1

C1: Cechowanie termopary i termistora.
Przemysław Kołoczek.

1. Wstęp.

Ćwiczenie miało na celu wycechowanie termopary (wyznaczenie zależności siły
elektromotorycznej od jej temperatury oraz stałej termopary), wyznaczenie stałej
termistora NTC oraz szerokości pasma wzbronionego materiału, z jakiego termistor ten
wykonano (na podstawie zależności oporu termistora od jego temperatury). Podczas
doświadczenia zaobserwowano zjawisko Seebecka, które polega na powstawaniu
niezerowego napięcia i przepływie prądu wskutek różnych temperatur na łączach dwóch
wzajemnie połączonych przewodników. W przypadku termopary na styku metali
występuje potencjał kontaktowy, powstający na skutek różnych koncentracji elektronów i
różnych prac wyjścia elektronów z metalu. Jego wartość jest zależna od rodzaju metali i
od temperatury złącza. Wartość napięcia między stykami jest proporcjonalna do różnicy
temperatur na złączach. Z kolei w przypadku termistora podłożem zjawiska Seebecka jest
przeskok elektronów przewodnictwa z pasma walencyjnego na pasmo przewodnictwa
pod wpływem wzrostu temperatury półprzewodnika, z którego termistor wykonano.
Zależność oporu termistora od jego temperatury nie jest liniowa. W przypadku termistora
NTC maleje wykładniczo. Dokonując pomiarów tejże zależności możliwe jest wyznaczenie
szerokości pasma wzbronionego dla półprzewodnika, z którego zbudowany jest termistor
i określenia jaki to materiał.

2. Opis doświadczenia.

Przygotowaną na statywie termoparę podłączono do miliwoltomierza, a termistor – do
omomierza. Urządzenia włączono, ustawiono właściwe zakresy pracy i odczekano aż do
ustabilizowania się wskazań mierników. Pobrano lód do termosa, zalano wodą i zatkano
korkiem z otworem. Napełniono zlewkę wodą i postawiono na grzejniku elektrycznym.
Jeden z końców termopary, termistor i termometr umieszczono w zlewce z wodą, z kolei
drugi koniec termopary – w mieszaninie wody i lodu. Ponownie odczekano aż do
ustabilizowania się wskazań mierników i odczytano ich wskazania oraz temperaturę wody.
Włączono grzejnik, ustawiono odpowiedni poziom mocy i odczytywano wartości napięcia
i oporu, co 2°C aż do ustabilizowania się temperatury wody i wskazań mierników,
mieszając co jakiś czas wodę. Grzejnik wyłączono i ponownie odczytywano wartości
napięcia i oporu w analogiczny sposób jak podczas ogrzewania wody. Aby przyspieszyć
ochładzanie wody, włączono wentylator i umieszczono przed zlewką z wodą, a po
pewnym czasie ostrożnie wyjęto układ termopara – termistor – termometr z wody.
Wskazania mierników odczytywano aż do osiągnięcia przez powyższy układ temperatury
początkowej. Po wykonanych pomiarach wyłączono mierniki, rozłączono obwód, wodę ze
zlewki i termosu wylano do zlewu, użyty sprzęt odłożono na miejsce.

3. Plan pracy.

a) Przygotować termoparę, termistor NTC, termometr na statywie, miliwoltomierz,

omomierz, zlewkę z wodą na płycie grzejnej.

b) Podłączyć termoparę do miliwoltomierza, podłączyć termistor do omomierza.
c) Pobrać lód i wodę do termosa, zanurzyć jeden z końców termopary do mieszaniny

wody i lodu, zanurzyć drugi koniec termopary oraz termistora do wody w zlewce.

2

d) Zanotować temperaturę, wartości napięcia i oporu przy ustabilizowanym napięciu na

miliwoltomierzu i oporze na omomierzu.

e) Włączyć płytę grzejną, odczytywać temperaturę, wartości napięcia i oporu, co 2°C, aż

do ustabilizowania się temperatury wody.

f) Zanotować temperaturę, wartości napięcia i oporu przy ustabilizowanych wskazaniach

omomierza i woltomierza po ustabilizowaniu się temperatury wody.

g) Wyłączyć płytę grzejną, włączyć wentylator, odczytywać temperaturę, wartości

napięcia i oporu, co 2°C podczas ochładzania się wody, aż do ustabilizowania się
temperatury wody.

h) Uporządkować stanowisko pracy.

4. Wyniki.

Tabela 1. Wyniki pomiarów.

Ogrzewanie

Ochładzanie

Temperatura

T [°C]

Napięcie

U [mV]

Opór

R [kΩ]

Temperatura

T [°C]

Napięcie

U [mV]

Opór

R [kΩ]

24

0,314

10,09

84

2,940

0,94

26

0,540

8,21

82

2,810

1,03

28

0,725

6,78

80

2,710

1,09

30

0,840

6,05

78

2,650

1,18

32

0,925

5,55

76

2,555

1,28

34

1,005

5,14

74

2,450

1,40

36

1,090

4,75

72

2,340

1,53

38

1,180

4,35

70

2,220

1,65

40

1,270

4,02

68

2,105

1,80

42

1,340

3,78

66

2,000

1,95

44

1,420

3,52

64

1,905

2,12

46

1,510

3,27

62

1,780

2,34

48

1,580

3,08

60

1,670

2,54

50

1,660

2,89

58

1,570

2,77

52

1,750

2,65

56

1,475

3,01

54

1,830

2,52

54

1,370

3,30

56

1,920

2,33

52

1,280

3,58

58

2,010

2,16

50

1,195

3,90

60

2,105

2,00

48

1,145

4,24

62

2,200

1,85

46

1,070

4,57

64

2,280

1,74

44

1,000

4,87

66

2,370

1,62

42

0,915

5,30

68

2,490

1,50

40

0,835

5,71

70

2,570

1,40

38

0,760

6,15

72

2,670

1,30

36

0,685

6,64

74

2,755

1,21

34

0,540

7,65

76

2,870

1,11

32

0,510

8,08

78

2,910

1,08

30

0,470

8,45

80

3,010

1,00

28

0,420

8,90

82

3,140

0,93

26

0,395

9,14

84

3,240

0,87

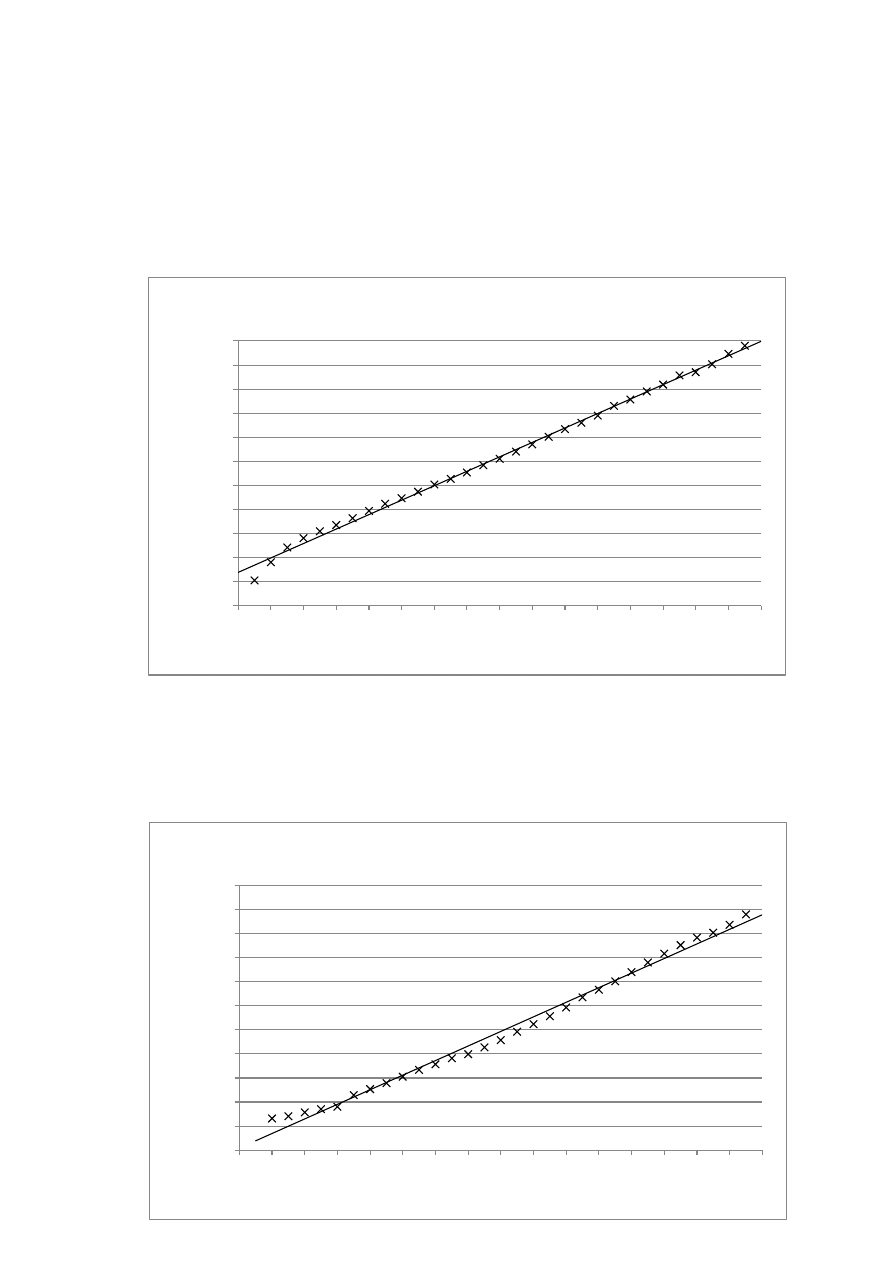
3

Wykres 2. Zależność napięcia od temperatury termopary podczas ogrzewania.

Wykres 1. Zależność napięcia od temperatury termopary podczas ochładzania.

5. Opracowanie wyników.

a) Termopara.

Sporządzono wykresy zależności napięcia od temperatury, dopasowano do nich linię
trendu i wyświetlono ich równania, a także wyznaczono niepewności pomiarowe
współczynników otrzymanych prostych, zarówno dla ogrzewania i ochładzania za
pomocą arkusza kalkulacyjnego Excel (funkcja REGLINP):





















𝛼 = 0,045 𝑚𝑉/𝐾

∆𝛼 = 0,00048 𝑚𝑉/𝐾

𝛽 = −0,58 𝑚𝑉

∆𝛽 = 0,027 𝑚𝑉

y = 0.045x - 0.5756

R² = 0.9967

0.000

0.300

0.600

0.900

1.200

1.500

1.800

2.100

2.400

2.700

3.000

3.300

22

26

30

34

38

42

46

50

54

58

62

66

70

74

78

82

86

U [m

V]

T [°C]

Termopara - ogrzewanie

y = 0.0455x - 0.9755

R² = 0.9913

0.000

0.300

0.600

0.900

1.200

1.500

1.800

2.100

2.400

2.700

3.000

3.300

22

26

30

34

38

42

46

50

54

58

62

66

70

74

78

82

86

U [m

V]

T [°C]

Termopara - ochładzanie

4

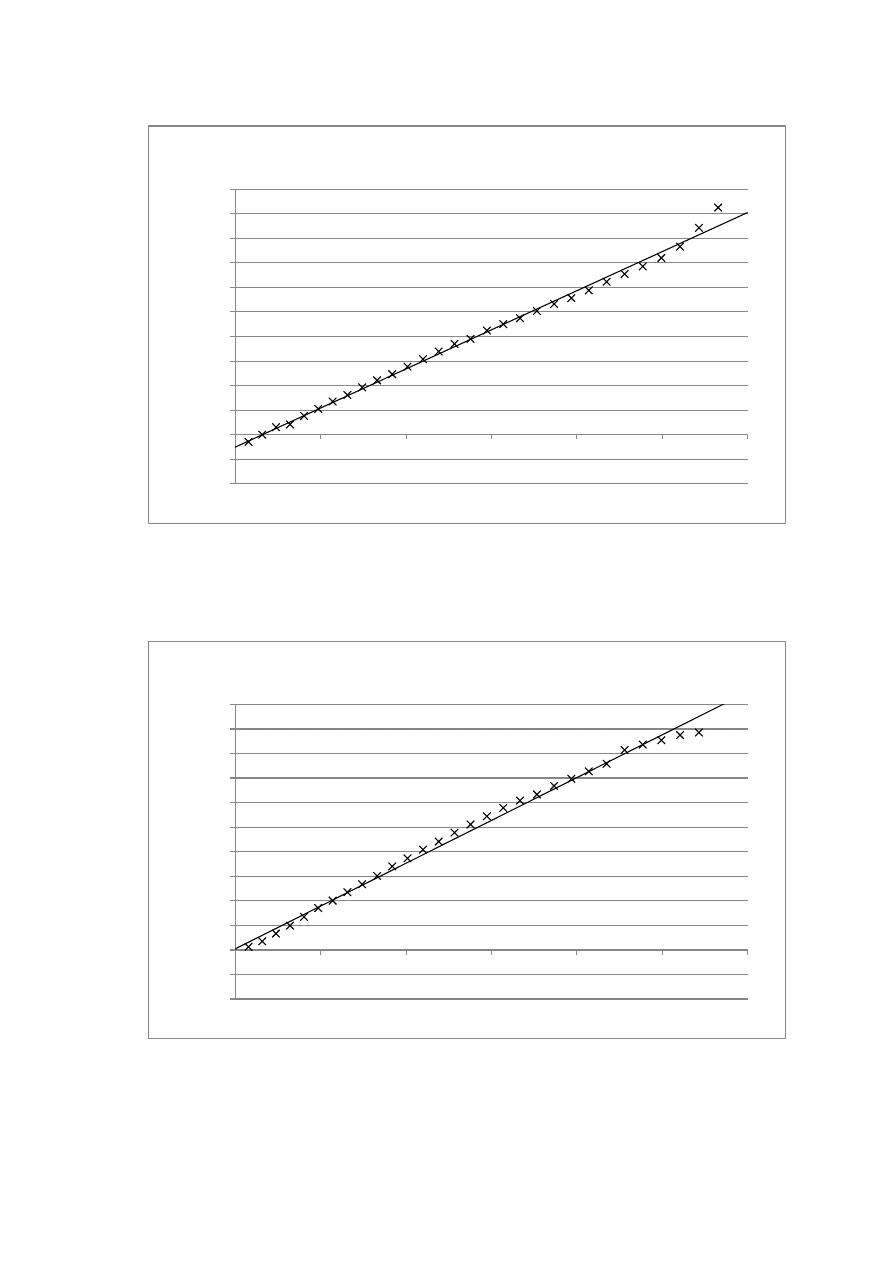
Wykres 3. Zależność oporu od temperatury termistora podczas ogrzewania.

Wykres 4. Zależność oporu od temperatury termistora podczas ochładzania.

𝛼 = 0,045 𝑚𝑉/𝐾

∆𝛼 = 0,00081 𝑚𝑉/𝐾

𝛽 = −0,98 𝑚𝑉

∆𝛽 = 0,04 𝑚𝑉

b) Termistor.

Sporządzono wykresy zależności oporu od temperatury. Ponadto sporządzono wykresy
zależności logarytmu naturalnego oporu od odwrotności temperatury w kelwinach,
dopasowano do nich linię trendu i wyświetlono ich równania, a także wyznaczono
niepewności pomiarowe współczynników otrzymanych prostych, zarówno dla
ogrzewania i ochładzania za pomocą arkusza kalkulacyjnego Excel (funkcja REGLINP):

0.00

1.00

2.00

3.00

4.00

5.00

6.00

7.00

8.00

9.00

10.00

11.00

22

26

30

34

38

42

46

50

54

58

62

66

70

74

78

82

86

R

[

kΩ

]

T [°C]

Termistor - ogrzewanie

0.00

1.00

2.00

3.00

4.00

5.00

6.00

7.00

8.00

9.00

10.00

11.00

22

26

30

34

38

42

46

50

54

58

62

66

70

74

78

82

86

R

[

kΩ

]

T [°C]

Termistor - ochładzanie

5

Wykres 5. Zależność logarytmu naturalnego oporu od odwrotności temperatury termistora (ogrzewanie).

Wykres 6. Zależność logarytmu naturalnego oporu od odwrotności temperatury termistora.(ochładzanie).

𝛼 = 3983,9 𝐾

∆𝛼 = 50,019 𝐾

𝛽 = −11,282 𝑘Ω

∆𝛽 = 0,15358 𝑘Ω

𝛼 = 4361,9 𝐾

∆𝛼 = 63,436 𝐾

𝛽 = −12,203 𝑘Ω

∆𝛽 = 0,19412 𝑘Ω

y = 3983.9x - 11.282

R² = 0.9954

-0.50

-0.25

0.00

0.25

0.50

0.75

1.00

1.25

1.50

1.75

2.00

2.25

2.50

0.0028

0.0029

0.0030

0.0031

0.0032

0.0033

0.0034

ln

R

[

kΩ

]

1/T [1/K]

Termistor - ogrzewanie

y = 4361.9x - 12.203

R² = 0.9941

-0.50

-0.25

0.00

0.25

0.50

0.75

1.00

1.25

1.50

1.75

2.00

2.25

2.50

0.0028

0.0029

0.0030

0.0031

0.0032

0.0033

0.0034

ln

R

[

kΩ

]

1/T [1/K]

Termistor - ochładzanie

6

Obliczono szerokość pasma wzbronionego oraz stałą termistora na podstawie wzoru:

𝑅(𝑇) = 𝑅

0

𝑒

𝑊

2𝑘𝑇

⇒ ln 𝑅(𝑇) =

𝑊

2𝑘

∙

1

𝑇

+ ln 𝑅

0

i uzyskanej zależności liniowej:

𝑦 = 𝛼𝑥 + 𝛽

Ostatecznie:

𝛼 =

𝑊

2𝑘

⇒ 𝑊 = 2𝑘𝛼

𝛽 = ln 𝑅

0

⇒ 𝑅

0

= 𝑒

𝛽

gdzie:
R(T) – opór elektryczny w danej temperaturze [kΩ],
R

0

– stała termistora [kΩ],

W – szerokość pasma wzbronionego [J],
k – stała Boltzmanna,
T – temperatura [K].
α – współczynnik kierunkowy równania uzyskanej prostej [K],
β – wyraz wolny równania uzyskanej prostej [kΩ].

Termistor – ogrzewanie:

𝑘 = 1,38 · 10

−23

𝐽/𝐾 = 8,61 · 10

−5

𝑒𝑉/𝐾

𝛼 = 3983,9 𝐾

𝛽 = −11,282 𝑘Ω

𝑊 = 1,10 ∙ 10

−19

𝐽 = 0,6864 𝑒𝑉

𝑅

0

= 1,26 ∙ 10

−5

kΩ = 1,26 ∙ 10

−2

Ω

Termistor – ochładzanie:

𝑘 = 1,38 · 10

−23

𝐽/𝐾 = 8,61 · 10

−5

𝑒𝑉/𝐾

𝛼 = 4361,9 𝐾

𝛽 = −12,203 𝑘Ω

𝑊 = 1,20 ∙ 10

−19

𝐽 = 0,751 𝑒𝑉

𝑅

0

= 5,02 ∙ 10

−6

kΩ = 5,02 ∙ 10

−3

Ω

7

Obliczono niepewność szerokości pasma wzbronionego oraz niepewność stałej
termistora na podstawie wzorów:

∆𝑊 = |

𝜕𝑊

𝜕𝛼

∙ ∆𝛼| = 2𝑘∆𝛼

∆𝑅

0

= |

𝜕𝑅

0

𝜕𝛽

∙ ∆𝛽| = 𝑒

𝛽

∆𝛽

gdzie:
k – stała Boltzmanna,
Δα – niepewność współczynnika kierunkowego równania uzyskanej prostej [K],
β – wyraz wolny równania uzyskanej prostej [kΩ],
Δβ – niepewność wyrazu wolnego równania uzyskanej prostej [kΩ].

Termistor – ogrzewanie:

𝑘 = 1,38 · 10

−23

𝐽/𝐾 = 8,61 · 10

−5

𝑒𝑉/𝐾

∆𝛼 = 50,019 𝐾

𝛽 = −11,282 𝑘Ω

∆𝛽 = 0,15358 𝑘Ω

∆𝑊 = 1,38 ∙ 10

−21

𝐽 = 0,0086 𝑒𝑉

∆𝑅

0

= 1,93 ∙ 10

−6

𝑘Ω = 1,93 ∙ 10

−3

Ω

Termistor – ochładzanie:

𝑘 = 1,38 · 10

−23

𝐽/𝐾 = 8,61 · 10

−5

𝑒𝑉/𝐾

∆𝛼 = 63,436 𝐾

𝛽 = −12,203 𝑘Ω

∆𝛽 = 0,19412 𝑘Ω

∆𝑊 = 1,75 ∙ 10

−21

𝐽 = 0,011 𝑒𝑉

∆𝑅

0

= 9,74 ∙ 10

−7

𝑘Ω = 9,74 ∙ 10

−4

Ω

Wyniki końcowe:

Termistor – ogrzewanie:

𝑊 = (0,6864 ± 0,0086) 𝑒𝑉

𝑅

0

= (1,26 ± 0,19) ∙ 10

−2

Ω

Termistor – ochładzanie:

𝑊 = (0,751 ± 0,011) 𝑒𝑉

𝑅

0

= (5,02 ± 0,97) ∙ 10

−3

Ω

8

6. Omówienie wyników i podsumowanie.

Wykres 1 i Wykres 2 zachowują dobrą liniowość, co ukazują wysokie wartości R

2

(powyżej

0,9900). Obydwie stałe termopary są takie same zarówno dla ogrzewania jak i ochładzania
– wynoszą 0,045 mV/K, przy czym niepewność pomiarowa dla ogrzewania, równa 0,00048
mV/K jest około 2 razy mniejsza niż dla ochładzania, która jest równa 0,00081 mV/K.
Wartość wyrazu β dla ogrzewania, równa (-0,58 ± 0,027) mV jest około 2 razy większa niż
dla ochładzania, która jest równa (-0,98 ± 0,046) mV, a jej niepewność – 2 razy mniejsza
dla ogrzewania niż dla ochładzania.
Wykres 3 i Wykres 4 nie są liniowe jak należało oczekiwać, co jest dobrze widoczne na
Wykresie 3, gorzej – na Wykresie 4. Pozostałe wykresy (Wykres 5 i Wykres 6) zachowują
dość dobrą liniowość, o czym mówią wysokie wartości R

2

(ponad 0,9900). Na podstawie

otrzymanych wyników można stwierdzić, że obydwie szerokości pasma wzbronionego i
ich niepewności są zbliżone zarówno dla ogrzewania – (0,6864 ± 0,0086) eV – jak i
ochładzania – (0,751

± 0,011) eV. Z kolei stałe termistora i ich niepewności dla

ogrzewania – (1,26 ± 0,19) · 10

-2

Ω – i ochładzania – (5,02 ± 0,97) · 10

-3

Ω – różnią się aż o

rząd wielkości. Porównując otrzymane wyniki szerokości pasma wzbronionego z danymi
tablicowymi można stwierdzić, że materiał, budujący termistor to german (0,67 eV).
Powyższe rozbieżności mogą wynikać z niedokładności użytych przyrządów pomiarowych,
niedoskonałości ludzkiego oka podczas odczytywania temperatury, należy również wziąć
pod uwagę trudności podczas równoczesnego odczytywania wartości napięcia i oporu dla
danej temperatury.

7. Literatura.

[1] A. Magiera, I Pracownia Fizyczna, IF UJ, Kraków 2010.
[2] D. Halliday, R. Resnick, J. Walker, Podstawy Fizyki 3, PWN, Warszawa 2003.
[3] http://www.fizyka.pk.edu.pl/tabele/Polprzew.htm.

8. Załączniki.

Kserokopia wyników pomiarowych.