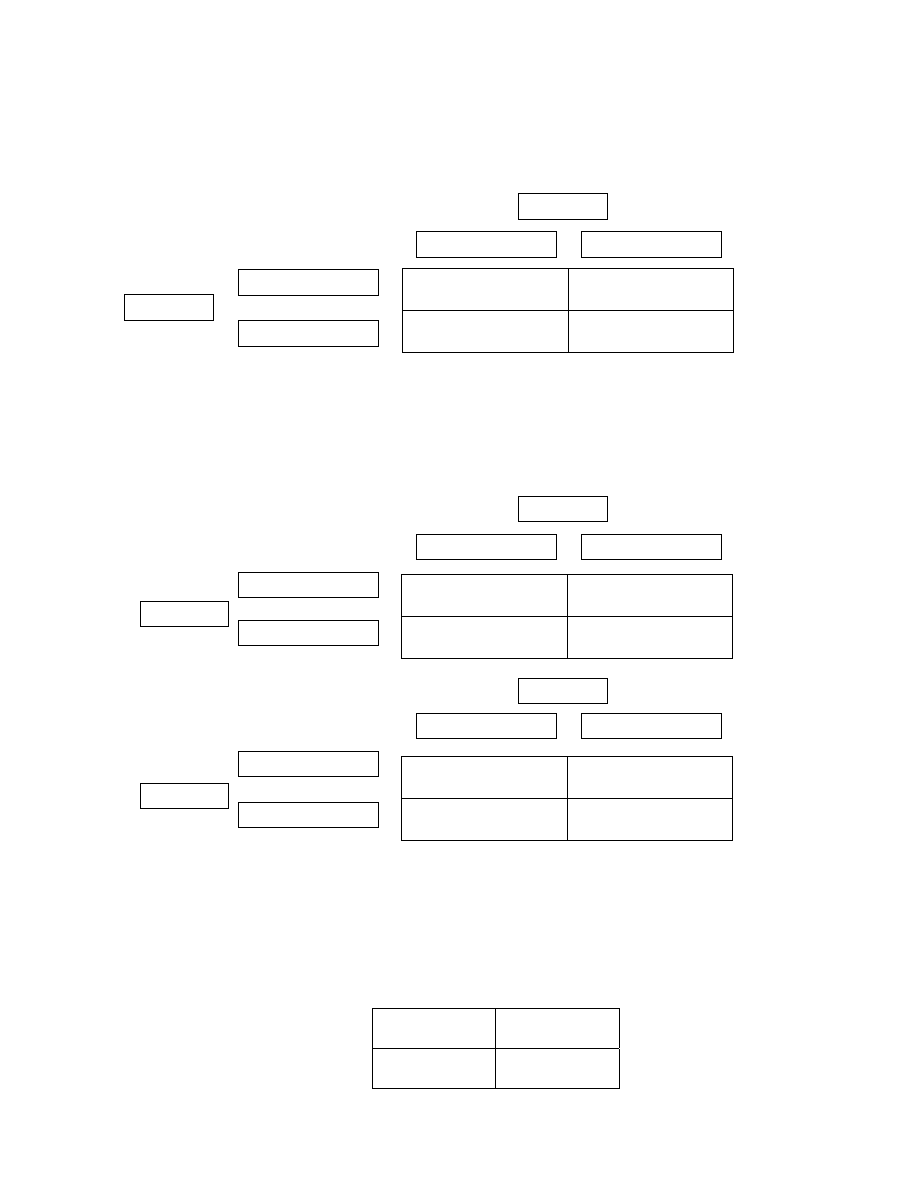
1

TEORIA GIER

Zadanie 1. Na rynku istnieją dwie firmy, które rozważają możliwość obniżenia ceny. Ich zysk w przypadku
różnych strategii przedstawia tabela. Czy gra posiada równowagę Nasha? Czy w przedstawionym przypadku
istnieje strategia dominująca? Jak zmieniłaby się sytuacja, gdyby firmy chciały się porozumieć? Jak zmieniłaby się
sytuacja, gdyby Firma 2 wiedziała, jaką decyzję podjęła Firma 1? Przedstaw ten problem przy pomocy drzewa
decyzyjnego.

9 9

15 5

5 15

12 12

Zadanie 2. Dwie firmy zawarły porozumienie o współpracy (kartel), ustalając wspólną politykę cenową. Jednak
obydwie mają możliwość sprzedawania poza kartelem po niższej cenie, co byłoby jednak sprzeczne z ich umową.
Na podstawie macierzy wypłat oceń, jakie zachowanie opłaca się firmom. Czy przedstawionych sytuacjach istnieją
strategie dominujące? Czy w tych grach występuje równowaga Nasha? Jeżeli tak – czy jest to rozwiązanie
optimum Pareto?

a)

25 25

12 30

30 12

20 20

b)

25 15

20 20

30 12

18 10

Zadanie 3. W 2000 r. dwa kraje członkowskie OPEC, Arabia Saudyjska i Iran wydobywały przeciętnie 5 mln i 2
mln baryłek ropy dziennie. Koszty produkcji wynosiły około $10 za baryłkę, a jej cena rynkowa kształtowała się na
poziomie $20. Zdolności wytwórcze w obu krajach pozwalały dodatkowo wydobywać 1 mln baryłek ropy
dziennie. Według ówczesnych ocen, każdy wzrost podaży o 1 mln baryłek prowadziły do spadku ceny ropy o $2.
Uzupełnij poniższą tabelę wypłat liczbami oznaczającymi odpowiednie wielkości zysku każdego z krajów.

I ran
2 mln baryłek 3 mln baryłek
5 mln baryłek
Arabia Saudyjska
6 mln baryłek

FIRMA 1

FIRMA 2

nie sprzedawać

sprzedawać

sprzedawać

nie sprzedawać

FIRMA 2

obniżyć cenę

nie obniżać ceny

obniżyć cenę

nie obniżać ceny

FIRMA 1

FIRMA 1

FIRMA 2

nie sprzedawać

sprzedawać

sprzedawać

nie sprzedawać

2

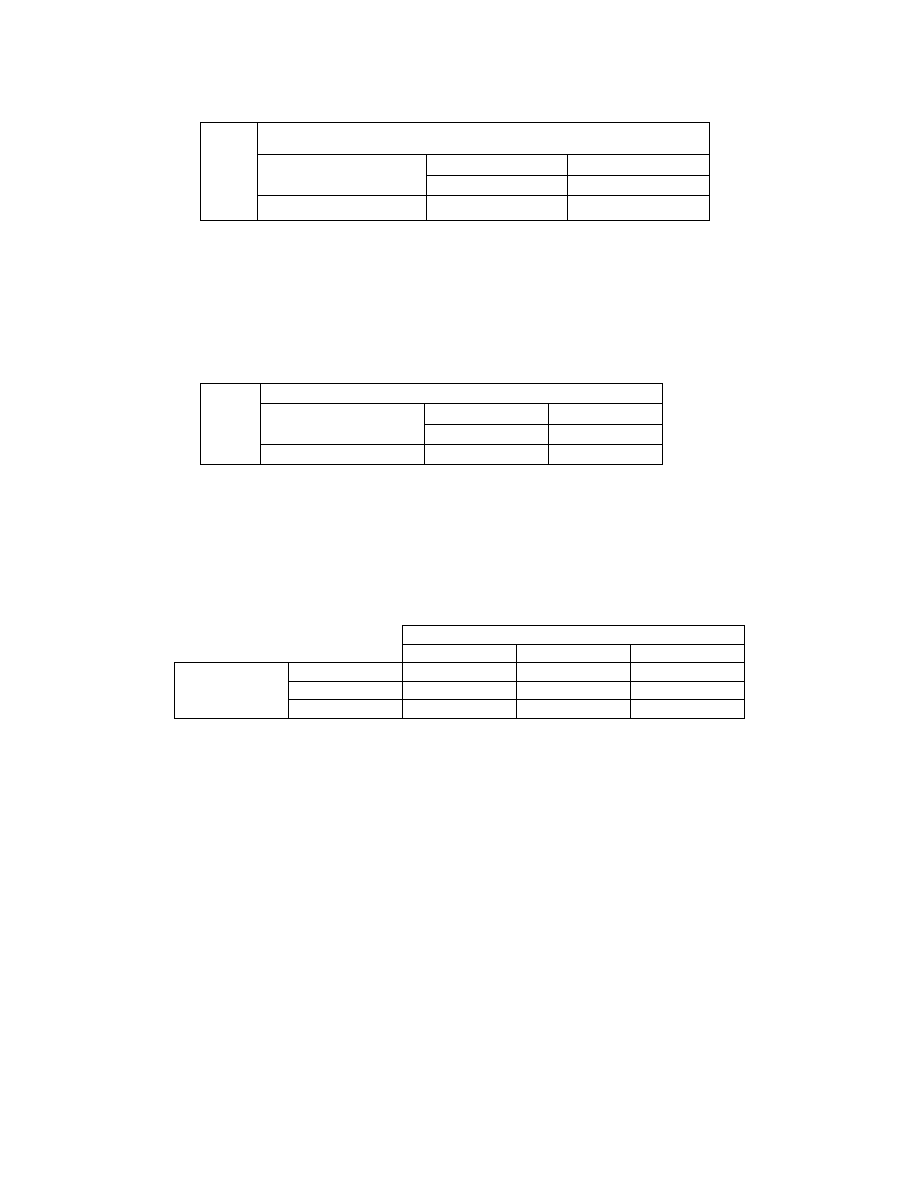
Zadanie 4. Na polskim rynku paliwowym Orlen jest przedsiębiorstwem znacznie większym od Rafinerii
Gdańskiej. Oba przedsiębiorstwa myślą o ekspansji, która prowadzi do różnych wyników, mierzonych poziomem
zysku w mln zł w zależności od zachowania rywala.

Rafineria Gdańska

inwestować nie

inwestować

inwestować

12 4

20 3

O
r
l
e
n

nie inwestować

15 6

18 5

a) którą strategię wybiorą rywale?
b) czy na rynku istnieje równowaga Nasha?

Zadanie 5. Dwóch nastolatków najeżdża na siebie samochodami po jednopasmowej drodze. Jeżeli żaden nie
zjedzie – gra zakończy się dla nich dramatycznie, obydwaj bowiem zginą. Jeżeli natomiast któryś z nich zjedzie z
drogi – żadnemu z nich nic się nie stanie, jednak ten który zjechał zostaje tchórzem, a ten, który nie zjechał –
bohaterem.

Michał

zjechać nie

zjechać

zjechać

0 0

-10 10

Marek

nie zjechać

10 -10

-100 -100

Na podstawie powyższej macierzy wypłat odpowiedz:
a) czy gra ma dominujące strategie?
b) czy występują tu stany równowagi Nasha?

Zadanie 6. Dwie firmy funkcjonujące na tym samym rynku mają ustalić cenę sprzedawanego przez siebie wyrobu.
Przewidywane zyski w zależności od ceny produktu przedstawia macierz wypłat. Czy w przedstawionej grze
istnieje równowaga Nasha?

Firma 1

1 zł 2

zł 3

zł

1 zł

0 0

50 -10

40 -20

2 zł

-10 50

20 20

90 10

Firma 2

3 zł

-20 40

10 90

50 50

Zadanie 7. Firma „Kangur” planuje wejście na rynek, na którym funkcjonują już dwie firmy: „Koala” i „Panda”.
Istniejące na rynku firmy rozważają możliwość zawarcia porozumienia i zablokowania nowej firmie wejścia na
rynek poprzez obniżenie cen. W tej chwili każda z nich ma 50% udział w rynku i osiąga zysk w wysokości 25 tys.
Jeżeli „Kangur” wejdzie na rynek - przejmie część rynku i wówczas zyski każdej z trzech firm wyniosą 15 tys.
Jeżeli Firmy „Koala” i „Panda” zdecydują się na obniżkę cen, spowoduje to spadek ich zysków do 20 tys., gdyby
„Kangur” nie zdecydowała się wejść na rynek, lub do 18 tys., jeżeli „Kangur” na rynek wejdzie, ale wówczas
„Kangur” poniósłby straty w wysokości 5 tys.
1) Przedstaw problem w postaci macierzy wypłat.
2) Przedstaw problem w postaci drzewa decyzyjnego.
3) Czy istnieje strategia dominująca?
4) Jakie decyzje podejmie „Kangur”, jeżeli wie, co postanowiły firmy funkcjonujące już na rynku?

Zadanie 8.

Sytuacja – jak w zadaniu 7, ale firmy „Koala” i „Panda” nie zawierają porozumienia. Przedstaw za

pomocą drzewa następująca sytuację: Gdyby firmy nie zdecydowały się porozumieć i tylko jedna z nich
obniżyłaby cenę, a „Kangur” wszedłby na rynek, wówczas jej zysk spadłby do poziomu 16 tys., zysk drugiej firmy
wyniósłby 13 tys., natomiast zysk „Kangura” 7 tys.; gdyby „Kangur” na rynek nie wszedł – wyniki firmy która
obniżyła cenę wyniosłyby 17 tys., wyniki drugiej firmy natomiast – 14 tys.
Rozpatrz sytuacje, w której znana jest decyzja pozostałych uczestników gry, przyjmując następującą kolejność:
a) Koala – Panda – Kangur;
b) Panda – Koala – Kangur.

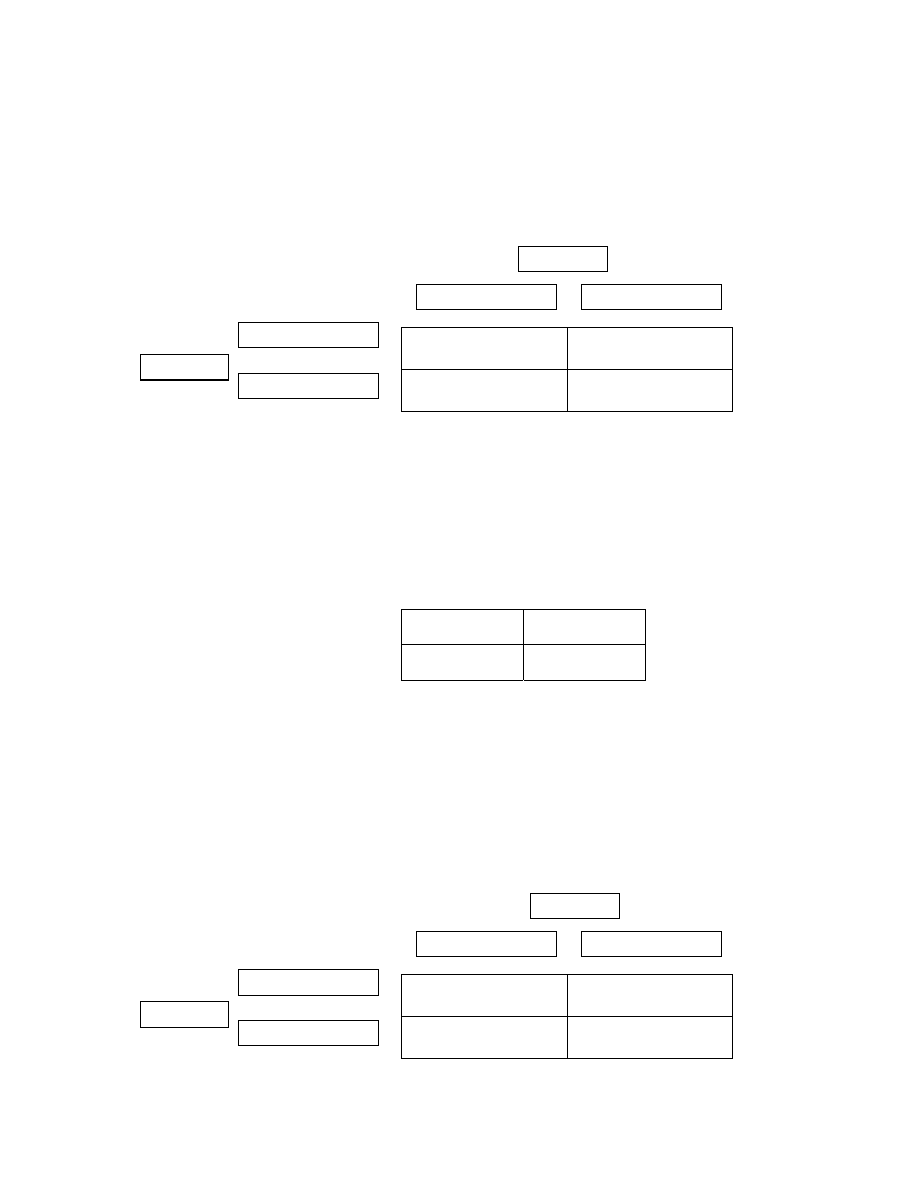
3

Zadanie 9. Na rynku funkcjonują dwie firmy, które planują przeprowadzenie kampanii reklamowej. Pierwotna
wartość rynku oszacowano na 100 tys. j.p. Koszt kampanii reklamowej wynosi 10 tys. j.p. Każde zainwestowane w
reklamę 10 tys. powoduje wzrost wartości rynku o 20 tys. W przypadku braku reklamy lub gdy obydwie firmy
przeprowadzą kampanię reklamową – firmy podzielą się rynkiem po połowie. W przypadku, gdy tylko jedna z firm
zdecyduje się przeprowadzić kampanię reklamową, zdobędzie ona 75% udziału w rynku.
1. Przedstaw w postaci macierzy wypłat.
2. Jaką decyzję podejmie Firma 2, jeżeli wie, że Firma 1 na pewno nie podejmie kampanii reklamowej (np. z

powodu braku środków na jej przeprowadzenie)?

3. Jak zmieni się sytuacja, jeżeli przyjmiemy, że Firma 1 rozpoczęła już kampanię reklamową?
4. Czy w grze występuje strategia dominująca?

Zadanie 10. Przedsiębiorstwo „M” i „N” rywalizują o pewien rynek i niezależnie od siebie muszą zdecydować o
wielkości wydatków na reklamę. Każde z niech jest w stanie wydać na ten cel 20 lub 10 mln zł. Jeśli firmy
wydadzą na reklamę po 20 mln każda, to podzielą się rynkiem o wartości 120 mln zł (zysk każdego
przedsiębiorstwa wyniesie 60 – 20 = 40 mln zł). Jeżeli jedno wyda 20 mln zł, a drugie 10 mln zł, to pierwsze
przejmie dwie trzecie rynku a drugie jedną trzecią. Jeżeli wydadzą po 10 mln, wówczas każda z nich przejmie
jedną trzecią potencjalnego rynku.

40 40

a) Wstaw liczby opisujące wielkość zysku do poniższej tabeli wypłat.
b) Zakładając niezależne działanie obu firm, jaki wybiorą poziom wydatków?
c) Czy opłacalne byłoby dla nich zawarcie porozumienia obejmującego całą gałąź i dotyczącego skali wydatków

na reklamę? Dlaczego?

Zadanie 11. Nad rzeką Styks istnieją dwie firmy. Prowadzona przez nie działalność wymaga budowy oczyszczalni
(dobro publiczne) u ujścia rzeki (koszt wybudowania oczyszczalni to 50 j.p.). Jeżeli przeprowadzą inwestycję
wspólnie, koszty poniosą po połowie każda. Za zanieczyszczanie Styksu płaci się karę 30 j.p. Przedstaw macierz
„wypłat” dla opisanej sytuacji. Czy strategia dominująca w tym przypadku prowadzi do optimum w sensie Pareto?
Jak zmieni się sytuacja, jeżeli kara wyniesie 60 j.p.

FIRMA 1

FIRMA 2

nie budować

budować

budować

nie budować

FIRMA 1

FIRMA 2

nie reklamować

reklamować

reklamować

nie reklamować

WYDATKI NA REKLAMĘ
FIRMY „M” w mln zł

10

20

WYDATKI NA REKLAMĘ FIRMY „N” w mln zł

10 20