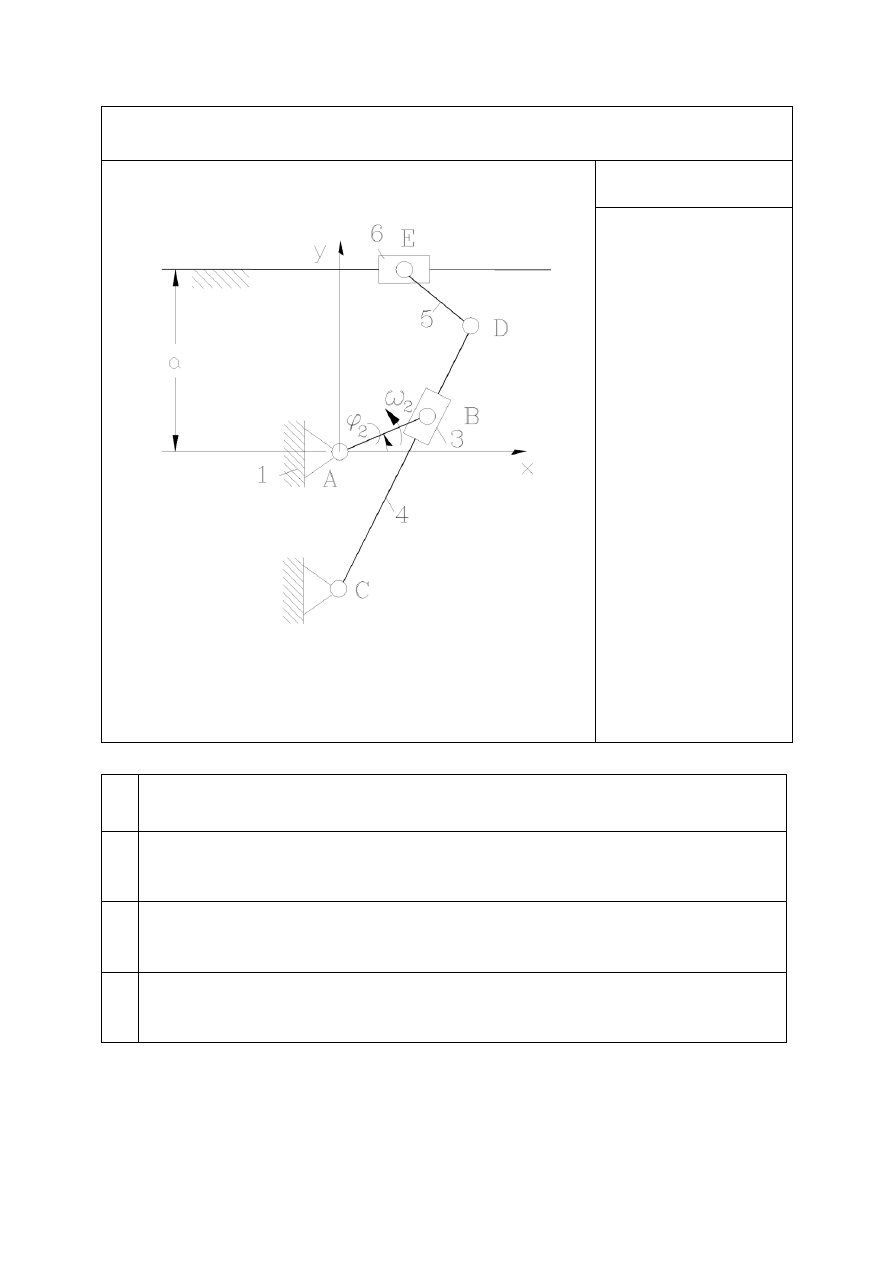
Zadanie projektowe nr K-1

Wymiary

AB = 0,15 m

AC=0,25 m

CD=0,53 m

DE=0,3 m

a=0,35 m



2

= ……

o



2

= ……rad/s



Lp.

Określić

1 Trajektorię punktu E (zakres pracy członu 6: x

Emin

, x

Emax

)

2

Przebiegi prędkości punktu E v

E

(



2

)

3 Przebiegi przyspieszenia punktu E a

E

(



2

)

Jak pokazano w [1]

1

, aby rozwiązać zadanie należy ułożyć układ funkcji opisujących

położenie członów mechanizmu:

f(w,q,x)=0,

(1)

gdzie:
w – wektor wymiarów(wartości stałych)
q – wektor napędów,
x – wektor zmiennych nieznanych.

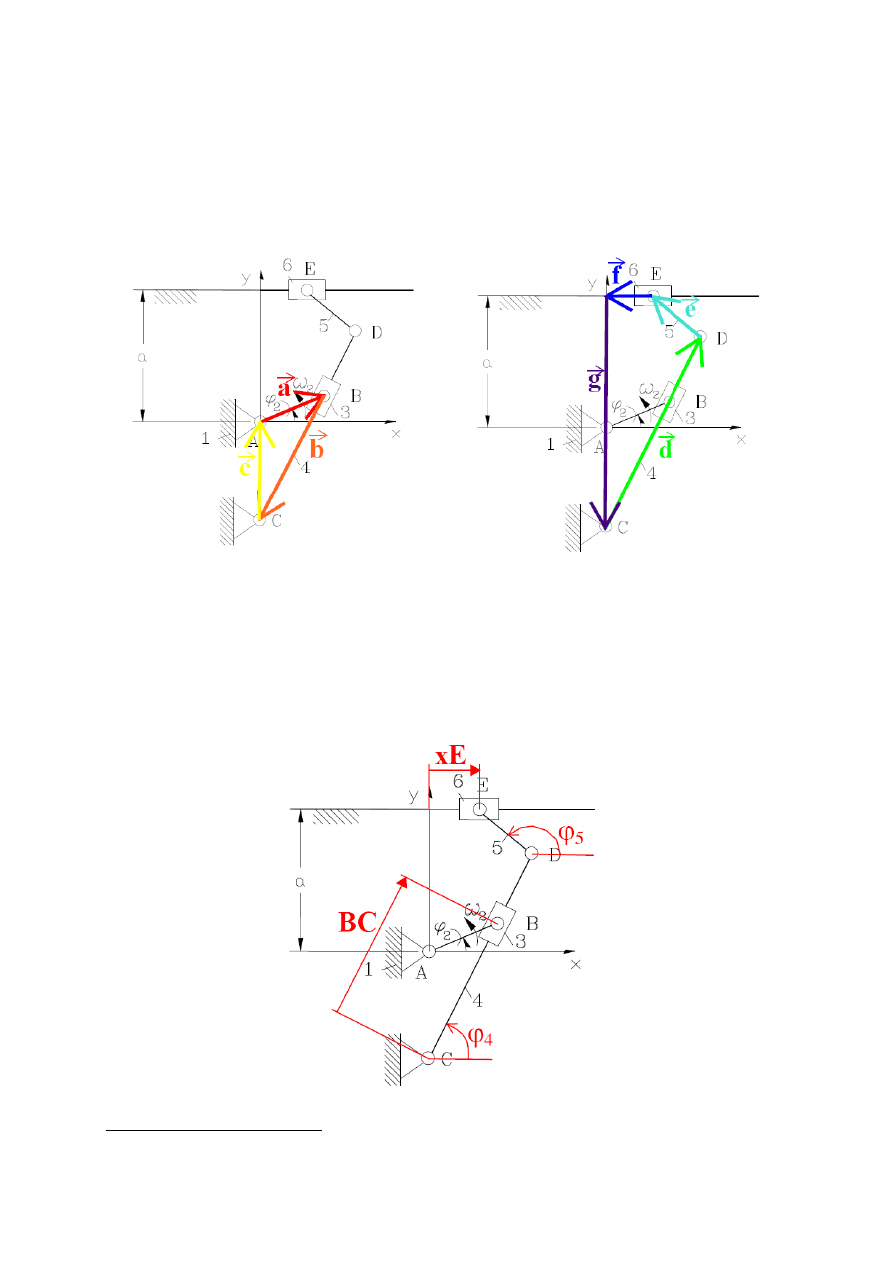
Rysunek 1. Przyjęte pętle wektorowe

Aby zapis był kompletny należy uzyskać n równań na n niewiadomych, czyli w tym
przypadku tyle ile wynosi wymiar wektora x (ile jest zmiennych niewiadomych).
Równania te, można uzyskać za pomocą tzw. równań konturowych. Są to równania sum
wektorów, które ułożone w pętle dają w wyniku 0. Na rys. 1 pokazano przyjęte pętle
wektorowe:

{

a⃗ + b

⃗ + c = 0

𝑑 + 𝑒 + 𝑓 + 𝑔 = 0

.

(2)

Rysunek 2. Zmienne zależne - nieznane

1

dział 3.3.2 – Uporządkowanie macierzowe (str. 132)

Jeżeli przyjąć za zmienne niewiadome wektor x, tak jak pokazano na rysunku 2:

x={BC,

φ

4

,

φ

5

,

xE }

T

Równania wektorowe (2) można zapisać, jako współrzędne wektorowe OX oraz OY (rzutując
wektory na osie głównego układu współrzędnych). W ten sposób otrzymamy 2 równania
z każdej pętli wektorowej. (2) przyjmuje postać:

𝑓(𝒘, 𝒒, 𝒙) =

{

AB cos(

φ

2

) −

BC

cos(

φ

4

) = 0

AB sin(

φ

2

) −

BC

sin(

φ

4

) + AC = 0

CD cos(

φ

4

) + DE cos(

φ

5

) −

𝑥𝐸

= 0

CD sin(

φ

4

) + DE sin(

φ

5

) − 𝑎 − 𝐴𝐶 = 0

.

(3)

Na czerwono zaznaczono zmienne niewiadome x, na zielono napęd q, reszta parametrów
zawartych w równaniach to wymiary (parametry stałe).
Tak zapisane równania można rozwiązać za pomocą programu MATLAB. Na początek
należy zdefiniować wszystkie wymiary oraz ustawić napędy. Należy rozpocząć o stworzenia
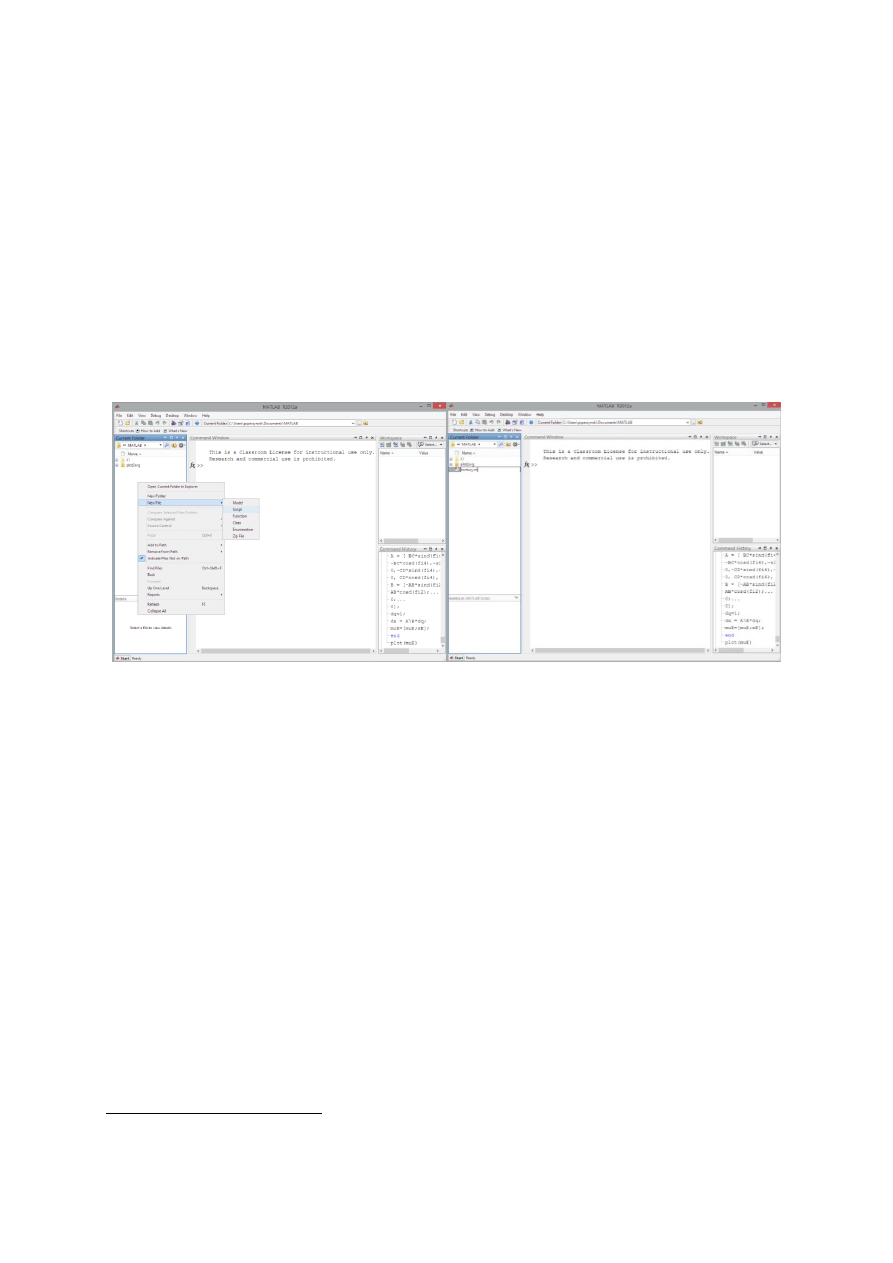
pustego pliku (skryptu) z rozszerzeniem .m, nazwiemy go kienmatyka_k1.m(rys. 3):

Rysunek 3. Tworzenie skryptu

Zaczynamy skrypt od wyczyszczenia przestrzeni roboczej, a następnie definiujemy wymiary:

clear

all

;

AB=0.15;

CD=0.53;

DE=0.3;

AC=0.25;

a =0.35;

fi2=30;

zmienna fi2 odpowiada kątowi napędu φ

2

, kolejno należy zdefiniować wskaźnik(uchwyt

2

)

do „funkcji nienazwanej”

3

, która zwróci nam wartość f(w,q,x) (3). W programie MATLAB

tworzy się go za pomocą znaku @:

f = @(X)([AB*cosd(fi2)-X(1)*cosd(X(2));

...

AB*sind(fi2)-X(1)*sind(X(2))+AC;

...

CD*cosd(X(2))+DE*cosd(X(3))-X(4);

...

CD*sind(X(2))+DE*cosd(X(3))-a-AC]);

2

ang. handle

3

ang. anonymous function

Funkcje sind oraz cosd odpowiadają funkcjom trygonometrycznym sin i cos, przyjmujące
argumenty kątowe w stopniach. Tak zdefiniowany wskaźnik na funkcję f można użyć,
do rozwiązania układu równań f(w,q,x)=0, za pomocą funkcji fsolve().
W następnym kroku należy zdefiniować wektor startowy zmiennych x, od którego zaczniemy
poszukiwanie rozwiązania:

x = [0.3,30,180,0];

wartości wektora x zostały przyjęte z góry i nie spełniają warunku (1): f(w,q,x)=0. Aby
znaleźć rozwiązanie użyjemy funkcji fsolve

4

w następujący sposób:

x = fsolve(f,x);

funkcja ta przyjmuje 2 parametry:

1. Wskaźnik na f.
2. Wektor startowy x, z którego zaczyna przeszukiwanie

Zwracana wartość to wektor rozwiązania, czyli szukane wartości x. Jeżeli informację, jakie
funkcja fsolve wypisuje na ekranie są niepożądane można je wyłączyć za pomocą
dodatkowych argumentów, przekazanych jako trzeci argument funkcji fsolve. Argumenty te
można złożyć za pomocą funkcji optimset

5

, np.:

x = fsolve(f,x,optimset(

'Display'

,

'off'

,

'TolFun'

,1e-12));

parametr „Display” definiuje, jakie informacje ma wypisać funkcja fsolve,
„TolFun” – tolerancja wartości funkcji f, poniżej której można zakończyć przeszukiwanie
rozwiązania.
Kolejnym krokiem jest rozwiązanie równania prędkości ẋ, w tym celu należy zróżniczkować
równania (1) po czasie, zakładając:

q=q(t)

x=x(t)

otzymamy rówanie:

Aẋ+Bq̇ =0,

(4)

gdzie:

𝐴 =

𝜕𝒇
𝜕𝒙

, 𝐵 =

𝜕𝒇
𝜕𝒒

to odpowiednio jakobiany ze względu na zmienne znane i nieznane. Aby rozwiązać równanie
prędkości ze względu na prędkości zmiennych nieznanych należy je przekształcić:

ẋ= -A

-1

Bq̇

Skrypt wygląda następująco:

A = [ BC*sind(fi4),-cosd(fi4),0,0;

...

-BC*cosd(fi4),-sind(fi4),0,0;

...

0,-CD*sind(fi4),-DE*sind(fi5),-1;

...

0, CD*cosd(fi4), DE*cosd(fi5),0];

B = [-AB*sind(fi2);

...

AB*cosd(fi2);

...

0;

...

0];

dq=1;

dx = -A\B*dq;

4

Szersze informacje znajdują się w pomocy do programu MATLAB, wywołując polecenia: „help fsolve”

lub „doc fsolve”

5

jw.: „help optimset” lub „doc optimset”

dq jest to pochodna napędu φ

2

, czyli prędkość kątowa ω

2

. W wyniku mamy prędkości ẋ

.

Jest to rozwiązanie jedynie dla jednej pozycji kąta φ

2

. Jeżeli chcemy wyznaczyć

charakterystykę dla całego zakresu pracy należy skrypt zapętlić w następujący sposób:

Wersja dla jednej pozycji

Skrypt zapętlony

→
→
→


























→
→
→
→
→
→

clear

all

;

AB=0.15;
CD=0.53;
DE=0.3;
AC=0.25;
a =0.35;

x = [0.3,30,180,0];

fi2=30;

f = @(X)([AB*cosd(fi2)-X(1)*cosd(X(2));

...

AB*sind(fi2)-X(1)*sind(X(2))+AC;

...

CD*cosd(X(2))+DE*cosd(X(3))-X(4);

...

CD*sind(X(2))+DE*sind(X(3))-a-AC]);

%x = fsolve(f,x);

x = fsolve(f,x,...
optimset(

'Display'

,

'off'

,

'TolFun'

,1e-12));

BC = x(1);
fi4 = x(2);
fi5 = x(3);
xE = x(4);

A = [ BC*sind(fi4),-cosd(fi4),0,0;

...

-BC*cosd(fi4),-sind(fi4),0,0;

...

0,-CD*sind(fi4),-DE*sind(fi5),-1;

...

0, CD*cosd(fi4), DE*cosd(fi5),0];
B = [-AB*sind(fi2);

...

AB*cosd(fi2);

...

0;

...

0];

dq=1;

dx = -A\B*dq;

clear

all

;

AB=0.15;
CD=0.53;
DE=0.3;
AC=0.25;
a =0.35;

x = [0.3,30,180,0];

wek_muE=[];wek_fi2=[];wek_t=[];wek_vE=[];
fi2_pocz=30;
for fi2=fi2_pocz:1:(fi2_pocz+360 )

f = @(X)([AB*cosd(fi2)-X(1)*cosd(X(2));

...

AB*sind(fi2)-X(1)*sind(X(2))+AC;

...

CD*cosd(X(2))+DE*cosd(X(3))-X(4);

...

CD*sind(X(2))+DE*sind(X(3))-a-AC]);

%x = fsolve(f,x);

x = fsolve(f,x,

...

optimset(

'Display'

,

'off'

,

'TolFun'

,1e-12));

BC = x(1);
fi4 = x(2);
fi5 = x(3);
xE = x(4);

A = [-cosd(fi4), BC*sind(fi4),0,0;

...

-sind(fi4),-BC*cosd(fi4),0,0;

...

0,-CD*sind(fi4),-DE*sind(fi5),-1;

...

0, CD*cosd(fi4), DE*cosd(fi5),0];
B = [-AB*sind(fi2);

...

AB*cosd(fi2);

...

0;

...

0];

dq=1;

dx = -A\B*dq;

t = ((fi2-fi2_pocz)*pi/180)/dq;
wek_muE=[wek_muE;xE];
wek_vE=[wek_vE;dx(4)];
wek_fi2=[wek_fi2;fi2];
wek_t=[wek_t;t];
end

Zmienne „wek_t”, „wek_fi2”, „wek_muE”, „wek_vE” są wektorami, które przechowują
wartości czasu, kąta φ

2

, położenia punktu E oraz prędkości v

E

. Przed pętlą tworzone są, jako

wektory stałe, a następnie dopisywane są wartości charakterystyk na koniec wektora za
każdym wywołaniem pętli symulacji. Na czerwono oraz strzałkami po lewej stronie
zaznaczone zostały różnice pomiędzy skryptami.
Aby rozwiązać przyspieszenia należy zaimplementować w powyższym skrypcie równanie
przyspieszeń:

Aẍ+Ȧẋ+Bq̈+Ḃq̇ =0.

Literatura:

1. Anotni Gronowicz, „Podstawy Analizy układów kinematycznych”, Oficyna

Wydawnicza Politechniki Wrocławskiej 2003