PRZYKŁADY ZASTOSOWANIA

PRZYKŁADY ZASTOSOWANIA

PRZYBLIŻONYCH METOD

PRZYBLIŻONYCH METOD

ANALITYCZNYCH

ANALITYCZNYCH

ROZWIĄZYWANIA RÓWNANIA

ROZWIĄZYWANIA RÓWNANIA

OPERATOROWEGO

OPERATOROWEGO

0

)

(



 f

u

L

Wykład

Wykład



Metody bazujące na danym równaniu

Metody bazujące na danym równaniu

operatorowym:

operatorowym:



-

-

metody ważonych residuów:

metody ważonych residuów:



-metoda Galerkina

-metoda Galerkina



-metoda najmniejszych kwadratów

-metoda najmniejszych kwadratów



-metoda kollokacji

-metoda kollokacji

Wykład

Wykład

Metody bazujące na funkcjonale:

Metody bazujące na funkcjonale:

-metoda Treftza

-metoda Treftza

-metoda Kantorowicza

-metoda Kantorowicza

We wszystkich tych metodach

We wszystkich tych metodach

postuluje się rozwiązanie przybliżone

postuluje się rozwiązanie przybliżone

w postaci:

w postaci:

i

N

i

i

a

y

x

y

x

y

x

u

y

x

u

)

,

(

)

,

(

)

,

(

ˆ

)

,

(

1

0















Wykład

Wykład

gdzie:

gdzie:

funkcja będąca dokładnym

funkcja będąca dokładnym

rozwiązaniem równania operatorowego

rozwiązaniem równania operatorowego

funkcja przybliżona

funkcja przybliżona

funkcja bazy, spełniająca

funkcja bazy, spełniająca

niejednorodne warunki brzegowe

niejednorodne warunki brzegowe

)

,

( y

x

u

)

,

(

ˆ

y

x

u

0



Wykład

Wykład

funkcja bazy spełniające

funkcja bazy spełniające

jednorodne warunki brzegowe

jednorodne warunki brzegowe

współczynniki

współczynniki

Funkcje bazy muszą spełniać warunki

Funkcje bazy muszą spełniać warunki

brzegowe zadania. Funkcje te należy

brzegowe zadania. Funkcje te należy

dobrać. Współczynniki a wyznacza

dobrać. Współczynniki a wyznacza

się .

się .

i



i

a

Wykład

Wykład

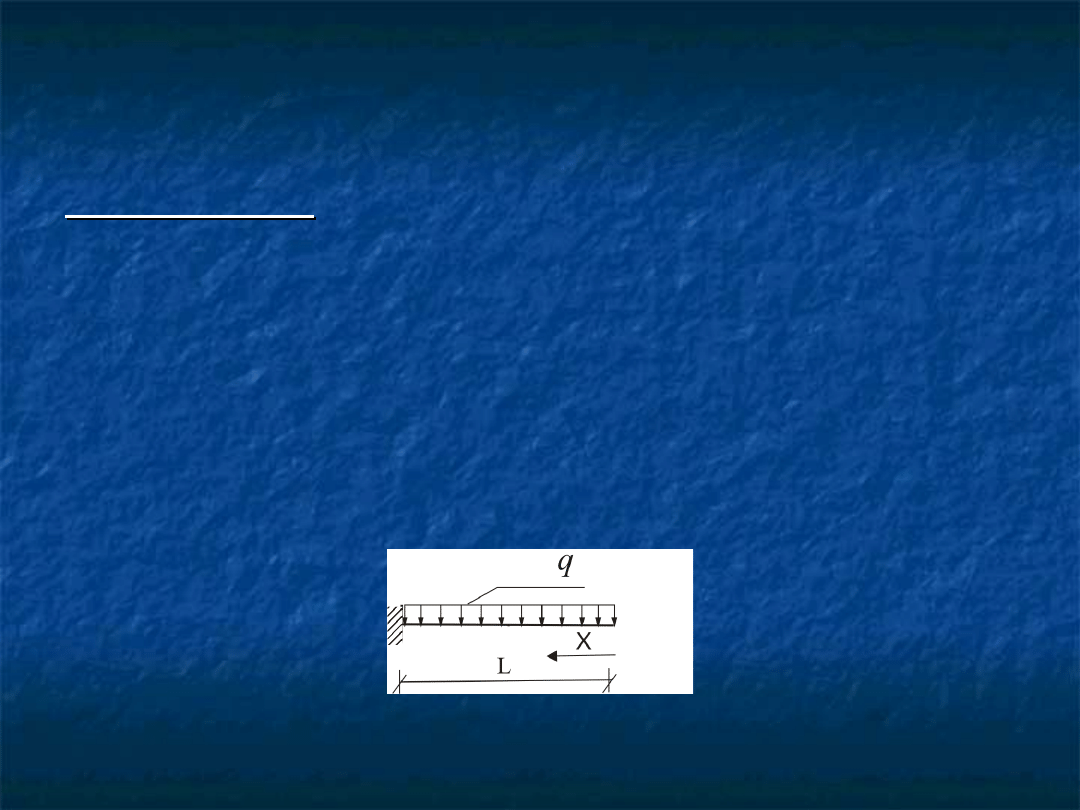
Przykład 1

Przykład 1

Do wyznaczenia jest funkcja

Do wyznaczenia jest funkcja

momentów zginających we

momentów zginających we

wsporniku. Do rozwiązania stosuje się

wsporniku. Do rozwiązania stosuje się

metody przybliżone oparte na danym

metody przybliżone oparte na danym

równaniu operatorowym.

równaniu operatorowym.

Wykład

Wykład

Rozwiązanie dokładne:

Rozwiązanie dokładne:

Poszukujemy

Poszukujemy

rozwiązania metodą:

rozwiązania metodą:

-Galerkina

-Galerkina

-kollokacji

-kollokacji

-najmniejszych

-najmniejszych

kwadratów

kwadratów

2

)

(

2

qx

x

M





Wykład

Wykład

Równanie różniczkowe wiążące

Równanie różniczkowe wiążące

moment zginający z obciążeniem:

moment zginający z obciążeniem:

(1)

(1)

Warunek brzegowy:

Warunek brzegowy:

0

)

(

,

0

)

(









l

x

l

x

M



qx

x

M

qx

x

T

dx

dM















)

(

)

(

0

Wykład

Wykład

Postuluje się rozwiązanie w ogólnej postaci:

Postuluje się rozwiązanie w ogólnej postaci:

Ograniczamy się do jednego wyrazu

Ograniczamy się do jednego wyrazu

szeregu

szeregu

i dobieramy tak aby spełnić w.b.

i dobieramy tak aby spełnić w.b.

(2)

(2)

(3)

(3)

i

N

i

i

a

y

x

y

x

y

x

u

y

x

u

)

,

(

)

,

(

)

,

(

ˆ

)

,

(

1

0















1



)

(

1

1

1

x

a

M





3

1

)

(

x

x 



Wykład

Wykład

Podstawiając (2) do (1):

Podstawiając (2) do (1):

(3)

(3)

Równanie różniczkowe możemy zapisać:

Równanie różniczkowe możemy zapisać:

(4)

(4)

Jeżeli podstawimy do niego (3) to prawa

Jeżeli podstawimy do niego (3) to prawa

strona tego równania będzie różna od zera

strona tego równania będzie różna od zera

(bo nie jest to rozwiązanie dokładne).

(bo nie jest to rozwiązanie dokładne).

3

1

1

x

a

M 

0

)

(







qx

x

M

Wykład

Wykład

Tą różnicę która pojawi się po prawej

Tą różnicę która pojawi się po prawej

stronie nazywamy

stronie nazywamy

residuum.

residuum.

Residuum równania (4):

Residuum równania (4):

Warunek na wyznaczenie -

Warunek na wyznaczenie -

warunek ortogonalizacji.

warunek ortogonalizacji.

qx

x

a

qx

x

M

r











2

1

1

1

3

)

(

1

a

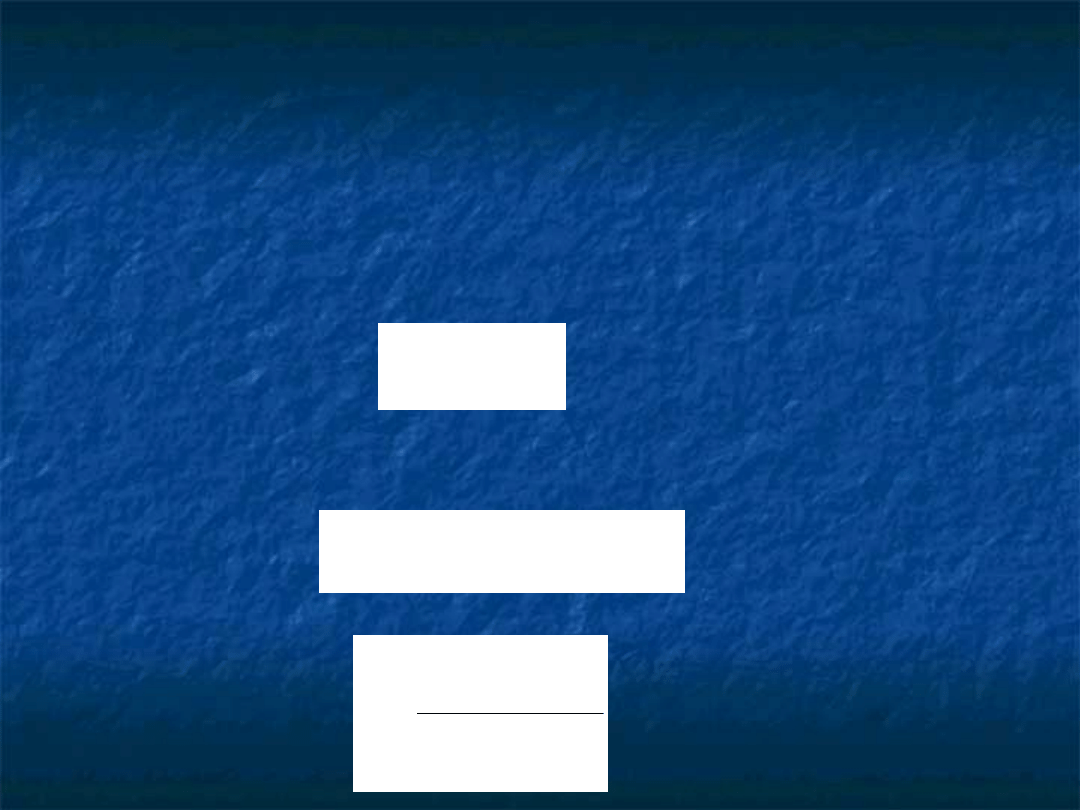
Wykład

Wykład

Warunek ten ma postać:

Warunek ten ma postać:

Mamy zatem:

Mamy zatem:

Stąd:

Stąd:

0

1

0

1





dx

W

r

l

0

)

(

)

3

(

1

2

0

1







dx

x

W

qx

x

a

l









l

l

dx

x

W

x

dx

x

xW

q

a

0

1

2

0

1

1

)

(

3

)

(

Wykład

Wykład

W zależności od tego jaką postać

W zależności od tego jaką postać

przyjmiemy dla funkcji wagi

przyjmiemy dla funkcji wagi

otrzymamy rozwiązania dla różnych

otrzymamy rozwiązania dla różnych

metod.

metod.

1.

1.

METODA GALERKINA

METODA GALERKINA

-Funkcja wagi taka sama jak funkcja

-Funkcja wagi taka sama jak funkcja

bazy:

bazy:

)

(

1

x

W

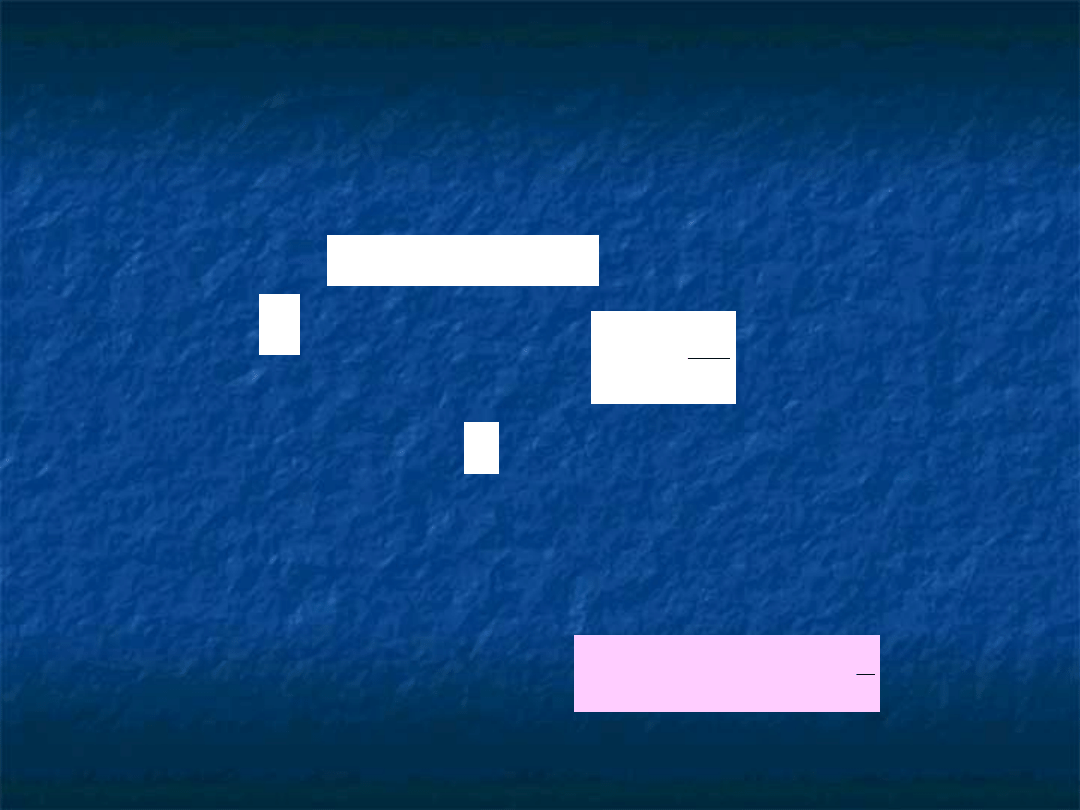
Wykład

Wykład

Tak więc:

Tak więc:

Obliczając otrzymamy:

Obliczając otrzymamy:

Zatem podstawiając do przyjętego

Zatem podstawiając do przyjętego

rozwiązania przybliżonego

rozwiązania przybliżonego

otrzymuje się :

otrzymuje się :

Rozwiązanie przybliżone:

Rozwiązanie przybliżone:

3

1

1

)

(

)

(

x

x

x

W







1

a

l

q

a

5

2

1





1

a

l

q

x

x

a

x

M

3

3

1

1

4

,

0

)

(







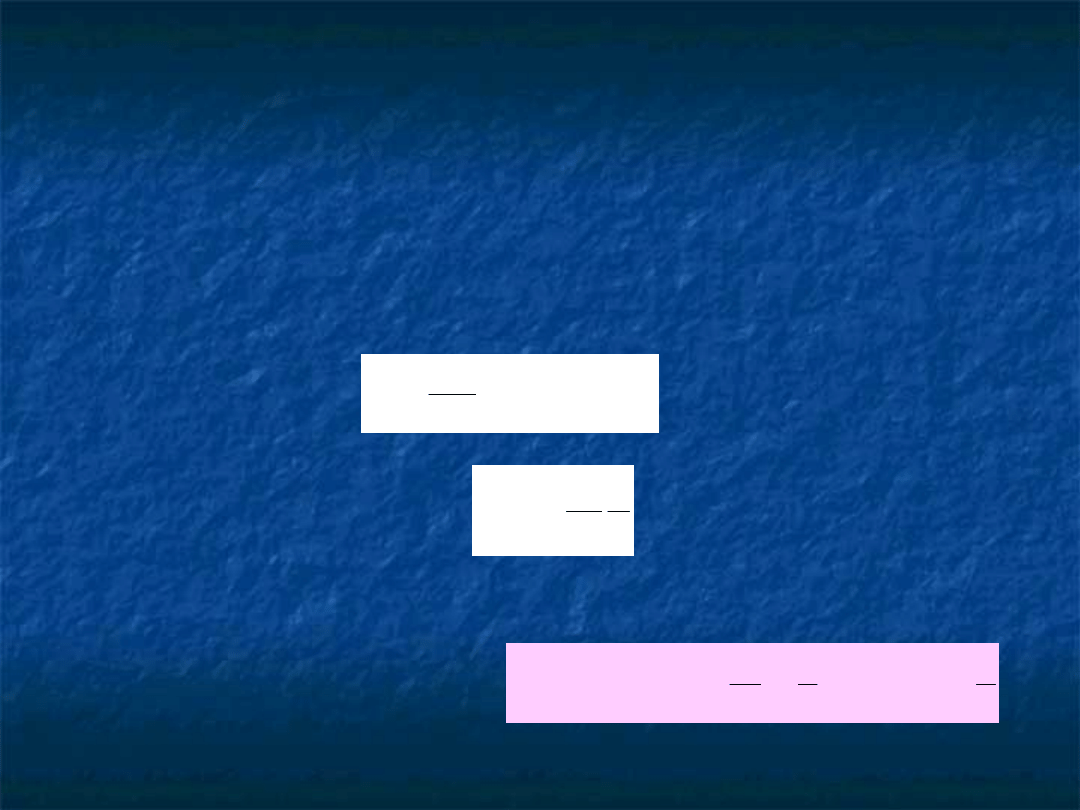
Wykład

Wykład

2.

2.

METODA NAJMNIEJSZYCH KWADRATÓW

METODA NAJMNIEJSZYCH KWADRATÓW

Funkcja wagi – pochodna funkcji bazy.

Funkcja wagi – pochodna funkcji bazy.

Tak więc:

Tak więc:

Po obliczeniu:

Po obliczeniu:

Zatem:

Zatem:

Rozwiązanie przybliżone:

Rozwiązanie przybliżone:

2

1

1

1

3

)

(

x

x

dx

d

W













l

q

a

12

5

1





l

q

x

l

q

x

x

a

x

M

3

3

3

1

1

416

,

0

12

5

)

(











Wykład

Wykład

3.METODA KOLLOKACJI

3.METODA KOLLOKACJI

Funkcja wagi – funkcja delta Diraca

Funkcja wagi – funkcja delta Diraca

Tak więc:

Tak więc:

Po obliczeniu:

Po obliczeniu:



















0

0

0

0

)

(

x

x

x

x

x

x



)

(

)

(

1

l

x

x

W







l

q

a

3

1





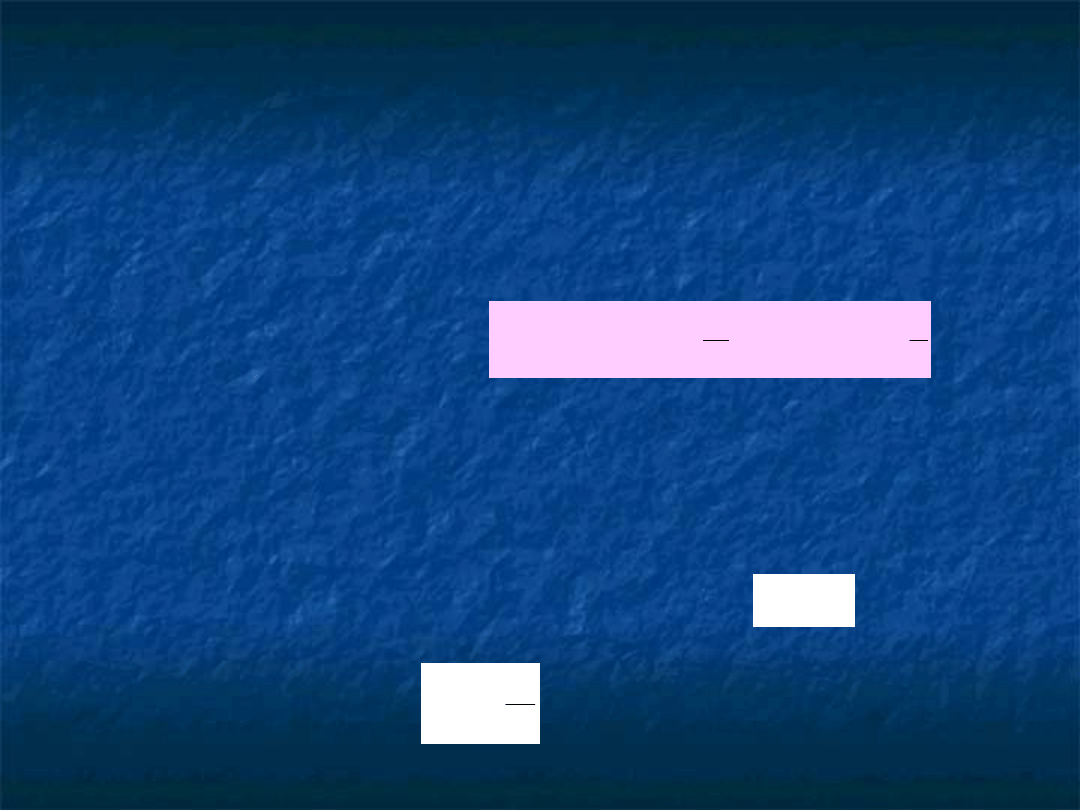
Wykład

Wykład

Rozwiązanie przybliżone:

Rozwiązanie przybliżone:

4. Uogólnienie metod:

4. Uogólnienie metod:

METODA

METODA

WAŻONYCH

WAŻONYCH

RESIDUÓW

RESIDUÓW

Funkcja wagi równa jedności:

Funkcja wagi równa jedności:

Po obliczeniu:

Po obliczeniu:

l

q

x

x

l

q

x

a

x

M

3

3

3

1

1

333

,

0

3

)

(











1

1



W

l

q

a

2

1





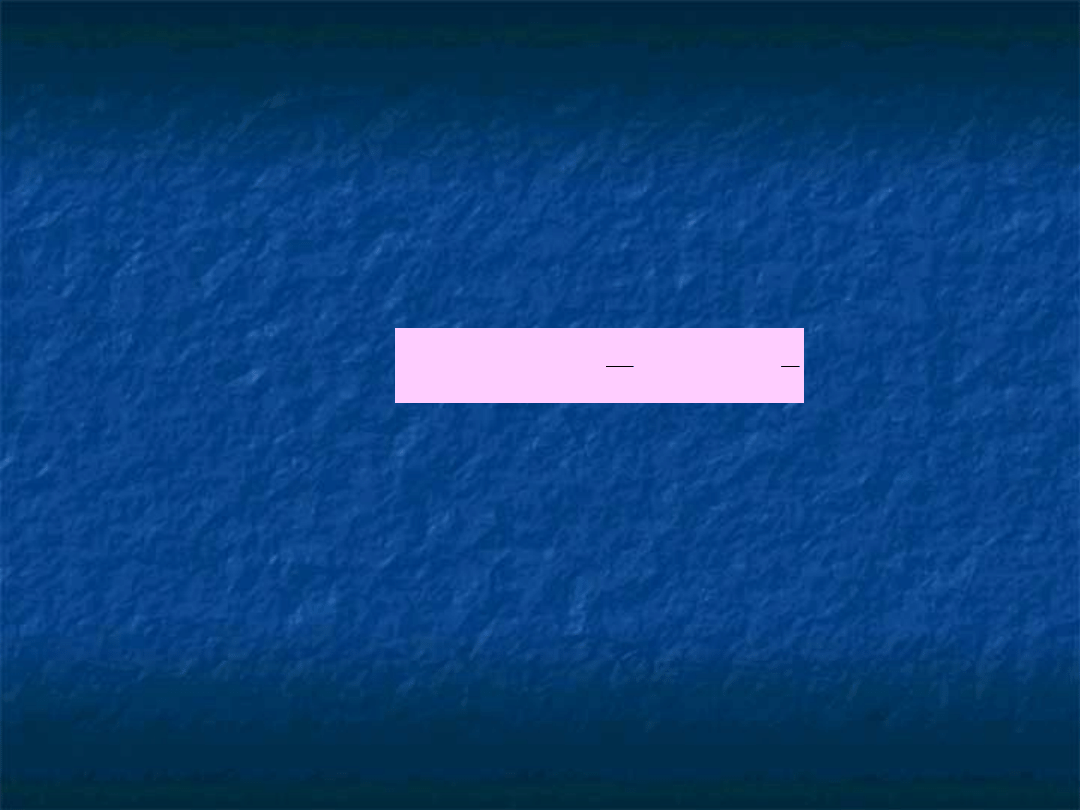
Wykład

Wykład

Rozwiązanie przybliżone:

Rozwiązanie przybliżone:

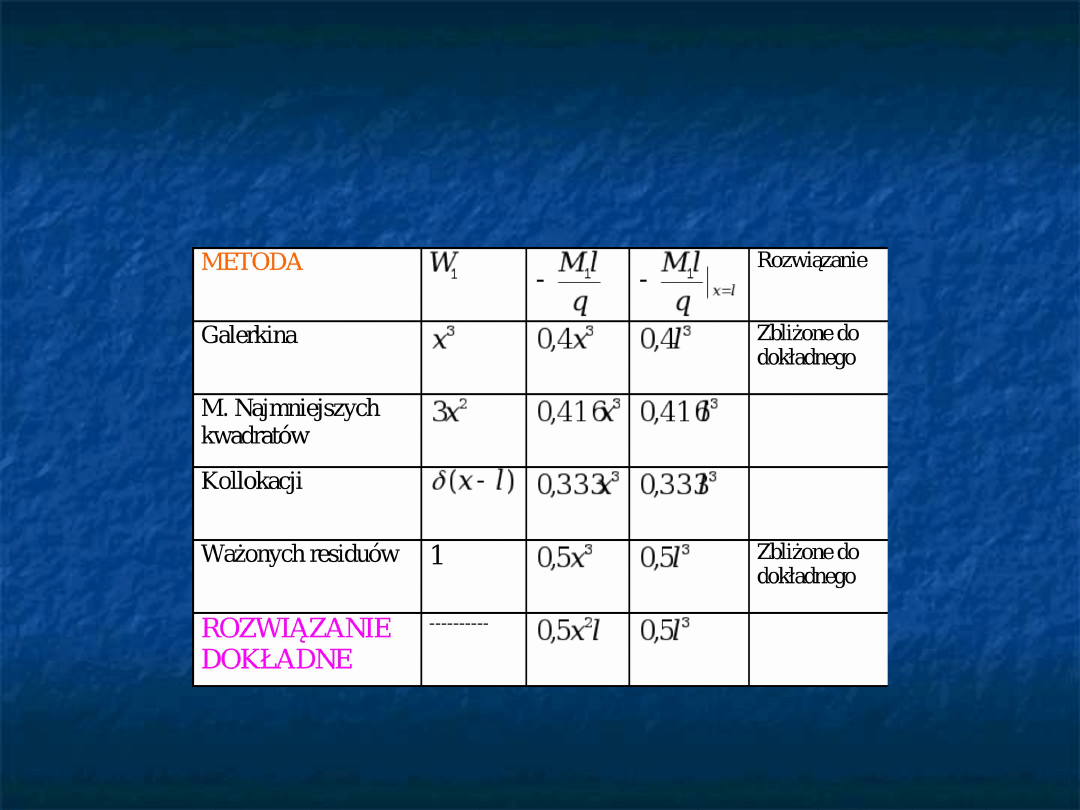
PORÓWNANIE METOD

PORÓWNANIE METOD

l

q

x

x

l

q

x

a

x

M

3

3

3

1

1

5

,

0

2

)

(











Wykład

Wykład

Wykład

Wykład

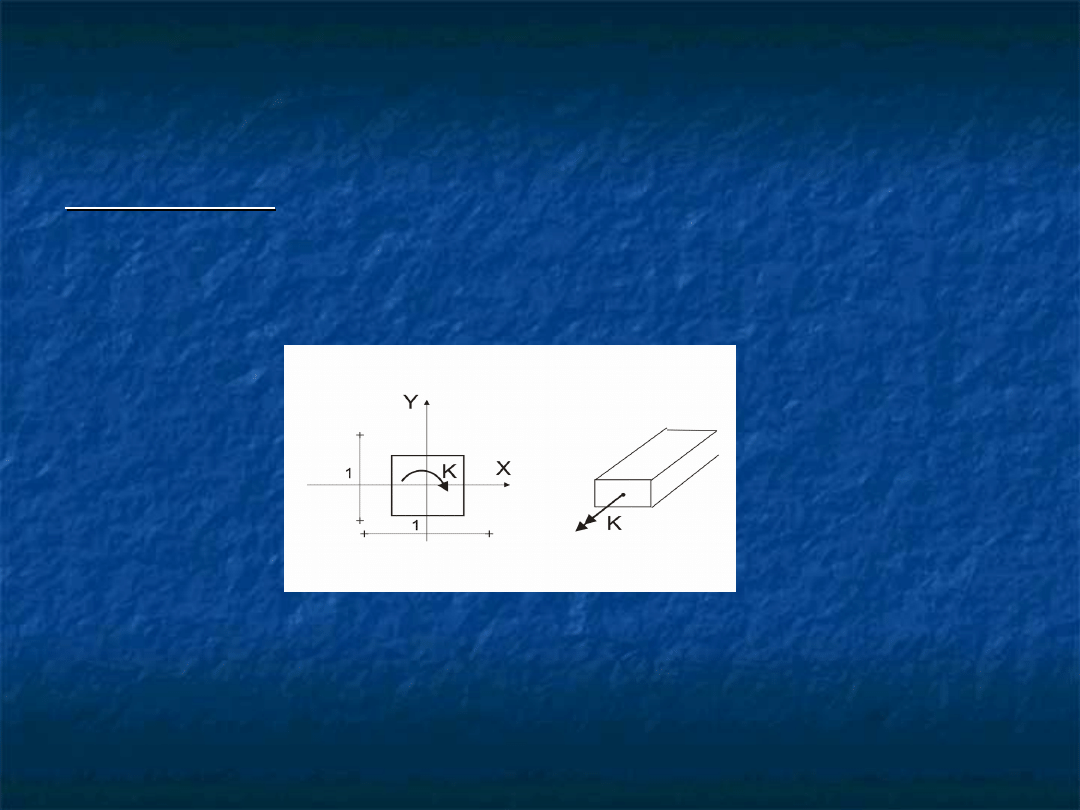
Przykład 2

Przykład 2

Do wyznaczenia jest funkcja naprężeń dla

Do wyznaczenia jest funkcja naprężeń dla

skręcanego pręta o przekroju kwadratowym.

skręcanego pręta o przekroju kwadratowym.

Rozwiązanie –

Rozwiązanie –

METODA RITZA

METODA RITZA

Wykład

Wykład

Równanie różniczkowe:

Równanie różniczkowe:

(1)

(1)

gdzie: - funkcja naprężeń

gdzie: - funkcja naprężeń

Warunki brzegowe:

Warunki brzegowe:

1

2

2

2

2



























y

x





)

,

( y

x



1

0

)

,

(

1

0

)

,

(













x

y

x

x

y

x





Wykład

Wykład

Funkcjonał równoważny równaniu (1)

Funkcjonał równoważny równaniu (1)

ma postać:

ma postać:

(2)

(2)

Poszukujemy rozwiązania

Poszukujemy rozwiązania

przybliżonego w postaci:

przybliżonego w postaci:

dxdy

y

x

F

























































 

1

1

1

1

2

2

2

)

(









i

N

i

i

a









1

Wykład

Wykład

Przyjmujemy np. 2 wyrazy szeregu,

Przyjmujemy np. 2 wyrazy szeregu,

czyli N=2. Funkcje bazy przyjmuje się:

czyli N=2. Funkcje bazy przyjmuje się:

(3)

(3)

Postuluje się zatem rozwiązanie:

Postuluje się zatem rozwiązanie:

(4)

(4)

)

)(

1

)(

1

(

)

1

)(

1

(

2

2

2

2

2

2

2

1

y

x

y

x

y

x



















)

)(

1

)(

1

(

)

1

)(

1

(

2

2

2

2

2

2

2

1

2

2

1

1

2

y

x

y

x

a

y

x

a

a

a



























Wykład

Wykład

Podstawiając równanie (4) do

Podstawiając równanie (4) do

funkcjonału (3) sprowadzamy

funkcjonału (3) sprowadzamy

funkcjonał do funkcji wielu

funkcjonał do funkcji wielu

zmiennych:

zmiennych:

Mamy zatem zagadnienie poszukiwania

Mamy zatem zagadnienie poszukiwania

funkcji wielu zmiennych:

funkcji wielu zmiennych:

)

,

(

)

(

2

1

a

a

F

F





2

,

1

0

)

,

(

2

1









i

a

a

a

F

i

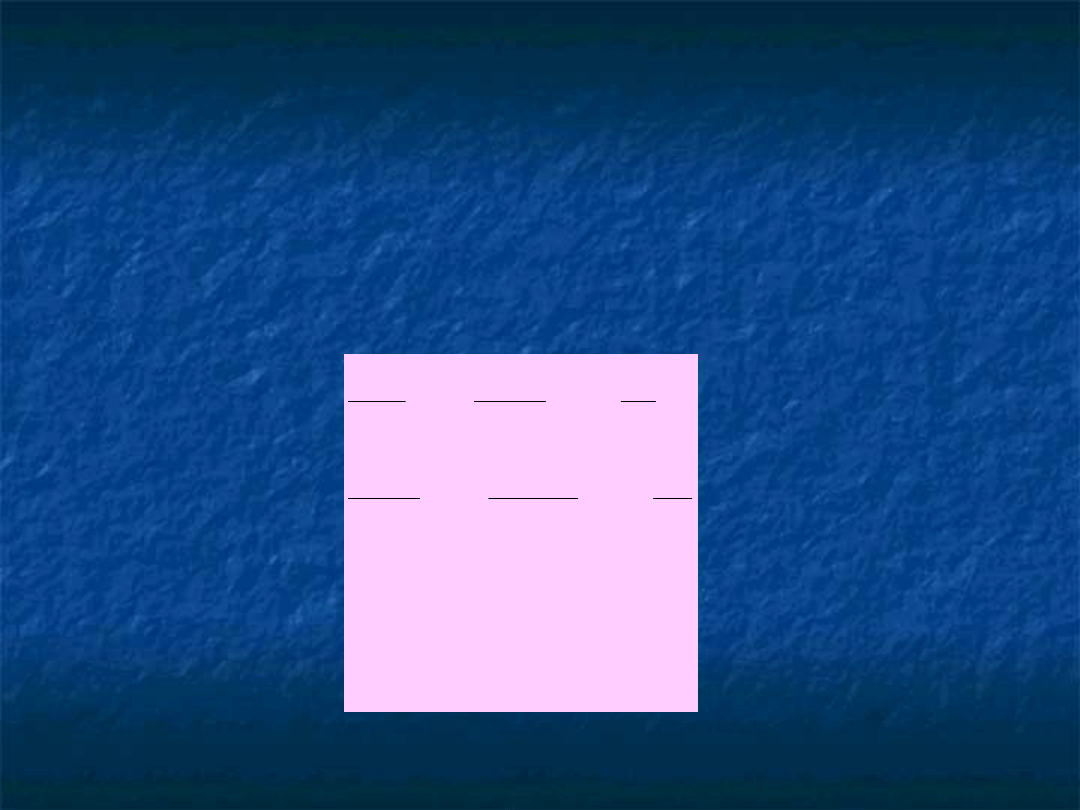
Wykład

Wykład

Minimalizując otrzymamy:

Minimalizując otrzymamy:

0592

,

0

292

,

0

45

42

4725

11264

525

1024

9

16

525

1024

45

266

2

1

2

1

2

1















a

a

a

a

a

a

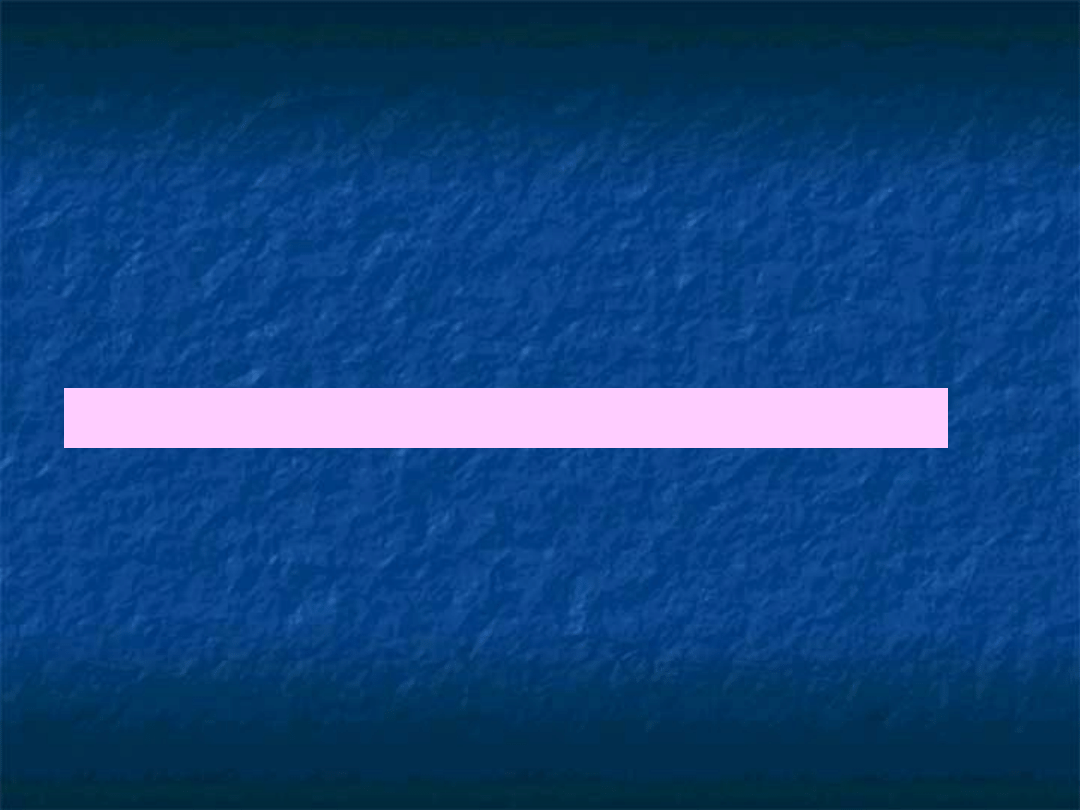
Wykład

Wykład

Zatem rozwiązanie przybliżone ma

Zatem rozwiązanie przybliżone ma

postać:

postać:





)

(

0592

,

0

292

,

0

)

1

)(

1

(

)

,

(

2

2

2

2

2

y

x

y

x

y

x











