Maciej Mysłowski
Grupa 19 IMIR
Mechanizm-7A
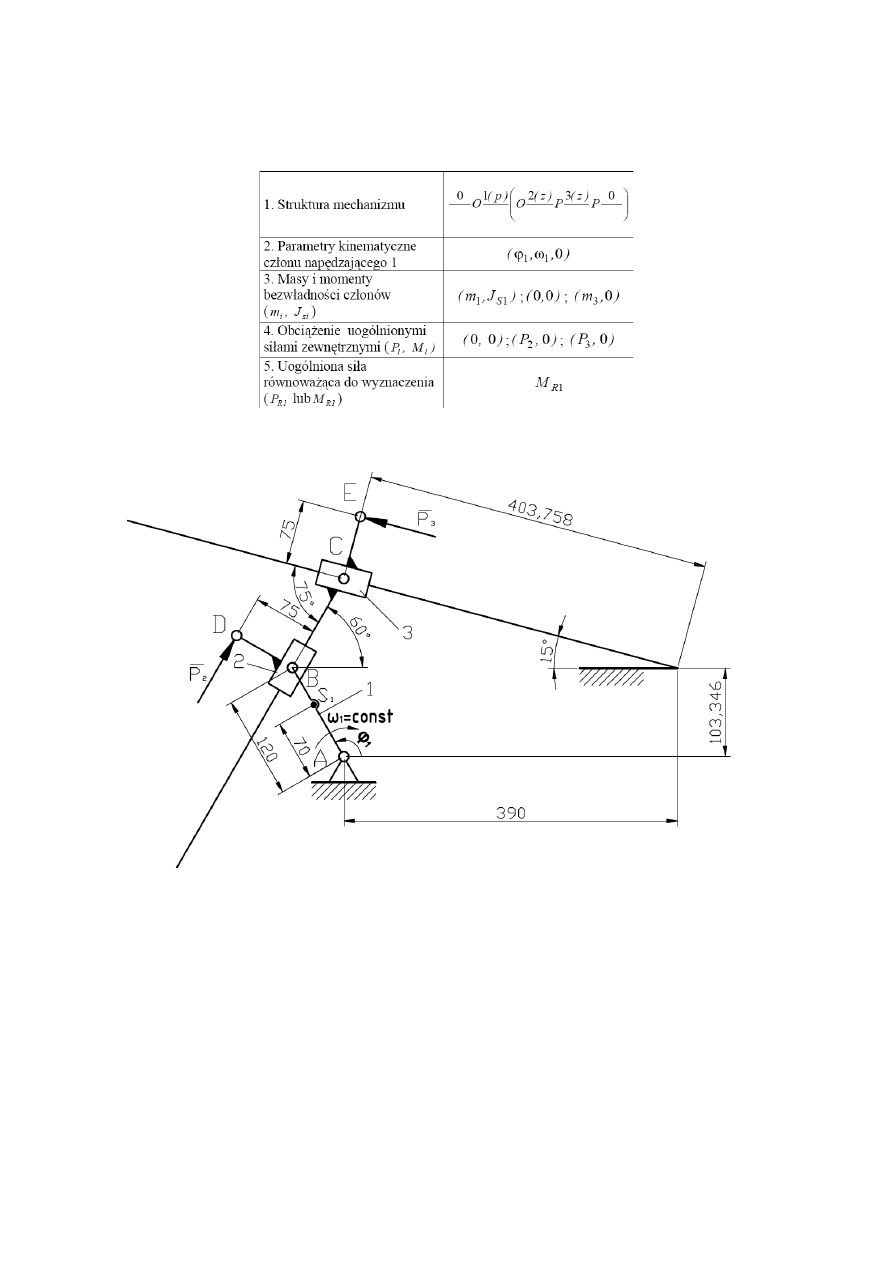
1.
Synteza strukturalna i geometryczna mechanizmu:
1.1. Nazwa strukturalna: Mechanizm korbowo-suwakowy
Nazwa funkcjonalna: Mechanizm dźwigniowy suwakowy
1.2. Ruchliwość mechanizmu:
n=3
p
5
=4
p
4
=0
(
)
∑
=
−
−
=
5
4
3
3
i
i
p
i
n
w
1
4
2
3
3
=
⋅
−
⋅
=
w
Ruchliwość mechanizmu wynosi 1.
2.
Analiza kinematyczna mechanizmu
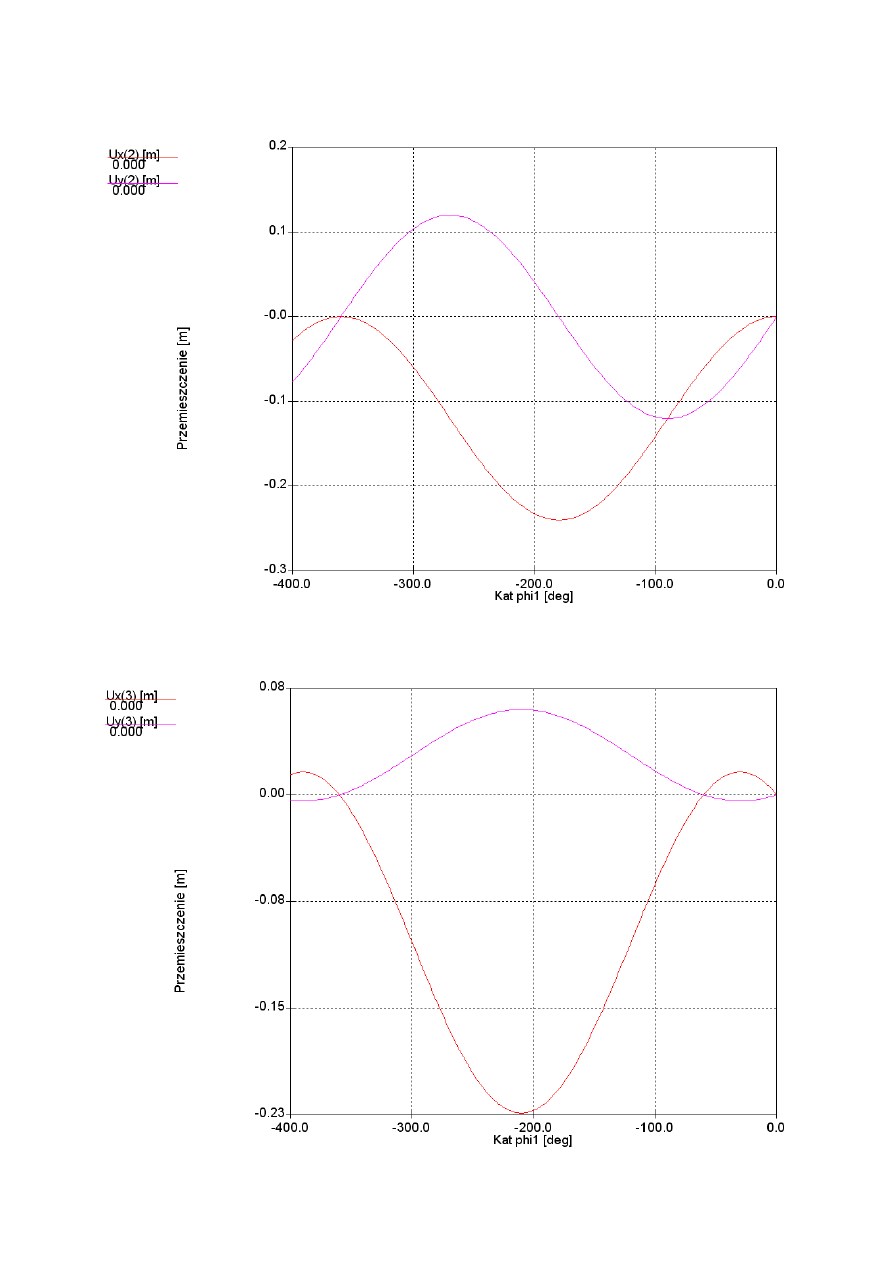
2.1. Wykresy przemieszczeń punktów charakterystycznych w zależności od kąta obrotu członu 1:
Wykres przemieszczeń punktów B, D, członu 2 poruszającego się ruchem postępowym.
Wykres przemieszczeń punktów C oraz E w względem osi x i y. Ze względu na ruch postępowy
członu 3 charakterystyki przemieszczeń wszystkich jego punktów są identyczne i są
charakterystykami przemieszczeń członu.
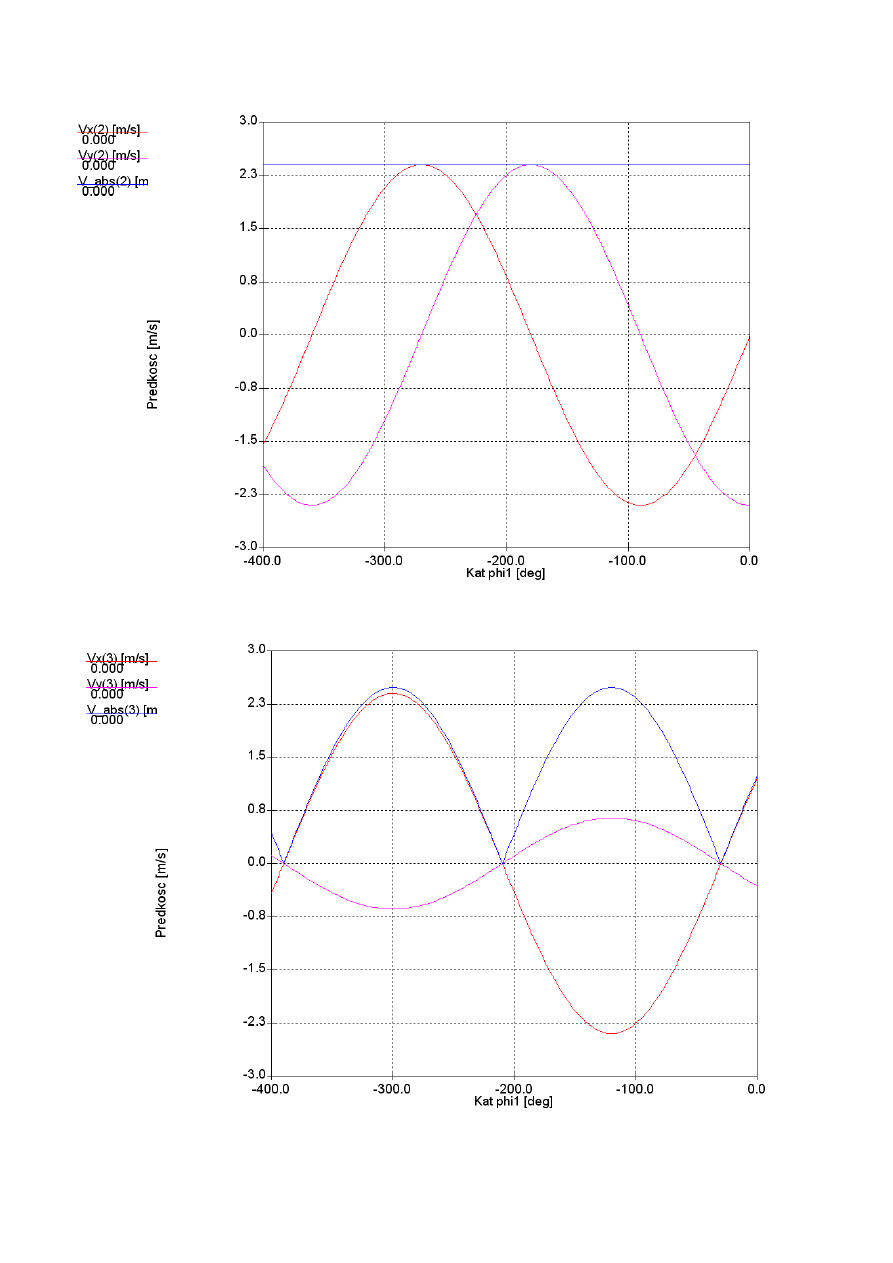
2.2. Wykresy prędkości punktów charakterystycznych w zależności od kąta obrotu członu 1:
Wykres prędkości punktów B, D, członu 2 poruszającego się ruchem postępowym.
Wykres prędkości punktów C oraz E. Ze względu na ruch postępowy członu 3 charakterystyki
prędkości wszystkich jego punktów są identyczne i są charakterystykami prędkości członu.
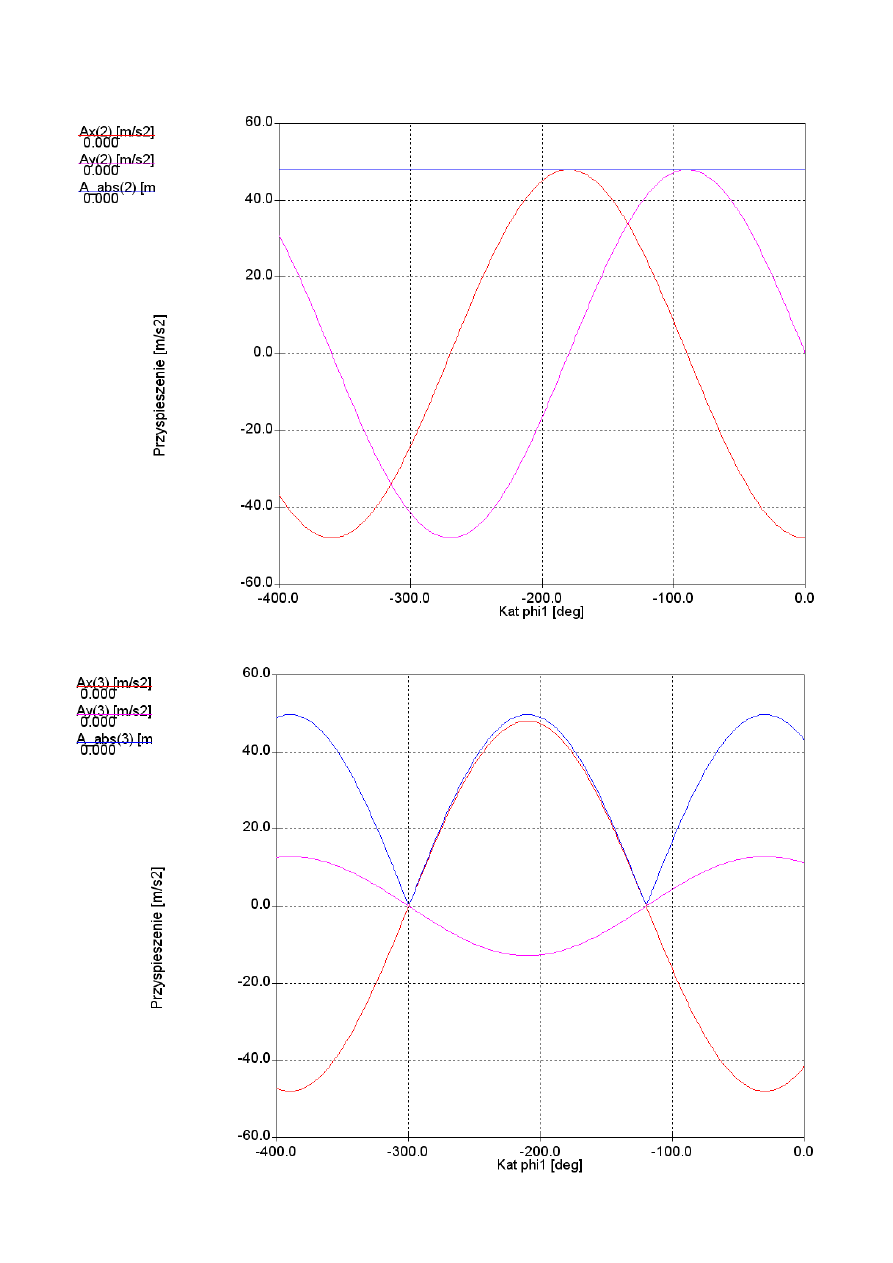
2.3. Wykresy przyspieszeń punktów charakterystycznych w zależności od kąta obrotu członu 1:
Wykres przyspieszeń punktów B, D, członu 3 poruszającego się ruchem postępowym.
Wykres przyspieszeń punktów C oraz E. Ze względu na ruch postępowy członu 3 charakterystyki
przyspieszeń wszystkich jego punktów są identyczne i są charakterystykami przyspieszenia członu.
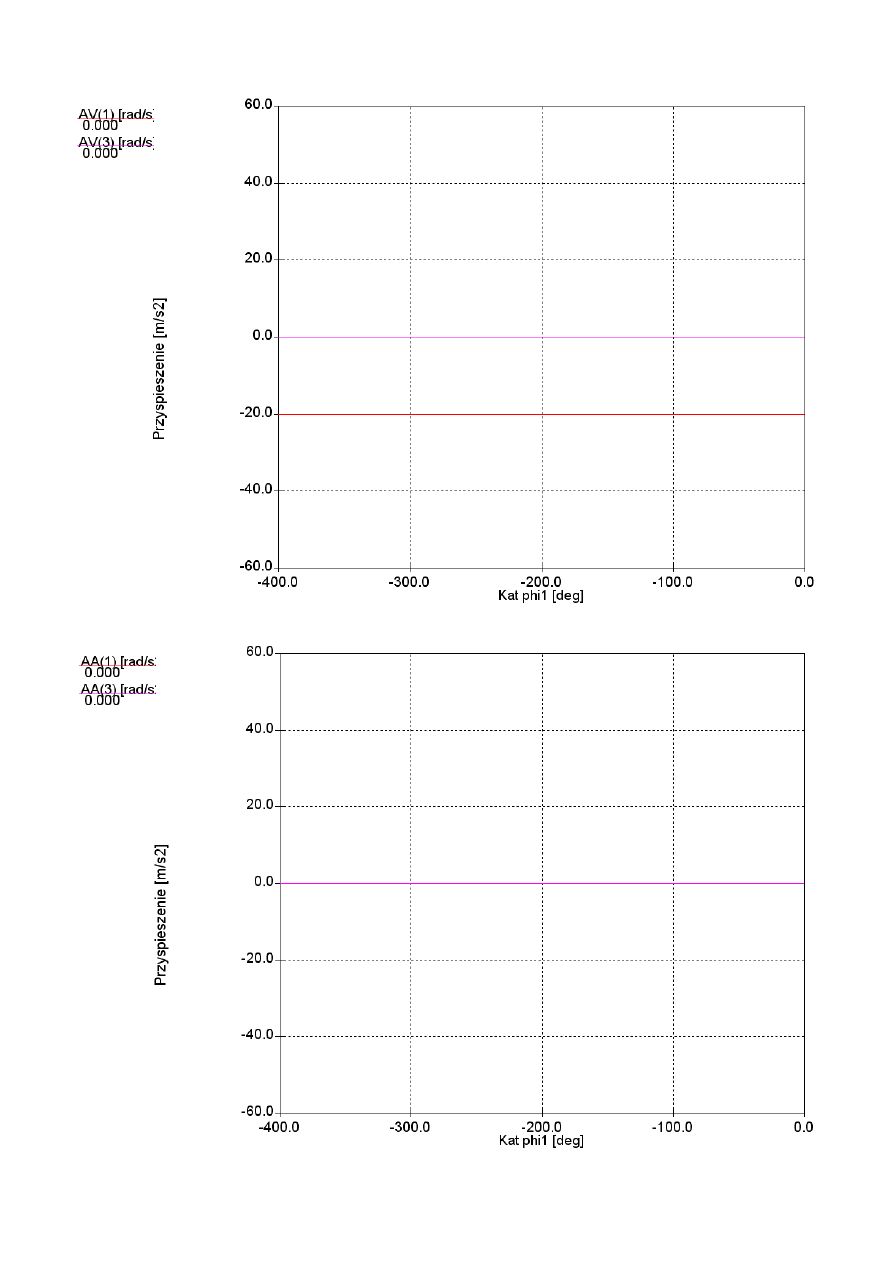
2.4. Wykresy prędkości kątowych członów 1 i 3 w zależności od kąta obrotu członu 1:
2.5. Wykresy przyspieszeń kątowych członów 1 i 3 w zależności od kąta obrotu członu 1:
Ze względu na ruch postępowy członów 2 i 3 ich prędkości i przyspieszenia kątowe są równe zero.
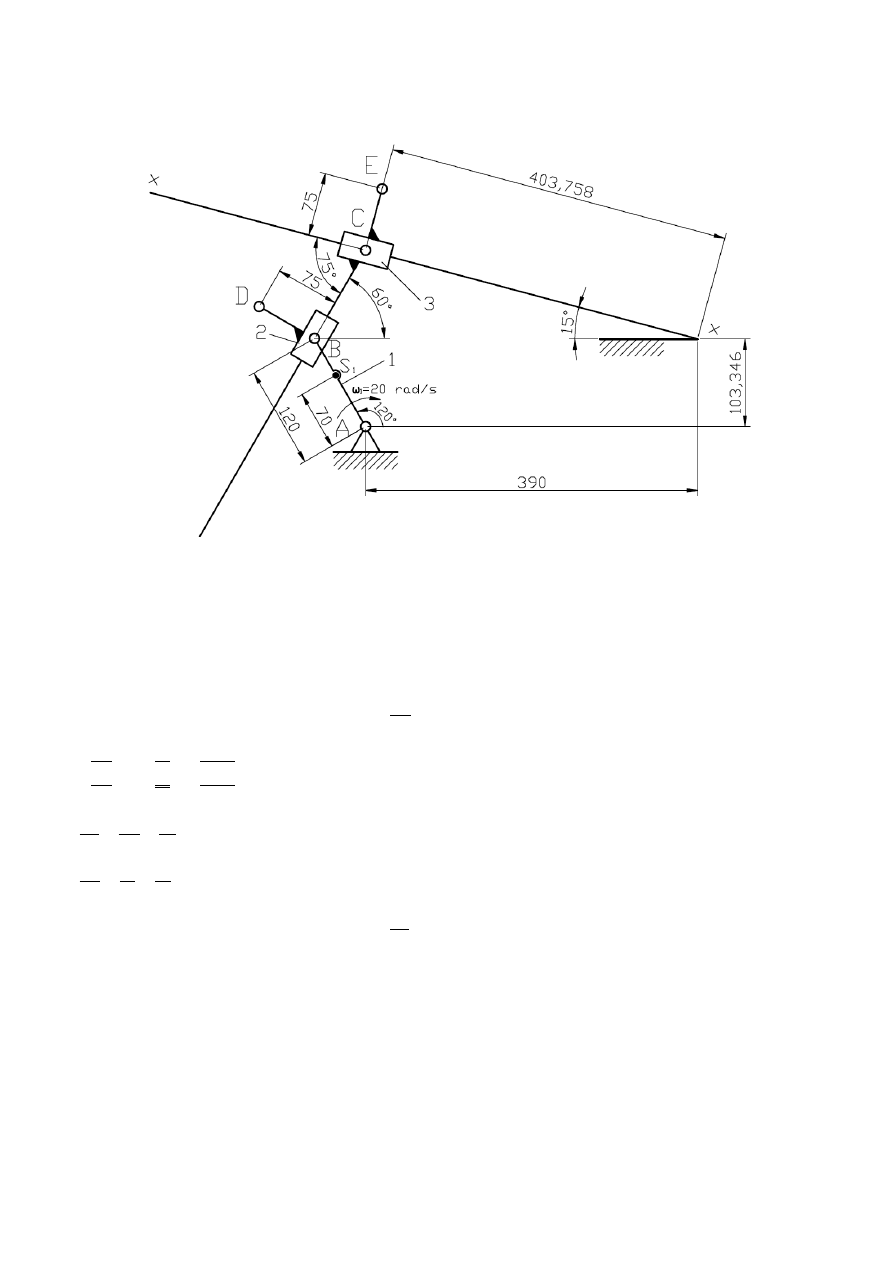
2.6. Wyznaczenie prędkości i przyspieszeń liniowych oraz prędkości i przyspieszeń kątowych
charakterystycznych punktów mechanizmu metodą grafoanalityczną dla wybranego położenia
mechanizmu.
Schemat mechanizmu w podziałce 1:5
Przyjmuję wymiary geometryczne jak na rysunku oraz:
ω
1
=const=20 rad/s
φ
1
=120º
Obliczenia prędkości:
s
m
AB
v
B
/
4
,
2
12
,
0
20
1
1
=
⋅
=
⋅
=
ω
AB
v
B
⊥
1
BC
v
AB
v
x
x
v
B
B
B
B
||
||
2
3
3
+
⊥
=
−
D
B
B
v
v
v
=
=
2
1
E
C
B
v
v
v
=
=
3
s
m
AS
v
S
/
4
,
1
07
,
0
20
1
1
1
=
⋅
=
⋅
=
ω
AB
v
S
⊥
1
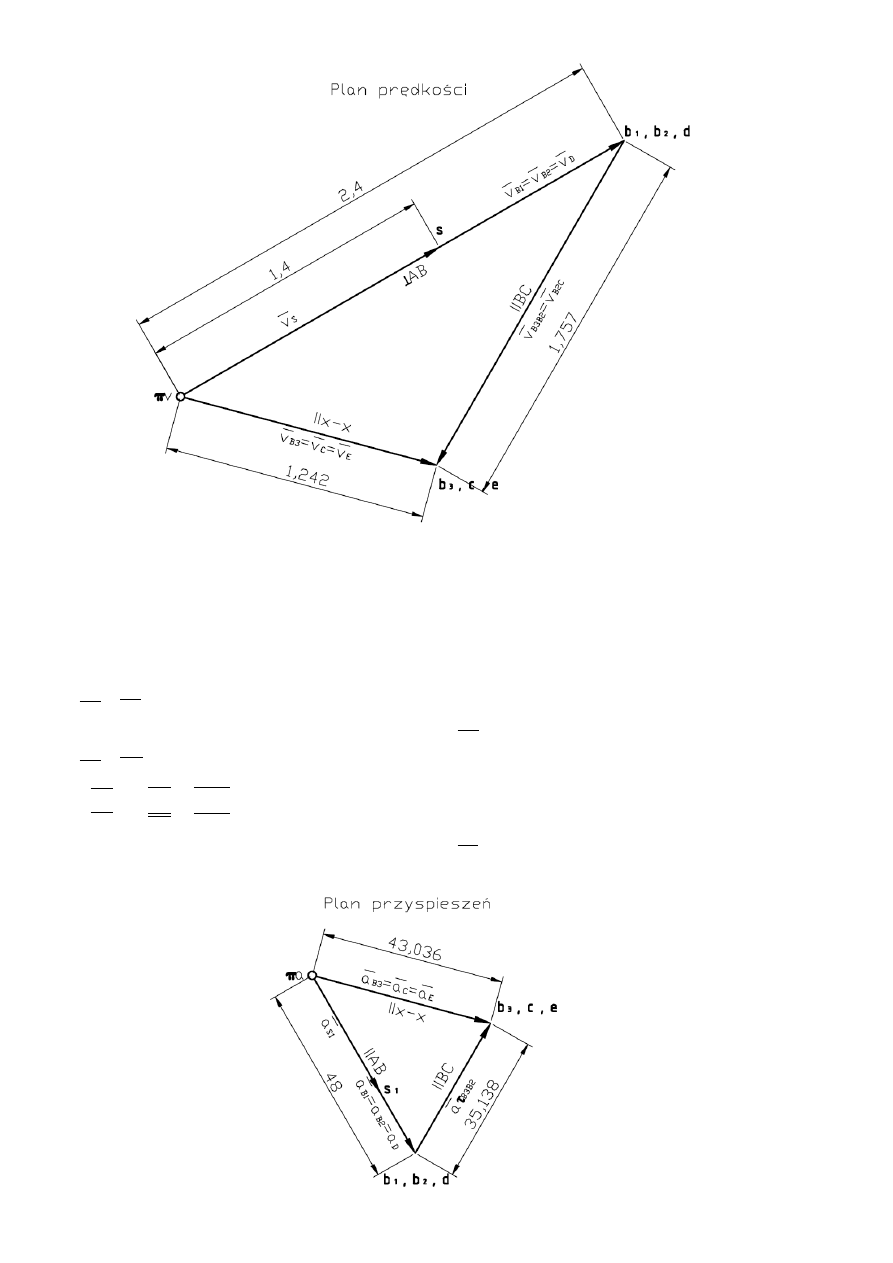
50mm:1m/s
Z planu prędkości otrzymuje się:
s
m
v
v
C
B
B
B
/
757
,
1
2
3
2
=
=
s
m
v
v
v
E
C
B
/
242
,
1
3
=
=
=
Obliczenia przyspieszeń:
Ponieważ ω
1
=const
0
1
=
τ
B
a
wtedy:
n
B
B
a
a
1
1
=
2
2
2
1
1
1
/
48
12
,
0
20
s
m
AB
a
a
n
B
B
=
⋅
=
⋅
=
=
ω
AB
a
B
||
1
2
1
B
B
a
a
=
BC
a
AB
a
x
x
a
B
B
B
B
||
||
||
2
3
2
3
τ
+
=
−
2
2
1
2
1
1
/
28
07
,
0
20
s
m
AS
a
S
=
⋅
=
⋅
=
ω
AB
a
S
||
1
1mm:1m/s
2
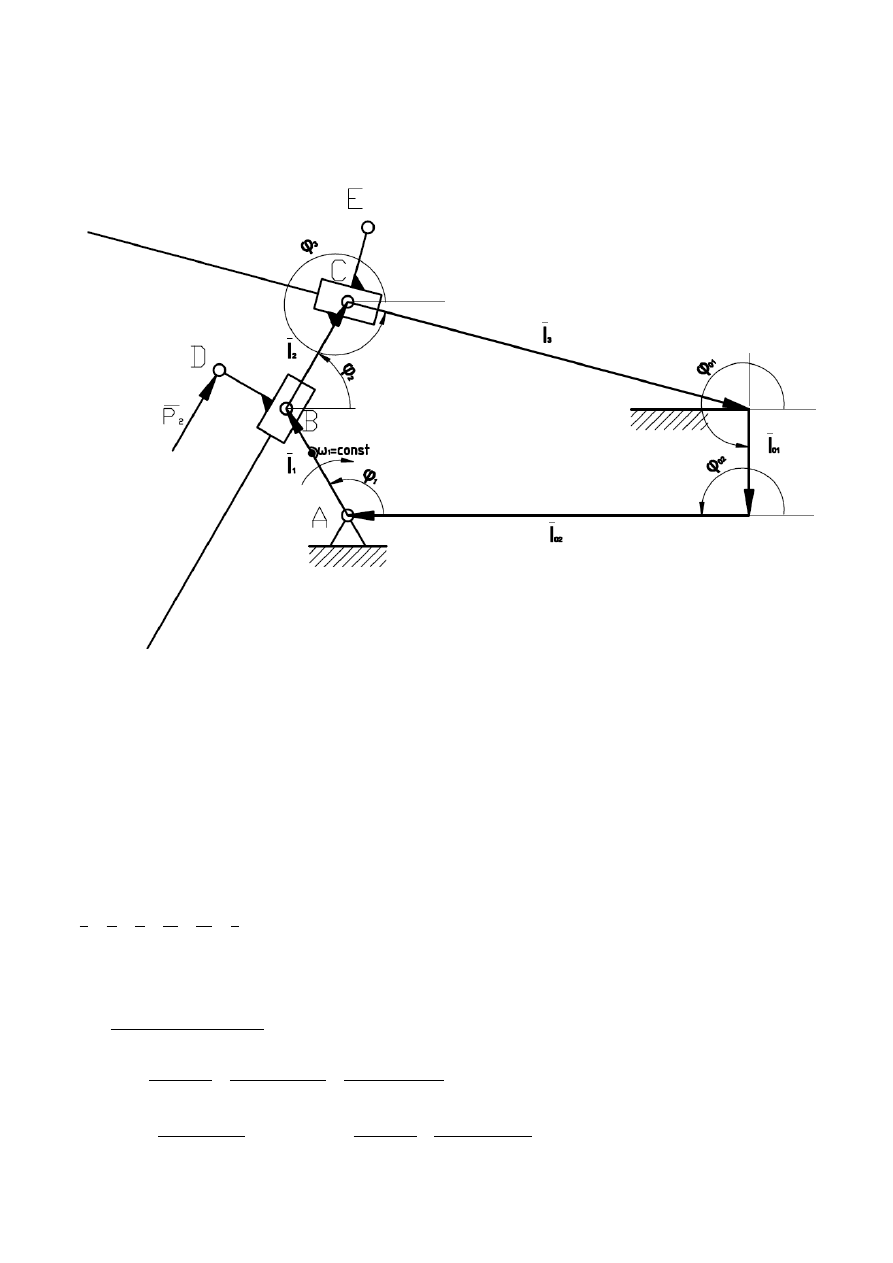
Z planu przyspieszeń otrzymuje się:
2
3
2
/
138
,
35
s
m
a
B
B
=
τ
2
3
/
036
,
43
s
m
a
a
a
E
C
B
=
=
=
2.7. Analiza metodą analityczną
Dane:
Należy przyjąć 2n-3 parametrów, gdzie n liczba boków wieloboku, 2·5-2=8
Przyjęte parametry:
φ
1
=φ
1
(t)
φ
2
=const=60º
φ
3
=const=345º
φ
01
=const=270º
φ
02
=const=180º
l
1
=1,2 m
l
01
=0,10335 m
l
02
=0,39 m
0
02
01
3
2
1
=
+
+
+
+
l
l
l
l
l
0
cos
cos
cos
02
3
3
2
2
1
1
=
−
+
+
l
l
l
l
ϕ
ϕ
ϕ
0
sin
sin
sin
01
3
3
2
2
1
1
=
−
+
+
l
l
l
l
ϕ
ϕ
ϕ
2
3
3
1
1
01
2
sin
sin
sin
ϕ
ϕ
ϕ
l
l
l
l
−
−
=
0
cos
sin
cos
sin
sin
cos
sin
sin
cos
cos
02
3
3
2
2
3
3
2
2
1
1
2
2
01
1
1
=
−
+
−
−
+
l
l
l
l
l
l
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
0
sin
cos
sin
sin
cos
cos
sin
cos
sin
cos
02
2
2
1
1
2
2
01
1
1
2
2
3
3
3
=
+
+
−
−
=
−
l
l
l
l
l
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
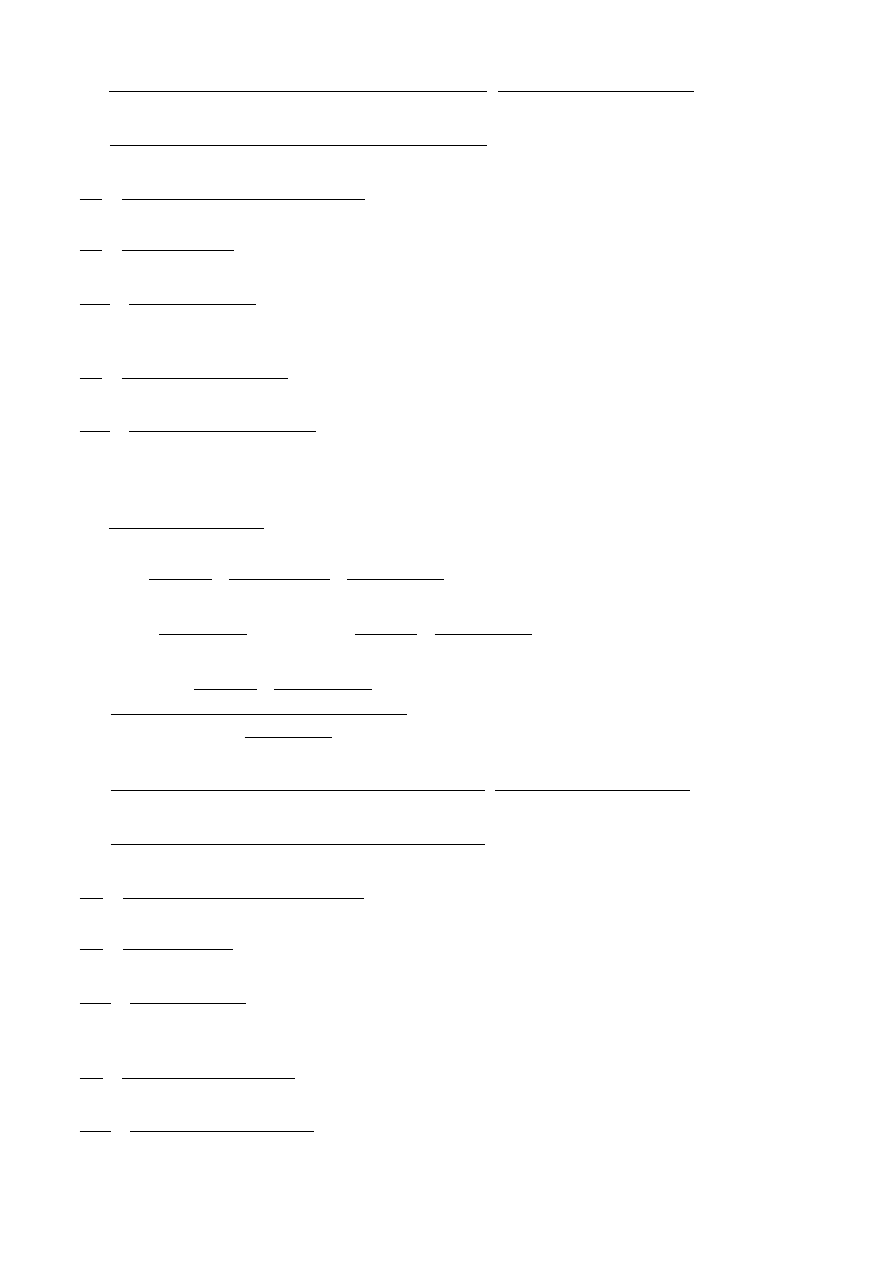
2
3
2
3
2
2
2
02
2
1
2
01
2
1
1
3
cos
sin
sin
cos
sin
sin
sin
cos
sin
cos
sin
cos
1
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
−
⋅
⋅
+
+
−
−
=
l
l
l
l
l
(
)
3
2
2
02
2
1
2
01
2
1
1
3
sin
sin
cos
sin
cos
sin
cos
1
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
−
+
+
−
−
=
l
l
l
l
l
(
)
3
2
2
1
1
2
1
1
1
3
sin
cos
cos
sin
sin
1
ϕ
ϕ
ϕ
ϕ
ω
ϕ
ϕ
ω
−
+
=
l
l
dt
dl
(
)
(
)
3
2
2
1
1
1
3
sin
cos
ϕ
ϕ
ϕ
ϕ
ω
−
−
=
l
dt
dl
(
)
(
)
3
2
2
1
1
2
1
2
3
2
sin
sin
ϕ
ϕ
ϕ
ϕ
ω
−
−
−
=
l
dt
l
d
Dla położenia analizowanego w metodzie grafoanalitycznej otrzymuje się:
(
)
(
)
s
m
dt
dl
/
242
,
1
345
60
sin
60
120
cos
12
,
0
20
3
=
−
−
⋅
=
(
)
(
)
2
2
3
2
/
036
,
43
345
60
sin
60
120
sin
12
,
0
400
s
m
dt
l
d
−
=
−
−
⋅
−
=
Wektor zmniejsza swą długość wektory przyspieszenia stycznego i prędkości mają zwroty przeciwne.
3
1
1
2
2
01
3
sin
sin
sin
ϕ
ϕ
ϕ
l
l
l
l
−
−
=
0
cos
sin
cos
sin
sin
cos
sin
sin
cos
cos
02
2
2
3
3
1
1
3
3
2
2
3
3
01
1
1
=
−
+
−
+
+
l
l
l
l
l
l
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
02
3
3
1
1
3
3
01
1
1
3
3
2
2
2
sin
cos
sin
sin
cos
cos
sin
cos
sin
cos
l
l
l
l
l
+
+
−
−
=
−
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
3
3
2
2
02
3
3
1
3
3
01
1
1
2
sin
cos
sin
cos
sin
cos
sin
sin
cos
cos
1
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
−
+
+
−
−
=
l
l
l
l
l
3
2
3
2
3
3
3
02
3
1
3
01
3
1
1
2
cos
sin
sin
cos
sin
sin
sin
cos
sin
cos
sin
cos
1
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
−
⋅
⋅
+
+
−
−
=
l
l
l
l
l
(
)
2
3
3
02
3
1
3
01
3
1
1
2
sin
sin
cos
sin
cos
sin
cos
1
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
−
+
+
−
−
=
l
l
l
l
l
(
)
2
3
3
1
1
3
1
1
1
2
sin
cos
cos
sin
sin
1
ϕ
ϕ
ϕ
ϕ
ω
ϕ
ϕ
ω
−
+
=
l
l
dt
dl
(
)
(
)
2
3
3
1
1
1
2
sin
sin
ϕ
ϕ
ϕ
ϕ
ω
−
+
=
l
dt
dl
(
)
(
)
2
3
3
1
1
2
1
2
2
2
sin
cos
ϕ
ϕ
ϕ
ϕ
ω
−
+
=
l
dt
l
d
Dla położenia analizowanego w metodzie grafoanalitycznej otrzymuje się:
(
)
(
)
s
m
dt
dl
/
4
,
2
60
345
sin
345
120
sin
12
,
0
20
2
−
=
−
+
⋅
=
(
)
(
)
2
2
2
2
/
48
60
345
cos
345
120
cos
12
,
0
400
s
m
dt
l
d
−
=
−
+
⋅
=
Wektor zmniejsza swą długość przyspieszenie styczne i prędkość mają zwroty zgodne.
Dla trzech metod: grafoanalitycznej, analitycznej i analizy w programie SAM otrzymano jednakowe
wartości prędkości i przyspieszeń dla wybranego położenia mechanizmu.
3.
Analiza kinetostatyczna
Przyjmuję następujące parametry:
m
1
=0,3kg
m
3
=06kg
P
2
=100N
P
3
=120N
Siły bezwładności:
Człon 1:
1
1
1
S
a
m
B
−
=
,
N
B
4
,
8
28
3
,
0
1
=
⋅
=
Człon 3
3
3
3
S
a
m
B
−
=
,
N
B
8216
,
25
036
,
43
6
,
0
3
=
⋅
=
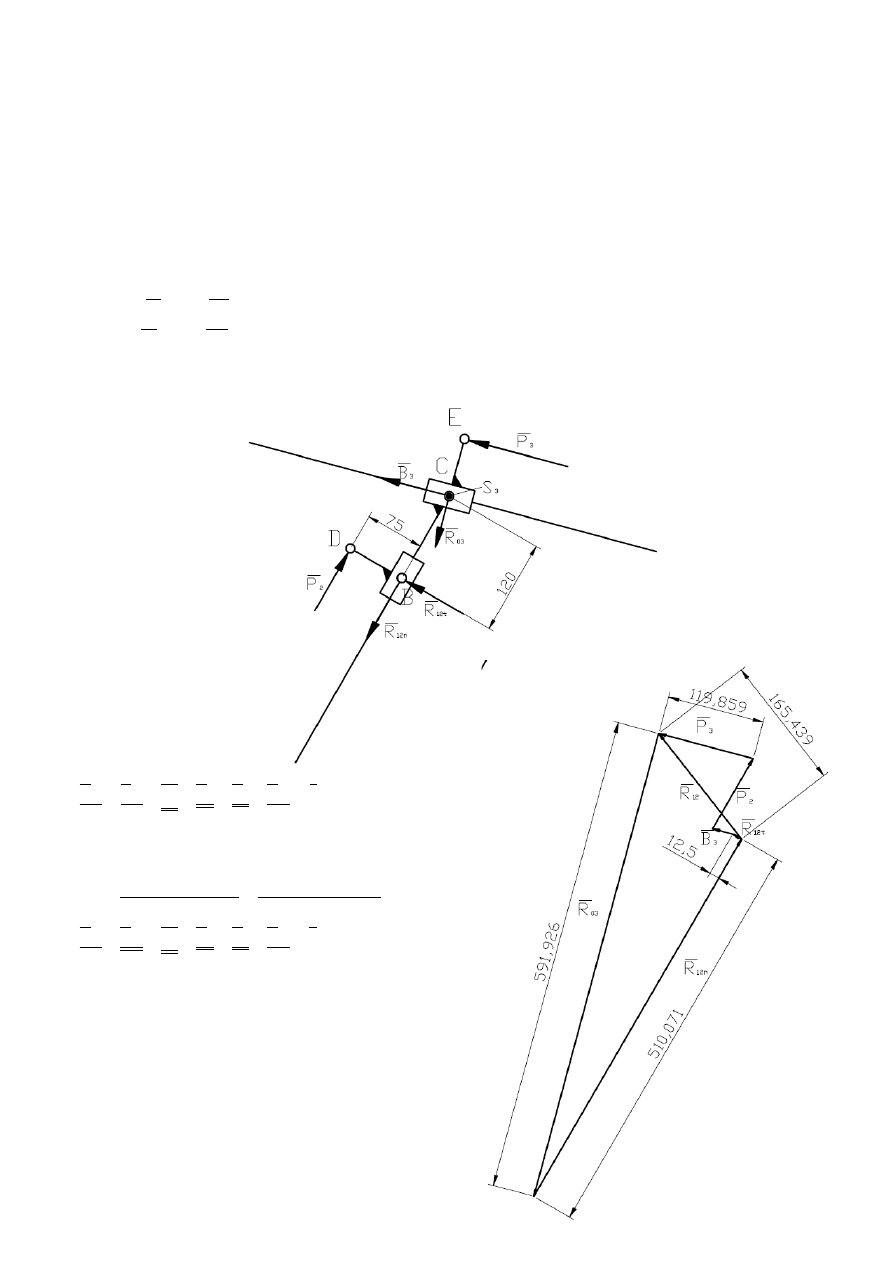
Siły ciężkości jako bardzo małe w porównaniu z siłami przyłożonymi i bezwładności można
zaniedbać
0
03
1
3
3
12
12
=
+
+
+
+
+
n
t
n
R
P
P
B
R
R
0
)
3
(
=
∑
iC
M
0
12
2
3
=
⋅
−
⋅
−
⋅
CD
R
BD
P
CE
P
t
N
CD
BD
P
CE
P
R
t
5
,
12
120
75
100
75
120
2
3
12
=
⋅
−
⋅
=
⋅
−
⋅
=
0
03
1
3
3
12
12
=
+
+
+
+
+
n
t
n
R
P
P
B
R
R
N
R
n
926
,
591
03
=
N
R
439
,
165
12
=
0
)
1
(
=
∑
iA
M
0
1
1
21
=
−
⋅
r
M
h
R
Nm
h
R
M
r
705
,
2
01635
,
0
439
,
165
21
1
=
⋅
=
⋅
=
Obliczenia metodą mocy chwilowych:
0
3
3
2
1
1
1
1
=
⋅
+
⋅
+
⋅
+
⋅
+
⋅
E
C
D
S
r
v
P
v
B
v
P
v
B
M
ω
0
180
cos
180
cos
0
cos
90
cos
0
cos
3
3
2
1
1
1
1
=
⋅
+
⋅
+
⋅
+
⋅
+
⋅
E
C
D
S
r
v
P
v
B
v
P
v
B
M
ω
Nm
v
P
v
B
v
P
M
E
C
D
r
944
,
2
20
242
,
1
120
242
,
1
82
,
25
4
,
2
100
1
3
3
2
1
=
⋅
+
⋅
+
⋅
−
=
⋅
+
⋅
+
⋅
−
=
ω
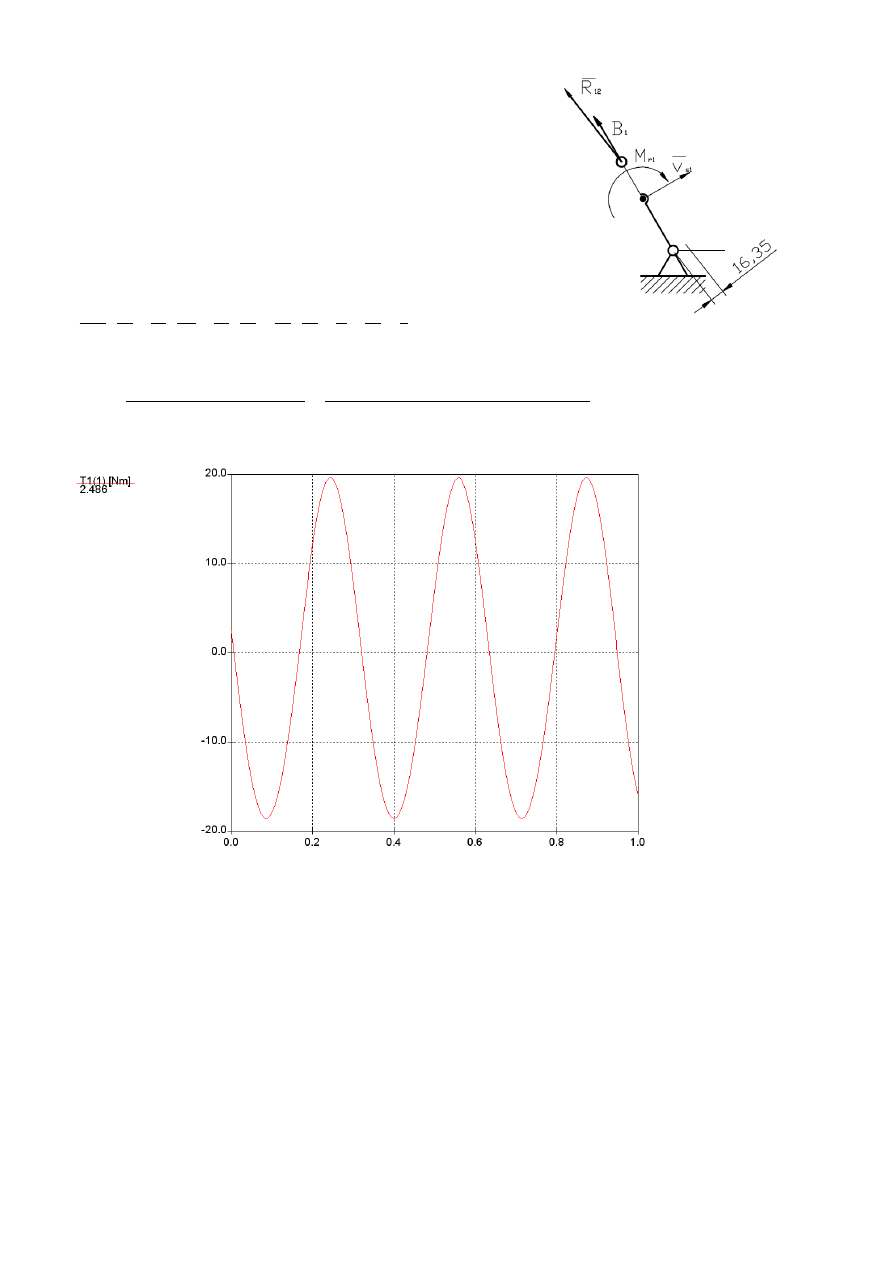
Analiza momentu programem SAM (Położenie w chwili t=0 dla danego położenia).
Porównanie otrzymanych momentów równoważących:
Metoda grafoanalityczna:
2,705 Nm
Metoda mocy chwilowych
2,944 Nm
Analiza programem SAM
2,486 Nm
Wyszukiwarka
Podobne podstrony:
mechanika 3 id 290735 Nieznany
manual mechanika 2 2 id 279133 Nieznany
Mechanisms 1 S id 291610 Nieznany
mechanikakinematyka id 291582 Nieznany
Przekladnie mechaniczne id 4047 Nieznany
Egzamin mechanika3 id 152505 Nieznany
przekladnie mechaniczne id 4048 Nieznany
Dodatek B Mechanika id 138691 Nieznany
mechanika 3 id 290735 Nieznany
manual mechanika 2 2 id 279133 Nieznany
mechanika plynow id 291486 Nieznany
Mechanika budowli 4 id 290783 Nieznany
mechanika do poprawki id 290847 Nieznany
mechanika plynow id 291242 Nieznany
mechanizmy lewopolkulowe id 291 Nieznany
MECHANIKA PLYNOW 1 id 291255 Nieznany
MECHANIKA PLYNOW 2(1) id 291256 Nieznany
mechanika inzynieria id 291479 Nieznany
więcej podobnych podstron