
Matematyka dyskretna cz. I
Logika, teoria mnogoœci, relacje, moc zbiorów, typy porz¹dkowe,
kongruencje
Zadania dla studentów informatyki
Katarzyna Lubnauer
Maria Wolska
id8989562 pdfMachine by Broadgun Software - a great PDF writer! - a great PDF creator! - http://www.pdfmachine.com http://www.broadgun.com

2
Logika
1.
Niech p, q, r nastêpuj¹ce zdania logiczne:
p- pada deszcz
q- s¹ chmury na niebie
r – œwieci sùoñce
Zapisz przy pomocy symboli logicznych nastêpuj¹ce zdania:
a)
Pada deszcz i œwieci sùoñce.
b)
Jeœli pada deszcz to s¹ chmury na niebie.
c)
Deszcz pada wtedy i tylko wtedy gdy s¹ chmury na niebie.
Które z tych zdañ s¹ zawsze prawdziwe?
2.
Zbadaj wartoœã logiczn¹ zdañ:
a)
Je¿eli 2+2=4 to 2+3=4.
b)
Je¿eli 2+3=4 to 2+2=4.
c)
Je¿eli 2+2=4 i 2+3=6 to 2x = 5.
d)
2+2=5 wtedy i tylko wtedy gdy 2+3 =4.
e)
2+2=4 lub 2+3=5.
3.
Mama. logik z zawodu powiedziaùa synowi: Jeœli nie odrobisz pracy domowej,
to nie obejrzysz filmu. Syn odrobiù lekcje i bez bajki zostaù wysùany do ùó¿ka. Czy
mama dotrzymaùa sùowa.
4.
Zbadaj wartoœã logiczn¹ zdañ:
a)
p
p
,
b)
q
p
,
c)
p
q
,
d)
q
p
r
q
p
,
e)
q
p
q
p
q
p
.
5.
Sprawdê które z poni¿szych zdañ s¹ tautologiami:
a)
q
p
p
q
,
b)
q
p
q
p
,
c)
q
p
q
p
,
d)
]
[
]
[
r
q
p
r
q
p
,
e)
p
p
q
p
.

3
6.
Okreœl koniunkcje za pomoc¹
a)
negacji i alternatywy
b)
negacji i implikacji.
7.
Okreœl równowa¿noœã za pomoc¹ koniunkcji, alternatywy i negacji.
8.
Zakùadaj¹c i¿ zdanie
q
p
jest faùszywe podaj wartoœã logiczn¹ zdania
p
q
.
9.
Zakùadaj¹c i¿ zdanie
r
q
p
)
(
jest faùszywe podaj wartoœã logiczn¹ zdania
r
q
p
r
q
.
10.Niech trójk¹t jest prostok¹tny ,wówczas suma kwadratów dùugoœci dwóch
krótszych boków równa jest kwadratowi dùugoœci najdùu¿szego boku. Zapisz
twierdzenie w postaci implikacji. Sformuùuj twierdzenie odwrotne, zbadaj jego
prawdziwoϋ.
11.Znajdê twierdzenie przeciwne, odwrotne i przeciwstawne do danego. Zbadaj
wartoœã logiczn¹ ka¿dego z tych twierdzeñ:
a)
Je¿eli
0
0
y
i
x
to
.
0
xy
b)
Je¿eli n jest liczb¹ naturaln¹ i parzyst¹ to
2
n
jest liczb¹ naturaln¹
parzyst¹.
c)
Niech n liczba naturalna. Je¿eli n jest liczb¹ parzyst¹ to
2
n
jest liczb¹
parzyst¹.
d)
Je¿eli x=0 lub y=0 to
0
xy
.
12.Udowodnij i¿ iloczyn dwóch liczb parzystych jest wielokrotnoœci¹ 4.
13.Udowodnij i¿ liczba
n
n
2
gdzie
N
n
jest liczb¹ parzyst¹. Podaj jaki typ
dowodu zastosowaùeœ.
14.Udowodnij i¿ liczba
n
n
3
gdzie
N
n
jest liczb¹ podzieln¹ przez 6. Podaj jaki
typ dowodu zastosowaùeœ.
15.Udowodnij i¿ liczba
n
n
3
gdzie
N
n
jest liczb¹ parzyst¹. Podaj jaki typ
dowodu zastosowaùeœ.
16.Udowodnij i¿ liczba
2
4
n
n
gdzie
N
n
jest liczb¹ podzieln¹ przez 3. Podaj
jaki typ dowodu zastosowaùeœ.
17.Udowodnij wynikania:
a)
Je¿eli
1
2
y
x
to
1
x
lub
1
y
.
b)
Je¿eli
0
xy
to
0
x
lub
0
y
.

4
c)
Je¿eli œrednia arytmetyczna n liczb jest wiêksza od a to przynajmniej
jedna z tych liczb jest wiêksza od a.
18.Udowodnij i¿
2
jest liczb¹ niewymiern¹. Podaj jaki typ dowodu
zastosowaùeœ.
19.Udowodnij i¿
3
jest liczb¹ niewymiern¹. Podaj jaki typ dowodu
zastosowaùeœ.
20.Udowodnij i¿
2
log 3
jest liczb¹ niewymiern¹. Podaj jaki typ dowodu
zastosowaùeœ.
21.Udowodnij i¿
3
log 5
jest liczb¹ niewymiern¹. Podaj jaki typ dowodu
zastosowaùeœ.
22.Udowodnij nastêpuj¹ce nierównoœci dla dowolnych
R
y
x,
:
a)
x
x
,
b)
0
0
max
,
x
y
x
y
x
y
,
c)
y
x
y
x
,
d)
y
x
y
x
,
e)
x
y
x
y
,
f)
x
y
x
y
,
g)
xy
x y
,
h)
x
x
y
y
.
Podaj jaki typ dowodu zastosowaùeœ.
23.Zapisz nastêpuj¹ce zdania w notacji polskiej (beznawiasowej):
a)
s
r
q
p
,
b)
s
r
q
p
,
c)
q
p
q
p
.
24.Przeksztaùã zdania z notacji beznawiasowej w notacje nawiasow¹:
a)
pq
q
p
,
b)
pqr
r
pq
.

5
Zbiory.
1.
Niech
13
,
12
,
6
,
17
,
8
,
6
,
5
,
1
,
17
,
5
,
3
,
1
,
10
,
8
,
6
,
4
,
2
,
17
,....,
3
,
2
,
1
,
0
D
C
B
A
U
.
Wyznacz zbiory:
a)
B
A
b)
B
A
c)
C
A
d)
c
B
C
A
e)
D
C
f)
C
B
g)
ile podzbiorów ma zbiór C
2.
Niech
5
,
4
,
2
A
,
parzyste
jest
n
n
B
:
N
,
0
:
p
e
nieparzyst
jest
p
p
C
Z
.
a)
Wyznacz
C
B
C
B
C
A
B
A
,
,
,
b)
Wypisz wszystkie podzbiory zbioru A
c)
Nie wyznaczaj¹c ich zgadnij, które ze zbiorów s¹ nieskoñczone:
A
B
B
A
B
A
B
A
,
,
,
.
3.
Wypisz kilka elementów poni¿szych zbiorów oraz zapisz te zbiory w inny
sposób:
a)
3
.
:
przez
podziel
n
N
n
A
b)
1
:
2
x
x
B
R
c)
2
2
:
x
x
C
R
d)
1
0 :
2
D
x
x
x
R
.
e)
4.
W przestrzeni
R
znajdê nastêpuj¹ce zbiory:
a)
3
,
2
5
,
1
,
b)
,
2
3
,
1
,
c)
7
,
2
5
,
0
,
d)
7
,
2
5
,
0

6
e)
c
,
0
f)
4
,
0
5.
Dla podanych zbiorów A,B wyznaczyã zbiory
B
A
B
A
B
A
\
,
,
. Wynik
zaznacz na osi liczbowej:
a)
8
5
1
:
,
0
1
16
4
1
3
:
2
2
x
x
x
B
x
x
x
x
x
A
R
R
b)
0
1
log
2
1
log
:
,
2
1
log
2
log
3
:
2
x
x
x
B
x
x
x
A
R
R
c)
1
1
1
:
,
2
2
1
:
x
x
x
B
x
x
A
R
R
d)
1
2
1
:
,
9
4
3
:
1
x
x
x
B
x
x
x
A
R
R
e)
1
1
1
:
,
1
:
x
x
x
B
x
x
x
A
R
R
f)
3
2
:
,
1
1
:
2
2
x
x
B
x
x
x
x
x
A
R
R
g)
5
1
:
,
0
4
1
3
:
2
2
x
x
B
x
x
x
x
x
x
A
R
R
h)
3
1
2
:
,
1
1
log
:
2
x
x
x
B
x
x
A
x
R
R
6.
Niech
2
:
2
.
:
,
,
,
,
,
,
,
,
*
*
w
dlug
w
C
i
w
dlug
w
B
yyy
xxx
yy
xx
y
x
A
y
x
a) Wyznacz zbiory
C
A
A
C
C
A
C
A
,
\
,
\
,
.
b) Wyznacz zbiory
A
B
C
B
C
B
B
A
\
,
,
,
.
c) Wyznacz zbiory
*
*
,
B
A
.
d) Wypisz wszystkie podzbiory
.
e) Ile zbiorów nale¿y do
2
.
7.
Wykazaã, ¿e dla dowolnych zbiorów A,B,C zachodzi równoœã
a)
B
A
A
B
A
\
\
b)
B
A
B
A
A
\
c)
B
A
B
A
A
\
\
d)
A
C
B
C
A
B
C

7
e)
C
A
B
A
C
B
A
\
\
\
f)
C
B
A
C
B
A
\
\
\
8.
Udowodnij uogólnione prawo De Morgana:
c
c
c
c
C
B
A
C
B
A
.
9.
Udowodnij prawdziwoœã nastêpuj¹cych zdañ nie u¿ywaj¹c diagramów Venna:
a)
B
A
A
i
A
B
A
dla dowolnych zbiorów A,B.
b)
Jeœli
C
A
i
B
A
, to
C
B
A
.
c)
Jeœli
C
B
i
C
A
to
C
B
A
.
d)
B
A
wtedy i tylko wtedy gdy
c
c
A
B
.
10.Dla dowolnego A okreœlonego w przestrzeni X okreœl zbiór
A
A
,
A
,
X
A
.
11.Wykazaã, ¿e dla dowolnego A,B,C zachodz¹ równoœci:
a)
A
B
B
A
b)
C
B
A
C
B
A
12.Podaj¹c odpowiednie przykùady wykazaã, ¿e równoœci
a)
A
B
B
A
\
b)
A
B
B
A
\
NIE zachodz¹ dla dowolnych zbiorów A,B. Zilustruj rozwi¹zanie diagramami
Venna.
13.Narysuj diagram Venna dla czterech dowolnych zbiorów A,B,C,D i zaznacz
na nim zbiór
c
c
c
D
C
B
A
.
14.Zbadaj czy poni¿sze zdania s¹ prawdziwe czy faùszywe. Prawdziwe zdania
udowodnij a dla faùszywych znajdê kontrprzykùad.
a)
C
A
B
A
implikuje B=C
b)
C
A
B
A
implikuje B=C
c)
C
A
B
A
i
C
A
B
A
implikuje B=C
d)
B
A
B
A
implikuje A=B
e)
C
A
B
A
implikuje B=C
f)
B
B
A
B
A
c
c
g)
B
C
A
C
B
A
\
\
15.Poka¿, ¿e
B
A
jest najmniejszym zbiorem zawieraj¹cym jednoczeœnie zbiory
A oraz B.
16.Rozwi¹¿ równanie :

8
2
1
,
1
1
,
0
X
17.Niech
5
,
1
4
,
2
,
5
,
3
,
1
C
i
B
A
. Rozwi¹¿ równanie
C
B
X
A
.
18.Niech
d
b
a
B
i
c
b
a
A
,
,
,
,
.
a)
Wypisz lub narysuj wszystkie pary uporz¹dkowane zbiorów
A
A
i
B
A
.
b)
Wypisz lub narysuj wszystkie pary uporz¹dkowane zbioru
y
x
B
A
y
x
:
,
.
19.Niech
3
,
2
,
1
,
0
S
i niech
3
,
1
T
.
a)
Wypisz lub narysuj elementy zbioru
S
T
i
T
S
.
b)
Wypisz lub narysuj elementy zbioru
n
m
T
S
n
m
:
,
.
c)
Wypisz lub narysuj elementy zbioru
n
m
S
T
n
m
:
,
.
d)
Wypisz lub narysuj elementy zbioru
3
:
,
n
m
T
S
n
m
.
e)
Wypisz lub narysuj elementy zbioru
5
:
,
mn
T
S
n
m
.
f)
.Wypisz lub narysuj elementy zbioru
n
m
S
S
n
m
:
,
.
20.Narysuj zbiory
A
B
B
A
,
dla:
a)
3
,
2
,
1
,
0
B
A
b)
3
,
0
,
1
,
2
B
A
c)
2
,
1
,
0
B
A
d)
,
2
,
1
,
B
A
.
21.Wypisz wszystkie elementy tych spoœród zbiorów które maj¹ nie wiêcej ni¿ 6
elementów oraz wypisz 6 elementów z tych zbiorów które maj¹ wiêcej
elementów.
a)
m
n
n
m
:
,
2
N
b)
2
:
,
2
m
n
n
m
N
c)
4
:
,
2
nm
n
m
Z
d)
x
x
y
x
2
2
:
,
R
e)
5
,
max
:
,
2
n
m
n
m
N
f)
1
,
max
:
,
2
n
m
n
m
N
.
22.W prostok¹tnym ukùadzie wspóùrzêdnych zaznaczyã zbiory A,B,
B
A
B
A
,
:

9
a)
0
:
,
,
0
sin
:
,
2
2
tgy
y
x
B
y
x
y
x
A
R
R
b)
0
cos
:
,
,
0
sin
:
,
2
2
y
x
y
x
B
y
x
y
x
A
R
R
c)
0
cos
:
,
,
0
:
,
2
2
y
x
y
x
B
y
x
tg
y
x
A
R
R
d)
0
:
,
,
0
:
,
2
2
tgx
y
x
B
y
x
tg
y
x
A
R
R
e)
1
:
,
,
log
log
:
,
2
2
y
x
y
x
B
x
y
y
x
A
y
x
R
R
23.Zaznacz zbiory
A
B
B
A
,
w ukùadzie wspóùrzêdnych:
a)
2
1
:
,
2
:
y
y
B
x
x
A
R
R
b)
1
2
:
,
1
2
:
y
y
B
x
x
A
R
R
c)
3
0
:
,
0
4
1
2
:
2
2
y
y
B
x
x
x
x
x
A
R
R
d)
0
27
16
:
,
5
1
:
3
2
x
x
x
B
y
y
A
R
R
e)
1
1
1
2
:
,
3
1
log
:
2
2
y
y
y
B
x
x
A
R
Z
f)
1
6
5
log
:
,
0
1
3
5
3
2
:
2
5
,
0
2
x
x
x
B
t
t
t
t
A
R
R
24.Wyka¿ równoœci:
a)
C
A
B
A
C
B
A
b)
C
A
B
A
C
B
A
10
Kwantyfikatory
1.
Oceñ wartoœã logiczn¹ zdañ i zapisz negacje ka¿dego zdania:
a)
x
x
x
2
R
b)
1
2
1
2
x
x
x
x
x N
c)
2
1
1
1
x
x
x N
d)
0
1
2
1
3
x
x
x N
e)
0
2
3
4
2
2
2
x
x
x
x R
f)
0
3
2
2
4
2
2
2
x
x
x
x R
g)
y
x
x
y
y
x
3
3
,
R
h)
3
,
2
,
1
,
3
3
,
A
gdzie
x
y
y
x
A
y
x
i)
10
2
2
n
m
n
m
N
N
j)
y
x
y
x
N
Z
k)
4
2
x
y
y
x
R
R
2.
Okreœl wartoœã logiczn¹ zdañ, dla
N
m
n
,
:
a)
]
2
[
m
n
n
m
b)
]
2
[
m
n
m
n
c)
]
2
[
n
m
n
m
d)
]
2
[
n
m
m
n
e)
}]
2
{
[
m
n
m
n
3.
Okreœl wartoœã logiczn¹ zdañ, dla
R
y
x,
:
a)
]
0
[
xy
x
y
b)
]
0
[
xy
y
x
c)
]
1
[
xy
x
y

11
d)
]
1
[
xy
y
x
4.
Niech p(x,y) , p(y) funkcje zdaniowe, znajdê kontrprzykùady do nastêpuj¹cych
implikacji:
a)
y
p
y
p
y
y
b)
)
,
(
)
,
(
y
x
p
y
x
p
y
x
x
y
c)
y
p
y
p
y
y
5.
Wska¿ zmienne wolne i zwi¹zane w nastêpuj¹cych wyra¿eniach:
a)
y
z
x
y
x
y
x
b)
y
x
x
x
y
c)
0
x
x
x
x
d)
A
x
x
e)
x
g
x
f
g
f
X
x
6.
Zapisz posùuguj¹c siê symbolik¹ logiczn¹ nastêpuj¹ce zdania:
a)
Liczby 2 i 3 nie maj¹ wspólnych dzielników ró¿nych od 1.
b)
Istnieje liczba naturalna od której nie jest mniejsza ¿adna inna liczba
naturalna.
c)
Ukùad równañ :
5
3
3
3
b
a
i
b
a
nie ma rozwi¹zañ.
7.
Podaj przykùad takich funkcji zdaniowych
X
x
x
x
,
,
, dla których
implikacje s¹ faùszywe:
a)
x
x
x
x
X
x
X
x
X
x
b)
x
x
x
x
X
x
X
x
X
x
8.
Niech formuùa r(x,y) oznacza, ¿e x jest rodzicem y, niech m(x) oznacza, i¿ x
jest mê¿czyzn¹. Zdefiniuj za pomoc¹ formuù r oraz m nastêpuj¹ce zdania:
a)
„x jest bratem y”
b)
„x jest siostr¹ cioteczn¹ y”
c)
„x jest pradziadkiem y”

12
Uogólnione sumy i iloczyny zbiorów
1.
Policz iloczyn i sumê uogólnion¹ ci¹gu zbiorów:
a)
2 , 2
n
n
n
A
b)
1 1
,
n
B
n n
c)
1
, 2
n
n
C
n
d)
1, 2,..., 3
n
n
D
e)
1
,
n
n
E
n
f)
R
R
t
t
x
x
F
t
,
sin
:
g)
0
,
1
:
R
R
t
xt
x
G
t
h)
R
R
t
t
x
x
H
t
,
1
:
i)
R
R
t
t
x
x
I
t
,
:
2.
Policz granice doln¹ i górn¹ ci¹gu zbiorów
a)
,
n
A
n n
b)
1 1
,
n
B
n n
c)
1
, 2
n
n
C
n
d)
1, 2,..., 3
n
n
D
3.
Zbiór wszystkich liczb naturalnych dodatnich przedstaw jako sume
nieskoñczon¹ ci¹gu zbiorów nieskoñczonych i parami rozù¹cznych.
Wskazówka:
2 1, 2
3, 2
5, 2
7,..., 2
,... ,
n
n
n
n
n
n
Z
k
n
N
, k liczba nieparzysta.
4.
Udowodnij korzystaj¹c z rachunku funkcyjnego nastêpuj¹ce twierdzenia
algebry zbiorów:
a)
B
A
B
A
\
,
b)
T
t
t
t
T
t
t
T
t
t
B
A
B
A
,
c)
T
t
t
T
t
t
T
t
t
t
B
A
B
A
,

13
d)
T
t
t
T
t
t
T
t
t
t
B
A
B
A
.

14
Relacje
1.
Niech
4
,
3
,
2
,
1
S
oraz
8
,
7
,
6
,
5
T
, oraz niech R relacja w zbiorze
T
S
.
Wypisz wszystkie pary nale¿¹ce do relacji R:
a)
10
,
y
x
R
y
x
b)
10
,
y
x
R
y
x
c)
parzyste
jest
y
x
R
y
x
,
2.
Dla relacji
4
3
2
1
,
,
,
R
R
R
R
w zbiorze
4
,
3
,
2
,
1
,
0
S
okreœl jakie wùasnoœci z poœród
poni¿szych speùniaj¹:
(Z) zwrotnoϋ
(PZ) przeciwzwrotnoϋ
(S) symetrycznoϋ
(AS) antysymetrycznoϋ
(P) przechodnioϋ
a)
parzyste
jest
y
x
R
y
x
1
,
b)
y
x
R
y
x
2
,
c)
0
,
3
y
x
R
y
x
d)
parzyste
jest
y
x
R
y
x
4
,
.
3.
Zbadaj jakie wùasnoœci spoœród wymienionych powy¿ej ma w zbiorze
,
,
,
S
relacja okreœlona tabel¹:
\
gdzie ‘+’ oznacza, ¿e dana para jest w relacji a’ –‘ , ¿e nie jest.
4.
W zbiorze N okreœlone s¹ nastêpuj¹ce relacje dwuargumentowe:
a)
parzyste
y
x
R
y
x
1
,
b)
3
.
,
2
przez
podziel
y
x
R
y
x
c)
5
,
3
y
x
R
y
x
d)
2
,
min
,
4
y
x
R
y
x
e)
x
y
R
y
x
5
,
gdzie
x
y
oznacza i¿ y jest podzielne przez x

15
f)
2
,
6
y
x
R
y
x
Zbadaj ich wùasnoœci i dla relacji równowa¿noœci znajdê klasy abstrakcji.
5.
W zbiorze X okreœlone s¹ nastêpuj¹ce relacje dwuargumentowe:
a)
X zbiór prostych na pùaszczyênie. Dwie proste l,k s¹ w relacji
gdy s¹
do siebie równolegùe (ozn.
k
l
)
b)
X zbiór prostych na pùaszczyênie. Dwie proste l,k s¹ w relacji
gdy s¹ do
siebie prostopadùe (ozn. l
k)
c)
X zbiór ludzi na ziemi . Dwaj ludzie s¹ w relacji ze sob¹ gdy maj¹
wspólnego rodzica (matkê lub ojca)
d)
X zbiór ludzi na ziemi . Dwaj ludzie s¹ w relacji ze sob¹ gdy maj¹
wspóln¹ matkê.
Zbadaj ich wùasnoœci i dla relacji równowa¿noœci znajdê klasy abstrakcji.
6.
Dla relacji z zadania drugiego narysuj rysunki przedstawiaj¹cy relacje miêdzy
elementami zbioru S. Jeœli element (x,y) nale¿y do relacji to ù¹czymy je strzaùk¹
o pocz¹tku w x i koñcu w y. Jeœli miêdzy jakimiœ punktami wystêpuj¹ strzaùki w
obu kierunkach to zastêpujemy je lini¹. Czym wyró¿niaj¹ siê rysunki ilustruj¹ce
relacje równowa¿noœci? Jakie wùasnoœci relacji mo¿esz odczytaã z rysunku.
7.
Zbiór liczb caùkowitych podzieliliœmy na zbiory rozù¹czne
3
,
2
,
1
,
0
,
,....
3
,
2
,
1
:
4
n
dla
k
n
k
Z
n
. Znajdê relacjê dla której s¹ to klasy
abstrakcji.
8.
Niech
d
c
b
a
X
,
,
,
oraz niech
X
S
2
zbiór wszystkich podzbiorów zbioru X.
Niech R relacja w zbiorze S okreœlona nastêpuj¹co:
B
A
R
B
A
,
. Wyka¿, ¿e
jest to relacja równowa¿noœci i znajdê klasê abstrakcji do której nale¿y element
b
a
A
,
.
9.
Niech X pewien zbiór niepusty oraz niech
X
S
2
zbiór wszystkich podzbiorów
zbioru X. Niech ponadto
X
a
oraz R relacja w zbiorze S okreœlona nastêpuj¹co:
B
A
a
B
A
R
B
A
,
. Wyka¿, ¿e jest to relacja równowa¿noœci i znajdê
jej klasy abstrakcji.
10.W zbiorze par uporz¹dkowanych
y
x,
gdzie x równe 0 lub 1 i y jest równe 0
lub 1 okreœlono relacje R w nastêpuj¹cy sposób
0
0
0
0
,
,
y
y
x
x
y
x
R
y
x
.
Zbadaj czy jest to relacja równowa¿noœci i jeœli odpowiedê jest twierdz¹ca znajdê
jej klasy abstrakcji.

16
11.W zbiorze trójek uporz¹dkowanych
z
y
x
,
,
gdzie x,y,z równe 0 lub 1
,okreœlono relacje R w nastêpuj¹cy sposób
n
n
y
x
y
y
y
R
x
x
x
3
2
1
3
2
1
,
,
,
,
dla
nieparzystej liczby wskaêników n=1,2,3. Zbadaj czy jest to relacja
równowa¿noœci i jeœli odpowiedê jest twierdz¹ca znajdê jej klasy abstrakcji.
12.Niech w zbiorze liczb naturalnych okreœlona bêdzie relacja
m
mod
w
nastêpuj¹cy sposób:
m
b
a
m
b
a
mod
mod
,
gdzie
km
b
a
m
b
a
k
def
Z
mod
.
Dla m=3 zbadaj czy jest to relacja równowa¿noœci i jeœli odpowiedê jest
twierdz¹ca znajdê jej klasy abstrakcji.
13.W teorii liczb okreœla siê relacjê zwan¹ kongruencj¹. Wyka¿, ¿e je¿eli
m
d
c
i
m
b
a
mod
mod
to
a)
m
d
b
c
a
mod
,
b)
m
d
b
c
a
mod
,
c)
m
d
b
c
a
mod
.
17
Funkcje
1.
Definiujemy funkcjê
R
R
:
f
okreœlon¹ wzorem :
0
,
1
0
,
1
,
2
3
x
dla
x
x
dla
x
x
dla
x
x
f
.
a)
Oblicz f(0), f(1), f(-1), f(2).
b)
Naszkicuj wykres funkcji f i na jego podstawie okreœl Im(f).
c)
Narysuj funkcje
1
,
,
f
f
f
.
2.
Które z poni¿szych rysunków przedstawiaj¹
a)
wykres funkcji
b)
wykres funkcji ró¿nowartoœciowej
c)
wykres funkcji „na” przedziaù
1
,
0
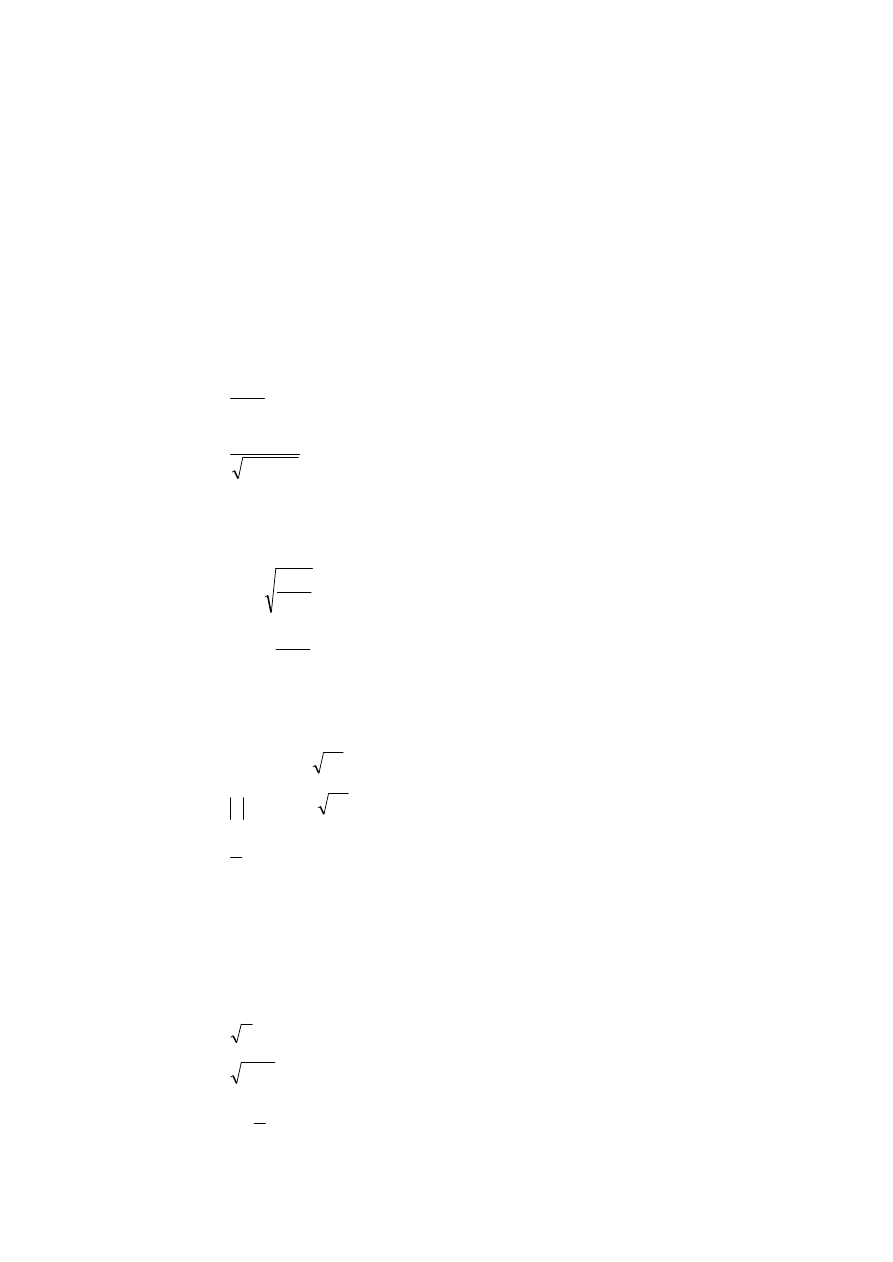
18
3.
Niech
5
,
4
,
3
,
2
,
1
S
oraz zdefiniujmy nastêpuj¹ce funkcje:
a)
n
n
f
6
b)
3
,
max n
n
f
c)
2
,
min n
n
f
d)
n
n
f
,
5
min
.
Zbadaj które z nich s¹ wzajemnie jednoznaczne z S w S.
4.
Wyznacz dziedzinê funkcji:
a)
1
2
x
x
x
f
b)
x
x
x
f
4
1
2
c)
x
x
f
sin
log
d)
e
e
x
f
x
ln
e)
x
x
x
x
f
1
1
3
f)
x
x
x
f
1
2
arcsin
5.
Czy funkcje f i g okreœlone nastêpuj¹co:
a)
2
2
2
2
z
z
g
i
x
x
f
b)
2
z
z
g
i
x
x
f
c)
2
z
z
g
i
x
x
f
d)
1
z
g
i
x
x
x
f
e)
z
z
z
g
i
x
f
2
2
cos
sin
1
f)
ctgz
tgz
z
g
i
x
f
1
s¹ równe?
6.
Okreœliã dziedzinê i zbiory wartoœci funkcji:
a)
3
x
x
f
b)
2
x
x
f
c)
x
x
f
1
sin
19
d)
x
x
x
f
1
e)
x
x
x
f
cos
sin
f)
4
2
2
x
x
x
f
g)
x
x
f
sin
log
7.
Dane s¹ funkcje
x
x
x
f
3
3
,
2
2
2
x
x
g
,
4
x
x
h
,
x
x
k
2
. Znajdê
funkcje:
a)
h
g
f
b)
h
h
f
c)
k
f
d)
g
g
e)
g
h
.
8.
Udowodnij i¿ nastêpuj¹ce funkcje s¹ ró¿nowartoœciowe na wskazanych
zbiorach:
a)
0
,
,
2
x
x
f
b)
R
,
3
x
x
f
c)
R
,
1
5
x
x
f
d)
1
,
1
1
x
x
x
f
e)
0
,
x
x
x
f
f)
0
\
,
1
R
x
x
x
f
9.
Zbadaj ró¿nowartoœciowoœã oraz wùasnoœã„na” funkcji
Z
Z
Z
Z
:
g
okreœlonej wzorem:
a)
m
n
m
n
g
,
,
b)
m
n
m
n
g
3
,
2
,
c)
m
n
m
m
n
g
,
,
d)
4
,
,
n
m
n
g
Dla funkcji odwracalnych znajdê funkcjê odwrotn¹.
10.Zbadaj odwracalnoœã poni¿szych funkcji dziaùaj¹cych z R w R oraz znajdê
funkcje odwrotn¹:
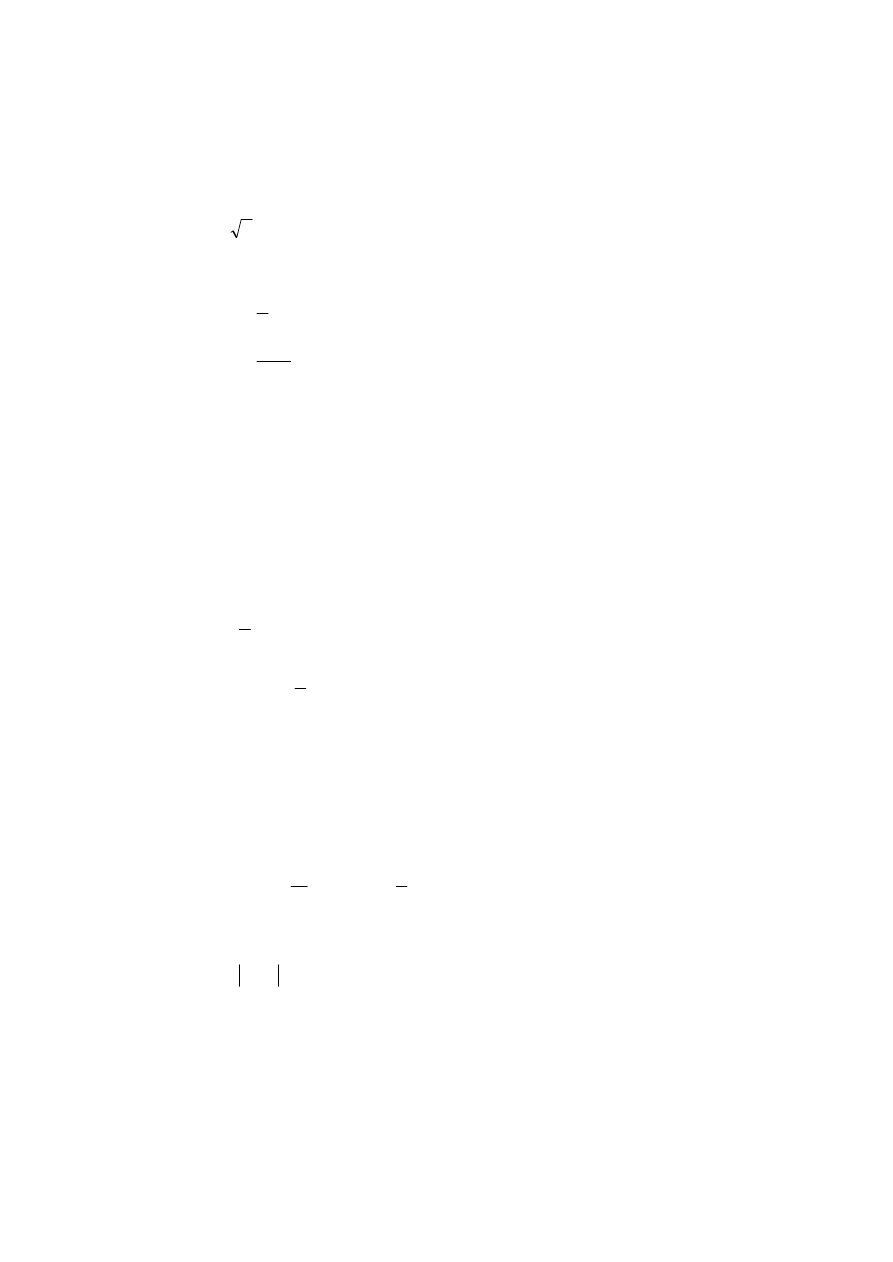
20
a)
3
2
x
x
f
b)
2
3
x
x
f
c)
3
2
x
x
f
d)
3
3
x
x
f
11.Definiujemy funkcje
N
N
:
f
oraz
N
N
:
g
w nastêpuj¹cy sposób:
n
n
f
2
,
.
2
1
.
2
nieparzyst
n
dla
n
parzyst
n
dla
n
n
g
.
Pokazaã, ¿e
N
N
g
f
oraz
f
g
.
12.Niech
2
x
x
f
. Znajdê obraz zbioru A oraz przeciwobraz zbioru B wzglêdem
f:
a)
4
,
1
,
3
,
2
B
A
,
b)
9
,
2
,
0
B
A
c)
3
,
,
3
B
A
.
13.Niech
x
x
f
1
. Znajdê obraz zbioru A oraz przeciwobraz zbioru B wzglêdem f:
a)
4
,
2
1
,
3
,
1
B
A
,
b)
9
,
2
,
0
B
A
.
14.Niech
x
x
f
2
cos
. Znajdê obraz zbioru A oraz przeciwobraz zbioru B
wzglêdem f:
a)
0
:
x
x
A
R
,
b)
n
x
n
x
A
4
3
4
:
R
,
c)
1
0
:
y
y
B
R
.
15.Niech
2
x
x
f
. Znajdê obraz zbioru A oraz przeciwobraz zbioru B
wzglêdem f:
a)
1
,
0
A
b)
2
,
0
B
c)
0
,
2
B

21
d)
6
,
2
B
16.Niech
2
2
x
x
f
. Znajdê obraz zbioru A oraz przeciwobraz zbioru B
wzglêdem f:
a)
2
,
0
A
,
b)
2
,
0
A
,
c)
2
,
0
B
d)
0
,
2
B
e)
6
,
2
B
17.Niech
2
x
x
f
oraz niech
3
,
2
A
. Znajdê f(A) oraz
A
f
f
1
.

22
Równolicznoœã zbiorów
1.
Wyka¿, ¿e przedziaùy:
a)
1
,
0
2
,
0
i
b)
d
c
i
b
a
,
,
c)
1
,
0
1
,
0
i
d)
1
,
0
1
,
0
i
s¹ równoliczne.
2.
Wyka¿, ¿e zbiór liczb naturalnych i zbiór liczb parzystych s¹ równoliczne.
3.
Wyka¿ równolicznoœã zbioru liczb naturalnych ze zbiorem liczb caùkowitych.
4.
Wyka¿ równolicznoœã zbioru liczb naturalnych podzielnych przez 6 ze zbiorem
liczb naturalnych podzielnych przez 3.
5.
*Wyka¿ równolicznoœã zbioru liczb naturalnych ze zbiorem liczb pierwszych.
6.
Wyka¿, ¿e funkcja
1
2
1
2
,
,
:
n
m
m
n
f
f
N
N
N
, odwzorowuje wzajemnie jednoznacznie zbiór
N
N
N
na
. (Zbiór liczb naturalnych bez zera)
7.
Udowodniã równolicznoœã zbioru liczb rzeczywistych z przedziaùem (0,1).
8.
Wyka¿, ¿e zbiór wszystkich trójk¹tów równobocznych na pùaszczyênie o
œrodku ciê¿koœci w pocz¹tku ukùadu wspóùrzêdnych i jednym z wierzchoùków o
wspóùrzêdnych caùkowitych jest zbiorem przeliczalnym.
9.
Zbadaj moc zbioru wszystkich kóù na pùaszczyênie, maj¹cych:
a)
Úrodek o wspóùrzêdnych wymiernych i r = 1
b)
Úrodek o wspóùrzêdnych wymiernych i
Z
k
k
r
,
2
.
10.Wyka¿, ¿e zbiór liczb wymiernych jest przeliczalny.
11.Wyka¿, ¿e zbiór A wszystkich ci¹gów o wyrazach równych 0 lub 1 jest
nieprzeliczalny.
12.*Wyka¿, ¿e zbiór liczb rzeczywistych jest nieprzeliczalny.
13.Wyka¿, ¿e zbiór liczb niewymiernych jest nieprzeliczalny.
14.Wyka¿, ¿e zbiór liczb postaci
k
n
gdzie
N
k
n,
jest przeliczalny.

23
Typy porz¹dkowe
1.
Niech
N
N
R
, i R jest relacj¹ podzielnoœci:
.
/
,
m
n
R
m
n
a)
Wykazaã, ¿e R jest relacj¹ porz¹dkuj¹c¹.
b)
Czy w zbiorze
R
,
N
jest element maksymalny.
2.
R
R
rodzina funkcji przeksztaùcaj¹cych zbiór R w R. Okreœlmy relacje
w
R
R
:
x
g
x
f
g
f
x
R
.
a)
Podaj przykùady takich funkcji, które s¹ w relacji
.
b)
Czy jest to relacja porz¹dkuj¹ca.
3.
1
,
0
1
,
0
rodzina funkcji przeksztaùcaj¹cych zbiór [0,1] w [0,1]. Okreœlmy
relacje
w
1
,
0
1
,
0
:
x
g
x
f
g
f
x
R
.
a)
Podaj przykùady takich funkcji, które s¹ w relacji
.
b)
Czy jest to relacja porz¹dkuj¹ca.
c)
Czy zbiór
,
1
,
0
1
,
0
posiada element maksymalny?
4.
Niech
x
y
xRy
/
;
1
\
1
N
N
,
a)
Czy relacja R porz¹dkuj¹ca w
1
N
?
b)
Wska¿ element maksymalny.
c)
Wska¿ element minimalny (o ile istnieje).
5.
Niech
1
,
0
,
3
,
2
,
1
B
A
, oraz niech
B
A
rodzina funkcji okreœlonych na A o
wartoœciach w wartoœciach zaœ R relacja okreœlona:
i
f
i
g
i
f
fRg
. Udowodnij i¿ relacja R porz¹dkuj¹ca. Wska¿ element
maksymalny i minimalny.
6.
Niech
7
,...,
2
,
1
X
oraz
y
x
xRy
/
2
. Udowodnij i¿ relacja R porz¹dkuj¹ca.
Wska¿ element maksymalny i minimalny.
Wyszukiwarka
Podobne podstrony:
logika zadania 1-2, logika
logika-testy, LogikaIIIgrupa2010czesc1, Zadania egzaminacyjne z logiki dla III grupy - egzaminator d
Logika formalna, logika-zadania
logika zadanie
logika-zadania, Administracja UKSW Ist, logika prawnicza
logika zadania
LOGIKA. Zadania z rozdziału VI, Studia, I ROK, I ROK, I SEMESTR, logika, LOGIKA EGZAMIN
Odpowiedzi 3-zestawy glownie 1, ☆☆♠ Nauka dla Wszystkich Prawdziwych ∑ ξ ζ ω ∏ √¼½¾haslo nauka, Logi
logika zadania, STUDIA, Analityka gospodarcza, Logika
logika-zadania (ćw 2 i 3), PRAWO - Studia, Logika
LOGIKA ZADANIA 1
odp3, ☆☆♠ Nauka dla Wszystkich Prawdziwych ∑ ξ ζ ω ∏ √¼½¾haslo nauka, Logika, zadania kolo1
LOGIKA - ZADANIA, Logika - zadania
LogikaPraktyczna - zadania, Socjologia, Logika
więcej podobnych podstron