Mateusz Stawowiak

Sprawozdanie nr 3

Charakterystyki częstotliwościowe podstawowych

obiektów dynamicznych

Interpretacja charakterystyki Nyquista:
Na podstawie przebiegu wykresu funkcji charakterystyki Nyquista możemy określić stabilność

jednowymiarowego układu zamkniętego. O stabilności mówi nam kryterium Nyquista:
a) Jeżeli układ otwarty jest stabilny to układ zamknięty jest też stabilny wtedy i tylko wtedy,

gdy wykres charakterystyki G(jω) przy wzroscie ω od 0 do ∞, nie obejmuje punktu o
współrzędnych (-1,j0).

b) Jeżeli układ otwarty nie jest stabilny i jego transmitancja ma r biegunów w prawej
półpłaszczyźnie zmiennej zespolonej to układ zamknięty jest stabilny wtedy i tylko wtedy, gdy

wykres charakterystyki G(jω) przy wzroscie ω od 0 do ∞, obejmuje punkt (-1,j0) r/2 razy.
Czasami można stosować tzw. „regułę lewej strony” - układ zamknięty jest stabilny, jeżeli przy

wzroście ω od 0 do ∞, wykres G(jω) leży po lewej stronie punktu (-1, j0)
Z wykresu charakterystyki Nyquista można odczytac także amplitudę - jako odległość danego

punktu charakterystyki od środka układu współrzędnych.
Interpretacja charakterystyk Bodego:

Wykresy Bodego to wykresy amplitudy od częstotliwości i fazy od częstotliwości. Są rysowane
w skali logarytmicznej. Pozwalają one wyznaczyć nam parametry takie jak: zapas

wzmocnienia i zapas fazy, które określają stabilność systemu, czyli mówią „jak daleko”
system znajduje się od granicy stabilności wyznaczonej przez punkt (-1,j0) (kryterium

Nyquista)
Zapas wzmocnienia (gain margin) - Gm=1/G, gdzie G jest wzmocnieniem przy

częstotliwości, dla której faza osiąga (-180

°

). Wartość ta oznacza o ile dB można zmienić

wzmocnienie zanim stracimy stabilność.

Zapas fazy (phase margin) – jest to wartość fazy dla częstotliwości, przy której wzmocnienie
wynosi 1 (0dB). Mów nam to, o ile stopni można zmniejszyć przesunięcie fazowe zanim

utracimy stabilność systemu.

Oznaczenia stosowane w sprawozdaniu:
M(f) – wzmocnienie (amplituda) od częstotliwości

P(f) – faza od częstotliwości
Rozwiązanie zadań wraz z kodem źródłowym w Matlabie:

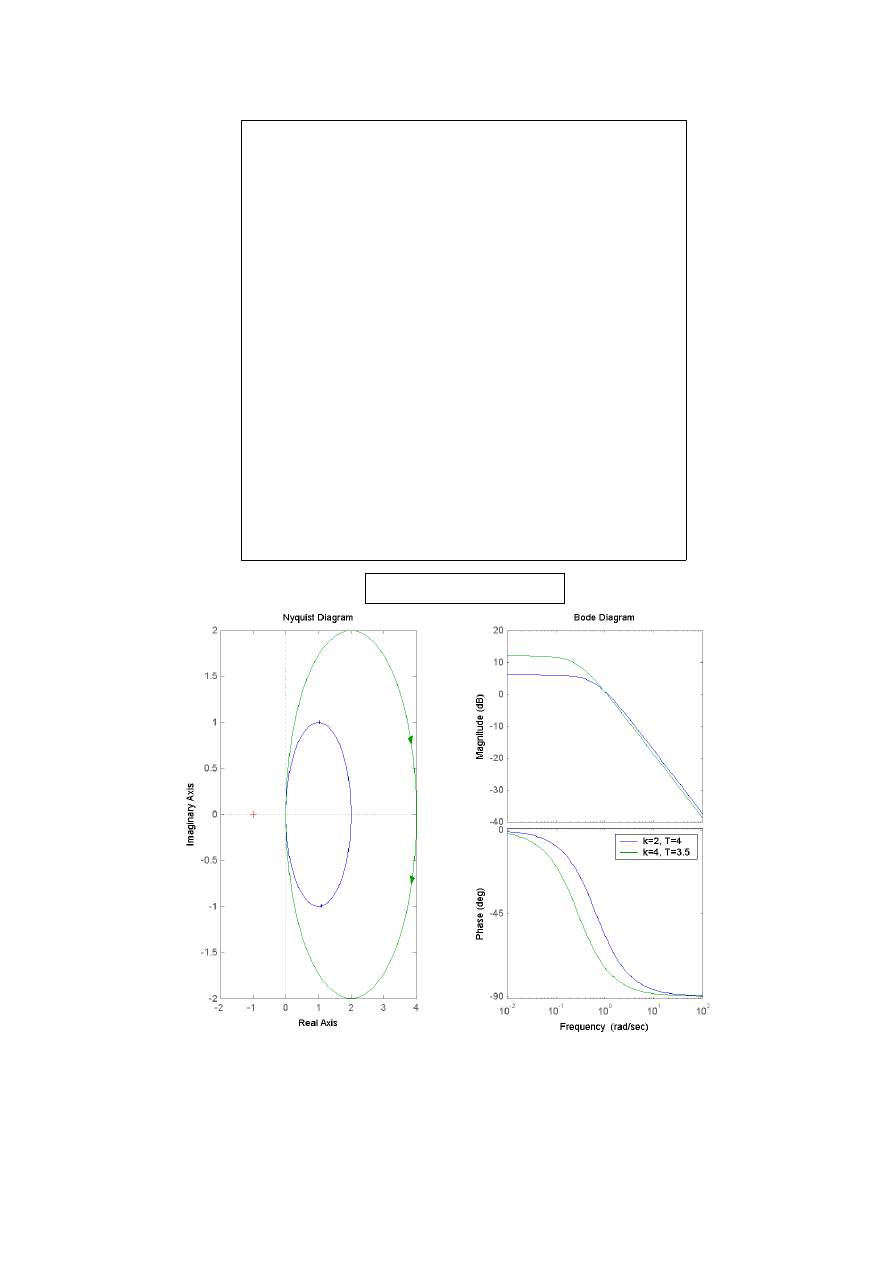
1. Obiekt inercyjny 1 rzędu

Zmiana parametru k nie wpływa na wykres P(f), ale wpływa na wygląd wykresu M(f), zgodnie z

zależnością: M(f_0)=20log_10(k). Parametr T ma wpływ na dynamikę wykresów. Im wartość
ta jest większa tym wykresy stają sie łagodniejsze. Wykres Nyquista jest elipsą o

promieniach: k i k/2, parametr T nie ma wpływu na wygląd charakterystyki Nyquista.

%Wartosci parametrów dla konkretnego obiektu:

k = [2 4];

T = [1.5 3.5];

%zapisanie liczniki i mianownika transmitancji

licz_1 = [0 k(1)];

mian_1 = [T(1) 1];

licz_2 = [0 k(2)];

mian_2 = [T(2) 1];

%Rysowanie charakterystyk cz stotliwo ciowych

ę

ś

figure(1);

subplot(1,2,1);

hold on;

nyquist(licz_1,mian_1);

nyquist(licz_2,mian_2);

subplot(1,2,2);

hold on;

bode(licz_1,mian_1);

bode(licz_2,mian_2);

legend('k=2, T=1.5','k=4, T=3.5',1);

Obiekt inercyjny 1 rzędu

2. Obiekt inercyjny 2 rzędu

System zachowuje się analogicznie jak w przypadku układu inercyjnego I rzędu: parametr k

nie wpływa na wykres P(f), ale wpływa na wygląd wykresu M(f), zgodnie z zależnością:
M(f_0)=20log_10(k). Natomiast parametry T1 i T2 wpływają na dynamikę wszystkich

wykresów. Im parametry te są mniejsze wykresy Bodego robią sie stromsze, a spirale na
wykresie Nyqusita szybciej zbiegają do 0.

%Wartosci parametrów dla konkretnego obiektu:

k = [2.5 1.8];

T1 = [3.8 2];

T2= [3.2 0.8];

%zapisanie liczniki i mianownika transmitancji

licz_1 = [0 0 k(1)];

mian_1 = [T1(1)*T2(1) T1(1)+T2(1) 1];

licz_2 = [0 0 k(2)];

mian_2 = [T1(2)*T2(2) T1(2)+T2(2) 1];

%Rysowanie charakterystyk cz stotliwo ciowych

ę

ś

figure(2);

subplot(1,2,1);

hold on;

nyquist(licz_1,mian_1);

nyquist(licz_2,mian_2);

subplot(1,2,2);

hold on;

bode(licz_1,mian_1);

bode(licz_2,mian_2);

legend('k=2.5, T1=3.8, T2=3.2','k=1.8, T1=2, T2=0.8',1);

Obiekt inercyjny 2 rzędu

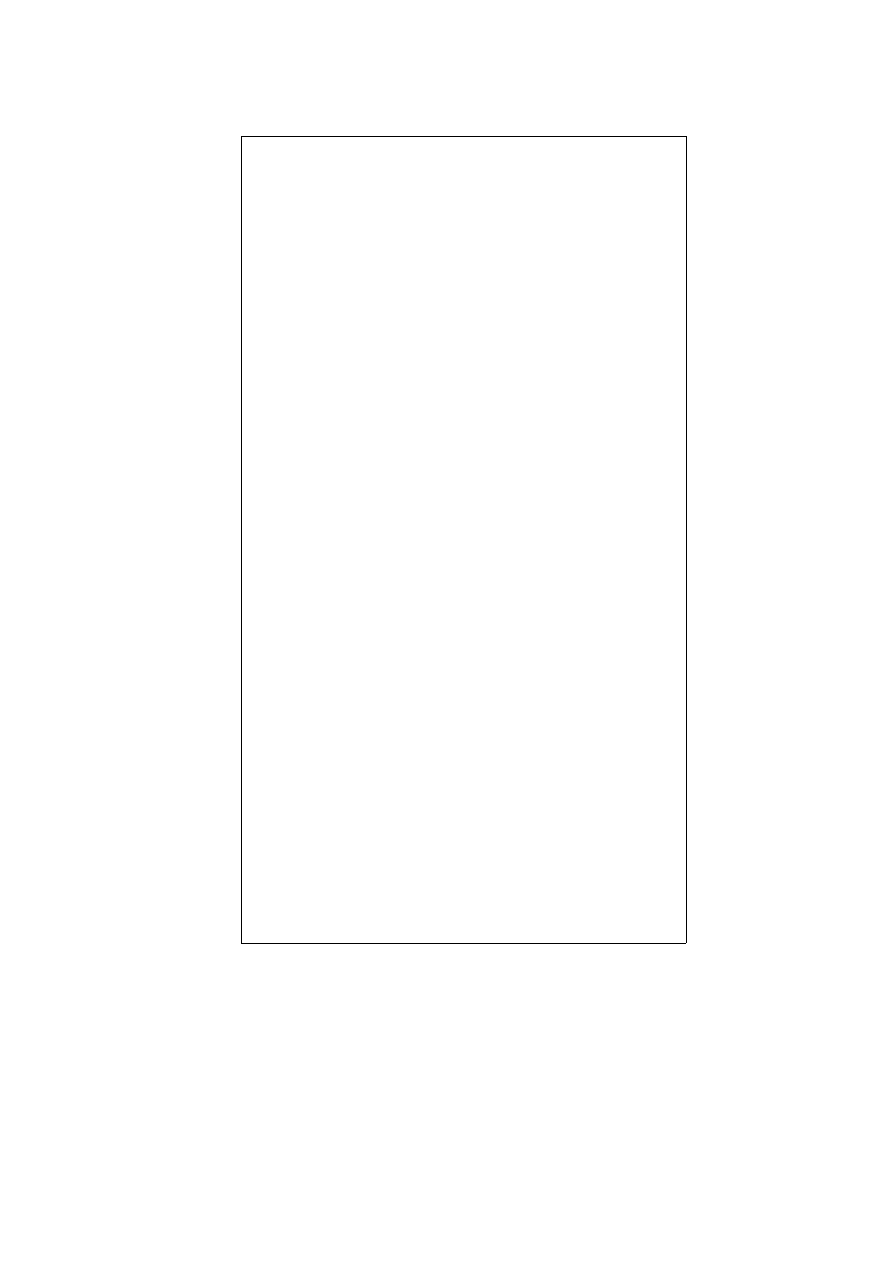
3. Obiekt oscylacyjny 2 rzędu

%Wartosci parametrów dla konkretnego obiektu:

k = [1.2 2];

T = [4 1];

ksi = [3.6 0.1];

%zapisanie liczniki i mianownika transmitancji

licz_1 = [0 0 k(1)];

mian_1 = [T(1)^2 2*ksi(1)*T(1) 1];

licz_2 = [0 0 k(2)];

mian_2 = [T(2)^2 2*ksi(1)*T(2) 1];

licz_3 = [0 0 k(1)];

mian_3 = [T(1)^2 2*ksi(2)*T(1) 1];

licz_4 = [0 0 k(2)];

mian_4 = [T(2)^2 2*ksi(2)*T(2) 1];

%Rysowanie charakterystyk cz stotliwo ciowych

ę

ś

figure(3);

subplot(1,2,1);

hold on;

nyquist(licz_1,mian_1);

nyquist(licz_2,mian_2);

subplot(1,2,2);

hold on;

bode(licz_1,mian_1);

bode(licz_2,mian_2);

legend('k=1.2, T=4, ksi=3.6','k=2, T=1, ksi=3.6',1);

figure(4);

subplot(1,2,1);

hold on;

nyquist(licz_3,mian_3);

nyquist(licz_4,mian_4);

subplot(1,2,2);

hold on;

bode(licz_3,mian_3);

bode(licz_4,mian_4);

legend('k=1.2, T=4, ksi=0.1','k=2, T=1, ksi=0.1',1);

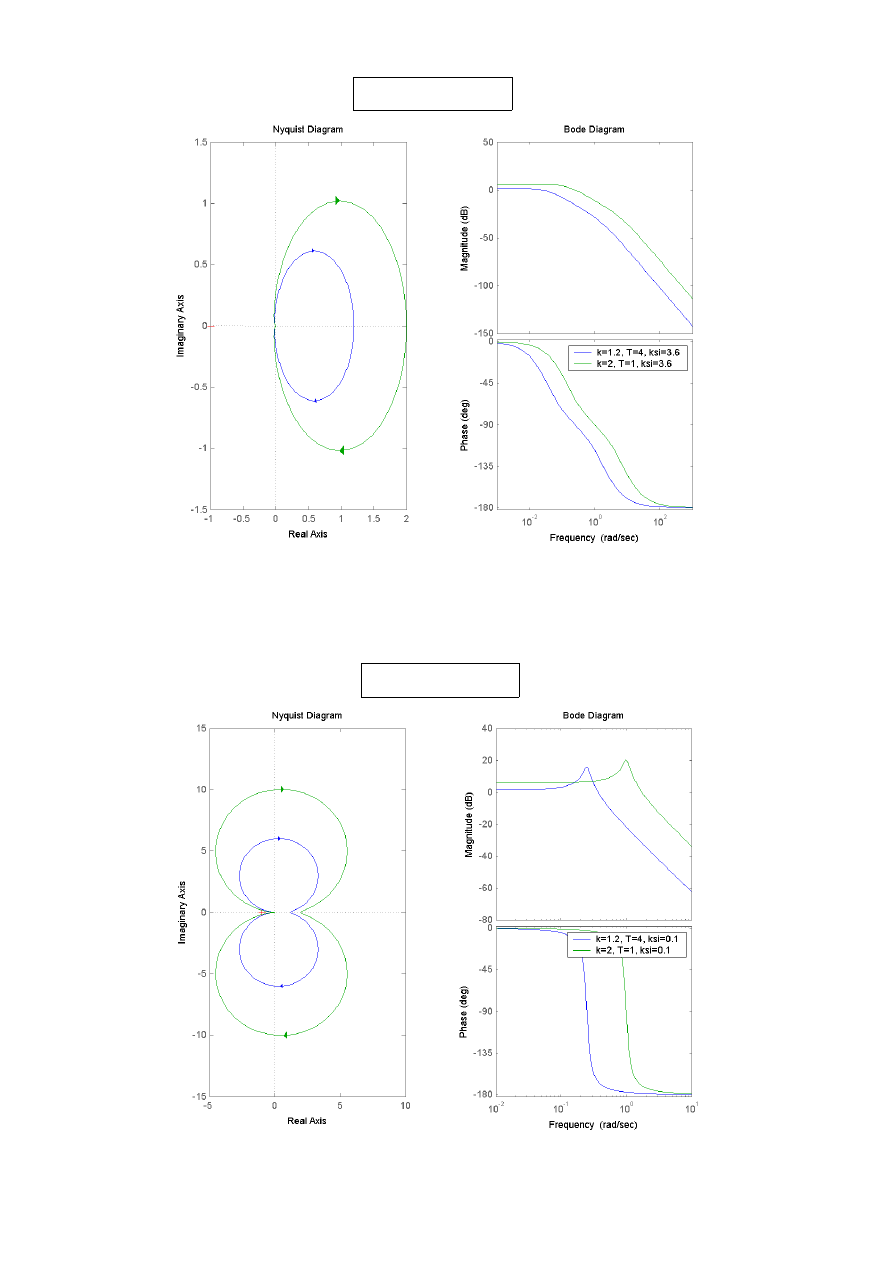
Wykresy dla ksi > 1

Wykresy dla ksi < 1

Dla ksi > 1

Parametr k nie wpływa na wykres P(f), ale wpływa na wygląd wykresu M(f), zgodnie z

zależnością: M(f_0)=20log_10(k). Zwiększenie wartości T powoduje, że wykresy Bodego przy
mniejszych częstotliwościach zaczynają zmniejszać swoje wartości. Choć dla wykresu P(f)

wartości w początkowym i końcowym punkcie, dla różnych T jest taka sama. Wykres Nyquista
jest elipsą o promieniach: k i k/2, parametr T nie ma wpływu na wygląd charakterystyki

Nyquista. Im większa jest wartość parametru ksi, tym wykres Nyquista coraz mnieje
przechodzi na lewą półpłaszczyznę zespoloną, dla P(f) powoduje, że na wykresie pojawiają się

punkty przegięcia (brak jednostajnego opadania).

Dla ksi < 1

Parametr k nie wpływa na wykres P(f), ale wpływa na wartość początkową M(f). Im wartość k
jest większa okręgi tworzące wykres Nyquista są większe. Wartość T ma taki sam wpływ na

P(f) i wykres Nyquista jak w przypadku dla (ksi>1). Na wykresie M(f) widoczny jest
charakterystyczny „pik”, którego odcięta jest równa 1/T. Im ksi jest mniejsze tym „pik” staje

sie wyrazniejszy, wykres P(f) staje sie na pewnym odcinku bardzo stromy (prawie pionowy), a
kształt wykresy Nyquista coraz bardziej przypomina okręgi.

4. Obiekt całkujący z inercją 1 rzędu

Wartość parametru k nie wpływa na wykres P(f), ale wpływa na wartość początkową M(f).

Zwiekszenie parametru T powoduje, że M(f) w środkowej części zaczyna szybciej opadać. A
P(f) szybciej się zmniejsza już od czestotliwości początkowej. Wartość T_i nie wpływa na

wykres P(f), a dla wykresu M(f) dla większych wartości parametru T_i wartość dla f_0 jest
mniejsza. Im wartość k jest większa tym hiperpole tworzące wykres Nyquista są bardziej

rozciągnięte wzdłuż osi rzeczywistej. Taki sam wpływ ma zwiększenie wartości T, a także
zmniejszanie wartosci parametru T_i.

%Wartosci parametrów dla konkretnego obiektu:

k = [2.2 5.2];

T = [0.5 3.5];

Ti = [0.6 2];

%zapisanie liczniki i mianownika transmitancji

licz_1 = [0 0 k(1)];

mian_1 = [T(1)*Ti(1) Ti(1) 0];

licz_2 = [0 0 k(2)];

mian_2 = [T(2)*Ti(2) Ti(2) 0];

%Rysowanie charakterystyk cz stotliwo ciowych

ę

ś

figure(5);

subplot(1,2,1);

hold on;

nyquist(licz_1,mian_1);

nyquist(licz_2,mian_2);

subplot(1,2,2);

hold on;

bode(licz_1,mian_1);

bode(licz_2,mian_2);

legend('k=2.2, T=0.5, Ti=0.6','k=5.2, T=3.5, Ti=2',1);

5. Obiekt różniczkujący rzeczywisty

Obiekt całkujący z inercją 1 rzędu

%Wartosci parametrów dla konkretnego obiektu:

T = [1.6 3.4];

Td = [2.8 1.8];

%zapisanie liczniki i mianownika transmitancji

licz_1 = [Td(1) 0];

mian_1 = [T(1) 1];

licz_2 = [Td(2) 0];

mian_2 = [T(2) 1];

%Rysowanie charakterystyk cz stotliwo ciowych

ę

ś

figure(6);

subplot(1,2,1);

hold on;

nyquist(licz_1,mian_1);

nyquist(licz_2,mian_2);

subplot(1,2,2);

hold on;

bode(licz_1,mian_1);

bode(licz_2,mian_2);

legend('T=1.6, Td=2.8','T=3.4, Td=1.8',1);

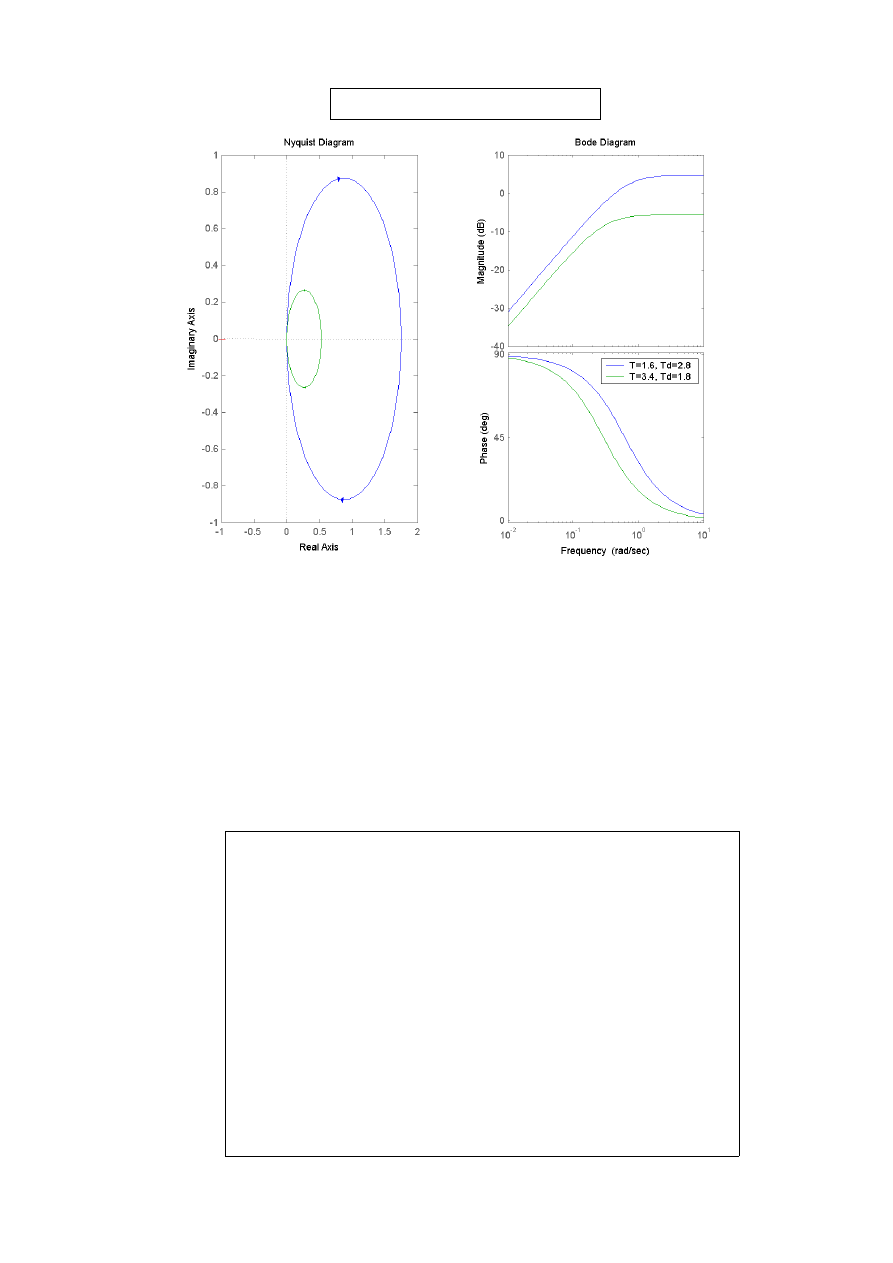
Zwiększenie wartości T powoduje, że wykres P(f) przy mniejszych częstotliwościach zaczyna
zmniejszać swoje wartości, wartości w początkowym i końcowym punkcie, dla różnych T są

takie same. Wykresy M(f) dla różnych T startuja z tego samego miejsca, lecz dla większych
wartości argumentów (częstotliwości) im T jest większe tym wcześniej i dla mniejszej wartości

amplituda utrzymuje tą samą wartość. Parametr Td nie ma wpływu na wykres P(f), dla M(f)
ma taki sam kształt lecz startuje z różnych wartości. Dla wykresu Nyquista im większa wartość

Td tym elipsy są większe.

6. Obiekt inercyjny 1 rzędu z opóźnieniem

%Wartosci parametrów dla konkretnego obiektu:

k = [1.4 1.8];

T = [4 2];

theta = [2 8];

%zapisanie liczniki i mianownika transmitancji

[licz_op_1 mian_op_1] = pade(theta(1), 4);

licz_iner_1 = [0 k(1)];

mian_iner_1 = [T(1) 1];

[licz_1 mian_1] = series(licz_op_1, mian_op_1, licz_iner_1, mian_iner_1);

[licz_op_2 mian_op_2] = pade(theta(2), 4);

licz_iner_2 = [0 k(2)];

mian_iner_2 = [T(2) 1];

[licz_2 mian_2] = series(licz_op_2, mian_op_2, licz_iner_2, mian_iner_2);

Obiekt różniczkujący rzeczywisty

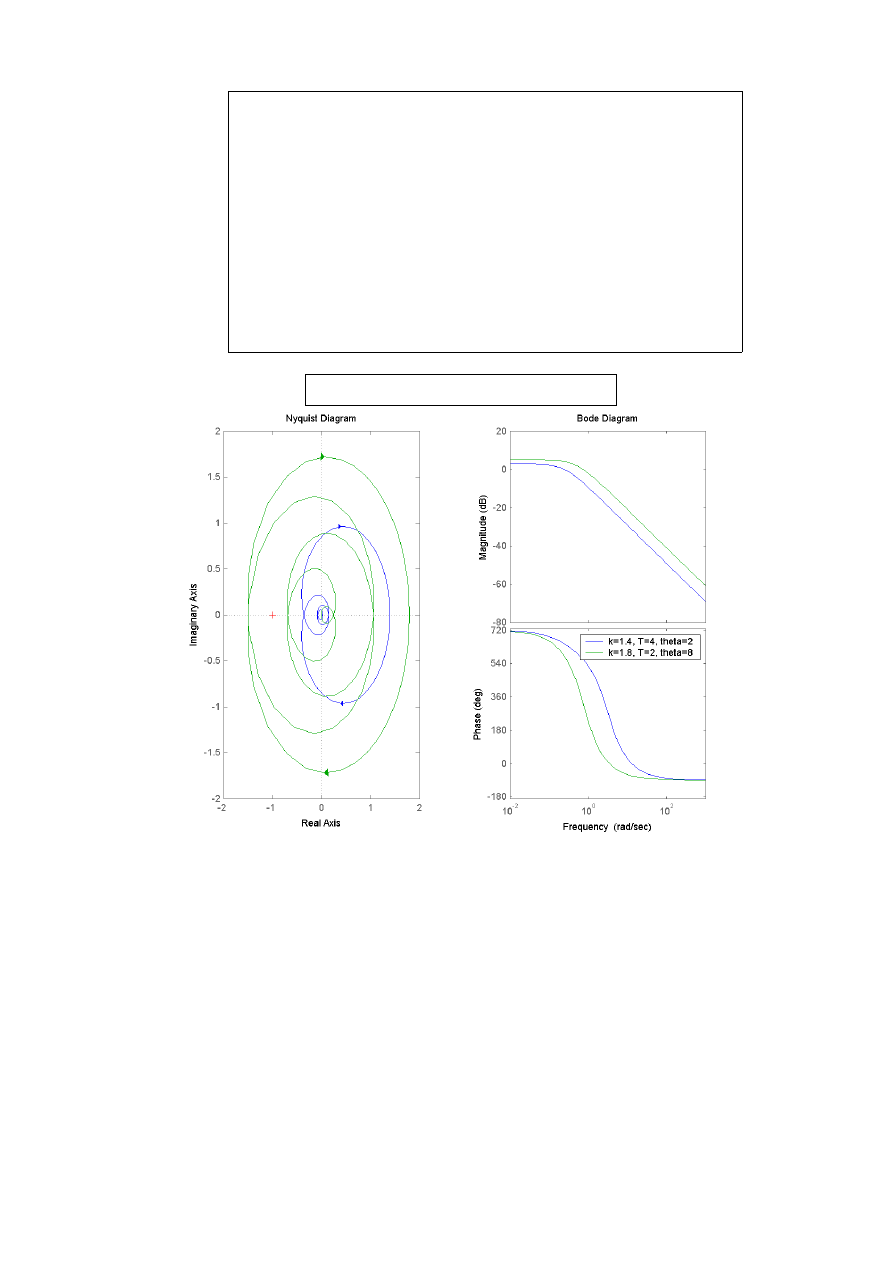
Im wartość parametru theta jest mniejsza, tym wykres Nyquista, który jest spiralą szybciej

zbiega do 0. Dla M(f) wartość ta praktycznie nie ma wpływu, wykresy różnią się nieznacznie.
Im theta jest mniejsza to wykres P(f) przy mniejszych częstotliwościach zaczyna zmniejszać

swoje wartości, wartości w początkowym i końcowym punkcie, dla różnych theta są takie
same. Parametr k ma taki sam wpływ na wykresy jak we wczesniejszych przypadkach. Im

wartość T jest większa tym wykres Nyquista szybciej zbiega do 0. Wykresy P(f) dla różnych T
są niemal identyczne. A wykres M(f) dla większych T zaczyna szybciej opadać.

%Rysowanie charakterystyk cz stotliwo ciowych

ę

ś

figure(7);

subplot(1,2,1);

hold on;

nyquist(licz_1,mian_1);

nyquist(licz_2,mian_2);

subplot(1,2,2);

hold on;

bode(licz_1,mian_1);

bode(licz_2,mian_2);

legend('k=1.4, T=4, theta=2','k=1.8, T=2, theta=8',1);

Obiekt inercyjny 1 rzędu z opóźnieniem