1

Szczególna Teoria Względności

Załó

ż

my,

ż

e pr

ę

dko

ść

ś

wiatła jest stała

wzgl

ę

dem eteru. Jaka jest wi

ę

c pr

ę

dko

ść

Ziemi wzgl

ę

dem eteru ?

Do

ś

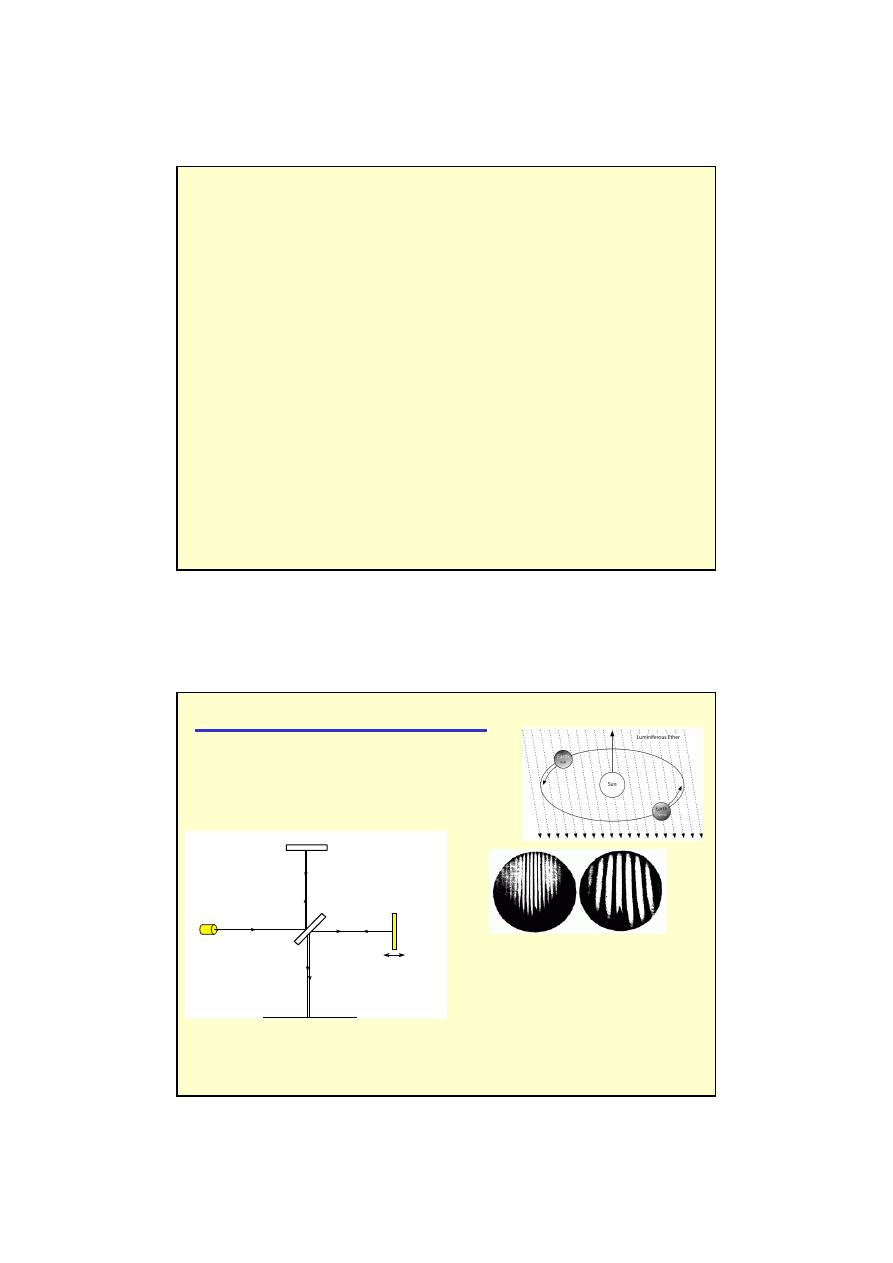
wiadczenie Michelsona i Morleya (1881 i 1887)

1) Załó

ż

my,

ż

e na ekranie obserwujemy maksimum

interferencyjne (pr

ąż

ki). Je

ś

li przesuniemy

zwierciadło ruchome o ¼ długo

ś

ci fali ( ¼

λ

) w

prawo, to promie

ń

2 przejdzie dodatkowo drog

ę

½

λ

i oba promienie na ekranie wygasz

ą

si

ę

w miejscach

gdzie si

ę

wzmacniały (maksima przejd

ą

w minima i

odwrotnie).
2) Zakłócenie ustawionego maksimum
interferencyjnego mo

ż

na by tak

ż

e uzyska

ć

, gdyby

pr

ę

dko

ś

ci

ś

wiatła w ramieniu 1 lub 2 ulegały

zmianie.

zwierciadło
półprzepuszczalne

zwier ciadło

ź

ródło światła

1

2

zwierciadło
ruchome

ekran

Zasada budowy interferometru Michelsona. Zwierciadło
„2” można przesuwać i w ten sposób doprowadzać do
powstawania kolejnych maksimów i minimów
interferencyjnych.

Kinematyka relatywistyczna

2

zwierciadło
półprzepuszczalne

zwierciadło

ź

ródło światła

1

2

zwierciadło

ekran

A

l

0

l

0

B

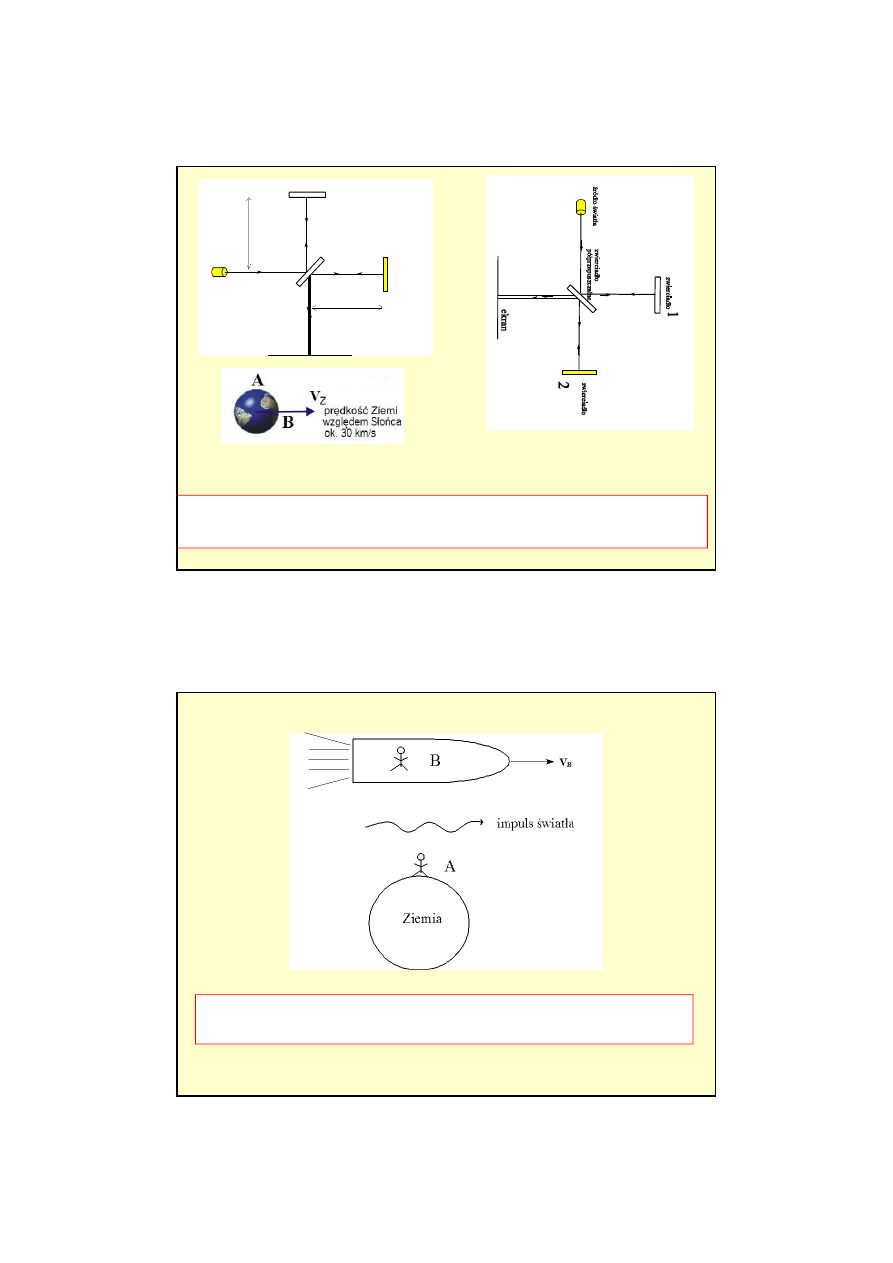
Je

ż

eli obrócimy interferometr o 90

0

,

obydwa lustra S

1

i S

2

zamieni

ą

si

ę

rolami,

a wi

ę

c:

Po obróceniu ramion pr

ąż

ki interferencyjne si

ę

przesun

ą

. Z przesuni

ę

cia tego mo

ż

na

wyznaczy

ć

v

Z

.

Do

ś

wiadczenie pokazało,

ż

e

v

Z

=0

(z dokł. 5 km/s) czyli albo Ziemia si

ę

nie

porusza (wzgl. eteru) albo pr

ę

dko

ść

ś

wiatła jest stała w ka

ż

dym układzie inercjalnym.

Zmierzona pr

ę

dko

ść

ś

wiatła jest taka sama w ka

ż

dym

układzie inercjalnym (np. dla obserwatora A oraz B) !!!

3

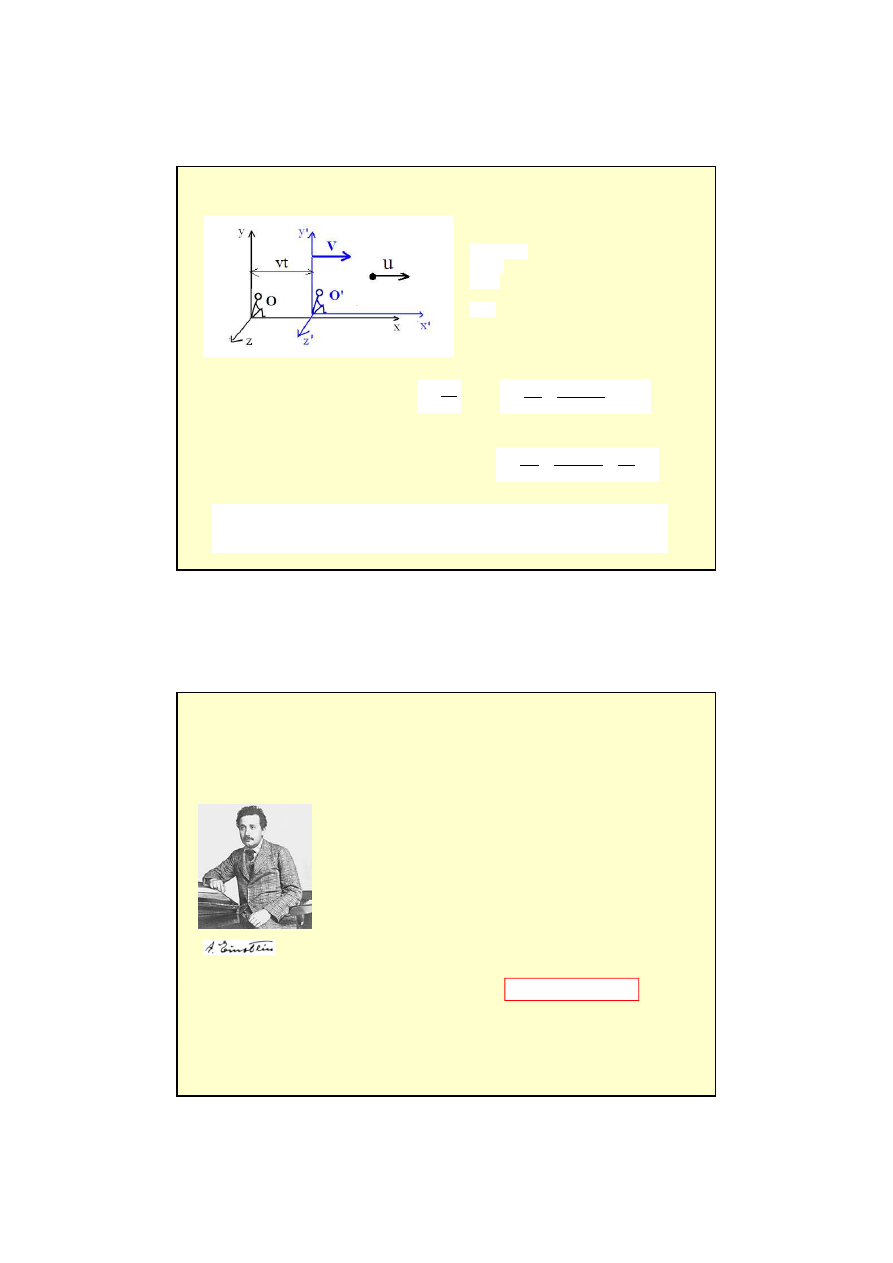
Vt

x

x

−

=

'

y

y

=

'

z

z

=

'

t

t

=

'

t

x

u

∆

∆

=

V

u

t

t

V

x

t

x

u

−

=

∆

∆

−

∆

=

∆

∆

=

'

'

'

składanie pr

ę

dko

ś

ci

a

t

u

t

V

u

t

u

a

=

∆

∆

=

∆

−

∆

=

∆

∆

=

)

(

'

'

'

przyspieszenie w układzie
poruszaj

ą

cym si

ę

Ta transformacja zastosowana do równa

ń

Maxwella nie daje tych samych wyników

dla omawianych układów inercjalnych.
Pr

ę

dko

ść

ś

wiatła nie jest stała dla transformacji Galileusza.

Transformacja Galileusza

Postulat II:

Pr

ę

dko

ść

ś

wiatła w pró

ż

ni jest jednakowa we

wszystkich kierunkach i w dowolnym obszarze danego inercjalnego
układu odniesienia i jednakowa dla wszystkich inercjalnych układów
odniesienia.

Postulat I

(zasada wzgl

ę

dno

ś

ci):

Wszystkie to

ż

same zjawiska fizyczne przebiegaj

ą

, przy

identycznych warunkach pocz

ą

tkowych, jednakowo w inercjalnych

układach odniesienia.
Inaczej mówi

ą

c, w

ś

ród IUO nie ma układu „uprzywilejowanego„

i stwierdzenie stanu absolutnego ruchu nie jest mo

ż

liwe.

c = 299 792 458 m/s

Postulaty szczególnej teorii wzgl

ę

dno

ś

ci szczególnej teorii wzgl

ę

dno

ś

ci,

Albert Einstein 1905.

4

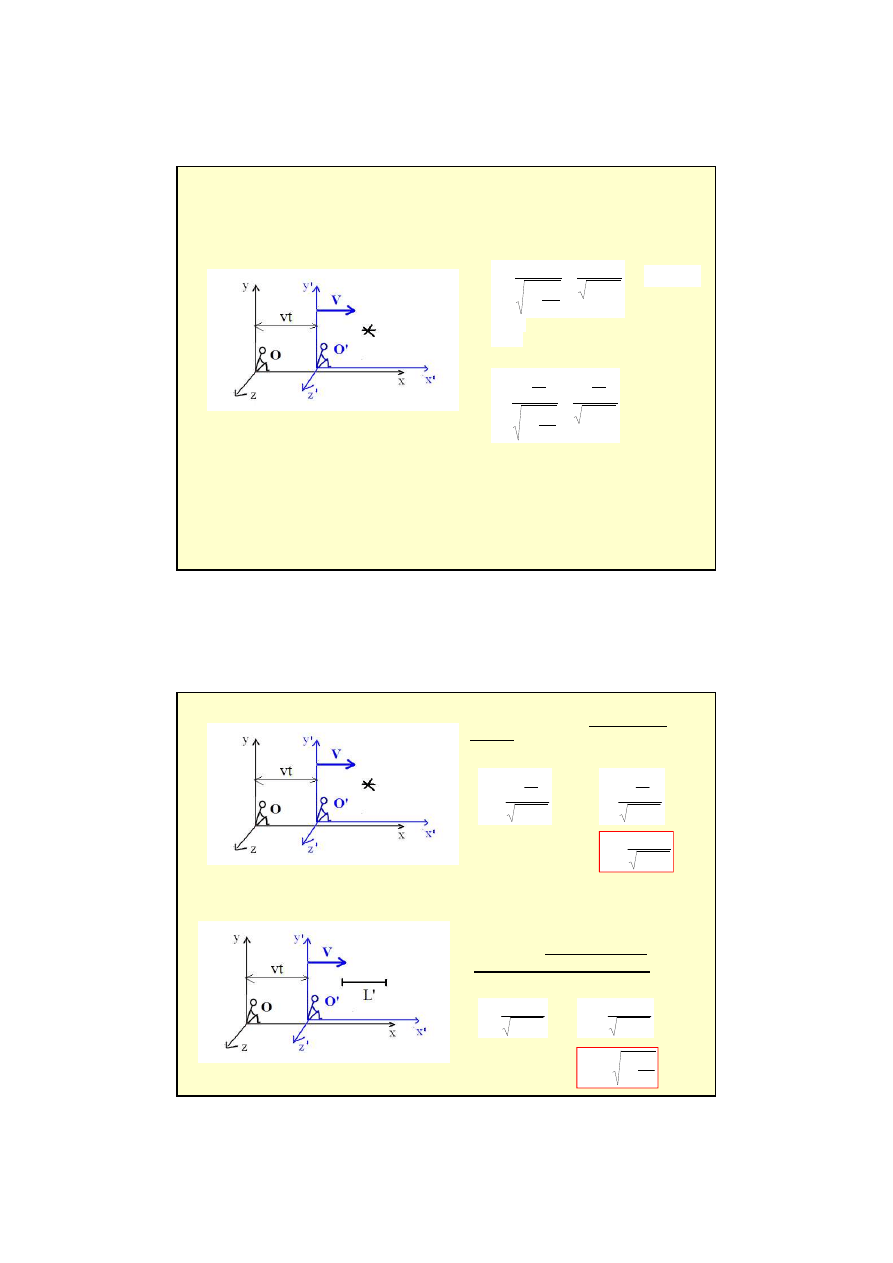
Szukamy transformacji współrz

ę

dnych, która uwzgl

ę

dnia niezale

ż

no

ść

pr

ę

dko

ś

ci

ś

wiatła od układu odniesienia.

2

2

2

1

1

'

β

−

−

=

−

−

=

Vt

x

c

V

Vt

x

x

y

y

=

'

z

z

=

'

2

2

2

2

2

1

1

'

β

−

−

=

−

−

=

x

c

V

t

c

V

x

c

V

t

t

β = V/c

Własno

ś

ci czasoprzestrzeni s

ą

inne ni

ż

przewiduje to transformacja Galileusza.

Dla

β

<< 1

otrzymujemy transformacj

ę

Galileusza.

Transformacja Lorentza

... czy dylatacja czasu i kontrakcja długo

ś

ci wynikaj

ą

z transformacji Lorentza???

Dwa zdarzenia zaszły w tym samym
miejscu

w układzie poruszaj

ą

cym

si

ę

(O’), w odst

ę

pie czasu .

Dylatacja czasu

0

'

=

∆

x

2

1

'

β

−

∆

=

∆

t

t

0

'

=

∆

x

0

'

≠

∆

t

0

'

≠

∆

t

2

2

1

'

β

−

−

==

x

c

V

t

t

2

2

1

'

'

β

−

+

=

x

c

V

t

t

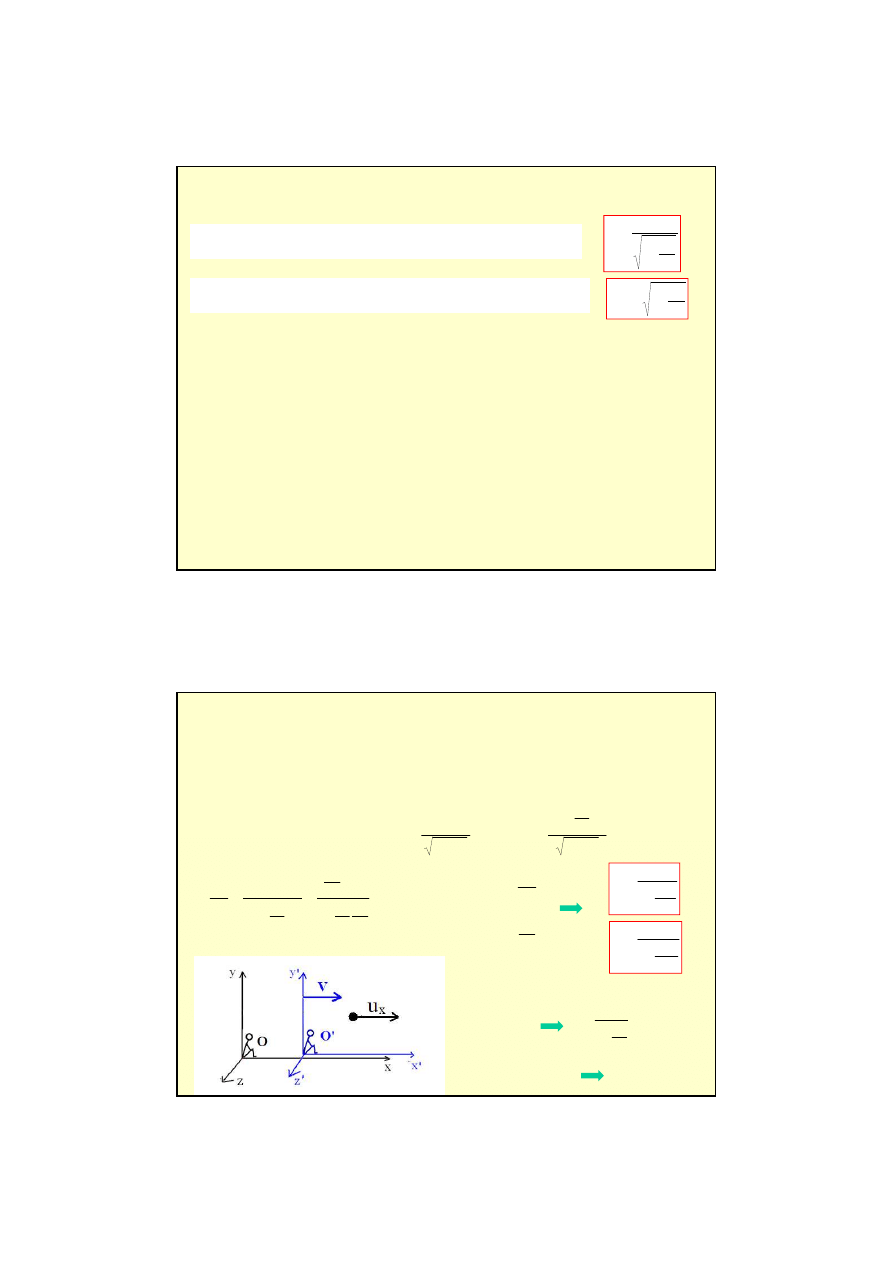
Pr

ę

t o długo

ś

ci (wzgl

ę

dem O’)

porusza si

ę

z pr

ę

dko

ś

ci

ą

V wzgl

ę

dem O.

Mierzymy długo

ść

w układzie O,

wyznaczaj

ą

c w tej samej chwili

współrz

ę

dne ko

ń

ca i pocz

ą

tku.

2

1

'

β

−

∆

=

∆

x

x

Skrócenie długo

ś

ci

2

2

1

'

c

V

L

L

−

=

'

'

L

x

=

∆

0

=

∆

t

2

1

'

β

−

−

=

Vt

x

x

L

x

=

∆

0

=

∆

t

5

Potwierdzenie dylatacji czasu i kontrakcji długo

ś

ci

2

2

1

'

c

V

t

t

−

∆

=

∆

1) Ka

ż

dy obserwator stwierdza,

ż

e poruszaj

ą

cy si

ę

zegar idzie wolniej

ni

ż

identyczny zegar w spoczynku (

dylatacja

czasu).

2

2

1

'

c

V

L

L

−

=

2) Ka

ż

dy obserwator stwierdza,

ż

e poruszaj

ą

cy si

ę

przedmiot jest krótszy

ni

ż

identyczny przedmiot w spoczynku (

kontrakcja

długo

ś

ci).

... a jak wygl

ą

da transformacja współrz

ę

dnych mi

ę

dzy układami inercjalnymi???

Dowody do

ś

wiadczalne

Miony docieraj

ą

do Ziemi cho

ć

maj

ą

zbyt krótki czas

ż

ycia (2 ms ).

W układzie zwi

ą

zanym z Ziemi

ą

jest to spowodowane dylatacj

ą

czasu (ich czas

ż

ycia

w układzie zwiazanym z Ziemi

ą

jest 30 razy dłu

ż

szy poniewa

ż

poruszaj

ą

si

ę

one z

pr

ę

dko

ś

ci

ą

99,3% pr

ę

dko

ś

ci

ś

wiatła).

Patrz

ą

c z układu odniesienia poruszaj

ą

cej si

ę

cz

ą

stki, atmosfera

Ziemi porusza si

ę

z pr

ę

dko

ś

ci

ą

ok. 99,3% pr

ę

dko

ś

ci

ś

wiatła wzgl

ę

dem spoczywaj

ą

cej

cz

ą

stki i tym samym, ze wzgl

ę

du na skrócenie długo

ś

ci, jest 30 razy cie

ń

sz

ą

warstw

ą

.

W ci

ą

gu 2 ms (czas

ż

ycia mionu) cała atmosfera zd

ąż

y przesun

ąć

si

ę

wzgl

ę

dem

cz

ą

stki i powierzchnia Ziemi dotrze do mionu.

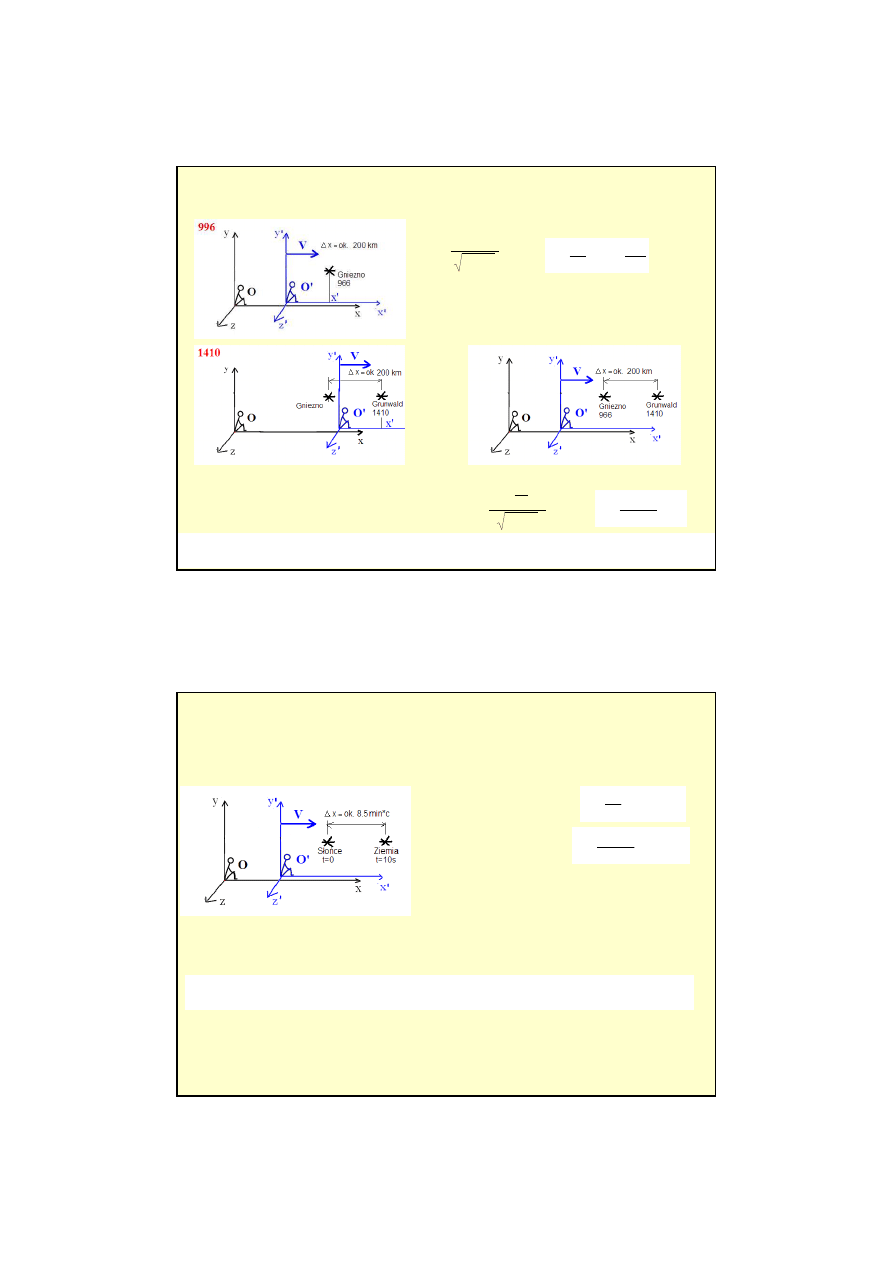
Obiekt ma pr

ę

dko

ść

u

x

'

w ruchomym układzie odniesienia (np. wzgl

ę

dem rakiety).

Jak

ą

pr

ę

dko

ść

u

x

zarejestruje nieruchomy obserwator, w układzie którego rakieta

porusza si

ę

z pr

ę

dko

ś

ci

ą

V

wzdłu

ż

osi

x

.

Z transformacji Lorentza:

2

1

'

β

−

∆

−

∆

=

∆

t

V

x

x

2

2

1

'

β

−

∆

−

∆

=

∆

x

c

V

t

t

t

x

c

V

V

t

x

x

c

V

t

t

V

x

t

x

∆

∆

−

−

∆

∆

=

∆

−

∆

∆

−

∆

=

∆

∆

2

2

1

'

'

'

'

'

t

x

u

x

∆

∆

=

t

x

u

x

∆

∆

=

Poniewa

ż

:

2

1

'

c

Vu

V

u

u

x

x

x

−

−

=

2

'

1

'

c

Vu

V

u

u

x

x

x

+

+

=

β = V/c

Składanie pr

ę

dko

ś

ci w transformacji Lorentza

dla u

x

= c

c

c

Vc

V

c

c

=

−

−

=

2

1

'

V =0.9c, u

x

’ = 0.9c

u

x

= 0.994c

Przykłady:

1)

2)

6

Zwi

ą

zek przyczynowo skutkowy a jednoczesno

ść

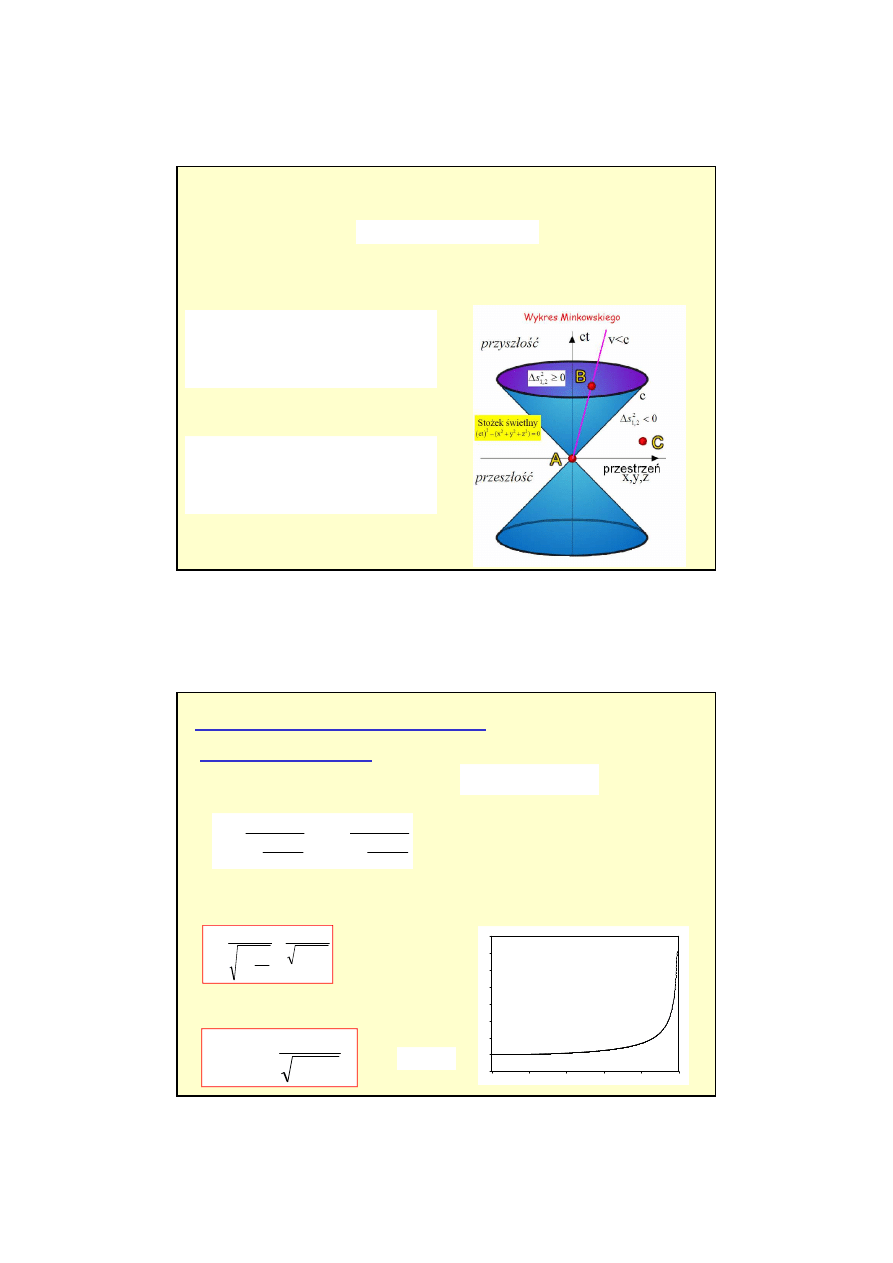
1) Czy istnieje układ, w którym bitwa pod Grunwaldem i chrzest Polski zaszły:

a) w tym samym miejscu:

rok

km

t

x

V

45

.

0

≈

∆

∆

=

0

1

'

2

=

−

∆

−

∆

=

∆

β

t

V

x

x

b) tym samym czasie:

0

1

'

2

2

=

−

∆

−

∆

=

∆

β

x

c

V

t

t

c

t

x

c

V

>>

∆

∆

=

/

2

Zdarzenia zajd

ą

w tym samym miejscu w układzie poruszaj

ą

cym si

ę

z pr

ę

dko

ś

ci

ą

ok. 0.45km/rok, z

Gniezna do Grunwaldu. Nie istnieje układ, w którym te zdarzenia s

ą

jednoczesne.

β = V/c

2) Po 10s od zaj

ś

cia protuberancji na Sło

ń

cu, na Ziemi wybuchł wulkan. Czy istnieje układ w

którym te zdarzenia zaszły:

a) w tym samym miejscu:

c

c

t

x

V

>

≈

∆

∆

=

*

51

b) tym samym czasie :

c

t

x

c

V

*

02

.

0

/

2

≈

∆

∆

=

Zdarzenia zajd

ą

w tym samym czasie w układzie poruszaj

ą

cym si

ę

z pr

ę

dko

ś

ci

ą

ok. 0.02*c.

Nie istnieje układ, w którym te zdarzenia zajd

ą

w tym samym miejscu.

7

Wielko

ść

fizyczna opisuj

ą

ca odległo

ść

mi

ę

dzy dwoma zdarzeniami nazywa si

ę

interwałem

zdefiniowanym nast

ę

puj

ą

co:

(

)

2

2

2

2

2

2

2

,

1

z

y

x

t

c

s

∆

+

∆

+

∆

−

∆

=

∆

Mo

ż

na wykaza

ć

,

ż

e interwał jest niezmiennikiem wzgl

ę

dem transformacji Lorentza, tzn. ma

tak

ą

sam

ą

warto

ść

w ka

ż

dym inercjalnym układzie odniesienia:

2

2

,

1

2

2

,

1

'

s

s

∆

=

∆

2

,

1

s

∆

1) Je

ś

li istnieje układ, w którym zdarzenia

zajd

ą

w tym samym miejscu to mo

ż

e istnie

ć

miedzy nimi zwi

ą

zek przyczynowy (te

zdarzenia nie mog

ą

by

ć

jednoczesne w

ż

adnym układzie). Wtedy :

0

2

2

,

1

≥

∆

s

2) Je

ś

li istnieje układ, w którym zdarzenia

zajd

ą

w tym samym czasie to nie mo

ż

e

istnie

ć

miedzy nimi zwi

ą

zek przyczynowy

(nie istnieje układ, w którym zdarzenia zajd

ą

w tym samym miejscu ). Wtedy :

0

2

2

,

1

<

∆

s

Geometria czasoprzestrzeni

DYNAMIKA RELATYWISTYCZNA

Pęd i masa relatywistyczna

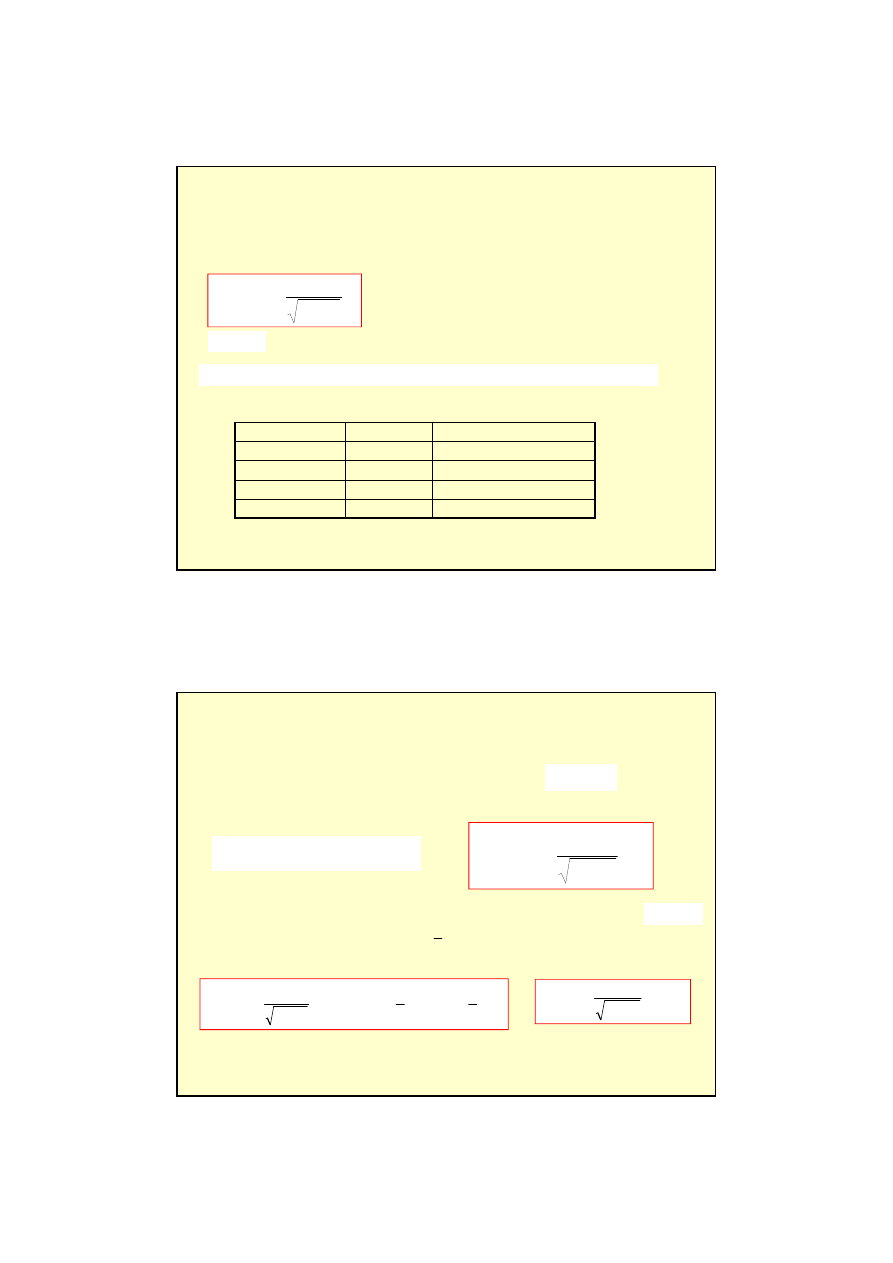
Je

ś

li ma pozosta

ć

słuszna zasada zachowania p

ę

du

, to masa ciała nie mo

ż

e

by

ć

wielko

ś

ci

ą

stał

ą

; musi ona zale

ż

e

ć

od pr

ę

dko

ś

ci wg. wzoru:

γ=

m/m

0

v/c

0.0

0.2

0.4

0.6

0.8

1.0

0

1

2

3

4

5

6

7

8

2

0

2

2

0

1

1

β

−

=

−

=

m

c

u

m

m

Sprawd

ź

my czy zasada zachowania p

ę

du:

∑

∑

=

i

i

xkonc

i

i

i

xpocz

i

u

m

u

m

,

,

obowi

ą

zuje

w układzie poruszaj

ą

cym si

ę

z pr

ę

dko

ś

ci

ą

V:

∑

∑

−

−

≠

−

−

i

i

xkonc

i

xkonc

i

i

i

xpocz

i

xpocz

i

c

Vu

V

u

m

c

Vu

V

u

m

2

,

,

2

,

,

1

1

problem: zas. zach. p

ę

du nie jest spełniona !!!

P

ę

d w mechanice relatywistycznej

definiujemy:

u

m

mu

p

2

0

1

β

−

=

=

β = u/c

8

Energia relatywistyczna

Aby utrzyma

ć

w mocy zasad

ę

zachowania energii w mechanice relatywistycznej,

pomi

ę

dzy mas

ą

całkowit

ą

a energi

ą

ciała (zwan

ą

energi

ą

całkowit

ą

) musi

zachodzi

ć

zwi

ą

zek :

2

2

0

2

1

c

m

mc

E

β

−

=

=

Jest to słynne równanie Einsteina

wyra

ż

aj

ą

ce

równowa

ż

no

ść

masy i energii.

Uwaga: Zasada zachowania energii obowi

ą

zuje dla energii całkowitej !!!

masa [kg]

energia

elektron

9.11×10

-31

8.19 ×10

-14

J (= 511 keV)

proton

1.67 ×10

-27

1.5 ×10

-10

J (= 938 MeV)

atom Uranu

3.95 ×10

-25

3.55 ×10

-8

J (= 225 GeV)

cz

ą

steczka kurzu

1 ×10

-13

1 ×10

4

J

β = u/c

Mo

ż

na wykaza

ć

,

ż

e gdy

u<<c

(tj. ) , wzory relatywistyczne przechodz

ą

w klasyczne:

u

m

u

m

mu

p

0

2

0

1

≈

−

=

=

β

2

0

2

2

0

2

2

0

2

1

1

...

2

1

1

1

1

1

u

m

c

m

c

m

E

k

≈













−

+

=

















−

−

=

β

β

0

→

=

c

u

β

Załó

ż

my najpierw,

ż

e ciało jest w spoczynku. Wtedy masa tego ciała jest równa

m

0

i jego energia, zwana

energi

ą

spoczynkow

ą

, wynosi:

2

0

0

c

m

E

=

Jaka jest wi

ę

c definicja energii kinetycznej ?

(

)

2

0

0

c

m

m

E

E

E

k

−

=

−

=















−

−

=

1

1

1

2

2

0

β

c

m

E

k

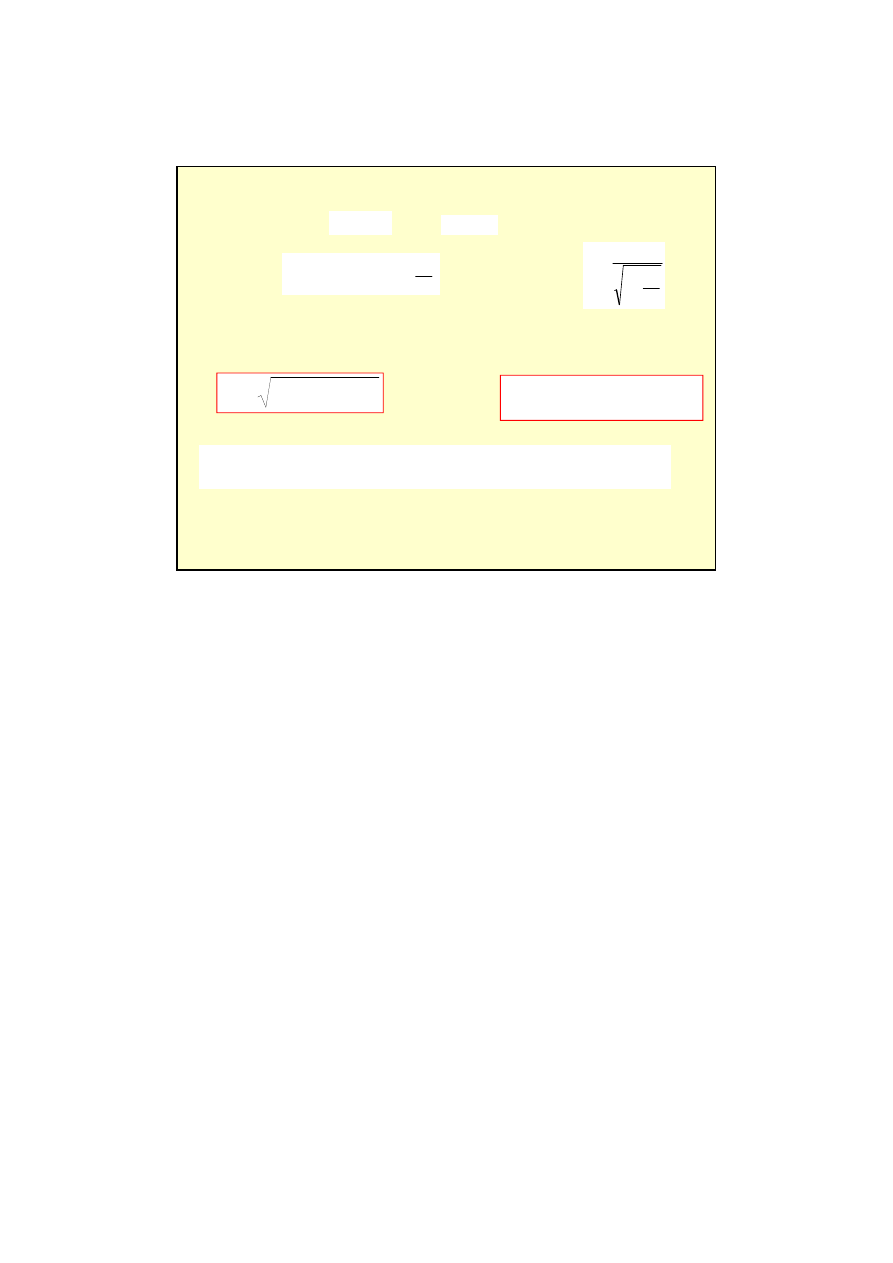
Relatywistyczna energia kinetyczna

jest równa:

β = u/c

9

2

mc

E

=

mu

p

=

oraz

)

1

(

2

2

4

2

2

2

2

c

u

c

m

c

p

E

−

=

−

2

2

0

1

c

u

m

m

−

=

st

ą

d:

podstawiaj

ą

c:

Zwi

ą

zek energii, masy i p

ę

du

4

2

0

2

2

2

c

m

c

p

E

=

−

otrzymamy:

2

2

4

2

0

c

p

c

m

E

+

=

Zauwa

ż

my,

ż

e wyra

ż

enie:

2

2

2

c

p

E

−

jest niezmiennikiem (podobnie jak

interwał ma tak

ą

sam

ą

warto

ść

we wszystkich układach inercjalnych).

lub