
Niezwykle szczególna teoria wzgl˛edno´sci
Andrzej Dragan


W
ST ˛
EP
N
iniejszy skrypt został przygotowany i udost˛epniony z my´sl ˛
a o studentach ucz˛eszczaj ˛
acych
na wykład ze szczególnej teorii wzgl˛edno´sci, który prowadziłem po raz pierwszy w 2001 roku
Szkole Nauk ´Scisłych Uniwersytetu Kardynała Stefana Wyszy´nskiego, a w kolejnych latach na
Wydziale Fizyki Uniwersytetu Warszawskiego. Pisany był jednak z nadziej ˛
a, ˙ze b˛edzie przy-
datny równie˙z wszystkim zainteresowanym samodzielnym studiowaniem podstaw teorii wzgl˛ed-
no´sci.
Szczególny nacisk podczas przygotowywania skryptu poło˙zony został na ograniczenie do ab-
solutnego minimum aparatu matematycznego potrzebnego do zapoznania si˛e z wyło˙zonym ma-
teriałem. Z wyj ˛
atkiem rozdziału 8 zawieraj ˛
acego rozwa˙zania dotycz ˛
ace elektrodynamiki klasy-
cznej, strona matematyczna prowadzonego wykładu nie wykracza stopniem trudno´sci poza el-
ementarne przekształcenia algebraiczne. W fachowej literaturze dotycz ˛
acej przedstawianych tu
zagadnie´n zawiło´sci analizy matematycznej przysłaniaj ˛
a cz˛esto spore i tak trudno´sci poj˛eciowe.
Niejednokrotnie natomiast zdarza si˛e, ˙ze rzeczy, których nie potrafimy wyja´sni´c własnej babci,
najcz˛e´sciej sami nie rozumiemy. Dlatego te˙z autor ma nadzieje, ˙ze niniejszy skrypt stanowi´c
b˛edzie po˙zyteczn ˛
a lektur˛e dla osób zapoznaj ˛
acych si˛e z teori ˛
a wzgl˛edno´sci po raz pierwszy,
a pozbawionych wiadomo´sci z zakresu matematyki wy˙zszej. Osoby zainteresowane bardziej
sformalizowanym i zmatematyzowanym podej´sciem, niew ˛
atpliwie ciekawym samym w sobie,
musz ˛
a si˛e niestety obej´s´c smakiem i si˛egn ˛
a´c po inn ˛
a pozycj˛e z bogatej literatury dotycz ˛
acej tego
tematu.
Zdaj˛e sobie spraw˛e z licznych pomyłek i nie´scisło´sci, które niechybnie zostały przeze mnie
popełnione i niedostrze˙zone, tym bardziej wdzi˛eczny b˛ed˛e za zwrócenie mi na nie uwagi przez
drogiego Czytelnika.
A
NDRZEJ
D
RAGAN
1

2

Spis tre´sci
1
T
RZ ˛
ESIENIE ZIEMI
7
1.1
T
RANSFORMACJA
L
ORENTZA
a’la M
INKOWSKI
1
. . . . . . . . . . . . . . . .
7
1.2
C
ZASOPRZESTRZE ´
N
! . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
1.3
T
RANSFORMACJA
L
ORENTZA JAKO OBRÓT
HIPERBOLICZNY
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
1.4
N
IC NIE MO ˙
ZE PORUSZA ´
C SI ˛
E SZYBCIEJ OD ´SWIATŁA
? . . . . . . . . . . . . . 14
1.4.1
D
YLEMAT
Z
WROTNICZEGO I RELATYWISTYCZNA DEFINICJA RUCHU
. 14
1.4.2
B
AJKA O STU KRASNOLUDKACH
. . . . . . . . . . . . . . . . . . . . . 15
1.4.3
L
ATARNIA MORSKA
. . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
1.5
P
ARADOKSY PRZYCZYNOWO
-
SKUTKOWE
. . . . . . . . . . . . . . . . . . . . 16
1.6
I
NTERWAŁ CZASOPRZESTRZENNY
. . . . . . . . . . . . . . . . . . . . . . . . 17
Pytania
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
Zadania . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
2
K
INEMATYKA RELATYWISTYCZNA
21
2.1
W
IELOZNACZNA JEDNOCZESNO ´S ´
C
. . . . . . . . . . . . . . . . . . . . . . . . 21
2.2
D
YLATACJA CZASU
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2.3
S
KRÓCENIE
L
ORENTZA
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
2.4
P
ARADOKS POCI ˛
AGU I DWORCA
. . . . . . . . . . . . . . . . . . . . . . . . . 24
2.5
C
ZY SKRÓCENIE
L
ORENTZA JEST RZECZYWISTE
?
. . . . . . . . . . . . . . . 25
2.6
E
LEKTRYZUJ ˛
ACY PARADOKS ELEKTRYCZNY
. . . . . . . . . . . . . . . . . . 27
2.7
P
ARADOKS BLI ´
ZNI ˛
AT
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
2.8
P
ARADOKS
R
OBERTA
K
ORZENIOWSKIEGO
. . . . . . . . . . . . . . . . . . . . 31
1
Geometryczne podej´scie do transformacji Lorentza zostało przedstawione na przykład w referencji [1].
3

4
SPIS TRE ´
SCI
2.9
R
ELATYWISTYCZNE TRANSFORMACJE PR ˛
EDKO ´SCI
. . . . . . . . . . . . . . . 34
Pytania
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
Zadania . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
3
N
IESZTYWNA BRYŁA SZTYWNA
41
3.1
M
ACHANIE DŁUGIM KIJEM
. . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
3.2
P
ARADOKS TYCZKARZA I STODOŁY
. . . . . . . . . . . . . . . . . . . . . . . 42
3.3
P
ARADOKS DWÓCH KWADRATÓW
. . . . . . . . . . . . . . . . . . . . . . . . . 43
3.4
P
ARADOKS KLOCKA I DZIURY W STOLE
2
. . . . . . . . . . . . . . . . . . . . . 44
3.5
N
API ˛
ECIA WEWN ˛
ETRZNE
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
Pytania
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48
Zadania . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48
4
K
ŁOPOTY Z TEORI ˛
A KWANTOW ˛
A
49
4.1
I
NTERFEROMETR
M
ACHA
-Z
EHNDERA
. . . . . . . . . . . . . . . . . . . . . . 49
4.2
Z
JAWISKO
EPR
I KWANTOWE ZACHWIANIE PRZYCZYNOWO ´SCI
. . . . . . . . 51
4.3
N
IERÓWNO ´SCI
B
ELLA
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
Pytania
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
Zadania . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
5
´S
WIATŁO
59
5.1
R
ELATYWISTYCZNY EFEKT
D
OPPLERA
. . . . . . . . . . . . . . . . . . . . . 59
5.2
E
FEKT
„
UNOSZENIA
”
´SWIATŁA W PORUSZAJ ˛
ACYM SI ˛
E
O ´SRODKU
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60
5.3
O
DBICIE ´SWIATŁA OD LUSTRA
. . . . . . . . . . . . . . . . . . . . . . . . . . 61
Pytania
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
Zadania . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63
6
P
OZORNE DEFORMACJE RUCHOMYCH OBIEKTÓW
65
6.1
O
BRAZ PORUSZAJ ˛
ACEGO SI ˛
E OKR ˛
EGU
. . . . . . . . . . . . . . . . . . . . . . 65
6.2
O
BRAZ PORUSZAJ ˛
ACEJ SI ˛
E KULI
3
. . . . . . . . . . . . . . . . . . . . . . . . . 68
Pytania
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
2
Problem ten został przedstawiony w pracy [2].
3
Zagadnienie przedstawione w tym podrozdziale pochodzi z pracy [5].

SPIS TRE ´
SCI
5
Zadania . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
7
D
YNAMIKA RELATYWISTYCZNA
73
7.1
C
ZTEROWEKTORY
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
7.2
C
ZTEROP ˛
ED
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74
7.3
E = mc
2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78
7.4
R
ELATYWISTYCZNA SIŁA I
II P
RAWO
N
EWTONA
. . . . . . . . . . . . . . . . 81
7.5
C
ZTEROPRZYSPIESZENIE
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82
7.6
R
UCH JEDNOSTAJNIE PRZYSPIESZONY
. . . . . . . . . . . . . . . . . . . . . . 83
Pytania
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85
Zadania . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
8
E
LEKTRODYNAMIKA RELATYWISTYCZNA
87
8.1
P
RELUDIUM
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
8.2
P
OTENCJAŁ PORUSZAJ ˛
ACEGO SI ˛
E ŁADUNKU
. . . . . . . . . . . . . . . . . . . 88
8.3
W
POSZUKIWANIU KOLEJNYCH CZTEROWEKTORÓW
. . . . . . . . . . . . . . 92
8.3.1
C
ZTEROGRADIENT
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93
8.3.2
C
ZTEROPR ˛
AD
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 94
8.3.3
C
ZTEROPOTENCJAŁ
. . . . . . . . . . . . . . . . . . . . . . . . . . . . 94
8.4
T
RANSFORMACJE PÓL
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 96
8.5
R
ELATYWISTYCZNA SIŁA
L
ORENTZA I ŁAMANIE
III
ZASADY
N
EWTONA
. . . 99
Pytania
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101
Zadania . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101
9
N
IESPODZIANKA
103
9.1
S
K ˛
AD SI ˛
E BIERZE TRANSFORMACJA
L
ORENTZA
?
4
. . . . . . . . . . . . . . . 103
Pytania
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 107
Zadania . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 107
B
IBLIOGRAFIA
109
4
Pomysł wyprowadzenia transformacji Lorentza przedstawion ˛
a metod ˛
a został omówiony w referencjach [8].

6
SPIS TRE ´
SCI

Rozdział 1
T
RZ ˛
ESIENIE ZIEMI
C
zy zastanawiali´scie si˛e kiedy´s w jaki sposób wytłumaczy´c osobie niewidomej od urodzenia, ˙ze
odległe przedmioty „s ˛
a” mniejsze od przedmiotów znajduj ˛
acych si˛e blisko? Przed nami podobne
zadanie. Ju˙z pod koniec pierwszego podrozdziału stanie si˛e jasne dlaczego. Oka˙ze si˛e zreszt ˛
a,
˙ze sami wyst ˛
apimy w roli osób niewidomych od urodzenia, którym rzeczywisto´s´c (jednak nie
do´swiadczana na codzie´n) wydaje si˛e niewiarygodna i niewyobra˙zalna.
1.1
T
RANSFORMACJA
L
ORENTZA
a’la M
INKOWSKI
1
P
unktem wyj´scia w naszym rozumowaniu b˛edzie przedziwny fakt, który znamy z do´swiad-
czenia: ´swiatło w pró˙zni zawsze porusza si˛e z pr˛edko´sci ˛
a c. Co rozumiemy przez „zawsze”?
Chodzi tu o propagacj˛e we wszystkich inercjalnych układach odniesienia. Na przykład ´swiatło
opuszczaj ˛
ace reflektory jad ˛
acego szybko samochodu oddala si˛e od kierowcy z pr˛edko´sci ˛
a c. Ale
z t ˛
a sam ˛
a pr˛edko´sci ˛
a zbli˙za si˛e ono do stoj ˛
acego na chodniku pieszego, niezale˙znie od wzgl˛ed-
nego ruchu samochodu i pieszego. Fakt ten jest niezwykle osobliwy, gdy˙z wydawa´c by si˛e
mogło, ˙ze ´swiatło powinno zbli˙za´c si˛e do pieszego z pr˛edko´sci ˛
a równ ˛
a c + V , gdzie V jest pr˛ed-
ko´sci ˛
a samochodu. Tak jednak nie jest. Oznacza to, ˙ze je´sli ´swiatło w pewnej chwili t
1
opu´sciło
punkt o współrz˛ednych (x
1
, y
1
, z
1
), a w chwili t
2
dotarło do punktu (x
2
, y
2
, z
2
), to zawsze, czyli
niezale˙znie od przyj˛etego inercjalnego układu odniesienia, ani pr˛edko´sci ´zródła spełnione jest
nast˛epuj ˛
ace równanie:
1
Geometryczne podej´scie do transformacji Lorentza zostało przedstawione na przykład w referencji [1].
7
8
ROZDZIAŁ 1.
TRZ ˛
ESIENIE ZIEMI
p
(x
2
− x
1
)
2
+ (y
2
− y
1
)
2
+ (z
2
− z
1
)
2
= c(t
2
− t
1
).
(1.1)
Jest to po prostu równanie: (droga) = (pr˛edko´s´c)×(czas) i pr˛edko´s´c c jest we wszystkich układach
jednakowa.
Rozwa˙zmy teraz proces polegaj ˛
acy na emisji i absorbcji impulsu ´swietlnego w dwóch kole-
jnych chwilach czasu w ró˙znych punktach. B˛edziemy bada´c nast˛epuj ˛
acy problem: czym b˛ed ˛
a
ró˙zni´c si˛e obserwacje dokonywane przez osob˛e stoj ˛
ac ˛
a w pobli˙zu od obserwacji osoby prze-
je˙zd˙zaj ˛
acej samochodem. W szczególno´sci, interesowa´c nas b˛edzie pytanie czy chwile emisji i
absorbcji impulsu w obu rozwa˙zanych układach b˛ed ˛
a jednakowe. Współrz˛edne i czas obserwa-
tora stoj ˛
acego na chodniku oznaczymy jak w poprzednim wzorze, a współrz˛edne osoby jad ˛
acej
samochodem b˛ed ˛
a tradycyjnie „primowane” - rysunek 1.1.
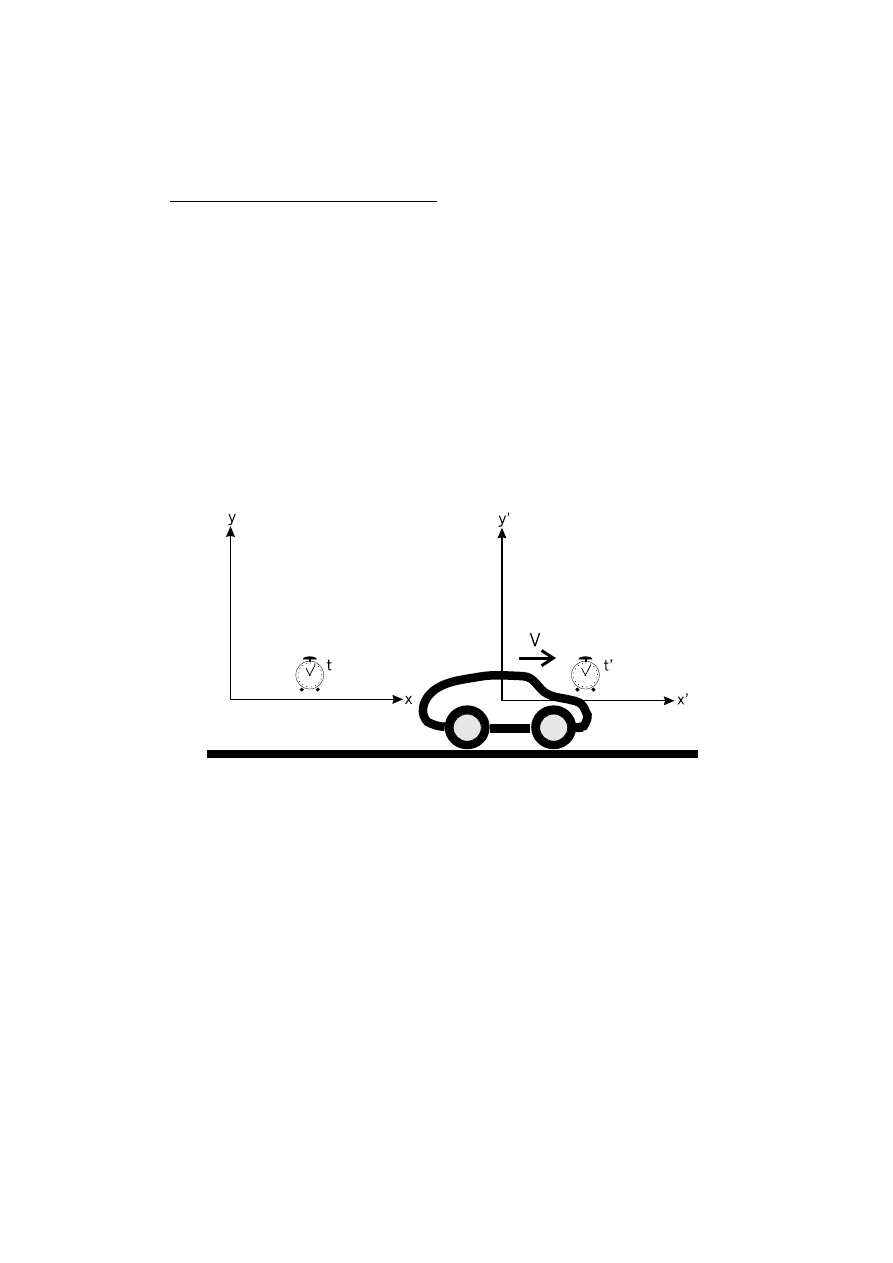
Rysunek 1.1:
Dwa układy współrz ˛ednych poruszaj ˛
ace si ˛e wzgl ˛edem siebie z pr ˛edko´sci ˛
a
V
wzdłu˙z osi
x
.
Pocz ˛
atki układów pokrywały si ˛e w chwili
t = t
0
= 0
. Przyj ˛eta notacja (zmienne primowane i nieprimowane)
b ˛edzie stosowana w całym wykładzie, chyba ˙ze zostanie wyra´znie powiedziane ˙ze jest inaczej.
Poniewa˙z obydwaj obserwatorzy potwierdz ˛
a poprawno´s´c równania (1.1) w swoich układach
odniesienia, to musi zachodzi´c nast˛epuj ˛
aca równo´s´c:
0 = c
2
∆t
2
− ∆x
2
− ∆y
2
− ∆z
2
= c
2
∆t
02
− ∆x
02
− ∆y
02
− ∆z
02
.
(1.2)
Zastosujmy teraz pro´sciutkie podstawienie: τ = ict, czyli wprowad´zmy tajemniczy „czas uro-
jony” (pami˛etaj ˛
ac, by nie przesadza´c z wyobra´zni ˛
a). Przepisuj ˛
ac poprzedni wzór otrzymujemy:
1.1.
TRANSFORMACJA LORENTZA A’LA MINKOWSKI
2
9
∆τ
2
+ ∆x
2
+ ∆y
2
+ ∆z
2
= ∆τ
02
+ ∆x
02
+ ∆y
02
+ ∆z
02
.
(1.3)
Wyra˙zenie (1.3) wygl ˛
ada jak równo´s´c dwóch odległo´sci w jakiej´s abstrakcyjnej, czterowymia-
rowej przestrzeni. Porzu´cmy na razie kwesti˛e interpretacji fizycznej tej przestrzeni i zastanów-
my si˛e nad stron ˛
a czysto matematyczn ˛
a. Mamy do czynienia z dwoma czterowymiarowymi
układami współrz˛ednych, pomi˛edzy którymi istnieje jaka´s transformacja zachowuj ˛
aca odległo´sci
pomi˛edzy punktami. Przykładem takiej transformacji mo˙ze by´c lustrzane odbicie albo zmiana
kierunku upływu czasu. Je´sli oba układy ró˙zniłyby si˛e wył ˛
acznie znakiem jednej ze współrz˛ed-
nych, oczywi´scie odległo´sci mi˛edzy dowolnymi dwoma punktami byłyby jednakowe w obu tych
układach, zgodnie ze wzorem (1.3). Inn ˛
a prost ˛
a transformacj ˛
a, która nie zmienia odległo´sci
jest obrót. Obroty, odbicia, przesuni˛ecia oraz ich zło˙zenia, to jedyne transformacje liniowe nie
zmieniaj ˛
ace odległo´sci pomi˛edzy dowolnymi punktami. Poniewa˙z rozwa˙zamy tu dwa porusza-
j ˛
ace si˛e wzgl˛edem siebie inercjalne układy odniesienia, interesuj ˛
a nas wył ˛
acznie takie trans-
formacje (współrz˛edne układów inercjalnych powinny transformowa´c si˛e liniowo - dyskusja
tego faktu odb˛edzie si˛e pó´zniej). Przej´scie do układu poruszaj ˛
acego si˛e nie wi ˛
a˙ze si˛e ani z
odbiciem współrz˛ednych przestrzennych, ani z odwróceniem biegu czasu, ani z przesuni˛eciem
współrz˛ednych, ani z przestrzennym obrotem, ani nawet ze zło˙zeniem tych wszystkich transfor-
macji. Zostaje nam tylko jedna mo˙zliwo´s´c: obrót w płaszczy´znie zawieraj ˛
acej „o´s czasu” τ oraz
jaki´s kierunek przestrzenny. Dla ustalenia uwagi przyj˛eli´smy, ˙ze samochód porusza si˛e wzgl˛e-
dem pieszego wzdłu˙z osi x, wi˛ec rozwa˙za´c b˛edziemy obrót w jedynej wyró˙znionej płaszczy´znie
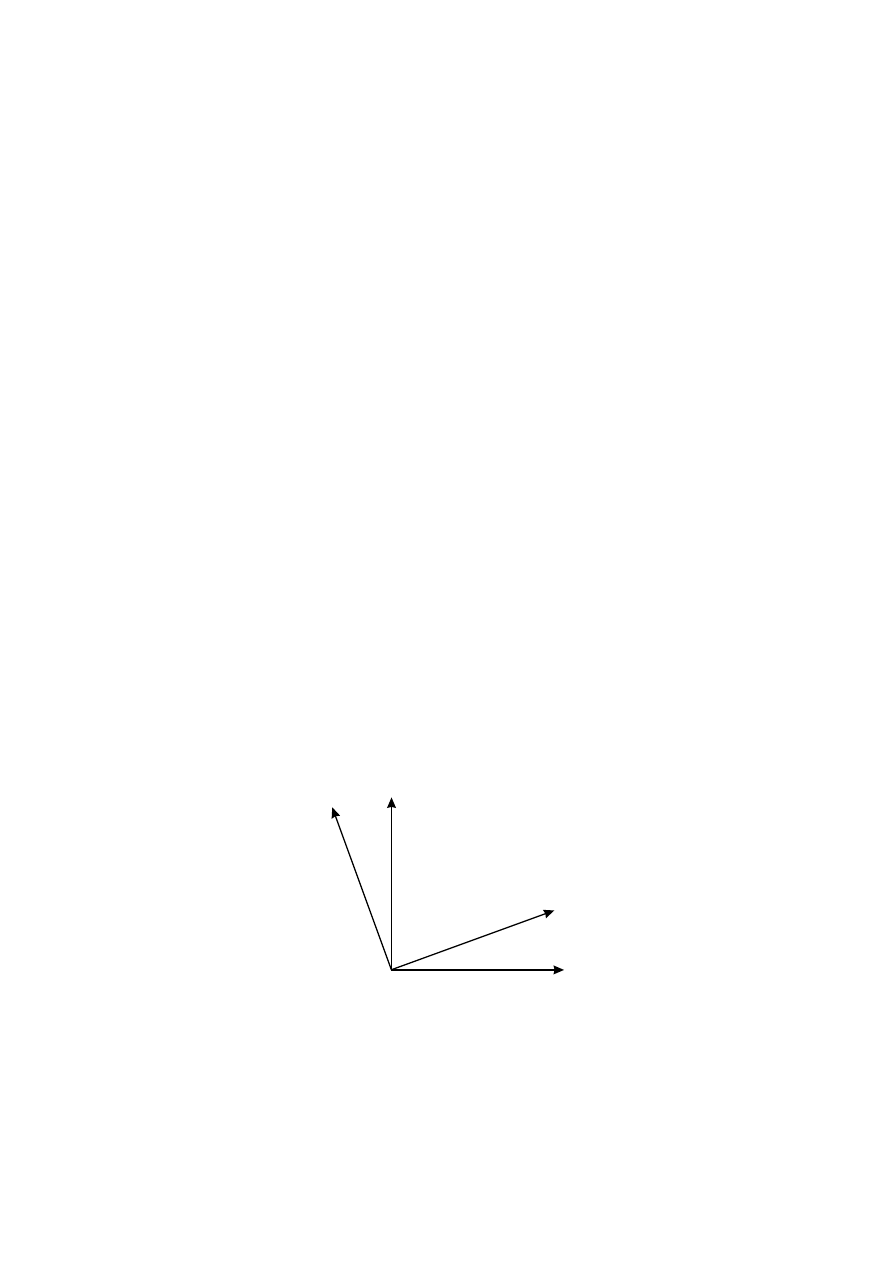
(τ, x) - rysunek 1.2. Je´sli przyjmiemy, ˙ze w chwili t = t
0
= 0 pocz ˛
atki obu układów odniesienia
t
x
x’
q
q
t
,
Rysunek 1.2:
Obrót układu współrz ˛ednych w płaszczy´znie
(τ, x)
.
pokrywały si˛e, to transformacja b˛edzie miała ogóln ˛
a posta´c:

10
ROZDZIAŁ 1.
TRZ ˛
ESIENIE ZIEMI
τ
0
= τ cos θ + x sin θ =
τ
√
1+tg
2
θ
+
x tg θ
√
1+tg
2
θ
x
0
= x cos θ − τ sin θ =
x
√
1+tg
2
θ
−
τ tg θ
√
1+tg
2
θ
,
(1.4)
gdzie θ jest k ˛
atem obrotu. Przypomnijmy, ˙ze transformacja ta ma zamienia´c poło˙zenie i chwil˛e
emisji ´swiatła widzianego przez obserwatora stoj ˛
acego na chodniku na współrz˛edne i czas zmie-
rzone przez osob˛e jad ˛
ac ˛
a samochodem wzdłu˙z osi x z pr˛edko´sci ˛
a V . Poniewa˙z jednak współ-
rz˛edne wszystkich punktów musz ˛
a tak˙ze transformowa´c si˛e liniowo, to układ równa´n (1.4) musi
opisywa´c przekształcenie dowolnego punktu czterowymiarowej przestrzeni.
We wprowadzonych transformacjach wyst˛epuje nieznany k ˛
at θ. Domy´slamy si˛e, ˙ze musi
on jako´s zale˙ze´c od pr˛edko´sci V (wiemy na przykład, ˙ze dla V = 0, równie˙z θ = 0), no bo od
czegó˙z by innego? Aby wyznaczy´c t˛e zale˙zno´s´c rozwa˙zmy ruch pocz ˛
atku układu współrz˛ednych
zwi ˛
azanego z samochodem: x
0
= 0. Z perspektywy obserwatora stoj ˛
acego na chodniku, punkt
ten oddala si˛e z pr˛edko´sci ˛
a V wzdłu˙z osi x. Korzystaj ˛
ac z drugiego z równa´n (1.4) dostajemy:
x
0
= 0 ⇒
x
τ
=
x
ict
=
V
ic
= tg θ.
(1.5)
Wstawiaj ˛
ac do równa´n (1.4) znalezion ˛
a warto´s´c tg θ, oraz powracaj ˛
ac do u˙zywania t zamiast τ
otrzymujemy znane wzory opisuj ˛
ace transformacj˛e Lorentza:
t
0
=
t−V x/c
2
√
1−V
2
/c
2
x
0
=
x−V t
√
1−V
2
/c
2
.
(1.6)
Wida´c, ˙ze transformacja zachowuje si˛e kulturalnie, dopóki rozwa˙zamy układy inercjalne porusza-
j ˛
ace si˛e z pr˛edko´sciami V < c. W przeciwnym wypadku pojawiaj ˛
a si˛e w niej liczby zespolone.
Transformacj˛e odwrotn ˛
a mo˙zemy znale´z´c na dwa sposoby: albo pomanipulowa´c równaniami
odwracaj ˛
ac zale˙zno´s´c, albo po prostu zamieni´c V na −V . Wynik oczywi´scie jest ten sam:
t =
t
0
+V x
0
/c
2
√
1−V
2
/c
2
x =
x
0
+V t
0
√
1−V
2
/c
2
.
(1.7)
Czas teraz na nieco gł˛ebsze przemy´slenia. Przede wszystkim widzimy, ˙ze gdy c −→ ∞,
znalezione transformacje przechodz ˛
a w co´s, co nazywa si˛e cz˛esto „transformacjami Galileusza”:

1.2.
CZASOPRZESTRZE ´
N!
11
(
t
0
= t
x
0
= x − V t.
(1.8)
W rzeczywisto´sci przed dokonaniem relatywistycznego przewrotu, nikt nie zapisywał tej trans-
formacji w powy˙zszy sposób. Nie uwa˙zano za konieczne rozwa˙zania czasu osobno w obu
układach współrz˛ednych. Czas rozumiano wył ˛
acznie jako pewien tajemniczy parametr nie zwi ˛
a-
zany z przestrzeni ˛
a, a cała transformacja była „trywialna” (nikt nie nazwałby tego nawet trans-
formacj ˛
a). „Po prostu” x
0
= x − V t.
Podej´scie Minkowskiego ujawnia jednak, ˙ze czas przypomina jeden z wymiarów przestrzen-
nych. Niew ˛
atpliw ˛
a ró˙znic ˛
a, cho´c nie wiadomo czy jedyn ˛
a, jest czynnik i, który wprowadzili´smy,
by „ujednolici´c” obraz czterowymiarowej przestrzeni.
1.2
C
ZASOPRZESTRZE ´
N
!
R
ozwa˙zania z poprzedniego podrozdziału prowadz ˛
a do niezwykle ciekawego wniosku: czas i
przestrze´n nie mog ˛
a by´c traktowane niezale˙znie. Z tego powodu wprowadza si˛e w teorii wzgl˛ed-
no´sci koncepcj˛e czterowymiarowej czasoprzestrzeni. Zrozumienie tego poj˛ecia pozwala oswoi´c
si˛e z przedziwnymi wnioskami z jakimi przyjdzie nam si˛e jeszcze zmierzy´c. Ró˙zne tempo up-
ływu czasu, fizyczna zmiana długo´sci poruszaj ˛
acych si˛e obiektów bez istnienia wewn˛etrznych
napi˛e´c w materiale - wszystko to staje si˛e niemal naturalne, gdy zdamy sobie spraw˛e, ˙ze prze-
j´scie do układu poruszaj ˛
acego si˛e odpowiada pewnemu obrotowi w czasoprzestrzeni. Pytania
typu „jaki jest naprawd˛e upływ czasu?” albo „jaka jest prawdziwa długo´s´c?” maj ˛
a taki sam
sens jak spieranie si˛e, jaki kolor ma sze´scian, którego ka˙zda ´sciana pomalowana jest inn ˛
a farb ˛
a.
Dla osoby patrz ˛
acej z jednej strony sze´scian jest niebieski, dla innej - czerwony. Kto ma racj˛e?
Pytanie o racj˛e jest, jak widzimy ´zle postawione. Wystarczy obróci´c sze´scian i obserwatorzy
zmieniaj ˛
a zdanie. Podobnie jest z obserwacj ˛
a ´swiata z ró˙znych, poruszaj ˛
acych si˛e wzgl˛edem
siebie układów inercjalnych.
1.3
T
RANSFORMACJA
L
ORENTZA JAKO OBRÓT
HIPERBOLICZNY
Z
auwa˙zyli´smy poprzednio, ˙ze zamieniaj ˛
ac czas rzeczywisty czasem urojonym, mo˙zemy odgad-
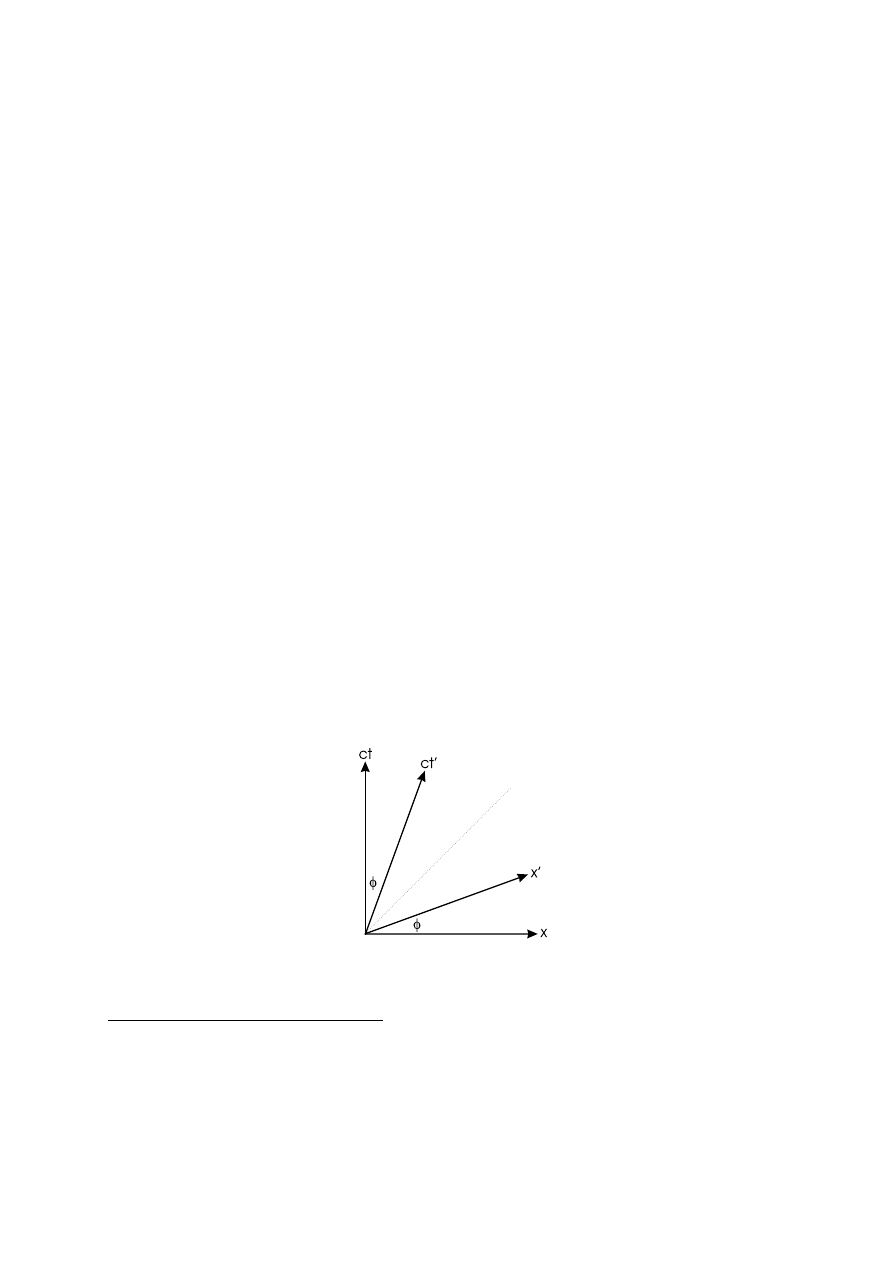
12
ROZDZIAŁ 1.
TRZ ˛
ESIENIE ZIEMI
n ˛
a´c, ˙ze transformacja Lorentza jest obrotem w „urojonej” czasoprzestrzeni. Spróbujemy teraz
stwierdzi´c jaka jest interpretacja geometryczna tej transformacji w „zwykłej”, rzeczywistej cza-
soprzestrzeni. Zapiszmy równania (1.4) przy u˙zyciu czasu rzeczywistego:
(
ict
0
= ict cos θ + x sin θ
x
0
= x cos θ − ict sin θ.
(1.9)
Aby pozby´c si˛e z transformacji liczb urojonych skorzystamy z elementarnych to˙zsamo´sci alge-
braicznych ł ˛
acz ˛
acych funkcje trygonometryczne z ich hiperbolicznymi odpowiednikami:
sin θ = −i sinh iθ
cos θ = cosh iθ.
(1.10)
Wstawiaj ˛
ac je do równa´n (1.9) i podstawiaj ˛
ac ϑ = iθ otrzymujemy:
(
ct
0
= ct cosh ϑ − x sinh ϑ
x
0
= x cosh ϑ − ct sinh ϑ.
(1.11)
Graficzna interpretacja transformacji Lorentza (1.11) znajduje si˛e na rysunku (1.3) przedsta-
wiaj ˛
acym osie dwóch układów inercjalnych poruszaj ˛
acych si˛e wzgl˛edem siebie. Równania osi
Rysunek 1.3:
Osie czasoprzestrzenne dwóch układów inercjalnych
2
.
2
W teorii wzgl˛edno´sci cz˛esto u˙zywa si˛e tego typu rysunków do opisu ró˙znych sytuacji. Nie robi si˛e tego nato-
miast w zasadzie nigdy w teorii Newtona. Jako ´cwiczenie warto si˛e zastanowi´c w jaki sposób wygl ˛
adałby rysunek
1.3 w wersji nierelatywistycznej. Wynik jest zaskakuj ˛
acy!

1.3.
TRANSFORMACJA LORENTZA JAKO OBRÓT
HIPERBOLICZNY
13
układu primowanego mo˙zemy wyznaczy´c korzystaj ˛
ac z transformacji Lorentza (1.11). O´s czasu
jest wyznaczona równaniem x
0
= 0, natomiast o´s przestrzenna jest zadana przez ct
0
= 0. Otrzy-
mujemy st ˛
ad, ˙ze tg φ = tgh ϑ = V /c, gdzie φ jest k ˛
atem wzgl˛ednego nachylenia osi obu układów
(rysunek 1.3). Wida´c, ˙ze osie układów, których pr˛edko´s´c d ˛
a˙zy do c b˛ed ˛
a zbli˙za´c si˛e do przery-
wanej linii. Tory „pod´swietlnych” cz ˛
astek rozpoczynaj ˛
acych swój ruch w x = x
0
= 0 musz ˛
a
znajdowa´c si˛e wewn ˛
atrz pionowego „sto˙zka” ograniczonego przerywan ˛
a lini ˛
a. Poniewa˙z brzeg
sto˙zka we wszystkich układach zadany jest tym samym równaniem, to cz ˛
astka, której pr˛edko´s´c
jest mniejsza od c w jednym układzie, b˛edzie równie˙z mniejsza od c w ka˙zdym innym układzie
inercjalnym.
Poprzez bezpo´srednie podstawienie wzorów (1.11), mo˙zemy sprawdzi´c, ˙ze zachodzi:
c
2
t
02
− x
02
= c
2
t
2
− x
2
,
(1.12)
co wraz z uzupełnieniem transformacji współrz˛ednych o warunki y
0
= y oraz z
0
= z daje
równo´s´c (1.2) od której rozpocz˛eli´smy nasze rozwa˙zania. Znalezione przez nas przekształce-
nie (1.11) jest hiperbolicznym obrotem, który odpowiada zwykłemu obrotowi, ale w przestrzeni
w której długo´s´c wektora nie jest sum ˛
a lecz ró˙znic ˛
a kwadratów poszczególnych składowych. W
tym sensie czasoprzestrze´n nie jest zwykł ˛
a, euklidesow ˛
a przestrzeni ˛
a, bo kwadrat długo´sci jest
w niej zdefiniowany jak w równaniu (1.2). Posiada ona jednak trójwymiarow ˛
a i euklidesow ˛
a
podprzestrze´n.
Zauwa˙zyli´smy, ˙ze wyra˙zenie:
∆s
2
= c
2
∆t
2
− ∆x
2
− ∆y
2
− ∆z
2
(1.13)
nie zmienia si˛e pod wpływem transformacji Lorentza, podobnie jak długo´s´c wektora w dowolnej
euklidesowej przestrzeni nie zmienia si˛e pod wpływem obrotów. Z tego powodu wielko´s´c ∆s
2
odgrywa bardzo wa˙zn ˛
a rol˛e w teorii wzgl˛edno´sci - nazywa si˛e j ˛
a interwałem czasoprzestrzennym
„pomi˛edzy” dwoma zdarzeniami oddzielonymi w czasie o ∆t, a w przestrzeni o ∆x, ∆y i ∆z.
Na przykład interwał czasoprzestrzenny pomi˛edzy zdarzeniami w których został wyemitowany,
a nast˛epnie pochłoni˛ety impuls ´swiatła zawsze wynosi zero (1.2).
Nasze rozwa˙zania obrotów w czasoprzestrzeni brzmi ˛
a niezwykle. Dlaczego jednak jad ˛
ac
autobusem nie doznajemy owych „hiperbolicznych obrotów” i wszystko wygl ˛
ada zupełnie „zwy-
czajnie”? Poniewa˙z parametr ϑ wyst˛epuj ˛
acy w przekształceniu (1.11) ϑ = atgh V /c mo˙zemy
14
ROZDZIAŁ 1.
TRZ ˛
ESIENIE ZIEMI
zazwyczaj (dla niewielkich pr˛edko´sci) przybli˙zy´c przez ϑ ≈ V /c, to powy˙zsza transformacja
uzyskuje przybli˙zon ˛
a posta´c:
(
ct
0
≈ ct − xϑ
x
0
≈ x − ctϑ.
(1.14)
Wida´c, ˙ze z pierwszego równania zostaje w przybli˙zeniu t
0
≈ t, a z drugiego x
0
≈ x − V t, czyli
transformacja Galileusza, do której jeste´smy przyzwyczajeni.
1.4
N
IC NIE MO ˙
ZE PORUSZA ´
C SI ˛
E SZYBCIEJ OD ´SWIATŁA
?
M
ówi si˛e cz˛esto, ˙ze „nic nie mo˙ze porusza´c si˛e szybciej od ´swiatła”, czyli wszystko porusza si˛e
od niego wolniej. Bez uprzedniego ustalenia co rozumiemy przez wszystko oraz przez porusza
si˛e, stwierdzenie to mo˙ze doprowadzi´c do wielu nieporozumie´n, co ilustruj ˛
a poni˙zsze (kontr)przy-
kłady.
1.4.1
D
YLEMAT
Z
WROTNICZEGO I RELATYWISTYCZNA DEFINICJA RUCHU
P
ewien Zwrotniczy obserwował kiedy´s dwa poci ˛
agi zbli˙zaj ˛
ace si˛e do siebie z ogromn ˛
a pr˛ed-
ko´sci ˛
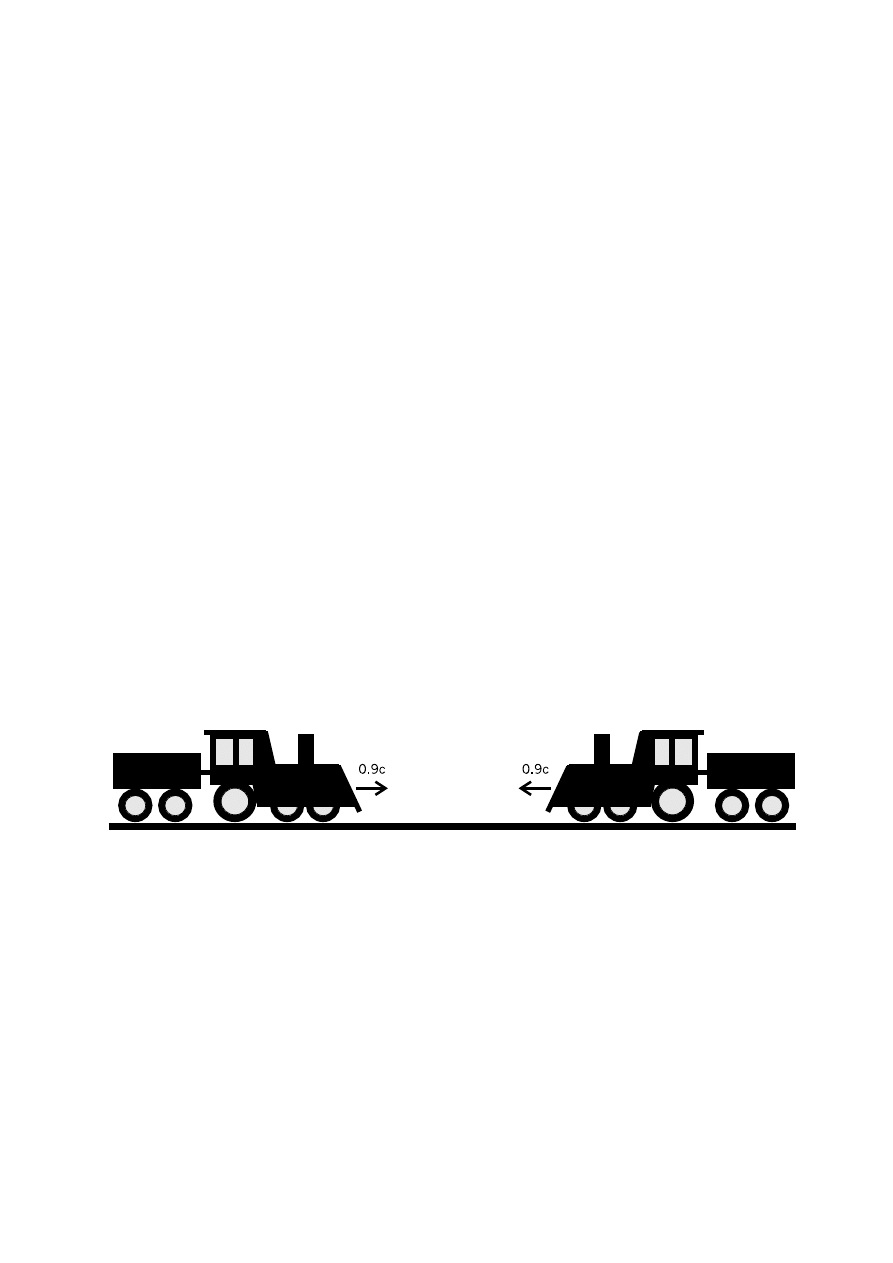
a - rysunek 1.4. Jeden z poci ˛
agów poruszał si˛e wzgl˛edem niego z pr˛edko´sci ˛
a 0.9c, a drugi
Rysunek 1.4:
Z jak ˛
a pr ˛edko´sci ˛
a poci ˛
agi zbli˙zaj ˛
a si ˛e do siebie według Zwrotniczego?
z pr˛edko´sci ˛
a −0.9c. Zwrotniczego zaintrygowało nast˛epuj ˛
ace pytanie: z jak ˛
a pr˛edko´sci ˛
a z jego
punktu widzenia, poci ˛
agi zbli˙zaj ˛
a si˛e do siebie? Stosuj ˛
ac bezmy´slnie regułk˛e „nic nie mo˙ze
porusza´c si˛e szybciej od ´swiatła” powiedzieliby´smy, ˙ze pr˛edko´sci w jaki´s dziwny sposób musz ˛
a
si˛e doda´c tak, ˙zeby wyszło co´s mniejszego od c. Otó˙z nie! Je˙zeli zdefiniujemy pr˛edko´s´c zbli˙za-
nia si˛e jako zmian˛e odległo´sci mi˛edzy poci ˛
agami w czasie, to nie mo˙ze wyj´s´c nic innego ni˙z
1.8c! Natomiast, gdyby´smy zapytali jednego z maszynistów, z jak ˛
a pr˛edko´sci ˛
a zbli˙za si˛e do

1.4.
NIC NIE MO ˙
ZE PORUSZA ´
C SI ˛
E SZYBCIEJ OD ´SWIATŁA?
15
niego drugi poci ˛
ag, bez w ˛
atpienia poda on pr˛edko´s´c mniejsz ˛
a ni˙z c - o tym b˛edzie mowa pó´zniej.
Chc ˛
ac u˙zywa´c powiedzonka „nic nie mo˙ze porusza´c si˛e szybciej od ´swiatła” musimy przede
wszystkim pami˛eta´c, ˙ze „porusza´c si˛e” oznacza tu „porusza´c si˛e wzgl˛edem mnie”. W teorii
wzgl˛edno´sci przez ruch rozumie si˛e zazwyczaj ruch wzgl˛edem ustalonego obserwatora, a nie jak
w przytoczonej sytuacji ruch wzgl˛edny dwóch obiektów z punktu widzenia osoby trzeciej. Jed-
nak, jak wynika z kolejnych przykładów, stwierdzenie, ˙ze nic nie porusza si˛e szybciej od ´swiatła
wymaga dalszego doprecyzowania.
1.4.2
B
AJKA O STU KRASNOLUDKACH
N
a przyj˛ecie urodzinowe Królewny ´Snie˙zki przyszło sto krasnoludków z całego lasu. Postanow-
iły one zrobi´c Królewnie przyjemno´s´c i na jej cze´s´c wykona´c „meksyka´nsk ˛
a fal˛e”, któr ˛
a widzia-
ły w telewizji podczas transmisji meczu. Poniewa˙z wszystkie krasnoludki dostały kiedy´s od
Królewny w prezencie po zegarku, postanowiły u˙zy´c ich do wykonania fali. Krasnoludki zsyn-
chronizowały swoje wspaniałe zegarki i ustawiły si˛e w szeregu w równych odst˛epach. Nast˛epnie
ka˙zdy krasnoludek podskoczył o ustalonej wcze´sniej godzinie, przy czym pierwszy z brzegu
podskoczył punktualnie o 12.00, nast˛epny sekund˛e po dwunastej, kolejny dwie sekundy po dwu-
nastej itd. Krasnoludki nie zwracały uwagi na stoj ˛
acych obok kompanów, tylko uwa˙znie patrzyły
na swoje zegarki i o umówionej godzinie podskakiwały. Zastanówmy si˛e teraz czy co´s ogranicza
pr˛edko´s´c takiej poprzecznej fali? Oczywi´scie nie! Krasnoludki mog ˛
a sta´c w dowolnie du˙zych
odległo´sciach, a ustalone odst˛epy czasu pomi˛edzy kolejnymi podskokami mog ˛
a by´c dowolnie
krótkie. W szczególno´sci, taka fala mo˙ze porusza´c si˛e szybciej od ´swiatła (gdyby wszystkie
krasnoludki podskoczyły jednocze´snie, powiedzieliby´smy, ˙ze fala porusza si˛e niesko´nczenie
szybko)! Sytuacja ta nie byłaby natomiast mo˙zliwa gdyby krasnoludki podskakiwały dopiero
w momencie gdy zobacz ˛
a, ˙ze kolega obok wła´snie podskoczył.
1.4.3
L
ATARNIA MORSKA
W
ydawałoby si˛e, ˙ze przynajmniej ´swiatło w pró˙zni powinno porusza´c si˛e z pr˛edko´sci ˛
a ´swiatła,
prawda? Przeanalizujmy nast˛epuj ˛
ac ˛
a sytuacj˛e: Na ´srodku okr ˛
agłej wyspy stoi latarnia morska,
której kopuła obraca si˛e, regularnie „przemiataj ˛
ac” wyrzucanym ´swiatłem pełny k ˛
at. Wyobra´zmy
sobie teraz, ˙ze wzdłu˙z całego brzegu wyspy został rozstawiony wysoki parawan, po którym
dookoła porusza si˛e plama ´swiatła z latarni. Jaka jest dopuszczalna pr˛edko´s´c tej plamy? Czy jest
to pr˛edko´s´c ´swiatła? Nic podobnego! ´Swiatło to mo˙ze porusza´c si˛e wzdłu˙z parawanu dowolnie
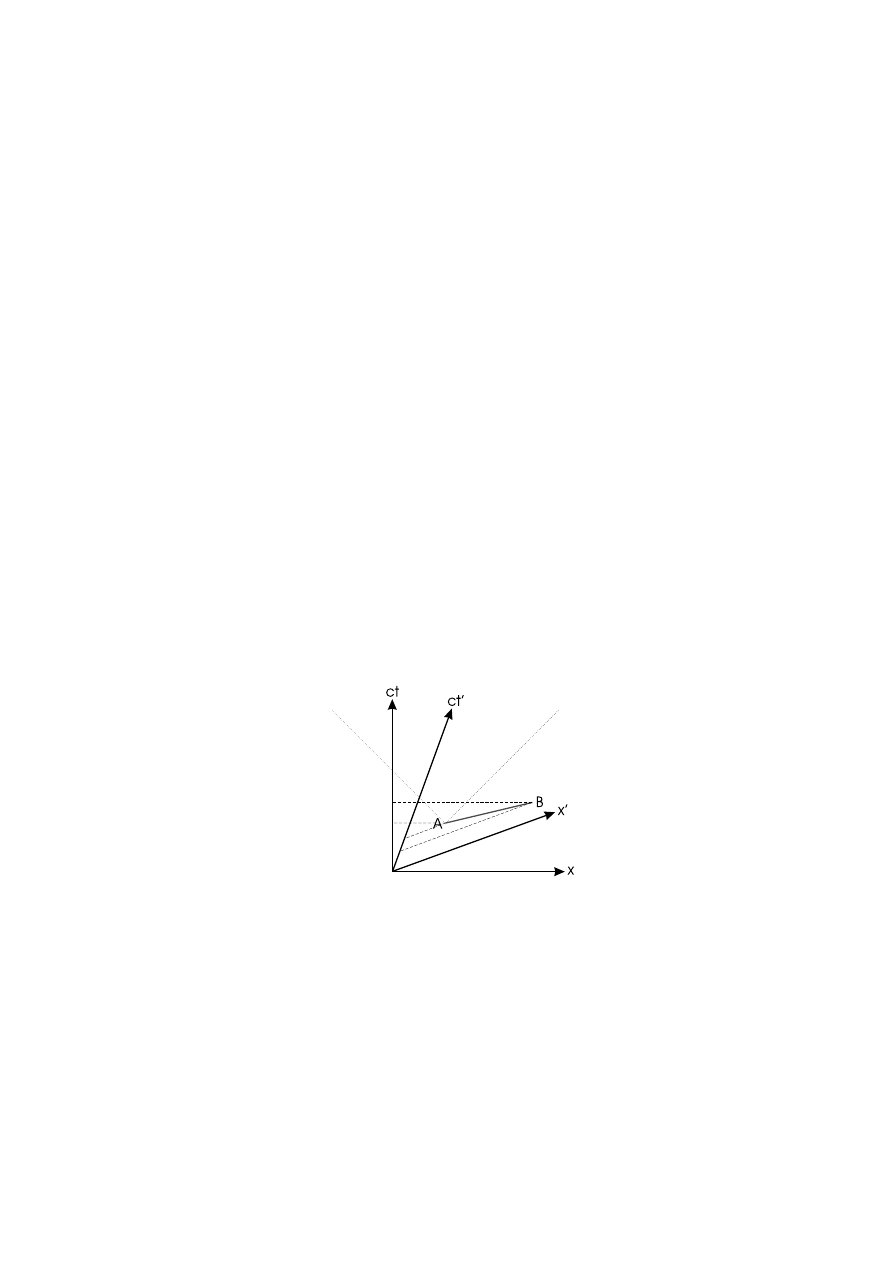
16
ROZDZIAŁ 1.
TRZ ˛
ESIENIE ZIEMI
szybko. Tym razem odpowied´z na pytanie jak to mo˙zliwe pozostawiamy Czytelnikowi.
Co w takim razie oznacza stwierdzenie, ˙ze nic nie mo˙ze porusza´c si˛e szybciej od ´swiatła?
Nasze w ˛
atpliwo´sci rozwieje chwilowo kolejny podrozdział.
1.5
P
ARADOKSY PRZYCZYNOWO
-
SKUTKOWE
W
yobra´zmy sobie, ˙ze co´s porusza si˛e z pr˛edko´sci ˛
a wi˛eksz ˛
a ni˙z c pomi˛edzy punktami A i B
wzdłu˙z pewnej trajektorii - rysunek 1.5 (trajektori˛e w czasoprzestrzeni nazywa si˛e lini ˛
a ´swiata
poruszaj ˛
acego si˛e obiektu). Mo˙ze to by´c meksyka´nska fala krasnoludków, plama ´swiatła latarni
morskiej, statek kosmiczny, cokolwiek. Z rysunku wida´c, ˙ze w układzie nieprimowanym porusza-
j ˛
acy si˛e obiekt był w punkcie A wcze´sniej ni˙z w punkcie B. Jednak˙ze je´sli linia ´swiata znaj-
duje si˛e poza obszarem dozwolonym dla obiektów poruszaj ˛
acych si˛e wolniej ni˙z c (kropkowany
sto˙zek), istniej ˛
a układy inercjalne w których zdarzenie w punkcie A nast ˛
api pó´zniej ni˙z zdarze-
nie w punkcie B. To znaczy, je´sli co´s porusza si˛e pomi˛edzy dwoma punktami A i B szybciej ni˙z
´swiatło, to w jednych układach odniesienia wida´c b˛edzie ruch z A do B, a w innych z B do A, jak
gdyby czas płyn ˛
ał wstecz. Na przykład je´sli meksyka´nska fala krasnoludków według Królewny
´Snie˙zki porusza si˛e w prawo, to dla przelatuj ˛acej na miotle Baby Jagi fala mo˙ze porusza´c si˛e w
lewo. Primowany układ Baby Jagi przedstawiono wła´snie na rysunku 1.5.
Rysunek 1.5:
Tor obiektu poruszaj ˛
acego si ˛e pomi ˛edzy punktami
A
i
B
z pr ˛edko´sci ˛
a ponad-
´swietln ˛
a. Kropkowane linie ograniczaj ˛
a obszar dozwolony dla obiektów poruszaj ˛
acych si ˛e z pr ˛edko´sciami
mniejszymi ni˙z
c
i zaczynaj ˛
acymi swój bieg w punkcie
A
. Linie przerywane rzutuj ˛
a punkty
A
i
B
na osie
czasu dwóch ró˙znych układów inercjalnych. Wida´c, ˙ze „kolejno´s´c nast ˛epstw” ulega odwróceniu.
Je˙zeli rozwa˙zanym, ponad´swietlnym obiektem jest na przykład statek kosmiczny, od razu
pojawia si˛e pewien paradoks: w jednych układach odniesienia załoga statku b˛edzie si˛e starze´c,

1.6.
INTERWAŁ CZASOPRZESTRZENNY
17
a w innych czas b˛edzie płyn ˛
a´c w odwrotn ˛
a stron˛e i załoga odmłodnieje. W drastycznej wer-
sji paradoksu w pewnych układach odniesienia kosmonauta mógłby najpierw umrze´c, a potem
si˛e urodzi´c. Poniewa˙z istnienie paradoksów tego typu nie mo˙ze by´c zaakceptowane, powszech-
nie twierdzi si˛e, ˙ze obiekty takie jak statek kosmiczny nie mog ˛
a porusza´c si˛e z pr˛edko´sciami
nad´swietlnymi. Przyjmuje si˛e, ˙ze nie mog ˛
a istnie´c ponad´swietlne sygnały nios ˛
ace jak ˛
akolwiek
informacj˛e, bo w pewnych układach odniesienia informacja mogłaby dotrze´c do odbiorcy zanim
została wysłana przez nadawc˛e. W szczególno´sci wolno nam z tego powodu rozwa˙za´c tylko
układy inercjalne poruszaj ˛
ace si˛e wzgl˛edem siebie z pr˛edko´sciami V < c. Okazuje si˛e jednak,
˙ze bardzo ciekawe i zupełnie nowe aspekty tego zagadnienia pojawiaj ˛
a si˛e wraz z mechanik ˛
a
kwantow ˛
a - b˛edzie o tym mowa pó´zniej. W ka˙zdym razie kwestia jest niezwykle delikatna, a na
pewno nie została dotychczas dobrze zrozumiana.
Zamian˛e kolejno´sci zdarze´n mo˙zna przeanalizowa´c przy pomocy wzorów transformacyjnych
(1.6). Niech zdarzenie A oznacza wysłanie pewnego sygnału, a B jego dotarcie do odbiorcy. Je´sli
w układzie nieprimowanym odległo´s´c przestrzenna pomi˛edzy A i B wynosi ∆x, a odst˛ep czasu
mi˛edzy nimi ∆t > 0, to w układzie primowanym odst˛ep czasu wyniesie:
∆t
0
=
∆t − V ∆x/c
2
p
1 − V
2
/c
2
.
(1.15)
Przyjrzyjmy si˛e licznikowi tego wyra˙zenia: ∆t − V ∆x/c
2
. Jest on dodatni w ka˙zdym układzie
inercjalnym poruszaj ˛
acym si˛e z pr˛edko´sci ˛
a V < c, o ile ∆x ≤ c∆t, czyli je˙zeli sygnał porusza
si˛e najwy˙zej z pr˛edko´sci ˛
a ´swiatła. Natomiast je´sli sygnał jest ponad´swietlny i ∆x > c∆t, to w
pewnych układach odniesienia ∆t
0
< 0. Oznacza to, ˙ze w tych układach sygnał propaguje si˛e
od odbiorcy do nadawcy. Powracamy zatem do wniosków wyci ˛
agni˛etych na podstawie analizy
rysunku 1.5.
1.6
I
NTERWAŁ CZASOPRZESTRZENNY
P
owrócimy teraz do poj˛ecia interwału czasoprzestrzennego. Zauwa˙zmy, ˙ze je˙zeli interwał ∆s
2
pomi˛edzy dwoma zdarzeniami jest ujemny, to zdarzenia te nie mog ˛
a by´c poł ˛
aczone ˙zadnym
pod´swietlnym sygnałem. Interwały ujemne nazywa si˛e „przestrzennymi”. Je˙zeli interwał jest
dodatni (interwał „czasowy”), to przesłanie pod´swietlnej informacji pomi˛edzy zdarzeniami jest
mo˙zliwe, natomiast je´sli wynosi on zero (interwał „zerowy”), to zdarzenia mog ˛
a zosta´c poł ˛
aczo-
ne tylko sygnałem poruszaj ˛
acym si˛e dokładnie z pr˛edko´sci ˛
a ´swiatła.

18
ROZDZIAŁ 1.
TRZ ˛
ESIENIE ZIEMI
Chcieliby´smy teraz omówi´c interesuj ˛
ac ˛
a wła´sciwo´s´c interwału czasoprzestrzennego od której
rozpocz˛eli´smy wykład. Wiemy, ˙ze pod wpływem transformacji Lorentza wyra˙zenie:
∆s
2
= c
2
∆t
2
− ∆x
2
− ∆y
2
− ∆z
2
(1.16)
nie zmienia swojej warto´sci przy zmianie układu odniesienia. Konsekwencje tego faktu s ˛
a
bardzo wa˙zne. Dzi˛eki niemu teoria wzgl˛edno´sci ma szans˛e w deterministyczny sposób opisy-
wa´c ´swiat. Wyobra´zmy sobie, ˙ze zdarzenie B oznacza wybuch bomby w pewnym miejscu i w
okre´slonej chwili. Je˙zeli bomba została uruchomiona zdalnym detonatorem umieszczonym w
innym punkcie przestrzeni i we wcze´sniejszej chwili A, to interwał czasoprzestrzenny pomi˛edzy
tymi dwoma zdarzeniami musi by´c czasowy lub zerowy. Z niezmienno´sci interwału wzgl˛edem
transformacji Lorentza wynika, ˙ze je˙zeli w pewnym układzie nast ˛
apił przyczynowo skutkowy
ci ˛
ag zdarze´n (czyli ci ˛
ag w którym zachodz ˛
ace zdarzenia wynikały ze zdarze´n wcze´sniejszych),
to kolejno´s´c tych zdarze´n w innych układach inercjalnych nie zmieni si˛e (czyli przyczynowo´s´c
b˛edzie zachowana). Je´sli bowiem w jednym układzie inercjalnym interwał mi˛edzy dwoma
zdarzeniami jest dodatni, to taki te˙z b˛edzie w dowolnym innym układzie. W naszym „bom-
bowym” przykładzie, detonator b˛edzie uruchamiany zanim wybuchnie bomba i odpowiednio
wcze´sniej we wszystkich mo˙zliwych układach inercjalnych.
Je˙zeli natomiast w pewnym układzie odniesienia dwa zdarzenia s ˛
a oddzielone interwałem
przestrzennym (czyli nie tworz ˛
a ci ˛
agu przyczynowo skutkowego), to b˛edzie tak równie˙z w
dowolnym innym układzie. Wynika to zreszt ˛
a bezpo´srednio z poprzedniego wniosku i odwracal-
no´sci transformacji Lorentza.
Jest teraz dobra okazja by wspomnie´c o bardzo wa˙znej zasadzie w teorii wzgl˛edno´sci. Za-
sadzie, z której dotychczas po cichu korzystali´smy nie b˛ed ˛
ac tego do ko´nca ´swiadomi. Brzmi
ona tak: ka˙zde zdarzenie widziane w jednym układzie inercjalnym, musi zachodzi´c równie˙z w
ka˙zdym innym inercjalnym układzie. Zatem nie da si˛e stwierdzi´c ˙ze układ inercjalny porusza si˛e
wzgl˛edem jakiegokolwiek wyró˙znionego ciała w inny sposób ni˙z poprzez obserwacj˛e ruchu tego
ciała. Wydaje si˛e oczywiste, prawda? Na przykład je´sli w jednym układzie wybuchła bomba, to
musi ona równie˙z wybuchn ˛
a´c w dowolnym (w szczególno´sci inercjalnym) układzie poruszaj ˛
a-
cym si˛e. Zasada ta oznacza, ˙ze nie istnieje ˙zaden wyró˙zniony układ inercjalny i z tego powodu
nazywa si˛e j ˛
a czasem zasad ˛
a demokracji układów inercjalnych. Wkrótce przekonamy si˛e, ˙ze
mimo pozornej „trywialno´sci” tego faktu, płyn ˛
a z niego bardzo wa˙zne i nietrywialne wnioski.

1.6.
INTERWAŁ CZASOPRZESTRZENNY
19
Pytania
• Czy mog ˛
a istnie´c nieliniowe transformacje zachowuj ˛
ace stało´s´c pr˛edko´sci ´swiatła we wszys-
tkich układach inercjalnych?
• Czym mo˙zna uzasadni´c wprowadzenie nowego poj˛ecia czasoprzestrzeni?
• Jaka jest interpretacja geometryczna transformacji Lorentza?
• Czy i kiedy zło˙zenie dwóch transformacji Lorentza jest przemienne?
• Czy zło˙zenie transformacji Lorentza dla ruchu z pr˛edko´sci ˛
a V i transformacji dla ruchu z
pr˛edko´sci ˛
a −V wzdłu˙z tego samego kierunku jest identyczno´sci ˛
a?
• Jak poprawnie u´sci´sli´c powszechnie u˙zywane sformułowanie mówi ˛
ace, ˙ze nic nie mo˙ze
porusza´c si˛e szybciej od ´swiatła?
• Jak ˛
a rol˛e w szczególnej teorii wzgl˛edno´sci odgrywa interwał czasoprzestrzenny?
• Dlaczego na rysunku 1.5 rzutowanie zdarze´n na o´s czasu dokonywane jest wzdłu˙z osi
przestrzennej, a nie prostopadle do osi czasu i analogicznie dla rzutowania na o´s przestrzenn ˛
a?
• W jaki sposób mo˙zna łatwo wyprowadzi´c posta´c transformacji Lorentza współrz˛ednej cza-
sowej przy znajomo´sci transformacji współrz˛ednych przestrzennych?
Zadania
• Podaj transformacj˛e Lorentza do układu odniesienia poruszaj ˛
acego si˛e z pr˛edko´sci ˛
a V
wzdłu˙z prostej le˙z ˛
acej w płaszczy´znie XY nachylonej pod k ˛
atem 45
◦
do osi X. W chwili
t = t
0
= 0 pocz ˛
atki obu układów inercjalnych pokrywały si˛e. Wskazówka: dogodnie
jest wyrazi´c transformacj˛e Lorentza dla dowolnie skierowanej pr˛edko´sci poprzez iloczyn
skalarny wektora poło˙zenia z wektorem pr˛edko´sci.
• Do milicjanta stoj ˛
acego po´srodku skrzy˙zowania zbli˙zaj ˛
a si˛e z jednakowymi pr˛edko´sciami
V = 0.9c dwa samochody: jeden od północy, a drugi od wschodu. Ze wzgl˛edu na awari˛e
sygnalizacji w chwili t = 0 dojdzie do zderzenia. Zanim dojdzie do wypadku, pomó˙z
milicjantowi odpowiedzie´c na nast˛epuj ˛
ace pytania: Z jak ˛
a pr˛edko´sci ˛
a z punktu widzenia

20
ROZDZIAŁ 1.
TRZ ˛
ESIENIE ZIEMI
milicjanta zbli˙zaj ˛
a si˛e do siebie samochody? Z jak ˛
a pr˛edko´sci ˛
a według jednego z kierow-
ców zbli˙za si˛e do niego drugi samochód? Czy w którym´s z wymienionych przypadków
milicjant powinien czu´c si˛e zaniepokojony przekroczeniem dozwolonej w obszarze zabu-
dowanym pr˛edko´sci c?
• Dla transformacji Galileusza narysuj osie współrz˛ednych czasoprzestrzennych obserwa-
tora poruszaj ˛
acego si˛e z pr˛edko´sci ˛
a V wzdłu˙z osi X. Podaj k ˛
aty wzgl˛ednego nachylenia
osi jako funkcje wzgl˛ednej pr˛edko´sci. Uwzgl˛ednij relacje pomi˛edzy jednostkami na osi-
ach.

Rozdział 2
K
INEMATYKA RELATYWISTYCZNA
2.1
W
IELOZNACZNA JEDNOCZESNO ´S ´
C
D
wa jednoczesne zdarzenia zachodz ˛
ace w ró˙znych punktach przestrzeni (na przykład jedno-
czesne tupni˛ecie dwoma butami) s ˛
a oddzielone interwałem przestrzennym. Wiemy, ˙ze takie
zdarzenia nie mog ˛
a by´c poł ˛
aczone ci ˛
agiem przyczynowo skutkowym, bo mógłby poł ˛
aczy´c je
jedynie sygnał poruszaj ˛
acy si˛e niesko´nczenie szybko. Podobnie w ka˙zdym innym układzie
odniesienia interwał b˛edzie przestrzenny. Jednak˙ze ze zmian ˛
a układu odniesienia wi ˛
a˙ze si˛e
niezwykła konsekwencja: je˙zeli zdarzenia s ˛
a jednoczesne w jednym układzie, to w wi˛ekszo´sci
innych, poruszaj ˛
acych si˛e wzgl˛edem niego inercjalnych układów, zdarzenia te nie b˛ed ˛
a jed-
noczesne! Sprawd´zmy, ˙ze jest tak w rzeczywisto´sci. Rozwa˙zmy dwa jednoczesne (∆t = 0)
zdarzenia oddalone o ∆x. W układzie poruszaj ˛
acym si˛e z pr˛edko´sci ˛
a V 6= 0 odst˛ep czasu
pomi˛edzy nimi odczytujemy ze wzorów (1.6):
∆t
0
=
∆t − V ∆x/c
2
p
1 − V
2
/c
2
=
−V ∆x/c
2
p
1 − V
2
/c
2
6= 0.
(2.1)
Oznacza to, ˙ze osoba przeje˙zd˙zaj ˛
aca w pobli˙zu poci ˛
agiem zaobserwuje, ˙ze najpierw tupn ˛
ał lewy,
a potem prawy but (lub odwrotnie). Jak to mo˙zliwe? Do podobnych wniosków dochodzili´smy
ju˙z w poprzednim rozdziale. Przypomnijmy sobie, ˙ze przej´scie do poruszaj ˛
acego si˛e układu
współrz˛ednych oznacza obserwacj˛e zjawisk z układu „obróconego” w czasoprzestrzeni. Na
tej samej zasadzie dwa ko´nce kija mog ˛
a by´c od jednego obserwatora równooddalone, ale od
drugiego, patrz ˛
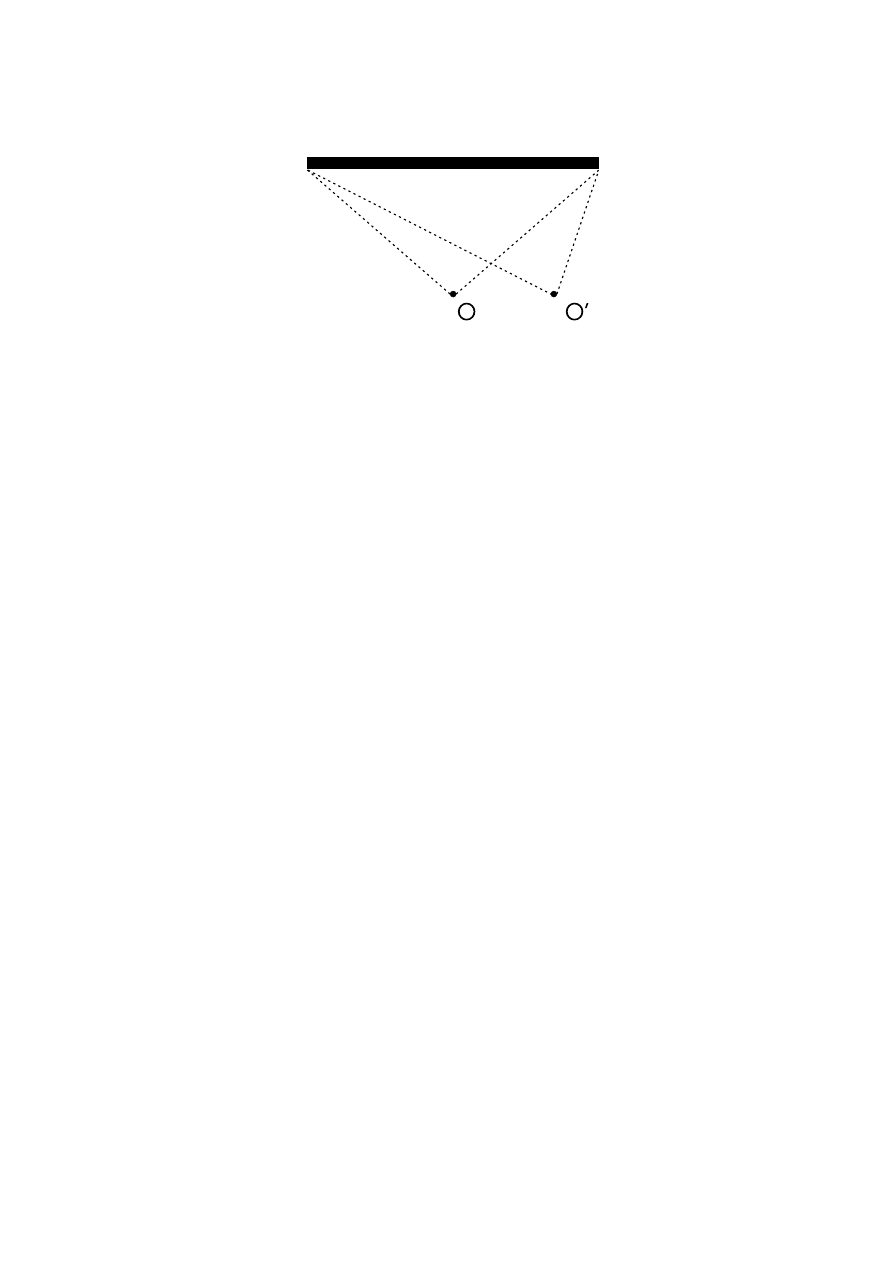
acego z boku, ka˙zdy koniec znajdzie si˛e w innej odległo´sci - rysunek 2.1. Wida´c
st ˛
ad, ˙ze zadawanie pytania „czy zdarzenia s ˛
a naprawd˛e jednoczesne, czy nie?” nie ma sensu.
21
22
ROZDZIAŁ 2.
KINEMATYKA RELATYWISTYCZNA
Rysunek 2.1:
Dwa ko ´nce kija znajduj ˛
a si ˛e w jednakowych b ˛
ad´z ró˙znych odległo´sciach w zale˙zno´sci od
obserwatora. Na tej samej zasadzie dwa zdarzenia zachodz ˛
ace jednocze´snie dla jednego obserwatora
nie musz ˛
a by´c jednoczesne dla innego.
Podobnie bezsensowne jest zadawanie pytania czy ko´nce kija s ˛
a „naprawd˛e” równooddalone.
Oczywi´scie zale˙zy od kogo! Nie istnieje „bezwzgl˛edne równooddalenie” podobnie jak nie ist-
nieje „bezwzgl˛edna równoczasowo´s´c” czyli „bezwzgl˛edna jednoczesno´s´c”.
2.2
D
YLATACJA CZASU
A
nalogi˛e z kijem mo˙zemy nadal eksploatowa´c. Na przykład obserwator patrz ˛
acy na kij „pod
k ˛
atem” mo˙ze uzna´c, ˙ze kij jest krótszy, a patrz ˛
ac zupełnie z boku mo˙ze wr˛ecz stwierdzi´c, ˙ze
długo´s´c kija wynosi zero (oczywi´scie nasz idealny kij jest niesko´nczenie cienki ;-). Czy to
samo mo˙ze dotyczy´c równie˙z czasu? Okazuje si˛e, ˙ze tempo upływu czasu w ró˙znych układach
inercjalnych jest ró˙zne. Rzu´cmy okiem raz jeszcze na rysunek 1.5. S ˛
a na nim narysowane dwa
zdarzenia A i B zrzutowane na osie czasu dwóch układów inercjalnych. Zwró´cmy uwag˛e, ˙ze
odst˛ep czasu na osi ct (czyli długo´s´c odcinka pomi˛edzy rzutami punktów A i B) jest inny ni˙z na
osi ct
0
. Aby jednak stwierdzi´c czy tempo upływu czasu zale˙zy od układu odniesienia musimy
przeanalizowa´c wskazania zegara umieszczonego nieruchomo w jednym z układów z punktu
widzenia drugiego układu.
Przeanalizujemy zmian˛e upływu czasu w sposób ilo´sciowy przy pomocy transformacji Lorentza.
Rozwa˙zmy zegar umieszczony w pocz ˛
atku x
0
= 0 układu inercjalnego poruszaj ˛
acego si˛e z pr˛ed-
ko´sci ˛
a V . Zegar odmierzył odst˛ep czasu ∆t
0
pomi˛edzy pewnymi dwoma zdarzeniami widzianymi
z punktu widzenia tego układu. Sprawd´zmy jakiemu odst˛epowi czasu ∆t odpowiada to w
układzie nieruchomym. Z transformacji (1.7) znajdujemy:

2.3.
SKRÓCENIE LORENTZA
23
∆t =
∆t
0
p
1 − V
2
/c
2
,
(2.2)
czyli ∆t
0
< ∆t. Według obserwatora nieruchomego czas w poruszaj ˛
acym si˛e układzie płynie
wolniej! Chod´z wygl ˛
ada to dziwnie, taki sam wniosek musi wyci ˛
agn ˛
a´c „obserwator primowany”
na temat upływu czasu w układzie nieprimowanym. Ten pozornie paradoksalny fakt zostanie
jeszcze omówiony dalej.
2.3
S
KRÓCENIE
L
ORENTZA
P
odobnym do spowolnienia upływu czasu zjawiskiem jest skrócenie poruszaj ˛
acych si˛e obiek-
tów w kierunku ruchu. Je˙zeli udało nam si˛e przełkn ˛
a´c geometryczn ˛
a interpretacj˛e zmiany układu
odniesienia, spowolnienie upływu czasu, skrócenie obiektów w ruchu nie powinno nas ju˙z dzi-
wi´c. Ilo´sciowa analiza tego skrócenia jest podobna do rozumowania z poprzedniego podrozdzia-
łu. Wyobra´zmy sobie kij o długo´sci ∆x
0
, spoczywaj ˛
acy w primowanym układzie wzdłu˙z osi x
0
.
Jak wygl ˛
ada kij z punktu widzenia układu nieprimowanego (wzgl˛edem którego poprzedni układ
porusza si˛e tradycyjnie z pr˛edko´sci ˛
a V wzdłu˙z osi x)? To znaczy ile wynosi w tym układzie
długo´s´c kija ∆x? Znajdujemy j ˛
a bez problemu korzystaj ˛
ac z transformacji (1.6). W tym celu
musimy obliczy´c ró˙znic˛e współrz˛ednych ∆x w tej samej chwili w układzie nieprimowanym, wi˛ec
bierzemy ∆t = 0:
∆x = ∆x
0
p
1 − V
2
/c
2
.
(2.3)
Jest to wła´snie słynne skrócenie Lorentza: im szybciej porusza si˛e kij, tym staje si˛e krótszy.
Chcieliby´smy teraz wyra´znie podkre´sli´c, dlaczego korzystali´smy z transformacji (1.6), a nie z
transformacji odwrotnej (1.7). Gdyby´smy skorzystali z tej drugiej bior ˛
ac ∆t
0
= 0, otrzymaliby´s-
my w wyniku raczej wydłu˙zenie, ni˙z skrócenie Lorentza. Otó˙z jest rzecz ˛
a niezwykle istotn ˛
a, ˙ze
mierz ˛
ac w wybranym układzie odniesienia jak ˛
a´s długo´s´c, czyli ró˙znic˛e współrz˛ednych dwóch
punktów, musimy zawsze oblicza´c odejmowane współrz˛edne w tej samej chwili czasu. Je˙zeli
mierzyliby´smy poło˙zenie ko´nców poruszaj ˛
acego si˛e kija w ró˙znych chwilach, kij w mi˛edzycza-
sie zd ˛
a˙zyłby si˛e troch˛e przesun ˛
a´c zafałszowuj ˛
ac wyniki naszych pomiarów. Dlatego wła´snie
musimy koniecznie przyj ˛
a´c, ˙ze poło˙zenie obu ko´nców obliczamy (lub mierzymy) jednocze´snie,
24
ROZDZIAŁ 2.
KINEMATYKA RELATYWISTYCZNA
czyli ∆t = 0, a nie ∆t
0
= 0. Poniewa˙z z pocz ˛
atku rozdziału wiemy, ˙ze poj˛ecie jednoczesno´sci
zale˙zy od układu odniesienia, oba podej´scia nie s ˛
a równowa˙zne.
Skrócenie o którym mówili´smy jest skróceniem w kierunku ruchu. Czy mo˙zliwe jest równie˙z
skrócenie w kierunku poprzecznym do kierunku ruchu? Załó˙zmy, ˙ze jest ono mo˙zliwe i przeana-
lizujmy nast˛epuj ˛
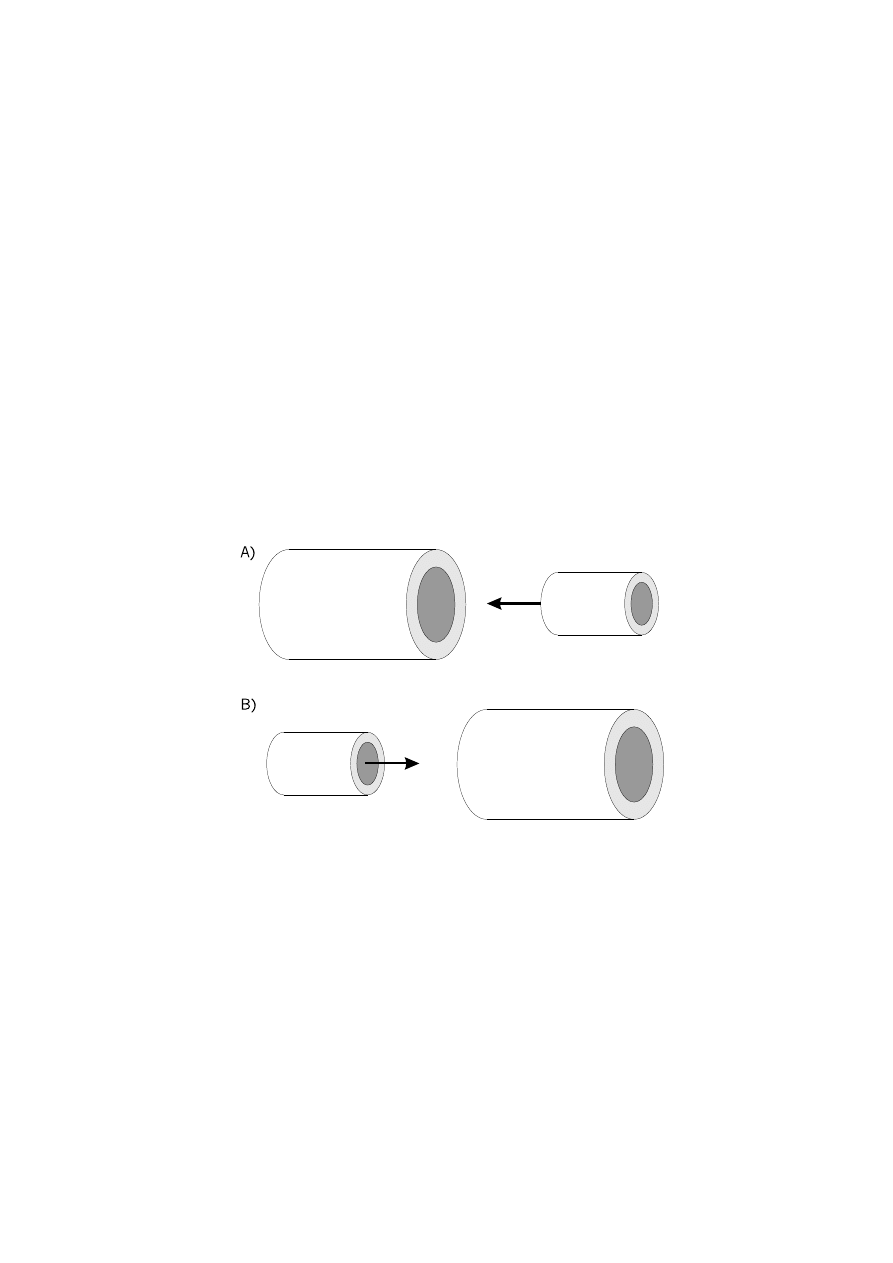
acy eksperyment my´slowy - rysunek 2.2. Rozwa˙zmy dwie identyczne, współ-
osiowe rury zbli˙zaj ˛
ace si˛e do siebie wzdłu˙z wspólnej osi symetrii. Je˙zeli podczas szybkiego
ruchu obiekty doznaj ˛
a skrócenia wzdłu˙z kierunku poprzecznego do pr˛edko´sci, to w układzie
zwi ˛
azanym z ka˙zd ˛
a z rur, druga b˛edzie zawsze w˛e˙zsza i przy odpowiednio du˙zej pr˛edko´sci
mo˙ze przelecie´c „na wylot”. Jest jasne, ˙ze to, która rura przeleci wewn ˛
atrz drugiej zale˙zy
od punktu widzenia. Zatem, je´sli jedn ˛
a z rur zast ˛
apimy wypełnionym w ´srodku walcem, to
w jednym układzie inercjalnym ciała bezpiecznie si˛e min ˛
a, a w drugim dojdzie do zderzenia.
Przykład ten ilustruje niemo˙zno´s´c istnienia skrócenia poprzecznego. Byłoby to niezgodne z za-
sad ˛
a demokracji: w ró˙znych układach odniesienia działyby si˛e ró˙zne rzeczy.
Rysunek 2.2:
Ruch wzgl ˛edny dwóch rur z hipotetycznym skróceniem poprzecznym. Widok z dwóch
układów odniesienia.
2.4
P
ARADOKS POCI ˛
AGU I DWORCA
Z
e skróceniem Lorentza wi ˛
a˙ze si˛e wiele „paradoksów”. Naturalnie owe paradoksy nie s ˛
a wcale
„paradoksalne” w tym sensie, ˙ze rzekome sprzeczno´sci s ˛
a czysto pozorne i, w przeciwie´nstwie

2.5.
CZY SKRÓCENIE LORENTZA JEST RZECZYWISTE?
25
do problemów zwi ˛
azanych ze skróceniem poprzecznym, po krótkim namy´sle mo˙zna wskaza´c
przyczyn˛e zamieszania i rozwi ˛
aza´c paradoks.
Paradoks poci ˛
agu i dworca jest nast˛epuj ˛
acy: wzdłu˙z peronu szybko przeje˙zd˙za poci ˛
ag. Gdyby
poci ˛
ag si˛e zatrzymał, jego długo´s´c byłaby dokładnie równa długo´sci peronu. Poniewa˙z jednak
wagony poruszaj ˛
a si˛e bardzo szybko, pojawia si˛e skrócenie Lorentza i w pewnej chwili cały skład
poci ˛
agu znajduje si˛e „wewn ˛
atrz” peronu. Jednak˙ze z punktu widzenia pasa˙zerów to peron ulega
skróceniu i w ˙zadnej chwili poci ˛
ag nie znajduje si˛e „wewn ˛
atrz” peronu. Jest wr˛ecz odwrotnie,
to peron mie´sci si˛e „wewn ˛
atrz” poci ˛
agu. Jak to mo˙zliwe?
Pozorna sprzeczno´s´c wynika z tego, ˙ze w problemie pojawia si˛e tylnymi drzwiami poj˛e-
cie jednoczesno´sci. Mówi ˛
ac, ˙ze w pewnej chwili poci ˛
ag znajduje si˛e wewn ˛
atrz peronu mamy
na my´sli, ˙ze czoło lokomotywy znajduje si˛e w obr˛ebie peronu jednocze´snie z tyłem ostatniego
wagonu. Naturalnie momenty w których mierzono na peronie poło˙zenie lokomotywy i ostat-
niego wagonu nie b˛ed ˛
a jednoczesne dla pasa˙zerów poci ˛
agu. Według nich poło˙zenie lokomo-
tywy zostanie zmierzone najpierw, a w chwil˛e pó´zniej, gdy poci ˛
ag zd ˛
a˙zy kawałek przejecha´c,
zmierzone zostanie poło˙zenie ostatniego wagonu i vice versa. Przykład ten powinien nauczy´c
nas ostro˙znego przygl ˛
adania si˛e wszelkim „paradoksom” teorii wzgl˛edno´sci. Powinni´smy by´c
szczególnie czujni, czy gdzie´s nie pojawia si˛e wła´snie zdradliwa jednoczesno´s´c.
2.5
C
ZY SKRÓCENIE
L
ORENTZA JEST RZECZYWISTE
?
Stawimy teraz czoła nast˛epuj ˛
acemu wa˙znemu pytaniu: czy skrócenie Lorentza jest rzeczywiste,
czy te˙z jest jedynie czym´s pozornym, matematyczn ˛
a ciekawostk ˛
a nie maj ˛
ac ˛
a zwi ˛
azku z rzeczy-
wisto´sci ˛
a? Musimy by´c udzielonej odpowiedzi absolutnie pewni, bowiem tylko wówczas mamy
szans˛e dobrze zrozumie´c relatywistyczny charakter rzeczywisto´sci. Pewno´s´c ta powinna nam
towarzyszy´c od samego pocz ˛
atku gdy analizowali´smy relatywistyczne transformacje zmiany
układu odniesienia. Rzeczy te s ˛
a jednak dla nas wci ˛
a˙z nowe i st ˛
ad konieczno´s´c oswojenia si˛e z
nimi (czemu zreszt ˛
a słu˙zy´c maj ˛
a równie˙z kolejne rozdziały).
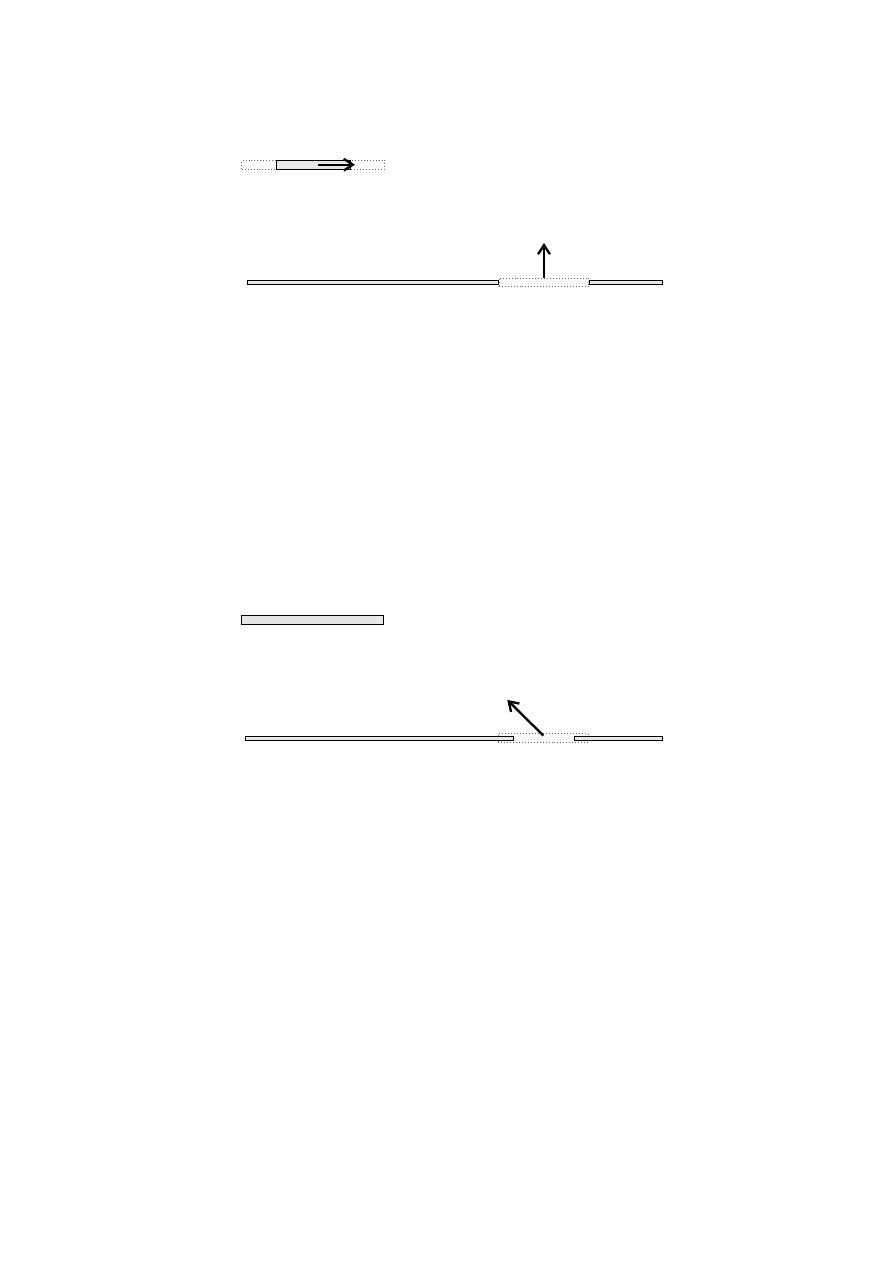
Rozwa˙zmy sytuacj˛e przedstawion ˛
a na rysunku 2.3. Mamy tam poruszaj ˛
acy si˛e poziomo pr˛et
oraz poruszaj ˛
ac ˛
a si˛e pionowo „dziur˛e”. Ich poło˙zenia i pr˛edko´sci mo˙zemy dobra´c w taki sposób,
aby, o ile skrócenie Lorentza jest rzeczywiste, pr˛et przeleciał przez dziur˛e bez szwanku. Gdyby
jednak skrócenie było jedynie matematycznym trikiem, musiałoby doj´s´c do zderzenia. Szek-
spirowski dylemat, który przed nami stoi, brzmi: przeleci czy nie przeleci? - oto jest pytanie!
Przede wszystkim kto´s z Was mógłby zauwa˙zy´c co nast˛epuje. Przejd´zmy do układu odniesie-
26
ROZDZIAŁ 2.
KINEMATYKA RELATYWISTYCZNA
Rysunek 2.3:
Poruszaj ˛
acy si ˛e poziomo pr ˛et oraz poruszaj ˛
ac ˛
a si ˛e pionowo „dziura”. Kropkowan ˛
a lini ˛
a
zaznaczono kształty spoczynkowe. Poło˙zenia i pr ˛edko´sci dobrane s ˛
a w taki sposób, aby skrócony pr ˛et
przeleciał przez dziur ˛e bez szwanku.
nia w którym pr˛et spoczywa, a dziura porusza si˛e uko´snie. Poniewa˙z dziura ma teraz dodatkow ˛
a
poziom ˛
a składow ˛
a pr˛edko´sci, musi pojawi´c si˛e dodatkowe poziome skrócenie - rysunek 2.4.
Zatem widzimy, ˙ze niezale˙znie czy skrócenie jest czy go nie ma - musi doj´s´c do zderzenia!
Czyli rozumuj ˛
ac dalej, stosujemy zasad˛e demokracji - i tak˙ze w pierwszym układzie odniesienia
zderzenie musi nast ˛
api´c, czyli skrócenie wcale nie jest rzeczywiste.
Ale czy rzeczywi´scie? :-)
Rysunek 2.4:
Ta sama sytuacja w układzie spoczynkowym pr ˛eta.
Otó˙z popełnili´smy powa˙zny bł ˛
ad! Rysunek 2.4 i przedstawione rozumowanie s ˛
a niepoprawne.
Wła´sciwa wersja wydarze´n w drugim układzie odniesienia przedstawiona jest na rysunku 2.5.
Musimy przecie˙z pami˛eta´c, ˙ze skrócenie jest zawsze w kierunku ruchu! Nie mo˙zemy uzyska´c
poprawnego skrócenia dokonuj ˛
ac go wzdłu˙z kierunku jednej składowej pr˛edko´sci, a nast˛epnie
wzdłu˙z kierunku drugiej składowej. Tak wła´snie uczynili´smy na rysunku 2.4 na którym wida´c
gołym okiem, ˙ze skrócenie nie jest wzdłu˙z kierunku pr˛edko´sci, czyli ´zle! Jednak na rysunku
2.5 jest ju˙z wszystko w porz ˛
adku - skrócenie jest, tak jak powinno, wzdłu˙z kierunku pr˛edko´sci.
Widzimy, ˙ze skrócenie Lorentza wymaga, by dziura si˛e obróciła.
Widzimy ponadto, ˙ze tak˙ze w tym układzie losy klocka zale˙z ˛
a od tego czy skrócenie jest

2.6.
ELEKTRYZUJ ˛
ACY PARADOKS ELEKTRYCZNY
27
Rysunek 2.5:
Ta sama sytuacja w układzie spoczynkowym pr ˛eta - tym razem wersja poprawna.
rzeczywiste czy nie! Je´sli jest - zderzenia nie b˛edzie w ˙zadnym z układów jak tego ˙z ˛
ada za-
sada demokracji. Je˙zeli nie jest, zderzenie b˛edzie (tak˙ze w obu układach). Zatem nic nie stoi
na przeszkodzie by twierdzi´c, ˙ze skrócenie Lorentza jest jak najbardziej rzeczywiste i pr˛et w
obydwu układach przeleci przez dziur˛e na wylot.
2.6
E
LEKTRYZUJ ˛
ACY PARADOKS ELEKTRYCZNY
Z
mienimy teraz na chwil˛e temat. Zajmiemy si˛e bowiem paradoksem, znanym jeszcze przed
pojawieniem si˛e teorii wzgl˛edno´sci, a zwi ˛
azanym z klasyczn ˛
a teori ˛
a elektromagnetyzmu. Jest
rzecz ˛
a ciekaw ˛
a, ˙ze spory i trudno´sci wokół tego problemu nie dawały si˛e przez kilkadziesi ˛
at lat w
˙zaden „klasyczny” sposób usun ˛
a´c i dopiero teoria wzgl˛edno´sci przyniosła ostateczne rozwi ˛
azanie.
Naprawd˛e, paradoks ten, jak i inne niepokonane wówczas sprzeczno´sci elektrodynamiki Maxwel-
la były bod´zcem do powstania szczególnej teorii wzgl˛edno´sci. Nie zapominajmy zreszt ˛
a, ˙ze
rozwa˙zaj ˛
ac na pocz ˛
atku tego wykładu zachowanie si˛e ´swiatła, zajmowali´smy si˛e w gruncie
rzeczy badaniem pró˙zniowych rozwi ˛
aza´n równa´n Maxwella. ´Swiatło jest w ko´ncu fal ˛
a elektro-
magnetyczn ˛
a!
Przyst ˛
apmy zatem do przedstawienia problemu. Rozwa˙zmy oboj˛etnie naładowany, pros-
toliniowy przewód elektryczny przez który płynie pr ˛
ad. Z mikroskopowego punktu widzenia
pr ˛
ad jest ruchem ujemnych elektronów z pewn ˛
a ´sredni ˛
a wypadkow ˛
a pr˛edko´sci ˛
a V na tle do-
datnich, nieruchomych jonów sieci krystalicznej przewodnika. Nat˛e˙zenie tego pr ˛
adu wynosi
I = e%
−
V S, gdzie %
−
jest g˛esto´sci ˛
a elektronów w przewodniku, a S polem przekroju drutu.
Wyobra´zmy sobie, ˙ze w odległo´sci r od przewodu, równolegle do niego porusza si˛e z t ˛
a sam ˛
a
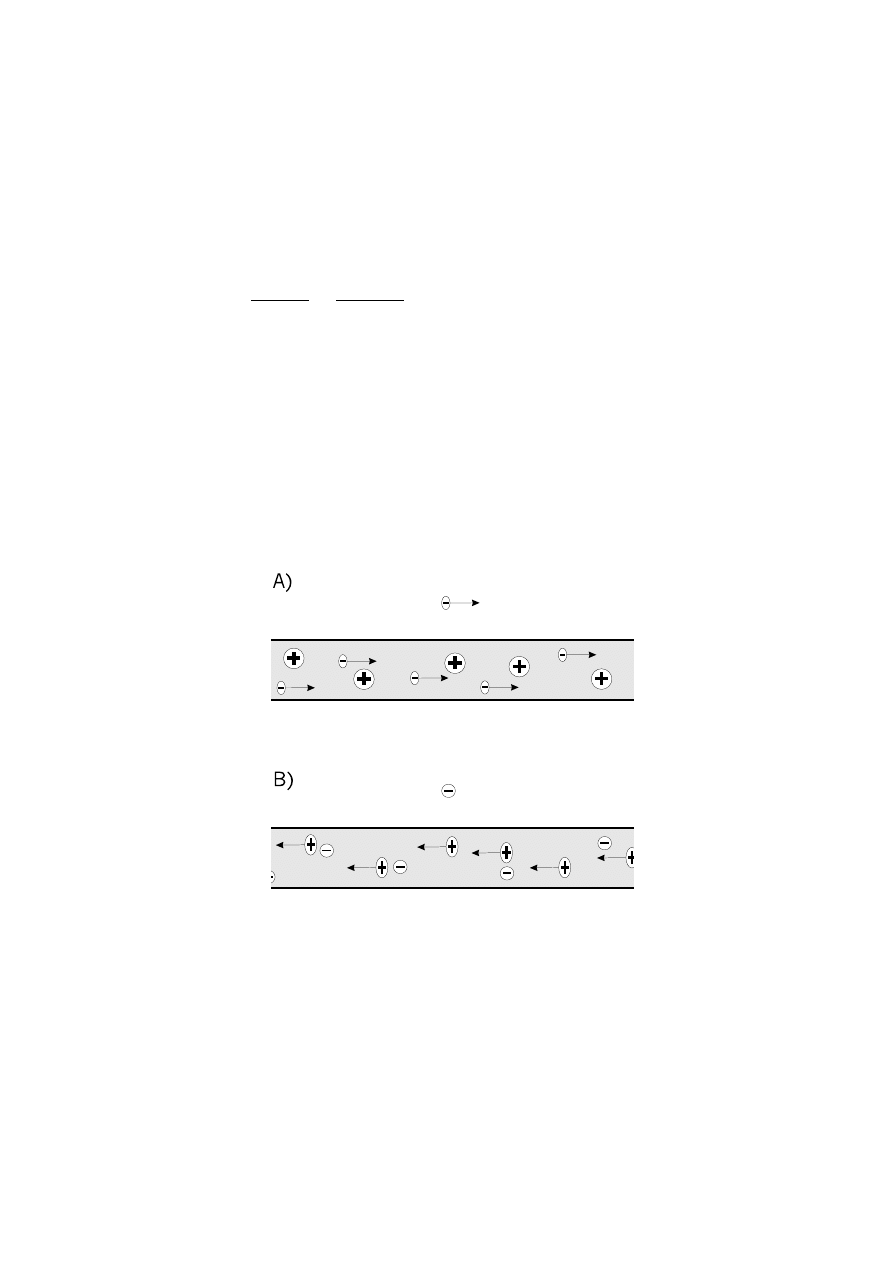
28
ROZDZIAŁ 2.
KINEMATYKA RELATYWISTYCZNA
pr˛edko´sci ˛
a V swobodny elektron - rysunek 2.6 A). Poniewa˙z ruch ładunków wewn ˛
atrz przewod-
nika wytwarza na zewn ˛
atrz pole magnetyczne B = I/2πε
0
c
2
r, w którym porusza si˛e elektron,
pojawi si˛e działaj ˛
aca na niego siła F skierowana ku przewodnikowi:
F = eV B =
eV I
2πε
0
c
2
r
=
e
2
%
−
SV
2
2πε
0
c
2
r
.
(2.4)
Siła ta spowoduje, ˙ze zewn˛etrzny elektron zacznie si˛e coraz bardziej zbli˙za´c do przewodu z
pr ˛
adem.
Kłopot pojawi si˛e w momencie, gdy rozwa˙zymy t˛e sam ˛
a sytuacj˛e w (primowanym) iner-
cjalnym układzie odniesienia poruszaj ˛
acym si˛e razem z elektronami - rysunek 2.6 B). Wówczas
pr ˛
ad elektronowy wynosi zero, ale pojawia si˛e analogiczny pr ˛
ad pochodz ˛
acy od dodatnich jonów
sieci poruszaj ˛
acych si˛e w przeciwnym kierunku. Pr ˛
ad ten naturalnie równie˙z wytwarza pole
magnetyczne. Kłopot w tym, ˙ze teraz zewn˛etrzny elektron nie porusza si˛e ju˙z w tym polu, lecz
spoczywa i dlatego nie działa na niego ˙zadna magnetyczna siła! Jak temu zaradzi´c?
Rysunek 2.6:
Ruch swobodnego ładunku w pobli˙zu przewodnika z pr ˛
adem widziany w dwóch układach
inercjalnych. Skrócenie Lorentza zostało celowo wyolbrzymione. W rzeczywisto´sci wypadkowa pr ˛edko´s´c
elektronów w przewodzie elektrycznym jest rz ˛edu centymetrów na minut ˛e.
Wida´c, ˙ze problem le˙zy gł˛eboko, bo we wzorze na sił˛e Lorentza: F = qv × B. Wyst˛epuje w
nim pr˛edko´s´c v ładunku q w polu magnetycznym B. Ale co to za pr˛edko´s´c? Pr˛edko´s´c wzgl˛edem
2.6.
ELEKTRYZUJ ˛
ACY PARADOKS ELEKTRYCZNY
29
czego? Przecie˙z mo˙zemy przej´s´c do układu w którym ładunek spoczywa - i co wtedy? Siła
przestanie działa´c?
Powró´cmy raz jeszcze do układu nieprimowanego i rozwa˙zmy fragment przewodu elek-
trycznego o długo´sci L. Całkowity ładunek zawarty wewn ˛
atrz tego fragmentu pochodzi cz˛e´s-
ciowo od elektronów Q
−
, a cz˛e´sciowo od dodatnich jonów Q
+
, w sumie wynosz ˛
aca 0 = Q
−
+
Q
+
= −eSL%
−
+ eSL%
+
(przewodnik jest nienaładowany). Wynika st ˛
ad oczywisty wniosek, ˙ze
g˛esto´s´c elektronów %
−
w przewodzie równa jest g˛esto´sci jonów %
+
. Co si˛e stanie gdy przejdzie-
my do układu poruszaj ˛
acego si˛e? Przede wszystkim musimy stanowczo stwierdzi´c, ˙ze ładunek
elementarny e nie zale˙zy od pr˛edko´sci nios ˛
acej go cz ˛
astki. Gdyby e zmieniał si˛e wraz pr˛edko´s-
ci ˛
a, to podgrzewane ciała ładowałyby si˛e elektrycznie, bo cz˛e´s´c ciepła przekazywana jest swo-
bodnym, lekkim elektronom, a cz˛e´s´c ci˛e˙zkim jonom sieci. W zwi ˛
azku z ró˙znic ˛
a mas, elektrony
nabieraj ˛
a o wiele wi˛ekszej pr˛edko´sci ni˙z jony i dlatego ka˙zda, cho´cby najmniejsza zale˙zno´s´c e od
pr˛edko´sci spowodowałaby powstanie nadwy˙zki (lub zmniejszenia) ujemnego ładunku wewn ˛
atrz
ciała, co nie jest jednak obserwowane.
Skoro zatem całkowita warto´s´c ujemnego ładunku elektronowego nie ulega zmianie (podob-
nie jak warto´s´c dodatniego ładunku jonowego), to mo˙ze zmienia si˛e jego g˛esto´s´c? Poniewa˙z
wybrany odcinek zawieraj ˛
acy poruszaj ˛
ace si˛e elektrony zmienia swoj ˛
a długo´s´c przy zmianie
układu odniesienia z L na L/
p
1 − V
2
/c
2
, to przy ustalonej warto´sci ładunku, musi zmienia´c
si˛e g˛esto´s´c elektronów (ta sama ilo´s´c elektronów znajduje si˛e teraz w dłu˙zszym odcinku drutu)!
Z równo´sci ładunków elektronowych zgromadzonych w ustalonym fragmencie przewodu Q
0
−
=
Q
−
oraz wzoru opisuj ˛
acego skrócenie Lorentza znajdujemy:
%
0
−
= %
−
p
1 − V
2
/c
2
.
(2.5)
Analizuj ˛
ac w podobny sposób ładunki pochodz ˛
ace od jonów sieci otrzymujemy:
%
0
+
=
%
+
p
1 − V
2
/c
2
.
(2.6)
Wypadkowa g˛esto´s´c ładunku zgromadzona w przewodniku w primowanym układzie odniesienia
wynosi e%
0
= −e%
0
−
+ e%
0
+
> 0. Oznacza to, ˙ze przewodnik w tym układzie jest naładowany
dodatnio i b˛edzie przyci ˛
agał zewn˛etrzny elektron sił ˛
a elektryczn ˛
a! Wszystko si˛e zatem zgadza,
przynajmniej jako´sciowo. W obydwu układach odniesienia sytuacja b˛edzie identyczna: ładunek
b˛edzie przyci ˛
agany przez przewodnik z pr ˛
adem. Ciekawe, ˙ze przyczyn ˛
a przyci ˛
agania w jednym
30
ROZDZIAŁ 2.
KINEMATYKA RELATYWISTYCZNA
układzie jest pole magnetyczne, a w drugim elektryczne. W dalszej cz˛e´sci przekonamy si˛e, ˙ze
w teorii wzgl˛edno´sci nie da si˛e nigdy oddzieli´c jednego pola od drugiego, bo warto´sci tych pól
zale˙z ˛
a od układu odniesienia. Natomiast efekt ko´ncowy - wpływ na ruch cz ˛
astek naładowanych
musi by´c we wszystkich układach odniesienia jednakowy.
Sprawd´zmy, ˙ze jest tak w rzeczywisto´sci i przeanalizujmy ilo´sciowo przyci ˛
aganie zewn˛etrzne-
go elektronu przez przewodnik w układzie primowanym. W tym układzie g˛esto´s´c ładunku w
przewodniku wynosi:
e%
0
= −e%
0
−
+ e%
0
+
=
e%
−
V
2
/c
2
p
1 − V
2
/c
2
.
(2.7)
Pole elektryczne pochodz ˛
ace od tej g˛esto´sci wynosi:
E =
e%
0
S
2πε
0
r
.
(2.8)
Zatem siła elektryczna F
0
z jak ˛
a swobodny ładunek jest przyci ˛
agany przez przewodnik w układzie
primowanym wynosi:
F
0
=
e
2
%
−
SV
2
2πε
0
c
2
r
p
1 − V
2
/c
2
.
(2.9)
Wida´c, ˙ze siły F i F
0
w obu układach s ˛
a niemal identyczne. Wzory (2.4) oraz (2.9) ró˙zni ˛
a
si˛e bowiem tylko o niewielki czynnik
p
1 − V
2
/c
2
. Pami˛etajmy jednak, ˙ze najwa˙zniejsze jest,
a˙zeby w obu układach siły te wywoływały jednakowy efekt, to znaczy tak ˛
a sam ˛
a zmian˛e p˛edu
swobodnego elektronu. Poprawne relatywistycznie II prawo Newtona jest postaci:
F =
dp
dt
,
(2.10)
o czym b˛edzie mowa w kolejnych rozdziałach. Oczekujemy, ˙ze p˛ed jaki uzyska elektron w
krótkim czasie ∆t w układzie nieprimowanym oraz odpowiadaj ˛
acym mu czasie ∆t
0
w układzie
primowanym b˛edzie taki sam, czyli musi zachodzi´c F ∆t = F
0
∆t
0
. St ˛
ad natychmiast wynika, ˙ze
F = F
0
p
1 − V
2
/c
2
, czyli wszystko si˛e zgadza!
Zwró´cmy teraz uwag˛e, ˙ze przedstawiony problem mo˙zna rozwi ˛
aza´c wył ˛
acznie stosuj ˛
ac re-
latywistyczne prawa. Obserwacja ta powinna nam u´swiadomi´c co´s bardzo wa˙znego: teoria elek-
tromagnetyzmu Maxwella jest teori ˛
a relatywistyczn ˛
a (z czego Maxwell nie mógł sobie rzecz

2.7.
PARADOKS BLI ´
ZNI ˛
AT
31
jasna zdawa´c sprawy). Oznacza to, ˙ze równa´n Maxwella nie trzeba b˛edzie modyfikowa´c by
otrzyma´c wersj˛e relatywistyczn ˛
a. Równania takie, jak je znamy s ˛
a ju˙z relatywistycznie niez-
miennicze. Zagadnieniom elektromagnetycznym i ich zwi ˛
azkowi z teori ˛
a wzgl˛edno´sci zostanie
po´swi˛econy jeden z dalszych, obszernych rozdziałów.
2.7
P
ARADOKS BLI ´
ZNI ˛
AT
O
mówimy teraz słynny paradoks bli´zni ˛
at. Brzmi on nast˛epuj ˛
aco: dwaj bracia bli´zniacy, Jacek
i Placek udali si˛e na stacj˛e kosmiczn ˛
a. Jacek wsiadł do rakiety i odbył dług ˛
a podró˙z, po czym
powrócił na Ziemi˛e. Z punktu widzenia Placka, pozostaj ˛
acego cały czas na Ziemi, upływ czasu
w rakiecie był spowolniony (rakieta cały czas poruszała si˛e z jak ˛
a´s du˙z ˛
a pr˛edko´sci ˛
a) i dlatego
jego brat Jacek po powrocie powinien zestarze´c si˛e mniej ni˙z on sam. Je˙zeli Placek czekał na
brata czas T , to według niego podczas całej podró˙zy kosmicznej Jacka a˙z do momentu jego
powrotu, upływ czasu w rakiecie powinien wynosi´c:
T
0
=
Z
T
0
dt
p
1 − V
2
(t)/c
2
< T,
(2.11)
gdzie V (t) jest zmienn ˛
a w czasie pr˛edko´sci ˛
a rakiety. Zatem po powrocie bracia powinni by´c
ju˙z w ró˙znym wieku. Kto´s mógłby tu spostrzec pewien pozorny paradoks: przecie˙z z punktu
widzenia Jacka, to Placek cały czas si˛e poruszał i po powrocie, to Placek powinien by´c młodszy.
Bł ˛
ad w tym rozumowaniu polega na tym, ˙ze układ Jacka nie jest inercjalny (bo rakieta musi
porusza´c si˛e z przyspieszeniem) i dlatego relatywistyczne wzory, które dotychczas wyprowadza-
li´smy i stosowali´smy nie s ˛
a w tym układzie poprawne.
W oparciu o t˛e prost ˛
a konsekwencj˛e szczególnej teorii wzgl˛edno´sci wykonywane były pewne
ciekawe eksperymenty. Na przykład jeden z dwóch zsynchronizowanych zegarów atomowych
umieszczano w ponadd´zwi˛ekowym samolocie, który odbywał dług ˛
a podró˙z, po czym wracał w
miejsce startu. Okazywało si˛e wówczas, ˙ze zegar, który odbył podró˙z nieznacznie si˛e pó´znił
w stosunku do zegara, który cały czas pozostawał nieruchomy. Zaobserwowane odst˛epstwo
zgadzało si˛e zreszt ˛
a idealnie ze wzorem (2.11).
2.8
P
ARADOKS
R
OBERTA
K
ORZENIOWSKIEGO
W
tym podrozdziale b˛edziemy mieli nareszcie okazj˛e prze´cwiczy´c w nieco bardziej zło˙zonym

32
ROZDZIAŁ 2.
KINEMATYKA RELATYWISTYCZNA
rachunku nasze nowe wiadomo´sci dotycz ˛
ace szczególnej teorii wzgl˛edno´sci. Oto kolejny zwi ˛
a-
zany z ni ˛
a „paradoks”.
Rozwa˙zmy bardzo szybki, relatywistyczny chód Roberta Korzeniowskiego. Poniewa˙z wew-
n ˛
atrz obiektów poruszaj ˛
acych si˛e z bardzo du˙zymi pr˛edko´sciami czas płynie wolniej dla obser-
watorów zewn˛etrznych, nale˙zy si˛e spodziewa´c, ˙ze zegarek na r˛ece Roberta Korzeniowskiego
b˛edzie chodził wolniej. Powolniejsze b˛edzie równie˙z bicie jego serca. A co mo˙zna powiedzie´c
o ruchu jego nóg? Czy im szybciej b˛edzie szedł tym wolniej porusza´c b˛edzie nogami? Czy w
granicy pr˛edko´sci ´swiatła wcale nie b˛edzie nimi poruszał? W jaki sposób mo˙zna chodzi´c nie
ruszaj ˛
ac nogami?
Rzeczywi´scie, z punktu widzenia obserwatora zewn˛etrznego, upływ czasu w układzie Ro-
berta Korzeniowskiego (wielko´sci w tym układzie oznacza´c b˛edziemy literkami z primem) jest
powolniejszy. Tempo upływu czasu ró˙zni si˛e o czynnik
p
1 − V
2
/c
2
, gdzie V jest pr˛edko´s-
ci ˛
a chodu. Nie oznacza to jednak, ˙ze mo˙zna przez ten˙ze czynnik skalowa´c pr˛edko´sci wszyst-
kich ruchów w poruszaj ˛
acym si˛e obiekcie! Prawo „spowolnianie upływu czasu” o podany
czynnik dotyczy obiektów nieruchomych (na przykład zegarów) w poruszaj ˛
acym si˛e układzie
odniesienia. Działa ono dobrze równie˙z dla obiektów poruszaj ˛
acych si˛e w układzie primowanym
powoli. Poniewa˙z jednak ruch nóg w układzie primowanym musi by´c równie szybki co ruch
piechura, musimy dokona´c transformacji Lorentza współrz˛ednych okre´slaj ˛
acych poło˙zenie nóg
oraz ´srodka masy chodziarza niezale˙znie. W tym celu wprowadzimy najprostszy z mo˙zliwych
model chodu.
W całym problemie wa˙zne s ˛
a naprawd˛e tylko trzy punkty: ´srodek masy (A), i poło˙zenie
dwóch stóp (B i C). Rozwa˙zmy sytuacj˛e z punktu widzenia Roberta Korzeniowskiego (czyli w
układzie primowanym). Przedstawia j ˛
a rysunek 2.7. W tym układzie ´srodek masy (A) jest nieru-
chomy, chodnik porusza si˛e do tyłu z pewn ˛
a pr˛edko´sci ˛
a −V , stopa aktualnie dotykaj ˛
aca ziemi
(C) równie˙z porusza si˛e z pr˛edko´sci ˛
a −V , a druga stopa, przenoszona do przodu (B) porusza si˛e
z pr˛edko´sci ˛
a V . Poniewa˙z zgodnie z przepisami chodu sportowego w ka˙zdej chwili czasu conaj-
mniej jedna stopa musi dotyka´c ziemi, Robert Korzeniowski chc ˛
ac i´s´c jak najszybciej, stawiaj ˛
ac
jedn ˛
a stop˛e jednocze´snie odrywa drug ˛
a. Powiedzmy, ˙ze w chwili t
0
= 0 stopa odrywana znajduje
si˛e w punkcie x
0B
= −d, a stopa stawiana w punkcie x
0C
= d. Natomiast przez cały czas ´srodek
masy A znajduje si˛e w punkcie x
0A
= 0. Zamiana ról nast˛epuje w chwili t
0
=
2d
V
. Przez nast˛epne
40 km ruch jest cyklicznie powtarzany.
Pytanie, które nas interesuje, to jak wygl ˛
ada chód z punktu widzenia obserwatora stoj ˛
acego na
chodniku (układ nieprimowany), dla którego ´srodek masy Roberta Korzeniowskiego porusza si˛e
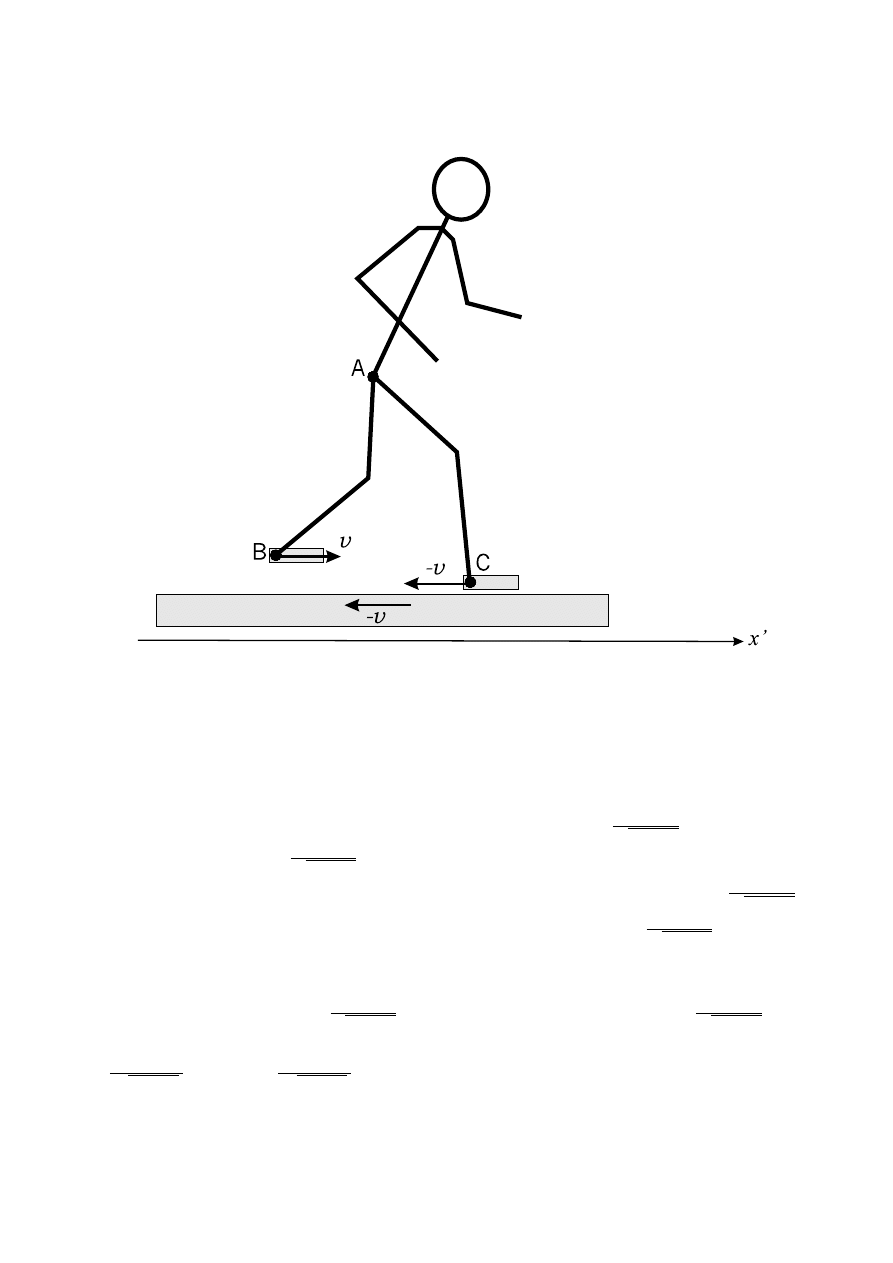
2.8.
PARADOKS ROBERTA KORZENIOWSKIEGO
33
Rysunek 2.7:
Prosty model chodu w inercjalnym układzie piechura.
zgodnie z równaniem x
A
= V t. Sprawd´zmy najpierw przy pomocy transformacji Lorentza jak
wygl ˛
adaj ˛
a czasoprzestrzenne współrz˛edne opisuj ˛
ace stawianie i odrywanie stóp. Rozpocznijmy
od pierwszego tupni˛ecia: stopa C postawiona zostaje w punkcie x
C
=
d
√
1−V
2
/c
2
, a stopa B oder-
wana w punkcie x
B
= −
d
√
1−V
2
/c
2
, czyli krok staje si˛e dłu˙zszy. Okazuje si˛e jednak, ˙ze stopy s ˛
a
stawiane i odrywane w ró˙znych chwilach: stopa B zostaje oderwana w chwili t
B
=
−dV /c
2
√
1−V
2
/c
2
jeszcze zanim zostanie postawiona stopa C, co ma miejsce w chwili t
C
=
dV /c
2
√
1−V
2
/c
2
(nawiasem
mówi ˛
ac mo˙ze to by´c przyczyn ˛
a dyskwalifikacji Roberta Korzeniowskiego, mimo i˙z ten twierdzi
˙ze stopy zmieniał jednocze´snie ;-). Rozwa˙zmy teraz drugie tupni˛ecie, w którym stopa B zostaje
postawiona w punkcie x
B
=
3d
√
1−V
2
/c
2
, a stopa C oderwana w punkcie x
C
=
d
√
1−V
2
/c
2
, za-
tem krok jest znowu dłu˙zszy. Odpowiednie chwile odpowiadaj ˛
ace tym zdarzeniom to t
B
=
2d/V +dV /c
2
√
1−V
2
/c
2
oraz t
C
=
2d/V −dV /c
2
√
1−V
2
/c
2
. Nast˛epnie proces powtarzany jest cyklicznie. Sprawd´zmy

34
ROZDZIAŁ 2.
KINEMATYKA RELATYWISTYCZNA
teraz, ˙ze czas oderwania stopy od ziemi wynosi:
∆t
↑
=
2d
V
1 +
V
2
c
2
q
1 −
V
2
c
2
,
(2.12)
natomiast czas w którym druga stopa dotyka ziemi to:
∆t
↓
=
2d
V
r
1 −
V
2
c
2
.
(2.13)
Mo˙zemy teraz odpowiedzie´c ju˙z w pełni na pytanie co dzieje si˛e z nogami podczas relatywis-
tycznego chodu według naszego prostego modelu. Czas trwania pełnego „okresu” w którym
stopa jest przenoszona, a nast˛epnie spoczywa na ziemi wynosi:
∆t = ∆t
↑
+ ∆t
↓
=
4d/V
q
1 −
V
2
c
2
(2.14)
i jest dłu˙zszy od czasu ∆t
0
widzianego przez Roberta Korzeniowskiego: ∆t
0
=
4d
V
. Zatem
odpowied´z na pytanie, czy im szybciej idziemy tym wolniej ruszamy nogami dla zewn˛etrznego
obserwatora jest, paradoksalnie, twierdz ˛
aca! W granicy V → c czas trwania pełnego kroku
staje si˛e wr˛ecz niesko´nczony! Jest i druga ciekawa obserwacja: w tej granicy obie stopy przez
wi˛ekszo´s´c czasu „frun ˛
a w powietrzu” robi ˛
ac ogromne kroki i prawie wcale nie dotykaj ˛
ac ziemi.
To ostatnie stwierdzenie staje si˛e wr˛ecz oczywiste, gdy zdamy sobie spraw˛e, ˙ze w układzie
Roberta Korzeniowskiego cały zewn˛etrzny ´swiat (zatem równie˙z chodnik) si˛e skraca. I mimo,
˙ze długo´s´c kroku według Korzeniowskiego jest zwyczajna, to skracanie chodnika powoduje,
˙ze ka˙zdy krok wi ˛
a˙ze si˛e z pokonaniem ogromnego dystansu. Nic wi˛ec dziwnego, ˙ze z punktu
widzenia s˛edziów kroki piechura staj ˛
a si˛e nienaturalnie długie. Poniewa˙z natomiast nogi Ko-
rzeniowskiego nie mog ˛
a si˛e wydłu˙za´c, to jedyn ˛
a mo˙zliwo´sci ˛
a zrealizowania tej sytuacji jest bieg
z wydłu˙zon ˛
a faz ˛
a lotu.
2.9
R
ELATYWISTYCZNE TRANSFORMACJE PR ˛
EDKO ´SCI
P
oznana dawka „paradoksów” teorii wzgl˛edno´sci jest na razie wystarczaj ˛
aca. Zajmiemy si˛e
teraz innym zagadnieniem. Zapomnijmy na chwil˛e o teorii wzgl˛edno´sci i spójrzmy raz jeszcze na
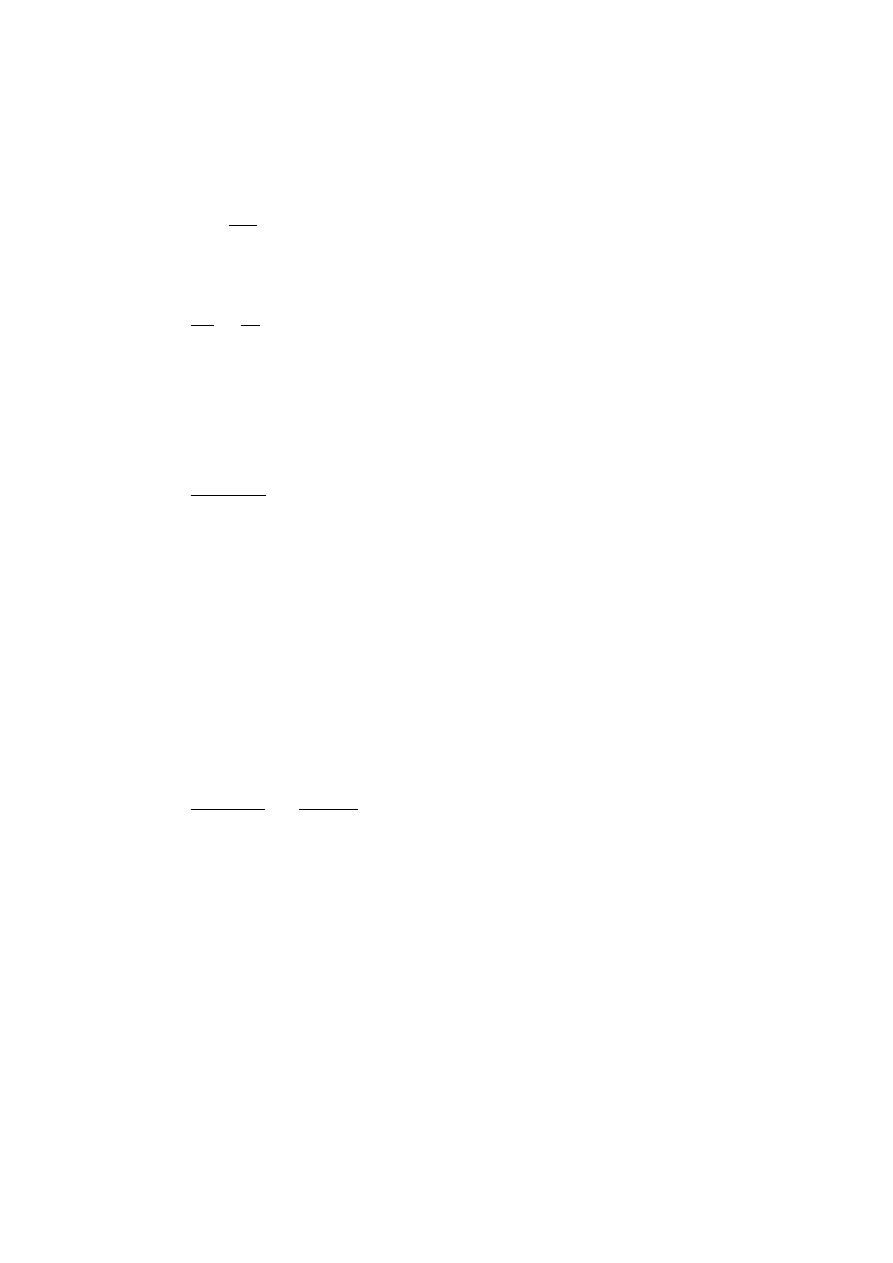
2.9.
RELATYWISTYCZNE TRANSFORMACJE PR ˛
EDKO ´SCI
35
transformacj˛e Galileusza (1.8). Rozwa˙zmy ruch punktu opisanego w układzie nieprimowanym
równaniem x(t), a w układzie primowanym równaniem x
0
(t
0
). Pr˛edko´s´c punktu w pewnej chwili
t wynosi v(t) =
dx(t)
dt
. Z jak ˛
a pr˛edko´sci ˛
a punkt ten poruszał si˛e b˛edzie w układzie primowanym?
Ró˙zniczkuj ˛
ac transformacj˛e Galileusza (1.8) bez trudu znajdujemy:
v
0
=
dx
0
dt
0
=
dx
dt
− V = v − V.
(2.15)
Wzór ten znamy oczywi´scie z codziennego do´swiadczenia wi˛ec niczym si˛e nie dziwimy. W
podobny sposób mo˙zemy jednak znale´z´c jego relatywistyczny odpowiednik ró˙zniczkuj ˛
ac trans-
formacj˛e Lorentza (1.6):
v
0
=
v − V
1 − vV /c
2
.
(2.16)
T ˛
a prost ˛
a metod ˛
a udało nam si˛e otrzyma´c wzór przy pomocy którego mo˙zemy odpowiada´c na
pytanie: z jak ˛
a pr˛edko´sci ˛
a porusza si˛e jaki´s punkt w układzie primowanym, je´sli wiadomo, ˙ze
w układzie nieprimowanym jego pr˛edko´s´c wynosi v. Co wi˛ecej, nasz wzór jest poprawny dla
dowolnego ruchu rozwa˙zanego punktu, niekoniecznie ruchu ze stał ˛
a pr˛edko´sci ˛
a. Ze stał ˛
a pr˛ed-
ko´sci ˛
a V musi si˛e natomiast porusza´c układ inercjalny z którego prowadzimy obserwacje.
Maj ˛
ac powy˙zszy wzór, pierwsz ˛
a rzecz ˛
a, któr ˛
a musimy sprawdzi´c jest rzekoma stało´s´c pr˛ed-
ko´sci ´swiatła. Je´sli w jednym układzie co´s porusza si˛e z pr˛edko´sci ˛
a v = c, to w drugim układzie,
poruszaj ˛
acym si˛e tradycyjnie z dowoln ˛
a pr˛edko´sci ˛
a V :
v
0
=
c − V
1 − cV /c
2
= c
1 − V /c
1 − V /c
= c.
(2.17)
Zatem wszystko si˛e zgadza! Pr˛edko´s´c ´swiatła po przej´sciu do dowolnego inercjalnego układu si˛e
nie zmieni. Doskonale. W podobny sposób mo˙zemy si˛e przekona´c, ˙ze je˙zeli w jednym układzie
odniesienia pr˛edko´s´c jakiego´s punktu jest mniejsza od c, to b˛edzie równie˙z mniejsza od c w
innym układzie. Na rysunku 2.8 znajduje si˛e wykres przykładowej zale˙zno´sci pr˛edko´sci obser-
wowanego punktu v
0
od pr˛edko´sci układu odniesienia V z którego prowadzona jest obserwacja.
Przyj˛eli´smy, ˙ze w układzie „spoczywaj ˛
acym” punkt porusza si˛e z pr˛edko´sci ˛
a v = 0.5c. Wida´c,
˙ze im szybciej porusza si˛e układ odniesienia, tym mniejsza jest obserwowana pr˛edko´s´c punktu.
Dla V = v pr˛edko´sci si˛e zrównuj ˛
a i ciało staje si˛e „nieruchome”. Zauwa˙zmy, ˙ze zale˙zno´s´c v
0
(V )
jest liniowa dla małych warto´sci V , jak w nierelatywistycznej mechanice.
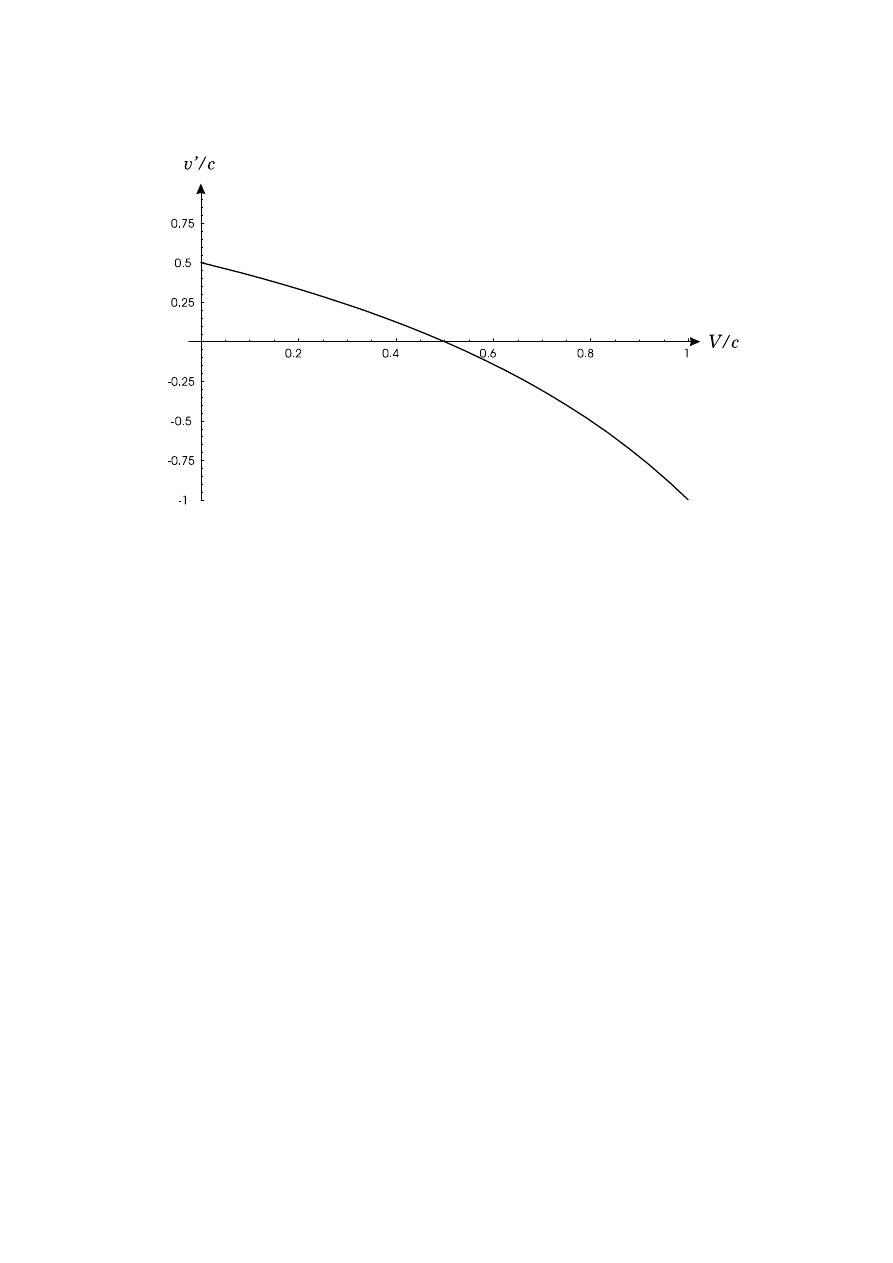
36
ROZDZIAŁ 2.
KINEMATYKA RELATYWISTYCZNA
Rysunek 2.8:
Zale˙zno´s´c pr ˛edko´sci poruszaj ˛
acego si ˛e ciała od pr ˛edko´sci układu odniesienia z którego
prowadzona jest obserwacja. W układzie nieruchomym ciało porusza si ˛e z pr ˛edko´sci ˛
a
v = 0.5c
. Im szyb-
ciej porusza si ˛e układ odniesienia, tym mniejsza jest obserwowana pr ˛edko´s´c. Dla
V = v
pr ˛edko´sci si ˛e
zrównuj ˛
a i ciało staje si ˛e „nieruchome”. Zauwa˙zmy, ˙ze zale˙zno´s´c
v
0
(V )
jest liniowa dla małych pr ˛edko´sci
V
, jak w mechanice nierelatywistycznej.
Za chwil˛e poznamy jednak co´s bardzo niezwykłego. W poprzednim przykładzie obiek-
tem obserwacji był punkt poruszaj ˛
acy si˛e z pr˛edko´sci ˛
a mniejsz ˛
a ni˙z c. Przeprowadzimy teraz
podobn ˛
a analiz˛e dla „obiektu” poruszaj ˛
acego si˛e z nad´swietln ˛
a pr˛edko´sci ˛
a. Pami˛etacie meksy-
ka´nsk ˛
a fal˛e krasnoludków na urodzinach Królewny ´Snie˙zki? Sprawdzimy teraz jak ˛
a pr˛edko´s´c
fali zaobserwuje przelatuj ˛
aca na miotle z pr˛edko´sci ˛
a V Baba Jaga poruszaj ˛
aca si˛e wzdłu˙z szeregu
podskakuj ˛
acych krasnoludków - rysunek 2.9.
Powiedzmy, ˙ze według Królewny meksyka´nska fala przesuwa si˛e z pr˛edko´sci ˛
a v = 1.5c.
Na rysunku 2.10 znajduje si˛e pr˛edko´s´c fali v
0
zarejestrowana przez Bab˛e Jag˛e w zale˙zno´sci od
pr˛edko´sci miotły V . Zale˙zno´s´c ta wydaje si˛e bardzo nieintuicyjna. Im szybciej Baba Jaga „goni”
fal˛e krasnoludków, tym szybciej ona ucieka! Dla V = c
2
/v pr˛edko´s´c fali staje si˛e niesko´nczona
(wszystkie krasnoludki podskakuj ˛
a jednocze´snie). Dopiero przy dalszym wzro´scie pr˛edko´sci
miotły kierunek fali odwraca si˛e i fala zaczyna si˛e porusza´c w przeciwn ˛
a stron˛e. Ten nieco-
dzienny, lecz prawdziwy efekt „uciekaj ˛
acych krasnoludków” przypomina ´swiat Alicji w Krainie
Czarów, nieprawda˙z? Krasnoludki uciekaj ˛
a Babie Jadze tym szybciej im szybciej goni je ona na

2.9.
RELATYWISTYCZNE TRANSFORMACJE PR ˛
EDKO ´SCI
37
Rysunek 2.9:
Baba Jaga przelatuj ˛
aca nad meksyka ´nsk ˛
a fal ˛
a krasnoludków.
swej miotle. Domy´slamy si˛e te˙z, ˙ze je˙zeli krasnoludki wykonałyby fal˛e poruszaj ˛
ac ˛
a si˛e dokład-
nie z pr˛edko´sci ˛
a ´swiatła, to niezale˙znie od pr˛edko´sci miotły, pr˛edko´s´c fali byłaby zawsze taka
sama - c.
Nasz wynik w postaci wzorów transformacyjnych pr˛edko´sci (2.16) nie jest jednak ogólny,
a dotyczy tylko jednowymiarowego ruchu wzdłu˙z osi x. Rozwa˙zmy zatem przypadek ruchu
trójwymiarowego widzianego z punktu widzenia układu spoczywaj ˛
acego oraz poruszaj ˛
acego si˛e
wzdłu˙z osi x. Je˙zeli ruch w układzie nieprimowanym opisywany jest wektorem pr˛edko´sci v =
(v
x
, v
y
, v
z
), to w układzie primowanym b˛edziemy mieli:
v
0
x
=
v
x
− V
1 − v
x
V /c
2
v
0
y
=
v
y
p
1 − V
2
/c
2
1 − v
x
V /c
2
(2.18)
v
0
z
=
v
z
p
1 − V
2
/c
2
1 − v
x
V /c
2
.
Powy˙zszy układ równa´n transformacyjnych mo˙zna równie˙z zapisa´c w ogólnej postaci dla dowol-
nej pr˛edko´sci V ruchu wzgl˛ednego dwóch układów odniesienia:
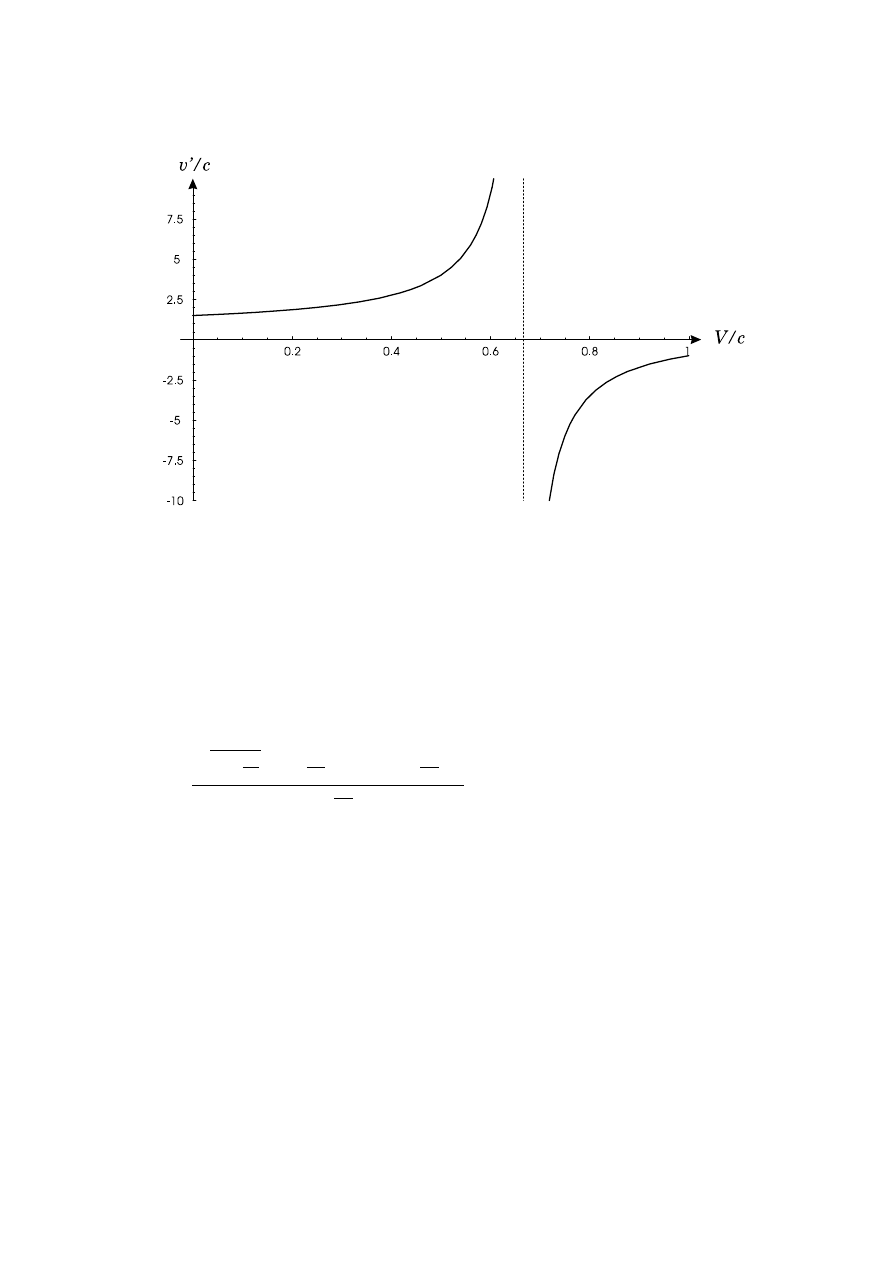
38
ROZDZIAŁ 2.
KINEMATYKA RELATYWISTYCZNA
Rysunek 2.10:
Efekt „uciekaj ˛
acych krasnoludków”. Bardzo nieintuicyjna zale˙zno´s´c nad´swietlnej pr ˛ed-
ko´sci z jak ˛
a porusza si ˛e „fala krasnoludków” od pr ˛edko´sci układu odniesienia z którego prowadzona jest
obserwacja. W układzie nieruchomym (
V /c = 0
) fala porusza si ˛e z pr ˛edko´sci ˛
a
v = 1.5c
. Im szybciej
porusza si ˛e układ odniesienia, tym wi ˛eksza jest obserwowana pr ˛edko´s´c, czyli im szybciej gonimy fal ˛e,
tym szybciej ona ucieka! Dla
V = c
2
/v
pr ˛edko´s´c fali staje si ˛e niesko ´nczona (wszystkie krasnoludki pod-
skakuj ˛
a jednocze´snie). Przy dalszym wzro´scie pr ˛edko´sci układu odniesienia kierunek fali odwraca si ˛e.
v
0
=
q
1 −
V
2
c
2
¡
v −
v·V
V
2
V
¢
−
¡
V −
v·V
V
2
V
¢
1 −
v·V
c
2
.
(2.19)
I pomy´sle´c jak bardzo sprawy mog ˛
a si˛e skomplikowa´c. Przypomnijmy tylko, ˙ze zwykły, niere-
latywistyczny odpowiednik powy˙zszego potwora to po prostu v
0
= v − V.
Pytania
• Czy dowolne dwa zdarzenia zachodz ˛
ace w ró˙znych miejscach, w pewnym układzie inerc-
jalnym s ˛
a jednoczesne?
• Czy dla dowolnej pary zdarze´n oddzielonych interwałem czasowym istnieje układ odniesienia
w którym te zdarzenia zachodz ˛
a w tym samym miejscu?

2.9.
RELATYWISTYCZNE TRANSFORMACJE PR ˛
EDKO ´SCI
39
• Czy kolejno´s´c zdarze´n oddzielonych interwałem zerowym zale˙zy od układu odniesienia?
• Czy dla ka˙zdej pary zdarze´n istnieje nietrywialna transformacja Lorentza nie zmieniaj ˛
aca
odst˛epu czasu mi˛edzy tymi zdarzeniami?
• Bli´zniak L spoczywaj ˛
acy w pewnym układzie inercjalnym obserwuje ruch bli´zniaka J ze
zmienn ˛
a w czasie pr˛edko´sci ˛
a v(t). Bli´zniak J na pocz ˛
atku i na ko´ncu ruchu trwaj ˛
acego T
spoczywa wzgl˛edem bli´zniaka L. O ile zestarzał si˛e bli´zniak J w czasie w którym bli´zniak
L zestarzał si˛e o T ?
• Czy przy zmianie układu odniesienia w ogólno´sci zmieniaj ˛
a si˛e tylko składowe pr˛edko´sci
ciał wzdłu˙z kierunku ruchu układu, czy tak˙ze w kierunkach poprzecznych?
• Uzasadnij czy to mo˙zliwe, by fala propaguj ˛
aca si˛e z pr˛edko´sci ˛
a wi˛eksz ˛
a ni˙z c poruszała
si˛e szybciej je´sli obserwator stara si˛e j ˛
a dogoni´c?
• Czy to prawda, ˙ze warto´s´c i kierunek pr˛edko´sci ´swiatła nie zale˙zy od układu odniesienia?
• Czy przej´scie z układu A do poruszaj ˛
acego si˛e wzgl˛edem niego z pr˛edko´sci ˛
a V układu
B, a nast˛epnie z układu B do układu C poruszaj ˛
acego si˛e wzgl˛edem B z pr˛edko´sci ˛
a V
wzdłu˙z tej samej osi jest równowa˙zne przej´sciu z układu A do układu D poruszaj ˛
acego si˛e
wzgl˛edem A z pr˛edko´sci ˛
a 2V ?
Zadania
• W przestrzeni kosmicznej porusza si˛e wzdłu˙z wspólnej prostej sto rakiet w taki sposób, ˙ze
druga oddala si˛e od pierwszej z pr˛edko´sci ˛
a 0.9c, trzecia od drugiej równie˙z z pr˛edko´sci ˛
a
0.9c i tak dalej a˙z do ostatniej rakiety. Jaka jest wzgl˛edna pr˛edko´s´c pierwszej i setnej
rakiety?
• Z oddalaj ˛
acego si˛e radialnie od Ziemi z pr˛edko´sci ˛
a v statku kosmicznego nadawana jest
audycja radiowa. Czas nadawania audycji w studio na statku wynosi τ = 30 minut. Jak
długa trwa odbiór audycji na Ziemi?

40
ROZDZIAŁ 2.
KINEMATYKA RELATYWISTYCZNA

Rozdział 3
N
IESZTYWNA BRYŁA SZTYWNA
P
rzed nami kolejny etap poznawania teorii wzgl˛edno´sci. Tym razem zwi ˛
azany z „brył ˛
a sztyw-
n ˛
a”. Cudzysłów znalazł si˛e tu nieprzypadkowo, bo jak si˛e wkrótce oka˙ze, poj˛ecie bryły sztywnej
w teorii wzgl˛edno´sci jest w pewnym sensie pozbawione sensu ;-). W mechanice nierelatywisty-
cznej bryła sztywna jest to ciało, w którym dowolnie wybrana para punktów nie zmienia wzgl˛ed-
nego poło˙zenia w czasie. W mechanice o´srodków ci ˛
agłych poj˛ecie to uogólni´c si˛e dopuszczaj ˛
ac
powstawanie odkształce´n i napi˛e´c w o´srodku tworz ˛
acym brył˛e. W przypadku relatywistycznym
od razu na my´sl przychodzi nam skrócenie Lorentza. Bryła sztywna poruszaj ˛
aca si˛e ze stał ˛
a pr˛ed-
ko´sci ˛
a staje si˛e spłaszczona, poniewa˙z jednak efekt ten jest czysto geometryczny, nie wywołuje
to powstawania ˙zadnych napi˛e´c wewn˛etrznych (co innego, gdy ciało nie porusza si˛e ruchem jed-
nostajnym - do tego tematu jeszcze powrócimy). Okazuje si˛e jednak, ˙ze nie to jest najwi˛ekszym
problemem. Aby zrozumie´c istot˛e kłopotów jakie pojawiaj ˛
a si˛e, gdy chcemy wprowadzi´c do
teorii wzgl˛edno´sci poj˛ecie bryły sztywnej, przemy´slmy nast˛epuj ˛
acy przykład.
3.1
M
ACHANIE DŁUGIM KIJEM
W
yobra´zmy sobie bardzo długi, lekki, sztywny i wytrzymały kij. Je˙zeli złapiemy za jeden
koniec i zaczniemy go obraca´c, to drugi koniec b˛edzie si˛e bardzo szybko poruszał. Wystarczy
do tego niewielki ruch r˛ek ˛
a, a je´sli kij jest bardzo lekki, to nie trzeba do tego nawet wielkiej siły.
Pytanie, czy maj ˛
ac dowolnie długi kij, mo˙zna wprawi´c w ten sposób jego przeciwległy koniec
w dowolnie szybki ruch? Oczywi´scie nie. Nie chodzi tu o ˙zaden praktyczny kłopot, ˙ze kij mu-
siałby by´c niesłychanie długi, a przy tym nic nie wa˙zy´c. Problem jest bardziej fundamentalny.
W chwili, gdy zaczniemy rusza´c r˛ek ˛
a, wzdłu˙z kija zacznie propagowa´c si˛e fala „d´zwi˛ekowa”
41
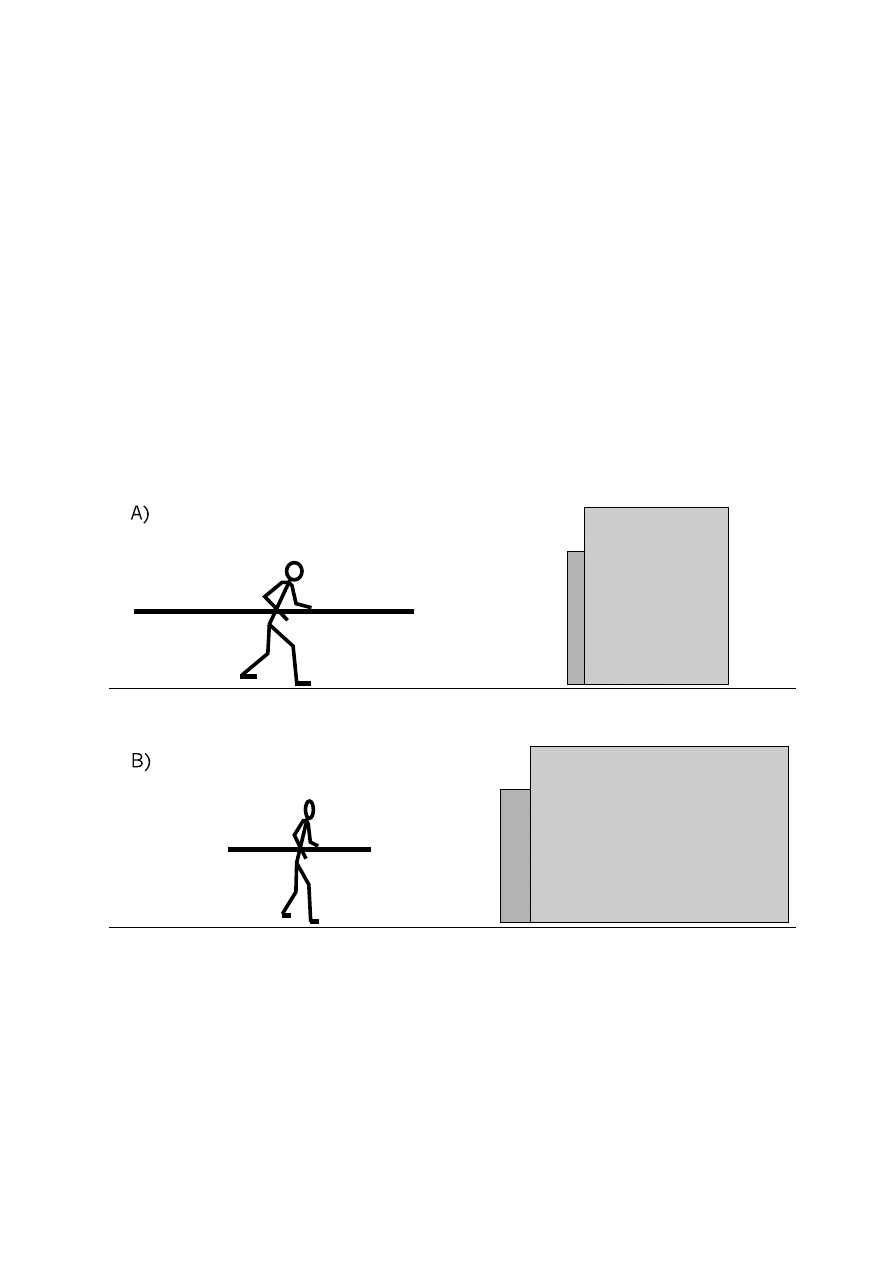
42
ROZDZIAŁ 3.
NIESZTYWNA BRYŁA SZTYWNA
nios ˛
aca o tym informacj˛e. Dlatego odległy koniec nie dowie si˛e od razu o tym, ˙ze zacz˛eli´smy
rusza´c kijem i przez jaki´s czas pozostanie nieruchomy. Zagadnienie, jaki b˛edzie naprawd˛e ruch
kija jest niezwykle trudne, bo do jego rozwi ˛
azania wymagana jest znajomo´s´c dynamiki tensora
napi˛e´c wewn ˛
atrz o´srodka z którego wykonany został kij. Nam jednak nie zale˙zy na znalezieniu
rzeczywistej reakcji całego kija na ruch trzymanego r˛ek ˛
a ko´nca. Wa˙zne jest jedynie, aby´smy si˛e
przekonali, ˙ze w teorii wzgl˛edno´sci nie mo˙zna mówi´c o „sztywno´sci” ciał. Idealne „nierelaty-
wistyczne” ciało sztywne, reaguje bowiem na dowoln ˛
a sił˛e zewn˛etrzn ˛
a jednocze´snie cał ˛
a swoj ˛
a
obj˛eto´sci ˛
a. Tego typu błyskawiczna reakcja jest w oczywisty sposób sprzeczna z zało˙zeniem, ˙ze
sygnały nie mog ˛
a porusza´c si˛e dowolnie szybko.
3.2
P
ARADOKS TYCZKARZA I STODOŁY
Rysunek 3.1:
Biegn ˛
acy tyczkarz z punktu widzenia dwóch układów odniesienia: swojego własnego i
układu stodoły. W pierwszym przypadku, stodoła (której drzwi s ˛
a otwarte) doznaje skrócenia Lorentza i
tyczka nie ma szans zmie´sci´c si ˛e w ´srodku. Jednak w układzie stodoły, to tyczka si ˛e skraca, zatem bez
problemu zmie´sci si ˛e w ´srodku i b ˛edzie mo˙zna nawet zamkn ˛
a´c za ni ˛
a drzwi.
P
ami˛etacie paradoks poci ˛
agu i dworca z rozdziału 2.4? Z punktu widzenia jad ˛
acego poci ˛
agu

3.3.
PARADOKS DWÓCH KWADRATÓW
43
skracał si˛e peron mieszcz ˛
ac si˛e „wewn ˛
atrz” poci ˛
agu. Z punktu widzenia osoby stoj ˛
acej na
peronie, to poci ˛
ag si˛e skracał i w pewnej chwili znajdował si˛e w cało´sci „wewn ˛
atrz” peronu.
Rozwi ˛
azanie problemu wymagało spostrze˙zenia, ˙ze w obu układach odniesienia równoczesno´s´c
oznaczała co innego. Jednak kto´s z Was mógł ju˙z wówczas zauwa˙zy´c kolejny problem zwi ˛
azany
z tym zagadnieniem. Oto on.
Wyobra´zmy sobie, ˙ze zamiast jad ˛
acego poci ˛
agu mamy biegn ˛
acego niezwykle szybko czło-
wieka trzymaj ˛
acego poziomo dług ˛
a tyczk˛e. Zamiast peronu jest natomiast stodoła z otwartymi
drzwiami, której długo´s´c jest równa długo´sci tyczki - rysunek 3.1. Biegn ˛
acy tyczkarz próbuje
zmie´sci´c si˛e wewn ˛
atrz skracaj ˛
acej si˛e (z jego punktu widzenia) stodoły - rysunek 3.1 A) i wszyst-
ko wskazuje na to, ˙ze mu si˛e to nie uda. Jednak z „punktu widzenia stodoły”, to tyczka si˛e skraca
mog ˛
ac bez problemu zmie´sci´c si˛e w ´srodku, a nawet mo˙zna b˛edzie zamkn ˛
a´c za ni ˛
a drzwi. Widzi-
my, ˙ze pojawia si˛e tu problem. Przecie˙z nie mo˙zemy si˛e zgodzi´c na to, ˙ze w jednym układzie
tyczkarz zmie´scił si˛e wewn ˛
atrz stodoły i drzwi zostały za nim zamkni˛ete, a w drugim układzie
pozostał na zewn ˛
atrz. Pami˛etamy przecie˙z o zasadzie demokracji układów inercjalnych!
Sytuacja w układzie stodoły nie budzi w ˛
atpliwo´sci: tyczkarz bez trudu zmie´sci si˛e wewn ˛
atrz
i b˛edzie mo˙zna zamkn ˛
a´c go razem z tyczk ˛
a w ´srodku. W momencie gdy zderzy si˛e on ze ´scian ˛
a
stodoły, jego pr˛edko´s´c spadnie do zera i tyczka wydłu˙zy si˛e wewn ˛
atrz stodoły utykaj ˛
ac pomi˛edzy
´scian ˛
a a zamkni˛etymi drzwiami. To samo musi si˛e wydarzy´c w układzie tyczkarza. Musimy
sobie zda´c spraw˛e z faktu, ˙ze w momencie gdy jeden koniec tyczki zostanie uderzony przez
tyln ˛
a ´scian˛e stodoły, drugi koniec stodoły nie zd ˛
a˙zy si˛e o tym dowiedzie´c natychmiast i jeszcze
przez jaki´s czas b˛edzie si˛e poruszał. Czas ten jest wystarczaj ˛
acy by cała tyczka zmie´sciła si˛e w
´srodku równie˙z w tym układzie. Łatwo sprawdzi´c, ˙ze nawet sygnał poruszaj ˛
acy si˛e z pr˛edko´sci ˛
a
´swiatła (a w rzeczywisto´sci z pr˛edko´sci ˛
a d´zwi˛eku) nie zd ˛
a˙zy przyby´c do drugiego ko´nca stodoły
zanim cała tyczka znajdzie si˛e wewn ˛
atrz, niezale˙znie od długo´sci stodoły ani pr˛edko´sci z jak ˛
a
si˛e porusza. Zatem z powodu relatywistycznej „niesztywno´sci” tyczki (i stodoły), paradoks daje
si˛e, jak wida´c, rozwi ˛
aza´c.
3.3
P
ARADOKS DWÓCH KWADRATÓW
Z
rzekom ˛
a sztywno´sci ˛
a „bryły sztywnej” wi ˛
a˙ze si˛e wiele innych interesuj ˛
acych paradoksów.
Oto kolejny: rozwa˙zmy ruch płaski dwóch kwadratów. Niech w spoczynkowym układzie od-
niesienia pierwszego kwadratu drugi porusza si˛e z pr˛edko´sci ˛
a v wzdłu˙z swojej przek ˛
atnej jak
na rysunku 3.2 A). Zgodnie ze szczególn ˛
a teori ˛
a wzgl˛edno´sci poruszaj ˛
acy si˛e kwadrat skraca
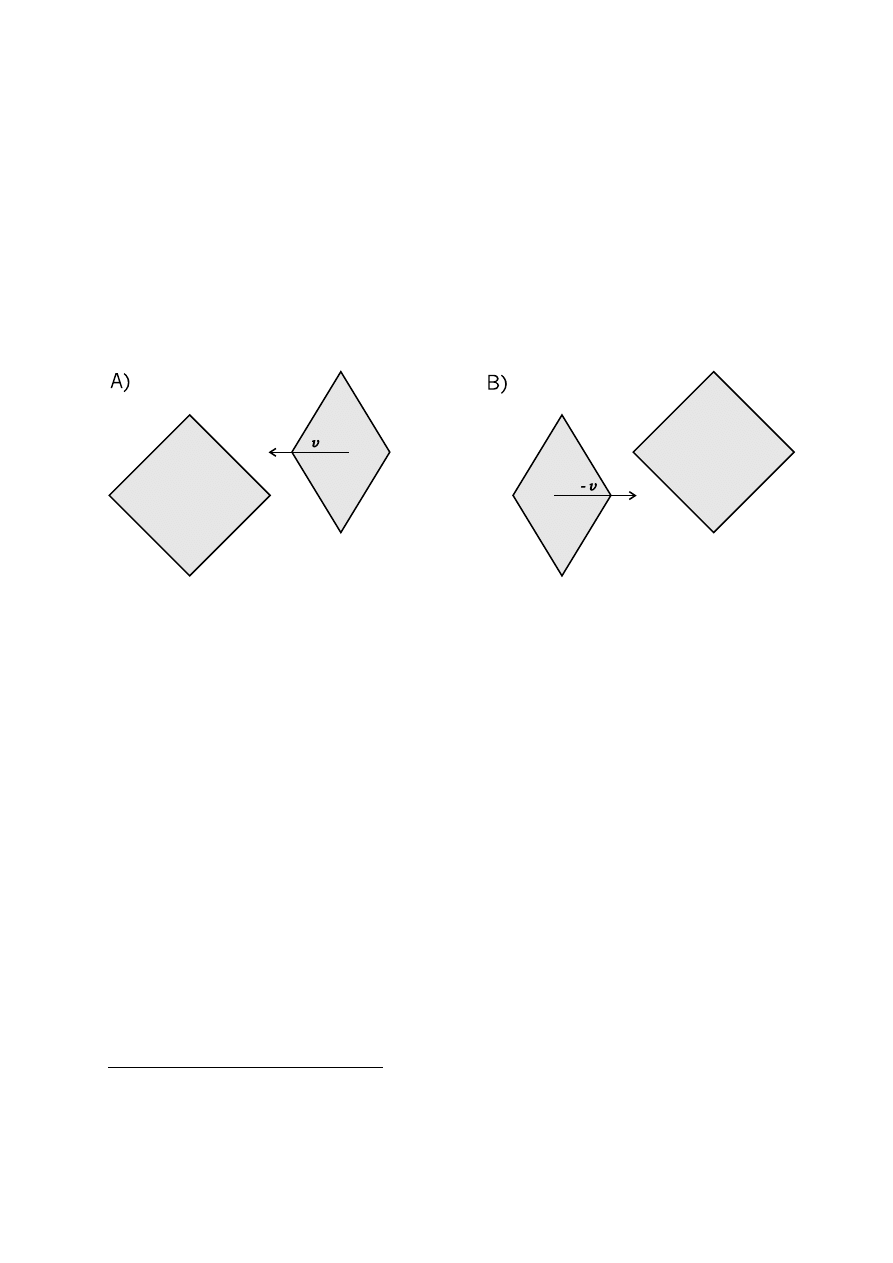
44
ROZDZIAŁ 3.
NIESZTYWNA BRYŁA SZTYWNA
si˛e w kierunku ruchu staj ˛
ac si˛e rombem. Z rysunku wida´c, ˙ze kwadraty zderz ˛
a si˛e, przy czym
wierzchołek pierwszego kwadratu uderzy w kraw˛ed´z drugiego pozostawiaj ˛
ac w niej zapewne
widoczne wgniecenie. To samo zderzenie „z punktu widzenia” drugiego kwadratu przedstaw-
iono na rysunku 3.2 B). Widzimy, ˙ze jako pierwsze zderz ˛
a si˛e wierzchołek drugiego kwadratu
z kraw˛edzi ˛
a pierwszego i widoczny ´slad uderzenia b˛edzie gdzie indziej. Poniewa˙z lokalizacja
„wgniecenia” nie mo˙ze zale˙ze´c od układu odniesienia, gdzie´s w przedstawionym rozumowaniu
musi tkwi´c bł ˛
ad. Jakie jest poprawne rozumowanie i gdzie jest ów bł ˛
ad?
Rysunek 3.2:
Zderzenie kwadratów w dwóch zwi ˛
azanych z nimi układach odniesienia.
W układzie odniesienia w którym kwadraty poruszaj ˛
a si˛e z równymi co do warto´sci, ale prze-
ciwnie skierowanymi pr˛edko´sciami, obydwa staj ˛
a si˛e jednakowymi rombami, które zderz ˛
a si˛e ze
sob ˛
a kraw˛edziami. Poniewa˙z w tym układzie oba wierzchołki doznaj ˛
a uderzenia jednocze´snie,
to w dowolnym innym układzie odniesienia punkt w którym zderzaj ˛
a si˛e kwadraty b˛edzie prze-
suwał si˛e wzdłu˙z kraw˛edzi z pr˛edko´sci ˛
a wi˛eksz ˛
a ni˙z c. Dlatego wgniecenia b˛ed ˛
a jednakowo
mocne na całej długo´sci zderzaj ˛
acych si˛e obszarów i punkty zderzaj ˛
ace si˛e w pierwszej kole-
jno´sci wcale nie pozostawi ˛
a wyra´zniejszych ´sladów. Wynika to z tego, ˙ze poszczególne zderza-
j ˛
ace si˛e punkty nie zd ˛
a˙z ˛
a „dowiedzie´c” si˛e, ˙ze doszło ju˙z do zderzenia pomi˛edzy ich s ˛
asiadami i
wytraci´c pr˛edko´sci decyduj ˛
acej o sile i impecie zderzenia.
3.4
P
ARADOKS KLOCKA I DZIURY W STOLE
1
O
mówimy teraz jeszcze jeden paradoks zwi ˛
azany z relatywistycznym ruchem bryły sztywnej.
Wyobra´zmy sobie kwadratowy (w swoim układzie spoczynkowym) klocek poruszaj ˛
acy si˛e po
1
Problem ten został przedstawiony w pracy [2].
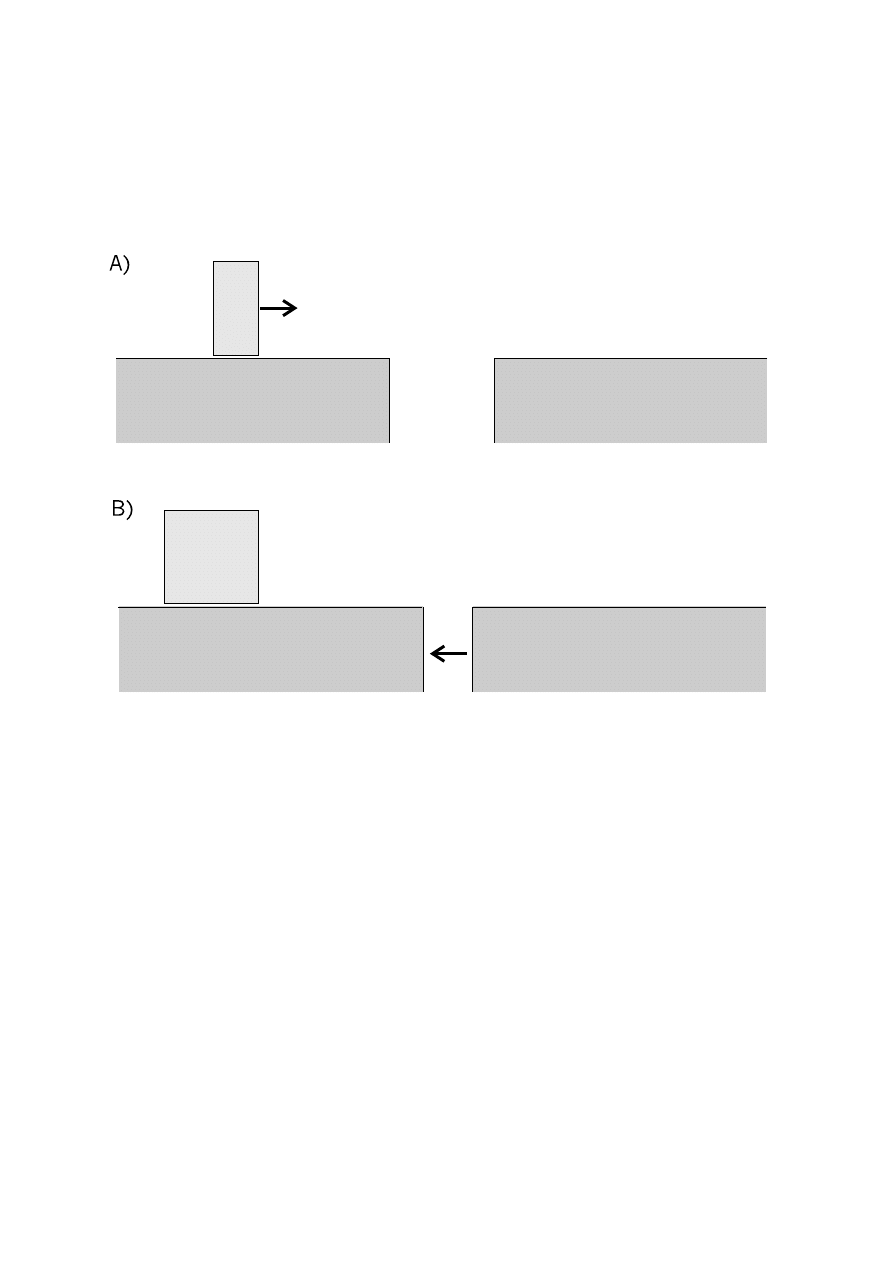
3.4.
PARADOKS KLOCKA I DZIURY W STOLE
2
45
dziurawym stole - rysunek 3.3. W układzie stołu klocek doznaje skrócenia Lorentza i dlatego
łatwo b˛edzie mu wpa´s´c do dziury (rysunek 3.3A). Z drugiej strony, z punktu widzenia klocka, to
dziura si˛e skraca uniemo˙zliwiaj ˛
ac klockowi wpadni˛ecie do ´srodka (rysunek 3.3B).
Rysunek 3.3:
Klocek poruszaj ˛
acy si ˛e po dziurawym stole z punktu widzenia dwóch inercjalnych układów
odniesienia: A) zwi ˛
azanego ze stołem, B) zwi ˛
azanego z klockiem.
Problem pozostawili´smy na koniec tego rozdziału, gdy˙z okazuje si˛e on by´c do´s´c skompli-
kowany. W momencie, gdy klocek znajdzie si˛e cz˛e´sciowo nad dziur ˛
a, b˛edzie na niego działał
pewien moment siły, który wywoła ruch obrotowy. To mo˙ze bardzo skomplikowa´c spraw˛e. Aby
nieco upro´sci´c sobie ˙zycie przyjmiemy, ˙ze dziura zamkni˛eta jest zapadk ˛
a, która w układzie stołu
zostaje nagle usuni˛eta. Dzieje si˛e to w momencie, gdy klocek w cało´sci znajdzie si˛e nad otwo-
rem. Nasz problem jest jednak nast˛epuj ˛
acy: kwadrat w swoim układzie odniesienia nigdy w
cało´sci nie znajduje si˛e nad otworem, bo w momencie, gdy tylni wierzchołek znajdzie si˛e nad
dziur ˛
a, przedni powinien ju˙z by´c po drugiej stronie. Czy oznacza to, ˙ze w tym układzie klocek
nie ma szans wpa´s´c do dziury? Oczywi´scie, nie. Zwró´cmy uwag˛e, ˙ze w układzie stołu cała
zapadka zostaje usuni˛eta jednocze´snie w chwili, gdy tylni wierzchołek znalazł si˛e nad otwo-
rem. Jednak w układzie klocka zapadka „znika” stopniowo, zaczynaj ˛
ac od drugiego brzegu
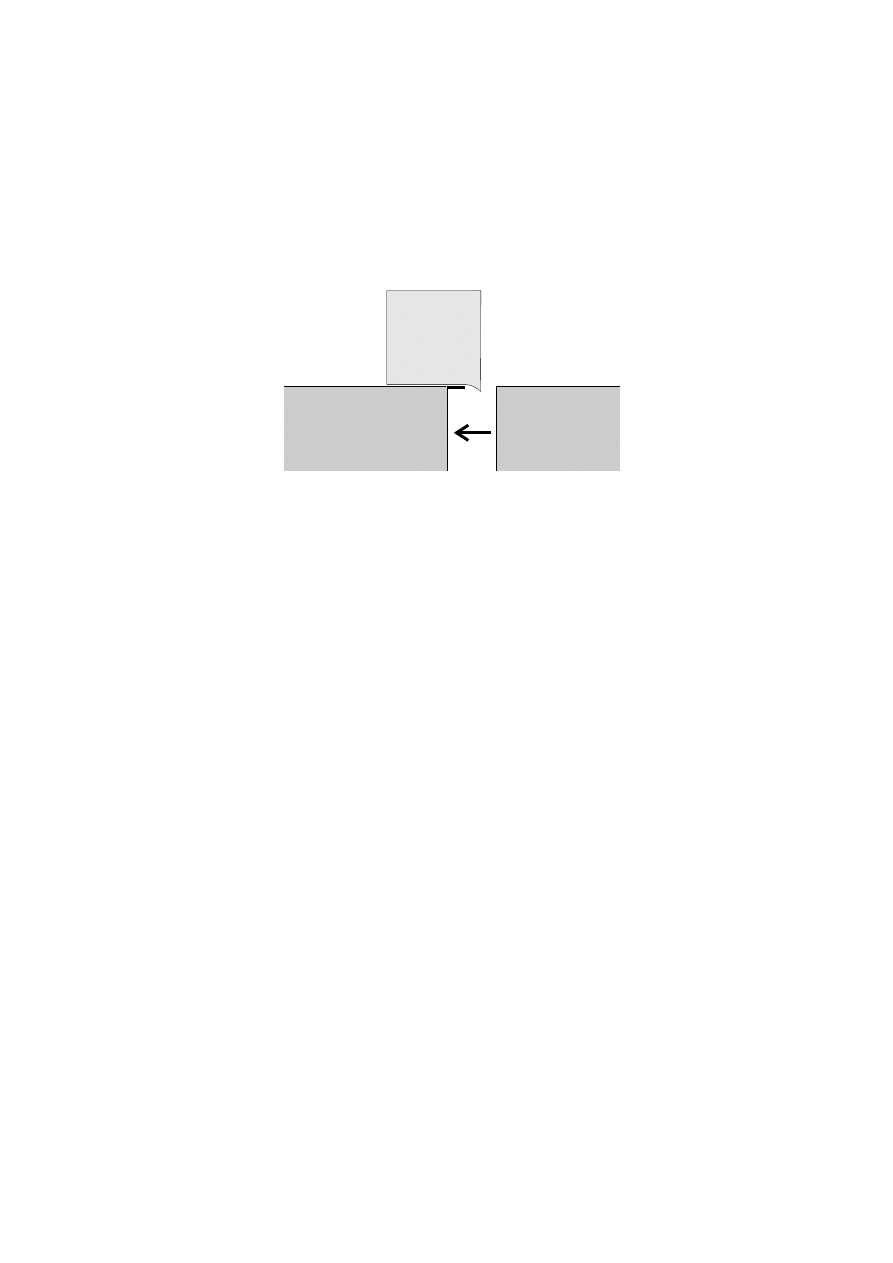
46
ROZDZIAŁ 3.
NIESZTYWNA BRYŁA SZTYWNA
dziury jeszcze zanim klocek znajdzie si˛e w cało´sci nad ni ˛
a. Pami˛etaj ˛
ac, ˙ze klocek nie mo˙ze
by´c uznany za brył˛e sztywn ˛
a zauwa˙zmy, ˙ze fragment spod którego usuni˛eto zapadk˛e zacznie
spada´c pomimo, ˙ze reszta klocka wci ˛
a˙z jeszcze znajduje si˛e na powierzchni stołu - rysunek
3.4. Z rysunku wida´c, ˙ze wewn ˛
atrz klocka pojawi ˛
a si˛e napi˛ecia, które strasznie skomplikuj ˛
a cał ˛
a
Rysunek 3.4:
Fragment klocka pod którym zapadka została usuni ˛eta „zsuwa si ˛e” do dziury zanim
jeszcze dowie si ˛e o tym reszta „kwadratu”. Prowadzi to naturalnie do powstawania silnych wewn ˛etrznych
napi ˛e´c.
dynamik˛e. Widzimy bowiem, ˙ze zwi˛eksza si˛e obj˛eto´s´c „kwadratowego” klocka. Napi˛ecia musz ˛
a
zatem istnie´c równie˙z w układzie inercjalnym zwi ˛
azanym ze stołem w którym cała zapadka znika
jednocze´snie. W momencie, gdy nacisk zapadki na klocek ustaje, jego dolna kraw˛ed´z zaczyna
swobodnie opada´c. Informacja o tym zaczyna si˛e rozchodzi´c pionowo wzdłu˙z klocka i dopiero
po pewnej chwili górna kraw˛ed´z równie˙z zaczyna spada´c. Powoduje to, ˙ze klocek rozci ˛
aga si˛e,
co wywołuje wła´snie wewn˛etrzne napi˛ecia w materiale.
Co gorsza, to jeszcze nie koniec komplikacji. ´Srodek masy klocka w układzie stołu pocz ˛
at-
kowo porusza si˛e poziomo, lecz po usuni˛eciu zapadki stopniowo nabywa pionowej składowej
pr˛edko´sci. Poniewa˙z skrócenie Lorentza ma miejsce zawsze w kierunku ruchu, to nawet je´sli
zaniedbamy efekty zwi ˛
azane z wewn˛etrznymi napi˛eciami, klocek zmieni kształt z prostok ˛
atnego
na równoległoboczny - rysunek 3.5 w zwi ˛
azku ze zmian ˛
a kierunku pr˛edko´sci . Oznacza to kolej-
ne ogromne komplikacje. Mo˙ze si˛e bowiem zdarzy´c, ˙ze pomimo i˙z ´srodek masy klocka spada,
to prawy, dolny wierzchołek podnosi si˛e ponad poziom stołu. W takiej sytuacji bardzo trudno
powiedzie´c, czy klocek wpadnie do dziury, czy nie. Potrzeba by tu bowiem szczegółowej anali-
zy zderzenia. Przykład ten pokazuje jak skomplikowany mo˙ze by´c relatywistyczny problem
bryły sztywnej. Pami˛etajmy, ˙ze zajmowali´smy si˛e geometri ˛
a kwadratu - jednym z najprostszych
mo˙zliwych przykładów.
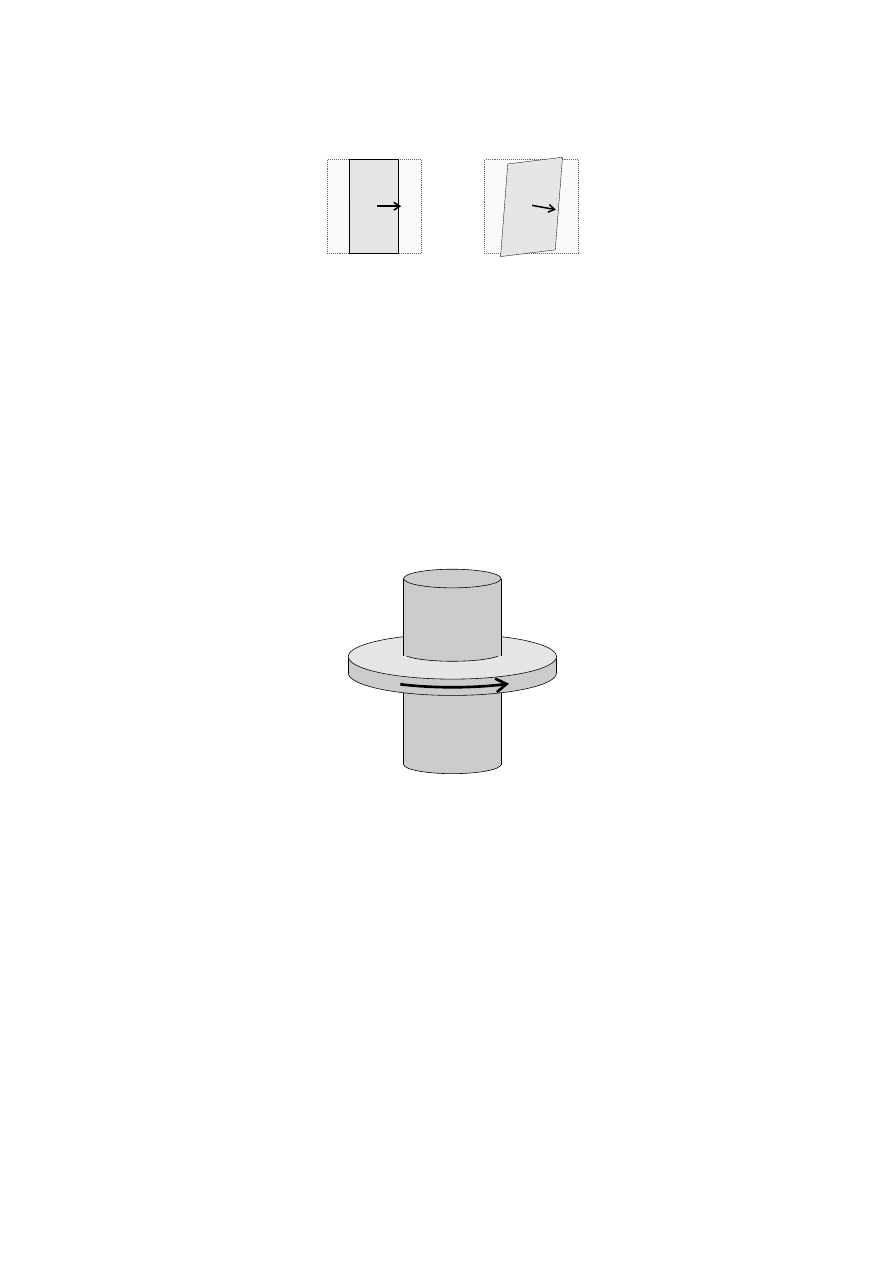
3.5.
NAPI ˛
ECIA WEWN ˛
ETRZNE
47
Rysunek 3.5:
Ze zmian ˛
a kierunku pr ˛edko´sci klocka wi ˛
a˙ze si ˛e równie˙z zmiana kierunku skrócenia
Lorentza. Klocek, który w układzie spoczynkowym jest kwadratowy, w układzie stołu zmienia si ˛e z pros-
tok ˛
ata w równoległobok.
3.5
N
API ˛
ECIA WEWN ˛
ETRZNE
W
iemy ju˙z, ˙ze w poruszaj ˛
acych si˛e ciałach czasami musz ˛
a pojawi´c si˛e napi˛ecia wewn˛etrzne
wywołane odkształceniami. Z cał ˛
a pewno´sci ˛
a jednak napi˛e´c tych nie ma w bryle poruszaj ˛
acej
si˛e ze stał ˛
a pr˛edko´sci ˛
a, bo nie ma ich w układzie spoczynkowym bryły. Napi˛ecia nie mog ˛
a si˛e
przecie˙z pojawi´c w wyniku przej´scia do innego inercjalnego układu odniesienia!
Rysunek 3.6:
Tarcza wiruj ˛
aca z relatywistyczn ˛
a pr ˛edko´sci ˛
a wokół nieruchomego rdzenia.
Wyobra´zmy sobie teraz okr ˛
agły pier´scie´n wiruj ˛
acy wokół pionowego trzpienia, jak na ry-
sunku 3.6. Analizuj ˛
ac ruch ka˙zdego elementu pier´scienia osobno stwierdzamy, ˙ze w wyniku
ruchu stycznego do okr˛egu powinny one dozna´c skrócenia Lorentza. Zatem obwód całego pier´s-
cienia powinien si˛e skróci´c, co wymagałoby zmniejszenia promienia. Mimo relatywistycznego
ruchu, spoczywaj ˛
acy rdze´n uniemo˙zliwia jednak pier´scieniowi zmian˛e kształtu. Nie mo˙ze si˛e
on zatem lorentzowsko skróci´c i z tego powodu paradoksalnie powstan ˛
a wewn ˛
atrz pier´scienia
napi˛ecia, mimo ˙ze jego kształt nie uległ wcale zmianie. Oczywi´scie napr˛e˙zenia te nie maj ˛
a nic
wspólnego z działaniem siły od´srodkowej. Maj ˛
a one charakter czysto relatywistyczny. Jednak˙ze

48
ROZDZIAŁ 3.
NIESZTYWNA BRYŁA SZTYWNA
W rzeczywisto´sci siła od´srodkowa odgrywa tu najwa˙zniejsz ˛
a rol˛e. Nie trzeba si˛e w zasadzie
martwi´c, czy pier´scie´n zmniejszy swój promie´n, tylko czy siła od´srodkowa go nie rozsadzi.
Pytania
• W jaki sposób z zasady demokracji wynika, ˙ze skrócenie poruszaj ˛
acych obiektów, poprzeczne
do kierunku ruchu jest niemo˙zliwe?
• Czy to prawda, ˙ze skrócenie Lorentza jest efektem pozornym i wynika z tego, ˙ze ´swiatło
opuszczaj ˛
ace obserwowany obiekt potrzebuje sko´nczonego czasu by dotrze´c do obserwa-
tora?
• Czy ciała poruszaj ˛
ace si˛e ze stał ˛
a pr˛edko´sci ˛
a doznaj ˛
a wewn˛etrznych napi˛e´c w zwi ˛
azku ze
skróceniem Lorentza?
Zadania
• Otwarta stodoła oraz tyczka maj ˛
a długo´s´c spoczynkow ˛
a L. W układzie stodoły biegn ˛
acy z
relatywistyczn ˛
a pr˛edko´sci ˛
a V tyczkarz mo˙ze by´c bez trudu zamkni˛ety wewn ˛
atrz. Rozwa˙z
sytuacj˛e w układzie tyczkarza, w którym w pewnym momencie pierwszy koniec tyczki
uderzy w tyln ˛
a ´scian˛e stodoły. Poka˙z, ˙ze i w tym układzie tyczka zostanie zamkni˛eta
wewn ˛
atrz. W tym celu udowodnij, ˙ze ˙zaden sygnał pochodz ˛
acy od uderzenia, a propagu-
j ˛
acy si˛e wzdłu˙z tyczki nie zd ˛
a˙zy dotrze´c do jej drugiego ko´nca zanim ten nie znajdzie
si˛e wewn ˛
atrz (ruchomej w tym układzie) stodoły oraz, ˙ze ˙zaden sygnał propaguj ˛
acy si˛e
wzdłu˙z stodoły nie zd ˛
a˙zy dotrze´c do jej drzwi zanim wewn ˛
atrz znajdzie si˛e cała tyczka.

Rozdział 4
K
ŁOPOTY Z TEORI ˛
A KWANTOW ˛
A
W
tym rozdziale zajmiemy si˛e czym´s co z pewno´sci ˛
a zdziwi niejednego z Was. Opowiemy
o przedziwnym zwi ˛
azku pomi˛edzy skwantowaniem energii a szczególn ˛
a teori ˛
a wzgl˛edno´sci -
jednym z najbardziej fascynuj ˛
acych i dot ˛
ad niezrozumiałych zagadnie´n mechaniki kwantowej.
Dla ustalenia uwagi, skupimy si˛e na kwantowych wła´sciwo´sciach ´swiatła, a wszystko o czym
powiemy b˛edzie wynika´c z „niegro´znego” z pozoru faktu istnienia fotonów...
4.1
I
NTERFEROMETR
M
ACHA
-Z
EHNDERA
S
pójrzmy na rysunek 4.1 na którym znajduje si˛e schemat interferometru Macha-Zehndera. Uk-
ład składa si˛e z dwóch luster, dwóch płytek ´swiatłodziel ˛
acych, które przepuszczaj ˛
a połow˛e
´swiatła, a połow˛e odbijaj ˛
a oraz dwóch detektorów ´swiatła czułych na pojedyncze fotony.
Co si˛e stanie, gdy z lewej strony o´swietlimy strumieniem ´swiatła doln ˛
a płytk˛e? Oczywi´scie,
cz˛e´s´c ´swiatła odbije si˛e od niej i pójdzie „górn ˛
a” drog ˛
a, a cz˛e´s´c przeniknie przez płytk˛e i dalej
b˛edzie podró˙zowa´c „dołem”. Obie wi ˛
azki odbij ˛
a si˛e od luster i natrafi ˛
a na kolejn ˛
a płytk˛e na
której ponownie si˛e nało˙z ˛
a. A co b˛edzie potem? Okazuje si˛e, ˙ze całe ´swiatło dotrze tylko do
jednego detektora, cho´c wydaje si˛e, ˙ze cz˛e´s´c powinna dotrze´c tak˙ze i do drugiego. Oto dlaczego
tak si˛e dzieje. Poniewa˙z drogi górna i dolna s ˛
a równej długo´sci, zmiana fazy fali elektromagne-
tycznej podró˙zuj ˛
acej obiema drogami jest identyczna. Jednak˙ze ka˙zdemu odbiciu fali (od lustra
lub płytki ´swiatłodziel ˛
acej) towarzyszy dodatkowa zmiana fazy o
π
2
. W formalizmie zespolonym
pole elektryczne przy ka˙zdym odbiciu nale˙zy pomno˙zy´c przez −i.
Przeanalizujmy teraz jakie pole elektromagnetyczne dociera do górnego detektora. Cz˛e´s´c
pola podró˙zowała górn ˛
a cz˛e´sci ˛
a interferometru odbijaj ˛
ac si˛e po drodze 3 razy, czyli nale˙zy je
49
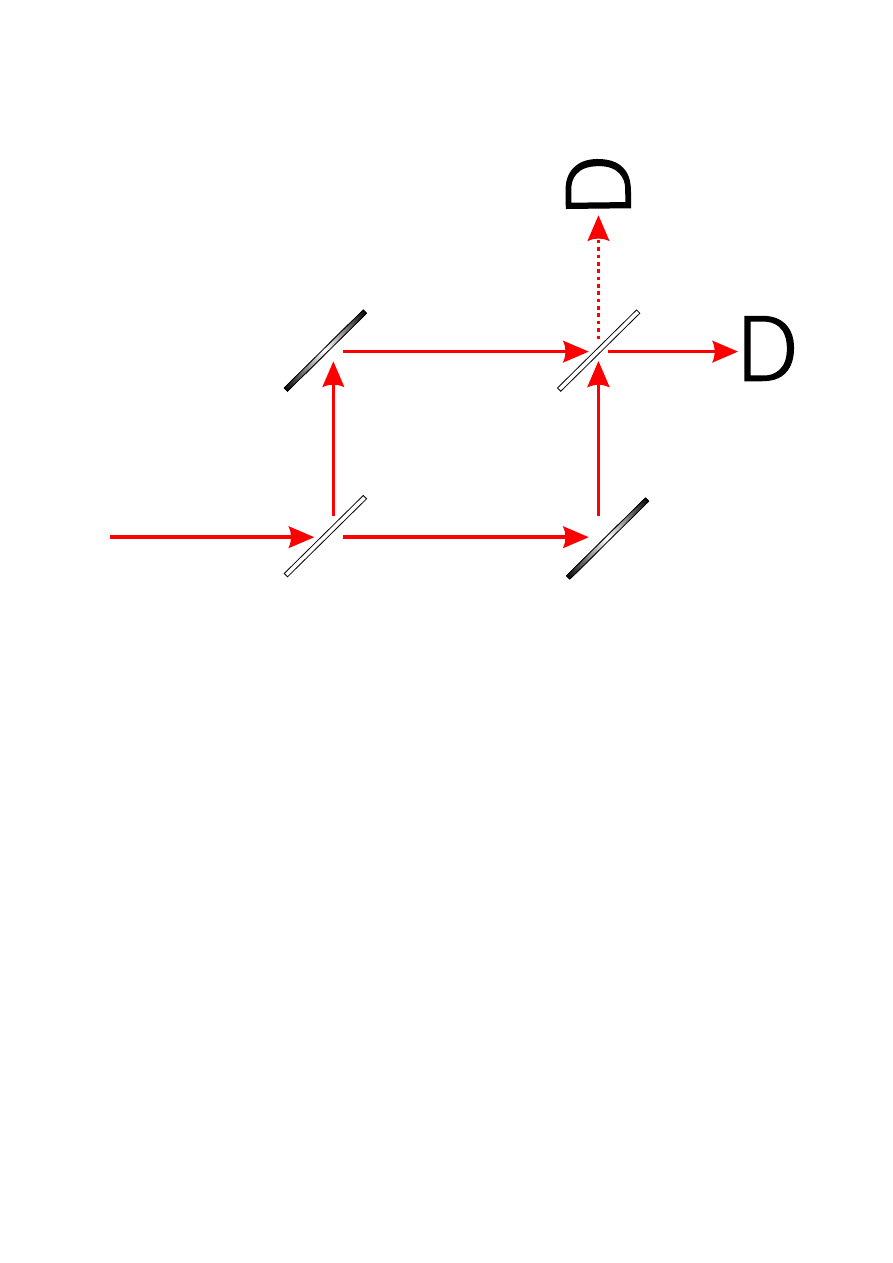
50
ROZDZIAŁ 4.
KŁOPOTY Z TEORI ˛
A KWANTOW ˛
A
Rysunek 4.1:
Schemat interferometru Macha-Zehndera.
pomno˙zy´c przez (−i)
3
= i. Pozostała cz˛e´s´c przechodz ˛
ac dołem odbiła si˛e tylko raz, czyli
mno˙zymy pole przez −i. Widzimy, ˙ze dodaj ˛
ac wkłady do całkowitego pola elektromagnety-
cznego pochodz ˛
ace od obu dróg otrzymujemy zero na powierzchni górnego detektora. Dlatego
wła´snie górny detektor niczego nie rejestruje. Analizuj ˛
ac w analogiczny sposób pole dociera-
j ˛
ace do dolnego detektora łatwo przekonujemy si˛e, ˙ze pola podró˙zuj ˛
ace alternatywnymi drogami
dodadz ˛
a si˛e. Wida´c, ˙ze pole nigdzie nie znika, tylko w cało´sci kumuluje si˛e w dolnym detek-
torze. Na razie wszystko jest do´s´c wiarygodne, jednak za chwil˛e dowiecie si˛e czego´s absolutnie
niesamowitego.
Poniewa˙z ka˙zdy strumie´n ´swiatła składa si˛e naprawd˛e z pojedynczych fotonów, zastanówmy
si˛e co b˛edzie si˛e działo gdy płytk˛e ´swiatłodziel ˛
ac ˛
a „o´swietlimy” pojedynczym fotonem. Do
którego detektora foton mo˙ze dotrze´c? Wydawa´c by si˛e mogło, ˙ze foton musi w jaki´s sposób
„zdecydowa´c si˛e” na jedn ˛
a z dróg i nie maj ˛
ac z czym interferowa´c b˛edzie równie cz˛esto wpadał
do jednego detektora co do drugiego, je´sli eksperyment b˛edziemy wielokrotnie powtarza´c. Co
prawda nie bardzo wiadomo co miałoby decydowa´c o wyborze przez foton tej a nie innej drogi,

4.2.
ZJAWISKO EPR I KWANTOWE ZACHWIANIE PRZYCZYNOWO ´SCI
51
ale czy przychodzi nam do głowy inne rozwi ˛
azanie? Okazuje si˛e, ˙ze musi nam przyj´s´c do głowy
inne rozwi ˛
azanie, bo nasze wnioski s ˛
a bł˛edne. W eksperymencie okazuje si˛e, ˙ze nawet u˙zywa-
j ˛
ac pojedynczych fotonów nie da si˛e „obudzi´c” górnego detektora. Znowu zawsze klika dolny!
Wygl ˛
ada wi˛ec na to, ˙ze foton z czym´s musi interferowa´c. Poniewa˙z w okolicy nie ma innych fo-
tonów musi zatem interferowa´c z samym sob ˛
a! Maj ˛
ac do dyspozycji dwa alternatywne sposoby
przebycia interferometru foton wybiera obydwa naraz podró˙zuj ˛
ac w pewnym sensie dwiema
drogami jednocze´snie! Powoli wkraczamy ju˙z na niebezpieczne tereny mechaniki kwantowej.
Dalej b˛edzie ju˙z coraz dziwniej. Pami˛etajmy jednak przez cały czas, ˙ze to nie wina teorii, ˙ze jest
dziwna. To raczej Natura jest przedziwna!
Z tego co powiedzieli´smy mo˙ze pozornie wynika´c, ˙ze z jednego fotonu robi ˛
a si˛e dwa. Czy
oznacza to, ˙ze energia nie jest zachowana? Aby to sprawdzi´c wystarczy postawi´c dwa detektory
tu˙z za pierwsz ˛
a płytk ˛
a ´swiatłodziel ˛
ac ˛
a. Zadaniem tych detektorów b˛edzie sprawdzenie któr˛edy
„naprawd˛e” podró˙zuje foton. I oto stanie si˛e co´s jeszcze dziwniejszego: b˛edzie klika´c zawsze
tylko jeden detektor, ale czasami pierwszy, a czasami drugi. To, który detektor kliknie w konkret-
nym przypadku jest zupełnie przypadkowe i niczym nieuzasadnione! Indeterminizm wyniku tego
eksperymentu jest, według doktryn mechaniki kwantowej fundamentalnym prawem przyrody.
Oto w jak dziwny sposób foton ratuje zasad˛e zachowania energii. Nasz eksperyment wygl ˛
ada
troch˛e tak, jakby foton poruszał si˛e dwiema drogami naraz, dopóki nikt nie próbuje sprawdzi´c
któr˛edy „naprawd˛e” przeszedł. Gdy jednak kto´s próbuje to zrobi´c stawiaj ˛
ac na dwóch drogach
detektory, foton zawsze zdecyduje si˛e na jedn ˛
a z alternatywnych mo˙zliwo´sci, zupełnie bez ˙zad-
nej przyczyny na t˛e, a nie inn ˛
a. W formalizmie kwantowomechanicznym taki „rozdwojony” stan
fotonu |Ψi zapisuje si˛e w nast˛epuj ˛
acy sposób:
|Ψi = |(foton przeszedł gór ˛
a)i + |(foton przeszedł dołem)i
(4.1)
i nazywa stanem superponowanym albo po prostu superpozycj ˛
a dwóch mo˙zliwo´sci. Na pozór
nasza kwantowa opowie´s´c nie ma nic wspólnego ze szczególn ˛
a teori ˛
a wzgl˛edno´sci, lecz za
chwil˛e przekonamy si˛e, ˙ze jednak ma, i to bardzo wiele.
4.2
Z
JAWISKO
EPR
I KWANTOWE ZACHWIANIE PRZYCZYNO
-
WO ´SCI
D
o fotonów jeszcze powrócimy, a tymczasem teraz zajmiemy si˛e słynnym „paradoksem” Ein-

52
ROZDZIAŁ 4.
KŁOPOTY Z TEORI ˛
A KWANTOW ˛
A
steina-Podolskiego-Rosena. Oto jak si˛e on przedstawia. Wyobra´zmy sobie nieruchom ˛
a, radioak-
tywn ˛
a (rozpadaj ˛
ac ˛
a si˛e) cz ˛
astk˛e, której całkowity, wewn˛etrzny moment p˛edu (nazywany spinem)
jest równy zero. Gdyby cz ˛
astka była zwykł ˛
a kulk ˛
a, to powiedzieliby´smy po prostu, ˙ze si˛e ona
nie kr˛eci, ale wiemy, ˙ze cz ˛
astki to nie s ˛
a zwykłe kulki. Dlatego nale˙zy powiedzie´c, ˙ze ich spin
wynosi zero. Z zasady zachowania p˛edu wynika, ˙ze je´sli cz ˛
astka ta rozpadnie si˛e na dwie iden-
tyczne, mniejsze cz ˛
astki, to polec ˛
a one w przeciwnych kierunkach. Oprócz zasady zachowania
p˛edu musi by´c równie˙z spełniona zasada zachowania momentu p˛edu z której wynika, ˙ze je´sli
spin poszczególnych produktów rozpadu nie jest równy zero, to zawsze spin pierwszej cz ˛
astki
musi by´c skierowany przeciwnie ni˙z spin drugiej. By´c mo˙ze słyszeli´scie, ˙ze spin cz ˛
astek ele-
mentarnych nie mo˙ze by´c dowolny. Na przykład spin elektronu w pewnym układzie jednostek
wynosi
1
2
. Oznacza to, ˙ze mo˙ze on by´c skierowany w dowolnym kierunku, ale jego warto´s´c musi
by´c dla ka˙zdego elektronu taka sama.
Dla ustalenia uwagi przyjmijmy, ˙ze produktami rozpadu s ˛
a wła´snie dwa elektrony. Skoro ich
spiny musz ˛
a by´c skierowane przeciwnie, to równie˙z dowolna składowa spinu musi mie´c ró˙zny
znak dla obu elektronów. Poniewa˙z składowe spinu elektronu mo˙zna mierzy´c eksperymentalnie,
to wnioskujemy st ˛
ad, ˙ze pomiar składowej spinu, na przykład wzdłu˙z osi z dla jednego elektronu
da zawsze wynik przeciwny ni˙z analogiczny pomiar składowej spinu dla drugiego elektronu.
W jaki sposób zapisa´c stan kwantowy pary elektronów wyprodukowanych w rozpadzie? S ˛
a
dwie mo˙zliwo´sci. Po pierwsze składowa spinu pierwszego elektronu mo˙ze by´c skierowana zgod-
nie z osi ˛
a z, a składowa spinu drugiego elektronu przeciwnie. Wówczas dwa elektrony byłyby
w stanie kwantowym | ↑i
1
| ↓i
2
. Jest te˙z druga, odwrotna mo˙zliwo´s´c w której elektrony s ˛
a w
stanie | ↓i
1
| ↑i
2
. Która z alternatyw zostanie w rzeczywisto´sci wybrana? W tym momencie na
my´sl przychodzi nast˛epuj ˛
aca analogia. Gdy zdejmiemy z nóg oba buty i jeden rzucimy w prawo,
a drugi w lewo, nie patrz ˛
ac który poleciał w któr ˛
a stron˛e, wydaje si˛e, ˙ze para butów b˛edzie
w podobnym stanie co para elektronów. Albo prawy but pofrun ˛
ał w prawo, a lewy w lewo,
albo na odwrót. Okazuje si˛e jednak, ˙ze sytuacja kwantowa jest diametralnie ró˙zna, bowiem
podobnie jak w przykładzie z poprzedniego podrozdziału zrealizowane zostan ˛
a obie alternatywy
jednocze´snie! W przypadku butów, ich skr˛etno´sci zostały ustalone ju˙z w momencie rzucania. W
przypadku elektronów, a˙z do momentu pomiaru kierunki ich spinów nie s ˛
a okre´slone. Całkowity
stan pary elektronów powstałych w rozpadzie jest postaci:
|Ψi = | ↑i
1
| ↓i
2
+ | ↓i
1
| ↑i
2
.
(4.2)

4.2.
ZJAWISKO EPR I KWANTOWE ZACHWIANIE PRZYCZYNOWO ´SCI
53
W gruncie rzeczy sytuacja jest bardzo podobna do omówionej w poprzednim podrozdziale.
Ró˙znica jest taka, ˙ze poprzednio rozwa˙zali´smy stan superponowany pojedynczego fotonu, a
teraz mówimy o superpozycji pary elektronów. Zanim nie wykonamy pomiaru, oba człony
superpozycji s ˛
a jednocze´snie „realizowane” i nie mo˙zna powiedzie´c czy „naprawd˛e” pierwsza
cz ˛
astka ma spin skierowany w gór˛e, czy w dół osi z. Bardzo podobny przykład został podany w
słynnej pracy Einsteina, Podolskiego i Rosena w której autorzy wyci ˛
agn˛eli wniosek, ˙ze je´sli
mechanika kwantowa jest „prawdziwa”, to elektrony musiałby si˛e ze sob ˛
a „skomunikowa´c”
dopiero w chwili pomiaru (je˙zeli ich spiny mierzone były jednocze´snie), aby unikn ˛
a´c złama-
nia zasady zachowania momentu p˛edu. Jednak˙ze tego typu komunikacja wymagałaby „u˙zycia”
przez elektrony sygnału poruszaj ˛
acego si˛e niesko´nczenie szybko, co jak wiemy jest do´s´c bolesne
z punktu widzenia szczególnej teorii wzgl˛edno´sci. Czy oznacza to, ˙ze mechanika kwantowa nie
jest dobr ˛
a teori ˛
a? Einstein uznał, ˙ze nie jest. My jednak spróbujemy mimo wszystko przyjrze´c
si˛e sprawie uwa˙zniej, tym bardziej, ˙ze pomimo swej „niecodzienno´sci” mechanika kwantowa
jeszcze ani razu, w ˙zadnym eksperymentalnym te´scie nie zawiodła. W dodatku, z nast˛epnego
podrozdziału dowiemy si˛e, ˙ze rzekome rozwi ˛
azanie problemu podane przez Einsteina nie jest
zgodne z rzeczywisto´sci ˛
a. Istnieje bowiem mo˙zliwo´s´c eksperymentalnej weryfikacji prawdzi-
wo´sci jego stwierdzenia.
Einstein nie mógł przełkn ˛
a´c faktu, ˙ze zjawisko o którym pisał wygl ˛
ada z punktu widzenia
mechaniki kwantowej dokładnie tak, jak gdyby elektrony wymieniały sygnały ponad´swietlne.
Pytanie, które si˛e narzuca to, czy mo˙zna by zastosowa´c efekt EPR do przesyłania informacji
ponad´swietlnych pomi˛edzy osobami dokonuj ˛
acymi pomiarów? Gdyby było to mo˙zliwe, wów-
czas zasady przyczynowo´sci uległyby zachwianiu o czym przekonali´smy si˛e ju˙z w rozdziale
1.5. Z drugiej strony osoba dokonuj ˛
aca pomiaru spinu dowiaduje si˛e jednocze´snie jaki b˛edzie
wynik analogicznego pomiaru na drugim elektronie mimo, ˙ze ten mo˙ze znajdowa´c si˛e ju˙z bardzo
daleko, a w przeciwie´nstwie do pary butów wynik nie był przed pomiarem okre´slony. Wygl ˛
ada
to tak, jakby´smy byli w stanie natychmiast dowiedzie´c si˛e o stanie odległego elektronu. Jednak˙ze
wynik naszego pomiaru jest, dokładnie jak w przypadku poprzedniego rozdziału, zupełnie przy-
padkowy. Co z tego, ˙ze natychmiast dowiadujemy si˛e o rezultacie odległego pomiaru, skoro nie
potrafimy wpływa´c na jego wynik? Nie potrafimy zmusi´c elektronu znajduj ˛
acego si˛e w ł ˛
acznym
stanie (4.1) do tego by jego spin był skierowany tak jak nam si˛e podoba. Dopiero gdyby to
nam si˛e udało, byliby´smy w stanie przesyła´c informacje przy pomocy „zjawiska EPR”. Natura
pomy´slała to naprawd˛e niezwykle chytrze. Cho´c mamy w r˛eku nielokalne (czyli oddziałuj ˛
ace na
odległo´s´c) zjawisko, nie potrafimy go u˙zy´c do kontrolowania obiektów na odległo´s´c ze wzgl˛edu

54
ROZDZIAŁ 4.
KŁOPOTY Z TEORI ˛
A KWANTOW ˛
A
na jego indeterminizm (fundamentaln ˛
a nieokre´slono´s´c wyników pomiarów). Pytanie czy to tylko
przypadek, zło´sliwe zrz ˛
adzenie losu, czy te˙z konsekwencja jakich´s bardziej fundamentalnych
praw? Tego nikt nie wie.
4.3
N
IERÓWNO ´SCI
B
ELLA
P
rzedziwna kwantowomechaniczna zasada mówi ˛
aca, ˙ze w ogólno´sci wynik pojedynczego po-
miaru nie jest przez nic okre´slony, budzi sprzeciw u wi˛ekszo´sci osób, które j ˛
a po raz pierwszy
poznaj ˛
a. Nic dziwnego. Słyszy si˛e na przykład: „Ja w to nigdy nie uwierz˛e! Na pewno ist-
nieje co´s, co sprawia, ˙ze foton odbija si˛e lub przechodzi przez płytk˛e ´swiatłodziel ˛
ac ˛
a. Prze-
cie˙z indeterminizm to absurd!”. Powstało nawet wiele konkurencyjnych teorii u˙zywaj ˛
acych za-
miast słowa „co´s”, terminu parametr ukryty. Teorie te mówi ˛
a: istniej ˛
a pewne, na razie niez-
nane (ukryte), parametry, które determinuj ˛
a wyniki pojedynczych pomiarów. Na przykład je´sli
chodzi o eksperyment z fotonem przechodz ˛
acym przez płytk˛e ´swiatłodziel ˛
ac ˛
a wydaje si˛e, ˙ze w
rzeczywisto´sci o tym czy foton odbije si˛e, czy przejdzie decyduje wła´snie jaki´s ukryty para-
metr. Podobnie na paradoks EPR patrzył Einstein. Twierdził on, ˙ze w momencie wytworzenia
pary elektronów, ich spiny s ˛
a ju˙z okre´slone. Okre´slone przez jaki´s niepoznany dot ˛
ad, ukryty
parametr.
Sytuacja radykalnie si˛e zmieniła, gdy w 1964 roku ukazała si˛e praca Bella zawieraj ˛
aca słynne
nierówno´sci nazwane pó´zniej jego nazwiskiem. Dzi˛eki nim, pojawiła si˛e mo˙zliwo´s´c ekspery-
mentalnego sprawdzenia, czy ukryte parametry istniej ˛
a, czy te˙z nie. Aby przedstawi´c ide˛e Bella,
powró´cmy do analizy paradoksu EPR. Przyjmijmy, ˙ze elektrony w chwili emisji ustalaj ˛
a mi˛edzy
sob ˛
a parametry: „ty bierzesz spin w gór˛e, ja bior˛e spin w dół i lecimy!”. Załó˙zmy, ˙ze obie cz ˛
astki
charakteryzuje parametr (lub zestaw parametrów) λ, okre´slaj ˛
acy kierunek spinu obu elektronów.
A jaka jest natura tych parametrów? Nie mam poj˛ecia i nic mnie to nie obchodzi! - mówi Bell.
Je˙zeli ukryte parametry rzeczywi´scie istniej ˛
a, to pr˛edzej czy pó´zniej zostan ˛
a odkryte, a na razie
po prostu zakładam, ˙ze jakie´s dziwne parametry nieznanej natury istniej ˛
a i decyduj ˛
a o wynikach
wszystkich pomiarów.
W eksperymencie my´slowym EPR u˙zyli´smy dwóch urz ˛
adze´n mierz ˛
acych spin wzdłu˙z tych
samych kierunków (wzdłu˙z osi z). Nic jednak nie zabrania nam ich zmieni´c! Mo˙zemy prze-
cie˙z urz ˛
adzenia mierz ˛
ace rzut spinu ustawi´c na pomiar ró˙znych składowych momentu p˛edu i
zobaczy´c jak wpłynie to na wyniki. Je´sli chcemy ukrytych parametrów, to musimy przyj ˛
a´c,
˙ze determinuj ˛
a one wynik ka˙zdego eksperymentu jaki przyjdzie nam do głowy wykona´c (czyli

4.3.
NIERÓWNO ´SCI BELLA
55
jak by´smy nie ustawili detektorów, wynik musi by´c zdeterminowany parametrem λ). Wynik
ka˙zdego eksperymentu mo˙ze by´c tylko: „w gór˛e” albo „w dół”. Trzeciego wyj´scia by´c nie mo˙ze.
Je˙zeli w wyniku pomiaru oka˙ze si˛e, ˙ze spin jest skierowany „w gór˛e”, to za wynik eksperymentu
przyjmiemy +1, a je´sli nie, to −1. Potem mo˙zemy wykona´c sto lub wi˛ecej eksperymentów i
obliczy´c jaki jest ´sredni wynik. Je´sli wyjdzie on zero, to znaczy, ˙ze tak samo cz˛esto spin trafia
si˛e skierowany „w gór˛e” jak i „w dół”. ´Srednia mo˙ze by´c te˙z dodatnia lub ujemna. Domy´slamy
si˛e co to oznacza. W pierwszym przypadku spin b˛edzie cz˛e´sciej ustawiony „w gór˛e”, a w drugim
cz˛e´sciej „w dół”. We´zmy sobie wi˛ec dwa detektory i jeden ustawmy w pewnym poło˙zeniu a, a
drugi w poło˙zeniu b. Nast˛epnie sprawd´zmy jakie s ˛
a wyniki pomiarów spinu dla obu cz ˛
astek. Oz-
naczmy przez A
a
(λ) wynik eksperymentu na pierwszym elektronie, a przez B
b
(λ) na drugim.
Jak wida´c, wyniki (mog ˛
ace jedynie przyj ˛
a´c warto´sci ±1) zale˙z ˛
a tylko od ustawienia detektorów
i ukrytego parametru. Co dalej? Powiedzmy sobie: te ukryte parametry, których nie znamy,
nie mog ˛
a by´c równie˙z przez nas nijak kontrolowane. Wi˛ec tak naprawd˛e, przypisywane s ˛
a one
elektronom losowo (w zasadzie, w naszej teorii musi istnie´c jaki´s czynnik, który decyduje o tym
jaki parametr zostaje w danym rozpadzie przypisany, ale my go nie potrafimy kontrolowa´c, wi˛ec
wychodzi na jedno).
Oznaczmy zbiór wszystkich mo˙zliwych parametrów przez Λ. Mo˙zemy jeszcze przyj ˛
a´c dla
ogólno´sci mo˙zliwo´s´c, ˙ze niektóre parametry trafiaj ˛
a si˛e cz˛e´sciej, a inne rzadziej, wi˛ec okre´slamy
jaki´s nieznany rozkład prawdopodobie´nstwa na zbiorze wszystkich parametrów p(λ). Im wi˛ek-
sza warto´s´c p(λ), tym cz˛e´sciej b˛edzie trafiał si˛e parametr λ. Suma wszystkich prawdopodo-
bie´nstw musi by´c równa jeden, tzn.
R
dλ p(λ) = 1. Skoro ju˙z to wszystko wiemy, mo˙zemy
przyst ˛
api´c do rachunków. Obliczmy najpierw, jaka jest ´srednia warto´s´c iloczynu wyników otrzy-
manych dla obu cz ˛
astek:
E(a, b) =
Z
Λ
dλ p(λ)A
a
(λ)B
b
(λ).
(4.3)
Dodam tu istotn ˛
a uwag˛e: powy˙zszy wzór kamufluje pewne wa˙zne zało˙zenie. Mianowicie takie,
ze wyniki obu pomiarów s ˛
a niezale˙zne. Innymi słowy, pomiary dokonane na odległych cz ˛
astkach
nie maj ˛
a na siebie wpływu (zało˙zenie to nazywa si˛e postulatem lokalno´sci). Formalne zas-
tosowanie tego zało˙zenia polega na stwierdzeniu, ˙ze wynik pomiaru spinów mo˙ze by´c zapisany
w postaci iloczynu wyników dla pierwszego i drugiego elektronu osobno (to wcale nie jest takie
oczywiste i po prostu zakładamy, ˙ze tak jest!). Skorzystamy teraz z elementarnego twierdzenia
całkowego: |
R
f (x)| ≤
R
|f (x)|. Mo˙zemy dokona´c serii pomiarów przy pewnych ustawie-

56
ROZDZIAŁ 4.
KŁOPOTY Z TEORI ˛
A KWANTOW ˛
A
niach detektorów i obliczy´c warto´s´c ´sredni ˛
a, nast˛epnie powtórzy´c procedur˛e zmieniaj ˛
ac jeden z
kierunków, a na ko´ncu odj ˛
a´c od siebie otrzymane wyniki i wzi ˛
a´c warto´s´c bezwzgl˛edn ˛
a. Otrzy-
mamy wówczas:
|E(a
0
, b) − E(a
0
, b
0
)| ≤
Z
Λ
dλ p(λ) |A
a
0
(λ)B
b
(λ) − A
a
0
(λ)B
b
0
(λ)|,
(4.4)
a jak si˛e uwa˙zniej przyjrze´c, to si˛e oka˙ze, ˙ze prawa strona mo˙ze by´c równie˙z zapisana w sprytny
sposób:
Z
Λ
dλ p(λ) |A
a
0
| |B
b
(1 ± A
a
B
b
0
) − B
b
0
(1 ± A
a
B
b
)|.
(4.5)
Znak ± mo˙zemy sobie wybra´c na ko´ncu jaki nam si˛e spodoba. Dla prostoty pomin˛eli´smy w
zapisie zale˙zno´s´c wyników od parametru λ. Wiemy, ˙ze dla ka˙zdego λ mamy |A
a
0
(λ)| = 1.
Zatem to ostatnie równa si˛e po prostu:
Z
Λ
dλ p(λ) |B
b
(1 ± A
a
B
b
0
) − B
b
0
(1 ± A
a
B
b
)| ≤
≤
Z
Λ
dλ p(λ)
¯
¯
¯|B
b
|(1 ± A
a
B
b
0
) + |B
b
0
|(1 ± A
a
B
b
)
¯
¯
¯ =
=
Z
Λ
dλ p(λ)
¯
¯
¯2 ± (A
a
B
b
0
+ A
a
B
b
)
¯
¯
¯ = 2 ± (E(a, b
0
) + E(a, b)).
(4.6)
W wyniku tych wszystkich zawiłych (cho´c przyznacie, niezbyt wyrafinowanych) rachunków,
dostajemy nierówno´s´c:
|E(a
0
, b) − E(a
0
, b
0
)| ≤ 2 ± (E(a, b
0
) + E(a, b)),
(4.7)
a z tego ju˙z łatwo otrzymujemy to, co nazywa si˛e szumnie „nierówno´sci ˛
a Bella” (wystarczy
sprytnie dobra´c znaki: raz plus, a raz minus w powy˙zszym wyra˙zeniu):
−2 ≤ S(a, b, a
0
, b
0
) ≤ 2,
(4.8)
gdzie

4.3.
NIERÓWNO ´SCI BELLA
57
S(a, b, a
0
, b
0
) = E(a, b) + E(a, b
0
) + E(a
0
, b) − E(a
0
, b
0
).
(4.9)
Chyba nikt nie spodziewa si˛e, ˙ze ten prosty wynik mo˙ze tak wiele znaczy´c! Zatem czeka Was
spora niespodzianka. Okazuje si˛e (te rachunki sobie ju˙z darujemy), ˙ze je´sli zapyta´c mechanik˛e
kwantow ˛
a, jaka jest warto´s´c kombinacji S dla pewnych szczególnych ustawie´n detektorów, to
oka˙ze si˛e, ˙ze mo˙zemy dosta´c wynik nawet S = 2
√
2. Ka˙zdy widzi, ˙ze łamie on nierówno´s´c Bella
(jest on przecie˙z wi˛ekszy ni˙z dwa!). Mamy nareszcie to, na co czekali´smy: znale´zli´smy mo˙zli-
wo´s´c eksperymentalnej weryfikacji przyj˛etych zało˙ze´n (determinizmu i lokalno´sci) w naszym
prostym modeliku. Wystarczy w odpowiedni sposób ustawi´c detektory, zmierzy´c przy ich po-
mocy spiny wielu par elektronów, obliczy´c warto´sci ´srednie i utworzy´c z nich kombinacj˛e S.
Je˙zeli otrzymany wynik przekroczy warto´s´c 2 (jak to przewiduje mechanika kwantowa), to
b˛edzie to bezpo´sredni dowód nieadekwatno´sci przyj˛etych zało˙ze´n do badanej sytuacji fizycznej!
Jaki jest werdykt? Eksperymenty badaj ˛
ace nierówno´sci Bella (w nieco zmienionej formie, przys-
tosowanej do mo˙zliwo´sci praktycznych) zostały ju˙z wykonane. Jak dot ˛
ad, ogłaszano jednogło´sne
werdykty na korzy´s´c mechaniki kwantowej: nierówno´sci Bella s ˛
a łamane! Có˙z to mo˙ze oz-
nacza´c? Na pewno tyle, ˙ze przyj˛ety przez nas ogólny model lokalnych teorii parametrów ukry-
tych nie jest poprawnym opisem praw przyrody. Wydaje si˛e, ˙ze nic sobie ona nie robi z naszych
zdroworozs ˛
adkowych oczekiwa´n.
Pytania
• Czy łamanie nierówno´sci Bella jest sprzeczne ze szczególn ˛
a teori ˛
a wzgl˛edno´sci?
• Czy ka˙zde zjawisko, które spełnia nierówno´sci Bella mo˙ze zosta´c opisane deterministy-
czn ˛
a teori ˛
a?
• Czy ka˙zde zjawisko, które łamie nierówno´sci Bella musi by´c uznane za niedeterministy-
czne?
• Czy ka˙zde zjawisko, które łamie nierówno´sci Bella musi by´c uznane za nielokalne?
Zadania

58
ROZDZIAŁ 4.
KŁOPOTY Z TEORI ˛
A KWANTOW ˛
A

Rozdział 5
´S
WIATŁO
Z
wycieczki po ´swiecie mechaniki kwantowej powracamy do teorii wzgl˛edno´sci. W tym roz-
dziale opiszemy kilka efektów relatywistycznych zwi ˛
azanych ze ´swiatłem. Oprócz słynnego
efektu Dopplera opowiemy tak˙ze o tym jak poruszaj ˛
acy si˛e o´srodek ci ˛
agnie za sob ˛
a propaguj ˛
ace
si˛e w nim ´swiatło oraz sprawdzimy, czy to prawda, ˙ze k ˛
at padania równy jest k ˛
atowi odbicia.
5.1
R
ELATYWISTYCZNY EFEKT
D
OPPLERA
Z
aczniemy od relatywistycznego efektu Dopplera, o którym ka˙zdy z Was zapewne słyszał.
Je˙zeli ´swiatło emitowane jest przez ruchome ´zródło, to pr˛edko´s´c fali ´swietlnej nie zale˙zy od
pr˛edko´sci ´zródła. Natomiast od pr˛edko´sci ´zródła zale˙zy cz˛esto´s´c emitowanej fali. St ˛
ad bierze si˛e
wła´snie słynne „przesuni˛ecie ku czerwieni” widma oddalaj ˛
acych si˛e gwiazd i galaktyk. Niek-
tórzy twierdz ˛
a równie˙z, ˙ze z tego samego powodu ´swiatła zbli˙zaj ˛
acego si˛e samochodu s ˛
a białe,
ale oddalaj ˛
acego si˛e s ˛
a ju˙z czerwone.
Rozwa˙zmy zatem ´zródło, które w swoim spoczynkowym układzie inercjalnym emituje we
wszystkich kierunkach ´swiatło o długo´sci fali λ
0
. Niech w innym inercjalnym układzie odniesienia
´zródło to porusza si˛e z pr˛edko´sci ˛
a v o składowych radialnej i transwersalnej (v
r
, v
ϕ
). Naszym
celem b˛edzie znalezienie długo´sci fali ´swiatła λ w tym układzie.
Jak wiadomo, ´swiatło nie jest niczym innym jak propaguj ˛
ac ˛
a si˛e fal ˛
a elektromagnetyczn ˛
a.
Powiedzmy, ˙ze dwa kolejne w˛ezły takiej fali zostały wyemitowane w chwilach t
e
1
i t
e
2
gdy ´zródło
znajdowało si˛e w odległo´sciach r
1
i r
2
od obserwatora. Chwile odbioru ´swiatła wynosz ˛
a: t
o
1
=
t
e
1
+
r
1
c
i t
o
2
= t
e
2
+
r
2
c
. Znajdujemy st ˛
ad zarejestrowan ˛
a długo´s´c fali:
59

60
ROZDZIAŁ 5.
´SWIATŁO
λ = c(t
o
2
− t
o
1
) = c(t
e
2
− t
e
1
)
µ
1 +
r
2
− r
1
c(t
e
2
− t
e
1
)
¶
=
c(t
0e
2
− t
0e
1
)
p
1 − v
2
/c
2
³
1 +
v
r
c
´
=
= λ
0
1 +
v
r
c
p
1 − v
2
/c
2
,
(5.1)
gdzie czasy „primowane” oznaczaj ˛
a czasy mierzone w układzie zwi ˛
azanym ze ´zródłem. Wzór,
który otrzymali´smy ró˙zni si˛e od nierelatywistycznego wzoru na przesuni˛ecie Dopplera trady-
cyjnie o czynnik
p
1 − v
2
/c
2
. Czynnik ten jest jednak bardzo wa˙zny, bo ujawnia mo˙zliwo´s´c
obserwowania przesuni˛ecia Dopplera dla ´zródła, które si˛e nie oddala, tylko obraca wokół obser-
watora. Jak wida´c, długo´sci fal elektromagnetycznych emitowanych przez oddalaj ˛
ace si˛e ´zródła
staj ˛
a si˛e wi˛eksze (czyli ´swiatło jest „bardziej czerwone”), podczas gdy ´zródła zbli˙zaj ˛
ace si˛e emi-
tuj ˛
a ´swiatło o mniejszej długo´sci (przesuni˛ecie „ku fioletowi”). To ostatnie stwierdzenie nie
jest jednak prawdziwe w ogólno´sci. Przyjrzyjcie si˛e wzorowi (5.1) - wynika z niego, ˙ze ´zródło
zbli˙zaj ˛
ace si˛e do obserwatora po pewnym spiralnym torze, mo˙ze nie doznawa´c przesuni˛ecia ku
fioletowi, a nawet by´c przesuni˛ete ku czerwieni! A kto´s mógłby pomy´sle´c, ˙ze efekt Dopplera
niczym go ju˙z nie zdziwi.
5.2
E
FEKT
„
UNOSZENIA
”
´SWIATŁA W PORUSZAJ ˛
ACYM SI ˛
E
O ´SRODKU
P
rzed nami kolejna niespodzianka. Zawsze gdy mówi si˛e, ˙ze pr˛edko´s´c ´swiatła wynosi c, nale˙zy
doda´c sakramentalne „w pró˙zni”. Wiadomo bowiem, ˙ze w o´srodkach takich jak szkło, czy woda,
pr˛edko´s´c ´swiatła jest mniejsza ni˙z c i nic nie stoi nawet na przeszkodzie, ˙zeby w tego typu
o´srodku od ´swiatła szybciej poruszał si˛e na przykład elektron. Pr˛edko´s´c fotonu w takim mate-
riale wynosi z grubsza
c
n
, gdzie n ≥ 1 jest współczynnikiem załamania. To dla o´srodka nieru-
chomego. A jaka jest pr˛edko´s´c ´swiatła w o´srodku o współczynniku załamania n i poruszaj ˛
acym
si˛e z pr˛edko´sci ˛
a v? Czy równie˙z wynosi
c
n
? Nic podobnego!
Aby dosta´c poprawn ˛
a pr˛edko´s´c ´swiatła w poruszaj ˛
acym si˛e o´srodku, nale˙zy po prostu prze-
transformowa´c pr˛edko´s´c
c
n
z układu w którym o´srodek spoczywa do układu w którym si˛e porusza.
Je˙zeli w układzie o´srodka ´swiatło propaguje si˛e w kierunku osi x i chcemy odpowiedzie´c na py-
tanie jaka b˛edzie pr˛edko´s´c ´swiatła w układzie w którym o´srodek porusza si˛e z pr˛edko´sci ˛
a V
wzdłu˙z osi −x, wystarczy zastosowa´c wzór (2.16):

5.3.
ODBICIE ´SWIATŁA OD LUSTRA
61
v
0
=
c
n
− V
1 −
V
nc
= c
c − nV
nc − V
.
(5.2)
Oznacza to ni mniej ni wi˛ecej, tylko ˙ze je´sli o´srodek porusza si˛e z pr˛edko´sci ˛
a −
c
n
, to w tym
układzie ´swiatło spoczywa! Kto by si˛e spodziewał? Efekt wygl ˛
ada dokładnie tak, jakby o´srodek
„ci ˛
agn ˛
ał” za sob ˛
a ´swiatło lub je „unosił”. Dokładnie w taki sam sposób w jaki płyn ˛
aca rzeka
unosi pływaj ˛
ac ˛
a po niej kaczk˛e.
5.3
O
DBICIE ´SWIATŁA OD LUSTRA
W
iemy, ˙ze ´swiatło odbija si˛e od spoczywaj ˛
acego lustra pod takim samym k ˛
atem pod jakim pada.
Poniewa˙z długo´s´c fali odbitego ´swiatła jest taka sama co długo´s´c fali ´swiatła padaj ˛
acego, to z
zasady zachowania p˛edu (składowej równoległej do powierzchni lustra) otrzymujemy równo´s´c
k ˛
atów padania i odbicia. Wiemy bowiem, ˙ze p˛ed ´swiatła zale˙zy od długo´sci fali. Jednak porusza-
j ˛
ace si˛e lustro mo˙ze zmieni´c cz˛esto´s´c odbijanego ´swiatła. Dlatego aby w odbiciu zachowana była
składowa p˛edu równoległa do powierzchni lustra, k ˛
at odbicia musi ró˙zni´c si˛e od k ˛
ata padania.
Nie poznali´smy jeszcze zasad relatywistycznej dynamiki, ale zwi ˛
azek pomi˛edzy obydwoma k ˛
a-
tami mo˙zna znale´z´c wył ˛
acznie przy u˙zyciu tego co ju˙z wiemy.
Rysunek 5.1:
Odbicie ´swiatła od nieruchomego lustra.
Rozwa˙zmy (primowany) układ współrz˛ednych w którym o´s x
0
jest prostopadła do nieru-
chomego lustra - rysunek 5.1. Poniewa˙z w tym układzie cz˛esto´s´c ´swiatła nie zmienia si˛e przy
odbiciu, to k ˛
at padania jest równy k ˛
atowi odbicia, θ
0
. Zatem składowa x
0
pr˛edko´sci fali pada-
j ˛
acej jest równa v
0p
x
= −c sin θ
0
, a fali odbitej v
0o
x
= c sin θ
0
. Odpowiednie składowe pr˛edko´sci w

62
ROZDZIAŁ 5.
´SWIATŁO
układzie w którym lustro porusza si˛e z pr˛edko´sci ˛
a V wzdłu˙z osi x mo˙zna łatwo znale´z´c korzys-
taj ˛
ac ze wzoru odwrotnego do (2.16):
v
p
x
=
−c sin θ
0
+ V
1 −
V
c
sin θ
0
= −c sin θ
p
(5.3)
v
o
x
=
c sin θ
0
+ V
1 +
V
c
sin θ
0
= c sin θ
o
,
gdzie θ
p
jest k ˛
atem padania ´swiatła, a θ
o
jest k ˛
atem odbicia. Widzimy, ˙ze dla V = 0 oba k ˛
aty s ˛
a
równe: θ
p
= θ
o
. Aby znale´z´c zale˙zno´s´c jednego k ˛
ata od drugiego, pozbywamy si˛e θ
0
z równa´n
(5.3) otrzymuj ˛
ac zwi ˛
azek:
sin θ
o
= sin θ
p
1 + 2
V
c
sin
−1
θ
p
+
V
2
c
2
1 + 2
V
c
sin θ
p
+
V
2
c
2
.
(5.4)
Zwró´cmy uwag˛e, ˙ze dla lustra którego pr˛edko´s´c d ˛
a˙zy do pr˛edko´sci ´swiatła mamy:
lim
V →c
sin θ
o
= 1,
(5.5)
czyli θ
o
d ˛
a˙zy do
π
2
. Łatwo jest „machaj ˛
ac r˛ekami” wytłumaczy´c, dlaczego k ˛
at odbicia jest wi˛ek-
szy ni˙z k ˛
at padania. Otó˙z ´swiatło padaj ˛
ace pod jakim´s k ˛
atem posiada pewn ˛
a składow ˛
a p˛edu
równoległego do powierzchni lustra. W wyniku odbicia składowa ta nie mo˙ze si˛e zmieni´c. Jed-
nak˙ze je˙zeli lustro porusza si˛e tak jak w omawianym przykładzie, to podczas odbicia skraca si˛e
długo´s´c fali ´swiatła, czyli zwi˛eksza si˛e jego p˛ed. Aby skompensowa´c t˛e zmian˛e p˛edu ´swiatło
musi odbi´c si˛e pod wi˛ekszym k ˛
atem dzi˛eki czemu p˛ed „poprzeczny” udaje si˛e zachowa´c. Oczy-
wi´scie je˙zeli pr˛edko´s´c lustra jest niewielka w porównaniu z pr˛edko´sci ˛
a ´swiatła V ¿ c, efekt
Dopplera prawie nie wyst˛epuje i k ˛
at padania jest niemal równy k ˛
atowi odbicia.
Pytania
• Czy ´zródło ´swiatła, którego odległo´s´c od inercjalnego obserwatora stale si˛e zwi˛eksza jest
zawsze charakteryzowana widmem przesuni˛etym ku czerwieni?
• Czy dowolne ´zródło ´swiatła, którego odległo´s´c od inercjalnego obserwatora stale si˛e zm-
niejsza jest zawsze charakteryzowana widmem przesuni˛etym ku fioletowi?

5.3.
ODBICIE ´SWIATŁA OD LUSTRA
63
• Czy k ˛
at padania ´swiatła na lustro jest zawsze równy k ˛
atowi odbicia?
• Czy pr˛edko´s´c ´swiatła w rzece wzgl˛edem brzegu rzeki zale˙zy od pr˛edko´sci wody?
Zadania
• ´Zródło ´swiatła porusza si˛e wzgl˛edem spoczywaj ˛
acego obserwatora wzdłu˙z krzywolin-
iowego toru ze z pewn ˛
a stał ˛
a co do warto´sci pr˛edko´sci ˛
a w taki sposób, ˙ze widmo ´swiatła
rejestrowane przez obserwatora jest dokładnie takie jak dla ´zródła spoczywaj ˛
acego. Dla
jakiej warto´sci pr˛edko´sci przeci ˛
a˙zenia, których doznaje ´zródło s ˛
a najwi˛eksze?

64
ROZDZIAŁ 5.
´SWIATŁO

Rozdział 6
P
OZORNE DEFORMACJE RUCHOMYCH
OBIEKTÓW
O
biekty poruszaj ˛
ace si˛e z du˙zymi pr˛edko´sciami ulegaj ˛
a skróceniu Lorentza. Wydawa´c by
si˛e mogło, ˙ze lec ˛
aca szybko na miotle Baba Jaga b˛edzie wygl ˛
adała na „krótsz ˛
a” ni˙z w czasie
spoczynku. Nic podobnego! Baba Jaga b˛edzie rzeczywi´scie krótsza, ale jej wygl ˛
ad b˛edzie zu-
pełnie inny. Brzmi od rzeczy? Problem polega na tym, ˙ze to co widzimy to ´swiatło docieraj ˛
ace
do naszych oczu od poruszaj ˛
acego si˛e obiektu. W wyniku tego, ˙ze rozwa˙zany obiekt sam porusza
si˛e z pr˛edko´sciami porównywalnymi z pr˛edko´sci ˛
a ´swiatła, jego obraz b˛edzie bardzo zniekształ-
cony. W tym rozdziale zajmiemy si˛e wła´snie tym zagadnieniem. Spróbujemy odpowiedzie´c na
pytanie, jak wygl ˛
adaj ˛
a proste, geometryczne obiekty w relatywistycznym ruchu.
6.1
O
BRAZ PORUSZAJ ˛
ACEGO SI ˛
E OKR ˛
EGU
R
ozpoczniemy od analizy obrazu okr˛egu poruszaj ˛
acego si˛e wzdłu˙z swojej ´srednicy. Wiemy ju˙z
z poprzednich rozdziałów, ˙ze rzeczywistym kształtem takiego „okr˛egu” jest elipsa. Musimy si˛e
teraz zastanowi´c w jaki sposób okre´sli´c jego wygl ˛
ad. Innymi słowy spróbujemy wywnioskowa´c
jak wygl ˛
adałaby fotografia okr˛egu.
Przede wszystkim b˛edziemy potrzebowa´c równania okre´slaj ˛
acego rzeczywiste poło˙zenie pun-
któw na okr˛egu. W jego układzie spoczynkowym mo˙ze ono na przykład by´c postaci x
02
+ y
02
=
R
2
, z
0
= d. Stosuj ˛
ac transformacj˛e Lorentza bez trudu znajdujemy równanie okre´slaj ˛
ace kształt
„okr˛egu” w układzie w którym porusza si˛e on wzdłu˙z osi x z pr˛edko´sci ˛
a V :
65

66
ROZDZIAŁ 6.
POZORNE DEFORMACJE RUCHOMYCH OBIEKTÓW
(x − V t)
2
1 − V
2
/c
2
+ y
2
= R
2
, z = d.
(6.1)
Rozwa˙zmy teraz promienie ´swiatła emitowane przez ten okr ˛
ag, które dotarły do aparatu fo-
tograficznego umieszczonego w pocz ˛
atku układu współrz˛ednych w chwili t
o
. Ich „równanie
ruchu” jest postaci: x
2
+ y
2
+ z
2
= c
2
(t
o
− t)
2
. Je˙zeli potraktujemy nasze równania jako układ,
to jego rozwi ˛
azaniem b˛edzie zbiór zdarze´n w czasoprzestrzeni w których zostało wyemitowane
´swiatło docieraj ˛
ace do aparatu. Z układu tego nale˙zy w pierwszej kolejno´sci wyeliminowa´c
t, gdy˙z nie interesuj ˛
a nas chwile emisji, tylko punkty z których ´swiatło zostało wyemitowane.
Wyznaczaj ˛
ac t z drugiego równania i wstawiaj ˛
ac do (6.1) dostajemy równanie czwartego stopnia:
(x − V t
o
+
V
c
p
x
2
+ y
2
+ d
2
)
2
1 − V
2
/c
2
+ y
2
= R
2
.
(6.2)
Rozwi ˛
azaniem równania jest krzywa czwartego stopnia, której kształt wyznaczyli´smy numerycznie
- rysunek 6.1. Wynik jest zaiste piorunuj ˛
acy. Na rysunku znajduj ˛
a si˛e zbiory punktów z których
emitowane było ´swiatło docieraj ˛
ace do aparatu w okre´slonych chwilach. Przyj˛eli´smy, ˙ze okr ˛
ag
o promieniu R = 1 poruszał si˛e z pr˛edko´sci ˛
a V = 0.9c, a jego odległo´s´c od płaszczyzny (x, y)
wynosiła d =
1
2
. Z rysunku wynika, ˙ze zbli˙zaj ˛
acy si˛e okr ˛
ag wygl ˛
ada na niesłychanie wydłu˙zony,
a oddalaj ˛
acy si˛e przypomina kształtem banan.
Wykonane fotografie b˛ed ˛
a nieco ró˙zni´c si˛e od obrazów znajduj ˛
acych si˛e na rysunku 6.1 je´sli
aparat b˛edzie ustawiony pod pewnym k ˛
atem do płaszczyzny ruchu okr˛egu. W zwi ˛
azku z tym,
obraz efektywnie ulegnie dodatkowemu „´sci´sni˛eciu” wzdłu˙z osi x. Oka˙ze si˛e, ˙ze po uwzgl˛ed-
nieniu tego ´sci´sni˛ecia, elipsa w chwili t
o
= 0 b˛edzie wygl ˛
ada´c jak idealny okr ˛
ag, o ile aparat
b˛edzie „celował” w jej ´srodek. Poniewa˙z jednak ludzkie oko (i mózg) posiada zdolno´s´c dostrze-
gania gł˛ebi obrazu, efekt ten b˛edzie w zasadzie „sztuczny” równie˙z dlatego, ˙ze widmo ´swiatła
ró˙znych punktów okr˛egu b˛edzie przesuni˛ete dopplerowsko w ró˙zny sposób. Punkty zbli˙zaj ˛
acego
si˛e okr˛egu, które s ˛
a bardziej odległe od obserwatora b˛ed ˛
a wydawa´c si˛e niebieskawe, a te bli˙zej
czerwonawe. Gdyby natomiast poruszaj ˛
acy si˛e okr ˛
ag został o´swietlony od tyłu, jego cie´n byłby
rzeczywi´scie okr ˛
agły w chwili t
o
= 0.
Podobn ˛
a analiz˛e mo˙zemy powtórzy´c dla dowolnego płaskiego ciała, którego kształt w spoczynku
opisuje równanie postaci F (x, y) = 0, poruszaj ˛
acego si˛e w swej płaszczy´znie z pr˛edko´sci ˛
a v
wzdłu˙z osi x. (F jest pewn ˛
a funkcj ˛
a dwóch zmiennych). Dla takiego kształtu, pozorny obraz
zarejestrowany przez aparat fotograficzny w chwili t
o
jest dany równaniem:
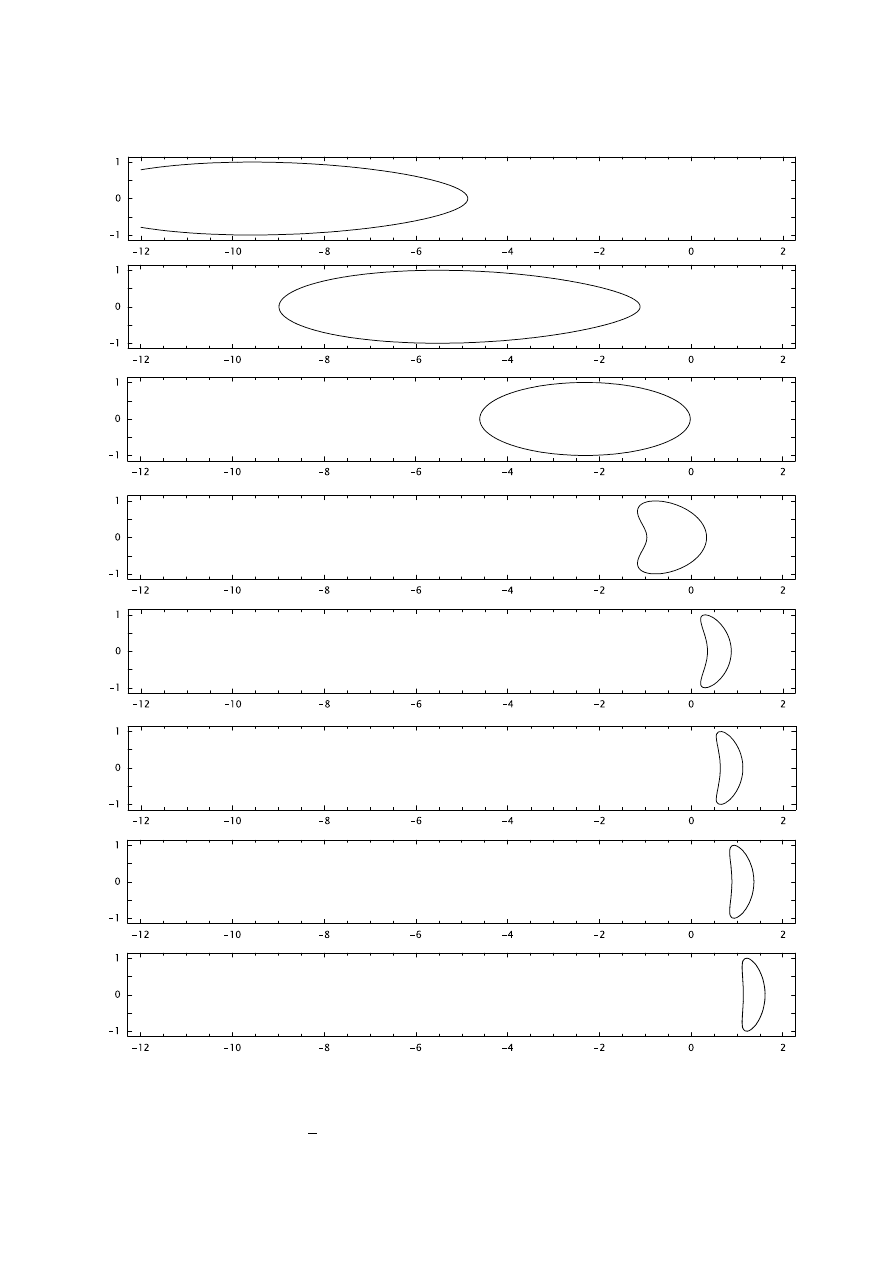
6.1.
OBRAZ PORUSZAJ ˛
ACEGO SI ˛
E OKR ˛
EGU
67
Rysunek 6.1:
Punkty poruszaj ˛
acego si ˛e okr ˛egu z których dobiega ´swiatło do aparatu fotograficznego.
„Zdj ˛ecia” robione s ˛
a w równych odst ˛epach czasu, pr ˛edko´s´c okr ˛egu wynosi
0.9c
, a odległo´s´c aparatu od
płaszczyzny ruchu równa jest
R
2
.
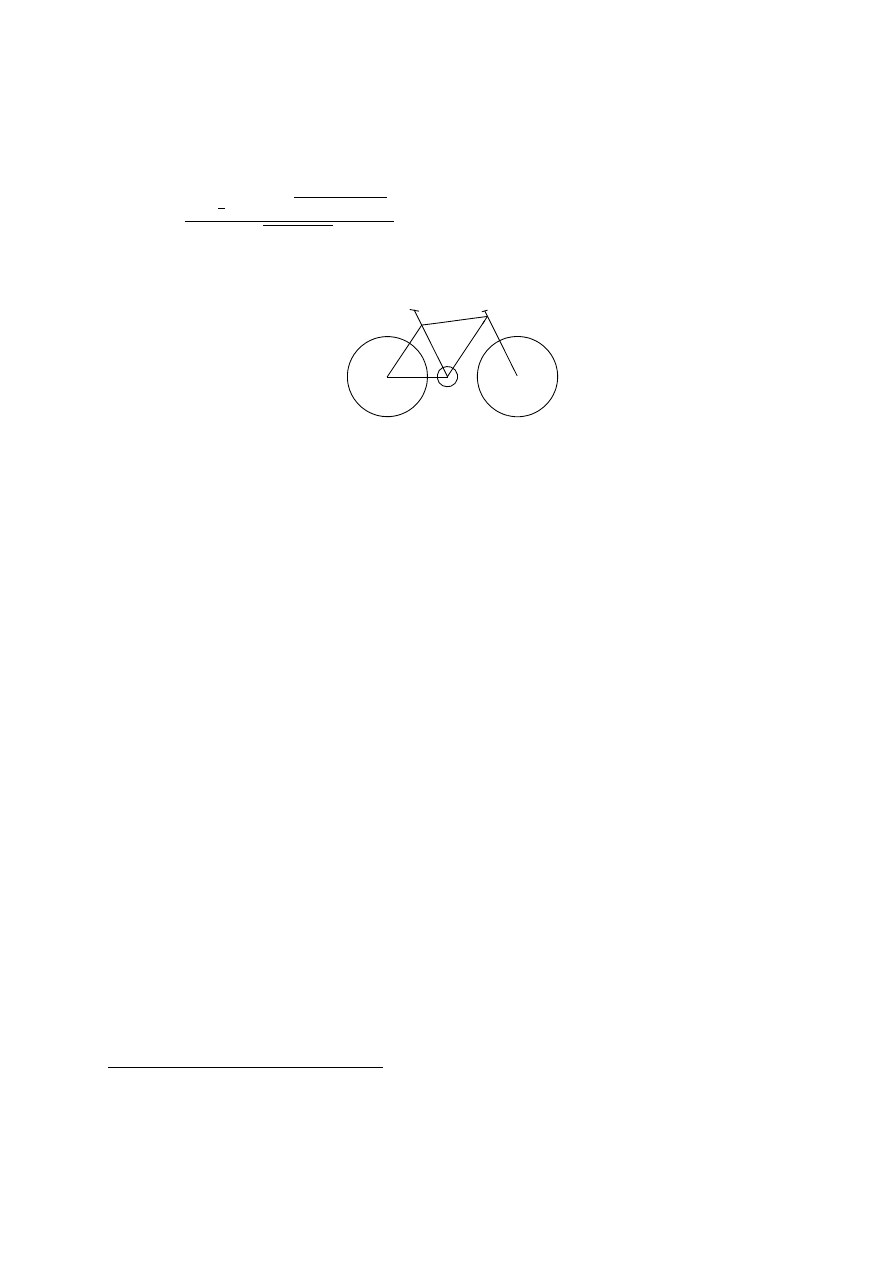
68
ROZDZIAŁ 6.
POZORNE DEFORMACJE RUCHOMYCH OBIEKTÓW
F
Ã
x −
v
c
(ct
o
−
p
x
2
+ y
2
+ d
2
)
p
1 − v
2
/c
2
, y
!
= 0.
(6.3)
Dla urozmaicenia przeanalizujmy jako przykład kontur przedstawiaj ˛
acy rower [4] - rysunek 6.2.
Rysunek 6.2:
Spoczywaj ˛
acy rower.
Analiza nie jest zbyt skomplikowana, bo rower składa si˛e wył ˛
acznie z odcinków i okr˛egów,
opisywanych elementarnymi równaniami. Dlatego posługuj ˛
ac si˛e równaniem (6.3) mo˙zemy
przeanalizowa´c wygl ˛
ad ka˙zdego z tych elementów osobno, a nast˛epnie zło˙zy´c otrzymane kształ-
ty w jedn ˛
a cało´s´c. Numeryczne rozwi ˛
azania tego równania znajduj ˛
a si˛e na rysunku 6.3. S ˛
a na
nim „fotografie” roweru jad ˛
acego z pr˛edko´sci ˛
a v = 0.8c wykonane z odległo´sci równej ´srednicy
koła roweru w kilku równych odst˛epach czasu. Przyznacie, ze zdj˛ecia s ˛
a niezwykle zaskaku-
j ˛
ace! Na trzecim od góry zdj˛eciu, ´srodek przeje˙zd˙zaj ˛
acego roweru akurat mijał obserwatora.
Wcze´sniejsze zdj˛ecia ukazuj ˛
a rower zbli˙zaj ˛
acy si˛e, podczas gdy na kolejnych rower ju˙z oddala
si˛e od aparatu.
6.2
O
BRAZ PORUSZAJ ˛
ACEJ SI ˛
E KULI
1
O
kazuje si˛e, ˙ze bardzo interesuj ˛
acymi własno´sciami „optycznymi” mo˙ze poszczyci´c si˛e porusza-
j ˛
aca si˛e kula. Przekonamy si˛e za chwil˛e, ˙ze niezale˙znie od kierunku i warto´sci pr˛edko´sci, cie´n
rzucany przez ni ˛
a na płaszczyzn˛e prostopadł ˛
a do kierunku padania promieni jest zawsze okr ˛
agły.
Rozwa˙zmy dowolny, spoczynkowy układ kuli - rysunek 6.4. W tym układzie „obwódka”
kuli jest okr ˛
agła. Mo˙zemy to stwierdzi´c badaj ˛
ac punkty na obwiedni kuli z których do obser-
watora docieraj ˛
a promienie ´swiatła w okre´slonej chwili. Przykładowy bieg tych promieni jest
przedstawiony na rysunku.
1
Zagadnienie przedstawione w tym podrozdziale pochodzi z pracy [5].
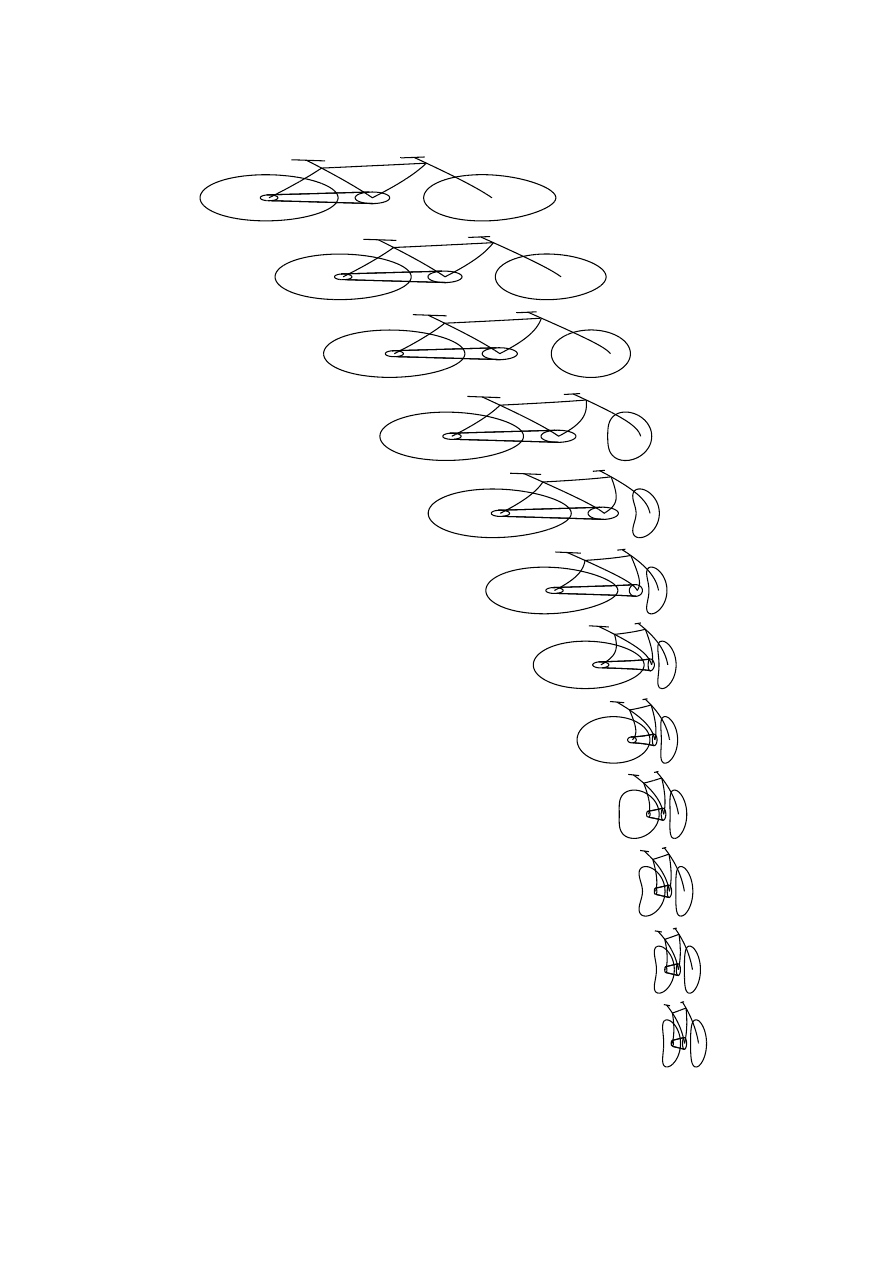
6.2.
OBRAZ PORUSZAJ ˛
ACEJ SI ˛
E KULI
2
69
Rysunek 6.3:
Fotografie roweru jad ˛
acego z pr ˛edko´sci ˛
a
v = 0.8c
wykonane z odległo´sci równej ´srednicy
koła roweru w kilku równych odst ˛epach czasu. W chwili wykonywania trzeciej fotografii ´srodek roweru
wła´snie mijał aparat fotograficzny.
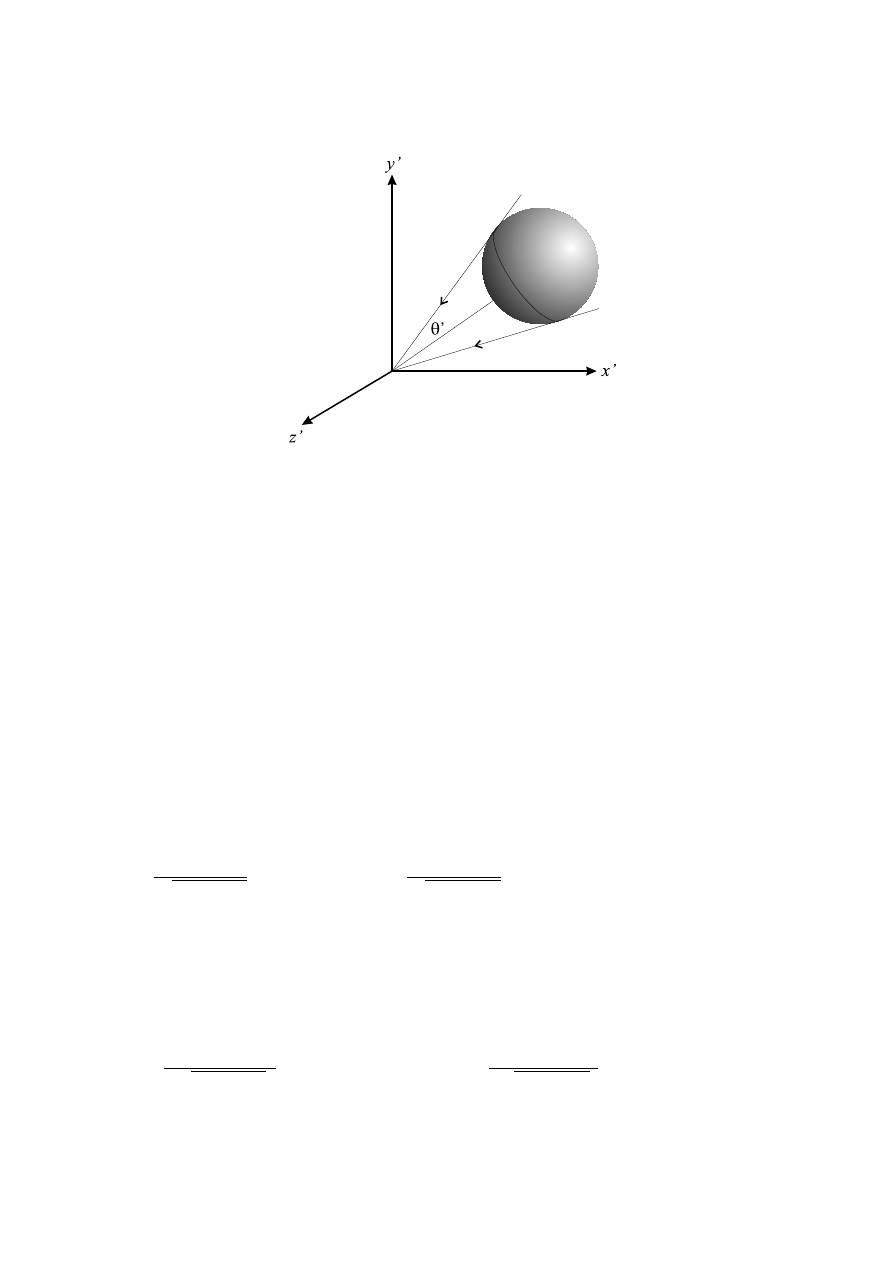
70
ROZDZIAŁ 6.
POZORNE DEFORMACJE RUCHOMYCH OBIEKTÓW
Rysunek 6.4:
Kula widziana w dowolnym spoczynkowym układzie odniesienia.
Oznaczmy w układzie spoczynkowym kuli wersor skierowany od obserwatora do ´srodka kuli
przez a
0
, natomiast wektor od obserwatora do punktu w którym promie´n ´swiatła rozpoczyna swój
bieg przez r
0
. K ˛
at pomi˛edzy a
0
oraz r
0
oznaczmy przez θ
0
. Wówczas równanie sto˙zka ´swietlnego:
r
0
· a
0
= x
0
a
0
x
+ y
0
a
0
y
+ z
0
a
0
z
= r
0
cos θ
0
= −ct
0
cos θ
0
(6.4)
okre´sla bieg promieni wyemitowanych w chwili t
0
< 0, które dotarły do obserwatora w chwili
t
0
o
= 0. Analogiczne równanie promieni docieraj ˛
acych do obserwatora poruszaj ˛
acego si˛e z pr˛ed-
ko´sci ˛
a V wzdłu˙z osi x w chwili, gdy obserwatorzy mijaj ˛
a si˛e jest postaci:
x − V t
p
1 − V
2
/c
2
a
0
x
+ ya
0
y
+ za
0
z
= −c
t − xV /c
2
p
1 − V
2
/c
2
cos θ
0
.
(6.5)
Otrzymali´smy je dokonuj ˛
ac transformacji Lorentza współrz˛ednych i czasu wyst˛epuj ˛
acych w
poprzednim równaniu. Po pomno˙zeniu obu stron przez dowoln ˛
a stał ˛
a N i drobnych przekształ-
ceniach dostajemy st ˛
ad:
x
a
0
x
− V cos θ
0
/c
p
1 − V
2
/c
2
N + yNa
0
y
+ zNa
0
z
= −ctN
cos θ
0
− V a
0
x
/c
p
1 − V
2
/c
2
.
(6.6)

6.2.
OBRAZ PORUSZAJ ˛
ACEJ SI ˛
E KULI
3
71
Przyjrzyjmy si˛e uwa˙znie otrzymanemu wyra˙zeniu, jest ono w zasadzie tej samej postaci co rów-
nanie (6.4), tylko zapisane przy u˙zyciu współrz˛ednych nieprimowanych oraz z innym wersorem
i k ˛
atem. Po podstawieniu
a
x
= N
a
0
x
− V cos θ
0
/c
p
1 − V
2
/c
2
a
y
= Na
0
y
(6.7)
a
z
= Na
0
z
cos θ = N
cos θ
0
− V a
0
x
/c
p
1 − V
2
/c
2
i wybraniu N w taki sposób by długo´s´c wersora a wynosiła 1, otrzymujemy równanie:
r · a = xa
x
+ ya
y
+ za
z
= −ct cos θ,
(6.8)
które jest tak˙ze równaniem sto˙zka, co oznacza, ˙ze cie´n rzucany przez poruszaj ˛
ac ˛
a si˛e kul˛e jest
wci ˛
a˙z okr ˛
agły. Co prawda wybrali´smy szczególn ˛
a chwil˛e obserwacji t
0
o
= t
o
= 0, jednak ze
wzgl˛edu na dowolno´s´c poło˙zenia kuli w układzie primowanym, nasz wynik jest zupełnie ogólny:
kula poruszaj ˛
aca si˛e z dowoln ˛
a, stał ˛
a pr˛edko´sci ˛
a zawsze rzuca okr ˛
agły cie´n. W ró˙znych układach
cie´n b˛edzie padał z ró˙znych kierunków a i b˛edzie miał ró˙zne rozmiary θ, jednak b˛edzie zawsze
okr ˛
agły.
Pytania
• Czy na podstawie analizy pozornego kształtu ruchomej kuli mo˙zemy co´s powiedzie´c o po-
zornym kształcie ruchomego okr˛egu w chwili, gdy okr ˛
ag ten mija obserwatora? Uzasadnij
odpowied´z analiz ˛
a równania (6.3).

72
ROZDZIAŁ 6.
POZORNE DEFORMACJE RUCHOMYCH OBIEKTÓW
Zadania
• Wzgl˛edem spoczywaj ˛
acego obserwatora porusza si˛e prostoliniowo i ze stał ˛
a pr˛edko´sci ˛
a
niewielki obiekt. Jego pozorna pr˛edko´s´c wynosi 2c. Jaka jest rzeczywista pr˛edko´s´c obiektu?
Obserwator znajduje si˛e w punkcie przecinaj ˛
acym tor ruchu.

Rozdział 7
D
YNAMIKA RELATYWISTYCZNA
D
otychczas zajmowali´smy si˛e w zasadzie relatywistyczn ˛
a kinematyk ˛
a i jej konsekwencjami.
To zabawne, ˙ze materiał ten w nierelatywistycznej mechanice jest niemal „trywialny” i na wi˛ek-
szo´sci wykładów po´swi˛eca mu si˛e z tego powodu bardzo niewiele czasu. O wiele szerszym
działem mechaniki jest nierelatywistyczna dynamika. Poniewa˙z w naszym wykładzie kładziemy
nacisk na nowe poj˛ecia i zjawiska niewyst˛epuj ˛
ace w wersji nierelatywistycznej, dynamice po´s-
wi˛ecimy jedynie jeden obszerny rozdział analizuj ˛
ac ró˙znice pomi˛edzy dynamik ˛
a relatywisty-
czn ˛
a i nierelatywistyczn ˛
a. Poniewa˙z istnieje mi˛edzy nimi cała masa podobie´nstw, nie b˛edzie
konieczne rozwa˙zanie wielu przykładów, bo ich nierelatywistyczne odpowiedniki s ˛
a zazwyczaj
szczegółowo omawiane na kursach mechaniki klasycznej. Uogólnienie na wersj˛e relatywisty-
czn ˛
a, o ile jest mo˙zliwe, jest zazwyczaj naturalne (wyj ˛
atkiem mo˙ze by´c szczegółowa analiza
ruchu bryły sztywnej).
7.1
C
ZTEROWEKTORY
P
odobnie jak w trójwymiarowej przestrzeni wygodnym poj˛eciem jest wektor posiadaj ˛
acy trzy
niezale˙zne składowe, tak w czterowymiarowej czasoprzestrzeni równie wygodnym obiektem jest
czterowektor. Oczywi´scie naturalnym kandydatem na czterowektor jest zbiór liczb okre´slaj ˛
acych
poło˙zenie i chwil˛e zaj´scia jakiego´s zjawiska (ct, x, y, z), albo w skrócie (ct, r). Czynnik c został
wprowadzony, aby wymiar wszystkich składowych czterowektora był jednakowy. Z poprzednich
rozdziałów wiemy ju˙z w jaki sposób transformuje si˛e czterowektor pomi˛edzy ró˙znymi układami
współrz˛ednych, przechodz ˛
ac z (ct, r) w (ct
0
, r
0
). Transformacja Lorentza opisuj ˛
aca owo przej-
´scie zachowuje, jak wiemy wielko´s´c (ct)
2
− r
2
, któr ˛
a mo˙zemy nazwa´c kwadratem „długo´sci”
73

74
ROZDZIAŁ 7.
DYNAMIKA RELATYWISTYCZNA
czterowektora. Ten prosty przykład podsuwa nam pomysł na uogólnienie poj˛ecia czterowek-
tora w nast˛epuj ˛
acy sposób. Czterowektorem (A
0
, A
1
, A
2
, A
3
) albo (A
0
, A) nazywamy wielko´s´c,
która pod wpływem przej´scia do układu inercjalnego poruszaj ˛
acego si˛e z pr˛edko´sci ˛
a V wzdłu˙z
osi x przechodzi w (A
0
0
, A
0
) równ ˛
a:
A
0
0
=
A
0
−A
1
V /c
√
1−V
2
/c
2
A
0
1
=
A
1
−A
0
V /c
√
1−V
2
/c
2
A
0
2
= A
2
A
0
3
= A
3
(7.1)
oraz analogicznie pod wpływem innych transformacji układu odniesienia. Nasza definicja mówi
po prostu, ˙ze czterowektorem jest wszystko co transformuje si˛e jak „czteropoło˙zenie” (ct, r),
czyli nie zmienia swojej czterowektorowej długo´sci. Czterowektory b˛edziemy oznacza´c małym
kwadracikiem A
¤
, aczkolwiek notacja ta zostanie wprowadzona wył ˛
acznie na potrzeby tego
wykładu (o dziwo nie ma sensownego zapisu czterowektora podobnego do stawiania strzałki
nad zwykłym wektorem).
Z łatwo´sci ˛
a sprawdzamy, ˙ze pod wpływem transformacji (7.1) wyra˙zenie A
2
0
−A
2
nie zmienia
swojej warto´sci, czyli jest równe A
02
0
− A
02
. Nie mo˙zemy przepu´sci´c tak niepowtarzalnej okazji
i nie nazwa´c powy˙zszego wyra˙zenia kwadratem długo´sci naszego dowolnego czterowektora.
Wszak˙ze w fizyce (jak równie˙z w matematyce) ka˙zdy niezmiennik jest wa˙zny i zostaje przeto ob-
darowany nazw ˛
a (wyznacznik macierzy w algebrze, długo´s´c i odst˛ep czasu w mechanice niere-
latywistycznej, ładunek elektryczny w elektrodynamice, kwadrat modułu funkcji falowej w me-
chanice kwantowej - wszystkie te wielko´sci s ˛
a wa˙zne dlatego, ˙ze si˛e nie zmieniaj ˛
a pod wpływem
pewnych przekształce´n). Mo˙zna bez trudu sprawdzi´c, ˙ze dla dowolnej pary czterowektorów A
¤
i B
¤
transformacja Lorentza nie zmienia warto´sci wyra˙zenia A
0
B
0
− A
1
B
1
− A
2
B
2
− A
3
B
3
, a
tak˙ze długo´sci czterowektora równego sumie (cztero)wektorowej A
¤
+ B
¤
.
7.2
C
ZTEROP ˛
ED
N
a razie zdefiniowali´smy sobie w abstrakcyjny sposób nowe i ogólne poj˛ecie czterowektora.
Przydałby si˛e teraz jaki´s przykład. Prosz˛e bardzo. Rozpatrzmy czterowektor nast˛epuj ˛
acej postaci:

7.2.
CZTEROP ˛
ED
75
v
¤
=
Ã
c
p
1 − v
2
/c
2
,
v
p
1 − v
2
/c
2
!
.
(7.2)
Czy rzeczywi´scie jest to czterowektor? Aby to sprawdzi´c, wystarczy zastosowa´c transformacj˛e
(7.1) i porówna´c wynik z obiektem uzyskanym z (7.2) poprzez transformacj˛e pr˛edko´sci wyst˛epu-
j ˛
acej we wzorze. Chwilowo odło˙zymy to zadanie do dalszej cz˛e´sci, a teraz przekonamy si˛e je-
dynie, ˙ze długo´s´c wyra˙zenia (7.2) rzeczywi´scie nie zmienia si˛e przy zmianie układu odniesienia.
Wynosi ona:
Ã
c
p
1 − v
2
/c
2
!
2
−
Ã
v
p
1 − v
2
/c
2
!
2
= c
2
.
(7.3)
Otrzymali´smy stał ˛
a c
2
, co oznacza, ˙ze po zastosowaniu transformacji Lorentza równie˙z otrzy-
mamy t˛e sam ˛
a stał ˛
a. Znaleziony czterowektor ma ju˙z nawet własn ˛
a nazw˛e: czteropr˛edko´s´c.
Nietrudno zreszt ˛
a zauwa˙zy´c czemu. Z czteropr˛edko´sci mo˙zemy zbudowa´c wiele innych czte-
rowektorów. Na przykład mno˙z ˛
ac wyra˙zenie (7.2) przez dowoln ˛
a stał ˛
a m otrzymamy nowy
czterowektor, którego kwadrat długo´sci wynosi m
2
c
2
:
p
¤
=
Ã
mc
p
1 − v
2
/c
2
,
mv
p
1 − v
2
/c
2
!
.
(7.4)
Jeste´smy ju˙z blisko słynnego mc
2
. Có˙z to za czterowektor? Aby zacz ˛
a´c rozumie´c co otrzyma-
li´smy, rozwi´nmy poszczególne składowe w szereg wokół małych pr˛edko´sci do drugiego rz˛edu
(wł ˛
acznie):
mc
p
1 − v
2
/c
2
≈ mc +
mv
2
2c
+ . . .
(7.5)
mv
p
1 − v
2
/c
2
≈ mv + . . .
Wzory zaczynaj ˛
a wygl ˛
ada´c znajomo: w rozwini˛eciu pierwszej składowej znajdujemy wyra˙zenie
na energi˛e kinetyczn ˛
a cz ˛
astki o masie m poruszaj ˛
acej si˛e z pr˛edko´sci ˛
a v. Znane z przedszkola
wyra˙zenie
mv
2
2
jest przeskalowane o addytywny czynnik mc
2
i dodatkowo podzielone przez c.
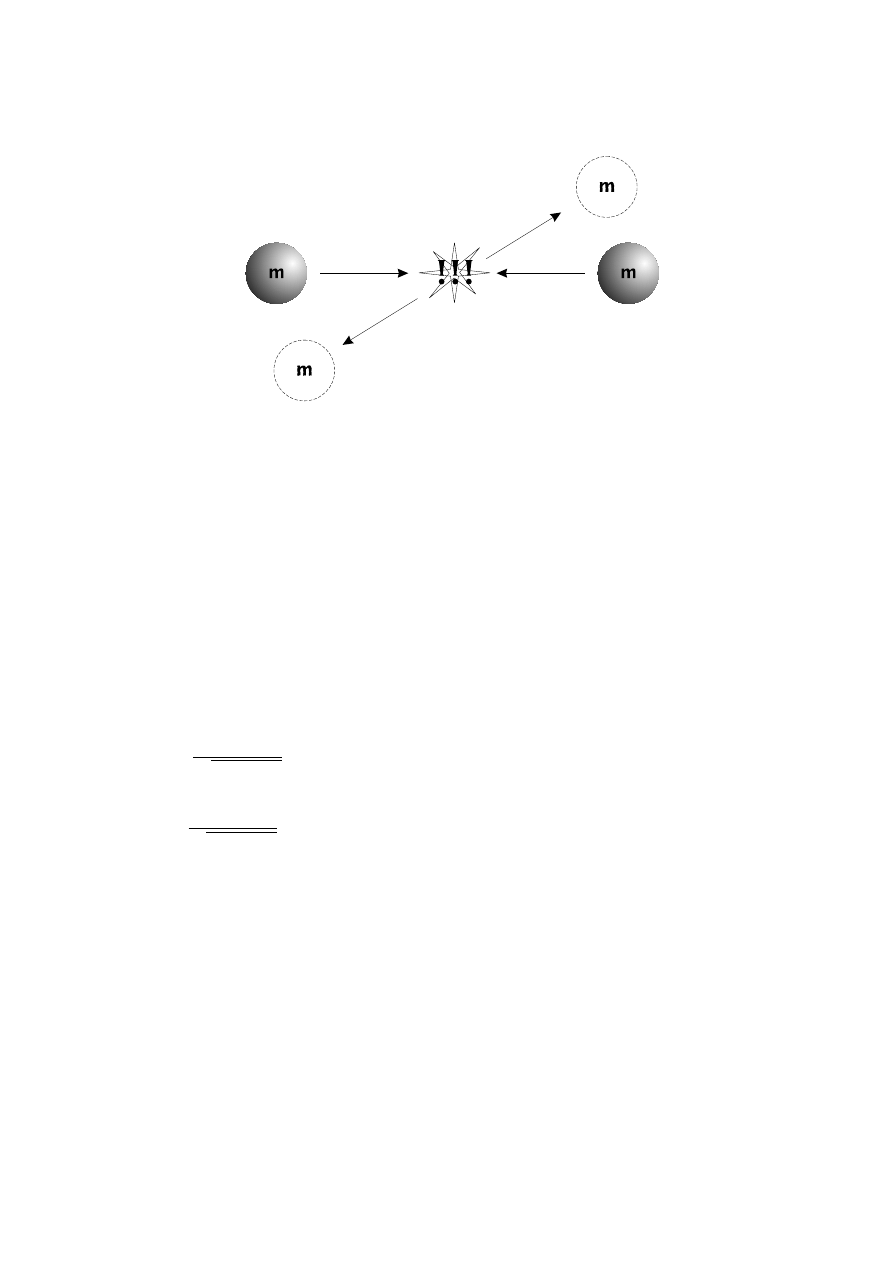
76
ROZDZIAŁ 7.
DYNAMIKA RELATYWISTYCZNA
Rysunek 7.1:
Dwie jednakowe kule zderzaj ˛
ace si ˛e spr ˛e˙zy´scie w układzie ´srodka masy.
Natomiast pierwszy człon rozwini˛ecia drugiego wyra˙zenia wygl ˛
ada jak p˛ed tej samej cz ˛
astki.
Czy to rzeczywi´scie mo˙zliwe, ˙ze otrzymane wyra˙zenia okre´slaj ˛
a relatywistyczn ˛
a energi˛e swo-
bodn ˛
a (podzielon ˛
a przez c dla ujednolicenia jednostek) i relatywistyczny p˛ed? Koniecznie to
sprawd´zmy rozwa˙zaj ˛
ac przypadek zderzenia spr˛e˙zystego dwóch ciał. Je˙zeli oka˙ze si˛e, ˙ze we
wszystkich mo˙zliwych układach odniesienia spełniona jest zasada zachowania naszych kandy-
datów na energi˛e swobodn ˛
a i p˛ed, to oznacza´c to b˛edzie, ˙ze zaproponowane wyra˙zenia, nazwi-
jmy je roboczo E i p:
E =
mc
2
p
1 − v
2
/c
2
(7.6)
p =
mv
p
1 − v
2
/c
2
,
rzeczywi´scie s ˛
a energi ˛
a i p˛edem. Rozpatrzmy najprostszy mo˙zliwy przypadek dwóch identycz-
nych kul zderzaj ˛
acych si˛e spr˛e˙zy´scie w układzie ´srodka masy - rysunek 7.1. Jak wida´c, do-
puszczamy sytuacj˛e ogóln ˛
a, w której zderzenie nie musi by´c centralne.
Po zderzeniu pr˛edko´sci obu kul musiały mie´c jednakow ˛
a warto´s´c i by´c przeciwnie skierowane.
Nie wynika to z zasady zachowania p˛edu czy energii (których przecie˙z jeszcze nie znamy), ale z
symetrii zagadnienia. Ponadto mo˙zemy równie˙z wywnioskowa´c stosuj ˛
ac argument symetrii, ˙ze
pr˛edko´sci kul po zderzeniu maj ˛
a t˛e sam ˛
a warto´s´c co przed zderzeniem. Wynika to z faktu, ˙ze
zderzenie całkowicie spr˛e˙zyste powinno by´c odwracalne w czasie. Gdyby w wyniku zderzenia
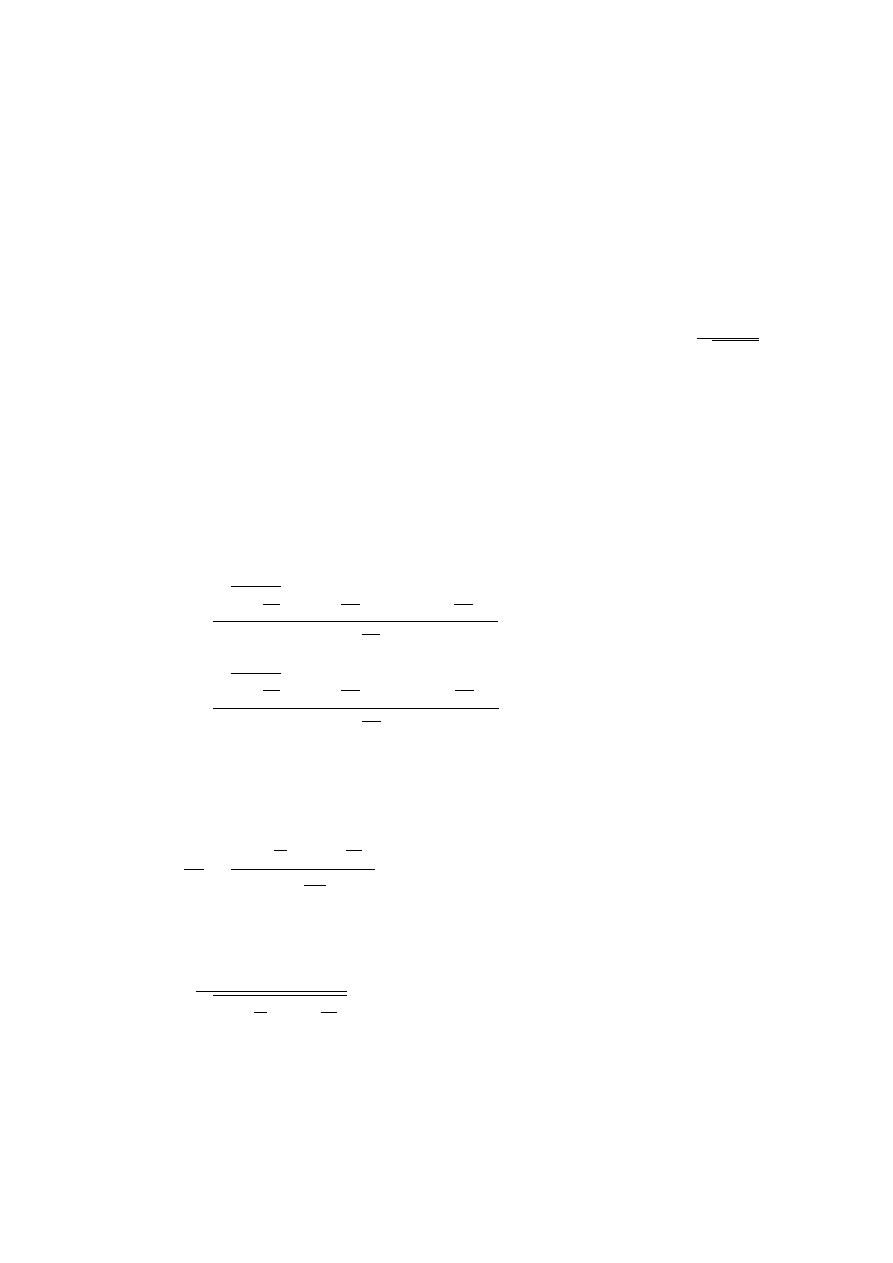
7.2.
CZTEROP ˛
ED
77
pr˛edko´sci zmalały, to my´slowo odwracaj ˛
ac proces w czasie okazałoby si˛e, ˙ze pr˛edko´sci wzrosły.
Zatem proces przebiegałby w ró˙zny sposób w zale˙zno´sci od kierunku upływu czasu i nie byłby
wcale odwracalny. Jedynym wyj´sciem jest przyj˛ecie, ˙ze w elastycznym zderzeniu jednakowych
kul w układzie ´srodka masy mog ˛
a zmieni´c si˛e jedynie kierunki pr˛edko´sci i to wył ˛
acznie w sym-
etryczny sposób (jak na rysunku 7.1).
Skoro tak, to w naszym zderzeniu zachowana jest zarówno suma wielko´sci E dla obu kulek
jak i suma (wektorowa) wielko´sci p dla obu kul. Sumy te wynosz ˛
a odpowiednio
2mc
2
√
1−v
2
/c
2
oraz
0, gdzie v jest pr˛edko´sci ˛
a kul. Musimy teraz pokaza´c, ˙ze zarówno suma E jak i suma p jest
zachowana w zderzeniu rejestrowanym przez dowolnego obserwatora inercjalnego. W tym celu
skorzystamy z ogólnego wzoru (2.19) transformuj ˛
acego pr˛edko´s´c v przy przej´sciu do układu
poruszaj ˛
acego si˛e z dowoln ˛
a pr˛edko´sci ˛
a V. W układzie ´srodka masy cz ˛
astki poruszały si˛e przed
zderzeniem z pewnymi pr˛edko´sciami ±v, a po zderzeniu z pr˛edko´sciami ±u, przy czym warto´sci
tych pr˛edko´sci były równe: u = v. Stosuj ˛
ac cierpliwie wzór (2.19) wyznaczamy pr˛edko´sci kul
przed i po zderzeniu w nowym inercjalnym układzie:
v
0
=
q
1 −
V
2
c
2
¡
±v ∓
v·V
V
2
V
¢
−
¡
V ∓
v·V
V
2
V
¢
1 ∓
v·V
c
2
(7.7)
u
0
=
q
1 −
V
2
c
2
¡
±u ∓
u·V
V
2
V
¢
−
¡
V ∓
u·V
V
2
V
¢
1 ∓
u·V
c
2
.
Zbadajmy teraz wyra˙zenie opisuj ˛
ace sum˛e „energii” obu cz ˛
astek przed zderzeniem w układzie
poruszaj ˛
acym si˛e. W tym celu sprawdzamy, ˙ze:
1 −
v
02
c
2
=
³
1 −
v
2
c
2
´ ³
1 −
V
2
c
2
´
¡
1 ∓
v·V
c
2
¢
2
(7.8)
i st ˛
ad wyznaczamy całkowit ˛
a „energi˛e” przed zderzeniem:
E
0
=
2mc
2
q¡
1 −
v
2
c
2
¢ ¡
1 −
V
2
c
2
¢.
(7.9)
Poniewa˙z otrzymane wyra˙zenie nie zale˙zy od wzgl˛ednej orientacji pr˛edko´sci v i V, a jedynie od
ich warto´sci, to obliczaj ˛
ac to samo dla cz ˛
astek po zderzeniu, otrzymamy identyczny wynik! O to

78
ROZDZIAŁ 7.
DYNAMIKA RELATYWISTYCZNA
nam wła´snie chodziło. Niezale˙znie od k ˛
ata rozproszenia w elastycznym zderzeniu dwóch iden-
tycznych cz ˛
astek, całkowita wielko´s´c E jest zachowana we wszystkich inercjalnych układach
odniesienia! Oznacza to, ˙ze od teraz mo˙zemy ju˙z oficjalnie nazywa´c wielko´s´c E =
mc
2
√
1−v
2
/c
2
energi ˛
a swobodn ˛
a cz ˛
astki o masie m i pr˛edko´sci v. Co prawda powinni´smy jeszcze wykaza´c,
˙ze energia swobodna jest równie˙z zachowana w zderzeniu elastycznym kulek o ró˙znych masach,
jednak to zadanie zostawimy zainteresowanemu Czytelnikowi. Podobnie zreszt ˛
a post ˛
apimy z
dowodzeniem „p˛edowo´sci” p. Procedura jest zaiste ta sama, zatem Czytelnik nie powinien
mie´c najmniejszych problemów z wykazaniem, ˙ze p jest w zderzeniu zachowany we wszyst-
kich układach.
W tym momencie powinno by´c ju˙z zupełnie jasne dlaczego czterowektor (7.4) nazywany
jest czterowektorem energii-p˛edu lub w skrócie czterop˛edem. Wypiszemy jeszcze wa˙zny i cz˛esto
stosowany zwi ˛
azek pomi˛edzy energi ˛
a i p˛edem cz ˛
astki swobodnej. Zastosujemy po prostu wzór
na kwadrat długo´sci czterowektora energii-p˛edu:
¡
E
c
¢
2
− p
2
= m
2
c
2
lub równowa˙znie:
E
2
= (mc
2
)
2
+ p
2
c
2
.
(7.10)
Mo˙zemy ju˙z teraz odpowiedzie´c na bardzo wa˙zne pytanie: co naprawd˛e sprawia, ˙ze nie da si˛e
rozp˛edzi´c cz ˛
astki do dowolnie du˙zej pr˛edko´sci? Dlaczego na przykład u˙zywaj ˛
ac bardzo du˙zej
energii do rozp˛edzenia cz ˛
astki nie pozwoli ona nada´c sobie pr˛edko´sci wi˛ekszej ni˙z c? Odpowied´z
na to pytanie kryje si˛e we wzorze na energi˛e swobodn ˛
a. Wynika z niego, ˙ze energia cz ˛
astki,
której pr˛edko´s´c zbli˙za si˛e do c gwałtownie wzrasta a˙z do niesko´nczono´sci. Oznacza to, ˙ze do
rozp˛edzenia masywnej cz ˛
astki do pr˛edko´sci ´swiatła trzeba by u˙zy´c niesko´nczonej energii, a to
jest oczywi´scie niemo˙zliwe.
Analizuj ˛
ac ten sam wzór mo˙zemy równie˙z stwierdzi´c, ˙ze cz ˛
astki, które nie posiadaj ˛
a masy,
a przenosz ˛
a energi˛e (na przykład fotony), musz ˛
a zawsze porusza´c si˛e z pr˛edko´sci ˛
a ´swiatła.
7.3
E = mc
2
N
adszedł wła´sciwy moment, aby zrozumie´c sens legendarnej formuły Einsteina E = mc
2
(btw,
wzór ten wzbudza szacunek ludno´sci cywilnej do tego stopnia, ˙ze na drzwiach toalety w jednym
z warszawskich klubów studenckich znalazła si˛e jego parafraza: E = wc
2
). Pod koniec tego
podrozdziału wszystko b˛edzie ju˙z jasne. Na pocz ˛
atek powró´cmy do rozwini˛ecia wyra˙zenia na
energi˛e swobodn ˛
a (podzielon ˛
a przez c) cz ˛
astki o masie m (7.5). W pierwszym członie pojawia
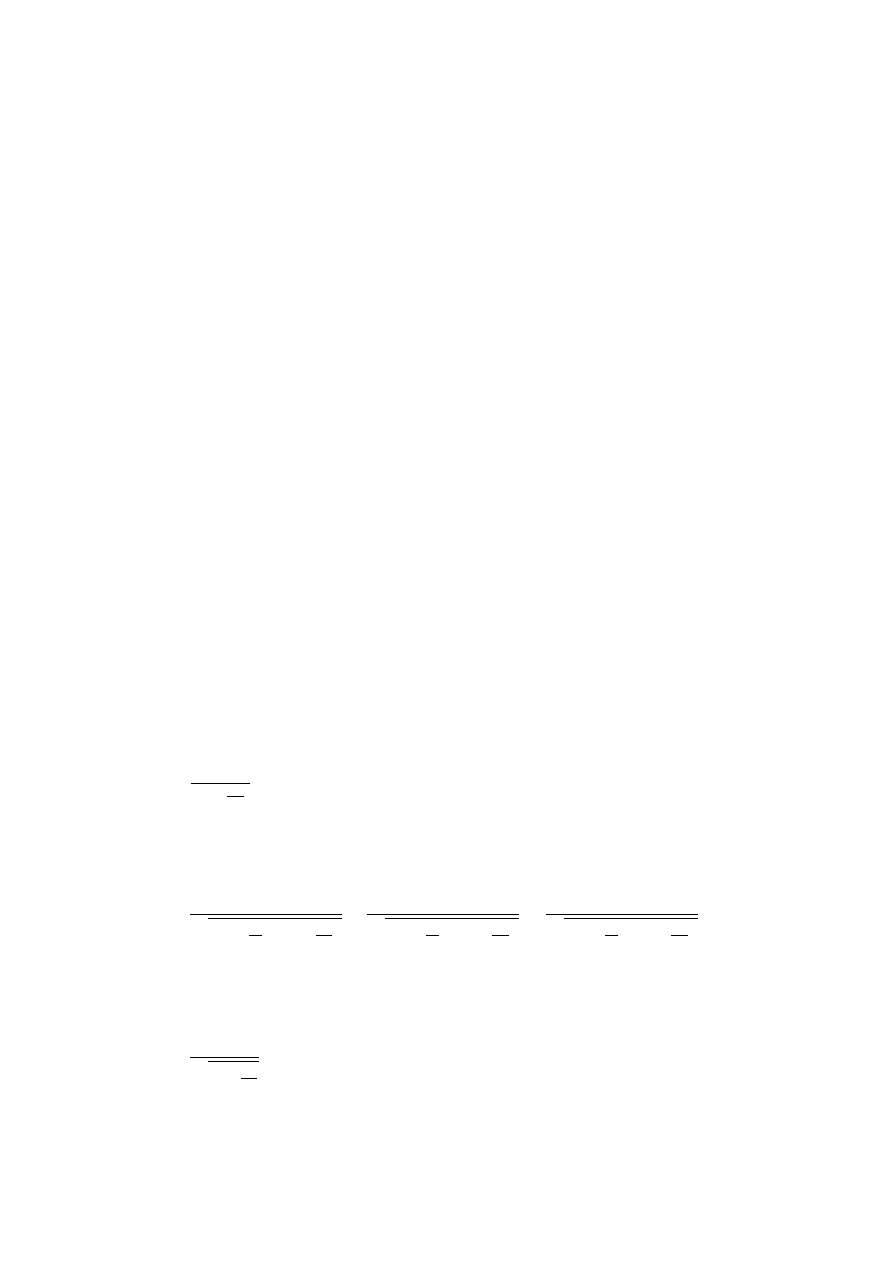
7.3.
E = MC
2
79
si˛e znajomy czynnik mc
2
nazywany niekiedy energi ˛
a spoczynkow ˛
a. Czy ma on jakie´s znacze-
nie? Kto´s z Was mógłby przecie˙z powiedzie´c, ˙ze energi˛e tak czy inaczej mo˙zemy zdefiniowa´c
z dokładno´sci ˛
a do dowolnej stałej addytywnej (a nawet multiplikatywnej przeskalowuj ˛
ac mas˛e).
Mogliby´smy na przykład rozwa˙za´c wyra˙zenie na energi˛e kinetyczn ˛
a postaci E − mc
2
, tak aby
energia cz ˛
astki spoczywaj ˛
acej wynosiła zero. Co prawda tego typu energia nie byłaby składo-
w ˛
a czterowektora energii-p˛edu o którym była mowa w poprzednim podrozdziale, ale czy jest to
wystarczaj ˛
acy powód by czynnik ten traktowa´c powa˙znie? Sama elegancja nie jest dowodem na
to, ˙ze energia spoczynkowa ma jakiekolwiek znaczenie fizyczne (dla niektórych elegancja mo˙ze
by´c jednak wa˙znym argumentem).
Aby przekona´c si˛e o znaczeniu czynnika spoczynkowego, przeanalizujmy idealnie nieelasty-
czne zderzenie dwóch jednakowych kulek o masie m. W układzie ´srodka masy kulki po prostu
sklej ˛
a si˛e ze sob ˛
a pozostaj ˛
ac po zderzeniu nieruchome. Co si˛e stanie z ich energi ˛
a? Wiemy to
chocia˙zby z mechaniki nierelatywistycznej: cz˛e´s´c energii kinetycznej zamieni si˛e na ciepło, a
cz˛e´s´c wywoła deformacj˛e materiału. Podobnie jak w mechanice nierelatywistycznej oczeku-
jemy, ˙ze niezale˙znie od tego czy energia mechaniczna jest zachowana, czy nie, zachowany
b˛edzie p˛ed. I rzeczywi´scie, w układzie ´srodka masy p˛ed jest zachowany. Sprawd´zmy jeszcze
dla pewno´sci czy podobnie jest w innych układach inercjalnych. Niech przed zderzeniem, w
układzie ´srodka masy kulki poruszaj ˛
a si˛e wzdłu˙z osi x z pr˛edko´sciami ±v. W układzie inercjal-
nym poruszaj ˛
acym si˛e tradycyjnie z pr˛edko´sci ˛
a V wzdłu˙z osi x pr˛edko´sci kulek przed zderze-
niem wynosz ˛
a:
v
0
=
±v − V
1 ∓
vV
c
2
,
(7.11)
a ich całkowity p˛ed jest równy:
p
0
=
m(v − V )
q¡
1 −
v
2
c
2
¢ ¡
1 −
V
2
c
2
¢ +
m(−v − V )
q¡
1 −
v
2
c
2
¢ ¡
1 −
V
2
c
2
¢ =
−2mV
q¡
1 −
v
2
c
2
¢ ¡
1 −
V
2
c
2
¢.
(7.12)
Natomiast pr˛edko´s´c zlepionych kulek wynosi po prostu −V , a ich p˛ed...
p
0
=
−2mV
q
1 −
V
2
c
2
(7.13)
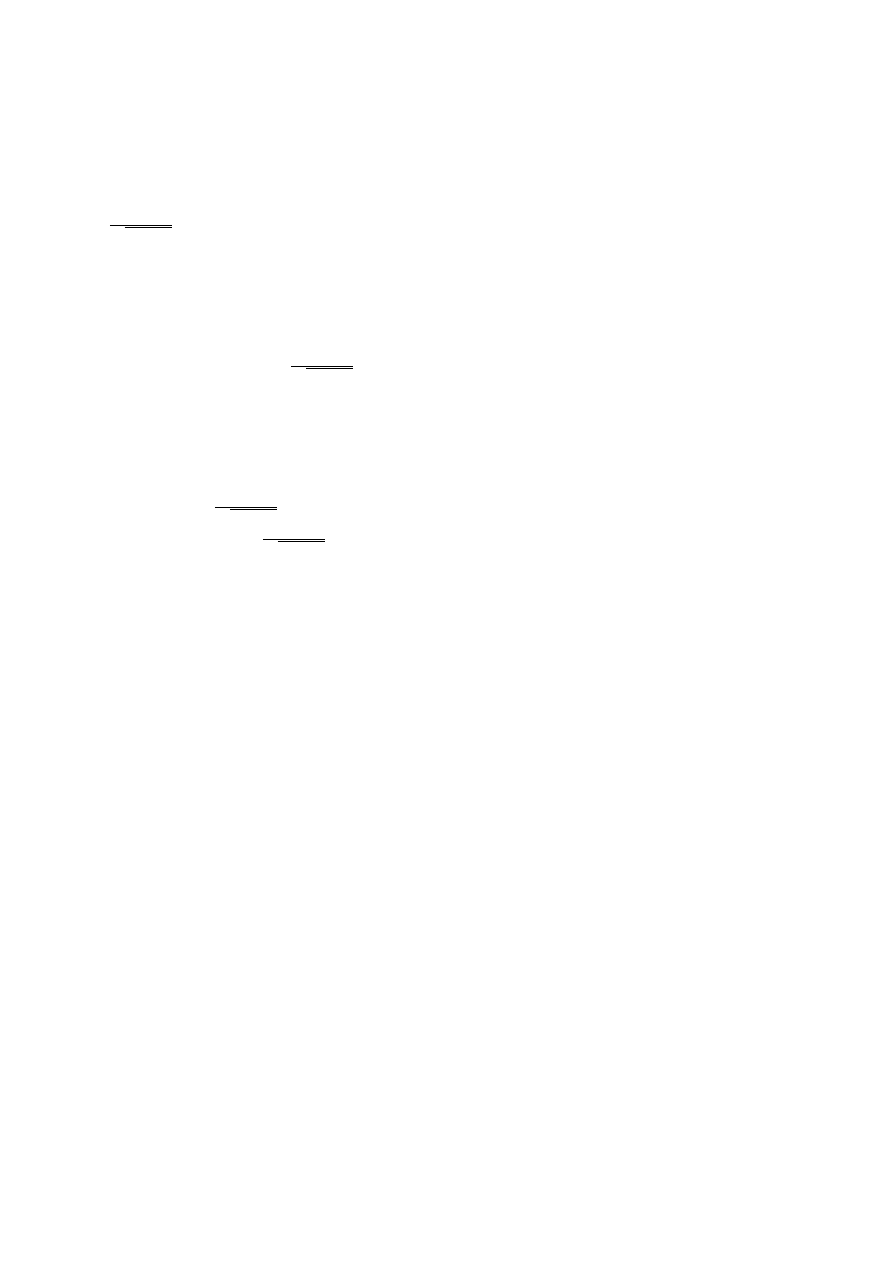
80
ROZDZIAŁ 7.
DYNAMIKA RELATYWISTYCZNA
...zaraz, zaraz, co´s tu si˛e nie zgadza! Wyra˙zenia na p˛ed przed zderzeniem (7.12) i po zderze-
niu (7.13) s ˛
a ró˙zne! Wygl ˛
ada to tak, jak gdyby masa zł ˛
aczonych kulek wynosiła nie 2m, ale
2m
√
1−v
2
/c
2
. Czy to mo˙zliwe? Przecie˙z to s ˛
a te same kulki co przed zderzeniem. Ró˙zni je naj-
wy˙zej temperatura, czyli energia wewn˛etrzna! Chwileczk˛e, ale wiemy, ˙ze energia wewn˛etrzna,
to po prostu ruch cz ˛
asteczek z których zbudowane s ˛
a nasze kulki. Wi˛eksza energia wewn˛etrzna
oznacza wi˛eksz ˛
a pr˛edko´s´c tych cz ˛
asteczek. Czy to jednak mo˙zliwe, ˙zeby masa poruszaj ˛
acych
si˛e cz ˛
asteczek realnie wzrastała ze wzrostem ich pr˛edko´sci? We wzorze na relatywistyczny p˛ed
(7.6) wyst˛epuje czynnik
m
√
1−v
2
/c
2
, który wygl ˛
ada jak „relatywistyczna masa” poruszaj ˛
acej si˛e
cz ˛
astki (lub kulki). Zauwa˙zmy, ˙ze je´sli na moment zało˙zymy, ˙ze czynnik ten wyznacza rzeczy-
wist ˛
a mas˛e poruszaj ˛
acego si˛e ciała, którego masa spoczynkowa wynosi m, to nasze kłopoty z
zachowaniem p˛edu w zderzeniu nieelastycznym znikn ˛
a! Powró´cmy raz jeszcze do układu ´srodka
masy przyjmuj ˛
ac nasz ˛
a robocz ˛
a hipotez˛e na temat zmiany masy. Energia, która znika w zderze-
niu jest równa
2mc
2
√
1−v
2
/c
2
− 2mc
2
. Według naszego pomysłu masa spoczynkowa sklejonych kulek
po zderzeniu wynosi
2m
√
1−v
2
/c
2
, a przed zderzeniem po prostu 2m. Zauwa˙zmy, ˙ze przyrosty tych
wielko´sci spełniaj ˛
a upragniony zwi ˛
azek:
∆E = ∆mc
2
,
(7.14)
który wynika z naszej roboczej hipotezy przyj˛etej na potrzeb˛e ratowania zasady zachowania p˛edu
w zderzeniach nieelastycznych.
Maj ˛
ac w pami˛eci mikroskopowy obraz kulek, potrafimy od pocz ˛
atku prze´sledzi´c losy zagu-
bionej energii. Pocz ˛
atkowo chłodne kulki posiadały pewn ˛
a energi˛e spoczynkow ˛
a oraz dodatkow ˛
a
energi˛e kinetyczn ˛
a. W momencie zderzenia energia kinetyczna została zamieniona na ciepło,
czyli energie kinetyczne cz ˛
asteczek materiału. Wzrost ich pr˛edko´sci spowodował wzrost ich mas
- czyli w opisie makroskopowym wzrost masy spoczynkowej zł ˛
aczonych kulek, a zatem równie˙z
ich energii spoczynkowych. Oznacza to, ˙ze wzrost masy spoczynkowej kulek mo˙zemy uwa˙za´c
za efekt kinetyczny pami˛etaj ˛
ac o ich budowie wewn˛etrznej. Problem pojawi si˛e, gdy zapytamy
o zderzenia nieelastyczne b ˛
ad´z rozpady cz ˛
astek elementarnych, nie posiadaj ˛
acych wewn˛etrznej
struktury. W tym przypadku, nasze relatywistyczne wzory na energi˛e i p˛ed s ˛
a nadal poprawne
i mamy ten sam problem: musi wzrosn ˛
a´c masa spoczynkowa, lecz tym razem efekt nie mo˙ze
by´c czysto kinetyczny, bo wewn ˛
atrz cz ˛
astek elementarnych nie ma ju˙z niczego co mogłoby si˛e
rusza´c! Nie pozostaje nam nic innego jak przyj ˛
a´c, ˙ze zwi ˛
azek pomi˛edzy mas ˛
a a energi ˛
a nie jest
prawem wył ˛
acznie kinetycznym, ale fundamentalnym prawem przyrody spełnionym nawet, gdy
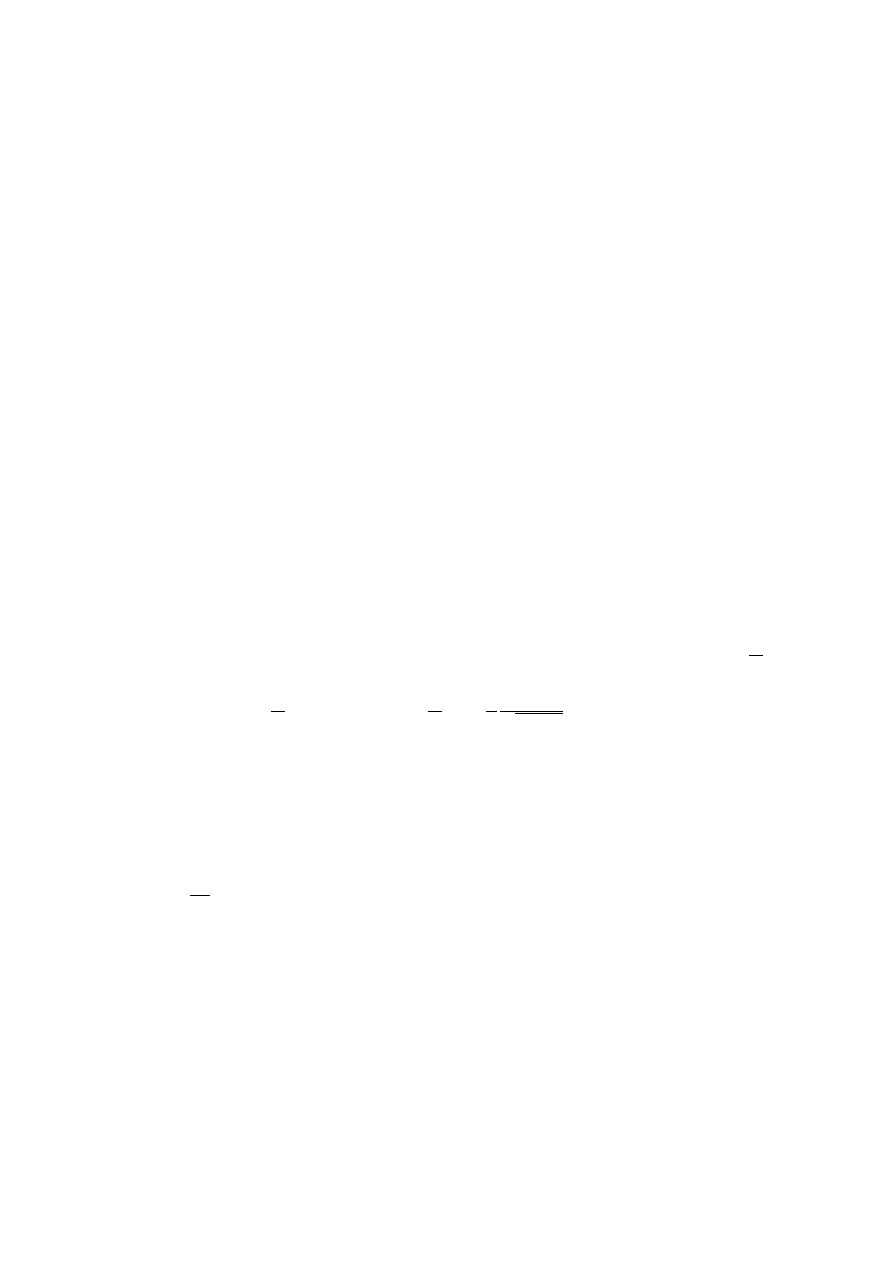
7.4.
RELATYWISTYCZNA SIŁA I II PRAWO NEWTONA
81
wewn ˛
atrz masy nie ma ˙zadnego ruchu. Napiszmy wi˛ec raz jeszcze:
E = mc
2
,
(7.15)
gdzie E jest energi ˛
a spoczywaj ˛
acej cz ˛
astki. Widzimy, ˙ze mc
2
nie jest wcale nieistotn ˛
a stał ˛
a,
a masa musi by´c jedn ˛
a z dost˛epnych form energii. Inaczej w zderzeniach nieelastycznych nie
byłby zachowany p˛ed. Nie jest to zreszt ˛
a wcale czysta teoria. Dzi˛eki poprawno´sci tego wzoru
powiodła si˛e przecie˙z budowa bomby atomowej!
7.4
R
ELATYWISTYCZNA SIŁA I
II P
RAWO
N
EWTONA
I
lekro´c rozwa˙zamy dowolny, zamkni˛ety układ ciał, spełniona jest zasada zachowania całkowite-
go p˛edu (a tak˙ze energii). Jednak˙ze cz˛esto rozwa˙za si˛e p˛ed pojedynczego ciała na które działaj ˛
a
ciała zewn˛etrzne, nieuwzgl˛ednione w układzie. Wówczas, naturalnie p˛ed rozwa˙zanego ciała nie
jest zachowany i mo˙ze si˛e zmienia´c. Mówimy wtedy, ˙ze za zmian˛e p˛edu odpowiedzialna jest
działaj ˛
aca siła. W gruncie rzeczy poj˛ecie siły jest obiektem czysto pomocniczym, ułatwiaj ˛
a-
cym opisywanie oddziaływa´n pomi˛edzy ciałami. W mechanice nierelatywistycznej siła pojawia
si˛e (i jest niejako definiowana) w równaniu Newtona F = ma lub równowa˙znie F =
dp
dt
. W
jaki sposób uogólni´c poj˛ecie siły na mechanik˛e relatywistyczn ˛
a? Zwró´cmy uwag˛e, ˙ze w teorii
wzgl˛edno´sci ma = m
dv
dt
to nie to samo, co
dp
dt
= m
d
dt
v
√
1−v
2
/c
2
! Nie do´s´c, ˙ze wektory te przyj-
muj ˛
a ró˙zne warto´sci, to mog ˛
a mie´c nawet ró˙zne kierunki! Aby zdefiniowa´c relatywistyczn ˛
a sił˛e
musimy si˛e zatem zdecydowa´c na jedn ˛
a z alternatywnych mo˙zliwo´sci. Ze wzgl˛edu na to, ˙ze p˛ed
relatywistyczny jest wielko´sci ˛
a maj ˛
ac ˛
a ogromne znaczenie (w ko´ncu w zamkni˛etych układach
jest zachowany), powszechnie definiuje si˛e sił˛e poprzez relatywistyczne II Prawo Newtona, czyli:
F =
dp
dt
.
(7.16)
Oczywi´scie w ka˙zdej chwili mo˙zemy rozwa˙zany układ rozszerzy´c na wszystkie oddziałuj ˛
ace
ciała i wówczas całkowita zmiana p˛edu b˛edzie wynosi´c zero, co oznacza, ˙ze b˛edzie musiało
by´c tak˙ze spełnione III Prawo Newtona mówi ˛
ace, ˙ze w oddziaływaniu dwóch ciał wyst˛epuj ˛
a
zawsze dwie siły o równych warto´sciach i przeciwnych kierunkach działaj ˛
ace na te ciała (sprawy
mog ˛
a si˛e jednakowo˙z nieco skomplikowa´c - do tego tematu powrócimy jeszcze analizuj ˛
ac siły
elektryczne i magnetyczne).

82
ROZDZIAŁ 7.
DYNAMIKA RELATYWISTYCZNA
Poniewa˙z przyrost czasu dt wyst˛epuj ˛
acy w powy˙zszym równaniu zale˙zy od układu odniesie-
nia, spodziewamy si˛e, ˙ze równie˙z siła b˛edzie jako´s zale˙ze´c od pr˛edko´sci V przyj˛etego układu
współrz˛ednych. W jaki sposób? Przypomnijmy sobie, ˙ze ju˙z kiedy´s natrafili´smy na ten problem
rozwa˙zaj ˛
ac w podrozdziale 2.6 zagadnienie zwi ˛
azane z przyci ˛
aganiem ładunku elektrycznego
przez przewód z pr ˛
adem. Zauwa˙zyli´smy wówczas, ˙ze wszystkie paradoksy znikaj ˛
a o ile przyj-
miemy, ˙ze siła F
0
działaj ˛
aca w układzie poruszaj ˛
acym si˛e z pr˛edko´sci ˛
a V mo˙ze by´c wyra˙zona
poprzez sił˛e F działaj ˛
ac ˛
a w układzie spoczywaj ˛
acym relacj ˛
a:
F
0
=
F
p
1 − V
2
/c
2
.
(7.17)
W ten sposób dostajemy wa˙zny wynik mówi ˛
acy, ˙ze je´sli siła transformuje si˛e zgodnie z po-
wy˙zszym prawem, to przyrost p˛edu pomi˛edzy okre´slonymi zdarzeniami jest zawsze taki sam:
dp = dp
0
. Jest to wynik zgodny z zasad ˛
a zachowania całkowitego p˛edu z czego oczywi´scie
bardzo si˛e cieszymy. Okazuje si˛e, ˙ze dodaj ˛
ac do siły jeszcze pewn ˛
a dodatkow ˛
a zerow ˛
a składow ˛
a,
mo˙zna zbudowa´c z nich nowy czterowektor nazywany czterosił ˛
a. Naturalnie, wówczas wzór
transformacyjny (7.17) trzeba b˛edzie równie˙z uzupełni´c o dodatkowy element, a˙zeby czterosiła
transformowała si˛e jak przystało na przyzwoity czterowektor. Wychodzi bowiem na to, ˙ze wzór
(7.17) jest poprawny tylko, gdy siła F działa na cz ˛
astk˛e spoczywaj ˛
ac ˛
a b ˛
ad´z poruszaj ˛
ac ˛
a si˛e
(jak w przykładzie z przewodnikiem elektrycznym) prostopadle do kierunku działania tej siły.
Szczegóły ´sledztwa pozostawiamy Czytelnikowi.
7.5
C
ZTEROPRZYSPIESZENIE
W
yra˙zenie (7.2) nazwali´smy czteropr˛edko´sci ˛
a. Dlaczego? Widzimy, ˙ze w granicy c −→ ∞
zerowa składowa czterowektora d ˛
a˙zy do 1, a pozostałe składowe do v. Jednak nie to jest powo-
dem nadania czterowektorowi (7.2) nazwy czteropr˛edko´sci. Przecie˙z wyra˙ze´n posiadaj ˛
acych
podobne przej´scie graniczne mo˙zemy wymy´sli´c dowoln ˛
a ilo´s´c! Wa˙zne jest tu co innego.
Rozwa˙zmy cz ˛
astk˛e poruszaj ˛
ac ˛
a si˛e z pr˛edko´sci ˛
a, której poło˙zenie w ka˙zdej chwili czasu
opisane jest czteropoło˙zeniem (ct, r) i która porusza si˛e z pr˛edko´sci ˛
a v =
dr
dt
. W jaki sposób
z czterowektora (ct, r) otrzyma´c czteropr˛edko´s´c? Na pewno nie, jak by´c mo˙ze si˛e narzuca,
poprzez ró˙zniczkowanie po czasie
d
dt
, gdy˙z dt zale˙zy od układu odniesienia! Zwró´cmy jednak
uwag˛e, ˙ze „czas własny” cz ˛
astki τ =
R p
1 − v
2
/c
2
dt poruszaj ˛
acej si˛e od punktu r
1
do punktu
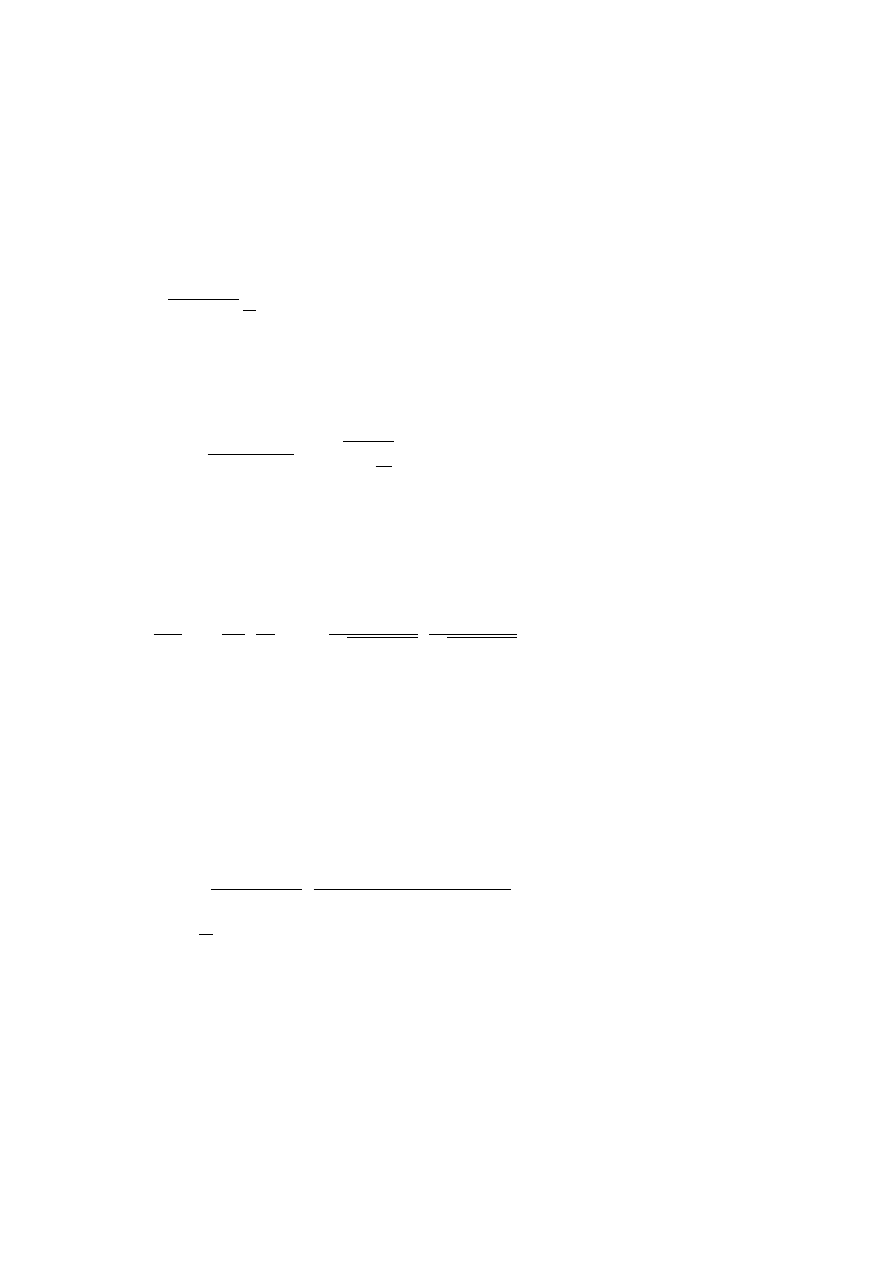
7.6.
RUCH JEDNOSTAJNIE PRZYSPIESZONY
83
r
2
nie zale˙zy od układu odniesienia. Na przykład je´sli w wagonie restauracyjnym poci ˛
agu za-
cz˛eto gotowa´c jajko w chwili gdy przeje˙zd˙zał on przez stacj˛e znajduj ˛
ac ˛
a si˛e w r
1
, a jajko ugo-
towało si˛e dokładnie gdy poci ˛
ag mijał inn ˛
a stacj˛e w r
2
, to czas τ jaki upłyn ˛
ał wewn ˛
atrz wagonu
oczywi´scie nie zale˙zy od tego kto i z jakiego układu odniesienia dokonuje obserwacji. Oz-
nacza to, ˙ze je´sli dowolne ciało przemie´sciło si˛e o dx z pr˛edko´sci ˛
a v, to odst˛ep czasu własnego
dτ =
p
1 − v
2
/c
2 dx
v
nie zale˙zy od układu odniesienia.
Na wszelki wypadek dojdziemy do tego samego wniosku jeszcze inn ˛
a metod ˛
a. Je˙zeli dwa
bardzo bliskie zdarzenia oddziela interwał czasoprzestrzenny ds, który jak wiemy nie zale˙zy od
układu odniesienia, to zauwa˙zmy, ˙ze:
ds =
√
c
2
dt
2
− dr
2
= c
r
1 −
v
2
c
2
dt = c dτ.
(7.18)
Czyli dτ jest tak˙ze niezale˙zne od obserwatora.
Wró´cmy wi˛ec do rozwa˙za´n na temat czteropr˛edko´sci: skoro długo´s´c czteropoło˙zenia r
¤
jest
niezale˙zna od układu odniesienia, to równie˙z niezale˙zna od niego b˛edzie długo´s´c czterowektora:
dr
¤
dτ
=
µ
dct
dτ
,
dr
dτ
¶
=
Ã
c
p
1 − v
2
/c
2
,
v
p
1 − v
2
/c
2
!
= v
¤
(7.19)
i wszystko staje si˛e jasne! Czteropr˛edko´s´c mo˙zna otrzyma´c ró˙zniczkuj ˛
ac po czasie własnym
czteropoło˙zenie. Widzimy ponadto, ˙ze mo˙zemy tak otrzymany czterowektor dalej ró˙zniczkowa´c
po czasie własnym τ otrzymuj ˛
ac czteroprzyspieszenie i tak dalej. Poniewa˙z, w przeciwie´nstwie
do czteroprzyspieszenia, owo „i tak dalej” jest prawie nigdy niepotrzebne, skupimy si˛e znalezie-
niu tylko tego pierwszego (czyli czteroprzyspieszenia). Ró˙zniczkuj ˛
ac ponownie (7.19) otrzymu-
jemy:
a
¤
=
µ
v · a/c
(1 − v
2
/c
2
)
2
,
a(1 − v
2
/c
2
) + v(v · a)/c
2
(1 − v
2
/c
2
)
2
¶
,
(7.20)
gdzie a =
dv
dt
. Powy˙zsze, przecudne wyra˙zenie, mimo odstraszaj ˛
acego wygl ˛
adu, oka˙ze si˛e
nieocenione, gdy zajmiemy si˛e analiz ˛
a relatywistycznego ruchu jednostajnie przyspieszonego.
7.6
R
UCH JEDNOSTAJNIE PRZYSPIESZONY
N
o wła´snie, jak w ogóle go zdefiniowa´c? Klasyczna definicja, mówi ˛
aca ˙ze ciało nabiera pr˛ed-

84
ROZDZIAŁ 7.
DYNAMIKA RELATYWISTYCZNA
ko´sci w jednostajnym tempie jest nie do przyj˛ecia! Przecie˙z wiemy, ˙ze ciało nie mo˙ze rozp˛edza´c
si˛e bez ogranicze´n. Z drugiej strony poj˛ecie ruchu jednostajnie przyspieszonego jest dobrze
okre´slone gdy ruch odbywa si˛e z pr˛edko´sci ˛
a zaniedbywalnie mał ˛
a w porównaniu z pr˛edko´sci ˛
a
´swiatła. W zwi ˛
azku z tym relatywistyczne uogólnienie polega na przyj˛eciu, ˙ze ruch jest jedno-
stajnie przyspieszony, je˙zeli ciało porusza si˛e ze stałym przyspieszeniem z punktu widzenia iner-
cjalnego układu chwilowo współporuszaj ˛
acego si˛e, tzn takiego w którym ciało w danej chwili
spoczywa. Konstrukcja pozornie karkołomna: w ka˙zdej chwili musimy znale´z´c układ w którym
ciało spoczywa, ale „porusza si˛e” z okre´slonym przyspieszeniem - je´sli to mo˙zliwe, to mówimy
o relatywistycznym ruchu jednostajnie przyspieszonym. Ma to zreszt ˛
a niejaki zwi ˛
azek z ogóln ˛
a
teori ˛
a wzgl˛edno´sci, wedle której stoj ˛
ac w rakiecie poruszaj ˛
acej si˛e ze stałym przyspieszeniem,
nasze wszystkie odczucia i eksperymenty b˛ed ˛
a dawa´c wyniki takie, jak gdyby´smy przez cały
czas spoczywali w jednorodnym polu grawitacyjnym. W ka˙zdym razie definicja wydaje si˛e jasna.
Pytanie, jak wygl ˛
ada ruch jednostajnie przyspieszony z punktu widzenia jednego, ustalonego
obserwatora, który przez cały czas spoczywa? Sprawd´zmy to rozwa˙zaj ˛
ac jednowymiarowy
przypadek ruchu wzdłu˙z osi x. Przy okazji prze´cwiczymy u˙zycie nowo poznanego formalizmu
czterowektorów.
Wiemy, ˙ze w danej chwili w układzie współporuszaj ˛
acym si˛e pr˛edko´s´c ciała wynosi zero,
a przyspieszenie a jest skierowane wzdłu˙z osi x. Zatem czteroprzyspieszenie (7.20) w tym
układzie upraszcza si˛e do:
a
0¤
= (0, a, 0, 0).
(7.21)
Natomiast w układzie, który cały czas spoczywa chwilowa pr˛edko´s´c ciała skierowana wzdłu˙z osi
x wynosi v. Jego chwilowe przyspieszenie wynosi po prostu
dv
dt
. Zatem czteropr˛edko´s´c w tym
układzie jest postaci:
a
¤
=
µ
v/c
(1 − v
2
/c
2
)
2
dv
dt
,
1
(1 − v
2
/c
2
)
2
dv
dt
, 0, 0
¶
.
(7.22)
Wiemy jednak, ˙ze długo´s´c czterowektora nie zale˙zy od układu odniesienia. Oznacza to, ˙ze za-
chodzi równo´s´c:
(a
¤
)
2
= (a
0¤
)
2
.
(7.23)
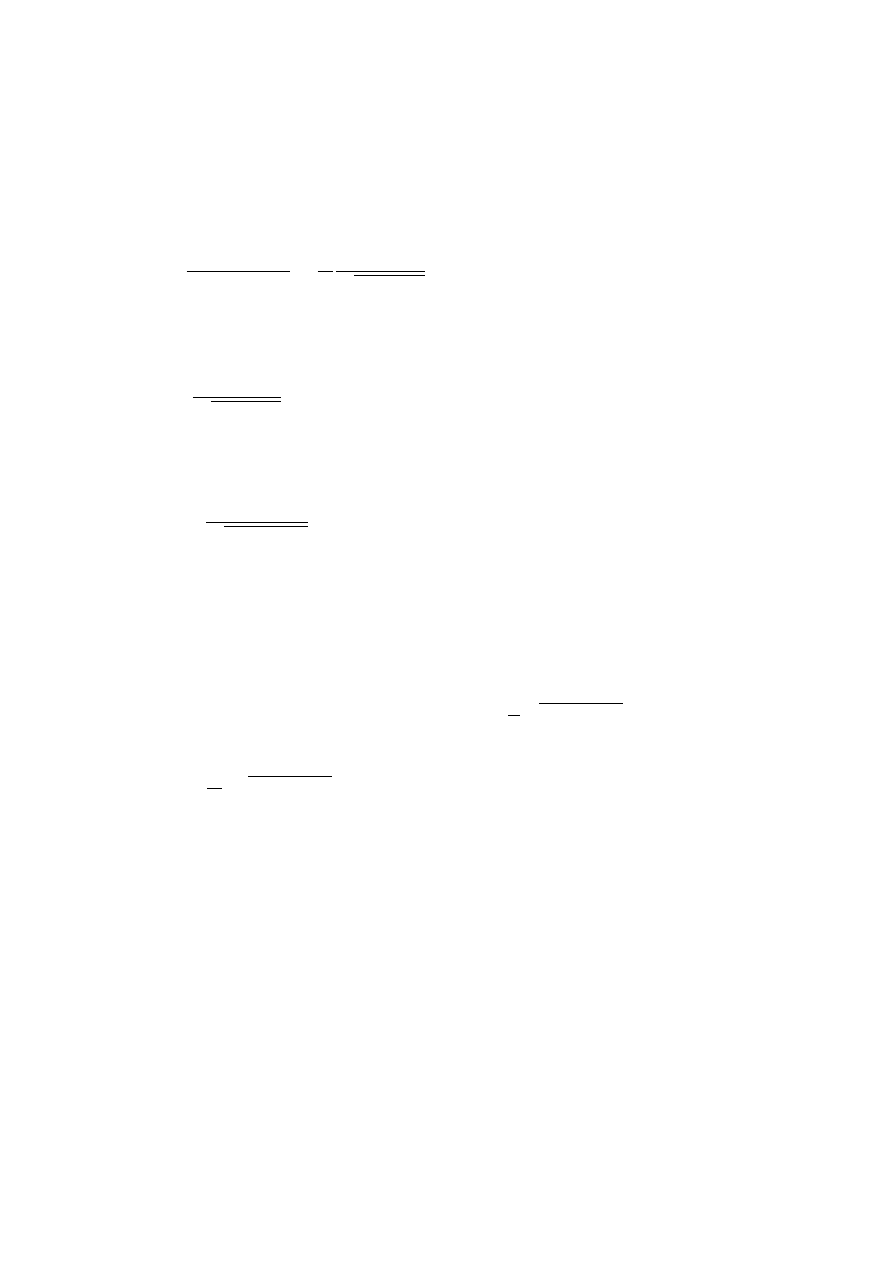
7.6.
RUCH JEDNOSTAJNIE PRZYSPIESZONY
85
Po podniesieniu do kwadratu i przyrównaniu obu czterowektorów otrzymujemy nast˛epuj ˛
ace rów-
nanie:
a =
dv/dt
(1 − v
2
/c
2
)
3/2
=
d
dt
v
p
1 − v
2
/c
2
.
(7.24)
Rozwi ˛
azaniem z warunkiem pocz ˛
atkowym v(0) = 0 jest:
at =
v
p
1 − v
2
/c
2
,
(7.25)
a po odwróceniu zale˙zno´sci:
v(t) =
at
p
1 + a
2
t
2
/c
2
.
(7.26)
Z gł˛ebok ˛
a ulg ˛
a stwierdzamy, ˙ze gdy czas d ˛
a˙zy do niesko´nczono´sci, pr˛edko´s´c d ˛
a˙zy do c, co
utwierdza nas w przekonaniu, ˙ze pr˛edko´sci ´swiatła przekroczy´c si˛e nijak nie da, nawet poruszaj ˛
ac
si˛e niesko´nczenie długo ze stałym przyspieszeniem.
Mo˙zemy jeszcze na dokładk˛e znale´z´c równanie ruchu ciała poruszaj ˛
acego si˛e ze stałym
przyspieszeniem. Szcz˛e´sliwie si˛e składa, ˙ze zadanie to jest w zasadzie trywialne, bo powy˙zsze
wyra˙zenie na pr˛edko´s´c jest pochodn ˛
a po czasie funkcji
c
2
a
p
1 + a
2
t
2
/c
2
, zatem:
x(t) =
c
2
a
(
p
1 + a
2
t
2
/c
2
− 1),
(7.27)
gdzie dodatkowa stała całkowania została wybrana w taki sposób, by w chwili pocz ˛
atkowej ciało
znajdowało si˛e w punkcie x = 0.
Pytania
• Podaj definicj˛e relatywistycznego ruchu jednostajnie przyspieszonego.
• Czy prawd ˛
a jest, ˙ze obiekt startuj ˛
acy z pewnego punktu i poruszaj ˛
acy si˛e relatywistycznym
ruchem jednostajnie przyspieszonym mo˙ze by´c dogoniony przez ´swiatło opuszczaj ˛
ace ten
punkt w dowolnej, pó´zniejszej chwili?

86
ROZDZIAŁ 7.
DYNAMIKA RELATYWISTYCZNA
• Czy wektor siły jest równy przestrzennej cz˛e´sci pewnego czterowektora?
• Czy iloczyn masy i przyspieszenia cz ˛
astki mo˙ze mie´c inn ˛
a warto´s´c ni˙z pochodna p˛edu tej
cz ˛
astki po czasie?
• Czy iloczyn masy i wektora przyspieszenia cz ˛
astki mo˙ze mie´c inny kierunek ni˙z pochodna
wektora p˛edu tej cz ˛
astki po czasie?
• Czy w zderzeniach nieelastycznych musi by´c zachowana całkowita energia swobodna
układu cz ˛
astek, czy jest tak tylko w przypadku zderze´n elastycznych? Jaka byłaby odpowied´z
w fizyce nierelatywistycznej?
• Czy podgrzewaj ˛
ac ciało zwi˛ekszamy jego mas˛e spoczynkow ˛
a?
Zadania
• Wyznacz wzory transformacyjne dla siły przy zmianie układu inercjalnego. Podaj posta´c
czterowektora, którego elementem jest siła. Jak ˛
a interpretacj˛e mo˙zna nada´c dodatkowej
składowej tego czterowektora?
• Wyznacz pr˛edko´s´c precesji orbity Merkurego zakładaj ˛
ac, ˙ze jego masa grawitacyjna wys-
t˛epuj ˛
aca w klasycznym wzorze Newtona na sił˛e grawitacyjnego oddziaływania dwóch ciał
zale˙zy od pr˛edko´sci jak: m(v) =
m
√
1−v
2
/c
2
. Pozostałe efekty grawitacyjne zwi ˛
azane z
konsekwencjami ogólnej teorii wzgl˛edno´sci pomi´n.
• Udowodnij, ˙ze swobodny elektron nie mo˙ze pochłon ˛
a´c fotonu.
• Udowodnij, ˙ze swobodna para elektron-pozyton nie mo˙ze w wyniku anihilacji wyemi-
towa´c pojedynczego fotonu.
• Czy prawd ˛
a jest, ˙ze obiekt startuj ˛
acy z pewnego punktu i poruszaj ˛
acy si˛e relatywistycznym
ruchem jednostajnie przyspieszonym mo˙ze by´c dogoniony przez ´swiatło opuszczaj ˛
ace ten
punkt w dowolnej, pó´zniejszej chwili?
• Punkty A i B poruszaj ˛
a si˛e relatywistycznym ruchem jednostajnie przyspieszonym wzdłu˙z
osi x w taki sposób, ˙ze odległo´s´c mi˛edzy nimi nie zmienia si˛e w czasie. Czy pr˛et umieszc-
zony pomi˛edzy A i B w którym´s momencie p˛eknie?

Rozdział 8
E
LEKTRODYNAMIKA RELATYWISTYCZNA
M
ateriał przedstawiony w tym rozdziale został oparty na podr˛eczniku R. P. Feynmana [7], jed-
nego z twórców elektrodynamiki kwantowej. Celem rozdziału jest wykazanie, ˙ze tytuł „elektro-
dynamika relatywistyczna” jest jak „masło ma´slane”. Elektrodynamika, w przeciwie´nstwie do
mechaniki Newtona, od pocz ˛
atku jest i była teori ˛
a relatywistyczn ˛
a!
8.1
P
RELUDIUM
W
równaniach Maxwella wyst˛epuj ˛
a dwie stałe, które mo˙zna wyznaczy´c eksperymentalnie:
stała dielektryczna ε
0
oraz przenikalno´s´c magnetyczna pró˙zni µ
0
:
∇ · E =
%
ε
0
∇ · B = 0
∇ × E = −
∂B
∂t
∇ × B = µ
0
j + µ
0
ε
0
∂E
∂t
Okazuje si˛e, ˙ze iloczyn tych dwóch stałych ma wymiar [
s
2
m
2
], czyli odwrotno´sci kwadratu pr˛ed-
ko´sci. Mo˙zemy zatem wprowadzi´c now ˛
a stał ˛
a o wymiarze pr˛edko´sci, z definicji równ ˛
a c =
1
√
µ
0
ε
0
. Jej warto´s´c mo˙zna wyznaczy´c eksperymentalnie na podstawie wyników pomiarów siły
87

88
ROZDZIAŁ 8.
ELEKTRODYNAMIKA RELATYWISTYCZNA
przyci ˛
agania dwóch ładunków elektrycznych oraz dwóch przewodów z pr ˛
adem, c ≈ 3 · 10
8
[
m
s
].
Jest to wła´snie pr˛edko´s´c ´swiatła, czyli pr˛edko´s´c propagacji pró˙zniowych rozwi ˛
aza´n równa´n
Maxwella. Aby si˛e przekona´c na przykład o tym, ˙ze zmiany potencjału elektrostatycznego ϕ
propaguj ˛
a si˛e z pr˛edko´sci ˛
a c, wystarczy kilka prostych przekształce´n równa´n (8.1) w wyniku
których otrzyma´c mo˙zna:
ε
0
µ
0
∂
2
ϕ
∂t
2
− 4ϕ = 0.
(8.1)
Jest to po prostu równanie falowe, którego rozwi ˛
azania rozchodz ˛
a si˛e jak wiadomo z pr˛edko´sci ˛
a
c = 1/
√
ε
0
µ
0
. I oto nam wła´snie chodziło. Zaczyna ju˙z pachnie´c teori ˛
a wzgl˛edno´sci!
8.2
P
OTENCJAŁ PORUSZAJ ˛
ACEGO SI ˛
E ŁADUNKU
P
rzeja˙zd˙zk˛e po relatywistycznych skłonno´sciach elektrodynamiki klasycznej rozpoczniemy od
ciekawego przykładu. Spróbujmy znale´z´c potencjał elektrostatyczny pochodz ˛
acy od porusza-
j ˛
acego si˛e ładunku punktowego. Sprawa niby prosta. Zaraz jednak oka˙ze si˛e, jak łatwo si˛e
pomyli´c.
Zacznijmy od wypisania ogólnego wyra˙zenia na potencjał elektrostatyczny w punkcie r
2
i chwili t pochodz ˛
acy od dowolnego rozkładu ładunku elektrycznego %(r, t) (jak wida´c do-
puszczamy mo˙zliwo´s´c zale˙zno´sci rozkładu ładunku od czasu):
ϕ(r
2
, t) =
Z
d
3
r
1
%(r
1
, t)
4πε
0
r
,
(8.2)
gdzie r = |r
2
− r
1
|. Oczywi´scie wzór ten jest niepoprawny, bo potencjał elektryczny w danej
chwili t nie mo˙ze zale˙ze´c od rozkładu ładunków w tej samej chwili! Potencjał ϕ nie mo˙ze
„dowiadywa´c si˛e” natychmiast o aktualnym rozkładzie ładunków, a wył ˛
acznie o rozkładzie
w chwilach wcze´sniejszych (w przeciwnym razie mo˙zna by u˙zywa´c pomiarów potencjału ϕ
do błyskawicznego przekazywania informacji). Ale poniewa˙z nie chcemy na razie stosowa´c
znajomo´sci teorii wzgl˛edno´sci, a jedynie prawa elektromagnetyzmu, wystarczy posłu˙zy´c si˛e
wnioskiem z poprzedniego podrozdziału: zaburzenia potencjału propaguj ˛
a si˛e z pr˛edko´sci ˛
a c.
Zatem poprawny wzór ma posta´c:
ϕ(r
2
, t) =
Z
d
3
r
1
%(r
1
, t
ret
)
4πε
0
r
,
(8.3)
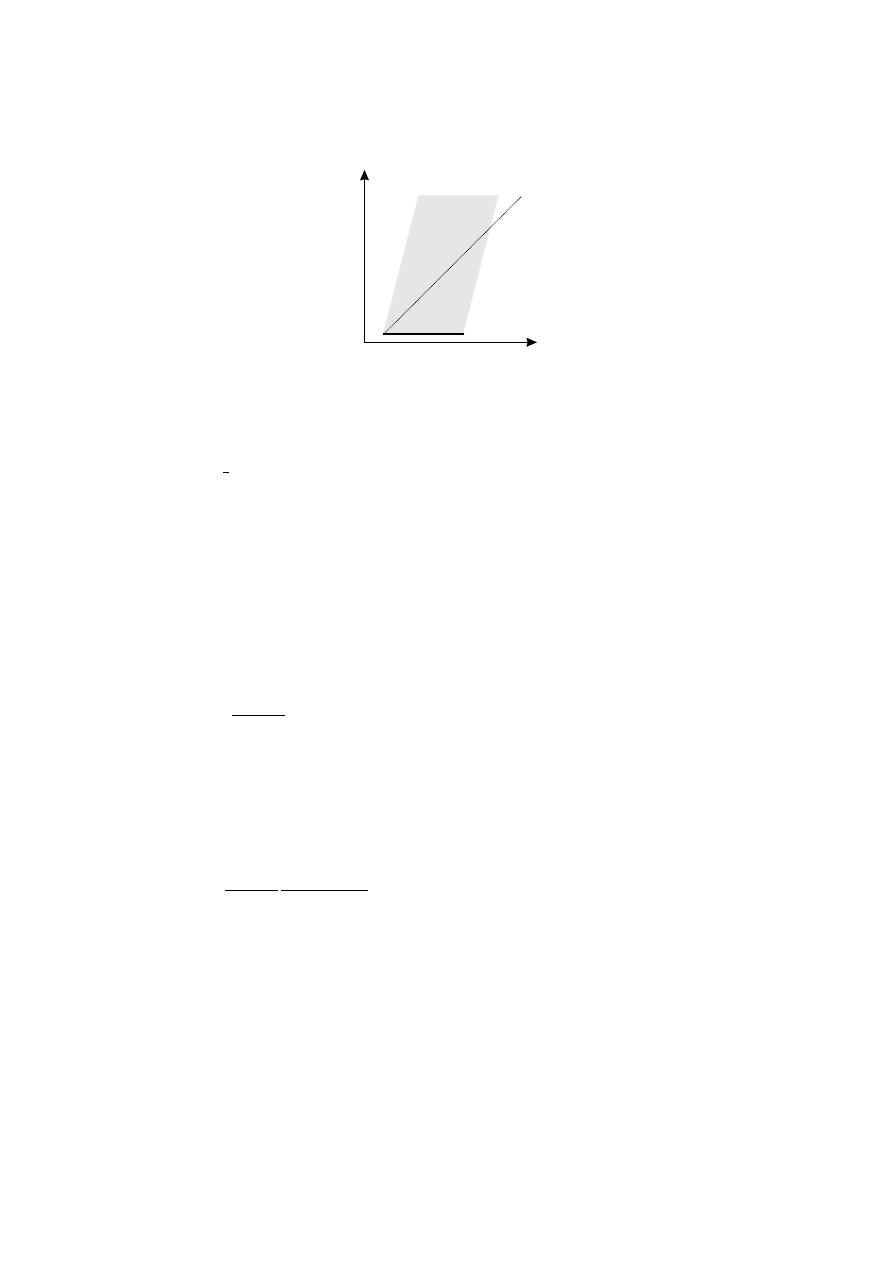
8.2.
POTENCJAŁ PORUSZAJ ˛
ACEGO SI ˛
E ŁADUNKU
89
ct
x
B
A
C
B’
Rysunek 8.1:
Diagram czasoprzestrzenny naładowanego odcinka AB. Szukamy potencjału w punkcie
C.
gdzie t
ret
= t −
r
c
jest tak zwanym czasem retardowanym (opó´znionym), czyli potencjał „czuje”
jedynie rozkład ładunków w chwilach wcze´sniejszych. W ten sposób uzyskujemy gwarancj˛e, ˙ze
zmiany potencjału propaguj ˛
a si˛e zawsze z pr˛edko´sci ˛
a c, dokładnie jak fale elektromagnetyczne
(czyli ´swiatło).
Spróbujmy wi˛ec odpowiedzie´c na interesuj ˛
ace nas pytanie: jaki jest potencjał generowany
przez punktowy ładunek q poruszaj ˛
acy si˛e z pr˛edko´sci ˛
a v? Oczywi´scie, naturalnym rozwi ˛
aza-
niem jest:
ϕ(r
2
, t) =
q
4πε
0
r
ret
,
(8.4)
gdzie r
ret
jest odległo´sci ˛
a mi˛edzy ładunkiem a punktem w którym badamy pole w odpowiednio
wcze´sniejszej (retardowanej) chwili. Okazuje si˛e, ˙ze znów jeste´smy w bł˛edzie. Poprawny wynik
jest nieco bardziej skomplikowany:
ϕ(r, t) =
q
4πε
0
r
ret
1
(1 − v
r
/c)
ret
,
(8.5)
czyli pojawia si˛e dodatkowo wyraz ze składow ˛
a pr˛edko´sci w kierunku punktu w którym badamy
pole, w chwili retardowanej.
Sk ˛
ad bierze si˛e dodatkowy człon? Najłatwiej to zrozumie´c rozwa˙zaj ˛
ac przykład krótkiego
odcinka AB naładowanego ładunkiem q i poruszaj ˛
acego si˛e wzdłu˙z prostej na której le˙zy. Spróbu-
jmy znale´z´c potencjał na tej prostej w punkcie C. Odpowiedni diagram czasoprzestrzenny przed-
stawiony jest na rysunku 8.1. Szary obszar reprezentuje fragment czasoprzestrzeni zajmowany

90
ROZDZIAŁ 8.
ELEKTRODYNAMIKA RELATYWISTYCZNA
przez poruszaj ˛
acy si˛e, naładowany odcinek. Do punktu C dociera informacja o rozkładzie
ładunku, której linia ´swiata została zaznaczona na diagramie przerywan ˛
a kresk ˛
a. Oznacza to,
˙ze do punktu C dociera informacja o ładunkach znajduj ˛
acych si˛e na przeci˛eciu przerywanej linii
´swiata oraz szarego obszaru. Wida´c, ˙ze pozorna długo´s´c naładowanego odcinka nie jest równa
AB, tylko AB’. Zatem potencjał w punkcie C jest taki, jak gdyby był generowany przez ładunek
równy nie q, tylko q
|AB’|
|AB|
. Oznacza to, ˙ze musimy odpowiednio zmodyfikowa´c wyra˙zenie na po-
tencjał pochodz ˛
acy od naładowanego odcinka. Poniewa˙z |AB| = |AB’|(1 − v/c), gdzie v jest
pr˛edko´sci ˛
a odcinka, to we wszystkich wyra˙zeniach zamiast q nale˙zy wstawia´c
q
1−v/c
. Nasz ˛
a anal-
iz˛e nietrudno uogólni´c na przypadek trójwymiarowy. Wówczas nale˙zy tylko zast ˛
api´c pr˛edko´s´c
v jej rzutem v
r
na kierunek w którym szukamy potencjału. Ot, i cała filozofia.
W wyniku dokonywanych przekształce´n okazało si˛e, ˙ze rezultat nie zale˙zy od długo´sci od-
cinka |AB|, wi˛ec nasze wzory s ˛
a poprawne równie˙z gdy odcinek jest niesko´nczenie krótki, czyli
gdy ładunek jest punktowy. W ten sposób docieramy szcz˛e´sliwie do poprawnego wyra˙zenia (8.5)
na potencjał generowany przez ładunek poruszaj ˛
acy si˛e z dowoln ˛
a pr˛edko´sci ˛
a. Wystarczy tylko,
znaj ˛
ac równanie ruchu ładunku, znale´z´c odpowiednie pr˛edko´sci i poło˙zenia retardowane. Wynik
nasz mo˙zemy jeszcze przepisa´c w równowa˙znej, eleganckiej postaci:
ϕ(r, t) =
q
4πε
0
(r − r · v/c)
ret
.
(8.6)
W identyczny sposób, korzystaj ˛
ac z zale˙zno´sci potencjału wektorowego A od rozkładu pr ˛
adów
elektrycznych mo˙zemy wyznaczy´c:
A(r, t) =
qv
ret
4πε
0
(r − r · v/c)
ret
.
(8.7)
Nasze wzory nosz ˛
a nazwy pochodz ˛
ace od nazwisk swoich pierwszych odkrywców. S ˛
a to poten-
cjały Lienarda-Wiecherta. Ostatni ˛
a rzecz ˛
a jak ˛
a teraz uczynimy, b˛edzie znalezienie tych potenc-
jałów dla najprostszego mo˙zliwego przypadku: ruchu ładunku q ze stał ˛
a pr˛edko´sci ˛
a v wzdłu˙z osi
x.
W przypadku jednostajnego ruchu mo˙zemy bez trudu obliczy´c retardowane czynniki wys-
t˛epuj ˛
ace w potencjałach Lienarda-Wiecherta. Po pierwsze retardowana odległo´s´c pomi˛edzy
poruszaj ˛
acym si˛e ładunkiem a punktem w którym badamy potencjał r
ret
wi ˛
a˙ze si˛e z czasem re-
tardowanym t
ret
w którym ładunek znajdował si˛e wła´snie w punkcie r
ret
zale˙zno´sci ˛
a:
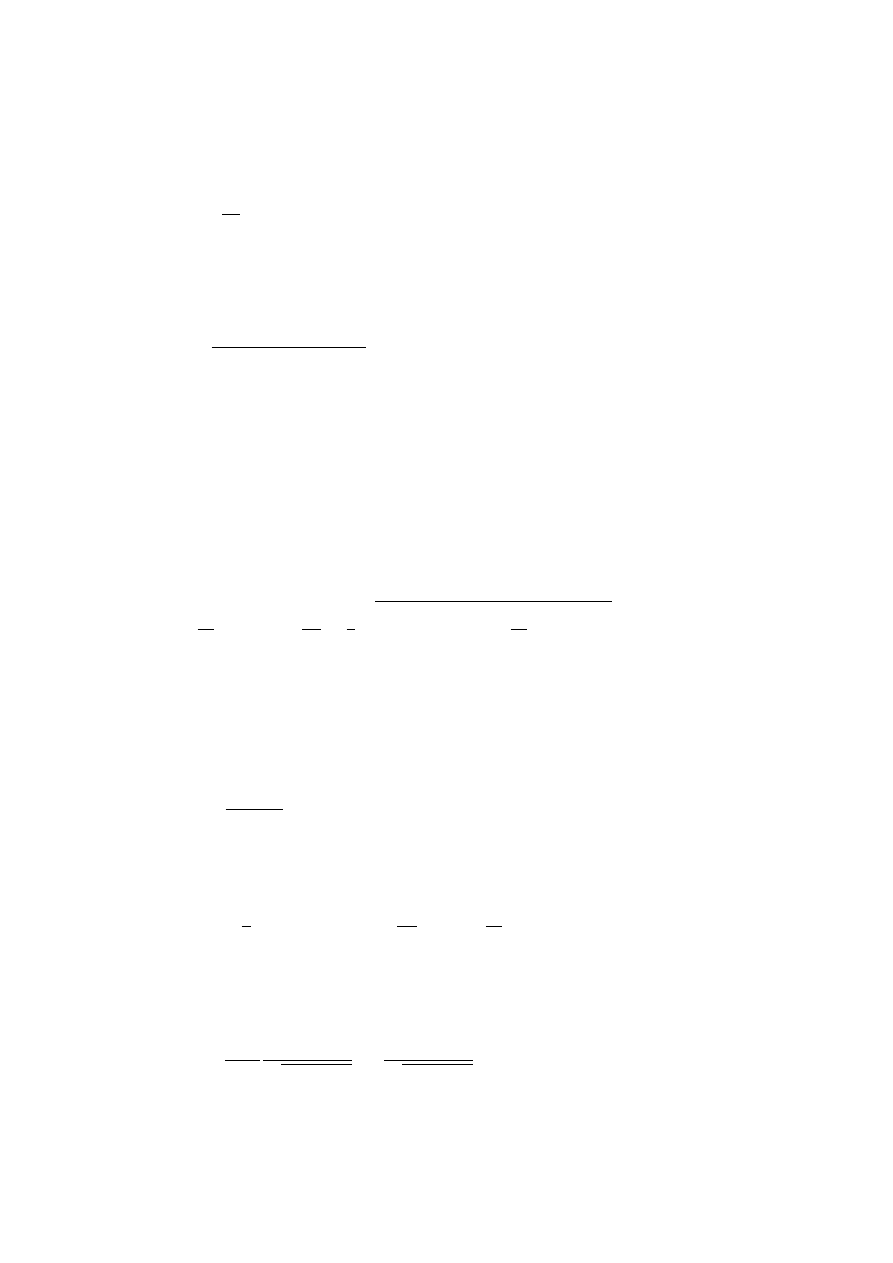
8.2.
POTENCJAŁ PORUSZAJ ˛
ACEGO SI ˛
E ŁADUNKU
91
t
ret
= t −
r
ret
c
.
(8.8)
Z drugiej strony, poniewa˙z równanie ruchu ładunku jest postaci x = vt, spełniony jest te˙z inny
zwi ˛
azek:
r
ret
=
p
(x − vt
ret
)
2
+ y
2
+ z
2
.
(8.9)
Wystarczy teraz rozwi ˛
aza´c układ powy˙zszych dwóch równa´n wyznaczaj ˛
ac t
ret
oraz r
ret
. Pozby-
waj ˛
ac si˛e z równa´n r
ret
dostajemy:
c
2
(t − t
ret
)
2
= (x − vt
ret
)
2
+ y
2
+ z
2
,
(8.10)
st ˛
ad natomiast
µ
1 −
v
2
c
2
¶
t
ret
= t −
vx
c
2
−
1
c
s
(x − vt)
2
+
µ
1 −
v
2
c
2
¶
(y
2
+ z
2
).
(8.11)
W celu obliczenia r
ret
wystarczy wykorzysta´c raz jeszcze wzór (8.8) razem z wyra˙zeniem powy˙zej.
Do obliczenia potencjału elektrostatycznego ϕ danego wyra˙zeniem (8.5), musimy ju˙z tylko
obliczy´c (1 − v
r
/c)
ret
. Retardowana składowa „radialna” v
r
jest równa:
(v
r
)
ret
= v
x − vt
ret
r
ret
.
(8.12)
Zatem retardowany mianownik wyra˙zenia (8.5) jest po prostu równy:
c(t − t
ret
) −
v
c
(x − vt
ret
) = c
·
t −
vx
c
2
−
µ
1 −
v
2
c
2
¶
t
ret
¸
.
(8.13)
Wstawiaj ˛
ac wyra˙zenie (8.11) dostajemy ostatecznie:
ϕ(r, t) =
q
4πε
0
1
p
1 − v
2
/c
2
Ã
x − vt
p
1 − v
2
/c
2
!
2
+ y
2
+ z
2
−1/2
.
(8.14)
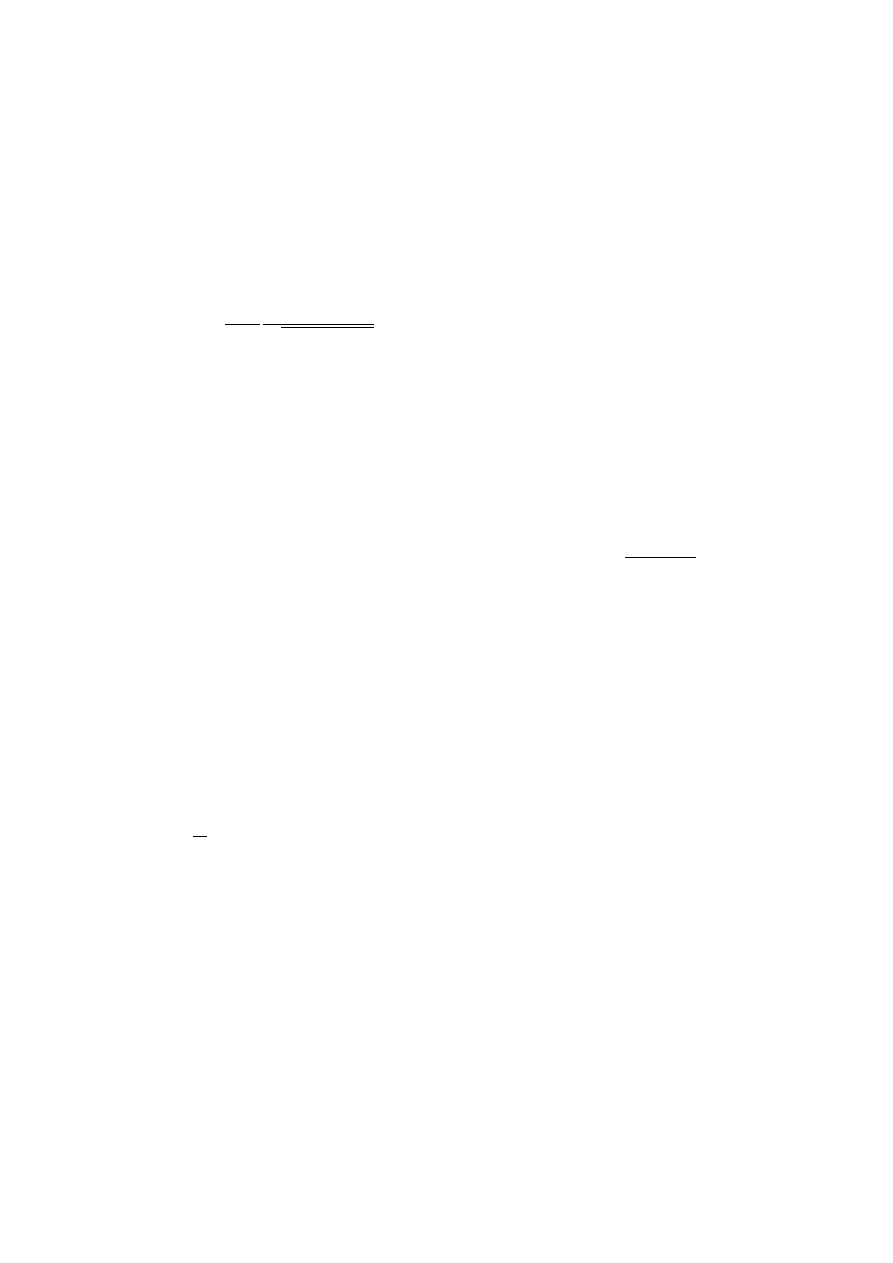
92
ROZDZIAŁ 8.
ELEKTRODYNAMIKA RELATYWISTYCZNA
Do´s´c kr˛ecenia! Wida´c ju˙z jak na dłoni, ˙ze z analizy równa´n Maxwella (8.1) mo˙zna wywnios-
kowa´c posta´c transformacji Lorentza! We wzorach pojawiaj ˛
a si˛e ju˙z znane z poprzednich roz-
działów Lorentzowskie czynniki. Aby wyprowadzi´c wzór (8.14) musieli´smy solidnie si˛e napra-
cowa´c. Wniosek jest taki, ˙ze wystarczyło wzi ˛
a´c potencjał ładunku spoczywaj ˛
acego:
ϕ(r, t) =
q
4πε
0
1
p
x
2
+ y
2
+ z
2
(8.15)
i dokona´c transformacji Lorentza współrz˛ednych x, y i z! Oczywi´scie, ˙ze tak! Przecie˙z nasza
podstawowa zasada mówi, ˙ze nie da si˛e stwierdzi´c czy to my poruszamy si˛e w pobli˙zu spoczy-
waj ˛
acego ładunku, czy jest odwrotnie. Zatem od samego pocz ˛
atku wystarczyło powiedzie´c, ˙ze
wynik b˛edzie taki jakby to ładunek spoczywał, a obserwator był w ruchu. Je´sli jednak nie zna
si˛e prawidłowych transformacji Lorentza (jak to miało miejsce w XIX wieku), mo˙zna znale´z´c
ich posta´c, jak zrobił wła´snie Lorentz, poprzez analiz˛e równa´n Maxwella.
Dobrze, dobrze, ale ró˙znica pomi˛edzy wzorami (8.14) i (8.15) nie sprowadza si˛e wył ˛
acznie
do transformacji Lorentza. Pojawia si˛e jeszcze dodatkowy czynnik
p
1 − v
2
/c
2
. Sk ˛
ad si˛e on
bierze? Otó˙z, gdyby go nie było, to całka z laplasjanu ϕ po całej przestrzeni byłaby ró˙zna
dla ładunku spoczywaj ˛
acego i poruszaj ˛
acego si˛e. Oznacza to, ˙ze w obu sytuacjach całkowity
ładunek w przestrzeni (czyli po prostu rozwa˙zany ładunek punktowy) byłby ró˙zny. Dodatkowy
wyraz pełni wi˛ec rol˛e czynnika normalizacyjnego, gwarantuj ˛
acego stało´s´c ładunku we wszyst-
kich układach odniesienia.
Wyprowadzili´smy tu posta´c potencjału elektrostatycznego ruchomego ładunku. Analogiczna
procedura prowadzi do wniosku, ˙ze potencjał wektorowy tego ładunku jest postaci:
A =
v
c
2
ϕ.
(8.16)
Wkrótce zreszt ˛
a oka˙ze si˛e, ˙ze zwi ˛
azek pomi˛edzy ϕ i A jest gł˛ebszy, wielko´sci te s ˛
a bowiem
składowymi jednego czterowektora.
8.3
W
POSZUKIWANIU KOLEJNYCH CZTEROWEKTORÓW
P
owoli naszym oczom ukazuje si˛e niezwykły, relatywistyczny charakter równa´n Maxwella.
Przyst ˛
apimy teraz do szczegółowej analizy tego zagadnienia. Do opisu wielko´sci fizycznych,
podobnie jak w mechanice klasycznej, u˙zyjemy poj˛ecia czterowektora.
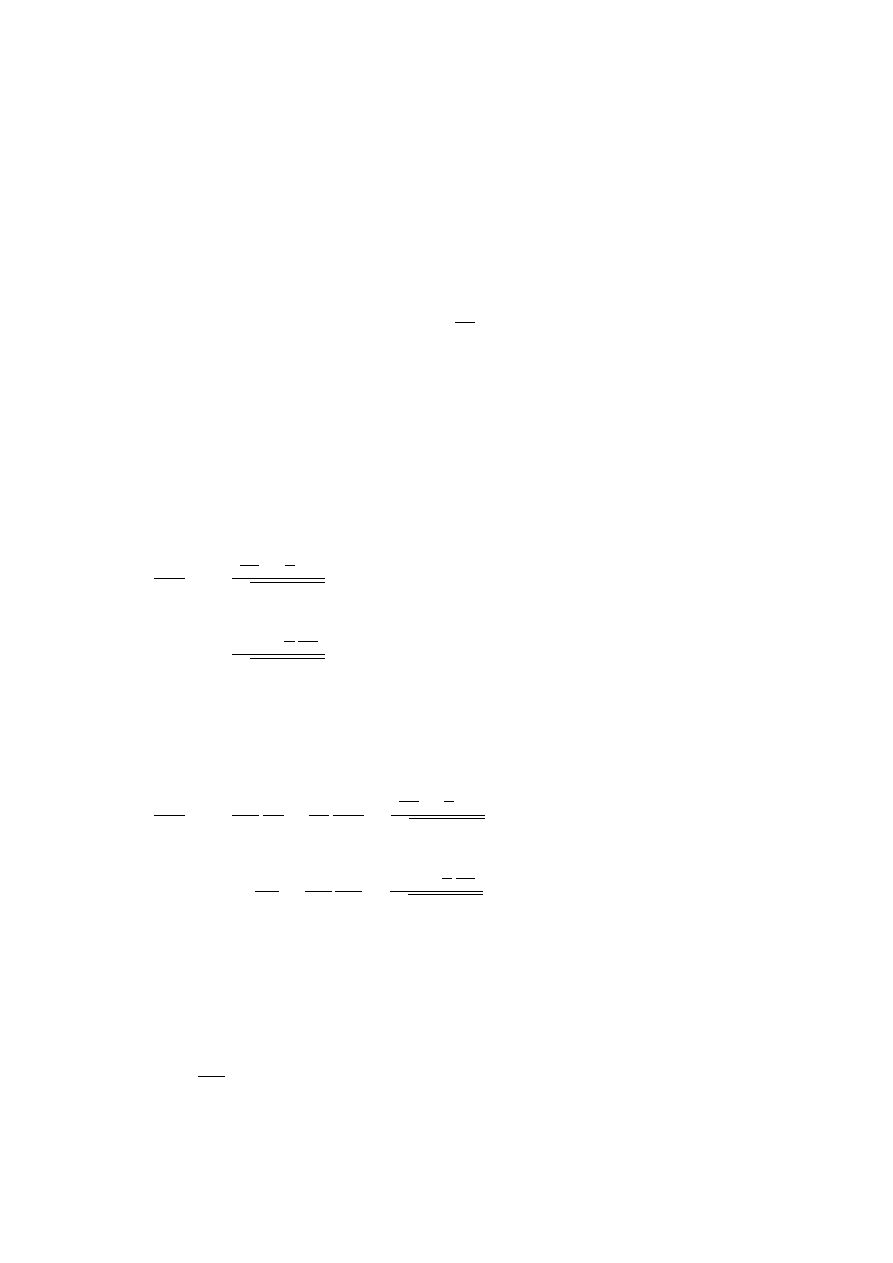
8.3.
W POSZUKIWANIU KOLEJNYCH CZTEROWEKTORÓW
93
8.3.1
C
ZTEROGRADIENT
P
oniewa˙z równania elektrodynamiki s ˛
a lokalnymi równaniami ró˙zniczkowymi, musimy si˛e naj-
pierw zastanowi´c w jaki sposób uogólni´c trójwymiarowy operator ró˙zniczkowy ∇, który w dzia-
łaniu na pole skalarne dawał pole wektorowe niezale˙zne od układu odniesienia. Podobnie, jak we
wcze´sniejszych rozdziałach wprowadzali´smy czteropoło˙zenie jako (ct, r), tak obecnie narzuca
si˛e nast˛epuj ˛
aca definicja czterogradientu: ¤ = (
∂
c ∂t
, ∇). Przekonajmy si˛e, czy tak zdefiniowany
obiekt posiada wymagane własno´sci, to znaczy czy zachodzi warunek:
¤ϕ(t, r) = ¤
0
ϕ(t
0
, r
0
).
(8.17)
Operator ¤
0
znajduj ˛
acy si˛e po lewej stronie równo´sci powinien transformowa´c si˛e jak przystało
na czterowektor:
∂
c ∂t
0
=
∂
c ∂t
−
V
c
∇
x
p
1 − V
2
/c
2
(8.18)
∇
0
x
=
∇
x
−
V
c
∂
c ∂t
p
1 − V
2
/c
2
.
Z drugiej strony, zwykłe zasady zamiany zmiennych przy ró˙zniczkowaniu wymagaj ˛
a by za-
chodził zwi ˛
azek
∂
c ∂t
0
=
∂
c ∂t
∂t
∂t
0
+
∂
∂x
∂x
c ∂t
0
=
∂
c ∂t
+
V
c
∇
x
p
1 − V
2
/c
2
(8.19)
∇
0
x
= ∇
x
∂x
∂x
0
+
∂
c ∂t
c ∂t
∂x
0
=
∇
x
+
V
c
∂
c ∂t
p
1 − V
2
/c
2
Wida´c, ˙ze z naszymi wzorami jest co´s nie tak, bo pojawia si˛e dodatkowy znak „−”. Wygl ˛
ada na
to, ˙ze nasz wybór czterogradientu nie był najlepszy. Jednak˙ze mo˙zemy w prosty sposób poprawi´c
nasz ˛
a definicj˛e otrzymuj ˛
ac operator transformuj ˛
acy si˛e jak nale˙zy. Wystarczy zdefiniowa´c:
¤ = (
∂
c ∂t
, −∇).
(8.20)

94
ROZDZIAŁ 8.
ELEKTRODYNAMIKA RELATYWISTYCZNA
Wida´c od razu, ˙ze ta definicja jest zgodna z transformacjami zamiany zmiennych ró˙zniczkowych
(8.19). Zatem powy˙zszy operator ¤ posiada odpowiednie własno´sci. Jest to wła´snie poszuki-
wany czterogradient.
8.3.2
C
ZTEROPR ˛
AD
W
ró´cmy ponownie do równa´n Maxwella. Jak wiemy, wynika z nich (lokalne) równanie ci ˛
agło´sci
ładunku elektrycznego:
∂%
∂t
+ ∇ · j = 0.
(8.21)
Oczywi´scie, równanie to wyra˙zaj ˛
ace lokaln ˛
a zasad˛e zachowania ładunku musi by´c spełnione
we wszystkich układach odniesienia. Matematycznie oznacza to, ˙ze posta´c tego równania nie
zmienia si˛e przy zmianie układu. Zwró´cmy uwag˛e, ˙ze lew ˛
a stron˛e tego równania mo˙zna za-
pisa´c jako czterowektorowy iloczyn czterogradientu i nast˛epuj ˛
acego nowego czterowektora j
¤
=
(c%, j):
¤j
¤
= 0.
(8.22)
I rzeczywi´scie, wszystko si˛e zgadza, bo wiemy ju˙z ˙ze iloczyn czterowektorów jest niezmienniczy
wzgl˛edem transformacji Lorentza. Znaczy to, ˙ze j
¤
jest rzeczywi´scie czterowektorem, nazy-
wanym czteropr ˛
adem. Jego „czasowa” składowa to g˛esto´s´c ładunku elektrycznego, a składowa
„przestrzenna” to g˛esto´s´c pr ˛
adu. Mo˙zemy zreszt ˛
a zauwa˙zy´c co´s ciekawego: jakakolwiek para
wielko´sci spełniaj ˛
acych równanie ci ˛
agło´sci we wszystkich układach inercjalnych musi tworzy´c
czterowektor. Czteropr ˛
ad jest tylko przykładem.
8.3.3
C
ZTEROPOTENCJAŁ
Z
apiszemy teraz równania Maxwella 8.1 w nieco zmienionej postaci. Dzi˛eki temu b˛edziemy
mogli zauwa˙zy´c co´s ciekawego. Przekonamy si˛e mianowicie jakie s ˛
a konsekwencje ich relaty-
wistycznej niezmienniczo´sci.
W tym celu, zamiast posługiwa´c si˛e polami E i B u˙zyjemy ich potencjałów. Z drugiego
z równa´n (8.1) wynika, ˙ze pole magnetyczne mo˙zna wyrazi´c jako rotacj˛e pola wektorowego:
B = ∇ × A. Wstawiaj ˛
ac to do trzeciego równania (8.1) dostajemy:
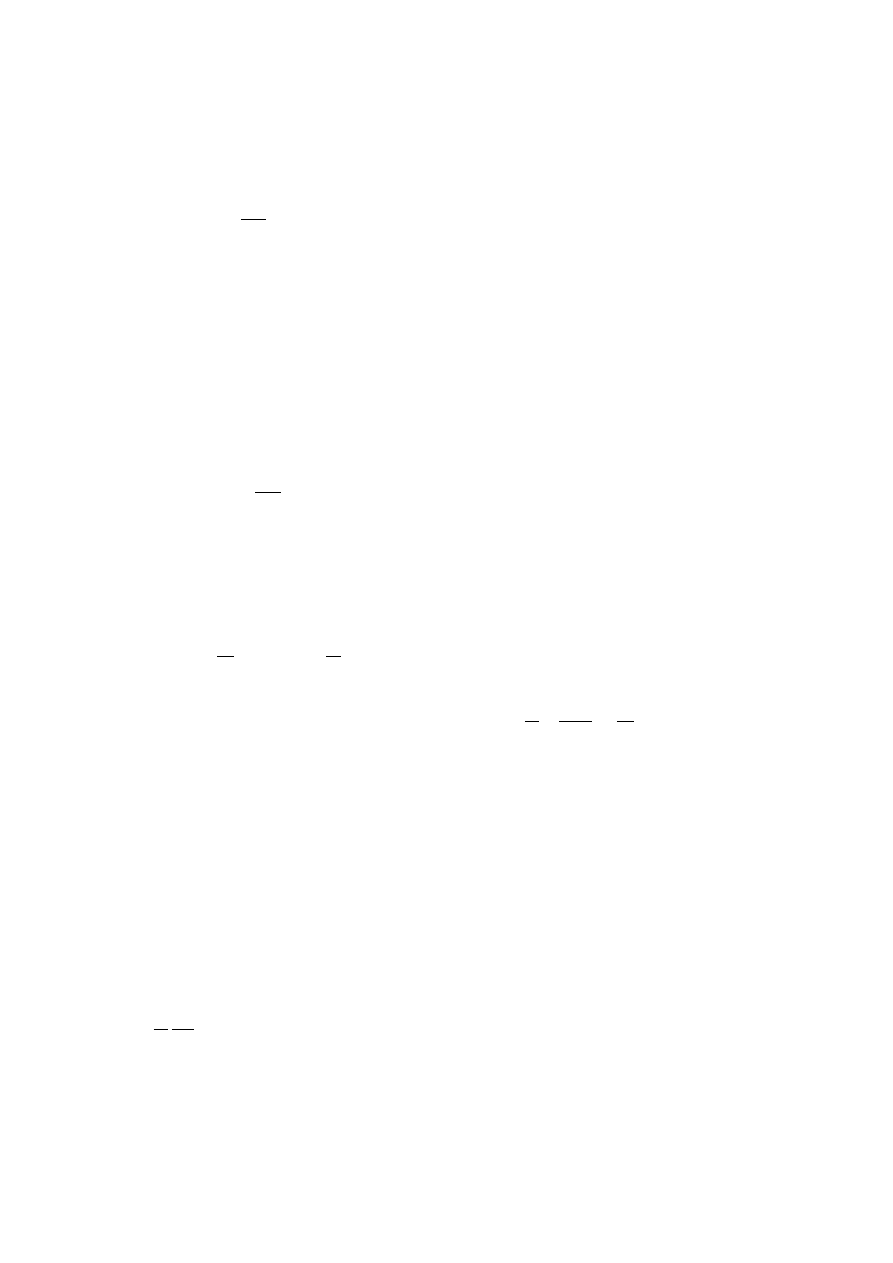
8.3.
W POSZUKIWANIU KOLEJNYCH CZTEROWEKTORÓW
95
∇ ×
µ
E +
∂A
∂t
¶
= 0
(8.23)
Poniewa˙z w przypadku elektrostatycznym rotacja pola elektrycznego znika, to zamiast niego
mo˙zemy posługiwa´c si˛e potencjałem skalarnym ϕ. Jest tak zawsze: ilekro´c rotacja jakiego´s pola
wektorowego znika, mo˙zemy równowa˙znie u˙zywa´c potencjału skalarnego z którego mo˙zemy
„odzyska´c” pole bior ˛
ac po prostu gradient. Wynika st ˛
ad, ˙ze wyra˙zenie znajduj ˛
ace si˛e pod ro-
tacj ˛
a w równaniu (8.23) mo˙zemy zast ˛
api´c (minus) gradientem pewnego potencjału skalarnego
ϕ. Wynika st ˛
ad, ˙ze:
E = −∇ϕ −
∂A
∂t
.
(8.24)
W szczególnym przypadku pól stałych w czasie dostajemy znany zwi ˛
azek E = −∇ϕ. Wsta-
wiaj ˛
ac wzór (8.24) do pozostałych dwóch równa´n Maxwella (8.1) dostajemy:
−4ϕ −
∂
∂t
∇ · A =
%
ε
0
∇ × (∇ × A) = ∇(∇ · A) − 4A = µ
0
j −
1
c
2
µ
∂
2
A
∂t
2
+
∂
∂t
∇ϕ
¶
.
Obydwa równania wygl ˛
adaj ˛
a teraz odra˙zaj ˛
aco. Zamiast obiecywanej prostoty mamy przed sob ˛
a
bardzo skomplikowanie wygl ˛
adaj ˛
ace wyra˙zenia. Jednak prostot˛e mo˙zna uzyska´c jednym spryt-
nym posuni˛eciem. Przypomnijmy sobie, ˙ze pole B nie okre´sla w sposób jednoznaczny potencja-
łu wektorowego A. Dowolno´s´c, która pozostaje, nazywana dowolno´sci ˛
a cechowania sprowadza
si˛e do faktu, ˙ze mo˙zemy narzuci´c dowolny warunek na dywergencj˛e potencjału wektorowego.
Aby upro´sci´c otrzymane wzory wybierzemy t˛e dywergencj˛e w bardzo szczególny sposób. Przyj-
miemy mianowicie warunek, zwany cechowaniem Lorentza:
1
c
2
∂ϕ
∂t
+ ∇ · A = 0.
(8.25)
Wówczas oba równania Maxwella uproszcz ˛
a si˛e do:

96
ROZDZIAŁ 8.
ELEKTRODYNAMIKA RELATYWISTYCZNA
µ
1
c
2
∂
2
∂t
2
− 4
¶
ϕ =
%
ε
0
(8.26)
µ
1
c
2
∂
2
∂t
2
− 4
¶
A =
j
c
2
ε
0
.
Nasze przekształcenia powoli zaczynaj ˛
a nabiera´c sensu. Teraz nast ˛
api rzecz najciekawsza. Otrzy-
mane wyra˙zenia mo˙zna zapisa´c w jeszcze prostszej postaci. Wystarczy wprowadzi´c nowy czterowek-
tor A
¤
= (
ϕ
c
, A), a wtedy mo˙zemy obydwa powy˙zsze równania zapisa´c jednym, czterowek-
torowym:
¤
2
A
¤
=
j
¤
c
2
ε
0
,
(8.27)
gdzie wykorzystali´smy zdefiniowany wcze´sniej operator ¤ (8.20). Wraz z warunkiem cechowa-
nia Lorentza i przepisem na wyra˙zanie pól E oraz B poprzez składowe czterowektora A
¤
,
mamy tu wszystkie równania Maxwella w jednym! Widzimy te˙z natychmiast, ˙ze je´sli A
¤
jest
rzeczywi´scie czterowektorem, to posta´c równania (8.27) nie zmienia si˛e przy przej´sciu do innego
układu inercjalnego. St ˛
ad za´s wynika, ˙ze równania Maxwella s ˛
a spełnione dla ka˙zdego obser-
watora inercjalnego. I czegó˙z jeszcze wi˛ecej pragn ˛
a´c od porz ˛
adnej teorii? A
¤
musi by´c zatem
czterowektorem. Nazywamy go czteropotencjałem.
8.4
T
RANSFORMACJE PÓL
S
koro A
¤
jest czterowektorem, to wiemy jak transformuje si˛e potencjał skalarny i wektorowy
przy zmianie układu odniesienia. Szukane przekształcenia s ˛
a po prostu transformacjami Lorentza.
Znaj ˛
ac własno´sci transformacyjne czteropotencjału powinni´smy równie˙z by´c w stanie odpowie-
dzie´c na kolejne pytanie: co dzieje si˛e z polem elektromagnetycznym przy zmianie układu?
W poprzednich rozdziałach otarli´smy si˛e ju˙z o ten problem. Doszli´smy wówczas do wniosku,
˙ze w ruchomym układzie mog ˛
a pojawi´c si˛e pola, których nie było w układzie spoczywaj ˛
acym.
W tym momencie mo˙zemy ju˙z zastanowi´c si˛e w jaki sposób wyznaczy´c te pola w sposób ogólny.
Poniewa˙z A
¤
jest czterowektorem, to przy przej´sciu do układu poruszaj ˛
acego si˛e z pr˛edko´sci ˛
a
V wzdłu˙z osi x, potencjały zmieniaj ˛
a si˛e zgodnie z wzorami Lorentza:

8.4.
TRANSFORMACJE PÓL
97
ϕ
0
(r
0
, t
0
) =
ϕ(r, t) − V A
x
(r, t)
p
1 − V
2
/c
2
(8.28)
A
0
x
(r
0
, t
0
) =
A
x
(r, t) − ϕ(r, t)/c
2
p
1 − V
2
/c
2
.
Widzimy, ˙ze poprawna transformacja wymaga przekształcenia nie tylko samych potencjałów,
ale tak˙ze współrz˛ednych od których te zale˙z ˛
a. Odpowied´z na pytanie o posta´c przetransfor-
mowanych pól wymaga ju˙z tylko odpowiedniego zró˙zniczkowania potencjałów. Pominiemy
szczegóły rachunkowe (zostawiamy je Czytelnikowi) i podamy od razu wynik:
E
0
x
= E
x
E
0
y
=
E
y
− V B
z
p
1 − V
2
/c
2
E
0
z
=
E
z
+ V B
y
p
1 − V
2
/c
2
(8.29)
B
0
x
= B
x
B
0
y
=
B
y
+ V E
z
/c
2
p
1 − V
2
/c
2
B
0
z
=
B
z
− V E
y
/c
2
p
1 − V
2
/c
2
gdzie opu´scili´smy w zapisie zale˙zno´s´c pól od odpowiednich współrz˛ednych (jest ona taka sama
jak we wzorach (8.28)).
Powy˙zsze, do´s´c skomplikowane wzory transformacyjne mo˙zemy te˙z zapisa´c w sposób bardziej
zwarty i ogólny:
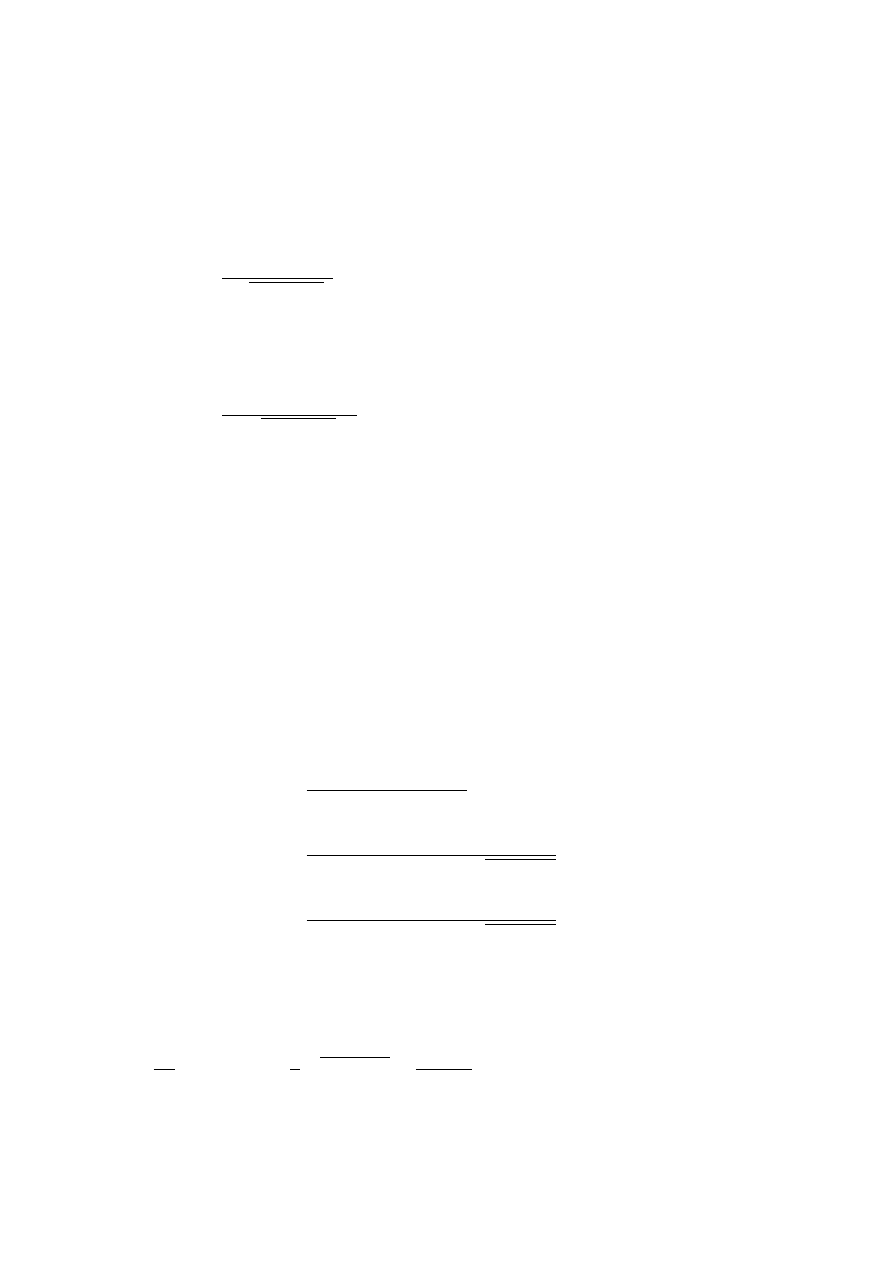
98
ROZDZIAŁ 8.
ELEKTRODYNAMIKA RELATYWISTYCZNA
E
0
q
= E
q
E
0
⊥
=
(E + V × B)
⊥
p
1 − V
2
/c
2
(8.30)
B
0
q
= B
q
B
0
⊥
=
(B − V × E/c
2
)
⊥
p
1 − V
2
/c
2
.
Widzimy teraz, jak na dłoni, ˙ze składowe pól równoległe do kierunku pr˛edko´sci nie zmieniaj ˛
a
si˛e, w przeciwie´nstwie do składowych poprzecznych. To spostrze˙zenie jest jednak nie do ko´nca
słuszne. Pami˛etajmy bowiem, ˙ze niezale˙znie od transformacji pól, nale˙zy tak˙ze przekształci´c
współrz˛edne.
Mo˙zemy to prze´sledzi´c na konkretnym przypadku. Rozwa˙zmy pole elektryczne ładunku
punktowego poruszaj ˛
acego si˛e ze stał ˛
a pr˛edko´sci ˛
a v wzdłu˙z osi x. Pole to mo˙zemy znale´z´c trans-
formuj ˛
ac pole ładunku spoczywaj ˛
acego w układzie nieprimowanym o współrz˛ednych x, y, z, t do
układu o współrz˛ednych primowanych x
0
, y
0
, z
0
, t
0
poruszaj ˛
acego si˛e z pr˛edko´sci ˛
a −v (wyj ˛
atkowo
w tym wykładzie przyj˛eta została notacja odwrotna do dotychczas stosowanej - układ primowany
porusza si˛e z pr˛edko´sci ˛
a −v, a nie v):
E
0
x
(x
0
, y
0
, z
0
, t
0
) =
qx
4πε
0
(x
2
+ y
2
+ z
2
)
3/2
E
0
y
(x
0
, y
0
, z
0
, t
0
) =
qy
4πε
0
(x
2
+ y
2
+ z
2
)
3/2
p
1 − v
2
/c
2
(8.31)
E
0
z
(x
0
, y
0
, z
0
, t
0
) =
qz
4πε
0
(x
2
+ y
2
+ z
2
)
3/2
p
1 − v
2
/c
2
,
gdzie współrz˛edne nieprimowane nale˙zy traktowa´c jako funkcje współrz˛ednych primowanych.
Zwró´cmy uwag˛e, ˙ze:
E
0
x
E
0
y
(x
0
, y
0
, z
0
, t
0
) =
x
y
p
1 − v
2
/c
2
=
x
0
− vt
0
y
0
,
(8.32)
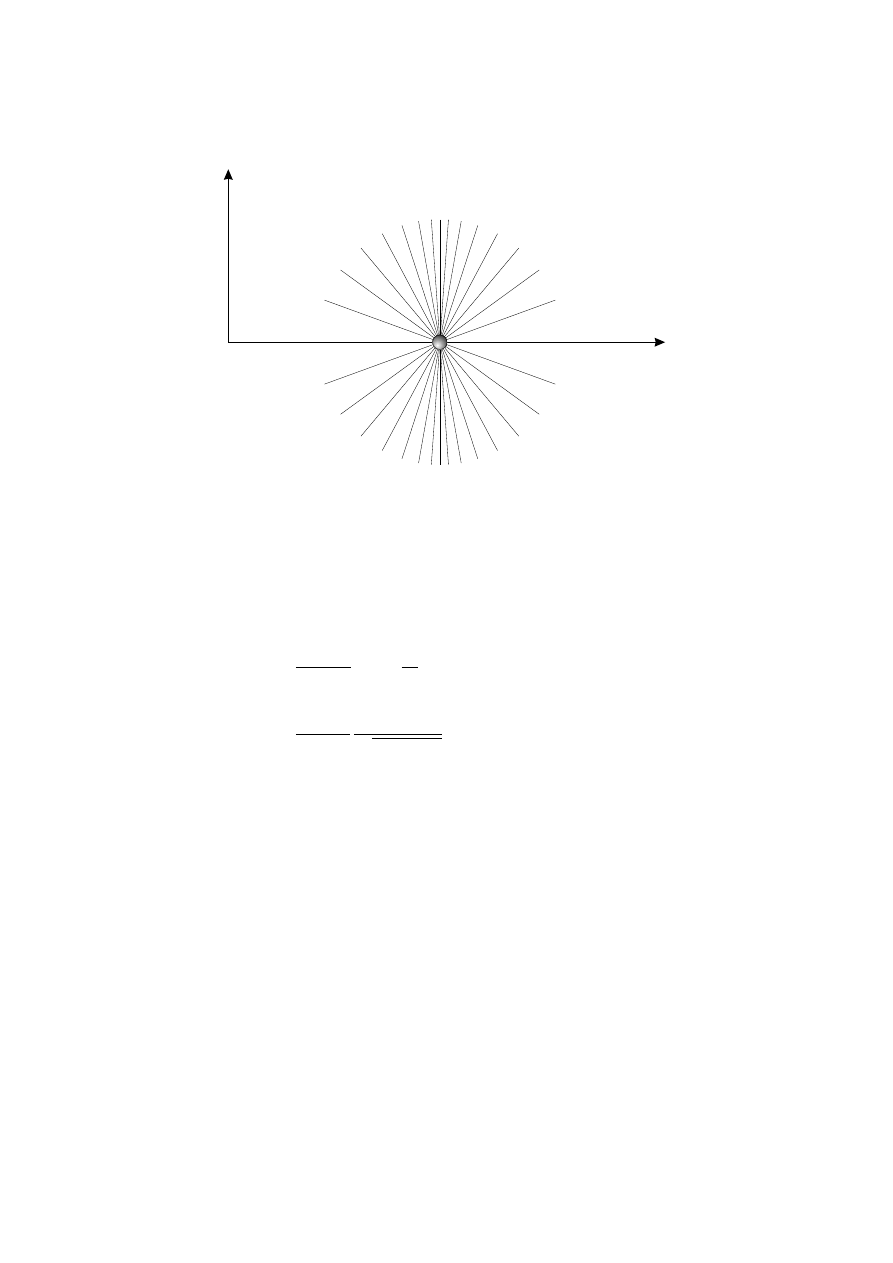
8.5.
RELATYWISTYCZNA SIŁA LORENTZA I ŁAMANIE III ZASADY NEWTONA99
x
y
Rysunek 8.2:
Linie pola elektrycznego ładunku poruszaj ˛
acego si ˛e ze stał ˛
a pr ˛edko´sci ˛
a wzdłu˙z osi
x
.
czyli pole poruszaj ˛
acego si˛e ładunku jest skierowane radialnie. Jednak˙ze pole wzdłu˙z toru ruchu
jest słabsze ni˙z pole w płaszczy´znie prostopadłej:
E
0
x
(x
0
, 0, 0, 0) =
q
4πε
0
x
02
µ
1 −
v
2
c
2
¶
(8.33)
E
0
y
(0, y
0
, 0, 0) =
q
4πε
0
y
02
1
p
1 − v
2
/c
2
.
Jest jednak jeszcze ciekawiej. Pole elektryczne ruchomego ładunku jest dokładnie takie, jak
gdyby cała przestrze´n razem z polem uległa skróceniu Lorentza! - rysunek 8.2. Powiedzieli´smy
„jak gdyby”, bo nie mo˙zemy wyobra˙za´c sobie, ˙ze pole elektromagnetyczne ruchomego ładunku
po prostu si˛e „´sciska”. Pami˛etajmy, ˙ze pojawia si˛e dodatkowe pole magnetyczne, którego nie ma
gdy ładunek spoczywa. Pole to „okr ˛
a˙za” prost ˛
a po której porusza si˛e ładunek, a na samej osi jest
równe zeru.
8.5
R
ELATYWISTYCZNA SIŁA
L
ORENTZA I ŁAMANIE
III
ZA
-
SADY
N
EWTONA
W
iemy ju˙z co nieco na temat pola elektromagnetycznego. Do pełni szcz˛e´scia brakuje nam ju˙z
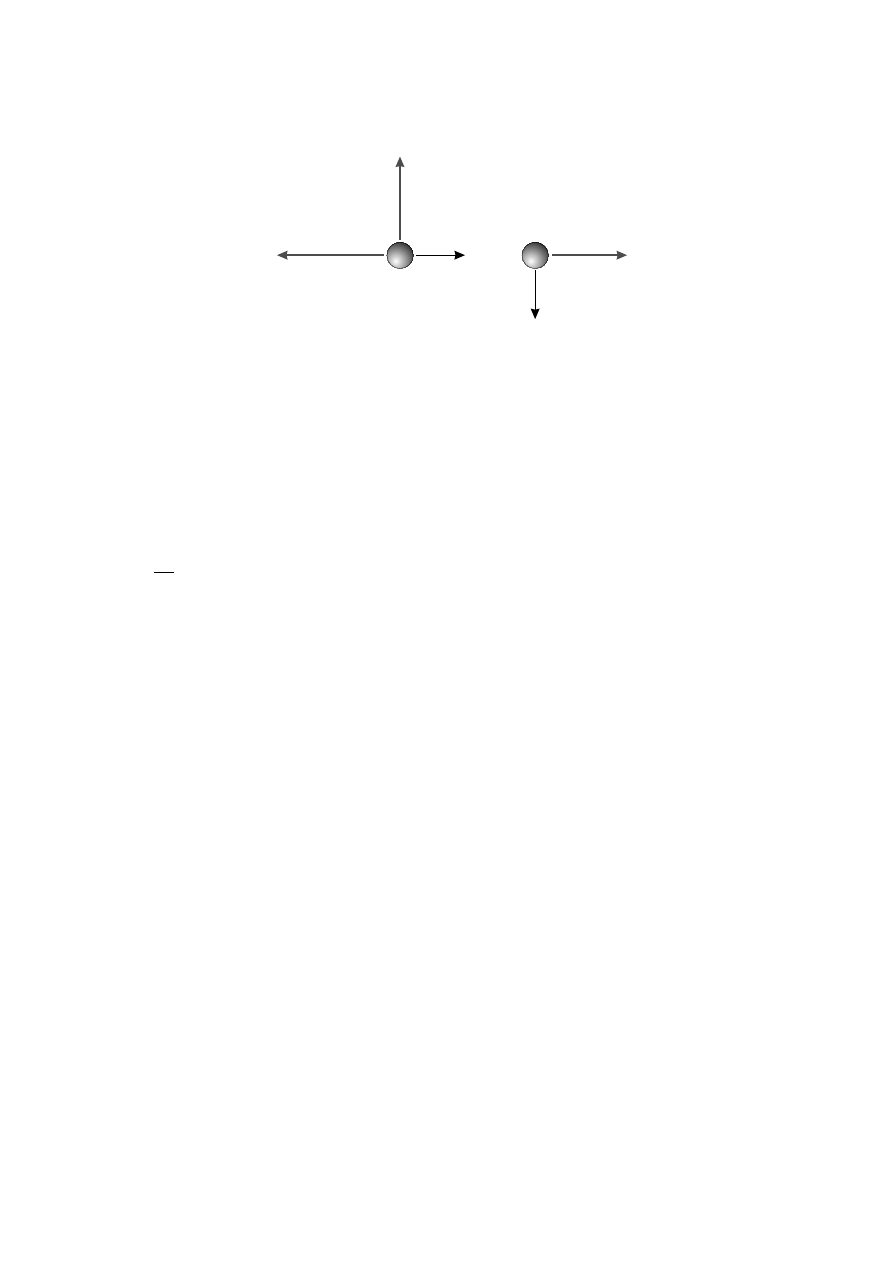
100
ROZDZIAŁ 8.
ELEKTRODYNAMIKA RELATYWISTYCZNA
V
V
F
F
F
1
2
3
Rysunek 8.3:
Czy III prawo Newtona jest łamane?
tylko wiedzy na temat tego w jaki sposób pole to wpływa na dynamik˛e ładunków elektrycznych.
Nie b˛edzie chyba niespodziank ˛
a II prawo Newtona (7.16) dla ładunku q umieszczonego w polu
E i B:
dp
dt
= q(E + v × B),
(8.34)
gdzie v jest pr˛edko´sci ˛
a ładunku w rozwa˙zanym układzie inercjalnym. Jest to po prostu siła
Lorentza, podobnie jak równania Maxwella, od pocz ˛
atku relatywistyczna.
Na koniec tego rozdziału podamy interesuj ˛
acy „paradoks”. Wyobra´zmy sobie dwa ładunki q
poruszaj ˛
ace si˛e jednostajnie wzdłu˙z prostopadłych prostych - rysunek 8.3. W rozwa˙zanej chwili
ładunek poruszaj ˛
acy si˛e pionowo akurat przecina tor ładunku poruszaj ˛
acego si˛e poziomo. Py-
tamy ile wynosz ˛
a siły działaj ˛
ace na oba ładunki. Udzielenie odpowiedzi nie jest trudne, bo
znamy wzór Lorentza oraz pole elektromagnetyczne poruszaj ˛
acego si˛e ładunku.
Siła działaj ˛
aca na ładunek poruszaj ˛
acy si˛e w dół jest czysto elektryczna, bo pole magnetyczne
na osi ruchu ładunku poruszaj ˛
acego si˛e poziomo znika. Na rysunku 8.3 jest to siła F
2
. Na drugi
ładunek działa analogiczna siła elektryczna F
1
, ale jej warto´s´c musi by´c wi˛eksza, gdy˙z pole
elektryczne w płaszczy´znie prostopadłej do ruchu jest silniejsze ni˙z wzdłu˙z toru - wzory (8.33).
Pojawia si˛e jeszcze dodatkowa siła magnetyczna F
3
działaj ˛
aca na ładunek poruszaj ˛
acy si˛e w
prawo. Działa ona prostopadle do obu pozostałych sił. Czy˙zby wi˛ec III prawo Newtona w teorii
wzgl˛edno´sci nie obowi ˛
azywało? Przypomnijmy w tym miejscu twierdzenie Noether: z symetrii
przestrzeni wzgl˛edem przesuni˛e´c musi wynika´c prawo zachowania p˛edu, z którego za´s wynika
III prawo Newtona. Rozwi ˛
azanie paradoksu pozostawiamy Czytelnikowi na długie, zimowe
wieczory...

8.5.
RELATYWISTYCZNA SIŁA LORENTZA I ŁAMANIE III ZASADY NEWTONA101
Pytania
Zadania
• W inercjalnym układzie odniesienia, w niesko´nczenie długim, prostoliniowym i oboj˛et-
nym elektrycznie przewodniku o polu przekroju poprzecznego S płynie pr ˛
ad o nat˛e˙zeniu
I. Oblicz pole elektromagnetyczne wytworzone przez przewodnik, a nast˛epnie dokonaj
transformacji tego pola do układu odniesienia poruszaj ˛
acego si˛e wzdłu˙z przewodnika z
pr˛edko´sci ˛
a V . Udowodnij, ˙ze identyczny wynik mo˙zna uzyska´c transformuj ˛
ac ´zródła pól
(g˛esto´sci ładunków oraz pr ˛
ady), a nast˛epnie obliczaj ˛
ac dla nich pola w nowym układzie.
• W inercjalnym układzie odniesienia, w niesko´nczenie długim, prostoliniowym i oboj˛etnym
elektrycznie przewodniku o polu przekroju poprzecznego S płynie pr ˛
ad o nat˛e˙zeniu I.
W pewnej odległo´sci d porusza si˛e z pr˛edko´sci ˛
a V prostopadł ˛
a do kierunku przepływu
pr ˛
adu ładunek q. Oblicz pole sił˛e oddziaływania przewodnika na ładunek, a nast˛epnie
podaj wynik w układzie zwi ˛
azanym z ładunkiem. Czy bez wykonywania oblicze´n mo˙zna
powiedzie´c sk ˛
ad si˛e bierze siła w drugim układzie?

102
ROZDZIAŁ 8.
ELEKTRODYNAMIKA RELATYWISTYCZNA

Rozdział 9
N
IESPODZIANKA
9.1
S
K ˛
AD SI ˛
E BIERZE TRANSFORMACJA
L
ORENTZA
?
1
N
a zako´nczenie wykładu zostawili´smy sobie nie lada niespodziank˛e. Pewnie ju˙z zd ˛
a˙zyli´scie si˛e
przyzwyczai´c do tego, ˙ze wszystkie dziwne rzeczy zwi ˛
azane z teori ˛
a wzgl˛edno´sci, wynikaj ˛
ace z
niezwykłego charakteru transformacji Lorentza bior ˛
a si˛e z zało˙zenia, ˙ze ´swiatło w pró˙zni porusza
si˛e zawsze ze stał ˛
a pr˛edko´sci ˛
a równ ˛
a c (albo wr˛ecz bezpo´srednio z postaci równa´n Maxwella).
Przez cały ten wykład byli´smy zaskakiwani konsekwencjami tego faktu. Czeka nas tym razem
by´c mo˙ze jeszcze wi˛eksze zaskoczenie. Czy bowiem, gdyby elektrodynamika nie istniała i nie
byłoby ´swiatła, teoria wzgl˛edno´sci tak˙ze nie mogłaby istnie´c? A mo˙ze by mogła?
Przekonamy si˛e, ˙ze istnienie fundamentalnej stałej przyrody - pr˛edko´sci c, która nie zale˙zy od
układu odniesienia mo˙zna wydedukowa´c w elementarny sposób z pewnych do´s´c „oczywistych”
zało˙ze´n, mi˛edzy innymi z zasady demokracji. Jak pami˛etacie zasada ta mówi, ˙ze prawa przyrody
we wszystkich układach inercjalnych s ˛
a jednakowe, czyli nie da si˛e stwierdzi´c „bezwzgl˛ednego
ruchu” wykonuj ˛
ac jakikolwiek eksperyment. Zasad˛e t˛e wielokrotnie stosowali´smy przy ró˙znych
okazjach i kto´s z Was mógłby powiedzie´c, ˙ze nie ma w niej niczego niezwykłego. W niniejszym
rozdziale b˛edziecie mieli szans˛e zmieni´c zdanie...
Powró´cmy zatem do samego pocz ˛
atku i spójrzmy na rysunek 1.1 od którego rozpocz˛eli´smy
cał ˛
a podró˙z. Rozpatrzmy nast˛epuj ˛
ace zagadnienie: mamy dwa inercjalne układy odniesienia,
poruszaj ˛
ace si˛e wzgl˛edem siebie z pr˛edko´sci ˛
a V i chcemy dowiedzie´c si˛e jak wygl ˛
ada transfor-
macja współrz˛ednych przestrzennych i czasów pomi˛edzy tymi układami. W pierwszym rozdziale
1
Pomysł wyprowadzenia transformacji Lorentza przedstawion ˛
a metod ˛
a został omówiony w referencjach [8].
103

104
ROZDZIAŁ 9.
NIESPODZIANKA
powiedzieli´smy, ˙ze taka transformacja powinna by´c liniowa i ˙ze jeszcze do tego wrócimy. Jest
teraz dobry moment, ˙zeby skupi´c si˛e na tym problemie. Dlaczego transformacja powinna by´c
liniowa? Z jakiego fundamentalnego prawa przyrody to niby wynika? Dowiemy si˛e tego na-
jpewniej sprawdzaj ˛
ac co by było, gdyby transformacja nie była liniowa we współrz˛ednych albo
w czasie. Wówczas bowiem przesuwaj ˛
ac pocz ˛
atek układu współrz˛ednych, albo przestawiaj ˛
ac ze-
garek, musieliby´smy zmieni´c cał ˛
a transformacj˛e, w innym wypadku transformacja „działałaby”
inaczej ni˙z przed przesuni˛eciem! To znaczy, ˙ze nieliniowa transformacja odró˙zniałaby ró˙zne
chwile czasu, albo ró˙zne punkty przestrzeni. Gdyby´smy na przykład przenie´sli cały wszech´swiat
w jakim´s kierunku o jeden metr, albo w czasie o jedn ˛
a sekund˛e, operacja ta nie powinna zmieni´c
niczego w dynamice wszech´swiata. Nie powinno to wpłyn ˛
a´c na wyniki ˙zadnych eksperymen-
tów. Podobnie jak jedyn ˛
a krzyw ˛
a, która nie wyró˙znia ˙zadnego punktu jest prosta, tak jedyn ˛
a
transformacj ˛
a „nieczuł ˛
a” na translacje jest transformacja liniowa. Oto cały powód.
Zatem z zało˙zenia jednorodno´sci czasoprzestrzeni płynie wniosek, ˙ze transformacja współ-
rz˛ednych musi by´c liniowa. Wyra´zmy zatem współrz˛edn ˛
a przestrzenn ˛
a x
0
w nowym układzie
inercjalnym (poruszaj ˛
acym si˛e tradycyjnie z pr˛edko´sci ˛
a V wzdłu˙z osi x) poprzez współrz˛edne i
czas w nieruchomym układzie:
x
0
= A(V ) x + B(V ) t.
(9.1)
Współczynniki A(V ) i B(V ) mog ˛
a zale˙ze´c oczywi´scie tylko od pr˛edko´sci wzgl˛ednej układów.
Na przykład dla transformacji Galileusza mamy: A = 1 i B = −V . Jednak˙ze na razie nie
znamy zale˙zno´sci współczynników transformacji A i B od pr˛edko´sci V . Wiemy jednak (zasada
demokracji), ˙ze transformacja odwrotna musi by´c postaci:
x = A(−V ) x
0
+ B(−V ) t
0
.
(9.2)
Co mo˙zemy powiedzie´c o ogólnej postaci A i B? Wyobra´zmy sobie, ˙ze kierunek czasu został
odwrócony: t 7→ −t. Wówczas, je˙zeli zamienimy dodatkowo V 7→ −V , to sytuacja (a zatem
i transformacja) nie powinna si˛e zmieni´c. Poniewa˙z po wprowadzeniu zmian znaków równanie
(9.1) przechodzi w:
x
0
= A(−V ) x − B(−V ) t,
(9.3)
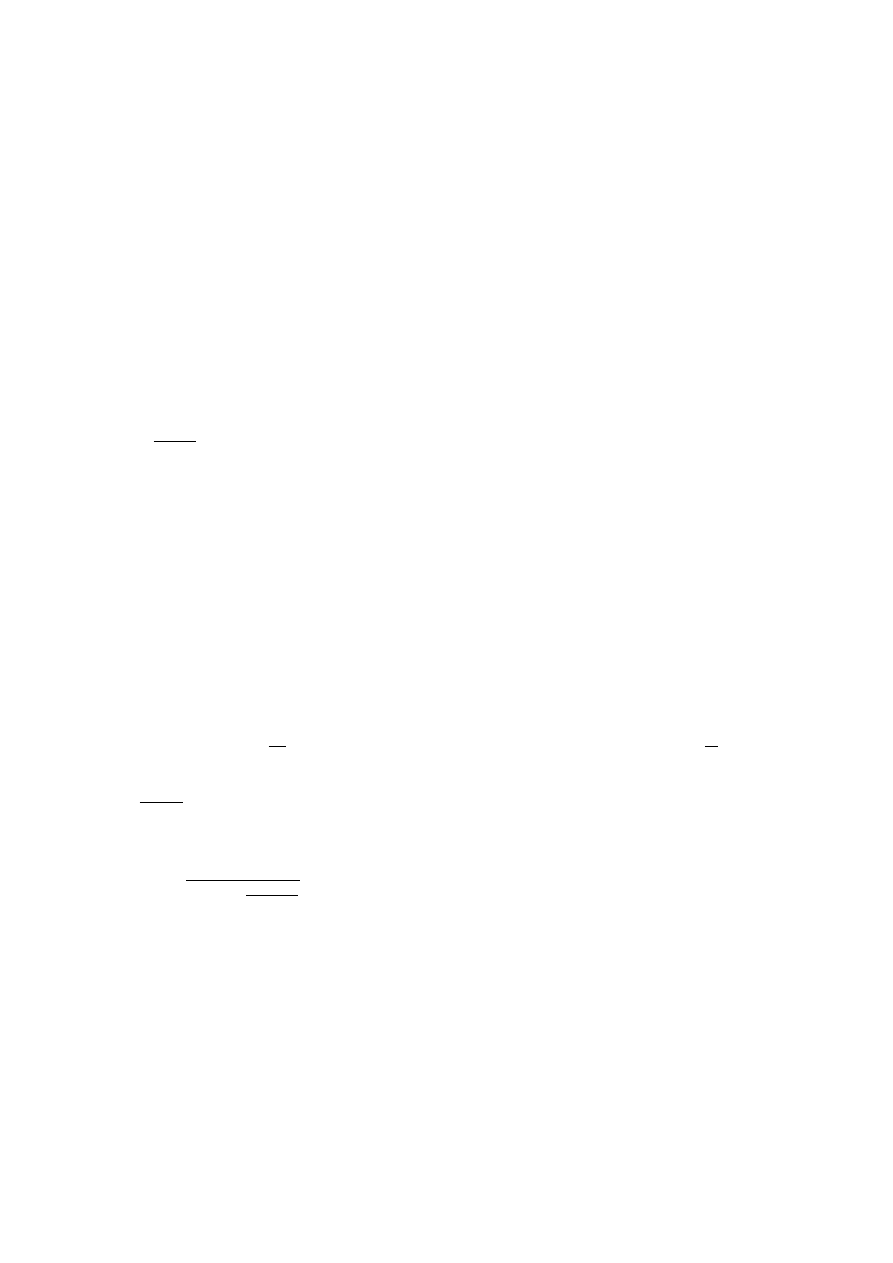
9.1.
SK ˛
AD SI ˛
E BIERZE TRANSFORMACJA LORENTZA?
2
105
otrzymujemy st ˛
ad dwa warunki:
A(−V ) = A(V )
(9.4)
B(−V ) = −B(V ).
Je˙zeli teraz rozwa˙zymy pocz ˛
atek układu primowanego x
0
= 0, którego równaniem ruchu w
układzie nieprimowanym jest x = V t, dostaniemy z równania (9.1) kolejny warunek:
B(V )
A(V )
= −V.
(9.5)
Mo˙zemy zatem przepisa´c równania (9.1) i (9.2) w nast˛epuj ˛
acej postaci:
x
0
= A(V )(x − V t)
x
= A(V )(x
0
+ V t
0
).
(9.6)
Z powy˙zszego układu równa´n mo˙zemy teraz wyprowadzi´c wzór transformacyjny dla pr˛edko´sci
jakiego´s punktu widzianego w dwóch układach inercjalnych. Wzór ten znajdziemy w taki sam
sposób w jaki zrobili´smy to w rozdziale 2.9. Powiedzmy, ˙ze w układzie primowanym co´s porusza
si˛e z pr˛edko´sci ˛
a v
0
=
dx
0
dt
0
. Szukamy odpowiedzi na pytanie z jak ˛
a pr˛edko´sci ˛
a v =
dx
dt
obiekt ten
b˛edzie poruszał si˛e w układzie nieprimowanym. Z pierwszego z równa´n (9.6) wyznaczamy
t =
x−x
0
/A
V
dzi˛eki czemu znajdujemy, ˙ze:
v =
v
0
+ V
1 + v
0
V
A
2
(V )−1
V
2
A
2
(V )
.
(9.7)
Wzór ten przypomina troch˛e relatywistyczny wzór odwrotny do (2.16). Wkrótce podobie´nstwo
stanie si˛e jeszcze bardziej uderzaj ˛
ace. Skorzystajmy raz jeszcze z zasady demokracji układów
inercjalnych. W rozwa˙zanej sytuacji mamy do czynienia z trzema obiektami: punktem, który
oddala si˛e z pr˛edko´sci ˛
a v
0
od pocz ˛
atku układu primowanego, który oddala si˛e z kolei z pr˛ed-
ko´sci ˛
a V od pocz ˛
atku układu nieprimowanego. Znaleziona pr˛edko´s´c v jest pr˛edko´sci ˛
a odda-
lania rozwa˙zanego punktu od pocz ˛
atku układu nieprimowanego. Zauwa˙zmy jednak, ˙ze je˙zeli
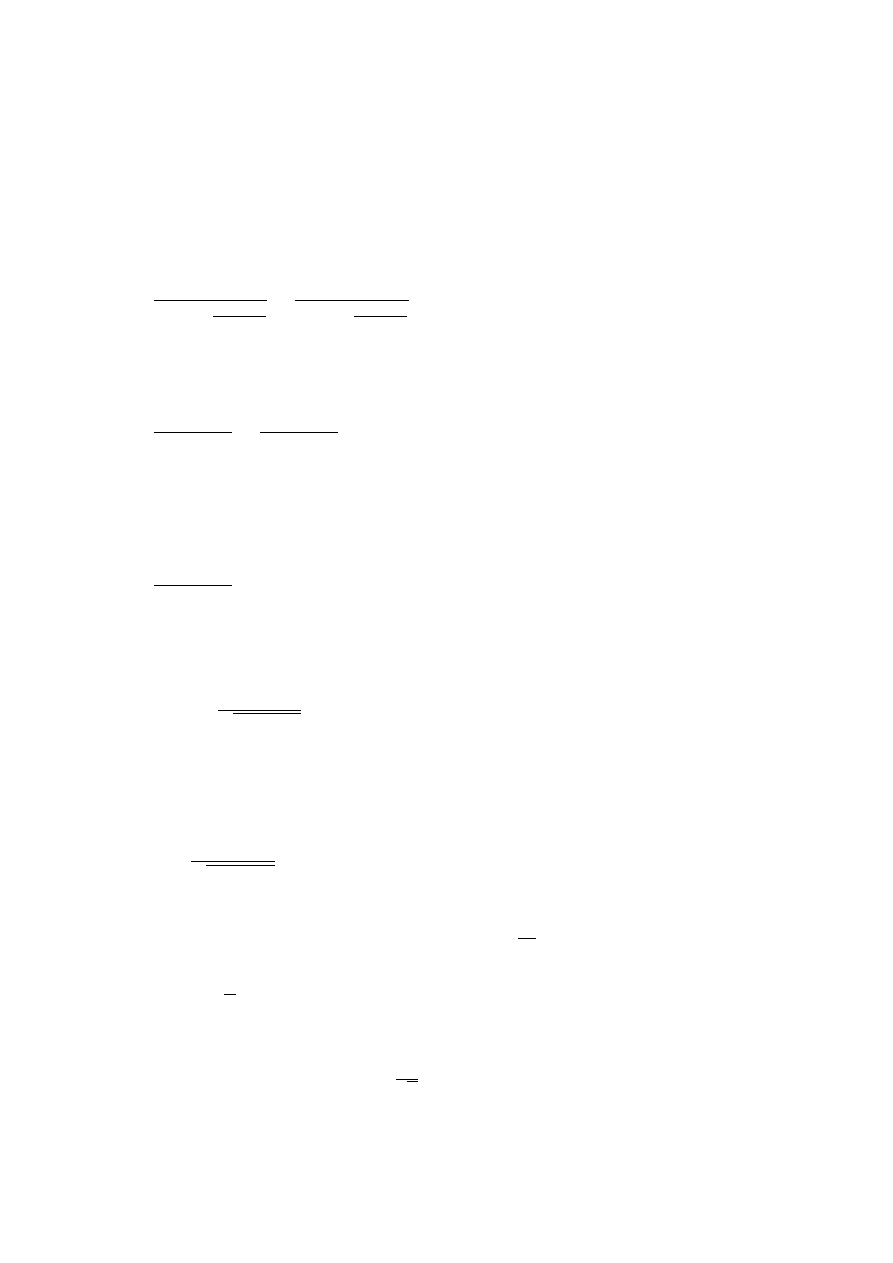
106
ROZDZIAŁ 9.
NIESPODZIANKA
odwrócimy role i zamienimy v
0
↔ V , to warto´s´c v nie powinna si˛e zmieni´c. Dlaczego? Dlat-
ego, ˙ze rozwa˙zany punkt porusza si˛e wzgl˛edem pocz ˛
atku układu nieprimowanego z tak ˛
a sam ˛
a
pr˛edko´sci ˛
a co ów pocz ˛
atek wzgl˛edem rozwa˙zanego punktu. Wynika st ˛
ad, ˙ze:
v
0
+ V
1 + v
0
V
A
2
(V )−1
V
2
A
2
(V )
=
V + v
0
1 + V v
0 A
2
(v
0
)−1
v
02
A
2
(v
0
)
,
(9.8)
z czego z kolei musi wynika´c, ˙ze
A
2
(V ) − 1
V
2
A
2
(V )
=
A
2
(v
0
) − 1
v
02
A
2
(v
0
)
.
(9.9)
Poniewa˙z jest to równo´s´c pewnej funkcji pr˛edko´sci w dwóch, dowolnych „punktach” V oraz v
0
,
oznacza to, ˙ze funkcja ta musi by´c stała:
A
2
(V ) − 1
V
2
A
2
(V )
= K.
(9.10)
Z tego warunku mo˙zemy bez trudu wyznaczy´c zale˙zno´s´c A(V ):
A(V ) =
1
√
1 − KV
2
.
(9.11)
Wstawiaj ˛
ac otrzymany wynik do pierwszego z równa´n (9.6) otrzymujemy w niespodziewany
sposób transformacj˛e Lorentza!
x
0
=
x − V t
√
1 − KV
2
.
(9.12)
Wygl ˛
ada na to, ˙ze wydarzył si˛e cud! Udało nam si˛e stwierdzi´c, ˙ze z zasady demokracji wynika
istnienie pewnej fundamentalnej stałej K, o wymiarze
s
2
m
2
, czyli odwrotno´sci kwadratu pr˛ed-
ko´sci! Nie potrafimy co prawda stałej tej obliczy´c i mo˙ze ona by´c równa zeru (jak w transforma-
cji Galileusza),
1
c
2
(jak w transformacji Lorentza) albo dowolnej innej warto´sci. Stał ˛
a t˛e mo˙zna
po prostu wyznaczy´c z do´swiadczenia. Cała reszta teorii wzgl˛edno´sci w zasadzie wynika, jak
ju˙z doskonale wiecie z transformacji współrz˛ednych. Jednym z wniosków jest oczywi´scie, ˙ze
„nic nie mo˙ze porusza´c si˛e szybciej ni˙z
1
√
K
” (patrz rozdział 1.4).

9.1.
SK ˛
AD SI ˛
E BIERZE TRANSFORMACJA LORENTZA?
3
107
W tym miejscu mogliby´smy ju˙z zako´nczy´c, gdyby nie fakt, ˙ze niemal˙ze przeoczyli´smy co´s
istotnego. Zwró´ccie uwag˛e, ˙ze nasza ogólniejsza posta´c transformacji pozwala przyj ˛
a´c tak˙ze
K < 0. Je˙zeli podstawimy K = −
1
c
2
, otrzymany układ równa´n transformacyjnych b˛edzie
postaci:
t
0
=
t
0
+V x
0
/c
2
√
1+V
2
/c
2
x
0
=
x
0
−V t
0
√
1+V
2
/c
2
.
(9.13)
Czy tego typu transformacja tak˙ze mogłaby opisywa´c ´swiat? Zapewne spełnia ona narzucone
przez nas warunki: zasad˛e demokracji oraz jednorodno´s´c czasoprzestrzeni. Có˙z zatem sprawia,
˙ze prawdziwa transformacja zawiera dodatni ˛
a stał ˛
a K? I co by było, gdyby K była ujemna?
Z pewno´sci ˛
a mo˙zna by udzieli´c odpowiedzi przynajmniej na ostatnie pytanie. Przypomnij-
my sobie, jak na pocz ˛
atku wykładu, w rozdziale 1.6 powiedzieli´smy, ˙ze stało´s´c interwału cza-
soprzestrzennego jest bardzo wa˙zna, bo dzi˛eki niej ´swiat mo˙ze zosta´c opisany przez szczególn ˛
a
teori˛e wzgl˛edno´sci w sposób deterministyczny. Okazuje si˛e, ˙ze teoria z ujemn ˛
a warto´sci ˛
a K
nie posiada tej wa˙znej własno´sci. Gdyby K było ujemne, kolejno´s´c nast˛epstw pozornie „przy-
czynowego” ci ˛
agu zdarze´n zale˙załaby od układu odniesienia. Poniewa˙z jednak na zbadanie tak
dziwnej teorii musieliby´smy po´swi˛eci´c kolejny skrypt, zadanie to pozostawimy Czytelnikowi.
Pytania
Zadania

108
ROZDZIAŁ 9.
NIESPODZIANKA

Bibliografia
[1] L. D. Landau i E. M. Lifszyc, Teoria Pola (PWN, Warszawa 1958).
[2] W. Rindler, Length Contraction Paradox, Amer. J. Phys. 29, 365 (1961).
[3] R. P. Feynman, Elementary Particles and the Laws of Physics (Cambridge University Press,
Cambridge 1995).
[4] A. Nowojewski, J. Kallas i A. Dragan, On the appearance of moving bodies, Amer. Math.
Month. 11 (2004); A. Nowojewski, J. Kallas i A. Dragan, O wygl ˛
adzie ciał w ruchu, Delta
(2003).
[5] M. L. Boas, Apparent Shape of Large Objects at Relativistic Speeds, Amer. J. Phys. 5, 283
(1961).
[6] G. D. Scott i H. J. Van Driel, Geometrical Appearances at Relativistic Speeds, Amer. J.
Phys. 38, 971 (1970).
[7] R. P. Feynman, Feynmana wykłady z fizyki (PWN, Warszawa 2001), tom II.
[8] P. Frank i H. Rothe, Über die Transformation der Raumzeitkoordinaten von ruhenden
auf bewegte Systeme, Ann. der Phys. 339, 825 (1911); A. Szymacha, Przestrze´n i ruch
(Wydawnictwo Uniwersytetu Warszawskiego, Warszawa 1997).
109
Wyszukiwarka
Podobne podstrony:
Niezwykle szczegolna teoria względności
Szczególna teoria względności Einstaina, Fizyka
szczególna teoria względności, Fizyka - hasło fizyka, Fizyka(1)
pawlikowski, fizyka, szczególna teoria względności
einstein-teoria-fiza, SZCZEGÓLNA TEORIA WZGLĘDNOŚCI - szybkość światła C w próżni jest jednakowa dla
9 szczegolna teoria wzglednosci Nieznany (2)
07 Szczegolna teoria wzglednosci
Logunow, Czugriew Szczególna teoria względności i efekt Sagnaca
,fizyka2,Szczególna teoria względności
SZCZEGÓLNA TEORIA WZGLĘDNOŚCI
Szczególna teoria względności 2
49 SZCZEGÓLNA TEORIA WZGLĘDNOŚCI 21 05 2006 r
SZCZEGÓLNA TEORIA WZGLĘDNOŚCI CZY NADAL OBOWIĄZUJE
Co to jest teoria względności podstawy geometryczne
F3 teoria wzglednosci
więcej podobnych podstron