1

Postulaty szczególnej teorii względności

Dla wszystkich obserwatorów w inercjalnych układach odniesienia prawa fizyki
są takie same – żaden z układów nie jest wyróżniony.

We wszystkich inercjalnych układach odniesienia i we wszystkich kierunkach
światło rozchodzi się w próżni z taką samą prędkością c=299792458 m/s.
Prędkość żadnego ciała przenoszącego energię lub informacje nie może
przekroczyć prędkości granicznej.

Potwierdzenie doświadczalne (CERN, 1964):
-mimo zwiększania energii kinetycznej elektronów, ich
prędkość nie przekracza prędkości światła
-prędkość światła wyemitowanego przez źródło
poruszające się z prędkością bliską c wynosi zawsze c
– tyle samo, co dla źródła w spoczynku.

Transformacja Galileusza i Lorentza

Galileusza (u<<c)

Lorentza (v

∼c)

2

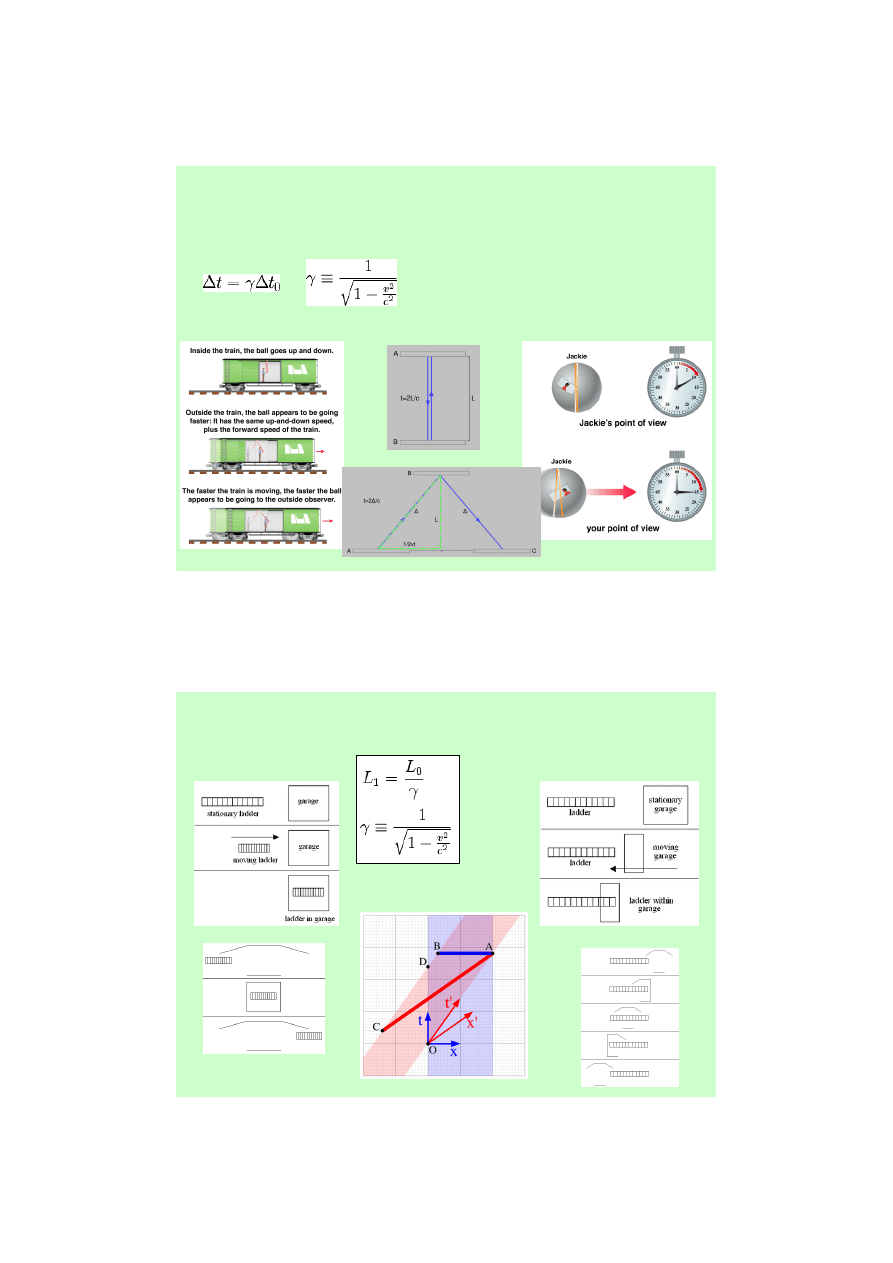
Dylatacja czasu

∆t – obserwator stacjonarny

∆t

0

– obserwator w ruchu

Skrócenie długości

„Paradoks drabiny”

3

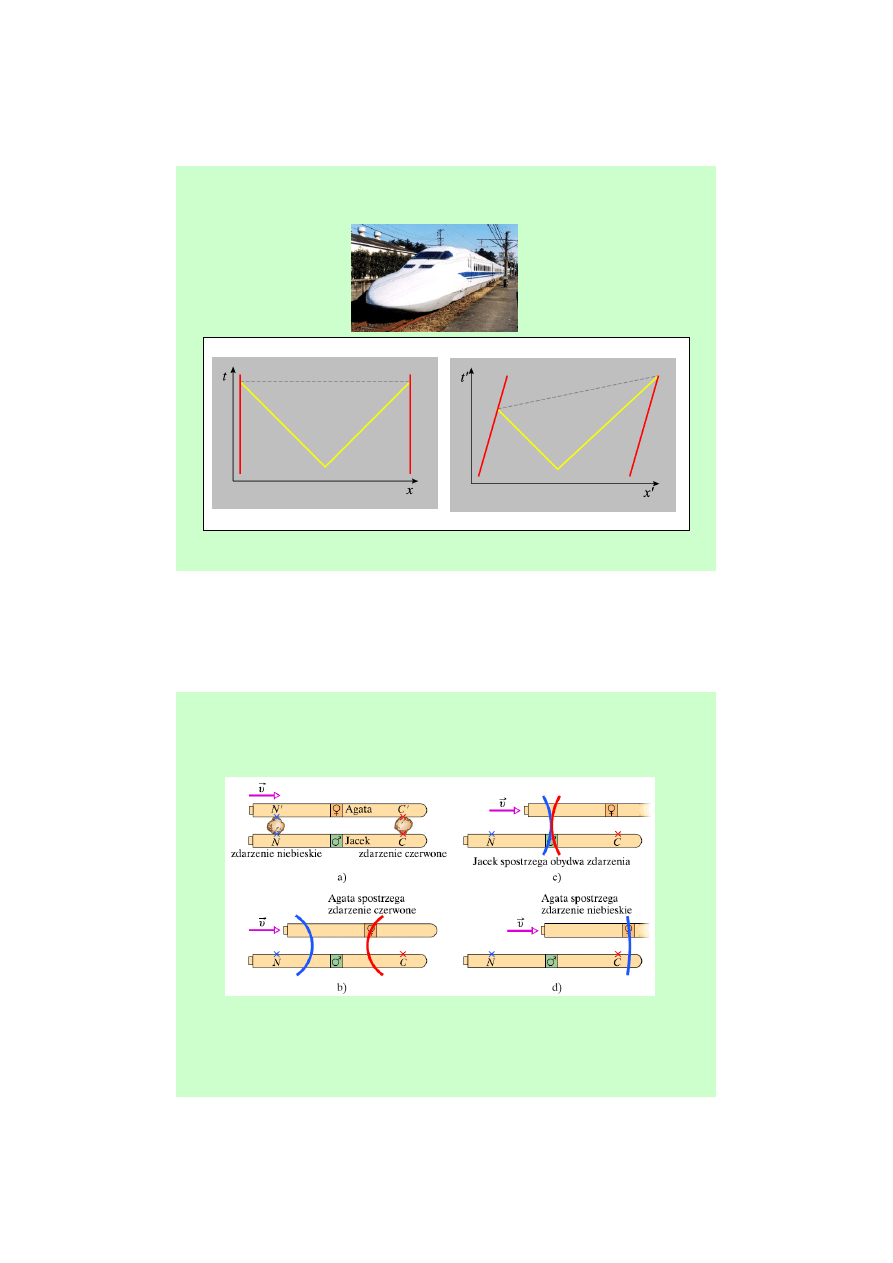
Względność jednoczesności

Obserwator w pociągu

Obserwator na stacji

Linia jednoczesności dla
obserwatora w pociągu

Względność jednoczesności

4

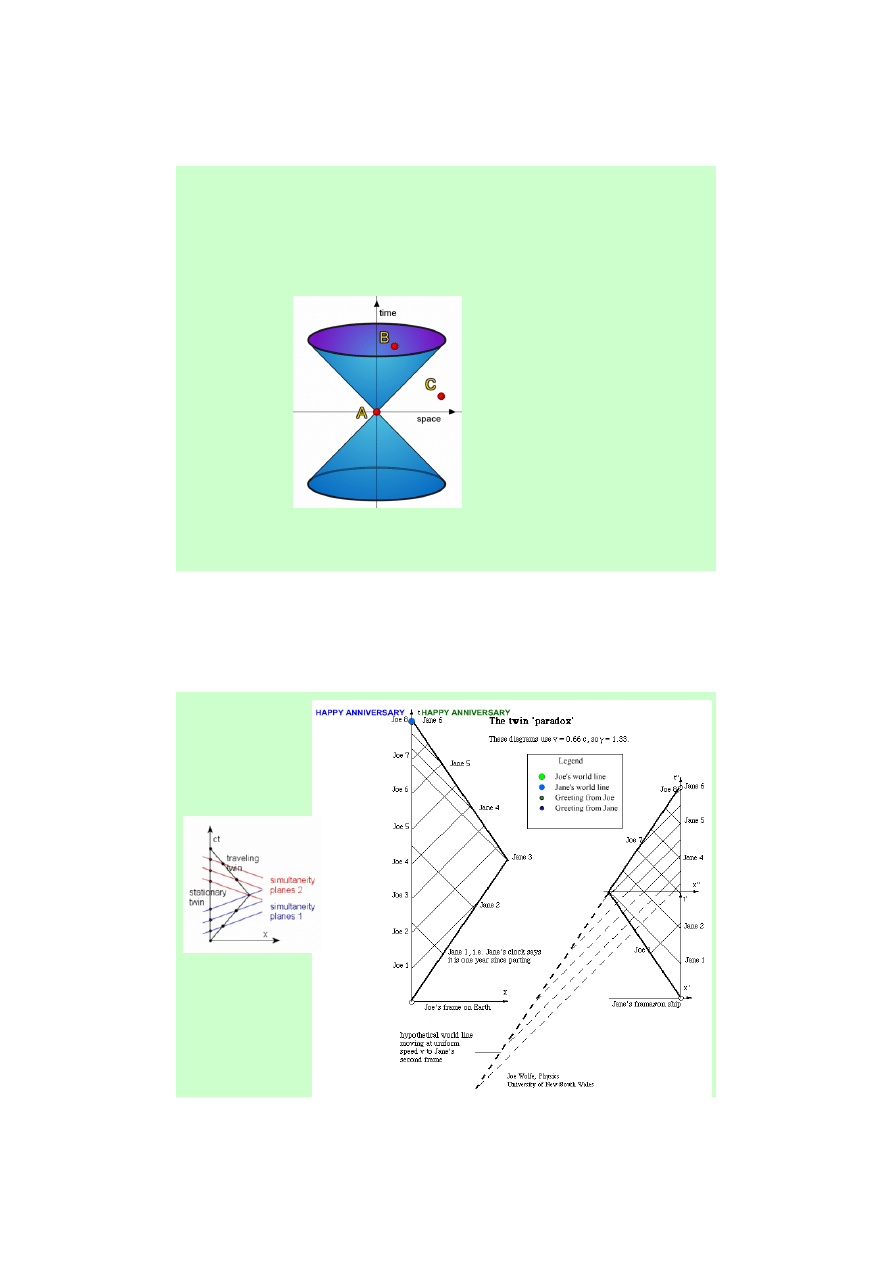
Stożek świetlny

Zdarzenie A wyprzedza
zdarzenie B we wszystkich
układach – może istnieć
zależność przyczynowo –
skutkowa.

Zdarzenie A może w niektórych
układach wyprzedzać zdarzenie
C, ale zdarzenie C może również
wyprzedzać zdarzenie A w
innych układach – nie może być
między nimi zależności
przyczynowo-skutkowej.

Stożek świetlny –
„horyzont zdarzeń”

Paradoks
bliźniąt

5

Paradoks bliźniąt

Układy rozważane w paradoksie
nie są równorzędne !

System GPS Global Positioning System

Wymagana
dokładność zegara:
20 ns/dobę

Efekty
relatywistyczne:
38000 ns/dobę

6

Dodawanie prędkości

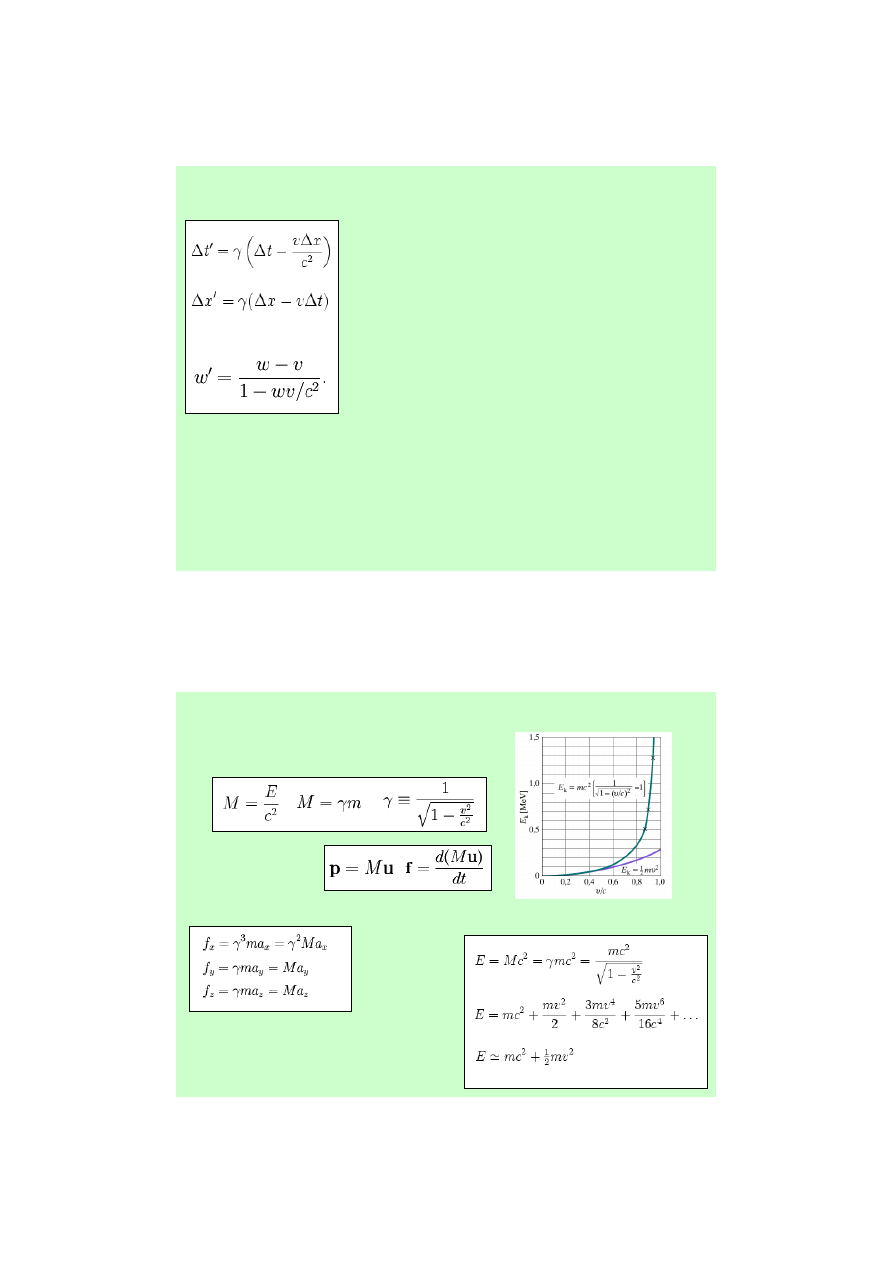
Pojęcie masy w fizyce relatywistycznej

Masa spoczynkowa i masa relatywistyczna

Definicja pędu i siły

Jeśli v dąży do c, siła dąży
do nieskończoności

Energia kinetyczna

7

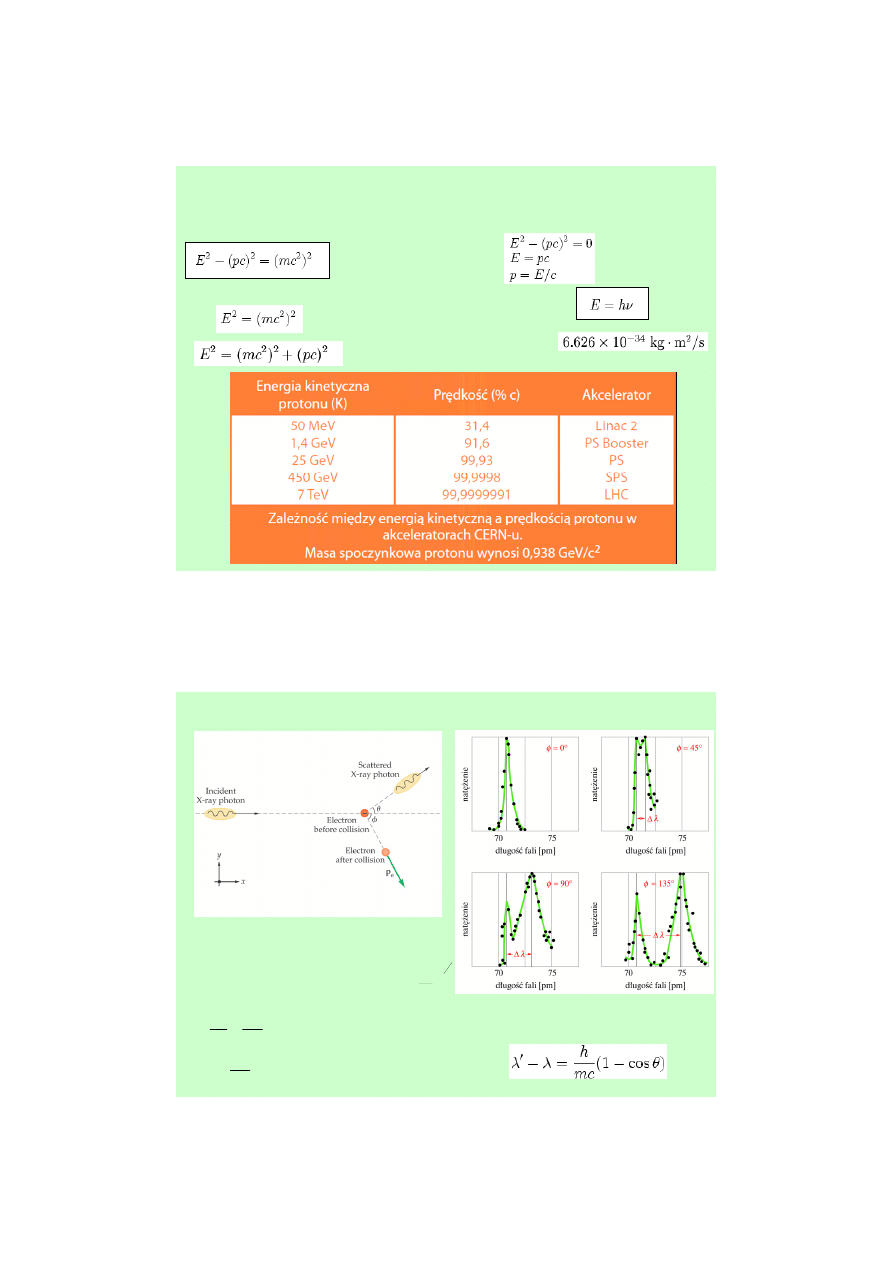
Energia i pęd w fizyce relatywistycznej

Energia i pęd

Masa spoczynkowa (p=0)

Foton – brak masy spoczynkowej

Foton – kwant energii

Stała Plancka

Efekt Comptona – zderzenie fotonu z elektronem swobodnym

φ

γ

θ

ν

sin

sin

0

mv

c

h

−

′

=

Przesunięcie Comptona nie zależy od
materiału rozpraszającego

φ

γ

θ

ν

ν

cos

cos

v

m

c

h

c

h

+

′

=

2

1

2

2

1

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

=

c

v

γ

2

2

c

m

h

mc

h

γ

ν

ν

+

′

=

+