K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
1
PiS15 W03: Zmienne losowe II
1. Charakterystyki liczbowe zm. l.
2. Charakterystyki położenia
Przykład 1
3. Charakterystyki rozrzutu
4. Momenty zwykłe
Przykład 2
5. Momenty centralne
6. Charakterystyki współzależności liniowej
Przykład 4, Przykład 5
7. Standaryzacja zmiennej losowej
8. Rozkład Bernoulliego i jego własności
9. Rozkład równomierny i jego własności
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
2
10. Proces Bernoulliego
11. Rozkład dwumianowy i jego własności
12. Rozkład jednostajny i jego własności
13. Rozkład normalny i jego własności
Przykład 6
Przykład 7
Przykład 8
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
3
1. Charakterystyki liczbowe zm. l.
Niech
na (
, B, P) określone będą zm. l. X
1
,…, X
n
o war-
tościach rzeczywistych.
Charakterystykami liczbowymi
zm. l.
(lub ich rozkładów prawdop.) nazywamy liczby charakteryzu-
jące zbiór wartości, jakie mogą one przyjmować, np. pod
względem wartości najbardziej prawdop., rozrzutu wokół
pewnej wartości, kształtu wykresu funkcji prawdop. lub
krzywej gęstości, a w przypadku kilku zm. l. współzależności
między nimi.
Charakterystyka liczbowa służy do syntetycznego opisu
wartości zm. l. Za pomocą kilku liczb można uzyskać w pro-
sty sposób dostatecznie dobre informacje o rozkładzie zm. l.
lub zależnościach pomiędzy zm. l.
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
4
2. Charakterystyki położenia
Charakterystykę liczbową zm. l. X nazywamy
charaktery-
styką położenia
, jeśli dodanie do zm. l. dowolnej stałej zmie-
nia wartość tej charakterystyki o tę stałą.
Do podstawowych charakterystyk położenia wartości zm.
l. należą:
a)
wartość oczekiwana
(ang. mean),
b)
wartość modalna
(ang. mode)
c)
kwartyle
(ang. quartile).
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
5
Wartością oczekiwaną
(wartością średnią, ang. expected va-
lue, mean) zm. l. X nazywamy liczbę m
X
E(X), przy czym
a) dla zm. l. typu dyskretnego
E(X)
x
i
p
i
b) dla zm. l. typu ciągłego
dx
x
xf
X
)
(
)
(
E
przy założeniu, że występujący szereg i całka są bezwzględ-
nie zbieżne. W przeciwnym przypadku powiemy, że zm. l. nie
ma wartości oczekiwanej.
Mianem wartości oczekiwanej jest miano badanej zm. l.
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
6
Własności wartości oczekiwanej
Na przestrzeni (
, B, P) określone są dwie zm. l. X i Y dla
których istnieją wartości oczekiwane oraz niech a, b, c
R,
wówczas
1. E(c)
c;
2. E(aX)
aE(X);
3. E(X
b)
E(X)
b;
4. E(X
Y)
E(X)
E(Y).
5. Jeżeli zm. l. X i Y są niezależne, to
E((X
EX)(Y
EY))
0.
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
7
Z własności 2, 3 i 4 wynika, że operator E jest operatorem li-
niowym. Własność 4 można uogólnić na przypadek skończo-
nej sumy zm. l.
Jeżeli zm. l. X i Y spełniają warunek z tezy własności 5, to
nazywamy je
nieskorelowanymi zm. l.
Jeżeli zm. l. X ma wartość oczekiwaną m, to zm. l.
Y
X
m
nazywamy zm. l. scentrowaną
(centred r.v.).
Przykład 1. Niech X będzie liczbą punktów stałych w loso-
wej permutacji zbioru {a, b, c}.
a) Wyznaczyć wartość oczekiwaną zm. l. X.
b) Uogólnić wynik na zbiór n elementowy.
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
8
Rozwiązanie.
a) Doświadczenie jest tu określone poprzez
permutację zbioru {a, b, c}. Stąd zbiór zdarzeń elementarnych
{(a, b, c), (a, c, b), (b, a, c), (b, c, a), (c, a, b), (c, b, a)}.
Każdy wynik zachodzi z prawdop. 1/6. Liczby punktów sta-
łych podane są w tablicy 1.1.
X
p
i
a b c
a c b
b a c
b c a
c a b
c b a
3
1
1
0
0
1
1/6
1/6
1/6
1/6
1/6
1/6
Tablica 1.1. Liczby punktów stałych.
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
9
Obliczamy E(X ) zm .l . typu dyskretnego
1
6
1
1
6
1
0
6
1
0
6
1
1
6
1
1
6
1
3
.
b) Wyznaczymy oczekiwaną liczbę punktów stałych w loso-
wej permutacji zbioru {1, 2, 3,…, n}. Dla każdego i, 1
i
n,
niech X
i
(
) równa się 1, jeśli losowa permutacja
ma punkt
stały na i-tym miejscu, i 0 w p. p. Dla każdego i,
E(X
i
)
1/n.
Niech Y oznacza liczbę punktów stałych w permutacji
Y(
)
X
1
(
)
X
2
(
)
…
X
n
(
).
Z własności liniowości dla n zm. l. wynika, że
E(Y)
E(X
1
)
E(X
2
)
…
E(X
n
), stąd E(Y)
1.
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
10
3. Charakterystyki rozrzutu
Charakterystykę liczbową zm. l. nazywamy
charaktery-
styką rozrzutu
, jeśli dodanie do zm. l. dowolnej stałej nie
zmienia wartości tej charakterystyki. Charakterystykami roz-
rzutu wartości zm. l. są:
a)
wariancja
(ang. variance),
b)
odchylenie standardowe
(ang. standard deviation),
c)
odchylenie ćwiartkowe
.
Względną charakterystyką rozrzutu jest
współczynnik
zmienności
(ang. coefficient of variation).
Niech
X będzie zm. l. określoną na (
, B, P) i ma wartość
oczekiwaną m
X
E(X).
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
11
Wariancją
(variance)
zm. l. X nazywamy wartość oczeki-
waną kwadratu scentrowanej zm. l., tj. liczbę
)
(
D
2
2
X
X
określoną wzorem:
D
2
(X)
E(X
m
X
)
2
,
przy czym
a) dla zm. l. typu dyskretnego
)
(
)
(
D
2
2
i
X
i
x
f
m
x
X
b) dla zm. l. typu ciągłego
dx
x
f
m
x
X
X
)
(
)
(
)
(
D
2
2
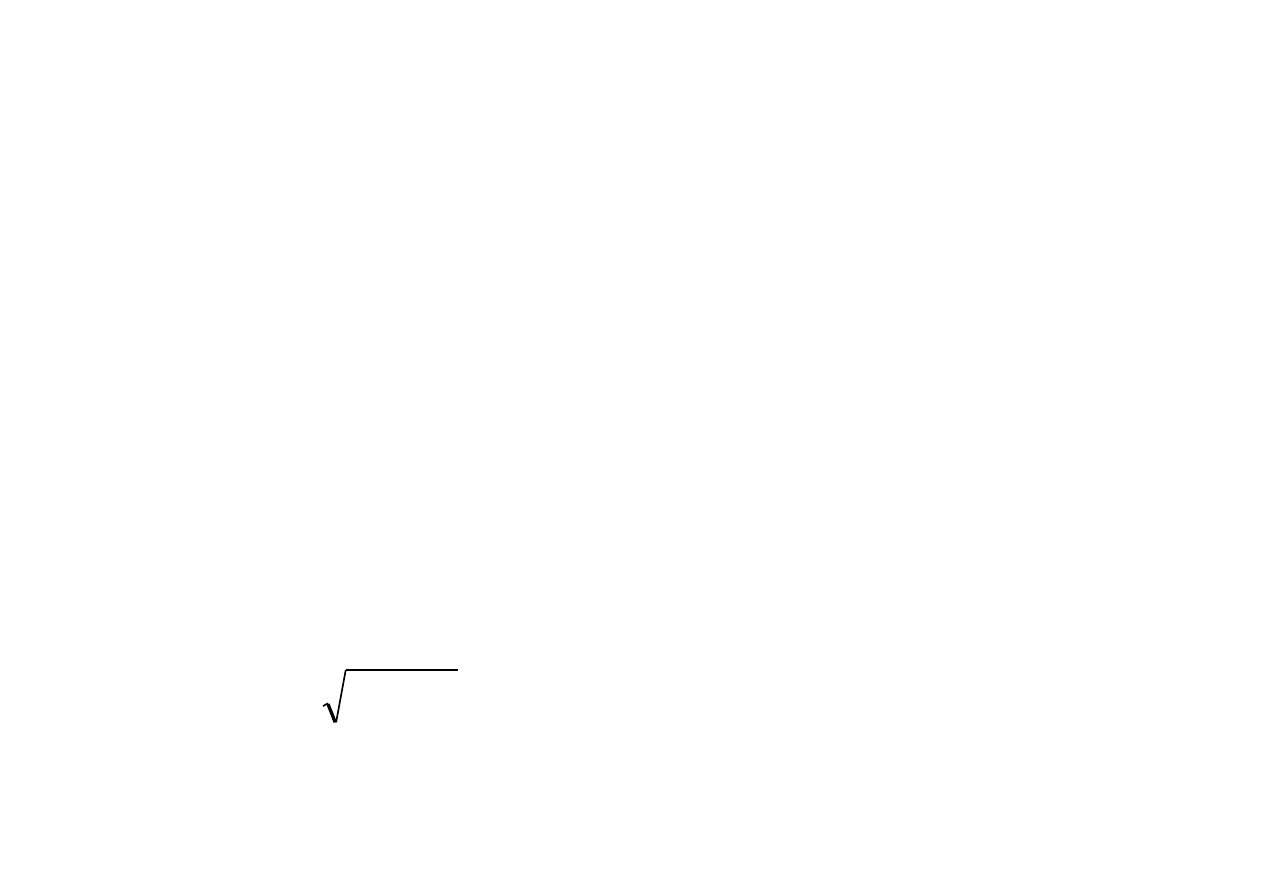
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
12
Wariancja zm. l. istnieje, gdy szereg (całka) występujący
w definicji wariancji jest zbieżny. Mianem wariancji jest
kwadrat miana badanej zm. l.
Niech na (
, B, P) określone będą zm. l. X i Y o skończo-
nych wariancjach oraz a, b
R. Wówczas
a) D
2
(a)
0
wariancja stałej zm. l. jest równa zero,
b) D
2
(X
a)
D
2
(X)
niezmienniczość na przesunięcie,
c) D
2
(aX)
a
2
D
2
(X) dla a
0;
Odchyleniem standardowym
(standard deviation) lub dysper-
sją zm. l. X nazywamy dodatni pierwiastek z wariancji, tj.
liczbę
)
(
D
2
X
X
. Mianem dyspersji jest miano badanej
zmiennej.
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
13
4. Momenty zwykłe
Momentem zwykłym
r
tego rzędu (r jest liczbą naturalną)
zm. l. X nazywamy charakterystykę liczbową określoną wzo-
rem:
m
r
(X)
E(X
r
)
Z istnienia momentów wyższych rzędów wynika istnienie
momentów niższych rzędów. Wartość oczekiwana jest mo-
mentem zwykłym rzędu pierwszego.
Związek między wariancją a momentami zwykłymi
Jeżeli istnieje wariancja D
2
(X) zm. l. X, to
)
(
)
(
)
(
D
2
1
2
2
X
m
X
m
X
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
14
Przykład 2. Losujemy liczbę z przedziału (a, b), gdzie a < b.
Niech X oznacza wylosowaną liczbę. Wyznaczyć wariancję
D
2
(X).
Rozwiązanie.
Wyznaczamy momenty
2
1
)
(
1
b
a
xdx
a
b
X
m
b
a
,
3
)
(
3
1
)
(
2
2
3
3
2
2
b
ab
a
a
b
a
b
dx
x
a
b
X
m
b
a
.
Stąd wariancja
.
12
/
)
(
)
(
D
2
2
1
2
2
a
b
m
m
X
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
15
5. Momenty centralne
Momentem centralnym
k-tego rzędu (k
1, 2,…) (
central
moment of order k
) zm. l. X nazywamy wartość oczekiwaną k-
tej potęgi scentrowanej zm. l., tj.
k
k
X
X
X
)
E
(
E
)
(
Wariancja jest momentem centralnym rzędu drugiego.
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
16
6. Charakterystyki współzależności liniowej
Jeżeli rozważamy kilka zm. l. określonych na tej samej
przestrzeni (
, B, P), to możemy badać je nie tylko z osobna,
ale również współzależności między nimi.
W szczególności, charakterystykami określającymi współ-
zależność liniową pomiędzy parą zm. l. są:
a) kowariancja,
b) współczynnik korelacji.
Niech na (
, B, P) określone będą zm. l. X
1
, X
2
,…, X
n
o
wartościach rzeczywistych.
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
17
Kowariancją zm. l. X
i
i X
j
(i, j
1, 2, …, n) spełniających
warunek E
X
i
X
j
<
, nazywamy wielkość
cov(X
i
, X
j
)
E((X
i
EX
i
) ( X
j
EX
j
))
Mianem kowariancji jest iloczyn mian badanych zmiennych.
Własności kowariancji:
1) cov(X
i
, X
j
)
cov(X
j
, X
i
),
2) cov(X
i
, X
i
)
D
2
(X
i
),
3) cov(X
i
, X
j
)
E(X
i
X
j
)
E(X
i
) E(X
j
),
4)
cov(X
i
, X
j
)
D(X
i
) D(X
j
) – nierówność Schwarza.
Z własności 3) wynika, że dla każdej pary niezależnych
zm. l. X
i
i X
j
cov(X
i
, X
j
)
0.
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
18
Odwrotne stwierdzenie jest fałszywe. Ilustruje to przykład.
Przykład 3. Obliczyć kowariancję oraz zbadać niezależność
zm. l. brzegowych dla wektora l. (X, Y) o łącznym rozkładzie:
X \Y
1
2
3
6
0,2
0
0,2
8
0
0,2
0
10 0,2
0
0,2
Rozwiązanie.
Po wykonaniu obliczeń mamy: E(X)
8, E(Y)
2, E(XY)
16, zatem cov(X, Y )
0, więc zm. l. X i Y są
nieskorelowane
, ale nie są niezależne, gdyż
P(X
6, Y
1)
0,2
(0,4) (0,4)
P(X
6) P(Y
1).
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
19
Niech na (
, B, P) określone będą zm. l. X
1
, X
2
,…, X
n
o
wartościach rzeczywistych.
Współczynnikiem korelacji
) zm. l.
X
i
, X
j
(i, j
1, 2,…, n) nazywamy charakterystykę liczbową
ij
określoną wzorem
)
(
D
)
(
D
)
,
(
Cov
j
i
j
i
ij
X
X
X
X
,
Współczynnik korelacji nie zależy od przyjętej skali oraz od
położenia początku układu współrzędnych, w którym są reje-
strowane zmienne.
Współczynnik korelacji jest wielkością bez miana.
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
20
Ponadto
1
(X
i
, X
j
)
1.
Własność
(X
i
, X
j
)
1 zachodzi wtedy i tylko wtedy, gdy
X
j
aX
i
b z prawdop. 1.
Przykład 4. (Palenie i rak). Zaprojektować badanie zależno-
ści chorowania na raka od palenia tytoniu w grupie 60 osób
dla których dane są zebrane w tablicy 1.
C\S
nie pali pali suma
bez raka
z rakiem
40 10
7 3
50
10
suma
47 13
60
Tablica 1. Palenie i rak
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
21
Projekt.
1. Oznaczenia i koncepcja badań. Niech
będzie zbiorem
badanych osób. Każda osoba
badana jest ze względu na
dwie dychotomiczne cechy, których modelami są zm. l. C i S
określona na
i o wartościach w zbiorze {0, 1}.
Niech C(
)
1, jeśli wylosowana osoba ma raka i 0 jeśli
nie ma oraz niech S(
)
1, jeśli osoba ta pali papierosy i 0 w
p.p.
2. Wyznaczamy łączny rozkład i brzegowe rozkłady.
Zauważmy, że
P(C
0; S
0)
40/60, P(C
0, S
1)
10/60, i tak dalej.
Łączny rozkład (C, S) jest dany w tablicy 2,
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
22
C\S
0 1
0
1
40/60 10/60
7/60 3/60
Tablica 2. Łączny rozkład.
Stąd rozkłady brzegowe zm. l. C i S:
60
/
13
60
/
47
1
0
S
f
,
60
/
10
60
/
50
1
0
C
f
.
3. Badamy niezależność. Zm. l. S i C nie są niezależne, gdyż
P(C
1, S
1)
3/60
0,05
natomiast
P(C
1) P(S
1)
0,036.
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
23
4. Obliczamy wartości oczekiwane i wariancje.
E(C)
10/60, E(S)
13/60,
E(C
2
)
10/60, E(S
2
)
13/60,
D
2
(C)
5/36, D
2
(S)
611/3600,
D(C)
0,372678, D(S)
0,411974.
5. Obliczamy kowariancję i współczynnik korelacji
E(CS)
3/60, cov(C, S)
5/360.
stąd
(X, Y)
0,090462.
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
24
7. Standaryzacja zmiennej losowej
Standaryzacją
zm. l. X o skończonej wartości oczekiwanej
m
X
i wariancji D
2
(X) > 0 nazywamy transformację
X
X
m
X
X
h
)
(
Zm. l. Z
h(X) nazywamy
standaryzowaną zm. l.
(
standardi-
zed r. v.
)
Standaryzacja zm. l. może być uogólniona na tak zwaną
„
zm. l. zredukowaną
”, która jest określana za pomocą innej
charakterystyki położenia i/lub innej charakterystyki rozrzutu.
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
25
Własności.
Niech Z będzie standaryzowaną zm. l. dla zm. l.
X, wówczas
a) E(Z)
0
wartość oczekiwana stand. zm. l. wynosi 0,
b) D
2
(Z)
1
wariancja stand. zm. l. wynosi 1,
c)
)
/
)
((
)
(
X
X
Z
X
m
x
F
x
F
.
Dowody. Własności a), b) d) wynikają z przekształceń:
0
)
E(
1
E
E(Z)
X
X
X
X
m
X
m
X
,
1
)
(
D
1
D
)
(
D
2
2
2
2
X
X
X
X
m
X
m
X
Z
.
x
X
x
F
X
P
)
(
)
/
)
((
)
/
)
(
(
P
X
X
Z
X
X
m
x
F
m
x
Z
.
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
26
8. Rozkład Bernoulliego i jego własności
Rozkładem Bernoulliego
) (zwa-
nym w polskiej literaturze rozkładem zero-jedynkowym) na-
zywamy rozkład zm. l. X dla której X(
)
{0, 1}. Wartość 1
przyjmuje z prawdop. p, a 0 z prawdop. q
1
p, czyli
.
0
,
1
dla
dla
1
)
;
(
x
x
p
p
p
x
f
B
Rozkład ten oznaczamy B(p). Zapis X ~ B(p) oznacza, że
zm. l. X ma rozkład Bernoulliego z parametrem p (p
(0, 1)).
Momenty zwykłe: E(X
k
)
1
k
p
0
k
(1
p)
p, dla k
1, 2,…
Stąd E(X) = p, E(X
2
) = p, D
2
(X)
p(1
p).
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
27
9. Rozkład równomierny i jego własności
Zm. l. X typu dyskretnego ma
rozkład równomierny
) na zbiorze X(
)
W, gdzie
W
{x
1
, x
2
,…, x
n
}, co oznaczamy X·~ U(W), jeżeli każdą z
wartości x
k
W przyjmuje z tym samym prawdop., tj.
f
U
(x
k
; W)
P(X
x
k
)
1/n.
Rozkład równomierny jest modelem losowania liczby
w totalizatorze sportowym, wyniku rzutu idealną kostką, lo-
sowania numeru produktu z ponumerowanej ich partii, itp.
Własności
X
U(W)
E(X)
(
x
k
)/n, D
2
(X)
(x
k
2
)/n
E
2
(X),
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
28
10. Proces Bernoulliego
Procesem Bernoulliego
1
) nazywamy
skończony lub nieskończony ciąg X
1
, X
2
,… identycznych i
niezależnych zm. l. (i.i.d.) o rozkładzie Bernoulliego, tj.
przyjmujących dwie wartości: 1 z prawdop. p zwanym sukce-
sem i 0 z prawdop. q
1
p zwanym porażką.
Z procesem Bernoulliego związane są rozkłady:
Bernoul-
liego
,
dwumianowy
i
Pascala
.
1
Jakub Bernoulli (1654-1705)
Matematyk szwajcarski, jeden z licznej rodziny Bernoullich, autor Ars conjectandi, pierw-
szego dzieła poświęconego rachunkowi prawdopodobieństwa.
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
29
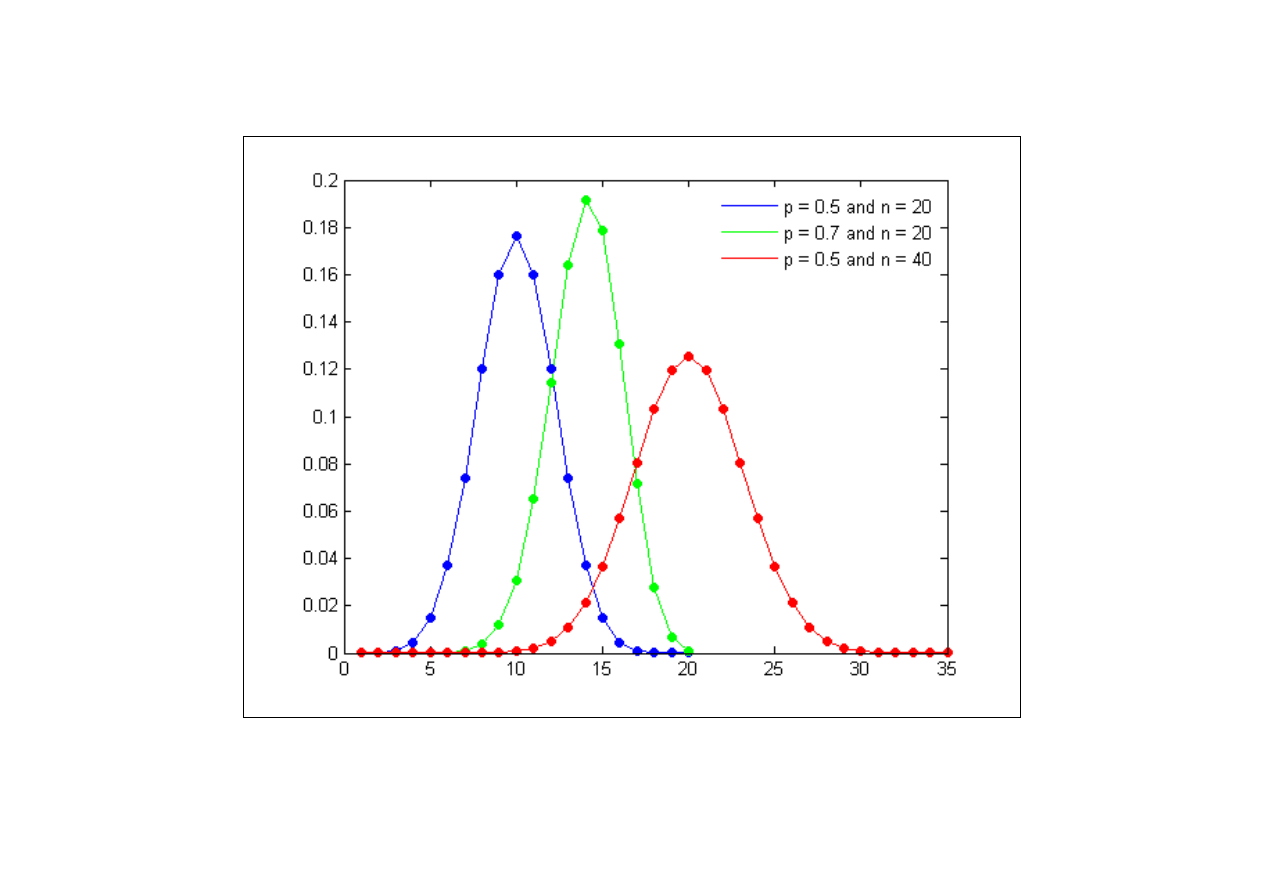
11. Rozkład dwumianowy i jego własności
Zm. l. X:
{0, 1,…, n} ma
rozkład dwumianowy
) z parametrami n i p (n
N, p
(0, 1)),
co oznaczamy X ~ B(n, p), jeżeli jej funkcja prawdop. (PMF)
f
B
wyraża się wzorem:
x
n
x
B
p
p
x
n
p
n
x
f
)
1
(
)
,
;
(
dla x
0, 1, 2,…, n.
Zm. l. X o rozkładzie B(n, p) zlicza liczbę sukcesów (jedy-
nek), w ciągu n niezależnych doświadczeń, których modelem
jest proces Bernoulliego.
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
30
Rys. 1. Łamane funkcji prawdop. rozkładów dwumianowych
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
31
1. Jeżeli X
i
~ B(p) dla i
0, 1, 2,…, n jest ciągiem zm. l.
iid o tym samym rozkładzie Bernoulliego, to ich suma
Y
n
X
1
X
2
…
X
n
ma rozkład dwumianowy Y
n
~ B(n, p).
2. Jeżeli X ~ B(n, p), to E(X)
np, D
2
(X)
np(1
p),
0
0
)
1
(
)
1
(
dla
dla
,
1
)
1
(
,
)
1
(
,
)
1
(
)
(
N
N
p
n
p
n
p
n
p
n
p
n
X
mo
,
gdzie symbol
x
oznacza część całkowitą z liczby x.
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
32
12. Rozkład jednostajny i jego własności
Zm. l. X:
(a, b) ma
rozkład jednostajny
na przedziale
[a, b]
), co oznaczamy X·~ U(a, b), je-
żeli jej gęstość prawdop. (PDF) wyraża się wzorem
).
,
(
),
,
(
dla
dla
0
1
)
,
;
(
b
a
x
b
a
x
a
b
b
a
x
f
U
Własności.
Niech X
k
~ U(a, b) dla k
1, 2,… wówczas
)
1
)(
(
)
(
E
1
1
k
a
b
a
b
X
k
k
k
,
stąd E(X)
(a
b)/2, D
2
(X)
(b
a)
2
/12.
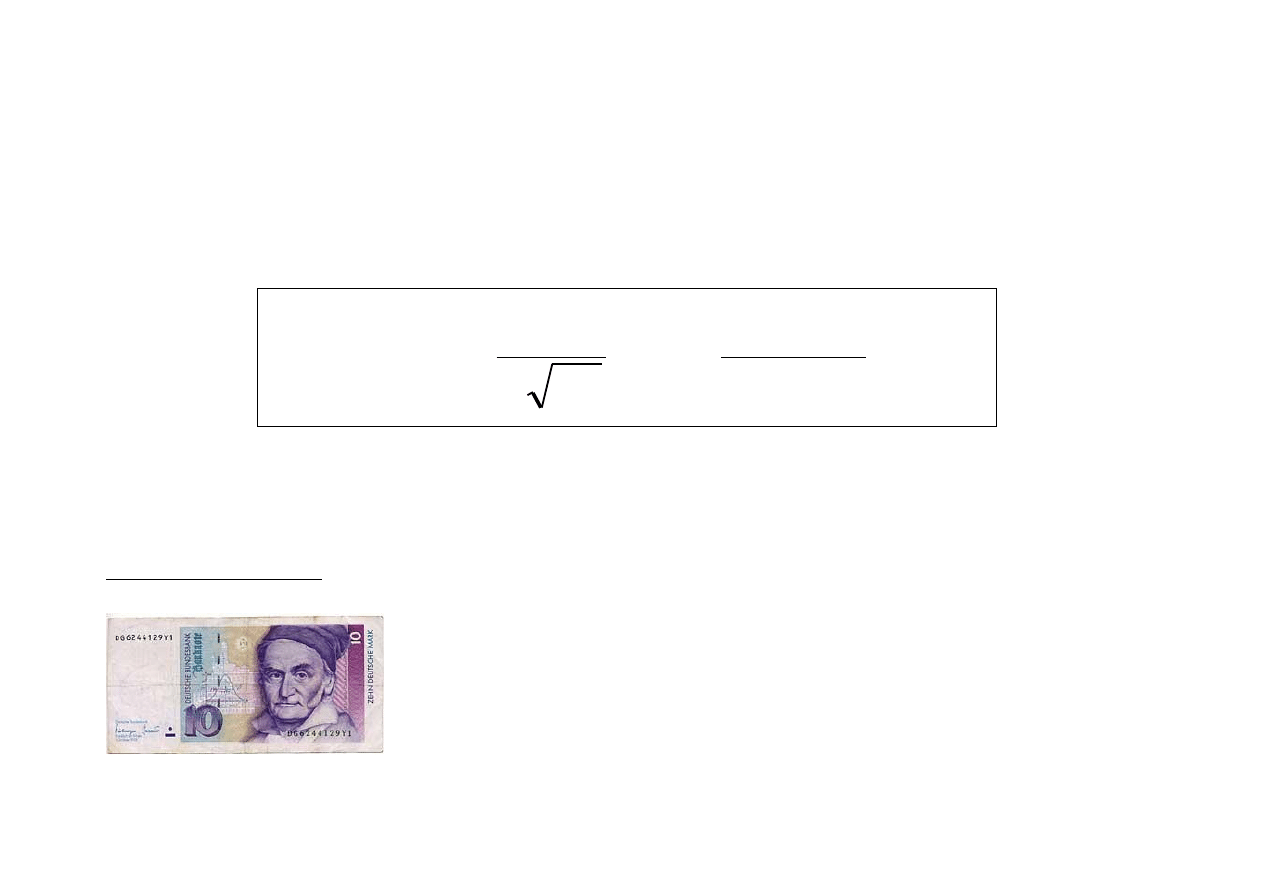
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
33
13. Rozkład normalny i jego własności
Zm. l. X typu ciągłego ma
rozkład normalny
z parametra-
mi m i
(m
R,
> 0), co oznaczamy X ~ N(m,
), jeśli
2
2
2
)
(
exp
2
1
)
,
;
(
m
x
m
x
f
N
, x
R.
Gęstość rozkładu normalnego została zaproponowana
przez
Gaussa
2
, jako model rozkładu częstości błędów pomia-
2
Carl Friedrich Gauss (1777-1855)
matematyk niemiecki. Jeden z najwybitniejszych matematyków wszystkich
czasów, zwany przez współczesnych książę matematyków. Profesor uniwersytetu w Getyndze.
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
34
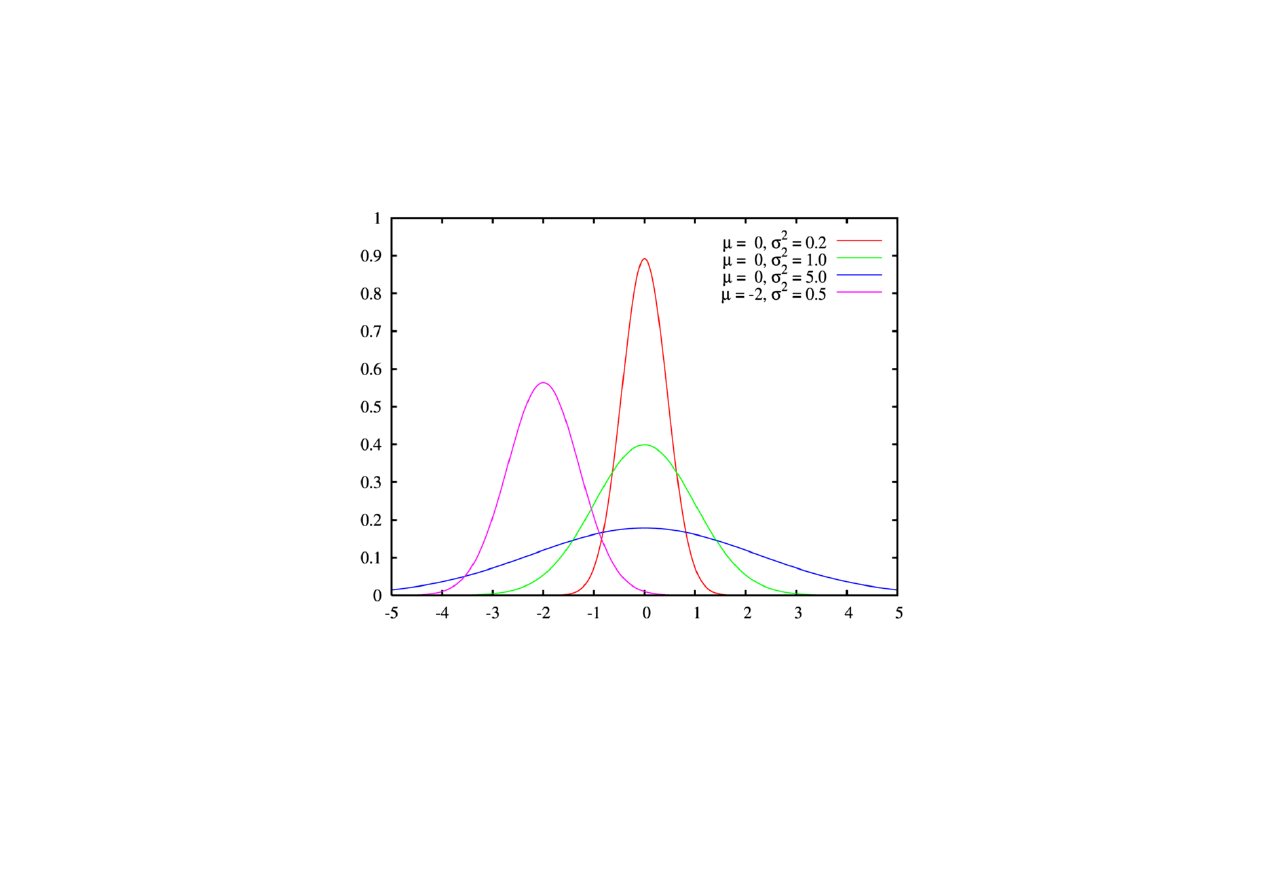
rowych. Na jego cześć krzywe gęstości rozkładów normal-
nych nazywamy
krzywymi Gaussa.
Rys. 3 Krzywe Gaussa.
Gęstość osiąga maksimum w punkcie x
m, natomiast dla
x
m
ma punkty przegięcia.
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
35
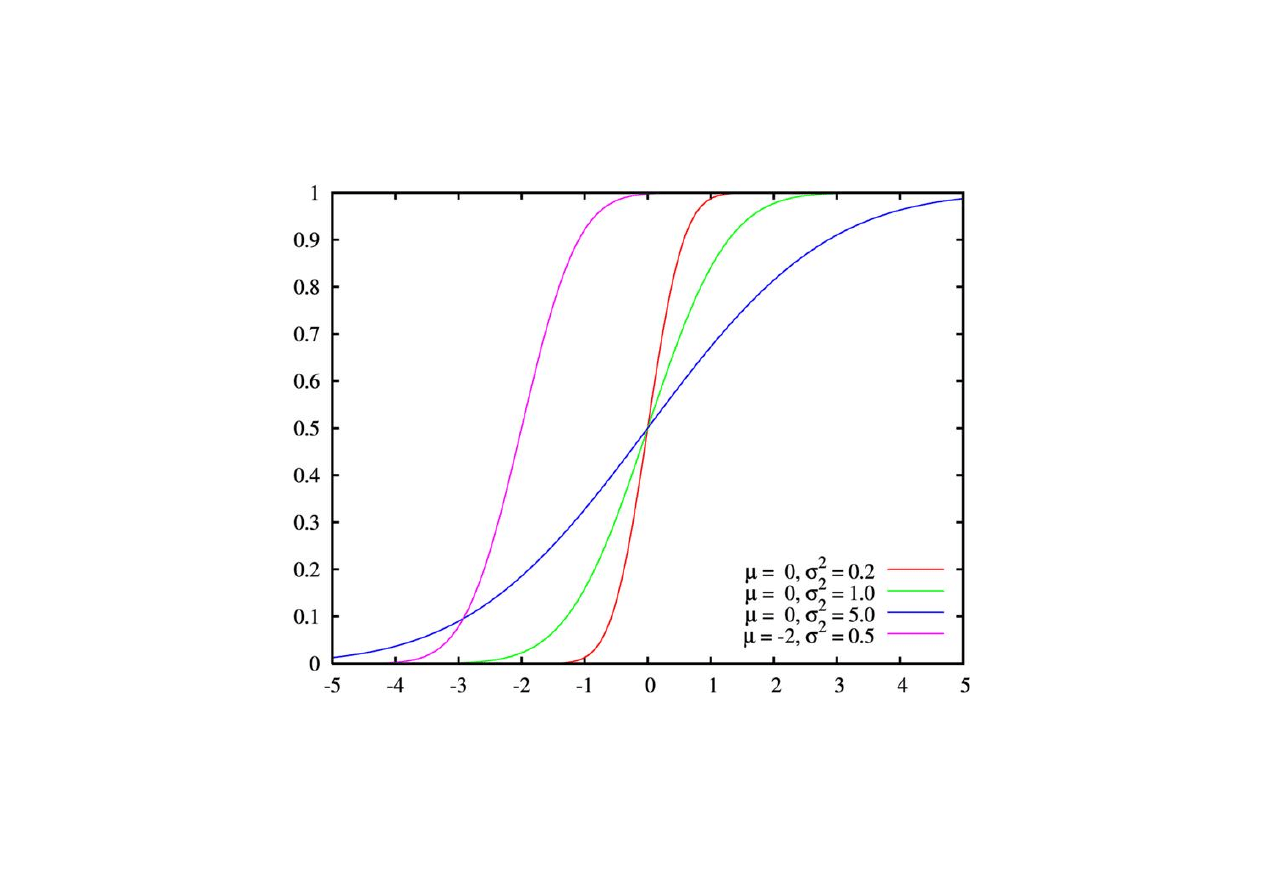
Własności: Jeżeli X ~ N(m,
), to E(X)
m, D
2
(X)
2
.
Rys. 4. Wykresy dystrybuant rozkładów normalnych
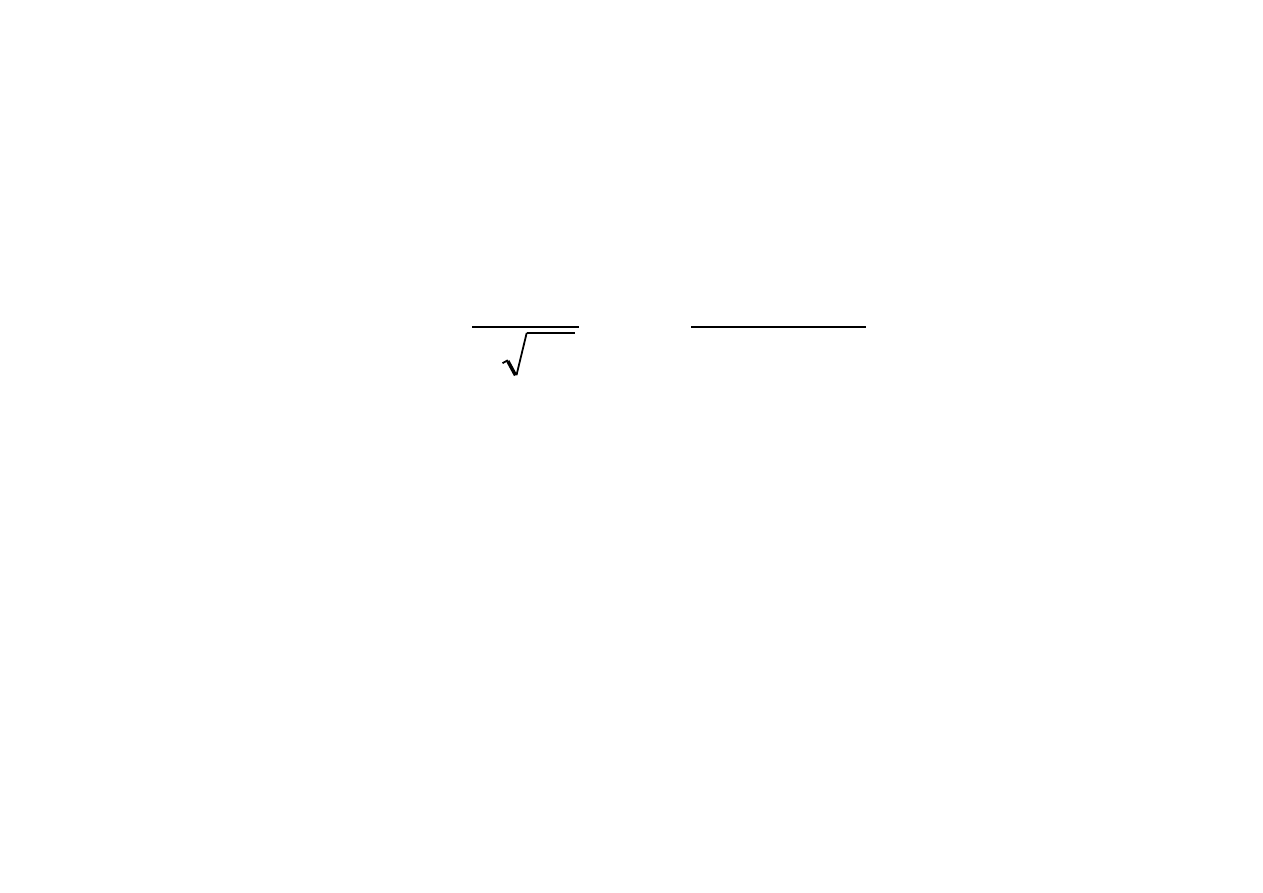
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
36
Przykład 6. Wytrzymałość lin stalowych (wyrażona w
[MPa]), pochodzących z masowej produkcji, jest zm. l. W i
PDF dana jest wzorem:
50
)
100
(
exp
2
1
)
,
;
(
2
w
m
w
f
, w
R.
Ile wynoszą średnia i wariancja wytrzymałości lin.
Odp.: E(W)
100 MPa, D
2
(W)
25 [MPa]
2
.
Zastosowanie rozkładu normalnego
Rozkład normalny jest najważniejszym i najczęściej sto-
sowanym rozkładem w MP i SM oraz najczęściej stosowa-
nym rozkładem w zastosowaniach inżynierskich i ekono-
micznych.
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
37
Standaryzowany rozkład normalny
Jeśli X ~ N(m,
) i zm. l. X poddamy standaryzacji Z, to Z~
N(0, 1). Rozkład N(0, 1) nazywamy
standardowym rozkła-
dem normalnym
.
Dystrybuanta stand. rozkładu normalnego
jest oznaczana
i ma postać
dx
x
z
z
2
exp
2
1
)
(
2
, z
R.
Z symetrii gęstości stand. rozkładu normalnego względem osi
Oy wynika zależność:
(
z)
1
(z).
Wartości funkcji
są stablicowane. Dla X ~ N(m,
) ko-
rzystamy z tej tablicy po jej standaryzacji.
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
38
Przykład 7. Wytrzymałość W (w [MPa]) lin stalowych, po-
chodzących z pewnej partii, ma rozkład jak w przykładzie 6.
Obliczyć prawdop. zdarzenia, że losowo wybrana lina z tej
partii będzie miała wytrzymałość większą niż 105 [MPa],
Rozwiązanie.
Z praw wielkich liczb możemy przyjąć, że czę-
stość przyjmowania wartości z przedziału (
; w) jest równa
prawdop. przyjmowania wartości z tego przedziału.
Obliczamy prawdop. zdarzenia W > 105 [MPa]
5
100
105
5
100
P
1
)
105
P(
1
)
105
(
P
W
W
W
)
1
(
1
)
1
(
P
1
Z
.
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
39
(w) odczytujemy z tablic lub obliczamy komputerowo.
Otrzymujemy
(1)
0,8413. Stąd prawdop., że losowo wy-
brana lina z rozważanej partii ma wytrzymałość większą niż
105 [MPa] wynosi 0,1587.
Kwantyle rozkładu normalnego
Niech F
X
(x; m,
) będzie CDF zm. l. X ~ N(m
X
,
X
).
Kwantyle zm. l. X wyznaczamy za pomocą funkcji kwanty-
lowej F
X
1
(p; m,
), która dla p
(0, 1) jest określona wzorem:
F
X
1
(p; m,
)
m
X
X
1
(p),
gdzie
1
(p) jest funkcją kwantylową rozkładu N(0, 1).
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
40
Ponieważ
1
(p)
1
(1
p),
więc wystarczy znać wartości tej funkcji dla p
(0,5; 1).
Wartości funkcji odwrotnej
1
podobnie jak samej dys-
trybuanty
są zestawiane w tablicach statystycznych. Często
stosowane kwantyle są zestawione w tablicy kwantyli.
p 0,75
0,90
0,95
0,975 0,99
0,995 0,999
z
p
0,6745 1,2816 1,6449 1,9600 2,3263 2,5758 3,0902
Tablica. Wybrane kwantyle rozkładu N(0, 1)
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
41
Przykład 8. Zużycie paliwa niezbędnego do przebycia przez
odrzutowiec odległości między dwoma miastami jest zm. l. X
o rozkładzie normalnym ze średnią m
5,7 ton i odchyleniu
standardowym
0,5 tony. Linia lotnicza chce ustalić taką
ilość paliwa, przy zatankowaniu której prawdop. dotarcia do
miejsca przeznaczenia wynosiłoby ponad 0,99.
Rozwiązanie.
Wiemy, że X ~ N(5,7; 0,5) [ton].
Mamy znaleźć taką wartość x dla której P(X < x)
0,99,
czyli kwantyl rzędu 0,99, tj. x
0,99
.
Kwantyl ten wyznaczamy z zależności
x
0,99
m
X
X
z
0,99
.
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
42
Ponieważ m
X
5,7;
X
0,5, z
0,99
1
(0,99)
2,3263, więc
x
0,99
6,86315 ton.
Należy zatankować 6,9 ton paliwa, gdyż daje to co najmniej
99% pewność, że wystarczy paliwa na cały lot.
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
43
Przykład projektu zaliczeniowego
Uwaga. Należy przytaczać wzory i składnie funkcji wykorzystywanych w roz-
wiązaniach. Udzielać pełnych odpowiedzi. Sporządzić tabelę ocen według
wzoru. W przypadku braku rozwiązania etapu, pod jego numerem, w polu
„uzyskano” wpisać „0”.
Etap
1 2 3 4 5 6 7 Łącznie
do uzyskania 1 2 3 1 2 1 3
13
uzyskano
Długość X (w mm) detalu produkowanego na pewnym automacie jest zmienną
losową o gęstości prawdopodobieństwa
R
x
x
x
f
X
,
08
,
0
)
20
(
exp
2
1
)
(
2
,
1. Rozpoznać rozkład długości detalu i ustalić parametry rozkładu.
2. Wyznaczyć współczynnik zmienności i drugi moment zwykły długości deta-
lu.
K.J. Andrzejczak, PiS15 W03: Zmienne losowe II
44
3. Obliczyć prawdopodobieństwa zdarzeń:
01
,
0
98
,
19
X
,
m
X
.
4. Obliczyć
dla
jakiej
wartości
stałej
b
zachodzi
równość
90
,
0
)
(
05
,
0
b
X
x
P
.
5. Wyznaczyć kwartyle długości detalu oraz obliczyć gęstości dla nich.
6. Wyznaczyć przedział, w którym mieści się 95% produkowanych detali, po
złomowaniu 5% detali o największej odchyłce długości od wymiaru prze-
ciętnego.
7. Detal spełnia normę długości, jeśli jego długość mieści się w przedziale
(19,6; 20,4). W celu sprawdzenia dokładności produkcji zmierzona zostanie
długość partii 180 losowo wybranych detali.
a) Wprowadzić zmienną losową opisującą wynik sprawdzenia normy długości
badanej partii detali i podać jej rozkład.
b) Obliczyć prawdop. zdarzenia, że w badanej partii detali, co najmniej 175 z
nich spełni normę długości.
c) Wyznaczyć dominantę liczby detali, które spełnią normę długości i praw-
dopodobieństwo dla niej.
