K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

1

PiS15 W02: ZMIENNE LOSOWE I

1.

Zmienna losowa i jej rozkład

2.

Niezależne zmienne losowe

Przykład 1
Przykład 2

3.

Pomiary bezpośrednie i ich skale

4.

Dystrybuanty i ich własności

Przykład 3

5.

Zmienna losowa typu dyskretnego i jej rozkład

Przykład 4

6.

Zmienna losowa typu ciągłego i jej rozkład

Przykład 5

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

2

7.

Parametry rozkładu

8.

Funkcja kwantylowa i kwantyle

9.

Do samodzielnego rozwiązania

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

3

1. Zmienna losowa i jej rozkład

Niech dana będzie przestrzeń probabilistyczna (

Ω

, B, P).

Zmienną losową (ozn. zm. l.) o wartościach rzeczywistych

(ang.

real-valued random variable

) nazywamy funkcję X

określoną na zbiorze

Ω

i przyjmującą wartości rzeczywiste:

X:

Ω

→

R,

spełniającą dla każdego x

∈

R warunek {

ω∈Ω

: X(

ω

)

≤

x}

∈

B.

Ogólniej wektor X

=

(X

1

,…, X

n

) taki, że X:

Ω

→

R

n

, tj. dla

i

=

1, 2,…, n, X

i

:

Ω

→

R, nazywamy

wektorem losowym

lub

wielowymiarową zm. l.,

jeżeli

B

R

R

∈

≤

ω

≤

ω

∈

ω

∀

∀

∈

∈

}

)

(

,...,

)

(

:

{

...

1

1

1

n

n

x

x

x

X

x

X

n

Ω

Ω

Ω

Ω

.

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

4

Współrzędne X

i

wektora l. nazywamy

zm. l. brzegowymi.

Jeżeli zbiór

Ω

jest skończony, to każda funkcja X:

Ω

→

R

jest zm. l.

Zbiór

wartości zm. l. X

X(

Ω

)

=

{x

∈

R

n

:

∃

ω∈Ω

x

=

X(

ω

)}

nazywamy jej obrazem.

Niech dana będzie przestrzeń probabilistyczna (

Ω

, B, P)

oraz określona na niej rzeczywista zm. l. X. Ponadto niech
B(R) będzie rodziną zbiorów borelowskich na prostej.

Funkcja P

X

określona w następujący sposób:

∀

A

∈

B(R)

P

X

(A)

=

P{

ω∈Ω

: X(

ω

)

∈

A}

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

5

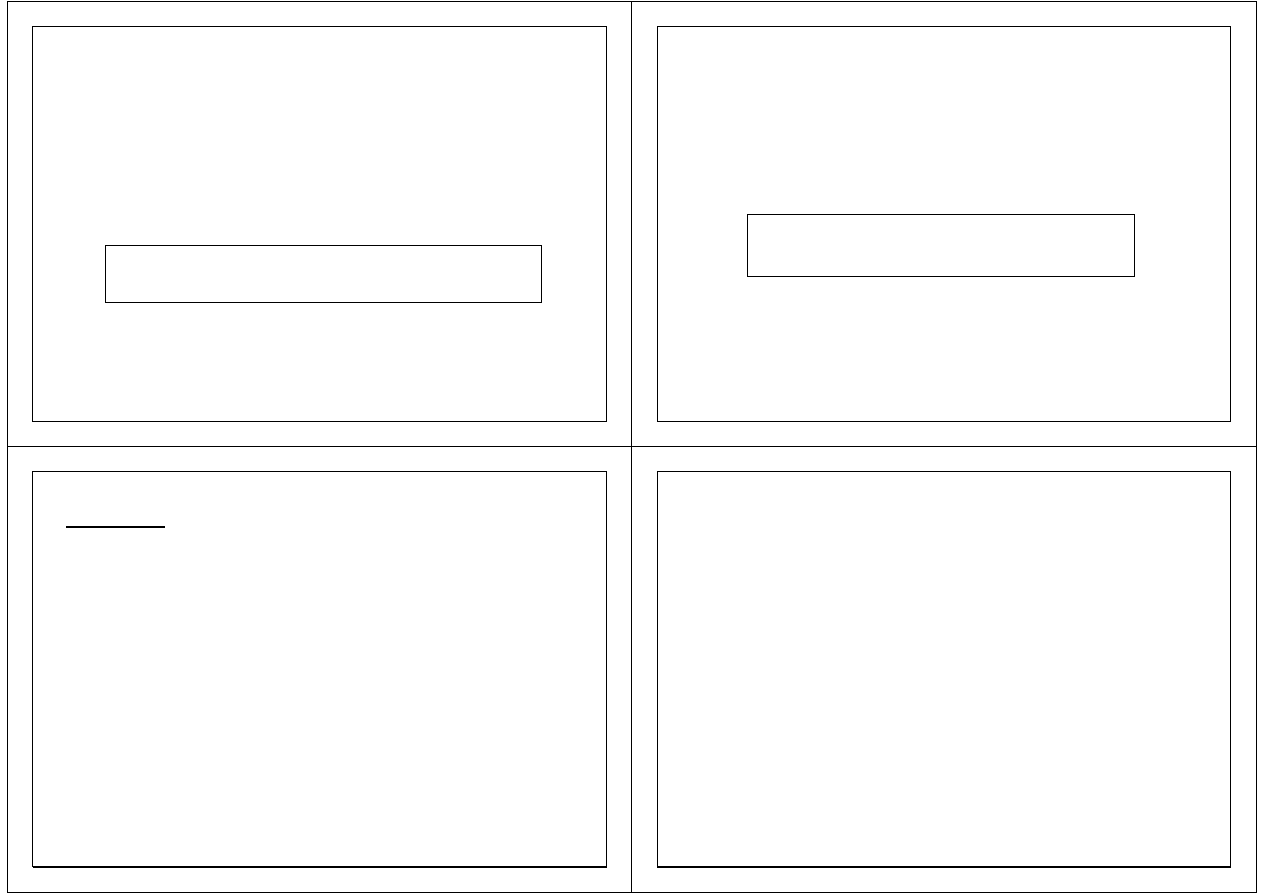
spełnia aksjomaty prawdop. Kołmogorowa. Nazywamy ją
rozkładem prawd. rzeczywistej zm. l. X.

2. Niezależne zmienne losowe

Rzeczywiste zm. l. X

1

, X

2

,…, X

n

określone na tej samej

przestrzeni (

Ω

, B, P) nazywamy niezależnymi zm. l., gdy dla

każdego ciągu zbiorów borelowskich B

1

, B

2

,…B

n

∏

=

=

∈

ω

∈

ω

=

∈

ω

∈

ω

n

i

i

i

n

i

i

i

B

X

B

X

1

1

}

)

(

:

P{

)}

)

(

(

:

P{

Ω

Ω

Ω

Ω

Ω

Ω

Ω

Ω

I

.

Uwaga.

1.

Dla x, x

1

, x

2

∈

R (gdzie x

1

< x

2

) zdarz. jest również zbiór

{

ω∈Ω

: X(

ω

) < x}, który ozn. X < x oraz zbiór X

≥

x i in.

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

6

Przykład 1. Określić zm. l. opisującą wynik badania jakości
pewnej partii wyrobów.

Rozwiązanie.

Jako zm. l. wystarczy obrać funkcję przyjmują-

cą dwie wartości, np. 1, jeżeli wylosowany wyrób

ω

okaże się

wadliwy oraz 0, jeżeli okaże się dobry. Funkcję tę można za-
pisać wzorem:

p.

p.

w

dobrego

wyrobu

dla

,

,

1

0

=

)

(







ω

X

, gdzie

ω∈Ω

.

Zm. l. X z przykładu 1 nazywa się zm. l. zero-jedynkową.

Tak określona zm. l. może być modelem dowolnego doświad-
czenia dychotomicznego, tj. takiego którego wynik zaliczyć
można jedynie do dwóch wykluczających się kategorii.

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

7

Przykład 2. Określić dwie zm. l. Z

1

i Z

2

opisujące wynik zali-

czenia przedmiotu i zbadać ich niezależność.

Rozwiązanie.

Zm. l. Z

1

i Z

2

są funkcjami

Z

1

, Z

2

: {A, B, C, D, E, F}

→

R,

które określamy następująco:

Z

1

(A)

=

5;

Z

2

(

ω

)

=

0 dla

ω

∈

{F},

Z

1

(B)

=

4,5;

Z

2

(

ω

)

=

1 dla

ω

∈

Ω

\{F},

Z

1

(C)

=

4;

Z

1

(D)

=

3,5;

Z

1

(E)

=

3;

Z

1

(F)

=

2.

Zm. l. Z

1

jest określona zgodnie z systemem ocen w szkolnic-

twie wyższym, a Z

2

informuje o zaliczeniu przedmiotu.

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

8

3. Pomiary bezpośrednie i ich skale

Pomiar bezpośredni

−−−−

doświadczenie polegające na przy-

porządkowaniu liczb przedmiotom (obiektom) lub wydarze-
niom zgodnie z pewnym zbiorem reguł określających jed-
nostki pomiaru, przyrządy pomiarowe, warunki pomiaru, itp.
Wynikiem pomiaru są dwa rodzaje wielkości, te które mówią
o liczebności zbioru obiektów, i te, które charakteryzują sto-
pień nasilenia zjawiska wyrażony w pewnej skali pomiarowej.

Skala pomiarowa

−−−−

zbiór W możliwych wyników pomiaru.

Zwykle skala jest podzbiorem zbioru liczb rzeczywistych wy-
rażonych w pewnych jednostkach miary.

Wyróżniamy następujące

skale pomiarowe:

dychotomicz-

na, nominalna, porządkowa, przedziałowa i ilorazowa.

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

9

4. Dystrybuanty i ich własności

Dystrybuantą

(ang.

cumulative distribution function

(CDF)) zm. l. X nazywamy funkcję rzeczywistą zmiennej rze-
czywistej F

X

: R

→

R, określoną wzorem:

F

X

(x)

=

P(X

≤

x)

=

P{

ω∈Ω

: X(

ω

)

≤

x}.

Uwaga.

Podana definicja dystrybuanty jest zgodna z nor-

mą PN-ISO 3534-1. W literaturze naukowej często dystrybu-
anta jest definiowana wzorem F

X

(x)

=

P(X < x).

Dla dwuwymiarowej zm. l. (X, Y) funkcję F

X,Y

, określoną

dla każdej pary liczb rzeczywistych (x, y), wzorem:

)

,

(

P

)

,

(

)

,

(

,

2

y

Y

x

X

y

x

F

y

x

Y

X

≤

≤

=

∋

a

R

nazywamy

dystrybuantą łączną

(the join CDF.)

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

10

Dystrybuantami

brzegowymi (marginal distribution func-

tion)

zm. l. X i Y nazywamy funkcje F

X

i F

Y

, gdzie

F

X

=

lim

y

→∞

F(x, y), F

Y

=

lim

x

→∞

F(x, y).

Twierdzenie o dystrybuancie

Funkcja F(x) jest dystrybuantą zm. l. o wartościach rzeczywi-
stych wtedy i tylko wtedy, gdy

1. jest funkcją niemalejącą, to znaczy spełnia formułę

∀

(x

1

, x

2

∈

R) (x

1

< x

2

⇒ F(x

1

)

≤

F(x

2

));

2. ma własności graniczne

0

=

)

(

lim

x

F

x

−∞

→

,

1

=

)

(

lim

x

F

x

+∞

→

,

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

11

3. jest funkcją co najmniej prawostronnie ciągłą

1

, tj.

∀

x

∈

R,

∀ε

>0,

)

(

)

(

lim

)

(

0

x

F

x

F

x

F

def

=

ε

+

=

+

→

ε

.

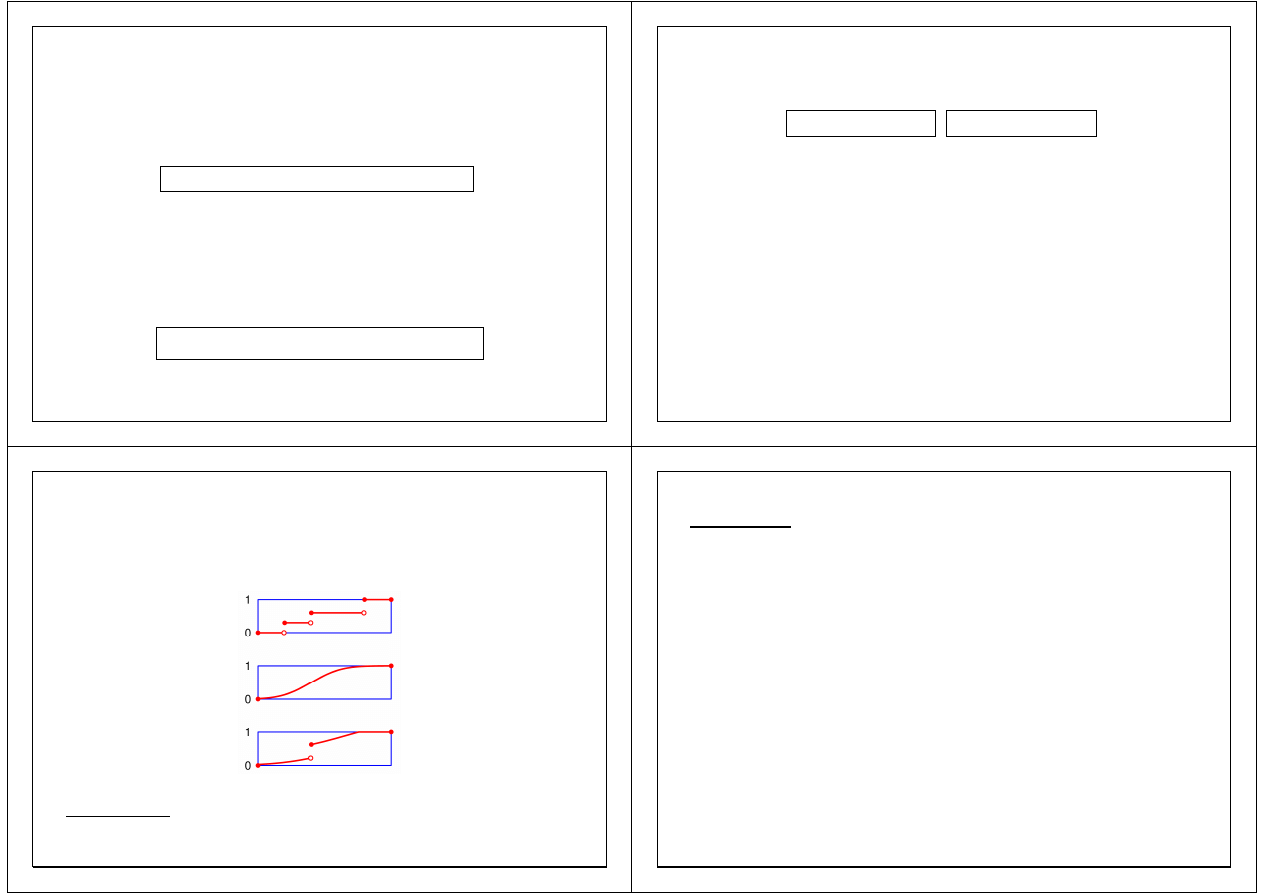
Rys. 1. Graficzne przedstawienie własności dystrybuanty

1

Przyjęta co najmniej prawostronna ciągłość jest zgodna z obowiązującą normą PN-ISO 3534-1:2002.

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

12

Przykład 3. Niech rozkład ocen z zaliczenia przedmiotu bę-
dzie równomierny.

a) Określić dwie różne zm. l. opisujące to doświadczenie.

b) Wyznaczyć dystrybuanty F

1

i F

2

.

c) Czy zm. l. opisujące to doświadczenie są niezależne ?

Rozwiązanie.

a) Niech

Ω

=

{A, B, C, D, F}, gdzie zdarzenia

elementarne oznaczają otrzymaną ocenę przez losowo wybra-
nego studenta. Zm. l. Z

1

i Z

2

określamy jak w przykładzie 2.

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

13

b) Dystrybuanty zm. l. Z

1

i Z

2

są określone wzorami:































≥

∈

∈

∈

∈

∈

<

=

.

5

),

5

;

5

,

4

[

),

5

,

4

;

4

[

),

4

;

5

,

3

[

),

5

,

3

;

3

[

),

3

;

2

[

,

2

dla

dla

dla

dla

dla

dla

dla

1

6

/

5

6

/

4

6

/

3

6

/

2

6

/

1

0

)

(

1

x

x

x

x

x

x

x

x

F

.

1

),

1

,

0

[

,

0

dla

dla

dla

1

6

/

1

0

)

(

2

≥

∈

<












=

y

y

y

y

F

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

14

c) Sprawdzamy niezależność Z

1

i Z

2

, np. czy

F

1

(3)F

2

(0)

=

F

1,2

(3, 0).

F

1

(3)

=

P(Z

1

≤

3)

=

P{E, F}

=

1/3,

F

2

(0)

=

P(Z

2

≤

0)

=

P{F}

=

1/6,

P(Z

1

≤

3, Z

2

≤

0)

=

P{F}

=

1/6, czyli F

1

(3) F

2

(0)

≠

F

(1, 2)

(3, 0).

Stąd wniosek, że zm. losowe Z

1

i Z

2

nie są niezależne.

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

15

5. Zmienna losowa typu dyskretnego i jej rozkład

Zm. l. X określoną na (

Ω

, B, P) nazywamy

zm. l.

typu dys-

kretnego

(

discrete R.V.

), jeżeli jej obraz X(

Ω

) jest zbiorem co

najwyżej przeliczalnym.

Dystrybuanta F

X

rzeczywistej zm. l. X jest wówczas funk-

cją przedziałami stałą. Skoki ma tylko w punktach nieciągło-
ś

ci x

1

, x

2

,…, x

n

,….

Skoki w tych punktach mają wartości p

1

, p

2

,…, p

n

,…,

gdzie p

i

=

P(X

=

x

i

)

=

P{

ω∈Ω

: X(

ω

)

=

x

i

} oraz

Σ

p

i

=

1.

Zm. l. typu dyskretnego jest modelem pomiarów w sła-

bych skalach. Modele jakościowego odbioru partii produktów
oraz rzutu kostką są przykładami zm. l. tego typu.

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

16

Funkcja prawdopodobieństwa

Niech X:

Ω

→ R będzie zm. l. typu dyskretnego.

Funkcją prawdopodobieństwa (probability mass function

PMF) nazywamy funkcję f

X

: R → [0, 1] określoną wzorem:

f

X

(x)

=

P(X

=

x)

=

P{

ω∈Ω

: X(

ω

)

=

x}.

Jeżeli obraz X(

Ω

)

=

{x

1

, x

2

, ... } oraz f

X

(x

k

)

=

p

k

, to PMF

jest podawana w postaci ciągu par {(x

k

, p

k

): k

=

1, 2,…}lub

dwuwierszowej tablicy

















=

...

...

3

2

1

3

2

1

p

p

p

x

x

x

f

X

.

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

17

Dla wektora l. (X, Y) z obrazami X(

Ω

) i Y(

Ω

), możemy

rozważać zdarzenia dla każdej pary ich wartości (x

i

, y

j

), gdzie

x

i

,

∈

X(

Ω

), y

j

∈

Y(

Ω

), tj.

{

ω∈Ω

: X(

ω

)

=

x

i

, Y(

ω

)

=

y

j

} (krótko {X

=

x

i

, Y

=

y

j

}).

Prawdop. P(X

=

x

i

, Y

=

y

j

) określa łączny rozkład pary (X, Y).

Funkcję f

X,Y

: R

2

→ [0, 1] określoną wzorem

f

X,Y

(x

i

, y

j

)

=

P(X

=

x

i

, Y

=

y

j

) ,

nazywamy

łączną funkcją prawd

. (the join PMF) dla pary X i

Y.

Brzegowe f. prawd. f

X

i f

Y

(“marginal” PMFs)

f

X

(x

i

)

=

P(X

=

x

i

)

=

p

i

•

, f

Y

(y

j

)

=

P(Y

=

y

j

)

=

p

•

j

,

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

18

otrzymujemy poprzez zsumowanie prawd. po wszystkich
wartościach pozostałej zm. l., tj.

f

X

(x

i

)

=

Σ

j

f

X,Y

(x

i

, y

j

), f

Y

(y

j

)

=

Σ

i

f

X,Y

(x

i

, y

j

).

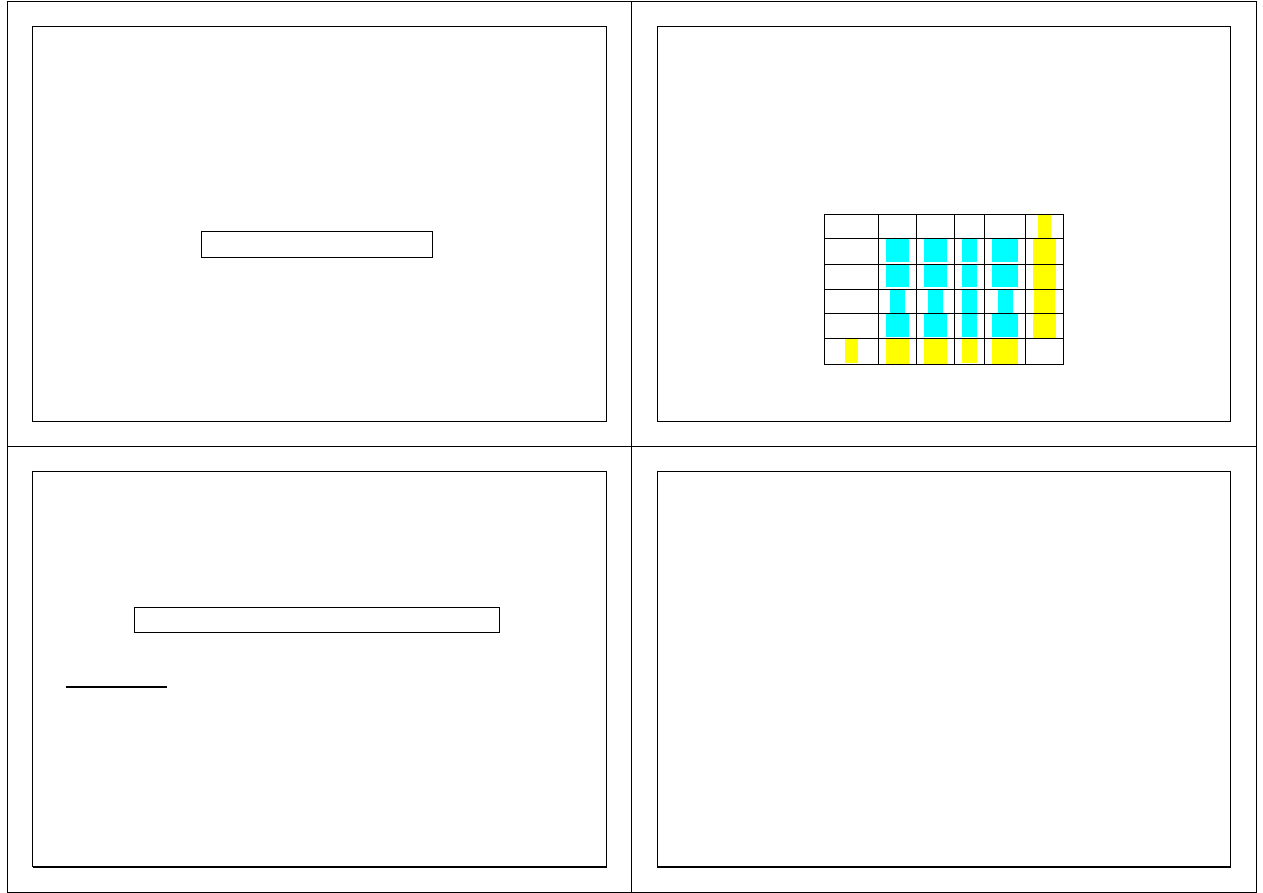
Elementy p

ij

łącznej funkcji prawd. zwykle umieszczamy w

tablicy dwudzielczej.

Tablica 1.

Schemat tablicy dwudzielczej

X \ Y y

1

y

2

... y

m

f

X

x

1

p

11

p

12

... p

1m

p

1

•

x

2

p

21

p

22

... p

2m

p

2

•

...

... ... ... ... …

x

n

p

n1

p

n2

... p

nm

p

n

•

f

Y

p

•

1

p

•

2

... p

•

m

1

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

19

Twierdzenie

(o funkcji prawd. niezależnych zm. l.). Zm. l.

X

1

, X

2

,…, X

n

o rozkładach typu dyskretnego są niezależne

wtedy i tylko wtedy, gdy dla każdego ciągu x

1

, x

2

,…, x

n

war-

tości zm. l.

P(X

1

=

x

1

, X

2

=

x

2

,…, X

n

=

x

n

)

=

Π

i

P(X

i

=

x

i

) .

Przykład 4. Uzyskanie promocji na następny semestr, przez
studenta pewnego kierunku studiów, jest związane z zalicze-
niem przez niego, w ustalonym terminie, co najmniej sześciu
przedmiotów spośród ośmiu. Zakładamy, że zaliczenie przez
studenta jednego przedmiotu nie zależy od wyników zalicze-
nia przez niego innych przedmiotów. Ponadto zakładamy, że
prawd. zaliczenia poszczególnych przedmiotów są równe i

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

20

wynoszą p. Rozważamy dwóch studentów A i B. Dla studenta
A niech p

=

0,9; natomiast dla studenta B niech p

=

0,7.

a)

Dla rozważanych studentów wyznaczyć funkcje prawd.

oraz dystrybuanty liczby zaliczonych przedmiotów.

b)

Podać najbardziej prawd. liczby zaliczonych przedmio-

tów przez studentów A i B.

c)

Obliczyć prawd. uzyskania promocji przez studentów A

i B.

Rozwiązanie.

Oznaczenia: X i Y oznaczają losowe liczby za-

liczonych przedmiotów odpowiednio przez studentów A i B.
Zm. l. X i Y przyjmują wartości ze zbioru {0, 1, 2,..., 8}.

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

21

a) Zdarzenie X

=

x zajdzie, jeśli student A zaliczy x przedmio-

tów i pozostałe, tj. 8

−

x nie zaliczy. Może tego dokonać na „8

po x” sposobów, czyli prawd. zdarzenia X

=

x dla x

∈

{0, 1,…,

8} wyraża się wzorem:

x

x

p

p

x

x

X

−

−















=

=

8

)

1

(

8

)

(

P

Podobnie dla studenta B. Funkcje prawd. oraz dystrybuanty
zm. l. X i Y, tj. dla p

=

0,9 i p

=

0,7 są zestawione w tablicy.

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

22

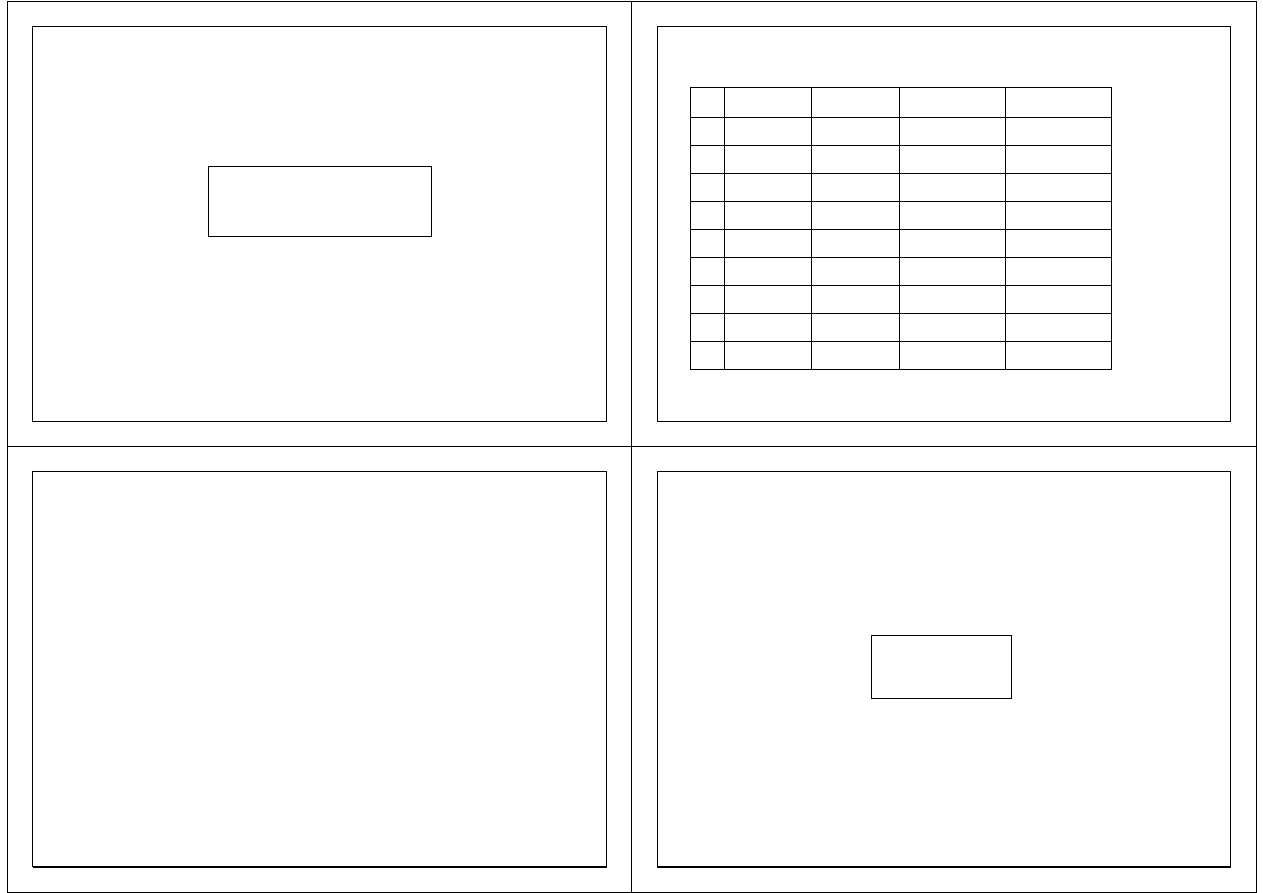
Tablica.

Funkcje prawd. i dystrybuanty

x P(X

=

x)

F

X

(x)

P(Y

=

x)

F

Y

(x)

0 1E-08

1E-08

0,00006561 0,00006561

1 7,2E-07 7,3E-07 0,00122472 0,00129033

2 2,27E-05 2,34E-05 0,01000188 0,01129221

3 0,000408 0,000432 0,04667544 0,05796765

4 0,004593 0,005024 0,1361367 0,19410435

5 0,033067 0,038092 0,25412184 0,44822619

6 0,148803 0,186895 0,29647548 0,74470167

7 0,382638 0,569533 0,19765032 0,94235199

8 0,430467 1

0,05764801 1

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

23

b) Najbardziej prawd. jest, że student A zaliczy 8 przedmio-
tów i prawdop. tego zdarzenia wynosi 0,430, natomiast dla
studenta B najbardziej prawd. jest, że zaliczy on 6 przedmio-
tów. Prawdop. tego zdarzenia wynosi 0,296.

c) Studenci A i B uzyskają promocje, jeżeli X

≥

6 i Y

≥

6.

Prawd. tych zdarzeń można obliczyć dwoma sposobami:

I: P(X

≥

6)

=

P(X

=

6)

+

P(X

=

7)

+

P(X

=

8);

II: P(X

≥

6)

=

1

−

P(X < 6)

=

1

−

P(X

≤

5)

=

1

−

F(5).

Podstawiając dane otrzymujemy P(X

≥

6)

=

0,961908, oraz

P(Y

≥

6)

=

0,55177381, czyli prawd. uzyskania promocji

przez studentów wynoszą odpowiednio 0,9619 i 0,5518.

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

24

6. Zmienna losowa typu ciągłego i jej rozkład

Zm. l. X o wartościach rzeczywistych nazywamy

zm. l.

ty-

pu

ciągłego

(

continuous random variable

), jeśli jej dystrybu-

anta F jest funkcją absolutnie ciągłą, tj. istnieje taka funkcja f

≥

0, że dla każdego x

∈

R

∫

∞

−

=

x

du

u

f

x

F

)

(

)

(

.

Obraz X(

Ω

) zm. l. typu ciągłego jest zbiorem nieprzeli-

czalnym, a prawd., że przyjmie szczególną wartość x wynosi
zero, tj. P(X

=

x)

=

0.

Zm. l. typu ciągłego zwykle jest modelem pomiaru wielko-

ś

ci fizycznych, np.: temperatury lub gęstości materiału.

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

25

Gęstością prawd.

(krótko gęstością, ang.

probability densi-

ty function

−

PDF) zm. l. X ciągłej, nazywamy funkcję f(x)

całkowalną w sensie Lebesque’a, która występuje pod zna-
kiem całki określającej jej dystrybuantę.

Krzywą gęstości

nazywamy wykres gęstości prawd. f(x).

Jeżeli gęstość jest różna od zera tylko w przedziale (a, b), to
mówimy, że rozkład jest skoncentrowany w tym przedziale.

Własności.

Funkcja f(x) jest gęstością pewnej ciągłej zm. l.

wtedy i tylko wtedy, gdy spełnia dwa warunki:
1. f (x)

≥

0 dla x

∈

R

−

warunek nieujemności,

2.

1

)

(

=

∫

+∞

∞

−

dx

x

f

−

warunek unormowania.

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

26

Graficzną interpretacją całki dla a, b

∈

R i a < b, jest pole ob-

szaru ograniczonego wykresem gęstości f(x), osią odciętych i
prostymi x

=

a, x

=

b.

Funkcje CDF, PDF i PMF charakteryzujące rozkład zm. l.

X nazywamy jej

charakterystykami funkcyjnymi

.

Przykład 5. Sprawdzić, czy funkcja

],

1

,

0

[

],

1

,

0

[

dla

dla

0

)

1

(

)

(

∉

∈









−

=

x

x

x

cx

x

f

gdzie c jest pewną stałą.

może być PDF np. stanu zasobów paliwa na stacji paliw, w
losowej chwili. Wyznaczyć jej dystrybuantę. Sporządzić wy-
kresy tych funkcji. Jakie zdarzenie może nas zainteresować ?

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

27

Jeżeli dana jest dystrybuanta F(x) zm. l. X typu ciągłego, to

gęstość:

dx

x

F

d

x

f

X

)

(

)

(

=

.

Charakterystyką funkcyjną

zm. l. X nazywamy każdą

funkcję w pełni charakteryzującą jej rozkład.

Wprowadzone funkcje CDF, PDF i PMF charakteryzujące

rozkład zm. l. X są jej

charakterystykami funkcyjnymi

.

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

28

7. Parametry rozkładu

Parametrem rozkładu

zm. l. X nazywamy wielkość stałą od

której zależy jej rozkład. Najczęściej stosowane rozkłady za-
leżą od jednego lub dwóch parametrów. Zapis

α∈

J, gdzie

J

⊆

R oznacza, że parametr

α

jest dowolną stałą ze zbioru J.

Jeśli dystrybuanta F(x) i gęstość (lub funkcja prawdop.)

f(x) zm. l. X zależą od parametrów

α

i

β

, to stosowany jest za-

pis

F(x;

α

,

β

) i f (x;

α

,

β

),

z podaniem zakresów wartości parametrów. Zapis ten podkre-
ś

la, że funkcje CDF, PDF i PMF są rodzinami funkcji zależ-

nymi od parametrów. Ustalenie wartości parametrów jest za-
daniem statystyki matematycznej.

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

29

8. Funkcja kwantylowa i kwantyle

Niech F będzie dystrybuantą zm. l. X. Funkcją kwantylową

(ICDF) nazywamy funkcję F

−

1

określoną wzorem

F

−

1

(p)

=

inf {x

∈

R: F(x)

≥

p} dla p

∈

(0, 1)

Jeżeli F jest funkcją ciągłą i rosnącą, to F

−

1

jest funkcją od-

wrotną w zwykłym sensie (inverse cumulative distribution
function) i wówczas

x

=

F

−

1

(p)

oznaczamy x

p

i nazywamy

kwantylem rzędu

p.

Kwantyle rzędów 0,25; 0,50 i 0,75 nazywamy

kwartylami

,

przy czym kwantyl x

0,5

nazywamy kwartylem środkowym lub

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

30

medianą

(ang. median), natomiast kwantyle x

0,25

i x

0,75

odpo-

wiednio

kwartylem dolnym i górnym

.

Zastosowanie:

Kwantyle rozkładów zm. l. mają zastosowanie

w statystyce m. in. do konstrukcji przedziałów ufności dla
nieznanych parametrów oraz do wyznaczania obszarów kry-
tycznych przy testowaniu hipotez statystycznych.

Do najczęściej stosowanych kwantyli należą kwantyle

rozkładów:

normalnego,
t-Studenta,
chi-kwadrat,
F-Snedecora.

Wartości tych kwantyli są stablicowane.

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

31

9.

Do samodzielnego rozwiązania

1.

(Sprawdzanie elementów) Spośród 3 dobrych i 2 wadli-

wych elementów losujemy jednocześnie 3 elementy. Niech
X oznacza liczbę wylosowanych elementów wadliwych, a Y
liczbę wylosowanych elementów dobrych.
a)

Wyznaczyć PMF oraz CDF zm. l. X.

b)

Wyznaczyć PMF oraz CDF zm. l. Y.

c)

Wyznaczyć łączną PMF i sprawdzić czy zm. l. X i Y są

niezależne.

Odp.: a) PMF:















=

3

,

0

6

,

0

1

,

0

2

1

0

X

f

, CDF:

.

2

,

2

1

,

1

0

,

0

gdy

gdy

gdy

gdy

,

1

,

7

,

0

,

1

,

0

,

0

)

(

≥

<

≤

<

≤

<

















=

x

x

x

x

x

F

X

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

32

2. (Dwie kostki) Doświadczenie polega na rzucie dwiema
prawidłowymi kostkami do gry. Zmienna losowa X jest równa

i) sumie ilości wyrzuconych oczek,
ii) iloczynowi ilości wyrzuconych oczek,
iii) maksimum ilości wyrzuconych oczek,
iv) minimum ilości wyrzuconych oczek,

a)

Wyznaczyć f. prawd. i sporządzić jej wykres.

b)

Wyznaczyć dystrybuantę i sporządzić jej wykres.

c)

Obliczyć prawd. zdarzeń: X

≤

10; X

≥

10.

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

33

3. (O gęstości prawdopodobieństwa). Dana jest funkcja

i)

f x

x

x

x

b

x

b

( ) =

dla < 0

dla 0

0 dla

0

10

/

≤ ≤

>











,

ii)

f x

x

x

x

x

b

( ) =

dla 0

< 1

dla 1

<

poza tym

≤

−

≤











2

0

,

a) Dla jakiej wartości b dana funkcja jest gęstością pewnej

zm. l. X ? Naszkicować krzywą gęstości.

b) Wyznaczyć i naszkicować dystrybuantę.
c) Obliczyć prawd. zdarzenia X > 1,5.
d) Ustalić x tak, aby P(X

≤

x)

=

0,1; P(X

≥

x)

=

0,1 ?

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

34

4. (O dystrybuancie). Dobrać stałe a, b tak, aby podana
funkcja była dystrybuantą zm. l. X typu ciągłego a) Wyzna-
czyć PDF zm. l. X.

b) Które zdarzenie X < ½, czy X > ½ jest bardziej prawd. ?

.

1

,

1

1

,

1

gdy

gdy

gdy

,

1

,

)

1

(

,

1

)

(

2

>

≤

<

−

−

≤












+

+

=

x

x

x

x

b

a

x

F

Odp.: a

=

−

1; b

=

¼.

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

35

5. (O zużyciu EE) Dzienne zużycie energii elektrycznej
(w setkach kWh) pewnej firmy jest zm. l. X o gęstości:

.

3

x

lub

0

,

3

0

gdy

gdy

,

0

),

2

3

(

9

1

)

(

2

≥

≤

<

<









−

+

=

x

x

x

x

x

f

Obliczyć prawd. zdarzenia,

a)

ż

e zużycie energii w ciągu losowo wybranego dnia bę-

dzie: i) większe niż 50 kWh; ii) między 100 a 200 kWh,

b)

ż

e w ciągu 30 losowo wybranych dni będzie 10 dni,

w których zużycie energii przekroczy 200 kWh.

K. J. Andrzejczak, PiS15 W02: Zmienne losowe I

36

6. Czas T eksploatacji (w jedn. czasu.) pewnych urządzeń jest
zm. l. typu ciągłego o rozkładzie zadanym funkcją

F t

t

t

t

b

t

b

( ) =

0

dla

1,

2(

/ )

dla 1 <

1

dla >

≤

−

≤











1 1

,

a) Wyznaczyć tak stałą b, aby funkcja była dystrybuantą.
b) Wyznaczyć gęstość czasu T eksploatacji urządzeń i spo-

rządzić krzywą gęstości.

c) Obliczyć prawd. zdarzeń:

−

1

≤

T

≤

3/2; T > (1

+

b)/2

i podać ich interpretację geometryczną.