Wykład 3

Zmienna losowa i jej rozkład

Aktualizacja: 28 marca 2008

3.1. Pojęcie zmiennej losowej

W całym niniejszym wykładzie przyjmujemy, że (Ω, P ) jest ustaloną przestrzenią proba-
bilistyczną.

Definicja 3.1.

Funkcję X : Ω → R przyporządkowującą każdemu zdarzeniu elementarne-

mu liczbę rzeczywistą nazywamy zmienną losową.

Definicja 3.2.

Mówimy, że zmienna losowa X jest typu skokowego (dyskretnego),

jeśli może przyjmować jedynie skończoną lub nieskończoną, ale przeliczalną liczbę warto-
ści

1

. Wartości zmiennej skokowej X oznaczać będziemy przez x

1

, x

2

, ....

Przykład 3.1.

Rozpatrujemy doświadczenie polegające na rzucie symetryczną monetą.

Niech E = {orzeł, reszka} . Określamy zmienna losową X w sposób następujący:

X(orzeł) = 1,

X(reszka) = 0.

Zmienna losowa przyjmuje wartości ze zbioru {0, 1}, ma więc charakter dyskretny. Po-
nieważ prawdopodobieństwa poszczególnych zdarzeń elementarnych wynoszą 0.5, tak więc
możemy zapisać:

P (X = 1) = P {orzeł} = 0.5,
P (X = 0) = P {reszka} = 0.5.

Gdybyśmy, zgodnie z przyjętą regułą, oznaczyli wartości zmiennej losowej jako x

1

= 0,

x

2

= 1, to mamy, że odpowiadające im prawdopodobieństwa to p

1

= 0.5, p

2

= 0.5.

Przykład 3.2.

Dla celów statystycznych wylosowano grupę n gospodarstw domowych,

dla których określono liczbę osób czynnych zawodowo w rodzinie X

S

. Zmienna X

S

=

0, 1, 2, 4, 5 jest zmienną losową dyskretną, natomiast prawdopodobieństwo, że i członków

1

Mówimy, że funkcja przyjmuje przeliczalną ilość wartości, jeśli wszystkie jej wartości można ustawić

w nieskończony ciąg x

1

, x

2

, . . . .

1

Wykład 3. Zmienna losowa i jej rozkład

danej rodziny jest czynnych zawodowo możemy określić jako częstość empiryczną (czyli
posługując się definicją klasyczną)

P (X

S

= i) =

n

i

n

,

gdzie n

i

jest liczbą rodzin w wylosowanej próbie dla których stwierdzono, że X

S

jest równe

i.

Definicja 3.3.

Mówimy, że zmienna losowa X jest typu ciągłego, jeśli zbiorem jej

wartości jest pewien przedział liczbowy.

W rzeczywistym świecie zmienne losowe o charakterze ciągłym w swej czystej postaci

występują rzadko. Pomiary wartości wyrażanych przez liczby rzeczywiste, prowadzone
są bowiem zwykle z określoną dokładnością (np. do jednej setnej, tysięcznej, itp.), a
więc liczba możliwych różnych pomiarów może być nawet skończona. Często jednak zbiór
wartości tego typu zmiennej jest tak liczny, że praktyce przyjąć musimy iż stanowi on
przedział liczbowy. Tego typu zmienne losowe nazywamy quasi ciągłymi lub po prostu
ciągłymi.

Przykład 3.3.

Jeśli analizujemy wybraną (bardzo dużą) grupę przedsiębiorstw przemysło-

wych w pewnym regionie kraju, z punktu widzenia ich zadłużenia bankowego (w milionach
złotych), to możemy określić zmienną losową X, przyjmującą wartości wszystkich moż-
liwych kwot tego zadłużenia. Są to wartości rzeczywiste, wypełniające pewien przedział,
którego granice określa najmniejsza (zerowa) i największa możliwa wielkość zadłużenia.

W rozważanym przypadku prawdopodobieństwo wystąpienia konkretnej wartości zadłu-

żenia, np. 3.65786 miliona złotych, może być dokładnie równe zero (P (X = 3.65786) =
0), pomimo, że liczba ta może należeć do przedziału będącego zbiorem wartości zmien-
nej. Możemy ustalać jedynie prawdopodobieństwo zadłużenia w pewnym przedziale. Np.
P (3.5 < X < 4.4) = 0.4107 oznacza, że na każde 100 losowo badanych przedsiębiorstw
trafimy około 41, których zadłużenie jest wyższe niż 3.5 mln złotych, ale niższe niż 4.5
mln złotych).
Zauważmy, że zmienna ta ma charakter quasi ciągły. Pomiary wielkości zadłużenia doko-
nywane są z określoną dokładnością (co najwyżej do jednego grosza). Tym niemniej zbiór
możliwych wartości zmiennej jest tak liczny, że musimy traktować ją jako ciągłą.

Z definicji zmiennej losowej wynika, że wartości zmiennej losowej związane są z pewny-

mi zdarzeniami losowymi. Tak więc (jak widzimy w przedstawionych wyżej przykładach),
występowanie określonej wartości zmiennej losowej wiąże się z prawdopodobieństwem
wystąpienia zdarzeń losowych do których jest ona przypisana. Zmienna losowa, w prze-
ciwieństwie do innych zmiennych znanych nam z matematyki definiowana jest nie tylko
przez zbiór możliwych wartości, ale również przez odpowiednie prawdopodobieństwa okre-
ślające jak często wartości te wystąpią w badanej sytuacji. Konkretna wartość (nazywana
często realizacją) zmiennej losowej zależy jedynie od przypadku. Sposób rozdysponowania
całej „masy” prawdopodobieństwa (równej 1) pomiędzy wartości jakie przyjmuje zmien-
na losowa określamy mianem rozkładu prawdopodobieństwa zmiennej lub krótko
rozkładu zmiennej. Pojęcie rozkładu zmiennej jest bardzo ważne, i wymaga bliższego
sprecyzowania. Opis rozkładu zmiennych losowych skokowych i ciągłych odbywa się w
różny sposób, dlatego potraktujemy je jako odmienne zagadnienia.

2

Wykład 3. Zmienna losowa i jej rozkład

3.2. Rozkład zmiennej losowej skokowej

Przypuśćmy, że zmienna losowa X, typu skokowego (dyskretna), przyjmuje wartości
x

1

, x

2

, . . . z prawdopodobieństwami odpowiednio p

1

, p

2

, . . . . Prawdopodobieństwa te speł-

niają oczywiście równość

n

X

i=1

p

i

= 1,

(3.1)

gdy zbiór wartości zmiennej losowej X jest skończony lub równość

∞

X

i=1

p

i

= 1

(3.2)

w przypadku nieskończonej liczby wartości zmiennej losowej X.

Rozkład dyskretnej zmiennej losowej możemy określić za pomocą funkcji prawdopo-

dobieństwa lub dystrybuanty.

Definicja 3.4.

Zbiór prawdopodobieństw postaci

P (X = x

i

) = p

i

,

i = 1, 2, . . .

(3.3)

spełniających warunek (

3.2

) nazywamy funkcją prawdopodobieństwa zmiennej lo-

sowej X typu skokowego albo rozkładem prawdopodobieństwa zmiennej losowej
typu skokowego.

Tak więc funkcja prawdopodobieństwa przypisuje wartościom zmiennej losowej praw-

dopodobieństwa ich realizacji. Jeśli zbiór wartości zmiennej jest skończony i stosunkowo
niewielki, rozkład zmiennej losowej przedstawiamy zwykle w formie tabelarycznej

x

i

x

1

x

2

. . . x

n

p

i

p

1

p

2

. . . p

n

Przykład 3.4.

Do tarczy oddaje się w sposób niezależny trzy strzały. Prawdopodobieństwo

trafienia w tarczę dla każdego strzału wynosi

1
2

. Zbiór zdarzeń elementarnych dla tego

doświadczenia przedstawia się następująco (T – trafienie, C – chybienie):

E = {CCC, CCT, CT C, T CC, CT T, T CT, T T C, T T T }.

Niech zmienna losowa X oznacza liczbę trafień w tarczę. Przyjmuje więc ona wartości:
x

1

= 0, x

2

= 1, x

3

= 2, x

4

= 3. Stosując elementarne zasady rachunku prawdopodobień-

stwa, możemy obliczyć:

P (X = 0) = p

1

=

1
8

,

P (X = 1) = p

2

=

3
8

,

P (X = 2) = p

3

=

3
8

,

P (X = 3) = p

4

=

1
8

.

3

Wykład 3. Zmienna losowa i jej rozkład

Łatwo widać, że p

1

+p

2

+p

3

+p

4

= 1, zatem obliczone prawdopodobieństwa można traktować

jako wartości funkcji prawdopodobieństwa zmiennej losowej X. W ujęciu tabelarycznym
funkcja ta przedstawia się następująco:

x

i

0

1

2

3

p

i

1
8

3
8

3
8

1
8

Przykład 3.5.

Wylosowaną grupę 1000 przedsiębiorstw przemysłowych przeanalizowano

pod względem współpracujących z nimi kooperantów. Zmienną losową X, określono jako
liczbę kooperantów. Określono, że może ona przyjmować wartości 2, 3, 4, 5 oraz 6. Obli-
czone liczby zakładów dla poszczególnych pięciu poziomów realizacji zmiennej wyniosły w
badanej grupie odpowiednio: 121, 362, 309, 184, 24. Na tej podstawie możemy oszacować
prawdopodobieństwa liczby kooperantów jako częstości empiryczne:

x

i

2

3

4

5

6

p

i

0.121 0.362 0.309 0.184 0.024

Oczywiście suma poszczególnych prawdopodobieństw jest równa 1, tak więc możemy je
traktować jako rozkład liczby kooperantów w zakładach przemysłowych.

Do opisu rozkładu prawdopodobieństwa zmiennej losowej służy również funkcja zwana

dystrybuantą.

Definicja 3.5.

Dystrybuantą zmiennej losowej X nazywamy funkcję F (x) określoną

na zbiorze liczb rzeczywistych, jako

F (x) = P (X ≤ x).

(3.4)

Znaczenie dystrybuanty polega między innymi na tym, że jak zobaczymy w przyszłości,
powyższa definicja stosuje się zarówno do zmiennych dyskretnych jak i ciągłych. W oby-
dwu przypadkach wartość dystrybuanty jest równa prawdopodobieństwu tego, że zmienna
losowa X przyjmie wartość nie większą od wartości argumentu.
Dla skokowej zmiennej losowej X, która przyjmuje wartości x

1

, x

2

, . . . z prawdopodobień-

stwami p

1

, p

2

, . . . , dystrybuanta ma postać

F (x) = P (X ≤ x) =

X

x

i

≤x

P (X = x

i

) =

X

x

i

≤x

p

i

,

−∞ < x < ∞.

(3.5)

Dystrybuantę zmiennej skokowej X zapisać możemy również następująco

F (x) =











































0

dla x < x

1

p

1

dla x

1

≤ x < x

2

p

1

+ p

2

dla x

3

≤ x < x

4

...

... ...

p

1

+ p

2

+ . . . + p

n−1

dla x

n−1

≤ x < x

n

1

dla x

n

≤ x

(3.6)

Powyższy zapis uwidacznia podstawowe własności dystrybuanty dyskretnej zmiennej lo-
sowej:

4

Wykład 3. Zmienna losowa i jej rozkład

Własność 3.1 (Własności dystrybuanty).

(D1)

0 ≤ F (x) ≤ 1,

(D2)

lim

x→−∞

F (x) = 0 oraz lim

x→∞

F (x) = 1,

(D3)

F jest funkcją niemalejącą (tzn. dla x

1

< x

2

zachodzi F (x

1

) ≤ F (x

2

) ) i przedziałami

ciągłą,

(D4)

F jest funkcją prawostronnie ciągłą.

Opierając się na znajomości dystrybuanty możemy wyznaczyć prawdopodobieństwo

zdarzenia polegającego na tym, że zmienna losowa przyjmuje wartości z przedziału (a, b] ,
tzn. zdarzenia a < X ≤ b. Zdarzenie to możemy przedstawić jako różnicę zdarzeń

(X ≤ b) − (X ≤ a),

których prawdopodobieństwa można określić znając dystrybuantę

P (a < X ≤ b) = P (X ≤ b) − P (X ≤ a) = F (b) − F (a).

(3.7)

W szczególności na podstawie dystrybuanty zmiennej skokowej możemy wyznaczyć war-
tość jej funkcji prawdopodobieństwa

P (X = x

i

) = P (x

i−1

< X ≤ x

i

) = F (x

i

) − F (x

i−1

) =

X

k≤i

p

k

−

X

k≤i−1

p

k

= p

i

.

(3.8)

Przykład 3.6.

Dla zmiennej losowej z Przykładu

3.4

postać dystrybuanty, zgodnie ze

wzorem (

3.6

), możemy zapisać jako

F (x) =































0 dla x < 0

1
8

dla 0 ≤ x < 1

4
8

dla 1 ≤ x < 2

7
8

dla 2 ≤ x < 3

1 dla 3 ≤ x

.

Przykład 3.7.

Dla zmiennej losowej z Przykładu

3.5

postać dystrybuanty, zgodnie ze

wzorem (

3.6

), możemy zapisać jako

F (x) =











































0

dla x < 2

0.121 dla 2 ≤ x < 3
0.483 dla 3 ≤ x < 4
0.792 dla 4 ≤ x < 5
0.976 dla 5 ≤ x < 6
1

dla 6 ≤ x

.

5

Wykład 3. Zmienna losowa i jej rozkład

3.3. Rozkład zmiennej losowej ciągłej

Zgodnie z wcześniejszą definicją zmiennej losowej ciągłej jej wartości wypełniają prze-
dział liczbowy, co oznacza, że zbiór zdarzeń elementarnych, na którym określono taką
zmienną jest nieskończony i nieprzeliczalny. Przypisanie więc każdej wartości zmiennej
losowej dodatniego prawdopodobieństwa jest niemożliwe. Opis rozkładu zmiennej losowej
ciągłej musi więc przebiegać inaczej niż w przypadku dyskretnym. Nie możemy bowiem
zdefiniować dla niej funkcji prawdopodobieństwa. Z tego powodu podstawową rolę w tym
przypadku gra pojęcie funkcji gęstości prawdopodobieństwa.

Definicja 3.6.

Funkcją gęstości prawdopodobieństwa zmiennej losowej typu cią-

głego nazywamy funkcję f określona na zbiorze liczb rzeczywistych o następujących wła-
snościach

(G1)

f (x) ≥ 0,

x ∈ R,

(G2)

b

R

a

f (x)dx = P (a < x ≤ b),

dla dowolnych a < b.

Własność 3.2.

Funkcja gęstości spełnia też warunek:

+∞

Z

−∞

f (x)dx = P (−∞ < x ≤ +∞) = 1.

(3.9)

Tak więc prawdopodobieństwo realizacji zmiennej losowej w dowolnym przedziale (a, b]
określone jest poprzez całkę oznaczoną z funkcji gęstości prawdopodobieństwa tej zmiennej
w przedziale od a do b.

Graficzną interpretacją całki

R

b

a

f (x)dx jest pole obszaru ograniczonego wykresem

funkcji f (x), osią odciętych i prostymi x = a i x = b (patrz Rysunek

3.1

).

b

x

a

f x

( )

Rysunek 3.1: Graficzna interpretacja całki

R

b

a

f (x)dx

Zauważmy, że prawdopodobieństwo tego, że zmienna losowa równa jest pewnej określonej
wartości zgodnie z podaną wyżej definicja wynosi 0, ponieważ:

P (X = a) = P (a < X ≤ a) =

a

Z

a

f (x)dx = 0.

6

Wykład 3. Zmienna losowa i jej rozkład

W związku z powyższym zachodzi również równość:

P (a ≤ X ≤ b) = P (a < X < b).

Przykład 3.8.

Autobus pewnej linii kursuje regularnie co 5 minut. Pasażer przychodzi na

przystanek w przypadkowym momencie, nie kierując się rozkładem jazdy. Niech zmienną
losową X będzie czas oczekiwania (w minutach) pasażera na autobus. Określimy funkcję
gęstości prawdopodobieństwa zmiennej losowej X oraz obliczymy prawdopodobieństwo tego,
że czas oczekiwania na autobus będzie liczbą z przedziału (1, 3].

Czas oczekiwania jest zmienną losową, mogącą przyjąć każdą wartość z przedziału

[0, 5]. Z warunków zadania wynika, że gęstość prawdopodobieństwa w tym przedziale jest
funkcją stałą. Wszystkie wartości zmiennej losowej są jednakowo prawdopodobne, ponieważ
pasażer nie zna czasów odjazdów. Możemy zatem zapisać:

f (x) =











0 dla

x < 0

c dla 0 ≤ x ≤ 5

0 dla

5 < x

gdzie c jest pewną stałą. Wartość stałej c wyznaczyć można z warunku normalizacyjne-
go (

3.9

), jaki musi spełniać funkcja gęstości, tzn. że całka z gęstości od minus do plus

nieskończoności musi być równa 1. Tak więc w tym przypadku mamy:

1 =

+∞

Z

−∞

f (x)dx =

0

Z

−∞

f (x)dx +

5

Z

0

f (x)dx +

+∞

Z

5

f (x)dx =

=

0

Z

−∞

0dx +

5

Z

0

cdx +

+∞

Z

5

0dx = 0 + [cx]

5
0

+ 0 = 5c,

zatem

5c = 1 ⇔ c =

1
5

.

Obliczając prawdopodobieństwo P (1 < x ≤ 3) skorzystamy z własności (G2)

P (1 < x ≤ 3) =

3

Z

1

f (x)dx =

3

Z

1

1
5

dx =

·

1
5

x

¸

3

1

=

2
5

.

Rozkład ciągłej zmiennej losowej również możemy scharakteryzować za pomocą dys-

trybuanty. Korzystając z definicji funkcji gęstości, dystrybuantę zmiennej losowej X typu
ciągłego określić możemy jako

F (x) = P (X ≤ x) =

x

Z

−∞

f (t)dt,

(3.10)

gdzie f (t) jest funkcją gęstości zmiennej losowej X. Jak widzimy dystrybuanta jest więc
funkcja pierwotną funkcji gęstości prawdopodobieństwa zmiennej, tzn. funkcja gęstości

7

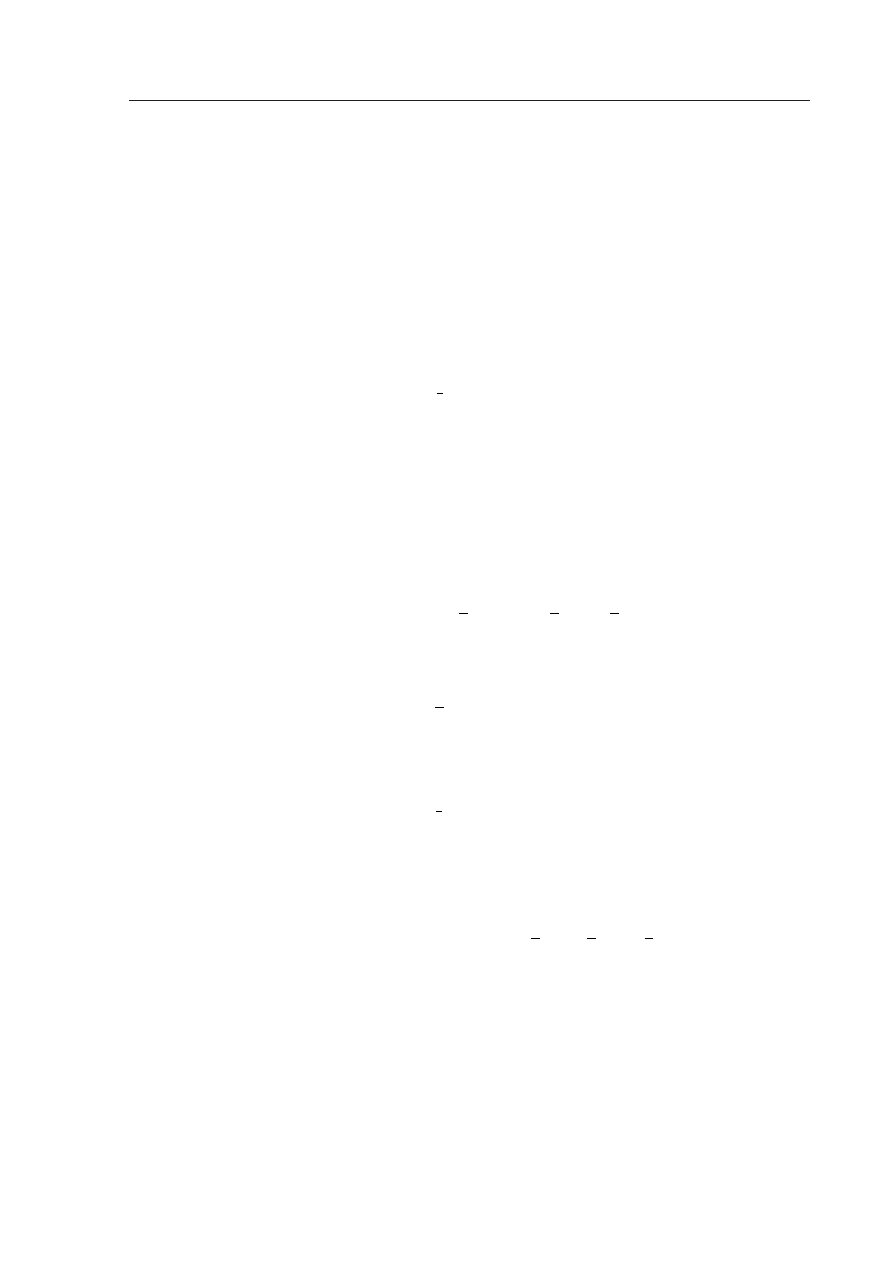
Wykład 3. Zmienna losowa i jej rozkład

jest pochodną dystrybuanty. Dystrybuanta ciągłej zmiennej losowej posiada podobne wła-
sności jak zmiennej skokowej (zob. Własność

3.1

) poza tym, że - w przeciwieństwie do

tamtej - jest funkcją ciągłą. Ponadto, również jak w przypadku dyskretnym:

P (a < X ≤ b) = P (X ≤ b) − P (X ≤ a) =

b

Z

−∞

f (x)dx −

a

Z

−∞

f (x)dx = F (b) − F (a) (3.11)

Przykład 3.9.

Określmy postać dystrybuanty dla zmiennej losowej z Przykładu

3.8

. Przy-

pomnijmy, że charakteryzowała się ona gęstością

f (x) =











0 dla

x < 0

1
5

dla 0 ≤ x ≤ 5

0 dla

5 < x

.

Tak więc dla x < 0 otrzymujemy

F (x) =

x

Z

−∞

0dt = 0,

dla 0 ≤ x ≤ 5

F (x) =

0

Z

−∞

0dt +

x

Z

0

1
5

dt = 0 +

·

1
5

t

¸

x

0

=

1
5

x,

dla x ≥ 5

F (x) =

0

Z

−∞

0dt +

5

Z

0

1
5

dt +

x

Z

5

0dt = 0 + 1 + 0 = 1.

Mamy więc

F (x) =











0

dla

x < 0

1
5

x dla 0 ≤ x ≤ 5

1

dla

5 < x

Korzystając z dystrybuanty również możemy obliczyć prawdopodobieństwo tego, że czas
oczekiwania na autobus będzie liczbą z przedziału (1, 3]

P (1 < X ≤ 3) = F (3) − F (1) =

1
5

· 3 −

1
5

· 1 =

2
5

.

8