Prawdopodobieństwo i statystyka
20.03.2006 r.
___________________________________________________________________________
Zadanie 1.
Zmienne losowe
są niezależne i mają jednakowy rozkład o gęstości
5
2
1
,
,
,
X
X
X
K
⎩
⎨
⎧
≤
>
=
−
0
0
0
)
(
x
gdy
x
gdy
e
x
p
x
θ
θ
θ
,
gdzie
0
>
θ
jest ustaloną liczbą. Niech Y oznacza zmienną losowa równą 1, gdy
, i równą 0 w pozostałych przypadkach. Niech
. Wyznaczyć
.
3
1
≥
X
∑
=
=
5
1
i
i
X
T
(
)
5
|
=
T
Y
E
(A) 0,05120
(B) 0,00256
(C) 0,02560
(D) 0,10240
(E) 0,01024
1
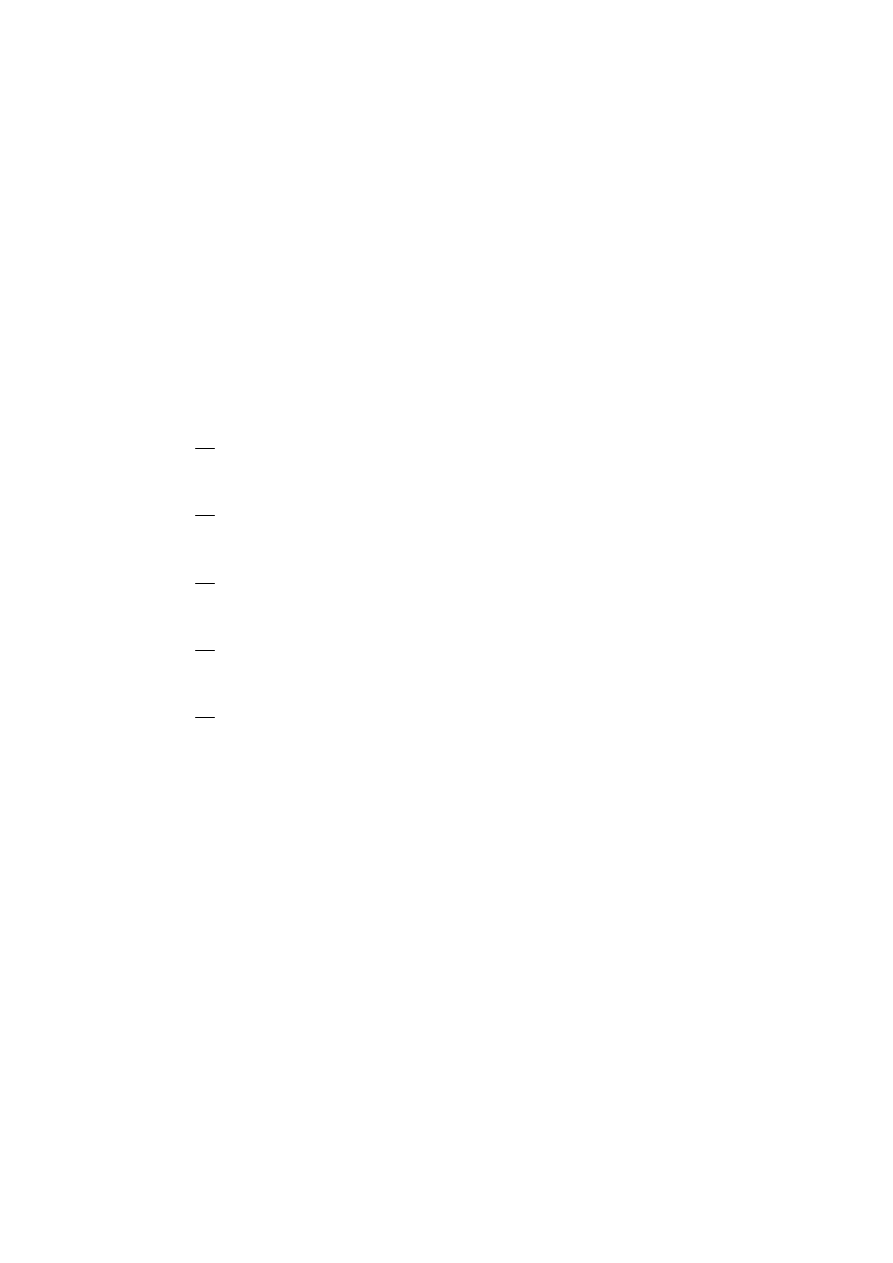
Prawdopodobieństwo i statystyka
20.03.2006 r.
___________________________________________________________________________
Zadanie 2.
Obserwujemy niezależne zmienne losowe
Zmienne losowe
mają ten sam rozkład o dystrybuancie
, a zmienne losowe
maja ten sam rozkład o dystrybuancie
. Dystrybuanta
spełnia warunek
4
3
2
1
3
2
1
,
,
,
,
,
,
Y
Y
Y
Y
X
X
X
.
3
2
1
,
,
X
X
X
1
μ
F
4
3
2
1
,
,
,
Y
Y
Y
Y
2
μ
F
μ
F
)
(
)
(
μ
μ
−
=
x
F
x
F
dla pewnej ustalonej, nieznanej, ciągłej, ściśle rosnącej dystrybuanty F.
Weryfikujemy hipotezę
2
1
0
:
μ
μ
=
H
przy alternatywie
2
1
1
:
μ
μ
>
H
stosując test o
obszarze krytycznym
}
13
:
{
>
=
S
S
K
,
gdzie S jest sumą rang zmiennych losowych
w próbce złożonej ze
wszystkich obserwacji ustawionych w ciąg rosnący. Wyznaczyć rozmiar testu.
3
2
1
,
,
X
X
X
(A)
35
11
(B)
35
12
(C)
35
10
(D)
35
9
(E)
35
8
2
Prawdopodobieństwo i statystyka
20.03.2006 r.
___________________________________________________________________________
Zadanie 3.
Zmienna losowa N ma rozkład Poissona z nieznanym parametrem
0
>
λ
. O
parametrze
λ
zakładamy, że podlega rozkładowi a priori gamma
.
Zmienna losowa
)
8
,
2
(
Gamma
θ
ma rozkład beta
. Zmienne N i
)
2
,
1
(
Beta
θ
są niezależne i
zmienne
θ
λ
i
są niezależne. Obserwujemy zmienną losową X, która przy znanych
wartościach
θ
i
N
ma rozkład dwumianowy
)
,
(
θ
N
bin
. Wyznaczyć wartości a i b
najlepszego liniowego predyktora zmiennej losowej N , to znaczy liczby a i b
minimalizujące wielkość
(
)
2
b
aX
N
E
−
−
.
A)
212
35
,
53
54
=
=
b
a
(B)
100
17
,
25
24
=
=
b
a
(C)
44
5
,
11
18
=
=
b
a
(D)
22
5
,
11
18
=
=
b
a
(E)
106
35
,
53
54
=
=
b
a
Uwaga.
Gęstość rozkładu gamma
)
,
(
β
α
Gamma
jest równa
x
e
x
x
p
β
α
α
β
α
α
β
−
−
Γ
=
1
,
)
(
)
(
dla
.
0
>
x
Gęstość rozkładu beta
)
,
(
β
α
Beta
jest równa
1
1
,
)
1
(
)
(
)
(
)
(
)
(
−
−
−
Γ
Γ
+
Γ
=
β
α
β
α
β
α
β
α
x
x
x
f
dla
)
1
,
0
(
∈
x
.
3
Prawdopodobieństwo i statystyka
20.03.2006 r.
___________________________________________________________________________
Zadanie 4.
Na podstawie prostej próby losowej
testowano hipotezę
przy alternatywie
, gdzie
jest parametrem odpowiadającym za
wariancję zmiennej losowej
za pomocą testu o obszarze krytycznym
20
2
1
,
,
,
X
X
X
K
1
:
2
0
=
σ
H
1
:
2
1
>
σ
H
2
σ
i
X
⎭
⎬
⎫
⎩
⎨
⎧
>
=
∑
=
20
1
2
i
i
t
X
K
.
Jeżeli dodatkowo wiadomo, że zmienne losowe
mają rozkład zadany gęstością
i
X
2
|
|
)
(
x
e
x
x
f
θ
θ
θ
−
=
, gdy
R
x
∈ ,
gdzie
0
>
θ
jest nieznanym parametrem, to przy poziomie istotności 05
,
0
=
α
,
wartość krytyczna t jest równa
(A) 55,7585
(B) 31,4104
(C) 18,3070
(D) 27,8793
(E) 15,7052
4
Prawdopodobieństwo i statystyka
20.03.2006 r.
___________________________________________________________________________
Zadanie 5.
Na podstawie prostej próby losowej
z rozkładu gamma o gęstości
n
X
X
X
X
,
,
,
,
3
2
1
K
⎩
⎨
⎧
≤
>
=
−
0
0
0
)
(
2
x
gdy
x
gdy
xe
x
f
x
θ
θ
θ
estymujemy parametr
θ
wykorzystując estymator największej wiarogodności
.
Wyznaczyć w przybliżeniu rozmiar próby n taki, że
θ
ˆ
95
,
0
05
,
0
|
ˆ
|
≈
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
≤
−
θ
θ
θ
P
.
Posłużyć się aproksymacją rozkładem normalnym. Wybrać spośród podanych liczb
najbliższe przybliżenie.
(A) 400
(B) 800
(C) 1600
(D) 3200
(E) 2400
5
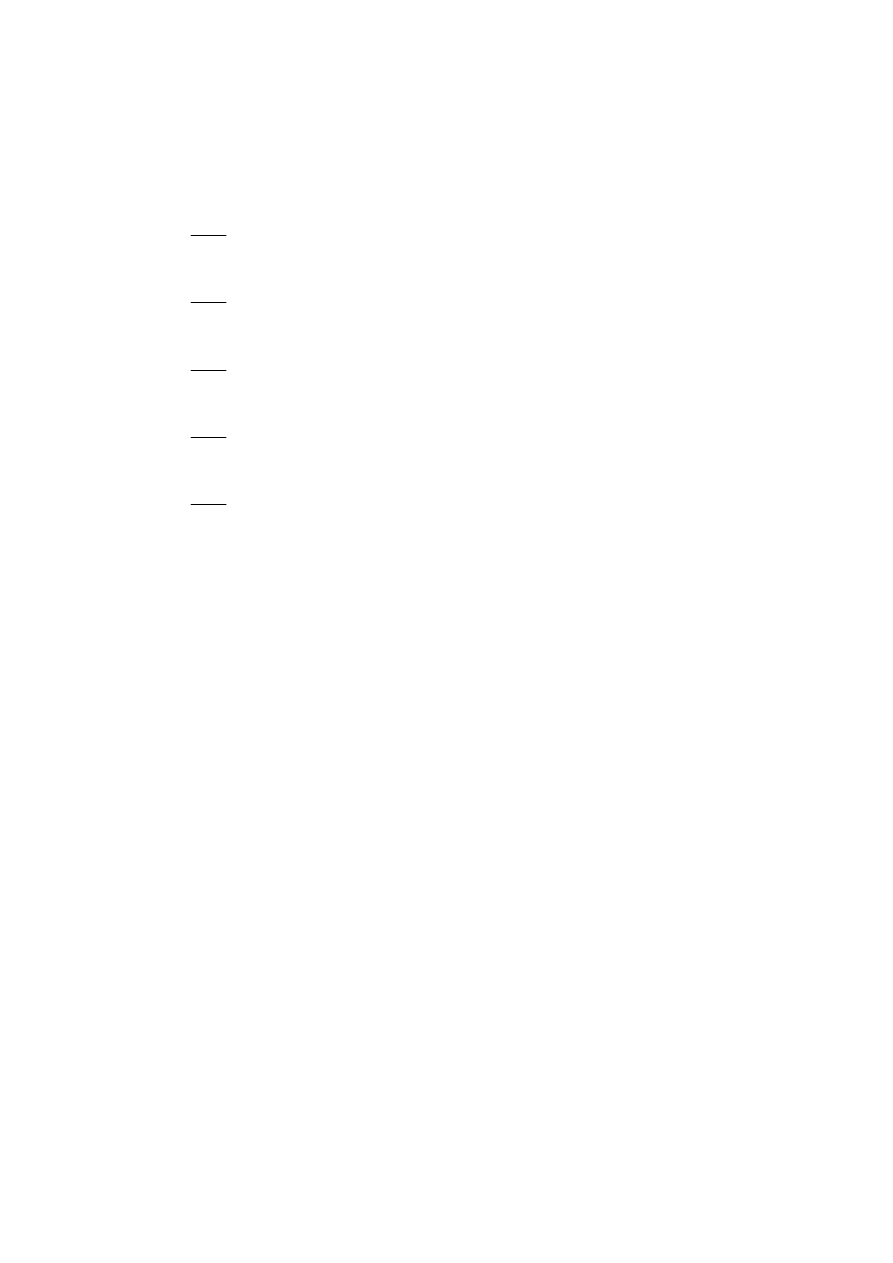
Prawdopodobieństwo i statystyka
20.03.2006 r.
___________________________________________________________________________
Zadanie 6.
Rzucono niezależnie 16 razy symetryczną monetą. Obliczyć prawdopodobieństwo, że
uzyskano 7 serii, jeśli wiadomo, że uzyskano 10 orłów i 6 reszek.
(A)
1001
210
(B)
1001
150
(C)
1001
75
(D)
1001
105
(E)
1001
45
Uwaga.
Serią nazywamy ciąg elementów jednego typu, przed i za którym występuje
element drugiego typu, na przykład w ciągu : aaabbbbaabbbbba jest 5 serii (3 serie
elementów typu a i 2 serie elementów typu b).
6
Prawdopodobieństwo i statystyka
20.03.2006 r.
___________________________________________________________________________
Zadanie
7.
Zmienne losowe X i Y są niezależne i każda ma rozkład prawdopodobieństwa o
gęstości
⎪⎩
⎪
⎨
⎧
≤
>
+
=
0
0
0
)
1
(
4
)
(
5
x
gdy
x
gdy
x
x
f
.
Rozważamy zmienną losową
(
)(
[
)
]
Y
X
X
U
+
+
+
=
1
1
ln
)
1
ln(
. Prawdziwe jest następujące
twierdzenie.
(A) Zmienna losowa U ma rozkład o gęstości
, gdy
3
3
)
1
(
140
)
(
x
x
x
p
−
=
)
1
,
0
(
∈
x
(B) Zmienna losowa U ma rozkład jednostajny na przedziale (0,1)
(C)
2
)
5
,
0
|
(
=
=
U
X
E
(D)
0
)
,
(
<
U
X
Cov
(E)
75
,
0
=
EU
7
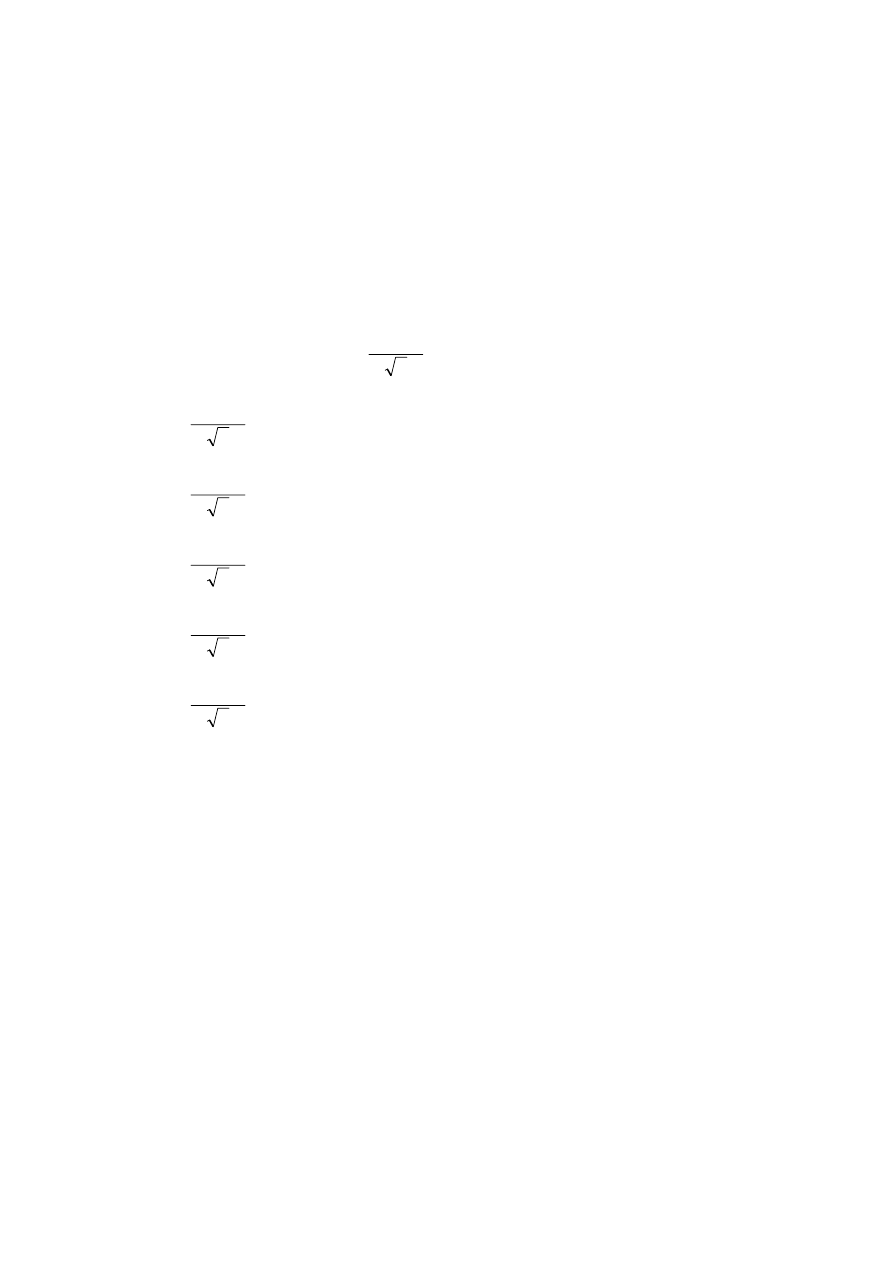
Prawdopodobieństwo i statystyka
20.03.2006 r.
___________________________________________________________________________
Zadanie
8.
Zmienne losowe
i
są niezależne. Każda ze
zmiennych losowych
ma jednakowy rozkład prawdopodobieństwa
n
Z
Z
Z
,
,
,
2
1
K
)
,
(
,
),
,
(
),
,
(
2
2
1
1
n
n
Y
X
Y
X
Y
X
K
i
Z
(
)
(
0
1
1
=
)
−
=
=
=
i
i
Z
P
p
Z
P
. Każda ze zmiennych losowych
ma jednakowy
rozkład prawdopodobieństwa taki, że
)
,
(
i
i
Y
X
m
EY
EX
i
i
=
=
i
i
współczynnik korelacji
2
σ
=
=
i
i
VarY
VarX
ρ
=
)
,
(
i
i
Y
X
Corr
. Niech
i
.
∑
=
=
n
i
i
i
n
X
Z
S
1
∑
=
=
n
i
i
i
n
Y
Z
T
1
Zbadać zbieżność rozkładów prawdopodobieństwa zmiennych
n
T
S
n
n
−
przy
+∞
→
n
(A)
)
2
)
1
(
2
,
0
(
2
2
2
p
m
p
N
n
T
S
n
n
+
−
→
−
ρ
σ
(B)
))
1
(
2
2
,
0
(
2
2
p
p
m
p
N
n
T
S
n
n
−
+
→
−
σ
(C)
))
1
(
)
1
(
2
,
0
(
2
ρ
σ
−
−
→
−
p
p
N
n
T
S
n
n
(D)
))
1
(
2
,
0
(
2
ρ
σ
−
→
−
p
N
n
T
S
n
n
(E)
n
T
S
n
n
−
nie jest ciągiem zbieżnym do rozkładu normalnego
8
Prawdopodobieństwo i statystyka
20.03.2006 r.
___________________________________________________________________________
Zadanie
9.
Wiadomo, że A, B, C są zdarzeniami losowymi takimi, że
5
2
)
(
=
B
P
4
1
)
|
(
=
B
A
P
4
1
)
|
(
=
A
C
P
5
3
)
(
=
∪ B
A
P
2
1
)
|
(
=
∩ B
A
C
P
.
Obliczyć ).
|
(
C
A
B
P
∩
(A)
Podane informacje nie wystarczają do wyznaczenia
)
|
(
C
A
B
P
∩
(B)
5
3
(C)
2
1
(D)
10
3
(E)
3
2
9
Prawdopodobieństwo i statystyka
20.03.2006 r.
___________________________________________________________________________
Zadanie
10.
Niech
będą niezależnymi zmiennymi losowymi o tym samym
rozkładzie jednostajnym na przedziale
6
2
1
,
,
,
X
X
X
K
[
]
θ
θ
,
−
, gdzie
0
>
θ
jest nieznanym
parametrem. Niech oznacza estymator największej wiarogodności parametru
θ
ˆ
θ
.
Obliczyć
(
)
θ
θ
θ
θ
ˆ
2
ˆ
<
<
P
.
(A) 0,8232
(B) 0,9998
(C) 0,9858
(D) 0,9844
(E) 0,8220
10
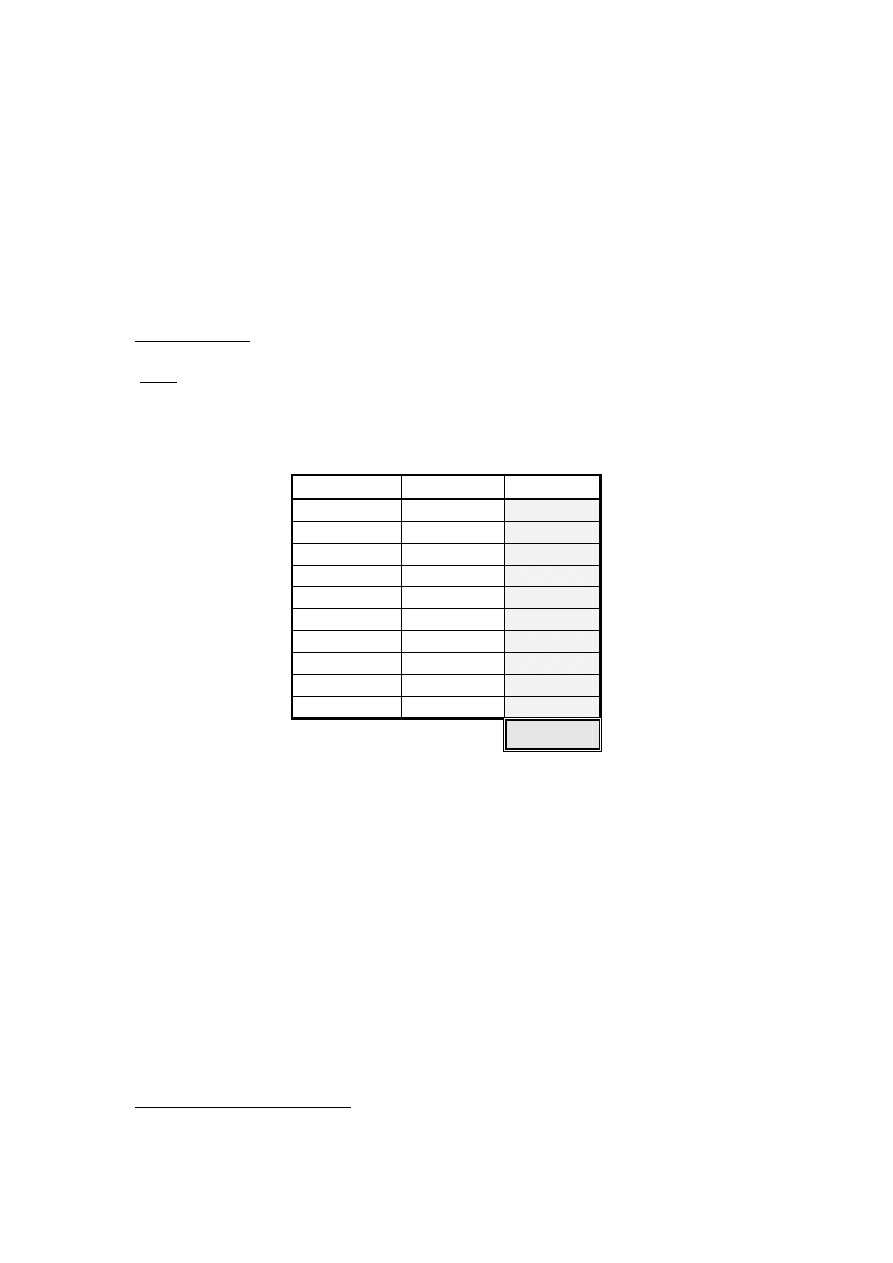
Prawdopodobieństwo i statystyka
20.03.2006 r.
___________________________________________________________________________
Egzamin dla Aktuariuszy z 20 marca 2006 r.
Prawdopodobieństwo i statystyka
Arkusz odpowiedzi
*
Imię i nazwisko : ...................... K L U C Z O D P O W I E D Z I ............................
Pesel ...........................................
Zadanie nr
Odpowiedź Punktacja
♦
1 C
2 A
3 A
4 D
5 B
6 B
7 B
8 D
9 E
10 D
*
Oceniane są wyłącznie odpowiedzi umieszczone w Arkuszu odpowiedzi.
♦
Wypełnia Komisja Egzaminacyjna.
11