Lecture Notes: Introduction to Finite Element Method

Chapter 1. Introduction

© 1998 Yijun Liu, University of Cincinnati

13

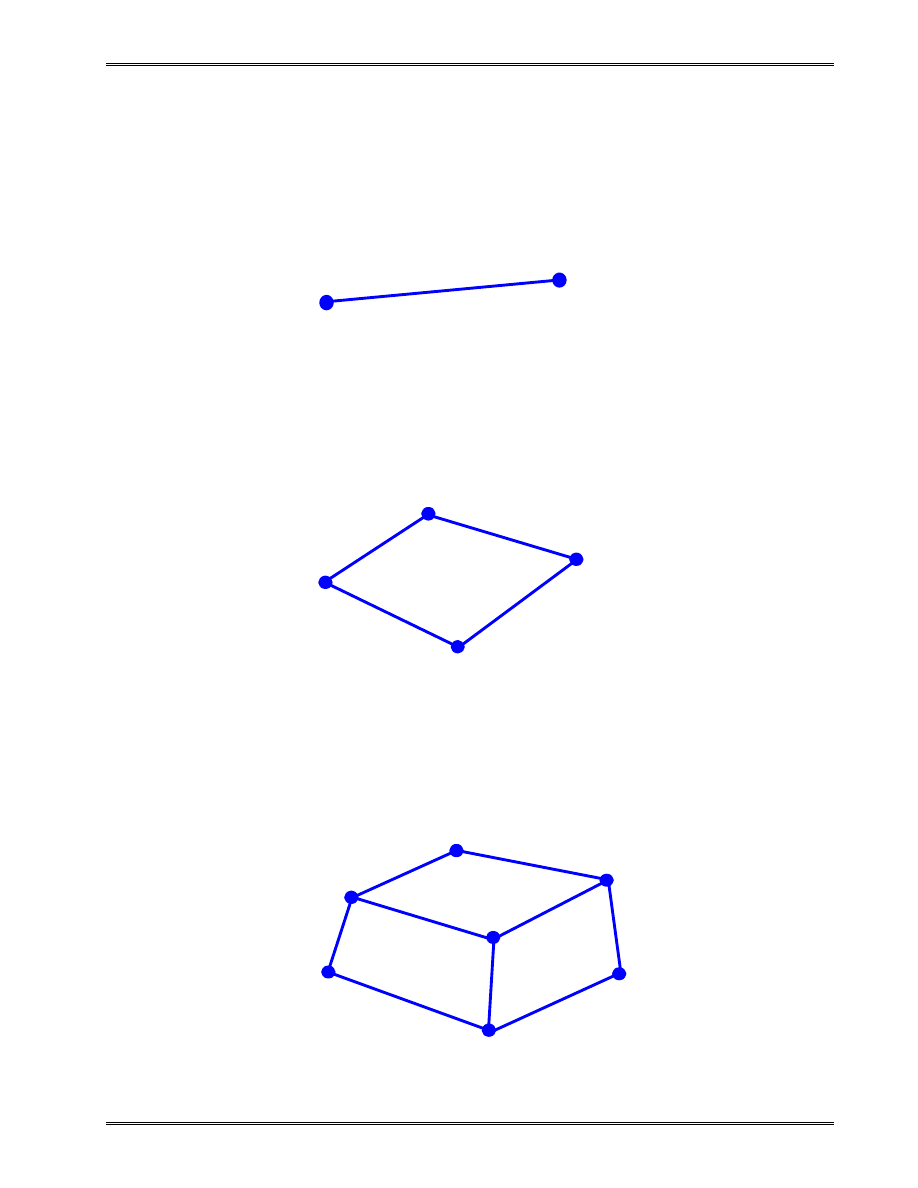
Types of Finite Elements

1-D (Line) Element

(Spring, truss, beam, pipe, etc.)

2-D (Plane) Element

(Membrane, plate, shell, etc.)

3-D (Solid) Element

(3-D fields - temperature, displacement, stress, flow velocity)

Lecture Notes: Introduction to Finite Element Method

Chapter 1. Introduction

© 1998 Yijun Liu, University of Cincinnati

14

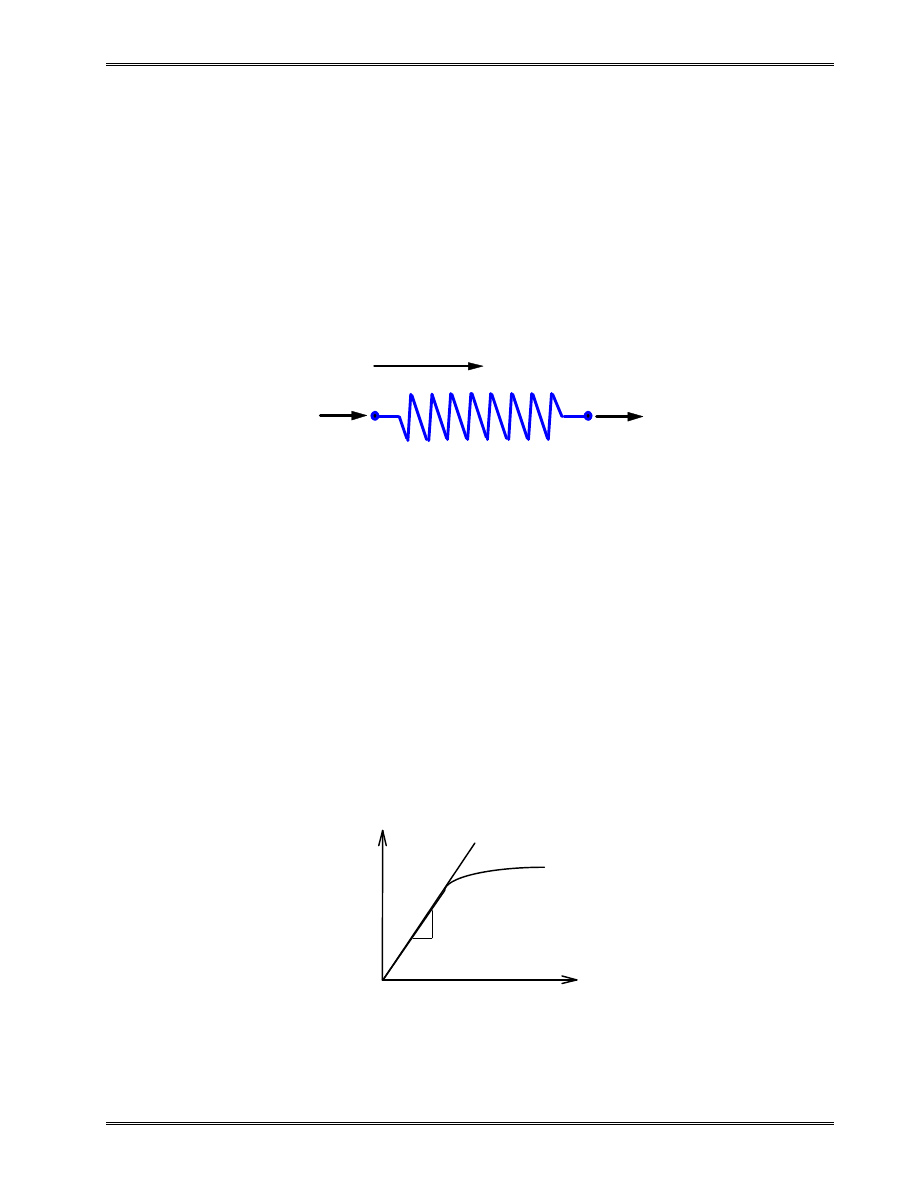
III. Spring Element

“

Everything important is simple

.

”

One Spring Element

Two nodes:

i, j

Nodal displacements:

u

i

, u

j

(in, m, mm)

Nodal forces:

f

i

, f

j

(lb, Newton)

Spring constant (stiffness):

k (lb/in, N/m, N/mm)

Spring force-displacement relationship:

F

k

= ∆

with

∆ =

−

u

u

j

i

k

F

=

/

∆

(> 0) is the force needed to produce a unit stretch.

k

i

j

u

j

u

i

f

i

f

j

x

∆

F

Nonlinear

Linear

k

Lecture Notes: Introduction to Finite Element Method

Chapter 1. Introduction

© 1998 Yijun Liu, University of Cincinnati

15

We only consider linear problems in this introductory

course.

Consider the equilibrium of forces for the spring. At node i,

we have

f

F

k u

u

ku

ku

i

j

i

i

j

= −

= −

−

=

−

(

)

and at node j,

f

F

k u

u

ku

ku

j

j

i

i

j

= =

−

= −

+

(

)

In matrix form,

k

k

k

k

u

u

f

f

i

j

i

j

−

−



















=













or,

ku

f

=

where

k = (element) stiffness matrix

u = (element nodal) displacement vector

f = (element nodal) force vector

Note that k is symmetric. Is k singular or nonsingular? That is,
can we solve the equation? If not, why?

Lecture Notes: Introduction to Finite Element Method

Chapter 1. Introduction

© 1998 Yijun Liu, University of Cincinnati

16

Spring System

For element 1,

k

k

k

k

u

u

f

f

1

1

1

1

1

2

1

1

2

1

−

−



















=













element 2,

k

k

k

k

u

u

f

f

2

2

2

2

2

3

1

2

2

2

−

−



















=













where

f

i

m

is the (internal) force acting on local node i of element

m (i = 1, 2).

Assemble the stiffness matrix for the whole system:

Consider the equilibrium of forces at node 1,

F

f

1

1

1

=

at node 2,

F

f

f

2

2

1

1

2

=

+

and node 3,

F

f

3

2

2

=

k

1

u

1,

F

1

x

k

2

u

2,

F

2

u

3,

F

3

1

2

3

Lecture Notes: Introduction to Finite Element Method

Chapter 1. Introduction

© 1998 Yijun Liu, University of Cincinnati

17

That is,

F

k u

k u

F

k u

k

k u

k u

F

k u

k u

1

1 1

1

2

2

1 1

1

2

2

2

3

3

2

2

2

3

=

−

= −

+

+

−

= −

+

(

)

In matrix form,

k

k

k

k

k

k

k

k

u

u

u

F

F

F

1

1

1

1

2

2

2

2

1

2

3

1

2

3

0

0

−

−

+

−

−



































=















or

KU

F

=

K is the stiffness matrix (structure matrix) for the spring system.

An alternative way of assembling the whole stiffness matrix:

“Enlarging” the stiffness matrices for elements 1 and 2, we

have

k

k

k

k

u

u

u

f

f

1

1

1

1

1

2

3

1

1

2

1

0

0

0

0

0

0

−

−



































=



















0

0

0

0

0

0

2

2

2

2

1

2

3

1

2

2

2

k

k

k

k

u

u

u

f

f

−

−



































=















Lecture Notes: Introduction to Finite Element Method

Chapter 1. Introduction

© 1998 Yijun Liu, University of Cincinnati

18

Adding the two matrix equations (superposition), we have

k

k

k

k

k

k

k

k

u

u

u

f

f

f

f

1

1

1

1

2

2

2

2

1

2

3

1

1

2

1

1

2

2

2

0

0

−

−

+

−

−



































=

+



















This is the same equation we derived by using the force
equilibrium concept.

Boundary and load conditions:

Assuming,

u

F

F

P

1

2

3

0

=

=

=

and

we have

k

k

k

k

k

k

k

k

u

u

F

P

P

1

1

1

1

2

2

2

2

2

3

1

0

0

0

−

−

+

−

−



































=















which reduces to

k

k

k

k

k

u

u

P

P

1

2

2

2

2

2

3

+

−

−



















= 









and

F

k u

1

1

2

= −

Unknowns are

U

= 









u

u

2

3

and the reaction force

F

1

(if desired).

Lecture Notes: Introduction to Finite Element Method

Chapter 1. Introduction

© 1998 Yijun Liu, University of Cincinnati

19

Solving the equations, we obtain the displacements

u

u

P k

P k

P k

2

3

1

1

2

2

2













=

+













/

/

/

and the reaction force

F

P

1

2

= −

Checking the Results

•

Deformed shape of the structure

•

Balance of the external forces

•

Order of magnitudes of the numbers

Notes About the Spring Elements

•

Suitable for stiffness analysis

•

Not suitable for stress analysis of the spring itself

•

Can have spring elements with stiffness in the lateral
direction, spring elements for torsion, etc.