PODSTAWY LINIOWEJ

TEORII SPRĘŻYSTOŚCI

•

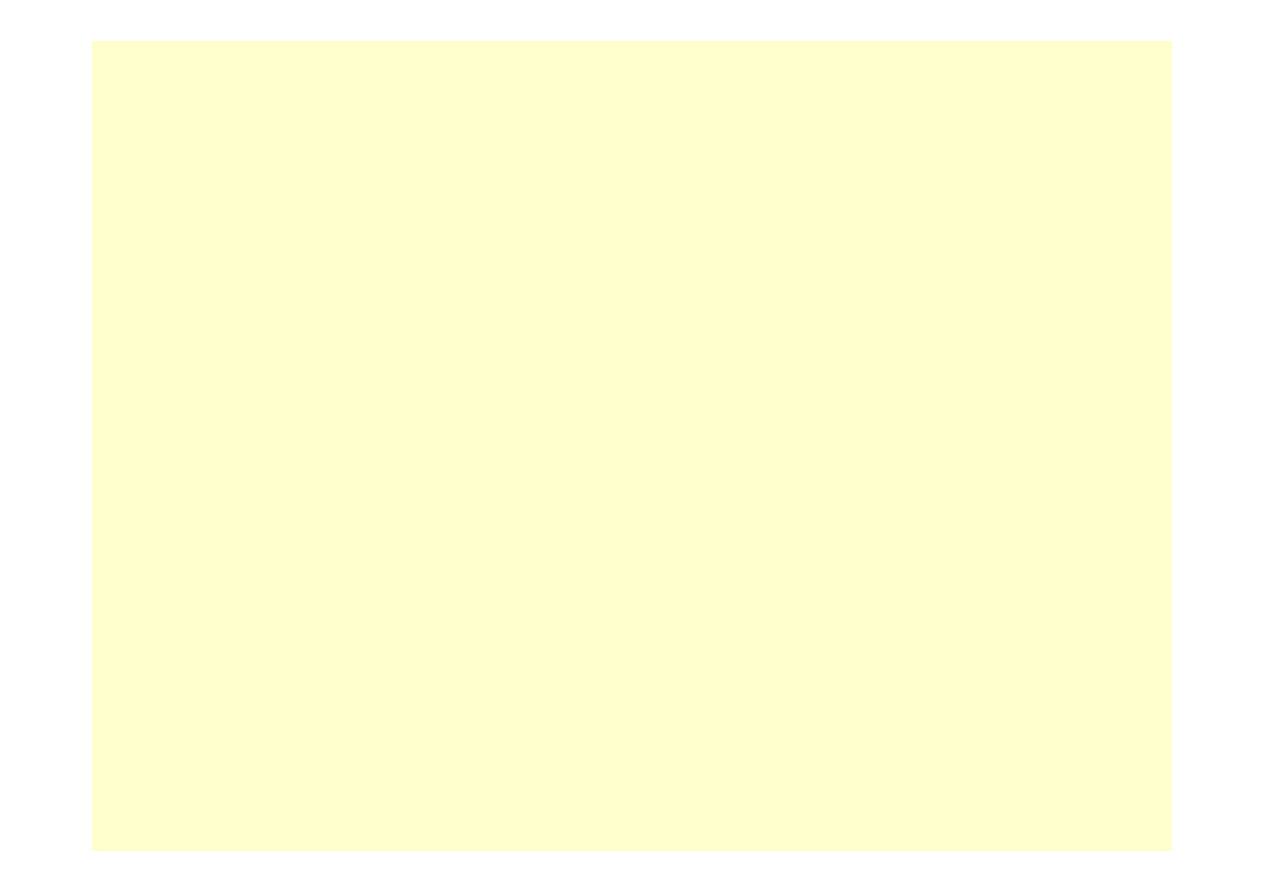
Przestrzenne zadanie brzegowe teorii
sprężystości

•

Metody rozwiązywania zadań brzegowych
teorii sprężystości

•

Rozwiązanie płaskiego zadania brzegowego
teorii sprężystości w naprężeniach

•

Rozwiązanie płaskiego osiowosymetrycznego
zadania brzegowego teorii sprężystości w
przemieszczeniach

•

Naprężenia kontaktowe

Przestrzenne zadanie brzegowe teorii sprężystości

1.

Ciało jest wypełnione w sposób ciągły materią zarówno przed, jak i po
odkształceniu (kontinuum materialne).

2.

Ośrodek ciągły jest fizycznie jednorodny i izotropowy.

3.

Przemieszczenia i odkształcenia pojawiają się w chwili przyłożenia
obciążeń wywołujących naprężenia.

4.

Istnieje naturalny beznapięciowy (beznaprężeniowy) stan ciała, do
którego powraca ono zawsze po odciążeniu.

5.

Odkształcenia i przemieszczenia są bardzo małe.

6.

Ośrodek ciągły (materiał) zachowuje się zgodnie z prawem Hooke’a.

7.

Funkcje określające naprężenia, przemieszczenia i odkształcenia są
ciągłe i różniczkowalne.

Klasyczna, liniowa teoria sprężystości jest mechaniką ciała (ośrodka)
odkształcalnego, opierająca się na następujących

założeniach

:

Przestrzenne zadanie brzegowej teorii sprężystości

można sformułować w następujący sposób:

Dane jest ciało liniowo sprężyste o dowolnym kształcie i wymiarach ( rys. 10.1 )

Przyjmujemy, że pozostaje ono w spoczynku. Znany jest sposób podparcia ciała i jego

własności sprężyste. Określone są siły

powierzchniowe q

i

masowe X

(

objętościowe X

ρ

)

działające na rozważane ciało. Poszukujemy natomiast wektorowego pola przemieszczeń
oraz tensorowych pól stanu naprężenia i odkształcenia w tym ciele. Innymi słowy, trzeba
znaleźć piętnaście funkcji współrzędnych punktu w ciele nieodkształconym.

Rys. 10.1

(

)

3

,

2

,

1

,

,

=

k

j

i

( )

k

i

x

u

(

)

3

,

2

,

1

,

=

k

i

(

)

3

,

2

,

1

,

,

=

k

j

i

( )

k

ij

i

ε

(

)

z

y

x

x

,

,

σ

(

)

z

y

x

xy

,

,

τ

(

)

z

y

x

y

,

,

σ

(

)

z

y

x

yz

,

,

τ

(

)

z

y

x

z

,

,

σ

(

)

z

y

x

zx

,

,

τ

(

)

z

y

x

u

,

,

(

)

z

y

x

v

,

,

(

)

z

y

x

w

,

,

(

)

z

y

x

x

,

,

ε

(

)

z

y

x

xy

,

,

γ

(

)

z

y

x

y

,

,

ε

(

)

z

y

x

yz

,

,

γ

( )

k

ij

x

=

σ

(

)

z

y

x

z

,

,

ε

(

)

z

y

x

zx

,

,

γ

lub w notacji inżynierskiej:

( 10.1 )

( 10.2 )

( 10.3 )

( 10.4 )

( 10.6 )

Poszukiwane funkcje:

( 10.5 )

Do znalezienia tych funkcji należy zastosować piętnaście podstawowych równań teorii

sprężystości, które zostały wcześniej wprowadzone. Tworzą one trzy grupy zależności:

A.

Równania wewnętrznej równowagi lokalnej

Są to trzy warunki Naviera, w których uwzględniono postulat Boltzmana, zwany
także warunkiem Cauchy’ego

0

,

=

ρ

+

σ

i

j

ji

X

(

)

3

,

2

,

1

;

3

,

2

,

1

=

=

j

i

ji

ij

σ

=

σ

( 10.7 )

( 10.8 )

(

)

3

,

2

,

1

;

3

,

2

,

1

=

=

j

i

albo w notacji inżynierskiej:

0

=

ρ

+

∂

τ

∂

+

∂

τ

∂

+

∂

σ

∂

X

z

y

x

zx

yx

x

0

=

ρ

+

∂

τ

∂

+

∂

σ

∂

+

∂

τ

∂

Y

z

y

x

zy

y

xy

0

=

ρ

+

∂

σ

∂

+

∂

τ

∂

+

∂

τ

∂

Z

z

y

x

z

yz

xz

yx

xy

τ

=

τ

zy

yz

τ

=

τ

xz

zx

τ

=

τ

( 10.9 )

( 10.10 )

B.

Związki geometryczne.

Wyróżnia się dwa rodzaje związków geometrycznych:

B1.

Zależność między składowymi stanu odkształcenia i przemieszczeniami,
czyli sześć związków Cauchy’ego.

(

)

i

j

j

i

ij

u

u

,

,

2

1

+

=

ε

(

)

3

,

2

,

1

;

3

,

2

,

1

=

=

j

i

ji

ij

ε

=

ε

( 10.11 )

( 10.12 )

albo w notacji inżynierskiej:

,

x

u

x

∂

∂

=

ε

,

y

v

y

∂

∂

=

ε

,

z

w

z

∂

∂

=

ε

,

x

v

y

u

xy

∂

∂

+

∂

∂

=

γ

,

y

w

z

v

yz

∂

∂

+

∂

∂

=

γ

,

z

u

x

w

zx

∂

∂

+

∂

∂

=

γ

( 10.13 )

B2. Warunki

ciągłości ( nierozdzielności ) odkształceń de Saint – Venanta,

których jest także sześć:

0

,

ln

j

=

mn

kl

ikm

e

e

ε

(

)

3

,

2

,

1

;

3

,

2

,

1

=

=

j

i

(

)

3

,

2

,

1

;

3

,

2

,

1

=

=

l

k

(

)

3

,

2

,

1

;

3

,

2

,

1

=

=

n

m

( 10.14 )

albo w notacji inżynierskiej:

,

2

2

2

2

2

y

x

x

y

xy

y

x

∂

∂

γ

∂

=

∂

ε

∂

+

∂

ε

∂

,

2

2

2

2

2

z

y

y

z

yz

z

y

∂

∂

γ

∂

=

∂

ε

∂

+

∂

ε

∂

x

z

z

x

zx

x

z

∂

∂

γ

∂

=

∂

ε

∂

+

∂

ε

∂

2

2

2

2

2

z

y

x

y

z

x

x

yz

zx

xy

∂

∂

ε

∂

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

γ

∂

−

∂

γ

∂

+

∂

γ

∂

∂

∂

2

2

x

z

y

z

x

y

y

zx

xy

yz

∂

∂

ε

∂

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

γ

∂

−

∂

γ

∂

+

∂

γ

∂

∂

∂

2

2

y

x

z

x

y

z

z

xy

yz

zx

∂

∂

ε

∂

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

γ

∂

−

∂

γ

∂

+

∂

γ

∂

∂

∂

2

2

( 10.15 )

C.

Związki fizyczne

Jest to uogólnione prawo Hooke’a, które może mieć dwojaką postać:

C1.

Sześć funkcji określających składowe stanu odkształcenia w zależności
od składowych stanu naprężenia:

ij

kk

ij

ij

E

E

δ

σ

ν

−

σ

ν

+

=

ε

1

(

)

3

,

2

,

1

,

,

=

k

j

i

( 10.16 )

albo w notacji inżynierskiej:

(

)

[

]

z

y

x

x

E

σ

+

σ

ν

−

σ

=

ε

1

(

)

[

]

x

z

y

y

E

σ

+

σ

ν

−

σ

=

ε

1

(

)

[

]

y

x

z

z

E

σ

+

σ

ν

−

σ

=

ε

1

,

G

xy

xy

τ

=

γ

,

G

yz

yz

τ

=

γ

G

zx

zx

τ

=

γ

( 10.17 )

C2.

Sześć funkcji określających składowe stanu naprężenia w zależności
od składowych stanu odkształcenia.

ij

kk

ij

ij

G

G

δ

ε

ν

−

ν

+

ε

=

σ

2

1

2

2

(

)

3

,

2

,

1

;

3

,

2

,

1

;

3

,

2

,

1

=

=

=

k

j

i

( 10.18 )

albo w notacji inżynierskiej:

(

)

⎥⎦

⎤

⎢⎣

⎡

ε

+

ε

+

ε

ν

−

ν

+

ε

ν

+

=

σ

z

y

x

x

x

E

2

1

1

(

)

⎥⎦

⎤

⎢⎣

⎡

ε

+

ε

+

ε

ν

−

ν

+

ε

ν

+

=

σ

z

y

x

y

y

E

2

1

1

(

)

1

1 2

z

z

x

y

z

E

ν

σ

ε

ε

ε

ε

ν

ν

⎡

⎤

=

+

+

+

⎢

⎥

+

−

⎣

⎦

xy

xy

G

γ

=

τ

yz

yz

G

γ

=

τ

zx

zx

G

γ

=

τ

( 10.19 )

W dynamicznym zadaniu brzegowym teorii sprężystości poszukiwane

funkcje ( 10.1 ), ( 10.2 ) i ( 10.3 ) albo ( 10.4 ),( 10.5 ) i ( 10.6 ) są dodatkowo zależne od
czasu t. W równaniach równowagi wewnętrznej należy uwzględnić siły bezwładności
d’Alemberta przyłożone do infinitezymalnego prostopadłościanu. Formuły
( 10.7 ) albo ( 10.9 ), w których prawe strony są odpowiednio równe :

2

2

..

t

u

i

u

i

∂

∂

ρ

=

ρ

(

)

3

,

2

,

1

=

i

,

2

2

t

u

∂

∂

ρ

,

2

2

t

v

∂

∂

ρ

,

2

2

t

w

∂

∂

ρ

albo

stają się

dynamicznymi równaniami ośrodka ( ciała ) odkształcalnego.

Metody rozwiązywania zadań brzegowych

teorii sprężystości

Poszukiwane funkcje ( 10.1 ), ( 10.2 ) i ( 10.3 ) albo ( 10.4 ),( 10.5 ) i ( 10.6 ) muszą być tak
dobrane, aby spełniały podstawowe równania teorii sprężystości A, B i C oraz warunki
brzegowe, a w przypadku zadania dynamicznego także warunki początkowe.

Rozwiązanie w naprężeniach

polega na tym, że w pierwszej kolejności wyznacza

się sześć funkcji określających składowe stanu naprężenia

( )

k

ij

x

σ

(

)

3

,

2

,

1

,

,

=

k

j

i

albo

(

)

,

,

, z

y

x

x

σ

(

)

,

,

, z

y

x

y

σ

(

)

,

,

, z

y

x

z

σ

(

)

,

,

, z

y

x

xy

τ

(

)

,

,

, z

y

x

yz

τ

(

)

.

,

, z

y

x

zx

τ

Należy w tym celu tak przekształcić podstawowe równania teorii sprężystości, aby uzyskać
układ równań różniczkowych ze względu na naprężenia. Trzy pierwsze równania tego
układu stanowią lokalne warunki równowagi wewnętrznej A. Aby uzyskać pozostałe
równania, należy składowe stanu odkształcenia, wyrażone przez składowe stanu
naprężenia w zależnościach C1, wprowadzić do warunków ciągłości odkształceń B2.
Po dokonaniu tej operacji i po przekształceniach, w trakcie których stosuje się również
równania równowagi lokalnej, otrzymujemy warunki nierozdzielności odkształceń
wyrażone przez naprężenia.

Jest to sześć równań Beltramiego - Michella >>>

Sześć równań Beltramiego – Michella:

(

)

k

k

ij

i

j

j

i

ij

kk

kk

ij

X

X

X

,

,

,

,

,

1

1

1

δ

ν

−

ν

−

+

−

=

σ

ν

+

+

σ

(

)

3

,

2

,

1

,

,

=

k

j

i

( 10.20 )

albo w notacji inżynierskiej:

0

2

1

1

3

2

2

2

=

ρ

∂

∂

+

ρ

⎟

⎠

⎞

⎜

⎝

⎛

∂

∂

+

∂

∂

+

∂

∂

ν

−

ν

+

∂

σ

∂

ν

+

+

σ

∇

x

X

z

Z

y

Y

x

X

x

śr

x

0

2

1

1

3

2

2

2

=

ρ

∂

∂

+

ρ

⎟

⎠

⎞

⎜

⎝

⎛

∂

∂

+

∂

∂

+

∂

∂

ν

−

ν

+

∂

σ

∂

ν

+

+

σ

∇

y

Y

z

Z

y

Y

x

X

y

śr

y

0

2

1

1

3

2

2

2

=

ρ

∂

∂

+

ρ

⎟

⎠

⎞

⎜

⎝

⎛

∂

∂

+

∂

∂

+

∂

∂

ν

−

ν

+

∂

σ

∂

ν

+

+

σ

∇

z

Z

z

Z

y

Y

x

X

z

śr

z

0

1

3

2

2

=

ρ

∂

∂

+

ρ

∂

∂

+

∂

∂

σ

∂

ν

+

+

τ

∇

x

Z

z

X

x

z

śr

xy

0

1

3

2

2

=

ρ

∂

∂

+

ρ

∂

∂

+

∂

∂

σ

∂

ν

+

+

τ

∇

z

X

y

Y

z

y

śr

yz

0

1

3

2

2

=

ρ

∂

∂

+

ρ

∂

∂

+

∂

∂

σ

∂

ν

+

+

τ

∇

y

X

x

Y

y

x

śr

xy

( 10.21 )

oznacza operator

harmoniczny Laplace’a
zwany laplasjanem.
Czytaj „ nabla dwa”.

( 10.22 )

-

2

2

2

2

2

2

2

z

y

x

∂

∂

+

∂

∂

+

∂

∂

=

∇

Poszukiwanych sześć funkcji

( )

k

ij

x

σ

(

)

3

,

2

,

1

,

,

=

k

j

i

albo

(

)

,

,

, z

y

x

x

σ

(

)

,

,

,

z

y

x

y

σ

(

)

,

,

, z

y

x

z

σ

(

)

,

,

,

z

y

x

xy

τ

(

)

,

,

,

z

y

x

yz

τ

(

)

,

,

, z

y

x

zx

τ

musi spełniać równania równowagi wewnętrznej A, równania Beltramiego – Michella oraz

warunki brzegowe:

jn

ji

ni

q

α

σ

=

(

)

3

,

2

,

1

;

3

,

2

,

1

=

=

j

i

albo w notacji inżynierskiej:

( )

( )

( )

zn

yn

xn

q

zx

yx

x

nx

cos

cos

cos

τ

+

τ

+

σ

=

( )

( )

( )

zn

yn

xn

q

zy

y

xy

ny

cos

cos

cos

τ

+

σ

+

τ

=

( )

( )

( )

zn

yn

xn

q

z

yz

xz

nz

cos

cos

cos

σ

+

τ

+

τ

=

( 10.23 )

( 10.24 )

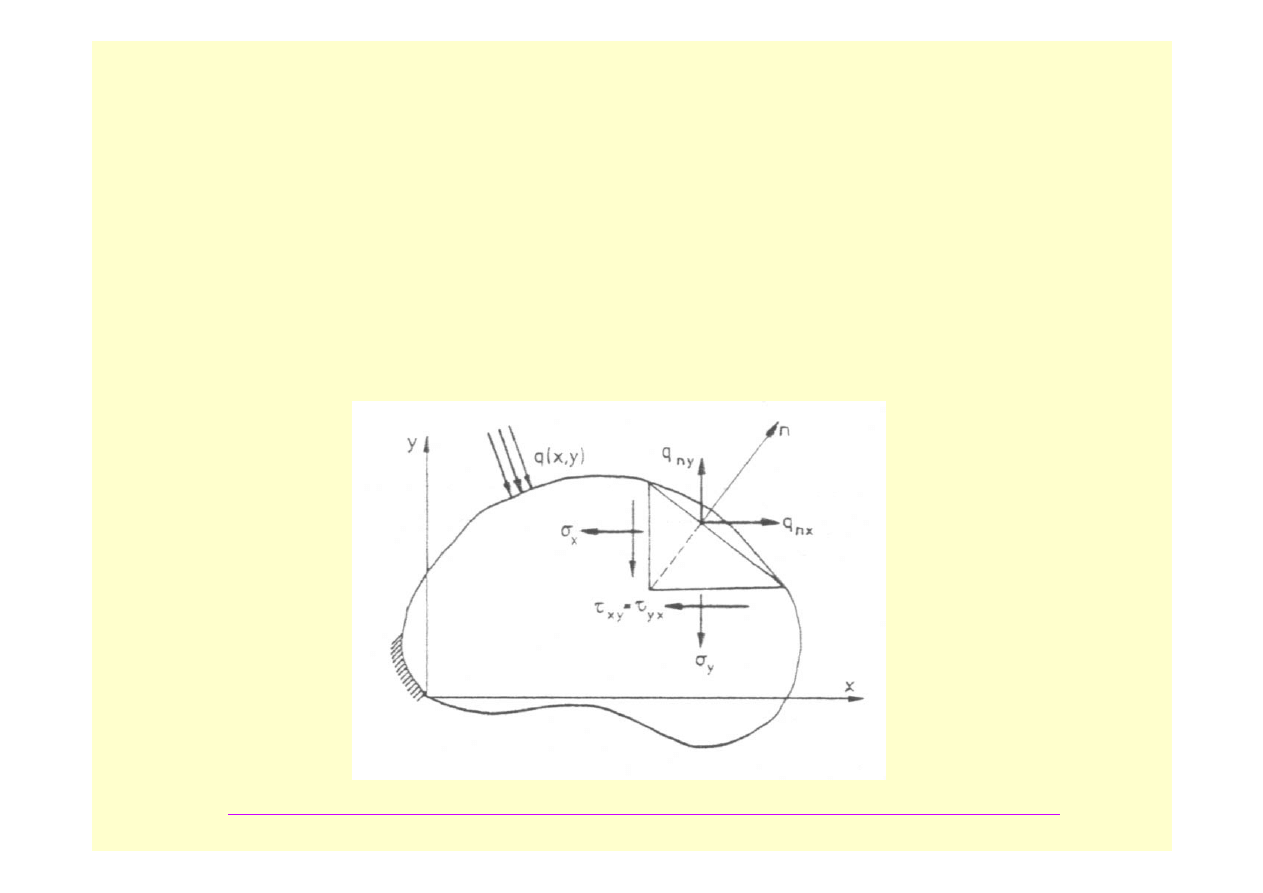
W tym przypadku n jest normalną do powierzchni zew. ciała w rozważanym

punkcie, której kierunek wyznaczają

albo cos( xn ), cos( yn ), cos( zn ).

(

)

3

,

2

,

1

=

α j

ij

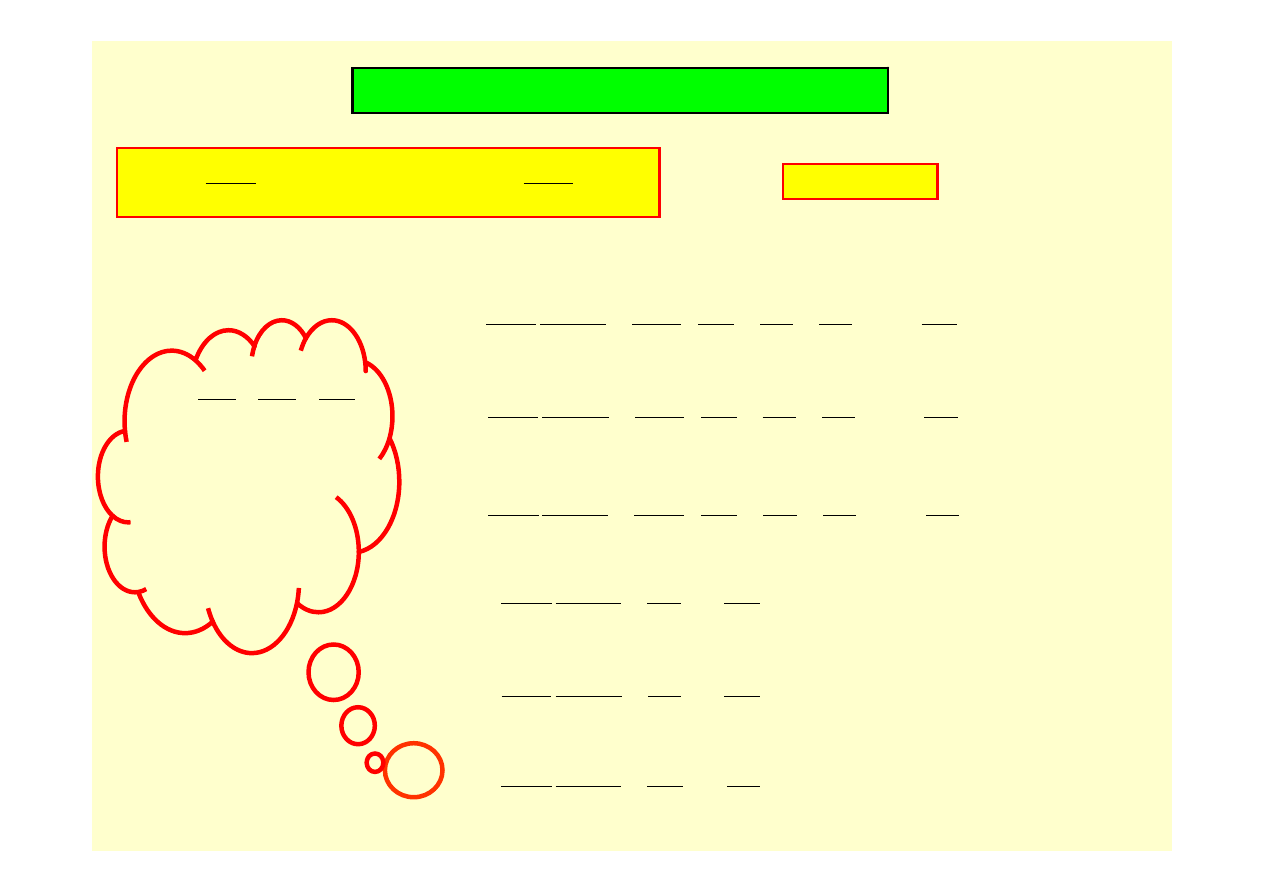
Ściana elementarnego czworościanu ( patrz obok )

prostopadła do n jest fragmentem powierzchni
ciała, na który działa obciążenie powierzchniowe
q( x, y, z ) o składowych q

ni

( i = 1, 2, 3 )

albo q

nx

, q

ny

, q

nz

. Pozostałe trzy wzajemnie

prostopadłe ściany,na których występują
naprężenia, znajdują się już wewnątrz ciała.
Warunki brzegowe wiążą znane powierzchniowe

obciążenia zewnętrzne ze stanem naprężenia

wewnątrz ciała.

Przy okazji omawiania warunków brzegowych warto przytoczyć

zasadę de Saint – Venanta

, która brzmi:

Zasada ta umożliwia modyfikację i upraszczanie warunków brzegowych. Wynika z

niej również, że stan naprężenia w pobliżu miejsca przyłożenia obciążenia powinien być
przedmiotem odrębnej analizy. Wiąże się to z naprężeniami stykowymi.

Różne, ale statycznie równoważne układy sił, przyłożone na niewielkiej części

powierzchni ciała, wywołują w punktach dostatecznie oddalonych od strefy działania
obciążenia praktycznie jednakowe stany naprężenia. Przez dostateczne oddalenie od strefy
działania obciążenia należy rozumieć odległość rzędu porównywalnego z liniowymi
wymiarami powierzchni, na którą działa układ sił zewnętrznych.

Rozwiązanie w przemieszczeniach

polega na tym, że w pierwszej kolejności

wyznacza się trzy funkcje określające przemieszczenia

albo

Należy w związku z tym przekształcić podstawowe równania teorii

sprężystości, aby uzyskać układ równań różniczkowych ze względu na przemieszczenia. W
tym celu składowe stanu odkształcenia wyrażone przez przemieszczenia zgodne z
zależnościami B1 wprowadzamy do uogólnionego prawa Hooke’a ( C2 ). Uzyskamy składowe
stanu naprężenia wyrażone przez przemieszczenia, które różniczkujemy i wstawiamy do
warunków równowagi wewnętrznej A. Po przekształceniach otrzymamy warunki równowagi
wewnętrznej wyrażone w przemieszczeniach, czyli trzy równania

Naviera – Lamego

:

( )

j

i

x

u

(

)

3

,

2

,

1

,

=

j

i

(

)

,

,

, z

y

x

u

(

)

,

,

, z

y

x

v

(

)

.

,

, z

y

x

w

(

)

0

,

,

=

+

+

λ

+

i

ji

j

jj

i

X

u

G

Gu

(

)

3

,

2

,

1

,

,

=

k

j

i

(

)

0

2

=

ρ

+

∇

+

∂

ϑ

∂

+

λ

Y

v

G

y

G

(

)

0

2

=

ρ

+

∇

+

∂

ϑ

∂

+

λ

X

u

G

x

G

(

)

0

2

=

ρ

+

∇

+

∂

ϑ

∂

+

λ

Z

w

G

z

G

;

z

w

y

v

x

u

z

y

x

∂

∂

+

∂

∂

+

∂

∂

=

ε

+

ε

+

ε

=

ϑ

-

2

1

2

ν

−

ν

=

λ

G

( 10.25 )

( 10.26 )

albo w notacji inżynierskiej:

stała Lamego

gdzie:

Funkcje

albo

muszą

spełniać układ równań różniczkowych cząstkowych Naviera – Lamego ( 10.25 ) lub ( 10.26 )
oraz warunki brzegowe. Są to warunki naprężeniowe ( 10.23 ) albo ( 10.24 ), które należy
również podać w przemieszczeniach. Aby uzyskać odpowiednie formuły, wystarczy w
naprężeniowych warunkach brzegowych ( 10.23 ) albo ( 10.24 ) składowe stanu naprężenia
wyrazić przez przemieszczenia, w analogiczny do stosowanego przy wyprowadzeniu równań
Naviera -Lamego. Mogą to być również

przemieszczeniowe warunki brzegowe

określające

przemieszczenia albo

na

części lub

na całym brzegu.

Rozwiązanie przestrzennego zadnia brzegowego teorii sprężystości wprost, tzn.

przez całkowanie układu cząstkowych równań różniczkowych jest bardzo trudne. Dlatego
stosuje się różne sposoby ułatwiające uzyskanie choćby przybliżonego rozwiązania.
Wprowadza się w tym celu uproszczone modele geometryczne ciała liniowo – sprężystego,
takie jak pręt, tarcza, płyta czy powłoka.

Stosuje się przybliżone metody rozwiązywania

równań różniczkowych. Korzysta się także z przybliżonych metod numerycznych
rozwiązywania zadań teorii sprężystości, takich jak metoda różnic skończonych, metoda
elementów skończonych czy metoda elementów brzegowych.

Metody te noszą nazwę metod

macierzowych lub komputerowych, ponieważ opierają się na rachunku macierzowym i są
przystosowane do obliczeń za pomocą komputera.

( )

j

i

x

u

(

)

3

,

2

,

1

,

=

j

i

(

)

,

,

, z

y

x

u

(

)

,

,

, z

y

x

v

(

)

z

y

x

w

,

,

( )

j

i

x

u

(

)

3

,

2

,

1

,

=

j

i

(

)

,

,

, z

y

x

v

(

)

z

y

x

w

,

,

(

)

,

,

, z

y

x

u

ROZWIĄZANIE PŁASKIEGO ZADANIA

BRZEGOWEGO TEORII SPRĘŻYSTOŚCI W

NAPRĘŻENIACH.

Wyróżnić trzeba dwa przypadki tego zadania, a mianowicie płaski stan naprężenia

lub odkształcenia. Poszukuje się odpowiednio funkcji

lub

Rozważymy szczegółowo pierwszy przypadek, który

zilustrowano na rys. 10.2, przedstawiającym tarcze przenoszącą obciążenia zewnętrzne q( x, y )
i utwierdzoną na części brzegu.

( )

,

,

y

x

x

σ

( )

,

,

y

x

y

σ

( )

y

x

xy

,

τ

( )

,

, y

x

x

ε

( )

,

,

y

x

y

ε

( )

.

,

y

x

xy

γ

Rys.10.2

Podstawowe równania teorii sprężystości przedstawiają się następująco: >>>

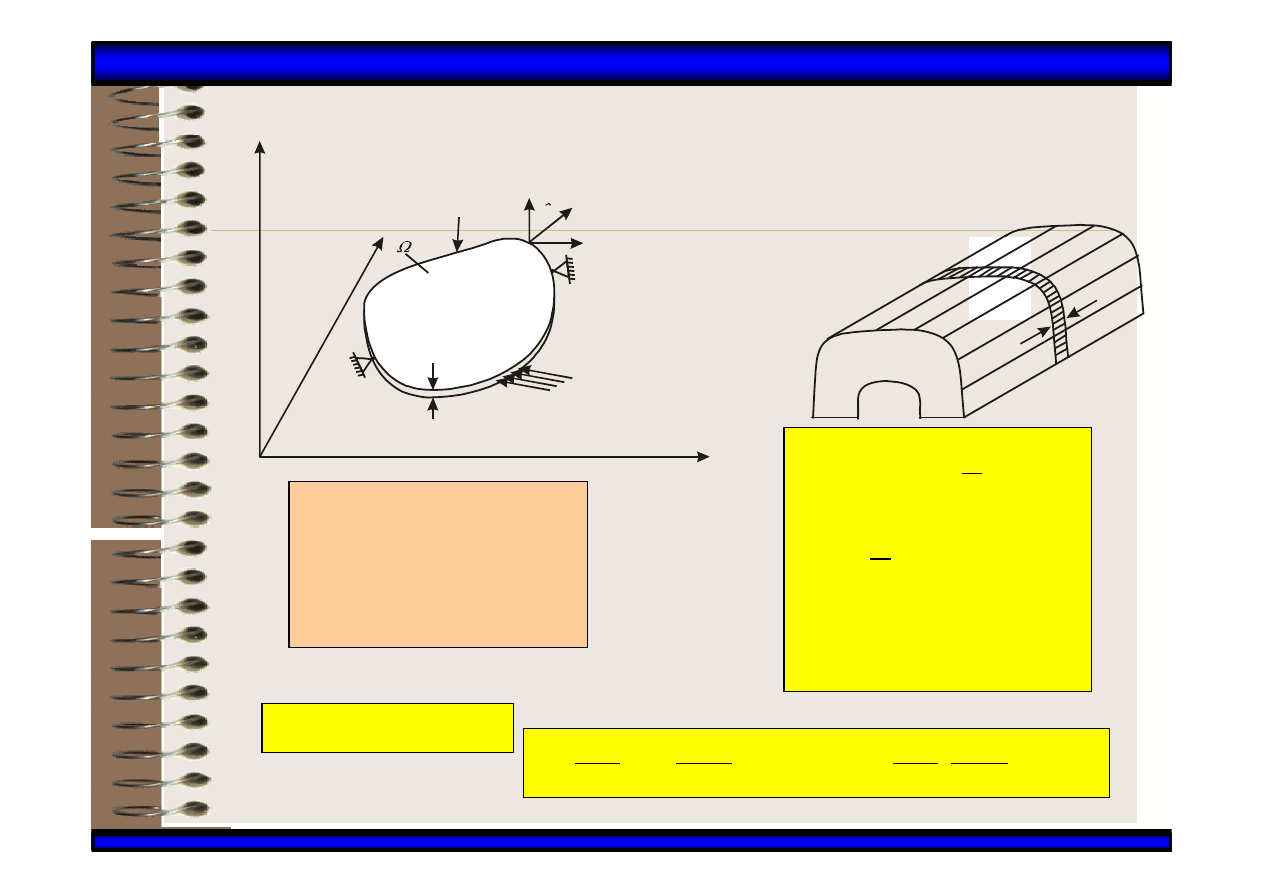
Płaskie zadania teorii sprężystości

Płaskie zadania teorii sprężystości

1

1

F

0

p

0

h

y

a)

n

y

n

n

x

x

b)

h

Płaski stan odkształcenia

Płaski stan naprężenia

0

[ ]

0

0

0

0

x

xy

yx

y

T

σ

σ

τ

τ

σ

⎡

⎤

⎢

⎥

= ⎢

⎥

⎢

⎥

⎣

⎦

1

0

2

1

[ ]

0

2

0

0

0

x

xy

yx

y

ε

γ

ε

γ

ε

⎡

⎤

⎢

⎥

⎢

⎥

⎢

⎥

= ⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦

(

)

(

)

1

1 2

1

1 2

z

z

x

y

z

x

y

E

E

ν

ν

σ

ε

ε

ε

ε

ε

ε

ν

ν

ν

ν

⎡

⎤

⎡

⎤

=

+

+

+

=

+

⎢

⎥

⎢

⎥

+

−

+

−

⎣

⎦

⎣

⎦

0,

z

ponieważ

σ

≠

0,

z

ponieważ

σ

≠

0

=

ρ

+

∂

τ

∂

+

∂

σ

∂

X

y

x

xy

x

0

=

ρ

+

∂

σ

∂

+

∂

τ

∂

Y

y

x

y

xy

,

x

u

x

∂

∂

=

ε

,

y

v

y

∂

∂

=

ε

x

v

y

u

xy

∂

∂

+

∂

∂

=

γ

y

x

x

y

xy

y

x

∂

∂

γ

∂

=

∂

ε

∂

+

∂

ε

∂

2

2

2

2

2

(

)

,

1

x

y

y

E

νσ

−

σ

=

ε

(

)

,

1

y

x

x

E

νσ

−

σ

=

ε

G

xy

xy

τ

=

γ

(

)

,

1

2

y

x

x

E

νε

+

ε

ν

−

=

σ

(

)

,

1

2

x

y

y

E

νε

+

ε

ν

−

=

σ

xy

xy

G

γ

=

τ

A. Lokalne warunki równowagi

( 10.28 )

( 10.27 )

( 10.29 )

B. Związki geometryczne

lub

C. Związki fizyczne

( 10.30 )

lub

( 10.31 )

Rozwiązanie płaskiego zadania brzegowego teorii sprężystości w naprężeniach

opiera się na warunkach równowagi wewnętrznej ( 10.27 ) oraz warunku nierozdzielności
przemieszczeń ( 10.29 ) wyrażonym w naprężeniach. Aby otrzymać to trzecie równanie,

wprowadzimy zależność ( 10.30 ) do ( 10.29 ) po uwzględnieniu , że

(

)

ν

+

=

1

2

E

G

(

)

(

)

(

)

⎥⎦

⎤

⎢⎣

⎡

τ

ν

+

∂

∂

∂

=

⎥⎦

⎤

⎢⎣

⎡

νσ

−

σ

∂

∂

+

⎥⎦

⎤

⎢⎣

⎡

νσ

−

σ

∂

∂

xy

x

y

y

x

E

y

x

E

x

E

y

1

2

1

1

2

2

2

2

2

Po wykonaniu różniczkowania i uporządkowaniu uzyskuje się:

(

)

y

x

x

x

y

y

xy

x

y

y

x

∂

∂

τ

∂

ν

+

=

∂

σ

∂

ν

−

∂

σ

∂

+

∂

σ

∂

ν

−

∂

σ

∂

2

2

2

2

2

2

2

2

2

1

2

( 10.32 )

Różniczkujemy pierwsze równanie ( 10.27 ) względem x, a drugie względem y, dodajemy
stronami i wyliczamy, co następuje:

ρ

⎟

⎠

⎞

⎜

⎝

⎛

∂

∂

+

∂

∂

−

∂

σ

∂

−

∂

σ

∂

−

=

∂

∂

τ

∂

y

Y

x

X

y

x

y

x

y

x

xy

2

2

2

2

2

2

( 10.33 )

Po wstawieniu wzoru ( 10.33 ) do ( 10.32 ) i po prostych przekształceniach otrzymujemy

równanie Levy’ego

:

(

)

(

)

ρ

⎟

⎠

⎞

⎜

⎝

⎛

∂

∂

+

∂

∂

ν

+

−

=

σ

+

σ

∇

y

Y

x

X

y

x

1

2

( 10.34 )

Dla przypadku płaskiego stanu odkształcenia, po analogicznych operacjach, równanie
Levy’ego ma następującą postać:

(

)

(

)

ρ

⎟

⎠

⎞

⎜

⎝

⎛

∂

∂

+

∂

∂

ν

−

−

=

σ

+

σ

∇

y

Y

x

X

y

x

1

1

2

(

)

0

2

=

σ

+

σ

∇

y

x

Jeśli siły masowe X, Y mają wartości stałe, równanie Levy’ego dla płaskiego stanu
naprężenia i odkształcenia jest identyczne

( 10.35 )

( 10.36 )

Upoważnia nas to do zajmowania się wyłącznie przypadkiem płaskiego stanu
naprężenia. Poszukiwane funkcje

muszą

spełniać

równania równowagi wewnętrznej ( 10.27 ), równanie Levy’ego ( 10.36 ) oraz
następujące warunki brzegowe:

( )

,

,

y

x

x

σ

( )

,

,

y

x

y

σ

( )

y

x

xy

,

τ

( )

( )

n

y

n

x

q

yx

x

nx

,

cos

,

cos

τ

+

σ

=

( )

( )

n

y

n

x

q

y

xy

ny

,

cos

,

cos

σ

+

τ

=

( 10.37 )

Rozwiązanie płaskiego zadania teorii sprężystości można uprościć, wprowadzając

funkcję

naprężeń Airy’ego

ψ ( x, y )

, za pomocą której można wyrazić składowe stanu naprężenia

następująco:

,

2

2

y

x

∂

ψ

∂

=

σ

,

2

2

x

y

∂

ψ

∂

=

σ

x

Y

y

X

y

x

xy

ρ

−

ρ

+

∂

∂

ψ

∂

−

=

τ

2

( 10.38 )

Łatwo sprawdzić, że jeśli X i Y mają wartości stałe, funkcje ( 10.38 ) spełniają warunki
równowagi ( 10.27 ). Po wstawieniu zależności ( 10.38 ) do równania Levy’ego ( 10.36 ) i
po prostych przekształceniach uzyskuje się

równanie biharmoniczne

ze względu na funkcję

naprężeń:

0

2

4

4

2

2

4

4

4

=

∂

ψ

∂

+

∂

∂

ψ

∂

+

∂

ψ

∂

y

y

x

x

0

4

2

2

=

ψ

∇

=

ψ

∇

∇

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

∂

∂

+

∂

∂

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

∂

∂

+

∂

∂

=

∇

=

∇

∇

2

2

2

2

2

2

2

2

4

2

2

y

x

y

x

( 10.39 )

czyli

( 10.40 )

Funkcja naprężeń

ψ( x, y ) musi być tak dobrana, aby spełniała równanie biharmoniczne,

a składowe stanu naprężenia przez nią wyrażone spełniały warunki brzegowe.

( 10.41 )

gdzie:

Przykład 10.1 >>>

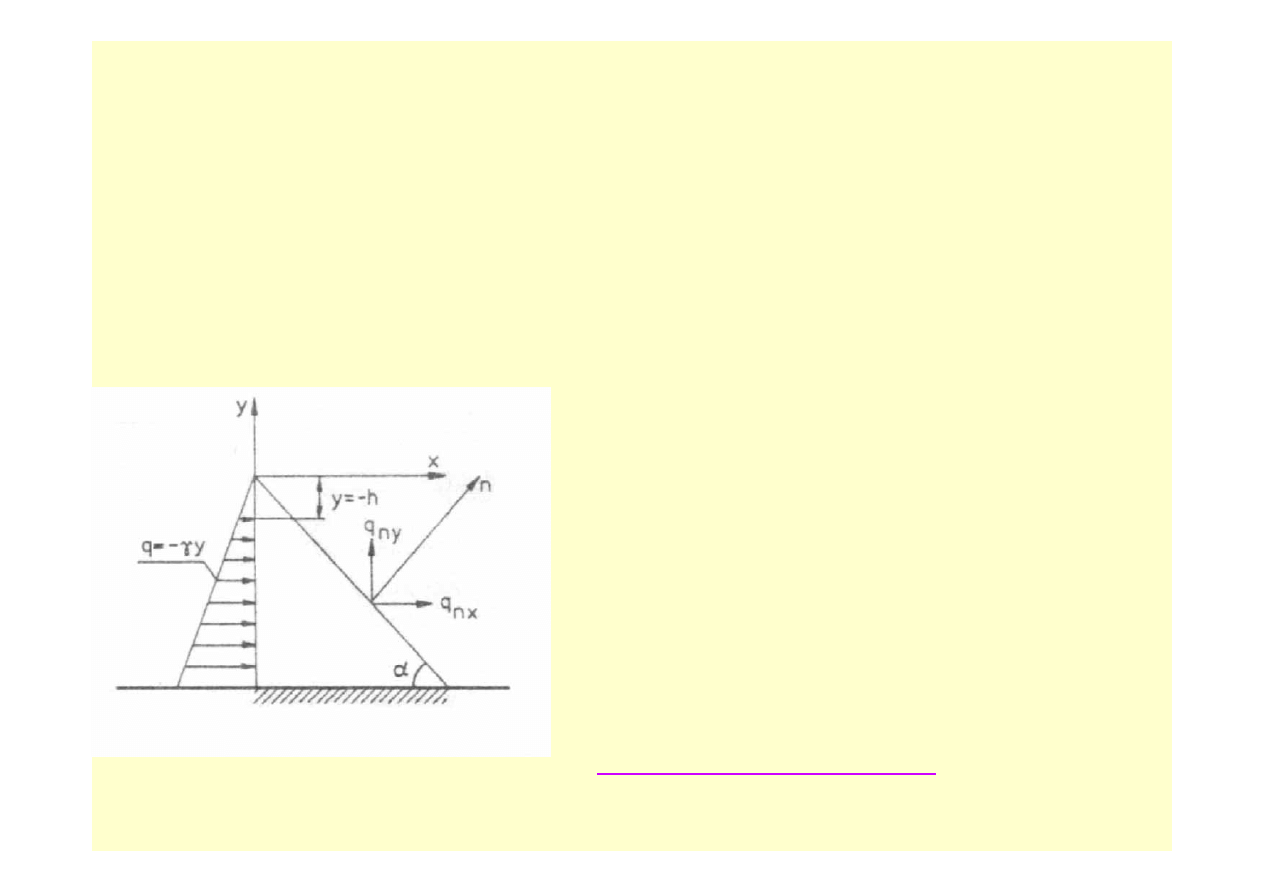
PRZYKŁAD 10.1

Płaska tarcza o grubości równej 1 jest zamocowana i obciążona w sposób pokazany na rys. 4.
Dane:

γ, p – ciężar jednostki objętości materiału tarczy, kąt α.

Poszukujemy rozwiązania w postaci wielomianu trzeciego stopnia

( )

3

2

2

3

,

dy

cxy

y

bx

ax

y

x

+

+

+

=

ψ

( 10.42 )

Funkcja ta może być funkcją naprężeń, ponieważ spełnia równanie biharmoniczne.

Składowe stanu naprężenia wyrażają następująco:

dy

cx

x

6

2

+

=

σ

by

ax

y

2

6

+

=

σ

px

cy

bx

xy

+

−

−

=

τ

2

2

( 10.43 )

Stałe a, b, c, d oblicza się z warunków brzegowych.

WARUNKI BRZEGOWE >>>

Rys.10.3

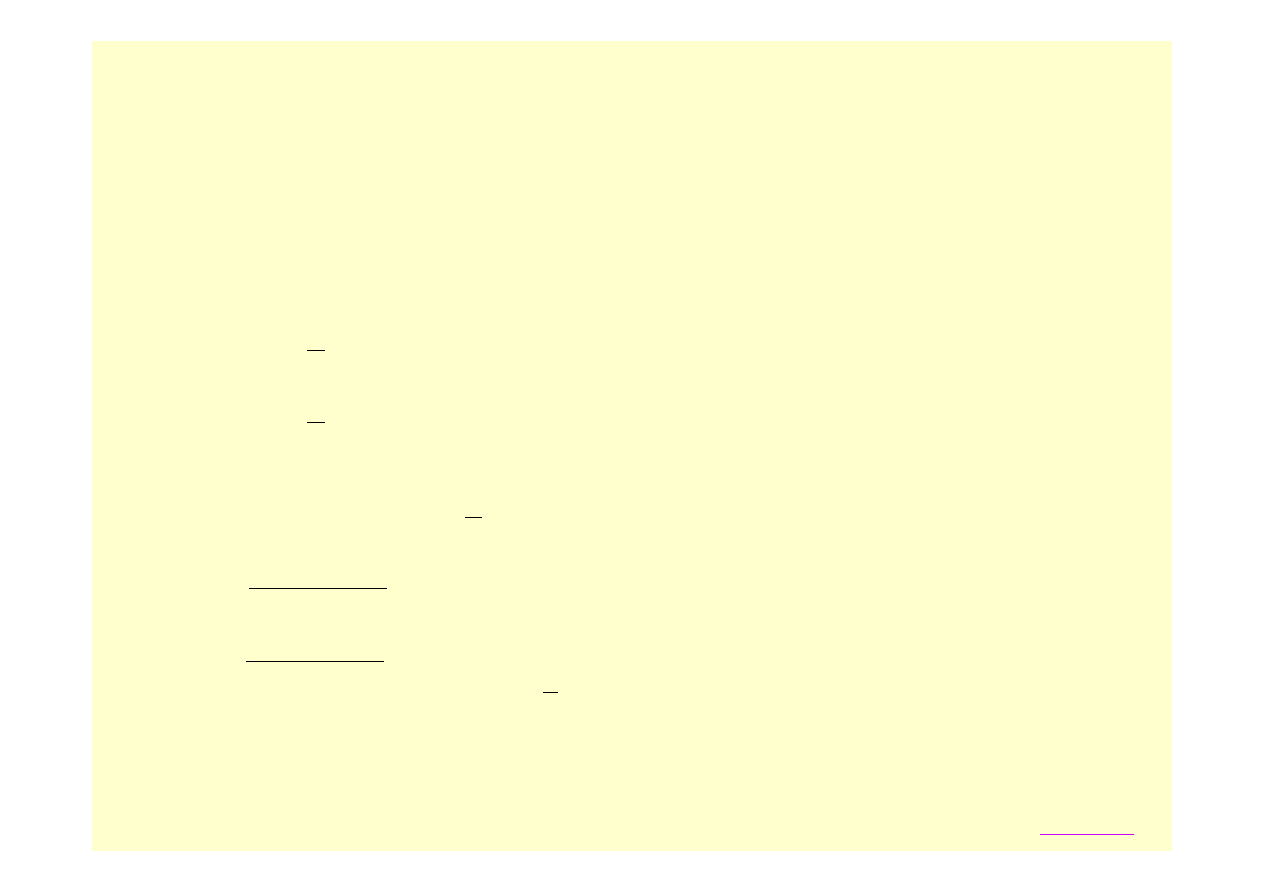
- na ścianie pionowej

WARUNKI BRZEGOWE:

,

0

=

x

,

0

=

τ

xy

,

0

=

x

y

q

x

γ

=

−

=

σ

,

α

−

= tg

x

y

,

0

=

nx

q

( )

( )

0

cos

cos

=

τ

+

σ

yn

xn

xy

x

,

α

−

= tg

x

y

,

0

=

ny

q

( )

( )

0

cos

cos

=

σ

+

τ

yn

xn

y

xy

1.
2.

3.

4.

- na ścianie pochyłej

gdzie:

( )

,

sin

2

cos

cos

α

=

⎟

⎠

⎞

⎜

⎝

⎛

α

−

π

=

xn

( )

( )

α

= cos

cos yn

Z warunku 1

0

2

=

− cy

0

=

c

Z warunku 2

y

dy

γ

=

6

γ

=

6

1

d

dalej >>>

Z warunku 3

(

)

0

cos

2

sin

6

1

6

=

α

−

−

α

γ

⋅

x

p

b

y

p

b

x

y

−

=

α

α

γ

2

cos

sin

p

b

tg

−

=

α

γ

−

2

2

p

tg

b

2

1

2

1

2

+

α

γ

−

=

Z warunku 4

(

)

(

)

0

cos

6

sin

2

2

=

α

+

α

γ

−

+

α

+

−

α

γ

py

tg

y

ax

px

px

tg

x

0

6

2

3

=

+

α

γ

−

+

α

γ

x

y

p

tg

x

y

a

tg

0

6

3

3

=

α

−

α

γ

+

+

α

γ

ptg

tg

a

tg

0

3

1

6

1

3

=

α

γ

−

α

=

tg

ptg

a

Po wstawieniu stałych a, b, c, d do formuł ( 10.43 ) otrzymuje się ostateczne rozwiązanie:

,

y

x

γ

=

σ

(

)

(

)

,

0

2

2

2

=

α

γ

−

+

α

α

γ

−

=

σ

y

tg

p

tg

tg

p

x

y

x

tg

xy

α

γ

=

τ

2

( 10.44 )

Po wstawieniu y = - h = const otrzymujemy:

y

x

γ

−

=

σ

(

)

(

)

0

2

2

2

=

α

γ

−

−

α

α

γ

−

=

σ

h

tg

p

tg

tg

p

x

y

α

γ

=

τ

2

tg

x

xy

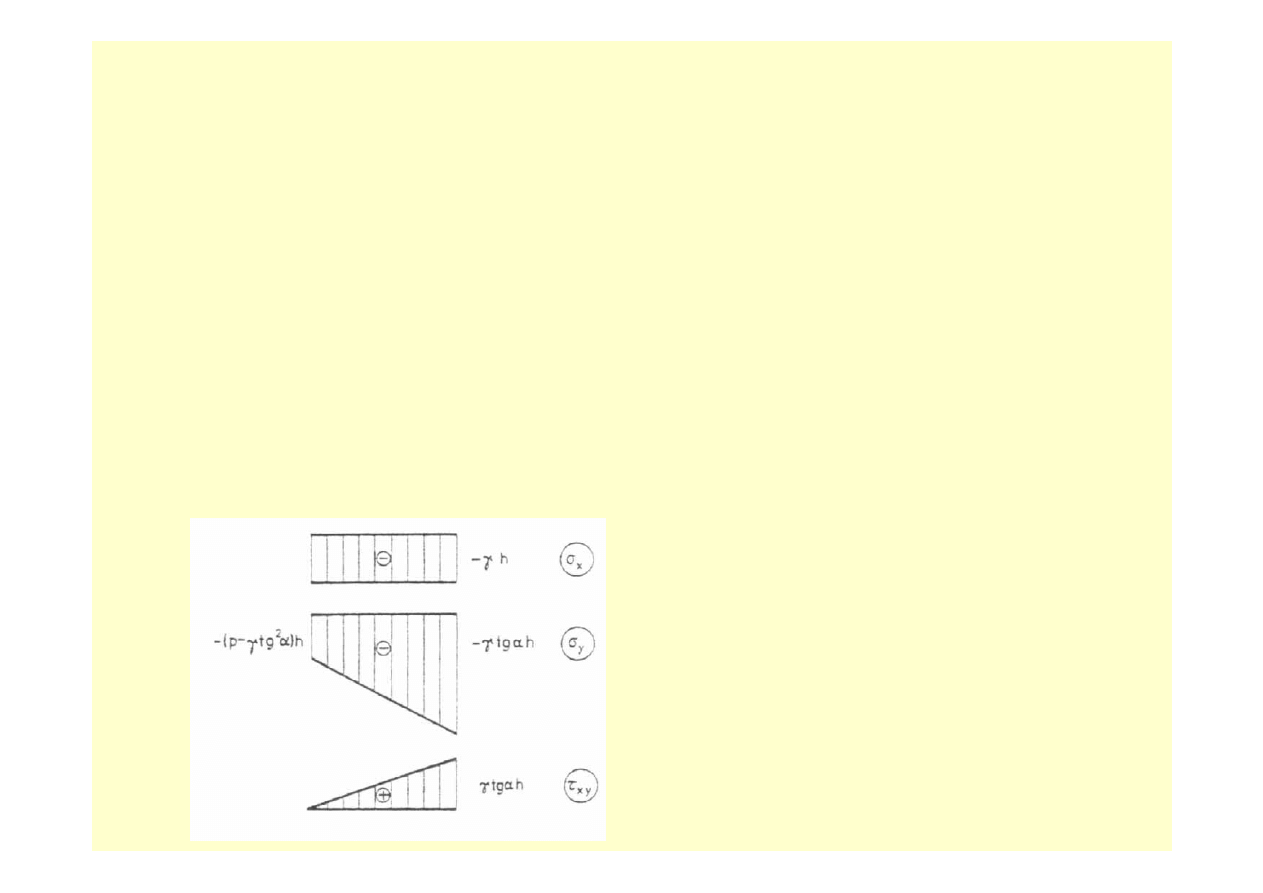
- wartość stała

- funkcja liniowa x

- funkcja liniowa x

( 10.45 )

Formuły ( 10.44 ) są błędne w pobliżu
miejsca utwierdzenia, ponieważ nie są tam
spełnione warunki brzegowe.

Opierając się na formułach ( 10.45 ), można sporządzić wykresy składowych stanu
naprężenia dla h = const ( rys. 10.4 )

Rys. 10.4

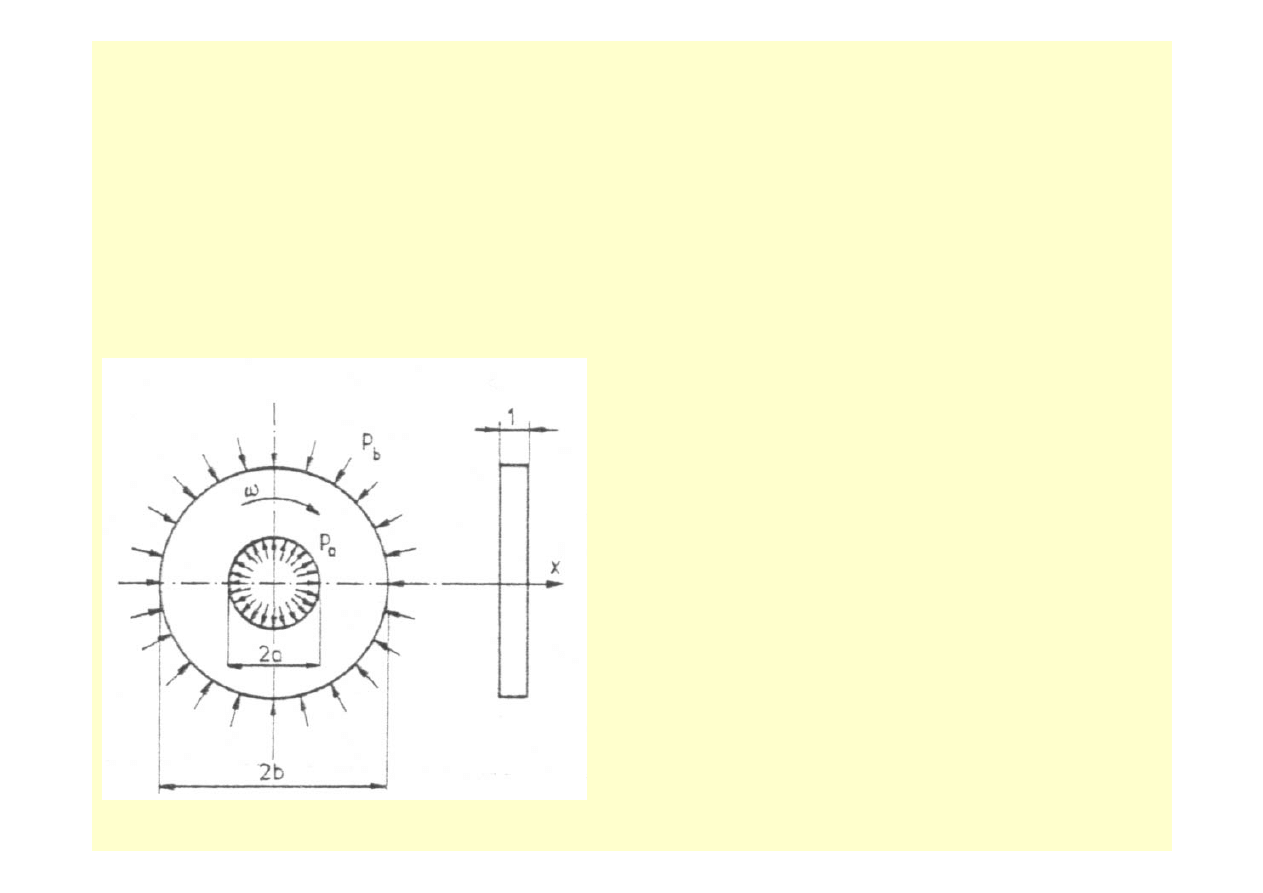
ROZWIĄZANIE PŁASKIEGO

OSIOWOSYMETRYCZNEGO ZADANIA BRZEGOWEGO
TEORII SPRĘŻYSTOŚCI W PRZEMIESZCZENIACH.

Pierścień o promieniu wewnętrznym a i zewnętrznym b oraz grubości 1 wykonany jest z
materiału o znanych stałych sprężystych

ν, E oraz gęstości ρ. Na powierzchni wewnętrznej i

zewnętrznej pierścienia, który wiruje ze stałą prędkością kątową

ω, działa promieniowe

obciążenie powierzchniowe p

a

i p

b

( rys. 10.5 )

Rys. 10.5

Tak sformułowane

płaskie osiowosymetryczne

,

dynamiczne zadanie brzegowe teorii sprężystości
wygodniej będzie rozwiązywać w biegunowym
układzie współrzędnych. Wymaga to
wyprowadzenia odpowiednich podstawowych
równań teorii sprężystości.

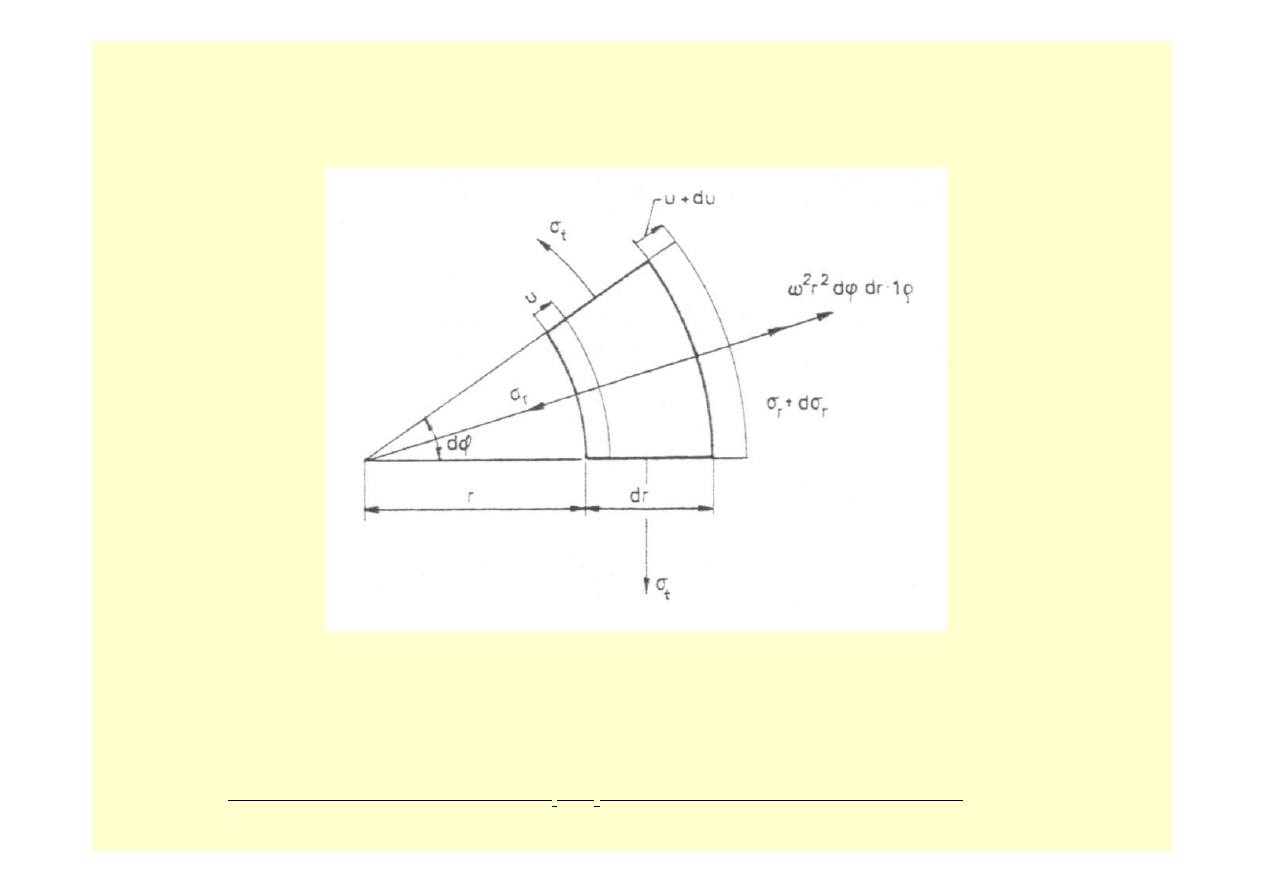
Wytniemy z rozważanego krążka segment ograniczony dwiema powierzchniami walcowymi o
promieniu r i r + dr oraz dwoma płaszczyznami przechodzącymi przez oś obrotu, które tworzą
kąt dwuścienny d

ϕ ( rys. 10.6 )

Ze względu na symetrię, w dowolnej płaszczyźnie przechodzącej przez oś obrotu naprężenie
styczne musi być równe zeru, a wiec jest to płaszczyzna główna stanu naprężenia. Występuje
w niej naprężenie

σ

t

zwane

obwodowym

. Na powierzchniach walcowych występują zatem

również tylko naprężenia normalne, zwane

promieniowymi

, równe odpowiednio

σ

r

oraz

σ

r

+ d

σ

r

. Obydwa naprężenia główne

σ

t

i

σ

r

zależą wyłącznie od promienia r.

Rys. 10.6

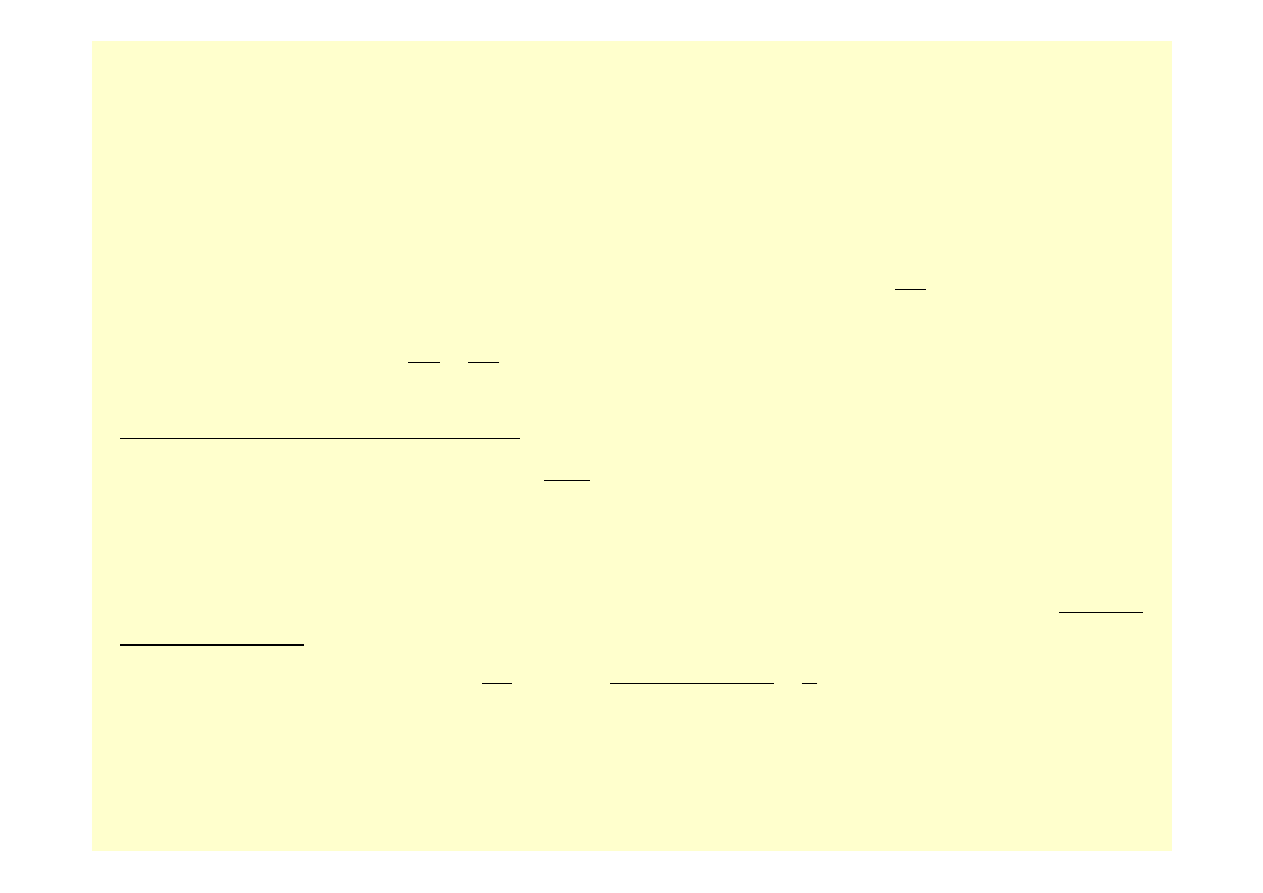
Zgodnie z zasadą d’ Alemberta, przyłożymy do segmentu siłę bezwładności równą
iloczynowi masy rd

ϕdrρ i przyspieszenia dośrodkowego ω

2

r, zwróconą od środka na

zewnątrz. Segment obciążony siłami powierzchniowymi oraz siłą bezwładności pozostaje w
równowadze, a więc suma rzutów tych sił na symetryczny kierunek promieniowy musi być
równa zeru:

(

)(

)

0

2

sin

2

2

2

=

ϕ

σ

−

ϕ

σ

−

ϕ

+

σ

+

σ

+

ϕ

ρ

ω

d

dr

rd

d

dr

r

d

drd

r

t

r

r

r

Po uwzględnieniu, że

oraz odrzuceniu małych wyższego rzędu otrzymujemy

równanie równowagi wewnętrznej A:

2

2

sin

ϕ

≈

ϕ d

d

2

2

r

r

dr

d

t

r

r

ρω

−

=

σ

−

σ

+

σ

( 10.46 )

Ze względu na osiową symetrię dowolny punkt tarczy dozna przemieszczenia u w kierunku
promieniowym. Ponieważ u jest funkcją r, wiec dwa punkty odległe od siebie o dr
przemieszczą się odpowiednio o u i u + du. Wynikają z tego następujące związki
geometryczne B:

,

dr

du

r

=

ε

(

)

r

u

r

r

u

r

t

=

π

π

−

+

π

=

ε

2

2

2

( 10.47 )

Odkształcenie promieniowe

ε

r

i obwodowe

ε

t

zależy tylko od r. Są to odkształcenia główne.

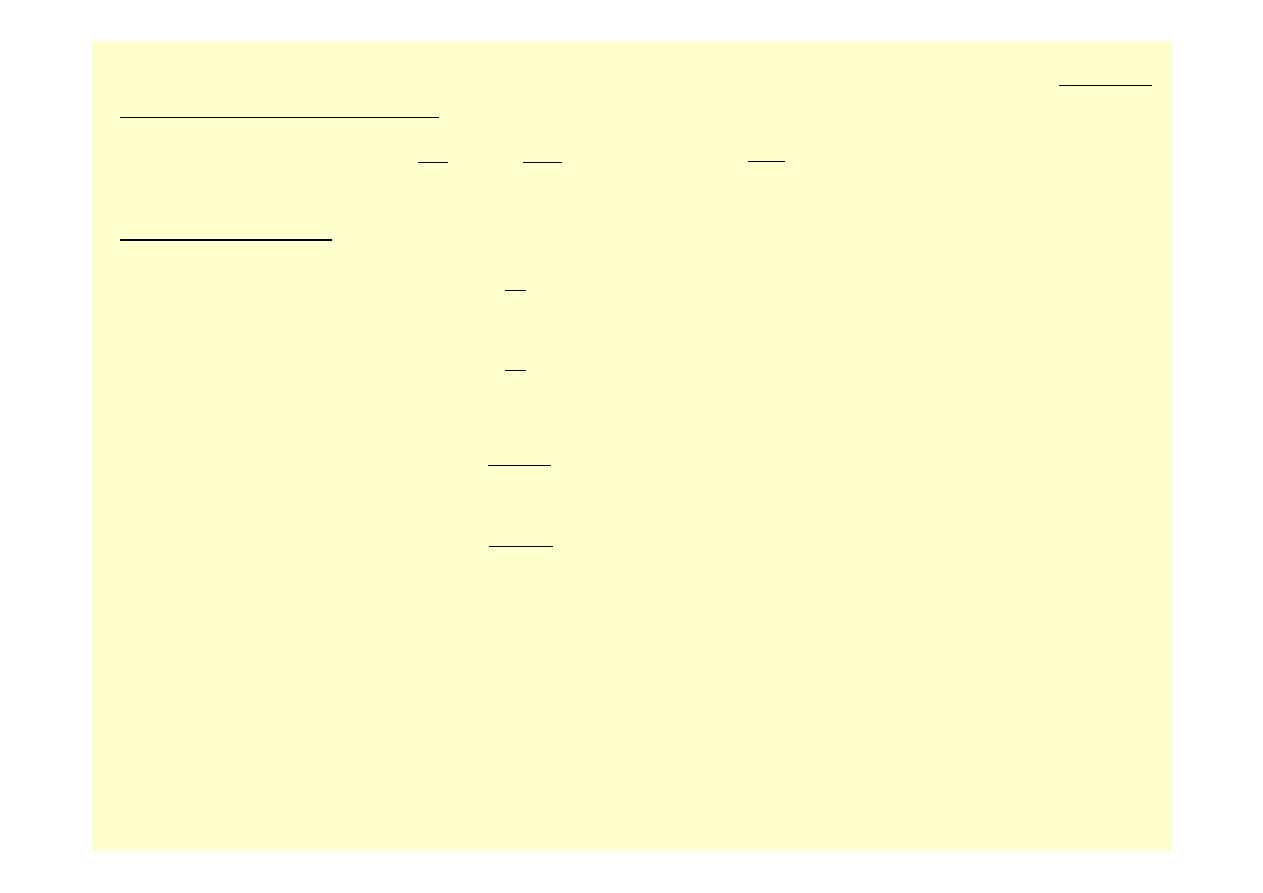
Po wyrugowaniu przemieszczenia u z zależności ( 10.47 ) otrzymamy warunek
nierozdzielności odkształceń:

,

r

u

t

ε

=

,

r

dr

d

dr

du

t

t

ε

+

ε

=

t

t

t

r

r

dr

d

ε

+

ε

=

ε

( 10.48 )

Związki fizyczne C będą miały następującą postać:

Rozwiązanie płaskiego osiowosymetrycznego, dynamicznego zadania teorii sprężystości w
przemieszczeniach będzie polegało na znalezieniu w pierwszej kolejności u( r ).

[

]

t

r

r

E

νσ

−

σ

=

ε

1

[

]

r

t

t

E

νσ

−

σ

=

ε

1

[

]

t

r

r

E

νε

+

ε

ν

−

=

σ

2

1

[

]

r

t

t

E

νε

+

ε

ν

−

=

σ

2

1

( 10.49 )

lub

( 10.50 )

Poszukujemy zatem pięciu funkcji

σ

r

( r ),

σ

t

( r ),

ε

r

( r ),

ε

t

( r ) i u( r ), które spełniają równania

A, B, C oraz warunki brzegowe.

Wstawiamy związki geometryczne ( 10.47 ) do prawa Hooke’a ( 10.50 )

⎥⎦

⎤

⎢⎣

⎡

ν

+

ν

−

=

σ

r

u

dr

du

E

r

2

1

⎥⎦

⎤

⎢⎣

⎡

ν

+

ν

−

=

σ

dr

du

r

u

E

t

2

1

( 10.51 )

Składowe stanu naprężenia wyrażone przez przemieszczenie zależnością ( 10.51 )
wprowadzamy do równania równowagi lokalnej ( 10.46 )

2

2

2

2

2

1

1

1

r

dr

du

r

u

E

r

u

dr

du

dr

d

r

E

r

u

dr

du

E

ρω

−

=

⎥⎦

⎤

⎢⎣

⎡

ν

+

ν

−

−

⎥⎦

⎤

⎢⎣

⎡

ν

+

ν

−

+

⎥⎦

⎤

⎢⎣

⎡

ν

+

ν

−

Po obustronnym pomnożeniu przez

i wykonaniu różniczkowania otrzymamy:

E

2

1

ν

−

2

2

2

2

2

1

r

E

dr

du

r

u

r

u

dr

du

r

dr

u

d

r

u

dr

du

ρω

ν

−

−

=

ν

−

−

ν

−

ν

+

+

ν

+

Po uproszczeniu i obustronnym podzieleniu przez r równanie równowagi lokalnej względem
przemieszczenia u( r ) będzie miało postać:

r

E

r

u

dr

du

r

dr

u

d

2

2

2

2

2

1

1

ρω

ν

−

−

=

−

+

( 10.52 )

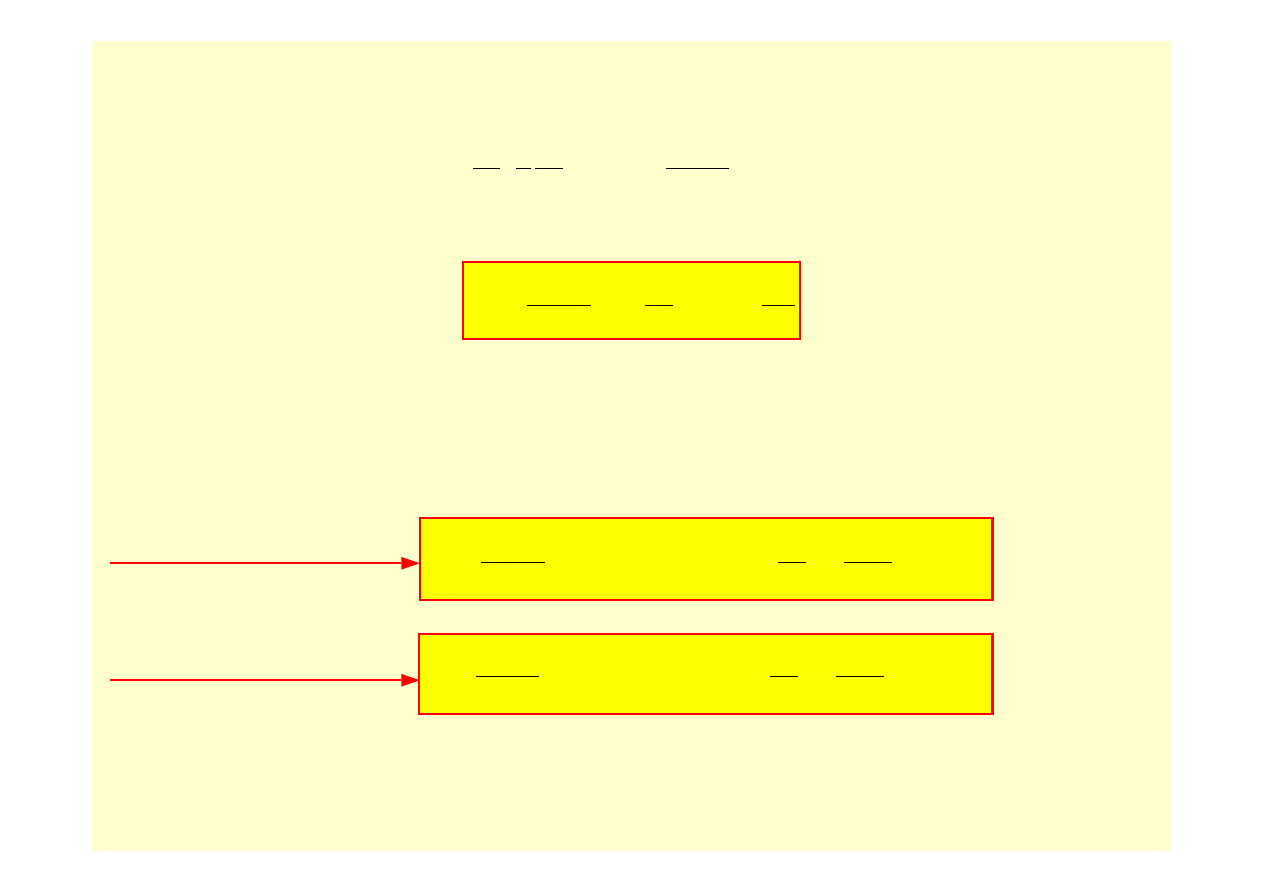
Lewa strona równania ( 10.52 ) może być zapisana jeszcze krócej

( )

r

E

ur

dr

d

r

dr

d

2

2

1

1

ρω

ν

−

−

=

⎥⎦

⎤

⎢⎣

⎡

( 10.53 )

Po dwukrotnym scałkowaniu otrzymamy:

r

C

r

C

r

E

u

2

1

3

2

2

8

1

+

+

ρω

ν

−

−

=

( 10.54 )

Stałe C

1

i C

2

należy wyliczyć z warunków brzegowych. Znajomość u( r ) umożliwia

wyznaczenie na podstawie zależności ( 10.51 ) składowych stanu naprężenia:
naprężenia promieniowego -

σ

r

( r ) i naprężenia obwodowego -

σ

t

( r )

(

)

(

)

(

)

2

2

2

2

1

2

3

8

1

1

1

1

r

r

C

C

E

r

ν

+

ρω

−

⎥⎦

⎤

⎢⎣

⎡

ν

−

+

ν

+

ν

−

=

σ

(

)

(

)

(

)

2

2

2

2

1

2

3

1

8

1

1

1

1

r

r

C

C

E

t

ν

+

ρω

−

⎥⎦

⎤

⎢⎣

⎡

ν

−

+

ν

+

ν

−

=

σ

( 10.55 )

naprężenie promieniowe

naprężenie obwodowe

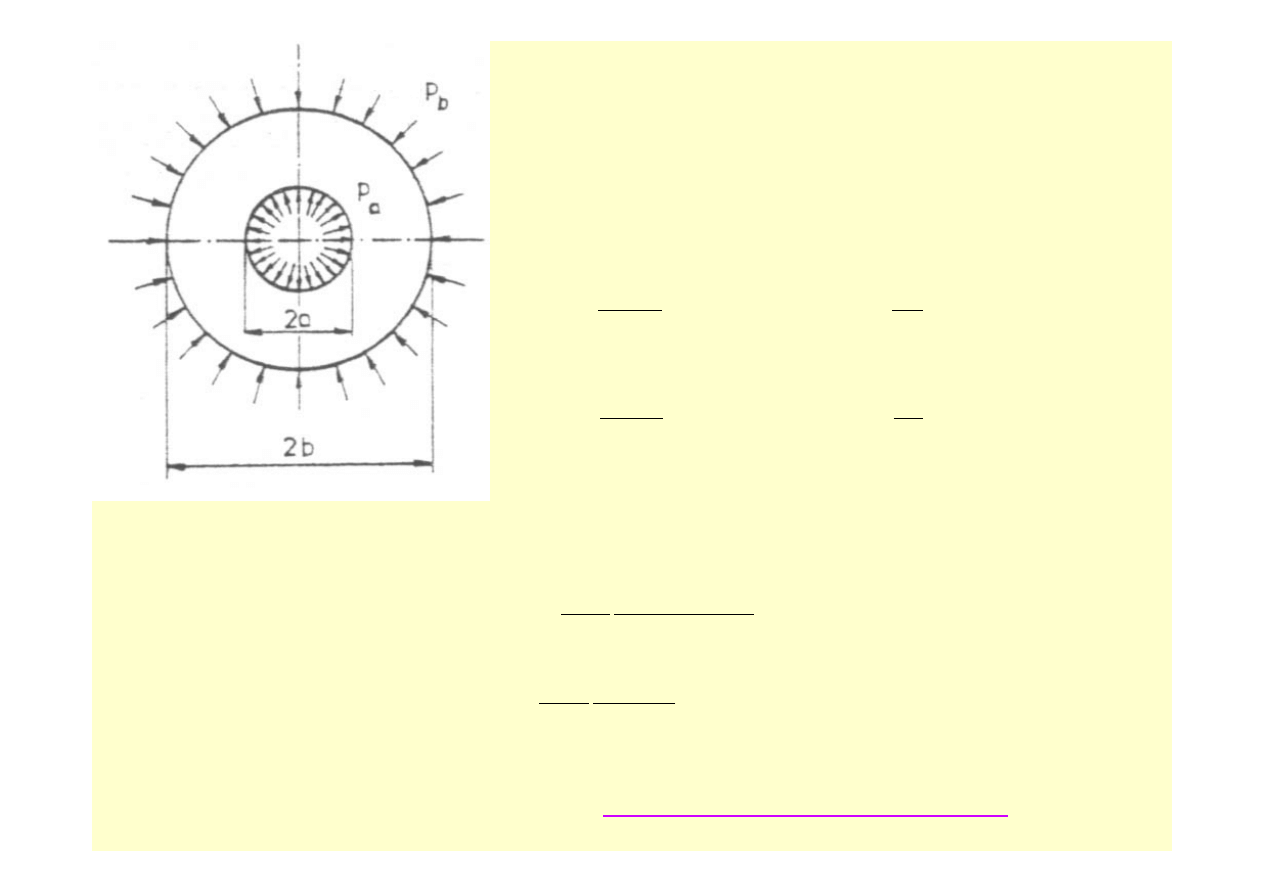
W przypadku rury grubościennej ( rys. 10.7 )

ω = 0, a

warunki brzegowe można sformułować następująco:
dla r = a,

σ

r

= -p

a

; dla r = b,

σ

r

= -p

b

, czyli

Rys.10.7

(

)

(

)

a

p

a

C

C

E

−

=

⎥⎦

⎤

⎢⎣

⎡

ν

−

+

ν

+

ν

−

2

2

1

2

1

1

1

1

(

)

(

)

b

p

b

C

C

E

−

=

⎥⎦

⎤

⎢⎣

⎡

ν

−

+

ν

+

ν

−

2

2

1

2

1

1

1

1

Wyliczone z tych równań stałe wynoszą:

2

2

2

2

1

1

a

b

b

p

a

p

E

C

b

a

−

−

ν

−

=

(

)

b

a

p

p

a

b

b

a

E

C

−

−

ν

+

=

2

2

2

2

2

1

Po wstawieniu stałych C

1

i C

2

do zależności ( 10.55 ) oraz

( 10.54 ) otrzymujemy wzory na

naprężenia i przemieszczenia w rurze

:

Warto zauważyć, że

nie zależy od r, a

więc

jest wartością stałą. Innymi słowy, grubość

rozważanego krążka zmienia się we wszystkich jego miejscach jednakowo i
dlatego rurę grubościenną można traktować jako zbiór płaskich tarcz.

2

2

2

2

2

2

2

2

2

a

b

p

p

r

b

a

a

b

b

p

a

p

b

a

b

a

r

t

−

−

−

−

=

σ

m

2

2

2

2

2

2

2

2

1

1

a

b

p

p

r

b

a

E

r

a

b

b

p

a

p

E

u

b

a

b

a

−

−

ν

+

+

−

−

ν

−

=

2

2

2

2

2

a

b

b

p

a

p

b

a

t

r

−

−

=

σ

+

σ

(

)

t

r

x

E

σ

+

σ

ν

−

=

ε

( 10.56 )

( 10.57 )

NAPRĘŻENIA I PRZEMIESZCZENIA W RURZE GRUBOŚCIENNEJ

Przykład 10.2. >>>

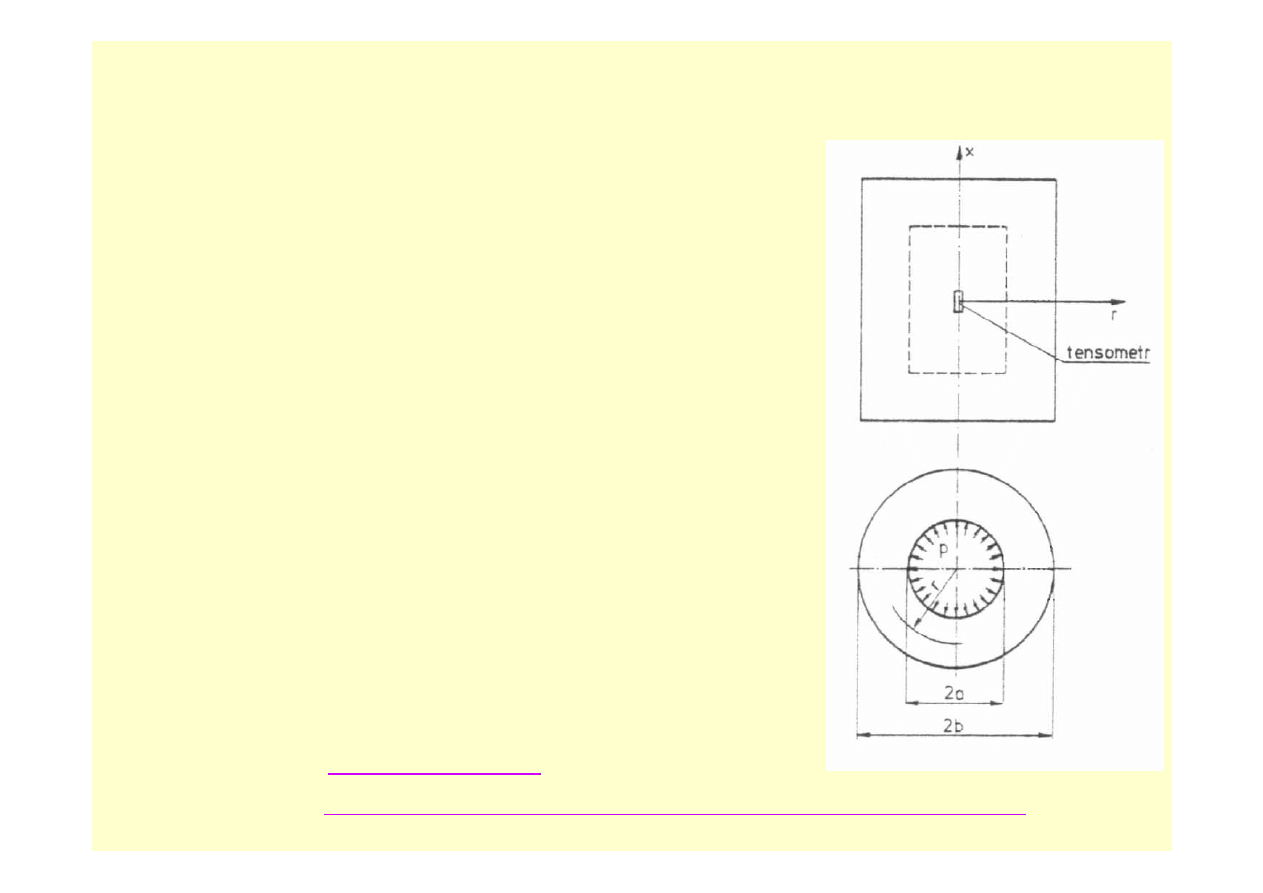
PRZYKŁAD 10.2

Zbiornik wysokociśnieniowy stanowi długa rura grubościenna
( rys. 10.8 ) o wymiarach a = 2 cm, b = 3 cm, l =100 cm.

Rozwiązanie >>>

Naprężenia i przemieszczenie w krążkach wirujących >>>

1.

Wyznaczyć nadciśnienie p panujące wewnątrz zbiornika,
jeśli wiadomo, że wywołuje ono na zewnątrz powierzchni
cylindra odkształcenie względne w kierunku tworzącej

ε

x

=10

-4

. Moduł sprężystości E = 2

⋅ 10

5

MPa, a

współczynnik Poissona

ν = 0,3.

2. Narysować wykresy

σ

r

,

σ

t

,

σ

x

.

3.

Obliczyć wg hipotezy maksymalnych naprężeń stycznych
maksymalne naprężenie redukowane w ścianach zbiornika.

Rys.10.8

Stan naprężenia w rurze grubościennej z dnem jest określony

następującymi wzorami:

( 10.58 )

( 10.59 )

( 10.60 )

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

−

−

=

σ

2

2

2

2

2

1

r

b

a

b

p

a

r

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

+

−

=

σ

2

2

2

2

2

1

r

b

a

b

p

a

t

p

a

b

a

x

2

2

2

−

=

σ

To ostatnie wyrażenie otrzymuje się z warunku, że suma rzutów na oś x sił działających na
część zbiornika, odciętą dowolną płaszczyzną prostopadłą do tej osi, musi być równa zeru.

[

]

t

x

x

E

νσ

−

σ

=

ε

1

naprężenie normalne w przekroju

prostopadłym do osi x.

dalej >>>

<<< powrót

(

)

,

2

2

2

p

a

b

a

b

r

x

−

=

σ

=

(

)

2

2

2

2

a

b

p

a

b

r

t

−

=

σ

=

2

2

2

2

2

a

b

p

a

p

a

E

x

−

ν

−

=

ε

(

)

(

)

ν

−

=

−

ε

2

1

2

2

2

p

a

a

b

E

x

(

)

(

)

MPa

62,5

2

1

2

2

2

=

ν

−

−

ε

=

a

a

b

E

p

x

(

)

(

)

MPa

62,5

-

p

-

2

2

2

2

2

2

=

=

−

−

=

σ

=

a

b

a

a

b

pa

a

r

r

(

)

(

) (

)

MPa

62,5

1

2

2

2

2

2

2

2

2

2

2

=

−

+

=

+

−

=

σ

=

a

b

a

b

p

a

a

b

a

b

pa

a

r

t

MPa

50

2

2

2

=

−

=

σ

p

a

b

a

x

MPa

225

=

σ

−

σ

=

σ

r

t

red

nadciśnienie panujące wew. zbiornika

max. naprężenie redukowane

w ścianach zbiornika

<<< powrót

Wykresy naprężeń>>>

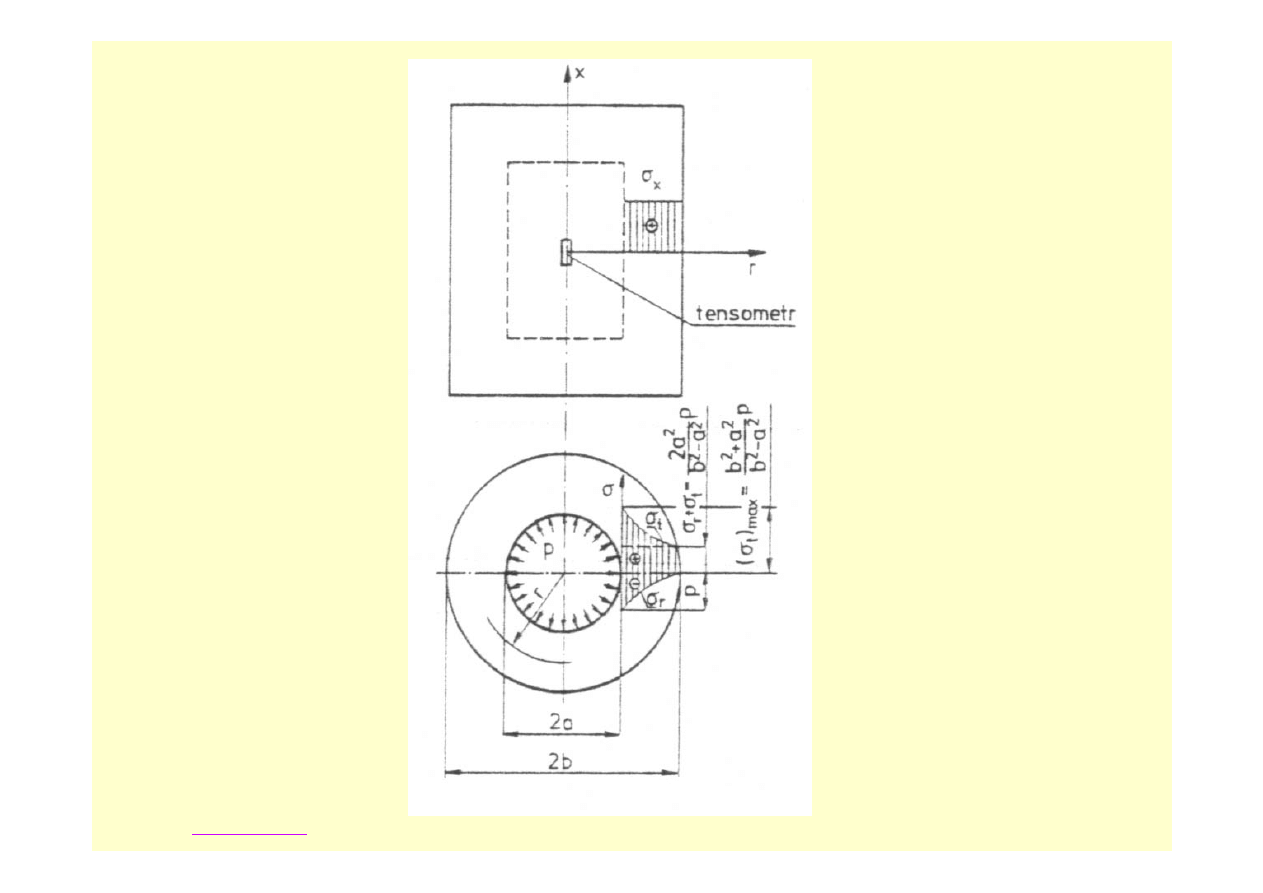
<<< powrót

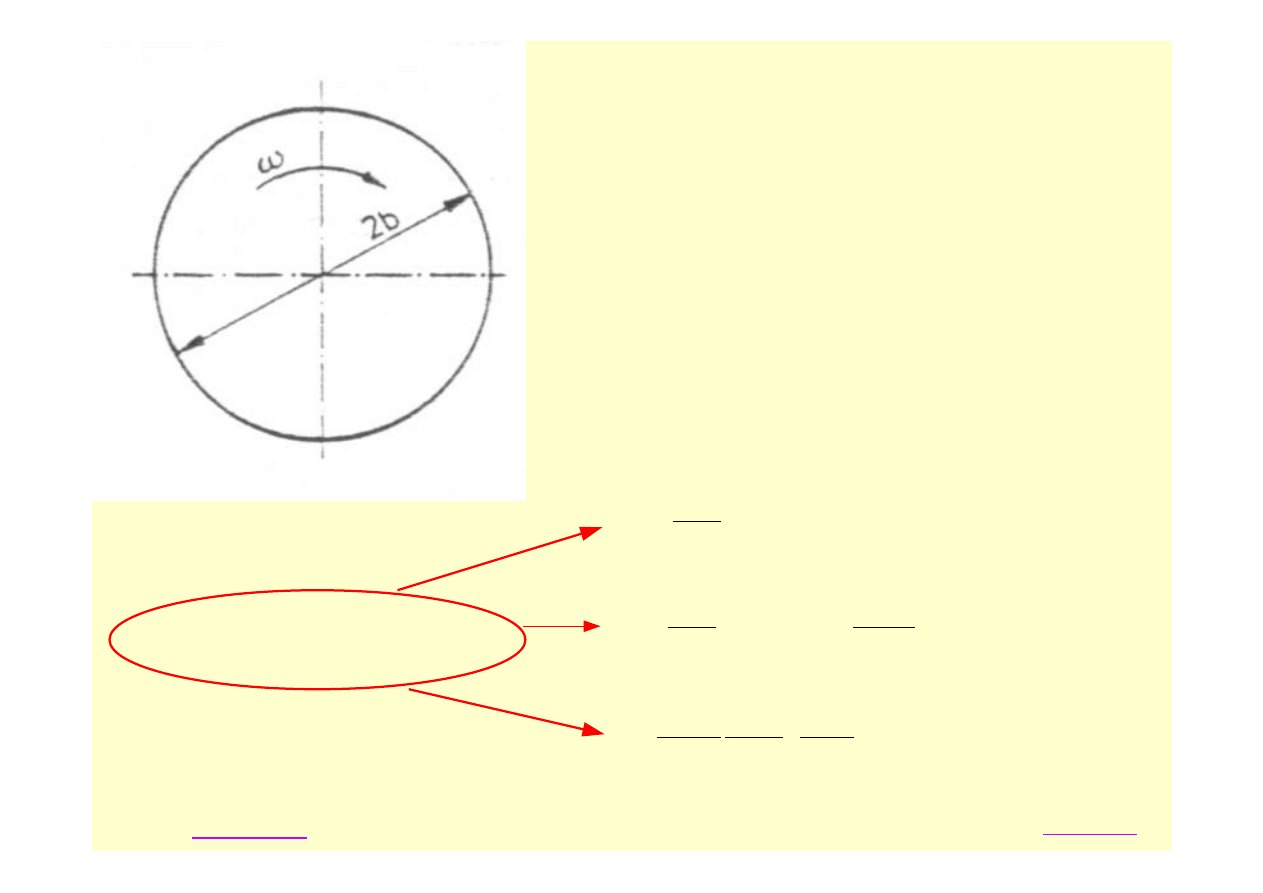
Rys. 10.9

W przypadku krążka wirującego bez otworu
( rys 10.9 ) a = 0, p

a

= 0, p

b

= 0, a warunki

brzegowe sformułować można następująco: dla r =
0 u = 0, dla r = b

σ

r

= 0. Pierwszy warunek

brzegowy może być spełniony tylko wówczas, gdy
C

2

= 0, w przeciwnym bowiem razie ostatni człon

wyrażenia ( 10.54 ) będzie równy
nieskończoności dla r = 0. Po wyliczeniu C

1

i

wstawieniu stałych do wzorów ( 10.55 ) i ( 10.54 )
otrzymujemy :

naprężenia i przemieszczenia

w krążkach wirujących

( 10.61 )

( 10.63 )

( 10.62 )

(

)

(

)

2

2

2

3

8

r

b

r

−

ν

+

ρω

=

σ

(

)

⎟

⎠

⎞

⎜

⎝

⎛

ν

+

ν

+

−

ν

+

ρω

=

σ

2

2

2

3

3

1

3

8

r

b

t

⎟

⎠

⎞

⎜

⎝

⎛

−

ν

+

ν

+

ρω

ν

−

=

2

2

2

2

1

3

8

1

r

b

r

E

u

dalej >>>

<<< powrót

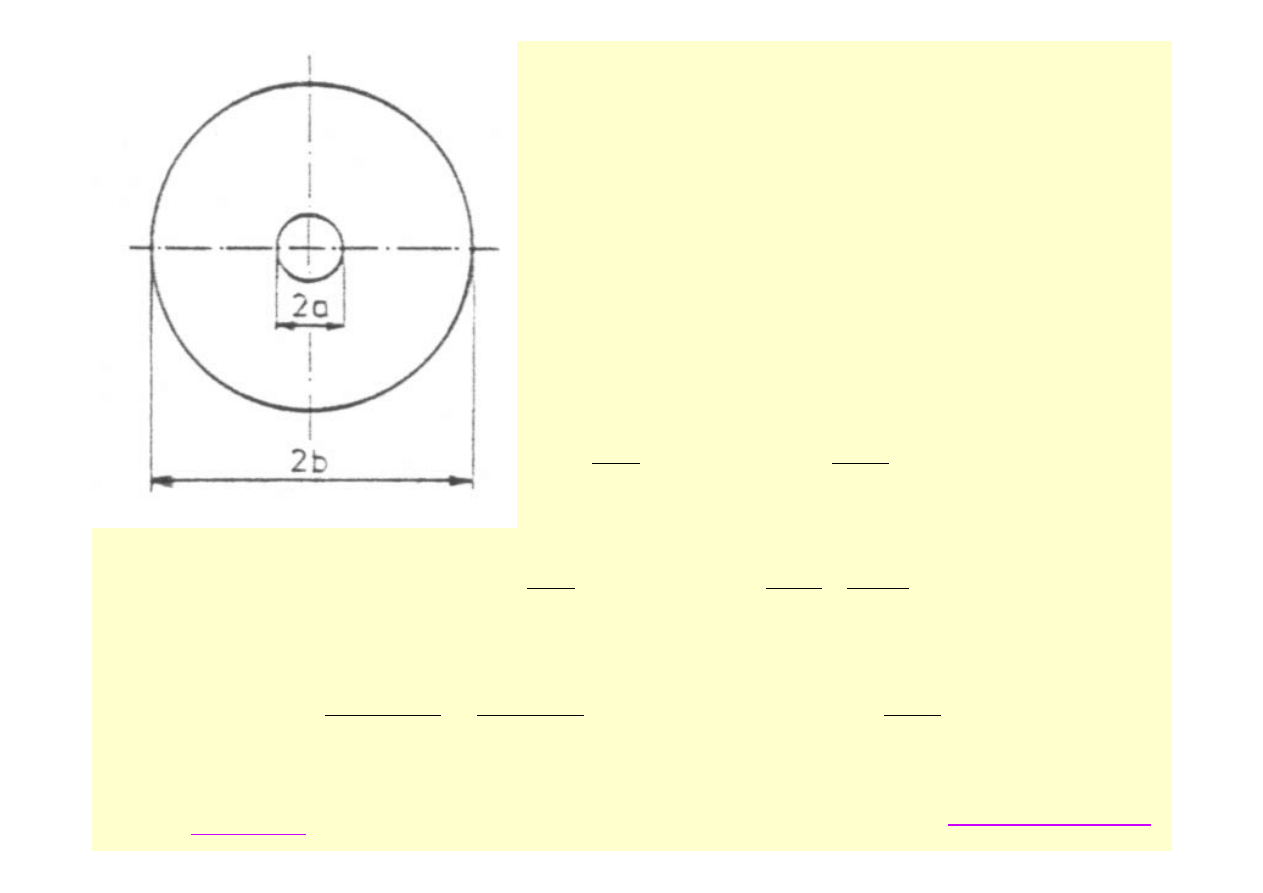
Rys.10.10

Jeśli krążek ma otwór ( rys .10.10 ), warunki
brzegowe sa następujące: dla r = a

σ

r

= 0 i dla

r = b

σ

r

= 0. Wzory na naprężenia i

przemieszczenia przybierają wtedy formę:

( 10.64 )

( 10.66 )

( 10.65 )

(

)

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

−

−

+

ν

+

ρω

=

σ

2

2

2

2

2

2

2

3

8

r

r

b

a

a

b

r

(

)

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

ν

+

ν

+

−

+

+

ν

+

ρω

=

σ

2

2

2

2

2

2

2

3

3

1

3

8

r

r

b

a

a

b

t

(

)

( )

(

)

(

)

(

)

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

ν

+

+

+

ν

−

+

ν

+

ν

−

−

ν

+

ρω

=

r

b

a

r

a

b

r

E

u

2

2

2

2

3

2

2

1

1

3

1

8

3

Przykład 10.3 >>>

<<< powrót

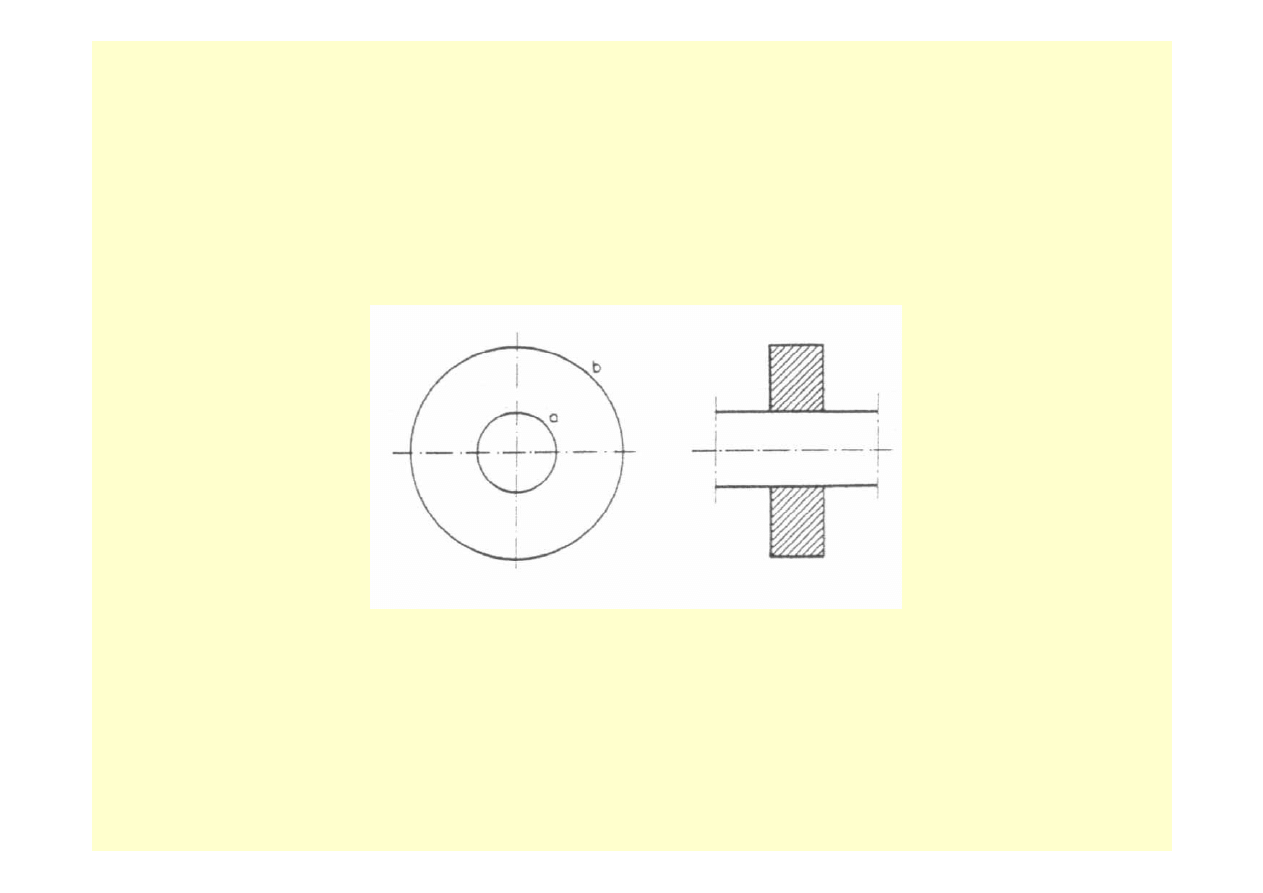
PRZYKŁAD 10.3

Na stalowy wał jest nasadzony krążek o stałej grubości. Różnica promieni wału i
otworu

δ = 0,005 mm ( rys. 10.11 ). Obliczyć liczbę obrotów na minutę, przy której

wzajemny nacisk wałka i krążka na powierzchni styku zmaleje do zera. Dane :
E = 2

⋅10

5

MPa,

ν = 0,28, a = 5 cm, b = 40 cm, ρ = 800 kg/m

3

.

Rys. 10.11

Wzajemny nacisk na powierzchni styku zmaleje do zera, jeśli różnica przemieszczeń
punktów leżących na powierzchni otworu i na powierzchni wałka osiągnie wartość:

( )

( )

δ

=

−

=

=

a

r

w

a

r

k

u

u

( 10.67 )

Wał traktujemy jako krążek bez otworu.

Dla wirującego nieobciążonego krążka o średnicy 2b z otworem o średnicy 2a, przy r = a,

otrzymamy:

( 10.69 )

( 10.68 )

(

)

(

)

(

)

(

)

⎥

⎦

⎤

⎢

⎣

⎡

ν

+

ν

−

−

ν

+

+

+

ν

−

ρ

ω

ν

+

=

3

2

2

2

2

2

2

3

1

1

1

8

3

a

a

b

a

a

b

a

E

u

k

Dla wirującego nieobciążonego krążka o średnicy 2a ( w formule ( 10.63 ) oznaczone
2b ) bez otworu i r = a

( )

⎟

⎠

⎞

⎜

⎝

⎛

−

ν

+

ν

+

ρ

ω

ν

−

=

2

2

2

2

1

3

8

1

a

a

E

a

u

w

Po wstawieniu zależności ( 10.68 ) i ( 10.69 ) do ( 10.67 ) otrzymuje się równanie, z
którego można wyliczyć

ω

(

)

(

)

(

)

(

)

( )

δ

=

⎟

⎠

⎞

⎜

⎝

⎛

−

ν

+

ν

+

ρ

ω

ν

−

−

⎥

⎦

⎤

⎢

⎣

⎡

ν

+

ν

−

−

ν

+

+

+

ν

−

ρ

ω

ν

+

2

2

2

2

3

2

2

2

2

2

2

1

3

8

1

3

1

1

1

8

3

a

a

a

E

a

a

b

a

a

b

a

E

czyli

stąd

(

)

δ

=

ρ

ω

ν

+

E

ab

4

3

2

2

(

)

1

-

s

437

3

2

=

ν

+

ρ

δ

=

ω

a

E

b

min

obr

4171

30 =

π

ω

=

n

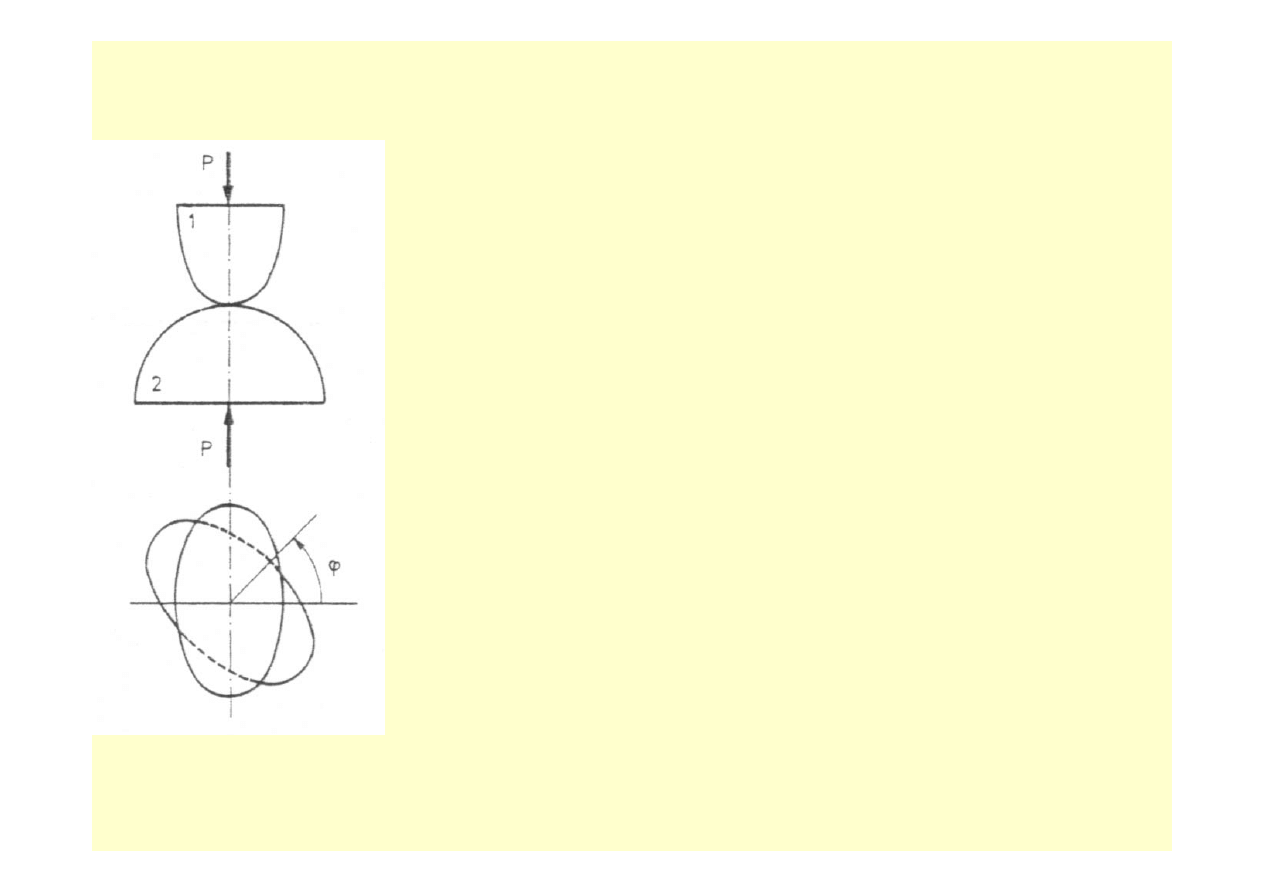
NAPRĘŻENIA KONTAKTOWE

Rys. 10.12

Teorię

naprężeń

stykowych, czyli kontaktowych

opracował Hertz. Jest to zagadnienie geometrycznie nieliniowe. Na
rysunku 10.12 pokazano dwa stykające się ciała. Mają one wspólną
normalną, wspólną płaszczyznę styczną w punkcie styku i są
wzajemnie dociskane siłami P. Dla ciała 1 min i max promień
krzywizny wynosi r

1

i r

1

’

, a stałe sprężyste E

1

i

ν

1

. Dla ciała 2

odpowiednie wielkości wynoszą r

2

i r

2

’

, a stałe sprężyste E

2

i

ν

2

.

Kąt między płaszczyznami największych krzywizn ( czyli
minimalnych promieni krzywizn, r

1

i r

2

) jest równy

ϕ.

Przyjmuje się następujące

założenia

:

2. Powierzchnie zewnętrzne ciał w otoczeniu punktu styku są

gładkie o regularnej krzywiźnie.

3. Odkształcenia ciał są niewielkie.

4.

Powierzchnia styku w stosunku do powierzchni ciał jest mała.

5.

Na powierzchni styku nie ma naprężeń stycznych, a jedynie
normalne.

1. Stykające się ciała są jednorodne, izotropowe i

liniowosprężyste

Po odkształceniu ciał spowodowanym ich wzajemnym dociśnięciem powstaje obszar
styku w postaci elipsy o osiach a i b ( a > b ), które można obliczyć ze wzorów

3

n

m

P

a

α

=

3

n

m

P

b

β

=

,

1

1

1

1

4

'

2

2

'

1

1

r

r

r

r

m

+

+

+

=

)

1

(

)

1

(

3

8

2

2

1

2

1

2

2

1

ν

−

+

ν

−

=

E

E

E

E

n

,

2

m

A

=

ϕ

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

−

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

−

+

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

−

+

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

−

=

2

cos

1

1

1

1

2

1

1

1

1

2

1

'

2

2

'

1

1

2

'

2

2

2

'

1

1

r

r

r

r

r

r

r

r

B

( 10.70 )

gdzie:

przy czym

α i β - współczynniki zależne od B/A, przy:

podane w

tablicy >>>

Tablica. Wartości

α, β, B/A

cd.>>>

0,4930
0,4897
0,4863
0,4828
0,4794

2,731
2,765
2,800
2,837
2,874

0,8661
0,8699
0,8737
0,8774
0,8811

0,6580
0,6359
0,6245
0,6127
0,6006

1,684
1,775
1,826
1,882
1,943

0,6113
0,6521
0,6716
0,6920
0,7126

0,5093
0,5061
0,5029
0,4996
0,4963

2,576
2,605
2,635
2,666
2,698

0,8468
0,8507
0,8545
0,8584
0,8623

0,8114
0,7717
0,7218
0,6992
0,6791

1,262
1,345
1,456
1,540
1,607

0,3204
0,3954
0,4795
0,5342
0,5819

0,5247
0,5217
0,5186
0,5155
0,5124

2,443
2,469
2,494
2,521
2,548

0,8270
0,8310
0,8350
0,8389
0,8428

1,0000
0,9696
0,9318
0,8791
0,8472

1,000
1,032
1,076
1,148
1,198

0,0000
0,0466
0,1075
0,1974
0,2545

β

α

B/A

β

α

B/A

0,3551
0,3223
0,2814
0,2232

5,091
6,159
8,062

12,789

0,9705
0,9818
0,9909
0,9937

0,5366
0,5336
0,5307
0,5277

2,350
2,372
2,395
2,419

0,8110
0,8150
0,8190
0,8230

0,4076
0,4029
0,3981
0,3932
0,3830

3,899
3,986
4,079
4,178
4,395

0,9428
0,9458
0,9488
0,9517
0,9574

0,5508
0,5480
0,5452
0,5423
0,5395

2,245
2,265
2,286
2,306
2,328

0,7907
0,7948
0,7988
0,8029
0,8069

0,4576

0,438

0,4499
0,4460
0,4297

3,132
3,181
3,233
3,286
3,526

0,9030
0,9065
0,9100
0,9134
0,9269

0,5646
0,5618
0,5591
0,5564
0,5536

2,153
2,171
2,189
2,207
2,226

0,7702
0,7743
0,7784
0,7825
0,7866

0,4759
0,4723
0,4687
0,4650
0,4613

2,914
2,954
2,996
3,040
3,085

0,8849
0,8885
0,8922
0,8958
0,8994

0,5881
0,5752
0,5726
0,5699
0,5672

2,011
2,087
2,103
2,119
2,136

0,7332
0,7538
0,7579
0,7620
0,7661

β

α

B/A

β

α

B/A

( )

2

2

1

2

3

,

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

π

=

b

y

a

x

ab

P

y

x

p

ab

P

p

π

=

2

3

max

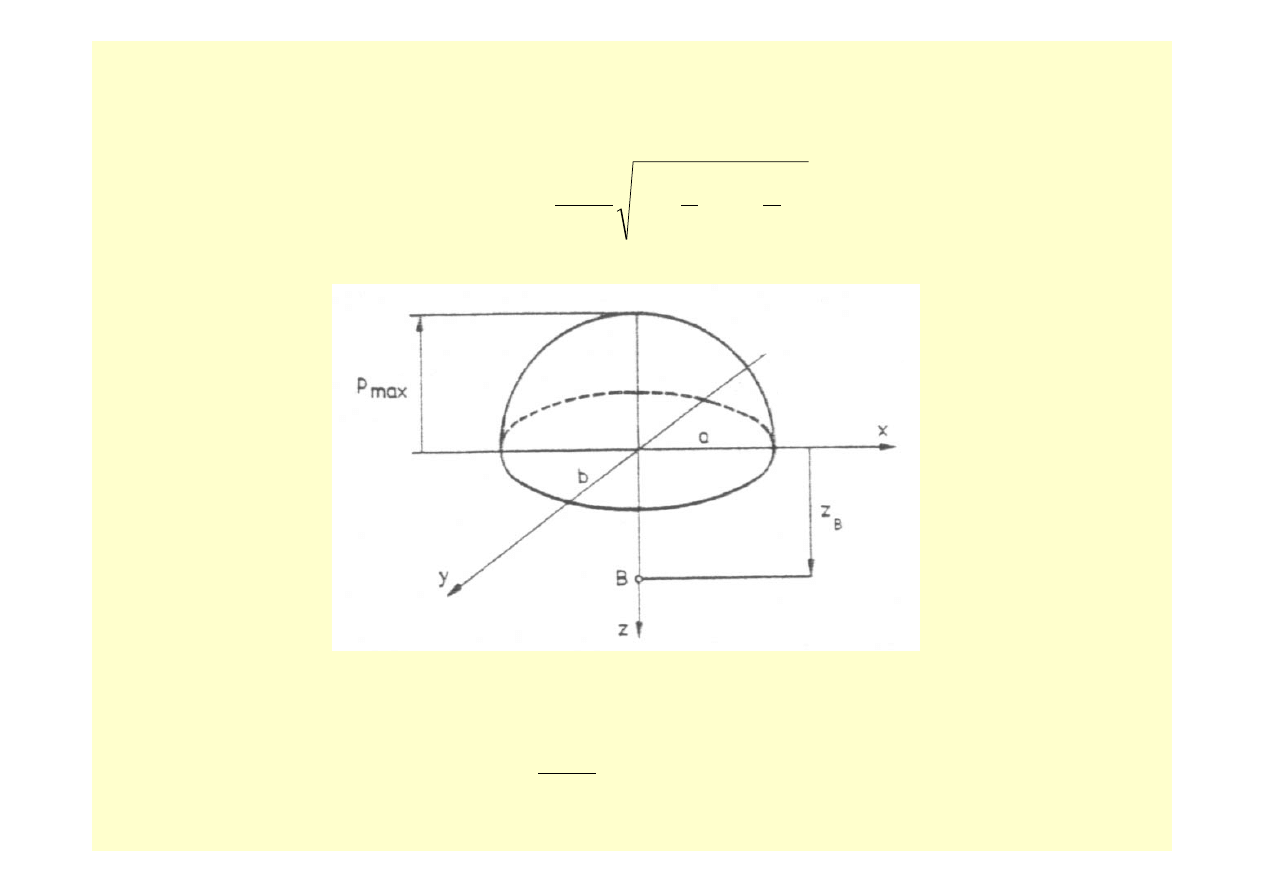
Rozkład

nacisków powierzchniowych

na obszarze styku jest elipsoidą ( rys. 10.13 ) o

następującym równaniu:

Rys. 10.13

( 10.71 )

Wartość p

max

największego ciśnienia na powierzchni styku dla x = 0 i y = 0 wynosi:

( 10.72 )

(

)

'

2

1

2

1

4

P

r

r

r

r

k

b

+

π

=

b

P

p

π

=

'

max

2

( 10.73 )

Jeśli elementy dociskane są walcami o osiach równoległych, obszar styku jest

prostokątem o szerokości 2b, przy czym:

Rozkład nacisków na obszarze styku jest walcem o przekroju półeliptycznym, a p

max

wynosi:

( 10.74 )

Siła docisku na jednostkę

długości wspólnej tworzącej

2

2

2

1

2

1

1

1

E

E

k

ν

−

+

ν

−

=

Największe naprężenie redukowane występuje w tak zwanym

punkcie

Bielajewa

, którego położenie na osi symetrii określa współrzędna z

B

. Według hipotezy

maksymalnych naprężeń stycznych przy

ν = 0,3 dla kołowego obszaru styku ( ściskania

kul ) z

B

/b = 0,481 i

σ

red

/p

max

= 0,620,natomiast dla prostokątnego obszaru styku (ściskania

walców ) z

B

/b = 0,780 i

σ

red

/p

max

= 0,608 . Według hipotezy energii odkształcenia

postaciowego wielkości te zmieniaja się odpowiednio w przedziale od z

B

/b = 0,481 i

σ

red

/p

max

= 0,620 do z

B

/b = 0,697 i

σ

red

/p

max

= 0,567. Wartości naprężenia redukowanego

w punkcie Bielajewa przekraczają często R

e

, a nawet R

m

. Materiał wytrzymuje to,

ponieważ panuje tam stan naprężenia bliski przestrzennemu równomiernemu ściskaniu
( dla takiego stanu naprężenia obydwie hipotezy tracą sens ).

Wartości jednostkowe nacisku dopuszczalnego k

dH

są znaczne, np. dla stali StOS wynoszą

440 MPa, a dla stali 18G2 nawet 880 MPa, ponieważ stany naprężenia w obszarze styku są
bliskie równomiernemu przestrzennemu ściskaniu.

Kryterium nacisku powierzchniowego

można sformułować następująco:

( 10.75 )

dH

k

p

max

≤

LITERATURA

Bąk R., Burczyński T.: Wytrzymałość materiałów z elementami ujęcia
komputerowego. WNT, Warszawa 2000