1

Wielkość fizyczna

to każda

mierzalna

właściwość lub cecha

przedmiotu lub zjawiska.

Pomiar

wielkości fizycznej polega na porównaniu danej wiel-

kości fizycznej z wielkością tego samego rodzaju przyjętą

jako wzorzec, jako jednostka miary.

Miarą

wielkości fizycznej

A

jest

iloczyn liczby {A},

która

wskazuje ile razy dana wielkość fizyczna jest większa lub

mniejsza od przyjętej jednostki miary

[A]

i

jednostki miary

użytego wzorca [A]:

A = {A} · [A]

2

Wykonując pomiar trzeba:



Zdefiniować odpowiednią

jednostkę miary,



Użyć właściwego

narzędzie pomiarowe,



Pamiętać, że działania związane z wykonaniem pomiaru

obarczone są

niedokładnościami.

Trzeba poznać zasady ustalania wartości tych niedokład-

ności:

rachunek błędów pomiaru.

Interpretację uzyskanych wyników ułatwia

właściwa prezen-

tacja uzyskanych wyników pomiaru.
Trzeba umieć sporządzać

tabele wyników i wykresy.

W

ielkości podstawowe układu SI

Pozostałe wielkości fizyczne, otrzymane z równań definicyjnych,

tworzą wielkości

pochodne,

a jednostki ich miary oparte na jed-

nostkach podstawowych układu SI nazywamy

jednostkami głów-

nymi.
Prędkość jest wielkością pochodną, bo:

a jej jednostką główną w układzie SI jest:

Wielkość podstawowa

Symbol

Jednostka miary

Długość

L

1 metr

m

Masa

M

1 kilogram

kg

Czas

T

1 sekunda

s

Natężenie prądu elektrycznego

I

1 amper

A

Temperatura

Q

1 kelwin

K

Liczność materii

N

1 mol

mol

Światłość

J

1 kandela

cd

3

Zakres wartości mierzonych wielkości może być bardzo sze-

roki, dlatego oprócz jednostek głównych stosuje się ich wielo-

korotności i podwielokrotności.

Przedrostek

Symbol

Mnożnik

giga

G

10

9

mega

M

10

6

kilo

k

10

3

hekto

h

10

2

deka

da

10

1

decy

d

10

−1

centy

c

10

−2

mili

m

10

−3

mikro

μ

10

−6

nano

n

10

−9

piko

p

10

−12

Najważniejsze właściwości narzędzia pomiarowego:



błąd wskazania (niedokładność wzorcownia),



czułość,



obszar mierniczy, czyli zakres mierzonych wielkości,



wpływ narzędzia pomiarowego na wielkość mierzoną.

Producent narzędzia pomiarowego powinien dostarczyć

informacji o dokładności wskazania przyrządu pomiaro-

wego. Mierniki elektryczne charakteryzuje tzw.

klasa do-

kładności:

gdzie: ΔA

oznacza błąd pomiaru wielkości A,

A

maks

górną granicę zakresu pomiarowego.

4

Gdy

brak

informacji o dokładności wywzorcowania przy-

rządu pomiarowego przyjmuje się, że

błąd pomiaru ró-

wny jest działce elementarnej narzędzia pomiarowego.

Chociaż może wydawać się nam, że wartość możemy

odczytać z większą dokładnością, nie ma to sensu, bo:

Trzeba pamiętać, że dokładnie odczytać nie oznacza

dokładnie zmierzyć.

R

achunek błędów pomiaru

Rozpatrzmy przykład pomiaru długości przy pomocy linijki.

Producent nie podał dokładności wskazania linijki, ale naniósł po-

działkę co 1 mm.
Oznacza to, że gwarantuje możliwość pomiaru długości z dokład-

nością do 1 mm.

I jest to pierwsze źródło błędu tego pomiaru.

Ale to nie jest jedyne źródło niepewności pomiarowej.....

Jaka jest długość tego klocka?

3,2 cm, 3,3 cm a może 3,25 cm?

5

Analizując czynności wykonywane podczas tego pomiaru
znajdujemy kolejne źródła niepewności:



Czy linijka ułożona jest równolegle do klocka?



Czy zero linijki „pokrywa się” z początkiem klocka?



Czy powtarzając pomiar przykładamy linijkę za każdym razem

identycznie?



Biorąc linijkę w rękę ogrzewamy ją; jak jej rozszerzenie wpły-

nie na wynik pomiaru?



Jaką wartość uzyska się wykonując pomiar przy pomocy linijki

wykonanej przez innego producenta?

Są to podstawowe problemy, przed którymi stanie każdy, kto chce

rzetelnie wykonać ten pomiar.

Przykład ten wskazuje, że wykonując jakikolwiek pomiar nie

możemy uniknąć popełnienia błędu pomiaru. Jest on „wpisany”

w procedurę pomiaru.

Błąd wskazania

przyrządu

pomiarowego

Błąd metody pomiaru:



przybliżony wzór,



niewłaściwe wykorzystanie
przyrządu pomiarowego.

6

W wyniku pomiaru otrzymujemy wartość

A

,

jako miarę danej wiel-

kości fizycznej. Nie jest ona jednak równa

rzeczywistej wartości

A

0

mierzonej wielkości fizycznej. Różnicę pomiędzy wielkością zmie-

rzoną i wartością rzeczywistą nazywamy

błędem pomiaru

δA

:

δA  A A

0

Wykonując pomiar nie jesteśmy w stanie określić ani wartości

A

0

,

ani

δA

.

Wartość

δA

możemy jedynie

oszacować

(ΔA)

i w ten sposób okre-

ślić przedział, w którym znajduje się rzeczywista wartość

A

0

wielko-

ści mierzonej:

A

0



AΔA, AΔA

Częściej do opisu tego przedziału będziemy korzystać z zapisu:

A  ΔA

Postaramy się teraz przedstawić zasady szacowania wartości

ΔA

błędu pomiarowego.

Wykonując kilkakrotnie pomiar tej samej wielkości fizycznej w tych

samych warunkach przy użyciu tego samego narzędzia pomiaro-

wego, można zauważyć, że:

albo:



wyniki kolejnych pomiarów nie różnią się od siebie o więcej

niż najmniejsza działka przyrządu pomiarowego,

albo:



wyniki kolejnych pomiarów różnią się od siebie o więcej niż

najmniejsza działka przyrządu pomiarowego.

W pierwszym przypadku mówimy o

błędzie systematycznym.

W drugim mówimy o

błędzie przypadkowym.

7

Błędy systematyczne

zawsze w ten sam sposób wpływają na wy-

niki pomiarów wykonywanych przy pomocy tej samej metody i apa-

ratury pomiarowej, a ich źródła mogą być następujące:



błąd wskazania przyrządu pomiarowego (określony przez klasę dokładno-

ści przyrządu lub różnicę pomiędzy najbliższymi działkami przyrządu).

Stanowi on podstawową, minimalną wartość błędu systematycznego,



niewłaściwa obsługa przyrządu pomiarowego (konieczne jest przestrze-

ganie instrukcji obsługi przyrządu pomiarowego),



zła metoda pomiaru (np.: pomiar ciśnienia krwi

metodą sfigmomanometry-

czną

, pomiar oporu elektrycznego przy pomocy obwodu elektrycznego złożo-

nego z amperomierza i woltomierza),



przybliżony charakter stosowanych wzorów (np.: wyznaczanie przyspie-

szenia ziemskiego g na podstawie pomiaru okresu drgań wahadła pobudzone-

go do dużych wychyleń i wykorzystując do obliczeń podręcznikowy wzór na

okres, który został wyprowadzony przy założeniu małych wychyleń wahadła),



pominięcie wpływu stałych czynników związanych z budową narzędzia

pomiarowego, np. wadliwie wykonana skala przyrządu, jej złe wywzorcowanie

(zła kalibracja) lub „starzenie” się przyrządu, w wyniku czego otrzymuje się

wartości pomiaru zawsze z nadmiarem lub zawsze z niedomiarem,



z przyczyn zawinionych przez eksperymentatora (np.: odczyt z paralaksą).

Oszacowanie wartości błędu systematycznego „sprowadza się” za-

tem do dokładnego przeanalizowania poszczególnych etapów po-

miaru. Wartość tego błędu można zmniejszyć jedynie w wyniku

udoskonalenia stosowanej metody pomiaru i/lub użycia dokładniej-

szych przyrządów pomiarowych.

Dokładne określenie wartości tego błędu nie jest łatwe!!!

W ramach pomiarów wykonywanych w pracowni biofizyki wyzna-

czając błędy systematyczne ograniczymy się do określenia błędu

wskazania przyrządu pomiarowego.

Wracając do przykładu pomiaru długości klocka przy pomocy linijki z podziałką na-

niesioną z dokładnością 1 mm, można stwierdzić, że błąd pomiaru długości wyno-

si co najmniej 1 mm. W warunkach pracowni przyjmujemy, że tyle wynosi wartość

błędu systematycznego pomiaru długości. Zakładamy, że pomiar wykonano na ty-

le rozsądnie, że pozostałe źródła niepewności są małe w porównaniu z dokładnoś-

cią wywzorcowania linijki. Długość klocka wynosi (3,3 ± 0,1) cm.

8

Rozpatrzmy przykład:

Wykonano pomiar napięcia woltomierzem o klasie dokładności 1,5 i

zakresie pomiarowym 250 V. Odczytano wartość napięcia 123,6 V.

Pomiar jest prawdopodobnie obarczony błędem systematycznym.

Jego wartość szacujemy na podstawie

klasy dokładności

przyrzą-

du pomiarowego

:

W rozpatrywanym przypadku:

Zwróćmy uwagę na sposób zapisu błędu.

Zapisując błąd powinniśmy zaokrąglić go do pierwszej cyfry znaczą-

cej, pierwszej różnej od zera cyfry w wyniku obliczeń błędu.

Wskazuje ona miejsce dziesiętne, na którym występuje błąd.

Szerokość przedziału, w którym znajduje się rzeczywista wartość

wielkości mierzonej zależy od oszacowanej wartości błędu. Stąd,

aby nie zawężać tego przedziału, należy zawsze wartość błędu zao-

krąglać w górę.

W rozpatrywanym przykładzie:

ΔU = 3,75 V ≈ 4 V

Czasami jednak zaokrąglenie wartości błędu w górę, do pierwszej cyfry

znaczącej, zbyt mocno zwiększa jego wartość, np. zaokrąglenie wartości
błędu pomiaru masy Δm =109 mg do wartości 200 mg

.

W sytuacji, gdy zaokrąglenie błędu w górę, do pierwszej cyfry zna-

czącej, zwiększa wartość błędu o więcej niż 10% jego wartości,

pozostawia się w wyniku błędu 2 pierwsze cyfry znaczące.
Ale nigdy w błędzie nie może być trzech lub więcej cyfr znaczących.

9

Stąd poprawnie zaokrąglając wartość błędu pomiaru masy:

zamiast Δm = 200 mg napiszemy Δm =110 mg

(zero na końcu nie jest znaczące).

Następnie możemy przystąpić do zaokrąglania wyniku pomiaru.

Wynik pomiaru zaokrąglamy do miejsca dziesiętnego, na

którym kończy się błąd pomiaru po jego prawidłowym za-

okrągleniu.

Poprawny zapis rozpatrywanego przez nas wyniku pomiaru ma po-

stać:

U =

(123,6 ± 3,75) V ≈

(124 ± 4) V

Wynik pomiaru i błąd przed

zaokrągleniem:

(136,521 ± 0,115) cm
(136,521 ± 0,195) cm

(0,036255 ± 0,000111) m

(65,273 ± 0,321)·10



3

μF

(251,6767 ± 0,07943) mA

(379823,1245 ± 1245,75) cm

2

Wynik pomiaru i błąd po

zaokrągleniu:

(136,52 ± 0,12) cm

(136,5 ± 0,2) cm

(0,03626 ± 0,00012) m

(65,27 ± 0,33) nF

(251,68 ± 0,08) mA

(379800 ± 1300) cm

2

= (37,98 ± 0,13) m

2

Przykłady zaokrąglania wartości błędu pomiaru i wyniku pomiaru:

10

Zwróćmy uwagę na różne sposoby zapisu błędu pomiaru:



błąd bezwzględny, np.: błąd pomiaru długości ΔL = 0,1 cm,

wtedy piszemy L = (3,3 0,1) cm,



błąd względny, , w naszym przypadku ,



błąd względny procentowy

, w naszym przypadku 3,1%,



w postaci przedziału L   3,2; 3,4  cm.

Błędy przypadkowe

Gdy wykonujemy pomiary przy użyciu przyrządów pomiarowych o

dużej dokładności (gdy błąd wskazania przyrządu jest mały), zda-

rza się często, że wyniki kilku kolejnych pomiarów różnią się od

siebie o wartość większą od dokładności przyrządu pomiarowego.

W takim przypadku mówimy, że pomiary obarczone są

błędem przypadkowym.

Ich źródło może być różnej natury:



związane z właściwościami mierzonej wielkości fizycznej

pomiar tętna poszczególnego osobnika, czy pomiar tętna w danej populacji,

pomiar średnicy drutu itp.,



związane z właściwościami przyrządu pomiarowego

tarcie łożysk w wadze, drgania lusterka w galwanometrze itp.,



zawinione przez eksperymentatora

przy pomiarze czasu stoperem - różne chwile włączenia i wyłączenia stopera

przy kolejnych pomiarach czasu itp.

11

Błędów przypadkowych nie można wyeliminować!

Można jednak, w odróżnieniu od błędów systematycznych, dokła-

dnie określić ich wartość.
Sposób szacowania wartości błędów przypadkowych wyjaśnia te-

oria Gaussa.

Istotę tej metody wyjaśnimy na przykładzie pomiaru tętna pew-

nego osobnika. Wyniki pomiaru zebrano w poniższej tabeli.

Carl Friedrich

Gauss, ur. 30 IV 1777, Brunszwik, zm. 23 II

1855, Getynga, niem. matematyk, fizyk, astronom i geodeta;

profesor uniw. i dyr. obserwatorium astr. w Getyndze; rozwinął

m.in. teorię liczb, geometrię nieeuklidesową, teorię funkcji

zespolonych; zajmował się też elektrycznością, magnetyzmem,

teorią potencjału.

Widzimy, że wyniki kilku kolej-

nych pomiarów tętna dla tego

samego osobnika, wykonanych

w tych samych warunkach, róż-

nią się od siebie o więcej niż

błąd wskazania przyrządu po-

miarowego; trzeba zatem wyko-

nać

co najmniej 10 pomiarów.

Dalej wykonujemy obliczenia,

tak jak wskazuje tabela.

Obliczamy kolejno:


średnią,



odchylenia od średniej,



obliczenia wykonujemy z do-

kładnością do 3 cyfr znaczą-

cych,



sumę kwadratów odchyleń

poszczególnych wyników od

wartości średniej.

12

Jako oczekiwaną (najbardziej prawdopodobną) wartość tętna badane-

go osobnika przyjmuje się

wartość średnią

określoną wzorem:

gdzie: n oznacza liczbę wykonanych pomiarów.

W naszym przypadku z obliczeń otrzymujemy:

Miarą błędu pomiarów w takim przypadku, jest tak zwane

odchylenie

standardowe

(średnie odchylenie kwadratowe, błąd średni poszczególnego po-

miaru)

zdefiniowane wzorem:

W rozpatrywanym przypadku wartość liczbowa odchylenia standardowe-

go wynosi:

Teraz rozumiemy dlaczego w powyższej tabeli zamieszczono dodat-

kowe kolumny, ułatwiają one obliczenie wartości odchylenia standar-
dowego.

Odchylenie standardowe jest miarą błędu pomiaru; zaokrąglamy je-
go wartość zgodnie z przyjętymi zasadami zaokrąglania błędów po-

miarowych do co najwyżej 2 cyfr znaczących.

Ponieważ końcowa wartość błędu nie może posiadać więcej niż 2 cyf-

ry znaczące, w pośrednich rachunkach związanych z szacowaniem
błędu, wystarczy prowadzić obliczenia z dokładnością do trzech cyfr

znaczących, tak jak to zostało przedstawione w tabeli.

Jaki jest sens odchylenia standardowego?

Wyjaśnimy to na przykładzie

bardziej licznej

próby pomiarów tętna...

13

Zaznaczmy wartość średnią..

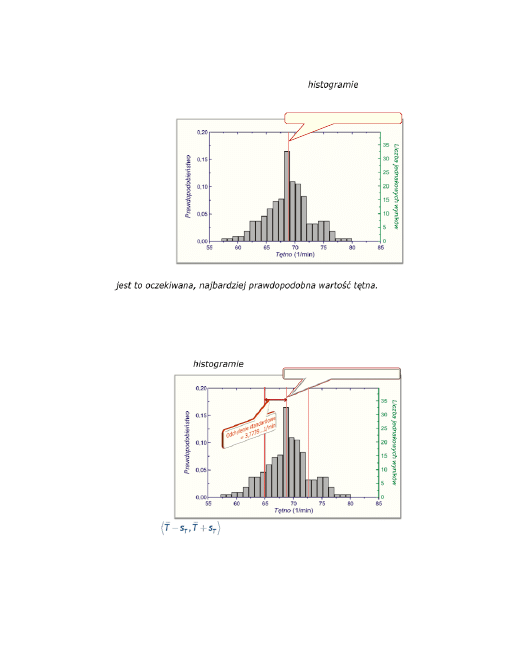
Wyniki tych pomiarów ilustrujemy na poniższym histogramie.

Zaznaczmy wartość średnią.. i już rozumiemy co oznacza stwierdzenie,

że jest to oczekiwana, najbardziej prawdopodobna wartość tętna.

Prawdopodobieństwo danego wyniku równe jest stosunkowi liczby danych

wyników do liczby wszystkich wyników.

Wartość średnia = 69,8134... 1/min

Wartość średnia = 69,8134... 1/min

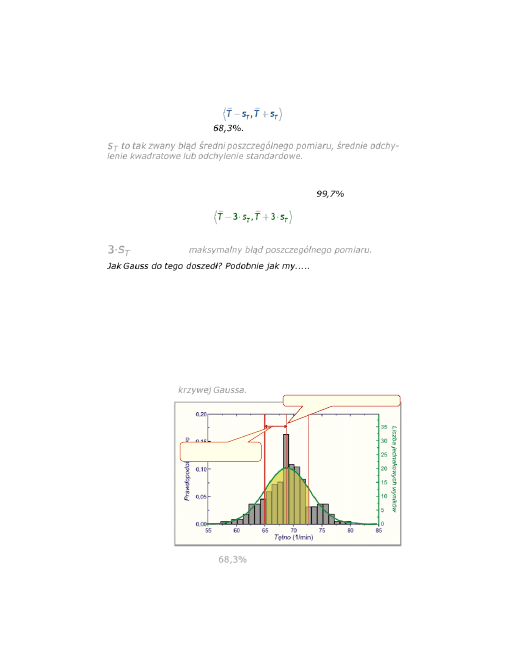
Zaznaczmy teraz na histogramie odchylenie standardowe.

W przedziale

znajduje się 147 wyników pomiaru tętna z

218 wszystkich pomiarów, czyli około

68%

wyników.

Musimy się zatem zgodzić z następującą interpretacją odchylenia stan-
dardowego....

14

Zgodnie z teorią Gaussa wartość tętna i-tego pomiaru leży w przedziale:

z prawdopodobieństwem 68,3%.

s

T

to tak zwany błąd średni poszczególnego pomiaru, średnie odchy-

lenie kwadratowe lub odchylenie standardowe.

Określony wyżej przedział trzeba zwiększyć, aby zwiększyć szansę

znalezienia się w nim kolejnego pomiaru.

Wartość i-tego pomiaru z prawdopodobieństwem 99,7% leży w prze-
dziale trzykrotnie szerszym:

o ile wykonano co najmniej 10 pomiarów.

3·

s

T to tak zwany maksymalny błąd poszczególnego pomiaru.

Jak Gauss do tego doszedł? Podobnie jak my.....

Wartość średnia = 69,8134... 1/min

Zauważył, że gdyby pomiarów było bardzo dużo to histogram miałby

następującą postać...

Przyjąłby kształt krzywej Gaussa.

Zaznaczone pole stanowi

68,3%

całego pola pod krzywą Gaussa.

Odchylenie standardowe

= 3,7739...1/min

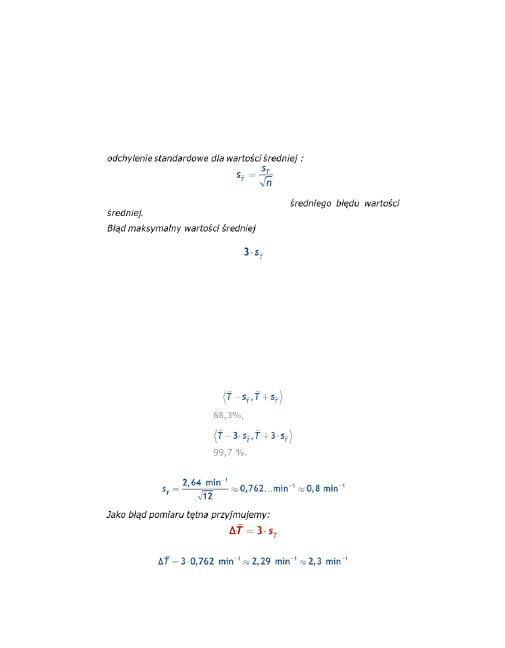
15

Teoria Gaussa dostarcza jeszcze dodatkowych informacji o wykona-

nych pomiarach. Bez wykonywania następnych kilku serii pomiaro-
wych możemy, na podstawie jednej serii pomiarowej, określić tzw.

odchylenie standardowe dla wartości średniej :

Parametr, który opisuje rozkład średnich z wielu serii pomiarowych.

Wielkość ta stanowi miarę tak zwanego średniego błędu wartości

średniej.

Błąd maksymalny wartości średniej dla próbki zawierającej więcej niż

10 pomiarów określony jest wzorem:

Zatem na podstawie jednej serii pomiarowej możemy wnioskować, że

rzeczywista wartość średnia znajduje się w przedziale:

z prawdopodobieństwem 68,3%,
a w przedziale:

z prawdopodobieństwem 99,7 %.

W rozpatrywanym przez nas przykładzie n=12−krotnego pomiaru tę-

tna:

Jako błąd pomiaru tętna przyjmujemy:

W rozpatrywanym przypadku:

16

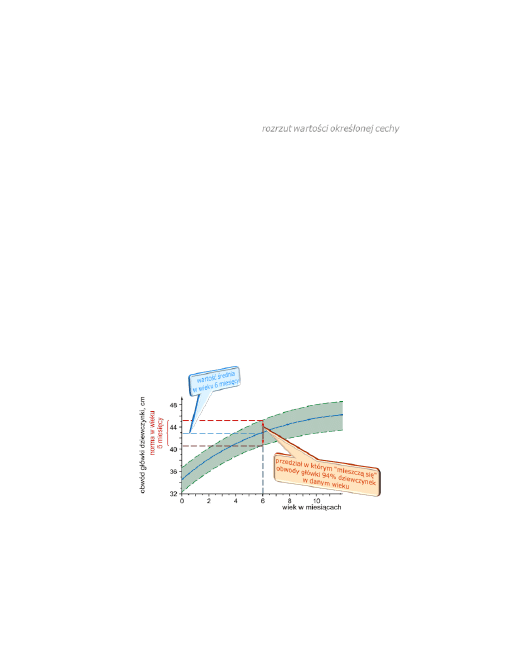
Metodą Gaussa można także określić

rozrzut wartości określonej cechy

elementów pewnego zbioru. Jeśli cecha (np. średnica krwinki) pewnej
populacji zmienia się i przyjmuje wartości różniące się od siebie o war-

tość większą niż dokładność użytego narzędzia pomiarowego, to odchy-
lenie standardowe określa rozrzut wartości tej cechy.

W takim przypadku trzykrotna wartość odchylenia standardowego jest
miarą wielkości przedziału, w którym znajduje się 99,7% otrzymanych

wyników (przedział, w którym znajduje się średnica 99,7% krwinek

danej populacji).

Zatem wykorzystując odchylenie standardowe można określać różne

normy i wykreślać normogramy,

np. tzw. siatka centylowa .........

Obwód główki dziewczynki w funkcji jej wieku.
Linia ciągła wyznacza wartość średnią, linie przerywane wyznaczają

przedział, którego szerokość zależy od wartości odchylenia standar-
dowego w danym wieku.

17

Błąd wielkości złożonej

Poznaliśmy metody umożliwiające określenie wartości liczbowej błędu

pomiaru bezpośredniego. Teraz trzeba wyjaśnić, jak postąpić w przy-
padku wyznaczania błędów pomiaru wielkości złożonej.

Zmierzono boki prostokąta a i b? Jaką powierzchnię ma ten prostokąt?

Bezpośrednie pomiary długości boków prostokąta obarczone są błędem

systematycznym i wynoszą odpowiednio:

a = (25,7

±

0,1) cm i b = (5,7

±

0,1) cm.

Pole prostokąta S = a·b, jest wielkością złożoną:

S = 25,7·5,7 cm

2

= 146,49 cm

2

W jaki sposób oszacować błąd pomiaru pola?

Można to zrobić dwoma sposobami:



w oparciu o liczbę cyfr znaczących w wynikach bezpośrednich



i bardziej formalnie ....

Im więcej cyfr znaczących ma wynik pomiaru tym pomiar jest dokładniej-

szy. Zatem można sądzić, że liczba cyfr znaczących występujących w wy-

niku pomiarów złożonych zależy od liczby cyfr znaczących występujących

w czynnikach zmierzonych bezpośrednio.
O liczbie cyfr znaczących w końcowym wyniku decyduje czynnik najmniej

dokładny.

Wynik końcowy ma tyle cyfr znaczących ile czynnik, który ma ich

najmniej.

a = (25,7 ± 0,1) cm

ma 3 cyfry znaczące i

b = (5,7 ± 0,1) cm

ma dwie,

więc zgodnie z omówioną regułą wynik końcowy winien mieć tylko dwie

cyfry znaczące:

S = 25,7·5,7 cm

2

= 146,49 cm

2



15

0 cm

2

Oczywiście nie wiemy ile wynosi błąd

S

,

ale podejrzewamy, że jest na

miejscu dziesiętnym ostatniej cyfry znaczącej wyniku, czyli na miejscu

dziesiątek i wynik zapiszemy w postaci:

S = (

15

0 ±

1

0) cm

2

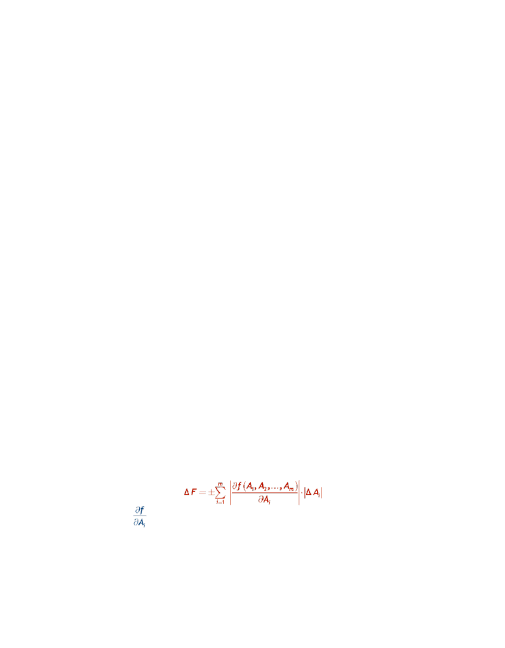
18

Można też obliczyć możliwe największą wartość pola:

S

maks

= (25,7+0,1)·(5,7+0,1) cm

2

= 149,64 cm

2

i najmniejszą:

S

min

= (25,7−0,1)·(5,7−0,1) cm

2

= 143,36 cm

2

Zatem pole prostokąta leży w przedziale:

＜

143,36 cm

2

; 149,64 cm

2

＞

Co możemy zapisać w postaci:

S = (146,5 ± 3,14) cm

2

≈ (146,5 ± 3,2) cm

2

Można też skorzystać z bardziej „matematycznej” recepty obliczania

błędu pomiaru wielkości złożonej.

Załóżmy, że wykonano

m

pomiarów bezpośrednich wielkości

A

i

(i=1,2,3,.,m)

i oszacowano błędy tych wielkości

ΔA

i

.

Interesuje nas wartość

F

i błąd

ΔF

wielkości

złożonej

wyrażonej, jako

funkcja

f

bezpośrednio zmierzonych wielkości

A

i

:

F = f (A

1

, A

2

,...., A

m

)

Maksymalny błąd

ΔF

pomiaru obliczamy wtedy z zależności:

gdzie oznacza tak zwane pochodne cząstkowe f względem A

i

.

19

Rozpatrzmy kilka szczególnych postaci funkcji

f:



jeśli zmierzone bezpośrednio wielkości są dodawane lub odejmo-

wane, to błąd wyniku

(sumy lub różnicy)

jest

zawsze sumą błędów

wielkości zmierzonych bezpośrednio:

jeśli

F = A +/− B

, wtedy zawsze

ΔF = ΔA + ΔB

,



jeśli funkcja

f

ma postać iloczynową:

F = f (A, B, C,…) = A

a

· B

b

· C

c

·…

to błąd wielkości złożonej ΔF oblicza się ze wzoru:

Jeśli zastosować ten schemat do obliczanego pola

prostokąta S = A

1

·B

1

,

to błąd pola

ΔS

obliczymy ze wzoru:

I dalej:

Zauważmy dużą zgodność wszystkich obliczeń wartości błędu.

2

l

T

π

g

 

Przykład:

Wyznaczenie wartości przyspieszenia ziemskiego g na podstawie pomiaru

okresu T drgań wahadła matematycznego o długości l:

Po przekształceniu wzoru otrzymuje się:

Wyznaczenie g wymaga bezpośredniego pomiaru T i l.
Pomiar l = (2,00±0,01) m obarczony był błędem systematycznym. Z ko-

lei okres drgań mierzono stoperem z dokładnością ±0,2 s. Stwierdzono

rozrzut wyników pomiaru większy niż 0,2 s. Zatem pomiar obarczony był

błędem przypadkowym. Na podstawie wykonanych 10 pomiarów okresu

drgań wahadła matematycznego otrzymano wartość T = (2,8±0,4) s.
Błąd przyspieszenia obliczymy z wzoru:

20

2

2

2

2

2

4

4 3,142 2,00

m

10,073636...

2,8

s

π l

g

T















 



 

 

2

m

Δ

10,1 0,291

2,94...

3

s

g





2

m

(10 3)

s

g

Warto zauważyć, że pośrednie obliczenia błędu wykonywano z dokładno-

ścią do 3 cyfr znaczących (dlaczego?). Teraz wystarczy obliczyć wartość g:

zatem:

i ostatecznie:

Zastosujmy teraz do oszacowania błędu pomiaru g receptę o cyfrach znaczących.

 l

= (2,00 ± 0,01) m ma trzy cyfry znaczące,



T = (2,8 ± 0,4) s

ma dwie cyfry znaczące.

Obliczona wartość przyspieszenia ziemskiego może mieć tylko dwie cyfry znaczące.

Po zaokrągleniu g do dwóch cyfr znaczących otrzymamy wartość g = 10 m/s

2

.

Ostatnia cyfra tego wyniku (0) jest cyfrą niepewną, o czym informuje zapis:

g = (10 ± 1) m/s

2

Umiejętność takiego szacowania błędów pomiaru jest niezwykle praktyczna.

Opracowywanie wyników pomiarów

Jeżeli badane są zależności pomiędzy wielkościami, powiedzmy x

i y, w celu ułatwienia analizy otrzymanych danych, wyniki pomia-

rów winny być odpowiednio zaprezentowane:



uszeregowane i zebrane w odpowiedniej tabeli,



przedstawione na odpowiednim wykresie.

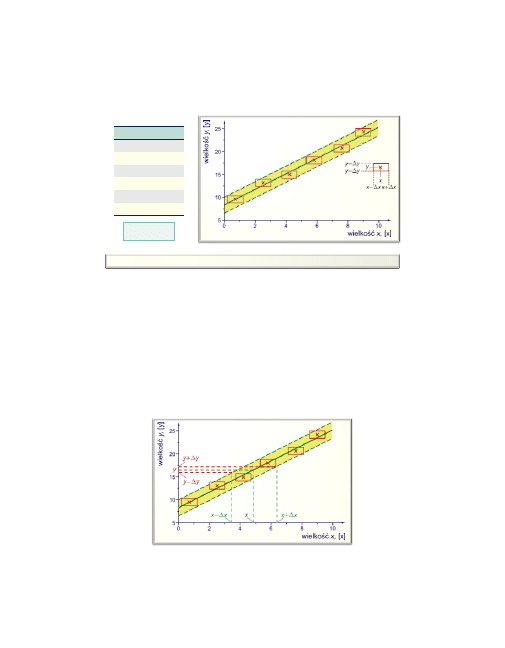
Na poniższym rysunku przedstawiono przykład poprawnie sporzą-

dzonego wykresu. Zaznaczono na nim niezbędne elementy zapew-

niające jego czytelność i przejrzystość.

21

Dobieramy jednostki.....

Sporządzamy wykres ........

Analizujemy otrzymane wyniki:

Zaznaczamy błędy pomiarów (prostokąty błędów) ..

Przeprowadzamy „linię najlepszego dopasowania” ....

Zaznaczamy „krzywe ufności”...

lp

x [x] y [y]

1

0,7

9,5

2

2,5

13,1

3

4,2

14,9

4

5,8

18,0

5

7,6

20,6

6

9,0

24,2

Δx=±0,5 [x]

Δy=±0,8 [y]

Często na wykresie zaznacza się także przebieg tzw. „krzywych uf-

ności”, które biegną równolegle do linii najlepszego dopasowania i

„obejmują” prostokąty błędów.

Wykreślenie krzywych ufności umożliwia np. oszacowanie błędu Δx niezna-

nej wielkości x, która odpowiada znanej (zmierzonej) wartości y ± Δy.

Rycina ilustruje sposób szacowania wielkości x i Δx. Dla dokładnego wyz-

naczenia tych wielkości może być przydatna

metoda interpolacji liniowej.

22

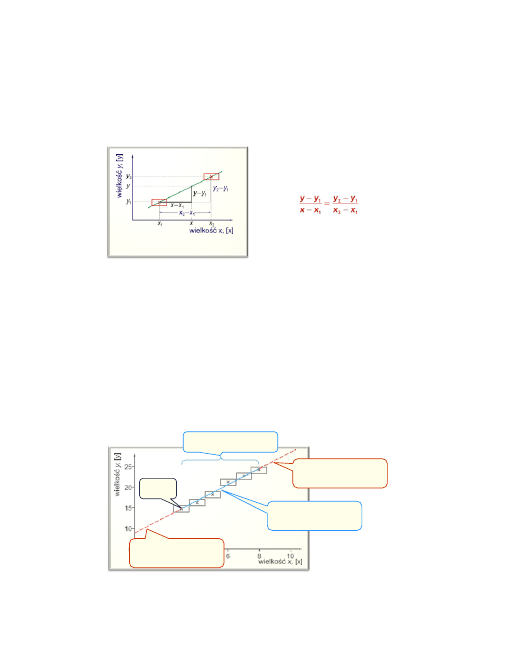
Z ryciny tej, dla zaznaczonych na

niej wielkości po zastosowaniu twie-

rdzenia Talesa, wynika że:

Jeżeli znane są np. wartości:

x

1

, x

2

, y

1

, y

2

i x

to z powyższego równania można

obliczyć wartość

y.

Na kolejnym rysunku pokazano, jak metodą interpolacji liniowej wyzna-

czyć można wartość wielkości y odpowiadającą wielkości x (lub na odwrót).

Nazwa interpolacja liniowa oznacza, że zakładamy, że rozpatrywane wiel-

kości łączy

zależność liniowa.

Interpolacja liniowa

Często istnieje też konieczność wyznaczenia wartości

y dla x leżącego poza zakre-

sem wykonanych pomiarów

.

Szacowanie wartości tej wielkości obarczone jest

większym ryzykiem

niż w przypa-

dku interpolacji, gdyż nie można być pewnym, jak będzie zmieniać się dana wiel-

kość poza zakresem wykonanych pomiarów.
W przypadku, jeśli punkty pomiarowe układają się wzdłuż linii prostej, w niewiel-

kiej odległości od przedziału, w którym wykonano pomiary, linię można

„przedłu-

żyć”

i odczytać odpowiednie współrzędne.

Procedurę taką nazywa się ekstrapola-

cją liniową.

punkty

pomiarowe

najlepiej dopasowana linia w

przedziale,

w którym wykonano pomiary

przedział wielkości x,

w którym wykonano pomiary

liniowa ekstrapolacja

poza zakres wykonanych

pomiarów

liniowa ekstrapolacja

poza zakres wykonanych

pomiarów

23

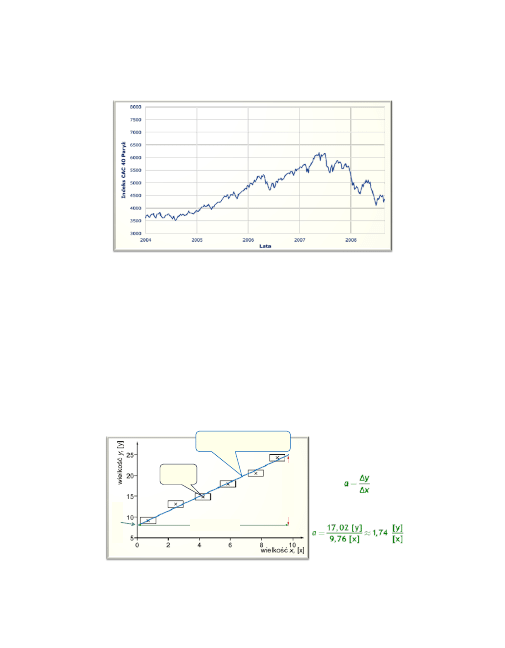
Łatwo pokazać, że interpolacja nieliniowa nie jest tak prosta, jak liniowa.

Rozpatrzmy przykład zmian wartości indeksu giełdowego w funkcji czasu

notowań.

0d 2004 r. do końca I kwartału 2006 r. indeks zmieniał się tak …
A jak pójdzie dalej? Jak będzie wyglądać nasza ekstrapolacja?
A jak dalej? W takiej sytuacji ekstrapolacja już nie jest łatwa?
Próbujemy dalej?

Często wykonuje się badania zależności, które w myśl przesłanek teoretycznych są
zależnościami liniowymi:

y =

a

·

x + b

Współczynnik kierunkowy

a

oraz parametr

b

posiadają określony sens fizyczny, za-

wierają informacje o badanym zjawisku. Zachodzi często konieczność wyznacze-

nia ich wartości.
W oparciu o wyżej przedstawione „przepisy” wykreślamy najpierw przebieg linii

najlepszego dopasowania.

Następnie wyznaczamy b.

punkty

pomiarowe

najlepiej dopasowana linia

y = a·x + b

b

=

7,

94

[

y]

Następnie wyznaczamy

a:

x = 9,76 [x]



y

=

17

,0

2

[y

]

Obliczamy wartość

a:

24

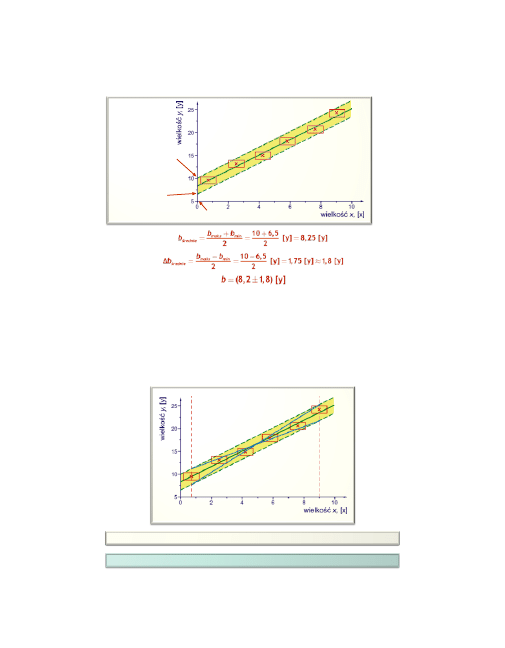
Sposób oszacowania wartości błędu

Δb

współczynnika

b

wyjaśnia rysunek.

b

maks

=

10 [y]

b

min

=

6,5 [y]

I

dalej:

x = 0 [x]

Sposób oszacowania wartości błędu współczynnika kierunkowego

Δa

przedstawia kolejny rysunek.

Zaznaczamy przedział, w którym wykonano pomiary...

Zaznaczamy linię o maksymalnym współczynniku kierunkowym a

maks

.

Zaznaczamy linię o minimalnym współczynniku kierunkowym a

min

.

Obliczamy wartości a

min

i a

maks

.

25

Po zaznaczeniu krzywych ufności, wyznacza się przebieg dwóch linii o ma-

ksymalnej,

a

maks

i minimalnej,

a

min

wartości współczynnika kierunkowego.

Wartość średnią współczynnika kierunkowego obliczamy ze wzoru:

Błąd

Δa

wartości współczynnika kierunkowego wyraża wzór:

Wreszcie końcowa wartość współczynnika kierunkowego wynosi:

Wreszcie zdarza się konieczność badania

zależności nieliniowych.

W niektórych przypadkach funkcji typu:

wystarczy wprowadzić nowe zmienne, odpowiednio:

i nowe funkcje mają postać liniową, odpowiednio:

Następnie, postępując zgodnie z omówionymi wyżej zasadami dotyczący-

mi wykresów liniowych, można dokonać ich analizy.

26

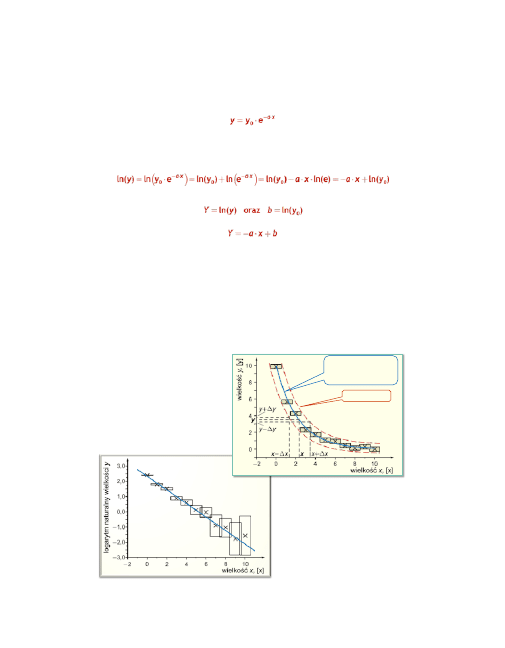
Ważny przypadek to często stosowana funkcja wykładnicza:

gdzie:

e

oznacza podstawę logarytmu naturalnego (e≈2,72),

y

0

oraz

a

to pewne parametry tej funkcji.

„Wyprostowanie” tej zależności uzyskuje się po obustronnym zlogarytmo-

waniu powyższego równania:

Po wprowadzenie następujących podstawień:

Otrzymujemy zależność:

Otrzymana liniowa zależność stanowi podstawę do dalszej analizy tego wy-

kresu wcześniej opisanymi metodami.
Kolejna rycina ilustruje rezultaty takiego przekształcenia.

Wykres zależności wykładniczej.
Zaznaczono sposób określenia krzy-

wych ufności, sposób odczytu nie-

znanych wartości x, gdy dane są

wartości y i sposób szacowania war-

tości błędów tak odczytanych wiel-

kości.

Ten sam wykres po wykorzystaniu,

opisanego wyżej, podstawienia przyj-

muje postać liniową.
Otrzymana liniowa zależność stano-

wi podstawę do dalszej analizy te-

go wykresu wcześniej opisanymi

metodami.

najlepiej dopasowana,
metodą najmniejszych

odchyleń, funkcja f(x)

krzywa ufności

27

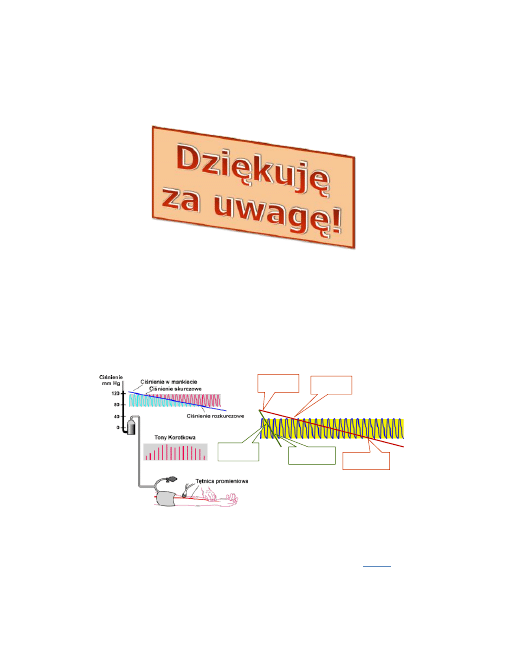
Pomiar ciśnienia skurczowego i rozkurczowego krwi metodą sfigmomano-

metryczną (konstruktor Riva Roci). W metodzie tej trzeba bardzo wolno

zmniejszać ciśnienie w mankiecie, w przeciwnym przypadku otrzymujemy

wyniki, które obarczone są błędem metody pomiaru.

powrót

ciśnienie w

mankiecie

ciśnienie

skurczowe

ciśnienie

rozkurczowe

ciśnienie

skurczowe

ciśnienie

rozkurczowe