Metody Obliczeniowe

Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o ,   s e m e s t r   5 ,   r o k   a k a d e m i c k i   2 0 1 3 / 1 4

Magdalena Rucka

Aproksymacja i interpolacja funkcji

materiały do wykładu nr 6a

Metody Obliczeniowe

Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o ,   s e m e s t r   5 ,   r o k   a k a d e m i c k i   2 0 1 3 / 1 4

Magdalena Rucka

2

Aproksymacja i interpolacja funkcji

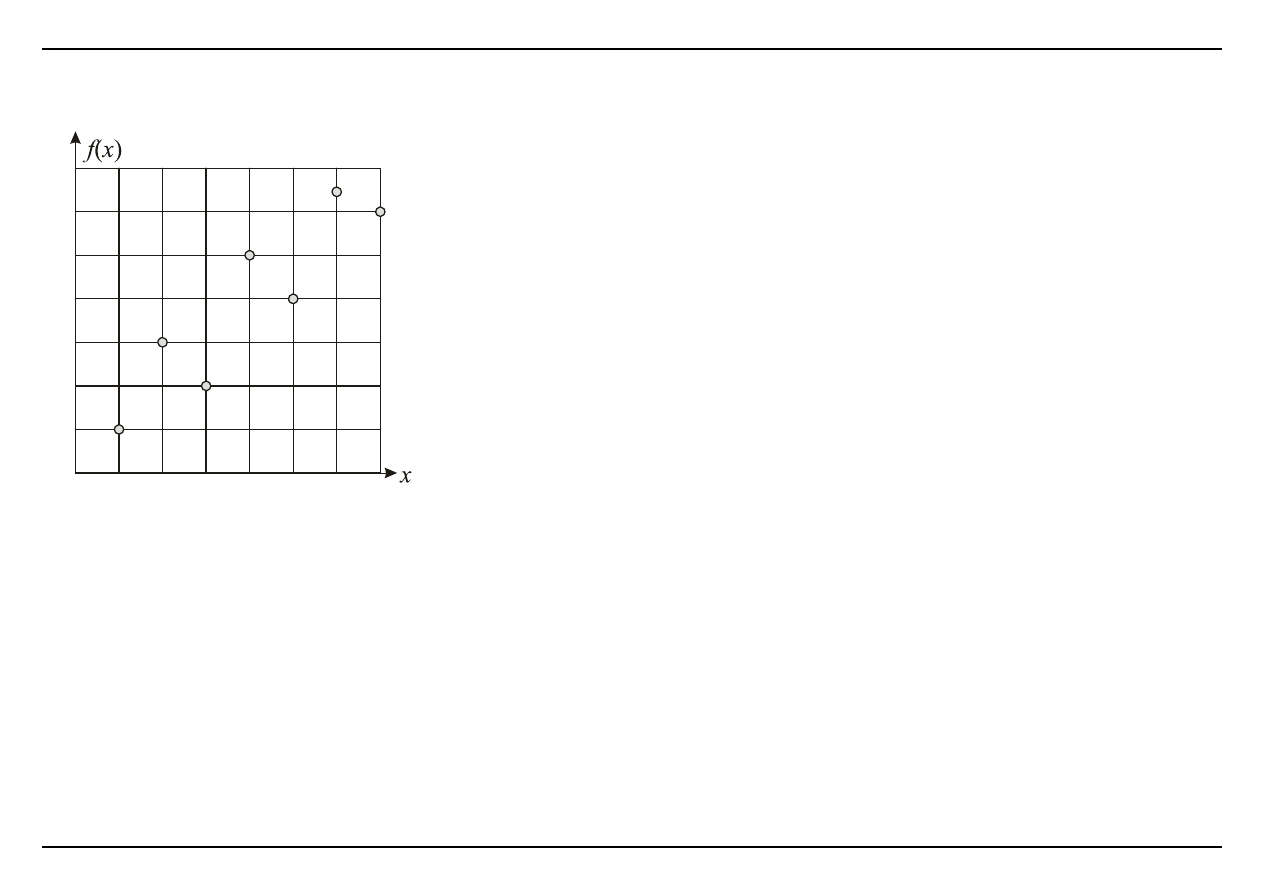
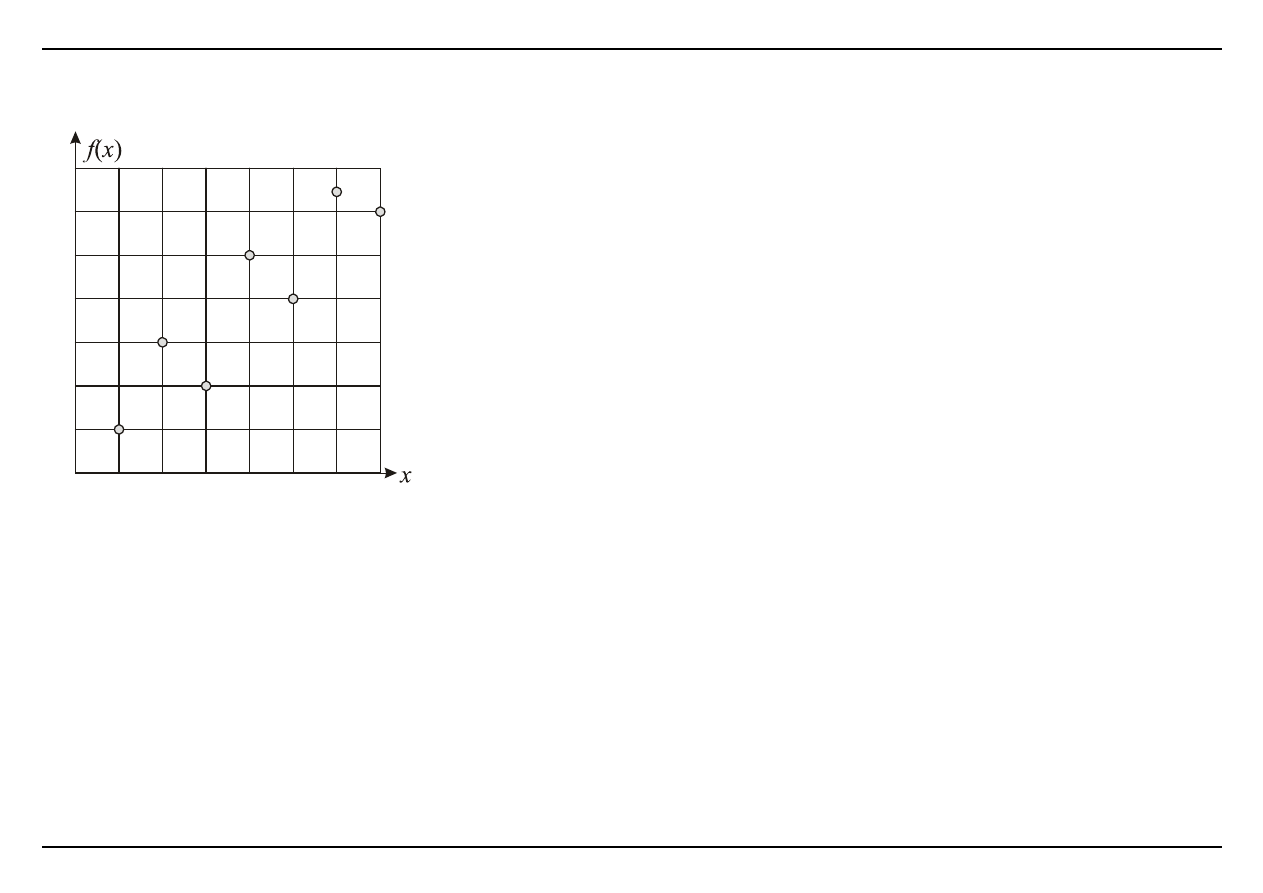
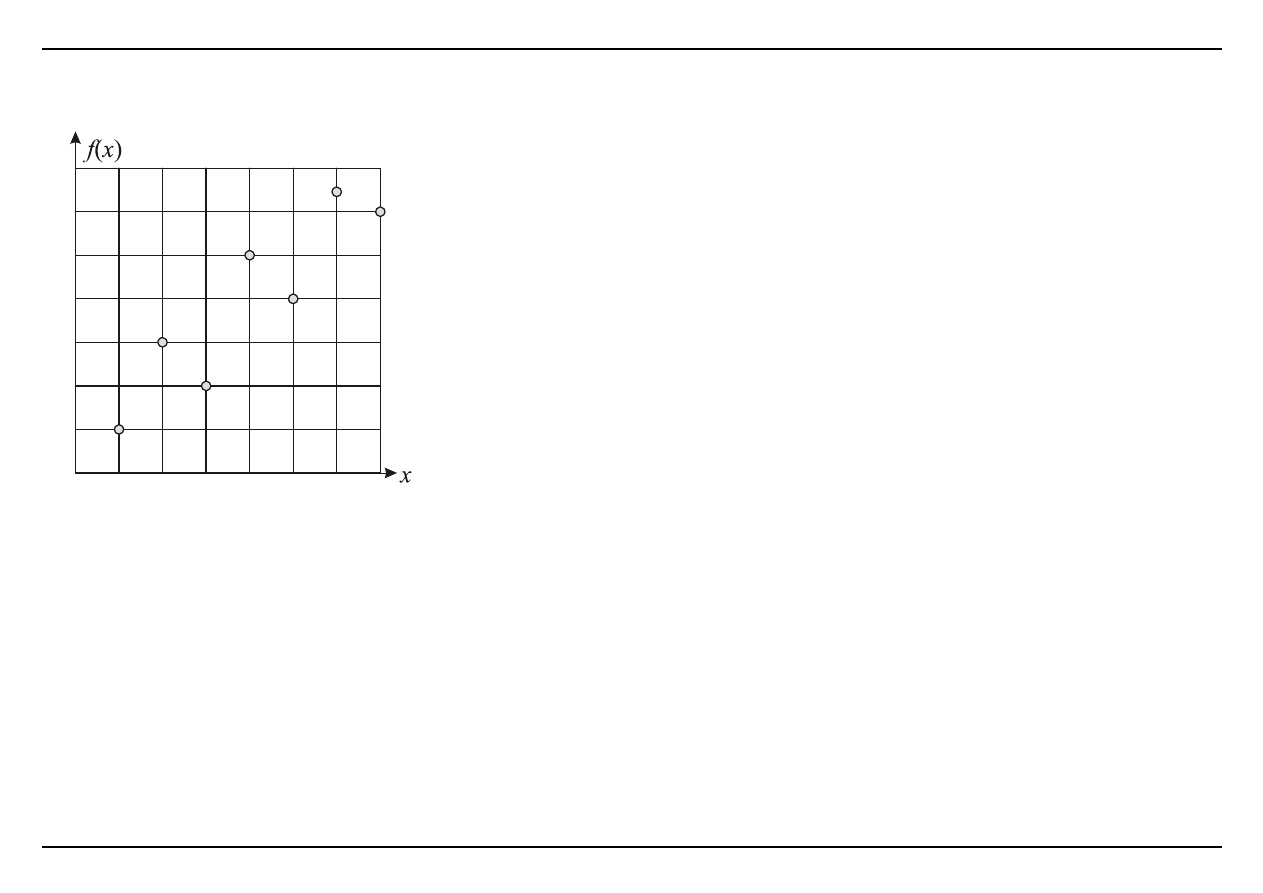
Punkty pomiarowe

Metody Obliczeniowe

Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o ,   s e m e s t r   5 ,   r o k   a k a d e m i c k i   2 0 1 3 / 1 4

Magdalena Rucka

3

Aproksymacja i interpolacja funkcji

Interpolacja

•

interpolacja wielomianowa Newtona (liniowa, kwadratowa, sześcienna)

•

interpolacja wielomianowa Lagrange’a

•

interpolacja wielomianowa Hermite’a

•

interpolacja trygonometryczna

Metody Obliczeniowe

Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o ,   s e m e s t r   5 ,   r o k   a k a d e m i c k i   2 0 1 3 / 1 4

Magdalena Rucka

4

Aproksymacja i interpolacja funkcji

Aproksymacja

•

minimum sumy błędów

•

minimum sumy wartości bezwzględnej błędów

•

minimum największego błędu (kryterium „minimax”)

•

minimum sumy kwadratów błędu

Metody Obliczeniowe

Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o ,   s e m e s t r   5 ,   r o k   a k a d e m i c k i   2 0 1 3 / 1 4

Magdalena Rucka

5

Aproksymacja i interpolacja funkcji

Interpolacja

2

0

1

2

( )

...







 

n

n

f x

a

a x

a x

a x

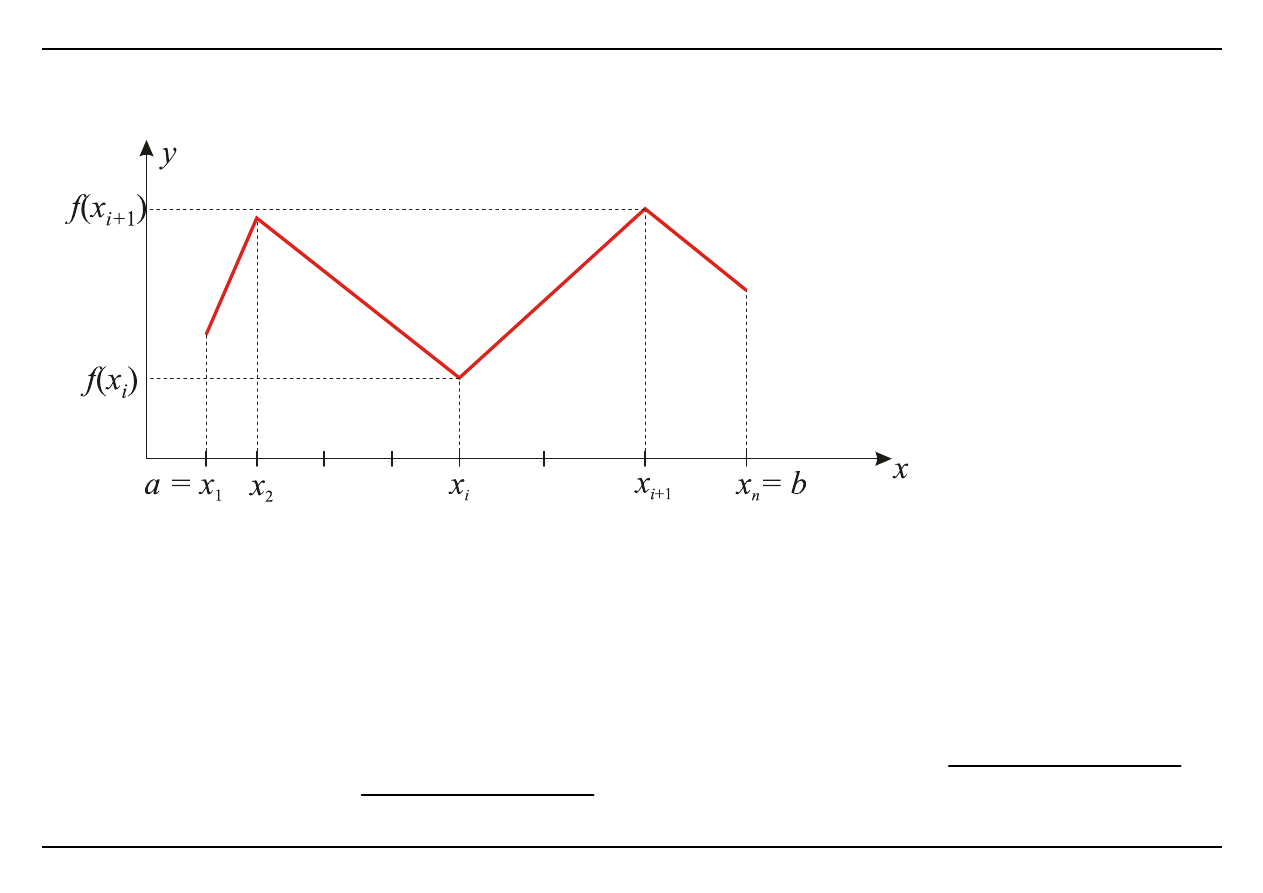
1. Interpolacja Newtona

Metody Obliczeniowe

Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o ,   s e m e s t r   5 ,   r o k   a k a d e m i c k i   2 0 1 3 / 1 4

Magdalena Rucka

6

Aproksymacja i interpolacja funkcji

a) interpolacja liniowa

0

1

( )

 

F x

b

b x

0

( )



i

b

f x

1

1

1

(

)

( )











i

i

i

i

f x

f x

b

x

x

1

1

(

)

( )

( )

( )













i

i

i

i

i

f x

f x

F x

f x

x

x

x

Metody Obliczeniowe

Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o ,   s e m e s t r   5 ,   r o k   a k a d e m i c k i   2 0 1 3 / 1 4

Magdalena Rucka

7

0

1

2

3

4

5

6

0

0.2

0.4

0.6

0.8

1

1.2

1.4

1.6

1.8

2

x

y

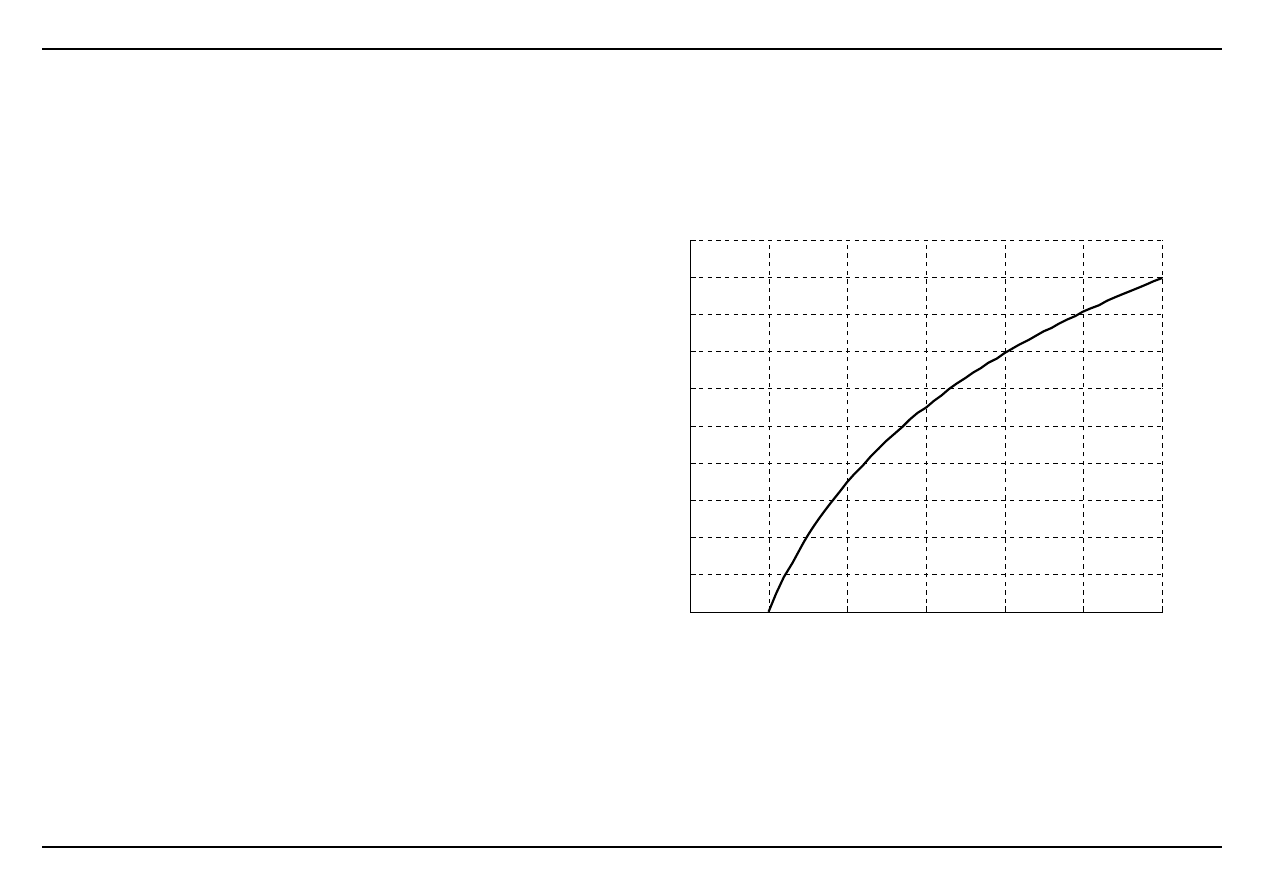
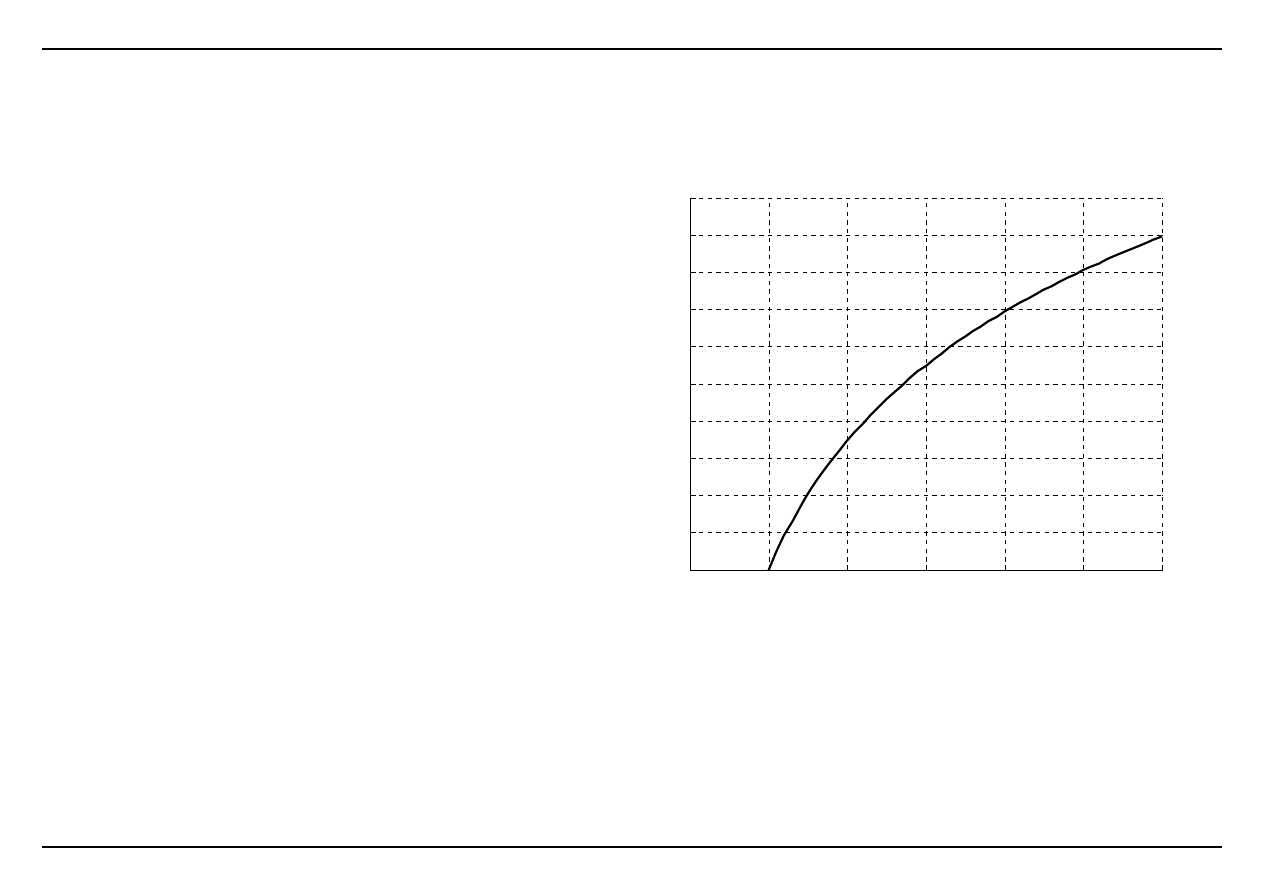
Przykład 

(Chapra S.C., Numerical Methods for Engineers. McGraw‐Hill Book Company, 1988)

Oszacować wartość ln2 stosując interpolację liniową w przedziale <1; 6>.

Aproksymacja i interpolacja funkcji

ln(2)

0.69314718



Metody Obliczeniowe

Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o ,   s e m e s t r   5 ,   r o k   a k a d e m i c k i   2 0 1 3 / 1 4

Magdalena Rucka

8

0

1

2

3

4

5

6

0

0.2

0.4

0.6

0.8

1

1.2

1.4

1.6

1.8

2

x

y

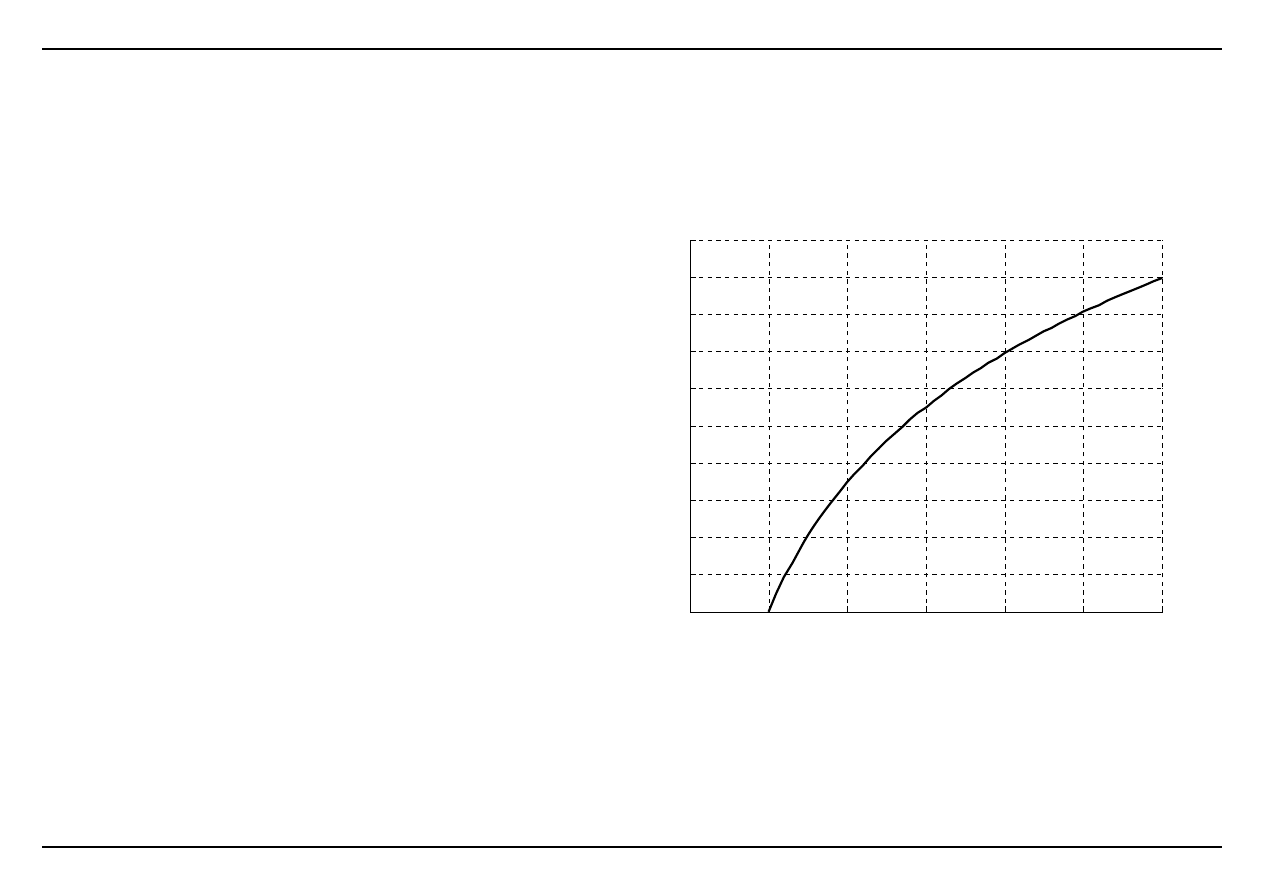
Przykład 

(Chapra S.C., Numerical Methods for Engineers. McGraw‐Hill Book Company, 1988)

Oszacować wartość ln2 stosując interpolację liniową w przedziale <1; 4>.

Aproksymacja i interpolacja funkcji

ln(2)

0.69314718



Metody Obliczeniowe

Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o ,   s e m e s t r   5 ,   r o k   a k a d e m i c k i   2 0 1 3 / 1 4

Magdalena Rucka

9

Aproksymacja i interpolacja funkcji

b) interpolacja kwadratowa

0

1

1

2

1

( )

(

)

(

)(

)





 









i

i

i

F x

b

b x

x

b x

x

x

x

1

1

,









i

i

x

x

x

0

1

(

)





i

b

f x

1

1

1

( )

(

)











i

i

i

i

f x

f x

b

x

x

1

1

1

1

2

1

1

(

)

( )

( )

(

)



























i

i

i

i

i

i

i

i

i

i

f x

f x

f x

f x

x

x

x

x

b

x

x

Metody Obliczeniowe

Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o ,   s e m e s t r   5 ,   r o k   a k a d e m i c k i   2 0 1 3 / 1 4

Magdalena Rucka

10

Przykład 

(Chapra S.C., Numerical Methods for Engineers. McGraw‐Hill Book Company, 1988)

( )

0.46209813(

1) 0.051873116(

1)(

4)



 





F x

x

x

x

Aproksymacja i interpolacja funkcji

(2)

0.56584436



F

0

1

2

3

4

5

6

0

0.2

0.4

0.6

0.8

1

1.2

1.4

1.6

1.8

2

x

y

Oszacować wartość ln2 stosując interpolację kwadratową w przedziale <1; 6>.

Metody Obliczeniowe

Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o ,   s e m e s t r   5 ,   r o k   a k a d e m i c k i   2 0 1 3 / 1 4

Magdalena Rucka

11

Aproksymacja i interpolacja funkcji

c) interpolacja Newtona dla wielomianu dowolnego stopnia

0

0

(

)



b

f x

Znane: wartości funkcji f(x) w (n+1) punktach

0

1

, ,...,

n

x x

x

Poszukiwana: funkcja interpolacyjna stopnia n

0

1

0

0

1

1

( )

(

) ...

(

)(

)...(

)



 



 







n

n

F x

b

b x

x

b x

x

x

x

x

x

1

1

0

[ ,

]



b

f x x

2

2

1

0

[

, ,

]





b

f x x x

1

1

0

[

,

,..., ,

]





n

n

n

b

f x x

x x

( )

(

)

[ ,

]







i

j

i

j

i

j

f x

f x

f x x

x

x

[ ,

]

[

,

]

[ ,

,

]









i

j

j

k

i

j

k

i

k

f x x

f x x

f x x x

x

x

1

1

1

2

0

1

1

0

0

[

,

,

,

]

[

,

,

,

]

[

,

,

,

]





















n

n

n

n

n

n

n

f x x

x

f x

x

x

f x x

x x

x

x

Metody Obliczeniowe

Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o ,   s e m e s t r   5 ,   r o k   a k a d e m i c k i   2 0 1 3 / 1 4

Magdalena Rucka

12

Aproksymacja i interpolacja funkcji

2. Interpolacja Lagrange’a

1

( )













n

j

i

j i

i

j

j

x

x

L x

x

x

1, 2,3,...,



i

n

1 dla

( )

0 dla









 





i

j

ij

i

j

L x

i

j

,

1, 2,3,...,



i j

n

1

( )

( ) ( )







n

i

i

i

f x

L x f x

Metody Obliczeniowe

Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o ,   s e m e s t r   5 ,   r o k   a k a d e m i c k i   2 0 1 3 / 1 4

Magdalena Rucka

13

Przykład

Obliczyć macierz sztywności 2‐węzłowego elementu prętowego.  

Aproksymacja i interpolacja funkcji

2

1

1

2

( )







x

x

L x

x

x

1

2

2

1

( )







x

x

L x

x

x

1

2

[

( )

( )]

 N x N x

N

'

'

1

2

[

( )

( )]

 N x N x

B

( )





T

e

L

EA

dx

K

B B

Metody Obliczeniowe

Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o ,   s e m e s t r   5 ,   r o k   a k a d e m i c k i   2 0 1 3 / 1 4

Magdalena Rucka

14

Aproksymacja i interpolacja funkcji

Aproksymacja

Kryteria błędów

 minimum sumy kwadratów błędu

0

1







y

a

a x e

0

1



  

e

y

a

a x

 minimum sumy błędów





0

1

1

1







 

 

n

n

i

i

i

i

i

e

y

a

a x

 minimum sumy wartości bezwzględnej błędów

 minimum największego błędu (kryterium „minimax”)

0

1

1

1







 





n

n

i

i

i

i

i

e

y

a

a x

1

2

min(max( ,

,...,

)

n

e e

e





2

2

0

1

1

1









 





n

n

r

i

i

i

i

i

S

e

y

a

a x

Metody Obliczeniowe

Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o ,   s e m e s t r   5 ,   r o k   a k a d e m i c k i   2 0 1 3 / 1 4

Magdalena Rucka

15

Aproksymacja i interpolacja funkcji

Metoda najmniejszych kwadratów – wariant liniowy

Cel:  wpasowanie prostej 

0

1







y

a

a x e

w zbiór danych

( ,

)

i

i

x y

i

= 1, 2, …, n

pomiarowych 

Kryterium błędu: 
minimum sumy kwadratów





2

2

0

1

1

1









 





n

n

r

i

i

i

i

i

S

e

y

a

a x

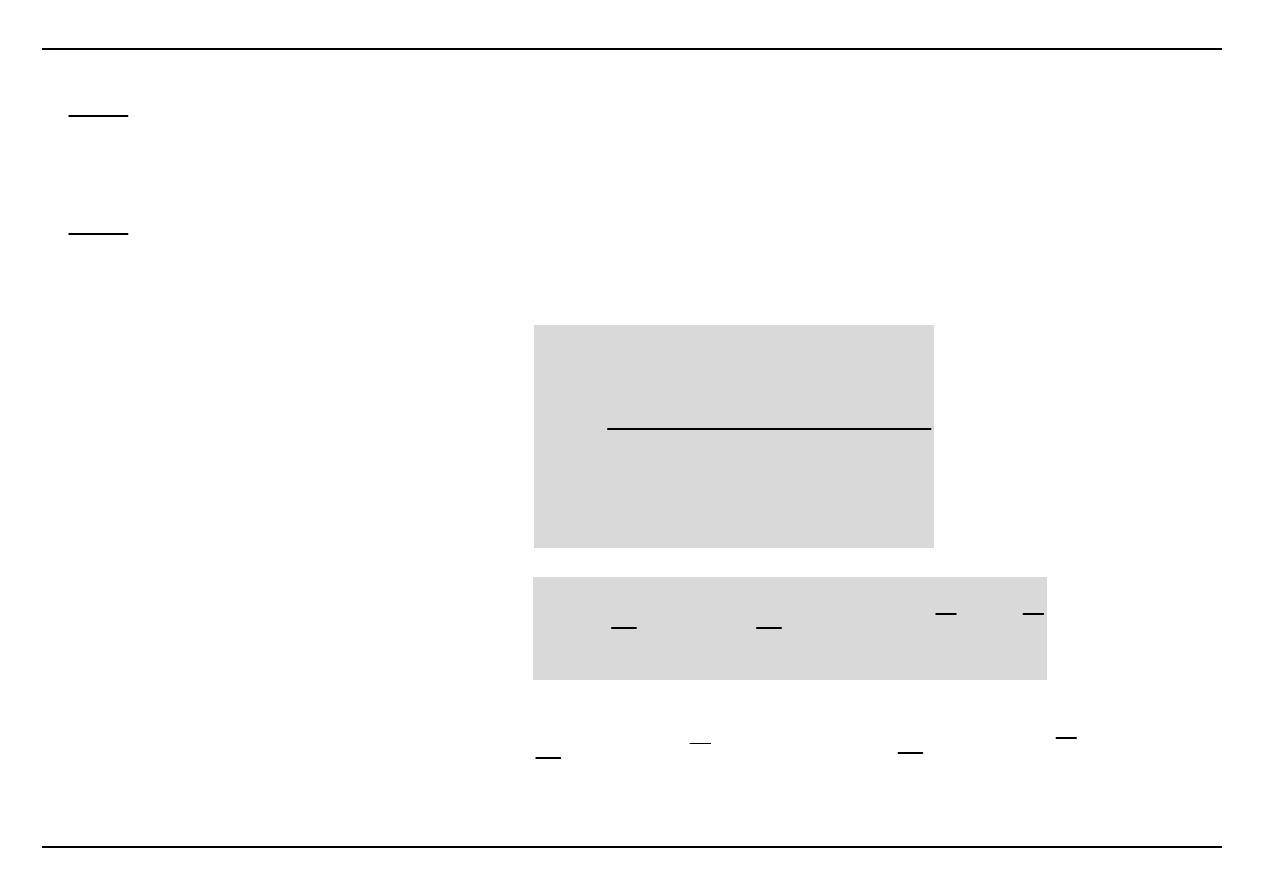
Cel: wyznaczyć wartości a

0

i a

1

tak, by zminimalizować S

r









0

1

1

0

0

1

1

1

2

2









 

 















 

 





 







n

r

i

i

i

n

r

i

i

i

i

S

y

a

a x

a

S

y

a

a x x

a

Metody Obliczeniowe

Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o ,   s e m e s t r   5 ,   r o k   a k a d e m i c k i   2 0 1 3 / 1 4

Magdalena Rucka

16

Aproksymacja i interpolacja funkcji

0

1

0

0

















 



r

r

S

a

S

a

0

1

1

1

1

2

0

1

1

1

1

0

0



































 









n

n

n

i

i

i

i

i

n

n

n

i

i

i

i

i

i

i

y

a

a x

y x

a x

a x





0

0

1







n

i

a

na

0

1

1

1

2

0

1

1

1

1







































n

n

i

i

i

i

n

n

n

i

i

i

i

i

i

i

na

a x

y

a x

a x

y x

1

1

1

1

2

2

1

1



















 









 





n

n

n

i

i

i

i

i

i

i

n

n

i

i

i

i

n

x y

x

y

a

n

x

x



0

1

1

1

1

1

1









 





n

n

i

i

i

i

a

y

x a

y

a x

n

n

1

1







n

n

i

y

y

n

1

1







n

n

i

x

x

n

Metody Obliczeniowe

Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o ,   s e m e s t r   5 ,   r o k   a k a d e m i c k i   2 0 1 3 / 1 4

Magdalena Rucka

17

Aproksymacja i interpolacja funkcji

Ocena dokładności aproksymacji

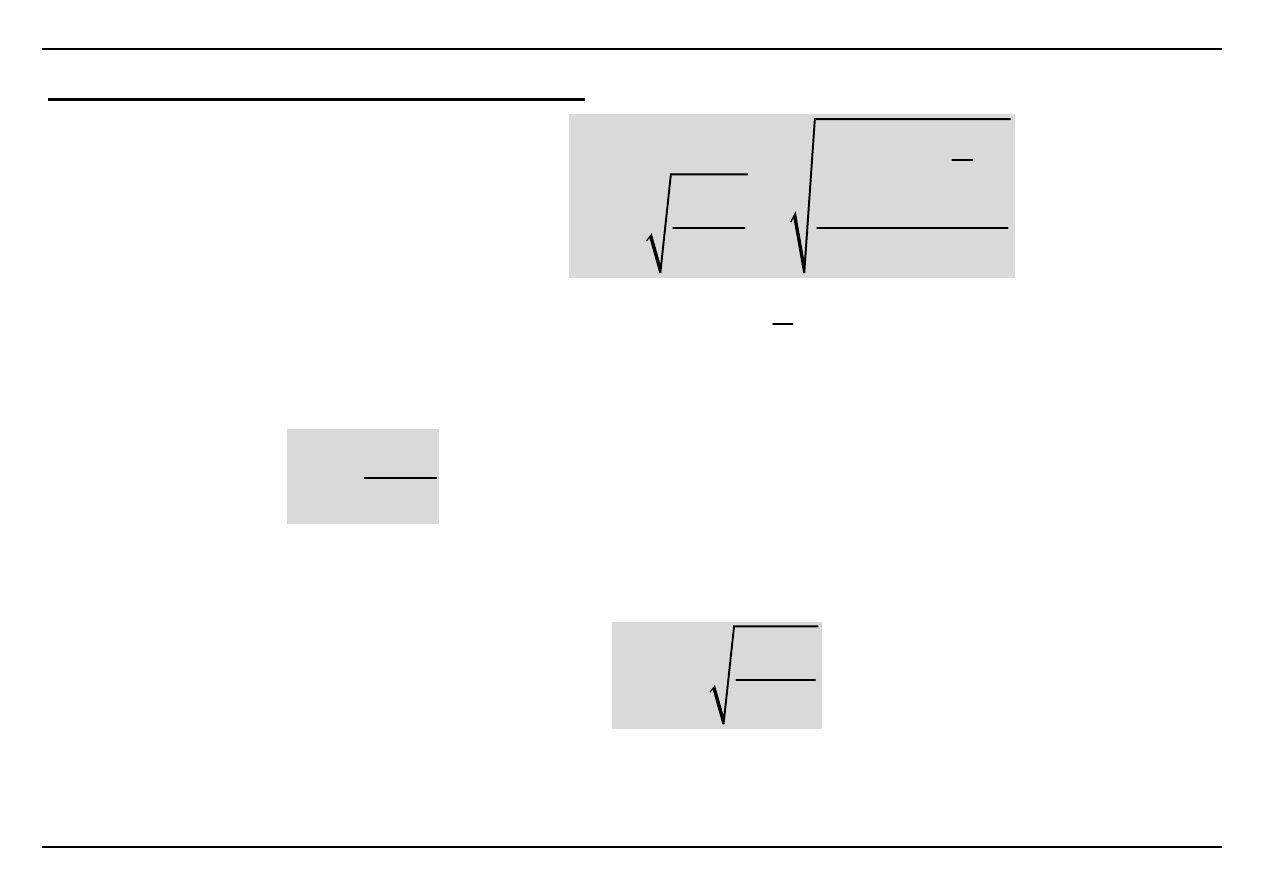
 Odchylenie standardowe:





2

1

1

1















n

i

t

i

y

y

y

S

s

n

n





2

1









n

t

i

i

S

y

y

 Wariancja:

 Standardowy błąd przybliżenia:

2

1





t

y

S

s

n

/

2





r

y x

S

s

n

Metody Obliczeniowe

Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o ,   s e m e s t r   5 ,   r o k   a k a d e m i c k i   2 0 1 3 / 1 4

Magdalena Rucka

18

Aproksymacja i interpolacja funkcji

Ocena dokładności aproksymacji

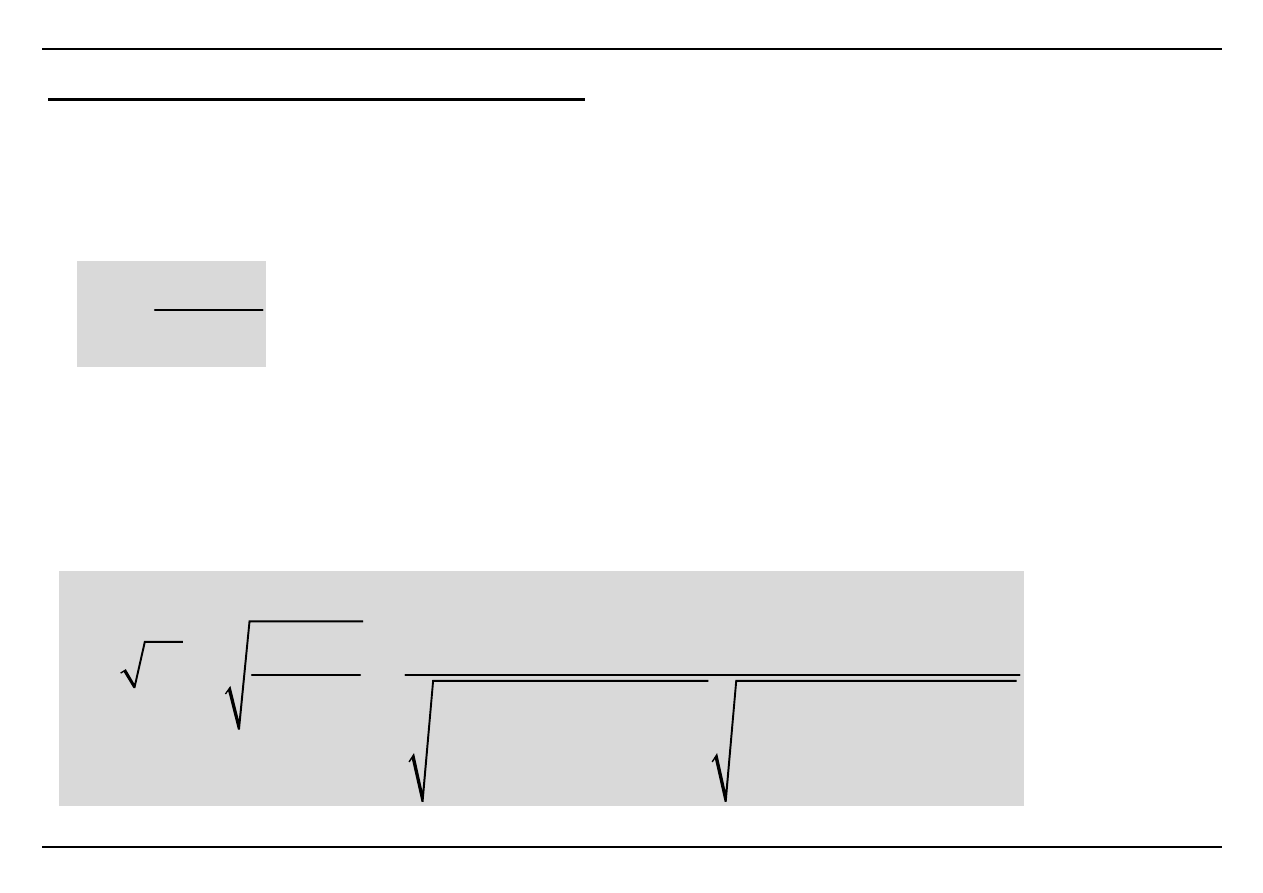
 Współczynnik determinacji

 Współczynnik korelacji

2





t

r

t

S

S

r

S

2

1

1

1

2

2

2

2

1

1

1

1























































 









n

n

n

i

i

i

i

t

r

i

i

i

n

n

n

n

t

i

i

i

i

i

i

i

i

n

x y

x

y

S

S

r

r

S

n

x

x

n

y

y

Metody Obliczeniowe

Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o ,   s e m e s t r   5 ,   r o k   a k a d e m i c k i   2 0 1 3 / 1 4

Magdalena Rucka

19

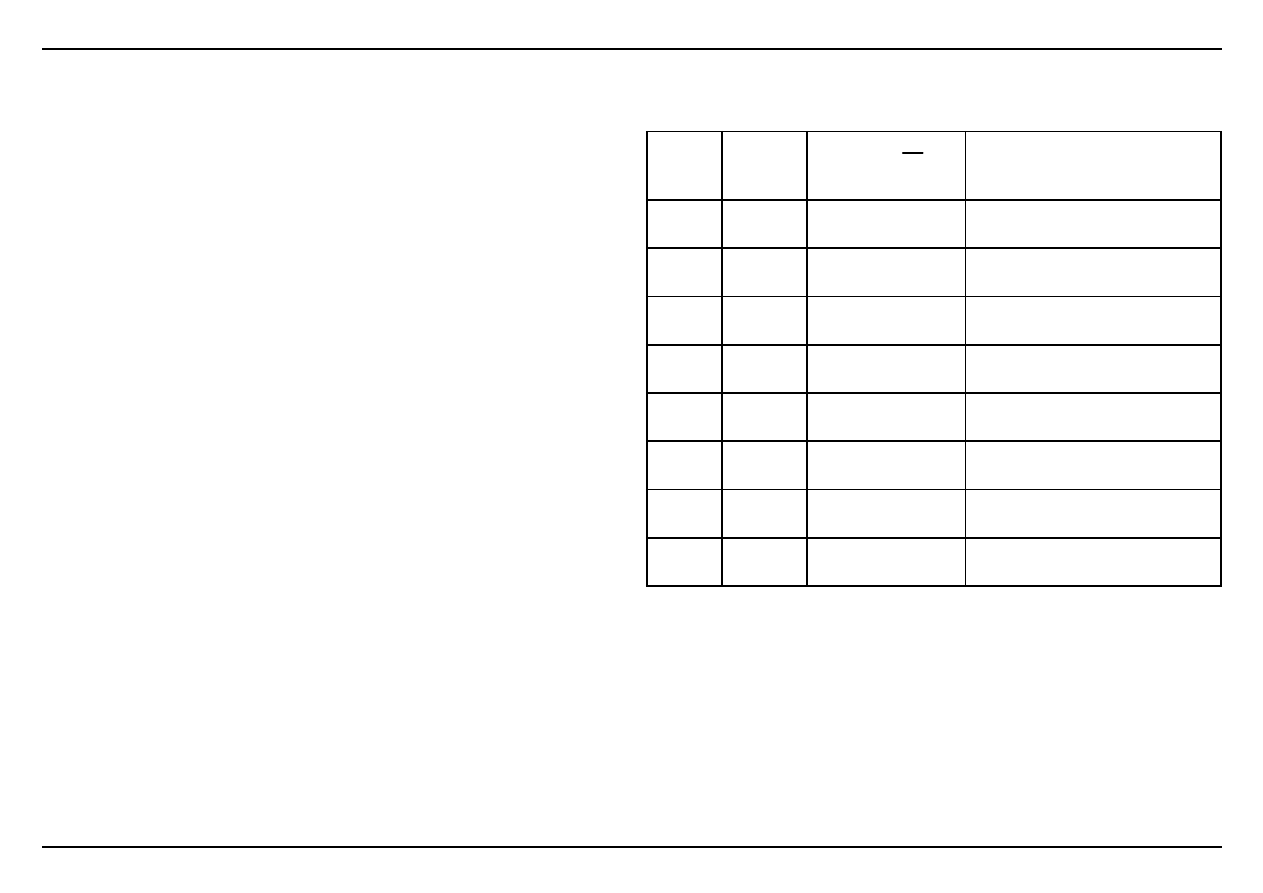
Przykład: 

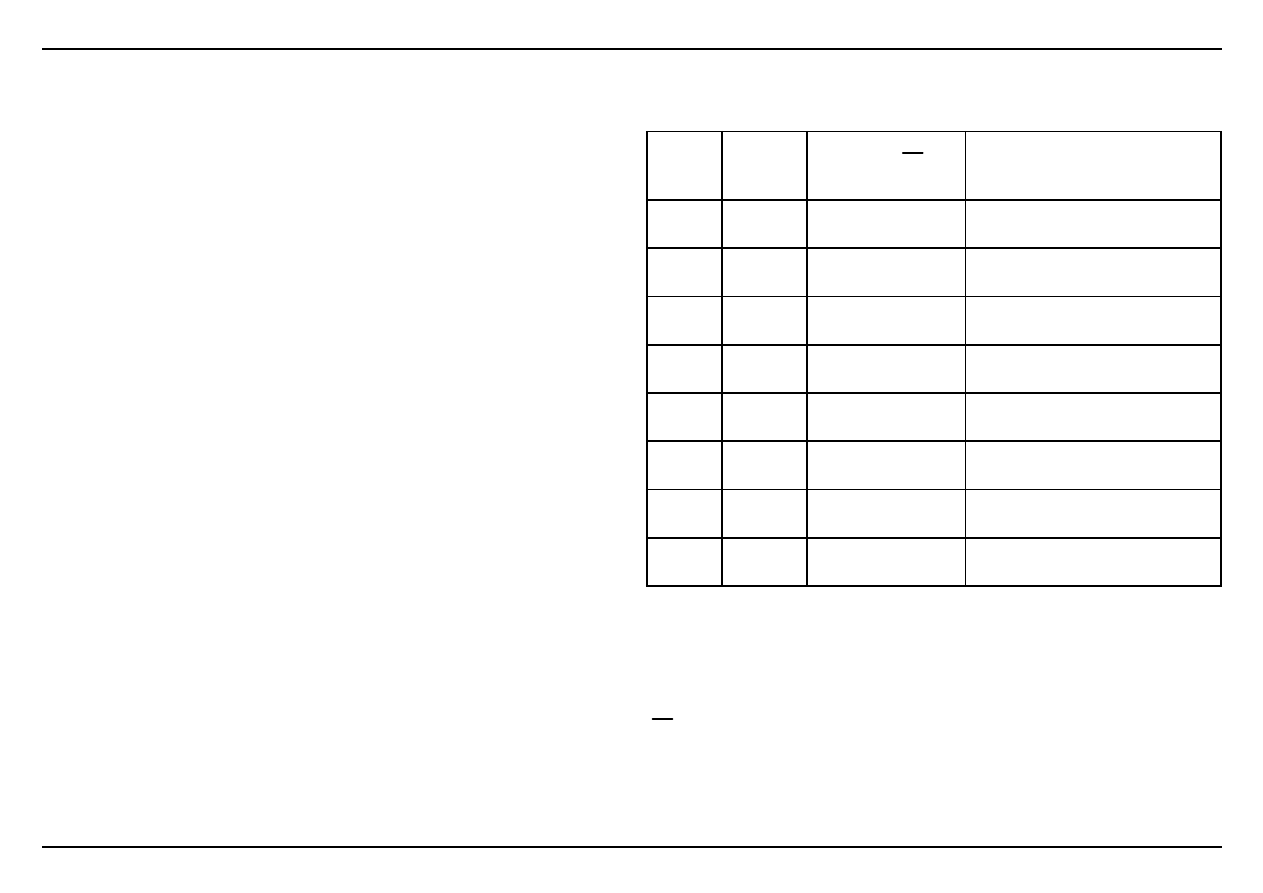
Wykonać aproksymację liniową pomierzonych danych 

Aproksymacja i interpolacja funkcji

xi=[0 1 2 3 4 5 6 7];

yi=[0.3 1.3 1.9 3.5 3 5.5 5 7];

i

x

i

y





2



i

y

y





2

0

1

 

i

i

y

a

a x

0

1

2

3

4

5

6

7

0.3

1.3

1.9

3.5

3

5.5

5

7

9.8439

4.5689

2.3639

0.0039

0.1914

4.2539

2.4414

12.6914

0.0003

0.0133

0.0345

0.2633

0.7887

0.5051

0.4768

0.1667

1





n

i

27.5



n

1







n

i

i

x

1







n

i

i

y

1







n

i

i

i

x y

 

2

1







n

i

i

x



y

Metody Obliczeniowe

Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o ,   s e m e s t r   5 ,   r o k   a k a d e m i c k i   2 0 1 3 / 1 4

Magdalena Rucka

20

Aproksymacja i interpolacja funkcji

xi=[0 1 2 3 4 5 6 7];

yi=[0.3 1.3 1.9 3.5 3 5.5 5 7];

i

x

i

y





2



i

y

y





2

0

1

 

i

i

y

a

a x

0

1

2

3

4

5

6

7

0.3

1.3

1.9

3.5

3

5.5

5

7

9.8439

4.5689

2.3639

0.0039

0.1914

4.2539

2.4414

12.6914

0.0003

0.0133

0.0345

0.2633

0.7887

0.5051

0.4768

0.1667

1





n

i

27.5

Metody Obliczeniowe

Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o ,   s e m e s t r   5 ,   r o k   a k a d e m i c k i   2 0 1 3 / 1 4

Magdalena Rucka

21

Aproksymacja i interpolacja funkcji

xi=[0 1 2 3 4 5 6 7];

yi=[0.3 1.3 1.9 3.5 3 5.5 5 7];

0

1

2

3

4

5

6

7

0

1

2

3

4

5

6

7

x

y

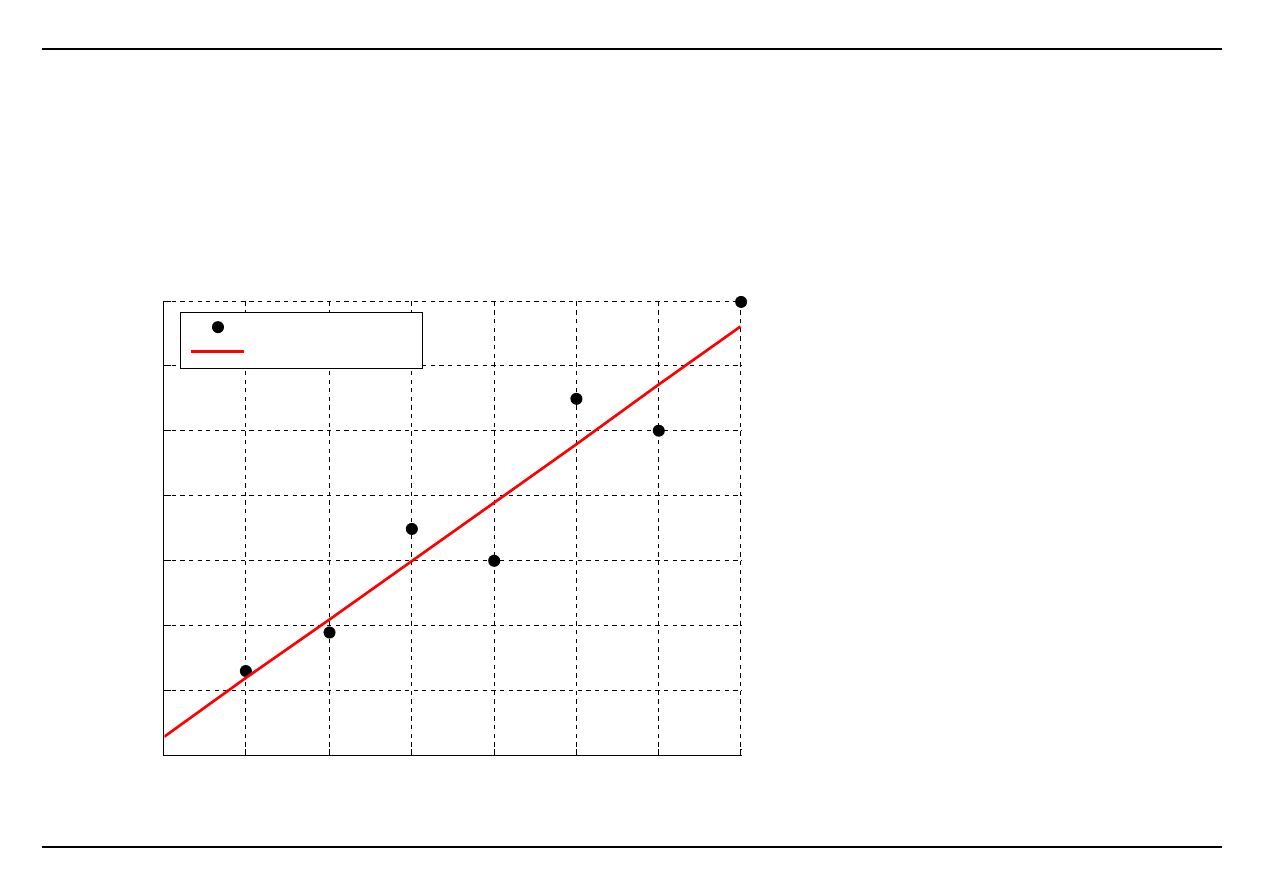
r

2

=0.93815

punkty pomiarowe
aproksymacja liniowa

Metody Obliczeniowe

Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o ,   s e m e s t r   5 ,   r o k   a k a d e m i c k i   2 0 1 3 / 1 4

Magdalena Rucka

22

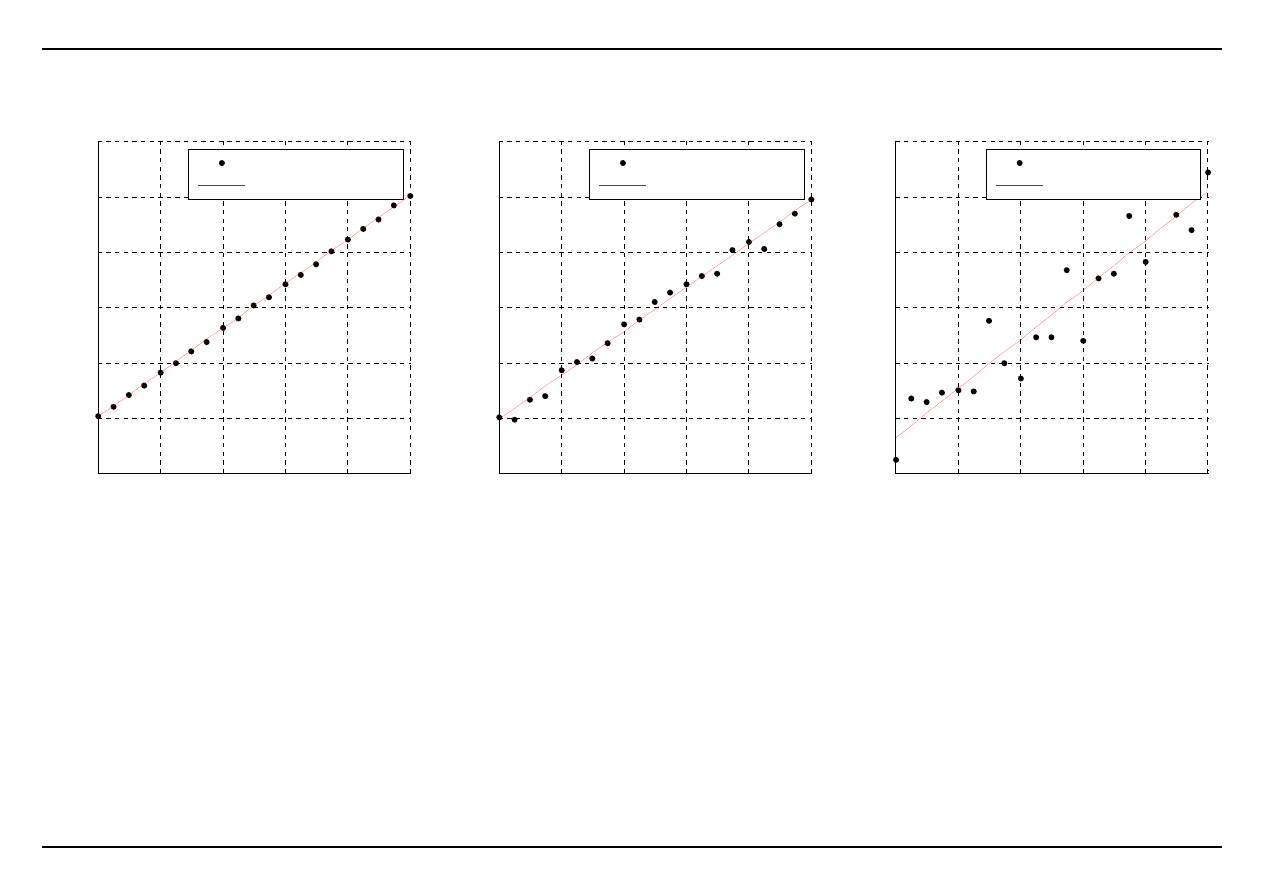
Przykład: 

Dane są wyniki uzyskane w próbie rozciągania osiowego. Dokonać 
aproksymacji liniowej danych pomiarowych, a następnie wykonać ocenę 
dokładności aproksymacji. Na podstawie funkcji aproksymującej obliczyć 
moduł sprężystości.

Aproksymacja i interpolacja funkcji

0

0.2

0.4

0.6

0.8

1

x 10

-3

-50

0

50

100

150

200

250





[M

Pa

]

proba rozciagania nr 1

0

0.2

0.4

0.6

0.8

1

x 10

-3

-50

0

50

100

150

200

250





[M

Pa

]

proba rozciagania nr 2

0

0.2

0.4

0.6

0.8

1

x 10

-3

-50

0

50

100

150

200

250





[M

Pa

]

proba rozciagania nr 3

Metody Obliczeniowe

Katedra Mechaniki Budowli i Mostów, Wydział Inżynierii Lądowej i Środowiska, Politechnika Gdańska
B u d o w n i c t w o ,   s e m e s t r   5 ,   r o k   a k a d e m i c k i   2 0 1 3 / 1 4

Magdalena Rucka

23

0

0.2

0.4

0.6

0.8

1

x 10

-3

-50

0

50

100

150

200

250





[M

Pa

]

r

2

=0.99976

E=200.1162 GPa

punkty pomiarowe
aproksymacja liniowa

0

0.2

0.4

0.6

0.8

1

x 10

-3

-50

0

50

100

150

200

250





[M

Pa

]

r

2

=0.99152

E=198.3946 GPa

punkty pomiarowe
aproksymacja liniowa

0

0.2

0.4

0.6

0.8

1

x 10

-3

-50

0

50

100

150

200

250





[M

Pa

]

r

2

=0.89768

E=223.0484 GPa

punkty pomiarowe
aproksymacja liniowa