Short

Short

-

-

circuits in networks with neutral not

circuits in networks with neutral not

effec

effec

t

t

iv

iv

e

e

ly

ly

grounded

grounded

2 / 31

Types

Types

of

of

neutral

neutral

handling

handling

The type of neutral earthing determines the zero sequence impedance and has

a dominating influence on the short-circuit current through earth.

The different types of neutral handling in power systems are as follows:

ƒ

Low-impedance earthing –

grounded / earthed network

3-phase network having its neutral connected with the earth through resistance or
reactance of sufficiently low value, which assures appropriate network operating
conditions during ground short-circuits.

This type of earth connection refers to HV networks.

ƒ

Isolated neutral –

isolated network

It is a network having no connection with the earth with the exception of such a
connection through high impedance of protection, measurement or signalling
devices.

Isolated networks are LV (690 V) or MV networks of small values of single-phase
short-circuits.

3 / 31

Types

Types

of

of

neutral

neutral

handling

handling

ƒ

Resonance earthing – compensated network

It is 3-phase network having its neutral connected with the earth through
reactance, value of which is selected to compensate single-phase short-circuit
current. The compensation means spontaneous extinguishing short-circuit arc.

Compensated networks – MV networks of high values of single-phase short-circuit
curents.

ƒ

Earthing with current limitation – resistor earthed neutral

It is 3-phase MV network having its neutral connected with the earth through
resistance which assures appropriate network operation conditions during earth
short-circuits.

ƒ

Directly earthed neutral – T type LV network

3-phase or single-phase network with direct neutral connection with the earth.

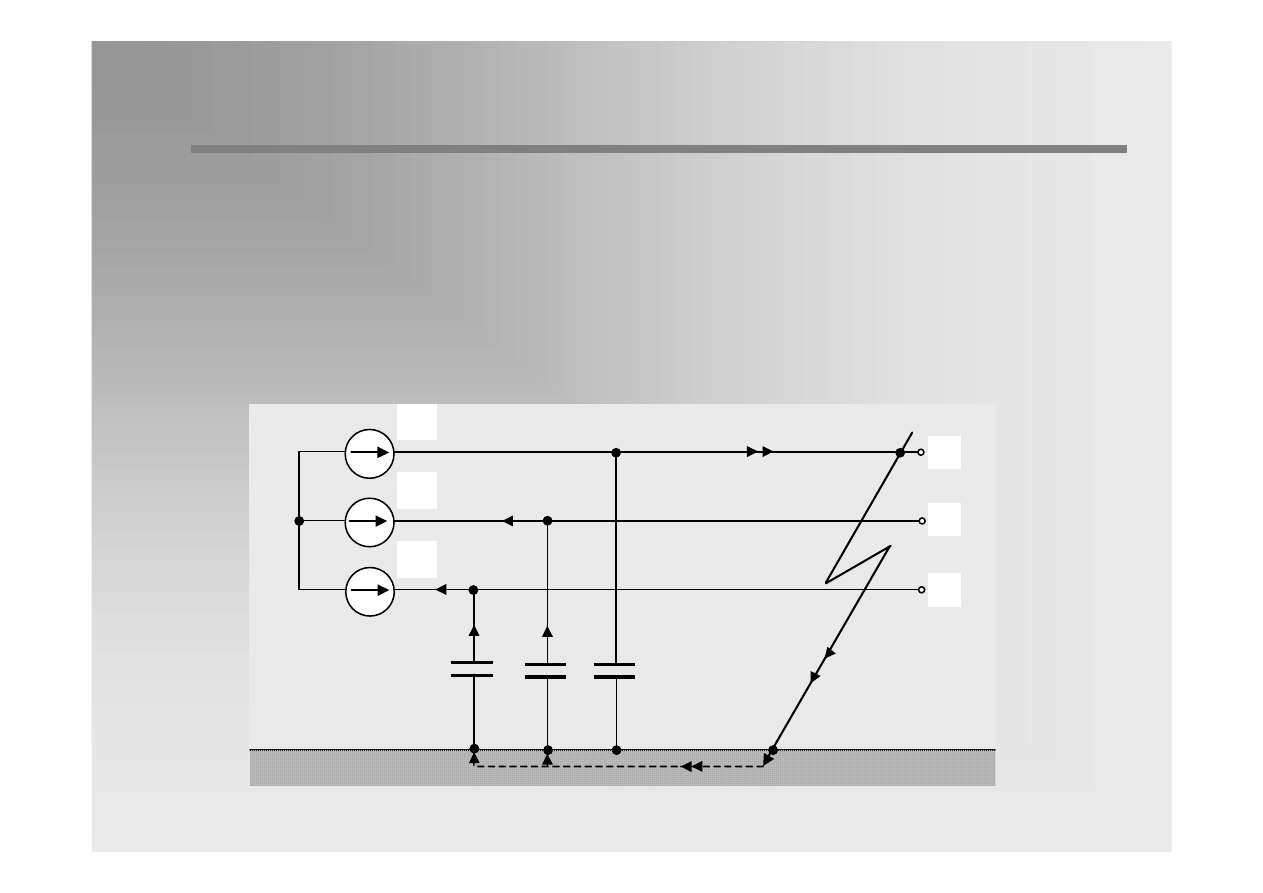
4 / 31

Short

Short

-

-

circuit in isolated network

circuit in isolated network

E

R

E

S

E

T

R

S

T

ƒ

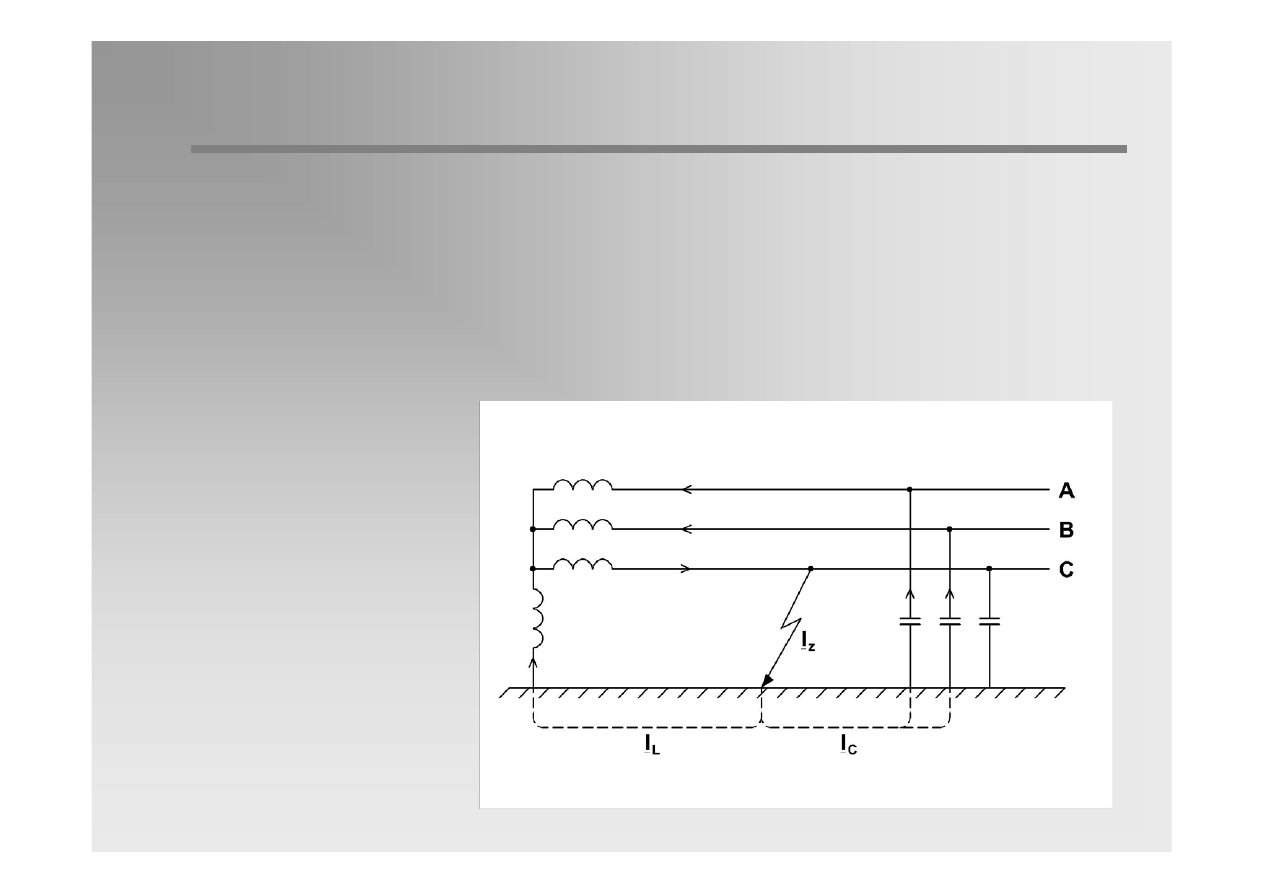
In isolated network the current of single-phase short-circuit flows in the

circuits constituted by the network phase-to-earth capacitances. Its value

is small, because network capacitance present high impedances for the

current flow.

ƒ

The earth-fault current has capacitive character.

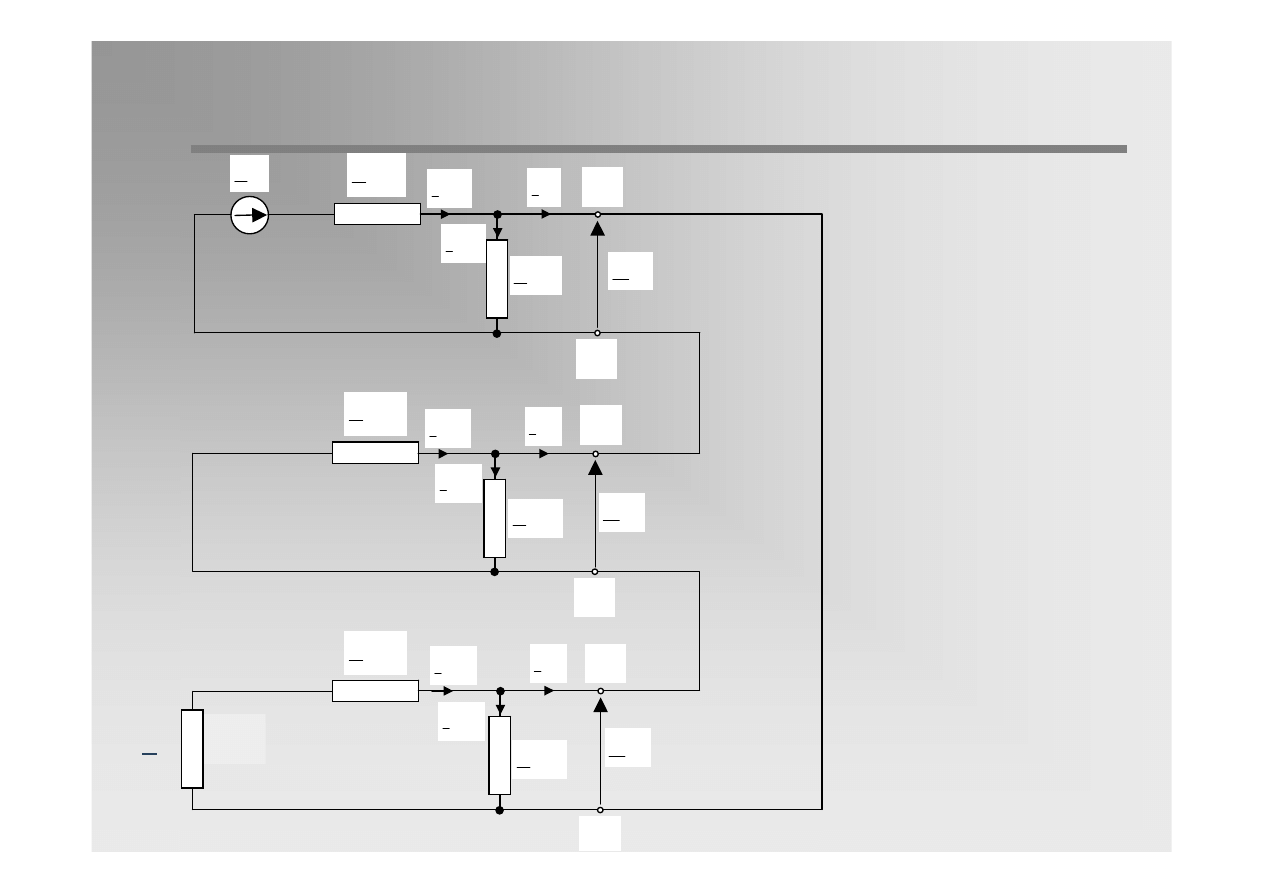
5 / 31

Short

Short

-

-

circuit in isolated network

circuit in isolated network

Equivalent circuit diagram
of a single-phase short-
circuit in isolated network.

( )

1

I

( )

1

E

( )

x

1

Z

( )

1

U

( )

x

2

Z

( )

2

U

P

(1)

K

(1)

K

(2)

( )

x

0

Z

( )

0

U

K

(0)

( )

X

1

I

( )

Y

1

I

( )

0

I

P

(0)

( )

X

0

I

( )

Y

0

I

( )

2

I

P

(2)

( )

X

2

I

( )

Y

2

I

( )

Y

0

Z

( )

Y

2

Z

( )

Y

1

Z

u

Z

3

3Z

u

The zero sequence
impedance is determined
by the capacitance phase-
to-earth and is
significantly higher than
the positive-sequence
impedance.

6 / 31

Earth

Earth

-

-

fault

fault

current in short

current in short

-

-

circuit location

circuit location

( )

( )

1 Y

1 X

Z

Z

>>

( )

( )

2 Y

2 X

Z

Z

>>

( )

( )

0 Y

0 X

Z

Z

>>

( )

( )

( )

( )

( )

( )

1 X

1 Y

1

1 X

1 X

1 Y

Z

Z

Z

Z

Z

Z

=

≈

+

( )

( )

( )

( )

( )

( )

2 X

2 Y

2

2 X

2 X

2 Y

Z

Z

Z

Z

Z

Z

=

≈

+

( )

( )

(

)

( )

( )

( )

( )

0 X

u

0 Y

0

0 Y

0 X

u

0 Y

Z

3Z Z

Z

Z

Z

3Z

Z

+

=

≈

+

+

( ) ( ) ( )

( )

( )

( )

( )

( )

( )

( )

( )

1

1

1

2

0

1

2

0

1 X

2 X

0 Y

E

E

I

I

I

Z

Z

Z

Z

Z

Z

=

=

=

≈

+

+

+

+

Taking into account that:

one can determine sequence component

impedances:

As a result, we can obtain the following current sequence
components:

The positive and negative
sequence series
impedances in the
denominater of the
equations can be
neglected compared with
those of shunt branches.
On the contrary, in zero
sequence we can omit
shunt zero sequence
impedance.

7 / 31

Earth

Earth

-

-

fault

fault

current

current

at

at

short

short

-

-

circuit location

circuit location

( )

( )

( )

0 Y

1 X

2 X

Z

Z

Z

>>

=

( ) ( ) ( )

( )

( )

1

1

2

0

0 Y

E

I

I

I

Z

=

=

≈

( )

( )

0 Y

0

1

Z

j C

=

ω

( ) ( ) ( )

( ) ( )

1

2

0

1

0

I

I

I

j C

E

=

=

= ω

( ) ( )

R

1

0

I

j 3 C

E

= ω

( )

1

E

( )

1

U

( )

0

U

( )

0

C

Furthermore, assuming that

one can write

Since

thus

Phase current:

Simplified equivalent circuit for

single-phase short-circuit in

isolated network

The capacitive earth-fault current is significantly lower
than a typical short-circuit current, in most cases even
lower than the normal operating current. The single
phase fault in a system with isolated neutral is called
earth-fault instead of short-circuit.

8 / 31

Voltage

Voltage

at

at

short

short

-

-

circuit location

circuit location

( )

( ) ( )

( )

( )

( )

( )

1

0

0

0

1

0

0 Y

E

U

Z

I

Z

E

Z

= −

= −

= −

( )

( )

( ) ( )

( )

( )

( )

( )

( )

1

1

1 1

1

1 X

1

1

0 Y

E

U

E

Z I

E

Z

E

Z

=

−

=

−

≈

( )

( ) ( )

( )

( )

( )

1

2

2

2 X

2

0 Y

E

U

Z

I

Z

0

Z

= −

= −

≈

( )

( )

( )

R

0

1

2

U

U

U

U

0

=

+

+

=

( )

( )

( )

( )

( )

( )

o

2

2

j210

1

1

S

0

1

2

U

U

a U

a U

a

1 E

3 E e

=

+

+

=

−

=

( )

( )

( )

(

)

( )

( )

o

2

j150

1

1

T

0

1

2

U

U

a U

a U

a 1 E

3 E e

=

+

+

== −

=

Voltage sequence components at short-circuit location:

Phase voltages:

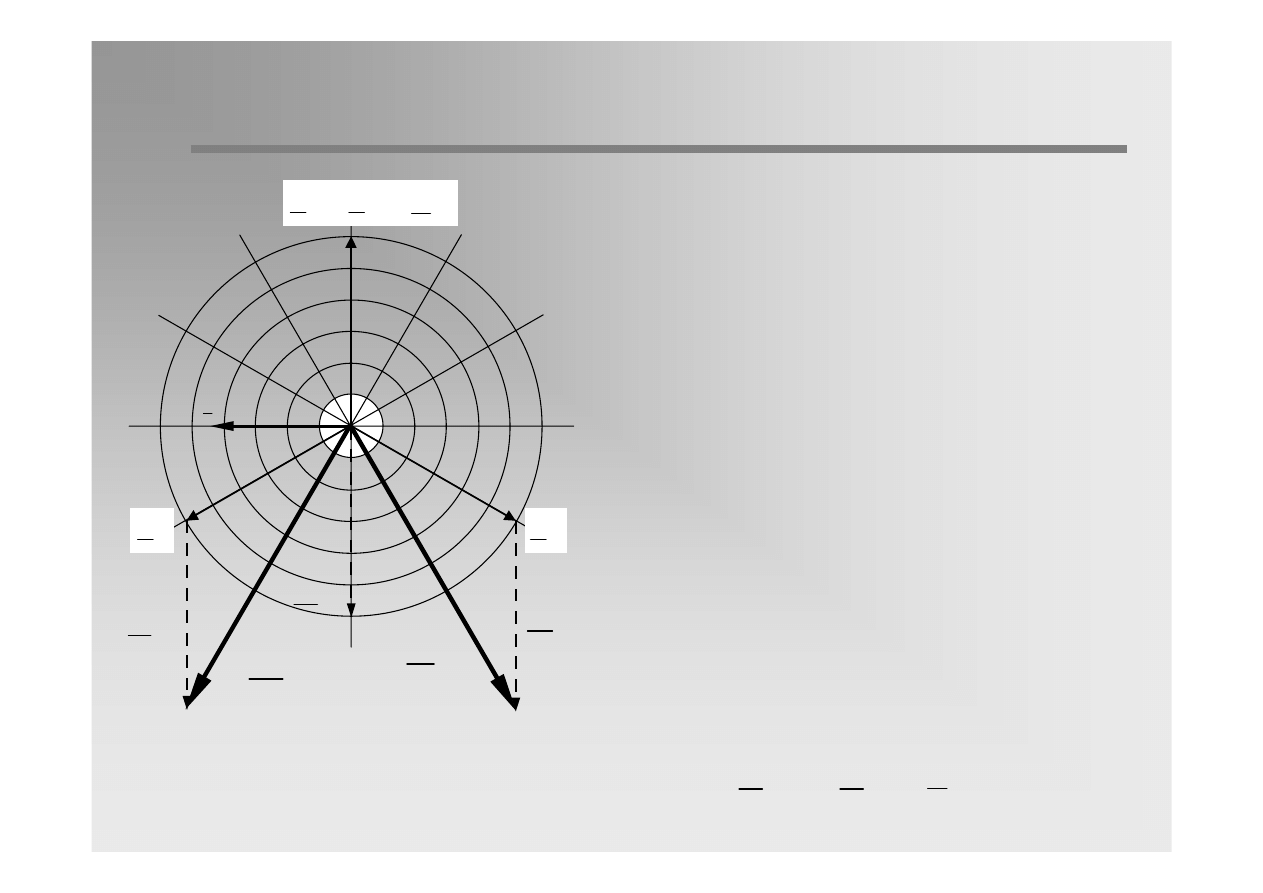
9 / 31

Earth

Earth

-

-

fault

fault

current

current

in

in

isolated

isolated

network

network

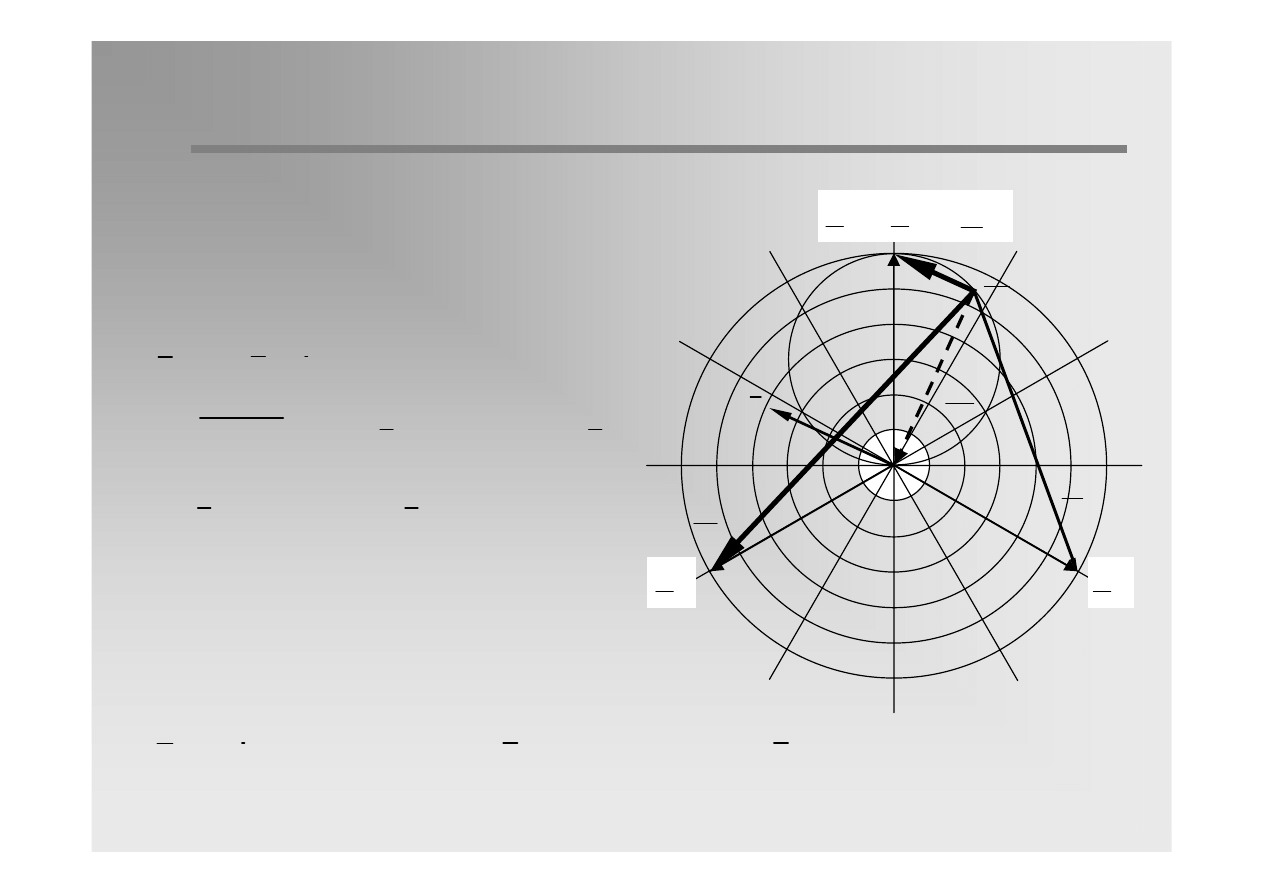
Vector diagram of voltages and currents in
short-circuit location during earth-fault.

( )

( )

1

1

R

U

E

E

=

=

S

E

T

E

R

I

( )

0

U

( )

0

U

S

U

( )

0

U

T

U

( )

( )

1

0

u

E

U

U

=

−

=

The phase-to-earth voltages of the non-faulted

phases are increasing to the amount of the

phase-to-phase voltage.
The voltage of the faulted phase is identical to

the voltage of the earth.
The voltage potential of the neutral N is given,

by definition, as the mean value of the three

phases which is not changed by the earth

fault.
A voltage displacement between neutral and

earth equal line-to-earth voltage is originating

from the fault. The voltage displacemnet is

equal to the voltage of the zero sequence

component.

10 / 31

Network operation during earth

Network operation during earth

-

-

fault

fault

Advantages

ƒ

Typically, earth fault is an intermittent arc fault. Since fault currents are small
they can be extinguished by themselves. Exterior factors like wind or cable
isolation are favourable to that.

ƒ

As a result of self-extinguishing most earth-faults disappear spontaneously
(70% in overhead lines 20-30% in cable lines).

ƒ

Three voltages phase-to-phase remain symmetrical. As a result, in LV network
phase and line voltages are the same before and after a fault. Consumer
devices operate normally.

ƒ

The low value of fault current and the lack of disturbances in load operation
make the long operation of network with earth-fault possible.

11 / 31

Network operation during earth

Network operation during earth

-

-

fault

fault

Disadvantages:

ƒ

Phase voltages at non-faulted phases increase to the value of

√3 U

f

ƒ

Persistent arc, which ignites and extinguishes at every current zero-
crossing causes transient overvoltages of multiplication factor (2÷3,5) U

f..

Due to the system damping, the overvoltage factor will be below 3 in most
of the cases.

ƒ

The capacitive earth-fault current and the recovery voltage at the fault
location have a phase displacement of nearly 90º. The earth-fault arc is
extinguished app. 10 ms after ignition of the earth-fault when the current
has its zero-crossing. At the same time the voltage at the faulted phase
reaches peak value (due to displacement) and may cause a reignition of the
earth-fault.

ƒ

The repetition of fault is possible. In case of double earth-fault short-circuit
current is similar to two-phase fault (app. 0,87 of 3-phase fault).

12 / 31

Network operation during earth

Network operation during earth

-

-

fault

fault

Disadvantages:

ƒ

As an effect of arc burning the following phenomena can occur at the fault
location:

•

Melting of conductors, destruction of insulators

•

Disturbances in protection operation

•

Possibility of the smelting of active iron in electric machines

ƒ

Single-phase faults cause the hazard of electric shock for the sake of touching
voltages occurrence.

ƒ

Earth-fault currents can cause smelting the armaments of reinforced concrete
poles.

ƒ

In overhead lines it can be observed that the impedance of ground round the
poles (pylon) incerases its resistivity (evaporation of water, slag forming).

13 / 31

Network operation during earth

Network operation during earth

-

-

fault

fault

The earth-fault value depends
on the type of network and
increases with increasing line
length:

Wire

cross-

section

mm

2

Line nominal voltage

6 kV

10 kV

15 kV

30 kV

Belted cable

70

0.130

0.120

0.087

0.056

95

0.145

0.130

0.100

0.060

Single-phase screend cable

70

-

-

0.185

0.133

95

-

-

0.198

0.141

Overhead lines

0.003

(

)

[ ]

Z

N

k k

n n

N

k

n

I

U k l

k l

U (0,1l

0.003l )

A

=

+

≅

≅

+

l

k

– total cable line length

l

n

– total overhead line length

k – coefficients (table) [A/kV km]

The value of current does not

depend on fault location in the

network.

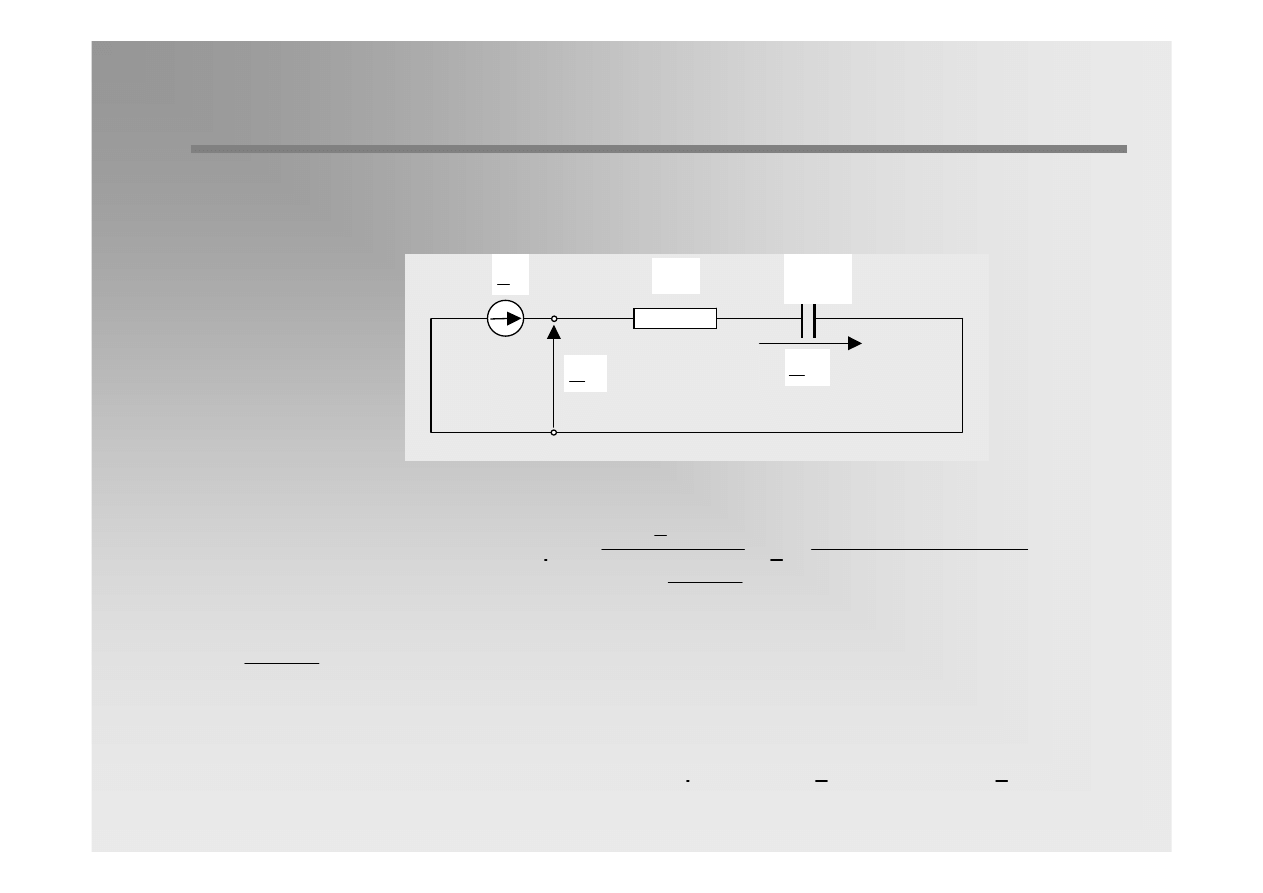
14 / 31

Earth

Earth

-

-

fault

fault

through an arc

through an arc

Short-circuit current in the fault location

( )

( )

( )

( )

( )

( )

( )

(

)

2 2

1

0

0

0

1

2

2 2

0

0

j C

C

3R

E

I

E

1

1

C

3R

3R

j C

τ

τ

τ

ω

+ ω

=

=

+ ω

+

ω

( )

(

)

2

2 2

0

1

C

3R

1

τ

+ ω

≈

( )

0

1

3R

C

τ

<<

ω

( )

( ) ( )

( )

( )

2 2

0

1

1

0

0

I

j C E

C

3R E

τ

= ω

+ ω

Taking into account:

The following equation can be obtain:

( )

1

E

( )

1

U

( )

0

U

τ

R

3

( )

0

C

C

(0)

15 / 31

Earth

Earth

-

-

fault

fault

through an arc

through an arc

Voltage at short-circuit location

( )

( )

1

1

R

U

E

E

=

=

S

E

T

E

R

I

( )

0

U

R

U

S

U

T

U

( )

( ) ( )

( )

( ) ( )

( )

( )

(

)

( )

( )

( )

0

0

0

2 2

1

1

0

0

0

1

1

0

U

Z

I

1

j C E

C

3R E

j C

E

j C

3R E

τ

τ

= −

=

= −

ω

+ ω

=

ω

= −

+ ω

( )

( )

( )

( )

(

)

( )

2

2 2

0

1

1

R

0

0

U

3I R

j C

3R E

C

3R

E

τ

τ

τ

=

= ω

+ ω

16 / 31

Earth

Earth

-

-

fault flow

fault flow

A

B

L

( )

( )

( )

( )

( )

( )

( )

( ) ( )

1

1 A

1

1 Y

1

1

1

1 YA

1 Y

U

I

I

Z

E

I

I

I

Z

=

+

=

=

+

=

+

( )

( )

( )

( )

( ) ( )

2

2 A

2

2

0

2 Y

U

I

I

I

I

Z

=

+

=

=

( )

0 A

I

0

=

( )

1

I

( )

1

E

( )

x

1

Z

( )

1

U

( )

x

2

Z

( )

2

U

P

(1)

K

(1)

K

(2)

( )

x

0

Z

( )

0

U

K

(0)

( )

X

1

I

( )

Y

1

I

( )

0

I

P

(0)

( )

X

0

I

( )

Y

0

I

( )

2

I

P

(2)

( )

X

2

I

( )

Y

2

I

( )

Y

0

Z

( )

Y

2

Z

( )

Y

1

Z

u

Z

3

I

(1)

I

(2)

I

(0)

I

(0)A

I

(2)A

I

(1)A

17 / 31

Earth

Earth

-

-

fault flow

fault flow

( )

( )

( )

( )

1

(1)

1 YA

1

1 Y

E

I

j C E

Z

=

= ω

( )

( )

1 Y

1

1

Z

j C

=

ω

( )

( )

0

1

C

C

<

( )

( ) ( )

( )

( ) ( )

0

1

1

0

1

1 Y

I

j C E

I

j C E

= ω

<

= ω

Line charging current:

Usually

Then earth-fault current is lower than line charging current.

In next considerations the charging current will be omitted.

18 / 31

Earth

Earth

-

-

fault flow

fault flow

( )

1

s

m

1

C

=

γ − γ

[

]

s

2h

lg

r

km/ F

0,02415

⎛

⎞

⎜

⎟

⎝

⎠

γ =

μ

Maxwell coefficients

:

h – mean height of hanging of phase wire above the ground
r – wire cross-section
H – mean distance of phase wire from the mirror reflection of other wires in earth
b

sr

– mean distance between wires

( )

0

s

m

1

C

2

=

γ + γ

[

]

sr

m

H

lg

b

km/ F

0,02415

⎛

⎞

⎜

⎟

⎝

⎠

γ =

μ

Positive and zero sequence capacitance of the line:

19 / 31

Earth

Earth

-

-

fault flow

fault flow

( )

0

I

( )

2

I

( )

1

I

( )

0

I

3

( )

0

I

Z

I

(1)B

(0)

I

I

=

( )

( )

1 A

'

0

I

I

=

( )

( )

2 A

'

0

I

I

=

( )

0 A

'

I

0

=

A

B

L

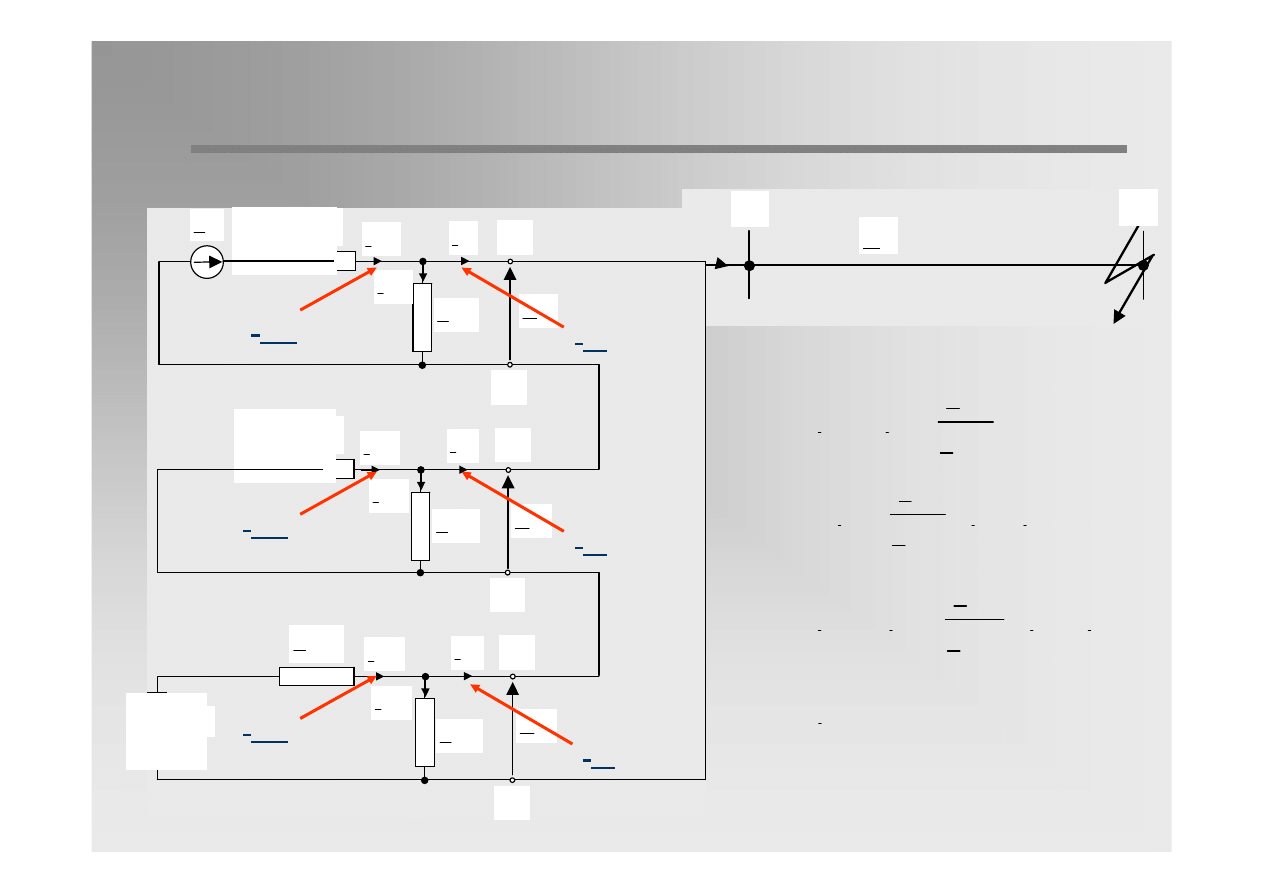
Earth-fault current

(2)B

(0)

I

I

=

(0)B

(0)

I

I

=

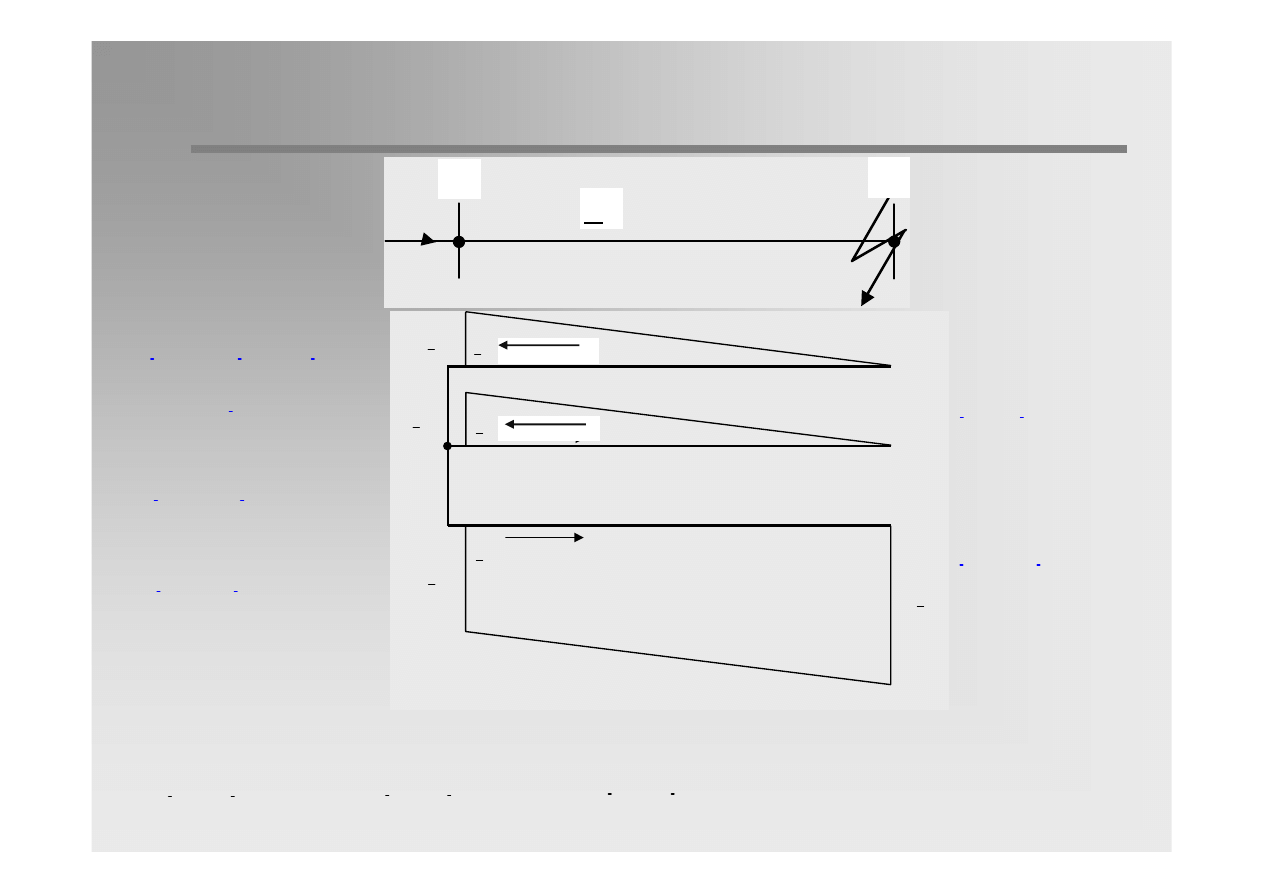
At any point α:

α

α =

A

AB

L

L

α

=

'
(1)

(0)

I

I

α

=

'
(2)

(0)

I

I

α

= α

'
(0)

(0)

I

I

I

(0)

20 / 31

Earth

Earth

-

-

fault flow

fault flow

RB

(0)

I

3I

=

SB

TB

I

I

0

=

=

'

RA

(0)

I

2I

=

'

2

SA

(0)

(0)

(0)

I

a I

aI

I

=

+

=

= −

'
TA

(0)

I

I

= −

A

B

L

Phase currents:

α

=

+ α

'

R

(0)

I

I (2

)

α

=

α −

'
S

(0)

I

I (

1)

α

=

α −

'
T

(0)

I

I (

1)

'
T

I

'

S

I

'
R

I

( )

0

I

3

( )

0

I

−

( )

0

I

−

( )

0

I

2

At any point α:

21 / 31

Earth

Earth

-

-

fault flow

fault flow

A

B

L

K

( )

1

I

( )

2

I

( )

0

I

I

(0)

'
T

I

'
S

I

'
R

I

( )

0

I

3

( )

0

I

−

( )

0

I

−

( )

0

I

2

( )

0

I

3

Z

I

3I

(0)

3I

(0)

22 / 31

Earth

Earth

-

-

fault flow

fault flow

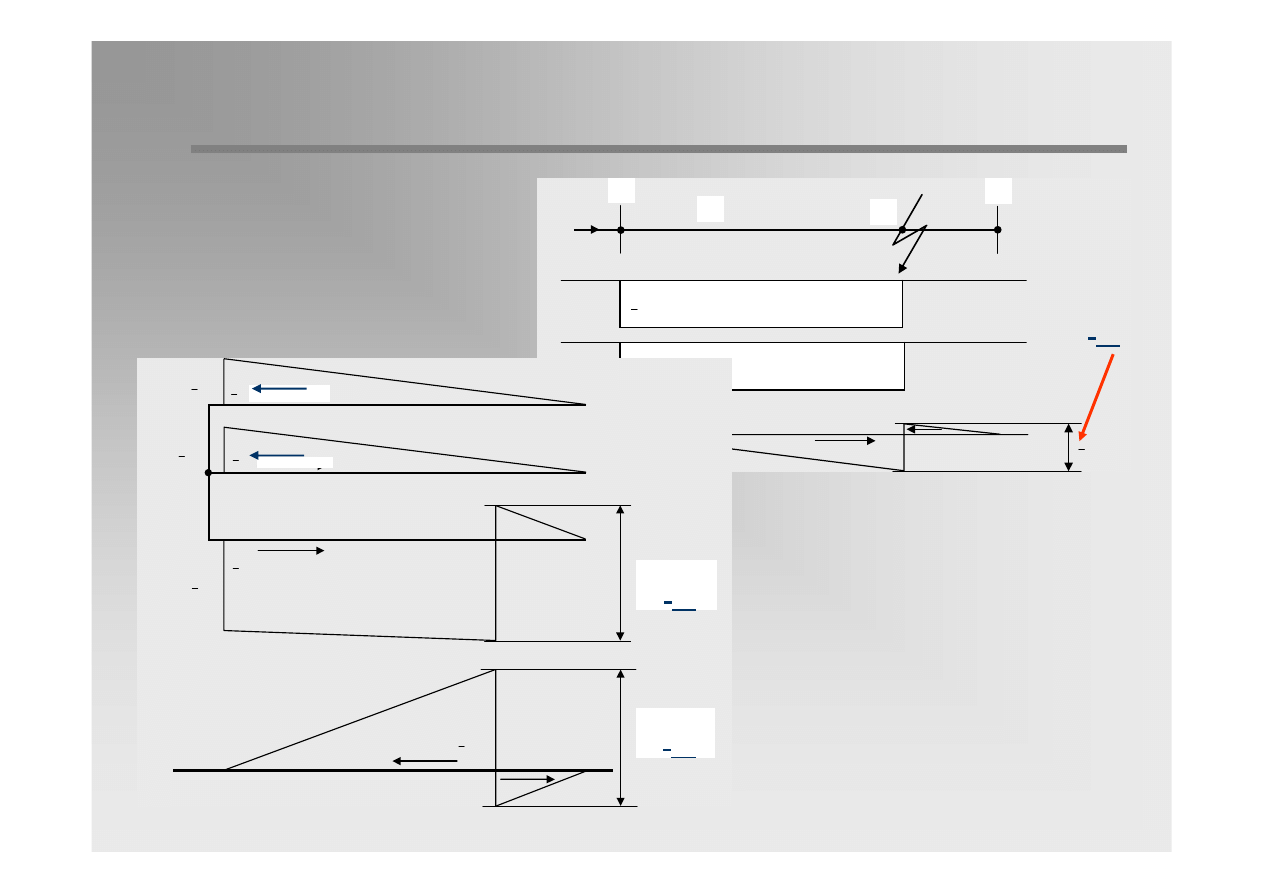
Principles of short-circuit current flow

Earth-fault current is equal 3 times zero sequence current. It flows

through the earth, zero sequence admittances, line wires and
transformer windings.

1.

Currents in non-faulted phases increases along the line from zero at
the end to the value of I

0

at the beginning.

2.

Current in faulted phase increases along the line from zero at both
ends to the value of I

0

at the fault location. Moreover, through the

faulted phase wire the sum of non-faulted phase currents 2 I

0

is

flowing to the fault location.

3.

Earth-fault current 3I

0

is flowing in earth from the fault location to the

end points of the line, where it reaches zero value.

23 / 31

Resonance

Resonance

earthing

earthing

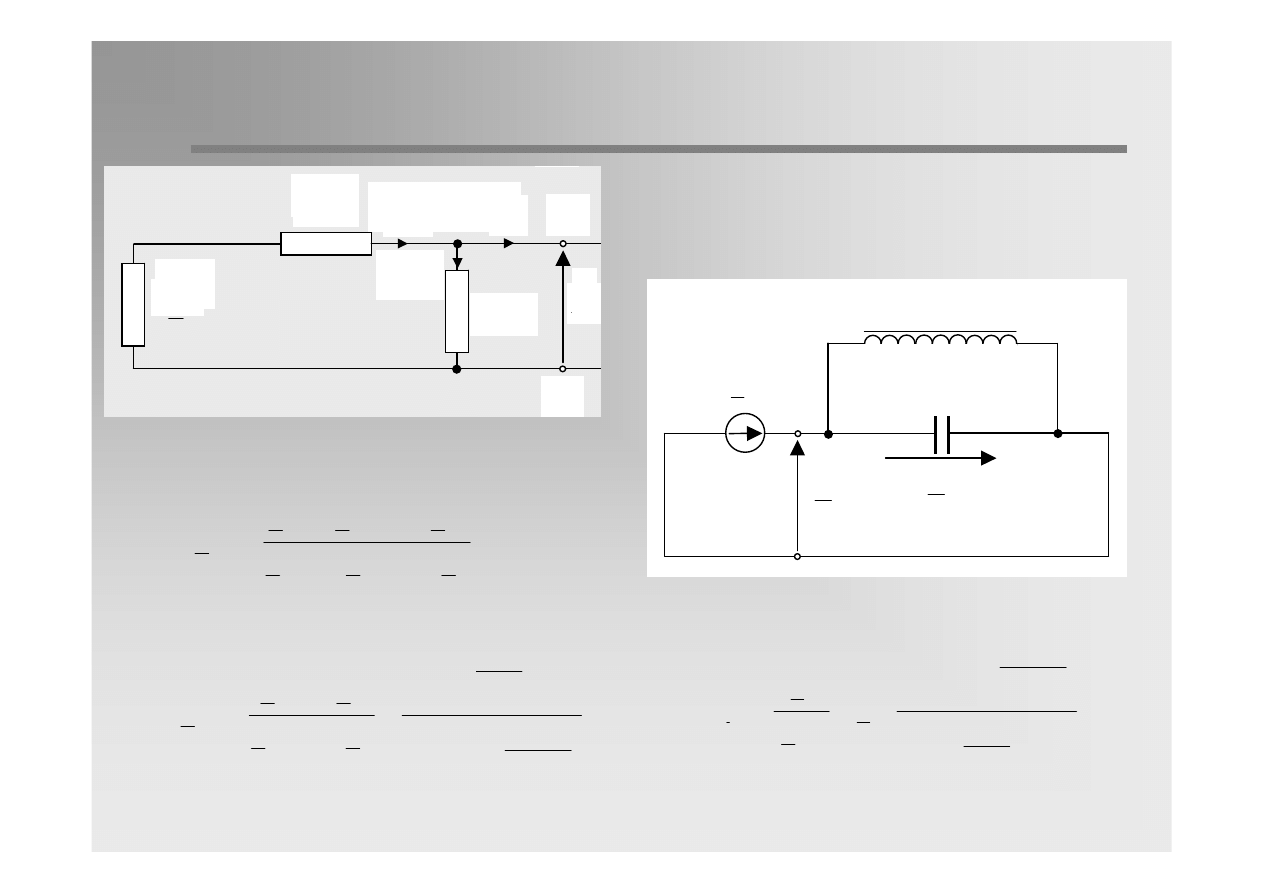
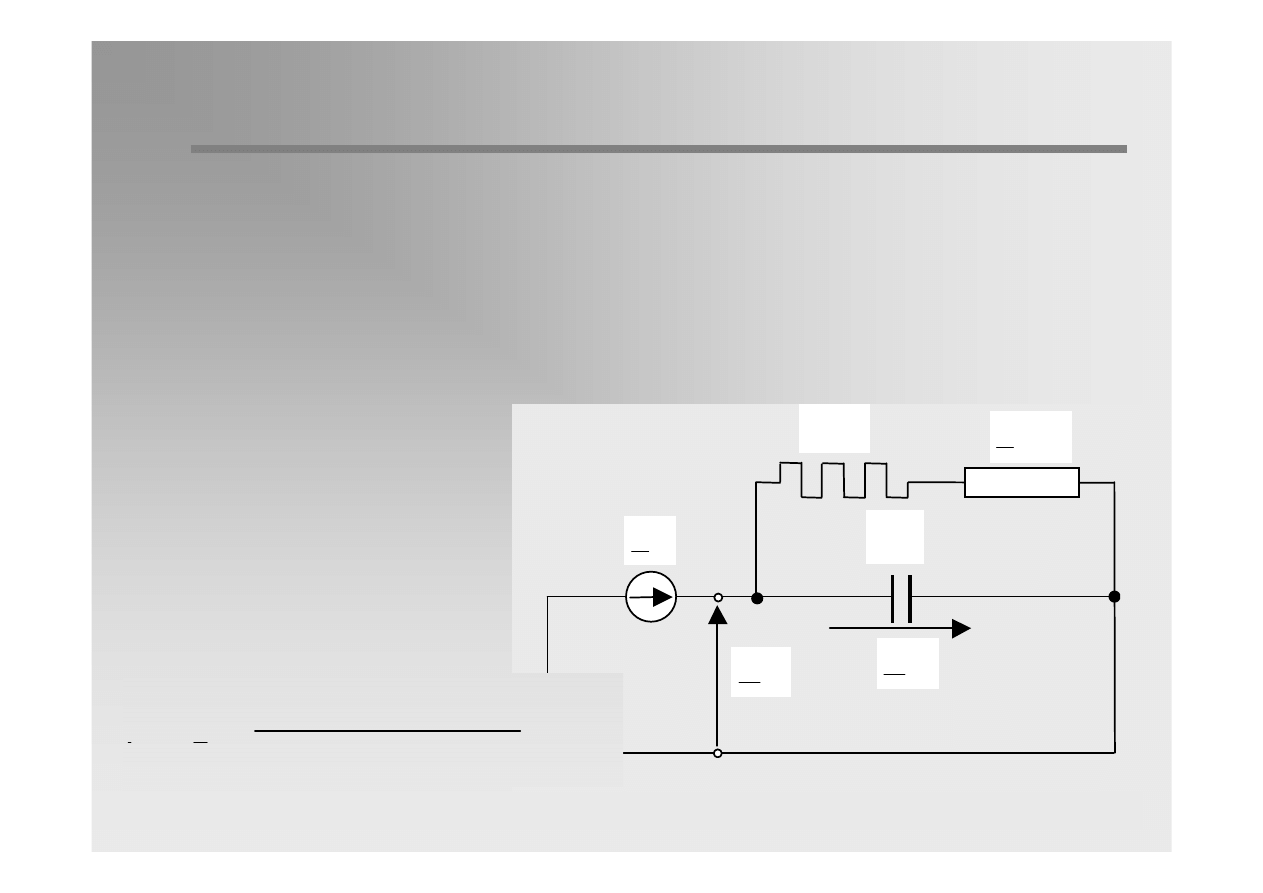
Resonanse earthing is applied if earth-fault current exceed limit values.

Resonance earhing is realized by earthing of one or several neutrals of
transformers through reactances (Petersen-coils), normally adjustable,
which will be set in resonance to the phase to earth capacitances of the
system.

The system in widely in
operation in Europen
countries in MV networks.

24 / 31

Resonance

Resonance

earthing

earthing

( )

x

0

Z

(

0

U

K

(0)

( )

0

I

P

(0)

( )

X

0

I

( )

Y

0

I

( )

Y

0

Z

u

Z

3

Z

(0)Y

Z

(0)X

u

u

Z

j L

= ω

(0)Y

(0)X

u

(0)

(0)Y

(0)X

u

Z

(Z

3Z )

Z

Z

Z

3Z

+

=

+

+

u

(0)Y

u

(0)

(0)

(0)Y

u

u

(0)

L

3

Z

3Z

C

Z

1

Z

3Z

j(3 L

)

C

=

=

+

ω −

ω

u

(1)

(0)

R

(1)

u

(0)

(0)

1

j(3 L

)

3E

C

I

E

L

Z

C

ω −

ω

≅

=

( )

1

E

( )

1

U

( )

0

U

( )

0

C

u

L

3

25 / 31

Resonance

Resonance

earthing

earthing

At the state of resonance the value of earth current is equal zero.

u

(0)

1

3 L

0

C

ω −

=

ω

=

=

ω

ω

u

u

2

(0)

(0)

1

1

L

or X

3 C

3

C

L

C

I

k

1

I

=

>

Then

so:

In order to avoid high overvoltages in case of exact resonance tuning
a small overtuning of up to 10 percent is recommended in practice,
resulting in an ohmic-inductive residual current at the fault location.

The Petersen coil can only be tuned for one frequency in resonance. Harmonics present
in the system voltage are increasing the residual current at the faul location.

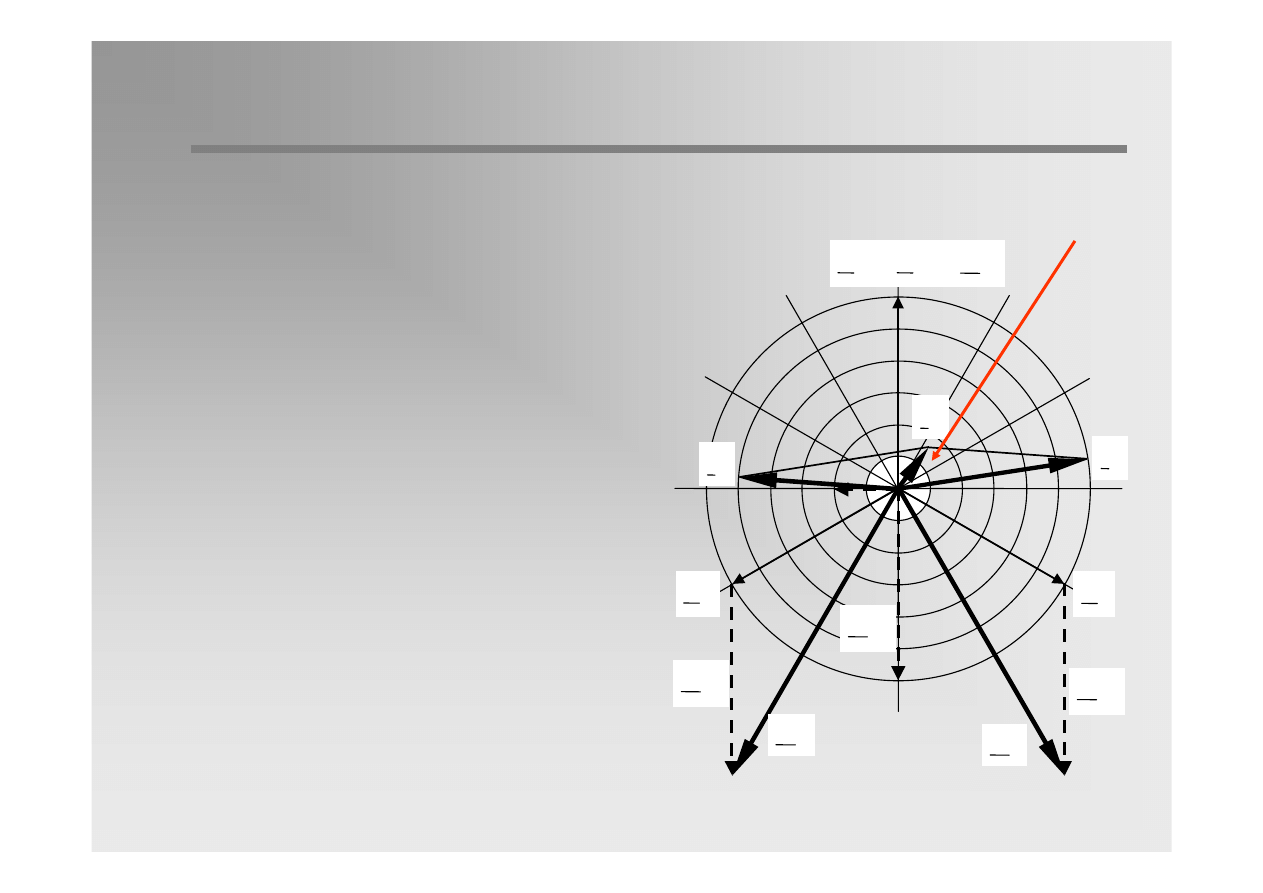
26 / 31

Resonance

Resonance

earthing

earthing

Vector diagram for the state of overtuning, with
taking into account ohmic components of
capacitive and inductive currents.

( )

( )

1

1

R

U

E

E

=

=

S

E

T

E

S

U

T

U

( )

0

U

( )

0

U

( )

0

U

C

I

L

I

r

I

Residual current

The task of resonance earthing is to reduce
the earth-fault current at the fault location to
the minimum or nearly to the minimum by
adjusting the Petersen coil to resonance or
nearly to resonance with phase-to-earth
capacitances. The omic part of the residual
current cannot be compensated by this. If
residual current is small enough, a self-
extinguishing of the arc is possible.
As the phase-to-earth capacitances are
changing during system operation, eg. due
to switching of lines, the Petersen coil has
to be also changed.

27 / 31

Resonance

Resonance

earthing

earthing

Compensated network has the characteristics similar to isolated

network characteristics, however the conditions for self-extinguishing

are better because of lower current value.
Petersen coil is connected to the earth through grounding transformer.

28 / 31

Resonance

Resonance

and

and

resistance

resistance

eathing

eathing

(AWSC)

(AWSC)

Normally, the network operates with resonace earthing. If the earth-fault
current is not self-extinguishing after a few seconds from the beginning of
a fault a resistor is connected in parallel with Petersen coil in order to
force ohmic component of the curent and prompt protection to operate.

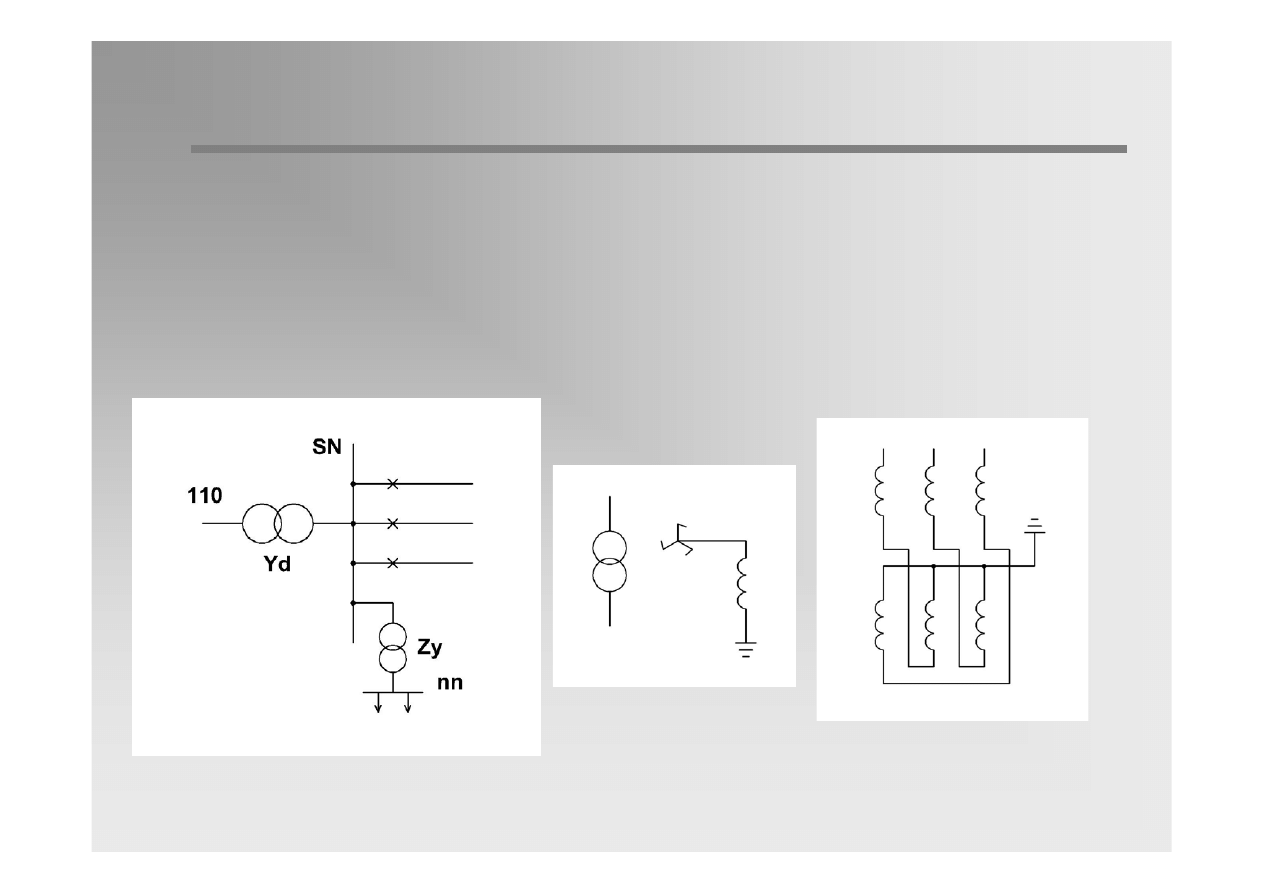
W

R

3

( )

1

E

( )

1

U

( )

0

U

( )

0

C

K

L

3 ω

K

R

3

( )

TU

0

Z

( )

( )

1

1

R

W

W

3E

E

I

3R

R

=

=

At the state of resonance tuning:

Automatics of ohmic
current component forcing
– AWSC (in Polish)

29 / 31

Resonance

Resonance

and

and

resistance

resistance

eathing

eathing

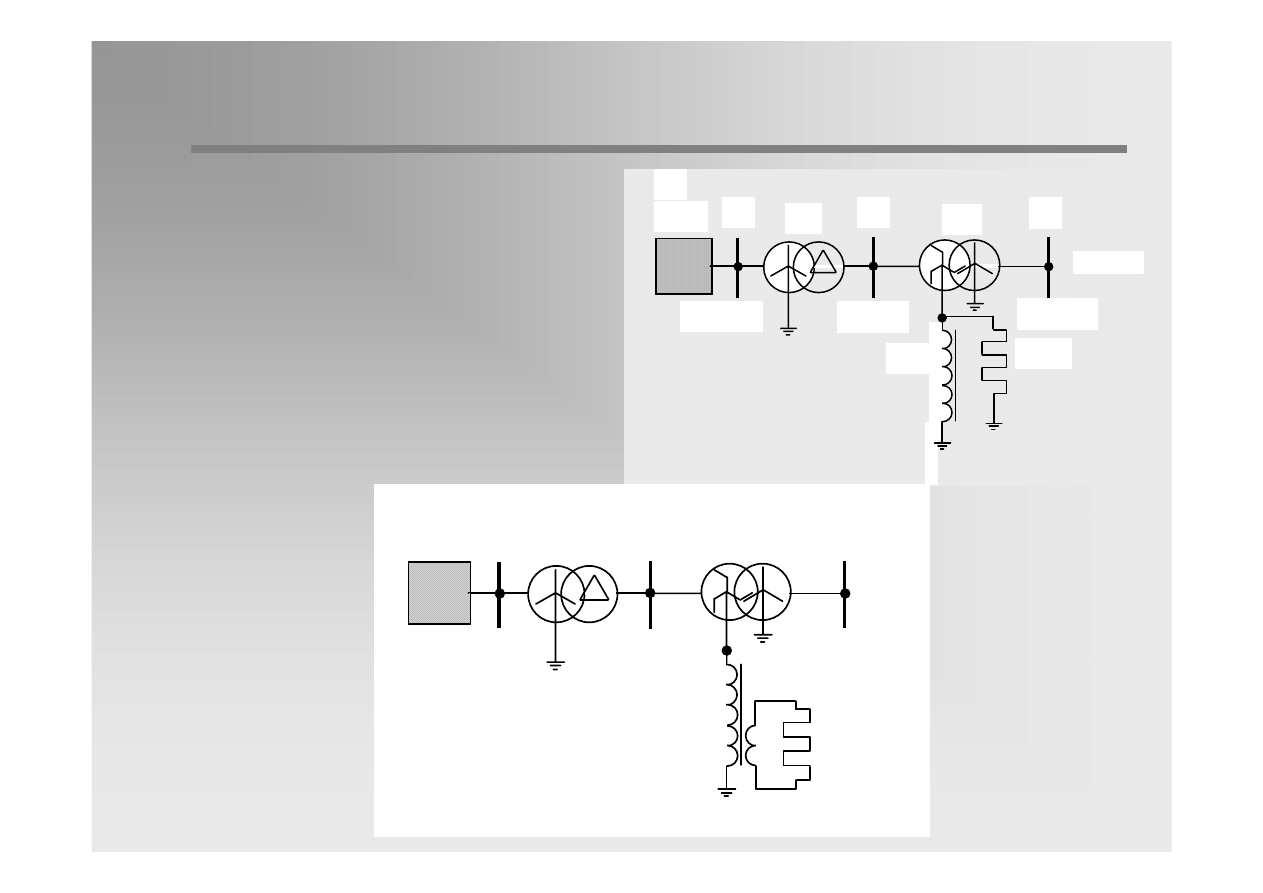
TZ

A

B

15 kV

0.4 kV

TU

D

110 kV

UE

DU

RW

a)

TZ

A

B

15 kV

0.4 kV

TU

D

110 kV

UE

DU

RW

b)

This manner joins the
advantages of compensation in
the field of fault elimination with
advantages of low-impedance
earthing in the field of correct
protection performance.

30 / 31

Earthing

Earthing

with

with

current

current

limitation

limitation

( )

1

E

( )

1

U

( )

0

U

( )

0

C

U

R

3

( )

TU

0

Z

( )

( )

( )

( )

R

1

0

U

0 TU

0 TU

1

I

3E

jB

R

3R

jX

⎛

⎞

⎜

⎟

=

+

⎜

⎟

+

+

⎝

⎠

To realise the scheme of earthing with current limitation the neutrals of

some or all transformers are earthed through reactances or resistances

to such an amount that the condition for the single-phase short-circuit is

fulfilled. The criterion for the design of the earthing conditions is the value

of the single-phase short-circuit current which can be limited to some kA

comparing to low-impedance earthing.

31 / 31

MV

MV

networks

networks

–

–

summary

summary

Most MV networks operate with resonance earthing.

Advantages:

ƒ

Decreasing earth-fault currents

ƒ

The possibility of load supply despite a fault

ƒ

Decreasing electric shock hazard and harmful effects of short-

circuit currents

ƒ

Cheap solutions of earthing systems and protection

Advantages of compensation are limited by the following factors

:

ƒ

Increasing the area of network

ƒ

Higher harmonics in the fault-current and the lack of possibility of

their compensation

ƒ

Not very precise regulation of extinguishing devices and high

residual currents which makes impossible the fault to self-

extinguish

32 / 31

MV

MV

networks

networks

–

–

summary

summary

Applied solutions:

¾

Resonance earthing and:

•

Division of large networks into smaller parts

•

Improvement of measurement methods and Petersen coils
tuning

•

Installing Petersen coils with smooth regulation under load
conditions

•

Application of forcing resistors

¾

Development of perm earthing with current limitation (mainly
through resistor)