2013-04-17 

1 

30 

Metody   probabilistyczne 

 

 

Weryfikacja hipotez statystycznych 

Hipotezy parametryczne 

cz.2 

31 

Testowanie hipotezy o dwóch wskaźnikach struktury (p) 



Badanie dwu skończonych  populacji generalnych ze względu na 
wyróżnioną cechę

. Zachodzi konieczność weryfikacji hipotezy o równości 

wskaźników struktury w obu zbiorowościach. 

Założenie: Cecha ma w populacjach rozkład dwupunktowy z parametrem 

odpowiednio p

1

  i p

2

 

oznaczającym prawdopodobieństwo, że cecha przyjmie 

wyróżnioną wartość.   
Próby muszą być duże  (n

1

≥100) i (n

2

≥100). 

Formułowanie hipotezy:  



Hipoteza zerowa (H

0

) 

jest hipotezą „o równości” i brzmi: H

0

: p

1

 = p

2 

gdzie p

1

 i  p

2

  

są konkretną wartością (liczbą). 



Hipoteza alternatywna (H

1

) 

może być sformułowana trojako (najczęściej w 

zależności od wyniku uzyskanego w próbie): 
H

1

: p

1

 



 p

2        

 (albo H

1

: p

1

 < p

2

    

albo też H

1

: p

1

 > p

2

)  



Wybór hipotezy alternatywnej (H

1

) ma decydujące znaczenie dla 

sformułowania obszaru odrzucenia, 



Rozkład różnicy między wskaźnikami struktury                     można 
aproksymować za pomocą rozkładu normalnego o parametrach 













2

2

1

1

,

n

m

n

m





























2

2

2

1

1

1

2

1

1

1

,

n

p

p

n

p

p

p

p

N

2013-04-17 

2 

32 

Testowanie hipotezy o dwóch wskaźnikach struktury (p) 

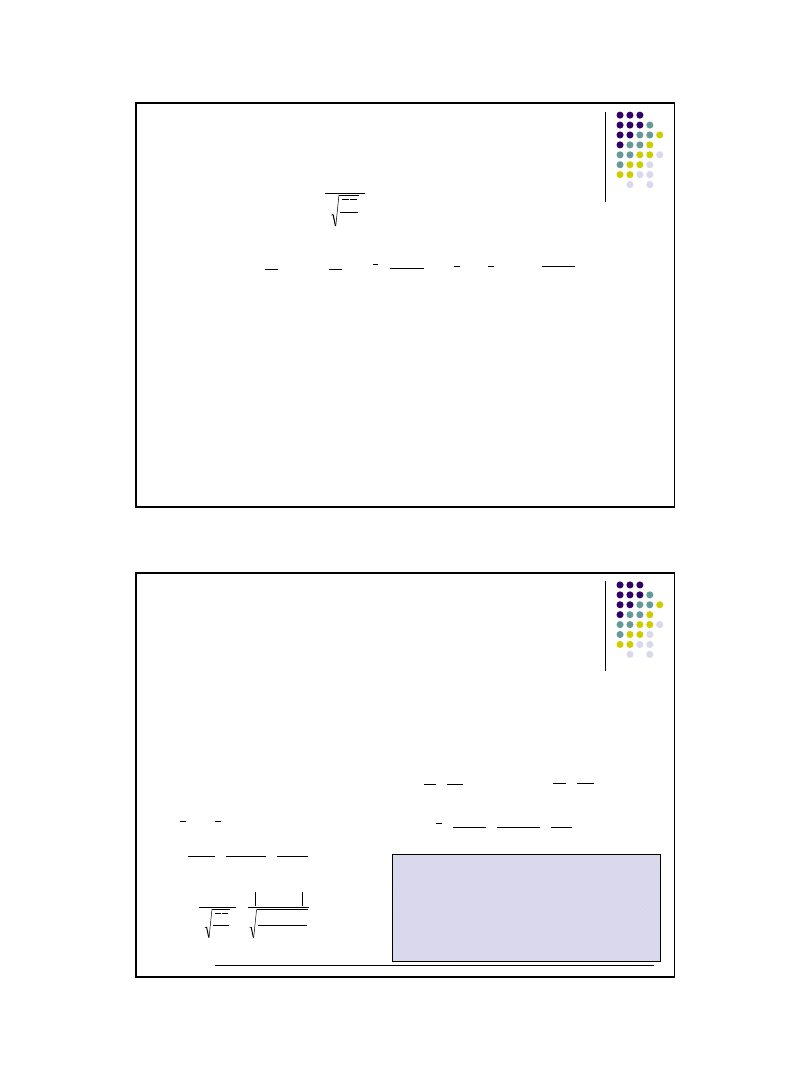
Sprawdzian: 

 
 
 
 

gdzie:

              ,               ,                 ,                   ,      



która ma w przybliżeniu rozkład asymptotycznie normalny N(0 ; 1), dla 
której P{|U|



u



}=



. 

Wnioskowanie  



Jeżeli wartość sprawdzianu U znajdzie się: 

1.

 w obszarze odrzucenia, to odrzucamy H

0

 i przyjmujemy H

1

. 

2.

poza obszarem odrzucenia, to nie mamy podstaw do odrzucenia 
H

0

. 

 

Brak podstaw do odrzucenia oznacza, że obie próby pochodzą z 

tej samej populacji 

n

q

p

p

p

U

*
2

*

1





1

1

*

1

n

m

p



2

2

*
2

n

m

p



2

1

2

1

n

n

m

m

p







p

q





1

2

1

2

1

*

n

n

n

n

n





33 

Testowanie hipotezy o dwóch wskaźnikach struktury (p) 

- 

przykład 



Zweryfikować przypuszczenie kobiety i mężczyźni jednakowo często 
dojeżdżają do pracy komunikacją zbiorową. 



Wylosowano 500 mężczyzn i 600 kobiet. Okazało się, że 200 mężczyzn i 
250 kobiet korzysta z komunikacji zbiorowej. Na poziomie istotności α=0,05 
zweryfikować hipotezę, że odsetek jeżdżących pojazdami komunikacji 
zbiorowej kobiet i mężczyzn jest jednakowy. 



Dane: n

1

=500,    n

2

=600,    m

1

=200,    m

2

=250,     α=0,05, 



H

o

 : p

1

=p

2

  wobec H

1

 : p

1

≠p

2 

 

4

,

0

500

200

1

1

*

1







n

m

p

42

,

0

600

250

2

2

*
2







n

m

p

41

,

0

1100

450

600

500

250

200

2

1

2

1

















n

n

m

m

p

59

,

0

41

,

0

1

1











p

q

727

,

272

1100

300000

600

500

600

*

500

*

2

1

2

1













n

n

n

n

n

671

,

0

273

59

,

0

*

41

,

0

42

,

0

4

,

0

*
2

*

1











n

q

p

p

p

U

Wniosek: 
u

0,025

 = 1,96 

– gdyż obszar jest dwustronny 

u

emp

< u

0,025

, czyli brak podstaw do 

odrzucenia hipotezy H

0

 

=> mężczyźni i 

kobiety jednakowo często korzystają z 
komunikacji zbiorowej. 

2013-04-17 

3 

34 

Testowanie hipotezy o wariancji populacji generalnej σ

2 

 

Założenie: Populacja generalna ma rozkład normalny N(μ, 



)  

o nieznanych parametrach 

μ i 



.  

Z populacji tej wylosowano niezależnie n elementów do próby 
 

Formułowanie hipotez:  



Hipoteza zerowa: H

0

 : 



2

= 



0

2

 , wobec 



hipotezy alternatywnej H

1

: 



2



 



0

2

 ,  

(albo H

1

: 



2



 



0

2

 , 

albo też H

1

: 



2

 < 



0

2

 ) 

gdzie: 



0

2

 

jest hipotetyczną wartością wariancji 



2

 . 

 



H

1

: 



2



 



0

2

 - 

najczęściej gdyż sytuację, w której wariancja jest 

wysoka uznaje się niekorzystną. 

35 

Testowanie hipotezy o wariancji populacji generalnej σ

2 

Model 1  



Założenia: 

próba mała (n≤30);  μ i 



 - nieznane 



Sprawdzian: 

Test istotności dla tej hipotezy jest następujący. Z wyników n elementowej 

próby losowej obliczmy wartość s

2

, a następnie wartość statystyki: 

 
 
 
 



Test istotności: 

Statystyka ta ma przy założeniu prawdziwości hipotezy H

0

 

rozkład χ

2

  z n-1 

stopniami swobody.  

Dla ustalonego z góry poziomu istotności 



  i dla n-1 stopni swobody 

odczytujemy z tablicy rozkładu χ

2

 

taką wartość krytyczną, aby spełniona 

byłą równość P{χ

2

 



 

χ

α

2

 }= 



. (obszar prawostronny) 

 



















n

i

i

x

x

s

n

ns

1

2

2

0

2

0

2

2

0

2

2

1

ˆ

*

1









2013-04-17 

4 

36 

Testowanie hipotezy o wariancji populacji generalnej 

σ

2 

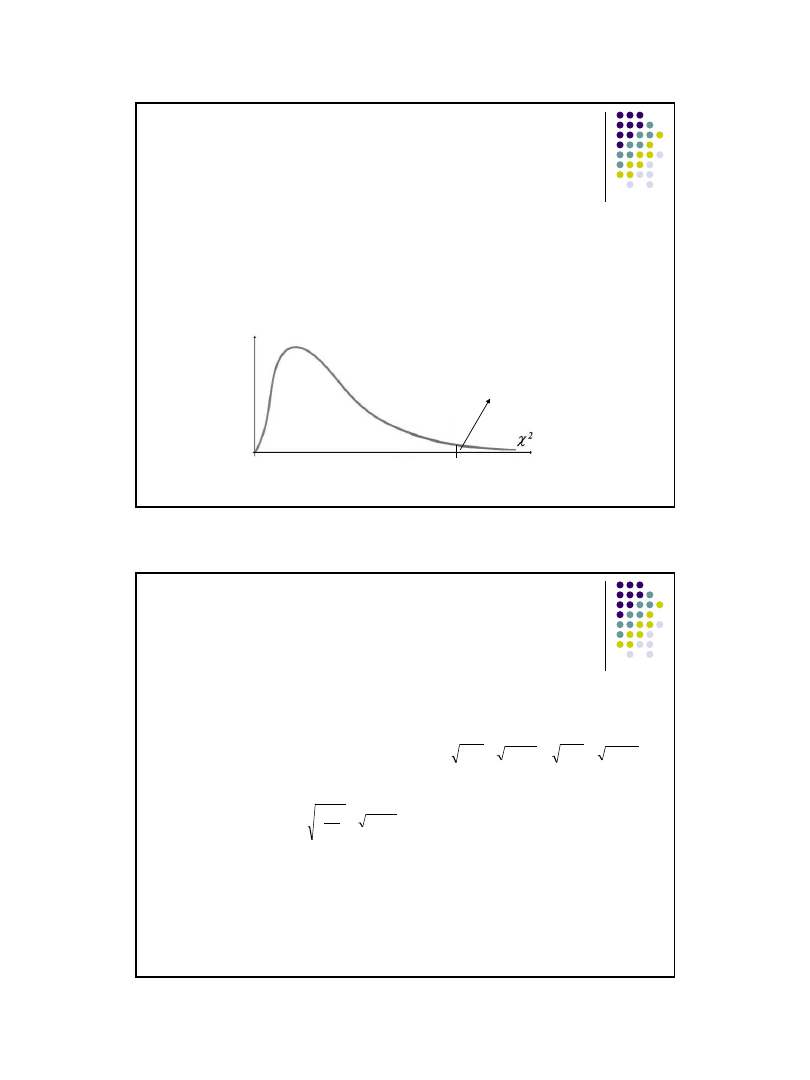
Wnioskowanie  



Nierówność χ

2

 



  

χ

α

2

 

określa prawostronny obszar krytyczny, tzn. gdy 

z porównania wartości χ

2

 

obliczonej z próby z wartością krytyczną  

zajdzie nierówność χ

2

 



 

χ

α

2

 

, hipotezę H

0

 

odrzucamy na korzyść 

alternatywy H

1

. 



Natomiast, gdy zajdzie nierówność χ

2

 



 

χ

α

2

 , nie ma podstaw do 

odrzucenia hipotezy H

0

, że wartość wariancji 



2

  populacji generalnej 

jest 



0

2

. 

 

 

χ

α

2 

α 

37 

Testowanie hipotezy o wariancji populacji generalnej σ

2 

Model 2 
Założenia: 

próba duża (n>30);  μ i 



 - nieznane 

 



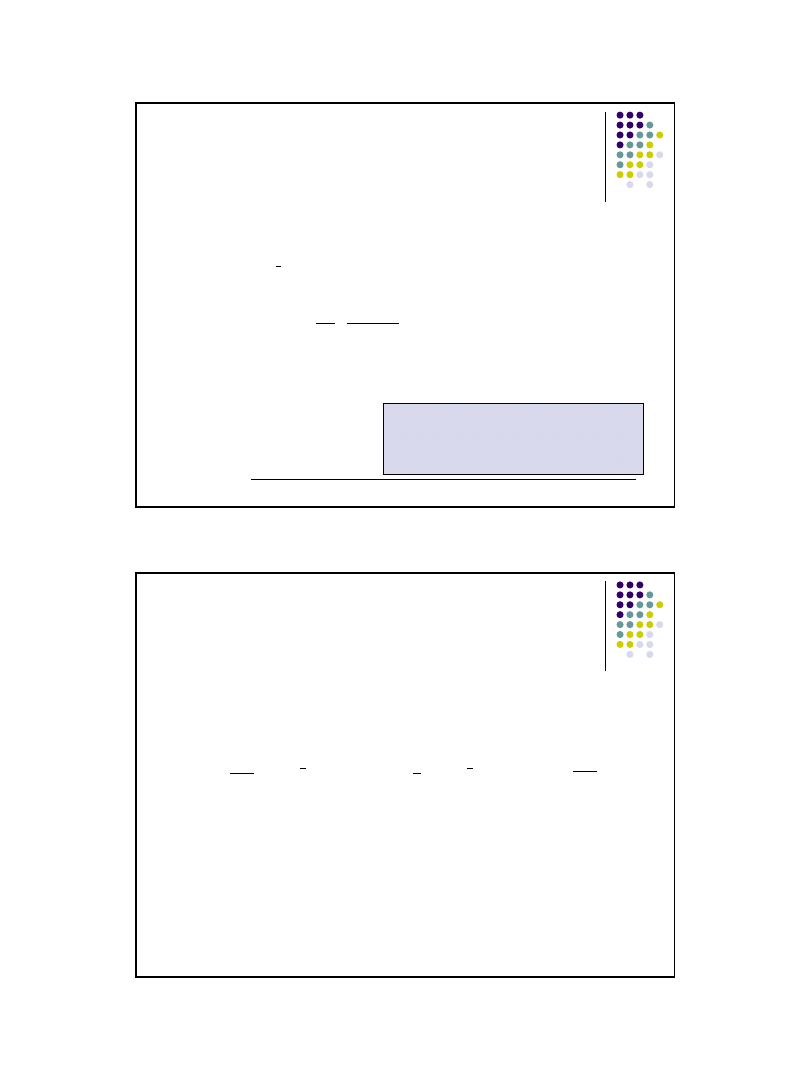
Sprawdzian: 
Wartość χ

2

 

należy przekształcić na  

 

gdzie: k 

– liczba stopni swobody k=n-1 

 

 

 



Test istotności: 

Statystyka ta przy założeniu prawdziwości hipotezy H

0

  

dla ustalonego 

U ma w przybliżeniu rozkład asymptotycznie normalny  

N(0 ; 1), dla którego P{U



u



}=



. 

 

3

2

2

1

2

2

2

2













n

k

U





3

2

2

2

2

0







n

ns

U



2013-04-17 

5 

38 

Testowanie hipotezy o wariancji populacji generalnej 

σ

2  

- 

przykład 



Pewnego dnia dokonano 15 pomiarów opóźnień pociągów 
przyjeżdżających do stacji Kraków Główny. Na podstawie wyników 
pomiarów otrzymano wartość średniego opóźnienia 23min i s

2

 = 523,07. 

Zakłada się, że czas opóźnień pociągów ma rozkład N(μ,σ). Sprawdzić na 
poziomie istotności  α=0,05 hipotezę, że wariancja opóźnień wynosi 400. 



Dane:  n=15,           , s

2

 = 523,07, 

σ

0

2

=400,         

α=0,05,  



Hipotezy: H

0

: 

σ

2

=400        H

1

: 

σ

2

>400 



Statystyka:  

 

 



Wnioskowanie:  obszar krytyczny:   

 

23



x

615

,

19

400

07

,

523

*

15

2

0

2

2











nS

emp

685

,

23

2

1

15

;

05

,

0







2

1

15

;

05

,

0

2









emp

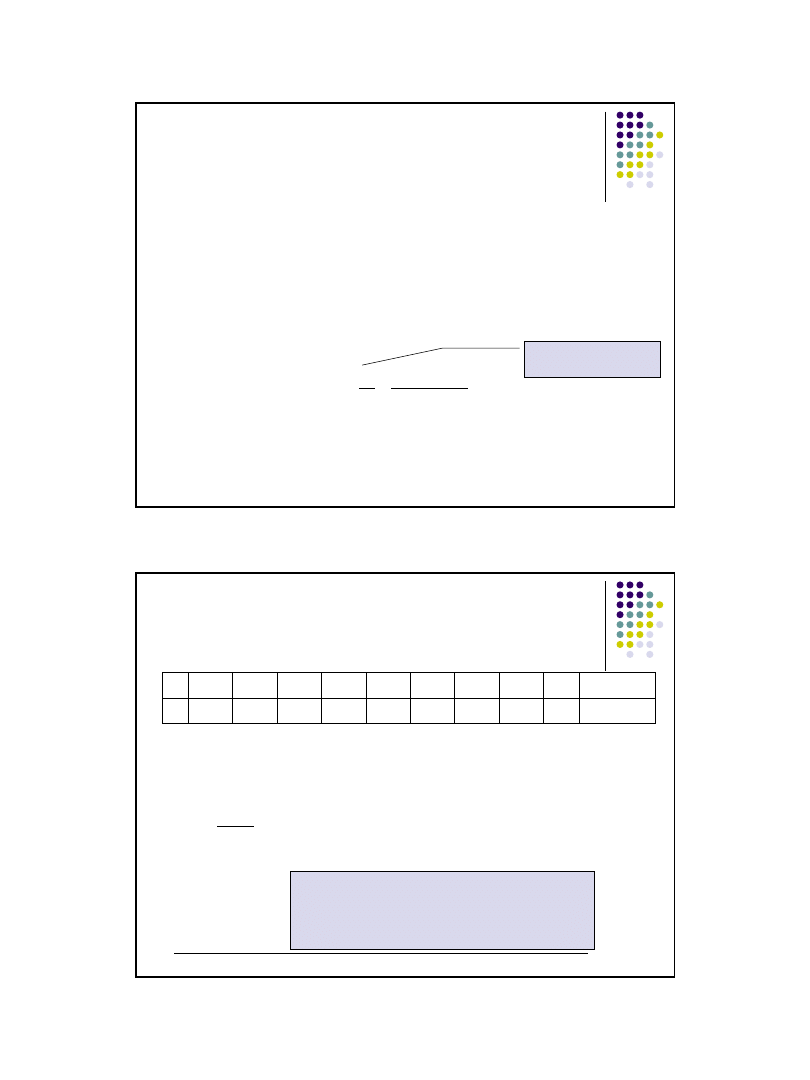
Wniosek: 
Nie ma podstaw do odrzucenia hipotezy 
głoszącej, że wariancja opóźnień całej 
populacji kształtuje się na poziomie 400. 

39 

Test dla dwóch wariancji 

 



Test służy do sprawdzenia hipotezy o jednakowym stopniu rozproszenia 

wartości badanej cechy w dwóch populacjach. 
 



Estymatory wariancji: 
 

 
 















n

i

i

x

x

n

s

1

2

2

1

1

ˆ













n

i

i

x

x

n

s

1

2

2

1

lub 

→ 

2

2

1

ˆ

s

n

n

s





2013-04-17 

6 

40 

Test dla dwóch wariancji 



Model 

Założenia: 



Dane są dwie populacje generalne mające odpowiednio rozkłady normalne  
N(

μ

1

, 



1

) i N(

μ

2

, 



2

), gdzie parametry tych rozkładów są nieznane, 



Wylosowano niezależnie dwie próby o liczebności n

1

 i n

2

 

elementów, 

Formułowanie hipotez 



Należy sprawdzić hipotezę H

0

: 



1

2

 = 



2

2

,     

wobec hipotezy alternatywnej  H

1

: 



1

2

 > 



2

2

. 

(postać najczęściej) 



Sposób postępowania: z obu prób wyznaczyć:         i 
 

Sprawdzian statystyka F: 

 

 



statystyka F

, przy założeniu prawdziwości hipotezy H

0

, ma  

rozkład F Snedecora z n

1

 

– 1 i n

2

 

– 1 stopniami swobody, 

Wnioskowanie: 



jeżeli F ≥ F



, to hipotezę H

0

 

należy odrzucić na rzecz hipotezy alternatywnej H

1

. 

2

1

ˆs

2

2

ˆs









1

/

1

/

ˆ

ˆ

2

2

2

2

1

2

1

1

2

2

2

1









n

s

n

n

s

n

s

s

F

W liczniku zawsze 

większa  z wariancji 

41 

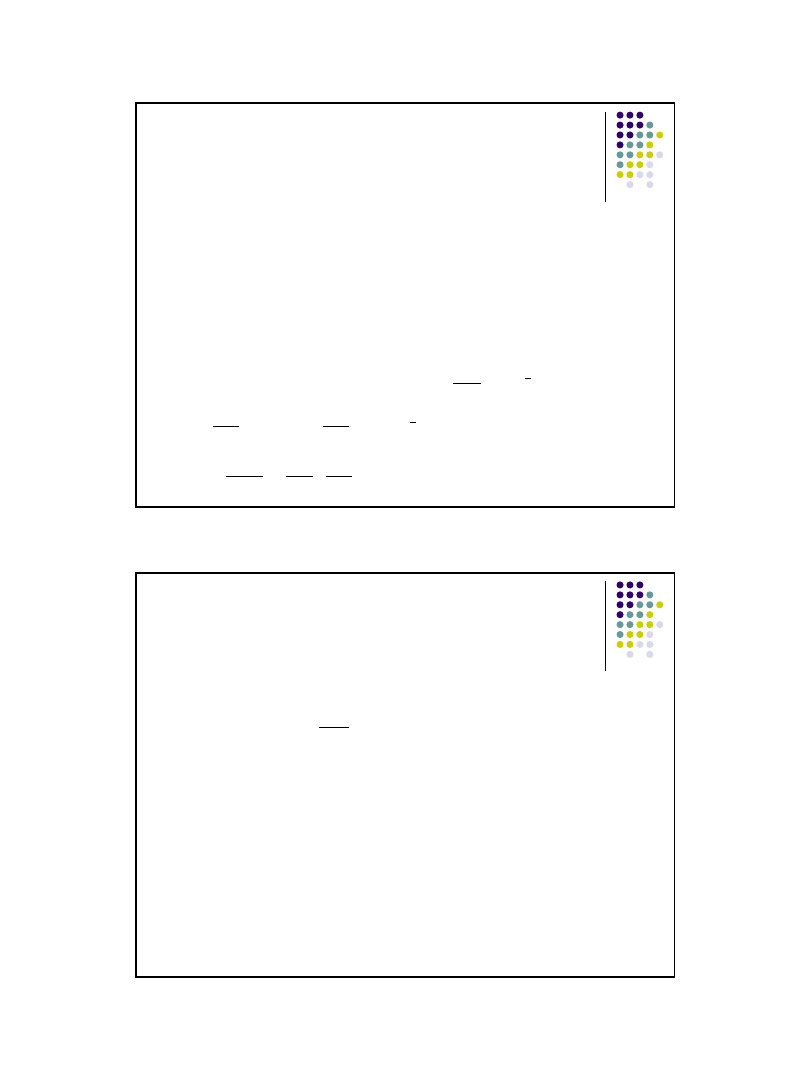
Test dla dwóch wariancji - przykład 



Wyniki dwóch czasu prowadzenia pojazdu przez kierowców.  
Poziom istotności  α=0,05. 
 

 

 

 



Zweryfikować hipotezę o równości wariancji wyników obu kierowców. 



Dane: n

1

=8,  n

2

=9, 



H

0

: 



1

2

 = 



2

2           

wobec

    

H

1

: 



1

2

 > 



2

2

 

 

I 

7,48 

7,88 

8,00 

7,15 

7,26 

7,33 

7,71 

7,18 

II 

7,62 

7,83 

8,03 

7,97 

7,17 

8,08 

7,92 

7,93  7,58 

28

,

1

0837

,

0

1072

,

0





F

F



=3,5   stąd    F=1,28 < F



=3,5

  

Wniosek: 
Brak podstaw do odrzucenia H

0

, że wariancje 

wyników czasu prowadzenia pojazdów przez 
obu kierowców są jednakowe. 

1072

0

s

2

1

,

ˆ



0837

0

s

2
2

,

ˆ



2013-04-17 

7 

42 

Test jednorodności wielu wariancji 

Test Bartletta jest stosowany do sprawdzenia założenia o jednakowych 

wariancjach we wszystkich badanych populacjach. 

Model 
Założenia: 



danych jest k populacji normalnych N(

μ

i 

, 



i

) (i = 1, 2, ..., k), 



z każdej populacji wylosowano niezależnie n

i

 

elementów, 



wyniki każdej próby są oznaczone x

ij

 (i = 1, 2, ..., k, j = 1, 2, ..., n

i

). 

Formułowanie hipotez: 



należy sprawdzić hipotezę H

0

 : 



1

2

 =  



2

2

 = ... = 



k

2

. 



hipoteza alternatywna H

1

 

: nie wszystkie wariancje są  równe. 

Sposób postępowania: 



z wyników k prób należy obliczyć:  















i

n

j

i

ij

i

i

x

x

n

s

1

2

2

1

1

ˆ































k

i

n

j

i

ij

k

i

i

i

i

x

x

k

n

s

n

k

n

s

1

1

2

1

2

2

1

ˆ

*

1

1

~

































k

i

i

k

n

n

k

c

1

1

 

 

1

1

1

3

1

1

gdzie: 







k

i

i

n

n

1

43 

Test jednorodności wielu wariancji 

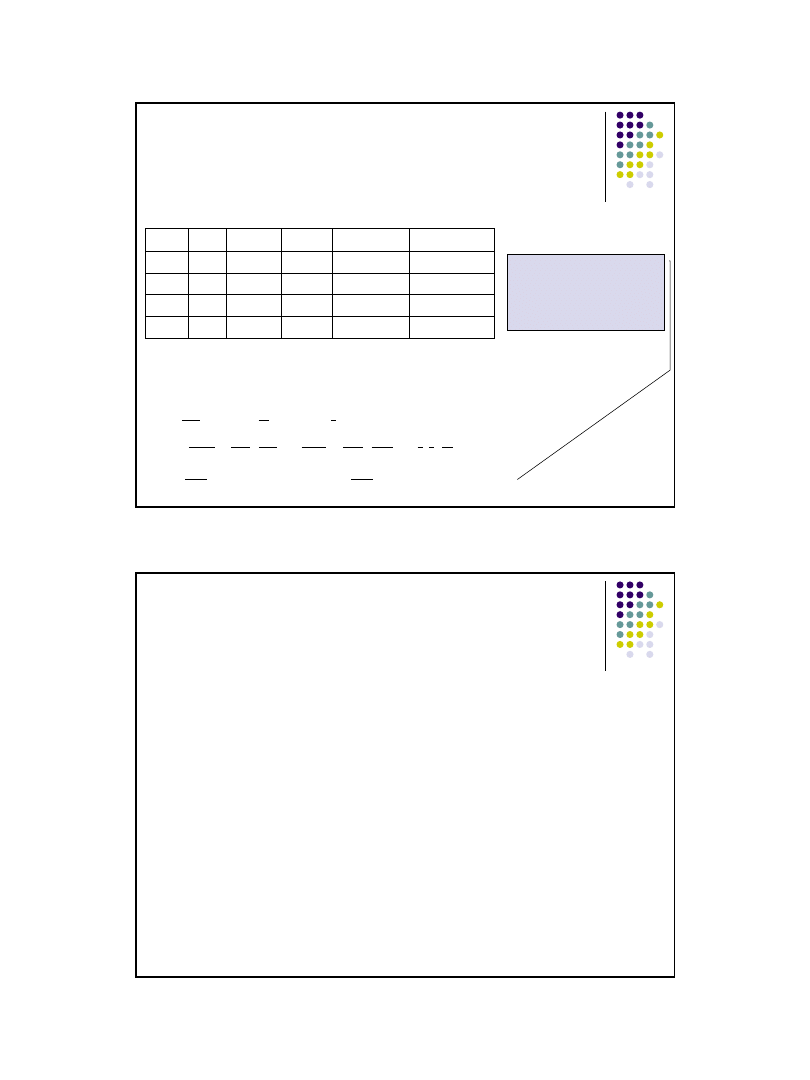
Statystyka: 



dla ustalonego poziomu istotności α i dla k –1 stopni swobody należy 
odczytać wartość χ

α

2

 . 

 

 

 

log 

– logarytm  dziesiętny 

 

Wnioskowanie: 



jeżeli χ

2

 



 

χ

α

2

 

, to hipotezę H

0

 

należy odrzucić.  



jeżeli χ

2

 < 

χ

α

2

  brak podstaw do odrzucenia hipotezy H

0. 





























k

i

i

i

s

n

s

k

n

c

1

2

2

2

1

303

2

ˆ

log

*

~

log

*

,



2013-04-17 

8 

44 

Test jednorodności wielu wariancji - przykład 



Zbadano  liczbę  pasażerów  przewożonych  linią  tramwajową  w godzinach  szczytu 
w kolejnych  3 dniach  roboczych  tygodnia.  Otrzymano  następujące  wariancje 
liczby pasażerów  przewożonych  20, 100, 70. Przyjmując poziom  istotności 
α=0,05 zweryfikować  hipotezę,  że wariancja  liczby pasażerów  w kolejne  dni 
tygodnia  jest jednakowa. 

lp 

s

i

2 

log(s

i

2

) 

(n

i

-1) 

(n

i

-1)*(s

i

2

) 

(n

i

-1)*log(s

i

2

) 

1 

20 

1,301 

9 

180 

11,709 

2 

100 

2,000 

9 

900 

18,000 

3 

70 

1,845 

9 

630 

16,606 

suma 

1710 

46,315 

n

i

= 

10 

s

2

= 

63,333 

c= 

1,049 

n= 

30 

n-k= 

27 

χ

2

= 

5,111 

k= 

3 

log(s

2

) 

1,802 

χ

2

0,05,2

= 

5,991 









3

,

63

190

*

3

1

70

100

20

27

9

ˆ

*

1

1

~

1

2

2





















k

i

i

i

s

n

k

n

s









049

,

1

27

1

9

3

6

1

1

3

30

1

 

 

1

10

1

1

3

3

1

1

1

 

 

1

1

1

3

1

1

1

1













 





























































k

i

k

i

i

k

n

n

k

c











 







111

,

5

315

,

46

333

,

63

log

3

30

049

,

1

303

,

2

ˆ

log

*

1

ˆ

log

*

303

,

2

1

2

2

2

































k

i

i

i

s

n

s

k

n

c



Wniosek 

Nie ma podstaw do 

odrzucenia hipotezy, że 

wariancje są jednakowe 

45 

Test analizy wariancji dla wielu średnich 

Klasyfikacja pojedyncza 



Podstawowe narzędzie statystyki eksperymentalnej, 
 



Pozwala na sprawdzenie, czy pewne czynniki, które można regulować w 
toku eksperymentu, wywierają wpływ (jak duży) na kształtowanie się 
średnich wartości badanych cech, 
 



Polega na porównaniu wariancji wynikającej z działania danego czynnika z 
wariancją resztkową mierzącą losowy błąd eksperymentu. 
 



Klasyfikacja pojedyncza

 

– suma kwadratów wariancji ogólnej jest rozbijana 

na dwa składniki mierzące zmienność między grupami (populacjami) i 
wewnątrz grup

. 

2013-04-17 

9 

46 

Test analizy wariancji dla wielu średnich 

Model 
Założenia: 



danych jest k 

populacji o rozkładzie normalnym N(μ

i

, 



i

) lub o rozkładzie 

zbliżonym do normalnego, 



wariancje wszystkich k 

populacji są równe (



1

2

 = 



2

2

 = ... = 



k

2

 = 



2

),  

ale 

nie muszą być znane, 



z każdej z tych populacji wylosowano niezależnie próby o liczności n

i

 

elementów, 



wyniki prób oznaczone są przez x

ij

 (i = 1, 2, ..., k,  j = 1, 2, ..., n

i

)  

przy czym x

ij

 = 

μ

i

 + 



ij

,  

gdzie: 



ij

 

jest wartością zmiennej losowej nazywanej składnikiem losowym, 

mającej rozkład N(0, 



), 

Źródło zmienności 

Suma kwadratów 

Stopnie 

swobody 

Wariancja 

Test F 

między 

populacjami 

(grupami) 

k - 1 

wewnątrz grup 

(składnik losowy) 

n - k 

47 

Test analizy wariancji dla wielu średnich 

cd 

Formułowanie hipotez: 



należy zweryfikować hipotezę H

0

 : 

μ

1

 = 

μ

2

 =... = 

μ

k

. 



hipoteza alternatywna H

1

 

: nie wszystkie średnie badanych populacji  są  

równe 

Sposób postępowania: 



z wyników poszczególnych prób należy obliczyć średnie grupowe   
i średnią ogólną     : 
 



wypełnić tablicę analizy wariancji: 

i

x

x







i

n

j

ij

i

i

x

n

x

1

1









k

i

n

j

ij

i

x

n

x

1

1

1

 







k

i

i

i

n

x

x

1

2

 

2

2

2

1

ˆ

ˆ

s

s

F















k

i

n

j

i

ij

i

x

x

1

1

2

 

1

)

(

ˆ

1

2

2

1











k

n

x

x

s

k

i

i

i

k

n

x

x

s

k

i

n

j

i

ij

i













1

1

2

2

2

)

(

ˆ

2013-04-17 

10 

48 

Test analizy wariancji dla wielu średnich 

cd 

 

Sprawdzian 



obliczoną w tablicy wartość F należy porównać z wartością krytyczną F



 

odczytaną z tablic rozkładu F Snedecora dla ustalonego poziomu istotności 



 

i dla liczby stopni swobody k-1 i n-k, 

 

Wnioskowanie: 



jeżeli F ≥ F



 

to hipotezę H

0

 

należy odrzucić, 



jeżeli F < F



 brak podstaw do odrzucenia hipotezy H

0.

 

 

49 

Test analizy wariancji dla wielu średnich - przykład 



Koszt wytworzenia pewnego usługi transportowej trzema różnymi metodami 
ma rozkład normalny o jednakowej wariancji dla każdej z metod. Na 
poziomie istotności α=0,05 zweryfikować hipotezę, że średnie koszty 
materiałowe są jednakowe dla wszystkich metod produkcji usługi. 

Metoda 

n

i 

s

i

2 

n

i

*s

i

2 

1 

5 

20 

100 

50 

250 

55,56 

2 

6 

30 

180 

175 

1050 

266,67 

3 

7 

20 

140 

121,43 

850 

77,78 

suma 

18 

  

420 

  

2150 

400 

Średnia                                             

420/18=23,33 

Źródło zmienności 

Suma 

kwadratów 

Stopnie 

swobody 

Wariancja 

Test F 

między grupami 

400 

k-1=2 

200,0 

F

emp

=1,39 

wewnątrz grup 

2150 

n-k=15 

143,3 

F

α,2,15

=3,68 

F<F

α

 

stąd nie ma podstaw  do odrzucenia  hipotezy  Ho 

o równości  średnich  kosztów  produkcji  usługi 

i

x

i

i

x

n *

 

i

i

n

 

x

x

2



x