2013-05-14
1
Metody probabilistyczne
Weryfikacja hipotez statystycznych
Hipotezy nieparametryczne
Część 2
42
Test sumy rang Kruskala Wallisa
(rozwinięcie testu U Manna-Whitneya)
Jeden z wygodniejszych i dość precyzyjnych testów nieparametrycznych
dla wielu prób.
Zastępuje, w pewnym zakresie, test analizy wariancji dla średnich
(nie wymaga, aby populacje miały rozkład zbliżony do normalnego).
Model
– skala porządkowa 2 i więcej prób niezależnych
Założenia:
danych jest k
populacji generalnych o dowolnych rozkładach z ciągłymi
dystrybuantami F
1
(x), F
2
(x), ..., F
k
(x),
z każdej populacji wylosowano niezależnie n
i
elementów do próby
(i = 1, 2, ..., k),
Formułowanie hipotezy:
należy sprawdzić hipotezę, że wszystkie próby pochodzą z jednej
populacji; H
0
: F
1
(x) = F
2
(x)= ...= F
k
(x).
Sposób postępowania:
wszystkim wynikom prób należy nadać rangi od 1 do n,
dla każdej próby oddzielnie wyznacza się sumy rang R
i
,
2013-05-14
2
43
Test sumy rang Kruskala Wallisa
(rozwinięcie testu U Manna-Whitneya)
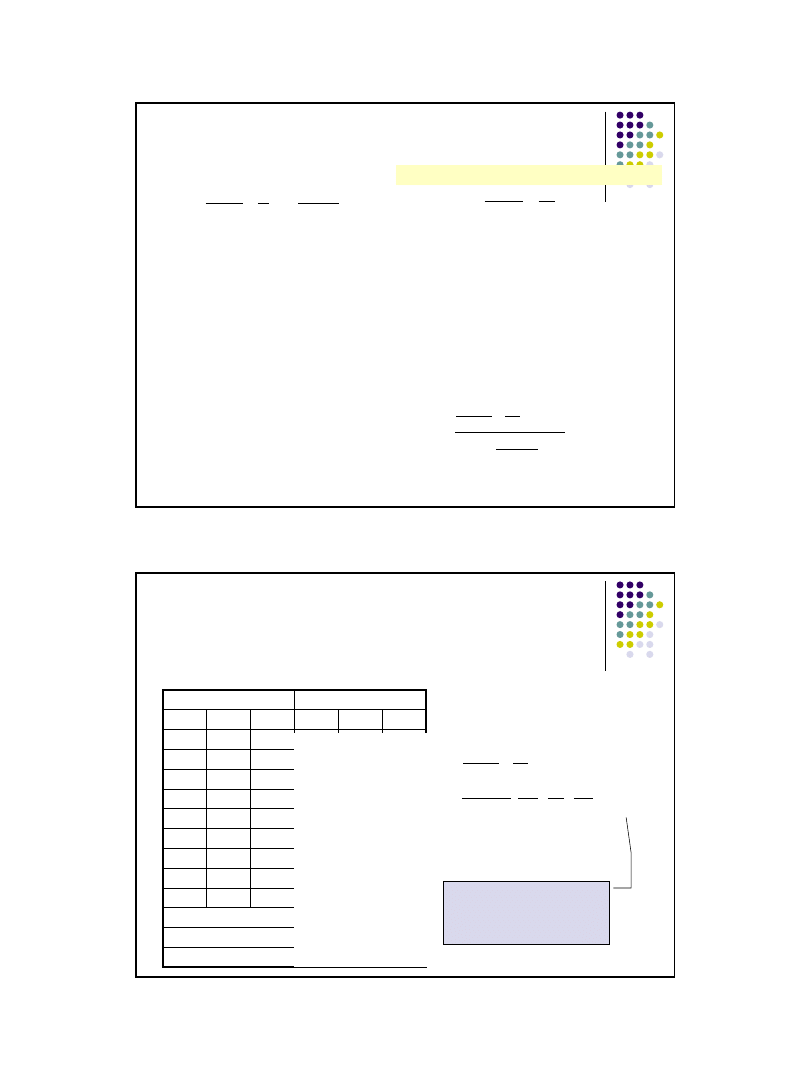
Sprawdzian
– wartość statystyki:
gdzie: - oczekiwana suma rang,
k
– liczba niezależnych prób,
R
i
– suma rang i-tej próby,
n
i
– liczebność i-tej próby
Wnioskowanie:
jeżeli hipoteza H
0
jest prawdziwa, to statystyka ta ma asymptotyczny rozkład
2
o k-1 stopniach swobody,
jeżeli zachodzi nierówność
2
≥
2
to hipotezę H
0
odrzucamy
– prawostronny obszar krytyczny
Jeżeli występują rangi wiązane:
gdzie: t
– liczba obiektów powiązanych daną rangą.
2
1
2
2
1
1
1
12
n
n
R
n
n
n
i
i
k
i
i
1
3
1
12
1
2
2
n
n
R
n
n
k
i
i
i
2
1 /
n
n
i
k
i
i
n
n
1
n
n
t
t
n
n
R
n
n
k
i
i
i
3
3
1
2
2
1
1
3
1
12
można sprowadzić do postaci prostszej:
44
Test sumy rang Kruskala Wallisa
– skala porządkowa
– 2 i więcej prób niezależnych - przykład
Na poziomie istotności =0,05 należy ocenić zgodność ocen funkcjonowania
transportu zbiorowego przez respondentów o różnym poziomie
wykształcenia.
Wykształcenie
Rangi łączone
P
Ś
W
P
Ś
W
54
17
13
20
4
3
33
10
60
11
1
22
42
47
37
15
17
13
63
26
36
24
7
12
40
12
61
14
2
23
49
22
28
18
6
9
50
43
56
19
16
21
33
27
10
8
19
5
Suma R
i
121
68
111
n
i
7
9
8
Suma R
i
2
/n
i
2091,6 513,78 1540.1
9
,
7
1
24
3
8
111
9
68
7
121
)
1
24
(
*
24
12
2
2
2
2
1
3
1
12
1
2
2
n
n
R
n
n
k
i
i
i
H
0
: oceny nie
różnią się istotnie
H
1
: oceny różnią się istotnie
χ
2
0,05,(3-1)
=5,991
Wniosek:
H
0
należy odrzucić.
Oceny różnią się istotnie
2013-05-14
3
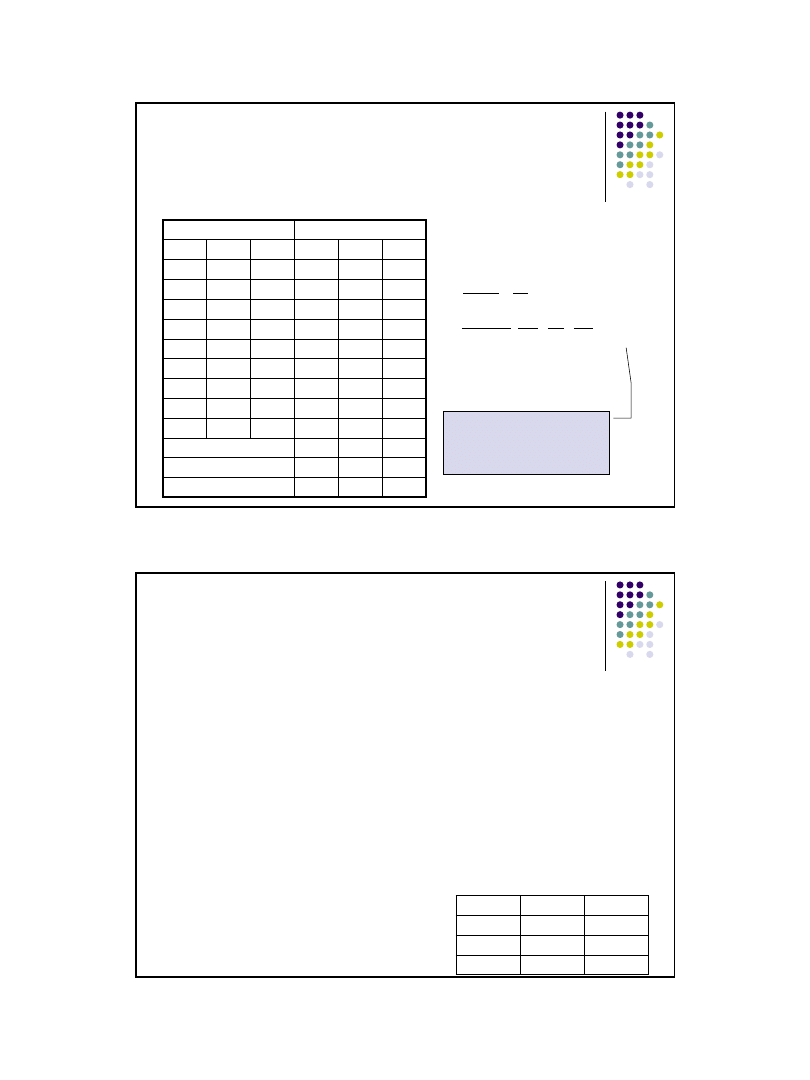
45
Test sumy rang Kruskala Wallisa
– skala porządkowa
– 2 i więcej prób niezależnych - przykład
Na poziomie istotności =0,05 należy ocenić zgodność ocen funkcjonowania
transportu zbiorowego przez respondentów o różnym poziomie
wykształcenia.
Wykształcenie
Rangi łączone
P
Ś
W
P
Ś
W
54
17
13
20
4
3
33
10
60
11
1
22
42
47
37
15
17
13
63
26
36
24
7
12
40
12
61
14
2
23
49
22
28
18
6
9
50
43
56
19
16
21
33
27
10
8
19
5
Suma R
i
121
68
111
n
i
7
9
8
Suma R
i
2
/n
i
2091,6 513,78 1540.1
9
,
7
1
24
3
8
111
9
68
7
121
)
1
24
(
*
24
12
2
2
2
2
1
3
1
12
1
2
2
n
n
R
n
n
k
i
i
i
H
0
: oceny nie
różnią się istotnie
H
1
: oceny różnią się istotnie
χ
2
0,05,(3-1)
=5,991
Wniosek:
H
0
należy odrzucić.
Oceny różnią się istotnie
46
Test mediany
Stosuje się dla sprawdzania hipotezy, że dwie (lub więcej) próby pochodzą z
jednej populacji, ale nie ma przyporządkowania wynikom jednej próby
wyników drugiej próby.
Model -
skala porządkowa - 2 i więcej prób niezależnych
Założenia:
dane są dwie populacje generalne o rozkładach z dowolnymi dystrybuantami
F
1
(x) i F
2
(x),
pobrano losowo dwie (trzy lub więcej) prób o liczebnościach n
1
i n
2
(n
3
… )
(liczebności stosunkowo duże),
Formułowanie hipotezy:
należy sprawdzić hipotezę, że obie próby pochodzą z jednej populacji;
H
0
: F
1
(x) = F
2
(x).
Sposób postępowania:
z wyników obu prób utworzyć jeden ciąg niemalejący, ustawiając wyniki w
kolejności rosnącej,
wyznaczyć medianę me,
pogrupować wyniki w tablicę:
Wyniki
> me
≤ me
Próba 1
Próba 2
Próba 3
2013-05-14
4
47
Test mediany -
skala porządkowa
– 2 i więcej prób niezależnych
Sprawdzian
– statystyka:
traktując tablicę wyników jak tablicę niezależności obliczyć wartość
statystyki
2
:
Wnioskowanie:
odczytać z tablic rozkładu
2
wartość krytyczną dla
2
dla (r-1)*(s-
1) stopni swobody i zadanego poziomu istotności
,
jeżeli zachodzi nierówność
2
>=
2
to hipotezę H
0
odrzucamy
– prawostronny obszar krytyczny
s
j
ij
ij
ij
r
i
n
n
n
1
'
2
'
1
2
48
Test mediany -
skala porządkowa
– 2 i więcej prób niezależnych - przykład
Zbadać na poziomie istotności α=0,05 zależność czasu przejazdu linii
w zależności od dnia tygodnia.
Rozkład liczebności w punkcie mediany M
e
= 10:
Wyniki
> me
≤ me
Razem
Roboczy
4
11
15
Sobota
7
7
14
Niedziela
10
1
11
Razem
21
19
40
556
,
10
225
,
5
40
11
19
1
...
125
,
7
40
15
19
11
875
,
7
40
15
21
4
2
2
1
2
'
2
'
1
2
s
j
ij
ij
ij
r
i
n
n
n
991
,
5
2
1
2
1
3
;
5
,
0
χ
2
> χ
α
2
Wniosek:
Hipotezę o niezależności czasu trwania kursu
od dnia tygodnia należy odrzucić
2013-05-14
5
49
Testy zgodności
Dwie próby zależne
Test McNemara,
Test znaków,
Test znaków rangowanych Wilcoxona,
50
Próby zależne
Charakteryzują się powtarzaniem pomiarów:
przed i po zastosowaniu jakiegoś środka reklamowego,
przed i po eksperymencie,
Opisują sytuacje, gdy opinie jednych grup zależą od innych.
Muszą być dokonywane na tych samych obiektach => próby są
jednakowo liczne,
2013-05-14
6
51
Test McNemara
Model
– 2 próby zależne – skala nominalna
Założenia:
dane są dwie populacje generalne o dowolnych rozkładach badanej cechy,
wylosowano dwie próby o licznościach odpowiednio n,
Formułowanie hipotezy:
H
0
: nie zanotowano zmiany przed i po eksperymencie,
Sposób postępowania:
zbudować tablicę 4-polową
obliczyć wartość statystyki χ
2
:
Wnioskowanie:
zbudować prawostronny obszar krytyczny testu tak, aby: P{χ
2
≥χ
α
2
}=α
dla stopni swobody s=(k-1)*(r-1)=1
jeżeli χ
2
≥ χ
α
2
, to hipotezę H
0
należy odrzucić,
jeżeli χ
2
<
χ
α
2
, brak podstaw do odrzucenia hipotezy H
0
.
przed
po
nie
A
B
tak
C
D
B
C
B
C
2
2
1
52
Test McNemara -
przykład
Zbadano opinie 100 pasażerów PKP. 20 osób deklarowało zakup nowego
produktu, po reklamie zainteresowanie wzrosło do 60 osób.
Na poziomie
istotności α=0,05 zweryfikować hipotezę, czy reklama wpłynęła na wzrost
zakupów.
Hipoteza: reklama nie ma wpływu na zakupy produktu.
Wniosek:
H
0
należy odrzucić. Reklama
wpłynęła istotnie na wzrost zakupów
s=(2-1)*(2-1)=1 - liczba stopni swobody
χ
2
0,05,1
=3,841
przed
po
nie
A
80
B
40
120
tak
C
20
D
60
80
100
100
200
02
,
6
40
20
1
40
20
1
2
2
2
B
C
B
C
2013-05-14
7
53
Test znaków
Służy do testowania hipotezy, że dwie próby pochodzą z jednej populacji.
Ograniczenie
– wyniki porównywanych dwu jednakowo licznych prób
stanowią pary odpowiadających sobie wzajemnie liczb.
Model
– skala porządkowa – 2 próby zależne
Założenia:
dane są dwie populacje generalne o ciągłych dystrybuantach,
wylosowano jednakową liczbę parami odpowiadających sobie n elementów,
Formułowanie hipotezy:
należy sprawdzić hipotezę, że obie próby pochodzą z tej samej populacji,
tzn. hipotezę H
0
: F
1
(x) = F
2
(x) wobec H
1
: F
1
(x
) ≠ F
2
(x).
Sposób postępowania:
należy zbadać znak różnicy par wyników w obu próbach i określić liczbę r
tych znaków, których jest mniej,
Wnioskowanie:
z tablic
rozkładu liczby znaków odczytać dla ustalonego poziomu istotności
i dla liczby par wyników n taką wartość r
, że P{ r ≤ r
α,n
}= α
– obszar krytyczny lewostronny,
jeżeli r ≤ r
α,n
, to hipotezę H
0
należy odrzucić.
54
Test znaków - przykład
Dla oceny wpływu szkolenia na technikę jazdy wylosowano 14 kierowców .
Wyniki przedstawiono w tablicy:
Na poziomie istotności α = 0,05 ocenić czy szkolenie miało wpływ na
technikę jazdy.
H
0
: technika jazdy przed i po szkoleniu nie uległa zmianie
Dane: n = 14, n
+
= 10, n
-
= 3 => r = 3,
r
0,05,14
= 2
r > r
α
Przed
50
20
25
80
50
70
70
25
70
65
80
10
60
50
Po
60
40
40
60
40
80
80
30
90
70
60
20
80
50
+
+
+
-
-
+
+
+
+
+
-
+
+
0
Wniosek
Nie ma podstaw do odrzucenia
hipotezy o jednakowej technice jazdy
przed i po szkoleniu.
2013-05-14
8
55
Test rangowanych znaków Wilcoxona
Istotą testu jest rangowanie – nadanie kolejnych numerów, według
rosnących wartości różnic dodatnich oraz ujemnych branych oddzielnie.
Model
– skala porządkowa – 2 próby zależne
Założenia:
dane są dwie populacje generalne o ciągłych dystrybuantach F
1
(x) i F
2
(x),
wylosowano jednakową liczbę n elementów do dwu prób, których wyniki
odpowiadają sobie parami,
Formułowanie hipotezy:
należy zweryfikować hipotezę, że obie próby pochodzą z tej samej
populacji, tzn. hipotezę H
0
: F
1
(x) = F
2
(x).
Sposób postępowania:
należy obliczyć różnice wyników obu prób dla wszystkich par wyników,
nadać wartościom bezwzględnym różnic numery poczynając od 1 dla
najmniejszej wartości,
zapisać rangi w dwóch grupach, oddzielnie dla różnic dodatnich oraz
ujemnych,
sumując rangi w obu grupach uzyskuje się sumę rang R+ dla różnic
dodatnich i sumę rang R- dla różnic ujemnych,
56
Test rangowanych znaków Wilcoxona
– skala porządkowa – 2 próby zależne
Sprawdzian - statystyka
znaleźć wartość statystyki R, jako mniejszą z tych dwu sum rang,
tzn: R = min{ R+ ; R- },
Wnioskowanie:
Obszar krytyczny lewostronny:
P{ R ≤ R
} =
α
Jeżeli R ≤ R
α
, to hipotezę H
0
należy odrzucić.
Jeżeli n>25 należy skorzystać z granicznego rozkładu normalnego N( μ
R
,σ
R
),
gdzie:
Statystyka:
4
1
n
n
R
24
1
2
1
n
n
n
R
R
R
R
U
2013-05-14
9
57
Test rangowanych znaków Wilcoxona
– skala porządkowa – 2 próby zależne - przykład
Na poziomie istotności α = 0,05 ocenić wpływ reklamy na sprzedaż nowego
produktu. W tabeli przedstawiono wyniki oceny 11 respondentów
przedstawiono w tabeli.
∑R+ = 26, ∑R- = 29 => min{R+, R-} = 26
Z tablic znaków rangowanych dla n=11 i α = 0,05 R
α
= 11
Przed
15
20
8
11
9
25
32
18
22
25
30
Σ
Po
18
15
12
15
16
22
26
20
20
20
30
znaki
+
-
+
+
+
-
-
+
-
-
wartość
3
-5
4
4
7
-3
-6
2
-2
-5
0
Rangi+
3,5
5,5
5,5
10
1,5
0
26
Rangi-
7,5
3,5
9
1,5
7,5
29
Wniosek
Nie ma podstaw do odrzucenia H
0
.
Reklama nie wpłynęła na wzrost sprzedaży.
58
Testy zgodności
Trzy i więcej prób zależnych
Test Q Cochrana,
Test ANOVA Friedmana z rangami,
2013-05-14
10
59
Test Q Cochrana
Uogólnienie testu McNemary.
Stosuje się dla sprawdzania hipotezy:
o postawach pod wpływem wielokrotnie powtarzanego bodźca, albo
dla dokonania dychotomicznego podziału zbiorowości respondentów
odpowiadających „tak” lub „nie” na kolejne pytania.
Zmienna dychotomiczna
przyjmuje wartości 1 lub 0.
Model - skala nominalna -
2 i więcej prób zależnych
Założenia:
wyniki obserwacji (odpowiedzi na kolejne pytania) zapisać w tablicy o liczbie
wierszy odpowiadającej liczbie przebadanych obiektów i liczbie kolumn
równej liczbie pomiarów zmiennej zależnej,
liczba wierszy powinna być duża.
Formułowanie hipotezy:
należy sprawdzić hipotezę, że próby pochodzą z jednej populacji;
H
0
: F
1
(x) = F
2
(x
) = … F
n
(x).
60
Test Q Cochrana - skala nominalna
– 2 i więcej prób zależnych
Statystyka:
gdzie: C
j
– liczba jedynek j-tej kolumnie,
C
sr
– średnia z C
j
,
R
i
– liczba jedynek w i-tym wierszu,
k
– liczba pomiarów zmiennej zależnej,
n
– liczba obiektów.
Wnioskowanie:
odczytać z tablic rozkładu
2
wartość krytyczną dla
α
2
dla (k-1) stopni
swobody i zadanego poziomu istotności
,
jeżeli zachodzi nierówność
2
≥
α
2
to hipotezę H
0
odrzucamy.
P{
2
≥
α
2
}=α - prawostronny obszar krytyczny.
n
i
i
n
i
i
k
j
k
j
j
j
n
n
i
i
k
j
sr
j
R
R
k
C
C
k
k
R
k
R
C
C
k
k
Q
1
2
1
1
2
1
2
1
1
2
1
1
2013-05-14
11
61
Test Q Cochrana - skala nominalna
– 2 i więcej prób zależnych - przykład
Zbadano wpływ reklamy na zmiany sprzedaży w 10 sklepach, na podstawie
3 pomiarów: przed, w trakcie i po akcji reklamowej.
Poziom istotności α = 0,05. Oznaczenia: 0 – spadek, 1 – wzrost sprzedaży.
H
0
: reklama nie wpłynęła na wielkość sprzedaży.
Lp.
przed
w czasie
po
Razem
R
i
2
1
0
1
1
2
4
2
0
1
1
2
4
3
0
0
1
1
1
4
1
1
1
3
9
5
0
1
1
2
4
6
0
1
1
2
4
7
0
1
1
2
4
8
0
1
1
2
4
9
1
1
1
3
9
10
0
0
1
1
1
∑
2
8
10
20
44
C
j
2
4
64
100
168
α = 0,05,
k=3,
χ
α
2
= 5,991
n
i
i
n
i
i
k
j
k
j
j
j
R
R
k
C
C
k
k
Q
1
2
1
1
2
1
2
1
13
16
208
44
20
3
20
168
3
1
3
2
Q
Wniosek:
H
0
należy odrzucić.
Reklama istotnie wpłynęła na
zmiany w wielkości sprzedaży
62
Test ANOVA Friedmana z rangami
Rozwinięcie testu Wilcoxona. Jest on nieparametryczną alternatywą analizy
wariancji dla klasyfikacji pojedynczej z powtarzanymi pomiarami zmiennej
zależnej.
Służy do sprawdzania hipotezy, czy k≥2 prób losowych zależnych pochodzi
z jednej populacji.
Rozkład populacji może być dowolny, ale ciągły.
Model -
skala porządkowa – 2 i więcej prób zależnych
Założenia:
wyniki obserwacji (odpowiedzi na kolejne pytania) zapisać w tablicy o liczbie
wierszy odpowiadającej liczbie przebadanych obiektów i liczbie kolumn
równej liczbie pomiarów zmiennej zależnej.
Formułowanie hipotezy:
należy sprawdzić hipotezę, że wszystkie próby pochodzą z jednej populacji;
H
0
: F
1
(x) = F
2
(x
) = … = F
k
(x).
2013-05-14
12
63
Test ANOVA Friedmana z rangami-
skala porządkowa
– 2 i więcej prób zależnych
Statystyka:
gdzie: R
j
– suma rang dla j-tego pomiaru,
n
– liczba porównywanych elementów,
k
– liczba pomiarów,
Wnioskowanie:
odczytać z tablic rozkładu
2
wartość krytyczną dla
α
2
dla (k-1) stopni swobody
i zadanego poziomu istotności
,
jeżeli zachodzi nierówność
2
>=
α
2
to hipotezę H
0
odrzucamy,
jeżeli zachodzi nierówność
2
<
α
2
to nie ma podstaw do odrzucenia hipotezy,
że k prób (k≥2) losowych pochodzi z jednej populacji.
Jeżeli występują rangi wiązane:
gdzie:
– t
j
-
liczba rang w każdej grupie rang powiązanych dla i-tego wiersza.
1
3
1
12
1
2
2
k
n
R
k
k
n
k
j
j
1
1
1
3
1
12
2
1
1
2
2
k
nk
T
k
n
R
k
nk
r
i
i
k
j
j
i
i
i
t
t
T
3
64
Test ANOVA Friedmana z rangami-
skala porządkowa
– 2 i więcej prób zależnych
Na czterech automatach produkowano uszczelki. W sposób losowy wybrano dni
tygodnia i w pewnym miesiącu ustalono liczbę uszczelek wadliwych z każdego
automatu. Zweryfikować hipotezę, że automaty istotnie różnią się ze wzgl.na liczbę
produkowanych wadliwych uszczelek.
j
Automat
Rangi
i
1 2 3 4
1
2
3
4
1 5 3 4 5
3,5
1
2
3,5
2 4 7 5 5
1
4
2,5
2,5
3 6 5 3 7
3
2
1
4
4 6 6 6 7
2
2
2
4
5 9 9 5 6
3,5
3,5
1
2
6 7 8 6 8
2
3,5
1
3,5
R
j
15
16
9,5
19,5
R
j
2
225 256 90,25 380,25 951,5
n=6, k=4,
α=0,05 χ
,k-1
2
=7,815
1
1
1
3
1
12
2
1
1
2
2
k
nk
T
k
n
R
k
nk
r
i
i
k
j
j
i
1
2
4
5
6
t
i
2
2
3
2
2
T
i
6
6
24
6
6
48
942
,
5
1
4
4
6
48
1
1
4
6
3
5
,
951
1
4
4
6
12
2
2
Wniosek:
Nie ma podstaw do odrzucenia H
0
Automaty nie odbiegają istotnie od
siebie w produkcji wadliwych
uszczelek.
Rangi dla każdego pomiaru
i
i
i
t
t
T
3
2013-05-14
13
65
Test ANOVA Friedmana z rangami-
skala porządkowa
– 2 i więcej prób zależnych
Na czterech automatach produkowano uszczelki. W sposób losowy wybrano dni
tygodnia i w pewnym miesiącu ustalono liczbę uszczelek wadliwych z każdego
automatu. Zweryfikować hipotezę, że automaty istotnie różnią się ze wzgl.na liczbę
produkowanych wadliwych uszczelek.
j
Automat
Rangi
i
1 2 3 4
1
2
3
4
1 5 3 4 5
3,5
1
2
3,5
2 4 7 5 5
1
4
2,5
2,5
3 6 5 3 7
3
2
1
4
4 6 6 6 7
2
2
2
4
5 9 9 5 6
3,5
3,5
1
2
6 7 8 6 8
2
3,5
1
3,5
R
j
15
16
9,5
19,5
R
j
2
225 256 90,25 380,25 951,5
n=6, k=4,
α=0,05 χ
,k-1
2
=7,815
1
1
1
3
1
12
2
1
1
2
2
k
nk
T
k
n
R
k
nk
r
i
i
k
j
j
i
1
2
4
5
6
t
i
2
2
3
2
2
T
i
6
6
24
6
6
48
942
,
5
1
4
4
6
48
1
1
4
6
3
5
,
951
1
4
4
6
12
2
2
Wniosek:
Nie ma podstaw do odrzucenia H
0
Automaty nie odbiegają istotnie od
siebie w produkcji wadliwych
uszczelek.
Wyszukiwarka
Podobne podstrony:
MP 8 hipot nieparam 1
MP 7 hipot param 1
MP 7 hipot parametryczne 2
MP W 06N
MP W 04N
R 4 2b mp
MP W 07N dodatek
testy nieparametryczne
R 4 1 mp
MP 6
MP 5
więcej podobnych podstron