2013-04-28

1

Metody probabilistyczne

Weryfikacja hipotez statystycznych

Hipotezy nieparametryczne

2

Testy nieparametryczne

Warunki konieczne do spełnienia w odniesieniu do wszystkich ww.

testów:



liczebność próby duża w porównaniu z liczebnością populacji generalnej
N,



próba powinna być próbą prostą (losowanie niezależne),



dopuszczalna wielkość błędu I-rodzaju (poziom istotności α) jest
najczęściej równa 0,05 lub 0,01.

Sprawdzana jest hipoteza

H

0

dotycząca rozkładu badanej cechy

w populacji generalnej, która nie określa wartości parametrów tego

rozkładu.

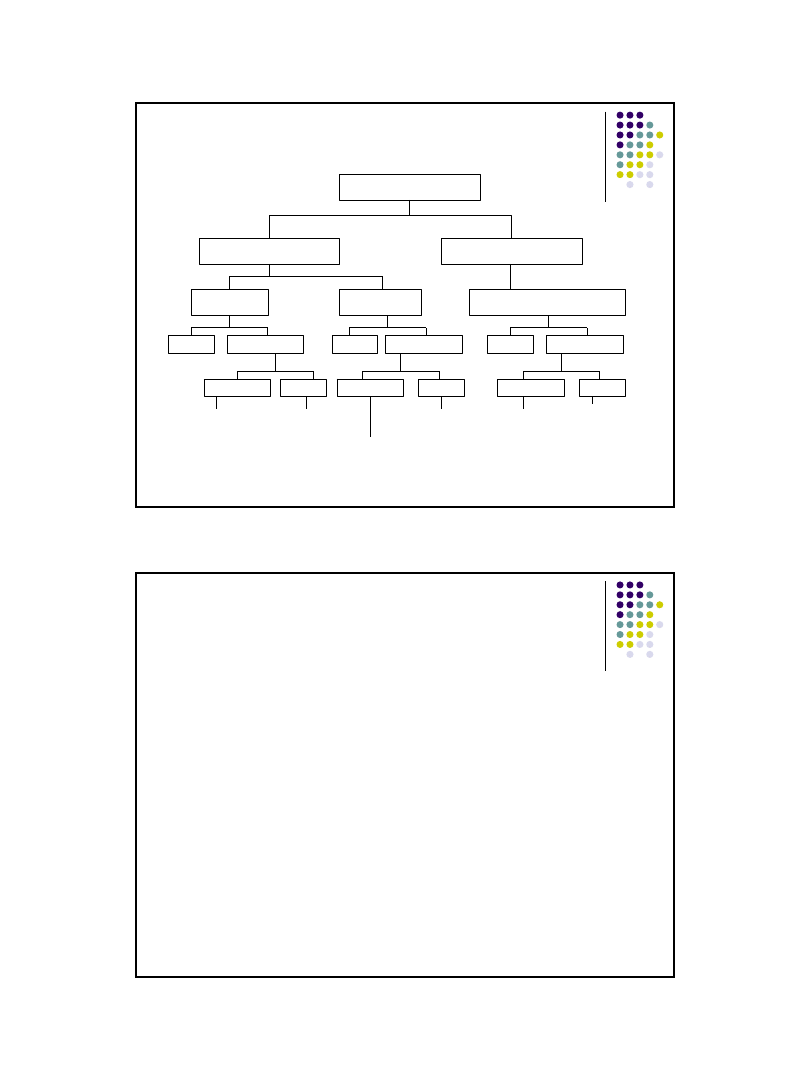
Podział testów nieparametrycznych

Testy zgodności

Testy losowości

próby

Testy niezależności

2013-04-28

2

3

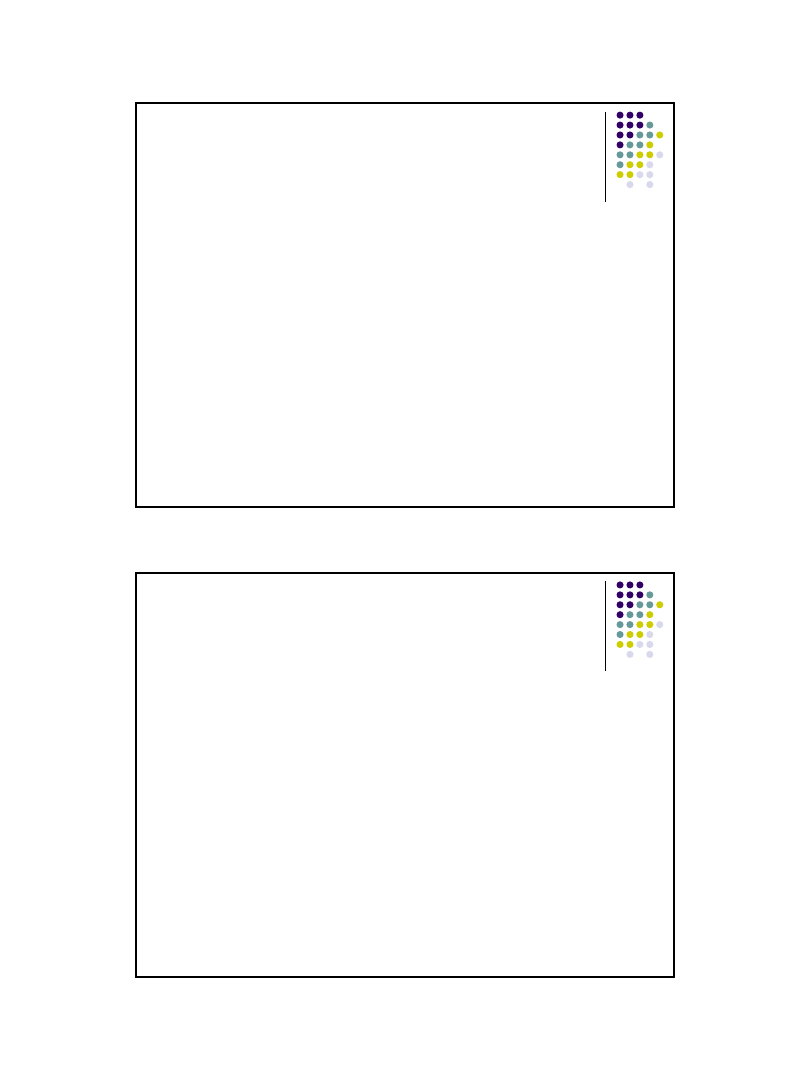
Testy statystyczne

(nieparametryczne i parametryczne)

Testy statystyczne

nieparametryczne

parametryczne

nominalna

porządkowa

przedziałowa i ilorazowa

skale

niezależności
chi

2

-McNemara
-QCochrana

-serii Walda-Wolfowitza
-U Manna-Whitneya
-Smirnowa-Kołmogorowa
-Kruskala Wallisa
-mediany

-znaków
-Wilcoxona
-Friedmana

-test z
-test t
-test F

-test t

jedna

jedna

jedna

dwie i

wiêcej

dwie i

wiêcej

dwie i wiêcej

niezależne

zależne

niezależne

niezależne

zależne

zależne

zmienne

test zgodności
chi

2

-Kołmogorowa
-serii

-test z
-test t

4

Testy zgodności

Testy zgodności – testy weryfikujące hipotezy dotyczące postaci

rozkładu populacji generalnej

H

0

: f(x)=f

0

(x) H

1

: f(x)≠ f

0

(x) H

0

: F(x)=F

0

(x) H

1

: F(x)≠ F

0

(x)

Przykłady testów zgodności:



Test

χ

2

Pearsona -

test dla jednej populacji zmiennej ciągłej lub

dyskretnej,



Test

λ Kołmogorowa test dla jednej populacji zmiennej ciągłej,



Test Shapiro

– Wilka - test dla jednej populacji; weryfikuje hipotezę, że

rozkład jest normalny,



Test

Kołmogorowa-Lillieforsa - test dla jednej populacji; weryfikuje

hipotezę, że rozkład jest normalny,



Test Kołmogorowa - Smirnowa – testuje hipotezy o jednakowym
rozkładzie dwóch populacji,

2013-04-28

3

5

Testy zgodności

Pojedyncza próba

6

Test zgodności



2

Dotyczy rozkładów ciągłych i dyskretnych,



Polega na porównaniu liczebności teoretycznej i empirycznej
ustalonych przedziałów klasowych.



Gdy rozbieżność między liczebnościami jest zbyt duża,
hipoteza, że populacja ma dany rozkład teoretyczny, musi zostać
odrzucona.



Ograniczenie

– duża liczebność próby



n

co najmniej kilkadziesiąt;



co

najmniej 8 wyników próby w każdym przedziale klasowym.



Statystyka

używana do weryfikacji hipotezy ma rozkład asymptotyczny



2

.

2013-04-28

4

7

Test zgodności



2

Model
Założenia:



populacja generalna ma dowolny rozkład o dystrybuancie należącej do
pewnego zbioru



rozkładów o określonym typie postaci funkcyjnej

dystrybuanty,



wylosowano niezależnie dużą próbę, której wyniki podzielono na k

rozłącznych klas o liczebności n

i

w każdej klasie ,

Formułowanie hipotezy:



należy sprawdzić, że populacja generalna ma rozkład typu



, tzn.



H

0

: F(x)





.



H

1

: F(x)



/



.

Sposób postępowania:



obliczyć dla każdej z k klas wartości badanej cechy X prawdopodobieństwo
(teoretyczne) p

i

, że zmienna losowa X o rozkładzie



przyjmie wartości

należące do klasy o numerze i (i = 1, 2, ..., k),



obliczyć liczność teoretyczną np

i

,





i

n

n

8

Test zgodności



2

Sprawdzian -

wartość statystyki:



która ma przy założeniu prawdziwości hipotezy H

0

asymptotyczny rozkład



2



o k-1 stopniach swobody lub



o k-r-1

stopniach swobody, jeżeli z próby oszacowano r parametrów

rozkładu,

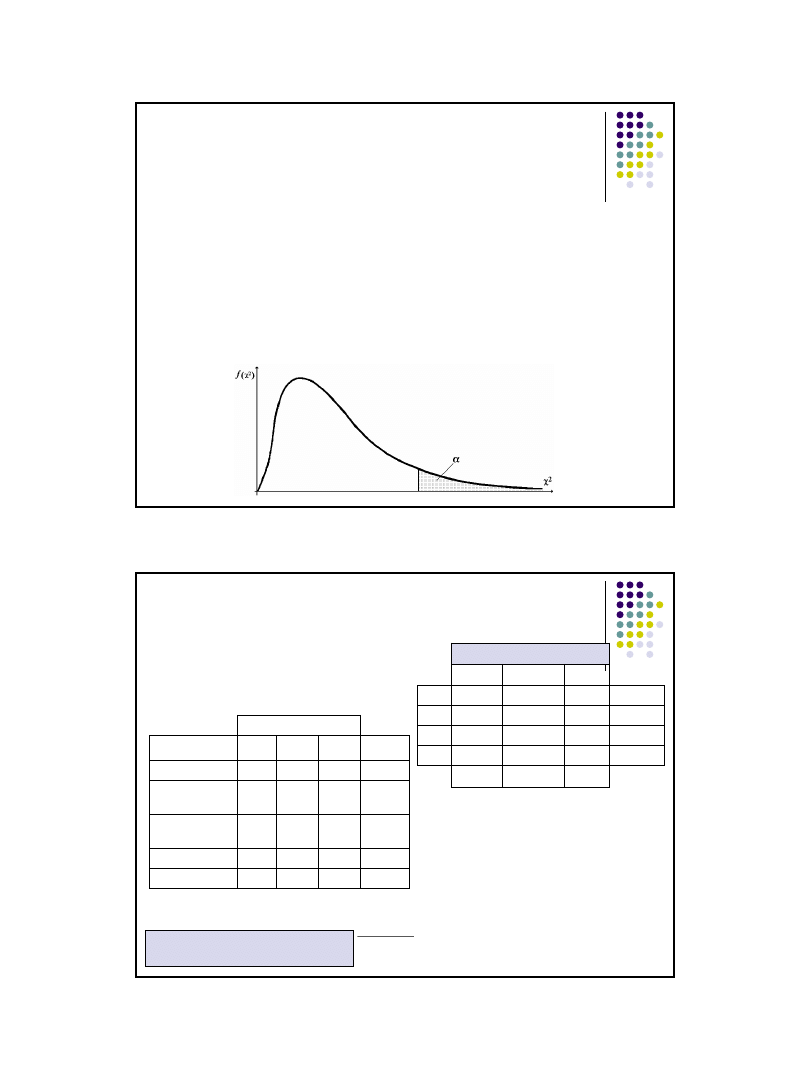
Wnioskowanie:



odczytać wartość krytyczną testu dla poziomu istotności



tak, aby

zachodziło:



Formułowanie wniosków:

jeżeli χ

2

≥ χ

α

2

, to hipotezę H

0

należy odrzucić na korzyść H

1

,

jeżeli χ

2

< χ

α

2

, brak podstaw do odrzucenia hipotezę H

0













k

i

i

i

i

np

np

n

1

2

2



















2

2

P

2013-04-28

5

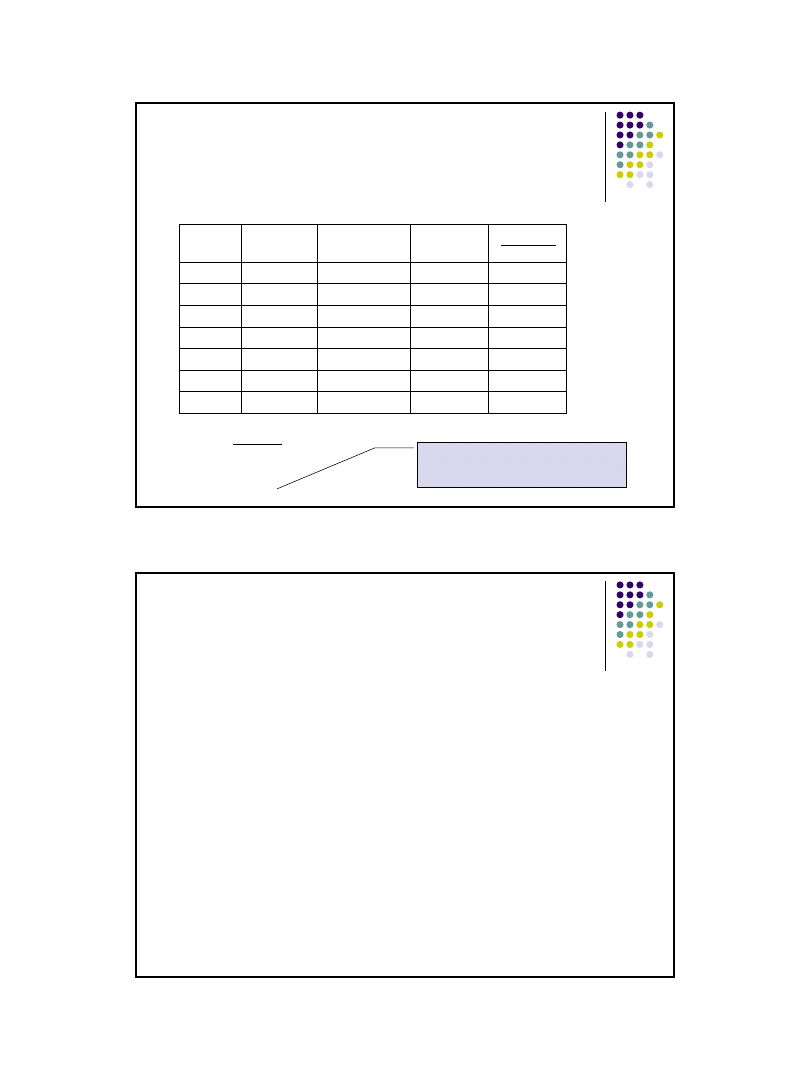
Wyniki
rzutów

n

i

p

i

n*p

i

1

42

0,167

33,3

2,253

2

41

0,167

33,3

1,763

3

27

0,167

33,3

1,203

4

25

0,167

33,3

2,083

5

41

0,167

33,3

1,763

6

24

0,167

33,3

2,613

suma

200

1

200

11,680

9

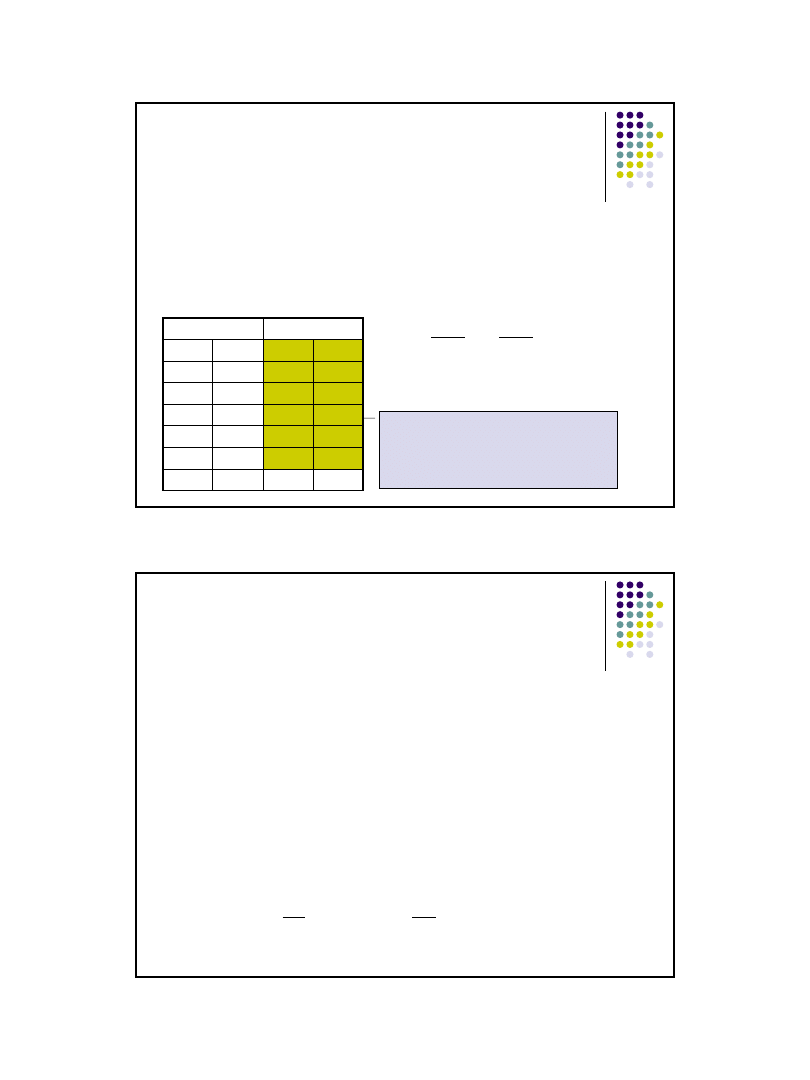
Test zgodności



2

-

przykład



Należy sprawdzić czy kostka do gry jest prawidłowo wyważona.
Dla zweryfikowania hipotezy należy przyjąć poziom istotności α=0,05.
W tym celu rzucono kostką 200 razy uzyskując wyniki:

i

i

i

p

n

p

n

n







2

)

(





68

,

11

1

2

2











k

i

i

i

i

np

np

n



χ

2

α,k-1

= 11,07

Wniosek:
Hipotezę H

0

należy odrzucić

10

Test zgodności



Kołmogorowa



Polega na porównaniu dystrybuanty empirycznej i teoretycznej.



Jeżeli populacja generalna ma rozkład zgodny z hipotezą, to wartości
dystrybuanty powinny być we wszystkich badanych punktach zbliżone.



Największa różnica między dwoma dystrybuantami służy do zbudowania
statystyki



, której rozkład (niezależny od postaci dystrybuanty

hipotetycznej) podał Kołmogorow.



Ograniczenia:



dystrybuanta hipotetyczna musi być ciągła,



parametry rozkładu hipotetycznego powinny być znane
(

jeżeli próba jest duża to dopuszcza się oszacowanie parametrów

z próby),



podział na klasy szeregu rozdzielczego przedziałowego o wąskich
przedziałach lub o jednakowej liczebności w klasach.

2013-04-28

6

11

Test zgodności



Kołmogorowa

Model
Założenia:



populacja generalna ma rozkład ciągły o dystrybuancie F(x),



z populacji wylosowano niezależnie do próby n elementów (co najmniej
kilkadziesiąt)

Formułowanie hipotezy:



należy zweryfikować hipotezę H

0

: F(x) = F

0

(x), H

1

: F(x

) ≠ F

0

(x),

gdzie F

0

(x

) jest konkretną, hipotetyczną i ciągłą dystrybuantą.

Sposób postępowania:



wyniki próby należy uporządkować w kolejności rosnącej lub pogrupować w
stosunkowo wąskie przedziały o prawych końcach x

j

i odpowiadających im liczebnościach n

j

,



dla każdego x

j

wyznaczyć wartość dystrybuanty empirycznej F

n

(x):

gdzie n

sk

– skumulowana od początku aż do x

k

liczebność:



dla każdego x

j

wyznaczyć wartość teoretycznej dystrybuanty F(x),



obliczyć dla każdego x

j

bezwzględną wartość różnicy |F

n

(x) - F(x)|,

 

n

n

x

F

sk

k

n









k

j

j

sk

n

n

12

Test zgodności



Kołmogorowa

Sprawdzian -

wartość statystyki:



oraz



która ma rozkład λ Kołmogorowa

Obszar krytyczny:



jeżeli n≤100 wartość krytyczną należy odczytać z tablic wartości D

n

(

α),



jeżeli n>100 dla ustalonego poziomu istotności



wartość krytyczną





można

odczytać z tablic granicznego rozkładu Kołmogorowa



i porównać w wartością empiryczną



,

Wnioskowanie:



jeżeli zachodzi nierówność λ ≥ λα, to hipotezę H

0

należy odrzucić,

jeżeli zachodzi nierówność λ < λα, brak podstaw do odrzucenia hipotezy H

0.

   

x

F

x

F

D

n

x





sup

n

D





2013-04-28

7

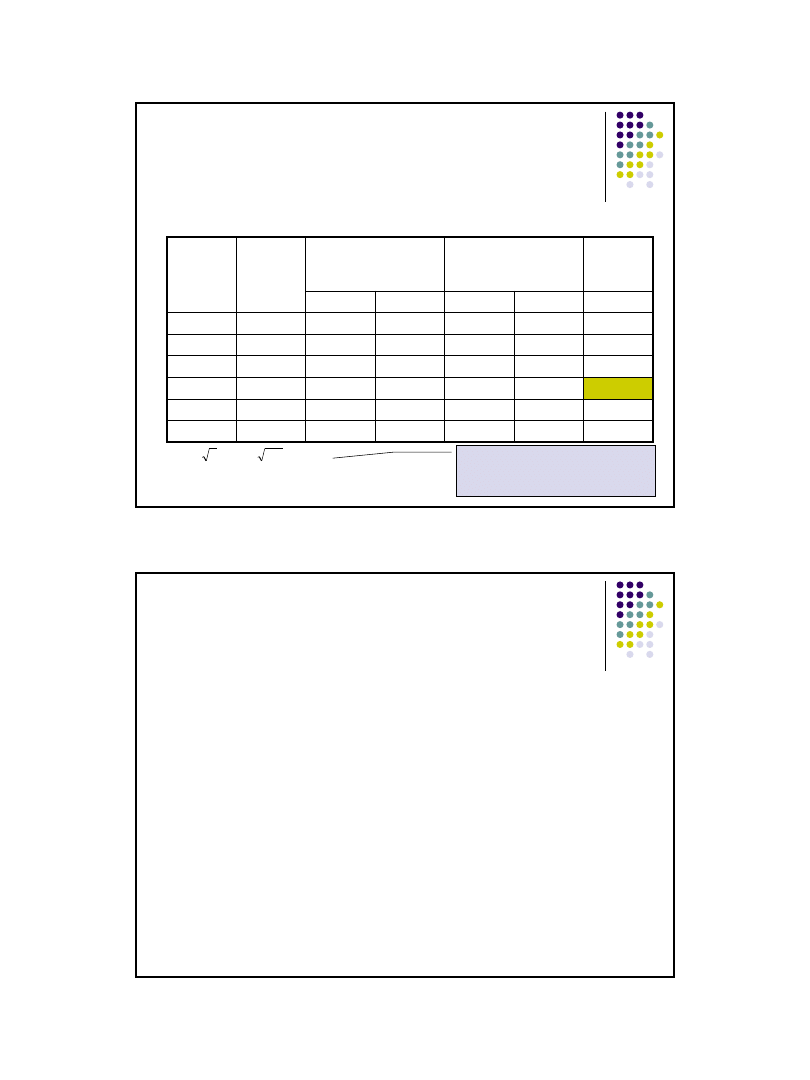
13

Test zgodności



Kołmogorowa - przykład



Dokonano ocen rangowych (w skali 1-

5) nowego produktu wśród 100

respondentów. Należy na poziomie istotności α=0,05 zweryfikować
hipotezę, że rozkład ocen wg przypisanych rang jest rozkładem
równomiernym.

Ranga

Liczba

respon-
dentów

Proporcje -

prawdopodobieństwa

Proporcje

skumulowane -

dystrybuanta

Różnice

Empirycz.

Teoret.

Empirycz.

Teoret.

|E-T|

1

12

0,12

0,20

0,12

0,20

0,08

2

24

0,24

0,20

0,36

0,40

0,04

3

32

0,32

0,20

0,68

0,60

0,08

4

24

0,24

0,20

0,92

0,80

0,12

5

8

0,08

0,20

1

1

0,00

Suma

100

1

1

2

,

1

100

*

12

,

0







n

D



Z tablic wartości krytycznych D

n

(

α)=0,134

Wniosek:
Nie ma podstaw do odrzucenia
hipotezy H

0

628

,

1

99

,

0





358

,

1

95

,

0





224

,

1

90

,

0





18

Testy zgodności

Dwie próby niezależne



Test serii,



Test serii Walda-

Wolfowitz’a,



Test U Manna-

Whitney’a,



Test Smirnowa-

Kołmogorowa

2013-04-28

8

19

Testy serii



Testy serii

służą do weryfikacji hipotezy:



o identyczności rozkładów

badanej cechy z dwóch lub

kilku populacji tzn, że dwie populacje mają ten sam rozkład
(dwie próby pochodzą z jednej populacji),



o losowości

(niezależności) próby,



Serią nazywa się każdy podciąg złożony z kolejnych
elementów jednego rodzaju utworzony w ciągu
uporządkowanych w dowolny sposób elementów dwu
rodzajów.



Gdy elementy danego ciągu są losowe, wtedy zarówno
długość serii jak i liczba serii utworzona w danym ciągu
jest losowa

20

Test serii

Model 1 -

Założenia:



dana jest populacja generalna o dowolnym rozkładzie,



pobrano próbę n elementową,

Formułowanie hipotezy:



należy sprawdzić hipotezę, że jest to próba losowa.

Sposób postępowania:



z uporządkowanego według kolejności pobierania elementów do próby

ciągu wyników próby obliczyć medianę me z próby,



każdemu wynikowi próby x

i

w tym uporządkowanym chronologicznie ciągu

należy przypisać symbol:



a

jeżeli x

i

< me



b

jeżeli x

i

> me



wynik x

i

= me

można odrzucić.



obliczyć w otrzymanym w ten sposób ciągu (np. aaabbaaab) liczbę serii k



przy założeniu losowości próby, liczba serii k ma znany i stablicowany

rozkład zależny tylko od n

1

i n

2

liczebności elementów a i b,

Wnioskowanie:



w oparciu o rozkład buduje się dwustronny obszar krytyczny dla testu dla

przyjętego poziomu istotności



tak, żeby zachodziły relacje:

P{ k ≤ k

1

} =

α/2 i P{ k ≤ k

2

} = 1 -

α/2



jeżeli k ≤ k

1

lub k ≥ k

2

, to hipotezę o losowości próby należy odrzucić

2013-04-28

9

21

Test serii

– losowość - przykład



Zbadano liczbę pasażerów w autobusach kolejno podjeżdżających na
przystanek. Na poziomie istotności α=0,1 zweryfikować hipotezę, że liczba
pasażerów jest liczbą losową.



Wyniki próby – liczba pasażerów:
48 46 20 18 51 47 29 40 35 12 10 => n=11



Hipoteza: próba jest losowa,



10 12 18 20 29 35 40 46 47 48 51 => Me = 35



k

emp

= 6,

α=0,1



k

1,

α/2

= 3, k

2,1-

α/2

= 8, -

dwustronny

obszar krytyczny



k

1

=3 ≤ k

emp

=6 ≤ k

2

=8

b b a a b b a b a a

Wniosek:

Nie ma podstaw do odrzucenia

hipotezy o losowości liczby

pasażerów w autobusach

22

Test serii

– identyczność rozkładów

Model

– 2 próby niezależne – skala nominalna

Założenia:



dane są dwie populacje generalne o dowolnych rozkładach badanej cechy,



wylosowano dwie próby o licznościach odpowiednio n

1

i n

2

,



stosowany dla zmiennych dychotomicznych

takich jak płeć (kobieta,

mężczyzna), decyzja (tak, nie), wybór (albo, albo)



Zmienna dychotomiczna

przyjmuje wartości 1 lub 0.

Formułowanie hipotezy:



należy zweryfikować hipotezę, że rozkłady obu populacji nie różnią się.



H

0

: F

1

(x) = F

2

(x) wobec H

1

: F

1

(x) ≠ F

2

(x)

Sposób postępowania:



uzyskane wyniki ustawić w jeden ciąg według kolejności pojawiania się,



oznaczyć elementy wg wartości zmiennej dychotomicznej za pomocą
symboli a

, a drugiej wartości za pomocą b,



odczytać liczbę serii k,

Wnioskowanie:



zbudować obustronny obszar krytyczny testu tak, aby:



P{k

1

≤k}=α/2 i P{k≤k

2

}=1-α/2



jeżeli k≤k

1

lub k≥k

2

, to hipotezę H

0

należy odrzucić.

2013-04-28

10

23

Test serii

– identyczność rozkładów - przykład



16 pasażerów przychodzących na przystanek to 10 kobiet i 6 mężczyzn.
Pojawiali się oni w następującej kolejności:
K K K M M K K K K M K M M M K K



Na poziomie istotności α=0,05 zweryfikować hipotezę, że kolejność
przychodzenia kobiet i mężczyzn jest przypadkowa.



Hipoteza: kobiety i mężczyźni przychodzą na przystanek przypadkowo,



Liczba serii k

emp

= 7, liczba elementów n=16, n

k

=10, n

m

=6,

α=0,05



k

1,

α/2

= 4, k

2,1-

α/2

= 11



k

1

=4 ≤ k

emp

=7 ≤ k

2

=11

Wniosek:
Nie ma podstaw do odrzucenia hipotezy,
że kolejność przychodzenia na
przystanek mężczyzn jest inna niż kobiet

24

Test serii

– identyczność rozkładów

– test Walda-Wolfowitza

Model

– 2 próby niezależne – skala porządkowa

2 szeregi ocen rangowych dokonanych przez dwie niezależne grupy

Założenia:



dane są dwie populacje generalne o dowolnych rozkładach badanej cechy,



wylosowano dwie próby o licznościach odpowiednio n

1

i n

2

,

Formułowanie hipotezy:



należy zweryfikować hipotezę, że rozkłady obu populacji nie różnią się.



H

0

: F

1

(x) = F

2

(x) wobec H

1

: F

1

(x) ≠ F

2

(x)

Sposób postępowania:



wyniki obu prób ustawić w jeden ciąg według rosnących wartości,



oznaczyć elementy jednej próby za pomocą symboli a, a drugiej próby za pomocą b,



odczytać liczbę serii k,

Wnioskowanie (próba mała):



zbudować obustronny obszar krytyczny testu tak, aby:
P{k

1

≤k}=α/2 i P{k≤k

2

}=1-α/2



jeżeli k≤k

1

lub k≥k

2

, to hipotezę H

0

należy odrzucić.

2013-04-28

11

25

Test serii

– identyczność rozkładów

– test Walda-Wolfowitza

Wnioskowanie -

dla większych prób



Rozkład r jest w przybliżeniu rozkładem normalnym o średniej:



I odchyleniu standardowym



Wykorzystuje się statystykę U:



Wnioskowanie stosowane również w hipotezach o losowości rozkładu



Uwaga: wykorzystuje się jedynie liczebności, a nie wartości
poszczególnych cech.

1

2

2

1

2

1









n

n

n

n

r









 



1

*

2

*

2

2

1

2

2

1

2

1

2

1

2

1













n

n

n

n

n

n

n

n

n

n

r



r

r

r

U









26

Test serii

– identyczność rozkładów – przykład

– test Walda-Wolfowitza



Pasażerowie dokonywali ocen funkcjonowania transportu zbiorowego w
mieście. Oceny mężczyzn:

50, 51, 37

,

Oceny kobiet:

44, 32, 44, 29, 55, 52, 44, 55, 61



Hipoteza: między ocenami mężczyzn i kobiet nie ma różnic, czyli obie próby
pochodzą z tej samej populacji



Na poziomie istotności α=0,05 zweryfikować hipotezę, że oceny kobiet i
mężczyzn nie różnią się,



Ciąg rosnący:

29 32

37

44 44 44

50 51

52 55 55 61



Liczba serii k

emp

= 5, liczba elementów n=12, n

k

=9, n

m

=3,

α=0,05



k

1,

α/2

= 2, k

2,1-

α/2

= 7,



k

1

=2 ≤ k

emp

=5 ≤ k

2

=7

Wniosek:

Nie ma podstaw do odrzucenia

hipotezy, że oceny kobiet

i mężczyzn nie różnią się istotnie.

2013-04-28

12

27

Test serii

– identyczność rozkładów

– test U Manna-Whitneya

Model

– 2 próby niezależne – skala porządkowa, gdy występują takie

same oceny między różnymi respondentami

2 szeregi ocen rangowych dokonanych przez dwie niezależne grupy

Założenia:



dane są dwie populacje generalne o dowolnych rozkładach badanej cechy,



wylosowano dwie próby o licznościach odpowiednio n

1

i n

2

,

Formułowanie hipotezy:



należy zweryfikować hipotezę, że rozkłady obu populacji nie różnią się.

Sposób postępowania:



przypisać uszeregowanym wg wartości ocenom respondentów rangi



zsumować rangi dla poszczególnych grup,



obliczyć wartość U:

gdzie: s

– suma mniejsza,

n

– liczebność próby, dla której suma jest mniejsza

Wnioskowanie:



zbudować obustronny obszar krytyczny testu tak, aby: P{U≤U

1

}=α

U

1

– tabela wartości krytycznych testu U Manna-Whitneya, U

2

= n

1

*n

2

– U

1



jeżeli U≤U

1

lub U≥U

2

, to hipotezę H

0

należy odrzucić.





2

1







n

n

s

U

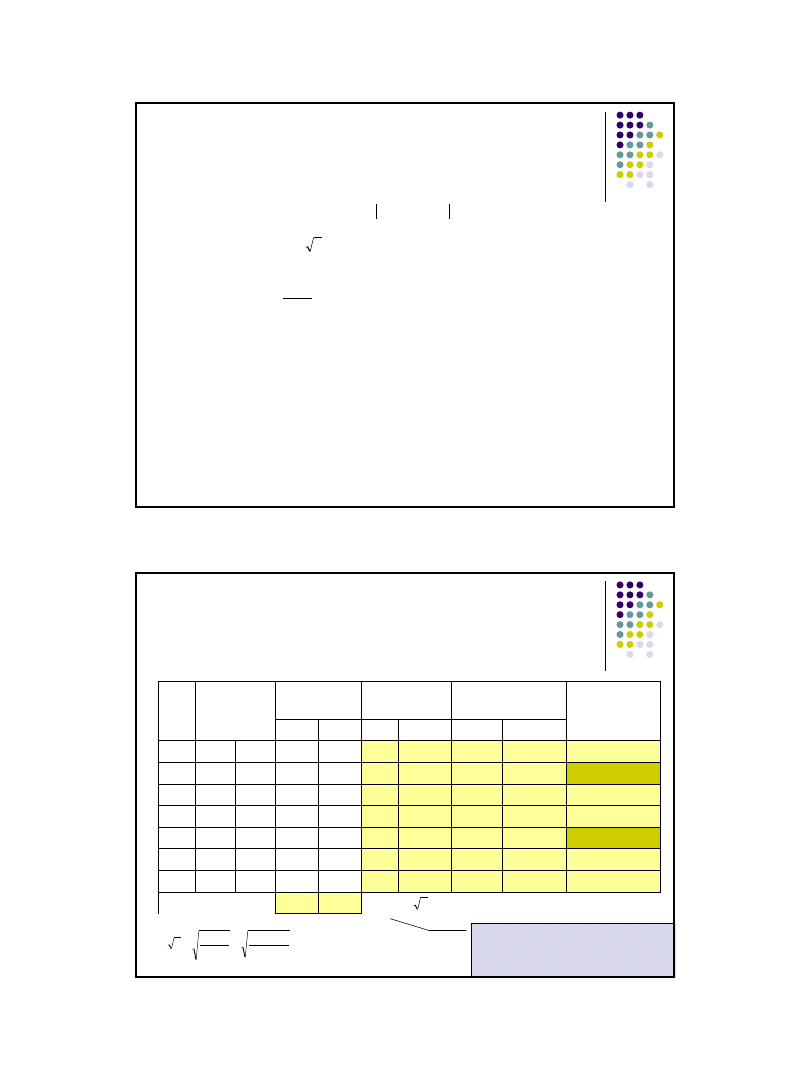
28

Test serii

– identyczność rozkładów

– test U Manna-Whitneya

Wnioskowanie -

dla większych prób



Rozkład U jest w przybliżeniu rozkładem normalnym o średniej:



I odchyleniu standardowym



Wykorzystuje się statystykę Z:



Uwaga: wykorzystuje się jedynie liczebności, a nie wartości
poszczególnych cech.

2

2

1

n

n

U











12

1

*

2

1

2

1







n

n

n

n

U



U

U

U

Z









2013-04-28

13

29

Test serii

– identyczność rozkładów

– test U Manna-Whitneya - przykład



Mieszkańcy dokonywali ocen funkcjonowanie wypożyczalni rowerów w

mieście. Oceny mężczyzn:

25, 18, 28, 30, 33

,

Oceny kobiet:

27, 15, 25, 30, 25, 18,

Na poziomie istotności α=0,05

zweryfikować hipotezę H

o

, że oceny kobiet i mężczyzn nie różnią się,



Hipoteza H

o

: między ocenami mężczyzn i kobiet nie ma różnic, czyli obie

próby pochodzą z tej samej populacji.



Uporządkowane oceny:

15 18

18 25

25 25 27

28 30

30

33

1 2 3 4 5 6 7 8 9 10 11

Wniosek:

Nie ma podstaw do odrzucenia

hipotezy H

o

, że oceny kobiet

i mężczyzn nie różnią się

Dane surowe

Rangi łączone

18

15

2,5

1

25

18

5

2,5

28

25

8

5

30

25

9,5

5

33

27

11

7

30

9,5

n

1

=5

n

2

=6

S

1

=36

S

2

=30









9

2

1

6

6

30

2

1















n

n

s

U

U

1,

α,n1,n2

=6 U

2

=n

1

*n

2

-U

1

=5*6-6=24

30

Test istotności Smirnowa-Kołmogorowa

Model -

2 próby niezależne – skala porządkowa

Założenia:



dane są dwie populacje generalne o rozkładach z ciągłymi dystrybuantami
F

1

(x) i F

2

(x),



pobrano dwie próby losowe o liczebnościach n

1

i n

2

,

Formułowanie hipotezy:



należy sprawdzić hipotezę, że obie próby pochodzą z tej samej populacji,
czyli H

0

: F

1

(x) = F

2

(x),

Sposób postępowania:



wyniki obu prób pogrupować w stosunkowo wąskie przedziały o tych
samych końcach x

j

,



dla każdego x

j

obliczyć wartości dystrybuant empirycznych z obu prób:

 

1

,

1

1

n

n

x

F

sk

n



 

2

,

2

2

n

n

x

F

sk

n



2013-04-28

14

31

Test istotności Smirnowa-Kołmogorowa

Sprawdzian -

wartość statystyki:



oraz: ,

gdzie:

Wnioskowanie:



dla ustalonego poziomu istotności



odczytać wartość krytyczną





i porównać w wartością empiryczną



,



jeżeli zachodzi nierówność λ ≥ λα, to hipotezę H

0

należy odrzucić.

 

 

x

F

x

F

D

n

n

x

2

1

*

sup





n

D

*





2

1

2

1

n

n

n

n

n





32

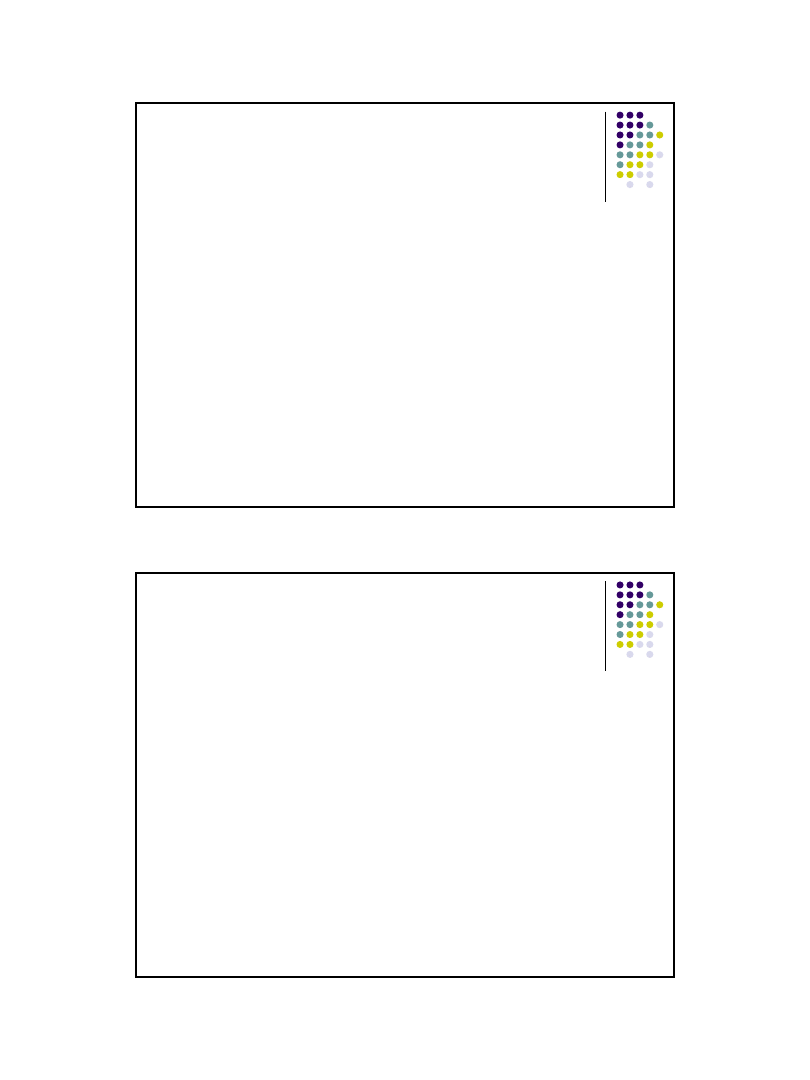
Test istotności Smirnowa-Kołmogorowa - przykład



Badane są rozkłady odstępów między przyjazdami kolejnych pojazdów na
przystanki A i B. Należy na poziomie istotności α=0,02 zweryfikować
hipotezę, że rozkłady odstępów pochodzą z tej samej populacji.

165

,

8

300

200

*

100

2

1

2

1









n

n

n

n

n

Nr

Przedziały

odstępów

czasu

Liczebności

Liczebności

skumulowane

Dystrybuanty

empiryczne

|F

nA

(x)-F

nB

(x)|

A

B

A

B

F

nA

(x)

F

nB

(x)

1

1,50

2,00

3

16

3

16

0,030

0,080

0,050

2

2,00

2,50

5

20

8

36

0,080

0,180

0,100

3

2,50

3,00

17

24

25

60

0,250

0,300

0,050

4

3,00

3,50

40

60

65

120

0,650

0,600

0,050

5

3,50

4,00

25

40

90

160

0,900

0,800

0,100

6

4,00

4,50

5

30

95

190

0,950

0,950

0,000

7

4,50

5,00

5

10

100

200

1,000

1,000

0,000

Liczebności prób

100

200

D

n

=0,100

λ

α

=1,52

816

,

0

165

,

8

*

100

,

0

*







n

D

n



Wniosek:
Nie ma podstaw do odrzucenia
hipotezy H

0

2013-04-28

15

33

Testy zgodności

Trzy i więcej prób niezależnych



Test niezależności χ

2

,



Test serii Kruskala-Wallisa,



Test mediany,

34

Test niezależności



2

skala nominalna (i każda inna)



Służy do sprawdzenia, czy dwie lub więcej badanych cech
(niekoniecznie mierzalnych) sa niezależne.
Zmienne losowe X i Y

są niezależne, gdy dla dystrybuant zachodzi

równość: F(x,y) = F

1

(x) F

2

(y)



Polega na porównaniu macierzy liczebności teoretycznych
i empirycznych.



Prawdopodobieństwami hipotetycznymi są oszacowane z próby
prawdopodobieństwa otrzymania jednocześnie określonej wartości (lub
kategorii jakościowej) cechy X oraz Y.



Ograniczeniem testu jest

duża liczebność próby i liczebność w

każdym przedziale klasowym n

ij

≥8

2013-04-28

16

35

Test niezależności



2

skala nominalna (i każda inna)

Model

– 2 i więcej prób niezależnych – skala nominalna

Założenia:



populacja generalna jest równocześnie badana ze względu na dwie cechy,
niekoniecznie mierzalne,



wylosowano niezależnie dużą próbę o liczebności n elementów,



należy zweryfikować hipotezę H

0

, że badane cechy są niezależne,

Sposób postępowania:



wyniki próby poklasyfikować w kombinowaną tablicę niezależności
o r wierszach i s kolumnach,



na boku tablicy jest r

grup wartości cechy X, a w nagłówku tablicy jest s grup

wartości cechy Y,



wnętrze tablicy wypełniają liczebności n

ij

(i = 1, 2, ..., r, j = 1, 2, ..., s)

oznaczające, ile elementów w próbie miało wartości obu cech należące do
kombinacji (i, j),

36

Test niezależności



2

skala nominalna (i każda inna)

– 2 i więcej prób niezależnych

Sposób postępowania c.d.:



sumowanie wierszy i kolumn macierzy liczebności empirycznych daje
liczebności brzegowe: ,



oszacować prawdopodobieństwa brzegowe: ,
zakładając prawdziwość hipotezy H

0

, należy obliczyć prawdopodobieństwa

hipotetyczne:



mnożąc te prawdopodobieństwa przez liczebność próby otrzymuje się
macierz liczebności teoretycznych [np

ij

],



Sprawdzian

– wartość statystykę:



Statystyka ta ma przy założeniu prawdziwości hipotezy H

0

asymptotyczny

rozkład



2

z (r

– 1)(s – 1) stopniami swobody

.









s

j

ij

i

n

n

1









r

i

ij

j

n

n

1

n

n

p

i

i







n

n

p

j

j







j

i

ij

p

p

p





















r

i

s

j

np

np

n

ij

ij

ij

1

1

2

2



2013-04-28

17

37

Test niezależności



2

skala nominalna (i każda inna)

– 2 i więcej prób niezależnych

Formułowanie hipotez:

H

0

: cecha Y

NIE ZALEŻY

od cechy X

H

1

: cecha Y

ZALEŻY

od cechy X

Wnioskowanie:



Obszar odrzucenia jest zawsze obszarem prawostronnym.



Jeżeli wartość sprawdzianu χ

2

znajdzie się:



w obszarze odrzucenia (tzn.

χ

2

>

χ

2

α

), to odrzucamy H

0

i przyjmujemy H

1

.



poza obszarem odrzucenia (tzn.

χ

2

≤ χ

2

α

), , to nie mamy podstaw do

odrzucenia H

0

.

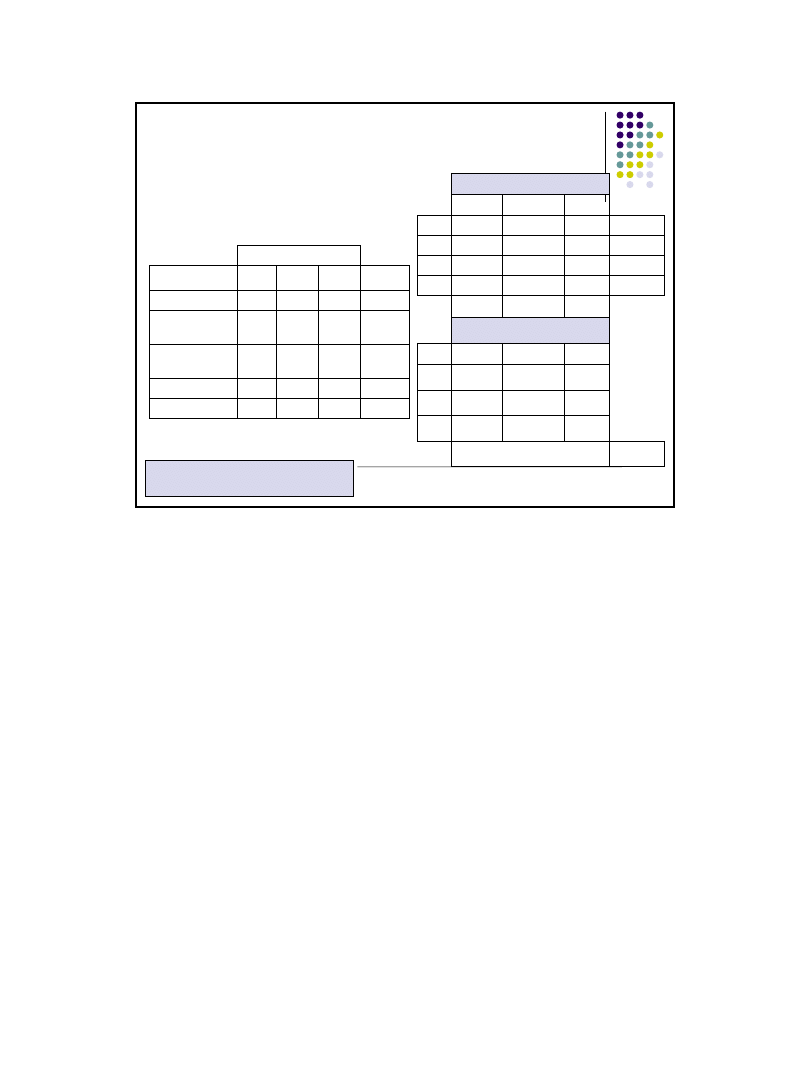
38

Test niezależności



2

skala nominalna (i każda inna)

– 2 i więcej prób niezależnych - przykład

Transport

Status

L

K

D

∑n

i.

Pracujący

100

80

220

400

Emeryci/

renciści

10

60

30

100

Uczniowie/

studenci

20

190

140

350

Niepracujący

10

100

40

150

∑n

.j

140

430

430

1000

ň

ij

=n

i.

* n

.j

/n

L

K

D

P

56

172

172

400

E/R

14

43

43

100

U/S

49

151

151

350

NP.

21

65

65

150

140

430

430

(n

ij

-ň

ij

)

2

/ň

ij

P

34,571

49,209

13,395

E/R

1,143

6,721

3,930

U/S

17,163

10,367

0,733

NP.

5,762

19,539

9,306

χ

2

171,840

Na poziomie istotności =0,05 zweryfikuj
hipotezę, czy wybór środka transportu
zależy od statusu zawodowego
H

0

: wybór środka nie zależy od statusu,

H

1

: wybór środka zależy od statusu,

χ

2

0,05;(4-1)(3-1)

=12,591

Wniosek:

H

0

należy odrzucić

2013-04-28

18

39

Test niezależności



2

skala nominalna (i każda inna)

– 2 i więcej prób niezależnych - przykład

Transport

Status

L

K

D

∑n

i.

Pracujący

100

80

220

400

Emeryci/

renciści

10

60

30

100

Uczniowie/

studenci

20

190

140

350

Niepracujący

10

100

40

150

∑n

.j

140

430

430

1000

ň

ij

=n

i.

* n

.j

/n

L

K

D

P

56

172

172

400

E/R

14

43

43

100

U/S

49

151

151

350

NP.

21

65

65

150

140

430

430

(n

ij

-ň

ij

)

2

/ň

ij

P

34,571

49,209

13,395

E/R

1,143

6,721

3,930

U/S

17,163

10,367

0,733

NP.

5,762

19,539

9,306

χ

2

171,840

Na poziomie istotności =0,05 zweryfikuj
hipotezę, czy wybór środka transportu
zależy od statusu zawodowego
H

0

: wybór środka nie zależy od statusu,

H

1

: wybór środka zależy od statusu,

χ

2

0,05;(4-1)(3-1)

=12,591

Wniosek:

H

0

należy odrzucić