- 1 -

Wersja 2.0

Portable

http://www.howtogeek.com/138545/tibi%E2%80%99s-mathematics-suite-is-a-useful-set-of-powerful-math-applications/

ZESTAW MATEMATYCZNY

Przekład

Robert Wi

ś

niewski

http://chomikuj.pl/bobwis

Przydatny i przyjazny dla u

ż

ytkownika zestaw aplikacji matematycznych, w tym:

•

Rozkład na czynniki pierwsze

•

Kalkulator graficzny

•

Kalkulator macierzowy

•

Kalkulator naukowy

Wymagania:: NET Framework 4.

- 2 -

SPIS TRE

Ś

CI

1. Zestaw matematyczny Tibi
1.1. Suita matematyczna
1.1.1. Wprowadzenie
1.1.2. Rozpoczynanie pracy
1.2. Skróty klawiszowe
1.2.1. Wprowadzenie
1.2.2. Ustawianie skrótów
1.2.3. Usuwanie skrótów
1.2.4. Ostrze

ż

enia

2. Rozkład na czynniki pierwsze
2.1. Rozpoczynanie pracy
2.2. Interfejs u

ż

ytkownika

2.3. Skróty klawiszowe
2.4. Ograniczenia

3. Kalkulator graficzny
3.1. Wprowadzenie
3.2. Ograniczenia
3.3. J

ę

zyk wyra

ż

e

ń

3.3.1. Wprowadzenie
3.3.2. Zmienne
3.3.3. Wst

ę

pnie zdefiniowane zmienne

3.3.4. Akceptowane operatory
3.3.5. Funkcje3.3.6. Wst

ę

pnie zdefiniowane funkcje

3.3.7. Składnia
3.4. Obliczanie wyra

ż

e

ń

3.4.1. Wprowadzenie
3.4.2. Rozpocz

ę

cie pracy

3.4.3. Zmienne
3.5. Całkowanie wyra

ż

e

ń

3.5.1. Wprowadzenie
3.5.2. Obliczanie
3.6. Wykre

ś

lanie wyra

ż

e

ń

3.6.1. Wykre

ś

lanie pojedynczych wyra

ż

e

ń

3.6.2. Wykre

ś

lanie wielokrotnych wyra

ż

e

ń

3.6.3. Nawigacja
3.7. Eksport i import wyra

ż

e

ń

3.7.1. Eksport
3.7.2. Import
3.8. Preferencje
3.8.1. Wprowadzenie
3.8.2. Dokładno

ść

wykresów

3.8.3. Dokładno

ść

liczb siatki

3.8.4. G

ę

sto

ść

siatki

3.8.5. Nawigacja i czuło

ść

skalowania

3.9. Problemy i ich rozwi

ą

zywanie

3.9.1. Aplikacja zawiesza si

ę

przy starcie

3.9.2. Wykres jest rysowany niepoprawnie
3.9.3. Aplikacja działa powoli
3.9.4. Uzyskuj

ę

niezdefiniowany bł

ą

d zmiennej

3.9.5. Uzyskuj

ę

niezdefiniowany bł

ą

d funkcji

3.9.6. Uzyskuj

ę

bł

ą

d pustego stosu

3.9.7. Uzyskuj

ę

bł

ą

d niedomkni

ę

tych nawiasów

3.9.8. Mam inne problemy nie opisane w typ przewodniku

- 3 -

4. Kalkulator macierzowy
4.1. Informacje ogólne
4.2. Ograniczenia
4.3. Przewodnik podstawowy
4.3.1. Wprowadzanie macierzy
4.3.2. Wykonywanie oblicze

ń

4.4. Okno kalkulatora macierzy
4.4.1. Przykładowe okno kalkulatora
4.4.2. Menu plików File
4.4.3. Menu macierzy Matrix
4.4.4. Menu pomocy Help
4.5. Skróty klawiszowe
4.6. Funkcje wszystkich przycisków
4.7. Edytor macierzy

5. Kalkulator naukowy
5.1. Interfejs u

ż

ytkownika

5.2. Ograniczenia
5.3. Przycisk drugiej funkcji
5.3.1. Opis
5.3.2. Przykład
5.4. Warto

ś

ci bezwzgl

ę

dne

5.4.1. Opis
5.4.2. Przykłady
5.5. Kombinatorka
5.5.1 Silnia
5.5.2. Permutacje
5.5.3. Permutacje na k-obiektach
5.5.4 Kombinacje
5.6. Stałe
5.6.1. Stała

ππππ

(pi)

5.6.2. Stała e
5.7. Cz

ęś

ci całkowite i ułamkowe

5.7.1. Cz

ęść

całkowita

5.7.2. Cz

ęść

ułamkowa

5.8. Skróty klawiszowe
5.9. Mno

ż

enie przez odwrotno

ść

5.10. Funkcje wszystkich przycisków

- 4 -

1. Zestaw matematyczny Tibi

1.1. Suita matematyczna

1.1.1. Wprowadzenie

Pakiet Tibi's Mathematics Suite jest zestawem przydatnych aplikacji matematycznych, które mo

ż

na

uruchamia

ć

niezale

ż

nie od siebie np. za pomoc

ą

przycisku w pasku zada

ń

lub za pomoc

ą

globalnych

skrótów klawiszowych.

Aktualnie zestaw ten składa si

ę

on z 5 osobnych modułów

•

Factorizator – Rozkład na czynniki pierwsze

•

Graphing Calculator – Kalkulator graficzny

•

Help Viewer – Pomocnik

•

Matrix Calculator – Kalkulator macierzowy

•

Scientific Calculator – Kalkulator naukowy

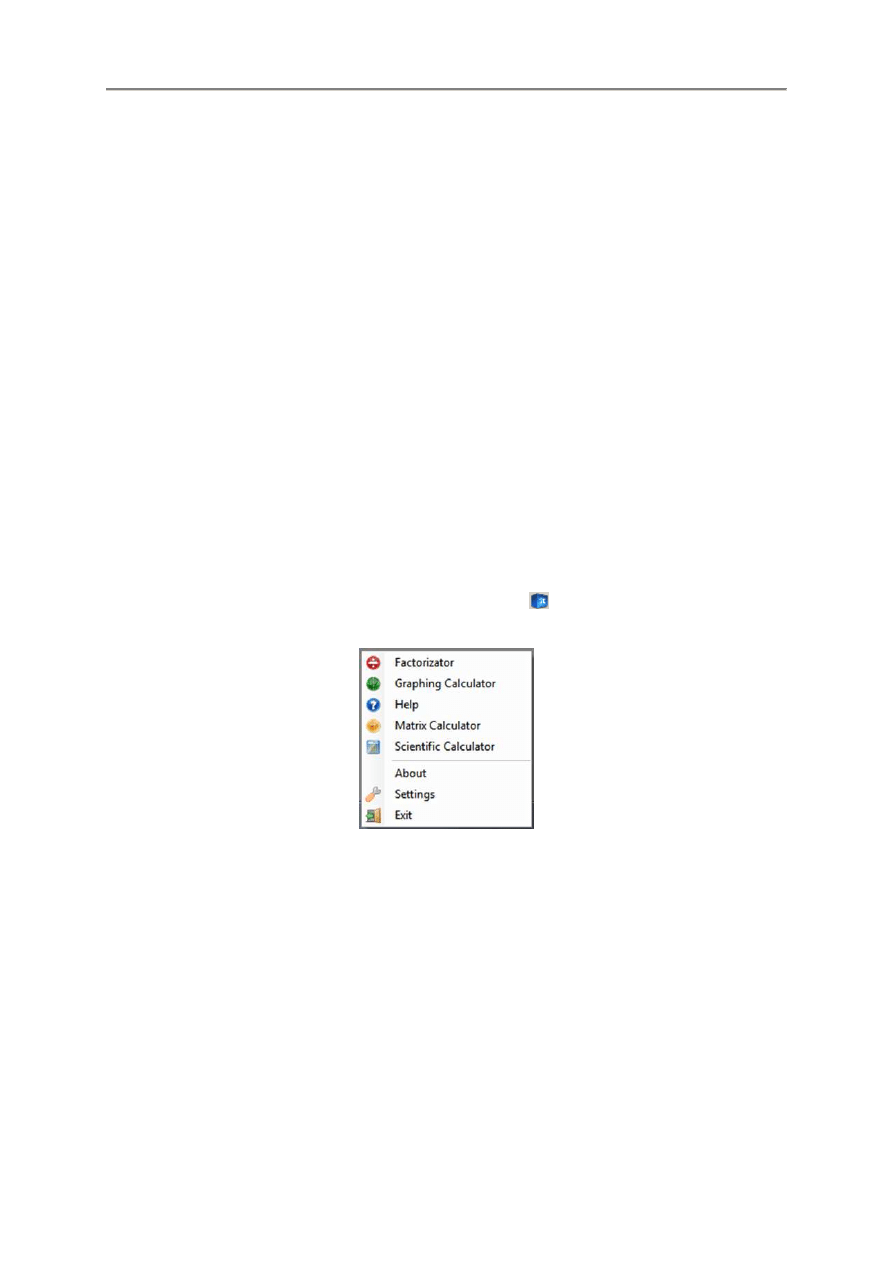
1.1.2. Rozpoczynanie pracy

Po klikni

ę

ciu prawym klawiszem myszki przycisku programu

w pasku zada

ń

, otwiera si

ę

menu

zawieraj

ą

ce wszystkie dost

ę

pne opcje pakietu.

Opcja Settings pozwala na ustawanie globalnych skrótów klawiszowych uruchamiaj

ą

cych wybrane

aplikacje.

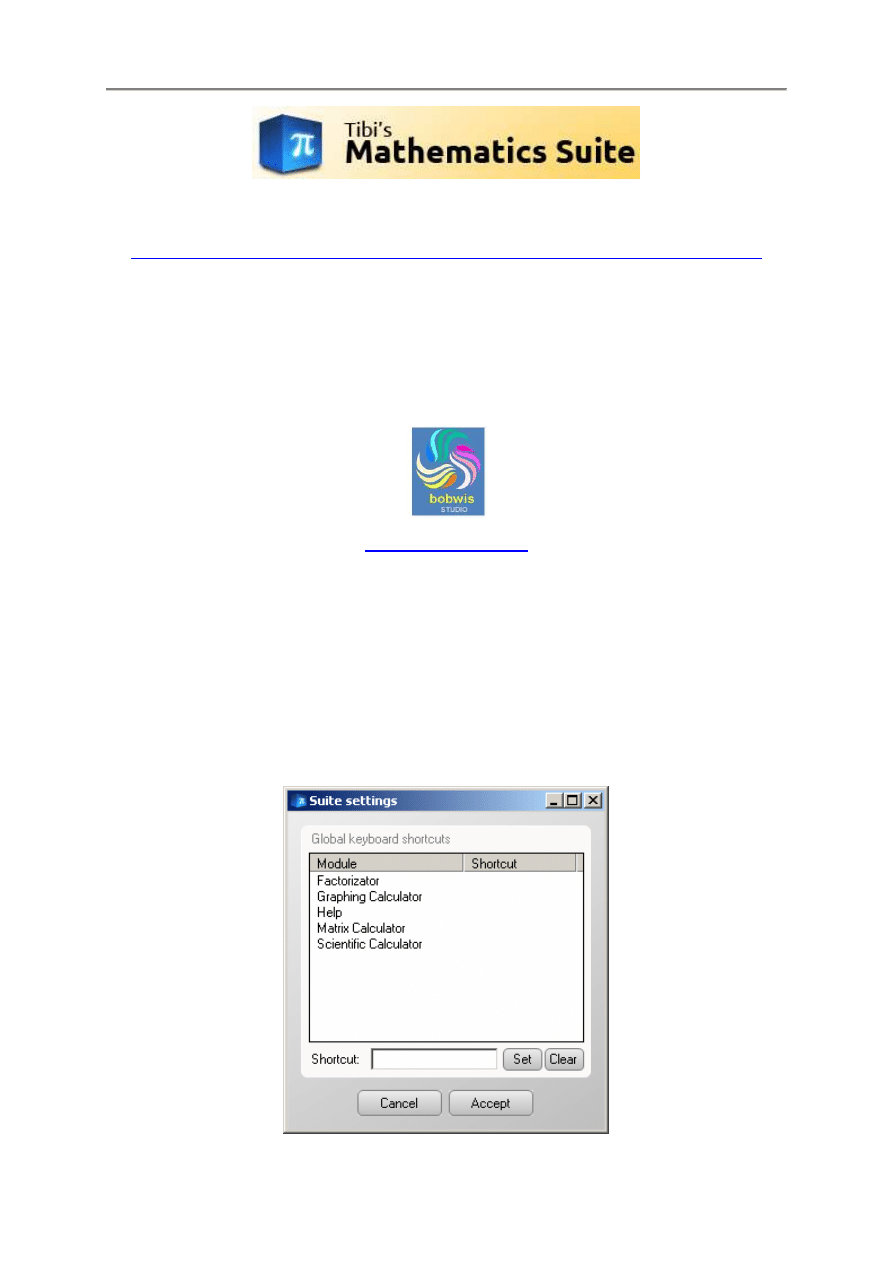
1.2. Skróty klawiszowe

1.2.1. Wprowadzenie

Skrót klawiszowy oznacza kombinacj

ę

klawiszy na klawiaturze, która wykonuje okre

ś

lone zadanie.

Zwykle skróty klawiszowe spełniaj

ą

przypisane zadanie gdy okno aplikacji jest otwarte. Natomiast

globalne skróty klawiszowe wykonuj

ą

swoje zadanie bez wzgl

ę

du na to czy okno aplikacji jest otwarte.

Przykładowo, w opcji tej mo

ż

na ustawia

ć

kombinacje klawiszy otwieraj

ą

cych kalkulator naukowy.

- 5 -

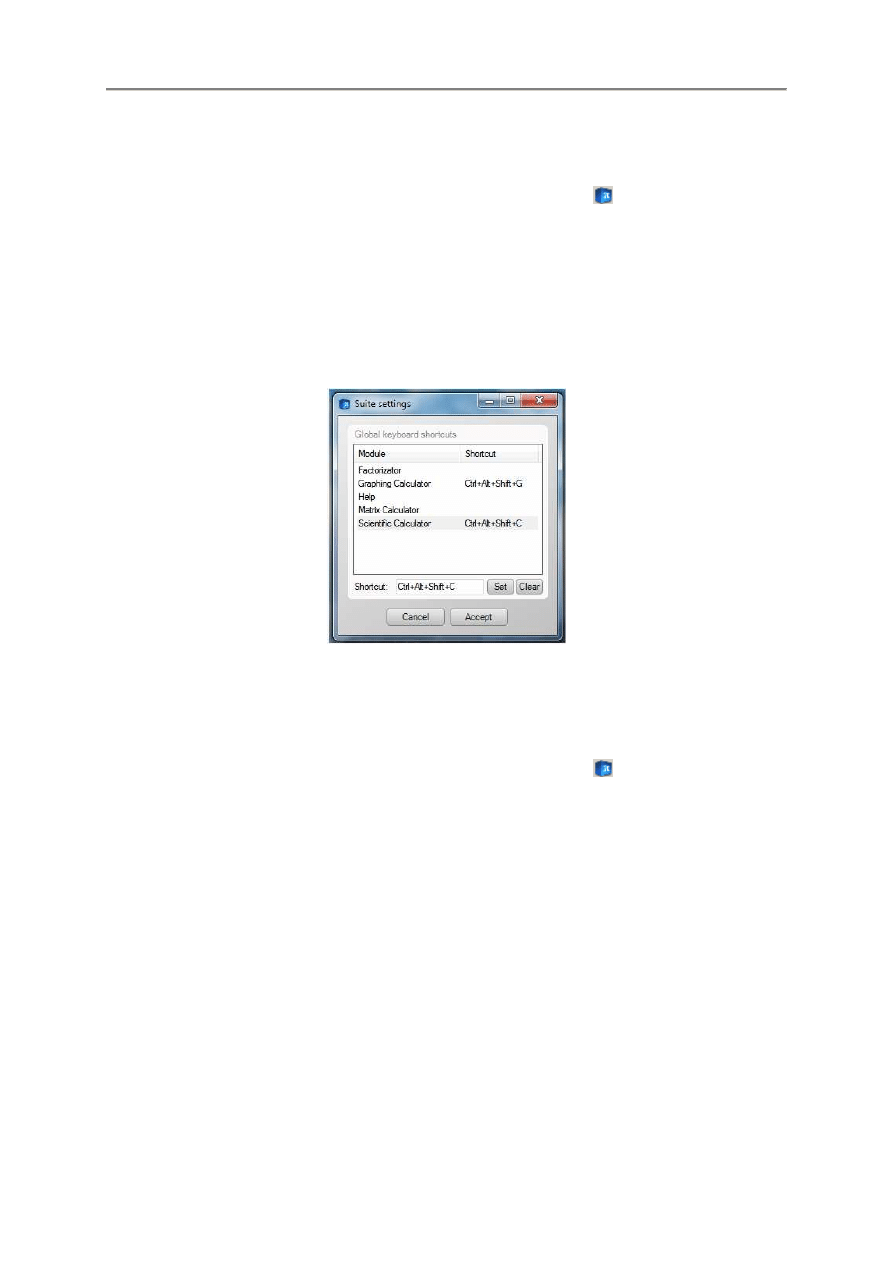
1.2.2. Ustawianie skrótów

W celu ustawienia globalnych skrótów klawiszowych nale

ż

y wykona

ć

poni

ż

sze kroki:

•

Krok 1 – Klikn

ąć

prawym klawiszem myszki przycisk programu

w pasku zada

ń

, po czym

w otworzonym menu wybra

ć

opcj

ę

Settings.

•

Krok 2 – Na wy

ś

wietlonej li

ś

cie wybra

ć

wymagan

ą

aplikacj

ę

.

•

Krok 3 – Klikn

ąć

pole edycji Shortcut i wcisn

ąć

wymagan

ą

kombinacj

ę

klawiszy.

•

Krok 4 – Klikn

ąć

przycisk Set aby potwierdzi

ć

wybór.

•

Krok 5 – Klikn

ąć

przycisk Accept aby zmodyfikowa

ć

ustawienia.

1.2.3. Usuwanie skrótów

W celu usuni

ę

cia globalnego skrótu klawiszowego nale

ż

y wykona

ć

poni

ż

sze kroki:

•

Krok 1 – Klikn

ąć

prawym klawiszem myszki przycisk programu

w pasku zada

ń

, po czym

w otworzonym menu wybra

ć

opcj

ę

Settings.

•

Krok 2 – Na wy

ś

wietlonej li

ś

cie wybra

ć

wymagan

ą

aplikacj

ę

.

•

Krok 3 – Klikn

ąć

przycisk Clear aby usun

ąć

skrót.

•

Krok 4 – Klikn

ąć

przycisk Accept aby zmodyfikowa

ć

ustawienia.

1.2.4. Ostrze

ż

enia

•

Zaleca si

ę

aby stosowa

ć

nietypowe kombinacje klawiszy. W przeciwnym razie mog

ą

wyst

ą

pi

ć

konflikty tych kombinacji z kombinacjami klawiszy innych aplikacji. Przykładowo, nie nale

ż

y

nigdy stosowa

ć

skrótów Ctrl + S, poniewa

ż

wiele aplikacji korzysta z nich do zapisywania.

Jednak kombinacja Ctrl + Alt + Shift + S jest dobry wyborem.

•

Nie nale

ż

y nigdy stosowa

ć

pojedynczego klawisza jako skrótu/ Przykładowo, ustawienie A

jako skrótu sprawi,

ż

e przy ka

ż

dym wpisaniu litery a w wyrazie, nast

ą

pi uruchomienie aplikacji.

•

Microsoft zaleca równie

ż

, aby korzysta

ć

z klawisza Windows tylko dla funkcji systemowych.

- 6 -

2. Rozkład na czynniki pierwsze

2.1. Rozpoczynanie pracy

Opcja Factorization jest aplikacj

ą

wy

ś

wietlaj

ą

c

ą

rozkład liczb naturalnych na czynniki pierwsze.,

Operacja ta jest zdefiniowana jako rozkład na liczby, które pomno

ż

one przez siebie daj

ą

oryginaln

ą

liczb

ę

. Korzystanie z tej aplikacji jest bardzo proste. Wystarczy w polu tekstowym Input Number

wpisa

ć

liczb

ę

i klikn

ąć

przycisk Calculate lub wcisn

ąć

klawisz Enter. Wynik operacji jest wy

ś

wietlany

w polu Factorization. Pierwsza kolumna reszt Remainder zawiera oryginalne liczby dzielone przez
ostatni dzielnik, a kolumna druga Divisor zawiera list

ę

dzielników.

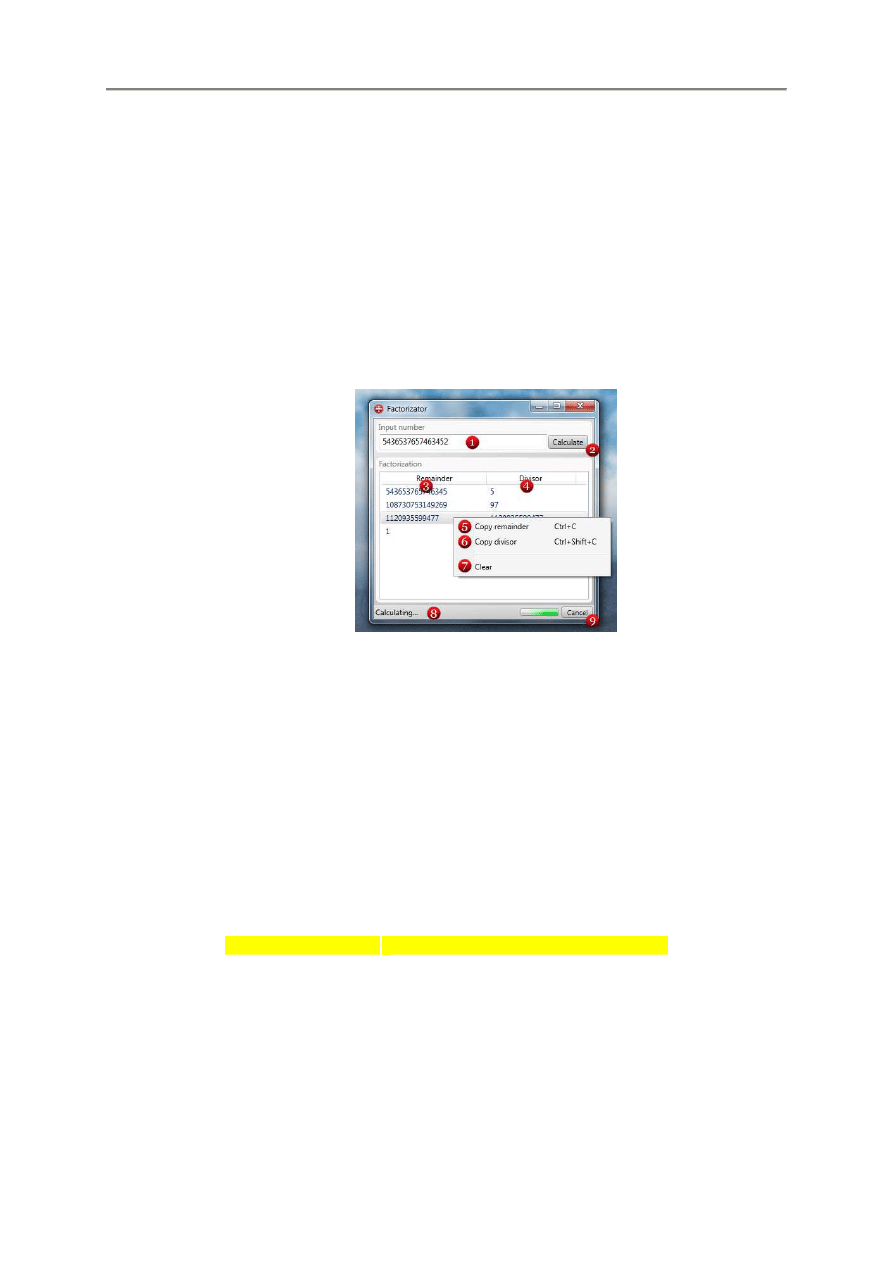
2.2. Interfejs u

ż

ytkownika

Wprowadzanie liczb

Przycisk obliczania Mo

ż

na zamiast niego wciska

ć

klawisz Enter)

Kolumna reszt

Kolumna dzielników

Menu kontekstowe – Kopiowanie reszt do schowka

Menu kontekstowe – Kopiowanie dzielników do schowka

Menu kontekstowe – Oczyszcza obszar faktoryzacji

Komunikat aktualnego stanu

Przycisk anulowania (pojawia si

ę

gdy obliczenia trwaj

ą

bardzo długo)

2.3. Skróty klawiszowe

Skrót klawiszowy

Operacja

Enter

Wykonuje obliczenia

F1

Otwiera plik pomocy

Ctrl + C

Kopiuje zaznaczon

ą

reszt

ę

do schowka

Ctrl + Shift + C

Kopiuje zaznaczony dzielnik do schowka

2.4. Ograniczenia

Kalkulator ten jest ograniczony do 128-bitowych liczb zmiennoprzecinkowych (w przybli

ż

eniu do

zakresu od ±1,0 × 10

-28

do ±7.9 × 10

28

, lub do 28-29 cyfr). Jednak z uwagi na to,

ż

e faktoryzacja

mo

ż

e by

ć

wykonywana tylko na liczbach całkowitych, liczby ułamkowe s

ą

obcinane.

- 7 -

3. Kalkulator graficzny

3.1. Wprowadzenie

Kalkulator graficzny Graphing Calculator jest narz

ę

dziem do obliczania, wykre

ś

lania i całkowania

wyra

ż

e

ń

(lub funkcji). Ma on wiele przydatnych mo

ż

liwo

ś

ci takich jak np. ł

ą

czenie wielu wykresów,

sterowniki nawigacji i skalowania oraz zapisywanie wykre

ś

lanych wyra

ż

e

ń

.

3.2. Ograniczenia

Wszystkie liczby s

ą

ograniczone do 64-bitowych liczb zmiennoprzecinkowych (w przybli

ż

eniu do

zakresu od ±5,0 × 10

-324

do ±1,7 × 10

308

, lub do 15-16 cyfr).

Innym ograniczeniem jest dokładno

ść

wykresów. Gdy wyra

ż

enie ma wiele asymptot pionowych,

wówczas wykres mo

ż

e by

ć

rysowany niepoprawnie.

3.3. J

ę

zyk wyra

ż

e

ń

3.3.1. Wprowadzenie

Kalkulator graficzny Graphing Calculator oblicza wyra

ż

enia oparte na dokładnym zestawie reguł,

które tworz

ą

j

ę

zyk. Z uwagi na to,

ż

e j

ę

zyk matematyczny jest zbyt zło

ż

ony i nie mo

ż

na zapisa

ć

go za

pomoc

ą

prostego tekstu, aplikacja ta (i wiele innych) korzysta z uproszczonego j

ę

zyka.

Gdy jeste

ś

cie zaznajomieni z programowaniem w takim j

ę

zyku jak C (np. C, C++, C#, Java), wówczas

j

ę

zyk tu stosowany jest bardzo podobny do tych j

ę

zyków programowania.

3.3.2. Zmienne

Zmienna jest symbolem, który mo

ż

e mie

ć

przypisan

ą

dowoln

ą

liczb

ę

. W tej aplikacji, symbol ten

reprezentowany jest ła

ń

cuchem znaków spełniaj

ą

cym poni

ż

sze zasady:

•

Zawsze zaczyna si

ę

liter

ą

•

Mo

ż

e zawiera

ć

tylko litery i cyfry. Nie mo

ż

e zawiera

ć

spacji, podkre

ś

lników ani innych symboli.

•

Zmienne rozró

ż

niaj

ą

du

ż

e i małe litery. Oznacza to,

ż

e alpha nie jest tym samym co Alpha.

Zalet

ą

korzystania ze zmiennych jest to,

ż

e mo

ż

na pomin

ąć

wpisywanie zło

ż

onych wyra

ż

e

ń

oraz łatwo

je odczytywa

ć

w ró

ż

nych wpisach. Zmienne s

ą

obsługiwane w programie Graphing Calculator

z pewnymi ograniczeniami, a wi

ę

c mo

ż

na z nich korzysta

ć

przy obliczaniu wyra

ż

e

ń

. Jednak

korzystanie z ró

ż

nych zmiennych przy wykre

ś

laniu wykresów oraz przy całkowaniu nie jest mo

ż

liwe.

Domy

ś

lnie mo

ż

na korzysta

ć

tylko z jednej zmiennej x przy wykre

ś

laniu i całkowaniu wyra

ż

e

ń

.

3.3.3. Wst

ę

pnie zdefiniowane zmienne

Program ma dwie wst

ę

pnie zdefiniowane zmienne:

•

pi (

ππππ

)

•

e

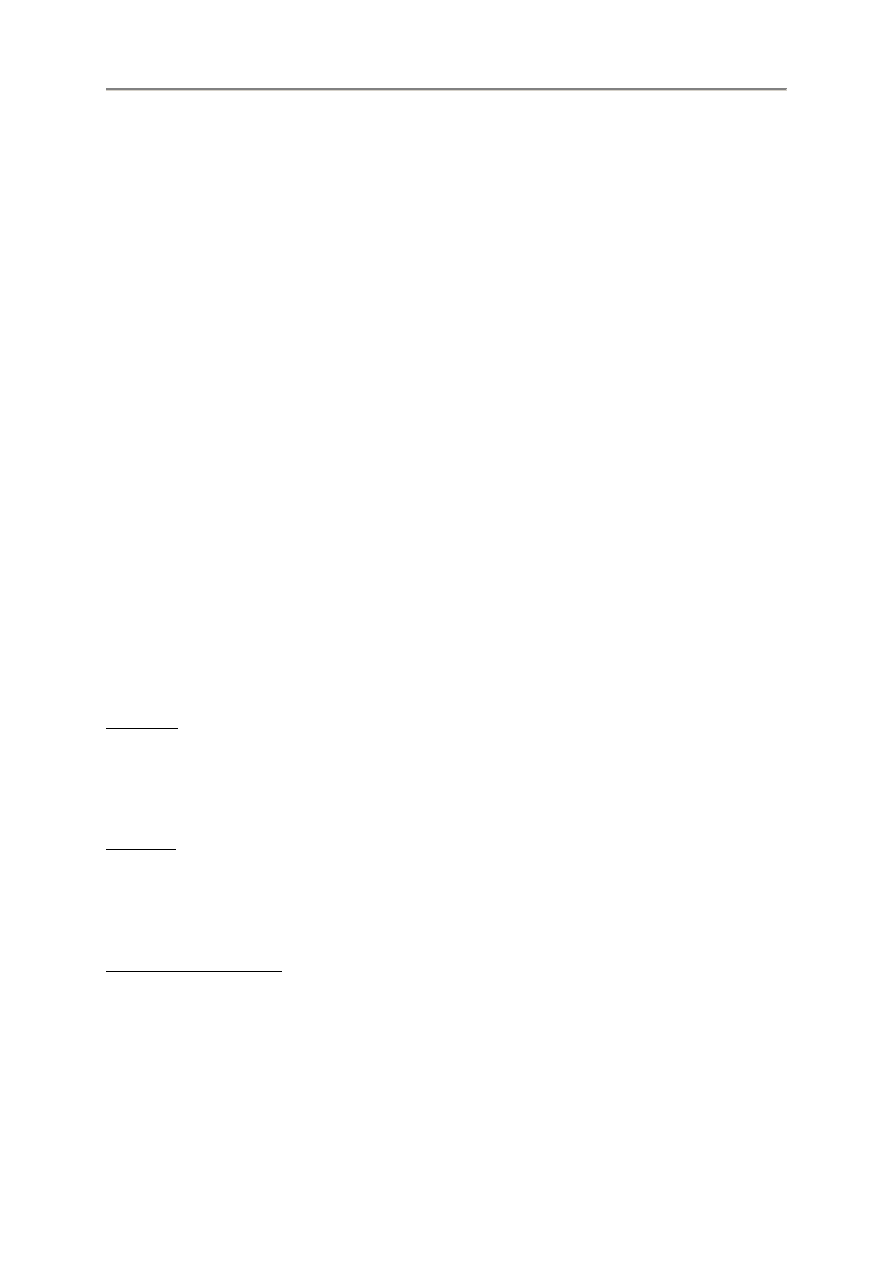
- 8 -

3.3.4. Akceptowane operatory

Akceptowane s

ą

poni

ż

sze operatory:

•

+

(dodawanie)

•

-

(odejmowanie)

•

*

(mno

ż

enie)

•

/

(dzielenie)

•

%

(reszta z dzielenia)

•

^

(pot

ę

gowanie)

Kolejno

ść

operacji jest równie

ż

respektowana.

Wy

ż

sza ranga oznacza wy

ż

szy priorytet.

Operacje o tej samej randze s

ą

wykonywane od lewej do prawej strony oprócz operatora

pot

ę

gowania.

•

Ranga 1:

+ -

•

Ranga 2:

* / %

•

Ranga 3:

^

3.3.5. Funkcje

Program Graphing Calculator obsługuje aktualnie tylko wst

ę

pnie zdefiniowane funkcje.

3.3.6. Wst

ę

pnie zdefiniowane funkcje

Mo

ż

na korzysta

ć

z poni

ż

szych funkcji:

Pierwiastki

sqrt(x)

Pierwiastek kwadratowy

cbrt(x)

Pierwiastek sze

ś

cienny

root(n, x) Pierwiastek n-tego stopnia

Logarytmy

lg(x)

Logarytm dziesi

ę

tny

ln(x)

Logarytm naturalny

log(b, x) Logarytm x o podstawie b

Funkcje trygonometryczne

sin(x)

Sinus

sinh(x) Sinus hiperboliczny

cos(x)

Cosinus

cosh(x) Cosinus hiperboliczny

tan(x)

Tangens

tanh(x) Tangens hiperboliczny

ctan(x) Cotangens*

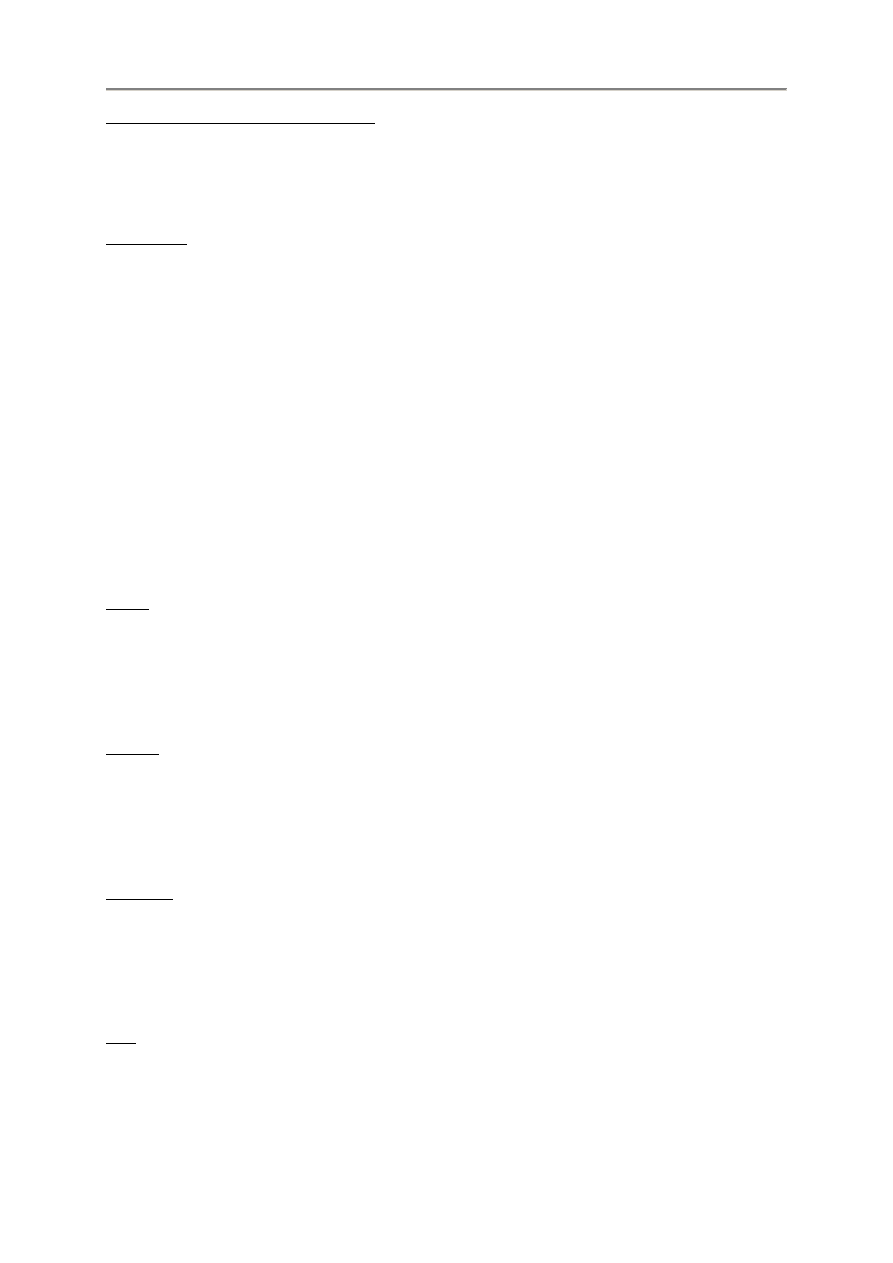
- 9 -

Odwrotno

ś

ci funkcji trygonometrycznych

arcsin(x) or asin(x)

Odwrotno

ść

sinusa

arccos(x) or acos(x) Odwrotno

ść

cosinusa

arctan(x) or atan(x) Odwrotno

ść

tangensa

Inne funkcje

ceil(x) or ceiling(x) Najmniejsza liczba całkowita wi

ę

ksza od x

floor(x)

Najwi

ę

ksza liczba całkowita mniejsza od x

int(x)

Cz

ęść

calkowita liczbty

truncate(x)

Obcina (usuwa)) cz

ęść

ułamkow

ą

liczby.

round(x, n)

Zaokragla liczbe do n cyfr dziesi

ę

tnych

abs(x)

Warto

ść

bezwzgl

ę

dna

max(x, y)

Maksimum

min(x, y)

Minimum

3.3.7. Składnia

Składnia tej aplikacji jest bardziej prosta ni

ż

w j

ę

zyku matematycznym.

Obowi

ą

zuj

ą

tu jednak poni

ż

sze zasady.

Liczby

•

Liczby w formacje naukowym nie s

ą

akceptowane

•

Grupowanie cyfr nie jest akceptowane

•

Cz

ęś

ci całkowite i ułamkowe liczb musz

ą

by

ć

oddzielane kropk

ą

(.), a nie przecinkiem(,).

Funkcje

•

Parametry funkcji musz

ą

by

ć

zamykane w nawiasach. Wyra

ż

enie sin x nie b

ę

dzie obliczane.

•

W funkcjach wieloparametrowych, parametry rozdziela si

ę

przecinkiem

•

Nazwy funkcji i zmiennych rozró

ż

niaj

ą

du

ż

e i małe litery.

Operatory

•

Operatory o tej samej randze s

ą

obliczane od lewej do prawej strony za wyj

ą

tkiem operatora

pot

ę

gowania, który jest obliczany od prawej do lewej strony. W przeciwnym razie

respektowana jest ranga operatorów.

•

Takie wyra

ż

enia jak 3x nie s

ą

akceptowane. Trzeba stosowa

ć

operator mno

ż

enia 3*x.

Inne

•

Wpisywane wyra

ż

e

ń

jako funkcji aktualnie nie jest obsługiwane, a wi

ę

c wyra

ż

enie f(x)=2*x

nie b

ę

dzie obliczane. Wpisanie jako y=2*x te

ż

nie b

ę

dzie obliczane.

- 10 -

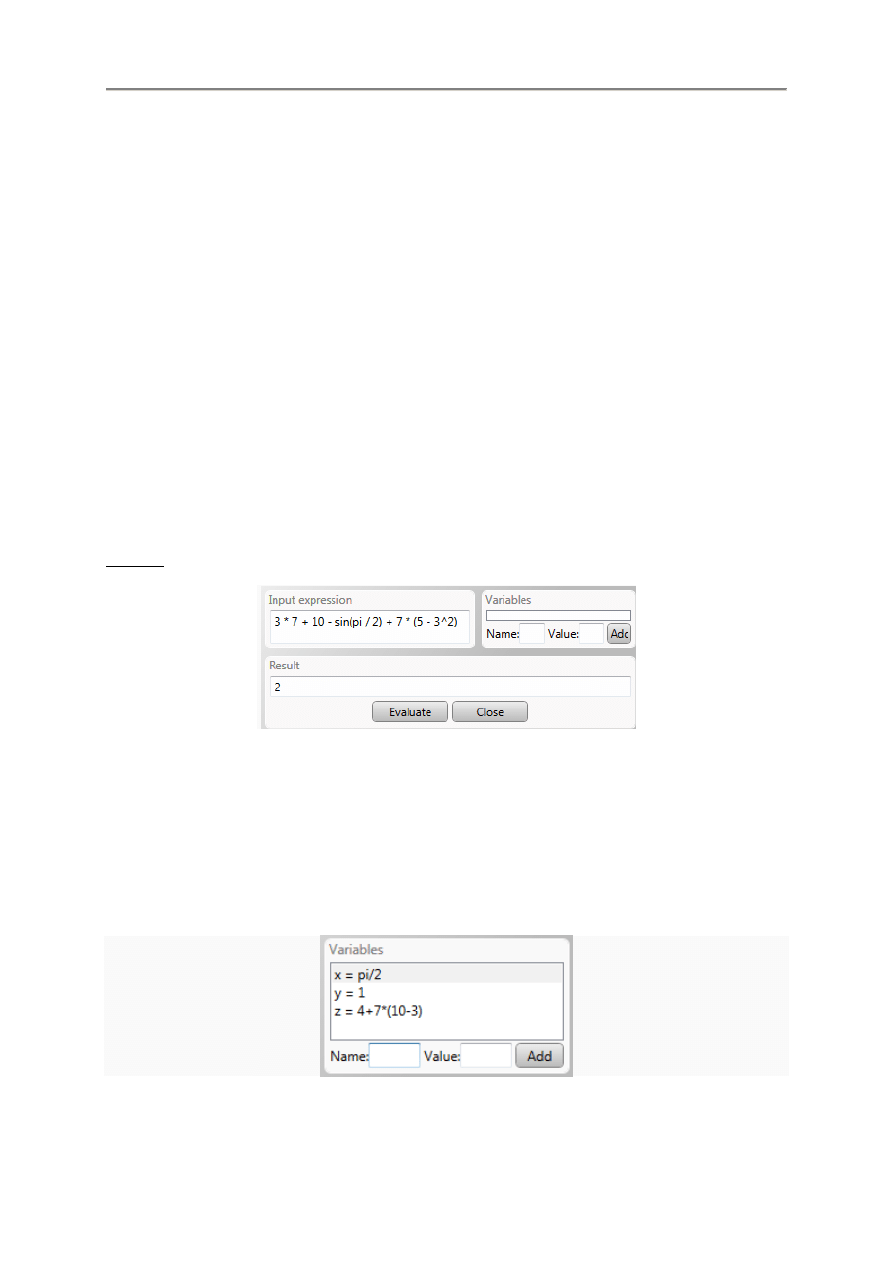
3.4. Obliczanie wyra

ż

e

ń

Dokumentacja ta opisuje jak korzysta

ć

z okna obliczania wyra

ż

e

ń

.

3.4.1. Wprowadzenie

Okno obliczania wyra

ż

e

ń

Evaluate

Expression jest narz

ę

dziem aplikacji Graphing Calculator, które

mo

ż

e oblicza

ć

wyniki wpisywanych wyra

ż

e

ń

matematycznych.

3.4.2. Rozpocz

ę

cie pracy

W celu obliczenia wyra

ż

enia nale

ż

y wykona

ć

poni

ż

sze kroki:

•

Krok 1 – W oknie aplikacji klikn

ąć

przycisk Evaluate

•

Krok 2 – W polu Input expression wpisa

ć

wymagane wyra

ż

enie

•

Krok 3 – Doda

ć

zmienne do listy zmiennych Variables je

ś

li jest to konieczne

•

Krok 4 – Klikn

ąć

przycisk Evaluate.

Przykład

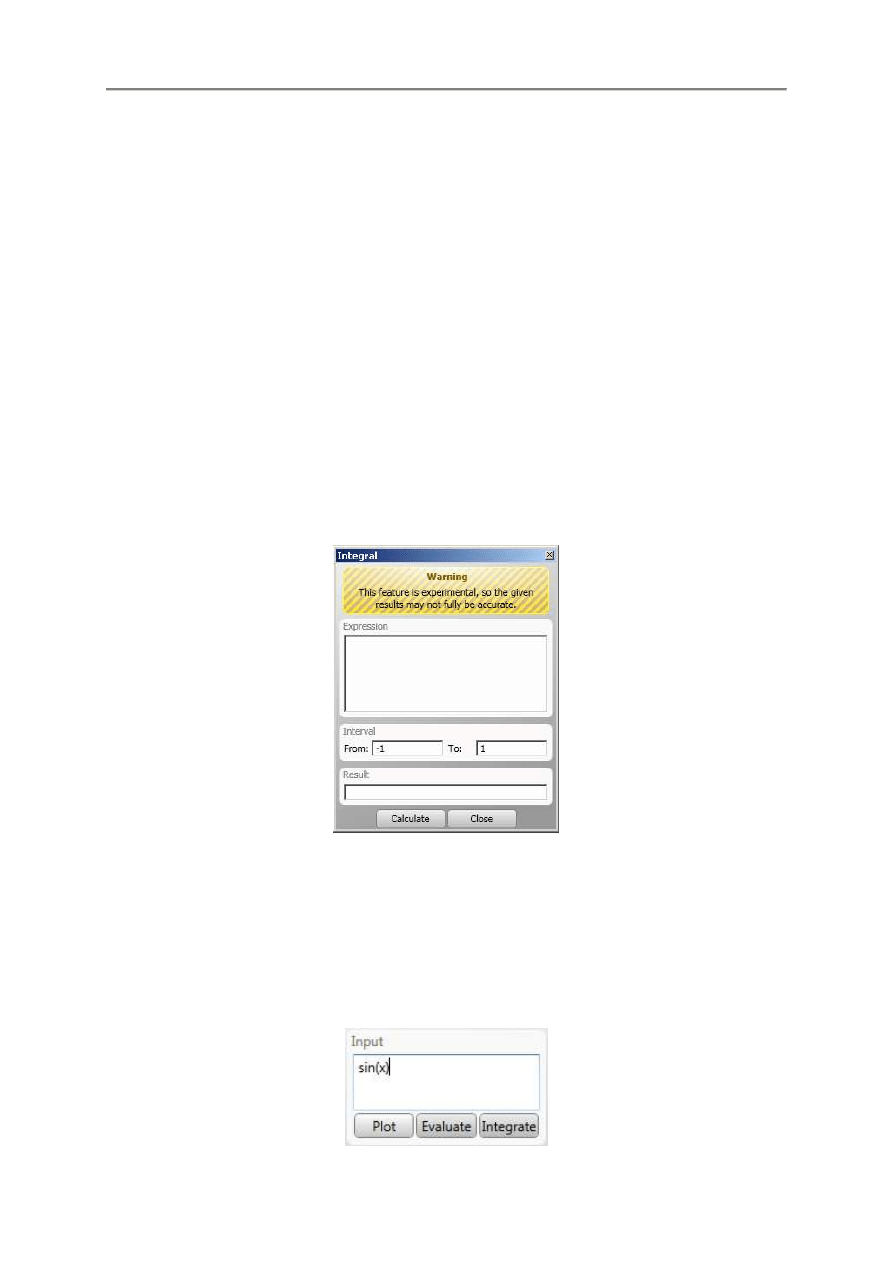
3.4.3. Zmienne

Aby skorzysta

ć

ze zmiennych w oknie oblicze

ń

, trzeba wpisa

ć

nazw

ę

zmiennej w polu Name oraz jej

warto

ść

w polu Value, po czym klikn

ąć

przycisk Add. Gdy zmienna o tej nazwie juz istnieje,

zostaniemy zapytani czy zast

ą

pi

ć

jej star

ą

warto

ść

.

Warto

ść

zmiennej mo

ż

e by

ć

równie

ż

wyra

ż

eniem, a nie tylko zwykł

ą

liczb

ą

.

Aby usun

ąć

zmienn

ą

z listy lub j

ą

edytowa

ć

, wystarczy klikn

ąć

ja prawym klawiszem myszki, po czym

w menu kontekstowym wybra

ć

odpowiednie polecenie Edit, Delete lub Clear List.

- 11 -

3.5. Całkowanie wyra

ż

e

ń

3.5.1. Wprowadzenie

Kalkulator całkowania Integral jest narz

ę

dziem aplikacji Graphing Calculator, które oblicza całk

ę

oznaczon

ą

wyra

ż

enia.

W otworzonym okienku dialogowym pojawia si

ę

ostrze

ż

enie,

ż

e opcja ta jest eksperymentalna i nie

była w pełni testowana.

3.5.2. Obliczanie

W celu obliczania całki oznaczonej wyra

ż

enia nale

ż

y wykona

ć

poni

ż

sze kroki:

•

Krok 1 – Klikn

ąć

przycisk Integrate

•

Krok 2 – W polu Expression wpisa

ć

wymagane wyra

ż

enie

•

Krok 3 – W polach Interval wpisa

ć

przedział całkowania

•

Krok 4 – Klikn

ąć

przycisk Calculate aby wykona

ć

obliczenia.

3.6. Wykre

ś

lanie wyra

ż

e

ń

3.6.1. Wykre

ś

lanie pojedynczych wyra

ż

e

ń

W celu wykre

ś

lenia wyra

ż

enia wystarczy wpisa

ć

w polu Input wymagane wyra

ż

enie i klikn

ąć

przycisk

Plot. Kolor wykre

ś

lanego wyra

ż

enia jest generowany losowo.

- 12 -

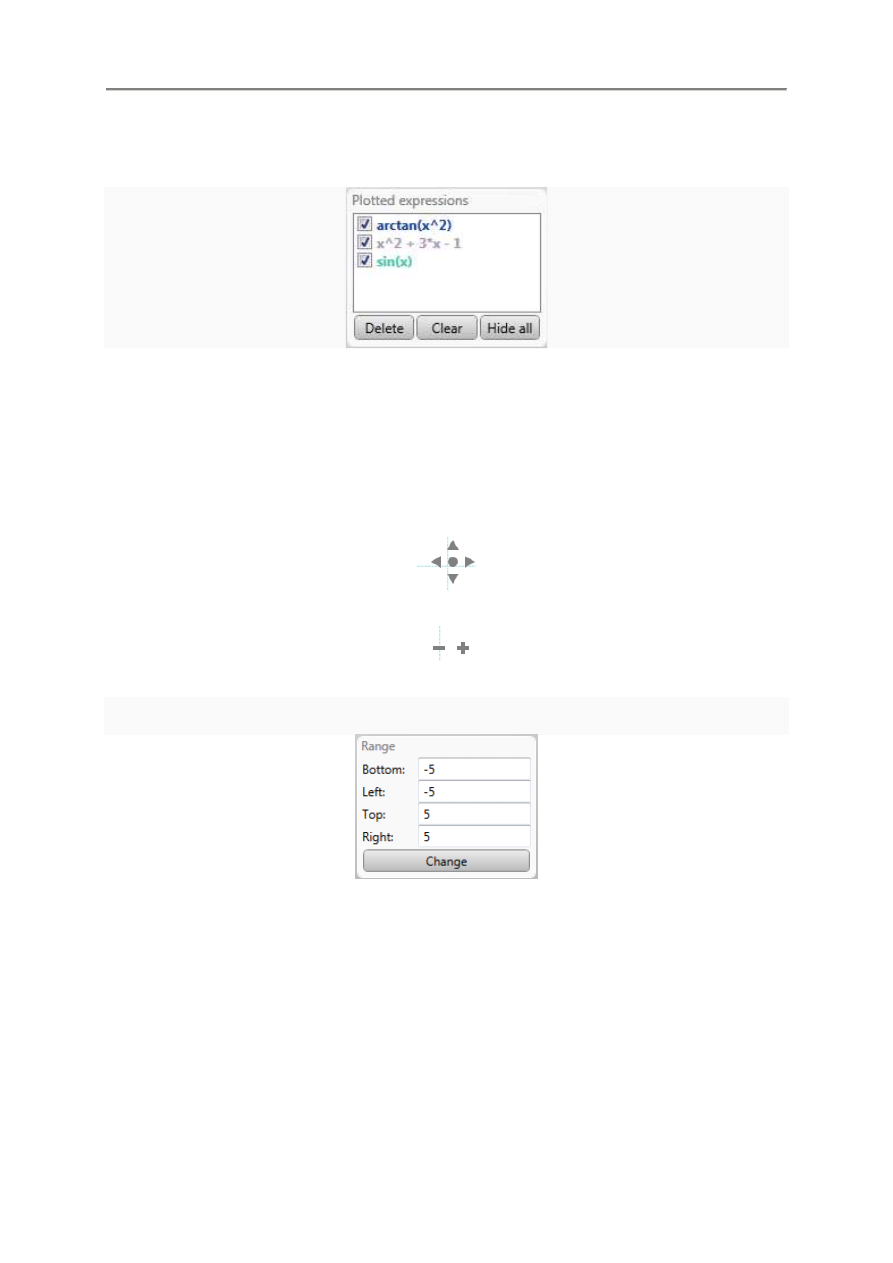
3.6.2. Wykre

ś

lanie wielokrotnych wyra

ż

e

ń

Po wykre

ś

leniu wyra

ż

enia, pojawia si

ę

ono na li

ś

cie Plotted expressions.

Tutaj mo

ż

na ukrywa

ć

i wy

ś

wietla

ć

wyra

ż

enia, usuwa

ć

je z listy klawiszem Delete a nawet opró

ż

nia

ć

cala list

ę

korzystaj

ą

c z przycisku Clear.

3.6.3. Nawigacja

Mo

ż

na porusza

ć

si

ę

po wykresie korzystaj

ą

c z przycisków znajduj

ą

cych si

ę

w prawym górnym rogu

lub z klawiszy kierunkowych na klawiaturze. Przycisk

ś

rodkowy przywraca wykres do oryginalnej

pozycji.

W dolnym prawym rogu wykresu znajduj

ą

si

ę

dwa przyciski skalowania. Mo

ż

na równie

ż

skalowa

ć

wykres korzystaj

ą

c kółka myszki lub z klawiszy + i – na klawiaturze.

W celu lepszego sterowania obszarem wykresu, mo

ż

na wpisa

ć

wymagane warto

ś

ci (lub wyra

ż

enia)

zakresów w odpowiednich polach sekcji Range.

3.7. Eksport i import wyra

ż

e

ń

3.7.1. Eksport

Mo

ż

na eksportowa

ć

list

ę

wyra

ż

e

ń

za pomoc

ą

polecenia menu File | Save Plotted Expressions lub

wciskaj

ą

c klawisze Ctrl + S. Wyra

ż

enia sa zapisywane w pliku XML, który mo

ż

na pó

ź

niej importowa

ć

.

3.7.2. Import

W celu importu zapisanego wyra

ż

enia, wybra

ć

polecenie menu File | Import.

- 13 -

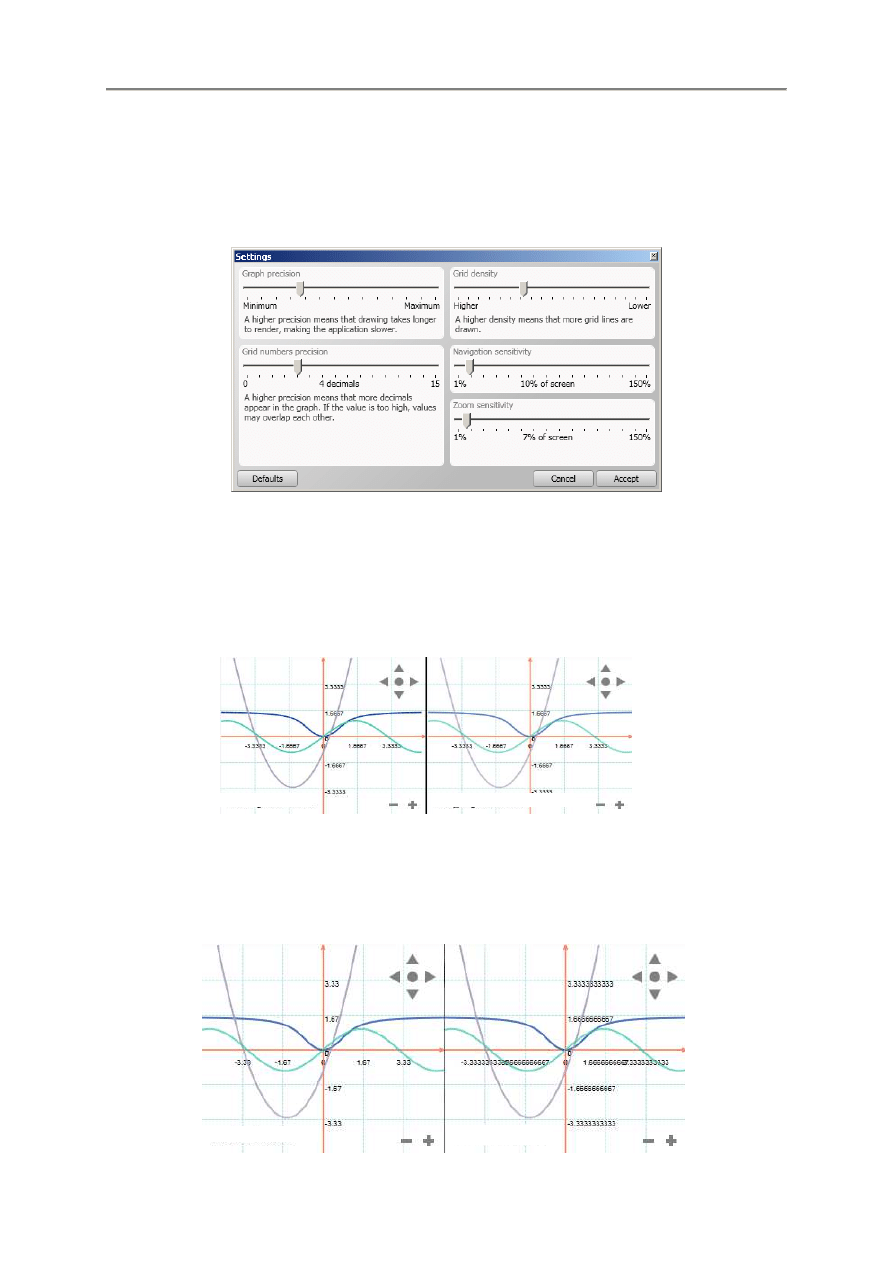
3.8. Preferencje

3.8.1. Wprowadzenie

W okienku dialogowym preferencji otwieranym poleceniem menu Application | Preferences mo

ż

na

konfigurowa

ć

wykresy,

3.8.2. Dokładno

ść

wykresów

Suwak w sekcji Graph Precision pozwala na ustawianie dokładno

ś

ci wykresów. Gdy dokładno

ść

jest

niska, rysowanie jest szybsze, jednak wygl

ą

d wykresu jest gorszy. Gdy dokładno

ść

jest wysoka,

rysowanie jest znacznie wolniejsze, ale wykres wygl

ą

da dokładniej.

3.8.3. Dokładno

ść

liczb siatki

Suwak w sekcji Grid Number Precision pozwala na ustawianie liczby znaków cyfr działek
wy

ś

wietlanych na wykresie. Gdy warto

ść

ta jest za wysoka, cyfry działek mog

ą

si

ę

na siebie nakłada

ć

.

Niska dokładno

ść

Wysoka dokładno

ść

2 znaki

10 znaków

- 14 -

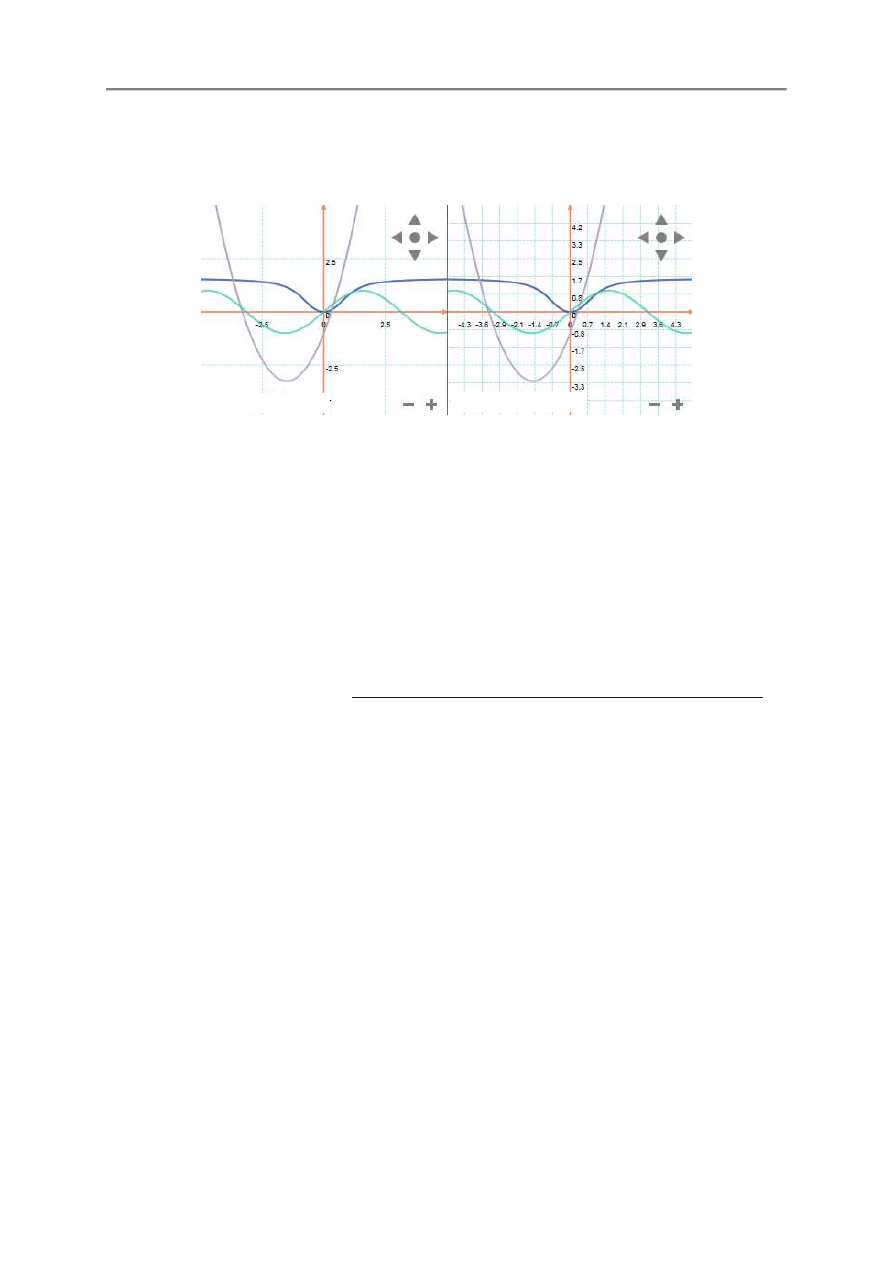
3.8.4. G

ę

sto

ść

siatki

Suwak w sekcji Grid Density pozwala na ustawianie ile linii siatki ma by

ć

wy

ś

wietlane.

3.8.5. Nawigacja i czuło

ść

skalowania

Ustawianie suwaków w sekcjach Navigation Sensitivity oraz Zoom Density pozwala na wybór
szybko

ś

ci przesuwania i skalowania wykresu.

3.9. Problemy i ich rozwi

ą

zywanie

3.9.1. Aplikacja zawiesza si

ę

przy starcie

Aplikacja ta wymaga zainstalowania .NET Framework 4.0. Je

ś

li nie jest jeszcze zainstalowana, mo

ż

na

ja

ś

ci

ą

gn

ąć

z Internetu pod adresem

http://www.microsoft.com/download/en/details.aspx?id=17718

3.9.2. Wykres jest rysowany niepoprawnie

Problemy z rysowaniem pojawiaj

ą

si

ę

gdy funkcja ma wiele asymptot pionowych lub gdy funkcja

zmienia si

ę

zbyt szybko.

Mo

ż

na wypróbowa

ć

wtedy zwi

ę

kszenie dokładno

ś

ci wykresu w okienku dialogowym preferencji.

3.9.3. Aplikacja działa powoli

Jest to znana niedogodno

ść

i ma miejsce przy wykre

ś

laniu funkcji. Wyst

ę

puje to podczas skalowania

okna lub przy poruszaniu si

ę

po wykresie.

Trzeba si

ę

z tym pogodzi

ć

lub wypróbowa

ć

obni

ż

enie dokładno

ś

ci wykresu w okienku dialogowym

preferencji.

3.9.4. Uzyskuj

ę

niezdefiniowany bł

ą

d zmiennej

Trzeba wtedy zidentyfikowa

ć

czy przypadkowo nie wpisali

ś

my niewła

ś

ciwej litery. Warto równie

ż

zapozna

ć

si

ę

z regułami składni wyra

ż

e

ń

.

Niska g

ę

sto

ść

Wysoka g

ę

sto

ść

- 15 -

3.9.5. Uzyskuj

ę

niezdefiniowany bł

ą

d funkcji

W takim przypadku trzeba sprawdzi

ć

reguły składni wyra

ż

e

ń

.

3.9.6. Uzyskuj

ę

bł

ą

d pustego stosu

Bł

ą

d ten pojawia si

ę

zwykle gdy nie podali

ś

my poprawnej liczby parametrów funkcji.Trzeba sprawdzi

ć

reguły składni wyra

ż

e

ń

.

3.9.7. Uzyskuj

ę

bł

ą

d niedomkni

ę

tych nawiasów

Bł

ą

d ten jest samoobja

ś

niaj

ą

cy. Nale

ż

y sprawdzi

ć

poprawno

ść

stosowanych nawiasów.

3.9.8. Mam inne problemy nie opisane w typ przewodniku

W takim przypadku mo

ż

na skontaktowa

ć

si

ę

z dostawc

ą

programu korzystaj

ą

c z dost

ę

pnych form

kontaktu. Nale

ż

y wówczas doł

ą

czy

ć

dokładny opis problemu oraz sytuacj

ę

w jakiej problem wyst

ą

pił,

doł

ą

czaj

ą

c ewentualnie zrzut ekranu. Plik informacyjny Log znajduj

ą

cy si

ę

w katalogu Logs b

ę

dzie

równie

ż

bardzo po

żą

dany.

4. Kalkulator macierzowy

4.1. Informacje ogólne

Kalkulator macierzowy Matrix Calculator słu

ż

y do obliczania macierzy matematycznych. Macierz taka

jest regularn

ą

tablic

ą

liczb, symboli lub wyra

ż

e

ń

. Indywidualne obiekty macierzy nosz

ę

nazwy

elementów lub wej

ść

.

4.2. Ograniczenia

Kalkulator ten jest ograniczony do 64-bitowych liczb zmiennoprzecinkowych (w przybli

ż

eniu do

zakresu od ±5,0 × 10

-324

do ±1,7 × 10

308

, lub do 15-16 cyfr).

Rozmiar macierzy jest ograniczony tylko wielko

ś

ci

ą

pami

ę

ci systemowej, ale nie jest wygodne

korzystanie z du

ż

ych macierzy (np. wi

ę

kszych od 100 x 100), poniewa

ż

powa

ż

nie zwalnia prac

ę

programu.

4.3. Przewodnik podstawowy

4.3.1. Wprowadzanie macierzy

W oknie aplikacji Matrix Calculator, macierze s

ą

zestawiane na li

ś

cie Matrices w lewym panelu.

Istniej

ą

ju

ż

tam domy

ś

lne macierze (zerowa i jednostkowa). Nie zachowuj

ą

si

ę

one jak zwykłe

macierze i rozmiar ich nie jest ustalony, a wi

ę

c s

ą

kompatybilne z ró

ż

nymi typami operacji z innymi

macierzami.

Wprowadzanie macierzy mo

ż

na wykona

ć

przez tworzenie macierzy lub przez import macierzy.

- 16 -

Tworzenie macierzy

•

Krok 1 – Najpierw otworzy

ć

menu Matrix i klikn

ąć

opcj

ę

New matrix. Alternatywnie, mo

ż

na

równie

ż

klikn

ąć

prawym klawiszem myszki na li

ś

cie Matrices i w otworzonym menu

kontekstowym wybra

ć

opcj

ę

New matrix.

•

Krok 2 – W otworzonym okienku dialogowym New matrix wybra

ć

szeroko

ść

oraz wysoko

ść

macierzy, po czym klikn

ąć

przycisk Apply.

•

Krok 3 – Wypełni

ć

pola utworzonej macierzy, nada

ć

jej nazw

ę

i opcjonalny opis, po czym

klikn

ąć

przycisk Accept.

Utworzone macierze mo

ż

na zapisa

ć

poleceniem menu File | Save As.

Import macierzy

Aktualnie, opcja ta jest jeszcze niedost

ę

pna.

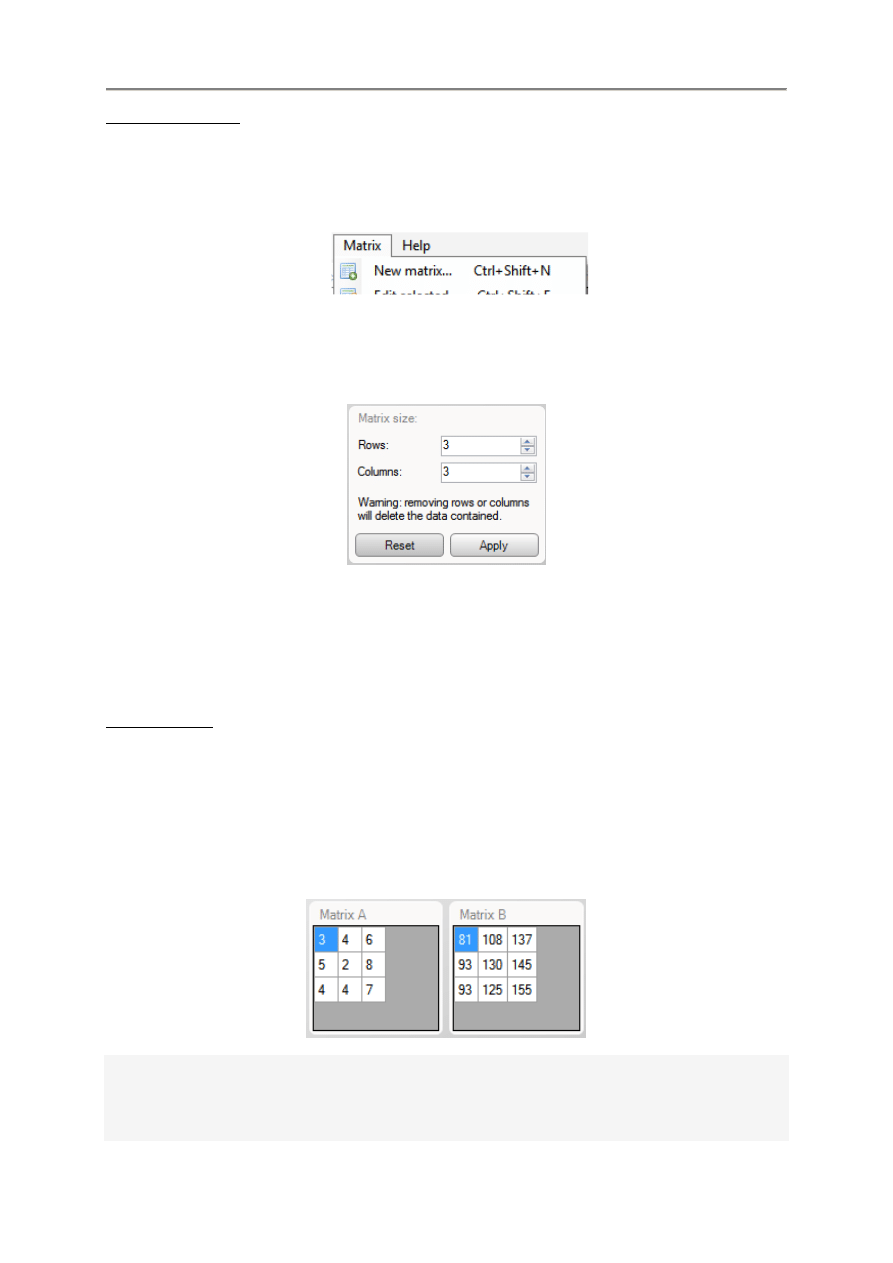
4.3.2. Wykonywanie oblicze

ń

W głównym oknie programu znajduj

ą

si

ę

dwa pola zwane slotami o nazwach Matrix A i Matrix B.

S

ą

to dwa obiekty stosowane w obliczeniach.

W celu wstawienia macierzy do slotu mo

ż

na przeci

ą

ga

ć

i upuszcza

ć

j

ą

z listy lub wybra

ć

polecenie

menu Matrix | Insert in slot albo wykona

ć

to samo za pomoc

ą

menu kontekstowego.

Po wstawieniu macierzy, klikn

ąć

przycisk odpowiedniej operacji. Gdy popełnimy bł

ą

d, wówczas

w slocie wyniku Result uka

ż

e si

ę

komunikat o bł

ę

dzie,

- 17 -

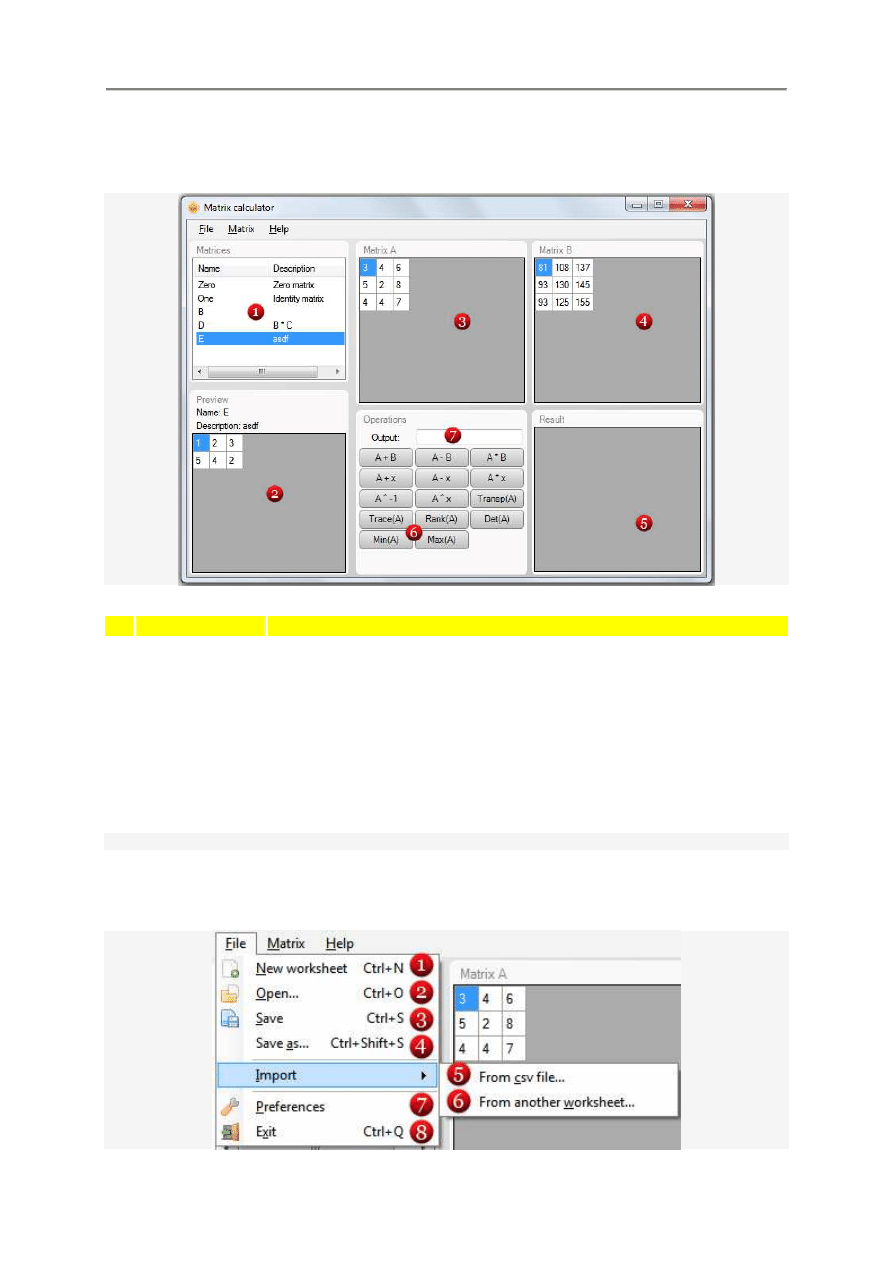
4.4. Okno kalkulatora macierzy

4.4.1. Przykładowe okno kalkulatora

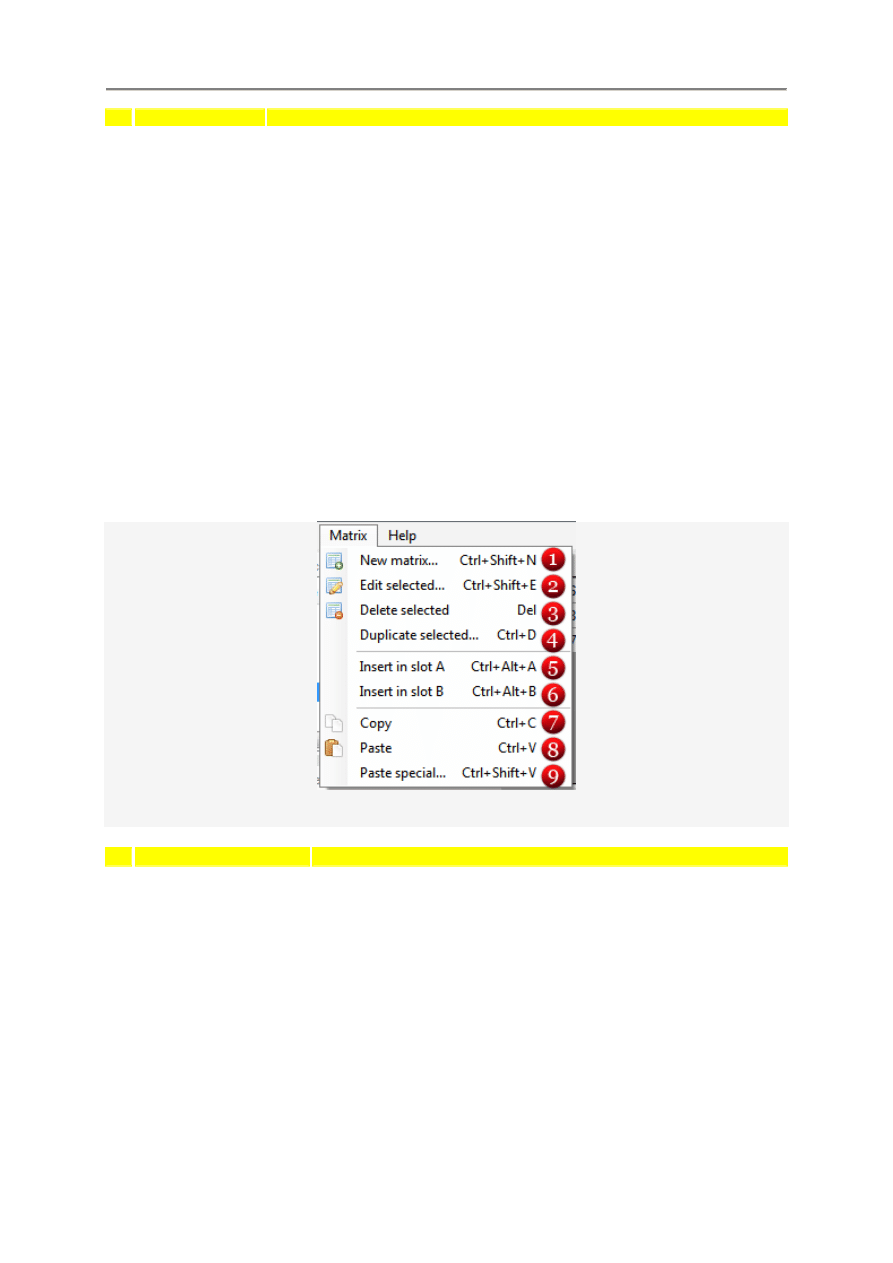
4.4.2. Menu plików File

Nazwa

Opis

Lista macierzy

Znajduj

ą

si

ę

tu wszystkie utworzone macierze

Panel podgl

ą

du

Wy

ś

wietlana jest tu macierz zaznaczona na li

ś

cie.

Slot A

Pierwszy składnik operacji

Slot B

Drugi składnik operacji

Wynik

Tu pojawia si

ę

wyniki operacji

Funkcje

Wszystkie zdefiniowane funkcje.

Komunikat

W razie bł

ę

du (np. niekompatybilne macierze), jest on tu wy

ś

wietlany

- 18 -

Nazwa

Opis

Nowy arkusz

Tworzy nowy arkusz

Otwórz...

Otwiera istniej

ą

cy arkusz *

Zapisz

Zapisuje aktualny arkusz *

Zapisz jako...

Zapisuje jako nowy arkusz *

Import z pliku csv ... Import macierzy z pliku CSV (opcja jeszcze nie dost

ę

pna)

Import z arkusza...

Import macierzy z istniej

ą

cego arkusza * (opcja jeszcze nie dost

ę

pna)

Preferencje

Otwiera okienko dialogowe preferencji

Wyj

ś

cie

Zamyka aplikacj

ę

* Arkusz jest zdefiniowany jako kolekcja macierzy.

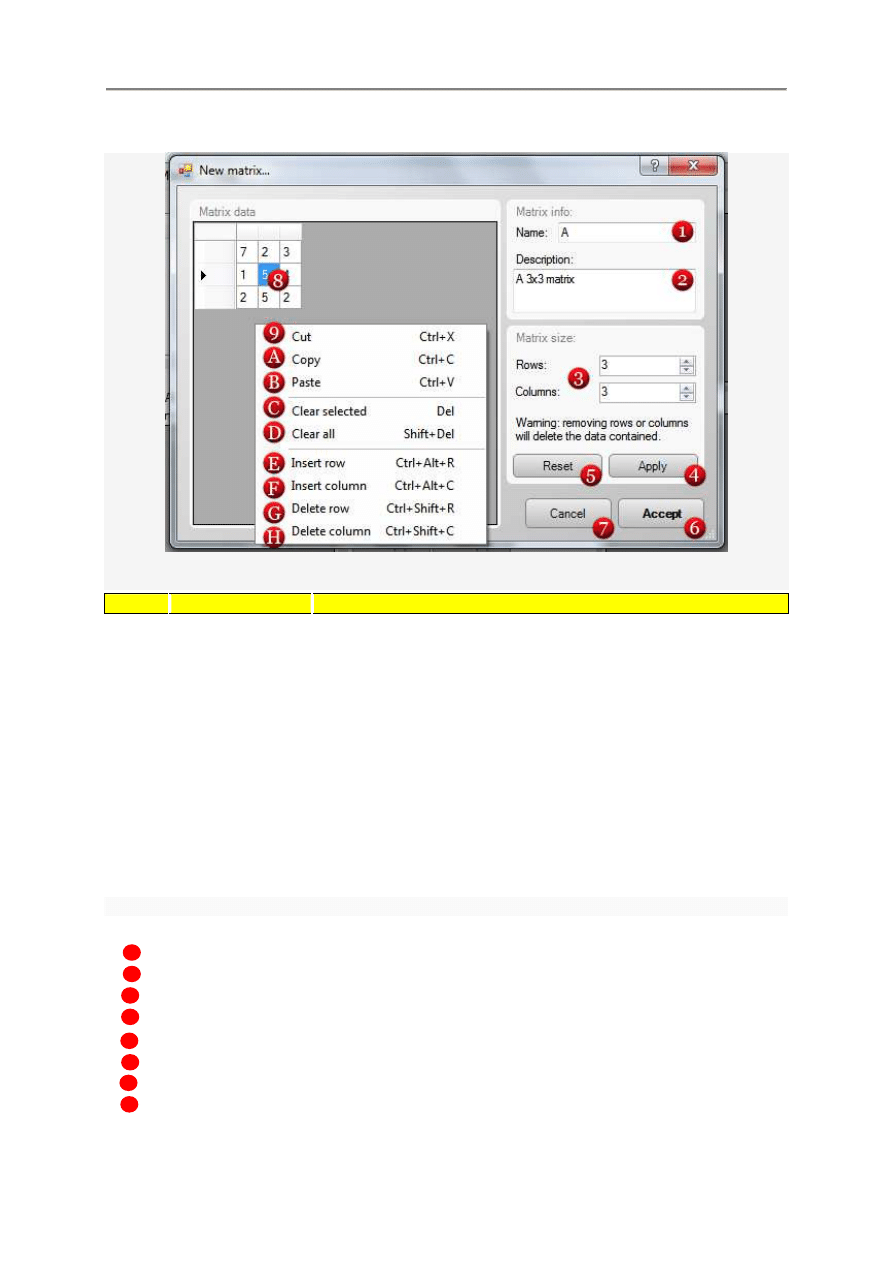
4.4.3. Menu macierzy Matrix

Menu to mo

ż

na równie

ż

otworzy

ć

jako menu kontekstowe (prawy klawisz myszki).

Nazwa

Opis

Nowa macierz...

Tworzy nowa macierz

Edycja zaznaczenia...

Edytuje zaznaczon

ą

macierz

Usuni

ę

cie zaznaczenia

Usuwa zaznaczone macierze

Duplikat zaznaczenia...

Tworzy now

ą

macierz opart

ą

na zaznaczonej

Wstaw w slot A

Wstawia macierz w slocie A (pierwszy czynnik)

Wstaw w slot B

Wstawia macierz w slocie A (drugi czynnik)

Kopiuj

Kopiuje zaznaczon

ą

macierz do pami

ę

ci (opcja jeszcze niedost

ę

pna)

Wklej

Wkleja macierz z pami

ę

ci (opcja jeszcze niedost

ę

pna)

Wklej specjalnie

Wkleja macierz z innej aplikacji (opcja jeszcze niedost

ę

pna)

- 19 -

4.4.4. Menu pomocy Help

Nazwa

Opis

O programie

Otwiera okienko z informacjami o programie Tibi's Mathematics Suite.

Pomoc

Wy

ś

wietla plik pomocy tej aplikacji

4.5. Skróty klawiszowe

Kombinacja klawiszy

Odpowiednik

Operacja

Ctrl + N

File - New worksheet

Tworzy nowy arkusz

Ctrl + O

File - Open...

Otwiera arkusz

Ctrl + S

File - Save

Zapisuje arkusz

Ctrl + Shift + S

File - Save As...

Zapisuje arkusz jako nowy plik

Ctrl + Q

File - Exit

Zamyka aplikacj

ę

Ctrl + Shift + N

Matrix - New matrix...

Tworzy now

ą

macierz

Ctrl + Shift + E

Matrix - Edit selected...

Edytuje zaznaczon

ą

macierz

Del

Matrix - Delete selected

Usuwa zaznaczon

ą

macierz

Ctrl + D

Matrix - Duplicate selected... Duplikuje zaznaczon

ą

macierz

Ctrl + Alt + A

Matrix - Insert in slot A

Wstawia macierz do slotu A

Ctrl + Alt + B

Matrix - Insert in slot B

Wstawia macierz do slotu A

Ctrl + C

Matrix - Copy

Kopiuje zaznaczon

ą

macierz

Ctrl + V

Matrix - Paste

Wkleja now

ą

macierz

Ctrl + Shift + V

Matrix - Paste special...

Wkleja z innej aplikacji

F1

Help - Help

Otwiera okno pomocnika

4.6. Funkcje wszystkich przycisków

Przycisk

Opis

A + B

Dodaje dwie macierze

A - B

Odejmuje macierz B od macierzy A

A * B

Mno

ż

y dwie macierze

A + x

Dodaje liczb

ę

do ka

ż

dego elementu macierzy A

A - x

Odejmuje liczb

ę

od ka

ż

dego elementu macierzy A

A * x

Mnozy liczbe przez kazdy element macierzy A

A ^ -1

Oblicza odwrotno

ść

macierzy A

A ^ x

Podnosi macierz A do całkowitej pot

ę

gi x

Transp(A) Oblicza transpozycj

ę

macierzy A

Trace(A) Oblicza

ś

lad macierzy A (suma elementów na przek

ą

tnej)

Rank(A) Oblicza rz

ą

d macierzy A

Det(A)

Oblicza wytznacznik macierzy A

Min(A)

Znajduje minimalny element macierzy A

Max(A)

Znajduje maksymalny element macierzy A

- 20 -

4.7. Edytor macierzy

Przycisk

Nazwa

Opis

Nazwa

Nazwa macierzy. Pole to jest wymagane

Opis

Opis macierzy. Pole to jest opcjonalne

Rozmiar macierzy

Zmiana liczby wierszy i kolumn macierzy

Przycisk
stosowania

Aktualizuje macierz z nowym rozmiarem

Przycisk
resetowania

Resetuje wiersze i kolumny

Przycisk
akceptacji

Zapisuje zmodyfikowan

ą

macierz i zamyka to okienko

Gdy istniej

ą

puste komórki, wypełniane s

ą

warto

ś

ciami 0

Przycisk
anulowania

Usuwa zmodyfikowan

ą

macierz, i zamyka to okienko

Siatka

Tu mo

ż

na edytowa

ć

elementy macierzy.

Menu kontekstowe siatki

Wytnij

Wycina zaznaczone komórki

Kopiuj

Kopiuje zaznaczone komórki do pami

ę

ci

Wklej

Wkleja komorki z pami

ę

ci

Usu

ń

zaznaczone

Ustawia warto

ś

ci zaznaczonych komórek na 0

Usu

ń

wszystkie

Ustawia warto

ś

ci calej macierzy na 0

Wstaw wiersz

Wstawia wiersz przed zaznaczon

ą

komórk

ą

Wstaw kolumn

ę

wia kolumn

ę

przed zaznaczon

ą

komórk

ą

Usu

ń

wiersz

Usuwa wiersz zawieraj

ą

cy zaznaczone komórki

Usu

ń

kolumn

ę

Usuwa kolumn

ę

zawieraj

ą

c

ą

zaznaczone komórki

A

H

G

F

B

C

D

E

- 21 -

5. Kalkulator naukowy

5.1. Interfejs u

ż

ytkownika

Wy

ś

wietlacz

Obszar indykatora
Usuwanie funkcji i pomoc
Operacje podstawowe
Klawisze numeryczne
Funkcje pami

ę

ci

Funkcje zaawansowane

5.2. Ograniczenia

Kalkulator ten jest ograniczony do 64-bitowych liczb zmiennoprzecinkowych (w przybli

ż

eniu do

zakresu od ±5,0 × 10

-324

do ±1,7 × 10

308

, lub do 15-16 cyfr).

5.3. Przycisk drugiej funkcji

5.3.1. Opis

Przycisk drugiej funkcji 2ndf jest stosowany do zmiany funkcji klikni

ę

tego

przycisku.

Zwykle, druga funkcja jest odwrotno

ś

ci

ą

funkcji przypasanej do przycisku.

Druga funkcja jest wy

ś

wietlana na szaro powy

ż

ej danego przycisku.

Mo

ż

na znale

źć

wi

ę

cej informacji o danej funkcji i drugiej funkcji danego

przycisku gdy wska

ż

emy go myszk

ą

Mo

ż

na równie

ż

korzysta

ć

z drugiej funkcji klikaj

ą

c dany przycisk prawym klawiszem myszki.

- 22 -

5.3.2. Przykład

Aby obliczy

ć

pierwiastek kwadratowy z liczby nale

ż

y klikn

ąć

przycisk drugiej funkcji 2ndf, po czym

klikn

ąć

przycisk x

2

. Uwaga: Mo

ż

na równie

ż

klikn

ąć

przycisk x

2

prawym klawiszem myszki.

5.4. Warto

ś

ci bezwzgl

ę

dne

5.4.1. Opis

W matematyce, warto

ść

bezwzgl

ę

dna (moduł) jest liczb

ą

oznaczana jako |n|, która jest równa tej

liczbie z pomini

ę

ciem jej znaku.

5.4.2. Przykłady

|6| = 6

|-4| = 4

5.5. Kombinatoryka

5.5.1 Silnia

W matematyce, silnia liczby naturalnej oznaczana jako n! jest iloczynem wszystkich liczb naturalnych
mniejszych lub równych n.

n! = 1

⋅⋅⋅⋅

2

⋅⋅⋅⋅

3

⋅⋅⋅⋅

...

⋅⋅⋅⋅

(n-1)

⋅⋅⋅⋅

n

Mo

ż

na to równie

ż

zapisa

ć

nast

ę

puj

ą

co:

1

!

n

k

n

k

=

=

∏

Zgodnie z konwencj

ą

, 0! = 1

Przykład:

5! = 1

⋅⋅⋅⋅

2

⋅⋅⋅⋅

3

⋅⋅⋅⋅

4 5 = 120

5.5.2. Permutacje

W matematyce, permutacja zestawu obiektów jest zdefiniowana jako szczególne uporz

ą

dkowanie tych

elementów, np. permutacje zestawu liczb {1, 2, 3} maj

ą

posta

ć

:

(1, 2, 3); (1, 3, 2); (2, 1, 3); (2, 3, 1); (3, 1, 2); (3, 2, 1);

Liczba permutacji tego zestawu wynosi n!

- 23 -

5.5.3. Permutacje na k-obiektach

Przykładowe permutacje dwóch elementów zestawu {1, 2, 3} maj

ą

posta

ć

:

(1, 2); (2, 1); (1, 3); (3, 1); (2, 3); (3, 2);

Liczba permutacji k-obiektów obliczana jest za pomoc

ą

poni

ż

szego wzoru:

Po uproszczeniu otrzymujemy:

5.5.4 Kombinacje

W matematyce, kombinacja jest metod

ą

wybierania pewnej liczby obiektów z du

ż

ego zestawu, gdzie

kolejno

ść

nie ma znaczenia.

Przykładowo, kombinacje 2 obiektów z zestawu {1, 2, 3} maj

ą

posta

ć

:

{1, 2}; {1, 3}; {2, 3};

Liczba permutacji obliczana jest za pomoc

ą

poni

ż

szego wzoru:

Po uproszczeniu otrzymujemy:

5.6. Stałe

•

ππππ

(pi)

•

e

5.6.1. Stała

ππππ

(pi)

Liczba

ππππ

(czasem zapisywana jako pi) jest stał

ą

matematyczn

ą

, która jest stosunkiem obwodu

dowolnego koła euklidesowego do jego

ś

rednicy.

Przybli

ż

ona warto

ść

ππππ

wynosi:

π

≈

3,141592

Liczba pi ma wiele zastosowa

ń

w matematyce, w nauce i w in

ż

ynierii co sprawia, ze jest jedn

ą

z najwa

ż

niejszych stałych.

- 24 -

5.6.2. Stała e

Liczba e jest wa

ż

na stal

ą

matematyczn

ą

, która jest podstaw

ą

logarytmów naturalnych.

Stała ta jest wynikiem poni

ż

szej granicy:

Jej przybli

ż

ona warto

ść

wynosi:

e

≈≈≈≈

2,71828

5.7. Cz

ęś

ci całkowite i ułamkowe

5.7.1. Cz

ęść

całkowita

W matematyce, cz

ęść

całkowita Floor liczby n, jest najwi

ę

ksz

ą

liczb

ą

całkowit

ą

mniejsz

ą

od n.

W matematyce, cz

ęść

całkowita Ceiling liczby n, jest najmniejsz

ą

liczb

ą

całkowit

ą

wi

ę

ksz

ą

od n.

Notacja:

Floor lliczby n;

⌊

⌊

⌊

⌊n⌋⌋⌋⌋

Ceiling lliczby n;

⌈

⌈

⌈

⌈n⌉⌉⌉⌉

Przykłady:

5.7.2. Cz

ęść

ułamkowa

W matematyce, ka

ż

da liczba rzeczywista mo

ż

e byc zapisana jako n + r, gdzie n jest liczba całkowit

ą

,

natomiast r jest (cz

ęść

ułamkowa) jest nieujemn

ą

liczb

ą

rzeczywist

ą

mniejsz

ą

od 1.

Cz

ęść

ułamkowa liczby n mo

ż

e by

ć

zapisana jako ró

ż

nica miedzy n, a jej cz

ęś

ci

ą

całkowit

ą

Floor.

Przykłady:

- 25 -

5.8. Skróty klawiszowe

Kombinacja klawiszy Przycisk równowa

ż

ny

Działanie

Num+ (+)

+

Dodaje liczby do siebie

Num- (-)

-

Odejmuje liczby od siebie

Num*

*

Mno

ż

y dwie liczby

Num/ (/)

/

Dzieii jedn

ą

liczb

ę

przez drug

ą

Escape

AC

Resetuje wszelkie obliczenia

Delete

Clear

Usywa aktualn

ą

liczbe

Backspace

⌫

Usuwa ostatnio wstawion

ą

liczb

ę

F1

Help

Otwiera pomoc tej aplikacji

Enter

=

Wykonuje obliczenia.

Ctrl + Q

Zamyka t

ą

aplikacj

ę

5.9. Mno

ż

enie przez odwrotno

ść

W matematyce, odwrotno

ść

liczby n jest liczb

ą

, która pomno

ż

ona przez n daje w wyniku liczb

ę

1.

Odwrotno

ść

liczby n oznacza si

ę

nast

ę

puj

ą

co:

5.10. Funkcje wszystkich przycisków

Przycisk

Opis

+

Dodaje liczby do siebie

-

Odejmuje liczby od siebie

*

Mnozy dwie liczby

/

Dzieii jedn

ą

liczb

ę

przez drug

ą

±

Zmienia znak

MOD

Oblicza reszt

ę

z dzielenia dwóch liczb

AC

Resetuje wszelkie obliczena

Clear

Usywa aktualn

ą

liczbe

⌫

Usuwa ostatnio wstawion

ą

liczb

ę

Help

Otwiera pomoc tej aplikacji

M+

Dodaje wy

ś

wietlan

ą

liczb

ę

do pami

ę

ci

M-

Odejmuje wy

ś

wietlan

ą

liczb

ę

od pami

ę

ci

MC

Oczyszcza pami

ęć

: Usuwa cal

ą

zawarto

ść

pami

ę

ci.

MS

Wstawianie do pami

ę

ci: Wstawia do pami

ę

ci zawarto

ść

wy

ś

wietlacza

MR

Wyciaganie z pami

ę

ci. Wy

ś

wietla zawarto

ść

pami

ę

ci

2ndf

Aktywuje drug

ą

funkcj

ę

nast

ę

pnego przycisku

e

n

Funkcja wykładnicza

- 26 -

ln

Oblicza logarytm naturalny

10

n

Oblicza 10 do pot

ę

gi n

log

Oblicza logarytm dziesi

ę

tny

log

n

x

Oblicza logarytm x o podstawie n

{x}

Oblicza ułamkow

ą

cz

ęść

liczby

[x]

Oblicza calkowit

ą

cz

ęść

liczby

-Abs

Oblicza ujemn

ą

warto

ść

liczby bezwzgl

ę

dnej

Abs

Oblicza warto

ś

c liczby bezwzgl

ę

dnej

1/x

Oblicza odwrotno

ś

c liczby

n

√

x

Oblicza n-ty pierwiastek liczby x

x

n

Oblicza x do potegi n-tej

arcsin

Oblicza arcus sinus liczby (wynik w radianach)

sin

Oblicza sinus liczby (w radianach)

arccos

Oblicza arcus cosinus liczby (wynik w radianach)

cos

Oblicza cosinus liczby (w radianach)

arctan

Oblicza arcus tangens liczby (wynik w radianach)

tan

Oblicza tangens liczby (w radianach)

√

x

Oblicza pierwiastek kwadratowy liczby x

x

2

Oblicza x do kwadratu

arcsinh

Oblicza arcus sinus hiperboliczny liczby

sinh

Oblicza sinus hiperboliczny liczby

arccosh

Oblicza arcus cosinus hiperboliczny liczby

cosh

Oblicza cosinus hiperboliczny liczby

arctanh

Oblicza arcus tangens hiperboliczny liczby

tanh

Oblicza tangens hiperboliczny liczby

3

√

x

Oblicza trzeci pierwiastek liczby x

x

3

Oblicza x do pot

ę

gi trzeciej

2

π

Wy

ś

wietla warto

ść

2

ππππ

π

Wy

ś

wietla stal

ą

ππππ

e

Wy

ś

wietla stal

ą

e

xPy

Oblicza rozmieszczenie y obiektów z liczby x

xCy

Oblicza kombinacje y obiektów z liczby x

x!

Oblicza silni

ę

x