v.5.1. Beta

FREEWARE

http://www.matrixer.narod.ru/

MATRIXER

Program ekonometryczny

MATRIXER v. 5.1. Instalka. Freeware. ENG (2004). Jest to program ekonometryczny, którego
autorem jest Alexander Tsyplakov. Program ten pracuje tylko w środowisku Windows. Można
korzystać z niego bezpłatnie tylko dla celów niekomercyjnych. Aplikacja ta jest przydatna nie tylko do
nauki ekonometrii, ale przede wszystkim w różnych pracach badawczych. Jego głównymi funkcjami są
różne metody analizy regresji (liniowa, nieliniowa, logitowa, probitowa, nieparametryczna),
zróżnicowane testy ekonometryczne oraz statystyki opisowe. Wszystkie analizy są ilustrowane
graficznie. Program obsługuje wektory i macierze (stąd jego nazwa) i można je importować ze źródeł
zewnętrznych (program otwiera pliki TXT oraz CSV).

Przekład:

Robert Wiśniewski

http://chomikuj.pl/bobwis

- 2 -

SPIS TREŚCI POMOCNIKA

HELP

1. Program Matrixer
2. Szybki start (wskazówki dla początkujących)
2.1. Jak importować dane
2.1.1. Jak importować dane z arkusza Excela przy korzystaniu ze schowka Windows
2.1.2. Jak importować niestandardowe dane przy korzystaniu ze schowka Windows
2.1.3. Jak importować dane z pliku tekstowego
2.2. Jak wpisywać dane
2.2.1. Wartości brakujące
2.2.2. Komentarze
2.2.3. Tryb wstawiania
2.3. Tekstowy format macierzy
2.4. Jak estymować regresję liniową
2.4.1. Jak estymować regresję liniową (za pomocą przycisku i menu) – 1
2.4.2. Jak wybierać zmienne
2.4.3. Jak estymować regresję liniową szybko i efektywnie – 2
2.5. Jak rysować wykres (diagram)
2.5.1. Jak rysować wykres korzystając z okna poleceń
2.5.2. Jak rysować wykres korzystając z menu Show
2.5.3. Jak rysować wykres korzystając z menu Panels
3. Macierze i zmienne w macierzach
3.1. Macierz modeli
3.2. Zmienne w macierzach
4. Skalary
5. Łańcuchy
6. Modele
7. Interfejs
7.1. Panel macierzy (zmienne)
7.2. Edytor tabel dla macierzy
7.3. Okno poleceń
8. Polecenia
9. Wykresy
9.1. Wykresy i diagramy
Przykład A
Przykład B
Przykład C
Przykład D
10. Polecenia przypisywania
11. Formuły
11.1. Podstawienia
11.2. Funkcje dynamiczne
12. Wyrażenia skalarne
13. Wyrażenia macierzowe
14. Funkcje
15. Estymacja modeli ekonometrycznych
15.1. Estymacja liniowych modeli regresji
15.2. Estymacja nieliniowych modeli regresji
15.3. Regresja logitowa i probitowa
16. Procedury statystyczne
16.1. Statystyki opisowe
16.2. Macierz korelacji
16.3. Funkcja autokorelacji
17. Wyniki estymacji
17.1. Estymacje i statystyka
17.2. Test usuwania zmiennych
17.3. Obserwacje wpływowe

- 3 -

17.4. Efekty drugiego rzędu
17.5. Histogram reszt standaryzowanych
17.6. Ograniczenia (parametrów funkcji)
18. Makra (grupy poleceń)
18.1. Pliki makr (pliki poleceń)
18.2. Edytor makr
18.3. Polecenia sterowania w makrach
18.4. Komunikaty i sygnały w makrach

1. Program Matrixer

Program Matrixer może być stosowany do analizy danych oraz do przeprowadzania różnych obliczeń
ekonometrycznych i statystycznych.

Korzystając z tego programu można estymować (i testować hipotezy) poniższych modeli:



Regresja liniowa.



Regresja nieliniowa



Regresja dwójkowa (logitowa i probitowa).



Inne modele.

Program Matrixer pracuje z obiektami poniższych typów:



Macierze.



Zmienne (kolumny macierzy).



Skalary.



Łańcuchy.



Modele.

Program Matrixer jest obsługiwany za pomocą:



Menu i skrótów klawiszowych (np. menu Panels).



Poleceń wprowadzanych w oknie poleceń Command Window.



Makr (bloków poleceń).

2. Szybki start (wskazówki dla początkujących)



Najpierw trzeba zaimportować dane lub je wprowadzić.



Przed rozpoczęciem pracy w programie Matrixer, warto zastanowić się chwilę nad
zrozumieniem jego ważnej właściwości. Dane dostępne w programie w danym momencie
znajdują się w jednym katalogu (katalog roboczy).



Przy wyjściu z programu, wszystkie macierze (tabele danych), jakie zostały utworzone
w bieżącej sesji (za wyjątkiem pamięci), są automatycznie przechowywane w katalogu
roboczym w plikach z rozszerzeniem MAT.



Przy uruchamianiu programu, wszystkie pliki poprzednio zapisane w katalogu roboczym są
automatycznie otwierane i są widoczne w panelu Matrices.



Właściwości te tłumaczą dlaczego program nie ma tradycyjnych poleceń menu zapisywania
Save oraz otwierania Open.



Po załadowaniu lub utworzeniu danych można rozpocząć z nimi pracę, np. estymować
regresję liniową lub narysować wykres.

2.1. Jak importować dane

Najprostszym sposobem jest import danych przy korzystaniu ze schowka Windows.



Załóżmy, że dane znajdują się w arkuszu Excela (lub w innym programie Windows
zawierającym edytor tabel). W takim przypadku patrz rozdział 2.1.1.

- 5 -



Nieco bardziej złożony jest import przy korzystaniu ze schowka, ale nie z edytora tabel
(np. WordPad, lub strona Web). Takie dane mogą być rozdzielane nie za pomocą symboli
tabulacji, ale za pomocą spacji lub przecinków i czasem mogą zawierać teksty. W takim
przypadku patrz rozdział 2.1.2.



Można również importować taki typ danych z pliku tekstowego. W takim przypadku patrz
rozdział 2.1.3.

2.1.1. Jak importować dane z arkusza Excela przy korzystaniu ze schowka Windows



Zaznaczyć prostokątny blok liczb w arkuszy Excela.



Skopiować dane do schowka Windows(zwykle można w tym celu skorzystać ze skrótu
klawiszowego CTRL + C).



Utworzyć w programie Matrixer nową macierz przez wciśnięcie klawisza INS w panelu
Matrices (patrz rozdział 7.1.) i w otworzonym okienku dialogowym wpisanie odpowiedniej
nazwy macierzy



W edytorze tabel Table Editor (patrz rozdział 7.2.) wkleić dane ze schowka przez
wciśnięcie klawiszy CTRL + V.



Zamknięcie edytora tabel powoduje zapisanie utworzonej macierzy.

Uwagi:



Edytory tabel można napotkać w wielu statystycznych lub ekonometrycznych programów
Windows. Opisana tu procedura pozwala na import danych z takich programów.



Symbolem separatora części dziesiętnych w liczbach Separatrix może być przecinek lub
kropka. Program Matrixer przy wprowadzaniu liczb zamienia przecinki na kropki.



Gdy do pierwszego wiersza kopiowany jest blok zawierający nazwy zmiennych, wówczas
Matrixer umieszcza te nazwy odpowiednio w nagłówkach nazw zmiennych (kolumn).



Można wstawiać bloki danych ze schowka do istniejących macierzy. Gdy wklejany blok nie
zawiera nazw, wówczas komórki mogą być przesuwane w dół w celu utworzenia wolnego
miejsca dla tego bloku. Gdy blok zawiera nazwy, wówczas zostaną utworzone nowe
zmienne (kolumny macierzy) z tymi nazwami. Istniejące kolumny mogą być wtedy
przesunięte w prawo,

2.1.2. Jak importować niestandardowe dane przy korzystaniu ze schowka Windows



Zaznaczyć fragment źródłowego programu z danymi.



Skopiować zaznaczony fragment danych do schowka Windows.



W programie Matrixer wybrać polecenie menu Matrix | Import | From Windows Clipboard
lub wcisnąć klawisze ALT + M w panelu Matrices.



Wprowadzić odpowiednią nazwę macierzy do której dane będą importowane.

Uwagi:



Przeczytać dokładnie uwagi podane w rozdziale 2.1.3.

- 6 -

2.1.3. Jak importować dane z pliku tekstowego



W programie Matrixer wybrać polecenie menu Matrix | Import | From File lub wcisnąć
klawisze ALT + M w panelu Matrices.



Wprowadzić odpowiednią nazwę macierzy do której dane będą importowane.

Uwagi:



Skorzystać z polecenia menu Matrix | Import | Options w celu sterowania jak dane mają
być importowane.



Najważniejszą opcją jest Presume columns of fixed width (stosuj kolumny o stałej
szerokości). Pozwala to na import sformatowanych danych rozdzielanych separatorem
w postaci spacji. Poniżej pokazano przykład takich danych:

Animal Y X

Rhesus monkey 6.800 179.003

Kangaroo 34.998 56.003

Gdy opcja ta nie jest zaznaczona (co jest ustawieniem domyślnym), wówczas program
zakłada, że pola danych są rozdzielane takimi separatorami jak przecinek, tabulator,
spacja. Itp. Ilustruje to poniższy przykład:

"ARGENTINA","Machinery",480,703,599

"ARGENTINA","Business Construction",1403,2057,"NA"

Gdy stosowane są przecinki jako separatory, wówczas format ten często nosi nazwę
plików CSV (Comma Separated Value). Inne warianty tego formatu mogą korzystać
z takich separatorów jak: średnik (;) lub pionowy słupek (|).



W zależności od wybranej opcji, przecinek może być interpretowany jako separator między
liczbami lub jako przecinek dziesiętny.



Skorzystać z opcji „Substitutions Text->Number” w celu wprowadzenia wartości
liczbowych dla pól nienumerycznych, np. takich jak Mężczyzna / Kobieta. Dla brakujących
wartości (takich jak NA), korzystamy z liczby 8934567 (patrz rozdział 2.3.).



Tekst można zastąpić komentarzami (patrz rozdział 2.2.2.). Należy usunąć zaznaczenie
pola Store Text as Comment aby tego uniknąć.



W celu importu nazw zmiennych, wcisnąć klawisze CTRL + N w edytorze tabeli i wkleić
nazwy zmiennych ze schowka (tak jak je przedtem kopiowaliśmy).



Skorzystać z edytora tabel do edycji utworzonej macierzy. Usunąć z macierzy wszystko to,
co program wstawi omyłkowo. W następstwie importu, dane nieliczbowe można zastąpić
wartościami brakującymi (patrz rozdział 2.2.1.). Dzięki temu edytor będzie wyglądał
następująco:

*-**-*

.



Nie należy oczekiwać poprawnych wynikowi gdy dane będą odbiegały od standardu.



Często przydatne jest edytowanie danych przed ich importem.



Program nie może importować danych bezpośrednio z pliku nietekstowego (binarnego),
takiego jak np. pliku Excela.

w celu importu danych z Excela należy korzystać z formatu CSV.

- 7 -

2.2. Jak wpisywać dane



Otworzyć istniejącą macierz w edytorze tabel lub utworzyć niwą macierz przez kliknięcie
klawisza INS panelu macierzy Matrices oraz wprowadzenie odpowiedniej nazwy.



Po ręcznym wprowadzeniu danych, zamknąć edytor tabel i zapisać macierz.

Wskazówki:



Wygodne może być przełączenie się w tryb wstawiania Insert Mode (patrz rozdział 2.2.3)
np. korzystając z klawiszy CTRL + I, co pozwoli na wpisywanie cyfr wewnątrz istniejącej
macierzy.



Przy wpisywaniu danych liczbowych wygodne jest korzystanie z klawiatury numerycznej,
która staje się aktywna po wciśnięciu klawisza Num Lock.



Wartości brakujące (patrz rozdział 2.2.1) można wprowadzać wpisując znak gwiazdki (*).



Przed wprowadzeniem danych za pomocą klawiatury należy rozważyć celowości importu
danych.



Przy wprowadzaniu dużych ilości danych, nie zapomnieć o zapisywaniu ich od czasu do
czasu, np. klawiszami CTRL + S.

2.2.1. Wartości brakujące

Przez wartości brakujące rozumiemy pustkę w danych. Matrixer może interpretować brakujące dane
w większości procedur. Wewnętrznie, oraz formacie tekstowym macierzy, do reprezentowania
brakujących wartości stosowana jest liczba

8934567

. Wartości brakujące widoczne są na ekranie

jako ciąg:

*-**-*

. W celu wpisywania wartości brakujących w formułach skalarnych (patrz rozdział 4)

stosuje się zapis:

@missing

(lub

@na

).



Obserwacje z brakującymi danymi są pomijane w modelach i na wykresach.



W modelach szeregów czasowych Time Series (takich jak np. ARIMA), wykorzystywane
są tylko przylegle obserwacje bez wartości brakujących.



Gdy argument funkcji nie spełnia jego dziedziny, (np.

sqrt(-1)

,

ln(0)

,

1/0

) , wówczas

wynik może być błędny na skutek brakujących wartości.



Wynik operacji, w której jeden z argumentów jest wartością brakującą, może być również
jest wartością brakującą, np.:

100/0+200

.



Edytorze tabel, wartości brakujące można wprowadzać za pomocą symbolu gwiazdki (*).

2.2.2. Komentarze

Komentarze Comments są tekstami, które objaśniają charakter danych liczbowych zawartych
w macierzy.

Komentarze są zapisywane i edytowane razem z macierzą i stanowią jej część.

- 8 -

2.2.3. Tryb wstawiania

Tryb wstawiania Insert Mode pozwala na ciągłe wprowadzanie danych do wnętrza macierzy
w edytorze danych. Po zakończeniu edycji jednej komórki, wstawiamy dane do komórki następnej, itd.

Aby zatrzymać takie ciągłe wprowadzanie danych, wystarczy wcisnąć klawisz ESC.

Tryb wstawiania uruchamia się klawiszami CTRL + I.

2.3. Tekstowy format macierzy

Plik programu Matrix w formacie tekstowym (czytelnym dla użytkownika) jest plikiem z rozszerzeniem
MAT. Można go oglądać i edytować w zwykłym edytorze tekstowym. Tak więc prostym sposobem
importu danych Matrix przez inne programy jest pobieranie ich z pliku formatu MAT.

Plik taki ma poniższą formę:



Pierwszy wiersz zawiera informacje i wymiarach macierzy, tzn. ich liczbie wierszy i kolumn
oddzielanych spacjami.



Dalej mogą istnieć wiersze komentarzy. Każdy wiersz komentarzy zaczyna się dwoma
ukośnikami // . Komentarze nie są konieczne i mogą być puste.



Wiersz następujący po komentarzach zawiera nazwy zmiennych oddzielone spacjami.
Gdy zmienna nie ma nazwy, wówczas zamiast niej wstawiany jest znak #. Jeśli wiersz
zmiennych jest pusty,, zmienne są traktowane jako nie mające nazw. Jednak sam ten
wiersz musi być obecny. W przeciwnym razie pierwszy wiersz liczb może być traktowany
rzez program jako łańcuch nazw.



Plik kończy się datą utworzenia macierzy, Każdy wiersz macierzy stanowi osobny wiersz
pliku. Liczby w każdym wierszu są oddzielane spacjami. Format ten jest dowolny. Dane
brakujące są reprezentowane liczbą

8934567

Poniżej przytoczono przykład omawianego pliku:

-----------------------------------

2 3

//

Tu może znajdować się komentarz

x y z

2.3 4.2 -99

1E-10 8934567 5

-----------------------------------

2.4. Jak estytymować regresję liniową

Istnieje kilka różnych sposobów estymacji regresji liniowej Linear Regression.

Możemy wybrać dowolny z nich.



Posługiwanie się interfejsem z przyciskami i menu (patrz rozdział 2.4.1)



Szybka i efektywna estymacja regresji (patrz rozdział 2.4.3)

- 9 -

2.4.1. Jak estymować regresję liniową (za pomoca przycisku i menu) – 1



Wybrać polecenie menu Panels | Regression | Linear Regression. Otworzy się okienko
dialogowe Linear Regression.



Kliknąć w okienku Linear Regression pierwszy przycisk Choose po czym w otworzonym
oknie Choose Variables wybrać zmienną zależną Dependend Variable (patrz rozdział
2.4.2).



Kliknąć w okienku Linear Regression drugi przycisk Choose oraz wybrać zmienną
niezależną Regressor .



Kliknąć przycisk RUN

.

Uwagi:



Trzeci wiersz Weights jest wykorzystywany przy stosowaniu regresji ważonej Weighted
Regression. Pozostawić ten wiersz pusty gdy estymujemy zwykłą regresję liniową.



Odpowiednie polecenia można również wprowadzać w oknie poleceń Command Window
(patrz rozdział 7.3). Można z nich później również do szybkiej estymacji tej samej regresji.



Zapisywać polecenia do historii poleceń History of Commands

gdy chcemy później

estymować tą samą regresję

2.4.2. Jak wybierać zmienne

Rozdział ten objaśnia jak wybierać zmienną lub grupy zmiennych w oknie Choose Variables.

Po lewej stronie tego okna znajduje się lista zmiennych (wektorów) znajdujących się w katalogu
roboczym. Obok każdej zmiennej znajduje się liczba wskazująca na jej długość (gdy mówimy
o zmiennych, rozumiemy, że są to kolumny macierzy lub kolumna macierzy)

Po prawej stronie znajduje się lista wybranych zmiennych (wektorów). Aby dodać zmienną do prawej

listy, można ją przeciągnąć myszką lub kliknąć przycisk ze strzałką

.

Aby usunąć zmienną z listy, kliknąć przycisk z krzyżykiem

.

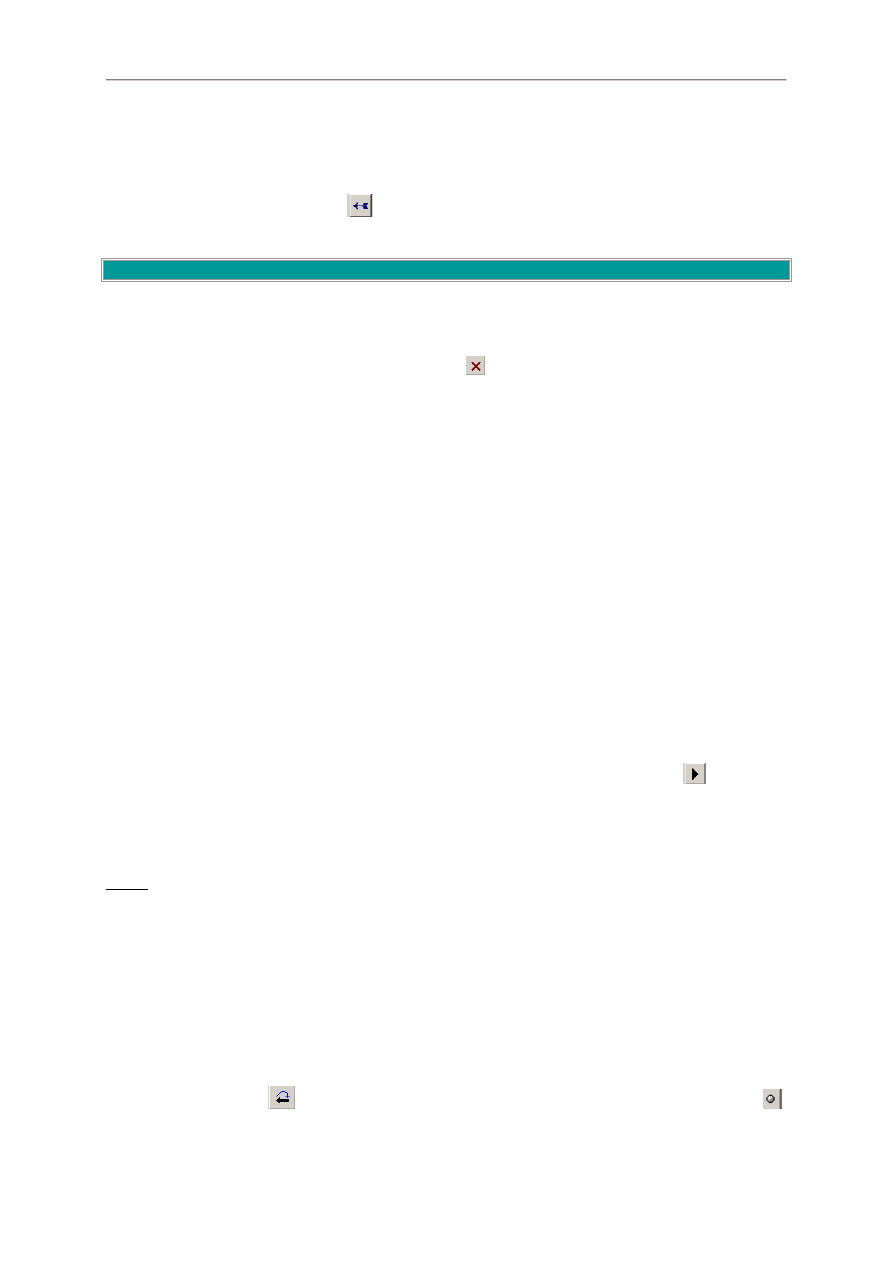
- 10 -



Pole Formula na dole tego okienka jest stosowane do wprowadzania formuł.

Zasady wpisywania formuł są podane w rozdziale 11.



Można dodawać człon stałej Constant lub czas trendu Trend przez klikanie odpowiednich

przycisków ze strzałkami

.

2.4.3. Jak estymować regresję liniową szybko i efektywnie – 2

Rozdział ten objaśnia jak uruchamiać regresję z poziomu okna poleceń Command Window.



Jeśli okno poleceń (patrz rozdział 7.3) nie jest puste można go oczyści klawiszem F10

lub przez kliknięcie przycisku z krzyżykiem

po lewej stronie tego okna.



Przeciągnąć zmienną zależną z panelu macierzy Matrices lub zmiennych Variables do
okna poleceń za pomocą myszki.

Można również wcisnąć klawisze CTRL + ENTER w panelu macierzy Matrices lub
zmiennych. Nazwa wybranej zmienne zostanie wstawiona do okna poleceń.



W oknie poleceń wstawić dwukropek (:) po zmiennej zależnej. Znak ten oddzieli lewą
stronę od prawej strony równania regresji. Mogą istnieć spacje przed lub za tym
separatorem.



Wpisać cyfrę 1 w oknie poleceń za symbolem dwukropka. Odpowiada to członowi wyrazu
wolnego (przecięcie) Intercept w liniowym równaniu regresji. Gdy nie chcemy uwzględniać
tej stałej Constant, wówczas nie wstawiamy cyfry 1 (ale czy naprawdę tego chcemy) ?



Wstawić do okna poleceń nazwę zmiennej niezależnej Regressor. Można to wykonać tak
jak poprzednio za pomocą myszki lub klawiszy CTRL + ENTER.



Po tych operacjach, okno poleceń może przybrać obraz podobny do poniższego:

y : 1 x1 x2 x3

Teraz możemy uruchomić to polecenie przez kliknięcie przycisku Run

z czarnym

trójkątem po lewej stronie okna poleceń lub przez wciśnięcie klawiszy SHIFT + ENTER.



Gdy program wyświetli komunikat o błędach, zapoznać się dokładnie z tym rozdziałem aby
zrozumieć co zrobiliśmy źle.

Uwagi:



Można korzystać z formuł w poleceniach regresji, np.:

ln(y)+10 : 1 exp(x1)/2 x2+x3



Regresory (zmienne niezależne) są oddzielane znakami spacji, a więc należy zachować
ostrożność przy korzystaniu ze spacji w formułach.



Program Matrixer zapamiętuje wcześniej uruchamiane polecenia.

Aby wywołać poprzednie polecenie, otworzyć historię poleceń przyciskiem History of

Commands

lub listę historii poleceń List of Command History przyciskiem

.

Obydwa te przyciski znajdują się w oknie poleceń.

- 11 -

2.5. Jak rysować wykres (diagram)

W programie Matrixer Istnieją trzy różne sposoby rysowania wykresów (diagramów).



Korzystanie z okna poleceń Command Window (patrz rozdział 2.5.1.)



Korzystanie z poleceń menu Show (patrz rozdział 2.5.2.)



Korzystanie z poleceń menu Panels (patrz rozdział 2.5.3.)

2.5.1. Jak rysować wykres korzystając z okna poleceń



Gdy okno poleceń Command Window (patrz rozdział 7.3) nie jest puste, można go

oczyści klawiszem F10 lub przez kliknięcie przycisku z krzyżykiem

po lewej stronie tego

okna.



Wpisać w tym oknie jedno z poleceń

plot!

,

scatter!

,

xyplot!

,

timeplot!

zależnie

od typu wykresu jaki chcemy wykreślić (patrz rozdział 9).



Gdy stosujemy polecenie rysowania wykresu punktowego rozrzutu

scatter!

lub wykresu

dwóch zmiennych z punktami połączonymi liniami

xyplot!

, wówczas przeciągamy

zmienną osi X z panelu macierzy Matrices lub zmiennych Variables do okna poleceń za
pomocą myszki.

Można również wcisnąć klawisze CTRL + ENTER w panelu macierzy lub zmiennych aby
wstawić wybrane zmienne do okna poleceń.



Następnie dodać do okna poleceń zmienną osi Y przez jej przeciąganie tak jak poprzednio
z panelu macierzy Matrices lub z panelu zmiennych Variables lub za pomocą klawiszy
CTRL + ENTER.



Zmienne są rozdzielane spacjami.

2.5.2. Jak rysować wykres korzystając z menu Show



Wybrać macierz w panelu macierzy Matrices lub zmienną w panelu zmiennych Variables.



Wybrać jedno z poniższych poleceń menu:

Show|Plot

Show|Scatter

Show|XY Plot



Otworzy się małe okienko dialogowe wyboru zmiennych do dodawania innych zmiennych.



Aby dodać inną zmienną, przeciągnąć ją z panelu Matrices lub Variables do tego okienka
korzystając z myszki.



Innym sposobem jest dodawanie zmiennej do już wybranej w panelu Martrices lub
Variables oraz kliknięcie przycisku Add w okienku wyboru zmiennych.



Kliknąć przycisk OK lub wcisnąć klawisz ENTER aby wyświetlić wykres.

- 12 -

2.5.3. Jak rysować wykres korzystając z menu Panels



Wybrać polecenie menu Panels | Plot.



W otworzonym okienku dialogowym Plot, w sekcji X axis, wybrać jeden z trzech typów
osi X: Observation Number (numer obserwacji), Variable (zmienna) lub Time (czas).



Gdy wybraliśmy opcję zmiennej Variable (patrz rozdział 2.4.2), ukaże się nowe pole
z przyciskiem Choose, którego kliknięcie pozwoli na wybranie zmiennej osi X.



W podobny sposób kliknąć przycisk Choose w sekcji Y axis po prawej stronie wybrać
odpowiednią zmienną osi Y.



Kliknąć przycisk Run

aby wyświetlić wykres.

Uwagi:



Odpowiadające polecenia zostaną wprowadzone w oknie poleceń Command Window.
Można z nich skorzystać do wprowadzenia zmian i szybkie wyświetlenie nowego wykresu.



Można wpisać to polecenie do listy historii Write to History w okienku dialogowym Plot
gdy chcemy potem rysować jeszcze raz ten sam wykres.



Skale osi Y (a także X) można wybierać jako logarytmiczne. W tym celu można w okienku
dialogowym Plot zaznaczać pola Logarithmic.



Można również wybierać wygląd dowolnej osi zmiennej Y. Domyślnie, punkty wykresu są
łączone odcinkami linii prostych Lines. Ponadto, można wybierać gwiazdki Stars oraz
słupki Bars tworzenia diagramów (wykresów).

3. Macierze i zmienne w macierzach

Dane liczbowe w programie Matrixer są przechowywane jako macierze. Każda macierz ma swoją
nazwę. Kolumny macierzy noszą nazwę zmiennych Variables i również mają swoje nazwy. Macierz
zawierająca jedną kolumnę może być traktowana jako zmienna i odpowiednio, zmienna może być
traktowana jako macierz zawierająca jedna kolumnę.
Macierz może zawierać teksty wraz z danymi liczbowymi (komentarze).
Panel macierzy Matrices jest wykorzystywany do pracy z macierzami. Panel ten wyświetla listę nazw
macierzy dostępnych w aktualnym katalogu roboczym oraz ich rozmiary. Edytor tabel Table Editor
jest stosowany do oglądania i edycji danych zawartych w macierzach.

Macierz może być trwała Permanent lub chwilowa (tymczasowa) Temporary. Nazwy macierzy
tymczasowych zaczynają się znakiem #. Macierze tymczasowe są usuwane po wyłączeniu programu.
Można korzystać z nazw macierzy zaczynających się od znaku # aby szybko oczyszczać aktualny
katalog od zbędnych plików. W celu usunięcia plików tymczasowych, można wcisnąć kombinację
klawiszy ALT + E w panelu Matrices lub w oknie poleceń Command Window.

Macierz może być przechowywana na dysku (w postaci plików) lub w pomięci RAM. Gdy program jest
po raz pierwszy uruchomiony, wszystkie nowo tworzone macierze są przechowywane w RAM,
ponieważ praca jest wtedy szybsza. Można przekształcać macierze z jednego formatu w drugi aby
chronić je w razie zawieszenia się systemu. Gdy program zostanie przerwany, wszystkie pliki będą
automatycznie zapisywane na dysku (patrz rozdział 2.3).

Istnieje również specjalny typ macierzy modelu Model Matrices (patrz rozdział 3.1)

- 13 -

3.1. Macierz modeli

Macierze modeli Model Matrices są specjalnym typem macierzy. Są one tworzone jako wynik
estymacji modelu (patrz rozdział 6). Nazwa macierzy modelu zaczyna się znakiem ukośnika (\).

Poniżej podano kilka rodzajów typowych macierzy modeli:

\Thetas

wektor parametrów,

\Resids

reszty,

\Fitted

wartości dopasowane.

Przykład:

b == \Thetas

3.2. Zmienne w macierzach

Zmienne Variables są kolumnami macierzy. Zmienna jest w pełni określona w poniższy sposób:

<name of matrix>[<name of variable>]

.

Można również korzystać z numerów kolumn [

numer]

zamiast nazw zmiennych. Przykładowo, zapis

data[3]

oznacza trzecią kolumnę w macierzy Data.

Do obsługi zmiennych wykorzystywany jest panel zmiennych Variables. Kliknięcie w tym panelu
wyświetla zmienne macierzy wybranej w panelu Matrices (patrz rozdział 7.1). Obsługa zmiennych jest
podobna do obsługi macierzy i poleceń przypisywania (patrz rozdział 10)

Macierz zawierająca jedną kolumnę może być traktowana jako zmienna i odpowiednio, zmienna może
być traktowana jako macierz zawierająca jedną kolumnę.



Przypisanie element – element.

<matrix assignment result> := <formula>

lub

<matrix assignment result> <coverage of observations> := <formula>



Przypisanie wyrażenia do macierzy.

<matrix assignment result> == <matrix expression>

lub

<scalar name> == <matrix expression>



Przypisanie wyrażenia do skalara.

<scalar name> := <scalar expression>



Przypisanie wyrażenia do łańcucha.

<string name> := <string expression>

- 14 -

4. Skalary

Skalary Scalars (wraz z macierzami) zawierają dane liczbowe, na których program wykonuje swoje
działania. Skalary są przechowywane tylko podczas pracy programu.

Skalary mogą zastępować stałe w wyrażeniach skalarnych Scalar Expressions (patrz rozdział 12),
formułach Formulas (rozdział 11) i wyrażeniach macierzowych Matrix Expression (rozdział 13).

Skalary można tworzyć za pomocą poleceń przypisania Assigment Command (patrz rozdział 10).

Istnieje osobne okno skalarów Scalars do oglądania i edycji skalarów utworzonych podczas pracy lub
tworzonych nowych skalarów. Okno to otwierane jest klawiszami CTRL + S.

Skalar @pi oznacza liczbę .

Skalary

@missing

oraz

@na

oznaczają brakującą wartość

Skalar

@timer

zawiera aktualną wartość czasu w sekundach

Przykład:

@A := 16; @n := 4;

x{1..100} := @A*sin(2*@pi*$i/@n);

y := if(x>=0,x,@missing);

Istnieje również specjalny rodzaj skalarów o nazwie „Model skalarów” Model Scalars.

5. Łańcuchy

Matrixer ma pewne możliwości obsługi łańcuchów. Łańcuchy są przechowywane tylko podczas pracy
programu.

Nazwy łańcuchów zaczynają się symbolami s_, Łańcuch można utworzyć jako wynik polecenia
przypisania.

Wyrażenie łańcuchowe jest mieszaniną tekstu i wyrażenia skalarnego. Tekst jest oznaczony znakami
z cudzysłowu (

"<text>"

). Indywidualne symbole ASCII można adresować jako

s_<n>

, gdzie n jest

symbolem kodu. Jako separator wyrażeń w łańcuchu stosowana jest spacja.

Przykład:

s_a := "Factorials: ";

s_path := "C:\Windows\Temp\";

for! @i 1 5;

s_f := @i "!=" exp(lngamma(@i+1));

s_a := s_a s_f s_32 " ";

print! (s_path "tempfile.txt") s_f;

endfor!;

wait! s_a;

Istnieje okno „łańcuchów” do oglądania i edycji łańcuchów utworzonych podczas pracy. albo do
tworzenia nowych łańcuchów (skrót klawiszowy CTRL + T)

- 15 -

6. Modele

Model macierzy

Model macierzy Model Matrices jest specjalnym rodzajem macierzy. Jest on tworzony w wyniku
estymacji modelu. Nazwa modelu macierzy się symbolem \. Poniżej przedstawiono kilka typowych
modeli macierz:

\Thetas

wektor parametrów,

\Resids

reszty,

\Fitted

dopasowane wartości.

Przykład:

b == \Thetas

7. Interfejs

7.1. Panel macierzy (zmienne)

Panel macierzy Matrices zawiera listę nazw macierzy znajdujących się w aktualnym katalogu
roboczym. Liczba wierszy i liczba kolumn każdej macierzy jest pokazana obok nazwy macierzy.
Liczby wierszu oraz liczby kolumn oddzielone są symbolem wskazującym na format macierzy.

Panel zmiennych Variables zawiera listę nazw zmienny występujących w macierzy zaznaczonej
w panelu macierzy (kliknąć w panelu zmiennych aby zobaczyć ich listę).

Poniżej zestawiono najważniejsze skróty klawiszowe tych paneli:

ENTER

– Widok i edycja aktualnej macierzy



– Przełączenie z panelu macierzy do panelu zmiennych



– Przełączenie z panelu zmiennych do panelu macierzy

TAB

– Przełączenie między panelami macierzy i zmiennych oraz oknem poleceń

INS

– Wstawia nową macierz

DEL

– Usuwa aktualną macierz / zmienną

ALT + N

– Zmienia nazwę aktualnej macierzy / zmiennej

ALT + C

– Kopiuje aktualną macierz / zmienną do schowka

Skrót klawiszowy CTRL + ENTER wstawia nazwę aktualnej macierzy / zmiennej do okna poleceń

Aby edytować aktualną macierz, wcisnąć klawisz ENTER lub podwójnie kliknąć myszką na macierzy.

7.2. Edytor tabel dla macierzy

Edytor tabel Table Editor jest stosowany do wprowadzania danych do nowo utworzonej macierzy
oraz do edycji już istniejących macierzy.

Edytor tabel jest bardzo podobny do edytorów tabel (arkuszy) innych programów, np. Excel. Jednak
w odróżnieniu od Excela, edytor tabel programu Matrixer jest z specjalnie zaprojektowany do edycji
danych numerycznych, np. w komórkach tabel można wprowadzać tylko liczby (jedna liczba w jednej
komórce).

- 16 -

Uwagi:



Schowek Windows może być wykorzystywany do kopiowania danych z edytora tabel
innych programów do macierzowego edytora tabel Matrixer i odwrotnie.



Należy zapoznać się ze wskazówkami o wprowadzaniu danych – patrz rozdział 2.2.



Można również oglądać i edytować komentarze do macierzy w edytorze tabel. W tym celu
należy przełączyć się na odpowiednie okno klawiszem TAB i kliknąć przycisk Comments
albo wcisnąć klawisz F3.

Skróty klawiszowe okna edycji tabel:

ESC

– Zamyka okno

CTRL + 

– Szybki skok w prawo

CTRL + 

– Szybki skok w lewo

ENTER, lub F2

– Edycja komórki

Podczas edycji komórki:

*

– Wstawia brakującą wartość

ESC

– Opuszcza komórkę bez zapisywania

ENTER

– Zapisuje zmiany i opuszcza komórkę

DEL

– Usuwa komórkę

INS

– Wstawia komórkę

CTRL + Y

– Usuwa wiersz

ALT + DEL

– Usuwa zmienną (kolumnę)

ALT + INS

– Dodaje zmienną (kolumnę)

ALT + N

– Zmienia nazwę zmiennej

CTRL + N

– Zmienia nazwy wszystkich zmiennych

CTRL + I

– Przełączenie w tryb wstawiania

F3

– Przełączenie do okna komentarzy

8. Polecenia

Polecenie Command można wykonać w oknie poleceń lub jako pojedyncze polecenie w makro.

8.1. Okno poleceń

Okno poleceń Command Windows stosowane jest do edycji i uruchamiania pojedynczych poleceń
lub bloków poleceń (makro).

Poniżej przytoczono niektóre polecenia:



Przypisanie element-element :

<matrix assignment result> := <formula>



Przypisanie macierzy:

<matrix assignment result> == <matrix expression>



Estymacja liniowa (patrz rozdziały 2.4.3 oraz 15.1):

<dependent variable> : <list of regressors>



Estymacja nieliniowa (patrz rozdział 15.1)::

nls! <dependent variable> : <formula>



Wykres:

plot! <variables list>



Histogram (patrz rozdział 9.1):



hist! <variable>

- 17 -

Uwagi:



Gdy program nie rozpoznaje niektórych poleceń, wówczas zawartość okna poleceń może
być traktowane jako wyrażenia skalarne. Wyświetlana jest wynikowa liczba. Jest to tzw.
tryb kalkulatora. Przykładowo, można w oknie poleceń napisać 2*2 i uruchomić to jako
polecenie. Wyświetlone zostanie okienko z wynikiem równy 4.



Podkreśla się, że wynikiem błędnego wpisu często jest generowany komunikat o błędzie.



Podwójne kliknięcie symbolu lub wyrazu wyświetla o nim wskazówkę informacyjną.



Polecenia, funkcje i inne identyfikatory specjalne są podświetlane.

Można z tego skorzystać do kontroli pisowni.

Skróty klawiszowe:



SHIFT + ENTER

– Uruchamia polecenie zawarte w oknie poleceń.



ALT + 

– Historia (poprzednie polecenia).



F10

– Oczyszcza okno poleceń.



TAB

– Przełącza do panelu macierzy

9. Wykresy

9.1. Wykresy i diagramy



Histogram:

hist! <variable>

Skrót: ALT + H



Wykres w funkcji liczby obserwacji:

plot! <list of variables>

Przykład:

plot! x y

Skrót: ALT + G



Wykres w funkcji czasu:

timeplot! <list of variables>

Przykład:

timeplot! x y



Wykres liniowy XY:

xyplot! <X-axis variable>

<list of Y-axis variables>

Przykład:

xyplot! x y1 y2

Skrót: ALT + Y



Wykres rozrzutu (gwiazdkowy):

scatter! <X-axis variable>

<list of Y-axis variables>

Przykład:

scatter! x y1 y2

Skrót: ALT + S



Ogólne polecenie (parametry opcjonalne podano w nawiasach kwadratowych):

plot! [(<kind of X axis>,<kind of Y axis>)] [<X-axis variable>,]
<list of Y-axis variables>

- 18 -

Typ osi Kind of Axis może być liniowy (lin) lub logarytmiczny (log). Gdy brak tego parametru,
wówczas obie osie są domyślnie liniowe.

Jeśli po pierwszej zmiennej następuje znak dwukropka (:), wówczas pierwsza zmienna będzie
traktowana jako zmienna osi X.
Po każdej zmiennej na liście zmiennych Y może wystąpić znak jeden z poniższych znaków
w dowolnej kombinacji |

-

oznacza linie prostą.

*

oznacza gwiazdkę

|

oznacza słupek

Gdy brak tych znaków, wówczas punkty wykresu będzie łączone odcinkami linii prostej.

Przykład A

A. Imitacja histogramu

@nbins := 10;

@min := minel(x);

@max := maxel(x);

@range := @max-@min;

@min := @min-@range/100;

@max := @max+@range/100;

@range := (@max-@min)/@nbins;

histogr == zerosvec(@nbins);

for! @i 1 rows(x);

@bin := int((x@(@i,1)-@min)/@range)+1;

histogr@(@bin,1) := histogr@(@bin,1)+1;

endfor!;

for! @bin 1 @nbins;

histogr@(@bin,2) := @min+@range*(@bin-0.5);

endfor!;

xyplot! histogr[2] histogr[1]|;

Przykład B

B. Marsaglia, Bray (1964)

@n := 1000;

x == onesvec(@n);

for! @i 1 div(@n,2);

loop!;

@v1 := 2*~u01-1;

@v2 := 2*~u01-1;

@r := sqr(@v1)+sqr(@v2);

break! @r<1;

endloop!;

@f := sqrt(-2*ln(@r)/@r);

@norm1 := @v1*@f;

@norm2 := @v2*@f;

@i2 := @i*2;

x@(@i2-1,1) := @norm1;

if! @i2<=@n;

x@(@i2,1) := @norm2;

endif!;

endfor!;

hist! x;

- 19 -

Przykład C

C. Metoda częściowego prawdopodobieństwa Coxa do estymacji modelu ryzyka.

Próba ta pozwala na odrzucanie linii podstawy funkcji ryzyka i estymowanie zależności regresji tylko
od czasu trwania procesu. Wyraz wolny jest również odrzucany, ponieważ jest to mnożnik „inii
podstawy”

Literatura: Cox, D.R. "Partial Likelihood," Biometrika, 62 (1975), 269-276.

Sorted == (Data[Y] Data[X1] Data[X2]) ? Data[Y];

Wszystkie zmienne są sortowane w kolejności rosnącego czasu

namevars! Sorted Y X1 X2;

mle! ln(fitted)-ln($csum(fitted)) \TT {>> fitted =
exp(%a1*Sorted[X1]+%a2*Sorted[X2]);

Przykład D

D. Estymacja metodą maksymalnego prawdopodobieństwa modelu autoregresji.

#y == clearrows(RTS[d]);

#y == sqr(#y);

#y == ln(#y+mean(#y)*0.02)

- mean(#y)*0.02/(#y+mean(#y)*0.02)+1.27;

#y == #y - mean(#y);

#start == 0.98|3|0.03;

mle! if($i>1,-0.5*(ln(2*@pi*f)+sqr(v)/f),@na)

>> h1 = if($i>1,%phi*$lag(h1+P1*v/f),0)

>> P1 = if($i>1,sqr(%phi)*$lag(P)+%S22,%S22/(1-sqr(%phi)))

>> f = P1+%S12

>> v = #y-h1

>> h = h1+P1*v/f

>> P = P1-sqr(P1)/f

&start #start &method simplex;

#p==flipv(\def_p);

#p1==flipv(\def_p1);

#h==flipv(\def_h);

#h1==flipv(\def_h1);

delete! #h_smooth;

@phi := \thetas@(1,1);

#h_smooth := if($i>1,#h+@phi*#p/$lag(#p1)*($l1-$lag(#h1)),#h);

#h_smooth == flipv(#h_smooth);

10. Polecenia przypisywania



Przypisanie element – element.

<matrix assignment result> := <formula>

lub

<matrix assignment result> <coverage of observations> := <formula>

- 20 -



Przypisanie wyrażenia do macierzy.

<matrix assignment result> == <matrix expression>

lub

<scalar name> == <matrix expression>



Przypisanie wyrażenia do skalara.

<scalar name> := <scalar expression>



Przypisanie wyrażenia do łańcucha.

<string name> := <string expression>

11. Formuły

11.1. Podstawienia

Polecenia przypisania



Przypisanie element-element:

<matrix assignment result> := <formula>

lub

<matrix assignment result> <coverage of observations> := <formula>



Przypisanie wyrażenia macierzowego:

<matrix assignment result> == <matrix expression>

lub

<scalar name> == <matrix expression>



Przypisanie wyrażenia skalarnego:

<scalar name> := <scalar expression>



Przypisanie wyrażenia łańcuchowego:

<string name> := <string expression>

11.2. Funkcje dynamiczne

Funkcje dynamiczne Dynamic Functions stosowane są w formułach.

Funkcje te wraz z podstawieniami pozwalają na pracę z modelami dynamicznymi.

- 21 -



Lag

$lag

lub

$lag<n>



Różnice

$diff

lub

$diff<n>



Różnice logarytmów

$diffln

lub

$diffln<n>



Suma skumulowana

$csum

or

$csum<n>



Zwłoka własna

$l

or

$l<n>

bez nawiasów

Przykład: – Generowanie szeregów AR(1):

x{1..100} := ar1

>> ar1 = if($i>1,@phi*$lag(ar1)+~n01,0);

lub

x{1..100} := @phi*$l1+~n01;

12. Wyrażenia skalarne



Operatory arytmetyczne

+

Sumowanie

-

Odejmowanie

*

Mnożenie

/

Dzielenie

^

Potęgowanie



Operatory relacyjne

=

Równe

<

Mniejsze od

<

Większe od

<=

Mniejsze lub równe

>=

Większe lub równe

<>

Różne

Wynikiem operacji relacyjnych jest 1 (prawda) lub 0 (fałsz).



Różne funkcje:

ln

Logarytm naturalny

exp

Wykładnik

sqrt

Pierwiastek kwadratowy

sqr

Kwadrat

abs

Wartość bezwzględna

Przykłady:

@omega := 2*@pi*~u01;

@y := if(@omega<@pi,cos(@omega),1/cos(@omega));

@sum := 0;

@n := rows(x);

for! @i 1 @n-1;

@sum := @sum+exp(x@(@i,1));

endfor!;

- 22 -

13. Wyrażenia macierzowe

Wyrażenia macierzowe Matrix Expression mają w zasadzie taką samą składnię jak wyrażenia
skalarne. Ponadto w różnych sytuacjach wyrażenia macierzowe są podobne do formuł i można z nich
korzystać w takim samym zakresie w operacjach podstawiani element-element. Jednak głównym ich
zadaniem jest wykonywanie różnych operacji macierzowych takich jak odwracanie lub transpozycja
macierzy



Operacje jednoargumentowe:

‘

Transpozycja

~

Odwrotność



Operacje dwuargumentowe:

+

Suma

-

Różnica

.

Iloczyn macierzy

*

Bezpośredni iloczyn macierzy (element po elemencie)

/

Bezpośrednie dzielenie macierzy

`

Iloczyn macierzowy z transpozycją pierwszej macierzy

~

Iloczyn macierzowy z odwrotnością pierwszej macierzy

& (lub spacja)

Konkatenacja w poziomie

|

Konkatenacja w pionie

:

Estymowane współczynniki regresji liniowej

?

Sortowanie macierzy wg wektorów



Funkcje:

inv

Odwrotność macierzy

diag

Macierz diagonalna

inner

Iloczyn wewnętrzny

sort

Sortowanie

onesvec

Wektor jednostkowy

acov

Funkcja auotokowariancji



Format polecenia przypisywania macierzy:

<name of resultant matrix>==<expression>



Przypisanie macierzy:

<matrix assignment result> == <matrix expression>

 Wyrażenie macierzowe można przypisać do skalara:

<scalar name> == <matrix expression>

Przykłady:

b == (x'x)~x'y;

d == A.c+d|e-v[1]&w[xx];

x == x1 x2 x3;

@rss == inner(e);

Aby dołączyć zwłokę do zmiennej, skorzystać z wyrażenia:

<variable> [<positive integer number with '+' or '-' sign>]

- 23 -

Uwagi:



W wyrażeniu macierzowym, spacje są stosowane do jako operatory konkatenacji
macierzy. W szczególności, gdy spacja znajduje się przed znakiem dodawania lub
odejmowania,, trzeba wstawić ronię z spację za tym znakiem, tak jak niżej:

1+2
lub
1 + 2



Gdy stosowane są operacje arytmetyki dwuargumentowej lub funkcje element-element,
wówczas w zakresie wymiarów macierzy są ostrzejsze niż w formułach.

14. Funkcje

Funkcje są stosowane w formułach, wyrażeniach skalarnych i w wyrażeniach macierzowych.

W programie Matrixer istnieją poniższe typy funkcji:



Funkcje macierzowe



Funkcje zwyczajne (element po elemencie)



Funkcje skalarne macierzy



Funkcje dynamiczne



Funkcje podmacierzowe



Funkcje do obliczania formuł i ich pochodnych względem parametrów.

15. Estymacja modeli ekonometrycznych

15.1. Estymacja liniowych modeli regresji

Najłatwiejszą i najszybszą metodą estymacji regresji liniowej w programie Matrixer jest rozpoczęcie od
wstawiania odpowiednich poleceń oknie poleceń. Polecenia te mają poniższą składnię:

<dependent variable> : <list of regressors>

tzn.

<zmienna zależna> : <lista regresorów>



Człon wyrazu wolnego Intercept na liście regresorów można wpisać jako 1,



Regresor można wyspecyfikować w postaci formuły.



Regresja ważona może być estymowana przez dodanie

&/ <weights>

. Zakłada się tu,

że wagi są proporcjonalne do pierwiastka kwadratowego z wariancji

Przykłady:

y : 1 x1 x2 x2[-1];

ln(data[cons]) : 1 ln(data[gnp]*10) ln(data[gnp])^2;

A[y] : 1 A[x] &/ A[w];

- 24 -

Po estymacji regresji, użytkownik może skorzystać z polecenia menu Show | Results, które pozwala
na oglądanie oraz analizowanie wyników lub skorzystanie w tym celu z klawiszy ALT + R.

Można również obliczać współczynniki OLS za pomocą operacji macierzowych:

Przykład:

b==Y:X

Tutaj Y jest zmienna zależną, natomiast X jest macierzą regresorów.

Ten sam wynik można uzyskać korzystając z poniższego wyrażenia macierzowego:

b==(X'X)~X'Y

15.2. Estymacja nieliniowych modeli regresji

Regresję nieliniową można estymować uruchamiając ją z okna poleceń za pomocą odpowiednich
poleceń, które mają poniższą poniższą składnię:

nls! <dependent variable> : <formula>

tzn.

nls! <zmienna zależna> : <formuła>

Nazwy estymowanych parametrów w formule zaczynają się znakiem %.

Opcje:



Algorytm numeryczny

&method <gnr|newton|gnrn|simplex|bfgsa|bfgsn|sa>



Wektor wartości początkowych parametrów

&start <variable>



Wektor dokładności parametrów

&deltas <variable>



Ogólna precyzja (parametr zbieżności)

&precision <number>



Maksymalna liczba iteracji

&maxstep <positive integer number>

Domyślnym algorytmem numerycznym jest metoda Gaussa-Newtona.

Dostępne są również inne algorytmy, takie jak metoda Newtona, metoda Simplex , etc.

Przykłady:

nls! D[Y] : %cnst + %a*D[Y] - %cnst*%a*z

nls! usa[labor] : %c1 + exp(-%c2 + usa[unempl])

- 25 -

15.3. Regresja logitowa i probitowa

Program Matrixer pozwala na wykonywania regresji dwójkowej Logit oraz Probit.

Polecenie dla regresji logitowej ma poniższą postać:

logit! <dependent variable> : <list of regressors>

Przykład:

logit! y: const x1 x2

Polecenie dla regresji probitowej ma poniższą postać:

probit! <dependent variable> : <list of regressors>

Zmienna zależna w tych modelach musi zawierać tylko wartości 0 oraz 1.

16. Procedury statystyczne

W oryginalnym pomocniku Help opisane są poniższe zagadnienia, z których przetłumaczono tu tylko
pierwszą pozycję (przypis tłumacza).



Statystyki opisowe



Macierz korelacji



Funkcja autokorelacji



Histogram



Gęstość widmowa. Spektrogram



Test ADF Dickeya-Fullera



Diagram normalności PP



Inne polecenie matematyczne i statystyczne



Dekompozycja macierzy

Niektóre procedury statystyczne sa zaimplementowane jako funkcje, np.:



Funkcje macierzowe: algebra macierzy



Funkcje rozkładów prawdopodobieństwa



Funkcje skalarne macierzy

16.1. Statystyki opisowe

Polecenie obliczania statystyk opisowych ma poniższą składnię:

descript! <variable>

Przykład:

descript! x

Procedura ta oblicza standardowe statystyki opisowe takie jak: minimum, maksimum, średnia
arytmetyczna. mediana odchylenie standardowe, asymetria, eksces, kurtoza, autokorelacja 1-go
stopnia, etc.

- 26 -

17. Wyniki estymacji

Po estymacji regresji, użytkownik może skorzystać z menu, Show | Results aby obejrzeć i analizować
wyniki regresji. Skrót do tego polecenie ma postać ALT + R.
W oryginalnym pomocniku Help opisane są poniższe zagadnienia, których tu nie tłumaczono (przypis
tłumacza).



Estymacje i statystyki



Histogram reszt standaryzowanych



Wartości odbiegające



Obserwacje wpływowe



Efekty drugiego rzędu



Test usuwania zmiennych



Ograniczenia (parametrów funkcji)



Diagnostyka

18. Makra (grupy poleceń)

Makra (makropolecenia) Macros są stosowane do uruchamiania grupy poleceń. Aktualnie są to
programy napisane wewnętrznym języku programowania Matrixera. Język ten nie jest zbyt złożony,
ale pozwala na automatyzacje rutynowych operacji.
W oryginalnym pomocniku Help opisane są poniższe zagadnienia, których tu nie tłumaczono (przypis
tłumacza).



Menu makropoleceń



Pliki makr (pliki poleceń)



Edytor makr



Polecenia sterowania w makrach



Komunikaty i sygnały w makrach,

- 27 -

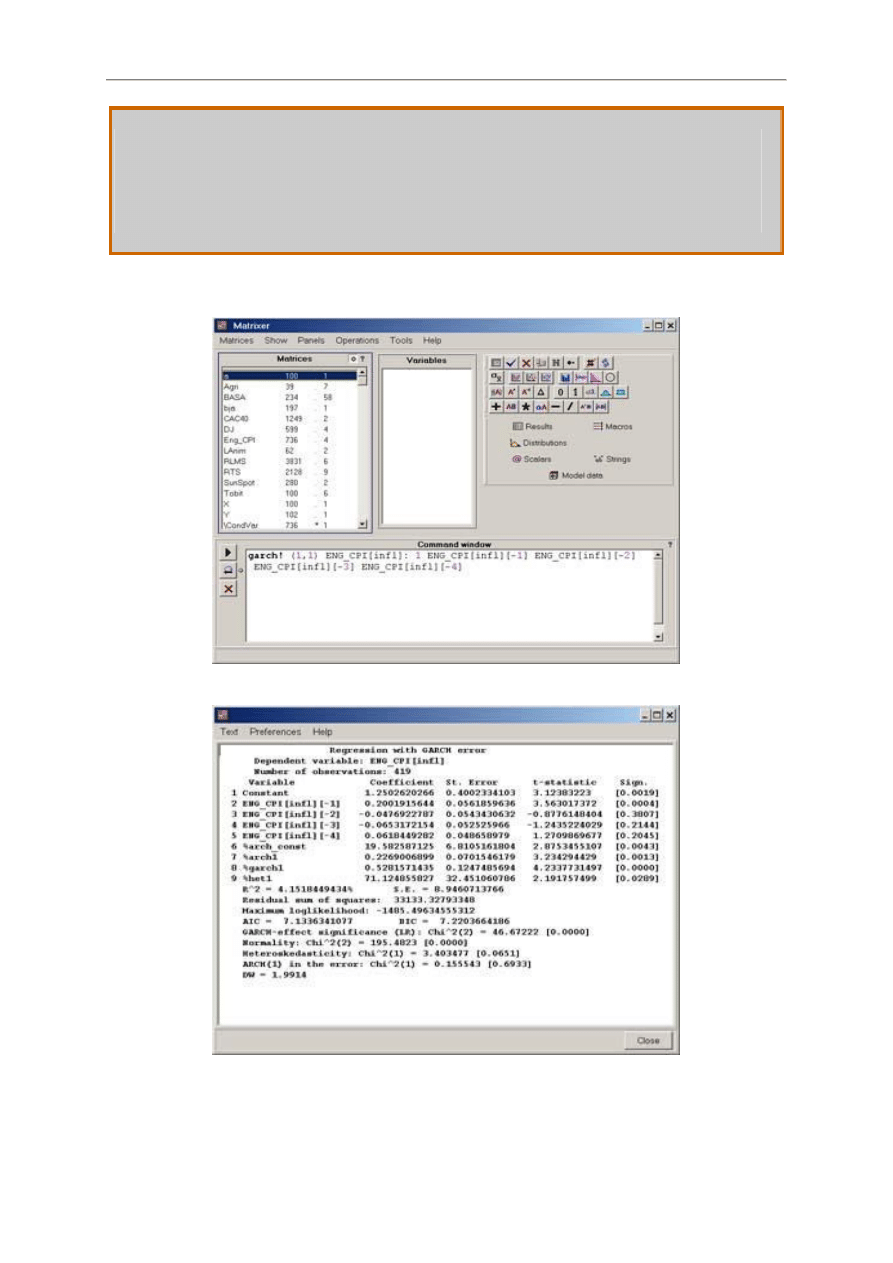
Przykładowe zrzuty ekranowe

ściągnięte ze strony domowej Matrixer

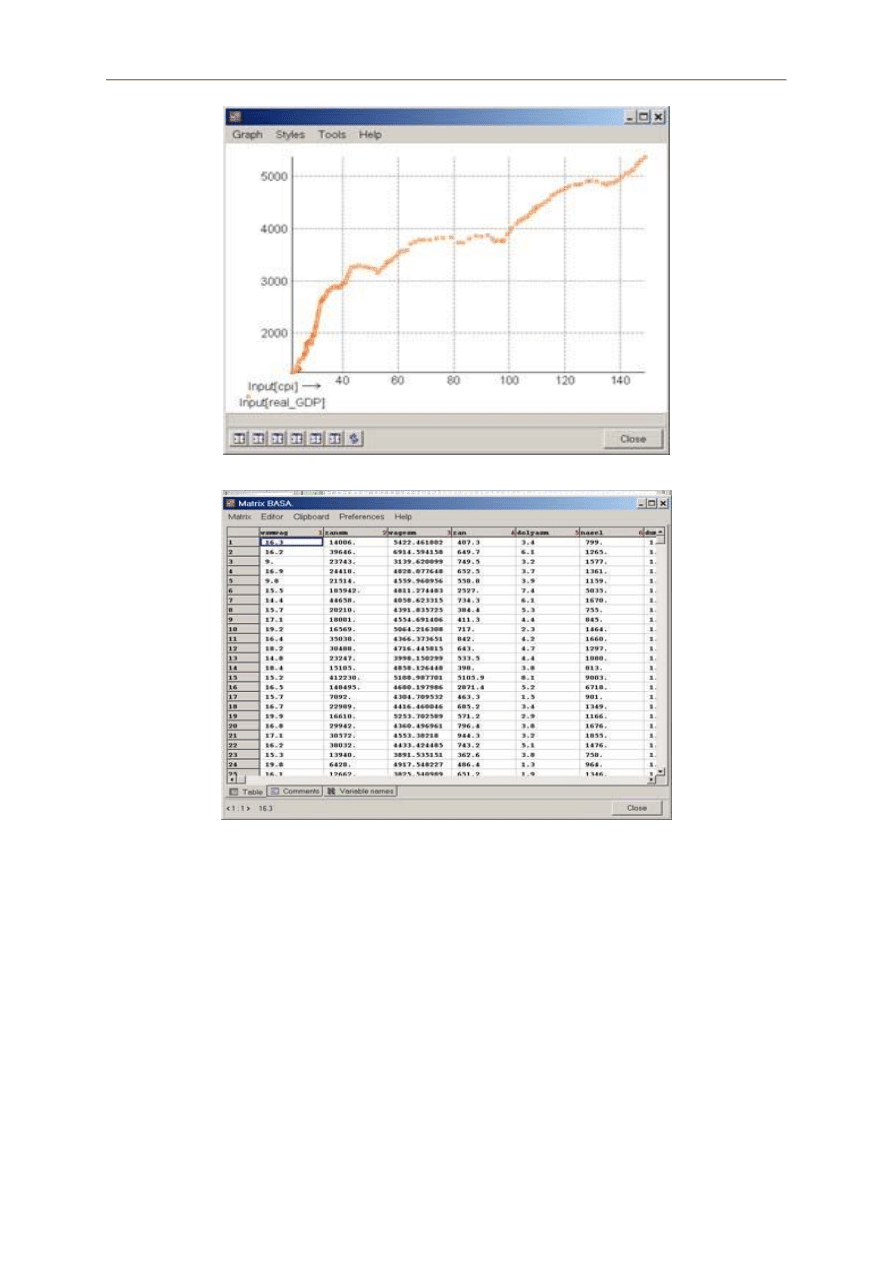
- 28 -