POMOCE DYDAKTYCZNE

WYBRANE ZAGADNIENIA PROJEKTOWANIA

ŚCIAN OPOROWYCH

Autor opracownia:

Dr inż. Adam Krasiński

Kierownik Katedry Geotechniki:

Prof. dr hab. inż. Bohdan Zadroga

Gdańsk, 2004

6. ŚCIANY OPOROWE

Ściany oporowe – są to konstrukcje, których głównym zadaniem jest podpieranie uskoków

naziomu gruntów rodzimych lub nasypowych, a głównym obciążeniem jest parcie podpieranego

gruntu.

Do konstrukcji oporowych zaliczamy:

1) Ściany lub mury oporowe

2) Ścianki szczelne i szczelinowe

3) Obudowy wykopów

ŚCIANY OPOROWE

Podział ścian oporowych

Ze względu na materiał:

- murowane (z cegły lub kamienia)

- betonowe

- żelbetowe

Ze względu na konstrukcję i kształt przekroju poprzecznego:

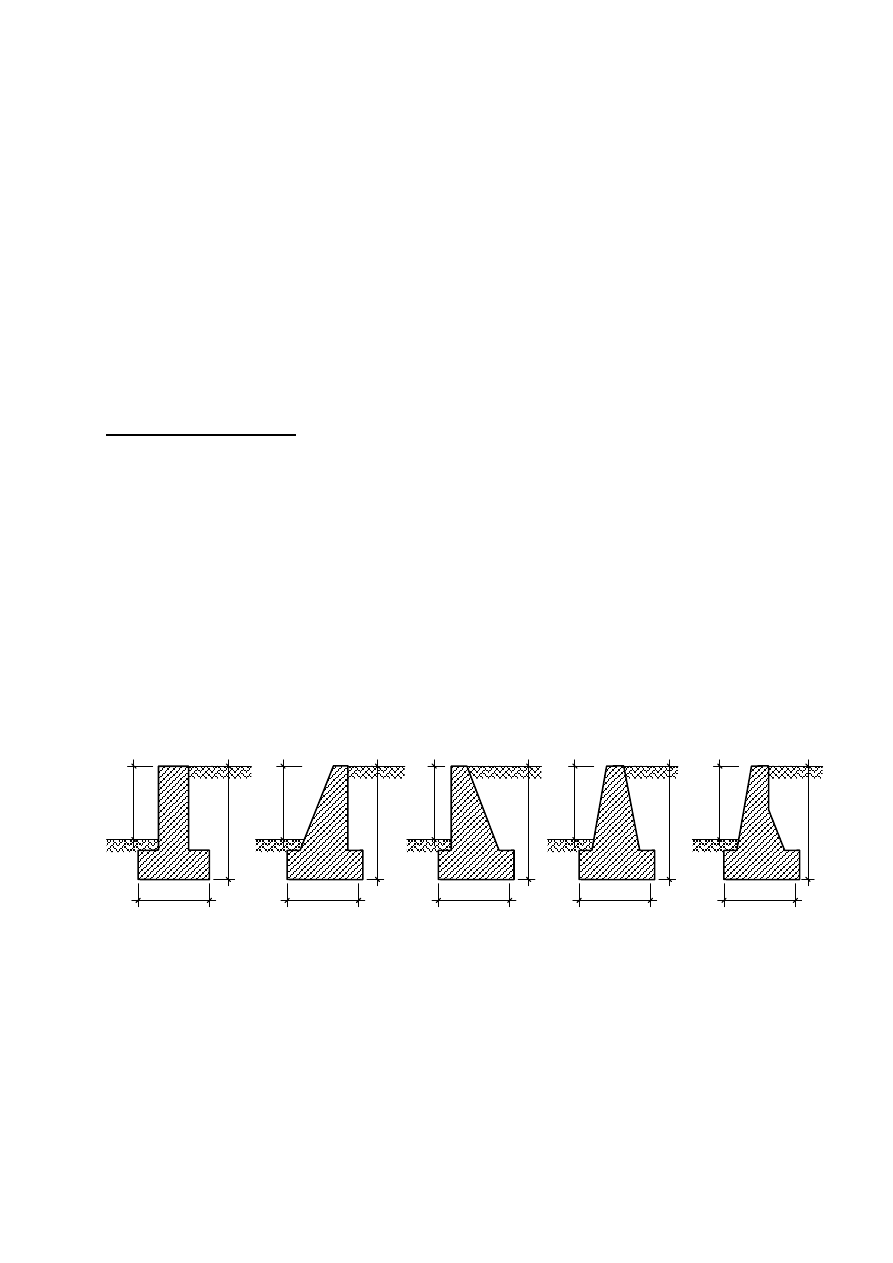
- masywne (najczęściej murowane lub betonowe) – ściany tego typu utrzymują stateczność

(przejmują parcie gruntu) dzięki swojej dużej masie. Kształty: prostokątny, schodkowy, trapezowy,

złożony (rys. 1)

H

n

≤

4 m

H

B=(0.5

÷0.7)H

H

n

≤

4 m

H

B=(0.5

÷0.7)H

H

n

≤

4 m

H

B=(0.5

÷0.7)H

H

n

≤

4 m

H

B=(0.5

÷0.7)H

H

n

≤

2.

5m

H

B=(0.5

÷0.7)H

Rys. 6.1. Rodzaje kształtów ścian oporowych masywnych.

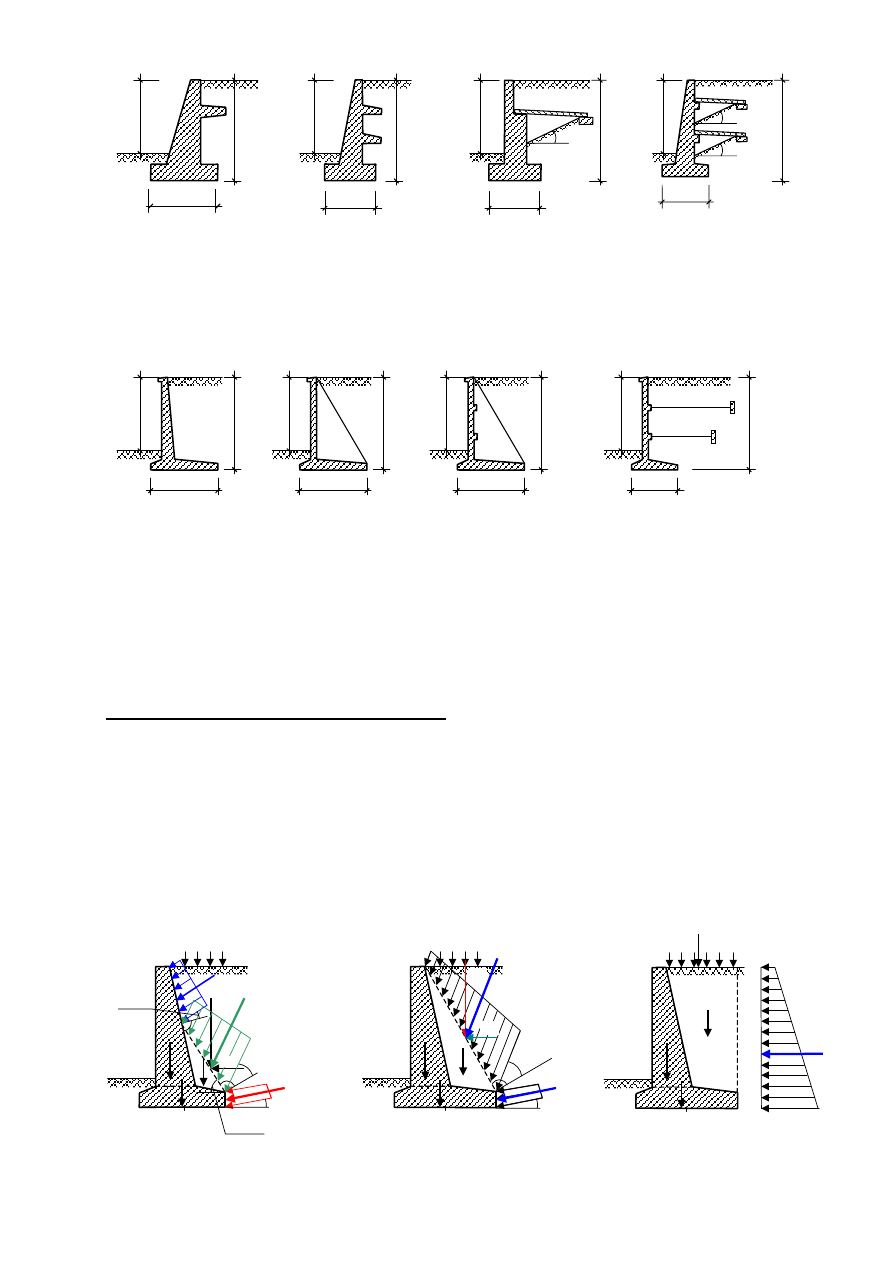
- półmasywne z elementami odciążającymi (betonowe lub żelbetowe) – ściany tego typu

utrzymują stateczność częściowo dzięki masie, częściowo dzięki redukcji parcia gruntu przez

elementy odciążające. Konstrukcje: ściany z jednym lub dwoma wspornikami, ściany z płytą

odciążajacą (rys. 2).

2

B=

∼0.5H

B=

∼0.5H

H

n

≤

6 m

H

ψ≤0.8φ

B=(0.5

÷0.7)H

H

n

≤

6 m

H

H

n

≤

6 m

H

B=

∼0.5H

ψ≤0.8φ

ψ≤0.8φ

H

n

≤

6 m

H

Rys. 6.2. Rodzaje ścian oporowych półmasywnych z elementami odciążającymi.

- lekkie (wyłącznie żelbetowe) – ściany te zachowują stateczność dzięki ciężarowi gruntu
zalegającego na wewnętrznej odsadzce fundamentowej. Konstrukcje: ściany płytowo-kątowe,
ściany płytowo-żebrowe, płytowe z elementami kotwiącymi (rys. 3).

H

n

≤

6 m

H

B=

∼0.4H

H

n

≤

8 m

H

B=0.6

÷0.7H

H

n

≤

8 m

H

B=0.6

÷0.7H

H

n

≤

4 m

H

B=0.6

÷0.7H

Rys. 6.3. Rodzaje ścian oporowych lekkich.

Zastosowanie ścian oporowych:

- podparcie tarasów pod zabudowę lub parkingi
- podparcie nasypów drogowych lub kolejowych na zboczach i dojazdach do wiaduktów
- podparcie skarp przy wjazdach do tuneli
- inne
Obliczanie i projektowanie ścian oporowych

Zbieranie obciążeń pionowych i poziomych

Na ściany oporowe działają różnorakie obciążenia, które rozdziela się na obciążenia pionowe
i poziome. Głównym obciążeniem jakie oddziaływuje na ściany oporowe jest parcie gruntu, które
w zależności od sposobu liczenia może być ukośne lub poziome. Ponadto na ścianę działają
obciążenia pionowe od ciężaru własnego jej elementów, ciężaru gruntu zasypowego
spoczywającego na odsadzkach fundamentowych oraz od dodatkowego obciążenia naziomu p.

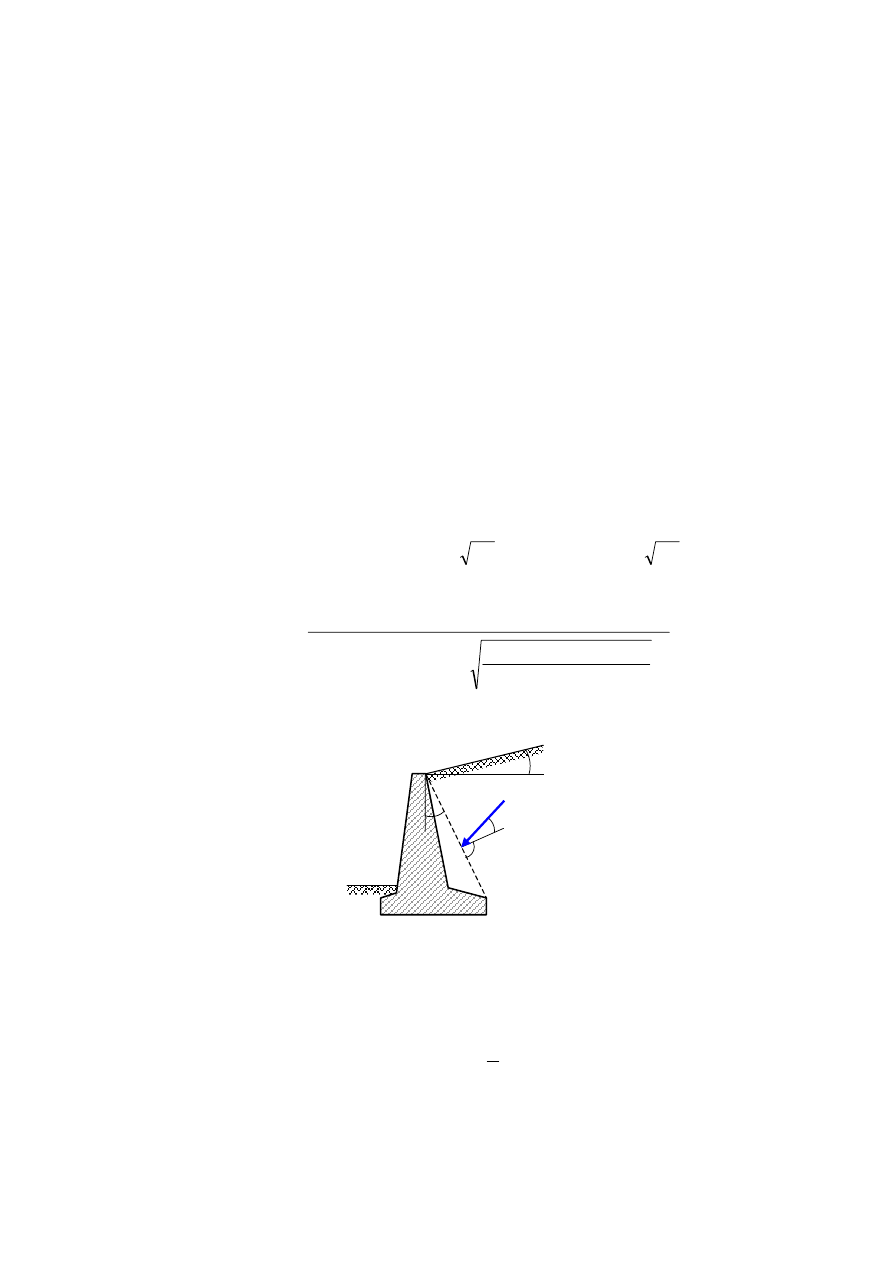
A) Sposób I

B) Sposób II

C) Sposób III (uproszczony)

.

p

0

δ

a2

=

φ/2

E

2

δ

a1

=

φ

E

1

h

E

1

v

E

1

G

3

G

1

G

2

δ

a3

=

φ/2

45

°+φ/2

.

E

2

h

.

E

2

p

0

δ

a1

=

φ/2

E

3

δ

a2

=

φ

E

2

v

E

1

G

3

G

1

G

2

P

p

0

E

G

3

G

1

G

2

Rys. 6.4. Sposoby zbierania obciążeń na ściany oporowe masywne i lekkie.

3

G

2

G

1

G

4

E

1

0

p

G

5

G

3

ϑ=45°+φ/2

R

p

= (G

4

+G

5

+P)/2

E

2

R

p

P

G

2

0

G

3

E

1

p

G

5

G

4

ϑ=45°+φ/2

E

2

φ

P

G

1

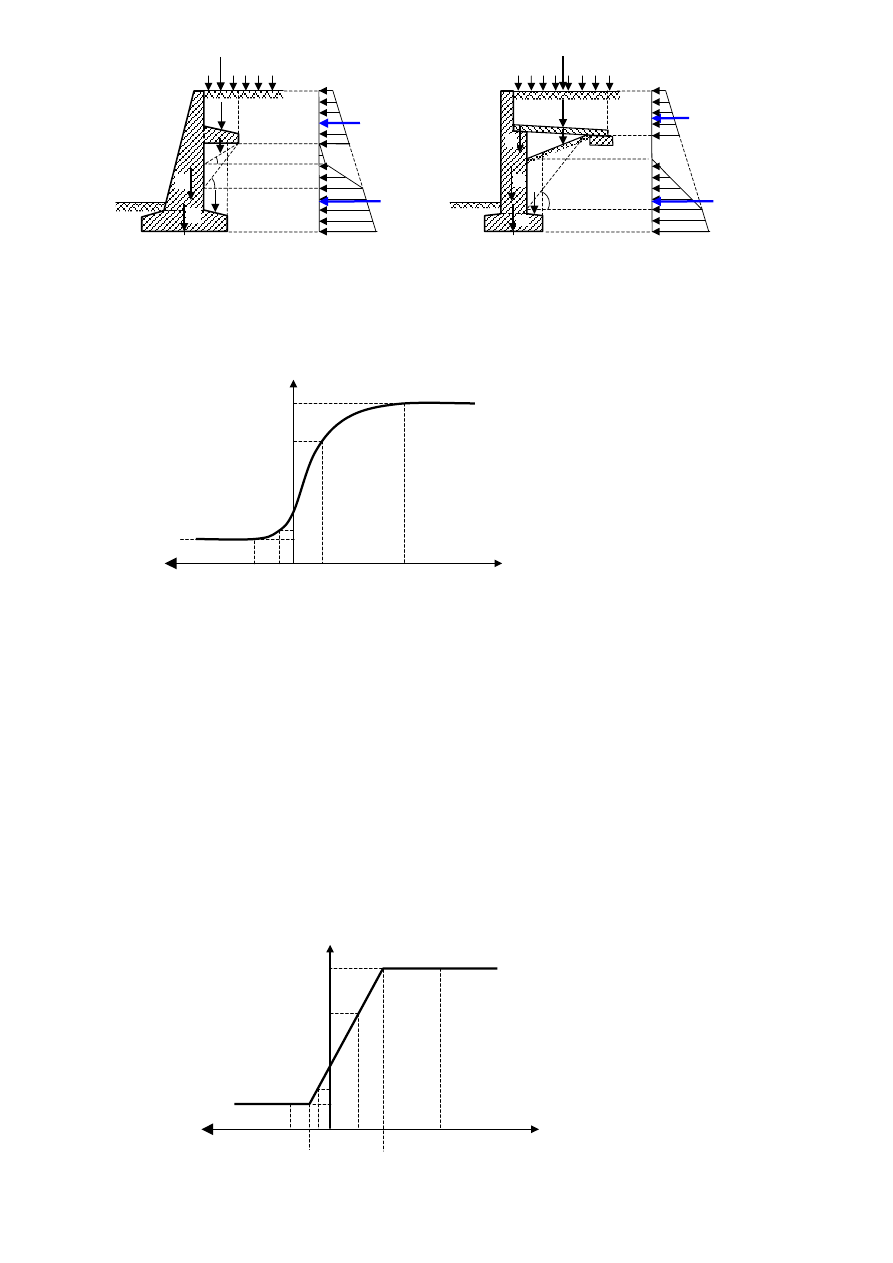
Rys. 6.5. Przyjmowanie obciążeń działających na ściany oporowe z elementami odciążającymi.

Zagadnienie parcia gruntu na ściany oporowe
Parcie i odpór gruntu jest oddziaływaniem, którego wartość zależy od przemieszczeń
i odkształcalności konstrukcji oporowej. Zależność parcia i odporu gruntu od przemieszczeń
konstrukcji oporowej można przedstawić graficznie, jak na rysunku poniżej.

δ

II

δ

a

δ (

do gruntu)

δ

p

strefa odporu

strefa parcia

E

II

E

0

E

a

E

I

0

δ

I

E

p

E

E

0

– parcie spoczynkowe – gdy

δ =0 (przem. zablokowane)

E

a

– parcie graniczne – gdy

δ ≥ δ

a

(ruch od gruntu)

E

p

– odpór graniczny – gdy

δ ≥ δ

p

(ruch do gruntu)

E

I

– parcie pośrednie – gdy 0 <

δ

I

<

δ

a

E

II

– odpór pośredni – gdy 0 <

δ

II

<

δ

p

δ (

od gruntu)

Rys. 6.6. Zależność parcia i odporu gruntu od przemieszczeń ściany oporowej.

Przyjęcie odpowiedniej wartości parcia w przypadku ścian oporowych nie jest sprawą oczywistą,
gdyż wartość ta zależy od przemieszczeń ściany, a przemieszczenia te z kolei są wynikiem miedzy
innymi parcia gruntu. Projektowanie ścian oporowych na parcie spoczynkowe (E

0

) jest zbyt

asekuracyjne i raczej niewłaściwe. Parcie takie przyjmuje się dla konstrukcji, które nie ulegają
żadnym przemieszczeniom – np. ściany tuneli lub dużych kolektorów i rurociągów. Projektowanie
z kolei na parcie graniczne (E

a

) może być zbyt ryzykowne, gdyż jest ono najmniejsze ze wszystkich

parć i występuje dopiero przy znacznych i nieskrępowanych przemieszczeniach ściany.
Ściany oporowe powinno się projektować na parcie pośrednie, przyjmowane w przybliżeniu

E

I

= (E

a

+ E

0

)/2

lub

E

I

= (2E

a

+ E

0

)/3

, bądź ustalane dokładniej na podstawie obliczeń iteracyjnych.

Ustalanie wartości parcia pośredniego według normy PN-83/B-03010

Wartość parcia pośredniego działającego na ścianę oporową ustala się w zależności od
przemieszczeń uogólnionych ściany z wykorzystaniem przybliżonego wykresu, podanego poniżej.

E

0

, E

a

, E

p

, E

I

, E

II

– jak na rys. 6

ρ (

od gruntu)

strefa odporu

strefa parcia

E

II

ρ

a

ρ (

do gruntu)

ρ

p

E

0

E

a

0

ρ

II

ρ

I

E

I

0.5

ρ

a

0.5

ρ

p

E

p

E

Rys. 6.7. Uproszczona zależność parcia i odporu gruntu od przemieszczeń uogolnionych.

4

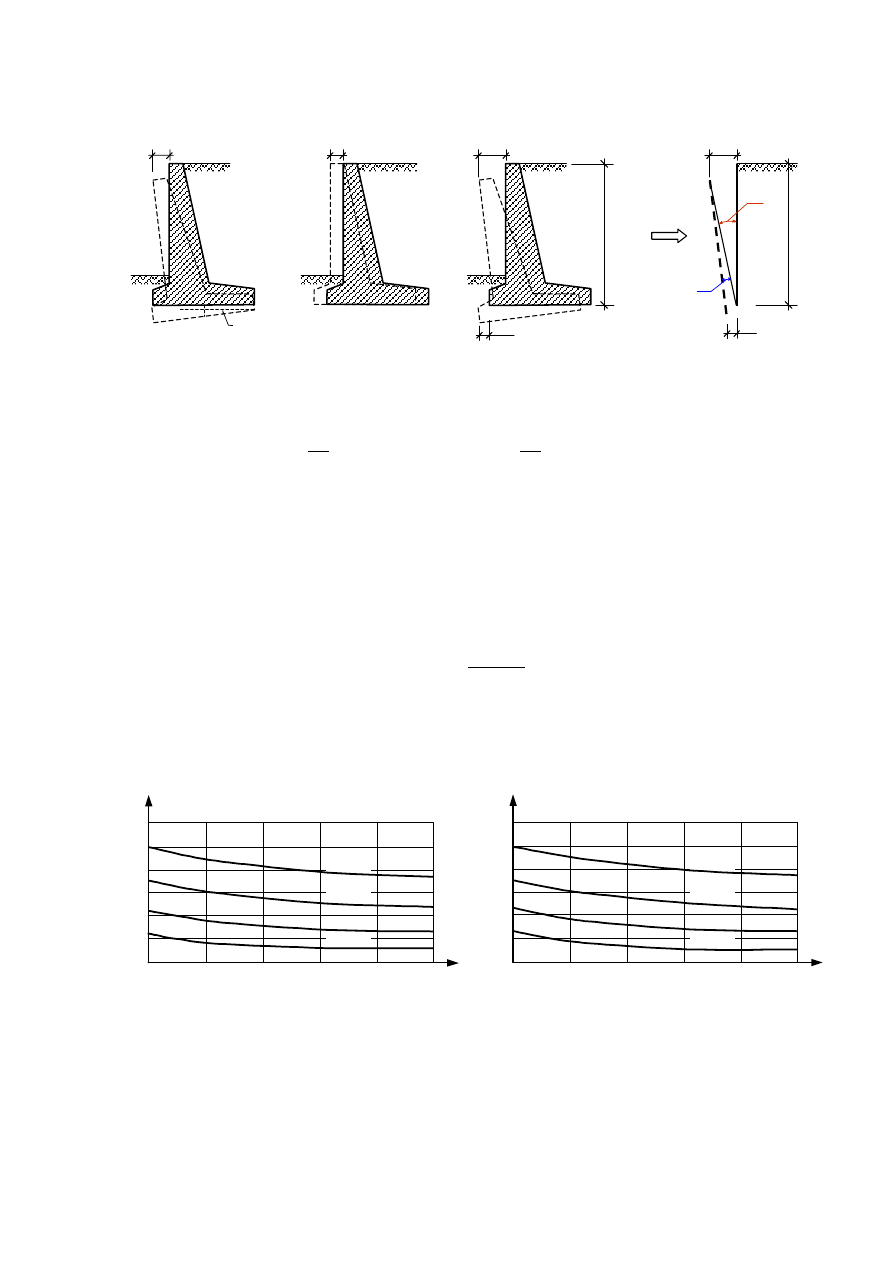
Przemieszczenia uogólnione oblicza się na podstawie przemieszczeń rzeczywistych ściany
oporowej: osiadań i przechyłki fundamentu oraz przesunięć poziomych (patrz rys. 8 poniżej).

H

ρ

B

ρ

A

f

A

A’

B’

A

B

f

B

H

f

A

=f

1

A’

B’

A

B

f

B

=f

1

+f

2

+ =

f

1

f

2

ϕ

s

0

s

2

s

1

Rys. 6.8. Wyznaczanie przemieszczeń uogólnionych ściany oporowej.

Przemieszczenia uogólnione oblicza się według wzorów:

H

f

B

A

=

ρ

[rad]

H

f

A

B

=

ρ

[rad] (1)

a całkowite przemieszczenie uogólnione jest sumą obu katów:

B

A

I

ρ

ρ

ρ

+

=

[rad]

(2)

Gdy przemieszczenie uogólnione

ρ

I

jest większe od połowy wartości przemieszczenia granicznego

(

ρ

I

≥ 0.5

ρ

a

), to przyjmuje się, że parcie pośrednie równe jest parciu granicznemu:

E

I

=

E

a

.

Natomiast w przypadku gdy 0 <

ρ

I

< 0.5

ρ

a

– parcie gruntu pośrednie należy obliczać następująco:

a

a

I

I

E

E

E

E

ρ

ρ

5

.

0

0

0

−

−

=

(3)

W bardzo podobny sposób należy wyznaczać odpór pośredni gruntu, jeśli zachodzi taka potrzeba.
Wartości uogólnionych przemieszczeń granicznych dla parcia

ρ

a

oraz dla odporu

ρ

p

odczytuje się

z nomogramów przedstawionych poniżej na rys. 9.

0.012

0.010

0.008

0.006

0.004

0.002

0.000

0 5 10

15

20

25

H [m]

ρ

a

φ

(n)

=10

°

φ

(n)

=20

°

φ

(n)

=30

°

φ

(n)

=40

°

0.12

0.10

0.08

0.06

0.04

0.02

0.00

0 5 10 15

20

25

H [m]

ρ

p

φ

(n)

=10

°

φ

(n)

=20

°

φ

(n)

=30

°

φ

(n)

=40

°

Rys. 6.9. Nomogramy do wyznaczania przemieszczeń granicznych

ρ

a

i

ρ

p

.

Można na nich zauważyć, że wartości

ρ

p

są 10-krotnie większe od wartości

ρ

a

.

5

Wartość jednostkową parcia spoczynkowego gruntu wyznacza się ze wzoru:

0

0

0

)

(

K

z

p

K

e

z

⋅

⋅

+

=

⋅

=

γ

σ

[kPa]

(4)

Współczynnik K

0

oblicza się ze wzorów:

a) dla gruntów rodzimych:

)

5

.

0

1

(

)

sin

1

(

3

2

1

0

ε

φ

ξ

ξ

ξ

tg

K

+

⋅

−

⋅

⋅

⋅

=

(5)

b) dla gruntów zasypowych:

[

)

5

.

0

1

(

)

15

.

4

5

)(

2

1

.

0

(

5

.

0

5

4

4

0

]

ε

ξ

ξ

ξ

tg

I

K

s

+

−

+

+

−

=

(6)

W powyższych wzorach:

ξ

1

÷

ξ

5

– współczynniki odczytywane z tablic 5 do 9 normy PN-83/B-03010

ε

– kąt nachylenia naziomu za ścianą (dla naziomu poziomego

ε

= 0)

I

s

– wskaźnik zagęszczenia gruntu zasypowego.

Dla piasków drobnych i średnich można wykorzystać przybliżoną, empiryczną formułę na I

s

w stosunku do I

D

, opracowaną przez Borowczyka i Frankowskiego (1981):

D

s

I

I

⋅

+

=

188

.

0

845

.

0

(7)

Parcie spoczynkowe działa zawsze poziomo i jego rozkład oraz wypadkową E

0

wyznacza się jak

pokazano na rys. 11b.
Wartość jednostkową parcia granicznego gruntu wyznacza się ze wzoru:

a

a

a

a

z

a

K

c

K

z

p

K

c

K

z

e

2

)

(

2

)

(

−

⋅

⋅

+

=

−

⋅

=

γ

σ

[kPa]

(8)

Współczynnik K

a

dla przypadku ogólnego oblicza się ze wzoru:

2

2

2

)

cos(

)

cos(

)

sin(

)

sin(

1

)

cos(

cos

)

(

cos













−

⋅

+

−

⋅

+

+

+

−

=

ε

β

δ

β

ε

φ

δ

φ

δ

β

β

φ

β

a

a

a

a

K

(9)

Wielkości (kąty) podane we wzorze (9) wraz z odpowiednimi znakami podano poniżej na rys. 10.

β

(+)

ε (+)

.

δ

a

(+)

E

a

Rys. 6.10. Oznaczenia kątów występujących we wzorze (9) wraz z przyjętą konwencją znaków.

W przypadku ściany pionowej i gładkiej oraz poziomego naziomu (

δ

a

=

β

=

ε

= 0) wzór (9)

sprowadza się do dużo prostszej i ogólnie znanej postaci:













−

=

2

45

2

φ

o

tg

K

a

(10)

W ścianach oporowych do zasypu najczęściej stosuje się grunty niespoiste, dla których wartość
spójności c, występującej we wzorze (8) równa jest zero (c = 0).

6

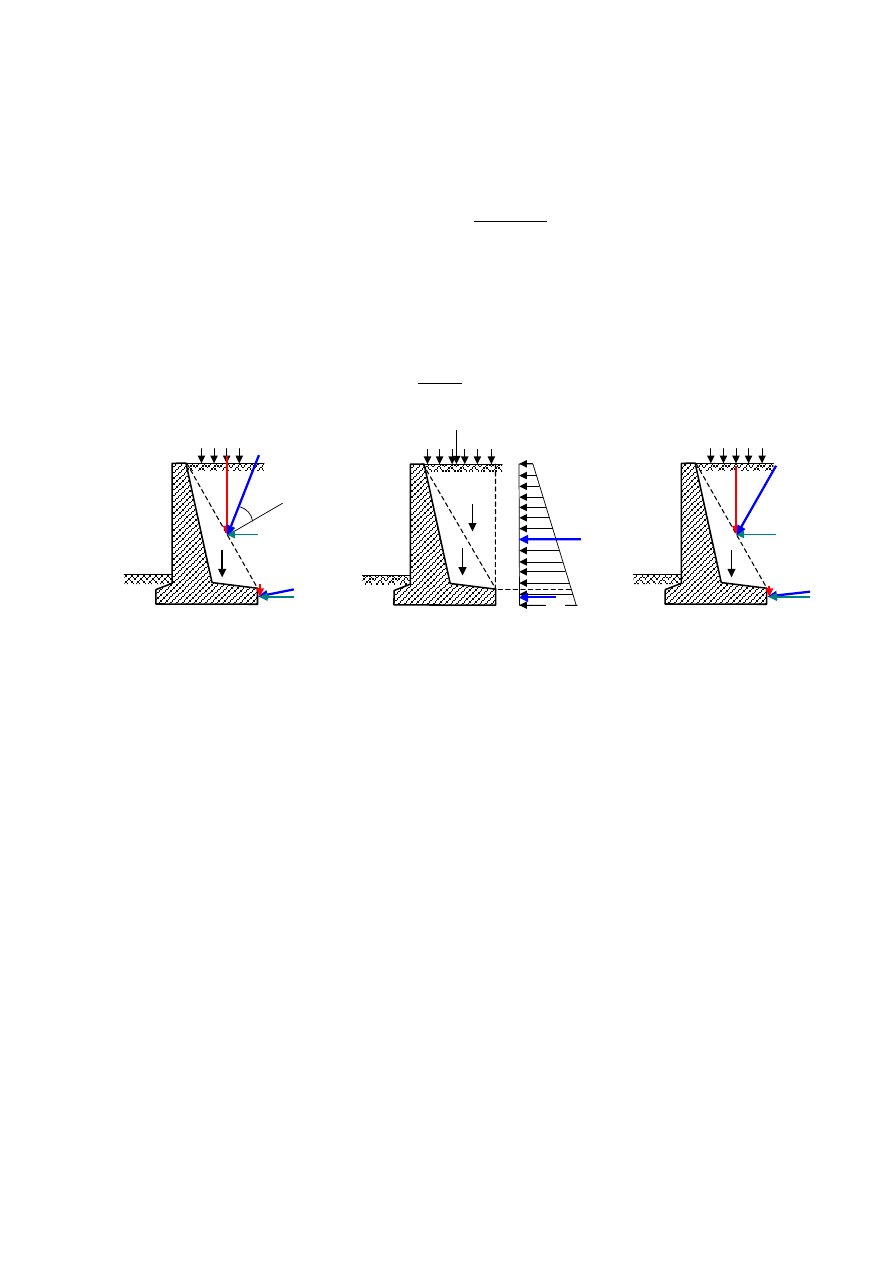
W przypadkach, w których parcie graniczne przyjmowane jest jako poziome (rys. 4c i 5),
wyznaczenie parcia pośredniego nie sprawia kłopotu. Problem pojawia się, gdy parcie graniczne
przyjmuje się ukośne (

δ

a

> 0) (rys. 4a,b). Wówczas składową poziomą parcia pośredniego E

I

h

wyznaczamy ze wzoru (3), w którym w miejsce E

a

wstawia się składową poziomą E

a

h

, natomiast

składową pionową E

I

v

można obliczyć ze wzoru:

a

v

a

I

v

I

E

G

G

E

ρ

ρ

5

.

0

)

(

−

′

−

′

=

(11)

w którym G’ jest ciężarem bryły gruntu zasypowego, pokazanej na rys. 11b. W wartości G’ należy
uwzględnić również ewentualne obciążenie naziomu p.
W przypadku parcia ukośnego działającego na pionową ścianę płyty fundamentowej, składową
pionową parcia pośredniego dla

ρ

I

< 0.5

ρ

a

wyznaczymy ze wzoru:

v

a

a

I

v

I

E

E

2

2

5

.

0

⋅

=

ρ

ρ

(12)

E

I2

v

E

I1

h

p

c)

E

I2

E

I1

h

E

I1

v

E

I1

G

E

02

G

E

a2

v

E

a1

h

E

a2

δ

a1

=

φ

E

a1

h

E

a1

v

E

a1

p

a) b)

G

P

p

E

01

G’

Rys. 6.11. Rozkłady i wypadkowe parcia gruntu na ścianę oporową: a) parcie graniczne, b) parcie spoczynkowe,

c) parcie pośrednie.

Proponuje się następujący iteracyjny tok postępowania przy ustalaniu wartości parcia pośredniego
działającego na ścianę oporową:

1) Zebranie obciążeń działających na ścianę oporową z wstępnym przyjęciem parcia granicznego

gruntu (E

a

).

2) Obliczenie przemieszczeń ściany oporowej (osiadań, przechyłki i przesunięcia poziomego –

rys. 15) i określenie przemieszczeń uogólnionych.

3) Określenie wartości parcia pośredniego E

I

. W przypadku, gdy parcie pośrednie wyjdzie równe

parciu granicznemu – będzie to koniec iteracji. Jeśli nie - przechodzimy do pkt. 4.

4) Ponowne obliczenie przemieszczeń ściany oporowej i przemieszczeń uogólnionych dla nowego

układu obciążeń (z parciem pośrednim z pkt. 3)

5) Określenie nowej wartości parcia pośredniego. W przypadku gdy parcie to będzie różniło się

mniej niż o 5% w stosunku do parcia ustalonego w pkt. 3 – kończymy iterację.

Zestawienie obciążeń działających na ścianę oporową

Po określeniu wszystkich obciążeń działających na ścianę oporową należy je zestawić wraz
z promieniami działania i momentami względem środka podstawy fundamentu „0”. Należy
oddzielnie zestawić obciążenia pionowe i oddzielnie poziome. W obciążeniach pionowych należy
policzyć 3 warianty: obciążenia charakterystyczne, obliczeniowe minimalne i obliczeniowe
maksymalne (tabl. 1), a w obciążeniach poziomych – 2 warianty: obciążenia charakterystyczne
i obliczeniowe maksymalne (tabl. 2).

7

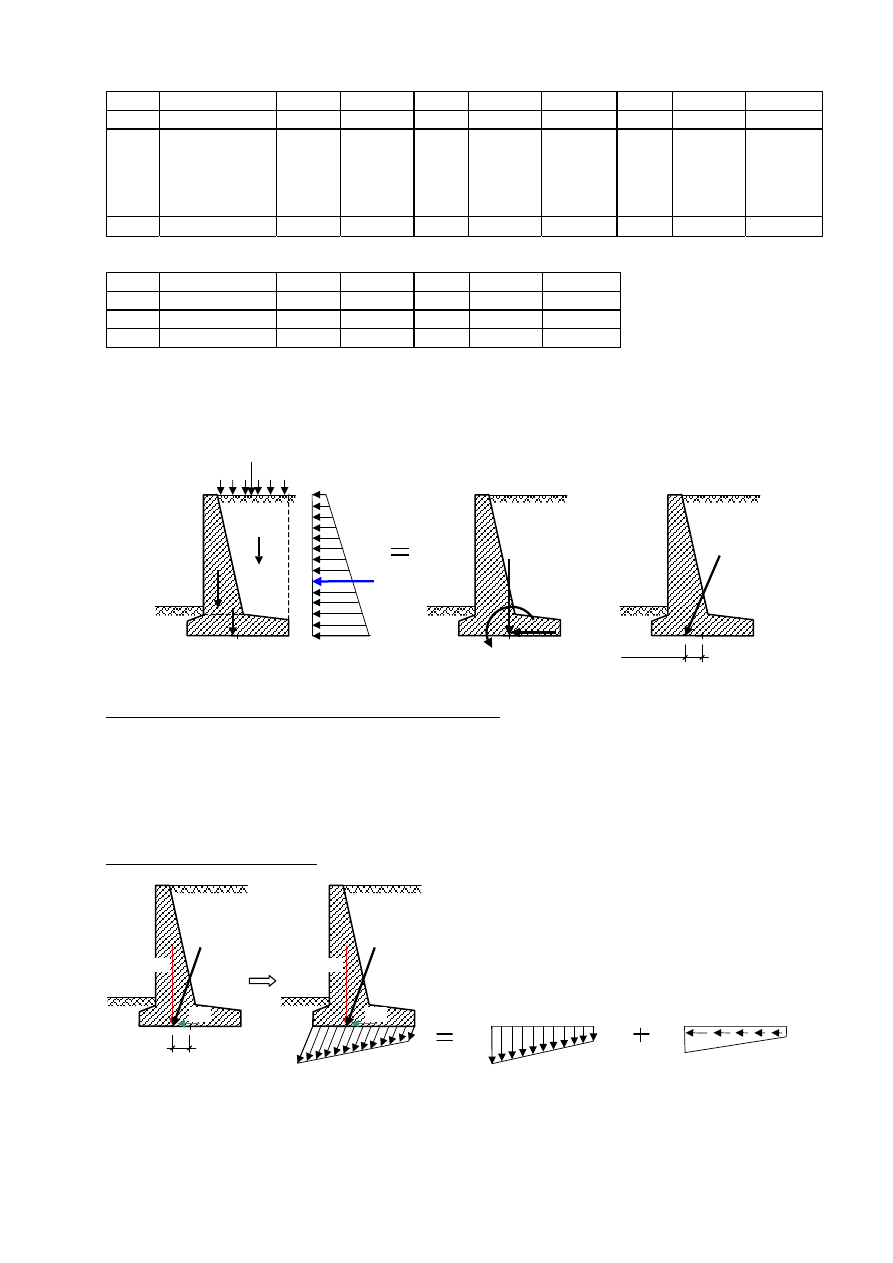
Tabl. 6.1. Obciążenia pionowe na 1 mb ściany

Obc. W.

charakt.

V

k

r

0

M

0

(V

k

)

γ

fmin

V

min

M

0

(V

min

)

γ

fmax

V

max

M

0

(V

max

)

[kN] [m]

[kNm]

[kN]

[kNm]

[kN]

[kNm]

G

1

G

2

...

(E

v

)

P

Σ

ΣV

k

-

ΣM

0

(V

k

)

-

ΣV

min

ΣM

0

(V

min

)

-

ΣV

max

ΣM

0

(V

max

)

Tabl. 6.2. Obciążenia poziome na 1 mb ściany

Obc. W.

charakt.

H

k

r

0

M

0

(H

k

)

γ

fmax

H

max

M

0

(H

max

)

[kN] [m]

[kNm]

[kN]

[kNm]

(E

h

)

Σ

ΣH

k

-

ΣM

0

(H

k

)

ΣH

max

ΣM

0

(H

max

)

W powyższych tablicach należy również uwzględnić ewentualne obciążenia zewnętrzne działające
na ścianę (np. gdy ściana jest jednocześnie przyczółkiem mostowym, to należy uwzględnić
obciążenia pionowe i poziome przekazywane z przęsła i z innych elementów).

Sprawdzenie położenia wypadkowej obciążeń w podstawie fundamentu i nacisków na grunt

P

E

B

=

ΣM

0

/

ΣV

lub

0

ΣQ

ΣM

0

ΣH

p

0

ΣV

0

E

G

3

G

1

G

2

Rys. 6.12. Sprowadzenie obciążeń działających na ścianę oporową do poziomu podstawy fundamentowej.

Należy przygotować następujące kombinacje obciążeń:
1. Obciążenia charakterystyczne - Komb. 1 :

ΣV

k

,

ΣH

k

,

ΣM

0k

=

Σ M

0

(V

k

) +

Σ M

0

(H

k

)

2. Obciążenia obliczeniowe

- Komb. 2:

ΣV

max

,

ΣH

max

,

ΣM

0odp

=

Σ M

0

(V

max

) +

Σ M

0

(H

max

)

- Komb. 3:

ΣV

min

,

ΣH

max

,

ΣM

0odp

=

Σ M

0

(V

min

) +

Σ M

0

(H

max

)

Naciski na podłoże gruntowe

q

1

=

ΣV/B⋅(1 + 6⋅E

B

/B)

q

2

=

ΣV/B⋅(1 - 6⋅E

B

/B)

t

1

q

2

q

1

ΣH

ΣV

ΣQ

ΣH

ΣV

E

B

0

ΣQ

t

2

Rys. 6.13. Rozkład nacisków na grunt przekazywanych przez podstawę ściany oporowej.

Warunki jakie powinny spełniać mimośród wypadkowej E

B

i naciski q:

- dla obciążeń charakterystycznych: Komb. 1: E

Bk

≤ B/6 oraz q

1

/q

2

≤ 3 ÷ 4

- dla obciążeń obliczeniowych: Komb. 2: E

B

≤ B/6,

Komb. 3 : E

B

= E

Bmax

≤ B/4

8

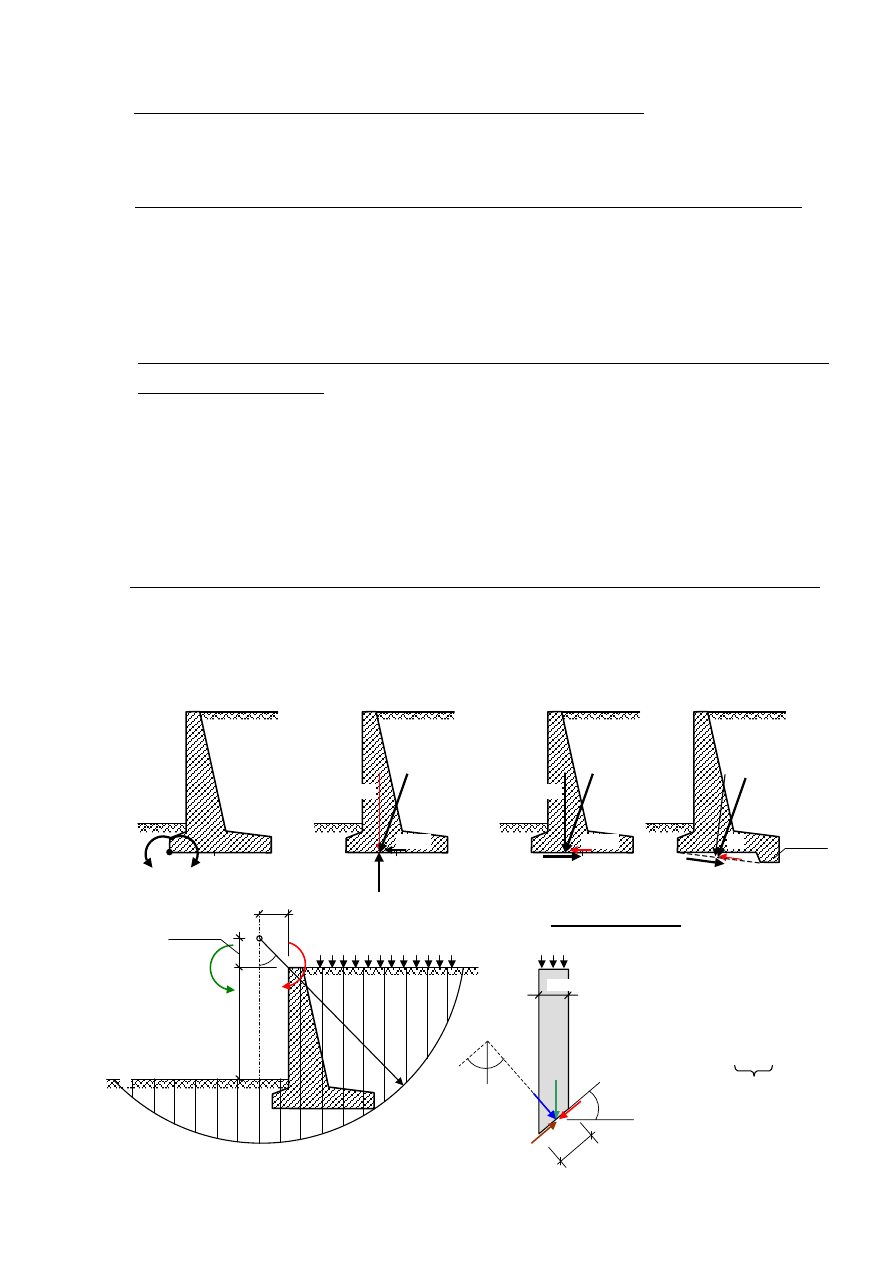
Sprawdzenie stanów granicznych nośności (SGN):

a) sprawdzenie stateczności na obrót (równowaga momentów) (rys. 14a):

ΣM

OA

≤ m

0

⋅ΣM

UA

, m

0

= 0.8

÷

0.9

(13)

najbardziej niekorzystny wariant obciążeń – Komb. 3

b) sprawdzenie nośności pionowej podłoża gruntowego (równowaga sił pionowych) (rys. 14b):

N

r

≤ m⋅Q

fNB

, m = 0.8

÷

0.9

(14)

należy sprawdzić Komb. 2 i Komb. 3 obciążeń, bo nie wiadomo, która z nich jest bardziej
niekorzystna. W Komb. 2 mamy maksymalne obciążenia pionowe N

rmax

, ale stosunkowo mały

mimośród E

B

, natomiast w Komb. 3 mamy mniejsze obciążenia pionowe N

rmin

, ale duży

mimośród E

B

, który może wpłynąć na znaczne obniżenie nośności podłoża Q

fNB

.

c) sprawdzenie nośności poziomej podłoża gruntowego (stateczność na przesuw lub równowaga

sił poziomych) (rys. 14c):

T

r

≤ m

t

⋅Q

tf

, m

t

= 0.9

÷ 0.95, Q

tf

= N

r

⋅

µ

+ a

⋅B, gdzie a = (0.2 ÷ 0.5) c

(r)

– adhezja (15)

najbardziej niekorzystny wariant obciążeń – Komb. 3

µ

≤ tg

φ

(r)

- współczynnik tarcia gruntu o podstawę fundamentu (wg normy - tabl. 3); w przypadku

fundamentów monolitycznych betonowanych wprost na nienaruszonym podłożu gruntowym
można przyjmować

µ

= tg

φ

(r)

. W przypadku nie spełnienia warunku można zastosować ostrogę

lub wymienić grunt.

d) sprawdzenie stateczności ogólnej uskoku naziomu – metodą Felleniusa (lub Bishopa) (rys. 14d)

M

o

≤ m⋅M

u

,

(16)

ΣM

o

,

⋅ΣM

u

– odpowiednio suma momentów obracających i utrzymujących

m – współczynnik korekcyjny, m = 0.6

÷ 0.85 – dla charakterystycznych obciążeń i parametrów,

m = 0.80

÷ 1.0 – dla obliczeniowych obciążeń i parametrów

R

B

R

T

M

n

i

i

n

i

i

u

⋅

+

⋅

=

∑

∑

=1

∑

=

⋅

=

n

i

i

o

R

B

M

1

Q

fNB

ΣM

UA

ΣM

OA

A

a)

0

ΣQ

0

N

r

=

ΣV

T

r

=

ΣH

b)

ΣQ

0

N

r

=

ΣV

T

r

=

ΣH

Q

tf

= N

r

⋅µ + a⋅B

c)

ΣQ

T’

r

ostroga

Q’

tf

= N’

r

⋅tgφ

(r)

+ c

(r)

⋅B’

N’

r

Metoda Felleniusa

M

u

M

O

dla

α

i

(+)

dla

α

i

(-)

α

i

(-)

N

i

= W

i

⋅cosα

i

B

i

= W

i

⋅sinα

i

T

i

= N

i

⋅tgφ

i

+ c

i

⋅l

i

, l

i

= b

i

/cos

α

i

l

i

b

i

= 0.1R

T

i

B

i

N

i

W

i

α

i

α

i

(+)

p

R

p

α

H

n

x

≈ 0.25H

n

y

≈ 0.25H

n

17

16

15

14

13 12

11 10

9

8

7

6

5

4

3

2

1

R

d)

0

Rys. 6.14. Schematy do sprawdzania warunków stanów granicznych nośności (SGN).

9

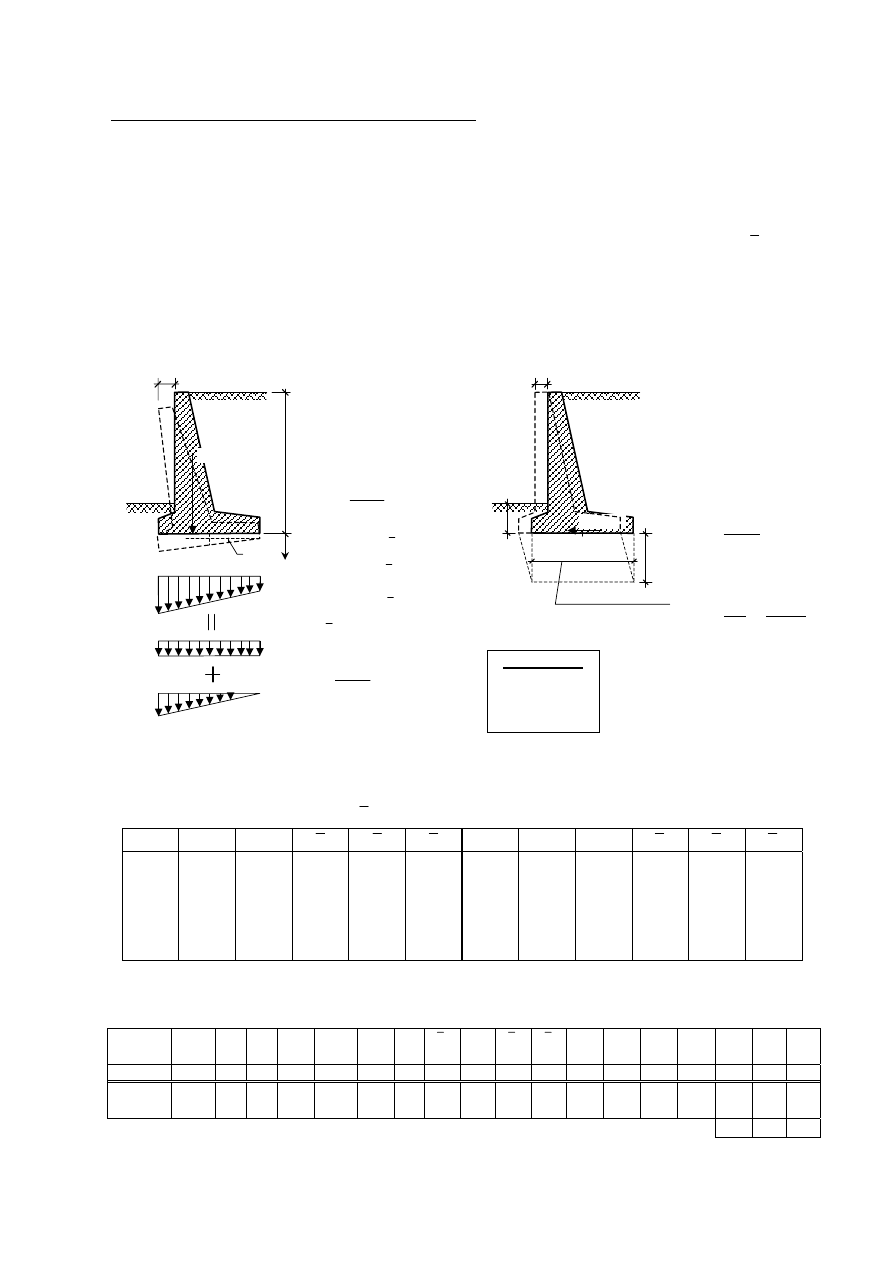
Obliczanie przemieszczeń i sprawdzenie stanów granicznych użytkowalności (SGU):

a) obliczenie osiadań i przechyłki ściany oporowej

Obliczenia osiadań i przechyłki ściany oporowej proponuje się wykonać metodą odkształceń
jednoosiowych. W tym celu trapezowy rozkład nacisków na grunt pod fundamentem ściany należy
rozłożyć na sumę rozkładu prostokątnego p

1

i trójkątnego p

2

. Następnie po podzieleniu podłoża

gruntowego na warstwy obliczeniowe o miąższości h

i

≤ 0.5B należy obliczyć wartości osiadań

punktów 0, 1 i 2, korzystając ze wzorów podanych na rys. 15a oraz współczynników k

j

i k

j

z tabl. 3.

Obliczenia proponuje się wykonać tabelarycznie (tabl. 4), poprzez sumowanie osiadań poszczegól-
nych warstw obliczeniowych do głębokości z

i

, na której spełniony jest warunek:

σ

jzi

≤ 0.3

σ

γ

zi

.

Wielkość z

i

odmierzamy zawsze od poziomu posadowienia do środka wysokości warstwy „i”.

Rys. 6.15. Schematy do obliczania przemieszczeń ścian oporowej.

Tablica 6.3. Wartości współczynników k

j

i k

j

(wg PN-83/B-03010-tabl. Z4-1)

z/B

k

0

k

1

k

0

k

1

k

2

z/B

k

0

k

1

k

0

k

1

k

2

0.00
0.25
0.50
0.75
1.00
1.50

1.000
0.960
0.820
0.668
0.542
0.396

0.500
0.496
0.481
0.450
0.410
0.332

0.50
0.48
0.41
0.33
0.28
0.20

0.50
0.42
0.35
0.29
0.25
0.19

0.00
0.08
0.13
0.15
0.16
0.15

2.00
2.50
3.00
4.00
5.00

0.306
0.245
0.208
0.160
0.126

0.275
0.231
0.198
0.153
0.124

0.15
0.13
0.11
0.08
0.06

0.15
0.12
0.10
0.08
0.06

0.14

0.10
0.08
0.06

0.13

Tablica 6.4. Obliczenia osiadań ściany oporowej

Profil

geotechn.

γ

i

(

‘

)

h

i

z

i

σ

γzi

0.3

σ

γzi

z

i

/B

k

0i

k

0i

k

1i

k

1i

k

2i

σ

0zi

σ

1zi

σ

2zi

M

0i

s

0i

s

1i

s

2i

[kN/m

3

]

[m]

[m]

[kPa]

[kPa]

- - - - - -

[kPa]

[kPa]

[kPa]

[MPa]

[mm]

[mm] [mm]

Σ

l

1

= 1.0 mb

Γ

,

Γ

i

– współczynniki

wpływu według
normy

- podłoże uwarstwione

∑

−

Γ

−

Γ

⋅

=

i

0

1

i

i

1

Hn

1

E

l

2

Q

f

2

,

1

,

0

j

;

M

h

s

i

0

i

jzi

j

=

⋅

σ

=

∑

2

i

0

1

i

0

zi

0

p

k

p

k

⋅

+

⋅

=

σ

2

i

1

1

i

1

zi

1

p

k

p

k

⋅

+

⋅

=

σ

2

i

2

1

i

1

zi

2

p

k

p

k

⋅

+

⋅

=

σ

B

s

s

2

1

−

=

ϕ

H

f

2

⋅

ϕ

=

k, k – współczynniki wpływu
według normy

Warunki SGU:

s < s

dop

ϕ < ϕ

dop

f = f

1

+ f

2

< f

dop

strefa odkształceń w
podłożu gruntowym

0

Q

Hn

=

ΣH

k

b)

D

h

w

B

f

1

p

1

p

2

p

1

q

2

(n)

q

1

(n)

s

1

s

2

z

H

s

0

N

n

=

ΣV

k

f

2

ϕ

a)

h

w

= 0.4(B+l

a

)

l

a

– długość wyparcia

strefy odporu

l

a

= D

⋅tg(45°+

φ

/2)

- podłoże jednorodne

0

1

Hn

1

E

l

2

Q

f

⋅

Γ

⋅

=

10

b) obliczenie przemieszczeń poziomych ściany oporowej

Przemieszczenia poziome ściany oporowej nie są efektem poślizgu ściany po gruncie, gdyż do tego
nie można dopuścić, lecz wynikają z odkształceń postaciowych bryły gruntowej, znajdującej się
pod fundamentem i sięgającej do głębokości h

w

.

Podstawowe wzory do obliczenia przemieszczenia poziomego f

1

ściany oporowej przedstawiono na

rys. 15b. Występujące w tych wzorach współczynniki

Γ

oblicza się ze wzoru:













⋅

−

+

+

⋅

−

⋅

+

=

Γ

Γ

Γ

m

arctg

m

m

1

)

2

3

(

)

1

ln(

)

1

(

2

)

1

(

2

ν

ν

π

ν

Γ

(17)

We wzorze tym

ν

jest współczynnikiem Poissona dla gruntu. Należy pamiętać, żeby wyrażenie

Γ

m

arctg

1

podawać w radianach.

W przypadku gdy wielkość h

w

zawiera się w jednej warstwie gruntowej, to mamy do czynienia

z podłożem jednorodnym i wówczas:

B

h

w

2

=

Γ

m

.

W przypadku gdy w zasięgu h

w

zawierają się dwie lub więcej warstw, to mamy do czynienia

z podłożem uwarstwionym i wówczas dla każdej warstwy obliczamy oddzielny współczynnik

Γ

i

dla

B

h

m

i

i

2

=

Γ

. Wielkość h

i

jest zagłębieniem spodu danej warstwy „i” w stosunku do spodu

fundamentu (nie mylić z miąższością tej warstwy). Dla ostatniej warstwy: h

i

= h

w

.

Zagadnienia dodatkowe
Odwodnienie gruntu zasypowego za ścianami oporowymi i izolacja ścian oporowych.
Posadowienie ścian oporowych na palach (patrz „fundamenty palowe).
Zbrojenie ścian oporowych.

Opracowanie:

dr inż. Adam Krasiński

(Katedra Geotechniki PG)

11

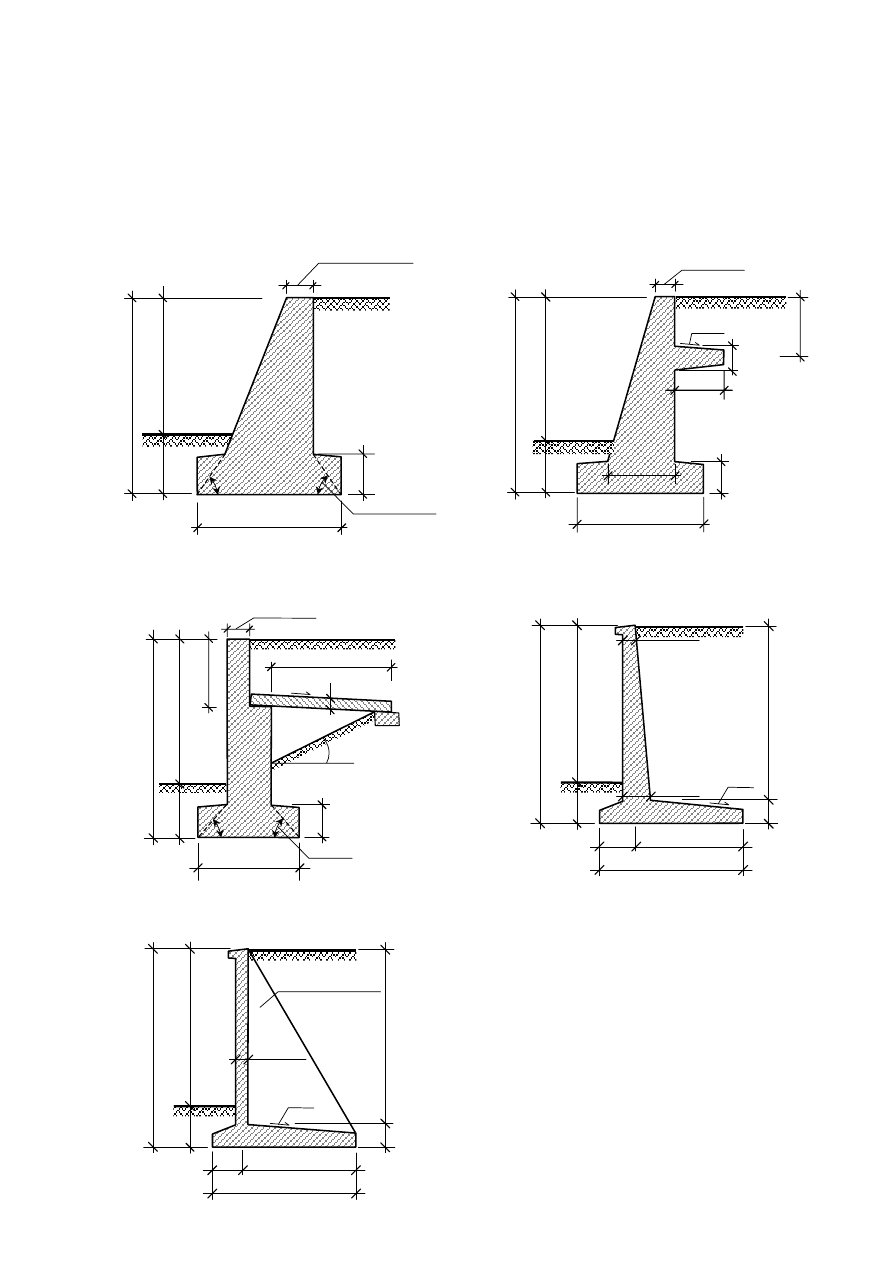
Załącznik 1. Zalecenia dotyczące przyjmowania wstępnego wymiarów ścian oporowych

1. Minimalna głębokość posadowienia ścian oporowych

D

≥ 0.5 m – grunty niewysadzinowe (grunty niespoiste)

D

≥ h

z

– grunty wysadzinowe (grunty spoiste)

h

z

– głębokość przemarzania gruntu (wg PN-81/B-03020)

2. Ściany masywne

3. Ściany półmasywne ze wspornikiem

B=(0.5

÷0.7)H

h

≥0.25B

H

n

≤

4 m

a

≥ 0.3m (beton)

a

≥ 0.5m (mur)

D

α

α ≥ 45° (beton)
α ≥ 60° (mur)

B=(0.5

÷0.6)H

h

≥0.2B

b

≥1/3B

≥0.3l

w

≥5%

a

≥ 0.25m

∼1/3H

l

w

=0.8

÷1.2m

H

n

≤

6 m

H

D

α

H

4.

Ściany półmasywne z płytą odciążającą 5. Ściany lekkie płytowo-kątowe

a

≥ 0.3m

∼1/3H

α ≥ 45°

α

α

h

≥0.25B

g

p

=(0.1

÷0.15)l

p

l

p

=2.5

÷3.5m

≥5%

D

ψ≤0.8φ

H

n

≤

6 m

H

B=

∼0.5H

≥5%

h

≥b

H

s

b

≥0.12H

s

a

≥0.15m

∼3/4B

∼1/4B

D

H

n

≤

4 m

H

B=0.6

÷0.7H

5.

Ściany lekkie płytowo-żebrowe

12

B=0.6

÷0.7H

H

a

≥0.20m

≥5%

żebra gr. 0.3

÷0.4m

co 2.0

÷3.0 m

h

≥0.12B

H

s

∼3/4B

∼1/4B

D

H

n

≤

8 m