ZADANIA Z TEORII OBWODÓW DLA TELEINFORMATYKI

ZESTAW 4

(17.11 – 24.11.2008)

Obowi

ą

zuj

ą

cy zakres materiału: Pobudzenie sinusoidalne. Metoda

symboliczna

analizy

stanu

ustalonego

przy

pobudzeniu

sinusoidalnym. Postulaty teorii obwodów.

Zad. 1. Znaleźć zespolone wartości skuteczne następujących prądów i napięć:

a) u t

t

( )

sin

=

−











12 2

150

7

12

π

,

b) i t

t

( )

cos

=

+











5 2

35

3

4

π

,

c) u t

t

t

( )

sin

cos

=

+











+

−











10

100

2

3

20

100

2

π

π

.

Zad. 2. Przedstawić jako funkcję czasu następujące prądy i napięcia:

a) U1 = -1 - j,

ω

= 120 rad/s,

b) I2 = 10j,

ω

= 300 rad/s,

c) U

e

e

j

j

3

2

3

1

3

8

4

=

+

−

π

π

,

ω

= 240 rad/s,

d) I4 = -2 + j4,

ω

=

π

.

Zad. 3. Za pomocą metody wskazów zespolonych wyznaczyć graficznie amplitudę i fazę

początkową przebiegu :

u(t) = 35sin(

ω

t) + 45cos(

ω

t).

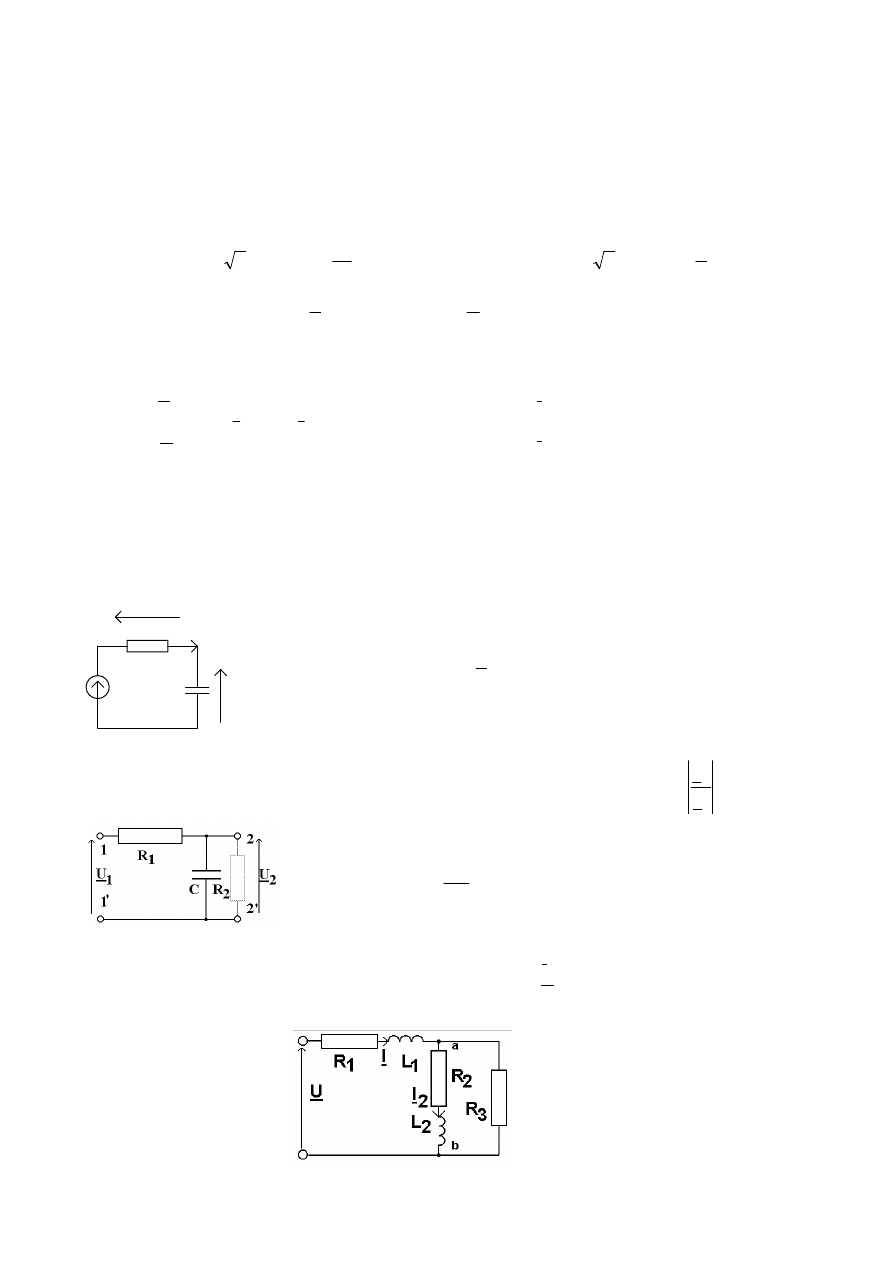
Zad. 4. Wyznaczyć napięcie u(t) na pojemności C. Narysować wykres wskazowy napięć i prądów

obwodzie.

Dane: e t

t

( )

sin

=

+











10

10

5

9

3

π

, C = 10

µ

F, R = 50

Ω

.

Zad. 5.

Wyznaczyć wartość rezystancji R2, którą należy podłączyć do zacisków 2, 2', żeby

u

u

k

2

1

=

.

Do obliczeń przyjąć następujące dane:

R1 = 100

Ω

,

1

50

ω

C

=

Ω

, k = 0.2.

Zad. 6. Jaka powinna być wartość rezystancji R3 aby prąd I2 płynący przez elementy R2 i L2

opóźniał się w fazie względem przyłożonego napięcia U o 90o. Przyjąć następujące dane :

R1 = 5

Ω

,

ω

L1 = 11

Ω

, R2 = 10

Ω

,

ω

L2 = 25

Ω

.

e(t)

R

C

u (t)

i(t)

u (t)

c

R