ZADANIA Z TEORII OBWODÓW DLA TELEINFORMATYKI

ZESTAW 6

(15.12.2008 – 05.01.2009)

Obowi

ą

zuj

ą

cy

zakres

materiału:

Pobudzenie

sinusoidalne.

Metoda

symboliczna analizy stanu ustalonego przy pobudzeniu sinusoidalnym.
Zasada

superpozycji.

Twierdzenie

Thevenina.

Dopasowanie

na

maksymaln

ą

moc czynn

ą

.

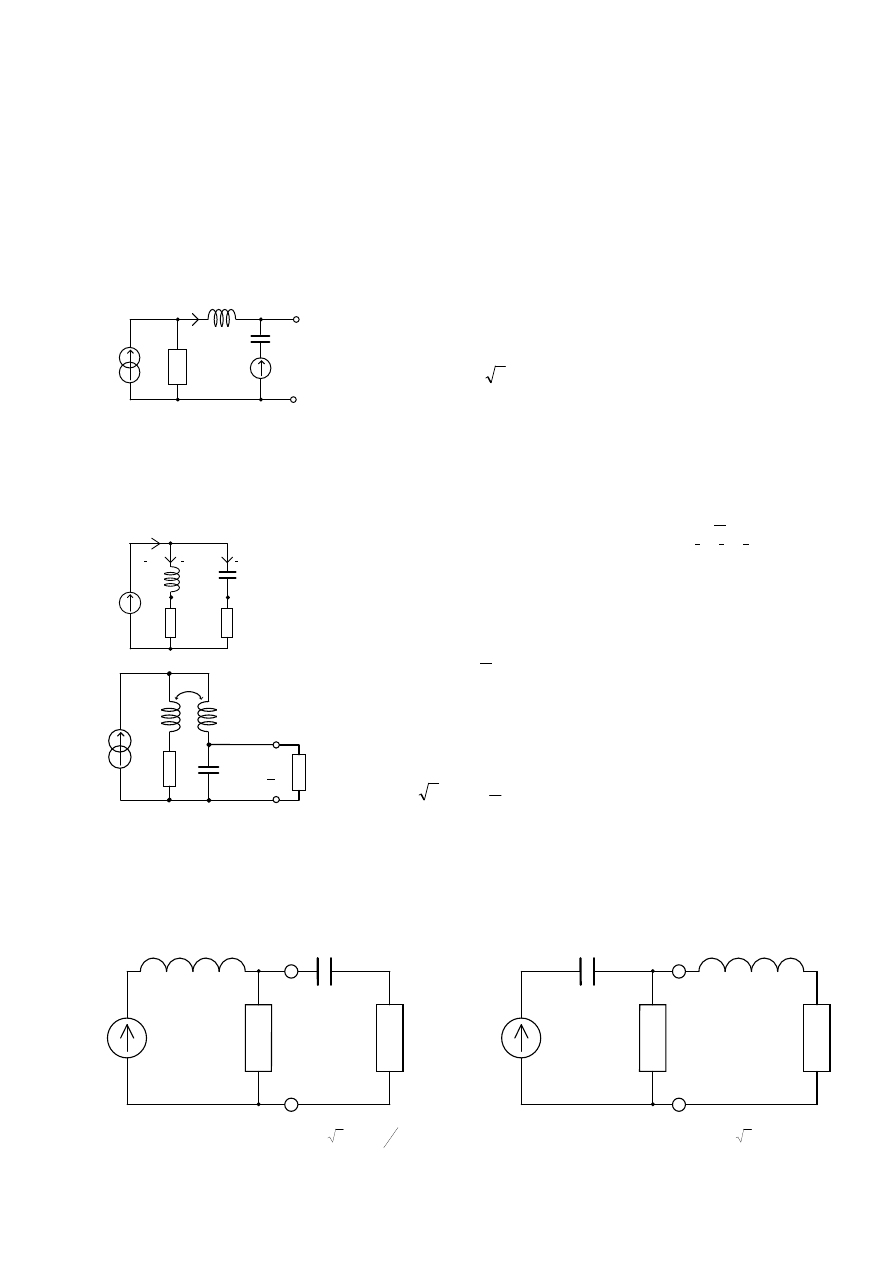
Zad. 1. Znaleźć schemat zastępczy wynikający z tw. Thevenina dwójnika 1, 2.

Dobrać tak elementy obciążenia, które należy dołączyć do
zacisków 1, 2, aby wydzieliła się w nim maksymalna moc
czynna. Obliczyć wartość tej mocy.

Dane: i

t

t

z

( )

cos

=

2

,

γ

= 2,

R = 1

Ω

, C = 1 F, L = 2 H.

Zad 2. Moc chwilowa doprowadzona do odbiornika, ze źródła o sinusoidalnym napięciu zmienia się

w przedziale 23 KVA do -5 kVA. Napisać wyrażenie na prąd i napięcie w funkcji czasu, jeżeli
u(0) = 500V, U

m

= 1835 V oraz f = 100Hz.

Zad 3. Dwie gałęzie podłączono równolegle do źródła napięcia sinusoidalnego o napięciu U = 130 V

(wartość skuteczna zespolona) (rys). Obliczyć prądy I

1

, I

2

, I oraz

wyznaczyć moc czynną i bierną, pobieraną przez każdą gałąź oraz
przez cały obwód. Znaleźć również napięcie między punktami A i B.
Dane:

X

L

=

ω

L = 6

Ω

, X

C

= 1/(

ω

C) = 5

Ω

, R

1

= 8

Ω

, R

2

= 12

Ω

.

Zad 4.Dla sieci przedstawionej na rysunku za pomocą tw. Nortona znaleźć

Yo , które zapewni dopasowanie na

maksymalną

moc

czynną

w

obciążeniu Y

0

.

Obliczyć tę moc.
Dane:

L1 = M = 1 H, L2 = 2H, C = 1 F, R = 1

Ω

,

iz(t) = 2

2

sin(

)

t

+ π

[A].

Zad 5.

Dobrać tak R

3

i C

4

(a) oraz R

2

i L

2

(b) by w tych dwójnikach wydzieliła się

maksymalna moc czynna. Obliczyć tę moc.

t

R

R

L

C

e( )

3

2

1

4

t

R

R

L

C

e( )

2

1

2

1

C

R

L

R

1

1

1

2

1

1

1

1

=

=

=

=

(a)

(b)

t

t

e

t

t

e

2

cos

2

)

(

)

4

sin(

2

2

)

(

=

−

=

π

C

L

1

2

i (t)

z

R

i(t)

i(t)

γ

L

R

C

u(t)

R

1

2

A

B

I

I

I

1

2

L

L

M

*

*

R

C

1

2

i (t)

z

Yo