L

ABORATORIUM FIZYCZNE

Instytut Fizyki Politechniki Krakowskiej

ĆWICZENIE

26

Polaryzacja światła

Ćwiczenie 26

2

W oddziaływaniu z materią, na
poziomie kwantowym należy po-
służyć się teorią korpuskularną
(cząsteczkową) światła. Np. w
zjawisku fotoelektrycznym światło
zachowuje się jak strumień czą-
stek, zwanych fotonami, z których
każda posiada określoną energię i
pęd. Podwójną naturę światła
określamy mianem dualizmu falo-
wo-korpuskularnego.

ĆWICZENIE

26

Polaryzacja światła

Barbara Oleś

1.

Wprowadzenie

Celem ćwiczenia jest badanie polaryzacji światła. Obejmuje ono obserwację zjawiska dwójłomno-

ści w kryształach oraz dwójłomności wymuszonej, sprawdzenie prawa Malusa, wyznaczenie właściwej
zdolności skręcającej roztworu cukru.

1.1

Natura światła

W zjawiskach dyfrakcji, interferencji i polaryzacji ujawnia się falowa natura światła. Tłumaczy ją

teoria falowa J.C.Maxwella, który w XIX wieku wykazał, że

światło jest falą elektromagnetyczną

, pole-

gającą na rozchodzeniu się zmiennych pól elektrycznych i magnetycznych. Zmienne okresowo w cza-
sie pole elektryczne wytwarza wokół siebie również zmienne okresowo wirowe pole magnetyczne

1

.

To zmienne pole magnetyczne jest z kolei źródłem zmiennego, wirowego pola elektrycznego

2

, wokół

którego znowu powstaje zmienne pole magnetyczne, itd.

Zmienne pola elektryczne i magnetyczne, wzajemnie się przenikające, które rozchodzą się w

przestrzeni tworzą

falę elektromagnetyczną

.

Do ilościowego opisu tych pól stosuje się wektor natę-

żenia pola elektrycznego oraz wektor indukcji magne-

tycznej . Wektory natężenia pola elektrycznego oraz

indukcji magnetycznej muszą opisywać zmiany pól w
czasie oraz przestrzeni i są dane funkcjami, których postać
jest podobna do funkcji opisującej fale mechaniczne. Wek-
tory te są zawsze prostopadłe do siebie i kierunku rozcho-
dzenia się fali, stąd światło jest

falą elektromagnetyczną

poprzeczną

, która może być spolaryzowana

3

.

1.2

Zjawisko polaryzacji światła

Ponieważ wiele urządzeń optycznych jak również nasze oczy reagują na składową pola elektrycz-

nego fali świetlnej, przyjęto wektor nazywać

wektorem świetlnym

. Konwencjonalne źródła światła,

żarówki, świetlówki wysyłają fale elektromagnetyczne, w których wektor w dowolnym punkcie
przestrzeni jest wprawdzie zawsze prostopadły do kierunku rozchodzenia się fal, ale jego kierunek
zmienia się przypadkowo (patrz: rys.1). Istnieją metody, żeby wymusić jeden, określony kierunek, do

1

Prawo Ampere’a.

2

Prawo Faraday’a.

3

Zjawisko polaryzacji występuje tylko dla fal poprzecznych, zarówno mechanicznych jak i elektromagnetycza-

nych.

Polaryzacja światła

3

którego wektor będzie równoległy, co oznacza, że jego drgania będą zachodzić tylko w jednej
płaszczyźnie.

Polaryzacja liniowa

fal świetlnych polega na otrzymaniu fali, w której wektor natężenia pola elek-

trycznego będzie miał określony kierunek w przestrzeni.

Płaszczyznę, w której leżą wektory natężenia pola elektrycznego nazywamy

płaszczyzną polary-

zacji

.

W szczególnym przypadku fali monochromatycznej

4

rozchodzącej się w próżni wzdłuż osi i spo-

laryzowanej w płaszczyźnie

, drgania wektora dane są równaniem

( , ) =

sin( −

+ ),

gdzie

= 2 / to liczba falowa, - częstość kołowa ( = 2 , – częstotliwość), - faza począt-

kowa. Dla wektora indukcji magnetycznej równanie ma analogiczną postać, tylko kierunek wektora

jest prostopadły do wektora . Rys.2 pokazuje, jak w danej chwili wygląda przestrzenna zmiana
wektorów obu pól. Argument funkcji sinus

Φ =

−

+

nosi nazwę

fazy

.

Światło może być również spolaryzowane kołowo lub eliptycznie. Wówczas koniec wektora natężenia

pola elektrycznego porusza się po linii śrubowej kołowej lub eliptycznej.

4

Fala monochromatyczna to fala o określonej długości

.

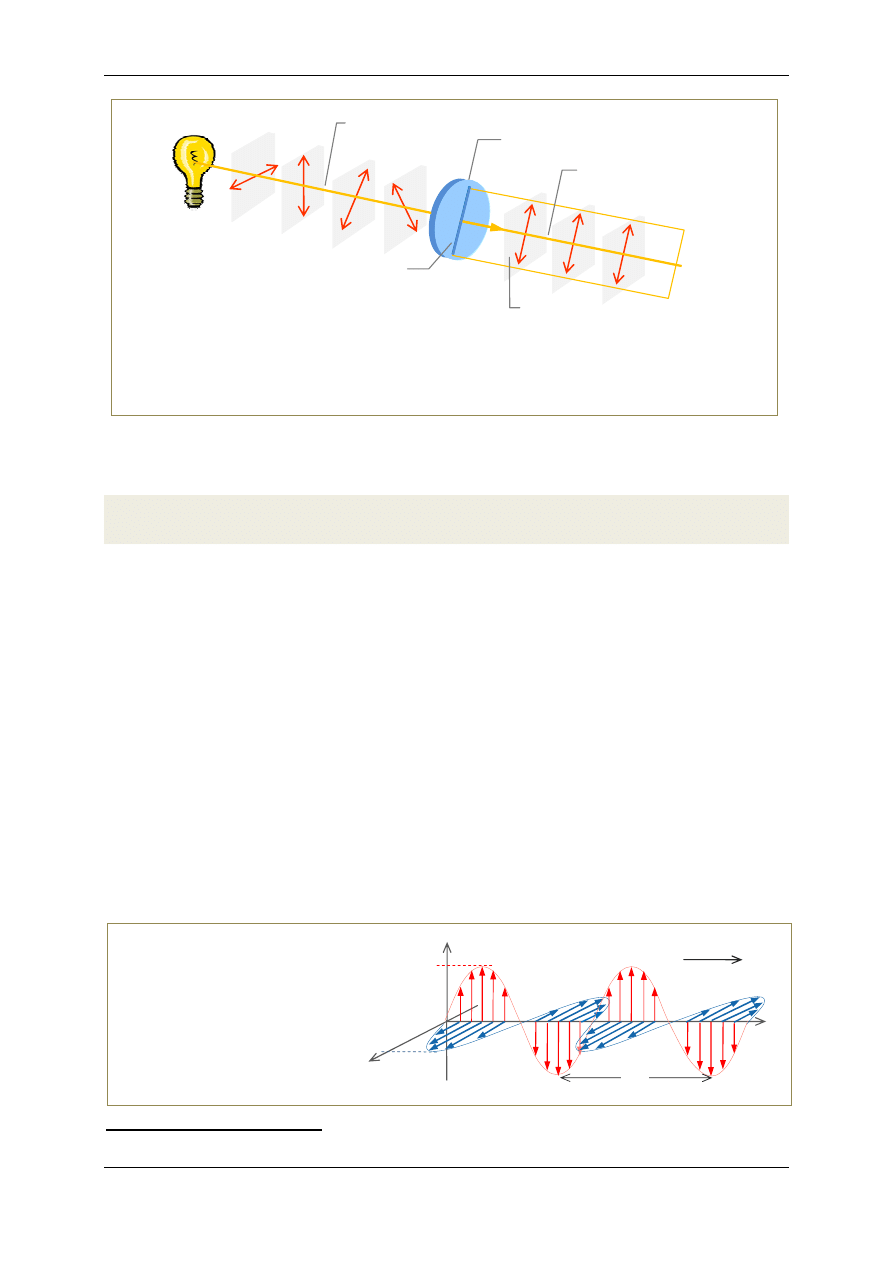
Rys.1. Światło emitowane przez żarówkę jest mieszaniną fal, których kierunki drgań wektorów są
zupełnie przypadkowe (ale zawsze prostopadłe do kierunku propagacji fali).

Filtr polaryzujący

ustawiony na drodze niespolaryzowanej wiązki światła wybiera tylko jeden kierunek wektora
dając światło spolaryzowane liniowo. Wektor drga wówczas w jednej płaszczyźnie.

światło
niespolaryzowane

filtr polaryzacyjny

światło
spolaryzowane

płaszczyzna polaryzacji

kierunek polaryzacji
filtra

kierunek rozchodzenia się fali

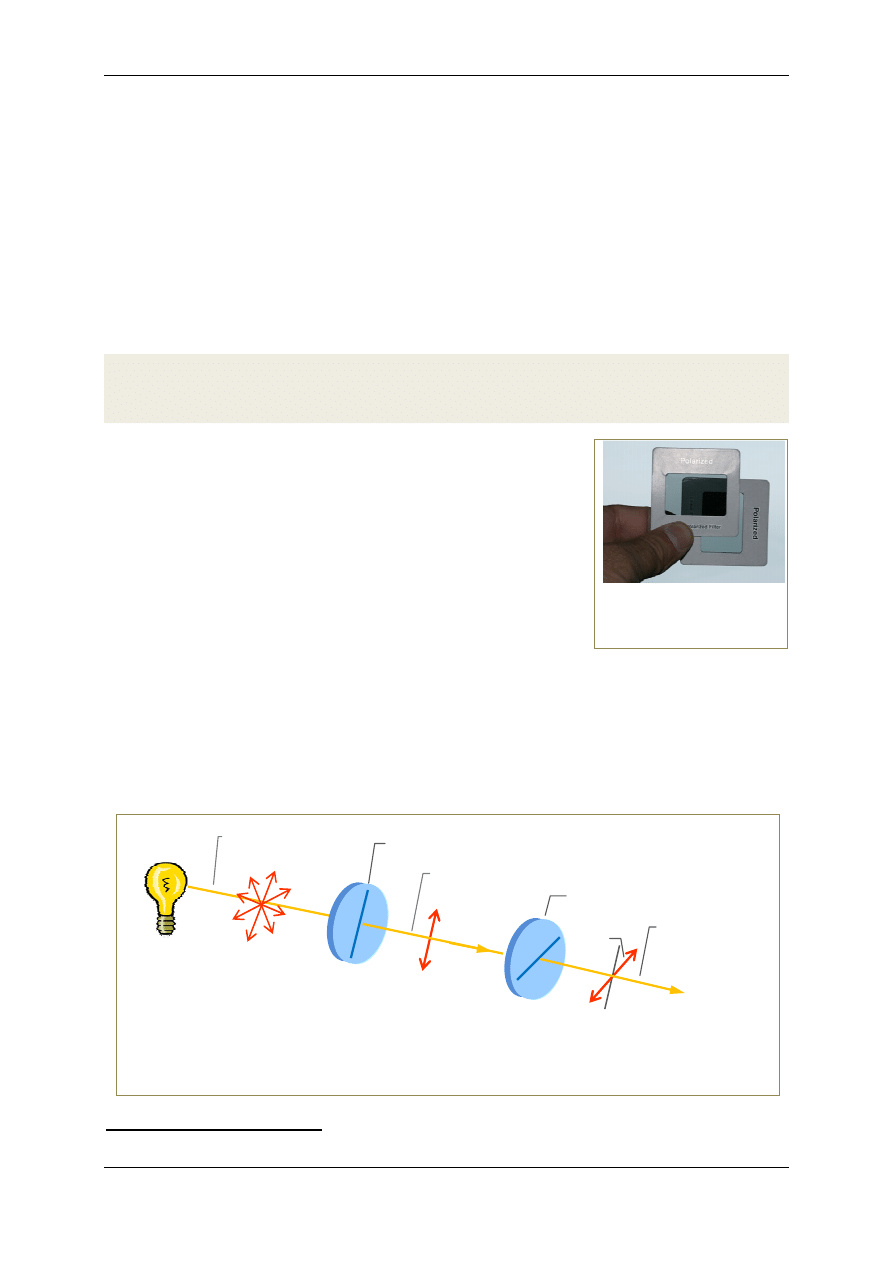
Rys.2. Liniowo spolaryzowana, mono-
chromatyczna fala elektromagnetycz-
na przedstawiona w postaci rozkładu
wektorów pola elektrycznego

i

magnetycznego wzdłuż kierunku jej
rozchodzenia się w ustalonej chwili .

Ćwiczenie 26

4

1.3

Metody polaryzacji światła

1.3.1

Filtry polaryzujące

Światło można spolaryzować przepuszczając go przez

polaroid

, folię polaryzującą zawierającą

długie cząsteczki jodosiarczanu chininy (herapatytu). W procesie produkcji cząsteczki ulegają upo-
rządkowywaniu w równoległe łańcuchy. Podczas przechodzenia światła przez folię, składowa pola

elektrycznego równoległa do łańcuchów wzbudza znajdujące się w nich elektrony do ruchu wzdłuż
cząsteczek. Energia fali związana z tą składową jest absorbowana przez elektrony

5

, a bez strat prze-

chodzi tylko ta część światła, która ma składową wektora prostopadłą do łańcuchów. Zatem kieru-
nek prostopadły do łańcuchów jest

kierunkiem polaryzacji

folii.

Światło niespolaryzowane po przejściu przez polaroid jest całkowicie spolaryzowane liniowo, a

kierunek jego polaryzacji jest zgodny z kierunkiem polaryzacji polaroidu (rys.1). Natężenie światła
spolaryzowanego jest równe połowie natężenia światła padającego na polaroid.

Rozważmy teraz sytuację, kiedy światło niespolaryzowane prze-

chodzi przez układ dwóch polaroidów. Pierwszy z nich nazwiemy

pola-

ryzatorem

, drugi

analizatorem

. Jeżeli kierunki polaryzacji polaryzatora

i analizatora są do siebie wzajemnie równoległe, to światło padające
na analizator jest w całości przepuszczane. Natomiast żadne światło
nie przejdzie przez analizator, jeżeli jego kierunek polaryzacji jest pro-
stopadły do kierunku polaryzacji pierwszego polaroidu. Mówimy
wówczas, że

polaryzatory są skrzyżowane

(rys.3).

Na rys.4 pokazana jest sytuacja pośrednia między wyżej wymie-

nionymi przypadkami granicznymi. Kierunek polaryzacji polaryzatora

tworzy kąt z kierunkiem polaryzacji analizatora. Wektor świetlny

wiązki padającej na analizator

możemy rozłożyć na dwie składowe, równoległą i prostopadłą do kierunku jego polaryzacji. Przez
analizator zostanie przepuszczona tylko część wiązki, która ma składową równoległą,

=

cos .

Ponieważ natężenie światła jest wprost proporcjonalne do kwadratu amplitudy wektora świetlnego,
natężenie światła wychodzącego z analizatora będzie dane wyrażeniem, które nosi nazwę prawa
Malusa

5

Taką selektywną absorpcję nazywamy dichroizmem.

Rys.4. Wiązka światła przechodzi przez dwa polaryzatory, których kierunki polaryzacji tworzą kąt

. Przez drugi filtr polaryzujący, analizator, przechodzi tylko część światła, której składowa wek-

tora natężenia pola elektrycznego jest równa

cos .

analizator

polaryzator

światło
spolaryzowane

światło
niespolaryzowane

światło
spolaryzowane

Rys.3. Skrzyżowane pola-
ryzatory nie przepuszczają
światła.

Polaryzacja światła

5

! = ! cos

"

, ($%&'( )&*+,&) (1.1)

gdzie

! jest natężeniem światła padającego na analizator, a kątem między kierunkami polaryzacji

polaryzatora i analizatora.

1.3.2

Zjawisko dwójłomności

Właściwości fizyczne wielu ciał o budowie krystalicznej zależą od kierunku, w którym są badane

6

.

W szczególności niektóre kryształy charakteryzuje

anizotropia optyczna

polegająca na tym, że współ-

czynnik załamania światła zależy od kierunku jego polaryzacji. Prowadzi to do rozszczepienia padają-
cego promienia światła niespolaryzowanego na dwa, o różnych, wzajemnie prostopadłych kierunkach
polaryzacji. Dla jednego z nich, zwanego

promieniem zwyczajnym

, współczynnik załamania

.

/

nie

zależy od kierunku rozchodzenia się światła w krysztale i spełnia prawo załamania Snella. Natomiast
współczynnik załamania

.

0

drugiego,

promienia nadzwyczajnego

, zależy od kierunku rozchodzenia

się światła w krysztale.

Zjawisko polegające na rozdzieleniu padającej na kryształ wiązki światła na dwie wiązki załamane

nosi nazwę

dwójłomności

(

podwójnego załamania

), a kryształy, w których ono występuje nazywamy

kryształami dwójłomnymi

.

Zjawisko podwójnego załamania można obserwować w krysztale kalcytu (rys.5), kwarcu, turmalinu i
innych. Zostało ono wykorzystane w pryzmacie Nicola, służącym do otrzymywania światła spolaryzo-
wanego liniowo. Pryzmat ten (nikol), zbudowany z dwóch odpowiednio wyciętych i złączonych ze
sobą pryzmatów z kalcytu, przepuszcza tylko promień nadzwyczajny eliminując promień zwyczajny,
który ulega całkowitemu wewnętrznemu odbiciu. Na jego wyjściu otrzymuje się światło całkowicie
spolaryzowane.

6

Ciała, których właściwości fizyczne nie zależą od kierunku, w którym są mierzone mówimy, że są

izotropowe

i

do nich należą szkło, pleksiglas.

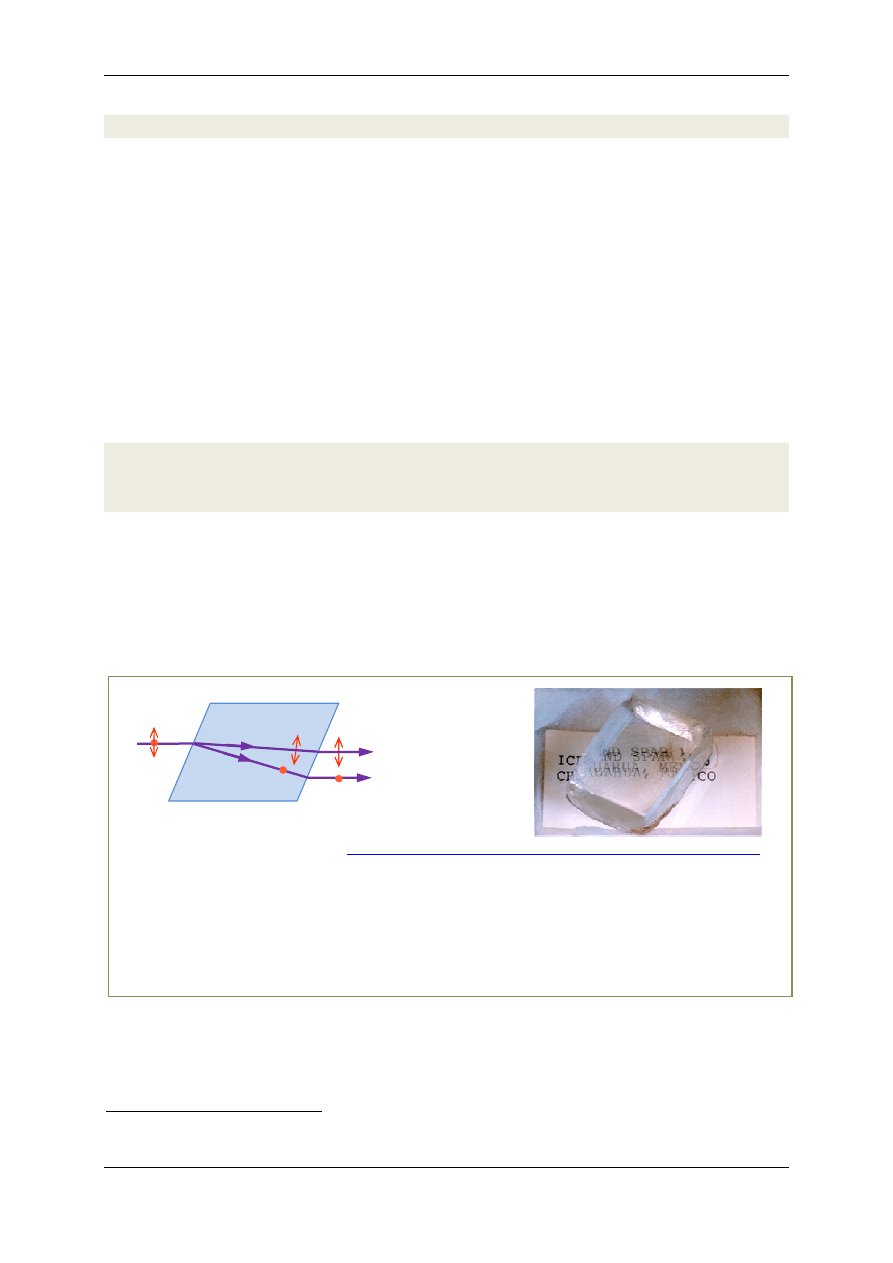
światło niespola-
ryzowane

kalcyt

promień nadzwyczajny

promień zwyczajny

Z

N

Rys.5. Dwójłomność w krysztale kalcytu. Promienie zwyczajny I nadzwyczajny wychodzące z kryształu są
spolaryzowane w kierunkach wzajemnie prostopadłych (kropki oznaczają kierunek prostopadły do płasz-
czyzny rysunku, a strzałki równoległy). Zjawisko dwójłomności może być obserwowane w krysztale kalcy-
tu, kładąc kryształ na zadrukowanej kartce papieru Widzimy wówczas podwojony obraz napisu. Obracając
kryształem zauważymy, że jeden obraz nie zmienia swojego położenia, drugi zatacza mały okrąg wokół
pierwszego. Za efekt ten odpowiedzialne są odpowiednio promienie zwyczajny i nadzwyczajny.

http://www.oberlin.edu/physics/catalog/demonstrations/optics/calcite.jpg

Ćwiczenie 26

6

1.3.3

Dwójłomność wymuszona

W przezroczystych ciałach izotropowych (np. w szkle

czy w pleksiglasie) dwójłomność może powstać w wyniku
mechanicznych naprężeń materiału. Zjawisko to nazywamy

dwójłomnością wymuszoną

.

Kiedy zwykły kawałek szkła umieścimy pomiędzy skrzy-

żowanymi polaryzatorami, przez analizator nie przejdzie
żadne światło. Sytuacja będzie taka jak na rys.3. Jednakże
ten sam kawałek poddany silnemu ściskaniu tak zmieni
polaryzację światła, że na wyjściu z analizatora będzie moż-
na obserwować jasne i ciemne pasma odpowiadające ob-
szarom o największym naprężeniu materiału (rys.6).

W materiale, w którym występują naprężenia, promień

świetlny rozdziela się na dwa promienie rozchodzące się z
różnymi prędkościami, których płaszczyzny drgań wektora
świetlnego pokrywają się z kierunkami naprężeń głównych.
Promienie wychodzące z analizatora interferują ze sobą, co
prowadzi to do pojawienia się ciemnych bądź jasnych prąż-
ków interferencyjnych. Analiza tych wzorów interferencyj-
nych dostarcza informacji o rozkładzie naprężeń.

Dwójłomność wymuszona jest wykorzystana w techni-

ce noszącej nazwę

elastooptyki

i służącej do badania rozkładu naprężeń w różnorodnych konstruk-

cjach (mostach, budynkach, narzędziach, itp.). W tym celu wykonane z przezroczystego materiału
modele umieszcza się pomiędzy skrzyżowanymi polaryzatorami i poddaje obciążeniom mechanicz-
nym. W zależności od naprężenia światło jest odmiennie spolaryzowane w różnych miejscach modelu
i powstają wzory. Są one barwne, gdy używa się światła białego, natomiast złożone tylko z jasnych i
ciemnych prążków, gdy zastosuje się światło monochromatyczne (rys.6).

1.4

Aktywność optyczna

Wiele ciał krystalicznych

7

i substancji organicznych ma zdolność skręcania płaszczyzny polaryzacji

spolaryzowanego liniowo światła. Nazywamy je substancjami

optycznie czynnymi

. Rozróżnia się sub-

stancje skręcające płaszczyznę polaryzacji światła w prawo i skręcające w lewo. Wszystkie substancje
optycznie czynne występują w dwóch odmianach – prawoskrętnej i lewoskrętnej.

Jeśli między dwa skrzyżowane polaryzatory wstawimy substancję optycznie czynną następuje

rozjaśnienie pola widzenia. Kąt skręcenia polaryzacji przez dane ciało jest równy kątowi, o jaki musi-
my skręcić analizator, aby ponownie uzyskać całkowite wygaszenie.

W roztworach kąt skręcenia płaszczyzny polaryzacji jest proporcjonalny do długości drogi

* prze-

bytej przez światło w roztworze i do jego stężenia

= 1 2

3

4

* . (1.2)

Współczynnik proporcjonalności

1 2

3

4

nosi nazwę

właściwej zdolności skręcającej

i zależy od rodzaju

substancji rozpuszczonej oraz długości fali (barwy) użytego światła. Zwykle grubość warstwy roz-

7

Np. mika, kwarc.

Rys.6. Światło spolaryzowane może
być wykorzystane do badania naprę-
żeń w modelach różnych obiektów i
narzędzi. Fotografia przedstawia
model muru poddanego obciążeniu i
umieszczony pomiędzy skrzyżowa-
nymi polaryzatorami. W pomiarach
użyto monochromatycznego światła
lampy sodowej. Widoczne są wzory
jasnych i ciemnych prążków, wynik
zmiany polaryzacji światła pod pły-
wem naprężenia. Obraz został już
przeanalizowany i naniesiono warto-
ści obliczonych naprężeń.

Polaryzacja światła

7

tworu podaje się w decymetrach, stężenie w gramach na 100 cm

3

i jednostką właściwej zdolności

skręcającej jest

1°

dm ∙ g/cm

:

.

Do pomiarów kąta skręcenia płaszczyzny polaryzacji używa się polarymetrów. Stosowane w cu-

krowniach tego typu przyrządy służą do określania stężenia cukru i noszą nazwę sacharymetrów.

2.

Metoda pomiaru

2.1

Sprawdzanie prawa Malusa

Prawo Malusa mówi, że natężenie

! światła przechodzącego przez dwa polaryzatory zależy od

względnej orientacji ich kierunków polaryzacji (wzór (1.1)). Z równania

! = ! cos

"

, którym wyraża

się to prawo, widać, że w celu
jego sprawdzenia należy zmierzyć
natężenie światła

! w zależności

od kąta

między kierunkami

polaryzacji polaryzatora i analiza-
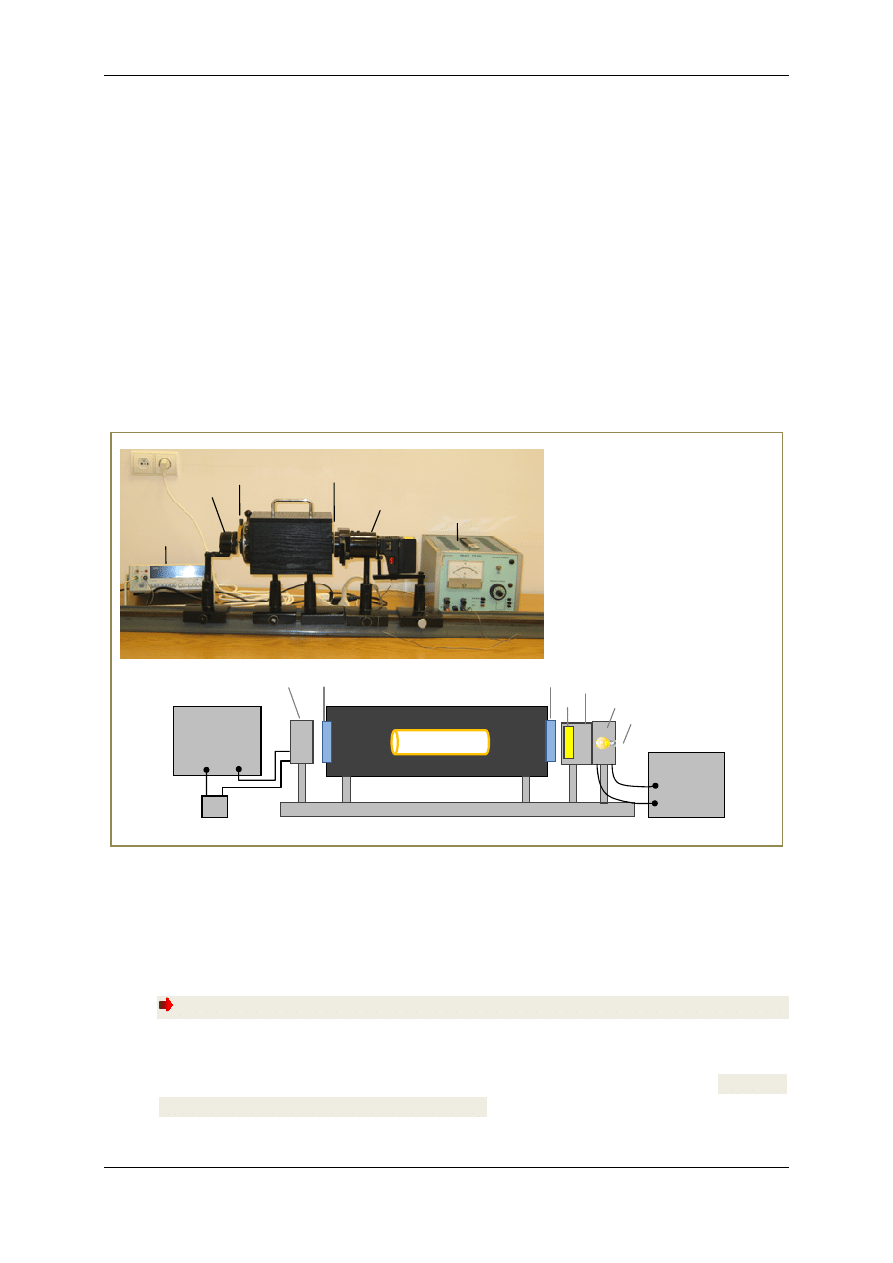
tora. Teoretyczny wykres

! w

funkcji we współrzędnych bie-
gunowych pokazany na rys. 7 ma
kształt półokręgu. Punkty pomia-
rowe idealnie zgadzające się z
przewidywaniami teoretycznymi
powinny wypadać na półokręgu o
promieniu

! /2.

2.2

Wyznaczanie właściwej zdolności skręcającej roztworu cukru

Właściwa zdolność skręcająca

1 2

3

4

jest zdefiniowana jako kąt, o który zostanie skręcona płasz-

czyzna polaryzacji światła o długości

= 589,9 nm przez warstwę roztworu grubości 1dm, w tempe-

raturze

20℃.

Właściwa zdolność skręcająca

1 2

3

4

wodnego roztworu cukru o danym stężeniu może być wy-

znaczona z pomiaru kąta skręcenia płaszczyzny polaryzacji . Ze wzoru (1.2) wynika, że

1 2

3

4

= * , (2.1)

gdzie

* jest grubością warstwy roztworu. Pomiar należy przeprowadzić z użyciem żółtego filtra, dają-

cego światło o wymaganej długości fali.

Temperatura ma niewielki wpływ na wartość

1 2

3

4

. Jeśli temperatura roztworu znacznie różni

się od temperatury

20℃, można dokonać korekty zmierzonej wartości 1 2

4

3

korzystając ze wzoru

1 2

3

4

= 1 2

3

" ℃

11,0 − 0,000471( − 20,0)2. (2.2)

90°

10°

B

C

"

!

!

D

E

|BE| = G!( )

|BD| = G!(10°)

Rys.7. Wykres prawa Malusa we współrzędnych biegunowych
z zaznaczonymi punktami pomiarowymi idealnego pomiaru,
które układają się na półokręgu o promieniu

H

I

! .

Ćwiczenie 26

8

3.

Wykonanie ćwiczenia

3.1

Opis aparatury

Fotografia i schemat aparatury stosowanej w ćwiczeniu są przedstawione na rys.8. Na ławie op-

tycznej ustawiono źródło światła, za nim kolimator i wysuwany żółty filtr interferencyjny. Wiązka
światła kierowana jest na polaryzator umocowany w przedniej ściance czarnej, światłoszczelnej osło-
ny. W jej tylnej ściance znajduje się skala kątowa z analizatorem, którym można obracać wokół osi.

Do pomiaru natężenia światła służy fotoopornik, połączony szeregowo z amperomierzem i bate-

ryjką. Zmiana natężenia światła zmienia wartość oporu fotodetektora, co pociąga za sobą zmianę
natężenia prądu płynącego w obwodzie, który jest proporcjonalny do natężenia światła. Fotopór nie
jest na stałe przymocowany do ławy, jego położenie można zmieniać.

Do zestawu pomiarowego należą również: pojemnik z roztworem cukru, kryształ kalcytu oraz ka-

wałki pleksiglasu i żywicy.

3.2

Sprawdzanie prawa Malusa

1.

Zapoznaj się z aparaturą znajdującą się na stole laboratoryjnym. Za zgodą opiekuna ćwiczenia
włącz zasilacz żarówki i amperomierz. Upewnij się, czy bateryjka jest podłączona do obwodu
fotodetektora, a filtr interferencyjny wysunięty.

Otwórz pokrywę osłony i usuń z niej pojemnik z cukrem, jeśli się w niej znajduje.

2.

Odsuń fotodetektor od osłony i spoglądając przez analizator obracaj nim obserwując pole wi-
dzenia (jeśli filtr interferencyjny został usunięty światło powinno być białe).

3.

Ustaw analizator w położeniu, w którym żadne światło przez niego nie przechodzi. Analizator
i polaryzator są teraz w położeniu skrzyżowanym. Oznacza to, że ich kierunku polaryzacji two-

Rys.8. Zdjęcie aparatury (a)
i jej schemat (b).

zasilacz

amperomierz

fotoopór

bateryjka

analizator

polaryzator

żarówka

filtr

roztwór cukru

kolimator

fotoopór

analizator

polaryzator

żarówka

zasilacz

amperomierz

Polaryzacja światła

9

rzą kąt

= 90°. Odczytaj kąt na skali, na jakim zatrzymał się znaczek w postaci rysy wyrytej

na obudowie analizatora – nie musi on być równy

90°! Zapamiętaj go!

4.

Dosuń fotodetektor do analizatora, odczytaj oraz zanotuj wartość prądu

J

K

płynącego w ob-

wodzie fotoopornika, który odpowiada

= 90°.

5.

Obracaj analizator co

10° i odczytuj wielkość J prądu odpowiadającą kolejnym kątom .

Wszystkie wyniki umieść w Tabeli 1.

Wyłącz amperomierz i odłącz bateryjkę.

3.3

Wyznaczanie właściwej zdolności skręcającej wodnego roztworu
cukru

1.

Wstaw w wiązkę światła żółty filtr interferencyjny. Patrząc przez analizator powinieneś wi-
dzieć światło żółte.

2.

Odsuń fotodetektor i ustaw analizator w położeniu, w którym pole widzenia będzie całkowi-
cie zaciemnione.
Zanotuj wartość kąta

C

. Wyznaczanie kąta

C

powtórz 5 razy.

3.

Do środka osłony, pomiędzy skrzyżowane polaryzatory wstaw pojemnik z roztworem cukru.
Powinieneś zaobserwować rozjaśnienie pola widzenia.

4.

Obracając analizatorem doprowadź ponownie pole widzenia do zaciemnienia.
Odczytaj wartość kąta

"

. Wyznaczanie kąta

"

powtórz 5 razy.

5.

Oszacuj połowę szerokości przedziału granicznego kąta

∆

M

(

J = 1,2). Nie sugeruj się tym, że

będzie nią najmniejsza działka skali. Staraj się znaleźć minimalny kąt, o który skręcając anali-
zator jesteś w stanie zauważyć rozjaśnienie pola widzenia.

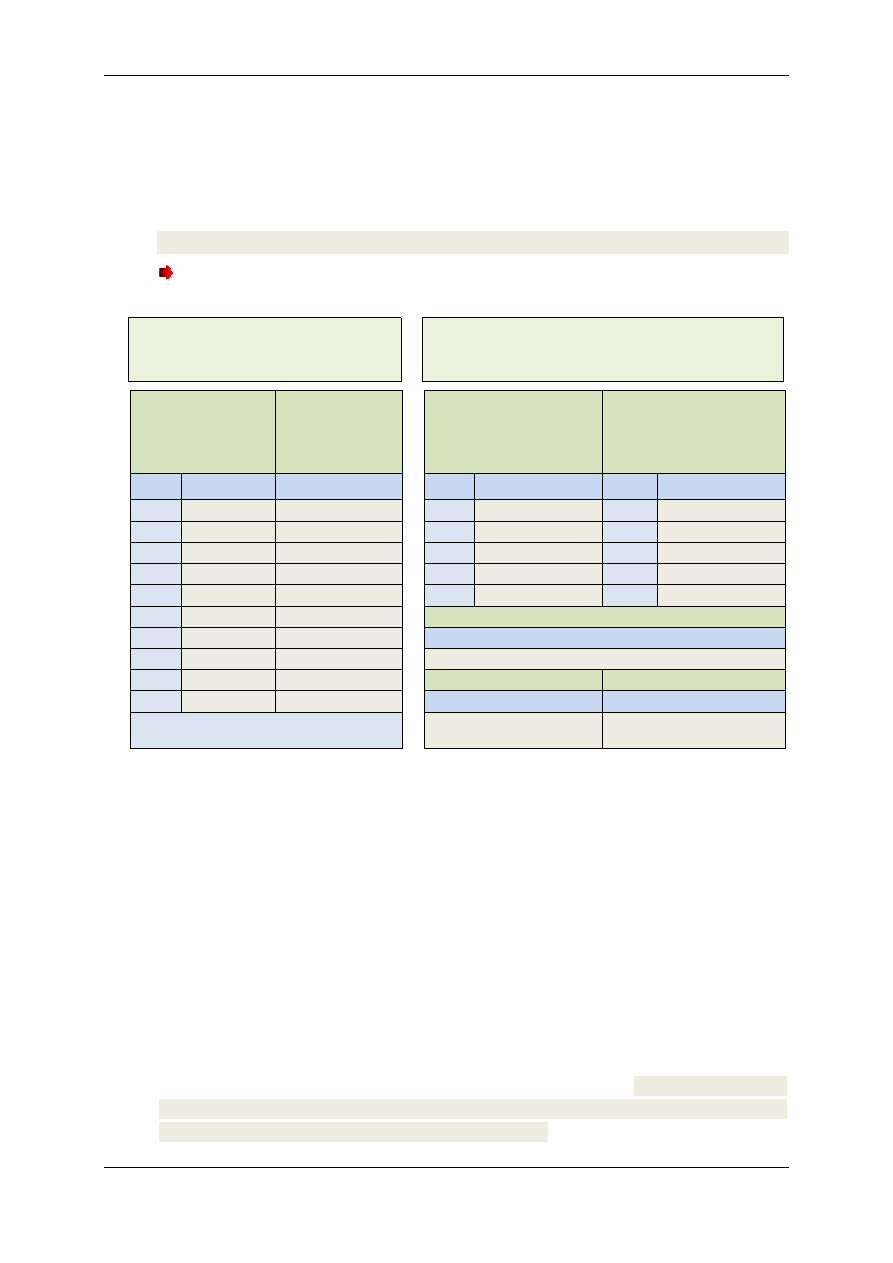
Tabela 1. Dane pomiarowe

Sprawdzanie prawa Malusa

Tabela 2. Dane pomiarowe

Wyznaczanie właściwej zdolności skręcają-

cej roztworu cukru

Kąt między kierun-

kami polaryzacji

polaryzatora i anali-

zatora

Natężenie prądu

elektrycznego w

obwodzie fotode-

tektora

Kąt odpowiadający całko-
witemu zaciemnieniu bez

roztworu

Kąt odpowiadający całkowi-

temu zaciemnieniu z roz-

tworem

Lp.

Kąt [

o

]

J [mA]

Lp.

C

[

o

]

Lp.

"

[

o

]

1.

90

o

1.

1.

2.

80

o

2.

2.

3.

70

o

3.

3.

4.

60

o

4.

4.

5.

50

o

5.

5.

6.

40

o

Połowa przedziału granicznego wyznaczania kąta

7.

30

o

∆

C

=

∆

"

[

o

]

8.

20

0

9.

10

o

Grubość warstwy roztworu

Stężenie roztworu

10.

0

o

* [dm]

[g/100cm

3

]

= 90° to kąt, gdy polaryzator i analizator są

w położeniu skrzyżowanym

Ćwiczenie 26

10

W przypadku wątpliwości jak obliczać niepewności lub w jakiej postaci zapisać końcowy wy-

nik (np. ile ma zawierać cyfr znaczących), proszę przeczytać odpowiedni fragment „Wprowadze-
nia do metod opracowywania danych pomiarowych”.

6.

Odczytaj z instrukcji znajdującej się w laboratorium grubość warstwy roztworu

* oraz jego

stężenie wraz z podanymi niepewnościami.
Wszystkie wyniki pomiarów umieść w Tabeli 2.

3.4

Obserwacja dwójłomności

3.4.1

Obserwacja dwójłomności naturalnej

1.

Odszukaj kryształ kalcytu. Połóż go na zadrukowanej kartce papieru.

2.

Wolno obracaj.

3.

Zanotuj swoje spostrzeżenia.

3.4.2

Obserwacja dwójłomności wymuszonej

1.

Obserwuj kawałek żywicy w świetle zwykłej lampki biurowej. Zanotuj swoje spostrzeżenia.

2.

Umieść kawałek żywicy w osłonie między dwoma skrzyżowanymi polaryzatorami. Dociśnij go
palcem. Użyj światła białego, a następnie przepuszczonego przez żółty filtr interferencyjny.

3.

Zanotuj swoje spostrzeżenia. Sporządź szkic wzorów, które obserwujesz w kawałku żywicy.

4.

Powtórz obserwacje dla kawałka pleksiglasu.

4.

Obliczenia

4.1

Sprawdzanie prawa Malusa

1.

Dla każdego kąta , oblicz pierwiastek kwadratowy ze zredukowanego natężenia prądu, tj. z

różnicy

J − J

K

,

GJ − J

K

(

J

K

odpowiada wartości prądu, gdy

= 90°). Wyniki obliczeń wpisz

do Tabeli 3.

2.

Narysuj na papierze milimetrowym wykres we współrzędnych biegunowych

GJ − J

K

w funkcji

kąta .

Narysuj oś

B , zaznacz na niej jednostkę i odmierz odcinek równy GJ − J

K

odpowiadający ką-

towi

0°. Zaznacz jego koniec małym krzyżykiem. To jest twój pierwszy punkt pomiarowy.

Narysuj półproste wychodzące z punktu

B pod kątami 10°, 20°, … . Na każdej zaznacz punkt,

którego odległość od

B będzie równa wartości GJ − J

K

, odpowiadającej kątowi, jaki półpro-

sta tworzy z osią . Wykreśl cyrklem półokrąg najlepiej dopasowany do punktów pomiaro-
wych.

3.

Dla każdego kąta , oblicz wartość

cos

"

oraz znormalizowanego prądu według wzoru

J

0OPQ

=

J − J

K

J − J

K

,

gdzie

J to prąd odpowiadający kątowi = 0°.

Polaryzacja światła

11

4.

Sporządź wykres znormalizowanego prądu

J

0OPQ

w funkcji

cos

"

.

Przyjrzyj się postaci prawa Malusa danej wzorem (1.1). Jaką funkcję powinieneś dopasować

do punktów pomiarowych? Możesz posłużyć się Excelem lub programem WykresLab.

4.2

Obliczanie właściwej zdolności skręcającej wodnego roztworu
cukru

Obliczenia wykonuj w sposób przejrzysty, pamiętaj o uwzględnianiu jednostek, gdy podstawiasz
wartości liczbowe do wzorów.

Po odpowiednim zaokrągleniu wyniki obliczeń wpisz do Tabeli 4.

1.

Oblicz wartości średnie

R

C

i

R

"

, a następnie kąt skręcenia polaryzacji światła przez warstwę

roztworu cukru

= R

C

− R

"

.

2.

Oblicz właściwą zdolność skręcającą

1 2

3

4

ze wzoru (2.1). Wyraź ją w jednostkach

1°

dm ∙ g/cm

:

.

3.

Oszacuj niepewność Typu B pomiaru kąta

M

,

+

S

(

M

), (J = 1,2)

8

.

4. Oblicz niepewności Typu A kątów

C

oraz

"

,

+

T

(

M

) , (J = 1,2).

5. Oblicz niepewność standardową złożoną

+

U

( ) kąta skręcenia płaszczyzny polaryzacji

8

Załóż trójkątny rozkład gęstości prawdopodobieństwa i oblicz niepewność standardową związaną z niejedno-

znacznością odczytu

+

(

J

)

= Δ

J

√

6

⁄

.

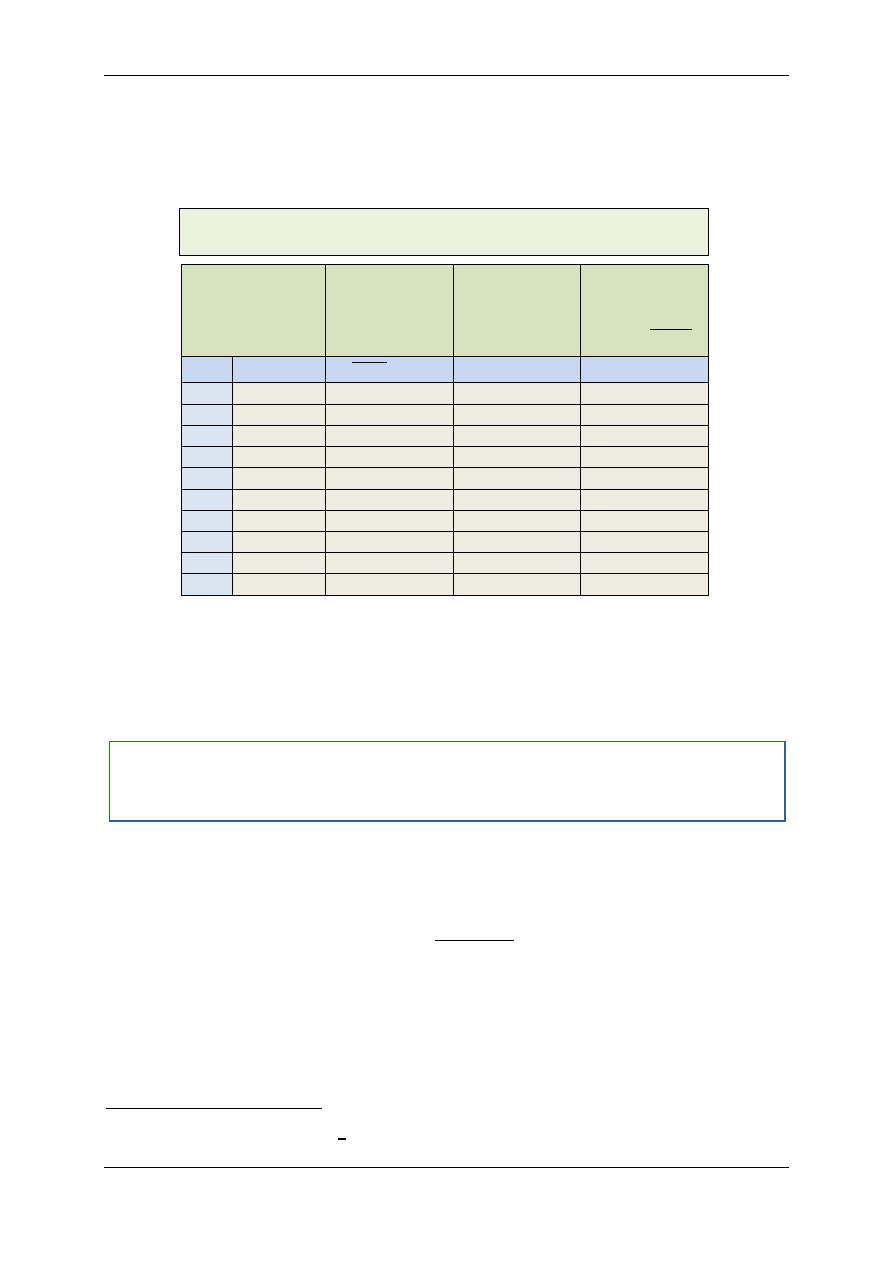
Tabela 3. Obliczenia

Sprawdzanie prawa Malusa

Kąt między kierun-

kami polaryzacji

polaryzatora i anali-

zatora

Pierwiastek ze

zredukowanego

prądu (

J − J

K

)

Kwadrat cosinusa

kąta

J

0OPQ

=

J − J

K

J − J

K

Znormalizowane

natężenie prądu

Lp.

Kąt [

o

]

GJ − J

K

[mA

1/2

]

cos

"

J

0OPQ

1.

90

o

2.

80

o

3.

70

o

4.

60

o

5.

50

o

6.

40

o

7.

30

o

8.

20

0

9.

10

o

10.

0

o

Ćwiczenie 26

12

+

U

( ) = G2+

S

(

M

)

"

+ +

T

(

C

)

"

+ +

T

(

"

)

"

.

6. Oblicz niepewność standardową złożoną

+

U

Z1 2

3

4

[

9

oraz niepewność względną

+

P,U

Z1 2

3

4

[

właściwej zdolności skręcającej

1 2

3

4

, wykorzystując obliczoną niepewność złożoną

+

U

( ) i

podane wartości niepewności stężenia roztworu cukru

+

S

( ) oraz grubości warstwy roz-

tworu

+

S

(*).

7. Oblicz niepewność rozszerzoną pomiaru właściwej zdolności skręcającej

\(1 2

3

4

) przy

współczynniku rozszerzenia

= 2.

5.

Dyskusja wyników

1.

Przedyskutuj wykresy: biegunowy

GJ − J

K

w funkcji kąta oraz znormalizowanego prą-

du

J

0OPQ

w zależności od kwadratu cosinusa kąta . Czy zgodne są one z teorią, czyli czy

potwierdzają prawo Malusa?

2.

Podaj poprawnie zapisane wyniki pomiarów właściwej zdolności skręcającej dla wodnego
roztworu cukru (łącznie z niepewnościami). Porównaj z wartościami z innych źródeł. Oceń
zgodność wyników.

3.

Zastanów się nad źródłami błędów, które miały wpływ na twoje wyniki pomiarów.

4.

Omów i wytłumacz obserwacje poczynione podczas badania zjawiska dwójłomności natu-
ralnej w kalcycie i dwójłomności wymuszonej w pleksiglasie i żywicy.

9

Wzory na

+

U

(1 2

3

4

) oraz +

P,U

(1 2

3

4

) wyprowadź samodzielnie w oparciu o wzór 7.8 podany w opracowaniu

„Obliczanie i wyrażanie niepewności pomiaru” – nie potrzebna jest do tego znajomość pochodnych, ponieważ
mamy do czynienia z przypadkiem funkcji będącej iloczynem potęg zmiennych niezależnych jak we wzorze 7.7).

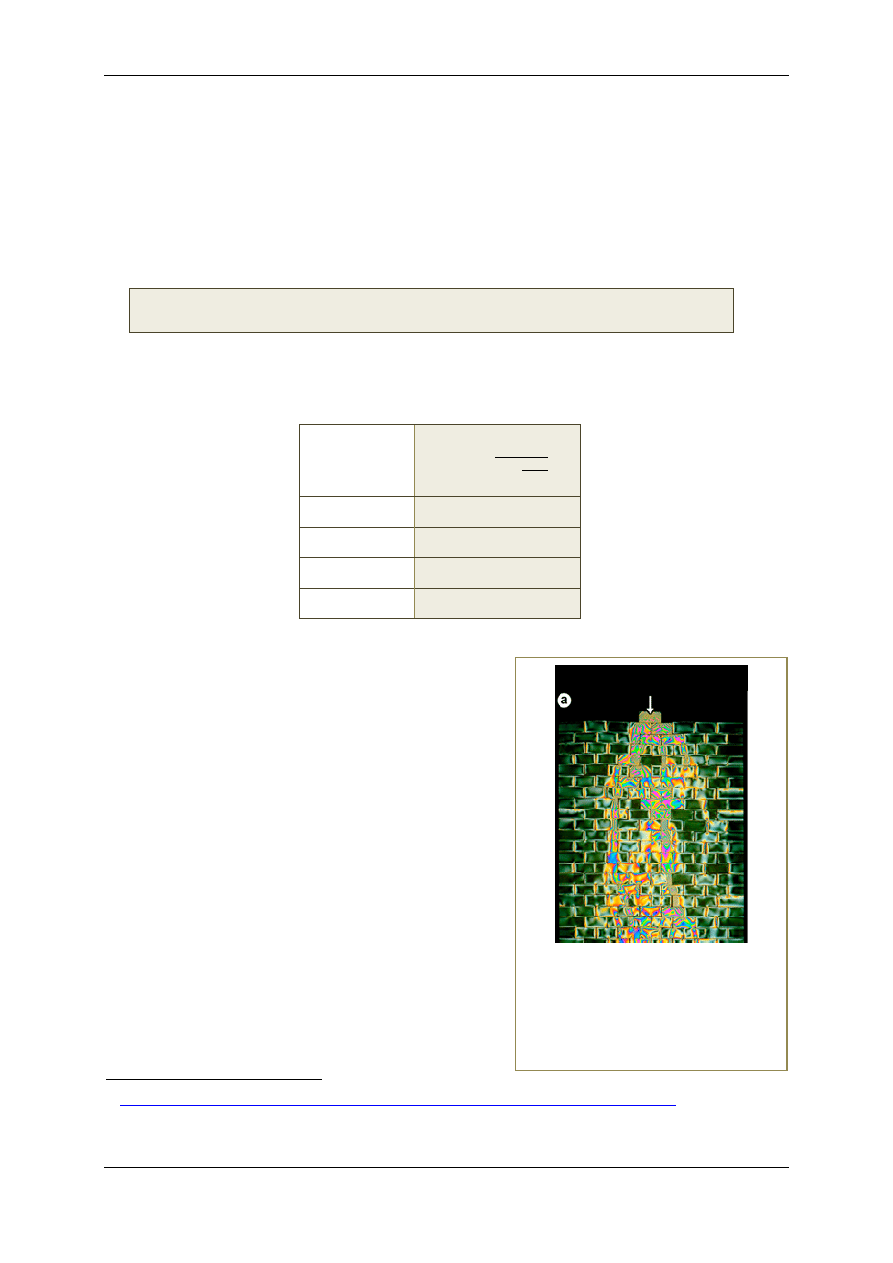
Tabela 4. Obliczenia właściwej zdolności skręcającej roztworu cukru

Średnia wartość kąta

C

(bez roztworu)

Średnia wartość kąta

"

(z roztworem)

Kąt skręcenia polaryzacji

światła przez warstwę

roztworu cukru

Właściwa zdolność

skręcająca roztworu

R

C

[

o

]

R

"

[

o

]

= R

C

− R

"

[

o

]

1 2

3

4

]

C°

^_∙`/a_

b

c

Niepewność standardowa

złożona kąta skręcenia

płaszczyzny polaryzacji

Niepewność względna

właściwej zdolności

skrę-

cającej

Niepewność standardo-

wa złożona

Niepewność rozszerzo-

na

+

U

( ) [

o

]

+

P,U

([ ]

3

4

)

+

U

Z[ ]

3

4

[ ]

C°

^_∙`/a_

b

c

\([ ]

3

4

) ]

C°

^_∙`/a_

b

c

Polaryzacja światła

13

6.

Uzupełnienia

6.1

Wartości tabelaryczne

[d]

e

fg°

wodnych roztworów wybranych

substancji

Tabelaryczna wartość

10

właściwej zdolności skręcającej

1 2

h

" °

roztworu wodnego cukru i

odpowiadająca jej niepewność

11

dla 589.4400 nm i

20.00℃ ± 0.01℃

.

właściwa zdolność skręcająca

1 2

h

" °

: 66.524

±

0.054

Wartości właściwej zdolności skręcającej

1 2

h

" °

dla wodnych

roztworów różnych substancji.

Substancja w

roztworze

1 2

h

" °

j

C°

^_∙

k

lmb

n

glukoza

+52.74

fructoza

-93.78

maltoza

+137.5

dekstroza

+194.8

6.2

Dwójłomność wymuszona

Dwójłomnością wymuszoną nazywamy zjawisko wy-

wołania dwójłomności w przezroczystych ciałach izotro-
powych (np. w szkle czy w pleksiglasie) w wyniku mecha-
nicznych naprężeń.

W materiale, w którym występują naprężenia, pro-

mień świetlny rozdziela się na dwa promienie rozchodzące
się z różnymi prędkościami, których płaszczyzny drgań
wektora świetlnego pokrywają się z kierunkami naprężeń
głównych. Doświadczenie pokazuje, że różnica współczyn-
ników załamania promienia zwyczajnego n

o

i nadzwyczaj-

nego n

e

jest proporcjonalna do naprężenia

σ

w danym

punkcie ciała

.

/

− .

0

= o(p

C

− p

"

), (i)

10

http://ts.nist.gov/MeasurementServices/ReferenceMaterials/archived_certificates/17e.pdf

11

Podana niepewność

\ jest niepewnością rozszerzoną dla poziomu ufności 95%, obliczoną ze wzoru

\( ) = +

U

( ), = 3,18.

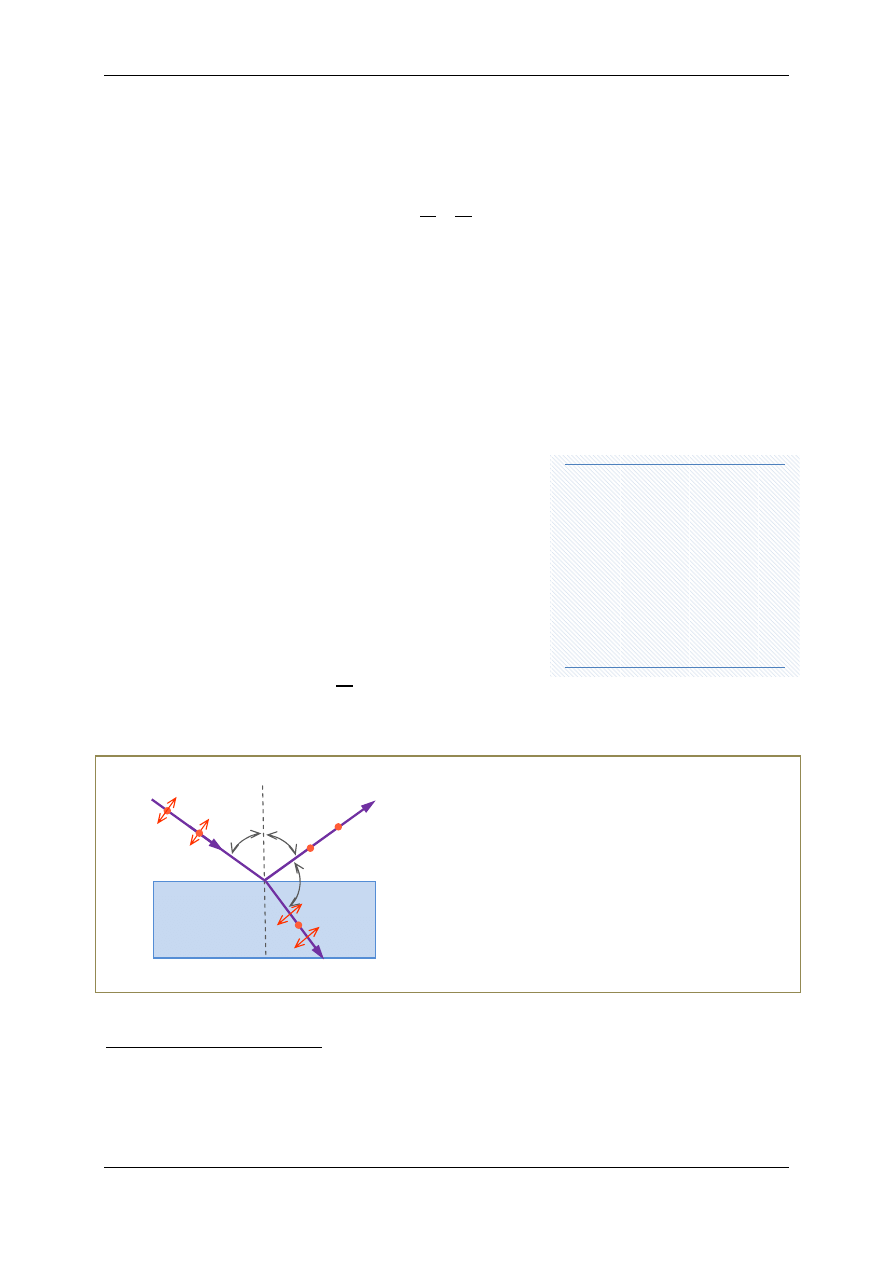
Rys.9. Obserwacja dwójłomności wy-
muszonej w modelu muru poddane-
go obciążeniu. W pomiarach użyto
światła białego. Widoczne są wzory
kolorowych i ciemnych prążków
Interferencyjnych (porównaj z rys.6).

Ćwiczenie 26

14

Światło słoneczne odbite od
mokrej nawierzchni drogi czy
powierzchni wody jest częścio-
wo spolaryzowane. Okulary
słoneczne firmy Polaroid mają
pionowy kierunek polaryzacji w
celu wyeliminowania światła
odbitego i zmniejszenia efektu
oślepiania.

C – współczynnik zależny od właściwości materiału,

σ

1

,

σ

2

- naprężenia główne.

Każdy z promieni przechodzi przez materiał z inną szybkością, co prowadzi do ich względnego

przesunięcia liniowego (różnicy dróg optycznych) na wyjściu z analizatora

r = s ∆ = s t

u

s

/

−

u

s

0

v = u(.

/

− .

0

), (ii)

gdzie

s - szybkość światła w powietrzu, u- grubość materiału. Ze wzorów (i) i (ii) wynika, że

r = ou(p

C

− p

"

).

Promienie wychodzące z analizatora interferują ze sobą i w zależności od wartości

δ

prowadzi to

do pojawienia się ciemnych bądź jasnych prążków interferencyjnych (izoklin

12

i izochrom

13

). Analiza

tych wzorów interferencyjnych dostarcza informacji o rozkładzie naprężeń.

6.3

Polaryzacja przez odbicie

Niespolaryzowane światło może zostać częściowo lub cał-

kowicie spolaryzowane liniowo przez odbicie od powierzchni
dielektryków, np. wody lub szkła. Przy kącie padania, zwanym

kątem Brewstera

, następuje pełna polaryzacja światła odbitego.

Wówczas promień odbity i załamany są do siebie wzajemnie

prostopadłe. Kierunek drgań wektora świetlnego w całkowi-
cie odbitym promieniu jest równoległy do płaszczyzny odbijają-
cej dielektryka ( patrz: rys.9).

Kąt Brewstera może zostać wyznaczony z prawa Brewstera

tg x

S

=

.

"

.

C

,

gdzie

.

C

i

.

"

są współczynnikami załamania

14

odpowiednio ośrodka pierwszego i ośrodka drugiego.

12

Izokliny są miejscami geometrycznymi punktów, w których kierunki naprężeń głównych są jednakowe.

13

Izochromy są miejscami geometrycznymi punktów, w których różnica naprężeń głównych jest wartością sta-

łą.

14

Współczynnik załamania ośrodka

. jest równy stosunkowi szybkości światła w próżni do jego szybkości w

danym ośrodku.

Rys.9. Kiedy światło pada na powierzchnię dielektryka
pod kątem Brewstera

x

S

, promień odbity i załamany są

do siebie prostopadłe. Kółka reprezentują składową
wektora równoległą do odbijającej powierzchni die-
lektryka (skierowaną prostopadle do powierzchni rysun-
ku), a strzałki składową do niej prostopadłą. Podczas
gdy promień odbity jest całkowicie spolaryzowany, za-
łamany jest spolaryzowany tylko częściowo.

normalna

promień padający

promień odbity

promień załamany

x

S

x

S

.

C

.

"

90°

Polaryzacja światła

15

7.

Literatura

1.

Praca pod red. B.Oleś i M.Duraj: Ćwiczenia laboratoryjne z fizyki, cz.1. wyd.4, Wydawnictwo
PK, Kraków 2008.

2.

D.Halliday, R.Resnick, J.Walker: Podstawy fizyki, t.4. wyd.1, PWN, Warszawa 2007.

3.

I.W.Sawieliew: Kurs fizyki, t.2, PWN, Warszawa 1989.

4.

Sz.Szczeniowski: Fizyka doświadczalna, cz.IV. wyd.IV, PWN, Warszawa 1967.

8.

Jeśli chcesz wiedzieć więcej

Krótkie i ciekawe demonstracje dotyczące zjawiska polaryzacji znajdziesz na filmach na YouTube.

Ćwiczenie 26

16

Spis treści

1.

WPROWADZENIE ..................................................................................................................................... 2

1.1

N

ATURA ŚWIATŁA

....................................................................................................................................... 2

1.2

Z

JAWISKO POLARYZACJI ŚWIATŁA

................................................................................................................... 2

1.3

M

ETODY POLARYZACJI ŚWIATŁA

..................................................................................................................... 4

1.3.1

Filtry polaryzujące ............................................................................................................................. 4

1.3.2

Polaryzacja przez odbicie .............................................................. Błąd! Nie zdefiniowano zakładki.

1.3.3

Zjawisko dwójłomności...................................................................................................................... 5

1.3.4

Dwójłomność wymuszona ................................................................................................................. 6

1.4

A

KTYWNOŚĆ OPTYCZNA

............................................................................................................................... 6

2.

METODA POMIARU ................................................................................................................................. 7

2.1

S

PRAWDZANIE PRAWA

M

ALUSA

.................................................................................................................... 7

2.2

W

YZNACZANIE WŁAŚCIWEJ ZDOLNOŚCI SKRĘCAJĄCEJ ROZTWORU CUKRU

............................................................... 7

3.

WYKONANIE ĆWICZENIA ......................................................................................................................... 8

3.1

O

PIS APARATURY

........................................................................................................................................ 8

3.2

S

PRAWDZANIE PRAWA

M

ALUSA

.................................................................................................................... 8

3.3

W

YZNACZANIE WŁAŚCIWEJ ZDOLNOŚCI SKRĘCAJĄCEJ WODNEGO ROZTWORU CUKRU

................................................ 9

3.4

O

BSERWACJA DWÓJŁOMNOŚCI

.................................................................................................................... 10

3.4.1

Obserwacja dwójłomności naturalnej ............................................................................................. 10

3.4.2

Obserwacja dwójłomności wymuszonej .......................................................................................... 10

4.

OBLICZENIA ............................................................................................................................................ 10

4.1

S

PRAWDZANIE PRAWA

M

ALUSA

.................................................................................................................. 10

4.2

O

BLICZANIE WŁAŚCIWEJ ZDOLNOŚCI SKRĘCAJĄCEJ WODNEGO ROZTWORU CUKRU

.................................................. 11

5.

DYSKUSJA WYNIKÓW............................................................................................................................. 12

6.

UZUPEŁNIENIA ....................................................................................................................................... 13

7.

LITERATURA ........................................................................................................................................... 15

8.

JEŚLI CHCESZ WIEDZIEĆ WIĘCEJ .............................................................................................................. 15