Sprawozdanie z ćwiczenia A-26.

Temat: Kinematyka cząstek elementarnych.

Cel ćwiczenia:

Celem ćwiczenia jest zapoznanie się z doświadczalnymi metodami analizy cząstek elementarnych oraz wyznaczenie kinematycznych wielkości opisujących te cząstki: masy, pędu i energii.

Podstawy fizyczne.

Fizyka cząstek elementarnych jest nauką, która stara się poznać podstawowe składniki budowy materii. Znane obecnie cząstki można podzielić na trzy grupy:

1. fotony;

2. leptony (cząstki obdarzone spinem połówkowym np.: elektrony)

3. hadrony

-mezony (cząstki o spinie całkowitym, lub równym zero)

-bariony (cząstki o spinie połówkowym np.: neutrony, protony)

W fizyce mikrocząstek oprócz zasad zachowania znanych z mechaniki (zasady zachowania energii i pędu) obowiązują jeszcze inne zasady. Podstawowe z tych zasad to:

-zasada zachowania ładunku;

-zasada zachowania liczby leptonowej;

-zasada zachowania liczby barionowej;

-zasada zachowania spinu.

Powyższym zasadom podlegają wszystkie zjawiska związane z cząstkami elementarnymi.

Ze względu na bardzo małe rozmiary cząstek oraz na bardzo krótki czas oddziaływania badanie ich polega raczej na analizie skutków oddziaływania, bądź obrazów reakcji (zdjęcia zawierające kaskady elektronowo-fotonowe), niż na badaniu samego procesu. Do rejestracji cząstek stosowane są detektory śladowe i licznikowe. Detektory śladowe pozwalają na utrwalenie torów cząstek naładowanych, cząstki neutralne można wykryć przez analizę produktów ich rozpadu (o ile posiadają one ładunek). Wśród detektorów śladowych można wyróżnić:

-emulsje jądrowe

-komory mgłowe

-komory pęcherzykowe

Zasada działania komór pęcherzykowych polega na tworzeniu się pęcherzyków pary wokół jonów powstałych na drodze cząstki naładowanej. Obraz torów otrzymuje się po sfotografowaniu wnętrza komory. Pomimo, iż zdjęcia wykonywane są kilkoma aparatami równocześnie metoda ta obdarzona jest dość znacznym błędem z uwagi na przeniesienie reakcji z przestrzeni na płaszczyznę. Często stosowane są komory ksenonowe, które z uwagi na dużą gęstość ośrodka pozwalają na analizę wszystkich produktów oddziaływania. Analizie tej poddawane jest zdjęcie zawierające ślad toru cząstki padającej (często są to mezony Pi), punkt oddziaływania z jądrami ksenonu, ślady torów wtórnych cząstek naładowanych (elektronu i pozytonu) powstałych z rozpadu fotonów o energii większej niż suma mas spoczynkowych powstałych cząstek. Cząstki te poruszając się w komorze tracą swoją energię przez jonizację atomów ośrodka oraz przez promieniowanie hamowania, w wyniku którego emitowane są fotony, które jeśli tylko posiadają odpowiednią energię to mogą znowu konwertować na pary elektronowo-pozytonowe. W ten sposób powstają kaskady. W wyniku oddziaływania cząstek padających z jądrami ksenonu mogą być wybijane nukleony, bądź produkowane nowe cząstki (głównie mezony Pi). Rezultat oddziaływania zależy od odległości zderzenia od centrum jądra. Emitowana cząstka bardzo szybko ulega rozpadowi na dwa fotony a informację o niej można uzyskać tylko poprzez analizę kaskad. W tym celu należy wyznaczyć energię powstałych fotonów oraz kąt między kierunkami ich ruchu. Energię fotonu można wyznaczyć z zależności:

gdzie:

- jest średnią sumą długości kaskad,

k - współczynnik proporcjonalności określający średnią stratę energii elektronów na jednostkę długości.

W celu wyznaczenia kąta między kierunkami kaskad należy skorzystać ze związków trygonometrycznych w trójkącie ABC (rysunek na kalce).

Ostatecznie energię cząstki można wyznaczyć z zależności:

Masę cząstki otrzymujemy z równania:

Obliczenia i wyniki pomiarów:

1. Średnia długość kaskad:

- kaskada 1:

- kaskada 2:

2.Energia fotonów (energia cząstki):

Błąd obliczeń energii (błąd systematyczny):

Energia cząstki wynosi:

3.Pęd cząstki określa wzór:

Wyliczenie kosinusa
:

Z trójkąta ABC (rysunek na kalce):

|AB|= 7,5
0,1 cm

|BC|= 6,1
0,1 cm

|AC|= 1,5
0,1 cm

z twierdzenia kosinusów:

4.Masa aktywna fotonów:

Błąd obliczenia masy:

Ostatecznie:

Błąd wyliczenia pędu:

Ostatecznie:

5.Wyliczanie pędów w kierunku osi X i Y (pędy fotonów):

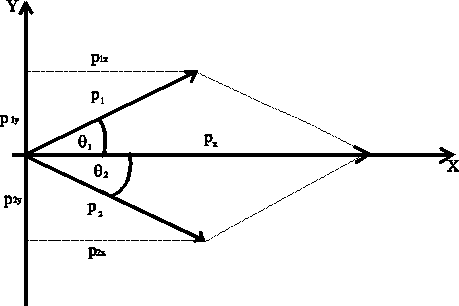
Z twierdzenia kosinusów:

gdzie:

Błąd wyliczenia pędów:

Ostatecznie:

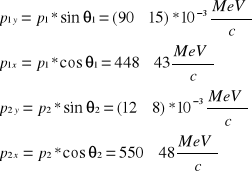
Dyskusja błędów.

Ze względu na powtarzalność pomiarów długości kaskad elektronowo-fotonowych przy liczeniu błędów uwzględniliśmy tylko błąd systematyczny. Wynika on głównie z niedokładności krzywomierza, która wynosiła
2cm. Błąd ten wynikał również z niepewności wyznaczonej stałej k (
0,5 MeV).

Błąd wyliczonej energii fotonów (energii cząstki) otrzymaliśmy metodą różniczki zupełnej.

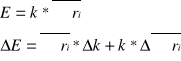
Tą samą metodą obliczyliśmy błąd z jakim została wyznaczona masa cząsteczki.

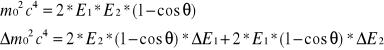
Gdzie:

,
-energie fotonów ,
-kąt między osiami kaskad

Na błąd wyznaczenia masy mogła mieć także wpływ niedokładność odczytu kosinusa
. Jest ona jednak stosunkowo nieduża i możemy ją pominąć.

Pęd cząstki został wyznaczony z dokładnością 42,5%, którą otrzymaliśmy metodą różniczki zupełnej:

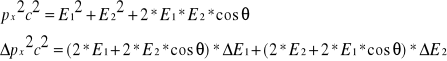
Identyczną metodą został wyznaczony błąd odpowiednich składowych pędów fotonów:

itd.

Przy wyliczaniu błędów składowych pędu zostały pominięte niepewności wynikające z wyznaczania kosinusów kątów
i
.

Wnioski.

Doświadczenie polegało na wyznaczeniu parametrów opisujących cząstkę powstałą w wyniku zderzenia mezonu Pi z atomem ksenonu. Wielkości te to: energia, pęd i masa. Zastosowana metoda już w samej sobie zawierała pewne niedoskonałości:

1. Analizie poddane zostało zdjęcie reakcji zachodzącej w przestrzeni trójwymiarowej i co za tym idzie utrwalone długości kaskad elektronowo fotonowych różnią się od wartości rzeczywistych. Wynika to z przeniesienia obrazu przestrzennego na płaszczyznę.

2. Przy wyznaczaniu energii powstałych fotonów pominięta została energia spoczynkowa pozytonów i negatonów, powstałych w wyniku rozpadu fotonów.

Jest to energia ok 1 MeV i jest ona nie duża w porównaniu z energią jaką pozytony i negatony tracą na drodze 1 cm (współczynnik k). Powyżej przedstawione wnioski oraz duża niekokładność krzywomierza miały zaczący wpływ na dokładność otrzymanych wyników pęd (42,5%), masa (43%).

Wyznaczona masa 159
68 MeV pozwala określić rodzaj powstałej cząstki. Z tablic odczytujemy, że jest to mezon
. Z zasady zachowania ładunku wnioskujemy, że musi to być cząstka nie posiadająca ładunku. Powyższym wymaganiom odpowiada mezon
. Dokładna masa takiej cząstki wynosi ok.135
, tak więc otrzymany przez nas wynik mieści się w granicach błędu.

Sprawozdanie z ćwiczenia A-26 Strona 5

---