Podobieństwo sygnałów – korelacja

Iloczyn skalarny wektorów/sygnałów

W przestrzeni L

2

ℝ

〈

x , y 〉=

∫

x t  y t dt

W przestrzeni ℝ

N

〈

x , y 〉=

1

N

∑

n=0

N −1

x n y n

Jeżeli 〈 x , y 〉=0 to x ⊥ y
a co jeżeli

〈

x , y 〉≠0

lub inaczej

∣〈

x , y 〉∣0

?

Korelacja

Korelacja w przestrzeni

L

2

ℝ

w przypadku stacjonarnym

R=

∫

x t x t− dt

po dyskretyzacji w przestrzeni ℝ

N

Rl =lim

n ∞

1

N

∑

n=0

N −1

x n x n−l

Korelacja w przestrzeni

ℝ

N

Z teorii procesów stochastycznych

R

x



k , m=

1



2

E[ x  k − x m−]

gdzie E [.] oznacza operator wartości oczekiwanej (w dużym uproszczeniu jest to wartość
średnia)



wartość średnia procesu losowego



wariancja procesu losowego

Konsekwentnie

R

xy



k , m=

1



x



y

E [ x k −

x



y  m−

y

]

Zwykle zakładamy że:

●

=

0

●

=

1

●

proces losowy (sygnał) jest stacjonarny wtedy

x  n , x n−l

lub

x  n , y n−l

- 1 -

Użyteczne definicje

R

x



l= E [x n x n−l] - autokorelacja

R

xy



l =E [ x n y n−l]

- korelacja wzajemna (kroskorelacja)

W praktyce można różnie liczyć estymator wartości oczekiwanej

R

x



l=

1

N

∑

n

x n x n−l  - estymator obciążony

R

x



l=

1

N −l

∑

n=0

N −l −1

x n x n−l  - estymator nieobciążony

Wyjaśnić pojęcia:

●

współczynnik korelacji

●

unormowany współczynnik korelacji ( 1/

x

2

)

●

funkcja korelacji

●

unormowana funkcja korelacji

●

miara podobieństwa sygnałów (dla l=0 otrzymujemy iloczyn skalarny !!!)

Przykład:

N=1000;n=(0:N-1);x=sin(2*pi*5/N*n+.3*pi)+randn(1,N);plot(n,x);

s1=sin(2*pi*5/N*n);s2=sin(2*pi*4/N*n);s3=sin(2*pi*13/N*n);s4=sin(2*pi*10/N*n)
;s5=sin(2*pi*4.8/N*n);

max(abs(xcorr(x,s1)))
max(abs(xcorr(x,s2)))

max(abs(xcorr(x,s3)))
max(abs(xcorr(x,s4)))

max(abs(xcorr(x,s5)))

Własności funkcji autokorelacji

1.

R

x



l= R

x

−

l

funkcja parzysta

2.

R

x



0≥R

x



l wartość maksymalna dla zerowego przesunięcia

- 2 -

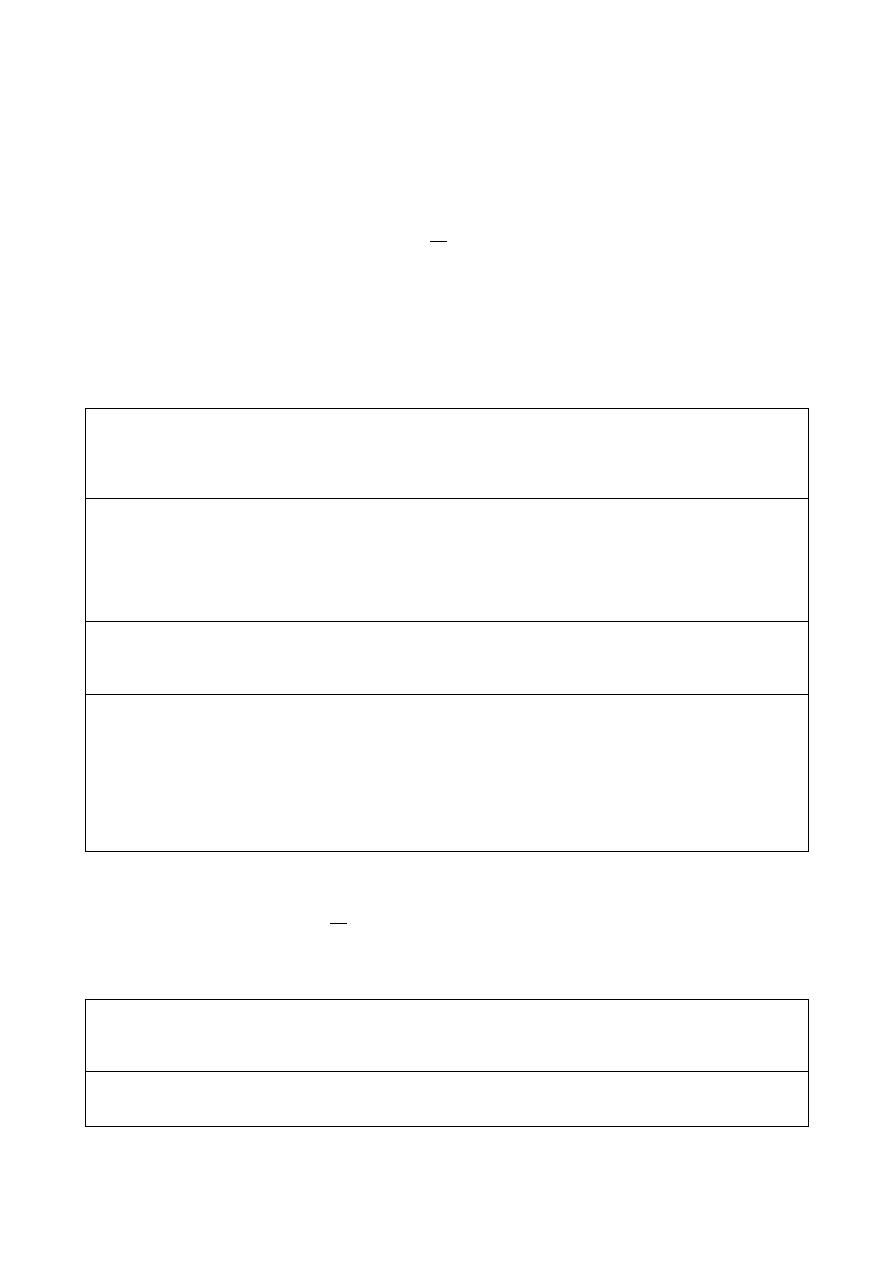
Transformacje czasowo-częstotliwościowe

Krótkoterminowa transformata Fouriera (ang. STFT)

STFT {x n}≡ X k , l =

∑

n =0

N −1

x n w n−l e

−

j 2 

N

k n

gdzie l – dyskretny czas, k – dyskretna częstotliwość
spektrogram to:

S  k , l=∣X  k , l∣

2

Przykład:

N=64;n=(0:N-1);

x=1.2*sin(2*pi*.13*n);y=2*sin(2*pi*.07*n);z=.8*sin(2*pi*.27*n);s=[x,y,z];
s=s+.1*randn(size(s));plot(s);

S=fft(s); M=size(S,2); f=(0:M-1)./M; plot(f,abs(S));

w=gausswin(N,3)';plot(w);

okno1=[w,zeros(1,N),zeros(1,N)];
okno2=[zeros(1,N),w,zeros(1,N)];

okno3=[zeros(1,N),zeros(1,N),w];
plot(okno1);hold on;plot(okno2);plot(okno3);hold off;

plot(s.*okno1);hold on;plot(s.*okno2);plot(s.*okno3);hold off;

S1=fft(s.*okno1); S2=fft(s.*okno2); S3=fft(s.*okno3);

M=size(S1,2); f=(0:M-1)./M;
plot(f,abs(S1),f,abs(S2),f,abs(S3));

N=256;n=(0:N-1);
x=sin(2*pi*.13*n);y=sin(2*pi*.07*n);z=sin(2*pi*.27*n);s=[x,y,z];

s=s+.7*randn(size(s));plot(s);
M=128; w=gausswin(M,3)'; plot(w);

tmp=[zeros(1,M/2),s,zeros(1,M/2)];plot(tmp);
L=3*N;S=zeros(L,M);

for l=(1:L), v=tmp(l:l+M-1).*w;V = fft(v);S(l,:)=abs(V).^2;end;
l=(0:L-1);f=(0:M-1)./M;imagesc(l,f,S');

Transformata Wignera-Villa

X

WV



k , l=

∑

n=0

N −1

x l x l−ne

−

j 2 

N

k n

!!! Problemy z częstotliwością Nquista !!!

N=100;n=(0:N-1);x=sin(2*pi*.13*n);y=zeros(1,N);z=sin(2*pi*.28*n);s=[x,y,z];

plot(s);
L= 3*N; l=(0:L-1); M=256; [TFR,nt,nf]=tfrwv(s',n,M);imagesc(nt,nf,TFR);

N=500;n=(0:N-1);f=linspace(.1,.3,N);x=sin(2*pi*f.*n);
M=128;[TFR,nt,nf]=tfrwv(x',n,M);imagesc(nt,nf,TFR);

- 3 -

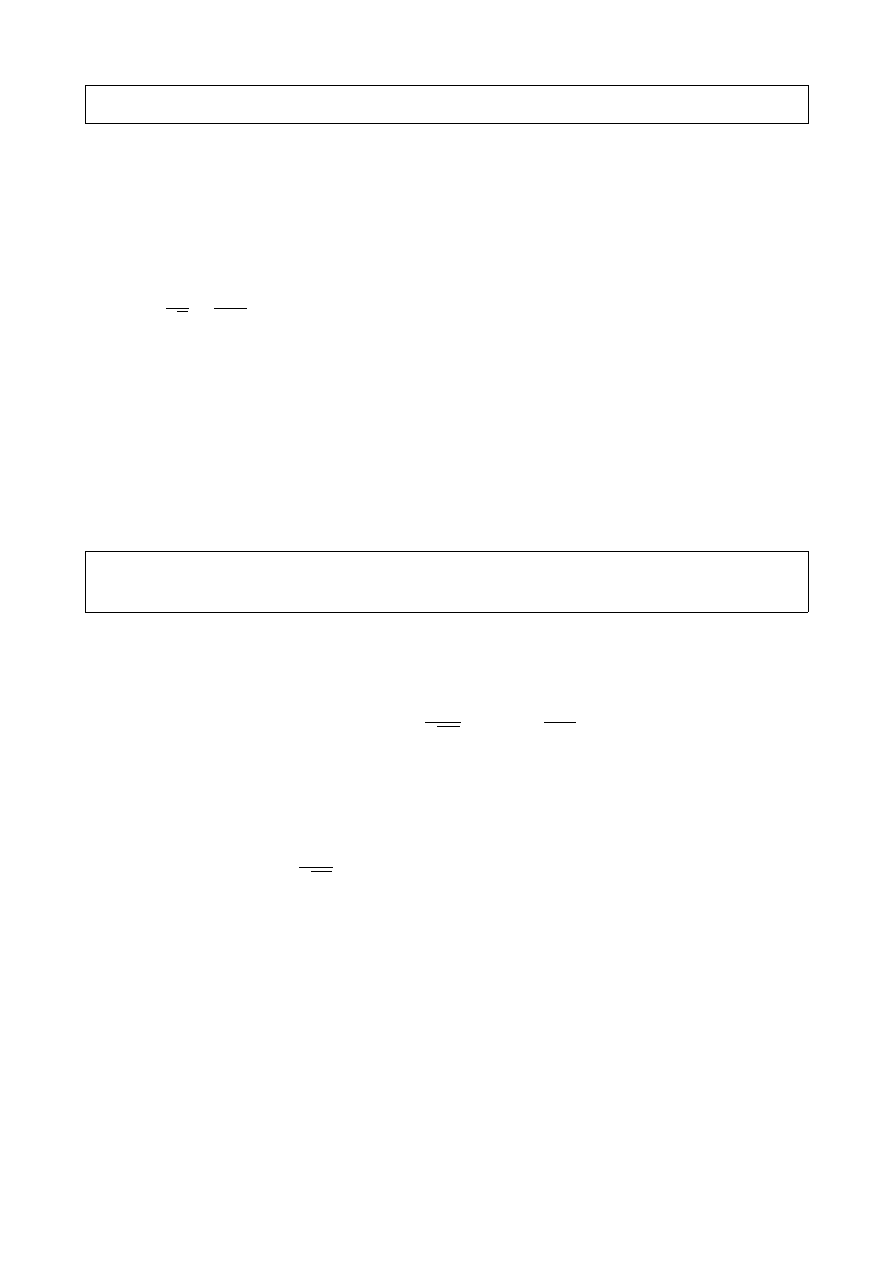
M=128;[TFR,nt,nf]=tfrwv(hilbert(x'),n,M);imagesc(nt,nf,TFR);

Dyskretna transformata falkowa (ang. wavelet)

Wavelet/Falka – (mała fala) sygnał okresowy szybko zanikający do zera

Falka ciągła:



a , b



t=

1



a





t−b

a



gdzie



t ∈L

2

ℝ

,

a , b∈ℝ ,

a0



t  prototyp falki, falka matka

–

b przesunięcie w czasie

–

a skalowanie w częstotliwości

Stąd nazwa transformacja „częstotliwość-skala” (skalogram)

Transformata falkowa to iloczyn skalarny badanego sygnału

z prototypami falek

Reprezentacja w przestrzeni

L

2

ℝ

W a ,b =

〈

x t , 

a , b



t

〉

=

∫

x t

a ,b



t dt=

1





a

∫

ℝ

x t

t−b

a



dt

przesunięcie w czasie:

y t= x t−u  ,

W

y



a ,b=W

x



a ,b−u 

przesunięcie w częstotliwości

y t= x  st ,

W

y



a , b=

1





s

W

x



sa , sb

Transformata odwrotna:

x t =

∫

ℝ

∫

ℝ

W a , b

a ,b



t  da db

Mamy bazę ortonormalną – rodzina falek, mamy współczynniki reprezentacji, mamy też
transformatę odwrotną ... piękne wzory tylko nie da się tego policzyć !!! ;)

- 4 -

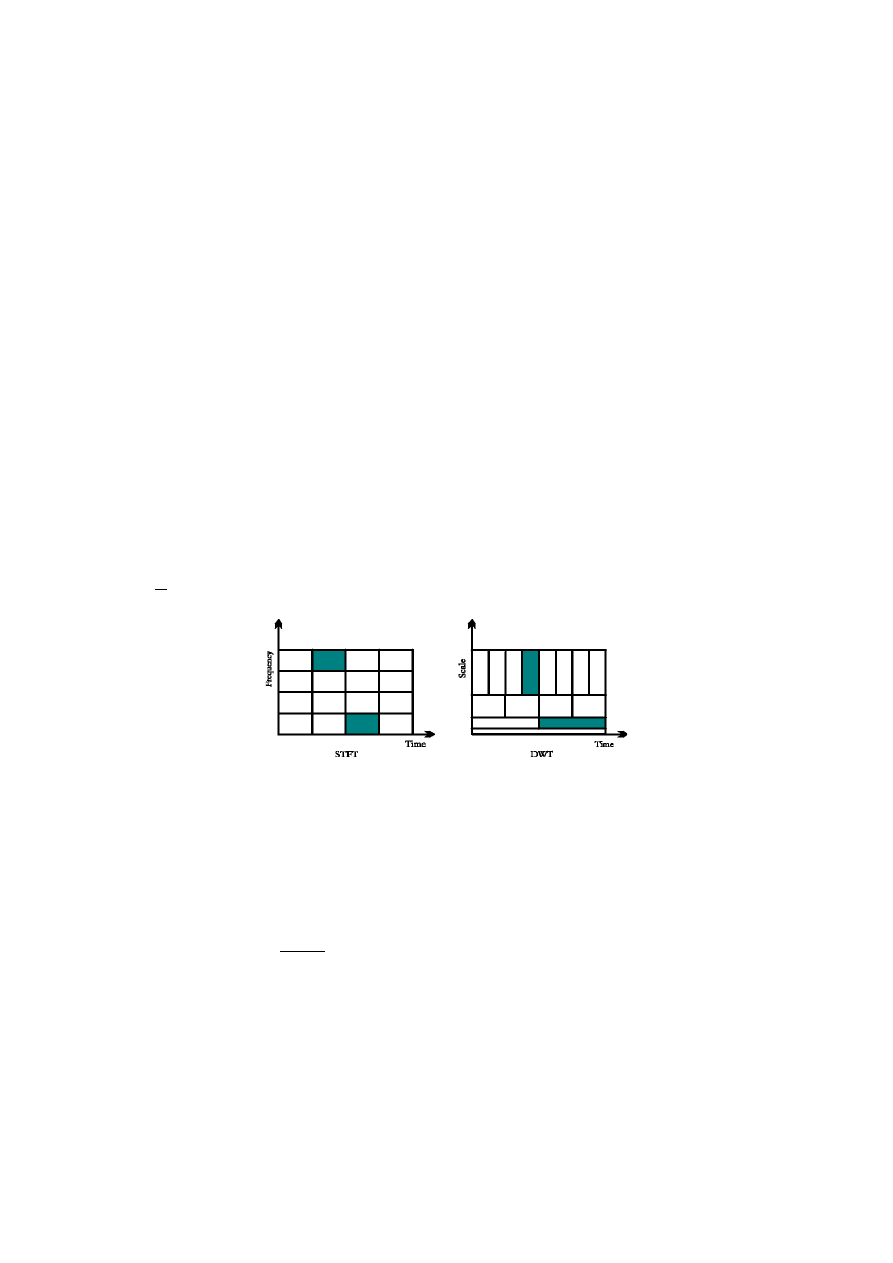
Reprezentacja w przestrzeni

ℝ

N

W a ,b =

〈

x n , 

a , b



n

〉

=

∑

n=0

N

x n 

a , b



n

Ważne definicje:

–

położenie i rozciągłość w czasie



t =

∫

ℝ

t∣

a ,b



t ∣dt



t

2

=

∫

ℝ



t−t

2

∣

a , b



t∣dt

–

położenie i rozciągłość w częstotliwości



=

∫

ℝ

∣

a ,b

∣

d 





2

=

∫

ℝ

− 



2

∣

a ,b

 ∣

d 

(rysunek z 

t

i 



)

Zasada nieoznaczoności Heisenberga:



t





≥

1
2

Przypadek dyskretny

Dwa rozwiązania:

1) nowe współrzędne skali



a

k

, l a

k

b gdzie l , k ∈ℤ



k , l



n=a

−

k / 2





n−l b

a

m



2) współrzędne skali z podziałem przez 2

a

k

=

a

0

k

, a

0

=

2  a

k

=

2

k

b

l

=

l b

0

a

0

k

, b

0

=

1  b

l

=

l2

k

- 5 -



k , l



n=

1



a

k





n−b

l

a

k



=

2

−

k /2



2

−

k

n−l 

Zatem w przestrzeni

ℝ

N

W  k , l=

〈

x  n ,

k ,l



n

〉

=

∑

n=0

N −1

x n 

k , l



n

i konsekwentnie transformata odwrotna:

x  n=

∑

k

∑

l

W  k , l

k ,l



n

Falka Morleta

Prototyp



n=

1



2 

e

−

j 

0

n

e

−

n

2

/

2

=

1



2 

e

−

j 

0

n n

2

/

2

=

e

−

2

2

 −

0



2

zwykle



0

=



2

ln 2

=

5.336

Meksykański kapelusz



n=1−n

2



e

−

n

2

/

2

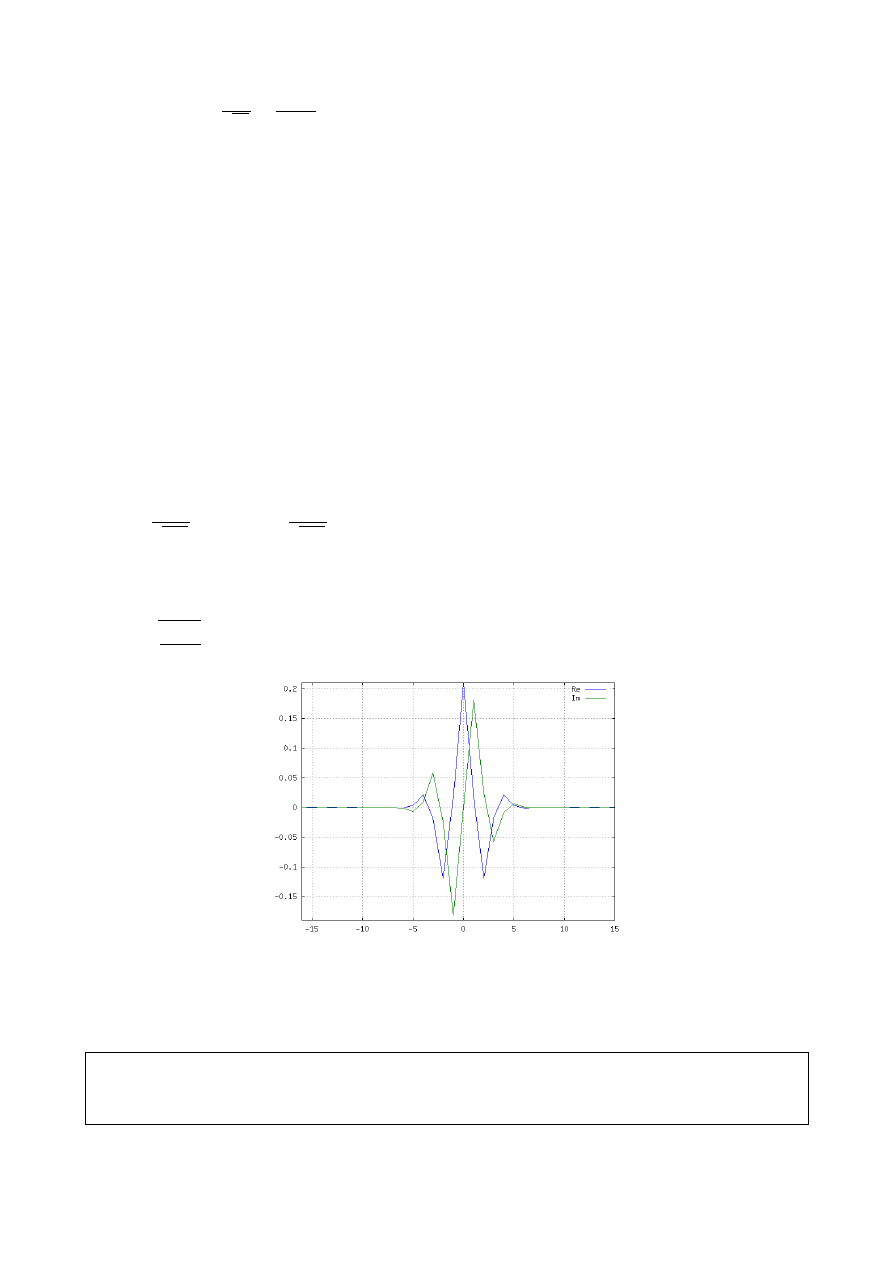
N=4;n=(-N:.1:N);
psi=(1-n.^2).*exp(-(n.^2)./2);

psi_1_0=sqrt(2)*(1-(n/2).^2).*exp(-((n/2).^2)./2);

- 6 -

plot(n,real(psi),';Re;',n,imag(psi),';Im;');

- 7 -