Dzień 3, matura podstawowa

Zobacz:

www.twojamatma.blogspot.com

Równania, nierówności, wyrażenia wymierne cz. I

1. Równanie

x

2

−4

(x

−4)(x+4)

= 0

A. nie ma rozwiązań

B. ma dokładnie jedno rozwiązanie

C. ma dokładnie dwa rozwiązania

D. ma dokładnie cztery rozwiązania

2. Równanie

(x+5)(x

−1)(x−4)

x

2

−16

= 0

A. nie ma pierwiastków

B. ma jeden pierwiastek

C. ma dwa pierwiastki

D. ma trzy pierwiastki

3. Równanie x

2

+ 3x

− 7 = 0 ma:

A. jedno rozwiązanie

B. nie ma rozwiązań

C. dwa rozwiązania

D. nieskończenie wiele rozwiązań

4. Rozwiązaniem równania

5

x

−3

− 2 = 0 jest liczba:

A.

−

11

2

B.

−

1
2

C.

1
2

D.

11

2

5. Rozwiązaniem równania 3(2

− 3x) = x − 4 jest:

A. x = 1

B. x = 2

C. x = 3

D. x = 4

6. Wskaż przedział, który jest zbiorem rozwiązań nierówności

x

4

+

1
6

<

x

3

:

A. (

−∞; −2)

B. (

−∞; 2)

C. (

−2; +∞)

D. (2; +

∞)

7. Dziedziną funkcji f , określonej wzorem f (x) =

3x

−1

x

2

−3x−4

jest zbiór:

A. R

B. R

− {

1
3

}

C. R

− {−1, 4}

D. R

− {−1,

1
3

, 4

}

8. Liczba 3 nie należy do dziedziny wyrażenia:

A.

x

−3

|x+3|

B.

2x

−1

|x−3|

C.

2x

−1

|x|+3

D.

x

−3

|2x−1|

Funkcja kwadratowa

9. Wykresem funkcji kwadratowej f (x) =

−3x

2

+ 3 jest parabola o wierzchołku w punkcie:

A.(3, 0)

B.(0, 3)

C.(

−3, 0)

D.(0,

−3)

10. Wskaż równanie osi symetrii paraboli określonej równaniem y =

−x

2

+ 4x

− 11:

A.x =

−4

B.x =

−2

C.x = 2

D.x = 4

11. Osią symetrii wykresu funkcji f (x) =

−6x

2

− 24x − 7 jest prosta o równaniu:

A.y = 2

B.x =

−2

C.x = 2

D.y =

−2

12. Największą wartością funkcji kwadratowej f (x) =

−2(x + 3)

2

− 4 jest:

A.3

B.

−2

C.

−4

D.4

1

Polub nas na

www.facebook.com/twojamatma

Dzień 3, matura podstawowa

Zobacz:

www.twojamatma.blogspot.com

13. Najmniejszą wartością funkcji f (x) = x

2

− 6x + 8 w przedziale < 4; 5 > jest:

A.0

B.3

C.9

D.

−16

14. Zbiorem wartości funkcji kwadratowej f (x) =

−(x + 6)

2

+ 4 jest przedział:

A. (

−∞; −6 >

B. (

−∞; 4 >

C. <

−6; +∞)

D. < 4; +

∞)

15. Wskaż funkcję kwadratową, której zbiorem wartości jest przedział <

−2; +∞):

A.y =

−2x

2

+ 2

B.y =

−(x + 1)

2

− 2

C.y = 2(x

− 1)

2

+ 2

D.y = (x + 1)

2

− 2

16. Funkcja f (x) = x

2

− 4x + 1 jest rosnąca w przedziale:

A. (

−∞; 2)

B. (

−∞; −3)

C. (

−3; +∞)

D. (2; +

∞)

17. Wykres funkcji kwadratowej f (x) = (x

− 3)

2

− 2 nie ma punktów wspólnych z prostą o równaniu:

A. y =

−3

B. y =

−1

C. y = 1

D. y = 3

18. Miejscami zerowymi funkcji kwadratowej y =

−3(x − 7)(x + 2) są:

A. x = 7, x =

−2

B. x =

−7, x = −2

C. x = 7, x = 2

D. x =

−7, x = 2

Własności wielokątów

19. Liczba przekątnych dziewięciokąta foremnego wynosi:

A.27

B.54

C.36

D.21

20. Suma miar kąrów wewnętrznych ośmiokąta wynosi:

A.360

◦

B.720

◦

C.1080

◦

D.1440

◦

21. Kąt wewnętrzny dziesięciokąta foremnego ma miarę:

A.144

◦

B.176, 4

◦

C.135

◦

D.120

◦

22. Jeden kąt trójkąta ma miarę 54

◦

. Z pozostałych dwóch kątów tego trójkąta jeden jest 6 razy więk-

szy od drugiego. Miary pozostałych kątów są równe:

A.21

◦

i 105

◦

B.11

◦

i 66

◦

C.18

◦

i 108

◦

D.16

◦

i 96

◦

23. Kąt przy podstawie w trójkącie równoramiennym ma miarę 70

◦

. Miara kąta między ramionami trójkąta

wynosi:

A.40

◦

B.55

◦

C.70

◦

D.110

◦

24. Różnica miar dwóch sąsiednich kątów wewnętrznych równoległoboku jest równa 30

◦

. Kąt rozwarty

tego równoległoboku jest równy:

A.105

◦

B.115

◦

C.125

◦

D.135

◦

2

Polub nas na

www.facebook.com/twojamatma

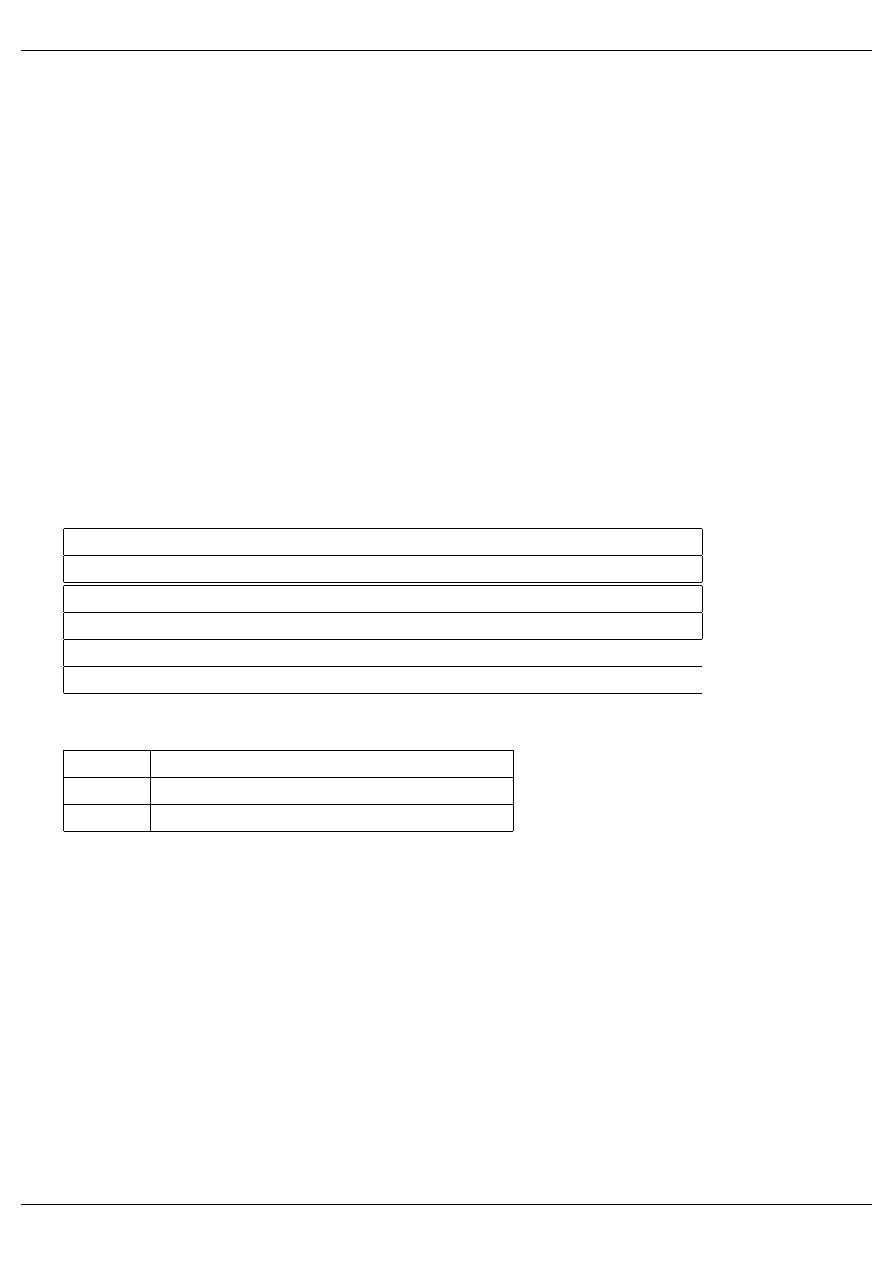
Dzień 3, matura podstawowa

Zobacz:

www.twojamatma.blogspot.com

Zadanie ostatnie - schemat I (xy):-)

25. Jasiek zatrudnił się na początku wakacji do zbierania truskawek. Każdego dnia zbierał taką samą liczbę

kilogramów i w sumie uzbierał 72 kilogramy. Gdyby każdego dnia zbierał o 2 kilogramy więcej, to tę samą

ilość truskawek uzbierałby w czasie krótszym o trzy dni. Oblicz ile kilogramów truskawek zbierał Jasiek

każdego dnia i w ciągu ilu dni je zbierał.

26. Pewien turystka pokonał trasę 112 km, przechodząc każdego dnia tę samą liczbę kilometrów. Gdyby

mógł przeznaczyć na tę wędrówkę o 3 dni więcej, to w ciągu każdego dnia mógłby przechodzić o 12 km

mniej. Oblicz, ile kilometrów dziennie przechodził ten turysta.

27. W czasie wakacji Marcin przejechał rowerem ze stałą prędkością odległość z miasteczka A do B liczącą

120 km. Gdyby jechał ze średnią prędkością o 5 km/h większą, to przejechałby tę odległość w czasie o 2

godziny krótszym. Wyznacz średnią rzeczywistą prędkość Marcina i rzeczywisty czas przejazdu.

ODPOWIEDZI:

- zadania zamknięte

1

2

3

4

5

6

7

8

9

10

C

C

C

D

A

D

C

B

B

C

11

12

13

14

15

16

17

18

19

20

B

C

A

B

D

D

A

A

A

C

21

22

23

24

A

C

A

A

- zadania otwarte

25

6 kg, 12 dni

26

28 km

27

15 km/h, 8 h

Niektóre z zadań wraz z dokładnymi rozwiązaniami, krok po kroku są dostępne na stronie:

www.twojamatma.blogspot.com

.

Wystarczy kliknąć po prawej na etykietę z nazwą ”działu”, do którego zadania należą!

Zapraszam!!!

3

Polub nas na

www.facebook.com/twojamatma