Dzień 4, matura podstawowa

Zobacz:

www.twojamatma.blogspot.com

Wykresy funkcji

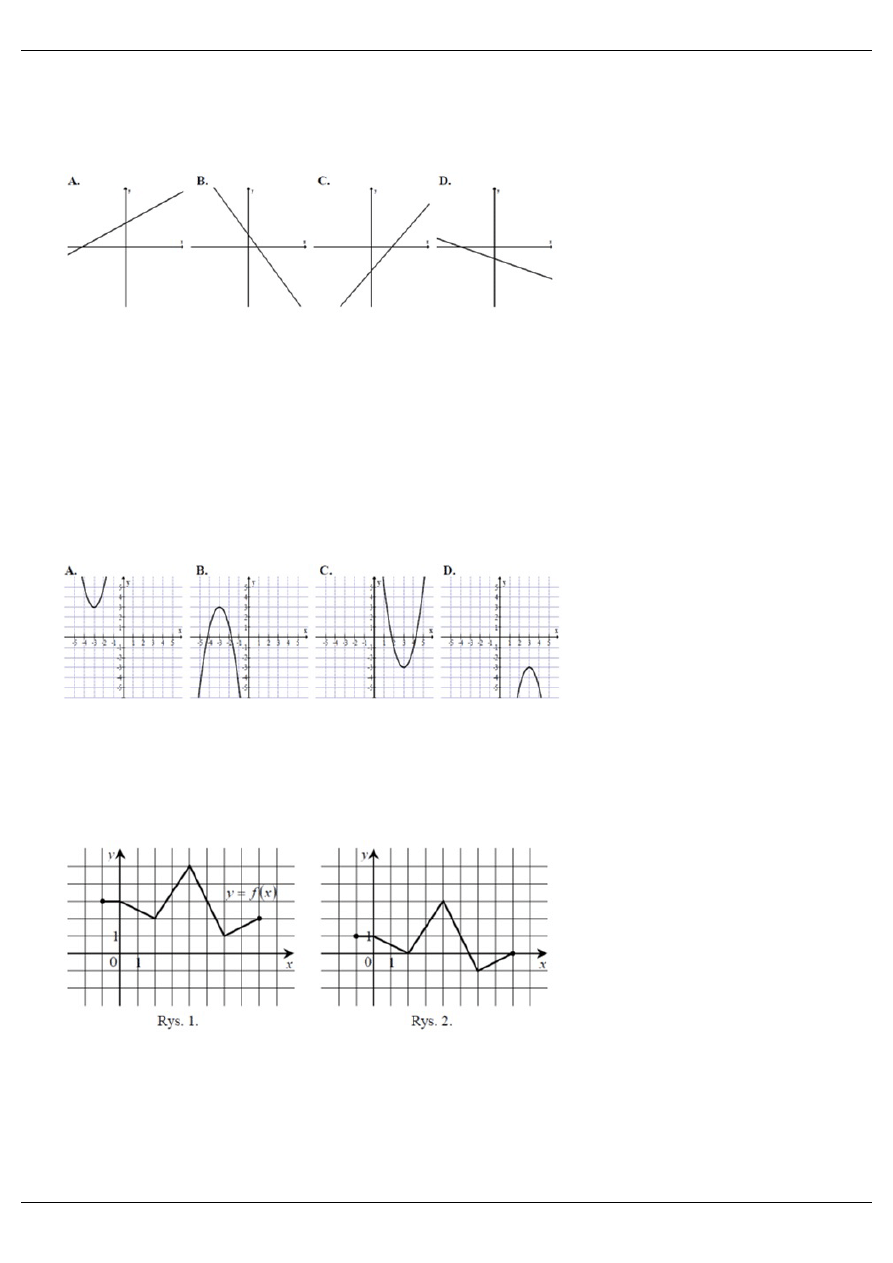
1. Na którym rysunku przedstawiono wykres funkcji liniowej y = ax + b takiej, że a > 0 i b < 0?

2. Dana jest funkcja liniowa y = ax + b, o któej wiadomo, że a < 0 i b > 0. Wykres tej funkcji prze-

chodzi przez następujące ćwiartki układu współrzędnych:

A. I, II, III

B. I, II, IV

C. II, III, IV

D. I, III, IV

3. Zbiorem wartości funkcji kwadratowej f jest przedział (

−∞, 3⟩. Na którym rysunku przedstawiono wy-

kres funkcji f ?

4. Na rysunku 1. jest przedstawiony wykres funkcji y = f (x). Funkcja przedstawiona na rysunku 2. jest

określona wzorem:

A. y = f (x) + 2

B. y = f (x)

− 2

C. y = f (x

− 2)

D. y = f (x + 2)

1

Polub nas na

www.facebook.com/twojamatma

Dzień 4, matura podstawowa

Zobacz:

www.twojamatma.blogspot.com

Zastosowanie tw. Pitagorasa

5. Podstawa trójkąta równoramiennego ma długość 6, a ramię ma długość 5. Wysokość opuszczona na pod-

stawę ma długość:

A. 3

B. 4

C.

√

34

D.

√

61

6. Wysokość CD trójkąta równoramiennego ABC jest równa 8, a ramię AC ma długość 10. Podstawa

AB tego trójkąta ma długość:

A. 12

B. 6

C.

√

89

D. 2

√

41

7. Przekątna AC prostokąta ABCD ma długość 11, a bok AB jest od niej o 5 krótszy. Oblicz długość

boku AD:

A.

√

157

B.

√

85

C. 5

D.

√

83

8. Ogród ma kształt prostokąta o bokach długości 20 m i 40 m. Na dwóch końcach przekątnej tego prosto-

kąta wbito słupki. Odległość między tymi słupkami jest:

A. równa 40 m

B. większa niż 50 m

C. większa niż 40 m i mniejsza niż 45 m

D. większa niż 45 m i mniejsza niż 50 m

9. Przekątna prostopadłościanu o wymiarach 3, 4, 5 ma długość:

A. 2

√

5

B. 2

√

3

C. 5

√

2

D. 2

√

15

Równanie okręgu

10. Okrąg o równaniu (x + 2)

2

+ (y

− 1)

2

= 13 ma promień równy:

A.

√

13

B.13

C.8

D.2

√

2

11. Dany jest okrąg o równaniu (x + 2)

2

+ (y

− 3)

2

= 5. Środek tego okręgu ma współrzędne:

A.(2,

−3)

B.(

−

√

2,

−

√

3)

C.(

−2, 3)

D.(

√

2,

√

3)

12. Wskaż równanie okręgu o środku S = (1,

−2) i promieniu r = 2.

A.(x

− 1)

2

+ (y + 2)

2

= 2

B.(x + 1)

2

+ (y

− 2)

2

= 2

C.(x

− 1)

2

+ (y + 2)

2

= 4

D.(x + 1)

2

+ (y

− 2)

2

= 4

13. Środek S okręgu o równaniu x

2

+ y

2

+ 4x

− 6y − 221 = 0 ma współrzędne:

A.(

−2, 3)

B.(2,

−3)

C.(

−4, 6)

D.(4,

−6)

14. Promień okręgu o równaniu x

2

+ y

2

+ 6x

− 2y + 3 = 0 jest równy:

A.5

B.7

C.

√

5

D.

√

7

15. Liczba punktów wspólmnych okręgu o równaniu (x + 3)

2

+ (y

− 1)

2

= 4 z osiami układu współrzędnych

jest równa:

A. 0

B. 1

C. 2

D. 4

2

Polub nas na

www.facebook.com/twojamatma

Dzień 4, matura podstawowa

Zobacz:

www.twojamatma.blogspot.com

16. Liczba punktów wspólnych okręgu o równaniu (x + 1)

2

+ (y + 3)

2

= 1 z prostą o równaniu y

− 2 = 0

jest równa:

A. 0

B. 1

C. 2

D. 3

Własności graniastosłupów i ostrosłupów

17. Liczba ścian bocznych graniastosłupa, który ma 12 wierzchołków, jest równa:

A. 12

B. 8

C. 6

D. 4

18. Graniastosłup ma 15 krawędzi. Ile wierzchołków ma ten graniastosłup?

A. 10

B. 5

C. 15

D. 30

19. Ostrosłup ma 18 wierzchołków. Liczba wszystkich krawędzi tego ostrosłupa jest równa:

A. 11

B. 18

C. 27

D. 34

20. Ostrosłup ma 12 krawędzi. Liczba wszystkich wierzchołków tego ostrosłupa jest równa:

A. 12

B. 9

C. 8

D. 7

21. Pewien wielościan ma 6 krawędzi. Liczba jego ścian jest równa:

A. 4

B. 6

C. 8

D. 10

Wielomiany

22. Wielomiany W (x) = ax(x + b)

2

i V (x) = x

3

+ 2x

2

+ x są równe. Oblicz a i b.

23. Rozłóż na czynniki możliwie najniższego stopnia wielomian W (x) = x

3

+ 5x

2

− 16x − 80.

24. Liczba 3 jest pierwiastkiem wielomianu W (x) = x

3

− 4x

2

− mx + 36. Wyznacz parametr m i pozostałe

pierwiastki tego wielomianu.

Ciągi

25. Ciąg (a

n

) jest określony wzorem a

n

=

n

−2

n+3

. Znajdź dziesiąty wyraz ciągu. Określ, który wyraz ciągu

jest równy

4
9

.

26. W ciągu arytmetycznym (a

n

) drugi wyraz jest równy 7, a szósty 17. Wyznacz pierwszy wyraz i różnicę

tego ciągu.

27. Pierwszy wyraz ciągu arytmetycznego jest równy (

−5), a suma dwudziestu początkowych wyrazów tego

ciągu jest równa 1230. Wyznacz różnicę tego ciągu.

28. Liczby x, y, 19 w podanej kolejności tworzą ciąg arytmetyczny, przy czym x + y = 8. Oblicz x i y.

3

Polub nas na

www.facebook.com/twojamatma

Dzień 4, matura podstawowa

Zobacz:

www.twojamatma.blogspot.com

29. Liczby 27, x, 3 są odpowiednio pierwszym, drugim i trzecim wyrazem malejącego ciągu geometrycznego.

Oblicz ósmy wyraz tego ciągu.

30. Suma początkowych n wyrazów pewnego ciągu arytmetycznego jest określona wzorem S

n

= n

2

− 2n,

dla n

­ 1. Wyznacz wzór na n-ty wyraz tego ciągu.

31. Ciąg (a, b, c) jest arytmetyczny i a + b + c = 33. Ciąg (a, b + 3, c + 13) jest geometryczny. Oblicz a, b i c.

ODPOWIEDZI:

- zadania zamknięte

1

2

3

4

5

6

7

8

9

10

C

B

B

B

B

A

B

C

C

A

11

12

13

14

15

16

17

18

19

20

C

C

A

D

C

A

C

A

D

D

21

A

- zadania otwarte

22

a = 1, b = 1

23

(x

− 4)(x + 4)(x + 5)

24

m = 9, x

∈ {−3, 4}

25

a

10

=

8

13

, a

6

26

a

1

= 4, 5 r = 2, 5

27

r = 7

28

x =

−1, y = 9

29

a

8

=

1

81

30

a

n

=

−2n − 3

31

a = 7, b = 11, c = 15 lub a = 28, b = 11, c =

−6

Niektóre z zadań wraz z dokładnymi rozwiązaniami, krok po kroku są dostępne na stronie:

www.twojamatma.blogspot.com

.

Wystarczy kliknąć po prawej na etykietę z nazwą ”działu”, do którego zadania należą!

Zapraszam!!!

4

Polub nas na

www.facebook.com/twojamatma