GI

04

-

01

1.

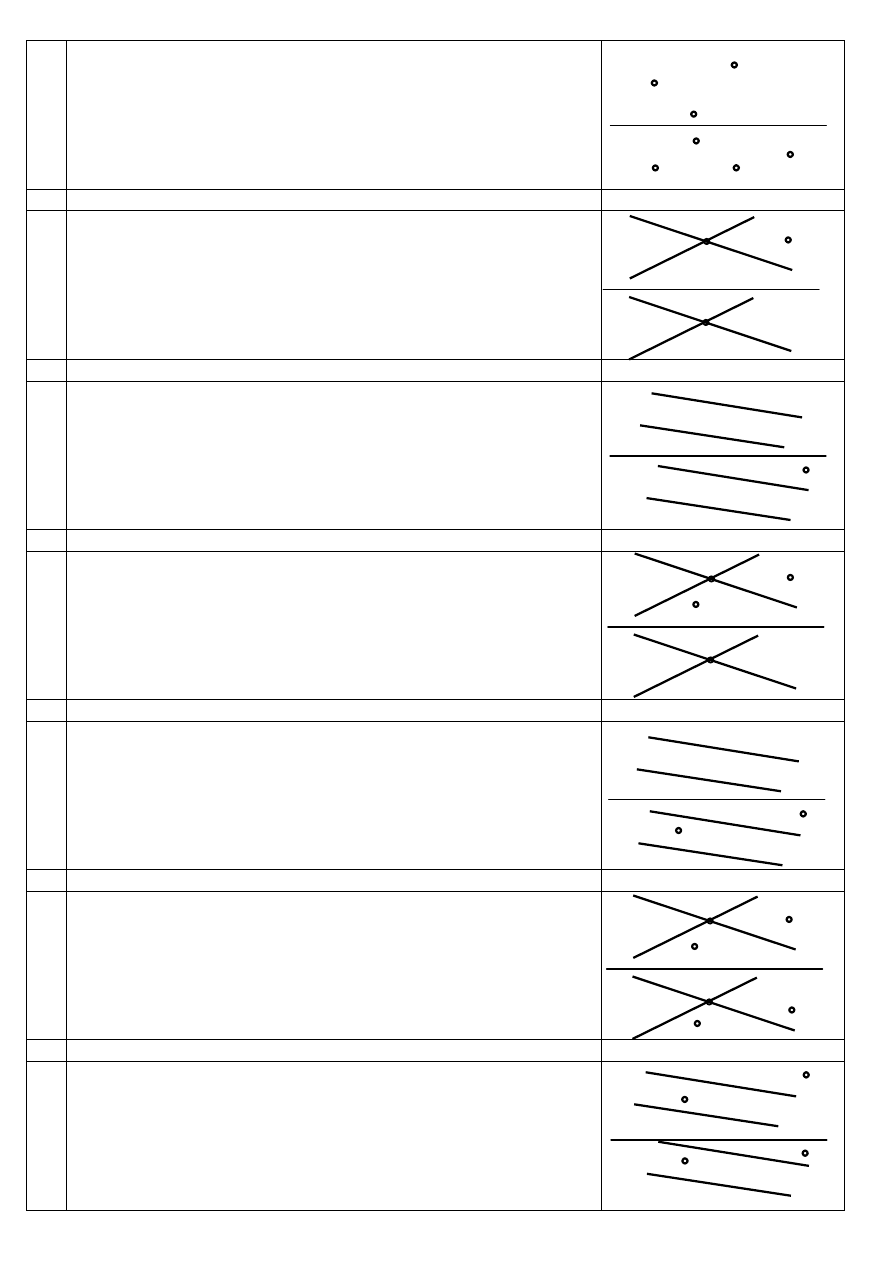
Dane są: płaszczyzna ω = ABC oraz 1 rzut punktu D.

2.

Znajdź drugi rzut punktu D, aby ten leżał na płaszczyźnie ω.

GI

04

-

02

1.

Dane są: płaszczyzna ω = ab oraz 1 rzut punktu D.

2.

Znajdź drugi rzut punktu D, aby ten leżał na płaszczyźnie ω.

`

GI

04

-

03

1.

Dane są: płaszczyzna ω = ab oraz 1 rzut punktu D.

2.

Znajdź drugi rzut punktu D, aby ten leżał na płaszczyźnie ω.

`

GI

04

-

04

1.

Dane są: płaszczyzna ω = ab oraz 1 rzut prostej c = CD.

2.

Znajdź drugi rzut prostej c, aby ta leżała na płaszczyźnie ω.

`

GI

04

-

05

1.

Dane są: płaszczyzna ω = ab oraz 1 rzut prostej c = CD.

2.

Znajdź drugi rzut prostej c, aby ta leżała na płaszczyźnie ω.

`

GI

04

-

06

1.

Dane są: płaszczyzna ω = ab oraz prosta c = CD.

2.

Znajdź punkt Q przebicia płaszczyzny ω prostą c.

`

GI

04

-

07

1.

Dane są: płaszczyzna ω = ab oraz prosta c = CD.

2.

Znajdź punkt Q przebicia płaszczyzny ω prostą c.

`

X

A

II

A

I

B

II

B

I

C

I

D

I

C

II

D

II

X

b

II

a

II

C

II

C

I

a

I

b

I

X

b

II

a

II

D

I

a

II

b

II

D

II

X

b

II

a

II

A

II

A

I

a

I

b

I

C

II

X

b

II

a

II

D

I

a

I

b

I

C

I

D

II

X

b

II

a

II

A

II

A

I

a

I

b

I

C

II

D

I

C

I

X

D

I

a

I

b

I

C

I

b

II

a

II

C

II

D

II

GI

04

-

08

1.

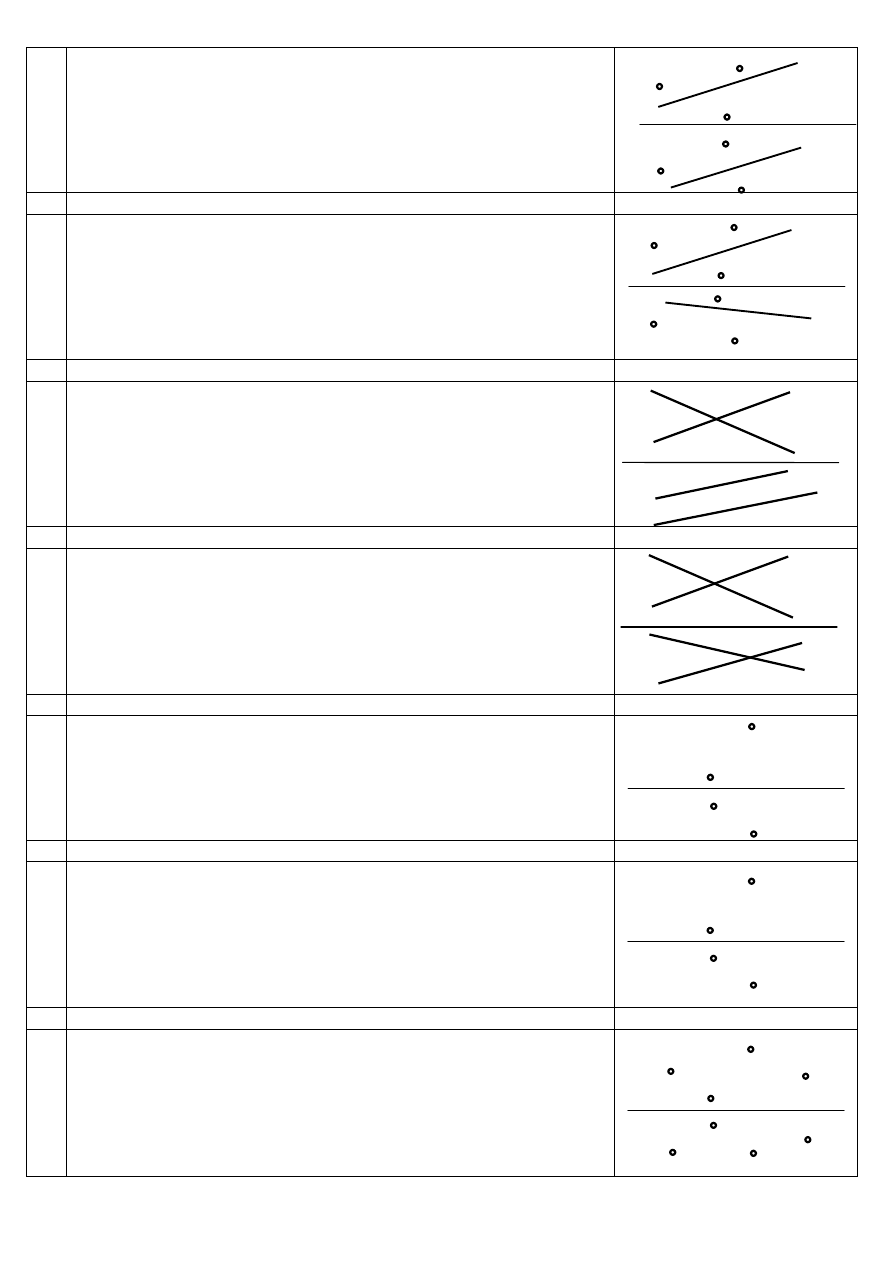
Dane są: trójkąt ABC oraz prosta c.

2.

Znajdź punkt Q przebicia trójkąta ABC prostą c, określ widoczność.

GI

04

-

09

1.

Dane są: trójkąt ABC oraz prosta c.

2.

Znajdź punkt Q przebicia trójkąta ABC prostą c, określ widoczność.

`

GI

04

-

10

1.

Dane są: dwie proste skośne c i d.

2.

Określ minimalną odległość miedzy prostymi c i d.

`

GI

04

-

11

1.

Dane są: dwie proste skośne c i d.

2.

Określ minimalną odległość miedzy prostymi c i d.

GI

04

-

12

1.

Dany jest odcinek A B.

2.

Zbuduj dowolny trójkąt równoboczny, którego 1 bokiem jest AB.

`

GI

04

-

13

1.

Dany jest odcinek A B.

2.

Zbuduj dowolny kwadrat, którego 1 bokiem jest AB.

`

GI

04

-

14

1.

Dane są: 2 trójkąty ABC i ACD o wspólnym boku AC.

2.

Określ kąt ψ pomiędzy oboma trójkątami..

`

X

A

I

B

I

C

I

c

I

A

II

B

II

C

II

c

II

X

A

II

B

II

C

II

c

II

A

I

B

I

C

I

c

I

c

I

X

d

I

d

II

c

II

X

d

II

c

II

d

I

c

I

X

A

II

A

I

B

I

B

II

X

A

II

A

I

B

I

B

II

X

A

II

A

I

B

II

B

I

C

I

D

I

C

II

D

II