klasyczne metody QSAR

Część IV: Klasyczne metody QSAR

7. Ilościowe zależności struktura chemiczna –
aktywność biologiczna

Rozwój

ilościowych metod określania aktywności

biologicznej skłonił wielu badaczy do poszukiwania metod
ilościowej analizy uzyskanych wyników. Tak powstały w
pierwszej połowie XX w.:

∗

farmakometria

∗

farmakokinetyka

∗

farmakodynamika.

Jednakże próby ilościowego powiązania budowy chemicznej z
aktywnością biologiczną przez szereg dziesięcioleci nie
dawały zadawalających wyników. Wydaje się, że główna
przeszkoda miała charakter psychologiczny: jak wyrazić
ilościowo jakościowe przecież informacje o budowie
chemicznej cząsteczki.
Pomoc

przyszła ze strony teoretycznej chemii

organicznej: prace Hammeta i Tafta nad wpływem
podstawników na szybkość przebiegu reakcji chemicznych
zapoczątkowały nowe spojrzenie na opis budowy chemicznej.
W opisie tym struktura chemiczna cząsteczki dzieli się na:

∗

stały w danej serii związków rdzeń

∗

fragmenty zmienne traktowane jako podstawniki rdzenia.

Pozwala to na ilościowy opis cząsteczki poprzez podanie
w p ł y w u p o d s t a w n i k ó w .

Z drugiej strony, nie do przecenienia jest również

zachodzący w tym czasie postęp w możliwościach
technicznych: rozwój i dostępność komputerów umożliwił
wykorzystanie różnorodnych metod numerycznych nie
stosowanych wcześniej ze względu na ich pracochłonność.
Na

początku lat '60 zakiełkowała nowa,

multidyscyplinarna gałąź wiedzy: i l o ś c i o w e
z a l e ż n o ś c i p o m i ę d z y s t r u k t u r ą
c h e m i c z n ą i a k t y w n o ś c i ą b i o l o g i c z n ą
(QSAR). W ramach QSAR wykorzystywana jest wiedza z
wielu tradycyjnych dziedzin nauki:

∗

chemia organiczna

∗

chemia fizyczna

∗

biochemia

∗

farmakologia i farmakometria

∗

statystyka matematyczna

∗

metody numeryczne

∗

techniki komputerowe.

Metody QSAR przez ostatnie 30 lat rozgałęziły się,

rozrosły, okrzepły i w tej chwili zajmują istotne miejsce w
poszukiwaniu i projektowaniu nowych leków, w tym również
chemoterapeutyków. Dobitnie świadczy o tym ilość publikacji
naukowych z tej dziedziny. W ostatnich latach wiele z nich
jest finansowanych przez liczące się ośrodki naukowe lub
duże firmy farmaceutyczne. Wynika to z faktu, że metody
ilościowego opisu zależności struktura - aktywność posiadają
zdolność do dostarczania informacji dwojakiej natury.
Z jednej strony uzyskane zależności traktowane być mogą
jako modele matematyczne pewnych procesów, którym
podlegają związki biologicznie czynne. Stanowią więc
wygodną metodę falsyfikacji pewnych teorii czy hipotez.
Przyczynia się to do istotnego przyspieszenia poznania wielu
bardzo skomplikowanych zjawisk zachodzących w
organizmach żywych. Oprócz tej roli poznawczej metody

QSAR mają również funkcje prognostyczne: pozwalają
oszacować aktywność biologiczną związków na podstawie ich
właściwości fizykochemicznych, a czasami tylko na
podstawie wzoru chemicznego, nawet bez konieczności ich
syntetyzowania. Przyczynia się to do znacznego
przyspieszenia i potanienia poszukiwania i projektowania
nowych leków.

W chwili obecnej metody QSAR przestały już być

wyłącznie ciekawostką teoretyczną, a stały się użytecznym
narzędziem o szerokich możliwościach.

Metody QSAR wykorzystują wiele, czasami dosyć

zaawansowanych, metod numerycznych. Celem naszego
wykładu jest zapoznanie Państwa z możliwościami
wykorzystania tych metod przy projektowaniu nowych
chemoterapeutyków, a nie ze stosowanymi metodami
numerycznymi. Jednakże nie będzie możliwe całkowite
pominięcie problemów numerycznych. Ograniczymy się
jednak w takich przypadkach do omówienia założeń
niezbędnych dla poprawnego doboru metodyki oraz do
poglądowych interpretacji sposobu działania algorytmów.
Nacisk położony będzie raczej na możliwe zastosowania
poszczególnych technik oraz sposoby prawidłowej
interpretacji wyników obliczeń.

W metodach QSAR spotkać można trzy

podstawowe sposoby opisu aktywności biologicznej:

∗

skala nominalna: w większości przypadków podział

badanych związków na dwie klasy, np. związki aktywne
i nieaktywne. W bardziej zaawansowanych metodach
istnieje możliwość zastosowania większej liczby klas.

∗

pojedynczy,

ilościowy test aktywności: zwykle w formie

ujemnego logarytmu ze stężenia wywołującego
standardową odpowiedź biologiczną. Z wykorzystaniem
tego opisu powstały pierwsze metody QSAR.

∗

bateria testów ilościowych: jednoczesne zastosowanie

wielu testów pozwala na pełniejszy opis zależności.
Stwarza jednak również określone problemy
obliczeniowe.

Również opis struktury związków dokonany być może na
wiele sposobów:

∗

jakościowy opis podstawników

∗

ilościowy opis właściwości fizykochemicznych całego

związku. Można tu rozróżnić przypadek ograniczonego
zestawu właściwości oraz wersję z baterią właściwości.

∗

ilościowe wielkości uzyskane z metod chemii

obliczeniowej, np. rzędy wiązań lub ładunki cząstkowe

∗

jakościowy opis elementów struktury

∗

struktura trójwymiarowa cząsteczki, ewentualnie z

opisem rozkładu pola elektrostatycznego generowanego
przez cząsteczkę

zależności od sposobu opisu aktywności

biologicznej i opisu budowy chemicznej stosowane są
odmienne techniki analizy ilościowych zależności
struktura - aktywność. Przed przystąpieniem do ich
systematycznego omawiania celowe jest jednak zapoznanie
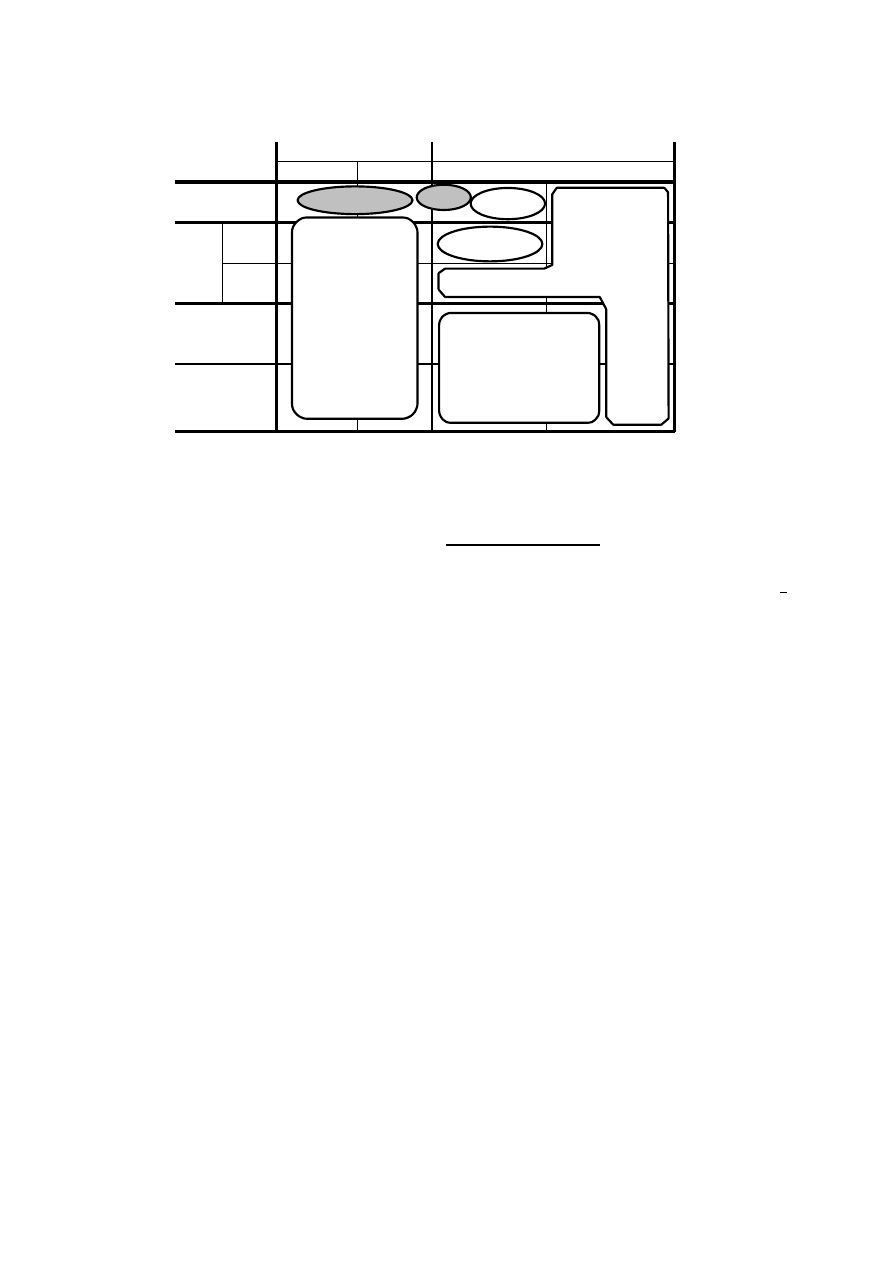
się z zakresem ich zastosowań, które ilustruje poniższy
schemat (Rys.7.1.).

Część IV: Klasyczne metody QSAR

Aktywność biologiczna

jakościowa

ilościowa

dwuklaso

wieloklaso

pojedyncze

bateria

struktury

Opis

jakościowy

podstawnik

właściw.

fiz.-

chem.

elementy
struktury

struktura
trójwymiarowa

pojedyn

cze

bateri

SAR

Rozpozna-

wanie

obrazów

nauczycielem

nRMO

F-W

m. Hanscha

Rozpoznawanie

obrazów

bez

nauczyciela

Metoda

głównych

składowych

regresja wielokrotna

Rys.7.1: Zakres typowych zastosowań różnych technik opisu zależności struktura - aktywność

W przypadku nominalnej skali aktywności

biologicznej (klasyfikacja aktywne - nieaktywne) stosuje się
zwykle tylko najprostszy sposób opisu budowy chemicznej:
jakościowy opis podstawników. W sytuacji takiej
zastosowanie ilościowych form opisu wydaje się być dosyć
trudne. Powszechnie za to stosuje się opisy jakościowe czyli
metodę SAR.

Nieregresyjne metody optymalizacji struktury

(nRMO) znajdują w zasadzie zastosowanie w przypadku
pojedynczych, ilościowych testów aktywności i jakościowym
opisie struktury, chociaż niektóre z nich mogą być również
zastosowane w przypadku jakościowego, wieloklasowego
opisu aktywności biologicznej.

W przypadku pojedynczych testów aktywności

szerokie zastosowanie znajdują metody regresyjne. Metoda
Free-Wilsona (F-W), jedna z dwóch pierwszych technik
QSAR, znajduje zastosowanie w przypadku jakościowego
opisu struktury chemicznej poprzez informacje o obecności
określonych podstawników w określonych miejscach rdzenia
cząsteczki.
Druga z najdłużej stosowanych metod QSAR, metoda
Hanscha, wymaga ilościowego opisu właściwości
fizykochemicznych analizowanych związków.

Do klasyfikacji i określania podobieństwa badanych

związków wykorzystuje się techniki matematyczne zwane
"rozpoznawaniem obrazów". W przypadku, gdy podział na
klasy znany jest przed wykonaniem obliczeń mamy do
czynienia z techniką "z nauczycielem", a zadanie sprowadza
się do określenia reguł klasyfikacji. Gdy podział na grupy nie
jest narzucony to odpowiednie techniki określane są mianem
"bez nauczyciele" i służą do określenia podobieństwa
pomiędzy poszczególnymi związkami należącymi do
analizowanego zbioru. Celem metod bez nauczyciele jest
często wykrycie tendencji pewnych elementów zbioru
związków do tworzenia mniej lub bardziej spójnych grup czy
klas.

W przypadku gdy choć jeden z opisów (aktywności

lub struktury) opiera się na bardzo licznym zestawie wielkości
(baterii testów) zwykłe metody regresyjne zawodzą. Stosuje
się wtedy technikę zwaną analizą głównych składowych dla
zredukowania liczby wielkości opisujących. Po takiej redukcji

wymiarowości problemu stosuje się typowe metody regresji
wielokrotnej.

8. Metody regresyjne.

Załóżmy, że zmienna niezależna y (w metodach
QSAR jest nią aktywność biologiczna) może być z rozsądnym
przybliżeniem wyrażona jako kombinacja liniowa k
zmiennych zależnych z:

...

yˆ

≈

Mamy wtedy do czynienia z najprostszym przypadkiem
metody regresyjnej tzw. r e g r e s j ą l i n i o w ą .
Występujące w regresji liniowej współczynniki ai obliczane

są z wykorzystaniem zasady m i n i m u m s u m y
k w a d r a t ó w r ó ż n i c zwanej także metodą
najmniejszych kwadratów. Zasada ta daje się wyrazić
wzorem:

(

)

min

yˆ

SKR

−

∑

Wartości ai dobierane (obliczane) są tak, aby spełniony był

warunek minimum SKR.

Jednym z problemów występujących przy analizie

regresji jest dobór ilości i rodzaju zmiennych niezależnych z
występujących w równaniu regresji. Wymaga się zwykle, aby
wszystkie człony równania były statystycznie istotne. Jednym
ze sposobów uzyskania równania regresji spełniającego ten
wymóg jest zastosowanie tzw. m e t o d y
o d r z u c a n i a . Obliczenia rozpoczyna się od równania
zawierającego wszystkie człony. Po wyznaczeniu
współczynników ai określa się ich istotność statystyczną. O

ile występują człony nieistotne usuwa się człon najmniej
istotny i ponownie wyznacza współczynniki, tym razem już
tylko k-1 współczynników. Usuwanie najmniej istotnych
członów i obliczanie nowych współczynników powtarza się
tak długo, aż wszystkie człony pozostające w równaniu
regresji będą statystycznie istotne.

Innym wymogiem stawianym prawidłowemu

równaniu regresji jest jego istotność jako całości. Najczęściej
stosowaną miarą tej istotności jest statystyka F Snedecora.
Uzyskanie równania charakteryzującego się wartością F
większą od krytycznej wskazuje, że równanie jako całość jest
statystycznie wiarygodne i może być użyte do przewidywania
wartości zmiennej zależnej (aktywności) na podstawie

Część IV: Klasyczne metody QSAR

znanych wartości zmiennych niezależnych. Informacje o
precyzji obliczania wartości zmiennej zależnej zawarte są w
innych wskaźnikach statystycznych obliczanych równolegle z
wartościami współczynników. Odchylenie standardowe
równania, s, podaje przeciętne odchylenie standardowe
prognozowanych wartości zmiennej zależnej. Rzeczywisty
błąd prognozowanych wartości zależy nie tylko od jakości
równania, ale również od wartości zmiennych niezależnych w
prognozowanym punkcie. Jego miarą jest wartość promienia
korytarza błędu w danym punkcie. Cenne informacje niesie
również współczynnik korelacji równania, r, a szczególnie
jego kwadrat zwany współczynnikiem determinacji. Określa
on jaki ułamek ogólnej zmienności zmiennej zależnej
wyjaśnić można przy pomocy danego równania regresji.

Przy pomocy metody najmniejszych kwadratów

wyznaczać można nie tylko wartości współczynników w
liniowych równaniach regresji, ale również współczynniki w
równań regresji krzywoliniowej. Najczęściej spotykanym
przykładem takiej regresji jest tzw. regresja wielomianowa.
Zmienna zależna opisywana jest w niej równaniem:

...

yˆ

≈

Jeśli w równaniu tym potraktujemy poszczególne potęgi
zmiennej z jako zmienne niezależne to otrzymamy typowe
równanie regresji liniowej. Tak więc również w przypadku
regresji krzywoliniowej zachowują moc omówione powyżej
mierniki istotności statystycznej i jakości prognozy.

Przykład 8.1: Zależność regresyjna.

-100 0

100 200 300 400 500 600 700

t [C]

100

200

300

400

500

600

R(t)

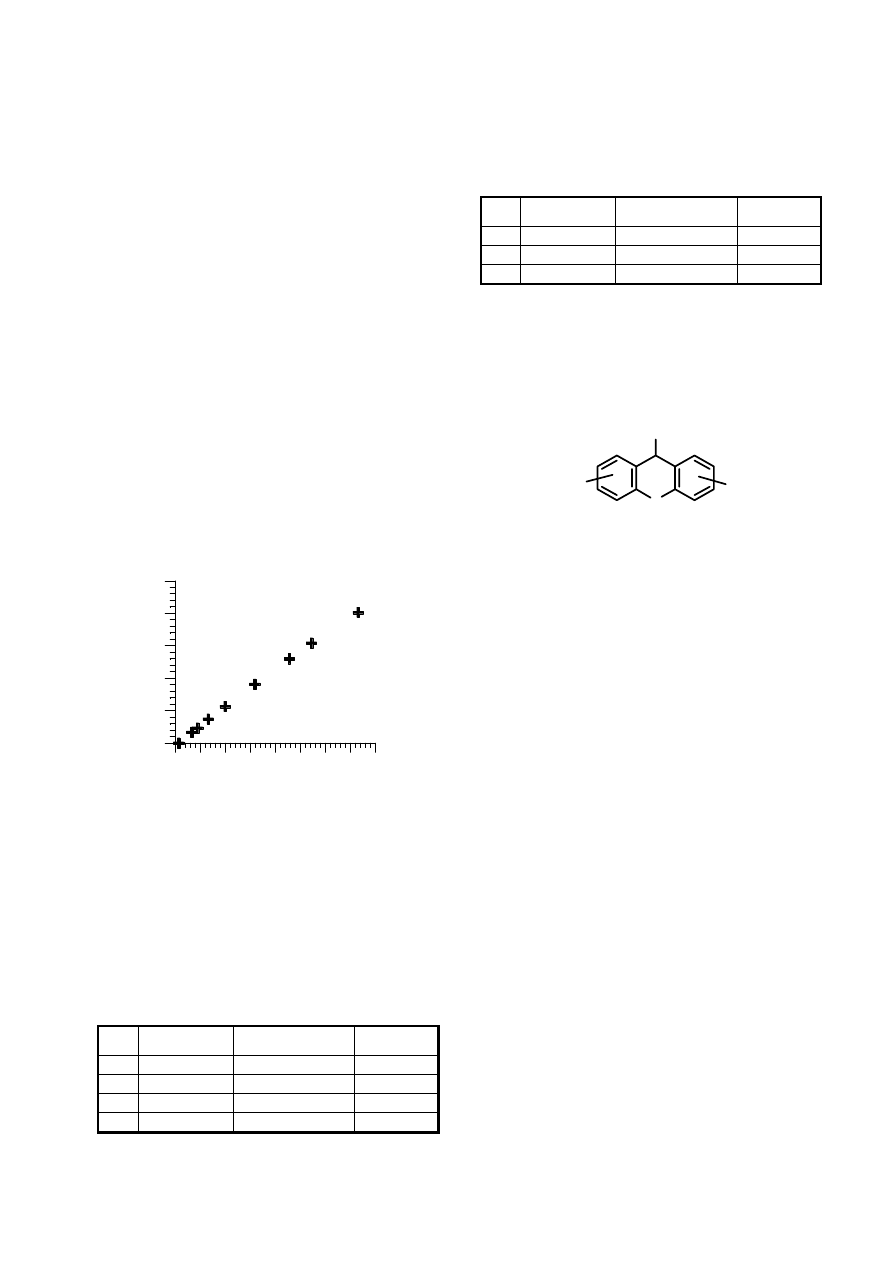
Rys.8.1: Zależność oporu platyny od temperatury.

Zmierzono opór elektryczny cewki platynowej

utrzymywanej w stałej temperaturze. Pomiary wykonano w 9
różnych temperaturach w zakresie od -85 do 630

°C. Zmierzony

opór zmieniał się od ok.100 do ok. 500 m

Ω (patrz rysunek

obok). Rozkład uzyskanych wyników sugeruje, że zależność
może być nieliniowa. Chcąc stworzyć model zależności oporu
od temperatury przyjęto model wielomianowy stopnia co
najwyżej trzeciego:

( )

Rˆ

≈

Nie znamy ani poprawnego stopnia wielomianu, ani wartości
współczynników. Spróbujmy zastosować metodę odrzucania
(Tab.VIII.1).

Tab.VIII.1. Wynik rozwiązania równania regresji stopnia
trzeciego

i współczynnik

odchylenie

standardowe

istotność

0 152,8411

1,04 376,82

1 0,6073

0,014

106,05

2 -0,000063

0,000072

-0,31

3 -0,000000035

0,0000000848

-1,52

s = 0,867

F = 68 612,6

R = 1,000

Równanie jako całość jest statystycznie bardzo istotne,
jednakże człon kwadratowy i sześcienny są nieistotne. Zgodnie
z metodą odrzucania usuwamy człon najmniej istotny (w
naszym przypadku człon sześcienny) i powtarzamy obliczenia
(Tab.VIII.2.).

Tab.VIII.2. Wynik rozwiązania równania regresji bez członu
sześciennego.

i współczynnik

odchylenie

standardowe

istotność

0 153,01

0,92

406,35

1 0,6118

0,0087

169,26

2 -0,092

0,016

11,75

s = 0,874

F = 101 243

R = 1,000

Po usunięciu członu sześciennego otrzymujemy równanie o
bardzo podobnych charakterystykach statystycznych, z tym, że
wszystkie jego człony są statystycznie istotne.
================================================

8.1. Metoda Free-Wilsona

N H R

Rys.8.2: Struktura serii pochodnych akrydyny

Rozważmy sytuację, gdy dysponujemy związkiem
chemicznym wykazującym interesujący nas rodzaj
aktywności biologicznej. Zadanie polega na znalezieniu
pochodnej o możliwie wysokiej aktywności. Jeśli z punktu
widzenia możliwości syntetycznych istnieje możliwość
wprowadzenia różnych podstawników w kilku miejscach
cząsteczki, to zastanówmy się ile takich pochodnych może
być. Dla przykładu poddajmy analizie serię pochodnych
akrydyny przedstawioną na Rys.8.2 przyjmując, że
modyfikować możemy:

∗

łańcuch boczny w pozycji 9 (4 różne podstawniki)

∗

lewy pierścień (3 podstawniki w czterech pozycjach 1

÷4)

∗

prawy pierścień (3 podstawniki w czterech pozycjach

÷8).

Liczba różnych pochodnych wynosi w tej sytuacji:

N = 4

× 34 × 34 = 26 244

Każdy związek należałoby zsyntetyzować i przetestować
biologicznie. Jest to ogromna praca wymagająca kolosalnych
nakładów. Pojawia się więc pytanie, czy nie dałoby się
zmniejszyć liczby związków dzięki zastosowaniu jakichś
reguł wyboru. Oczywiście można coś takiego zastosować.
Dobór związków opierać się może na szeregu kryteriach: od
zupełnej losowości po rozważania oparte na regułach
teoretycznej chemii organicznej. Zawsze jednak stracimy
część informacji i nie będziemy do końca pewni czy nie
pominęliśmy najlepszej pochodnej.
Istnieje

wszakże pewien sposób pozwalający

zminimalizować ryzyko pominięcia najlepszych pochodnych.
Można mianowicie zbudować i zweryfikować model
zależności aktywności biologicznej od obecności lub braku
określonego podstawnika w określonej pozycji w cząsteczce.
Przez wiele lat wydawało się jednak, że model taki musi
zawierać bardzo skomplikowane i niepoznane dotychczas
zależności funkcyjne. Jednakże w roku 1964 ukazała się
publikacja Free i Wilsona w której autorzy zaproponowali
bardzo prosty model. Przyjęli mianowicie założenie, że dany
podstawnik w danym miejscu cząsteczki ma na aktywność
biologiczną zawsze taki sam wpływ niezależnie od obecności
innych podstawników w innych miejscach.

Część IV: Klasyczne metody QSAR

W przypadku ogólnym założenie takie nie

wytrzymuje próby weryfikacji: znamy wiele przykładów gdy
podstawniki wzmacniają lub znoszą swój wpływ w zależności
od wzajemnego usytuowania. Widać to szczególnie wyrażnie
w przypadku pochodnych związków aromatycznych: dwa,
odpowiednio dobrane podstawniki w pozycji orto mogą
tworzyć dla siebie wzajemnie zawadę przestrzenną; z koleji
podstawniki w pozycji para mogą wywierać na siebie wpływ
poprzez efekty indukcyjne i/lub rezonansowe
Znane są jednak również bardzo liczne przykłady, gdy efekty
podstawników po prostu sumują się. Metoda zaproponowana
przez Free i Wilsona nie jest więc podejściem uniwersalnym i
wymaga w każdym indywidualnym przypadku potwierdzenia
słuszności założenia o a d d y t y w n o ś c i w p ł y w u
p o d s t a w n i k ó w .
Przyjmując słuszność tego założenia możemy zbudować
matematyczny model analizowanej zależności:

⋅

∑

gdzie:

i - numer związku

j - numer podstawnikopozycji

Ai - aktywność i-tego związku

aj - wkład podstawnikopozycji do aktywności

Xij - obecność podstawnikopozycji j w związku i

Wyjaśnienia wymaga określenie

podstawnikopozycja.

Ponieważ ten sam podstawnik umieszczony w różnych
pozycjach może wywierać różny wpływ na aktywność, więc
należy określić niezależnie wpływ danego podstawnika w
każdej z pozycji w której może występować. Takie połączenie
podstawnika z pozycją w strukturze bazowej w której
występuje nazywamy właśnie podstawnikopozycją.

W przypadku analizowanych wcześniej pochodnych

akrydyny możemy mieć np. sytuację przedstawioną w
Tab.VIII.3

Tab.VIII.3: Przykładowy zestaw podstawników jakie wystąpić mogą w pochodnych akrydyny (Rys.8.3) i odpowiadające im
podstawnikopozycje.
pozycja podstawnik

pozycja podstawnik

ł.boczny C2H4NHMe 1

NH2 10

OH 19

ł.boczny C2H4NMe2 2

3 NO2 11

Cl 20

ł.boczny C3H6NHMe 3

OMe

ł.boczny C3H6NMe2 4

3 NH2 13

OH 22

1 NO2 5

NO2 14

Cl 23

1 OMe

4 OMe

7 Me

1 NH2 7

NH2 16

OH 25

2 NO2 8

Cl 17

Cl 26

2 OMe

5 Me

8 Me

8 OH

Mamy więc 28 podstawnikopozycji. Rozstrzygnięcia wymaga
teraz problem liczby związków jakie należy zsyntetyzować,
aby wiarygodnie określić wpływ każdej podstawnikopozycji
na aktywność padanych pochodnych. Oddzielnym problemem
jest taki dobór syntetyzowanych związków, aby przy danej
ich liczbie N otrzymać jak najwięcej, jak najbardziej
wiarygodnej informacji o zależnościach
struktura - aktywność.
Ponieważ model zaproponowany przez Free i
Wilsona jest liniowy ze względu na nieznane wartości aj

można więc go zidentyfikować (wyznaczyć nieznane wartości
parametrów modelu) przy pomocy metody regresyjnej.
Bezwzględnie minimalna liczba związków niezbędnych dla
jednoznacznego wyznaczenia współczynników modelu
wynosi:

Nmin = Z + 1

gdzie:

Z - liczba podstawnikopozycji.

Model izdentyfikowany w oparciu o taki minimalny zestaw
związków nie posiada wszakże

żadnej zdolności

prognostycznej: odtwarza on d o k ł a d n i e (wraz z
błędami pomiarowymi) aktywności związków na podstawie
których został zidentyfikowany, ale błąd oszacowania
aktywności innego związku jest nieokreślony. Dopiero
zastosowanie liczby związków większej od Nmin pozwala z

jednej strony na wyeliminowanie błędów pomiarowych, a z
drugiej na statystyczne oszacowanie przedziału ufności
prognozy (korytarza błędu). Ponadto w przypadku
n i e z n a c z n y c h odstępstw od wymogu addytywności
wpływu podstawników dostatecznie duża liczba związków

pozwala na zachowanie rozsądnych zdolności
prognostycznych modelu Free-Wilsona.
Na podstawie teorii modeli regresyjnych można przyjąć, że
dostatecznie dobre modele zależności otrzymuje się w sytuacji
gdy Nrzecz jest większe lub równe Nmin + ∆, gdzie wartość ∆

powinna wynosić od 10 do 20. Tak więc w przypadku
analizowanych pochodnych akrydyny dla poprawnego
zastosowania metody Free-Wilsona należy dysponować serią
ok. 50 pochodnych (28 + 1 +20). W pierwszym momencie
może się to wydawać dużo, należy jednak pamiętać że
budujemy model opisujący aktywność ponad 26 tysięcy
związków.
Wiedząc już, ile powinna liczyć seria związków
niezbędna dla wyznaczenia wpływu podstawnikopozycji
należy rozstrzygnąć kwestię które z bardzo licznego zestawu
możliwych pochodnych powinny zostać użyte do identyfikacji
modelu. Nie ma tu, bo i nie może być, jednoznacznego
algorytmu doboru związków. Istnieje za to kilka reguł którym
powinien podlegać zbiór pochodnych aby tworzony model
miał dobre właściwości prognostyczne. I tak:

∗

każda podstawnikopozycja powinna wystąpić

conajmniej w dwóch związkach. Jeszcze korzystniejsze jest
gdy występuje w trzech lub czterech związkach. Zaczyna
wtedy działać statystyczne uśrednianie przypadkowych
błędów wyznaczania aktywności i model nabiera zdolności
prognostycznych.

∗

należy unikać związków podstawionych tylko w

jednej pozycji. Zbyt duża liczba takich związków utrudnia
spełnienie poprzedniej reguły. Jest to wymóg sprzeczny z
tendencją obowiązującą w badaniach SAR w których dąży się

Część IV: Klasyczne metody QSAR

do indywidualnego określenia wpływu każdego elementu
struktury.

∗

krotność występowania poszczególnych

podstawnikopozycji powinna być podobna. Przedział ufności
wpływu podstawnikopozycji zależy m.in. od krotności jej
występowania. Duże zróżnicowanie krotności
podstawnikopozycji powoduje, że niektóre z wpływów będą
wyznaczone z błędem dużo większym niż inne. Ponieważ
zwykle z góry nie wiadomo która podstawnikopozycja jest
istotna dla aktywności nie zachowanie tej reguły grozi
powstaniem sytuacji gdy wpływ ważnej podstawnikopozycji
określony zostanie z niedostatecznę precyzją.

∗

należy unikać korelacji podstawnikopozycji, tzn.

nadmiernie częstego występowania pewnej kombinacji

podstawnikopozycji. Z numerycznego punktu widzenia
oznacza to, że kolumny macierzy danych powinny być
możliwie ortogonalne (niezależne od siebie). Jeśli to tylko
możliwe podstawniki powinny być dobierane losowo.
Reguły te odbiegają na tyle istotnie od tradycyjnego
zestawu związków projektowanych dla badań SAR, że zwykle
dla prawidłowego zastosowania metody Free-Wilsona należy
przewidzieć jej zastosowanie już na etapie projektowania serii
związków (przed rozpoczęciem syntez). Przykładowy
fragment tablicy podstawnikopozycji dla omawianych
pochodnych akrydyny przedstawia Tab.VIII.4:

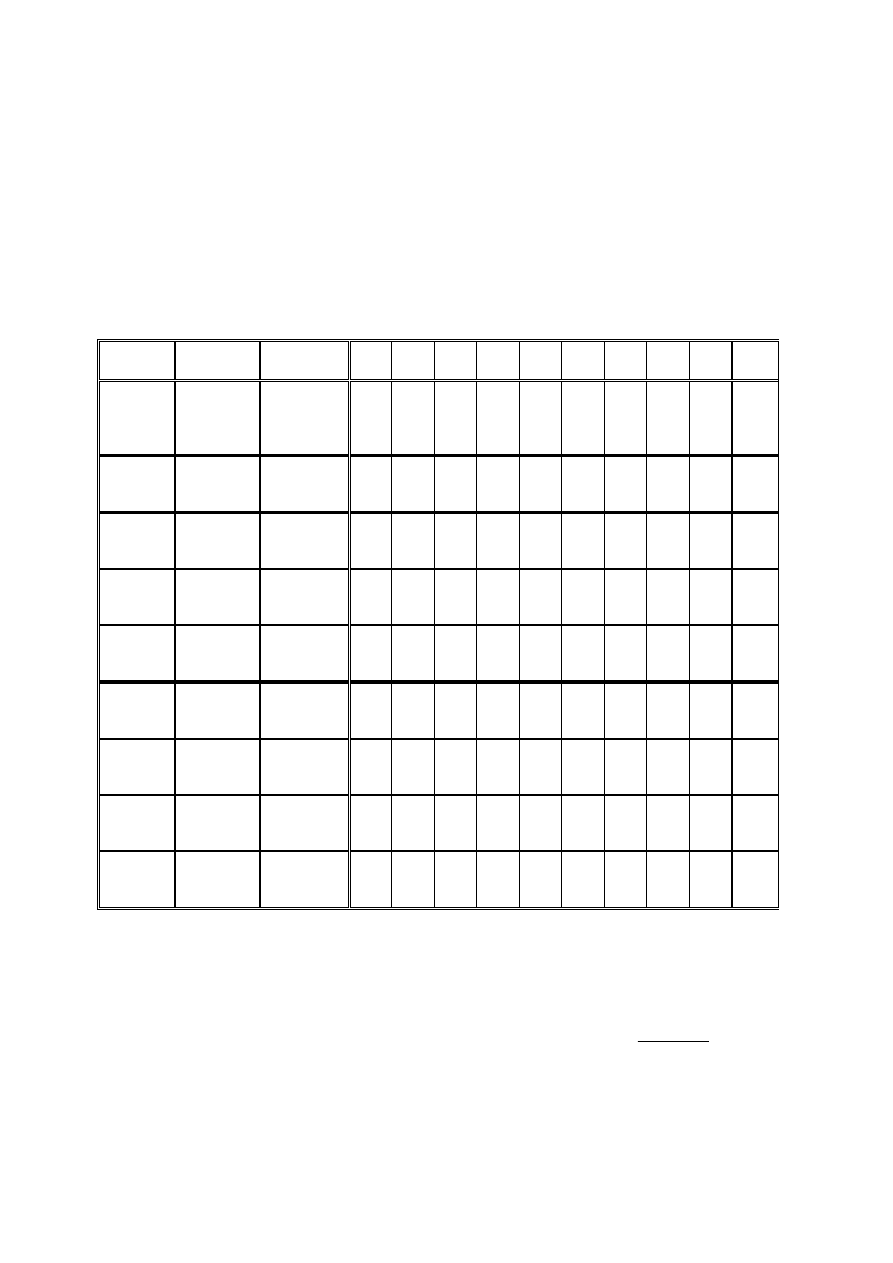
Tab.VIII.4: Fragment tablicy podstawnikopozycji dla zestawu pochodnych akrydyny

Pozycja Podstaw-

nikopoz.

Podstaw-nik

Z1 Z2 Z3 Z4 Z5 Z6 Z7 Z8 Z9 Z10

C2H4NHMe 1 1

łańcuch 2

C2H4NMe2 1 1 1

boczny 3

C3H6NHMe 1 1 1

C3H6NMe2 1 1

NO2

6 OMe

NH2

NO2

9 OMe

NH2

NO2

12 OMe

NH2

NO2

15 OMe

NH2

17 Cl

18 Me

19 OH

20 Cl

21 Me

22 OH

23 Cl

24 Me

26 Cl

27 Me

Należy zwrócić uwagę, że nie może wystąpić
sytuacja gdy w jednym związku występuje więcej niż jedna
podstawnikopozycja dla tej samej pozycji. Ponadto, w
omawianym przykładzie przyjęto założenie, że w każdym z
pierścieni (pozycje 1

÷4 i 5÷8) może w danym związku

wystąpić tylko jeden podstawnik.

Uzyskanie statystycznie istotnego rozwiązania

równania regresji jest jedynie pierwszym etapem metody
Free-Wilsona. Należy teraz sprawdzić, czy w tym konkretnym
przykładzie uzyskany model spełnia założenie o
addytywności wpływu podstawników. Z punktu widzenia
statystyki problem sprowadza się do weryfikacji hipotezy o
adekwatności modelu. Jeśli model jest adekwatny to wariancja
resztowa modelu nie powinna być większa od wariancji

oznaczeń aktywności. W przypadku nieaddytywnego wpływu
podstawników wariancja resztowa modelu zakładającego
addytywność będzie istotnie większa niż wariancja oznaczeń.
Hipotezę o adekwatności modelu testujemy testem

χ2:

(

)

2
e

yˆ

−

∑

gdzie:

- wariancja oznaczeń aktywności.

2
e

Sumę kwadratów różnic można wygodnie obliczyć ze wzoru:

(

)

(

)

yˆ

−

⋅

−

∑

gdzie:

s - odchylenie standardowe równania regresji

N - liczba związków

Część IV: Klasyczne metody QSAR

Z - liczba podstawnikopozycji.

Hipotezę o adekwatności modelu, czyli o addytywności
wpływu podstawników, odrzucamy jeśli:

−

≥

obliczona wartość statystyki

χ2 nie jest mniejsza od wartości

krytycznej znalezionej w tablicach dla poziomu istotności

α i

N-Z-1 stopni swobody. W przeciwnym przypadku nie ma
podstaw do odrzucenia testowanej hipotezy.
Jeśli potwierdzone zostanie założenie o
addytywności wpływu podstawników, to uzyskany model
regresyjny stanowi wiarygodne narzędzie do przewidywania
aktywności innych pochodnych. Szybkim sposobem
wyszukania pochodnej o przypuszczalnie najwyższej
aktywności jest przegłąd wartości wpływów
podstawnikopozycji. Należy przy tym pamiętać, że dla każdej
pozycji wybieramy podstawnik o największym wpływie.
Pozwala to zaproponować syntezę przypuszczalnie bardzo
aktywnego związku. Ponadto dla tego związku możemy
wyznaczyć na podstawie równania regresji jego
przypuszczalną aktywność.

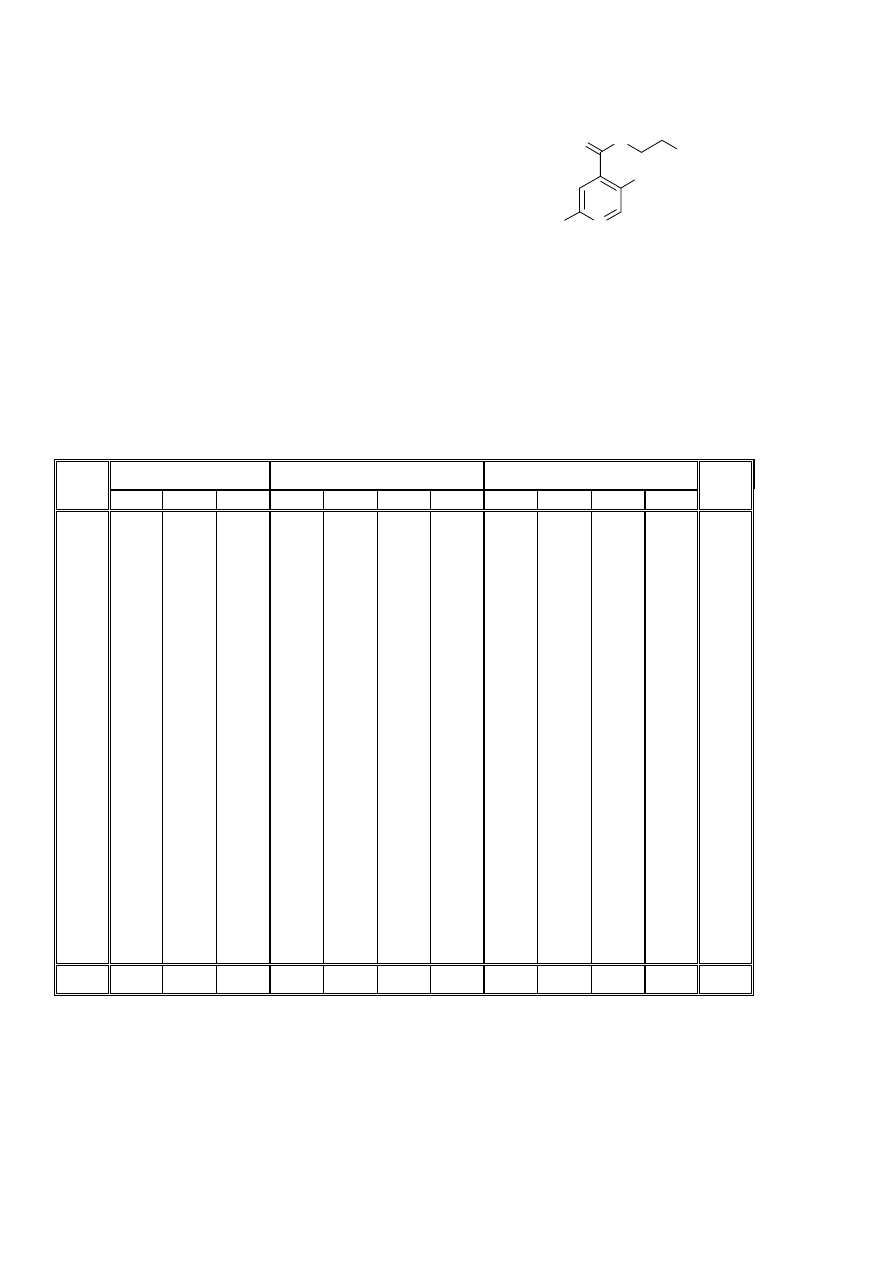
Przykład 8.2: Zastosowanie metody Free-Wilsona: dane
symulowane, przypadek addytywny.

Jako pierwszy rozważymy symulowany przykład

addytywnego wpływu podstawników w pochodnych kwasu
4-pirydylokarboksylowego (rysunek obok). Modyfikacje
chemiczne dotyczą terminalnego podstawnika w łańcuchu
amidu (X) oraz w pozycjach 2 (R2) i 5 (R5) pierścienia

pirydynowego. Obecna w łańcuchu amidu grupa hydroksylowa
może występować w formie wolnej (X = OH), jako eter metylowy
(X = OMe) lub ester acetylowy (X = OAc). W pozycji 2
występować może chlor, grupa metylowa, aminowa lub nitrowa,
a w pozycji 5 chlor, grupa metylowa, aminowa lub
hydroksylowa. Tak więc liczba podstawnikopozycji w
analizowanej serii pochodnych wynosi 3 + 4 + 4 = 11.
Zsyntetyzowano 25 pochodnych spełniających omówione
powyżej reguły.

Tab.VIII.5. Tablica podstawnikopozycji i aktywności biologicznej pochodnych kwasu 4-pirydylokarboksylowego (dane symulowane)

Nr X

R5 Akt.

OMe

OAc

Me Cl

NO2 NH2 Me Cl OH NH2 biol.

I 1 1 1

1,86

II 1 1 1

1,55

III 1 1 1

1,00

IV 1 1

0,04

0,99

VI 1

2,07

VII

0,57

VIII

1 1

0,75

1 1 1

1,28

1 1

2,18

1 1 1

2,41

XII

1 1 1

2,36

XIII

1 1 1

3,67

XIV

1 1

1,31

XV 1 1 1

2,18

XVI

1 1

0,23

XVII

0,57

XVIII

1 1 1

0,30

XIX

1 1

1,50

2,65

XXI

1 1

3,56

XXII

1 1

1,33

XXIII

1 1

2,39

XXIV

1,02

XXV

1 1

0,36

krotn.

5 6 5 5 4 6 5 4 4 4 4

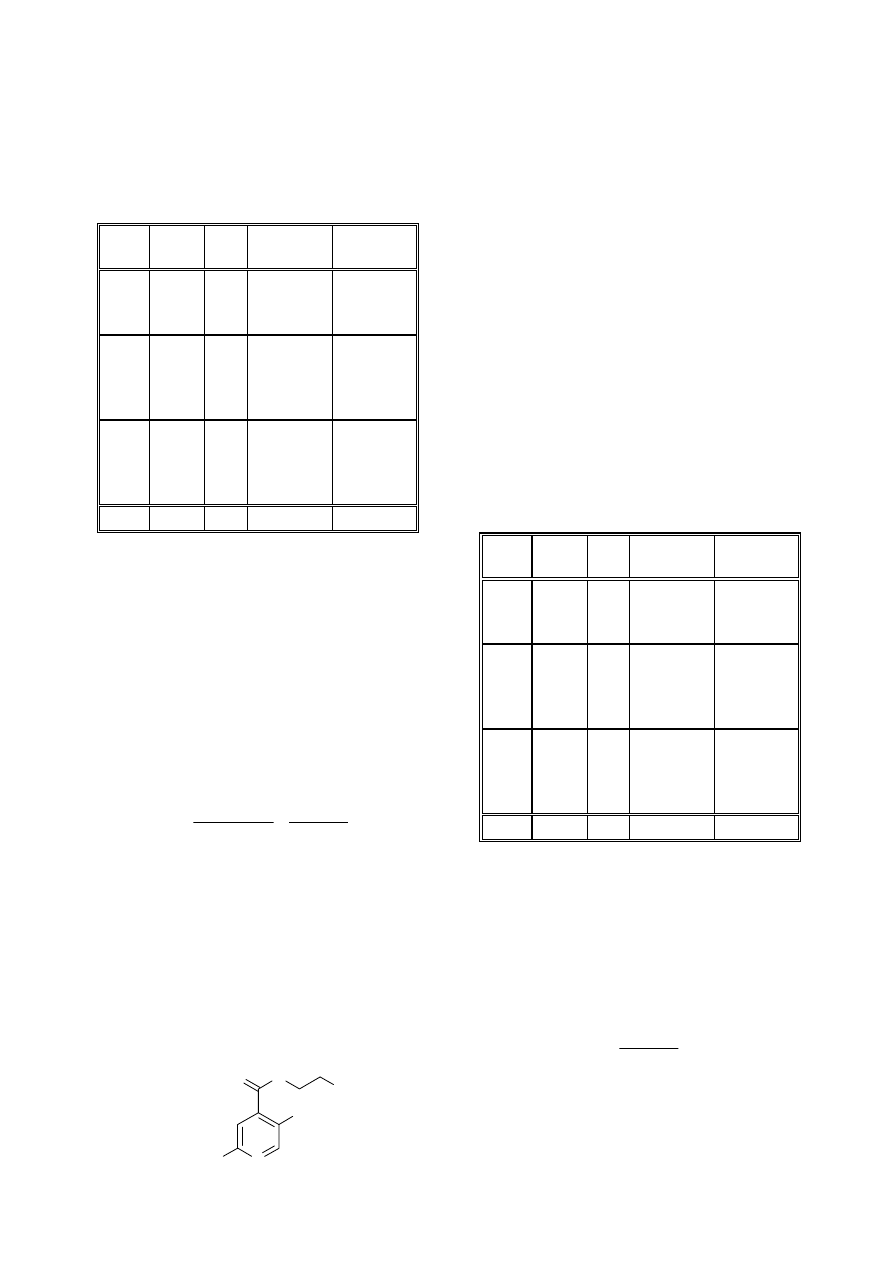
Część IV: Klasyczne metody QSAR

Po zastosowaniu metody Free-Wilsona powstał układ 25
równań z 12 niewiadomymi (11 współczynników przy
podstawnikopozycjach + wyraz wolny).
Rozwiązanie tego układu z wykorzystaniem algorytmu
odrzucania doprowadziło do modelu zawierającego 11 istotnych
parametrów:

Tab.VIII.6. Istotne współczynniki modelu Free-Wilsona dla
danych symulacyjnych (wersja z addytywnościa wpływu
podstawników

Poz. Podst. P.p. Wkład do

aktywności

Promień

przedziału

ufności

X OH 1

0,97

0,12

X OMe 2

0,29

0,12

X OAc 3

-0,51

0,13

Me 4

-0,23

0,13

R2 Cl 5

---

R2 NO2 6

0,91

0,13

R2 NH2 7

-0,56

0,12

R5 Me 8

0,98

0,12

R5 Cl 9 1,52 0,13
R5 OH 10

-0,49

0,14

R5 NH2 11

-0,54

0,14

µo

1,077 0,093

N = 25

Z = 10

s = 0,093

F = 274,1

F0,05;10;14 = 2,60

D = R2 = 0,995

R = 0,998

Uzyskane równanie regresji posiada wysoką istotność jako
całość (duża wartość testu F, współczynnik determinacji bliski
jedności). Dzięki zastosowaniu algorytmu odrzucania z
końcowego równaniu usunięty został człon opisujący wkład
wnoszony do aktywności przez atom chloru w pozycji R2.

Oznacza to, że z prawdopodobieństwem conajmnie 95% jego
wkład do aktywności nie jest istotny. Wszystkie pozostałe
człony mają istotny udział w aktywności badanej serii związków.
Należy teraz określić, czy uzyskany model adekwatnie opisuje
zmienność aktywności biologicznej w badanej serii. Potrzebna
jest do tego znajomość odchylenia standardowego pomiarów
aktywności biologicznej. Informacja taka powinna być dostępna
w pracowni wykonującej oznaczenia aktywności. W naszym
przykładzie przyjmiemy wartość tego odchylenia jako równą

σe

= 0,1 j.a. Możemy teraz obliczyć wartość statystyki

χ2:

(

)

093

2
e

⋅

−

Krytyczna wartość

χ0,05;14 = 23,69. Ponieważ wartość

krytyczna jest większa od obliczonej więc nie ma podstaw do
odrzucenia hipotezy o adekwatności uzyskanego modelu
zależności struktura - aktywność. Oznacza to, że w przypadku
badanej serii związków spełnione jest założenie o adekwatności
wpływu podstawników. Można więc uznać ten model za
posiadający zdolności prognostyczne i podjąć na jego
podstawie próbę znalezienia pochodnej o przypuszczalnie
najwyższej aktywności.
Należy w tym celu spośród podstawnikopozycji dotyczących
każdej z pozycji wybrać podstawnik posiadający największy
wkład do aktywności. W przypadku analizowanej serii będą to:
w

łańcuchu bocznym

⇒ OH z wkładem 0,97±0,12

w pozycji 2

⇒ NO2 z wkładem 0,91±0,13

w pozycji 5

⇒ Cl z wkładem 1,52±0,13

Tak więc można założyć, że najaktywniejszym związkiem
będzie pochodna o budowie przedstawionej obok. Jej
aktywność oszacować można na równą:

A = 1,077 + 0,97 + 0,91 + 1,52 = 4,47

±0,16

Należy pamiętać, że zaproponowana pochodna jest przypusz-
czalnie najaktywniejsza tylko w obrębie d z i e d z i n y
(przedziału ważności) modelu. W przypadku metody
Free-Wilsona dziedzinę ogranicza zestaw podstawnikopozycji.
Tak więc pochodna o przedstawionej powyżej strukturze jest
najaktywniejsza spośród 4

×5×5 = 100 możliwych pochodnych

zawierających w łańcuchu bocznym i pozycjach 2 i 5
wymienione powyżej podstawniki lub atom wodoru. Wadą
metody Free-Wilsona jest niemożliwość przewidzenia
aktywności dla innych podstawników niż uwzględnione w
analizowanym zestawie.
===============================================

Przykład 8.3.: Zastosowanie metody Free-Wilsona:
dane symulowane, przypadek braku addytywności

Dla zobrazowania sytuacji jaka powstaje, gdy

dochodzi do interakcji pomiędzy podstawnikami zmodyfikowano
nieznacznie Przykład 7-I. Modyfikacja polegała na tym, że dla
związków w których w pozycji 2 występowała grupa nitrowa a w
pozycji 5 grupa hydroksylowa lub aminowa (związki III, IX i XII)
zwiększono aktywność o 1 jednostkę.
Tak przygotowany zestaw poddano analizie regresjii z
zastosowaniem algorytmu odrzucania. Otrzymane wyniki
przedstawia Tab. VIII.7.

Tab.VIII.7. Istotne współczynniki modelu Free-Wilsona dla
danych symulacyjnych (wersja bez addytywnego wpływu
podstawników)

Poz. Podst. P.p. Wkład do

aktywności

Promień

przedziału

ufności

X OH 1 0,86 0,47
X OMe 2

---

X OAc 3

---

Me 4

---

R2 Cl 5

---

R2 NO2 6

1,41 0,45

R2 NH2 7

---

R5 Me 8

1,18 0,52

R5 Cl 9

1,58 0,53

R5 OH 10

---

R5 NH2 11

---

µo

0,65 0,27

N = 25

Z = 4

s = 0,44

F = 28,72

F0,05;4;20 = 2,87

D = R2 = 0,852

R = 0,923

Przede wszystkim widać, że w zaistniałej sytuacji wpływ 7
podstawnikopozycji okazał się statystycznie nieistotny.
Pozostały jedynie podstawnikopozycje o najsilniejszych
wkładach do aktywności. Zmniejszyła się też znacznie jakość
dopasowania, choć równanie jako całość pozostaje w dalszym
ciągu statystycznie istotne (F > Fkryt). W ślad za spadkiem

jakości dopasowania wzrosły też znacznie przedziały ufności
parametrów modelu. Sprawą kluczową jest jednak ocena
adekwatności modelu. Obliczona wartość testu

χ2 wynosi:

381

437

⋅

wobec wartości krytycznej

. Ponieważ wartość

obliczona jest większa od wartości krytycznej, więc model
j e s t n i e a d e k w a t n y . Tym samym wykazano, że
istnieje oddziaływanie pomiędzy podstawnikami, a więc ich
wpływ nie jest addytywny.

;

Można zauważyć, że pomimo nieadekwatności
modelu struktura pochodnej o przypuszczalnie najwyższej

Część IV: Klasyczne metody QSAR

aktywności przewidziana jest poprawnie: jest to ta sama
pochodna co w Przykładzie 8.2. Co więcej przewidywana
aktywność tej pochodnej A

4,5

±0,69 jest bardzo bliska

poprzedniej prognozie (4,47

±0,16). Sytuacja taka występuje

wtedy, gdy odstępstwa od addytywności nie dotyczą kombinacji
podstawników o najsilniejszym wkładzie do aktywności.
================================================
=

Od czasu zaproponowania metody przez Free i

Wilsona była ona testowana nie tylko na danych
symulacyjnych (jak powyżej), ale również na licznych
przykładach rzeczywistych. Jeden z takich przykładów
zostanie omówiony poniżej.

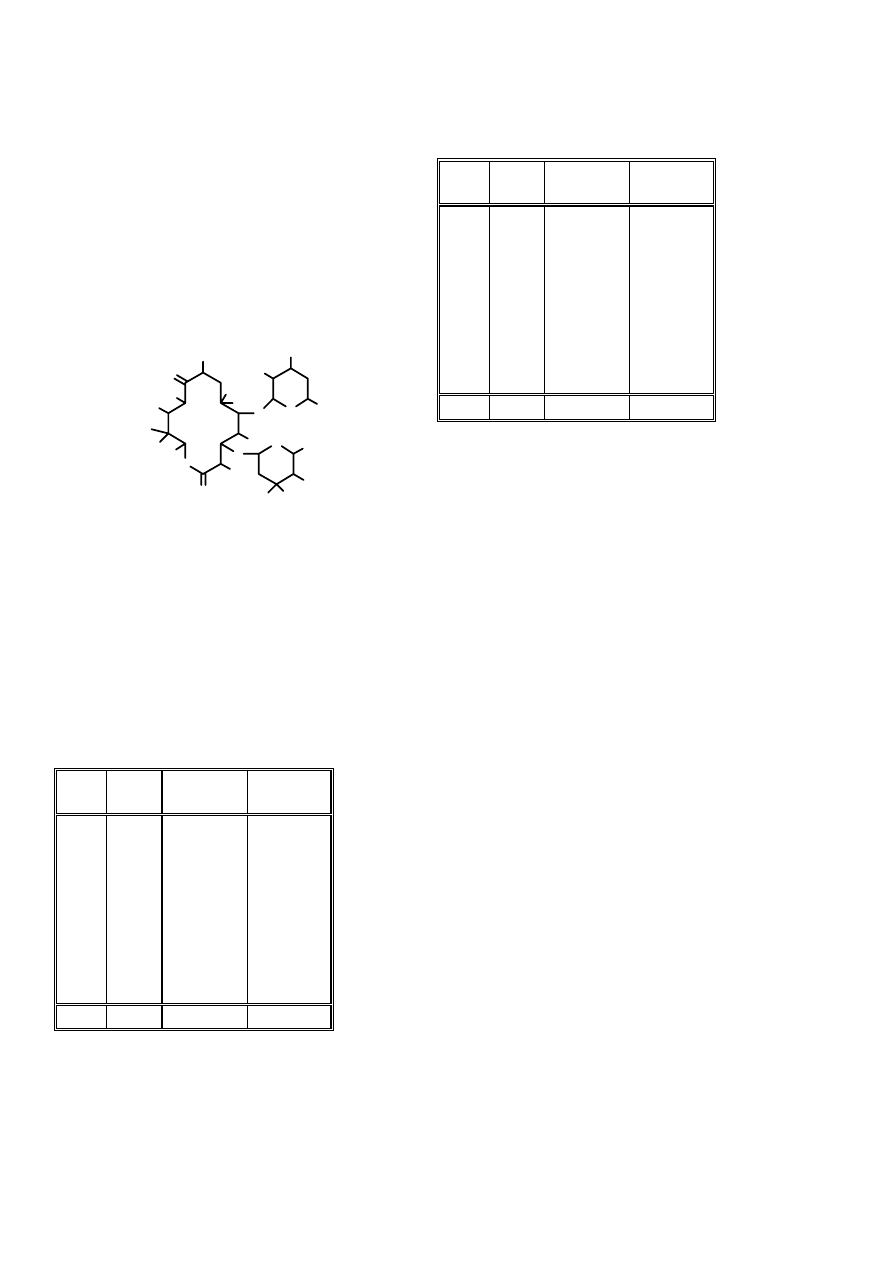
Przykład 8.4.: Zastosowanie metody Free-Wilsona:
dane rzeczywiste.

M e

O H

M e

O M e

M e

N M e

M e

Analizowany przykład ten dotyczy serii pochodnych antybiotyku
przeciwbakteryjnego erytromycyny B. Modyfikacje dotyczyły
wybiórczego acylowania trzech grup hydroksylowych (R1 i R2 w

cukrach i R3 w pierścieniu makrolidowym) oraz obecności lub

braku dodatkowej grupy hydroksylowej w pierścieniu
makrolidowym (R4). Jako pochodne grup hydroksylowych

stosowano:

R1 ⇒ formyl (For) lub acetyl (Ac)

R2 ⇒ For, Ac lub propionyl (Pro)

R3 ⇒ For, Ac lub Pro.

W tej sytuacji minimalna liczba pochodnych wynosi: Nmin = 1

+2 + 2

×3 + 1 = 10. W rzeczywistych modelach stosowano 28

lub 27 pochodnych. Aktywność wyznaczana była w formie
pIC50 na szczepach S.aureus i K.pneumonia z odchyleniem

standardowym

σe = 0,065.

Aktywność w stosunku do S.aureus wyznaczono dla
28 pochodnych. Po zastosowaniu metody Free-Wilsona wraz z
algorytmem odrzucania uzyskano wyniki:

Poz. Podst. Wkład do

aktywności

Promień

przedziału

ufności

R1 For

---

R1 Ac -0,15

0,06

R2 For

-0,28

0,07

R2 Ac -0,65

0,08

R2 Pro

-0,74

0,13

R3 For

---

R3 Ac -0,56

0,09

R3 Pro

-0,67

0,16

OH 0,21 0,07

µo

2,76 0,07

N = 28

Z = 7

s = 0,075

F = 172,45

F0,05;7;20 = 2,87

D = R2 = 0,984

R = 0,992

χ2 = 26,627

χ20,05;20 = 31,41

Uzyskane równanie jest statystycznie istotne,

wyjaśnia ponad 98% zmienności aktywności i opisuje
adekwatny model. Jednakże płynące z niego wnioski nie są
zbyt budujące dla autorów omawianej pracy: z modelu wynika
bowiem, że praktycznie żadna z badanych pochodnych

acylowych nie daje nadziei na uzyskanie pochodnej o wyższej
aktywności. Jedyny dodatni wkład do aktywności wnosi
obecność dodatkowej grupy hydroksylowej (R4).

W przypadku szczepu K. pneumonia stwierdzono

podobne zależności struktura - aktywność:

Poz. Podst. Wkład do

aktywności

Promień

przedziału

ufności

R1 For

---

R1 Ac -0,10 0,05
R2 For

-0,16 0,06

R2 Ac -0,44 0,07
R2 Pro

-0,60 0,10

R3 For

-0,17 0,09

R3 Ac -0,55 0,07
R3 Pro

-0,69 0,13

R4 OH

---

µo

2,94 0,05

N = 27

Z = 7

s = 0,061

F = 153,59

F0,05;7;19 = 2,87

D = R2 = 0,983

R = 0,991

χ2 = 16,73

χ20,05;19 = 30,14

Podstawowa różnica polega na tym, że wpływ dodatkowej
grupy hydroksylowej jest w przypadku K. pneumonia
statystycznie nieistotny. Tym samym w przypadku tego
drobnoustroju żaden z elementów struktury erytromycyny B
analizowanych w omawianej pracy nie wnosi dodatniego
wpływu do aktywności.
================================================

8.2. Metoda Hanscha.

Poważnym ograniczeniem metody Free-Wilsona
jest fakt, że optymalizacja obejmuje tylko te
podstawnikopozycje, które występują w badanych związkach.
Innym ograniczeniem jest wymóg jednoczesnych zmian w
kilku miejscach struktury bazowej. Wad tych pozbawiona jest
inna metoda regresyjna zaproponowana w latach '60 przez
Hanscha i Fujitę. Istotą tej metody jest założenie, że o
aktywności biologicznej decydują

właściwości

fizykochemiczne związków.
Fakt ten znany był od dziesiątków lat. Istniały jednak dwa
podstawowe problemy:

i) ile i jakie właściwości wpływają na aktywność

biologiczną

ii) jak i l o ś c i o w o opisać wpływ tych właściwości.

Zasługą Hanscha i Fujity było zaproponowanie logicznego
zestawu cech fizykochemicznych oraz wykazanie (prace
Hanscha), że cechy te rzeczywiście wpływają na aktywność
biologiczną bardzo różnorodnych grup związków. Autorzy
zaproponowali i uzasadnili w oparciu o podstawowe prawa
biofizyki konieczność zastosowania do opisu zależności
struktura - aktywność 3 parametrów fizykochemicznych:

♦

parametru lipofilowego opisującego zdolność

związku do przenikania przez błony biologiczne i tym samym
charakteryzującego właściwości transportowe i resorpcyjne
związku

♦

parametru elektronowego podstawników lub

cząsteczki jako całości. Parametr taki opisuje rozkład gęstości
elektronowej w cząsteczce, a tym samym reaktywność
związku i jego zdolność do elektrostatycznego oddziaływania
z celem molekularnym.

♦

parametru sterycznego opisującego geometrię

cząsteczki, a w szczególności zawadę przestrzenną w
sąsiedztwie miejsc reaktywnych lub ogólną wielkość i kształt
cząsteczki. Umożliwia to uwzględnienie dopasowania
związku do jego celu komórkowego.

Część IV: Klasyczne metody QSAR

W pierwszych swoich pracach Hansch zastosował

najprostszy z możliwych modeli opisujących zależność
aktywności biologicznej od właściwości fizykochemicznych -
model liniowy:
logA

ao + a1L + a2E + a3S

gdzie:

A - aktywność biologiczna

L - parametr lipofilowy

E - parametr elektronowy

S - parametr steryczny.

Wykazano, że model ten, pomimo swego skrajnego
prymitywizmu, całkiem dobrze (adekwatnie) opisuje wiele
przypadkach obserwowanych zależności
struktura - aktywność. Stwierdzono również, że w znacznej
liczbie przypadków zależność aktywności biologicznej od
lipofilowości nie jest liniowa, lecz charakteryzuje się
obecnością wyraźnego maksimum. W tej sytuacji Hansch
rozszerzył swój model dodając do niego człon kwadratowy.
Powstało w ten sposób tzw. pełne równanie Hanscha o
postaci:

logA = ao + a1L + a2L2 + a3E + a4S

Wartości liczbowe współczynników ai oblicza się metodą

regresji wielorakiej (ang. Multiple Regression Analysis MRA).
Ponieważ równanie Hanscha ma służyć m.in. do celów
prognostycznych (przewidywanie aktywności nowych
pochodnych), więc podstawowym wymogiem jest
wiarygodność uzyskanych wartości współczynników. Jednym
z podstawowych wielkości określających tą wiarygodność jest
liczba związków w badanej serii. Z rozważań statystycznych
wynika, że powinno ich być conajmniej po 4

÷ 5 na każdy

parametr. W przypadku pełnego równania Hanscha oznacza to
potrzebę użycia 5

× 4 = 20 związków.

Dla danej serii związków należy przede wszystkim określić
czy wszystkie człony równania mają statystycznie istotny
wpływ na aktywność. Dokonuje się tego poprzez ocenę
istotności wsółczynników równania. Ostateczne równanie
powinno być:

∗

istotne jako całość: test F Snedecora

∗

posiadać tylko istotne współczynniki: dla każdego

współczynnika test t Studenta

∗

być adekwatne: test

χ2.

W metodzie Hanscha kluczową rolę odgrywa

poprawny dobór właściwości fizykochemicznych
korelowanych z aktywnością biologiczną. W klasycznych
pracach Hanscha jako parametr lipofilowy wykorzystywany
był log(P), czyli współczynnik podziału w układzie
n-oktanol : woda. Jako parametr elektronowy podstawników
Hansch zastosował stałe Hammetta

σ, a jako parametr

steryczny podstawników stałe Tafta Es. Inni autorzy

wykorzystali inne właściwości fizykochemiczne do wyrażenia
trzech podstawowych zdaniem Hanscha parametrów:
lipofilowego, elektronowego i sterycznego. Poniżej omówione
zostaną

właściwości fizykochemiczne najczęściej

wykorzystywane do określania w/w parametrów.

8.2.1. Parametry lipofilowe.

Jak

już wspomniano, pierwszym parametrem

opisującym właściwości lipofilowe związków był logarytm
współczynnika podziału w układzie n-oktanol : woda (bufor).
Parametr ten jest ciągle używany, gdyż uznawany jest za
najlepszy, bezpośredni miernik lipofilowości. W zespole
Hanscha w trakcie wyznaczania wartości współczynników
podziału stwierdzono dla wielu podstawników, że ich wpływ
na logP jest stały i niezależny zarówno od struktury bazowej
do której ten podstawnik jest przyłączony jak i od obecności
innych podstawników. Wyrażając to samo inaczej, obserwacja
ta sugerowała, że wpływ podstawników na lipofilowość ma
charakter addytywny. Dalsze, szczegółowe prace zespołu
Hanscha doprowadziły do potwierdzenia tej hipotezy i
zaproponowania nowej stałej charakteryzującej podstawnik:

stałej lipofilowości

π. Definiowana jest ona dla danego

podstawnika X jako:

π = logPX - logPH

gdzie: PX - współczynnik podziału związku

podstawionego

PH -współczynnik podziału związku

niepodstawionego
Wartości stałych lipofilowości dla częściej spotykanych
podstawników przedstawia poniższa tabela.

Tab.VIII.8. Wartości stałych lipofilowości

π dla częściej

spotykanych podstawników

Podstawnik

Br 0,86

CHO

-0,65

CH3 0,50

CH=NOH

-0,38

CH2 0,50

COCH3 -0,55

CF3 0.88

CONH2 -1,49

etyl 1,02

COOCH3 -0,01

propyl 1,55

COOCH2CH3 0,51

i-propyl 1,53

CH2COOH -0,72

CH2OH -1,03

CH2CONH2 -1,68

CH2NH2 -1,04

CH2COOCH3 -0,69

CCH 0,40

4-pirydyl

0,32

CN -0,57

fenyl 1,89

Hansch zaproponował również sposób obliczania logP dla
całych związków bazując na danych dla kilkudziesięciu
związków bazowych, wartościach

π podstawników oraz

poprawkach na wiązania wielokrotne i rozgałęzienia. Np. :
wiązanie podwójne

∆π = -0,30

wiązanie potrójne

∆π = -0,52

rozgałęzienie

∆π = -0,20

CH2 w pierścieniu π = 0,41

-CH=CH-CH=CH-

π = 1,35

System ten posiadał jednak szereg niedogodności. Przede
wszystkim dla uwzględnienia wpływu sąsiedztwa
podstawników wymagał bardzo rozbudowanego systemu
poprawek, co w połączeniu z drugim mankamentem:
niejednoznacznością, czyniło go metodą obarczoną dużą dozą
subiektywizmu. Dwa poniższe przykłady obrazują zakres
niejednoznaczności tego systemu.
Dibenzyl:

φ-CH2-CH2-φ.

Logarytm

współczynnika podziału dla dibenzylu

obliczyć można z co najmniej trzech schematów:
a) 2

×logP(φH) + 2×π(CH2) = 2×2,13 + 2×0,5 = 5,26

b) logP(

φH) + 2×π(CH2) + π(φ) = 2,13 + 2×0,5 + 1,89 = 5,02

c) 2

×π(CH2) + 2×π(φ) = 2×0,5 + 2×1,89 = 4,78

Rzeczywista, zmierzona wartość logP dla dibenzylu wynosi
4,81.
Toluen:

φ-CH3

Również dla tak prostego związku jak toluen, logP
obliczyć można conajmniej 2 sposobami:
a) logP(

φH) + π(CH3) = 2,31 + 0,5 = 2,81

b) logP(CH4) + π(φ) = 0,9 + 1,89 = 2,79

W tym przypadku z obydwu sposobów otrzymujemy bardzo
zbliżone wartości logP.
Szczegółowa analiza tego typu niejednoznaczności
oraz szczególnie dużych różnic pomiędzy wartościami logP
obliczonych w/g różnych sposobów skłoniła Nysa i Rekkera
(1973) do zaproponowania innego modelu służącego do
oblicznia logP. W modelu tym nie wyróżnia się struktury
bazowej i podstawników, lecz całą strukturę traktuje się jako
złożoną z fragmentów. Każdy z fragmentów wnosi
addytywnie swój wkład do końcowej wartości logP:

Część IV: Klasyczne metody QSAR

∑

⋅

log

gdzie: fi - stała hydrofobowa fragmentu i

ai - liczba określająca ile razy fragment i występuje

w cząsteczce
n

łączna liczba fragmentów w cząsteczce.

Zgodnie z tym modelem logP dibenzylu oblicza się ze wzoru
(Tab.VIII.9):
logP(

φ-CH2-CH2-φ) = 2×f() + 2×f() = 2×1,896

+ 2

×0,527 = 4,85

Tabela VIII.9. Stałe hydrofobowe wyznaczone przez Nysa i Rekkera dla typowych składników związków organicznych.

Fragment falif.

faromat.

Fragment

faromat i fheterocykl

0,14

C r

0,158

CH 0,236

0,236

Ar 0,297

CH2 0,527

0,527

CHAr 0,344

CH3 0,702

0,702

(N)

-0,98

CH2=CH

0,93

(O)

0,10

CH=C

0,51

(S)

0,44

0,193 0,193

(NH)

-0,60

-0,51

0,425

pirolil

0,59

0,06

0,930

furanyl

1,22

0,24

1,169

tienyl

1,62

0,59

1,456

pirydynyl

0,543

-1,536 -0,458

chinolinyl

1,85

OH -1,440

-0,374

fenyl

(C6H5) 1,896

0CH3

-0,834

0,244

(C6H4) 1,732

-2,133

-1,07

(C6H3) 1,477

NH -1,864

-0,93

naftalenyl 3,17

NH2 -1,380

-0,911

NO2 -1,06

-0,089

COO

-1,003

0,000

COO

-1,281

-0,40

OCH2COOH 1,21

-0,609

CONH2

-1,99

-1,26

=C=0

-1,69

-0,99

-1,13

-0,20

Nys i Rekker obliczyli wartości stałych

hydrofobowych fi stosując metodę regresji krokowej dla

zestawu 154 związków o znanych logP. Obliczono zarówno
stałe hydrofobowe dla typowych fragmentów
kilkuatomowych (grup funkcyjnych, podstawników) jak i dla
pojedynczych atomów, w tym różnego typu atomów węgla w
pierścieniach aromatycznych i heterocyklicznych.
Stwierdzono przy tym, że atomy węgla wspólne dla pierścieni
skondensowanych mają wartość fi ok. dwa razy większą niż

inne aromatyczne atomy węgla. Autorzy oznaczyli je
symbolem C.Ar. Stałe hydrofobowe dla atomów i grup

funkcyjnych występujących w typowych związkach
organicznych zestawiono w Tab.VIII.9.
Poniższe przykłady obrazują sposób obliczania logP
przy pomocy stałych hydrofobowych oraz pozwalają
porównać uzyskane wartości z danymi doświadczalnymi.
n-propylobenzen:

φ-CH2-CH2-CH3

logP = f(

φ) + 2f(CH2) + f(CH3) = 1,896 +2×0,527 +

0,702 = 3,65

wartość doświadczalna : 3,69

eter fenylowo-allilowy:

φ-O-CH2-CH=CH2

logP = f(

φ) + f(-O-)arom + f(CH2) + f(CH=CH2) =

1,896 - 0,458 + 0,527 + 0,93 = 2,90

wartość doświadczalna : 2,94

2,4,6-trichlorofenol
logP = f(C6H3) - f(H)arom + f(OH)arom + 3×f(Cl)arom =

1,896 - 0,193 - 0,374 + 3

×0,93 = 3,70

chloropromazyna

C l

logP = 7

×f(CHAr) + 4×f(C.Ar) + f(CAr) + f(Cl)arom +

f(S)arom + f(NH)het + f(CH2) + 2×f(CH3) +

f(N)alif = 5,38

wartości doświadczalne : 5,16; 5,35 i 5,32

W przypadku związków ulegających dysocjacji w

pH fizjologicznym obliczanie logP bardzo się komplikuje.
Wartość logP formy zjonizowanej jest dużo mniejsza niż dla
formy niezdysocjowanej. Dla związków częściowo
zdysocjowanych w danym pH wprowadzono pojęcie
współczynnika dystrybucji który zastępuje współczynnik
podziału. W przypadku kwasów definiuje się go wzorem:

[ ]

−

gdzie indeks L dotyczy fazy lipidowej, a indeks W fazy
wodnej. Ponieważ istnieją trudności techniczne z
precyzyjnym pomiarem stężeń obu form kwasu w roztworach
wodnych, więc dla celów praktycznych wprowadzono wzory
przybliżone:
dla

kwasu:

(

)

log

−

log

dla

zasady:

(

)

log

−

log

Część IV: Klasyczne metody QSAR

Chromatograficzne metody wyznaczania parametrów
lipofilowych.

Dla niektórych związków bardzo trudno jest

wyznaczyć współczynnik podziału. Dotyczy to np. związków
nietrwałych, zanieczyszczonych lub tworzących stabilne
emulsje. Dla takich przypadków zaproponowano wyznaczać
parametr lipofilowy metodami chromatografii cienko-
warstwowej jako tzw. wartość Rm. Metoda okazała się tak

wygodna, że stosuje się ją również w przypadku związków
pozbawionych w/w niedogodności.
Zaletami metody chromatograficznej są: i) małe zużycie
związku; ii) brak wymogu specjalnej czystości; iii) możliwość
jednoczesnego (na jednej płytce) oznaczania kilku lub nawet
kilkunastu związków.
Stwierdzono,

że pomiędzy stałą Rm, a logarytmem

współczynnika podziału P istnieje zależność liniowa :

Rm = a×logP + b

gdzie stałe a i b zależą od warunków chromatografii, np.
podłoża i składu fazy ruchomej.

Dla wyeliminowania innych niż podział efektów

chromatograficznych (głównie sorpcji na żelu) stosuje się
neutralne nośniki, takie jak metylocelulozę, lub
chromatografię faz odwróconych. Istnieje prosta zależność
pomiędzy wielkością Rm a ruchliwością chromatograficzną

Rf:















−

log

W przypadku związków ulegających dysocjacji dla
zapewnienia stałego pH stosuje się buforowaną fazę ruchomą.

Burzliwy rozwój chromatografii HPLC, w tym

również na fazach odwróconych, spowodował, że ostatnio
głównie ta technika stosowana jest do chromatograficznego
wyznaczania parametrów lipofilowych. Okazało się przy tym,
że wielkością liniowo zależna od współczynnika podziału jest
skorygowany czas retencji, k’. Jest to jednocześnie typowy
parametr wyznaczany w technikach HPLC.
Inne parametry lipofilowe.
Oprócz

omówionych

powyżej, klasycznych metod

wyznaczania właściwości lipofilowych proponowano
zastosować szereg innych wielkości. Spośród nich pewne
zastosowanie znajdują:

∆Rm dla podstawników - wielkość proporcjonalna

do parametru

logS - rozpuszczalność związku w wybranym

rozpuszczalniku, np. wodzie lub chloroformie

[P] - parachora: wielkość addytywna wiążąca

objętość molową cieczy Vc i jej napięcie powierzchniowe σ.

W literaturze od wielu dziesiątków lat istnieją tablice parachor
atomowych i parachor wiązań.

Parametry lipofilowe podzielić można, ze względu

na sposób ich wyznaczania na dwie klasy:

∗

parametry doświadczalne dla których wyznaczenia

należy posiadać próbkę analizowanego związku i wykonać na
niej odpowiednie pomiary

∗

parametry teoretyczne (tablicowe) których wartość

można wyznaczyć dysponując jedynie wzorem związku.
Parametry doświadczalne, wyznaczane dla konkretnych
związków zapewniają bardziej adekwatny opis właściwości
związków. Mają więc istotne znaczenie na etapie
poszukiwania zależności. Wadą tak uzyskanej zależności jest
jednak niemożność projektowania na jej podstawie
konkretnych nowych pochodnych. Możliwe jest jedynie
wskazanie trendów (kierunków) zmian. Wady tej pozbawione
są modele oparte na parametrach obliczanych lub
tablicowych. Po uzyskaniu statystycznie istotnej zależności
można na jej podstawie oszacować aktywność związku
jedynie na podstawie jego wzoru.

8.2.2. Parametry elektronowe.

Przypuszczano od dawna, że rozkład ładunku w

obrębie cząsteczki ma istotny wpływ na jej reaktywność
chemiczną i efekty biologiczne. Brakowało jednak prostego
sposobu opisu zależności pomiędzy rozkładem ładunku a
właściwościami chemicznymi lub biologicznymi.

W roku 1935 Hammett stwierdził, że istnieje

liniowa zależność pomiędzy zmianami energii swobodnej
wywołanej wprowadzeniem podstawnika w pochodnych
kwasu benzoesowego, a ich powinowactwem elektronowym.
Zależność tę dla równowag dysocjacji można wyrazić
wzorem:

⋅

log

gdzie: Ks - stała dysocjacji podstawionego kwasu

benzoesowego

Ko - stała dysocjacji kwasu benzoesowego

σ - stała charakteryzująca podstawnik (stała

Hammetta)

ρ - stała zależna od warunków pomiaru

Stałe Hammetta stosuje się do układów aromatycznych w
których podstawnik jest w pozycji para lub meta do centralnej
grupy reagującej. Stałe te opisują w zasadzie wpływ
indukcyjny podstawnika. Przykładowe wartości stałych
Hammetta dla typowych podstawników przedstawia poniższa
tabela.

Tab.VIII.10. Wartości stałych Hammetta dla typowych podstawników.
Podstawnik pozycja

Podstawnik pozycja

para meta

-O- -1,000

-0,710

Cl 0,228

0,372

-NH2 -0,660

-0,160

-Br

0,232

0,931

-CH3 -0,170

-0,070

-J

0,276

0,352

-OH -0,357

0,000

-NO2 0,778

0,710

-OMe -0,268

0,115

-CF3 0,551

0,415

-F

0,062 0,337

-CN

0,628 0,678

Zasługą Hanscha i Fujity jest zastosowanie stałych
Hammetta jako opisu właściwości elektronowych serii
związków. Trzeba było dużej dozy odwagi intelektualnej aby
zastosować prosty parametr chemiczny dla opisu wpływu
modyfikacji chemicznej na oddziaływanie leku z jego
makromolekularnym celem komórkowym.

Oprócz

stałej Hammetta w metodzie Hanscha

stosowane są liczne inne parametry elektronowe. Niektóre z
nich są tylko modyfikacjami klasycznej stałej Hammetta. Do
takich parametrów należą:

σorto - stała Hammetta dla pozycji orto

σI - stała indukcyjna (alifatyczna)

Część IV: Klasyczne metody QSAR

σ - stała rezonansowa (alifatyczna)

σ* - stała polarności (alifatyczna)

F - aromatyczna stała indukcyjna

R - aromatyczna stała rezonansowa

Istnieją również stałe elektronowe oparte na odmiennych niż
stała Hammetta podstawach fizykochemicznych. Do
najczęściej stosowanych w badaniach QSAR należą:

pKa lub ∆pKa - stała dysocjacji lub jej zmiana w stosunku

do związku odniesienia

⋅

−

- polaryzowalność molowa

ε - stała dielektryczna
M - masa cząsteczkowa
ρ - gęstość
µ - moment dipolowy
δ - przesunięcie chemiczne w NMR
1/

λ - położenie maximum absorpcji w widmach UV/VIS

Rozwój metod obliczeniowych chemii kwantowej
spowodował, że jako parametry elektronowe w badaniach
QSAR zaczęto również stosować wielkości kwantowo-
chemiczne. Do najczęściej używanych parametrów tego typu
należą energie tzw. orbitali granicznych:

HOMO - energia najwyższego obsadzonego orbitalu (ang.
Highest Occupied Molecular Orbital)
LUMO - energia najniższego nieobsadzonego orbitalu
(ang. Lowest Unoccupied Molecular Orbital)

Wartości energii tych orbitali są miarą podatności cząsteczki
jako całości do oddawania (HOMO) lub przyjmowania
(LUMO) elektronów. Oprócz takich globalnych parametrów
elektronowych metody obliczeniowe chemii kwantowej
dostarczają również parametrów opisujących bardziej
"lokalne" właściwości fragmentów cząsteczki. Parametrami
takimi są np. ładunki cząstkowe wybranych atomów lub rzędy
określonych wiązań.
Obliczenia kwantowo-chemiczne pozwalają również na
oszacowanie wartości takich doświadczalnych parametrów
elektronowych jak np. moment dipolowy, energia jonizacji
lub wartość przesunięcia chemicznego w NMR.

Podobnie jak w przypadku parametrów lipofilowych

dysponujemy więc również w przypadku parametrów
elektronowych dwoma typami parametrów:

∗

parametrami doświadczalnymi dla których

wyznaczenia należy posiadać próbkę analizowanego związku
i wykonać na niej odpowiednie pomiary

∗

parametrami teoretycznymi (tablicowymi) których

wartość można wyznaczyć dysponując jedynie
proponowanym wzorem związku.

8.2.3. Parametry steryczne.

Przed opublikowaniem prac Hanscha i Fujity

wydawało się, że opis kształtu cząsteczki nastręczać będzie
szczególnie wiele problemów przy poszukiwaniu zależności
struktura - aktywność. Na szczęście rozwój w latach '50 i na
początku '60 tzw. fizycznej chemii organicznej będący
wynikiem sukcesu koncepcji wpływu podstawników na
właściwości chemiczne całej cząsteczki zapoczątkowany
pracami Hammetta i jego szkoły dostarczył niezbędnych
narzędzi.
Taft

badając wpływ podstawników na szybkość

hydrolizy estrów alkoholi alifatycznych i aromatycznych
kwasów karboksylowych podstawionych w pozycji meta
stwierdził, że oprócz stałej Hammetta, czyli wpływów
elektronowych, na szybkość hydrolizy wpływa również efekt
przestrzenny podstawników i zaproponował zależność:

log

⋅

Wielkość E

nazwana została stałą Tafta i jest szeroko

stosowana dla opisu zawady przestrzennej podstawników
zarówno w badaniu reaktywności chemicznej jak i zależności
struktura chemiczna - aktywność biologiczna.

Ogólna koncepcja wpływu zawady przestrzennej

została szeroko przyjęta i rozbudowana dla innych
szczegółowych przypadków. I tak wprowadzono:

- stałą Tafta dla podstawników w pozycji orto

o
S

- stałą Tafta dla podstawników w pozycji meta

- stałą Hancock'a uwzględniającą hiperkoniu-

gację wodorów

C
S

Stała Tafta i jej analogi znajduje zastosowanie jedynie w
przypadku serii związków będących prostymi, podstawionymi
w tym samym miejscu, pochodnymi tej samej sztywnej
struktury bazowej. Nie nadają się zupełnie do opisu bardziej
zróżnicowanych serii związków lub pochodnych o pewnej
swobodzie konformacyjnej. Dlatego opracowano całą gammę
parametrów opisujących wielkość i ogólny kształt cząsteczki:

∗

V - objętość molową

∗

- promień Van der Waalsa podstawnika

* V

- objętość cząsteczki z uwzględnieniem promieni

Van der Waalsa

∗

- odległość pomiędzy wybranymi atomami i i j

∗

parametry STERIMOL - grupa 5 parametrów
opisujących kształt cząsteczek. Parametry te nadają się
szczególnie dla sztywnych cząsteczek

∗

parametry Kiera: molecular connectivity

χ i molekularne

indeksy kształtu

κ - na bazie grafu reprezentującego

pozbawiony atomów wodoru szkielet cząsteczki można
otrzymać szereg parametrów opisujących topologię
cząsteczki

Dla poprawnego wyznaczenia wartości parametrów tego typu,
za wyjątkiem parametrów Kiera, potrzebna jest znajomość
rzeczywistego kształtu cząsteczek. Bardzo często
wykorzystuje się w tym celu metody modelowania
molekularnego w tym również półempiryczne metody chemii
kwantowej. Innym źródłem informacji o kształcie cząsteczki
mogą być struktury otrzymane metodami analizy dyfrakcyjnej
monokryształów.
Ponieważ kształt cząsteczki ma wiele aspektów i nie
wydaje się możliwe pełne jego określenie przy pomocy
pojedynczej wielkości liczbowej zaproponowano jego opis
przy pomocy rodziny parametrów z których każdy opisuje
inny jego aspekt. założeniu to legło u podstaw parametrów
typu STERIMOL oraz indeksów Kiera.

Parametry STERIMOL.

Bardzo prostym, ale skutecznym opisem kształtu sztywnych
cząsteczek są tzw. parametry STERIMOL. Opisują one 5
maksymalnych wymiarów cząsteczki. Przed przystąpieniem
do ich wyznaczania należy przyjąć określoną orientację
każdej z cząsteczek. Zwykle w tym celu wybiera się jeden z
atomów każdej z cząsteczek stanowiących badaną serię jako
tzw. atom bazowy i lokuje się go w początku układu
współrzędnych. Z kolei definiuje się dwa wiązania w których
ten atom uczestniczy i określa się ich orientację w stosunku
do układu współrzędnych.

C *

R N H

N O

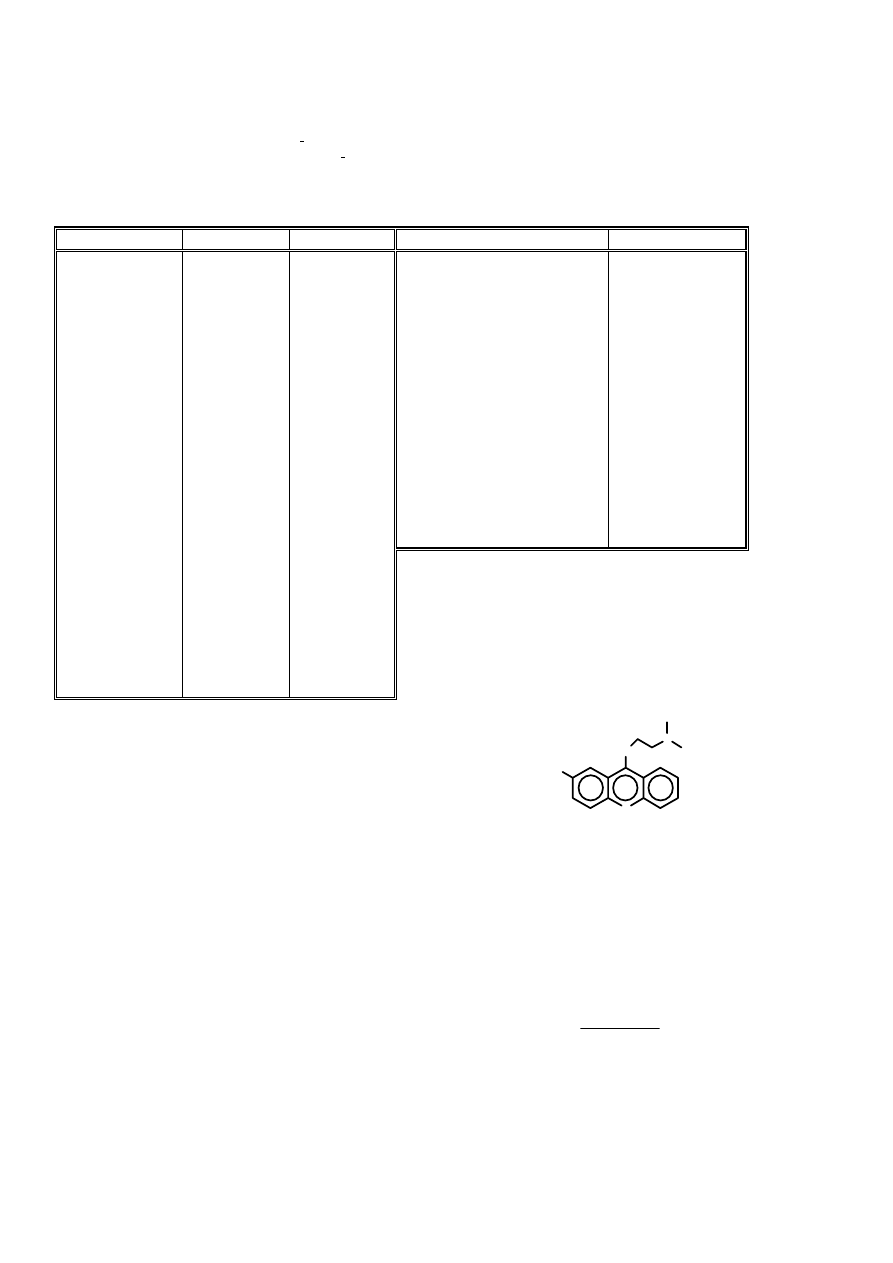
Prześledźmy to podejście na przykładzie pochodnych
1-nitro-9-aminoakrydyny. Jako atom bazowy wybierzmy
węgiel w pozycji 9 (na rysunku powyżej oznaczony
gwiazdką). Przyjmijmy ponadto, że:

Część IV: Klasyczne metody QSAR

wiązanie C9-N9 pokrywa się z osią Ox

układ pierścieni znajduje się w płaszczyźnie Oxy

pierścień z grupą nitrową leży z zakresie

dodatnich

współrzędnych y

Dla tak zorientowanej cząsteczki określa się teraz 5
charakterystycznych wymiarów:

- długość W, czyli maksymalny rozmiar wzdłuż osi Ox
- wysokość U, czyli maksymalny wymiar na dodatniej
części osi Oy
- głębokość D, czyli maksymalny wymiar na ujemnej
części osi Oy
- szerokość w lewo L, czyli maksymalny wymiar ujemny

na osi Oz

- szerokość w prawo R, czyli maksymalny wymiar
dodatni

na osi Oz.

Rys.8.3. przedstawia powyższe parametry dla cząsteczki
1-nitro-9-metyloaminoakrydyny.

Rys.8.3: Sposób definiowania parametrów STERIMOL na
przykładzie pochodnej 1-nitro-9-metyloaminoakrydyny. Kolorem
fioletowym zaznaczono atomy wykorzystywane przy orientacji
cząsteczki.

Parametry Kiera.

Innym bardzo popularnym podejściem do opisu

kształtu cząsteczek jest zastosowanie teorii grafów. W
odróżnieniu od parametrów STERIMOL nie jest przy tym
potrzebna znajomość rzeczywistego, trójwymiarowego
kształtu cząsteczki: wystarcza wzór strukturalny. W ujęciu
tym wzór cząsteczki traktowany jest jako graf: zespół węzłów
połączonych wiązadłami. Do najpopularniejszych parametrów
tego typu należą zaproponowane przez Kiera i Halla indeksy

(molecular connectivity) oraz zaproponowane przez Kiera

molekularne indeksy kształtu

. Parametry te opisują w

formie rodziny indeksów różne aspekty kształtu podstawnika
lub całej cząsteczki bazując na wzorze strukturalnym
pozbawionym atomów wodoru.
Rodzinę indeksów

, gdzie m = 0, 1, 2 i 3,

obliczyć można przypisując każdemu węzłowi grafu (atomowi
niewodorowemu) wielkość

określającą liczbę innych

węzłów bezpośrednio z nim związanych. Poszczególne
indeksy molecular connectivity obliczamy w/g poniższych
wzorów, przy czym:

indeks

jest sumą udziałów poszczególnych

atomów

[7.1.]

∑

indeks

jest sumą udziałów

r wiązań

[7.2.]

( )

∑

⋅

indeks

jest sumą udziałów

s trójek atomów

[7.3.]

(

)

∑

⋅

istnieją dwa indeksy

dla liniowego

ułożenia czwórki atomów i

dla ułożenia gwiaździstego

[7.4a.]

(

)

∑

⋅

[7.4b.]

(

)

∑

⋅

Obliczenia indeksów molecular connectivity dla 5 izomerów
heksamu przedstawia poniższy przykład.

Przykład 8.5. Indeksy molecular connectivity dla
izomerów heksanu.

Rozpocznijmy od wypisania struktur i wartości

dla

wszystkich 5 izomerów heksanu:

heksan

2-metylopentan

3-metylopentan

2,3-dimetylobutan

2,2-dimetylobutan

Teraz dla każdego z nich obliczmy indeksy Kiera.

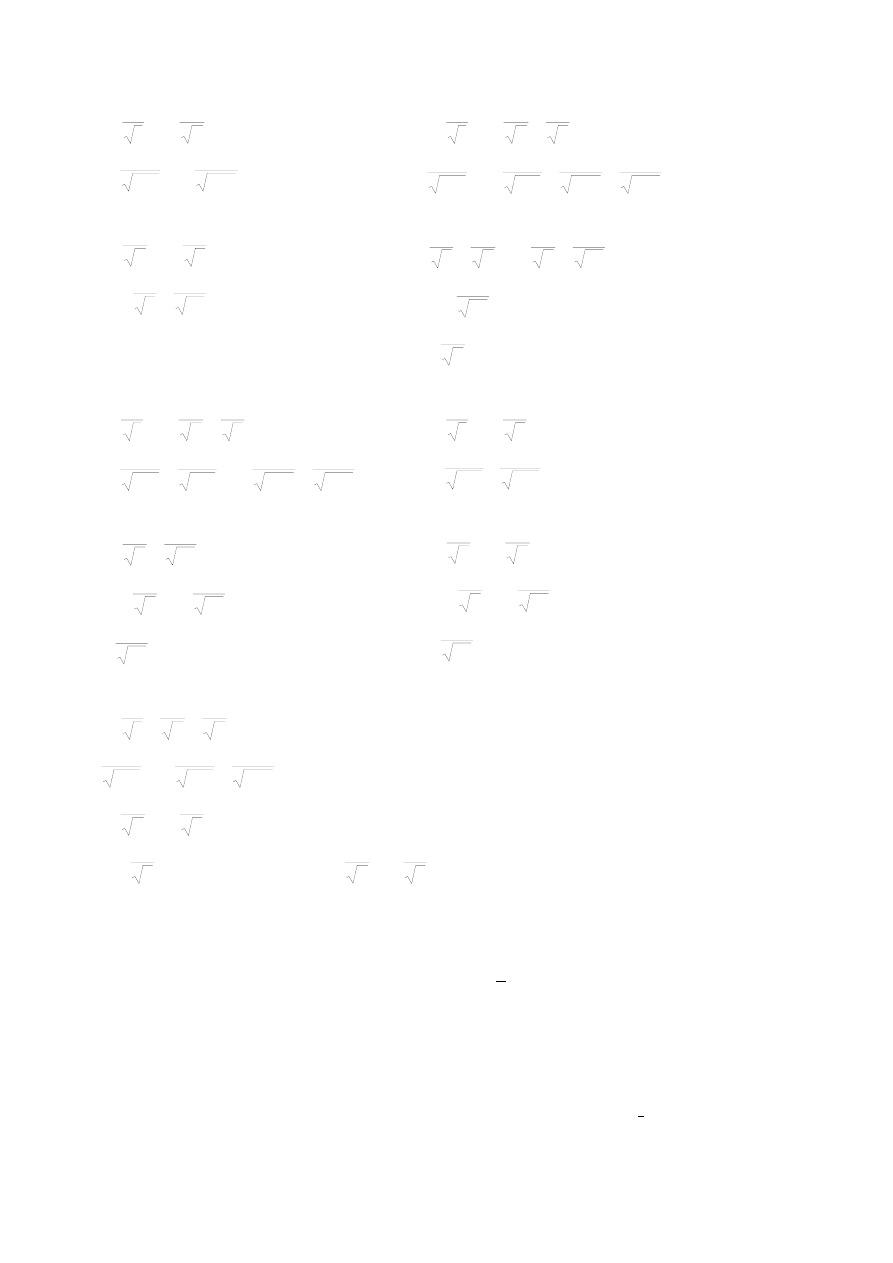
Część IV: Klasyczne metody QSAR

Heksan.

828

≈

⋅

914

≈

⋅

707

≈

⋅

957

≈

⋅

2-Metylopentan.

992

≈

⋅

770

≈

⋅

183

≈

⋅

866

≈

⋅

408

≈

3-Metylopentan.

992

≈

⋅

808

≈

⋅

922

≈

⋅

394

≈

⋅

289

≈

2,3-Dimetylobutan.

155

≈

⋅

643

≈

⋅

488

≈

⋅

394

≈

⋅

289

≈

2,2-Dimetylobutan.

207

≈

⋅

561

≈

⋅

914

≈

⋅

061

≈

⋅

561

≈

⋅

Dla

cząsteczek lub podstawników zawierających

atomy inne niż węgiel można zastosować dwa podejścia. Po
pierwsze można przyjąć, że ogólny kształt cząsteczki nie
zależy w istotny sposób od rodzaju atomów. Przy takim
założeniu np. indeksy dla alkoholu t-butylowego są takie same
jak dla 2,3-dimetylopropanu. Wykazano, że założenie to
można bezpiecznie stosować gdy cząsteczka zawiera oprócz
węgla atomy tlenu i azotu. W przypadku gdy w skład
cząsteczki wchodzą atomy których wielkość wyraŸnie
odbiega od wielkości atomów węgla (fluor, siarka, chlor i.t.p.)
poprawniejsze jest drugie podejście. Polega ono na
modyfikacji wartości

dla atomów odpowiednio do ich

wielkości.

Molekularne indeksy kształtu

bazują na trochę

innych podstawach (L.B.KIER, Quat.Struct.-Act.Relat. 4,109-

116(1985); L.B.KIER, Quant.Struct.-Act.Relat. 5,1-7(1986);
L.B.KIER, Quat.Struct.-Act.Relat. 6,8-12(1987)). W/g Kiera
są one miarą informacji niesionej przez fragmenty struktury o
długości

m atomów.

Indeks rzędu 0 dotyczy informacji zawartej w poszczególnych
atomach i obliczany jest w/g wzoru:
[7.5.]

⋅

gdzie:

A - liczba niewodorowych atomów cząsteczki

i - zawartość informatyczna obliczana zgodnie z

równaniem Shannona jako

( )

∑

−

log

gdzie

sumowanie biegnie po wszystkich k rodzajach rozróżnialnych
atomów, a pk jest prawdopodobieństwem znalezienia atomu

danego rodzaju.
Indeks rzędu 1 dotyczy wiązań i obliczany jest ze wzoru:

Część IV: Klasyczne metody QSAR

[7.6.]

(

)

( )

−

gdzie:

jest liczbą wiązań w cząsteczce pozbawionej

atomów wodoru.

Indeks rzędu 2 dotyczy trójek bezpośrednio z sobą
związanych atomów i obliczany jest ze wzoru:
[7.7.]

(

)(

)

( )

−

gdzie:

jest liczbą trójek atomów.

Indeks rzędu 3 dotyczy czwórek związanych z sobą atomów i
obliczany jest w/g jednego z poniższych wzorów:

[7.8.]

(

)(

)

( )

(

)(

)

( )













−

parzystego

dla

ego

nieparzyst

dla

Poniższy przykład zawiera wyniki obliczeń molekularnych
indeksów kształtu dla izomerów heksanu.

Przykład 8.6. Molekularne indeksy kształtu dla
izomerów heksanu

heksan

2-metylopentan

3-metylopentan

2,3-dimetylobutan

2,2-dimetylobutan

Rozpocznijmy od wyznaczenia zawartości informacji

dla wszystkich 5 izomerów heksanu:

heksan:

( )

4771

log

≈

⋅

2-metylopentan:

( )

6778

log

≈

⋅

3-metylopentan;

( )

5775

log

≈

⋅

2,3-dimetylobutan:

( )

2764

log

≈

2,2-dimetylobutan:

( )

5396

log

≈

⋅

Należy jeszcze ustalić liczbę par, trójek i czwórek atomów. Jest to bardzo podobne do postępowania omówionego w Przykł.7-V.
Możemy teraz obliczyć wartości poszczególnych indeksów:

heksan

2-metylopentan

3-metylopentan

2,3-dimetylobutan

2,2-dimetylobutan

i = 0,4771

2,863

= 0,6778
= 4,067

= 0,5775
= 3,465

= 0,2764
= 1,659

= 0,5396
= 3,238

= 5

κ =

= 5
= 6

= 4

2,813

= 5
= 1,800

= 6
= 1,250

= 7
= 0,918

= 3

5,333

= 3
= 5,333

= 4
= 3

= 3
= 5,333

Cechą charakterystyczną molekularnych indeksów kształtu,
odróżniającą je korzystnie od indeksów molecular
connectivity, jest możliwość przypisania każdemu z nich
interpretacji geometrycznej. I tak:

- wskaźnik symetrii. Jego wartość spada ze wzrostem

symetrii cząsteczki.

- wskaźnik wielkości. Wszystkie niecykliczne

cząsteczki o tej samej liczbie atomów niewodorowych
mają taką samą wartość

równą liczbie atomów A.

Tym samym jest to miara "wielkości" cząsteczki.
Obecność w cząsteczce fragmentów cyklicznych
obniża wartość indeksu i to tym bardziej im więcej
jest pierścieni.

- wskaźnik linearności. Wartości tego indeksu zależą od

stopnia rozgałęzienia cząsteczki i jej sferyczności.
Przyjmuje największe wartości dla struktur liniowych,
nierozgałęzionych.

- wskaźnik centralności rozgałęzienia. Wartości tego

indeksu kodują obecność i lokalizację rozgałęzienia w
strukturze niecyklicznej.

8.2.4. Parametry zero-jedynkowe.

Nie

wszystkie

elementy budowy chemicznej serii

związków daje się łatwo ująć w formę parametrów
lipofilowych, elektronowych lub sterycznych. Dotyczy to w
szczególności sytuacji gdy w obrębie analizowanej serii
znajduje się podgrupa związków wyróżniająca się jakimś
elementem struktury. Można wtedy wprowadzić dodatkowy
parametr przyjmujący wartość 1 gdy element ten jest w
strukturze obecny i 0 przy jego braku. Podejście takie jest w
istocie połączeniem metody Hanscha z koncepcją
Free-Wilsona. Zastosowanie jednego lub więcej parametrów
tego typu pozwala zastosować do opisu cząsteczki typowe
parametry lipofilowe, elektronowe i steryczne bez
konieczności poszukiwania specyficznych parametrów
dostarczających adekwatnego opisu różnych podgrup
występujących w naszej serii związków.

8.2.5. Interpretacja modelu Hanscha.

Uzyskanie adekwatnego opisu zależności

struktura - aktywność przy pomocy równania Hanscha niesie

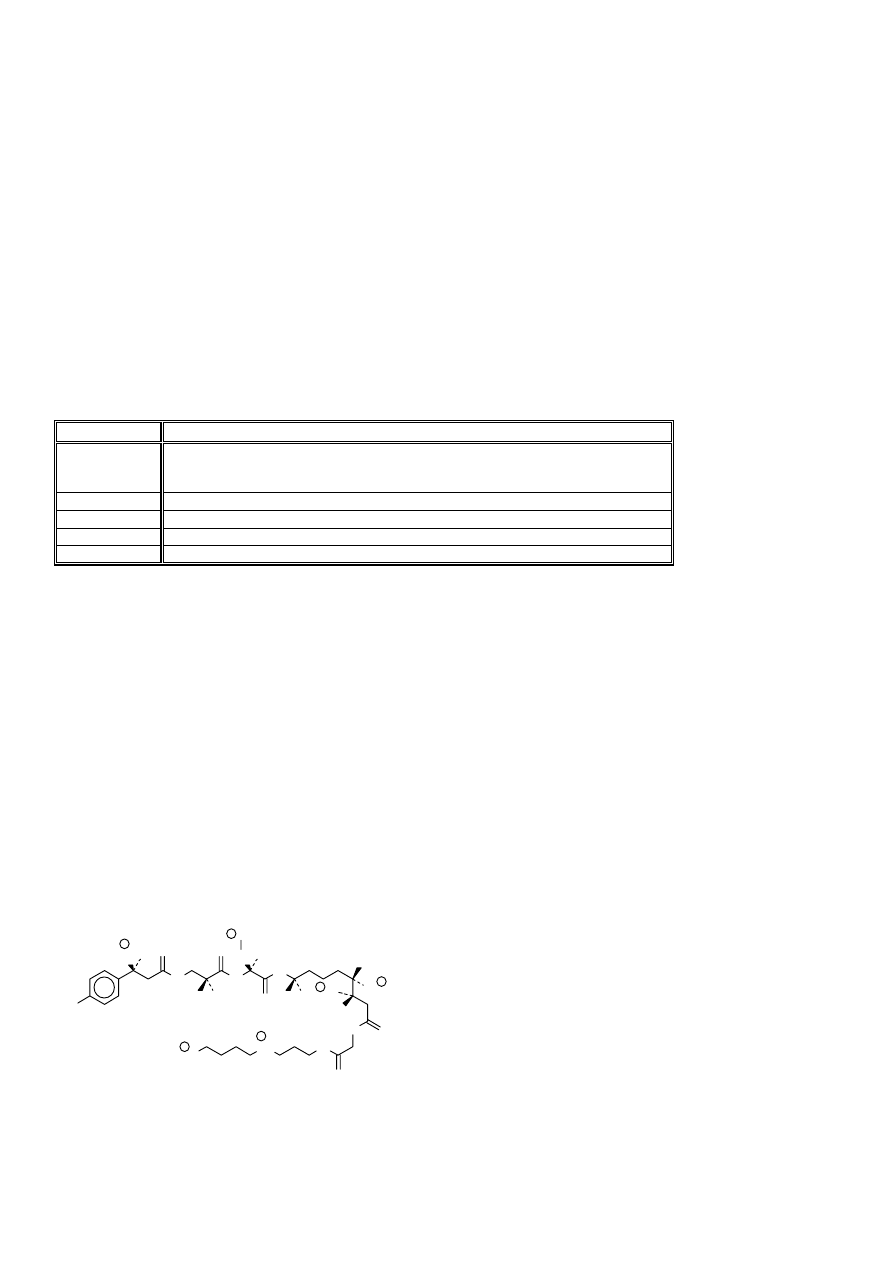
Część IV: Klasyczne metody QSAR

z sobą dwojakiego rodzaju korzyści: prognostyczne i
poznawcze.

Po pierwsze umożliwia ono przewidzenie kierunku

poszukiwań nowych pochodnych o korzystniejszych
właściwościach biologicznych i farmakologicznych. Jest to
dotychczas główny cel stosowania tej metody: uzyskanie
informacji prognostycznych. Do tej samej grupy informacji
należy również uzyskanie podstaw dla przerwania dalszych
poszukiwań gdy z analizy równania wynika, że nie ma
realnych szans na uzyskanie pochodnych o istotnie lepszych
cechach biologicznych. Warto wtedy czasami poszukać
podstawników o podobnych właściwościach fizyko-
chemicznych determinujących aktywność, ale jednocześnie
zmieniających cechy niekorzystne np. brak rozpuszczalności,
nietrwałość chemiczną lub też łatwiejszych w syntezie: tańsze
substraty, obejście zastrzeżeń patentowych.

Z drugiej strony, ponieważ w równaniu Hanscha

występują parametry mające określony sens fizyczny jest
możliwe uzyskanie tą drogą pośrednich informacji o
mechanizmie działania badanej grupy związków biologicznie

czynnych. Występowanie lub brak w uzyskanym modelu
określonych członów sugeruje istotność takich a nie innych
oddziaływań dla aktywności biologicznej w testowanym
układzie. Poniżej zestawiono typową interpretację roli
poszczególnych członów i parametrów w równaniu Hanscha.
Obecność w równaniu członu opisującego
w ł a ś c i w o ś c i l i p o f i l o w e (logP,

π lub RM)

oznacza, że w układzie istotny jest transport związku lub jego
wiązanie z elementami surowicy. Występowanie członu
kwadratowego pozwala wyznaczyć optymalne właściwości
lipofilowe. Brak tego członu wskazuję, że znajdujemy się z
dala od optimum (można się spodziewać poprawy
aktywności), a znak współczynnika dostarcza informacji o
kierunku zmian.
Istotność p a r a m e t r u e l e k t r o n o -
w e g o typu stałej Hammetta wskazuje na istotność efektów
elektronowych. W zależności od tego jaki konkretny rodzaj
stałej okaże się istotny mamy podstawy do snucia hipotez o
mechanizmie oddziaływania z receptorem:

Stała Sugestie

σm lub σp

Istotna rola zmian gęstości elektronowej w pierścieniu aromatycznym. Przypuszczalnie
istotną rolę odgrywa zmiana jonizacji cząsteczki i/lub oddziaływania ładunek-ładunek lub
ładunek-dipol.

σ-

Istotna rola oddziaływań z wolnymi parami elektronowymi

σ+

Istotna rola oddziaływań nukleofilowych

HOMO Cząsteczka ulega jonizacji (oddaje elektron lub przyjmuje proton)
LUMO Cząsteczka przyjmuje elektron lub parę elektronów

Obecność w równaniu Hanscha p a r a m e t r u
e l e k t r o n o w e g o opisującego rozkład elektronów w
cząsteczce wskazuje na znaczenie różnego rodzaju
oddziaływań pomiędzy polami elektrycznymi targetu i
związku biologicznie czynnego. Występowanie w równaniu
refrakcji molowej RM lub polaryzowalności

α sugeruje, że

pomiędzy lekiem i targetem dochodzi do indukowanych
interakcji dipol-dipol. Jeśli istotny dla aktywności
biologicznej jest moment dipolowy

µ to prawdopodobnie

mamy do czynienia z interakcją typu dipol-ładunek, a jeśli
kwadrat momentu dipolowego to interakcja typu dipol-dipol
indukowany.

8.2.6. Przykłady zastosowań.

Poniżej przedstawiono trzy przykłady zastosowania
metody Hanscha do poszukiwania zależności
struktura - aktywność dla różnych grup związków.

Przykład 8.7: Estry i amidy edeiny A

(J. Mazerski, B.

Woynarowska & E. Borowski, Proceedings of the XVth
European Peptide Symposium, Gdańsk 1978, str.373-375)

N H

C H

H O

N H

C O O

N H

H O

N H

H O

Edeina A

Edeina

należy do grupy antybiotyków peptydowych

produkowanych przez bakterię Bacillus brevis. Antybiotyki tej
grupy charakteryzują się szerokim spektrum
przeciwbakteryjnym i przeciwgrzybowym. Wykazują również
aktywność immunosupresyjną i cytotoksyczną. Niestety
charakteryzują się również bardzo wysoką toksycznością w
stosunku do organizmów wyższych. Celem omawianych tu

badań było określenie ilościowych zależności pomiędzy
właściwościami estrów i amidów edeiny A, a ich aktywnością w
stosunku do modelowych komórek pro- i eukariotycznych.
Zaplanowano otrzymanie 10 pochodnych tego antybiotyku na
grupie karboksylowej (patrz wzór powyżej):
- 4 estrów alkilowych: metylowego, etylowego, butylowego i
amylowego
- 3 amidów alifatycznych: etylowego, butylowego i heksylowego
- 3 amidów z dodatkową grupą aminową: 2-N,N-dimetylo-

aminoetylowego, 4-aminobutylowego i 5-N,N-dime

tyloaminoamylowego
Łącznie z edeiną oraz produktem wewnątrzcząsteczkowej
cyklizacji tworzy to serię 12 związków. Dla całej serii oznaczono
aktywność biologiczną w 3 testach mikrobiologicznych:
-

drożdze S.cerevisiae

- bakterie Gram+ B.subtilis

- bakterie Gram- E.coli

Jako miarę aktywności przyjęto pIC50.

Właściwości fizykochemiczne opisano przy pomocy:

2 parametrów lipofilowych
*

RM w układzie n-butanol/pirydyna/kwas

octowy/woda

6/2/3/5

celulozie
*

π z tablic

2 parametrów sterycznych

* refrakcja molowa MR

* molecular connectivity w/g Kiera

∆χ

5 parametrów binarnych opisujących:

* typ pochodnej (ester 1, amid 0)

* typ pochodnej (ester 0, amid 1)

obecność atomy azotu w podstawniku D

wypadkowy

ładunek cząsteczki q

ilość grup aminowych w cząsteczce n

Nie użyto parametrów elektronowych, gdyż przy zastosowanych
typach pochodnych nie mają one istotnego znaczenia.
Ponieważ nie należy używać w jednym równaniu
dwóch lub więcej parametrów tego samego typu w pierwszym
etapie analizy zastosowano pary równań zawierające RM i

refrakcję molową MR lub indeks Kiera. W każdym z równań
stosowano wszystkie parametry binarne. Przy ustalaniu równań
modelu zastosowano metodę odrzucania uzyskując dla
poszczególnych drobnoustrojów następujące pary równań:

Część IV: Metody QSAR

S.cerevisiae
(1) pIC50 = -2,2 RM - 0,038 MR + 0,50q - 2,69
R

0,913

(2) pIC50 = -1,4 RM - 0,044(∆χ)

2 - 0,91

0,848

B.subtilis
(3) pIC50 = -1,3 RM - 1,73

0,746

(4) pIC50 = -1,0 RM - 0,17(∆χ)

2 + 0,5(∆χ)- 1,85

0,928

E.coli
(5) pIC50 = -1,1 RM + 0,20q - 2,52

0,901

(6) pIC50 = -2,8(RM)

2-2,6R

M - 0,40(∆χ) +1,4DN - 1,61

0,981

Uzyskane zależności wskazują, że we wszystkich testach
aktywności istotny jest wpływ właściwości lipofilowych.
Jednakże zastosowany parametr empiryczny nie pozwala
przewidzieć właściwości związków na etapie ich projektowania.
Dlatego też w II etapie zastosowano wyłącznie parametry
tablicowe lub obliczane i uzyskano zależności:
S.cerevisiae
(7) pIC50 = 0,33π - 0,10(∆χ)

2 + 0,28q - 1,64

0,903

B.subtilis
(8) pIC50 = 0,44π -0,12(∆χ)

2 + 0,58n - 3,72

0,948

E.coli
(9) pIC50 = 0,50π -0,11(∆χ)

2 +0,99D

N - 0,79

0,956

Uzyskane równania wskazują, że model zależności powinien
zawierać parametr lipofilowy, steryczny oraz wskaźnik stopnia
jonizacji cząsteczki (q, n lub DN; poza edeiną i cykloedeiną

parametry te są identyczne). Zastanawiające jest podobieństwo
uzyskanych równań. Jedynie wpływ stopnia jonizacji jest dla
każdego testu istotnie różny.
Poszukując pochodnej o najwyższej aktywności widzimy że:

i) właściwości lipofilowe: korzystny jest wzrost

lipofilowości i to znaczny (brak istotności członu kwadratowego)

ii) właściwości steryczne: korzystny możliwie mały

podstawnik

iii) stopień jonizacji: im większy tym lepiej.

Charakterystyczne są sprzeczne przesłanki wynikające z tych
postulatów: wzrost lipofilowości i wzrost stopnia jonizacji, wzrost
lipofilowości i zmniejszenie podstawnika. W efekcie wydaje się,
że te sprzeczne wymagania najlepiej spełniają ester i amid
butylowy.
==============================================

Przykład 8.8: pochodne Ledakrinu (Zofia Mazerska -
doktorat).

N O

(C H

)

Analizie poddano serię 10 mono- i dialkilo

pochodnych 1-nitro-9-aminopropyloaminoakrydyny o
właściwościach przeciwnowotworowych. Jako miarę aktywności
przeciwnowotworowej przyjęto pED50 - ujemny logarytm z

dawki obniżającej o 50% ciężar guza w mysim mięsaku Sa-180.
Jako parametry fizykochemiczne przyjęto:

* parametr lipofilowy Hanscha

* 4 różne tablicowe parametry steryczne.

W I etapie analizowano 4 różne równania Hanscha (po jednym
dla każdego parametru sterycznego). Ze wszystkich po
zastosowaniu metody odrzucania otrzymano ten sam model:
pED50 = -0,074π

2 + 2,57

R = 0,848

Model ten był adekwatny. Tym samym wykazano, że efekty
steryczne wokół terminalnego atomu azotu nie mają istotnego
wpływu na aktywność przeciwnowotworową (przynajmniej w
tym teście).

-5.0

0.0

5.0

0.0

2.0

4.0

Analizując zakres

π jaki obejmują badane związki

zauważono ważny fakt: wszystkie wartości

π były dodatnie i

leżały w przedziałe od 0 do 3. W tej sytuacji nie dziwi wysoka
korelacja pomiędzy zmiennymi

π i π2 (r = 0,979). Nasuwało to

wątpliwości co do prawidłowego wyboru przez metodę
odrzucania kwadratu parametru lipofilowego, a nie samego
parametru, w trakcie usuwania nieistotnych parametrów. Po
świadomym usunięciu

π2 z danych początkowych uzyskano

równanie:
pED50 = -0,24π + 2,73

R = 0,834

I to równanie również było adekwatnym modelem zależności.
Jakość obu modeli jest praktycznie jednakowa i z punktu
widzenia statystyki są one równocenne. Jednakże wnioski z
nich płynące są diametralnie odmienne (patrz wykres obok).
Model kwadratowy sugeruje, że maksimum aktywności jest już
osiągnięte dla

π=0 (pEDmax = pED50(0) = 2,57 wobec

pED(n-Pro)=2,61, pED(di-Me)=2,53, pED(Et)=2,56). Model
liniowy zapowiada wzrost aktywności dla związków o ujemnym
π, np. pED(π=-1)=2,97, a pED(π=-2)=3,21. W tej sytuacji
rozróżnienie pomiędzy obu modelami było sprawą kluczową dla
dalszego poszukiwania nowych związków z tej grupy.
Zaprojektowano więc i wykonano syntezę 4 nowych
pochodnych: 3 o ujemnym

π:

-CH2-CH2-OH o π = -0,16
-CH(CH3)(CH2-OH)2 o π = -0,65
-C(CH2-OH)3 o π = -1,81
oraz pochodną n-heksylową o

π = 3,0 dla poszerzenia zakresu

zmienności.

W trakcie badań biologicznych żadna z pochodnych

nie była aktywniejsza niż związki wcześniej zsyntetyzowane.
Ponownie wyznaczono współczynniki równania Hanscha dla 4
zestawów parametrów i ponownie otrzymano z każdego
zestawu takie same równanie:
pED50 = -0,90π

2 + 0,083π + 2,47

R = 0,887

n = 14

s = 0,11

Równanie to opisuje paraboliczną zależność aktywności
przeciwnowotworowej od właściwości lipofilowych z maksimum
aktywności pEDmax = 2,47 przypadającym dla π~0,5. Tak więc

widać teraz, że bliższy prawdy był poprzednio model
kwadratowy.
Z uzyskanej zależności widać też wyraźnie, że nie należy się w
tej grupie pochodnych spodziewać związków o aktywności dużo
wyższej niż ok.

2,5, a ewentualne dalsze poszukiwania

pochodnych o lepszych właściwościach farmakologicznych(
mniejsza toksyczność, lepsza rozpuszczalność w wodzie)
dotyczyć powinny związków o

π ~ 0,5.

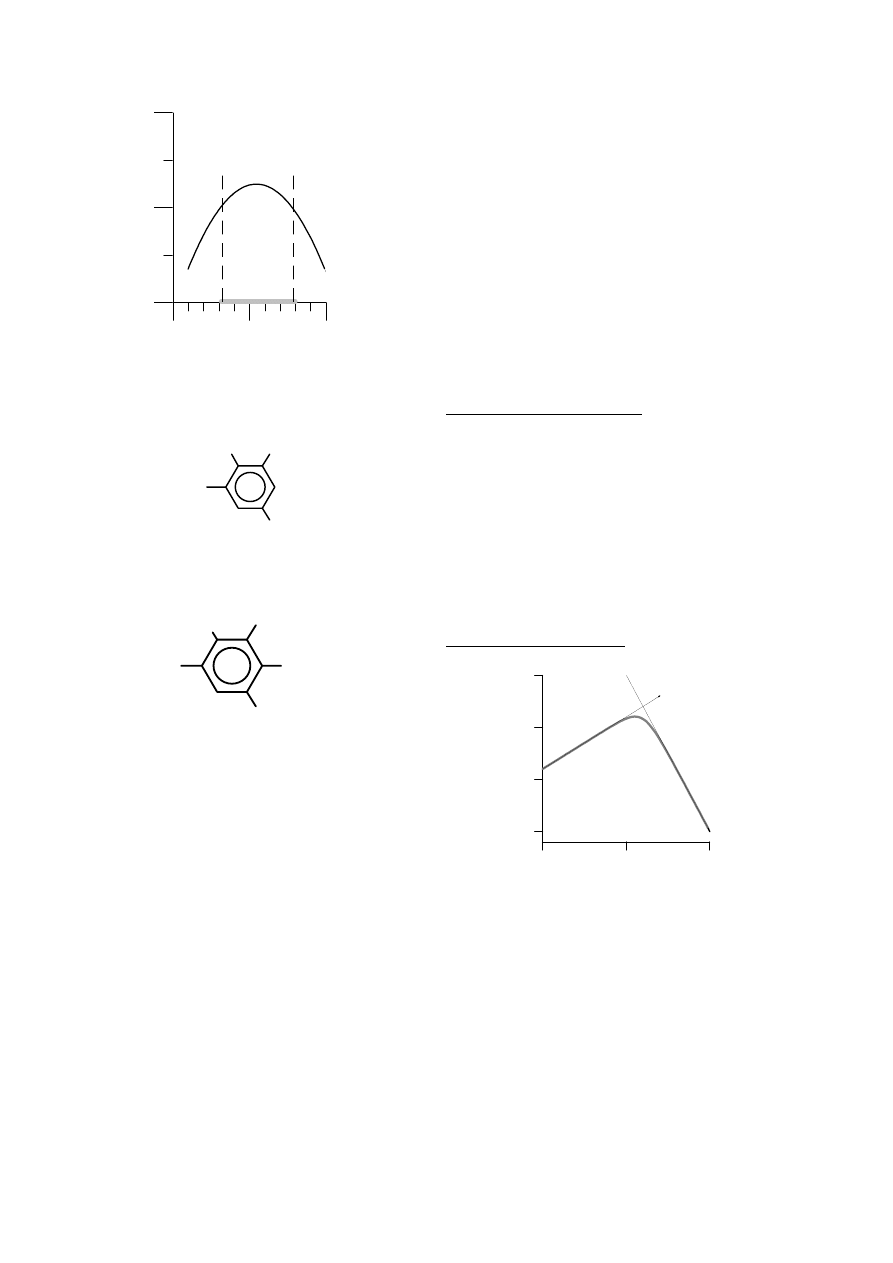
Część IV: Metody QSAR

-5.0

0.0

5.0

0.0

2.0

4.0

==============================================

Przykład 8.9: Długołańcuchowe fenole o właściwościach
cytotoksycznych (H.Itokawa, N.Totsuka et al.,
Chem.Pharm.Bull. 37,1619-1621(1989)).

2 9

(C O O H )

O H

(O H )

Autorzy

badając wyciąg z krzewu jarząbu

japońskiego (Ginkgo biloba L.) stwierdzili cytotoksyczność tych
wyciągów. Dalsze badania wykazały, że za aktywność
biologiczną odpowiedzialne są fenole zawierające 15 węglowy
łańcuch alifatyczny (patrz struktura po prawej).

Chcąc określić rolę poszczególnych elementów
struktury zsyntetyzowano 29 związków o wzorze ogólnym
zamieszczonym obok (po lewej). W pozycji R1 użyto 5 różnych

łańcuchów alifatycznych od C7 do C15, a w pozycjach od R2 do

R5 występowały grupy fenolowe lub atomy wodoru.

Jako

miarę aktywności biologicznej przyjęto pED50 w

hodowli komórkowej na linii komórek nowotworowych chomika
syryjskiego.

Jako parametry fizykochemiczne przyjęto: i) logP w

układzie n-oktanol/woda; ii) EHOMO - energię najwyższego

obsadzonego orbitalu molekularnego; iii)

ELUMO energię

najniższego nieobsadzonego orbitalu molekularnego. Energie
LUMO i HOMO mają swoje przybliżone interpretacje
chemiczne. Energia LUMO opisuje względne właściwości
elektronoakceptorowe (podatność na redukcję), a energia
HOMO właściwości elektronodonorowe (podatność na
utlenianie, łatwość protonowania).
Nie stosowano stałych Hammetta, gdyż nie są to parametry
addytywne i nie nadają się do stosowania w przypadku
pochodnych podstawionych jednocześnie w wielu miejscach.
Po zastosowaniu metody Hanscha uzyskano zależność:
pED50 = -0,016(logP)

2 + 0,28logP - 4,1E

LUMO + 1,1EHOMO

+ 10,58

R = 0,905 n = 29

s = 0,18

Aktywność cytotoksyczna badanych fenoli zależy głównie od
lipofilowości (optymalny logP = 8,3) i poziomu energetycznego
LUMO. Wpływ energii HOMO jest dużo mniej istotny. Związek o
w okiej aktywności powinien więc charakteryzować się:

∗

logP ~ 8, co odpowiada łańcuchowi C13

∗

niską (możliwie ujemną) energią LUMO

∗

wysoką (jak najmniej ujemną) energią HOMO.

Dwa ostatnie wymogi są przeciwstawne, lecz wpływ LUMO jest
ok. 4 razy silniejszy i on decyduje. Obliczono wartości energii
LUMO i HOMO dla różnych kombinacji grup hydroksylowych w
pozycjach od R2 do R5 i okazało się, że najkorzystniejszymi

wartościami tych energii charakteryzują się związki zawierające
2 grupy hydroksylowe w pozycjach R3 i R4. Związek o takiej

strukturze części aromatycznej i łańcuchu C13 wykazał

znaczącą aktywność przeciwnowotworową w dwóch testach na
mysich nowotworach przeszczepialnych.
=========================================

8.3. Inne metody regresyjne.

Duża popularność metody Hanscha (był okres w
latach '70, gdy cały QSAR utożsamiano z metodą Hanscha)
spowodował dążenie do jej poszerzenia na przypadki, gdy
klasyczna metoda zawodziła. Spośród licznych propozycji,
trwałe miejsce w QSAR znalazły 2 modyfikacje:

∗

uogólniony model kwadratowy

∗

zależność bilinearna Kubinyiego.

Poniżej zostaną one pokrótce omówione.

Uogólniony model kwadratowy.

W swej pełnej postaci:

logA = ao + a11π2 + a22σ2 + a33Es2 +a1π + a2σ + a3Es +

a12πσ + a13πEs + a23σEs

uogólniony model kwadratowy wymaga zidentyfikowania 10
współczynników czyli może być zastosowany tylko w
przypadku dużej serii związków (co najmniej 40

÷50). Ponadto

brak jest jak dotychczas uzasadnienia teoretycznego i
interpretacji sensu fizycznego członów opisujących wpływy
mieszane (ostatnia linia wzoru). Obydwa te wady powodują,
że w praktyce model ten bywa zwykle stosowany w wersji
skróconej zawierającej człony liniowe i 2 lub 3 człony
kwadratowe.

Model bilinearny Kubinyiego

logA

logP

W szeregu przypadkach zaobserwowano

niesymetryczną zależność aktywności biologicznej od logP
lub

π. Na lewo od optimum nachylenie jest inne niż na prawo.

Dla opisu takich przypadków Kubinyi zaproponował tzw.
zależność bilinearną o postaci:

logA = a

×logP - b×log(β×P + 1) + c

Przykład krzywej bilinearnej pokazano na wykresie obok. Dla
logP<<logPmax zależność dąży asymptotycznie do prostej o

równaniu:

logA = a

×logP + c

a dla logP >> logPmax dąży do prostej o równaniu:

logA = (a-b)

×logP + c - b×logβ

Podstawową niedogodnością modelu bilinearnego
jest konieczność nieregresyjnego, iteracyjnego wyznaczania
wartości współczynników. Typowe pakiety oprogramowania
statystycznego nie pozwalają na pokonanie tego problemu.
Dlatego też model bilinearny stosowany bywa jedynie
sporadycznie i tylko w przypadku wyraźnej asymetrii

Część IV: Metody QSAR

zależności aktywności biologicznej od właściwości
lipofilowych.

9. Nieregresyjne metody optymalizacji
struktury

W latach '70, po wykazaniu słuszności założeń

metody Hanscha, jedną z przeszkód w jej szerokim
stosowaniu okazała się bariera statystyczno-obliczeniowa.
Rozwiązanie równania Hanscha wymaga pewnego nakładu
pracy obliczeniowej, zwłaszcza gdy należy powtórzyć
kilkakrotnie obliczenia dla różnych zestawów parametrów lub
gdy odrzucamy człony nieistotne. Wykonanie takich obliczeń
ręcznie, nawet z zastosowaniem kalkulatora (a był to na
początku lat '70 jeszcze dosyć drogi i rzadki przyrząd),
wymaga kilku godzin żmudnych obliczeń. Dostęp do
komputerów był wtedy bardzo ograniczony. Ponadto
większość chemików, biologów i farmakologów nie posiadało
dostatecznej znajomości podstaw statystyki, aby z lawiny
równań produkowanych przez komputer wybrać prawidłowo
to najlepsze. Poniższy przykład ilustruje ten problem.

Przykład 9.1: Liczba uproszczonych równań
otrzymywanych z równania Hanscha.

Klasyczne,

pełne równanie Hanscha:

logA = ao + a1π

2 + a

2π + a3σ + a4Es

zawiera 4 człony. Przy rozpatrywaniu uproszczonych wersji
tego równania mamy:

♦ 4 równania z jedną zmienną

♦ 6 równań z dwiema zmiennymi

♦ 4 równania z trzema zmiennymi

♦ 1 równanie z czterema zmiennymi (pełne)

W sumie 15 równań. Dla każdego z tych równań należy
obliczyć współczynniki i charakterystyki statystyczne, a
następnie dokonać wyboru rónania lub równań najlepszych.
==============================================

Pojawiły się więc próby opracowania metod
projektowania nowych pochodnych bazujące na wiedzy o
wpływie właściwości fizykochemicznych na aktywność
biologiczną, ale bez korzystania z równań regresji. Szeroką
swego czasu popularność zdobyły dwie z nich:
 metoda

Darvasa



schematy operacyjne Toplissa

W chwili obecnej, gdy właściwie każdy badacz ma lub może
mieć dostęp do komputera osobistego, a rozwój
oprogramowania przeznaczonego do opracowywania danych
doprowadził do sytuacji gdy wyznaczanie współczynników
równań regresji jest sprawą trywialną, metody nieregresyjnej
optymalizacji struktury utraciły swoje znaczenie. Pomimo to
warto się zapoznać, choćby pobieżnie, z założeniami tych
metod.

9.1. Metoda Darvasa.

Pomysł opiera się na założeniu, że aktywność
biologiczna daje się opisać jako ciągła funkcja d w ó c h
parametrów fizykochemicznych:

♦

σ dla pochodnych aromatycznych

♦

i Es dla związków alifatycznych.

Postać matematyczna tej funkcji nie jest nam znana i nie
dążymy do jej poznania. Naszym celem jest znalezienie
maksimum tej funkcji (aktywności) dzięki jej "próbkowaniu"
poprzez syntezę i oznaczanie aktywności odpowiednio
dobranych pochodnych. Z algorytmicznego punktu widzenia
metoda Darvasa opiera się na metodzie simpleksów.

W pierwszym etapie należy określić zestaw

podstawników które można wprowadzić do struktury bazowej
bez nadmiernych problemów syntetycznych. Dla tak
dobranego zestawu pochodnych, w oparciu o tablicowe

wartości parametrów wykonujemy "mapę" - planszę metody-
w układzie

π-σ (dla aromatycznej struktury bazowej) lub π-Es

(dla alifatycznej struktury bazowej).

Wybieramy teraz trzy pochodne tworzące w pobliżu

środka mapy możliwie równoramienny trójkąt. Wybrane
związki syntetyzujemy i oznaczamy ich aktywność
biologiczną. Rozpoczynamy teraz poszukiwanie maksimum
aktywności biologicznej uproszczoną metodą sympleksów
(patrz przykład poniżej). Z wierzchołka trójkąta
odpowiadającego pochodnej o najniższej aktywności
prowadzimy środkową przeciwległego boku i w obszarze
mapy przez który przechodzi ta prosta poszukujemy punktu
tworzącego nowy, możliwie równoramienny trójkąt. Po
wybraniu nowego wierzchołka syntetyzujemy odpowiadający
mu związek i oznaczamy jego aktywność biologiczną.
Powstał w ten sposób nowy simpleks z którym postępujemy
analogicznie jak z simpleksem poprzednim.
Postępowanie przerywamy, gdy osiągneliśmy już maksimum
aktywności lub wyczerpały się możliwe do otrzymania
pochodne w kierunku oczekiwanego maksimum.

Przykład 9.2: Metoda Darvasa.

Tworzymy

mapę przedstawiającą właściwości

lipofilowe (

π) i elektronowe (σ) wybranych pochodnych

aromatycznych podstawionych w pozycjach 3- i 4-pierścienia
fenylowego.

4NH

4NHMe

4OMe

3Me

4Me

4COMe

4Cl

4Br

3Cl

3CF

4CN

3NO

4NO

3NO

;4Cl

3NO

;4CF

4CF

3Cl;4Cl

W pierwszym etapie zaplanowano syntezę trzech związków:
-

związku niepodstawionego (logA = 0,155)

- 4 -COCH3

(logA = 0,462)

- 4 -Cl

(logA = 0,301).

tworzących simpleks początkowy. Związek niepodstawiony
tworzy najgorszy wierzchołek i z niego prowadzimy środkową
przeciwległego boku.

4NH

4NHMe

4OMe

3Me

4Me

4COMe

4Cl

4Br

3Cl

3CF

4CN

3NO

4NO

3NO

;4Cl

3NO

;4CF

4CF

3Cl;4Cl

Jako nowy wierzchołek wybieramy np. pochodną 4 -NO2.

Powstaje w ten sposób drugi simpleks:

- 4 -Cl

(logA = 0,301)

- 4 -COCH3

(logA = 0,463)

- 4 -NO2 (logA = 0,845)

Najgorszym wierzchołkiem jest pochodna 4-chloro i z niej
prowadzimy środkową przeciwległego boku.

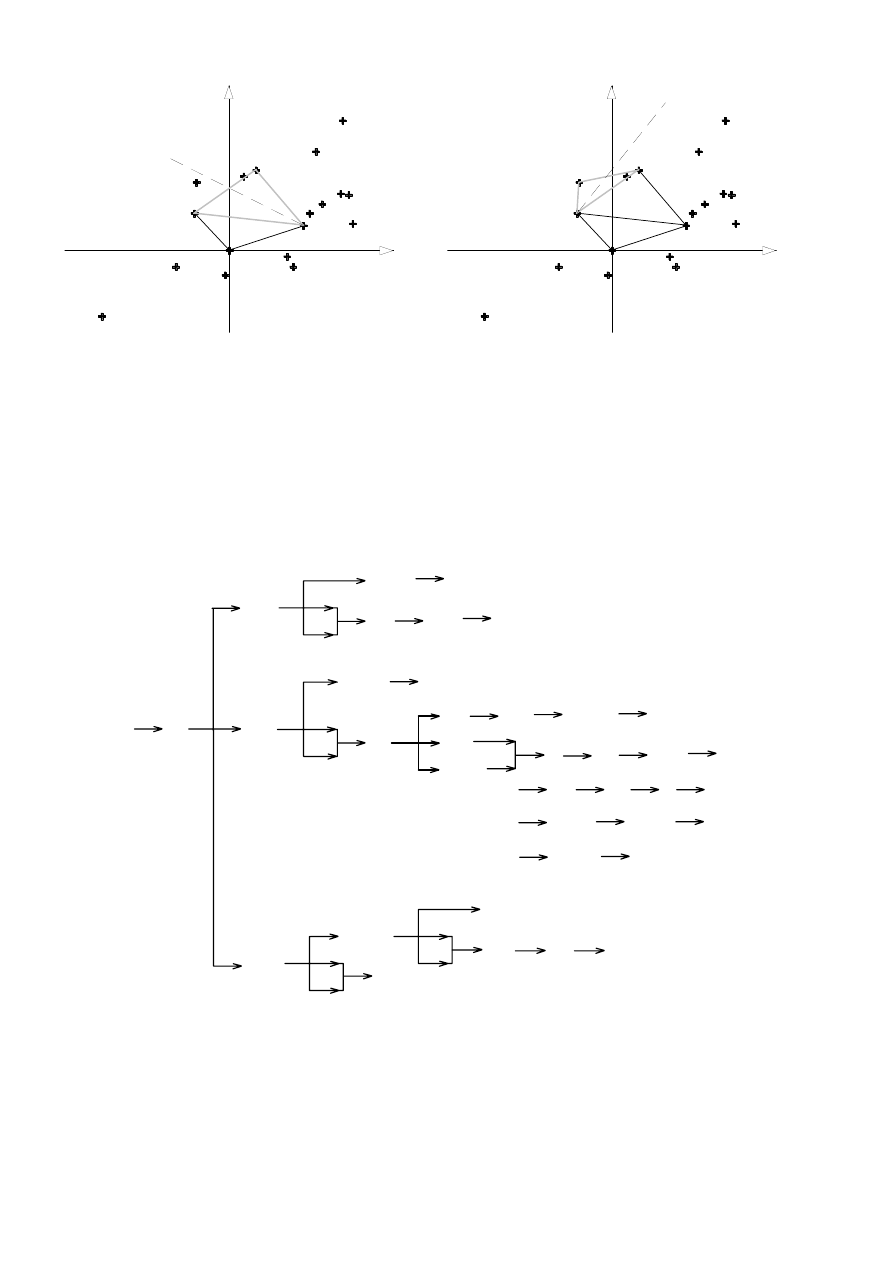
Część IV: Metody QSAR

4NH

4NHMe

4OMe

3Me

4Me

4COMe

4Cl

4Br

3Cl

3CF

4CN

3NO

4NO

3NO

;4Cl

3NO

;4CF

4CF

3Cl;4Cl

Jako nowy wierzchołek wybieramy np. 4-cyjano. Powstaje w ten
sposób trzeci simpleks:
4-COCH3 (logA = 0,463)

4-NO2

(logA = 0,845)

4-CN

(logA

1,020).

Środkowa wyprowadzona z wierzchołka 4-acetylo prowadzi
jednak w obszar mapy pozbawiony możliwych do
zsyntetyzowania pochodnych.

4NH

4NHMe

4OMe

3Me

4Me

4COMe

4Cl

4Br

3Cl

3CF

4CN

3NO

4NO

3NO

;4Cl

3NO

;4CF

4CF

3Cl;4Cl

W tej sytuacji jako najaktywniejszy związek uznajemy pochodną
4-cyjano.
=============================

8.2. Schematy operacyjne Toplissa.

Założeniem metody jest przyjęcie tezy Hanscha, że
aktywność biologiczna zależy od zmian właściwości
fizykochemicznych. Topliss opracował odpowiednie
schematy dla doboru podstawników w pierścieniu
benzenowym oraz dla doboru podstawników w układzie
alifatycznym (patrz poniżej).

Schemat I: Schemat Toplissa doboru podstawników pierścienia benzenowego.

CF ;

Cl;

C(CH )

3 3

CH ;

Cl;

CF ;

N(CH )

3 2

OCH

COCH

CONH

SO CH

SO NH

OCH

N(CH )

3 2

CH ;

N(CH )

3 2

CH ;

OCH

Schematy

umożliwiają wybór kierunku syntezy

następnych związków w zależności od wyników
biologicznych związków poprzednio zsyntetyzowanych.
Mogą one być szczególnie pomocne w pracach chemika-
syntetyka nie mającego możliwości lub chęci
przeprowadzenia obliczeń komputerowych.

W przypadku podstawników pierścienia

benzenowego startujemy od związku niepodstawionego.
Ponieważ w większości przypadków aktywność biologiczna

zależy od lipofilowości więc jako pierwszą pochodną Topliss
zaproponował pochodną 4-chloro (

π=0,70; σ=0,23; Es=0,27).

Pochodna ta może mieć aktywność lepszą (L), taką samą (T)
lub gorszą (G) niż związek niepodstawiony. Wzrost
aktywności może wynikać ze wzrostu lipofilowości i/lub
efektów elektronowych. Dlatego też w przypadku wzrostu
aktywności dla 4-chloropochodnej schemat proponuje "pójść
za ciosem" i dalej zwiększać oba efekty: pochodna 3,4-
dichloro (

π=1,25; σ=0,52).

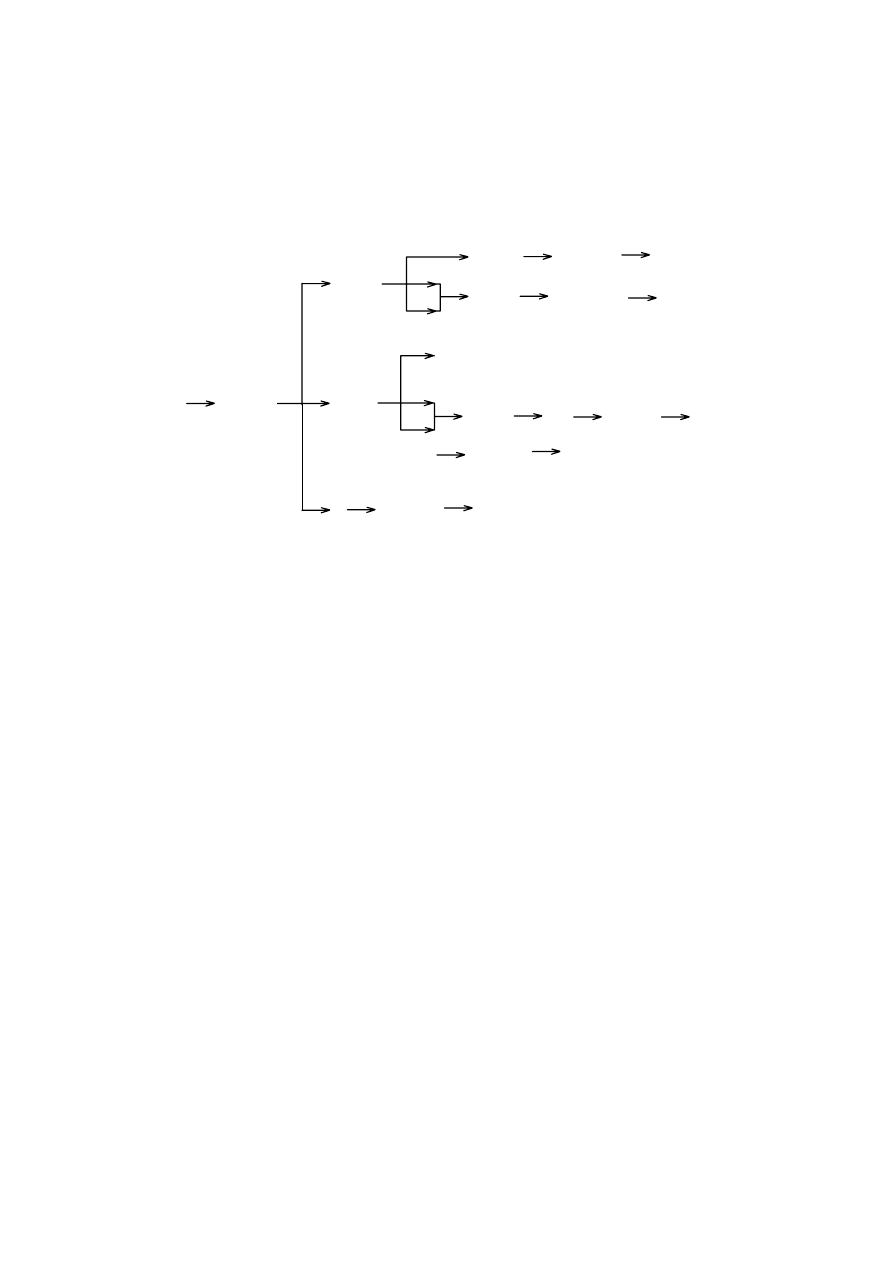
Część IV: Metody QSAR

Pochodna 3,4-dichloro może być bardziej aktywna niż 4-
chloro, mieć taką samą aktywność lub wykazywać spadek
aktywności. I tu znowu schemat przewiduje odpowiednie
postępowanie.
Analogiczne wnioskowanie przeprowadzić można w sytuacji
gdy 4-chloropochodna obniża aktywność.
Topliss

zaproponował również schemat doboru

podstawnika R w ugrupowaniach typu:

-CO-R

-NHR

-CO-NHR i

-NH-CO-R.
Schemat opiera się na parametrach

π, σ* i Es, z tym że

głównie brana jest pod uwagę lipofilowość i zawada
przestrzenna.

Schemat II: Schemat Toplissa doboru podstawników w układach alifatycznych.

C H

3 7

C H

5 9

C H

6 11

CH C H

6 11

CH CH C H

6 11

C H

4 7

CH C H

3 5

C H

4 7

CHCl

CH CF

CH SCH

CH C H

CH OCH

CH SO CH

Obydwie przedstawione tu nieregresyjne metody

optymalizacji struktury mają pewną istotną niedogodność: są
metodami krokowymi. Po syntezie kolejnego związku
czekamy (zwykle długo) na zbadanie jego aktywności
biologicznej i w oparciu o nią planujemy kolejną syntezę.
Prowadzi to do bardzo długiego toku poszukiwania. Jednakże
tylko metodą krokową można uzyskać maksymalny efekt przy
minimalnej ilości syntez.

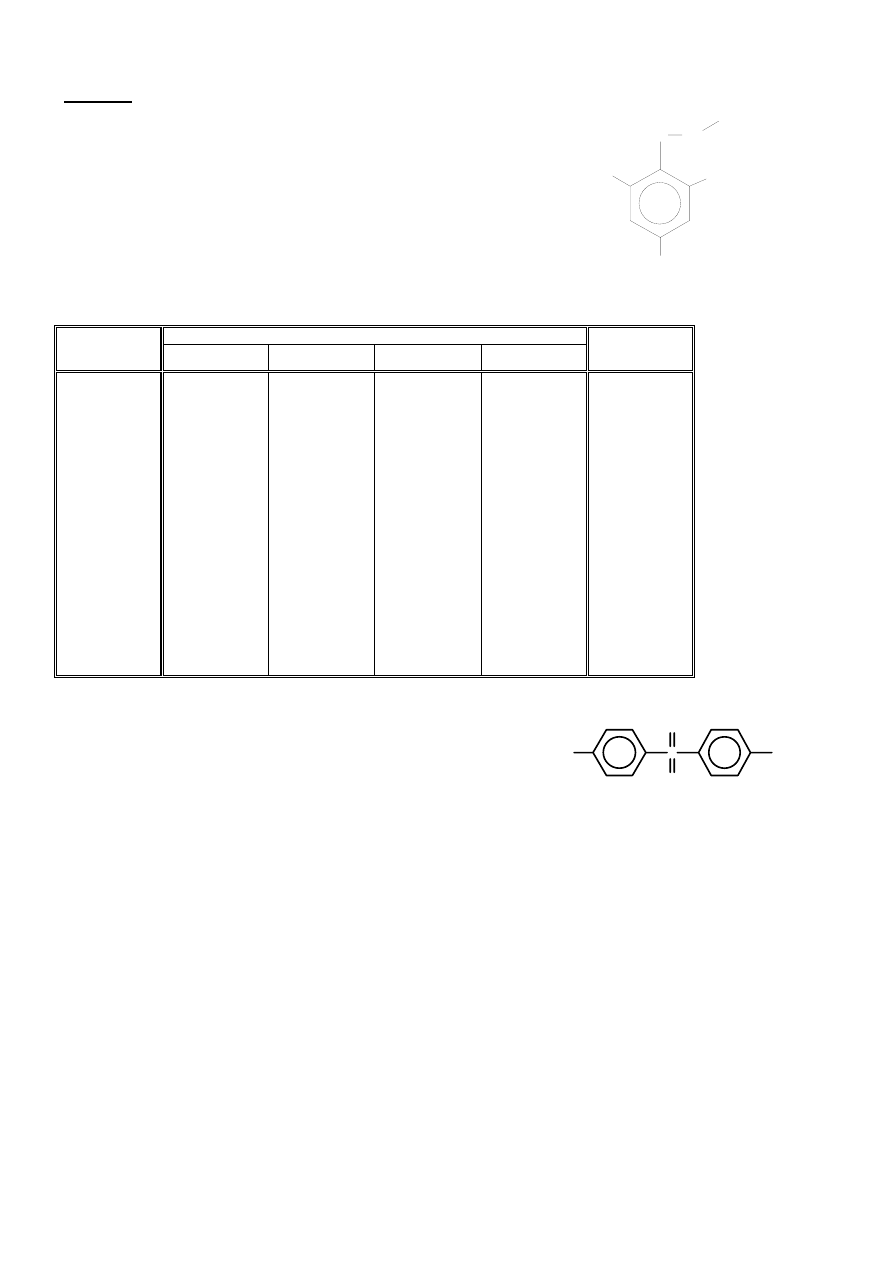
Część IV: Metody QSAR

ZADANIA

Zadanie 1: W oparciu o zamieszczoną poniżej tabelę struktur i aktywności

przeciwgrzybowych pochodnych etylobenzenu określ wpływ poszczególnych
podstawnikopozycji na aktywność biologiczną stosując metodę Free-Wilsona. W
tym celu:
i) określ jednoznacznie numery i nazwy poszczególnych podstawnikopozycji
ii) napisz w postaci jawnej macierz podstawnikopozycji i odpowiadajacy jej

wektor aktywności

iii) wprowadź powyższe dane do programu REGR, znajdź poprawne równanie

regresji i na jego podstawie dokonaj oszacowania aktywności pochodnej o
przypuszczalnie najwyższej aktywności.

iv) wiedząc że odchylenie standardowe oznaczeń aktywności wynosi 0,4 określ

addytywność wpływu podstawników.

Puste miejsca w tabeli oznaczają, że w tym miejscu występuje wodór.

związek

podstawniki

pMIC

B1 OH Me Me Me 2,54
B2 NH2 Me Me Me 1,83

B3 OH Me

Me 3,04

B4 OH Cl Cl Cl 1,93
B5 NH2 Cl OMe Me 2,28

0,18

OMe

1,27

B8 OH OMe

OMe

1,59

B9 OH OMe

Me Cl 1,51

B10 OH OMe OMe

2,50

B11 OH

0,53

B12 OH Cl Me

0,70

B13 OH

1,49

B14 NH2

0,80

B15 NH2

OMe

1,09

B16 NH2 Me OMe

2,05

B17 NH2 Me

Cl 1,48

B18

OMe 0,99

B19

OMe

OMe 0,57

Zadanie 2: W oparciu o zamieszczone poniżej dane znajdź zależność pomiędzy

aktywnością przeciwdrobnoustrojową (pIC50) 17 pochodnych 4-amino-

difenylosulfonu podstawionych w pozycji 4', a ich właściwościami fizyko-
chemicznymi.
Na podstawie uzyskanej zależności opisz cechy pochodnych o przewidywanej
wysokiej aktywności.

pIC50

Symbol podst.

M.smeg SM



π ppm

ICOOH

CO-1

NH2

-0.30

-1.23 .......... -0.253 0

CO-2

OCH3

-1.18 -0.02

..........

-0.127

CO-3

NO2

-1.94

-0.28 ..........

0.111 0

CO-4

-1.23

0.00 ..........

0.000 0

CO-5

-0.30

-0.67 .......... -0.156 0.45

CO-6

-1.65 0.71

..........

0.004

CO-7

NHCOCH3

-0.38 -0.97

..........

-0.114

CO-8

-1.68 0.86

..........

0.000

CO-9

NHCH3

-0.82 -0.47

..........

-0.253

CO-10

NHC2H5

-0.56 -0.08

..........

-0.250

CO-11

CH3

-1.21 0.56

..........

-0.091

CO-12

N(CH3)2

-0.26 0.18

..........

-0.237

CO-13

COOCH3

-0.36 -0.01

..........

0.005

CO-14

COOH

-2.06

-4.36 ..........

0.030 1

CO-15

CONHNH2

-0.73 -1.92

..........

-0.003

CO-16

NHCH2COOCH3

-0.76 -0.95

..........

-0.141

CO-17

NHCH2COOH

-1.69 -3.59

..........

-0.141

C H

N H

Wyszukiwarka

Podobne podstrony:
Metodyka masażu klasycznego, Metodyka masażu klasycznego
Metodyka masażu klasycznego, Metodyka kończyny dolnej
Założenia klasycznej metody najmniejszych kwadratów, Wykłady rachunkowość bankowość
Klasyczne metody rentgenowskie, Pielęgniarstwo licencjat cm umk, I rok, Radiologia
Masaż leczniczy klasyczny, Metodyka masażu klasycznego
Metody klasyczne 2
Metodyka masażu klasycznego, Studia, Fizjoterapia, Studia - fizjoterapia, Masaż, PODRĘCZNIKI (dyndi
Metodyka masażu klasycznego, Masaż kosmetyczny, Ruchy w masażu kosmetycznym wykonujemy 3- krotnie
6 METODY KLASYCZNE, II wojna światowa na morzu, Dydaktyka
METODYKA styl klasyczny zabka
Metodyka nauczania stylem klasycznym (Zabka), Pływanie
Ćwiczenie 6 Poznajemy metody usamodzielniające (zabawowo naśladowczą, zabawowo klasyczną i bezpośre
T 3[1] METODY DIAGNOZOWANIA I ROZWIAZYWANIA PROBLEMOW
10 Metody otrzymywania zwierzat transgenicznychid 10950 ppt
metodyka 3

więcej podobnych podstron