1

Instytut Mikroelektroniki i Optoelektroniki
Zespół Laboratoriów Przyrządów Półprzewodnikowych

Pomoce dydaktyczne oraz instrukcja wykonawcza

do ćwiczenia pod tytułem:

„Kontakt półprzewodnik-półprzewodnik – złącze p-n”

(Z)

Opracowanie: dr inż. Aleksander Werbowy

I

. Część teoretyczna

1.

Fale materii – energia elektronu w nieskończonej i skończonej studni potencjału

Immanentną cechą materii jest jej dualna korpuskularno-falowa natura. Oznacza to, że

poruszające się cząstki, jak np. elektrony można opisywać jako fale materii. Długość takiej
fali (nazywanej długością fali de Broglie’a) określa zależność:

h

p

λ

=

,

(1)

gdzie: h jest stałą Plancka zaś p – pędem poruszającej się cząstki.

Jednym z przejawów falowej natury elektronu jest kwantyzacją jego energii (tzn. fakt, iż

elektron może posiadać tylko ściśle określone wartości energii) w przypadku, gdy staje się on
zlokalizowany przestrzennie, czyli ograniczony w swoim istnieniu do pewnego skończonego
obszaru w przestrzeni. Taką pułapką jest tzw. studnia potencjału, tj. obszar o pewnych
skończonych rozmiarach ograniczony na krańcach barierami potencjału, zwanymi też
barierami energetycznymi (o nieskończonej (sytuacja wyidealizowana) lub skończonej
(sytuacje rzeczywiste) wysokości). Bariery potencjału uniemożliwiają po prostu ucieczkę
elektronom, których energia jest mniejsza od potencjału bariery. Dyskretyzacja energii
elektronu staje się widoczna w przypadku studni o rozmiarach nanometrowych (tj. rzędu
10

-9

m), a wiec porównywalnych z długością fali de Broglie’a elektronu. Dla rozmiarów

przestrzennych znacznie większych (albo dla bardzo dużych wartości liczb kwantowych
(np. głównej n)), zgodnie z zasadą korespondencji Bohra, efekt ten zanika, a dokładniej
rzecz ujmując staje się niedostrzegalny, gdyż skwantowane wartości energii elektronów
zaczynają się od siebie coraz mniej różnić, przechodząc płynnie w quasi ciągłe kontinuum
stanów, tj. z obszaru zjawisk i cech dających się poprawnie opisać tylko na gruncie fizyki
kwantowej do obszaru poprawnie opisywanego przez fizykę klasyczną.

W ogólności każda fala materii (a więc również ta związana z elektronem) poruszająca

się w przestrzeni tak, iż nie jest w żaden sposób ograniczona, tj. nie działa na nią żadna siła
wypadkowa (a więc np. cząstka-fala nie znajduje się w żadnym polu energii potencjalnej)
może przyjmować każdą dowolną (rozsądną) długość (czyli i częstość) – analogicznie jak
„klasyczna” fala biegnąca wzdłuż naprężonej nieskończonej (albo dostatecznie długiej, aby
z dobrym przybliżeniem za nieograniczoną ją uznać) liny. Natomiast w przypadku, gdy fala
materii zostanie w jakimś polu sił uwięziona (przypomnijmy, iż oznacza to jej lokalizację
przestrzenną), może przyjmować już jedynie wybrane długości. Inne, pośrednie, nie są
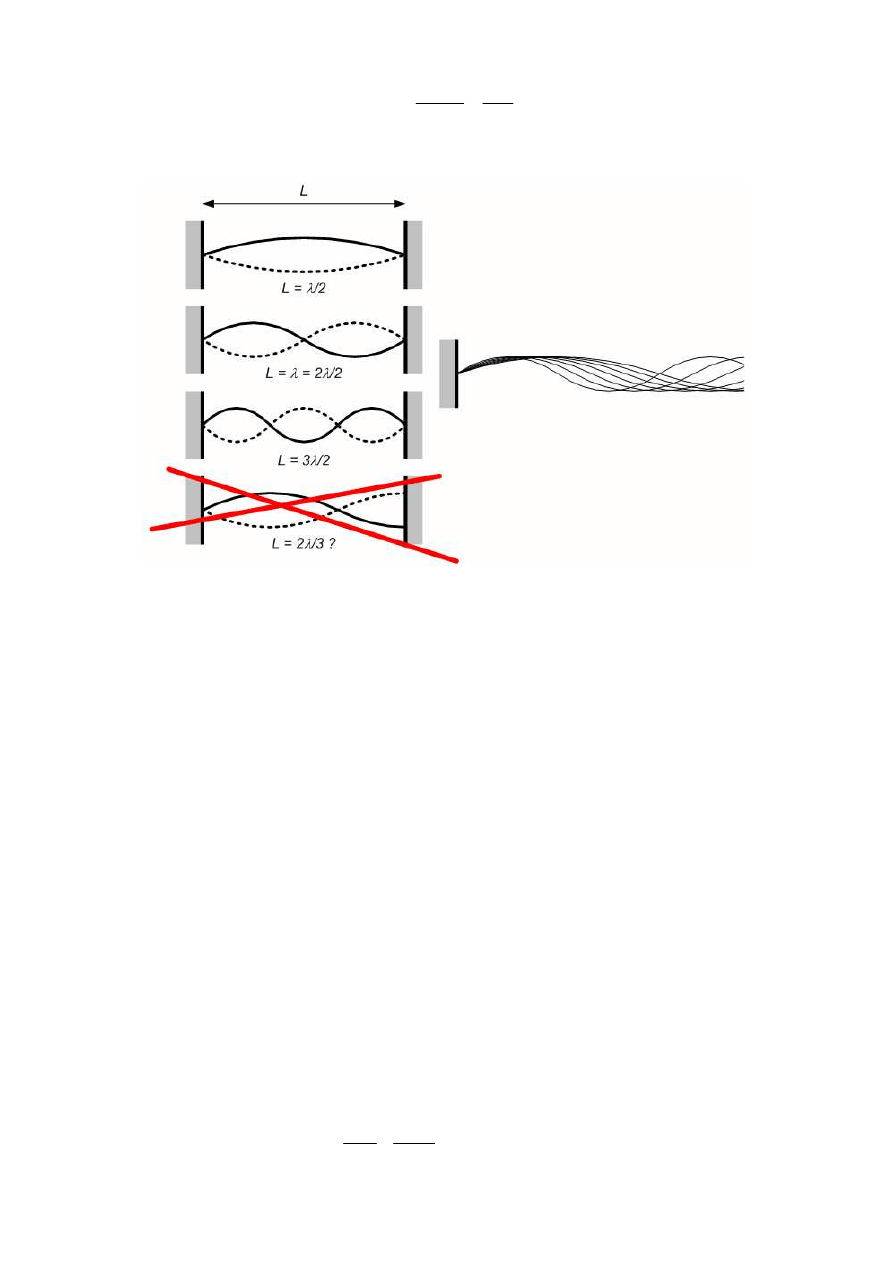
dopuszczalne. Podobnie, jak w linie skończonej (albo np. strunie gitary), w której może
rozchodzić się tylko fala stojąca (a nie biegnąca, jak w nieskończonej) i to tylko o pewnych
dyskretnych długościach, a więc i częstościach (rys. 1). W rozważaniach dotyczących fal
materii, zamiast długości czy częstości wygodniej jest zazwyczaj rozpatrywać ich energie E,
które można określić przekształcając odpowiednio wzór de Broglie’a (1):

2

2

2

2

2

2

e

e

h

p

E

m

m

λ

=

=

,

(2)

gdzie m

e

jest masą elektronu. A skoro długość fali w dyskutowanym przypadku może

przyjmować tylko określone wartości, to tym samym i jej energie będą skwantowane.

(a)

(b)

Rys.1 Fala stojąca w linie skończonej (a) i biegnąca w linie nieskończonej (b).

2.

Poziomy energetyczne elektronu w atomie izolowanym

Prostym przykładem rzeczywistej pułapki elektronowej jest każdy atom, a najprostszym –

atom wodoru. Dodatni ładunek protonu i ujemny elektronu powodują, iż obydwie cząstki
przyciągają się elektrostatycznie. To samo dzieje się w atomach cięższych pierwiastków, tyle
że z rosnącą liczbą atomową Z, czyli po prostu liczbą protonów w jądrze, w ten sam sposób
wzrasta liczba elektronów je otaczających. Można więc powiedzieć, że atom jest pułapką
dla elektronu lub elektronów ograniczając ich ruch do pewnego obszaru w przestrzeni
(aczkolwiek pamiętajmy o tym, że zawsze z pewnym niezerowym prawdopodobieństwem
elektron może być gdzie indziej, nawet na krańcu wszechświata !). Wobec tego, w świetle
wcześniejszej dyskusji, elektron może w atomie przebywać tylko w wybranych dyskretnych
stanach kwantowych o tj. stanach o pewnych wybranych energiach.

Rozpatrując atomy z tego punktu widzenia należy pamiętać, że formalnie rzecz ujmując

tak naprawdę zawsze określamy energię potencjalną układu elektron-proton (czyli całego
atomu). Zazwyczaj jednak (ale nie zawsze !) energię w całości można przypisać elektronowi,
ponieważ ma masę znacznie mniejszą od masy protonu (o 3 rzędy wielkości), więc niejako
to proton „rządzi” ruchem elektronu a nie na odwrót (po prostu obiekty mniej masywne
doznają w polu sił elektromagnetycznych znacznie większego przyspieszenia niż masywne).

Dozwolone wartości energii elektronu w atomie (nazywane też poziomami

energetycznymi czy powłokami elektronowymi) można określić rozwiązując równanie
Schrödingera ze skończoną energią potencjalną oddziaływania elektrostatycznego układu
protony-elektrony, czyli znajdując funkcje falowe opisujące stany elektronów w takiej
skończonej studni potencjału (poniżej podana jest wersja równania dla studni
jednowymiarowej):

( )

2

2

2

2

d

8

0

d

m

E U x

x

h

π

Ψ +

−

Ψ =









,

(3)

3

gdzie E jest całkowitą energią mechaniczną (tj. sumą energii potencjalnej i kinetycznej)
cząstki, zaś U(x) – energią potencjalną pola działających na nią sił.

Stan o najniższej energii jest tzw. stanem podstawowym. Jego energia nie może być

równa zeru, bo to oznaczałoby zerowanie kwadratu modułu funkcji falowej elektronu (czyli
gęstości prawdopodobieństwa), co z kolei byłoby równoznaczne z brakiem elektronu
w studni potencjału, czyli w atomie (lecz pamiętać należy, iż dotyczy to tylko fal materii (w
tym przypadku elektronów) zlokalizowanych – niezlokalizowane mogą mieć energię
zerową). Elektrony, jak wszystko w przyrodzie, dążą do osiągnięcia dostępnego stanu o jak
najniższej energii, więc w atomie w naturalny sposób będą obsadzać poziomy poczynając
od najniższego (względem jądra). Nie stłoczą się na jednym poziomie o najniższej energii, bo
elektrony (jak i wiele innych cząstek zwanych fermionami (zaliczają się do nich także
np. protony)) podlegają tzw. zakazowi Pauliego, regule, która mówi, że w dowolnym
układzie złożonym z oddziałujących na siebie cząstek (jak choćby właśnie elektrony
w atomie) nie może być nawet 2 o identycznym zestawie pewnych cech, tzw. liczb
kwantowych, określających dopuszczalne stany kwantowe w jakich te cząstki mogą się
znaleźć. Innymi słowy w atomie nie może być elektronów w tym samym, identycznym stanie
kwantowym. Z tego właśnie względu elektrony okupują coraz wyższe energetycznie
poziomy. Gdy mamy do czynienia z atomem o tak właśnie obsadzonych poziomach,
mówimy, że znajduje się on w stanie podstawowym (inaczej – niewzbudzonym). Rozwiązania
równania Schrödingera pokazują jednak, że w każdym atomie obok owych
„podstawowych” istnieją także „potencjalne” (oczywiście nadal dyskretne) poziomy
energetyczne, tj. takie, które mogą zostać zajęte przez elektrony, pod warunkiem, że zyskają
skądś potrzebną do takiego przeskoku energię (rozważamy tu oczywiście stany o energiach
mniejszych niż energia potencjalna układu jądro-elektron – jeśli elektron zyska energie
większą, to po prostu uwolni się z pola oddziaływania jądra i opuści studnie potencjału
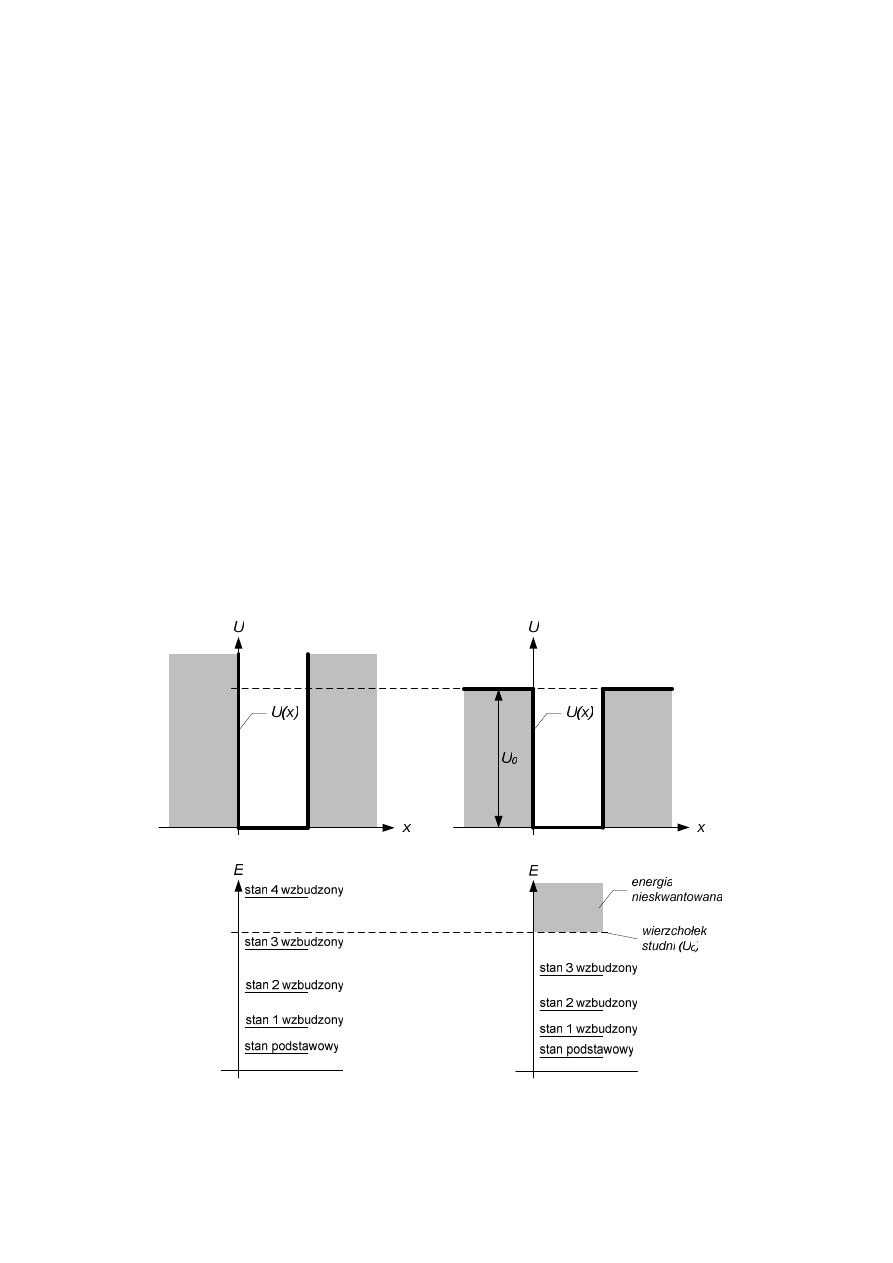
stając się elektronem swobodnym. Taką sytuację nazywamy jonizacją atomu (rys. 2).

(a)

(b)

Rys. 2 Nieskończona studnia potencjału (a) i skończona (b) oraz odpowiadające im

diagramy poziomów energetycznych

4

Jeśli elektron wędruje na wyższy poziom, mówimy o wzbudzeniu atomu/elektronu, ale jest

to generalnie stan „nienaturalny” i układ „z chęcią” powraca do stanu o najniższej możliwej
energii, czyli stanu podstawowego. Stany wzbudzone są więc krótkotrwałe (typowo
∆t

≅

10

-8

s), w rezultacie czego związane z nimi poziomy energetyczne nie są już „ściśle”

dyskretne, jak stany podstawowe, lecz nieco rozmyte. Jest to ponownie przejaw falowej
natury materii, tym razem manifestującej się w postaci nieoznaczoności charakteryzującej
pewne pary wielkości fizycznych. Opisuje to zasada nieoznaczoności Heisenberga ∆E∆t

≥

h,

która natychmiast pozwala wyznaczyć szerokość, czyli rozmycie energetyczne takich
poziomów w atomach:

h

E

t

∆ ≅

∆

(4)

Typowe rozmycie poziomu energetycznego stanu wzbudzonego jest w takim razie rzędu
10

-7

eV. Jeszcze raz należy podkreślić, że nie odnosi się to do stanów podstawowych

w atomie, gdyż czas przebywania w nich elektronów → ∞, w związku z czym ich rozmycie
energetyczne → 0 (rys. 3).

Rys. 3 Rozmycie energetyczne poziomów wzbudzonych w izolowanym atomie

3.

Poziomy energetyczne elektronu w krysztale; pasmowy model energetyczny ciała

stałego

W atomie izolowanym znajdującym się w stanie podstawowym poziomy energetyczne

przyjmują zatem dyskretne wartości (zaś wzbudzone są nieznacznie rozmyte). Sytuacja
zmienia się jednakże, gdy atomy zaczynają się do siebie zbliżać, czyli np. gdy powstawać
zaczyna ciało stałe. Wówczas bowiem atomy zaczynają one „odczuwać” swoją obecność,
co wynika z faktu, że funkcje falowe ich elektronów zaczynają się na siebie nakładać,
poczynając przy tym oczywiście od funkcji falowych elektronów najbardziej zewnętrznych,
tzw. walencyjnych. Pojawia się też skończone prawdopodobieństwo ich tunelowania
pomiędzy atomami. Powłoki wewnętrzne natomiast (nie mówiąc już o funkcjach falowych
protonów i neutronów tworzących jądro, czyli po prostu funkcjach falowych jądra
atomowego) prawie na siebie nie oddziałują, bo odległości rozdzielające atomy w ciele
stałym (tzw. stałe sieci krystalicznej) w porównaniu z ich rozmiarami przestrzennymi są
znacznie większe. W rezultacie obsadzające je elektrony są bardzo silnie zlokalizowane
i związane z „macierzystym” jądrem atomowym, przebywając tam praktycznie „zawsze”
(bo prawdopodobieństwo tunelowania przez tak wysokie i szerokie bariery energetyczne jest
bliskie 0). Ponowne zastosowanie zasady nieoznaczoności pokazuje że tym razem nawet
poziomy podstawowe w atomie są rozmyte (choć minimalnie, np. dla poziomu 1s w atomie
sodu ∆E

≅

10

-19

eV) – patrz rys. 4a.

W miarę zbliżania się atomów i rosnącego przekrywania się funkcji falowych elektronów,

przede wszystkim walencyjnych, zaczyna także działać zakaz Pauliego. Tym razem

5

manifestuje się jednak inaczej, niż w przypadku obsadzania dozwolonych poziomów
w atomie izolowanym. Formując ciało stałe, np. kryształ z dowolnych atomów, przysuwamy
ku sobie atomy, z których w każdym najniższe, podstawowe stany kwantowe są już
obsadzone. Pozostają w takim razie do dyspozycji jedynie stany wzbudzone, a jak wiemy
elektrony przebywają w nich krótko a ponadto przeniesienie na nie elektronów ze wszystkich
głębokich powłok (a więc bardzo silnie związanych z jądrem macierzystym) stanowiłoby
bardzo duży wydatek energetyczny. Znacznie korzystniejsze energetycznie okazuje się inne
rozwiązanie. Otóż gdy elektrony tylko zaczynają odczuwać wzajemne oddziaływanie,
wartości energii zajmowanych przez nie poziomów w każdym z atomów zaczynają się
rozszczepiać, tzn. przyjmować nieco inne wartości od tych w stanie izolowanym. I tak dla 2
zbliżających się atomów każdy dyskretny poziom rozszczepi się na 2 podpoziomy. Jeśli więc
przykładowo powstaje kryształ miedzi, której każdy atom otacza 29 elektronów (co oznacza,
że znajdują się one w 29 różnych stanach kwantowych), to po zbliżeniu 2 atomów
dostaniemy w sumie 2x29 czyli 58 podpoziomów itd. Innymi słowy, w układzie złożonym z N
atomów każdy poziom izolowanego atomu ulegnie rozszczepieniu na N podpoziomów. Ich
sumaryczna liczba z kolei wyniesie N

×

liczba poziomów elektronowych w pojedynczym

atomie. W ten sposób każdy dyskretny w izolowanym atomie poziom energetyczny
rozszczepia się na pasmo energetyczne złożone z N podpoziomów. Pasma powstałe
z najwyższych obsadzonych poziomów energetycznych w odizolowanych atomach są
najszersze – ich szerokość E wynosi zazwyczaj od jednego do kilku eV. Wynika z tego, że
np. w krysztale o objętości powiedzmy 1 cm

3

, czyli zawierającym ok. 10

22

atomów, nawet

w owych najszerszych pasmach odległość (energetyczna)

∆

E pomiędzy sąsiednimi

rozszczepionymi podpoziomami będzie rzędu E/10

22

eV, czyli jakieś 10

-22

eV ! Można więc

powiedzieć, że podpoziomy te tworzą de facto ciągłe (ściśle rzecz jasna biorąc quasi
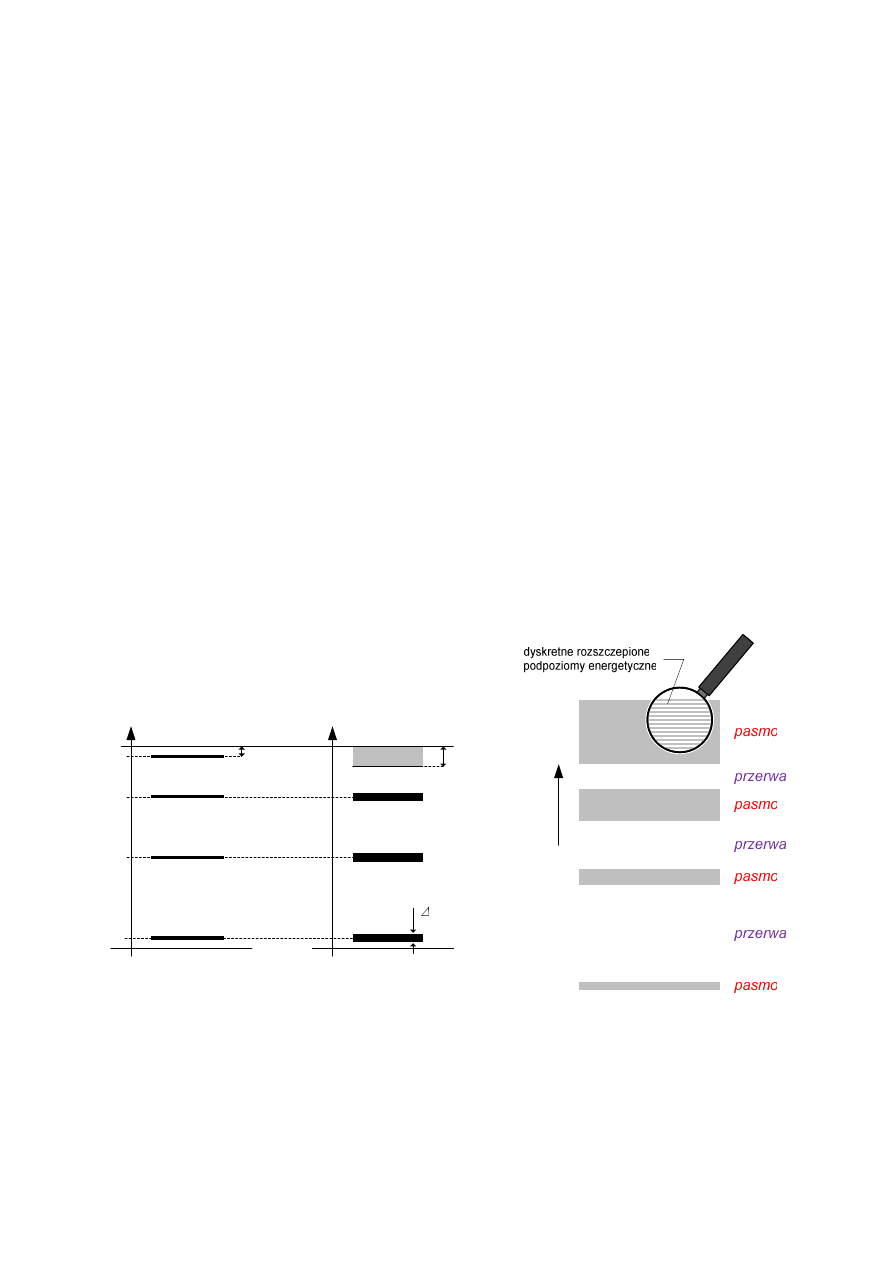
ciągłe) pasmo energetyczne (rys. 4b). Zwróćmy przy tym uwagę, że im większy kryształ
(więcej atomów), tym

∆

E mniejsza – w przypadku kryształu nieskończonego

∆

E spadłaby do

0 i pasma stałyby się faktycznie ciągłe.

E

atom Na

E

kryształ Na

3s

2p

2s

1s

2p

2s

1s

E

j

=5,14 eV

5,5 eV

E = 10

-19

eV

6N stanów

Konfiguracja elektronowa 1s

2

2s

2

2p

6

3s

1

3s

0

2N stanów

2N stanów

e

n

e

rg

ia

(a)

(b)

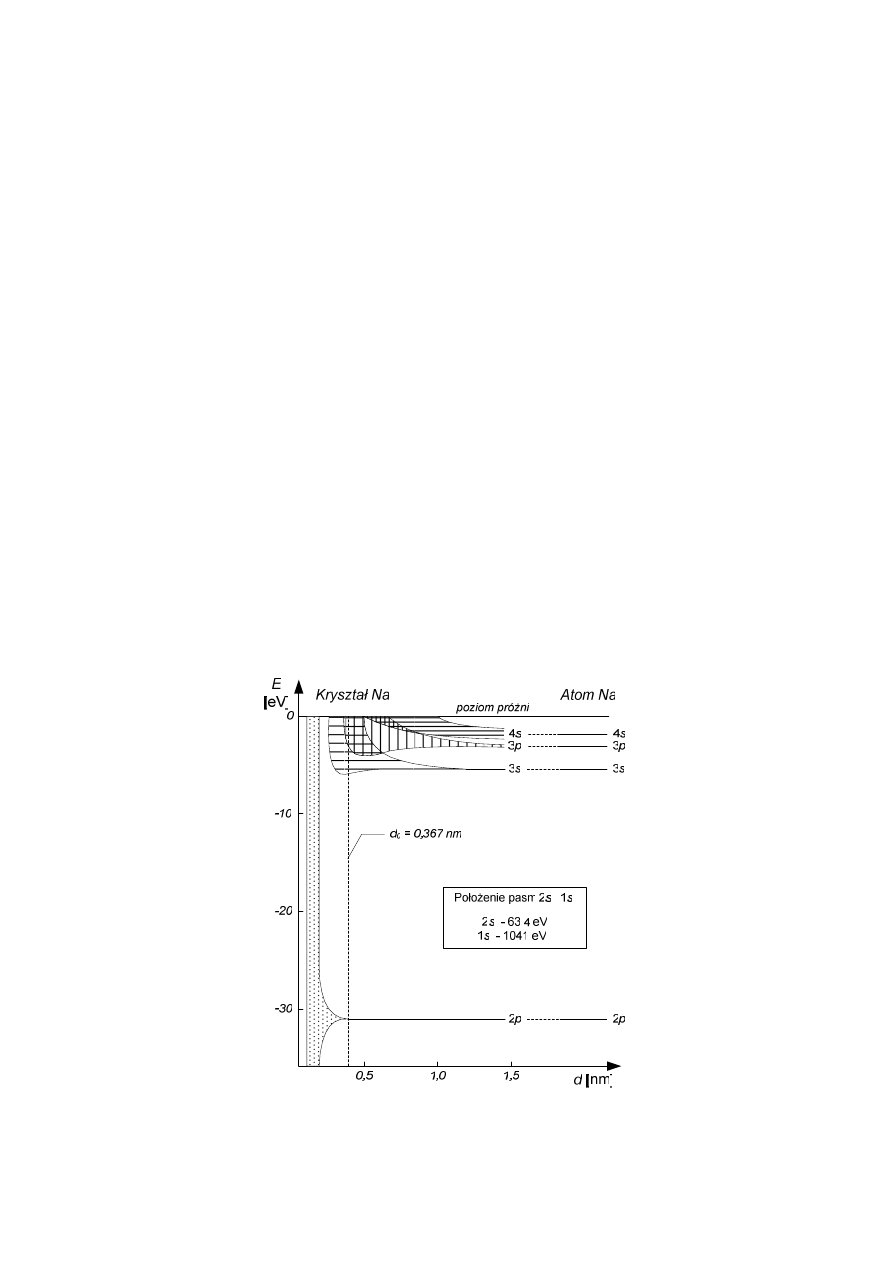
Rys. 4 Poziomy energetyczne w izolowanym atomie sodu i krysztale sodu (skala na osi energii

niezachowana) (a) oraz układ pasm i przerw energetycznych tworzących strukturę

energetyczną (model pasmowy) wyidealizowanego kryształu (b)

Pasma te, podobnie jak dyskretne poziomy w odizolowanych atomach, rozdzielone są

przez obszary energii zabronionych, tj. takich, których elektrony przyjmować nie mogą.

6

Warto tu zauważyć prawidłowość, że im głębiej w stronę jądra, tym szerokość pasm
dozwolonych mniejsza zaś przerw większa (ich szerokości stają się tego samego rzędu
właściwie dla najwyżej położonych pasm energetycznych oraz rozdzielających je przerwy
zabronionej). Reprezentacja graficzna takiego układu pasm i przerw energetycznych
tworzących strukturę energetyczną ciała stałego nazywamy modelem pasmowym (rys.4b).
Wiąże się to ze wzmiankowanym już faktem, iż funkcje falowe elektronów obsadzających
niższe poziomy energetyczne przekrywają się z funkcjami falowymi elektronów innych
atomów w znacznie mniejszym stopniu niż funkcje falowe elektronów z powłok
zewnętrznych, czyli po prostu słabiej ze sobą oddziałują, co skutkuje mniejszym
rozszczepieniem tych poziomów – można powiedzieć, że te głębsze poziomy są „bardziej”
ciągłe.

Podpoziomy energetyczne w pasmach kryształu, podobnie jak to się dzieje z dyskretnymi

poziomami w izolowanym atomie, obsadzane są poczynając od tych o najniższych
energiach, aczkolwiek występują pewne odstępstwa od tej reguły, bo atom, jak już wiemy,
musimy traktować całościowo. Otóż bywa, że w atomie (dotyczy to cięższych pierwiastków)
niektóre z niższych poziomów podstawowych nie są obsadzane, bo elektrony w stanie
podstawowym lokują się na poziomach wyższych. Wiąże się to z faktem, iż energia atomu
o tak ulokowanych elektronach jest niższa niż atomu, w którym elektrony zapełniałyby
literalnie poziomy od najniższego do najwyższego.

Najwyższe pasmo energetyczne obsadzone w temperaturze zera bezwzględnego

nazywamy pasmem walencyjnym bo zajmują je właśnie elektrony walencyjne, czyli
pochodzące z ostatniej, najbardziej zewnętrznej powłoki każdego z atomów. Natomiast
pierwsze z kolei całkowicie nieobsadzone w temperaturze 0 K pasmo nazywane jest
pasmem przewodnictwa. W modelach energetycznych (jak i wielu innych rozważaniach)
ograniczamy się zazwyczaj tylko do tych ostatnich pasm, bo właściwie o wszystkich
cechach materii w skali makroskopowej (czyli np. jej własnościach fizycznych czy
chemicznych) decyduje struktura atomowych powłok walencyjnych i oddziaływanie
obsadzających je elektronów (gdyż, jak wspomniano, głębiej zlokalizowane elektrony
praktycznie nie oddziałują z otoczeniem).

(a)

7

(b)

Rys. 5 Rozszczepianie się energetycznych poziomów przy tworzeniu się kryształów sodu (a)

i diamentu (b) oraz wynikające z tego struktury energetyczne obydwu materiałów

W zależności od rodzaju atomów tworzących ciało stałe ich poziomy energetyczne

mogą się rozszczepiać w taki sposób, że powstające pasma będą się na siebie się nakładać
albo i nie – wówczas będą rozdzielone obszarami energii niedozwolonych dla elektronów,
nazywanymi przerwami energetycznymi E

g

(rys. 5). W analogiczny sposób rozszczepiać się

będą również i „ewoluować” wyższe pasma, nieobsadzone w sytuacji, gdy atom pozostaje
w stanie podstawowym – są one przecież obszarami energii potencjalnie dostępnymi dla
elektronów, aczkolwiek zazwyczaj rozpatrywanie ich zachowania nie ma znaczenia
praktycznego.

4. Dielektryki, półprzewodniki i metale

Materiały, których pasmo walencyjne jest całkowicie obsadzone w temperaturze 0 K nie

mogą w takich warunkach przewodzić prądu, nawet przy dużych wartościach pola
elektrycznego, bo zapełniające to pasmo elektrony, ze względu na zakaz Pauliego, „nie
mają gdzie się ruszyć”, bo nie mają w swoim sąsiedztwie energetycznym stanów, na które
mogłyby przejść. A brak ruchu ładunku oczywiście oznacza brak przepływu prądu. Aby
w takim materiale elektron mógł się przemieścić, musiałby przeskoczyć do wyższego pasma,
gdzie ma dostępne wolne poziomy energetyczne. Jednak przerwa energetyczna E

g

między

tymi pasmami jest typowo rzędu jednego-kilku elektronowoltów. Takiej więc energii trzeba
dostarczyć elektronom, aby się tam znalazły i tym samym umożliwiły przepływ prądu.
Fizycznie równoważne jest to jednak dostarczeniu elektronom energii potrzebnej do
wyrwania elektronu walencyjnego z pola sił przyciągania elektrostatycznego atomu
macierzystego (czyli po prostu do zerwania wiązania). Tyle, że energia (kinetyczna), jaką
elektron może uzyskać pokonując średnią drogę swobodną w przyłożonym polu
elektrycznym o typowych dla struktur elektronicznych wartościach kształtuje się na poziomie
10

-8…4

eV, czyli o rzędy wielkości za mało. Do uzyskania zauważalnego przewodnictwa jest

zatem potrzebna jakaś inna metoda aktywacji elektronów. Zazwyczaj odbywa się
to poprzez dostarczenie im energii w postaci kwantów (np. promieniowania
elektromagnetycznego) o wartości większej od E

g

albo po prostu aktywacja termiczna.

W tym drugim jednak przypadku i tak mało skuteczna, gdyż prawdopodobieństwo
obsadzeń przez elektrony nieobsadzonych poziomów w danych warunkach (temperaturze)

8

podlega statystyce Fermiego-Diraca, z której wynika, że średnio, wskutek podgrzewania
materiału elektrony i tak mogą uzyskać przyrost energii na poziomie od kT do maksymalnie
kilku kT. A kT to przecież w temperaturze pokojowej zaledwie 0,026 eV. Zawsze oczywiście
istnieje w statystycznym rozkładzie energii cząstek wysokoenergetyczny „ogon”, ale
obejmuje niewielką ich liczbę, więc sama aktywacja termiczna w takim materiale jest mało
skuteczna. Temperatury, w których by zadziałała są na poziomie ponad 10

4

K (energia 1 eV

odpowiada temperaturze ponad 11 000 K !), a więc w zakresie, w którym żadne ciało stałe
nie może przecież istnieć.

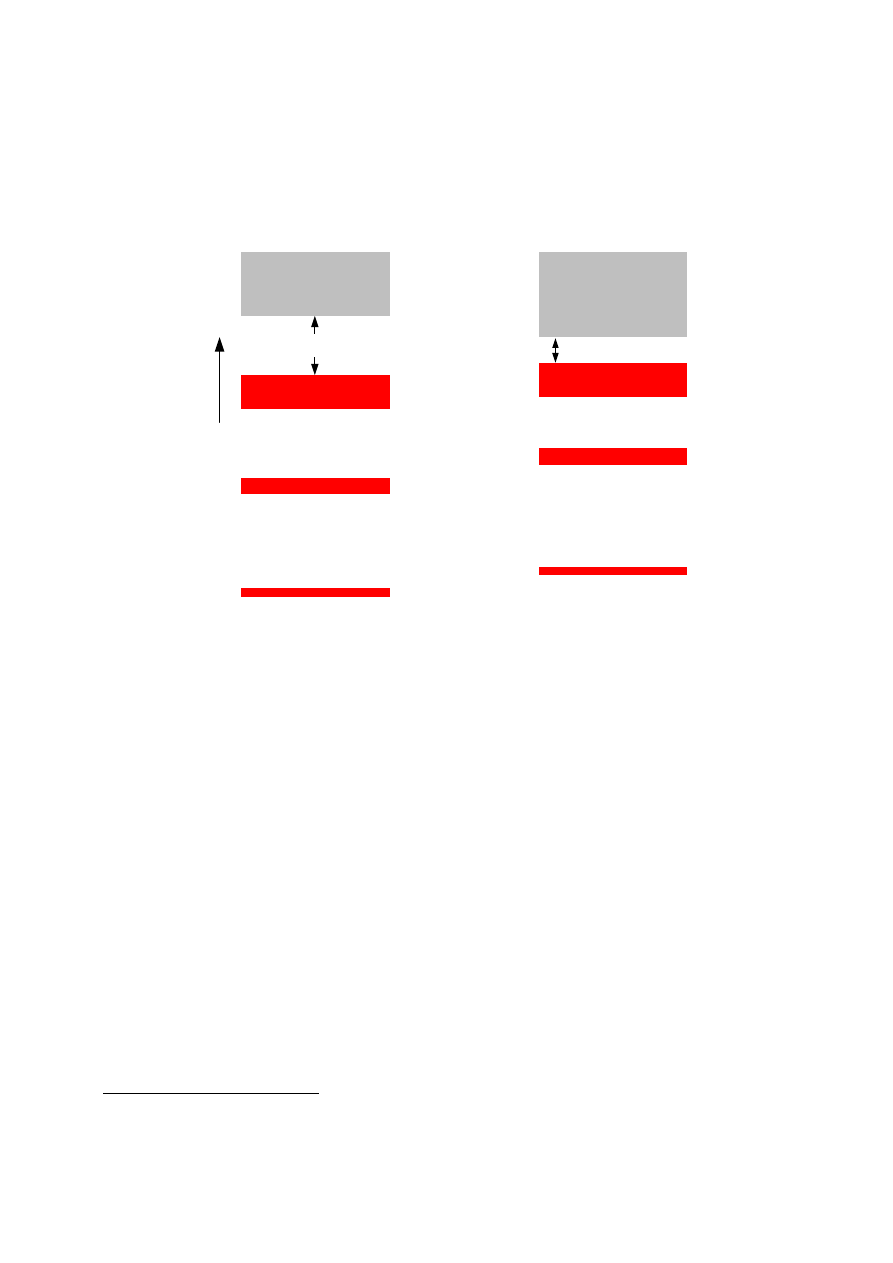
pasmo walencyjne

pasmo

przewodnictwa

e

n

e

rg

ia

pasmo walencyjne

pasmo

przewodnictwa

E

g

>

2...3 eV

E

g

<

2...3 eV

(a)

(b)

Rys. 6 Układ pasm i przerw tworzących strukturę energetyczną (model pasmowy) izolatora

(a) i półprzewodnika (b) (na czerwono zaznaczono poziomy całkowicie obsadzone)

Materiały o opisanych własnościach w ogólności nazywamy dielektrykami. W przypadku,

gdy szerokość ich przerwy energetycznej E

g

jest nie większa niż 2…3 eV określane są jako

półprzewodniki (rys. 6). Czyli półprzewodnik w tym ujęciu to po prostu dielektryk z względnie
wąską przerwą energetyczną, co oznacza, że w tych samych warunkach termicznych
charakteryzuje go większe prawdopodobieństwo pokonania przez niektóre elektrony
przerwy energetycznej (więcej z nich może tego dokonać, czyli łatwiej im zerwać wiązania),
a więc koncentracja tzw. swobodnych nośników ładunku jest w nich większa niż
w dielektrykach (choć i tak mała).

Inaczej wygląda sytuacja w materiałach, w których w ogóle nie ma przerwy zabronionej.

Można przy tym wyróżnić 2 przypadki. W pierwszym w temperaturze 0 K pasmo walencyjne
jest zapełnione częściowo. Najwyższy obsadzony w takich warunkach poziom nazywany jest
poziomem Fermiego, zaś odpowiadająca mu energia nosi nazwę energii Fermiego (E

F

),

która wynosi typowo kilka eV (np. w Cu E

F

= 7 eV)

1

. Drugi zaś przypadek obejmuje materiały,

w których pasmo walencyjne i przewodnictwa (powstające, przypomnijmy, z wolnych,
normalnie nieobsadzonych, czyli wzbudzonych poziomów atomowych) nakładają się
częściowo na siebie (takie zjawisko nazywamy hybrydyzacją pasma), co daje elektronom
z pasma walencyjnego (nawet jeśli je całkowicie zapełniają) obszar dostępnych,
nieobsadzonych poziomów w ich bezpośrednim sąsiedztwie energetycznym. W obydwu

1

Pokazuje to, jak mylne jest wyobrażenie, iż w temperaturze zera bezwzględnego panuje całkowity bezruch –
prędkość elektronu z poziomu Fermiego (v

F

), a więc o energii E

F

może być bardzo duża (we wspomnianej Cu

jest rzędu 1,6

×

10

6

m/s !!! – a wszystko to wynika z zakazu Pauliego).

9

przypadkach więc, zarówno częściowo zapełnione pasmo walencyjne jak i hybrydowe
pełnią rolę pasma przewodnictwa (rys. 7).

e

n

e

rg

ia

(a)

(b)

Rys. 7 Układ pasm i przerw tworzących strukturę energetyczną (model pasmowy) metali –

materiał z częściowo zapełnionym pasmem walencyjnym (a) oraz z częściowo

nakładającymi się na siebie pasmami walencyjnym i przewodnictwa (b)

W rezultacie materiały te, nawet w temperaturze zera bezwzględnego mogą przewodzić

prąd elektryczny, ponieważ w obydwu przypadkach w bezpośrednim energetycznym
sąsiedztwie elektrony z poziomu Fermiego i z nim sąsiadujących mają do dyspozycji quasi
kontinuum nieobsadzonych stanów energetycznych, które mogą swobodnie, nawet
w temperaturze 0 K zajmować. Jest to możliwe, gdyż poziomy te, jak już pokazano,
w typowych rozmiarów materiale odległe są od siebie o 10

-22…23

eV, podczas gdy typowe

pole elektryczne może im nadać energie rzędu 10

-8…4

eV. Materiały o takich własnościach

nazywamy metalami.

Oczywiście również podniesienie temperatury metalu spowoduje, iż część elektronów

zyska energię termiczną pozwalającą na przeniesienie się na wyższe, nieobsadzone poziomy
energetyczne. Nie wpływa to jednak w rzeczywistości w jakiś istotny sposób na
przewodnictwo elektryczne metali (w rzeczywistości ze wzrostem temperatury wręcz ono
spada, co tłumaczy dopiero kwantowa teoria przewodnictwa, którą jednak tu nie będziemy
się zajmować). Analogicznie, jak w przypadku dielektryków (i półprzewodników), statystyka
Fermiego-Diraca pokazuje, iż nawet w wysokich temperaturach rzędu 1000 K (0,086 eV),
a więc gdy materiał już zaczyna świecić, tylko bardzo mikroskopijna część ogólnej liczby
elektronów przewodnictwa (znajdujących się w pobliżu poziomu Fermiego) może zostać
wzbudzona termicznie, przechodząc na wyższe poziomy. Prawdopodobieństwo P(E)
obsadzenia stanu przekraczającego E

F

o E opisuje zależność:

( )

1

1

F

E E

kT

P E

e

−

=

+

(5)

Podstawiając do niej konkretne dane możemy np. się przekonać, że w temperaturze 1000 K
prawdopodobieństwo obsadzenia stanu przekraczającego E

F

o 5kT wynosi zaledwie 0,6 % !

Widać więc, że tym bardziej w przypadku półprzewodników sama aktywacja termiczna

praktycznie nic nie zmieni, gdyż ich przewodnictwo, nie tylko w temperaturze pokojowej
ale i w temperaturach bliskich stopienia bądź wyparowania, będzie znikomo małe, bo takaż
będzie liczba elektronów w paśmie przewodnictwa (w półprzewodnikach E

F

lokuje się

w przerwie zabronionej, więc wartości E-E

F

i tym samym wykładnika w zależności (5) są

10

jeszcze większe). Liczbę takich elektronów przypadających na jednostkę objętości
półprzewodnika nazywamy koncentracją samoistną n

i

. Przykładowo w temperaturze

pokojowej w krzemie kształtuje się ona na poziomie 10

10

cm

-3

, podczas gdy wszystkich

elektronów walencyjnych jest tam około 10

23

cm

-3

! Różnica między półprzewodnikiem

a dielektrykiem o typowych rozmiarach sprowadza się więc z tego punktu widzenia tylko
i wyłącznie do tego, że w tym pierwszym przypadku istnieje realne prawdopodobieństwo
tego, iż drgania termiczne w materiale są w stanie przenieść jakąś (choć bardzo małą)
część elektronów do pasma przewodnictwa (bo np. w Ge E

g

= 0,7 eV a w Si E

g

= 1,1 eV),

podczas gdy w drugim (np. w diamencie, w którym E

g

= 5,5 eV) jest to praktycznie

wykluczone. Niemniej w takim ujęciu zarówno półprzewodniki, jak i dielektryki w zasadzie
niewiele się różnią. Natomiast kardynalnie odróżniają się od metali. Przykładowo
koncentracja swobodnych nośników prądu w Cu, porównywalna z koncentracją atomów
miedzi, jest 10

11

razy większa niż w czystym Ge i aż 10

13

niż w czystym Si, bo w Ge tylko jeden

na 10 miliardów (1/10

10

) zaś w Si tylko jeden na bilion (1/10

12

) atomów oddaje swój elektron

walencyjny na rzecz przewodnictwa !

Jednak jednym z czynników, który zadecydował o karierze półprzewodników jest m.in.

fakt, że można w nich zmieniać koncentracje nośników prądu (a więc i przewodnictwo)
w bardzo szerokim (rzędy wielkości) zakresie.

pasmo walencyjne

pasmo

przewodnictwa

E

g

dziury

elektrony

Rys. 8 Model pasmowy półprzewodnika z zaznaczonymi elektronami przeniesionymi do

pasma przewodnictwa i „wytworzonymi” przez nie w związku z tym dziurami w paśmie

walencyjnym

Zacznijmy od tego, że te nieliczne elektrony z pasma walencyjnego, które pozyskają

dostatecznie dużą energię aby przejść do pasma przewodnictwa (czyli fizycznie, jak
pamiętamy, zerwać wiązanie kowalencyjne) i tym samym stać się nośnikami swobodnymi,
pozostawiają po sobie w paśmie walencyjnym wolne nieobsadzone stany energetyczne,
luki, które nazywane są dziurami (rys. 8). W takiej sytuacji pozostałe elektrony z pasma
walencyjnego zyskują pewną swobodę ruchu, bo zyskują pewną ilość nieobsadzonych teraz
stanów energetycznych, które mogą zajmować. Jeśli więc pojawi się teraz w materiale pole
elektryczne E, to elektrony w paśmie walencyjnym będą unoszone w kierunku przeciwnym
do zwrotu tego pola (jak zresztą każda ujemnie naładowana cząstka), przeskakując od luki
do luki. Bez dziur ich przemieszczanie się w polu elektrycznym nadal byłoby zablokowane.
W innym ujęciu można stwierdzić, że to położenia dziur będą się przemieszczać, tyle że
w przeciwnym kierunku (a więc zgodnie ze zwrotem pola elektrycznego). W rezultacie
dziury zachowują się jak dodatnio naładowane cząstki (o dodatnim ładunku
elementarnym). I w taki właśnie sposób rozpatrywany jest ruch elektronów w paśmie
walencyjnym – łatwiej jest analizować i opisywać przemieszczanie się takich luk, gdyż jest ich
po prostu mniej niż samych elektronów. W rezultacie na całkowity prąd elektryczny płynący
w półprzewodniku składa się sumaryczny przepływ swobodnych elektronów w paśmie
przewodnictwa (czyli tzw. prąd elektronowy I

e

) oraz przepływ dziur w paśmie walencyjnym

11

(czyli tzw. prąd dziurowy I

d

). Łatwo to sobie wyobrazić pamiętając, że prąd dziurowy to też

ruch elektronów, tyle że w paśmie walencyjnym. Właśnie fakt, iż w półprzewodnikach
w paśmie walencyjnym mogą powstawać wolne stany energetyczne (dziury), czyli że
elektrony mogą się jednocześnie przemieszczać na 2 poziomach energetycznych
(przewodnictwa i walencyjnym) stał się jednym z głównych czynników rozwoju elektroniki.

5. Półprzewodniki domieszkowane

Mimo, iż w czystym półprzewodniku, jak wspomniano, koncentracja swobodnych

nośników prądu jest bardzo mała, to sytuacja może ulec znaczącej zmianie, jeśli do
półprzewodnika (a w ogólności także i do izolatora) wprowadzimy odpowiednio dobrane
obce atomy, zwane domieszkami. Taki zabieg nazywamy domieszkowaniem, a realizowany
jest albo in situ, tj. w trakcie wytwarzania monokryształu półprzewodnikowego albo później,
metodą dyfuzji (zazwyczaj) wysokotemperaturowej atomów lub implantacji jonów domieszki
(czyli wysokoenergetycznego wstrzeliwania jonów domieszki w strukturę monokryształu).
Istotne jest przy tym, aby atomy te ulokowały się w węzłach sieci krystalicznej materiału, czyli
zastąpiły (często mówimy podstawiły) w nich atomy macierzyste. Zwykle jest ich niewiele
w porównaniu z liczbą atomów macierzystych – np. jeden na milion, choć we
współczesnych strukturach może być ich znacznie więcej, w skrajnych przypadkach nawet
jeden na 10 000 – ale nawet ta śladowa obecność może istotnie zmienić przewodność
półprzewodnika. Praktycznie wszystkie współczesne przyrządy półprzewodnikowe bazują na
materiałach domieszkowanych. Istnieją przy tym 2 rodzaje domieszkowania, zwane
domieszkowaniem typu n oraz domieszkowaniem typu p.

5.1 Półprzewodniki typu n

Rozpatrzmy kryształ krzemu. W izolowanych atomach tego pierwiastka w stanie

podstawowym (a więc niewzbudzonym) elektrony zajmują kolejne podpowłoki
energetyczne w następujący sposób:

1s

2

2s

2

2p

6

3s

2

3p

2

.

Tworząc kryształ każdy atom Si „przeznacza” parę elektronów z podpowłoki 3s oraz parę
z podpowłoki 3p na uformowanie mocnych 2-elektronowych wiązań kowalencyjnych
z każdym z 4 sąsiadujących atomów (każde 2 elektrony tworzące to wiązanie stają się
wspólne dla obydwu atomów – nazywamy je uwspólnionymi). W skali całego kryształu
wszystkie elektrony tworzące międzyatomowe wiązania kowalencyjne tworzą pasmo
walencyjne energii. Jak pamiętamy, aby jakikolwiek z tych elektronów mógł stać się
elektronem swobodnym, tj. znaleźć się w paśmie przewodnictwa musi uzyskać energię
potrzebną „fizycznie” do zerwania któregoś z tych wiązań. Minimalna wartość tej energii jest
właśnie równa energii przerwy zabronionej E

g

.

Jeśli jednak któryś z atomów Si zastąpimy atomem pierwiastka, który ma 5 elektronów

walencyjnych (np. fosforu), to 4 z nich, analogicznie do atomów krzemu utworzą z sąsiadami
wiązania kowalencyjne. Natomiast piąty elektron będzie w takiej sytuacji „nadmiarowym”,
słabo związanym z macierzystym rdzeniem atomu fosforu. W języku modelu pasmowego
możemy wówczas powiedzieć, że taki elektron zajmuje zlokalizowany stan energetyczny,
który znajduje się w obszarze pasma zabronionego w pewnej odległości (E

d

) poniżej dna

pasma przewodnictwa. Ponieważ ta „odległość” jest niewielka, znacznie mniejsza od E

g

(a przynajmniej dla domieszek, które chcemy wykorzystać w praktyce taka powinna być),
więc taka też jest energia potrzebna do wzbudzenia takiego elektronu, czyli przeniesienia
go do pasma przewodnictwa (rys. 9). Typowo jej wartość kształtuje się na poziomie setnych
części eV (np. w przypadku domieszkowania krzemu fosforem wynosi 0,044 eV), a to
oznacza, że w temperaturze pokojowej statystycznie rzecz biorąc praktycznie wszystkie
z takich elektronów są wzbudzone, a więc są swobodnymi elektronami pasma
przewodnictwa (mówimy o takiej sytuacji, że atomy domieszki są termicznie zjonizowane).
Domieszki dostarczające dodatkowych elektronów do pasma przewodnictwa nazywamy
donorami. W materiale takim w paśmie przewodnictwa jest znacznie więcej elektronów niż

12

dziur w paśmie walencyjnym, więc mówimy, że elektrony są tu nośnikami większościowymi
zaś dziury – mniejszościowymi.

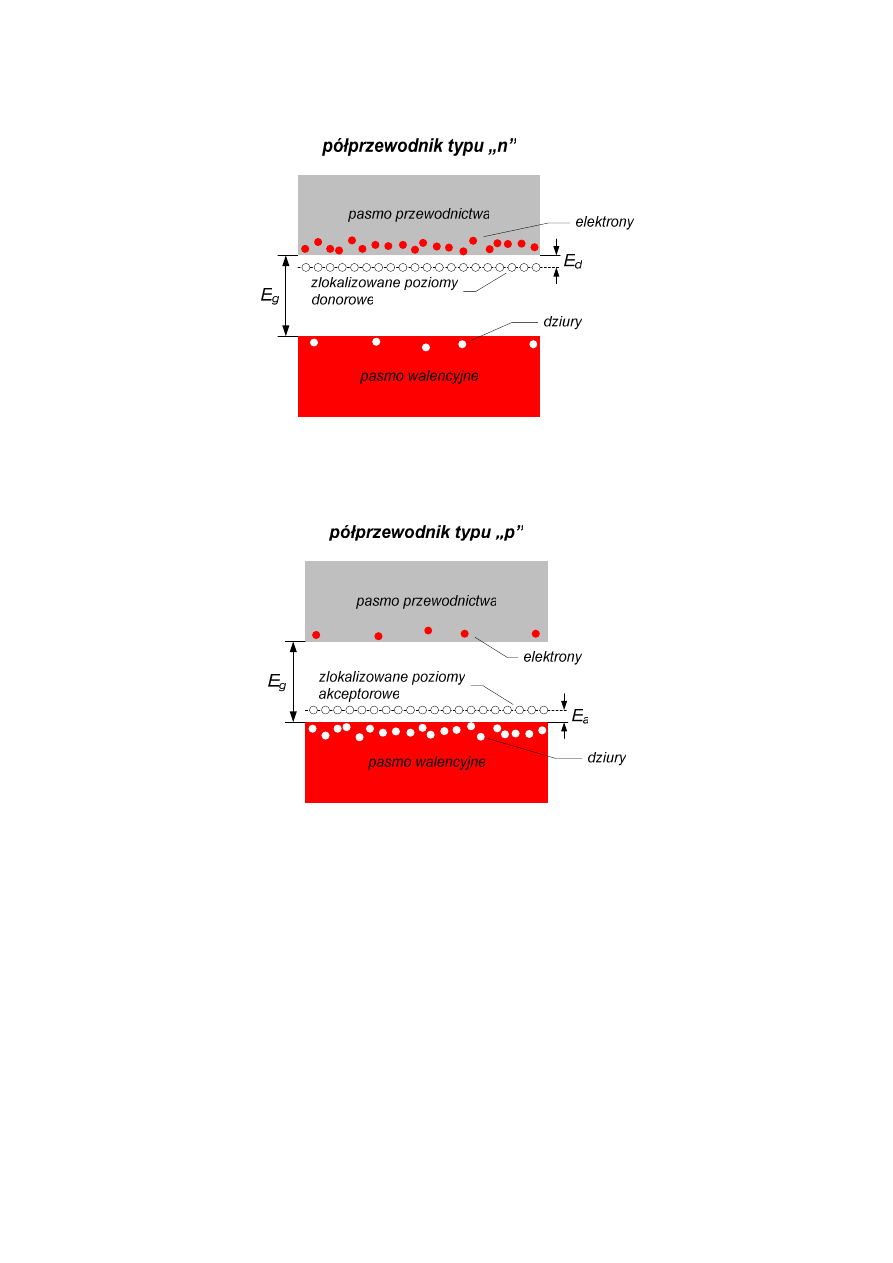
Rys. 9 Model pasmowy półprzewodnika typu n

5.2 Półprzewodnik typu p

Rys. 10 Model pasmowy półprzewodnika typu p

Z analogiczną poniekąd sytuacją będziemy mieli do czynienia, gdy niektóre z atomów

krzemu w sieci kryształu zastąpimy atomami pierwiastka, który ma tylko 3 elektrony
walencyjne (a więc o 1 mniej niż Si). Takim pierwiastkiem jest np. bor. Elektrony te w ten sam
sposób, jak opisano wyżej utworzą 3 dwuelektronowe wiązania kowalencyjne z sąsiednimi
atomami krzemu, natomiast w czwartym wiązaniu kowalencyjnym (a więc i w paśmie
walencyjnym) z czwartym sąsiadem będzie brakować jednego elektronu, czyli będzie tam
po prostu dziura. Może ona zostać zapełniona niewielkim kosztem energetycznym przez jakiś
elektron z sąsiedniego wiązania pomiędzy atomami Si-Si (czy B-Si). Powstałą w ów sposób
kolejną lukę elektronową w wiązaniu może zapełnić następny elektron z kolejnego wiązania,
itd. W rezultacie taka dziura w paśmie walencyjnym półprzewodnika zachowuje się jak
wiemy, jak dodatni nośnik ładunku i może się przemieszczać po całej sieci krystalicznej,
dając w przypadku obecności pola elektrycznego E przyczynek do przepływu prądu
całkowitego. W kategoriach modelu pasmowego możemy powiedzieć, że każdy atom
takiej domieszki tworzy zlokalizowany stan energetyczny znajdujący się w obszarze przerwy

13

zabronionej w pewnej odległości (E

a

) ponad wierzchołkiem pasma walencyjnego

półprzewodnika. Jak wspomniano, elektron z sąsiedniego wiązania bardzo łatwo może
obsadzić ten stan, pozostawiając dziurę w paśmie walencyjnym – energia do tego
potrzebna jest niewielka, np. w przypadku boru w krzemie wynosi 0,045 eV. A to znów
oznacza, że w temperaturze pokojowej praktycznie we wszystkich atomach takiej domieszki
owe stany są obsadzone przez elektrony z pasma walencyjnego, w efekcie czego pojawia
się w nim populacja dziur (rys. 10). Domieszki opisanego właśnie typu nazywane są z kolei
akceptorami. W takim półprzewodniku znacznie więcej jest dziur w paśmie walencyjnym niż
elektronów w paśmie przewodnictwa, dziury są więc nośnikami większościowymi zaś
elektrony mniejszościowymi.

W sytuacji, gdy w materiale znajdują się obydwa rodzaje domieszek, o dominującym

charakterze jego przewodnictwa (elektronowe czy dziurowe) decyduje, koncentracja której
z domieszek (donorowej czy akceptorowej) jest większa.

6. Złącze p-n

Jeśli połączymy ze sobą dwa półprzewodniki o przeciwnych typach przewodnictwa, to

otrzymamy fundamentalną dla całej elektroniki strukturę zwaną złączem p-n. Zwykłe
zetknięcie czy sklejenie takich materiałów zazwyczaj nie da oczekiwanego efektu, gdyż aby
takie złącze powstało pomiędzy obydwoma obszarami musi istnieć ciągłe przejście
pomiędzy ich strukturami krystalicznymi. Stąd w praktyce złącze p-n wytwarzane jest na
drodze domieszkowania materiału o danym typie przewodnictwa domieszką o typie
przeciwnym. W rezultacie w materiale powstają dwa obszary: jeden, w którym większa jest
koncentracja domieszki donorowej N

D

(materiał typu n), a tym samym i elektronów

w paśmie przewodnictwa oraz drugi obszar z większą koncentracją domieszki akceptorowej
N

A

(materiał typu p), czyli dziur w paśmie walencyjnym. Umownie obydwa obszary złącza

rozgranicza tzw. złącze metalurgiczne definiowane jako miejsce, a ściślej powierzchnia, na
której koncentracje domieszek donorowej i akceptorowej się zrównują. Rzeczywiste profile
rozkładów ich koncentracji charakteryzują pewne gradienty (tj. nie są one stałe w funkcji
odległości np. od powierzchni struktury czy też powierzchni metalurgicznej złącza). W wielu
jednak przypadkach (np. w celu uproszczenia modelowania takich struktur) rzeczywiste
rozkłady aproksymuje się profilem skokowym (mówimy wtedy, że złącze p-n jest skokowe)
albo liniowym (takie złącze nazywamy liniowym złączem p-n). Przyjmuje się więc, że stały
rozkład koncentracji domieszek zmienia się albo skokowo w obszarze złącza (ma to miejsce
w złączach epitaksjalnych, płytkich złączach dyfuzyjnych i otrzymywanych w wyniku
niskoenergetycznej implantacji jonów) lub łagodnie, co można przybliżyć rozkładem
liniowym (taki charakter posiadają głębokie złącza dyfuzyjne i otrzymywane wskutek
wysokoenergetycznej implantacji jonów). Ponadto należy zauważyć, że koncentracje
atomów domieszek akceptorowej i donorowej po obydwu stronach złącza mogą albo być
równe, tj. N

A

= N

D

(takie struktury w rzeczywistości stosowane są stosunkowo rzadko) albo

różne, tj. N

A

≠ N

D

. Złącze pierwszego z wymienionych typów nazywamy symetrycznym, zaś

drugiego – niesymetrycznym. Ponieważ obecnie w praktyce spotykane są przede wszystkim
złącza niesymetryczne (i skokowe), dalsza dyskusja ograniczona będzie właśnie do nich.
W sytuacji, gdy koncentracje po obydwu stronach złącza różnią się znacząco (o rzędy
wielkości) opisujemy je jako p

+

-n albo p-n

+

, gdzie symbol „+” wskazuje właśnie silniej

domieszkowany obszar. Przekrój takiej struktury i profil rozkładu domieszek ukazano na rys. 11.

Na początek rozważmy, jakie zjawiska fizyczne zajdą lub będą zachodzić w takim złączu,

na razie przy braku jakiejkolwiek zewnętrznej polaryzacji (czyli pod nieobecność
zewnętrznego pola elektrycznego).

Jak łatwo zauważyć, w obszarze złącza po obydwu jego stronach mamy do czynienia

z dużymi różnicami koncentracji nośników (po stronie p dominują bowiem dziury zaś po
stronie n – elektrony), co innymi słowy oznacza występowanie gradientu ich koncentracji.
Jeśli zatem materiały p i n utworzą rzeczywiste metalurgiczne złącze, to naturalną koleją
rzeczy ze względu na ów gradient koncentracji na początku wystąpi zjawisko dyfuzji

14

nośników z obszarów o ich większej koncentracji do mniejszej, czyli dziury zaczną przepływać
(dyfundować) z obszaru p do n, natomiast elektrony w kierunku przeciwnym (tj. z obszaru n
do p). W rezultacie w pewnym obszarze przyzłączowym po obydwu jego stronach
pozostaną nieruchome (bo tkwiące w sieci krystalicznej) jony domieszek, odsłonięte przez
odpływ swobodnych nośników większościowych (mówimy o tych domieszkach wówczas,
że są nieskompensowane). Będą to, odpowiednio, ujemne jony akceptorowe (N

A

-

) po

stronie p (bo dziury przepłynęły na drugą stronę, więc każdy akceptor ma w ich miejsce po
nadmiarowym elektronie) oraz dodatnie donorowe (N

D

+

) po stronie n (bo ich nadmiarowe

elektrony przedyfundowały na drugą stronę złącza), które utworzą tym sposobem
tzw. obszar ładunku przestrzennego, ujemnego po stronie p i dodatniego po stronie n. Ów
obszar ładunku przestrzennego po obydwu stronach złącza określany jest jako tzw. warstwa
zubożona – nazwa odzwierciedla fakt, że właśnie nośników większościowych wskutek
opisanych zjawisk obszar ten jest w znacznej mierze pozbawiony. Jeśli przyjmiemy
w uproszczeniu, że w warstwie zubożonej w ogóle nie ma swobodnych nośników prądu i jej
ładunek tworzą wyłącznie ładunki zjonizowanych domieszek, to rozkład ładunku w tym
obszarze będzie determinowany jedynie przez ich rozkład. Taki model rozkładu ładunku
nazywamy przybliżeniem warstwy zubożonej. Jest on słuszny dla złączy symetrycznych
i

w

większości

przypadków

wystarczający

do

zadowalającego

opisu

złączy

niesymetrycznych słabo domieszkowanych, natomiast niewłaściwy dla złączy silnie
asymetrycznych. W nich bowiem koncentracja nośników mniejszościowych jest w pewnym
obszarze większa od koncentracji zjonizowanych atomów domieszki (podczas gdy
w złączach słabo asymetrycznych tylko porównywalna), co model przybliżenia zubożenia
czyni całkiem nieadekwatnym.

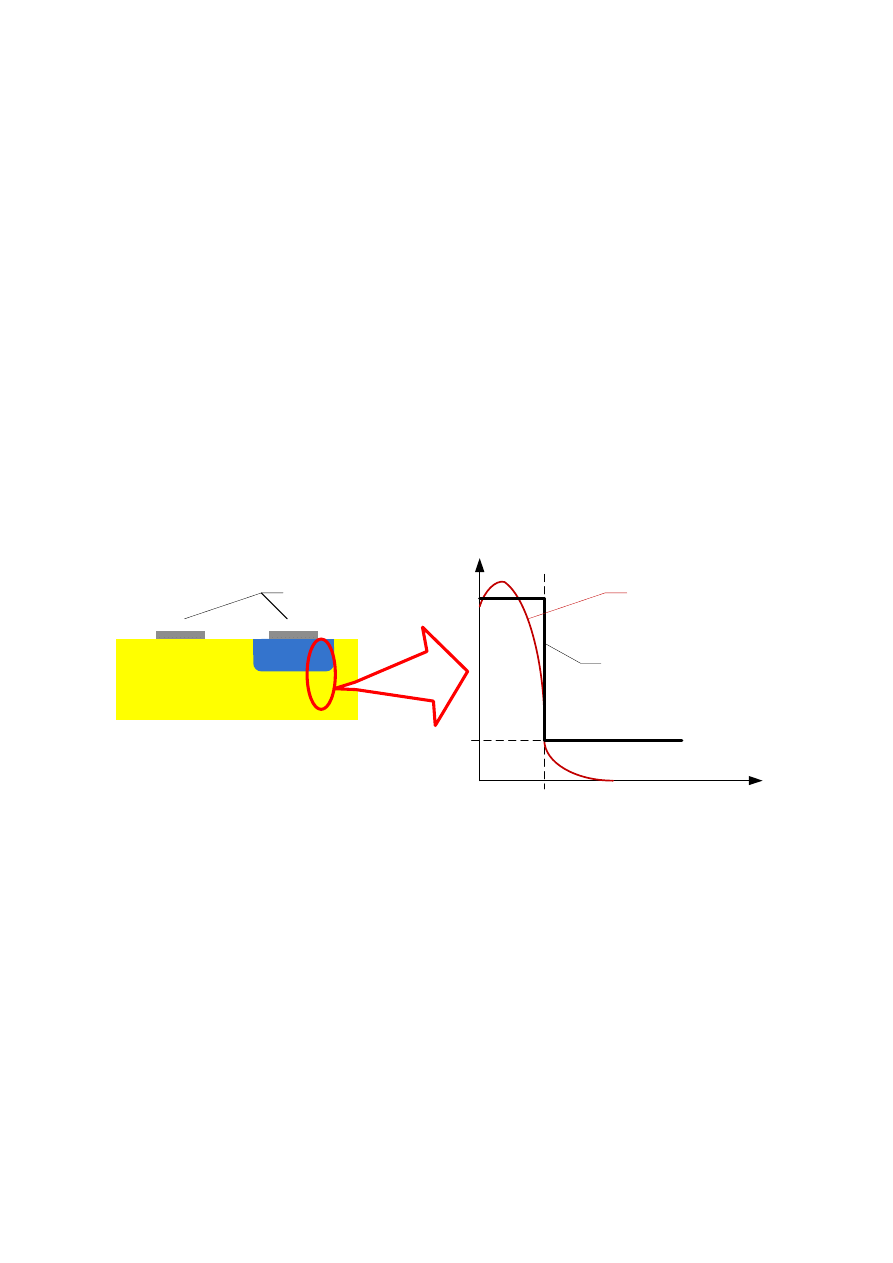
p

n

elektrody
(kontakty elektryczne)

N

D

N

A

p

n

x

x

j

rzeczywisty profil
rozkładu domieszek

aproksymacja profilu
rozkładu domieszek

0

(a)

(b)

Rys. 11 Przekrój przez typową rzeczywistą strukturę złącza p-n (a) oraz profil rozkładu

domieszek rzeczywisty i aproksymowany (złącze skokowe niesymetryczne p-n

+

) (b)

W rezultacie wywołanego odpływem nośników większościowych zaburzenia równowagi

rozkładu ładunku elektrycznego, w owym obszarze pojawi się pole elektryczne, o zwrocie,
zgodnie z przyjętą w fizyce konwencją, od obszaru dodatniego (n) do ujemnego (p). To
spowoduje wyhamowanie dalszego przepływu dyfuzyjnego z obszarów macierzystych
nośników większościowych, pojawiających się wskutek fluktuacji termicznych przypadkowo
na granicy obszaru ładunku przestrzennego. Elektrony będą zawracane do obszaru n zaś
dziury do obszaru p (stąd obszar ładunku przestrzennego nazywany jest warstwą zaporową).
Ponieważ w tym przypadku ich ruch jest wymuszony, czyli odbywa się pod wpływem pola
elektrycznego mówimy, że nośniki takie są przez nie unoszone – w przeciwieństwie do
mechanizmu transportu dyfuzyjnego, który jest tylko i wyłącznie efektem dążenia układu do
równowagi (tu wyrównania koncentracji) na drodze tylko i wyłącznie przypadkowych
ruchów cieplnych nośników. Innymi słowy można powiedzieć, że przepływ prądów

15

dyfuzyjnych w jedną stronę będzie skompensowany przepływem prądów unoszenia
w przeciwną i w efekcie złącze znajdzie się w stanie równowagi termodynamicznej.
Oczywiście zmiana temperatury, np. jej podniesienie spowoduje, że po obu stronach
pojawią się nośniki o energiach umożliwiających im pokonanie bariery pola elektrycznego,
lecz ich dyfuzja na drugą stronę spowoduje natychmiast dalszy wzrost ładunku
przestrzennego, czyli wzrost natężenia zatrzymującego ów przepływ pola, czyli ponowną
stabilizacje układu, tyle że z wyższą wartością pola elektrycznego.

Obecność pola elektrycznego w złączu sygnalizuje, że między obszarami ujemnego

i dodatniego ładunku przestrzennego wytworzy się jakaś różnica potencjałów, czyli po
prostu napięcie. Nazywamy je potencjałem (napięciem) wbudowanym (bo wytwarza się
samorzutnie, bez udziału jakichkolwiek pól przykładanych z zewnątrz) lub potencjałem
dyfuzyjnym

U

d

(gdyż

jest

efektem

procesu

transportu

dyfuzyjnego

nośników

większościowych). Z kolei w ramach modelu pasmowego określamy tę różnicę potencjałów
jako wysokość bariery, gdyż to ona właśnie stanowi barierę dla przepływu nośników
o energiach mniejszych od jej wysokości.

Obszary półprzewodników leżące poza warstwą zubożoną określane są jako quasi

neutralne elektrycznie, gdyż tam rozkłady koncentracji nośników większościowych
w zasadzie pokrywają się z rozkładami koncentracji domieszek (czyli innymi słowy są one
tam po prostu skompensowane).

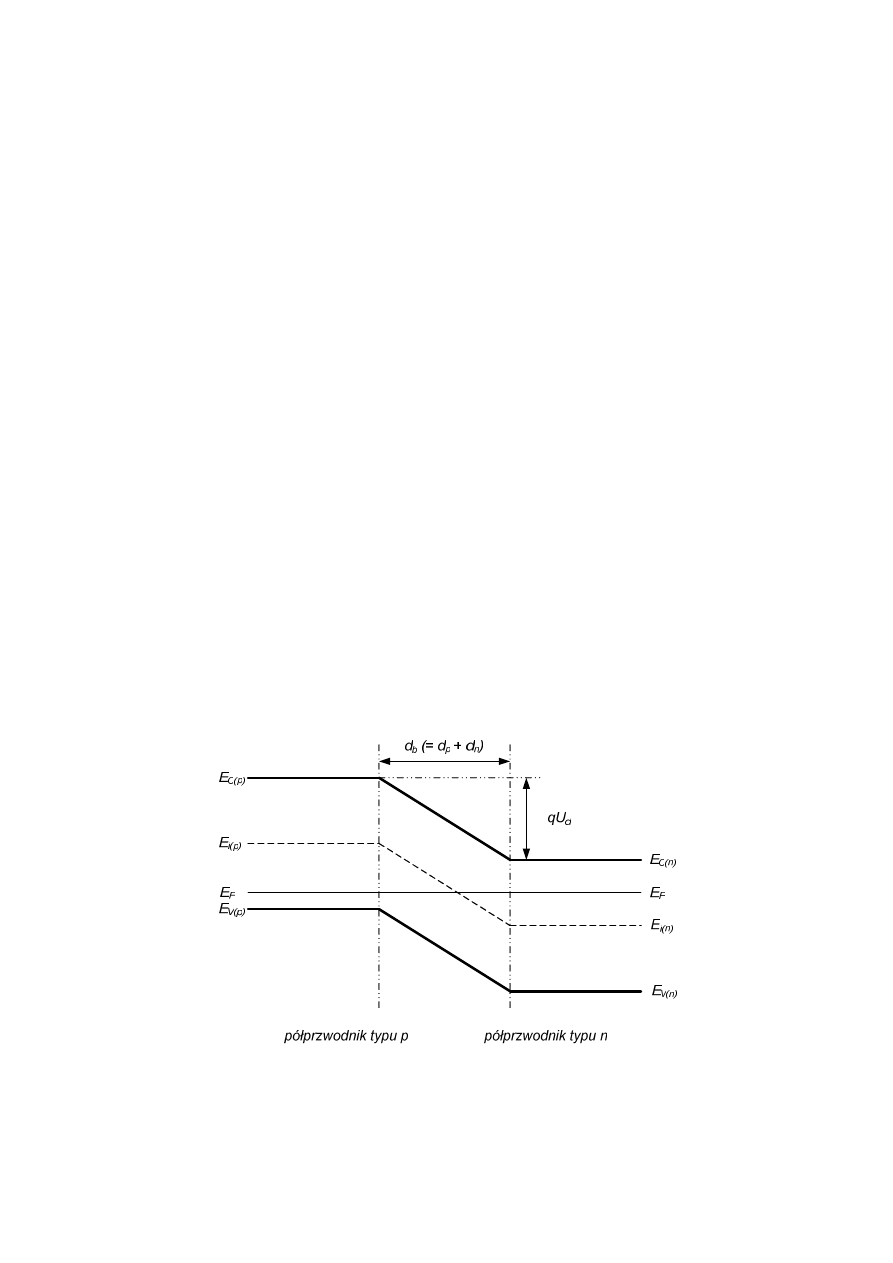
Model pasmowy złącza p-n w warunkach równowagi termodynamicznej ukazuje rys. 12.

Warto zwrócić uwagę na fakt, iż w takiej sytuacji położenie poziomu Fermiego E

F

reprezentowane jest przez ciągłą linię prostą w obszarze całego złącza (czyli po obu jego
stronach jego energia ma identyczną wartość).

Zakładając jak wcześniej, że koncentracje domieszek w całym obszarze warstwy

zubożonej są stałe, zaś koncentracje nośników swobodnych w porównaniu z nimi pomijalnie
małe, wartości ładunku przestrzennego Q

p

i Q

n

przypadającego na jednostkową

powierzchnię można wyrazić następująco:

p

A

p

Q

qN d

−

= −

(6a)

n

D

n

Q

qN d

+

=

,

(6b)

gdzie d

p

i d

n

oznaczają, odpowiednio, szerokość obszaru ładunku przestrzennego (warstwy

zubożonej) po stronie p oraz n złącza, zaś q jest ładunkiem elementarnym.

Rys. 12 Model pasmowy złącza p

+

-n w warunkach równowagi termodynamicznej

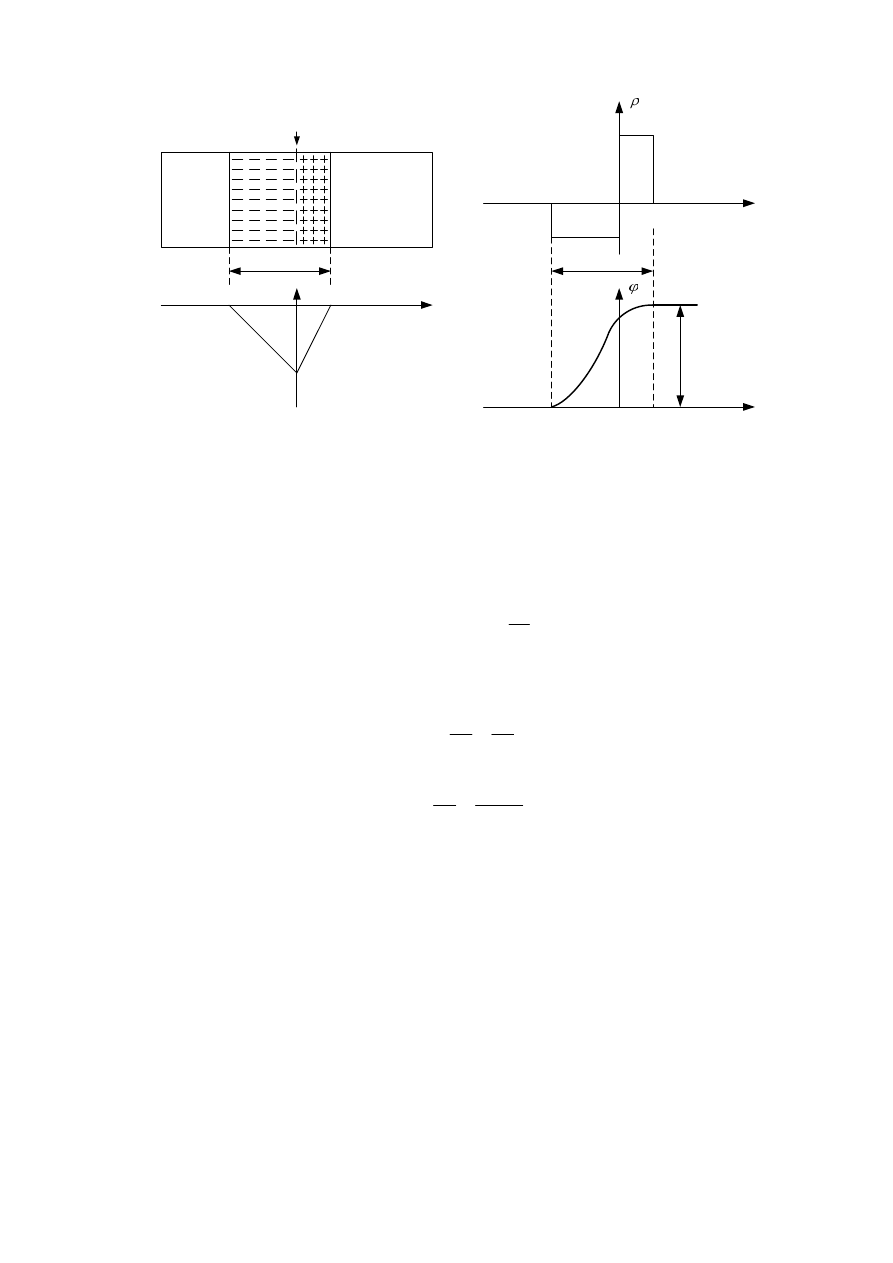
Przykładowe rozkłady ładunku elektrycznego w obszarze warstwy zubożonej oraz

natężenia pola elektrycznego i jego potencjału dla niesymetrycznego złącza skokowego
przedstawiono na rys. 13.

16

p

n

złącze

metalurgiczne

E

x

E

max

d

n

d

p

+

-

qN

A

qN

D

d

n

d

p

x

x

d

p

d

n

U

d

(a)

(c)

(b)

(d)

d

b

d

b

Rys. 13 Obszar ładunku przestrzennego (a) i jego rozkład (b) oraz rozkłady natężenia pola

elektrycznego (c) i jego potencjału (d) w niesymetrycznym złączu skokowym p-n

+

6.1 Potencjał wbudowany (napięcie dyfuzyjne)

Jak już wspomniano, w warunkach równowagi termodynamicznej w złączu p-n prądy

dyfuzji i unoszenia dla dziur, jak i elektronów się równoważą, co można zapisać, np. dla dziur
w postaci następującej:

d

0

d

p dyfuzyjny

p unoszenia

p

p

p

J

J

qD

q

pE

x

µ

+

= −

+

=

,

(7)

gdzie: kT/q = D

p

/

µ

p

(tzw. równanie Einsteina) zaś E jest natężeniem pola wbudowanego

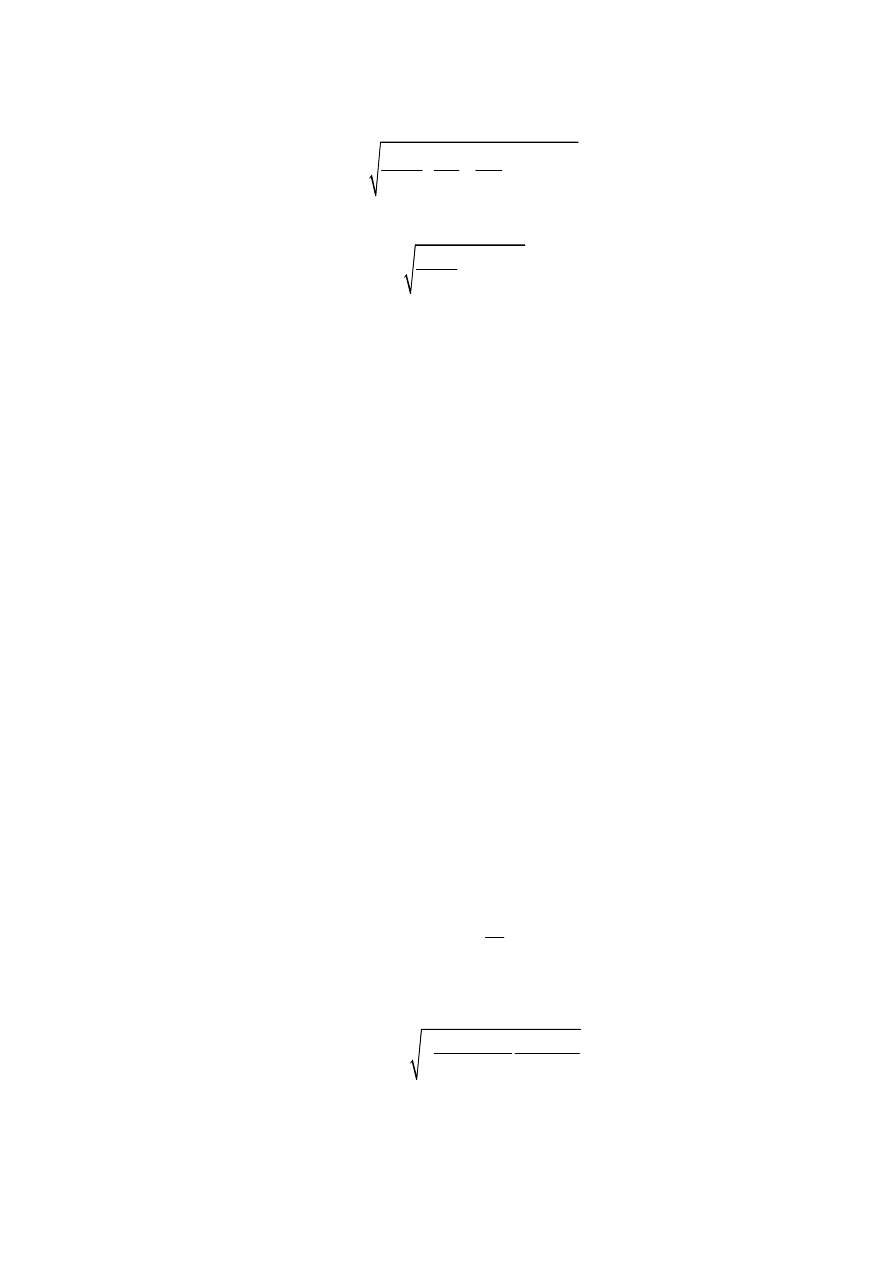
w złączu. Odpowiednie przekształcenia tej zależności prowadzą do wzoru na napięcie
dyfuzyjne U

d

:

ln

p

d

n

p

kT

U

q

p

=

,

(8)

co po uwzględnieniu, że p

p

≅

N

A

oraz np = n

i

2

daje ostatecznie:

2

ln

A

D

d

i

N N

kT

U

q

n

=

(9)

Prowadząc analogiczne rozważania dla elektronów otrzymamy dokładnie tę samą funkcję.
Należy tu podkreślić, że wartość napięcia dyfuzyjnego U

d

jest istotnie zależna od:

koncentracji domieszek donorowych i akceptorowych po obydwu stronach złącza, jak
i koncentracji samoistnej nośników n

i

(a więc szerokości przerwy zabronionej E

g

w materiale

czyli jego rodzaju) oraz temperatury. Podstawiając np. N

A

= N

D

= 10

16

cm

-3

widzimy, że

w temperaturze pokojowej U

d

w Si wynosi około 670 mV, natomiast w GaAs w przybliżeniu

1,04 V.

6.2 Szerokość obszaru zubożonego (warstwy zaporowej)

W ramach przyjętego wcześniej modelu przybliżenia warstwy zubożonej rozkład gęstości

ładunku

przestrzennego

po

obu

stronach

złącza

odpowiada

równomiernemu

(jednorodnemu) rozkładowi koncentracji atomów domieszek. Gęstość ładunku w warstwie
zubożonej wynosi więc –qN

A

po stronie obszaru typu p oraz qN

D

po stronie n. Ponieważ

złącze jako całość zachowuje obojętność elektryczną, zatem ładunek przestrzenny po jego
jednej stronie musi być równoważony przez taki sam co do wartości i przeciwny co do znaku
ładunek przestrzenny po drugiej stronie złącza. Możemy to zapisać jako:

17

0

A

p

D

n

qN d

qN d

−

+

−

+

=

(10)

Równanie to pokazuje, że pole elektryczne w całości odkłada się tylko na warstwie
zaporowej (a poza nią jest równe zeru) oraz, że szerokości obszarów zubożonych po obu
stronach złącza są odwrotnie proporcjonalne do koncentracji domieszek.

Rozwiązując dla takiego przypadku równanie Poissona (wiążącym rozkład potencjału

pola elektrycznego z rozkładem gęstości ładunku) i korzystając z prawa Gaussa (wiążącym
rozkład natężenia pola elektrycznego z rozkładem gęstości ładunku) możemy teraz określić
szerokości obszaru ładunku przestrzennego d

p

i d

n

po obydwu stronach złącza, jak również

jego całkowitą szerokość d

b

, (= d

p

+ d

n

):

(

)

0

2

s

D

p

d

A

A

D

N

d

U

q

N

N

N

ε ε

=

+

,

(11a)

(

)

0

2

s

A

n

d

D

A

D

N

d

U

q

N

N

N

ε ε

=

+

,

(11b)

0

2

1

1

s

b

d

A

D

d

U

q

N

N

ε ε





=

+









,

(12)

gdzie:

ε

0

i

ε

s

to, odpowiednio, przenikalność elektryczna próżni i względna przenikalność

elektryczna półprzewodnika (w tym przypadku Si).

Z obydwu powyższych równań wynika natychmiast, że w przypadku złączy

asymetrycznych (czyli o różnym poziomie domieszkowania obszarów p i n) szerszy jest obszar
ładunku przestrzennego po słabiej domieszkowanej stronie złącza, co odzwierciedla zgodny
z prawami elektrostatyki fakt, że pole elektryczne głębiej wnika do obszarów o mniejszej
przewodności (czyli w tym przypadku słabiej domieszkowanych).

Cała dotychczasowa dyskusja dotyczyła, przypomnijmy, sytuacji, gdy złącze p-n

znajduje się w warunkach równowagi termodynamicznej, tj. nie jest spolaryzowane żadnym
zewnętrznym napięciem. W sytuacji nierównowagowej musimy oczywiście uwzględnić
wpływ dodatkowego napięcia (potencjału) zewnętrznego na zjawiska zachodzące
w złączu. Po pierwsze napięcie to praktycznie w całości będzie odkładało się na warstwie
zaporowej, podobnie jak napięcie dyfuzyjne, sumując się z nim lub redukując jego
wartość, w zależności od znaku. Ze statystyki Maxwella-Boltzmanna wiadomo, że
prawdopodobieństwo przejścia cząstki ponad barierą potencjału E, czyli P(E), wynosi
exp(-E/kT).

W

rozważanym

przypadku

złącza

p-n

w

warunkach

równowagi

termodynamicznej barierą dla dyfundujących przez złącze nośników większościowych jest
pole elektryczne powstałe w warstwie ładunku przestrzennego. Wysokość tej bariery
(tj. energia, jaką muszą mieć nośniki aby ją pokonać) jest więc po prostu równa energii tego
pola elektrycznego, czyli E = qU

d

. Przykładając zewnętrzne pole elektryczne (czyli różnicę

potencjałów, czyli napięcie U), w zależności od tego, czy jego zwrot jest zgodny ze zwrotem
pola „własnego” warstwy zaporowej czy też nie, spowodujemy, odpowiednio, jego
wzmocnienie, albo redukcję, czyli po prostu podwyższenie lub obniżenie tej bariery. Tak więc
całkowita energia pola w warstwie ładunku przestrzennego będzie w takiej sytuacji
opisywana zmodyfikowana zależnością E = q(U

d

– U), zaś dyfundujące nośniki większościowe

w mniejszej lub też w większej ilości będą mogły przepływać na drugą stronę złącza. Tak czy
inaczej, dotychczasowa równowaga między prądami dyfuzyjnym i unoszenia zostanie
zakłócona (aczkolwiek przy niewielkich prądach niezbyt znacząco). Zewnętrzną różnicę
potencjałów (napięcie polaryzacji) U wstawiamy przy tym ze znakiem „+”, gdy jego spadek
jest przeciwny do spadku U

d

(bariera ulega obniżeniu) i ze znakiem „-”, gdy jest zgodny

ze spadkiem U

d

(bariera ulega podwyższeniu). Polaryzację zewnętrzną dodatnią

w powyższym sensie (tj. gdy potencjał wyższy (+) przyłożony jest do obszaru p, zaś niższy (-)
do obszaru n) nazywamy polaryzacją w kierunku przewodzenia, natomiast polaryzację
ujemną – zaporową.

18

W związku z powyższym, skoro całkowita wysokość bariery potencjału w złączu p-n jest

równa sumie (względnie różnicy) obydwu napięć, zmieniać się będzie także szerokość
obszaru ładunku przestrzennego:

(

)

0

2

1

1

s

b

d

A

D

d

U

U

q

N

N

ε ε





=

+

−









(13)

Łatwo zauważyć, że w przypadku złączy silnie asymetrycznych, np. p

+

-n, czyli w sytuacji, gdy

N

A

>> N

D

, powyższą zależność można uprościć do postaci:

(

)

0

2

s

b

d

D

d

U

U

qN

ε ε

≅

−

(14)

6.3 Pojemność złącza p-n

Jak pokazano wyżej, jeśli złącze p-n będzie polaryzowane napięciem zewnętrznym U,

(albo ogólniej, jeśli jego wartość będzie ulegać zmianom) zmieniać się będzie także
szerokość obszaru ładunku przestrzennego. Zmiany te mają charakter całkowicie
odwracalny, tzn. po wyłączeniu (lub ogólniej, po przywróceniu wyjściowej wartości)
napięcia polaryzacji U, szerokość warstwy zaporowej powróci do pierwotnych rozmiarów.

Obszar ten z punktu widzenia elektrostatyki stanowi kondensator płaski o okładkach

półprzewodnikowych wstępnie (tj. bez polaryzacji zewnętrznej) naładowany do napięcia
kontaktowego U

d

. Istotną rzeczą jest fakt, iż ze względu na półprzewodnikową naturę

materiału, każdą z okładek tworzy ładunek przestrzenny (jest on znaku dodatniego w części
półprzewodnika typu n i reprezentuje jedną okładkę oraz ujemnego w części typu p
i reprezentuje drugą okładkę), a nie powierzchniowy, jak to ma miejsce w „klasycznym”
kondensatorze o okładkach metalowych. W tym drugim przypadku przyłożenie napięcia
zewnętrznego wpływa tylko na gęstość zgromadzonego na okładkach ładunku, natomiast
odległość między samymi ładunkami pozostaje stała (bo nie zmienia się odległość między
okładkami), dzięki czemu pojemność takiego kondensatora nie zależy od przyłożonego
napięcia. Tymczasem w kondensatorze o okładkach półprzewodnikowych, jakim jest złącze
p-n, z kolei gęstość ładunku w każdym punkcie rozkładu ładunku przestrzennego nie zależy
od przyłożonego napięcia, natomiast zależy od niego szerokość tych obszarów. Pojemność
obszaru ładunku przestrzennego można sobie wyobrazić jako sumę elementarnych
pojemności (kondensatorów) połączonych równolegle, każda tworzona przez parę
elementarnych ładunków: elementarny ładunek dodatni po stronie n i ujemny po stronie p.
Skoro zmianom ulega szerokość warstwy zaporowej w funkcji napięcia, to w trakcie tego
procesu będą pojawiały się kolejne albo znikały dotychczas istniejące elementarne
kondensatory, zaś odległości między tworzącymi je kolejno parami ładunków będą,
odpowiednio, coraz większe lub mniejsze. Ponieważ pojemność jest odwrotnie
proporcjonalna do odległości pomiędzy ładunkami, wraz ze zmianami napięcia
zewnętrznego również pojemność obszaru ładunku przestrzennego czyli złącza p-n będzie
się zmieniać. W takim razie ogólnie pojemność złącza można zapisać jako:

0

T

s

b

A

C

d

ε ε

=

,

(15)

gdzie A jest powierzchnią złącza p-n.

Biorąc pod uwagę, że szerokość obszaru ładunku przestrzennego d

b

zależy od napięcia

(13) ostatecznie dostajemy:

(

)

0

2

s

A

D

T

d

A

D

N N

C

A q

U

U N

N

ε ε

=

−

+

(16)

I znów, jak poprzednio, dla złącza silnie asymetrycznego, np. p

+

-n, zależność tę można

uprościć do postaci:

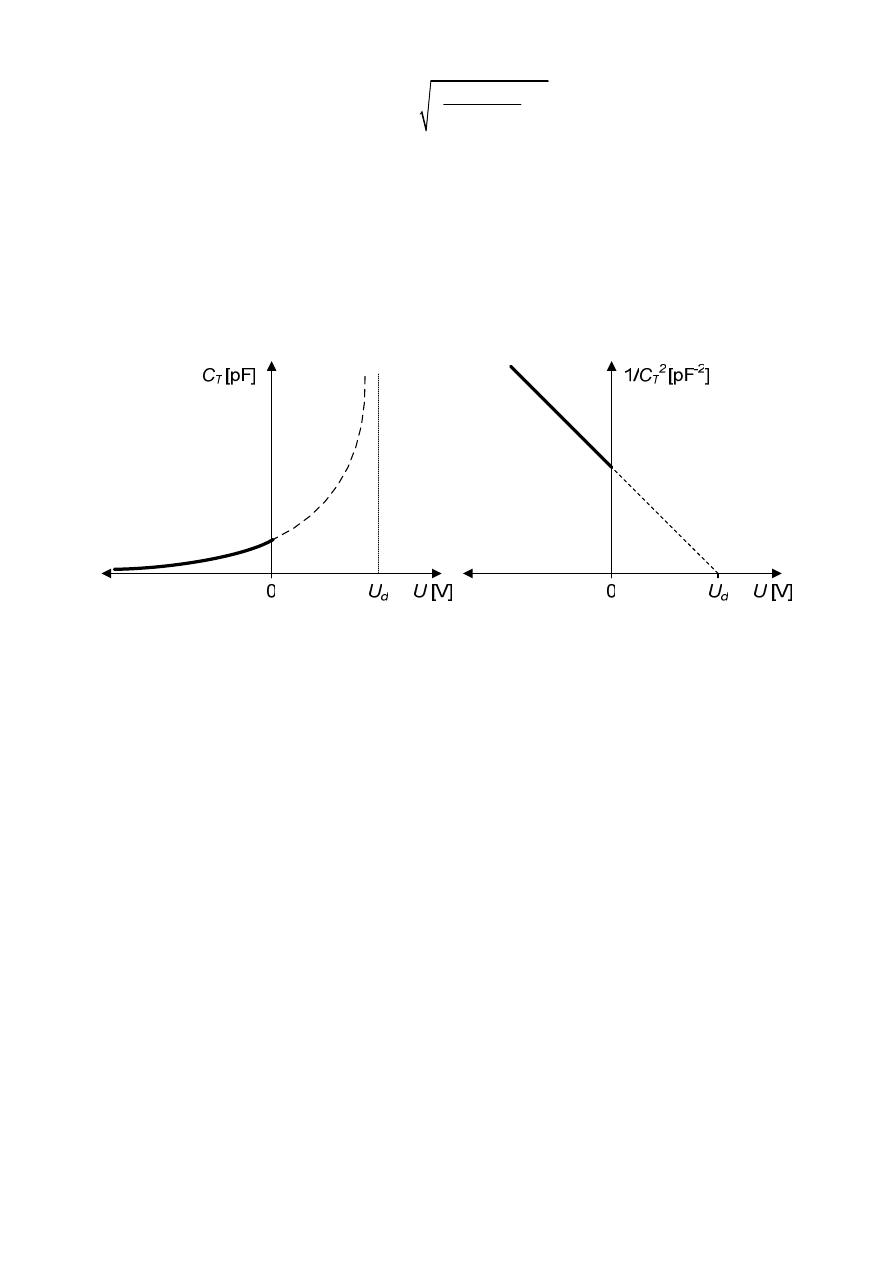
19

(

)

0

2

s

T

D

d

C

A q

N

U

U

ε ε

≅

−

(17)

Określona powyżej pojemność nazywana jest pojemnością (różniczkową) złącza lub

warstwy zubożonej złącza (C

T

). Ponieważ pojemność C

T

= f[ 1/(U)

2

] to 1/C

T

2

= f(U), co ilustrują

wykresy na rys. 14.

Widać, że mierząc pojemność złącza p-n w funkcji napięcia zewnętrznego (czyli

tzw. charakterystykę pojemnościowo-napięciową C-V złącza) a następnie sporządzając
wykres 1/C

T

2

= f(U) i liniowo go aproksymując do punktu przecięcia z osią napięć, można

wyznaczyć wartość napięcia dyfuzyjnego U

d

. Ponadto, gdy mamy do czynienia ze złączem

silnie asymetrycznym, którego charakterystykę C-V opisuje zależność (17), to można
z nachylenia wykresu 1/C

T

2

= f(U) również oszacować koncentrację domieszki po słabiej

domieszkowanej stronie złącza.

(a)

(b)

Rys. 14 Zależność pojemności różniczkowej złącza p-n od napięcia polaryzacji (a) oraz

przebieg zależności 1/C

T

2

= f(U) (b)

6.4 Charakterystyka prądowo-napięciowa (I-V) złącza p-n

Na zakończenie warto wspomnieć o charakterystyce prądowo-napięciowej I-V złącza

p-n, choć akurat w ramach tego ćwiczenia nie będzie ona mierzona.

Jak wcześniej wspomniano, polaryzowanie złącza p-n napięciem zewnętrznym może

obniżać lub podwyższać wysokość bariery energetycznej dla nośników większościowych
dyfundujących

na

drugą

stronę

złącza

(rys.

15).

Wspomniano

również,

że

prawdopodobieństwo przechodzenia cząstek ponad barierą (czyli de facto w ujęciu
statystycznym ich liczba) zależy eksponencjalnie od jej wysokości. Wobec tego w takiż
sposób zmieniać się będzie prąd złącza w funkcji przykładanego napięcia.

Przy polaryzacji zaporowej prąd dyfuzyjny maleje, stając się mniejszy niż w warunkach

równowagi termodynamicznej (czyli przy braku polaryzacji zewnętrznej). Obok niego jednak
przez złącze płynie także prąd nośników mniejszościowych – elektronów z obszaru p i dziur
z obszaru n – które pojawiając się wskutek fluktuacji termicznych na krawędzi warstwy
zaporowej są przez istniejące w niej pole elektryczne (w tym przypadku większe niż dla
polaryzacji przewodzenia) porywane i unoszone na drugą stronę złącza. Jak łatwo
zauważyć ten prąd zasadniczo nie zależy od wysokości bariery, bo dla niego ona w ogóle
nie istnieje ! Ponieważ jednak tworzą go nośniki mniejszościowe, których jest o rzędy wielkości
mniej niż większościowych (np = n

i

2

!), to jest on bardzo mały. W przypadku polaryzacji

w kierunku przewodzenia maskuje go duży prąd dyfuzyjny i dopiero gdy zostaje on
praktycznie wyeliminowany, co ma miejsce przy polaryzacji złącza w kierunku zaporowym,
staje się widoczny. Taki stan rzeczy skutkuje silnie asymetryczną charakterystyką I-V złącza
p-n (rys. 16), formalnie opisywaną przez wzór Shockley’a:

20

1

qU

kT

s

I

I

e





=

−









,

(18)

gdzie I

s

to tzw. prąd nasycenia.

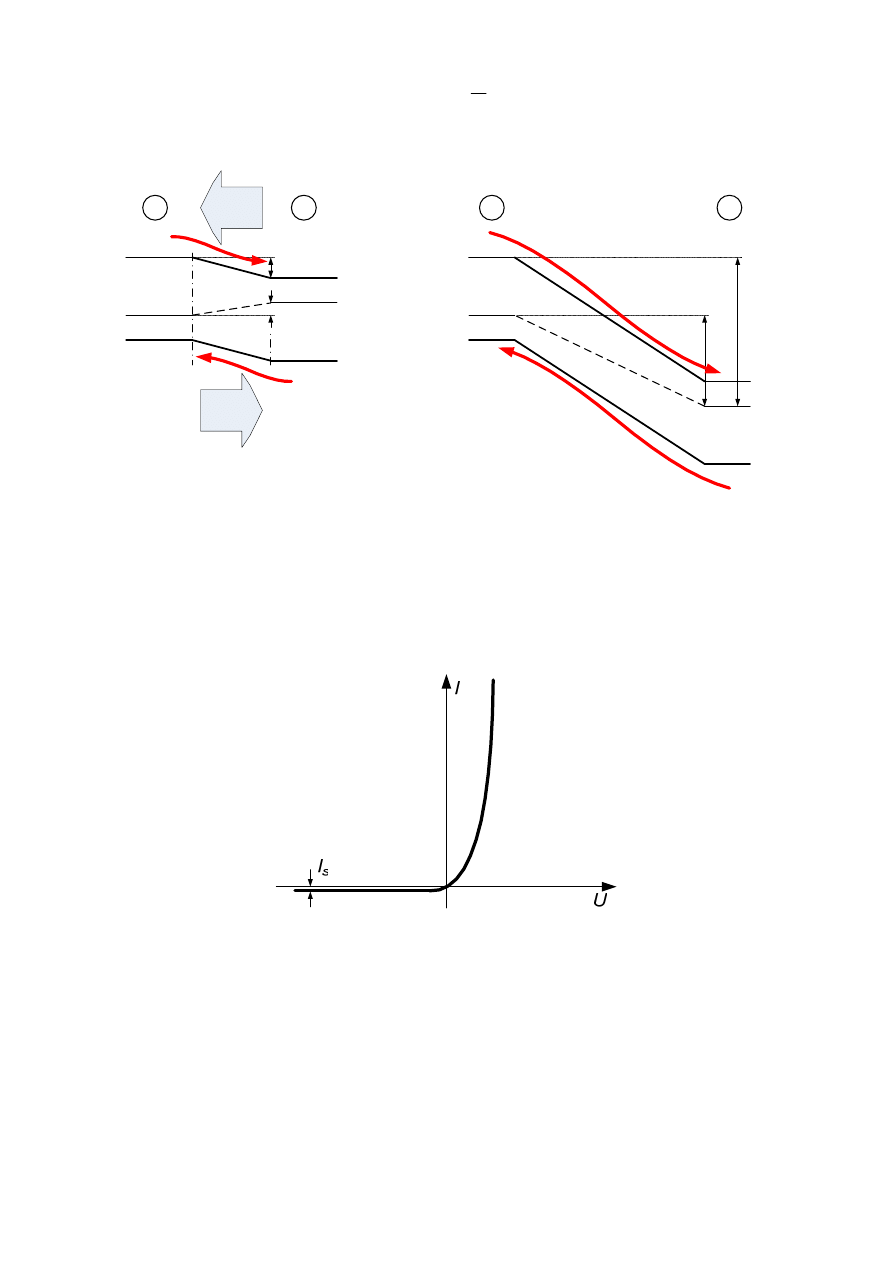
n

p

E

F(p)

E

V(p)

E

C(p)

p

E

C(n)

E

F(n)

E

V(n)

n

q(U

d

- U)

qU

I

n(dyf)

I

p(dyf)

I

p(u)

I

n(u)

qU

q(U

d

+ U)

E

F(p)

E

V(p)

E

C(p)

E

C(n)

E

F(n)

E

V(n)

I

n(u)

I

p(u)

(a)

(b)

Rys. 15 Modele pasmowe złącza p-n i płynące przez nie prądy przy polaryzacji złącza

w kierunku przewodzenia (a) i zaporowym (b)

Nie przesadzając można stwierdzić, że na tej właśnie asymetrii zbudowana jest cała

elektronika ciała stałego.

Rys. 16 Charakterystyka prądowo-napięciowa (I-V) złącza p-n

21

II

. Instrukcja wykonawcza do ćwiczenia pod tytułem:

„Kontakt półprzewodnik-półprzewodnik – złącze p-n” (Z)

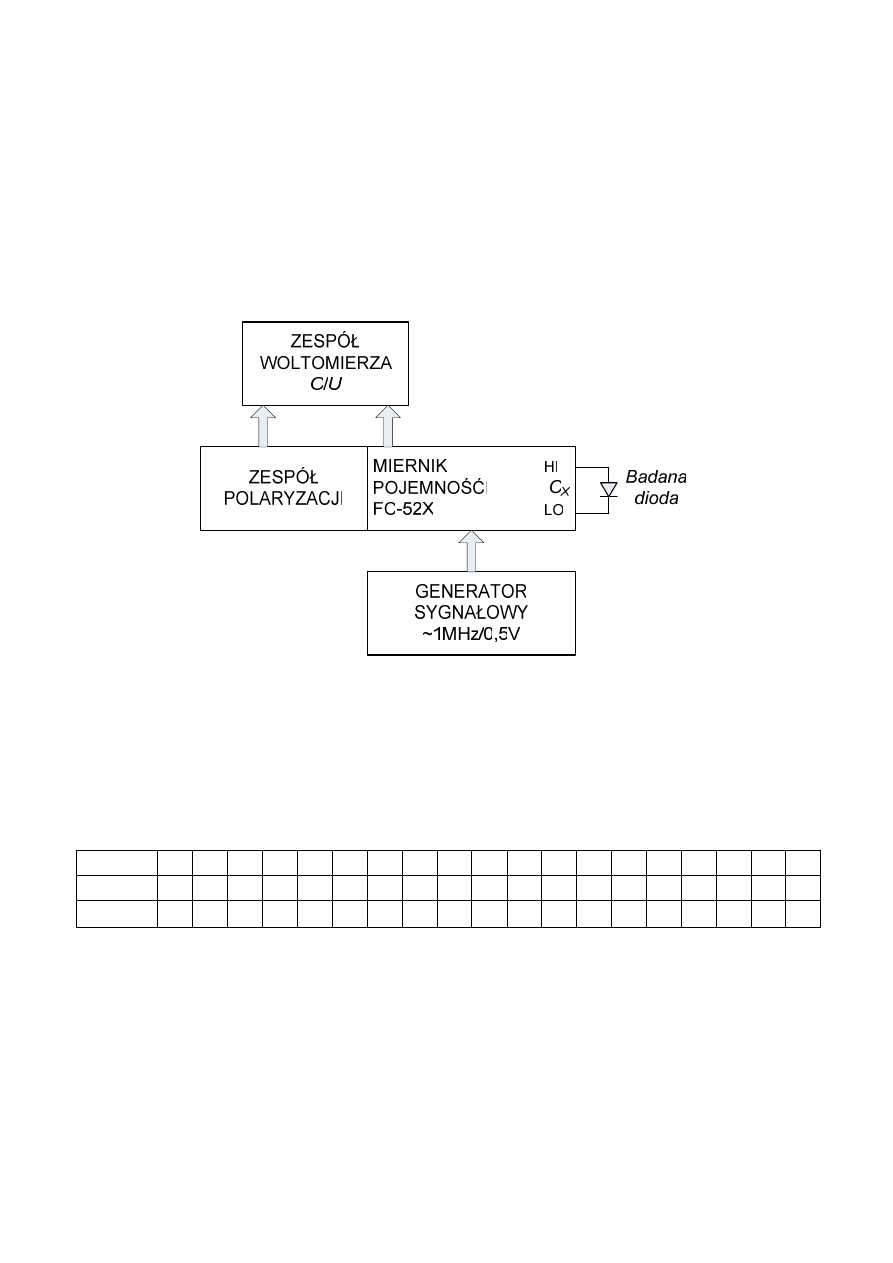
Schemat

zestawu

pomiarowego

wykorzystywanego

w

niniejszym

ćwiczeniu

przedstawiono na rys. A. Na schemacie tym:
– miernik pojemności różniczkowej jest miernikiem typu FC-520 lub FC-522,
– C

X

oznacza gniazda (HI, LO) dla uchwytu badanej diody,

– zespół woltomierza C/U z wyświetlaczem cyfrowym pozwala odczytywać wartość

napięcia lub pojemności (opis sposobu odczytu zamieszczony na obudowie),

– zespół polaryzacji pozwala na regulację napięcia polaryzacji złącza p-n (diody)

w zakresie napięć ujemnych i dodatnich (za pomocą regulatora wieloobrotowego).

Rys. A Schemat układu pomiarowego (instrukcja obsługi u Prowadzącego)

1.

W układzie pomiarowym jak na rys. A zmierz zależność pojemności różniczkowej C

T

badanej diody Si (tj. złącza p-n) w funkcji stałego napięcia polaryzacji U (czyli
tzw. charakterystykę pojemnościowo-napięciową (C-V) diody) w obszarze pracy
zaporowej (napięcia ujemne) w zakresie od 0 do -1,8 V co 0,1 V. Dla każdego punktu
pomiarowego oblicz także wartość odwrotności kwadratu zmierzonej pojemności
(tj. C

T

-2

[pF], czyli 1/ C

T

2

[pF]). Wyniki pomiarów oraz obliczeń zamieść w tabeli:

U [V]

0

-0,1 -0,2 -0,3 -0,4 -0,5 -0,6 -0,7 -0,8 -0,9 -1,0 -1,1 -1,2 -1,3 -1,4 -1,5 -1,6 -1,7 -1,8

C

T

[pF]

C

T

-2

[pF

-2

]

CZĘŚĆ OBLICZENIOWA

2.

Na arkuszu papieru milimetrowego formatu A3 (w układzie horyzontalnym
(tj. poziomym)) sporządź wykres tej charakterystyki, tj. C

T

[pF] = f(U) [V], a następnie na

innym arkuszu wykres zależności C

T

-2

[pF

-2

] = f(U) [V] (czyli 1/C

T

2

= f(U)).

Oczekiwany przebieg charakterystyk ukazuje rys. 14 (część I niniejszych materiałów).

3.

Ekstrapolując wykres charakterystyki C

T

-2

[pF

-2

] = f(U) [V] do punktu przecięcia z osią

napięcia

U

wyznacz

wartość

napięcia

dyfuzyjnego

(czyli

tzw.

potencjału

22

wbudowanego) U

d

(wartość U

d

należy odczytać i podstawiać w obliczeniach

z dokładnością 0,01 V (10 mV)).

4.

Zakładając, że złącze ma charakter asymetryczny (tzn. w tym przypadku jest typu p

+

-n)

wyznacz wartość koncentracji domieszki po słabiej domieszkowanej stronie złącza (czyli
w tym przypadku po stronie n, a więc domieszki donorowej N

D

) z dokładnością 2 cyfr po

przecinku z zależności:

( )

2

3

0

0

2

cm

T

d

D

r

C

U

N

q

A

ε ε

−









=













,

gdzie:

U

d

– napięcie dyfuzyjne [V],

q – ładunek elementarny (tj. elektronu) = 1,6×10

-19

[C],

ε

0

– przenikalność elektryczna próżni = 8,85×10

-14

[F/cm],

ε

r

– względna przenikalność elektryczna krzemu = 11,7,

C

T

(0) – pojemność złącza [F] przy U = 0 V,

A – pole powierzchni złącza [cm

2

] (wartość poda Prowadzący ćwiczenie)

5.

Korzystając z otrzymanej powyżej wartości N

D

wyznacz położenie poziomu Fermiego E

F

po stronie n złącza (czyli E

F

= E

F(n)

) z dokładnością 0,01 eV (czyli 10 meV) z następującej

zależności:

( )

ln

[eV]

D

F

i n

i

N

E

E

kT

n





−

≅

⋅









,

gdzie:

( )

( )

( )

2

C n

V n

i n

E

E

E

+

=

[eV] – poziom środka pasma zabronionego E

i(n)

(tzw. poziom

samoistny),
n

i

– koncentracja nośników w krzemie samoistnym (koncentracja samoistna)

= 10

10

[cm

-3

],

kT = 2,53×10

-2

[eV].

Szerokość przerwy zabronionej E

g

krzemu w temperaturze pokojowej (T = 293 K)

E

g

= E

C

– E

V

= 1,1 eV.

6.

W oparciu o znajomość położenia poziomu Fermiego E

F

po stronie n złącza (czyli

E

F

= E

F(n)

) oraz wyznaczoną uprzednio wartość napięcia dyfuzyjnego U

d

określ różnicę

E

F(p)

– E

V(p)

(czyli E

F

– qU

d

) (patrz rys. B), w stanie równowagi termodynamicznej (tj. przy

braku zewnętrznego napięcia polaryzującego (U = 0 V)), tzn. gdy E

F(p)

= E

F(n)

)

z dokładnością 0,01 eV (czyli 10 meV).

7.

Następnie, również dla stanu równowagi termodynamicznej (patrz pkt. 6), wyznacz
położenie poziomu środka pasma zabronionego E

i

po stronie p złącza, czyli E

i(p)

(patrz rys.

B) z dokładnością 0,01 eV (czyli 10 meV). Zauważ, że:

[ ]

( )

( )

( )

( )

( )

eV

2

2

C p

V p

C n

V n

i p

d

E

E

E

E

E

qU

+

+

=

=

+

8.

Oblicz koncentrację domieszki po silniej domieszkowanej stronie złącza (czyli w tym
przypadku po stronie p, a więc domieszki akceptorowej N

A

) z dokładnością 2 cyfr po

przecinku z zależności:

( )

( )

-3

cm

i p

F p

E

E

kT

A

i

N

n e

−





=





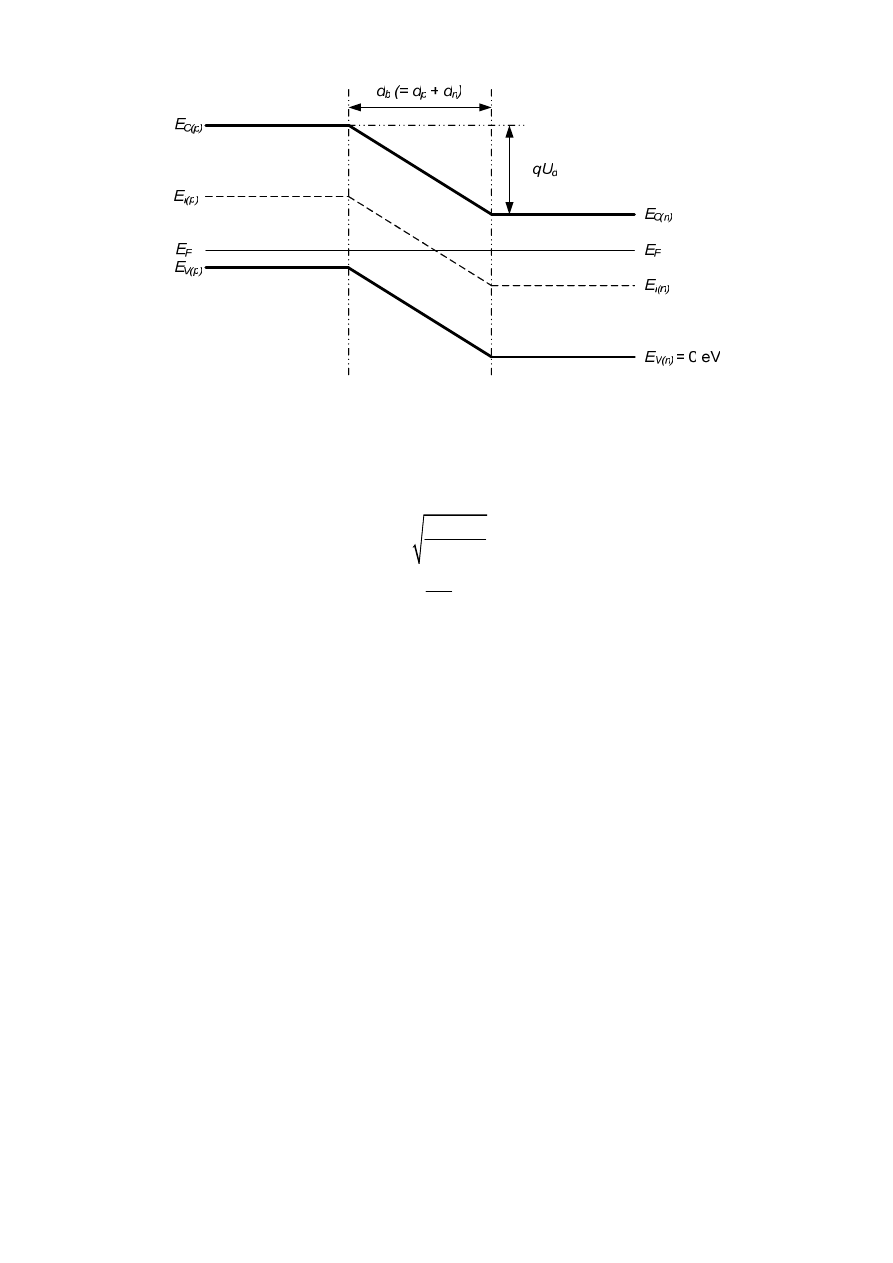
23

Rys. B Model pasmowy złącza p-n w warunkach równowagi termodynamicznej (tj. przy

braku zewnętrznego napięcia polaryzującego (U = 0 V))

9.

Wyznacz głębokości wnikania (tj. szerokości) warstw zaporowych do obszarów typu n
i typu p badanego złącza korzystając z zależności:

[ ]

0

2

cm

r

d

n

D

U

d

qN

ε ε

=

,

[ ]

cm

D

p

n

A

N

d

d

N

=

.

10.

Na podstawie uzyskanych wyżej wyników sporządź na papierze milimetrowym
w formacie A4 (w układzie wertykalnym (tj. pionowym)) model pasmowy badanego
krzemowego złącza p-n w stanie równowagi termodynamicznej. Przyjmij, że odległość
wierzchołka pasma podstawowego (walencyjnego) obszaru n (E

V(n)

) od osi x znajduje się

na poziomie 0 eV.

11.

Na końcu sprawozdania zamieść zestawienie wyników końcowych:

C(0) [pF]

U

d

[V] (z dokładnością 0,01 V)

N

D

[cm

-3

] (z dokładnością 2 miejsc po przecinku)

E

F

– E

i(n)

[eV] (z dokładnością 0,01 eV)

E

F

[eV] (z dokładnością 0,01 eV)

E

(p)

– E

V(p)

[eV] (z dokładnością 0,01 eV)

E

i(p)

[eV] (z dokładnością 0,01 eV)

N

A

[cm

-3

] (z dokładnością 2 miejsc po przecinku)

d

n

[nm]

d

p

[nm]