Instytut Mikroelektroniki i Optoelektroniki
Zespół Laboratoriów Przyrządów Półprzewodnikowych
Pomoce dydaktyczne oraz Instrukcja wykonawcza
do ćwiczenia pod tytułem:
„Oddziaływanie polowe w kondensatorze MOS”
(M)
Opracowanie: dr inż. Agnieszka Zaręba
mgr inż. Józef Maciak
I. Część teoretyczna
1. Zasada działania kondensatora MOS (ang. Metal-Oxide-Semiconductor)
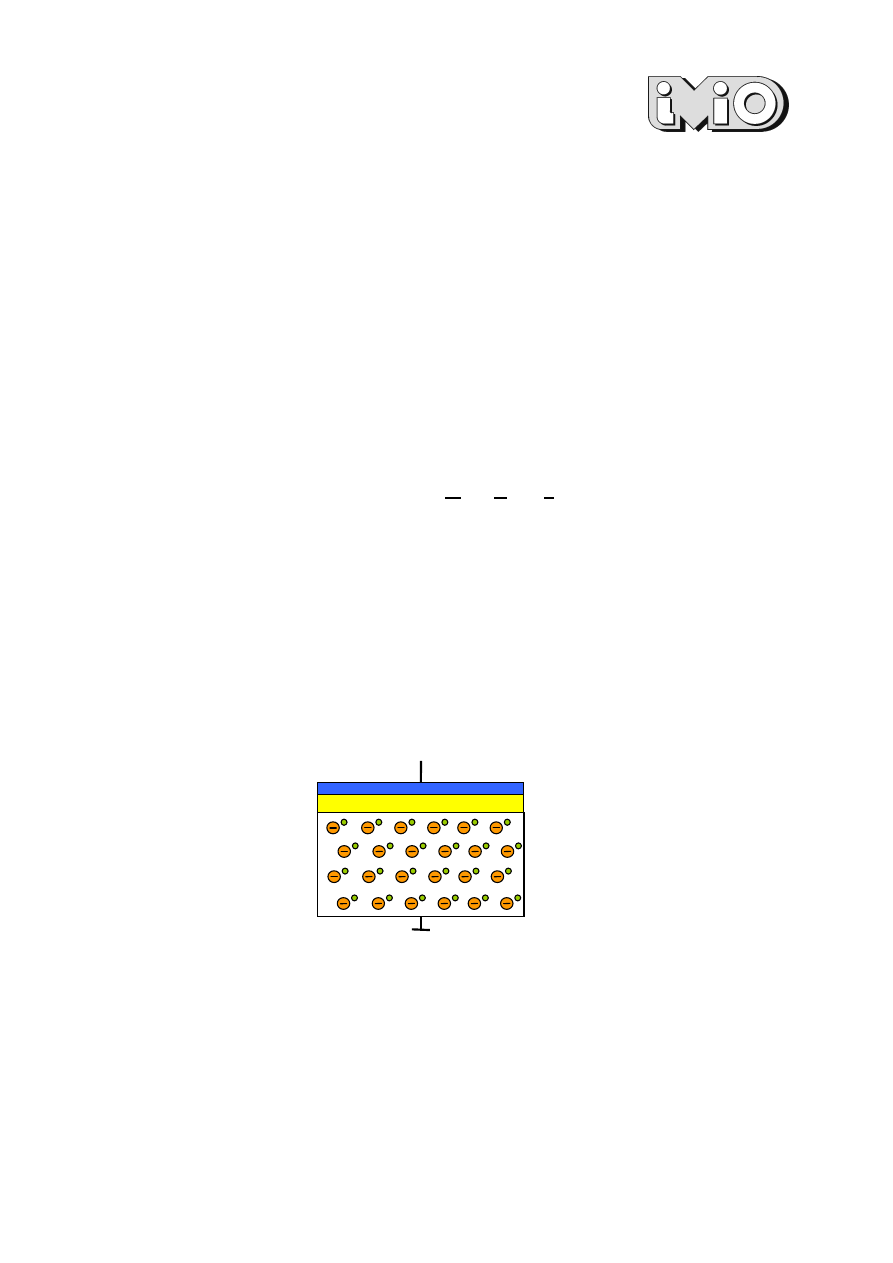
Na początek omówione zostaną właściwości idealnego kondensatora MOS z podłożem
półprzewodnikowym typu p. Jego schematyczny przekrój bez polaryzacji zewnętrznej
przedstawiono na rys. 1. W tym przypadku pominięto wszelkie ładunki, które mogą znajdować się
w warstwie tlenku podbramkowego oraz założono, że kontaktowa różnica potencjałów pomiędzy
elektrodą bramki (ang. Gate) a półprzewodnikiem jest równa zero (
ϕ
ms
= 0, pojęcie to zostanie
szerzej omówione w dalszej części instrukcji). W dalszych rozważaniach przyjęto ponadto, że
warstwa tlenku jest idealnym izolatorem.
Rys. 1. Schematyczny przekrój idealnego kondensatora MOS bez polaryzacji zewnętrznej.
W zależności od wartości napięcia bramki (U
G
) przypowierzchniowy obszar
półprzewodnika może znajdować się w trzech charakterystycznych stanach. Jest to związane z
oddziaływaniem pola elektrycznego wywołanego przez bramkę na swobodne nośniki ładunku w
półprzewodniku. Oddziaływanie to odbywa się jak w klasycznym kondensatorze, poprzez warstwę
izolatora.
Krzemowe podłoże
półprzewodnikowe
typu p
Tlenek podbramkowy SiO
2
Bramka metalowa
U
G
= 0
„Oddziaływanie polowe w kondensatorze MOS” (M)
2
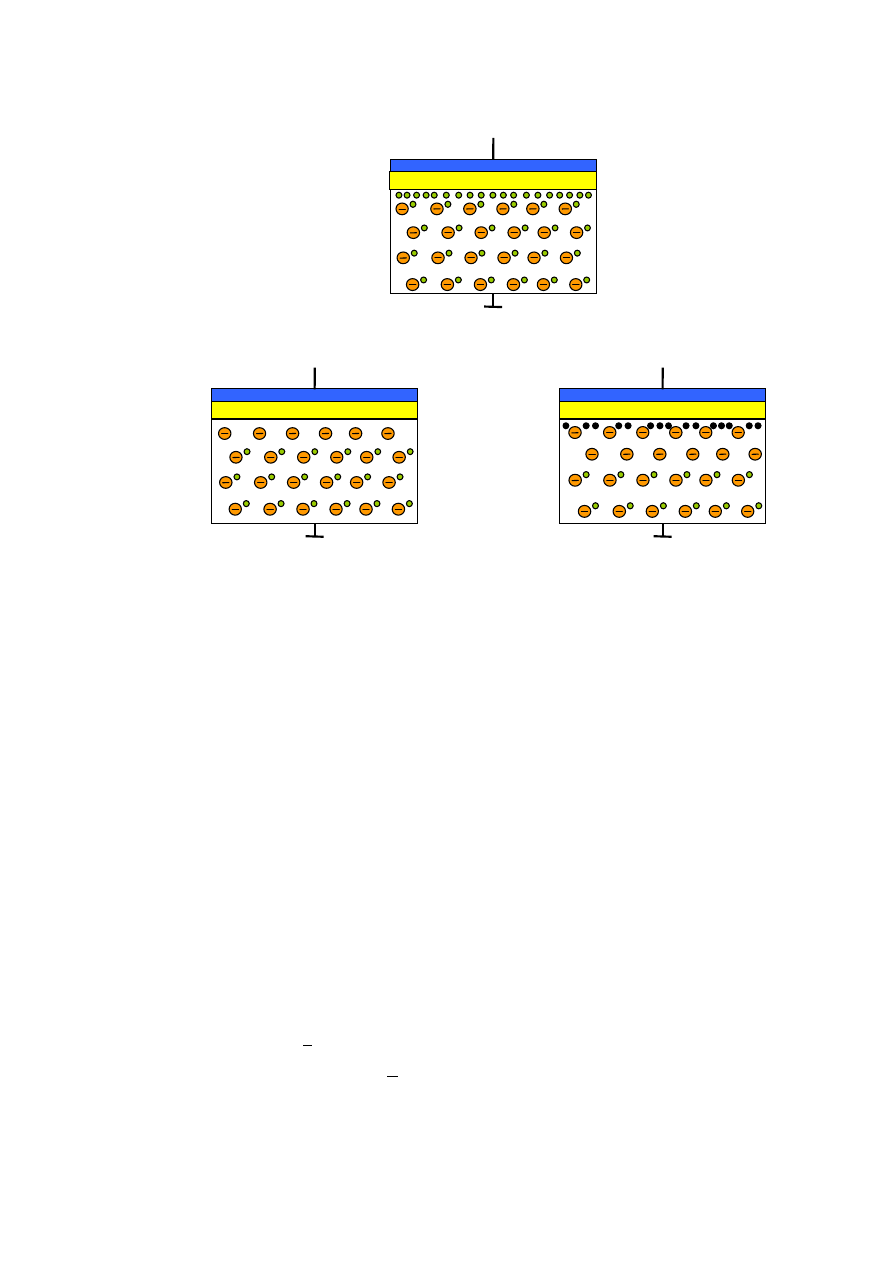
Rys. 2. Schematyczne przekroje tranzystora MOS, w którym przypowierzchniowa warstwa
półprzewodnika znajduje się w stanie: a) akumulacji, b) zubożenia c) inwersji.
Jeśli U
G
< 0, wówczas do znajdującego się pod bramką przypowierzchniowego obszaru
półprzewodnika przyciągane są dziury (rys. 2a.). W przypadku kondensatora z podłożem typu p
mamy do czynienia z gromadzeniem się nośników większościowych. W związku z tym stan
obszaru podbramkowego nazywa się stanem akumulacji.
W przypadku polaryzacji bramki niedużym napięciem dodatnim dziury są odpychane z
obszaru podbramkowego, gdzie pozostają nieruchome odsłonięte jony domieszki akceptorowej
(rys. 2b.). Pozbawiony swobodnych nośników ładunku obszar półprzewodnika nazywa się warstwą
zubożoną, a jego stan – stanem zubożenia.
Wraz ze wzrostem dodatniego napięcia ku powierzchni granicznej dielektryk-
-półprzewodnik przyciągana jest coraz większa liczba elektronów (w rozważanym przypadku
nośników mniejszościowych). Innymi słowy, w obszarze podbramkowym następuje odwrócenie
typu przewodnictwa, czyli panuje w nim stan inwersji (rys. 2c.). Dopóki koncentracja elektronów
na powierzchni (n
S
– od ang. Surface) jest mniejsza od koncentracji nośników większościowych w
objętości półprzewodnika (p
B
– od ang. Bulk) mówi się o stanie słabej inwersji. Dla większych
wartości U
G
, kiedy n
S
≥
p
B
następuje stan silnej inwersji. Napięcie bramki, od którego rozpoczyna
się ten stan nazywa się napięciem progowym (U
G
=
U
T
).
Warstwa
zubożona
Warstwa inwersyjna
U
G
>> 0
c) stan inwersji
Warstwa akumulacyjana
a) stan akumulacji
U
G
< 0
U
G
> 0
Warstwa
zubożona
b) stan zubożenia
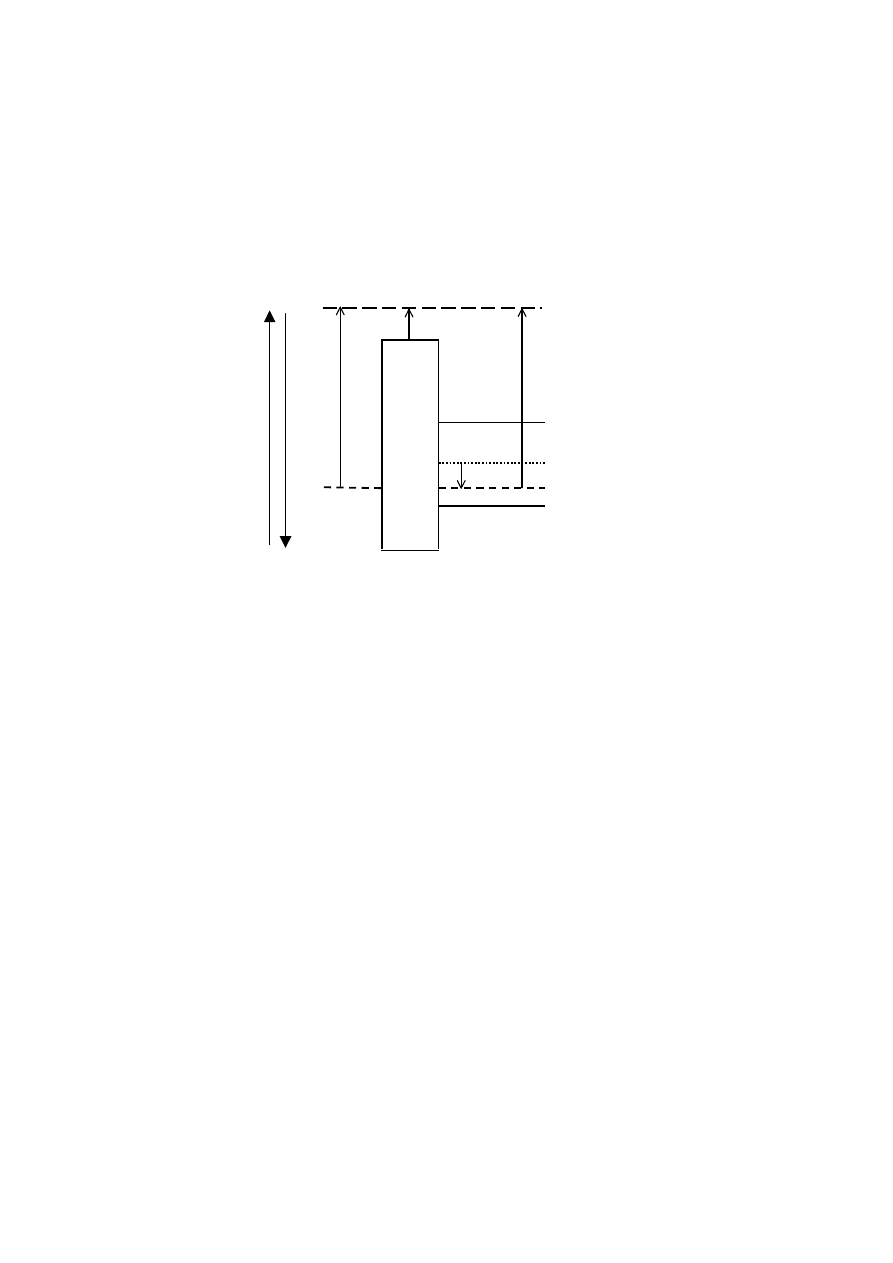
„Oddziaływanie polowe w kondensatorze MOS” (M)
3
2. Energetyczny model pasmowy struktury MOS.
Energetyczny model pasmowy idealnego kondensatora MOS przy U
G
= 0 przedstawiono na
rys. 3. W tym przypadku przy braku polaryzacji zewnętrznej pasma energetyczne w
półprzewodniku są wyprostowane. Wynika to z założenia, że kontaktowa różnica potencjałów
ϕ
ms
jest równa zero oraz że w tlenku podbramkowym nie ma żadnych ładunków. Nie ma więc żadnych
czynników zaburzających równomierny rozkład ładunków w półprzewodniku (patrz rys. 1.).
Rys. 3. Energetyczny model pasmowy idealnego kondensatora MOS przy braku polaryzacji
zewnętrznej (założono, że kontaktowa różnica potencjałów
ϕ
ms
= (
Φ
M
–
Φ
S
)/q = 0).
Na rys. 3. użyto oznaczeń:
E
C
– dno pasma przewodnictwa w półprzewodniku,
E
V
– wierzchołek pasma walencyjnego w półprzewodniku,
E
i
– poziom samoistny w półprzewodniku,
E
F
– poziom Fermiego w półprzewodniku,
ϕ
F
– potencjał Fermiego w półprzewodniku,
E
Fm
– poziom Fermiego w metalu,
Φ
M
– praca wyjścia z metalu (równa energii potrzebnej do przeniesienia elektronu z poziomu E
Fm
do poziomu próżni),
Φ
S
– praca wyjścia z półprzewodnika (równa energii potrzebnej do przeniesienia elektronu z
poziomu E
F
do poziomu próżni),
χ
i
– powinowactwo elektronowe dielektryka.
Przyłożenie do bramki napięcia ujemnego i wywołanie w przypowierzchniowym obszarze
półprzewodnika stanu akumulacji odpowiada na modelu energetycznym zagięciu pasm ku górze
(patrz rys. 4a.). Miarą zagięcia pasm na granicy dielektryk-półprzewodnik jest potencjał
E
C
E
F
E
i
E
V
E
Fm
Φ
M
Φ
S
q
χ
i
q
ϕ
F
Poziom energetyczny elektronu w próżni
E
ϕ
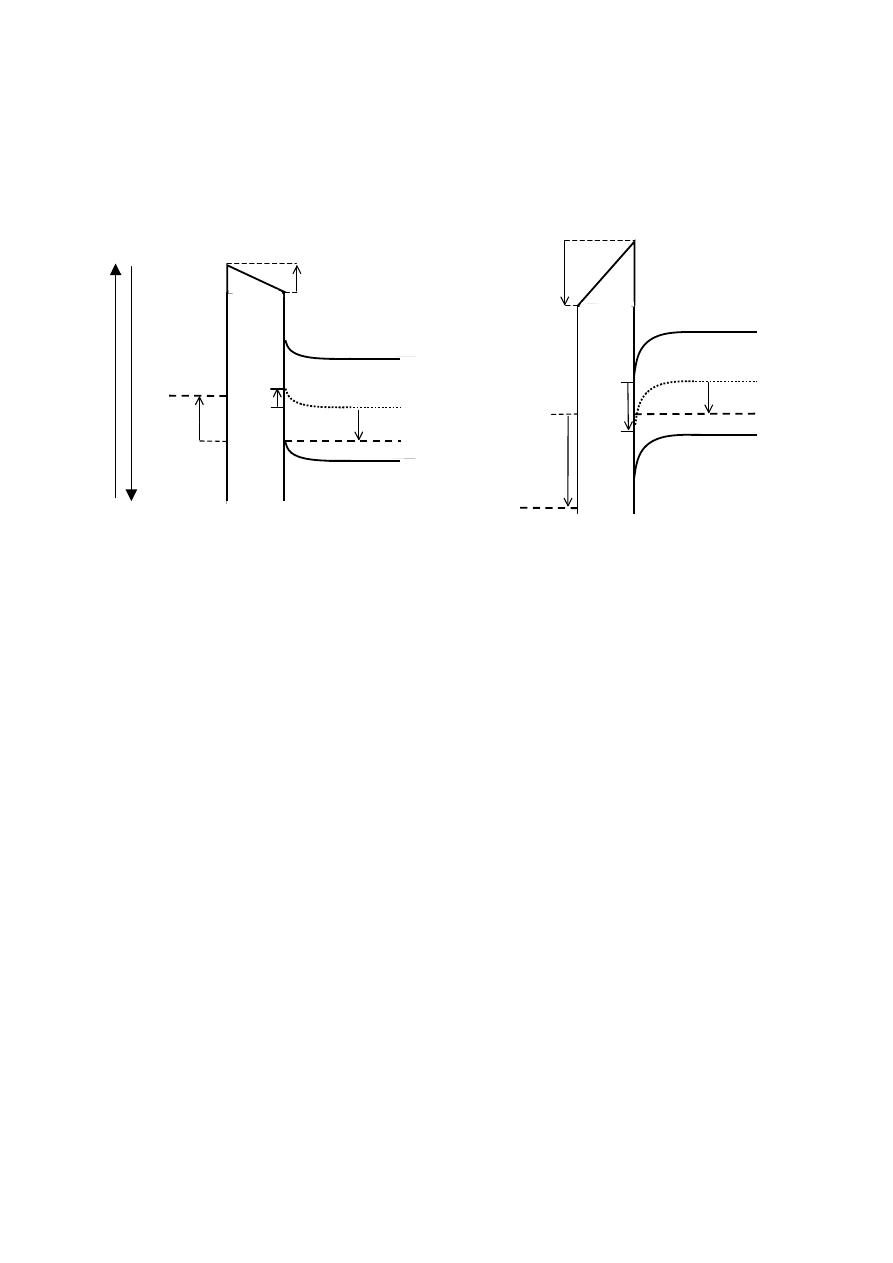
„Oddziaływanie polowe w kondensatorze MOS” (M)
4
powierzchniowy (
ϕ
S
), który jest równy spadkowi napięcia na przypowierzchniowej warstwie
półprzewodnika. Pozostała część napięcia U
G
odkłada się na warstwie tlenku (
ϕ
i
):
i
S
G
φ
φ
U
+
=
(1)
a)
b)
Rys. 4. Energetyczny model pasmowy kondensatora MOS w przypadkach, kiedy
przypowierzchniowy obszar półprzewodnika znajduje się w stanie: a) akumulacji, b) inwersji.
Przy dodatniej polaryzacji bramki pasma energetyczne w półprzewodniku zostaną zagięte ku
dołowi. Możliwe są następujące przypadki:
0 <
ϕ
S
<
ϕ
F
– stan zubożenia,
ϕ
F
≤
ϕ
S
< 2
ϕ
F
– stan słabej inwersji,
2
ϕ
F
≤
ϕ
S
– stan silnej inwersji.
3. Właściwości rzeczywistego kondensatora MOS
a) Kontaktowa różnica potencjałów
W rzeczywistym kondensatorze MOS praca wyjścia z materiału bramki nie jest równa pracy
wyjścia z półprzewodnika. W przypadku najczęściej stosowanych bramek metalowych praca
wyjścia z metalu jest mniejsza od pracy wyjścia z półprzewodnika (
Φ
M
<
Φ
S
), czyli kontaktowa
różnica potencjałów:
ϕ
ms
= (
Φ
M
–
Φ
S
)/q < 0
(2)
Innymi słowy, rysując model pasmowy kondensatora należy poziomy Fermiego w
materiałach po obu stronach dielektryka umieścić na różnych wysokościach, tak jak pokazano na
rys. 5a. Z fizycznego punktu widzenia oznacza to, że w strukturze kondensatora MOS panuje stan
E
ϕ
q
ϕ
F
E
F
E
V
E
C
E
i
q
ϕ
i
q
ϕ
S
E
Fm
qU
G
<0
q
ϕ
S
q
ϕ
i
q
ϕ
F
E
V
E
C
E
i
E
F
E
Fm
qU
G
>>0
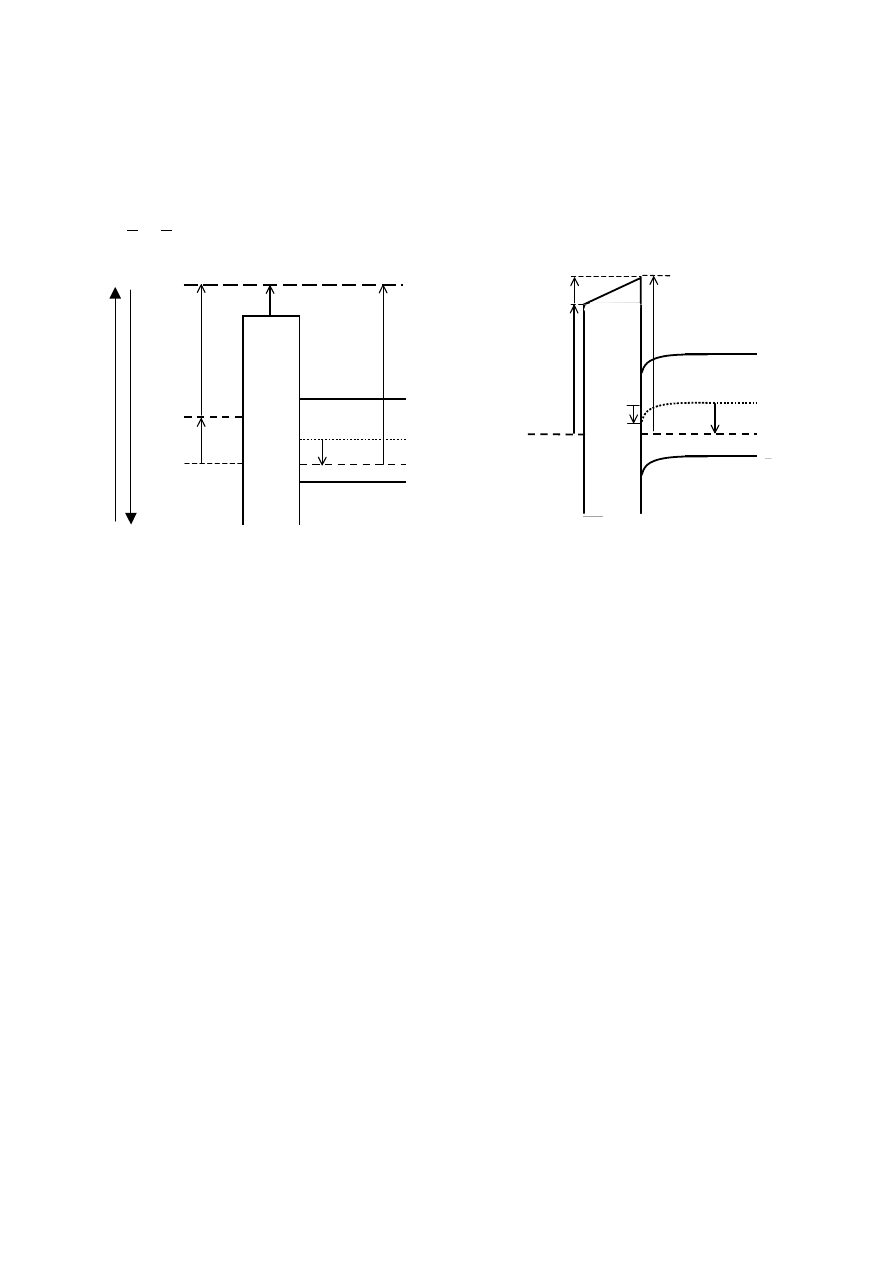
„Oddziaływanie polowe w kondensatorze MOS” (M)
5
nierównowagi termodynamicznej. Taki stan nierównowagi może zostać utrzymany, jeśli do bramki
zostanie przyłożone odpowiednie napięcie U
G
=
ϕ
ms
. Ponieważ w stanie tym żadne pasma
energetyczne nie ulegają zagięciu nazywa się go stanem płaskich pasm, a charakterystyczną
wartość napięcia bramki z nim związanego zwie się napięciem płaskich pasm i oznacza U
G
= U
FB
(ang. Flat Band).
Rys. 5. Energetyczny model pasmowy kondensatora MOS o
ϕ
ms
< 0: a) w stanie płaskich pasm
(U
G
= U
FB
), który jest stanem nierównowagi oraz b) w stanie równowagi termodynamicznej.
Jednakże bez oddziaływania zewnętrznego (przy U
G
= 0) struktura będzie dążyć do
osiągnięcia stanu równowagi, czyli wyrównania poziomów Fermiego. Oznacza to, że część
elektronów przepłynie z metalu do półprzewodnika. Spowoduje to równocześnie odepchnięcie
części dziur zgodnie z bilansem koncentracji nośników w stanie równowagi:
n
⋅
p = n
i
2
(3)
gdzie przez n
i
oznaczono koncentrację samoistną w półprzewodniku.
Po stronie półprzewodnika powstanie ujemny ładunek przestrzenny złożony zarówno z
elektronów, jak i z odsłoniętych centrów domieszkowych. Związana z tym ładunkiem bariera
potencjału zahamuje dalszy przepływ elektronów i ustali się stan równowagi. Odpowiadający mu
model pasmowy struktury MOS przedstawiono na rys. 5b.
b) Ładunki w tlenku
W rzeczywistych kondensatorach MOS w nieidealnej warstwie tlenku podbramkowego oraz
na nieidealnej powierzchni granicznej tlenek-półprzewodnik znajdują się nieskompensowane
ładunki elektryczne (np. jony metali alkalicznych, zerwane wiązania sieci krystalicznej). Są to
głównie ładunki dodatnie. W matematycznym opisie właściwości kondensatora zastępuje się je
E
ϕ
Φ
M
E
C
E
F
E
i
E
V
E
Fm
Φ
S
q
χ
i
q
ϕ
F
Poziom energetyczny elektronu w próżni
qU
G
=q
ϕ
ms
q
ϕ
i
q
ϕ
S
E
Fm
Φ
M
−
q
χ
i
E
F
E
V
E
C
E
i
q
ϕ
F
Φ
S
−
q
χ
i
−
q
ϕ
S

„Oddziaływanie polowe w kondensatorze MOS” (M)
6
przez równoważnie działający ładunek efektywny (Q
eff
) umiejscowiony w płaszczyźnie granicznej
tlenek-półprzewodnik. Jest to ładunek przypadający na jednostkę powierzchni, o wymiarze C/cm
2
.
Dodatni ładunek efektywny, tak jak kontaktowa różnica potencjałów, powoduje
indukowanie w półprzewodniku ładunku ujemnego. Aby skompensować działanie obu czynników i
doprowadzić przypowierzchniowy obszar półprzewodnika do stanu płaskich pasm należy
przyłożyć napięcie bramki równe:
ox
eff
ms
FB
C
Q
φ
U
−
=
(4)
gdzie C
ox
jest
pojemnością jednostkową tlenku podbramkowego, pojemnością przypadającą na
jednostkę powierzchni, o wymiarze F/cm
2
.
4. Matematyczny opis właściwości kondensatora MOS
Matematyczny opis przedstawionych powyżej stanów przypowierzchniowego obszaru
półprzewodnika uzyskuje się rozwiązując równanie Poissona:
( )
( )
( ) ( ) ( )
[
]
x
n
x
p
x
N
x
N
ε
q
ε
x
ρ
dx
φ
d
A
D
S
S
2
2
+
−
−
=
−
=
(5)
gdzie: q – ładunek elementarny = 1.6
⋅
10
-19
C,
ε
S
– przenikalność dielektryczna półprzewodnika,
N
D
(x), N
A
(x), p(x), n(x) – odpowiednio koncentracje: zjonizowanych domieszek
donorowych i akceptorowych oraz koncentracje dziur i elektronów w odległości x od
powierzchni półprzewodnika.
W przypadku półprzewodnika jednorodnie domieszkowanego:
( )
( )
B
B
A
D
A
D
p
n
N
N
x
N
x
N
−
≈
−
=
−
(6)
gdzie:
−
=
kT
φ
q
exp
n
n
F
i
B
– koncentracja elektronów w głębi półprzewodnika
=
kT
φ
q
exp
n
p
F
i
B
– koncentracja dziur w głębi półprzewodnika.
„Oddziaływanie polowe w kondensatorze MOS” (M)
7
Koncentracje swobodnych nośników ładunku można wyrazić wzorami:
( )
( )
(
)
( )
−
⋅
=
−
⋅
=
kT
x
φ
q
exp
p
kT
x
φ
φ
q
exp
n
x
p
B
F
i
(6a)
( )
( )
(
)
( )
⋅
=
−
⋅
=
kT
x
φ
q
exp
n
kT
φ
x
φ
q
exp
n
x
n
B
F
i
(6b)
gdzie k to stała Boltzmana, a T to temperatura bezwzględna.
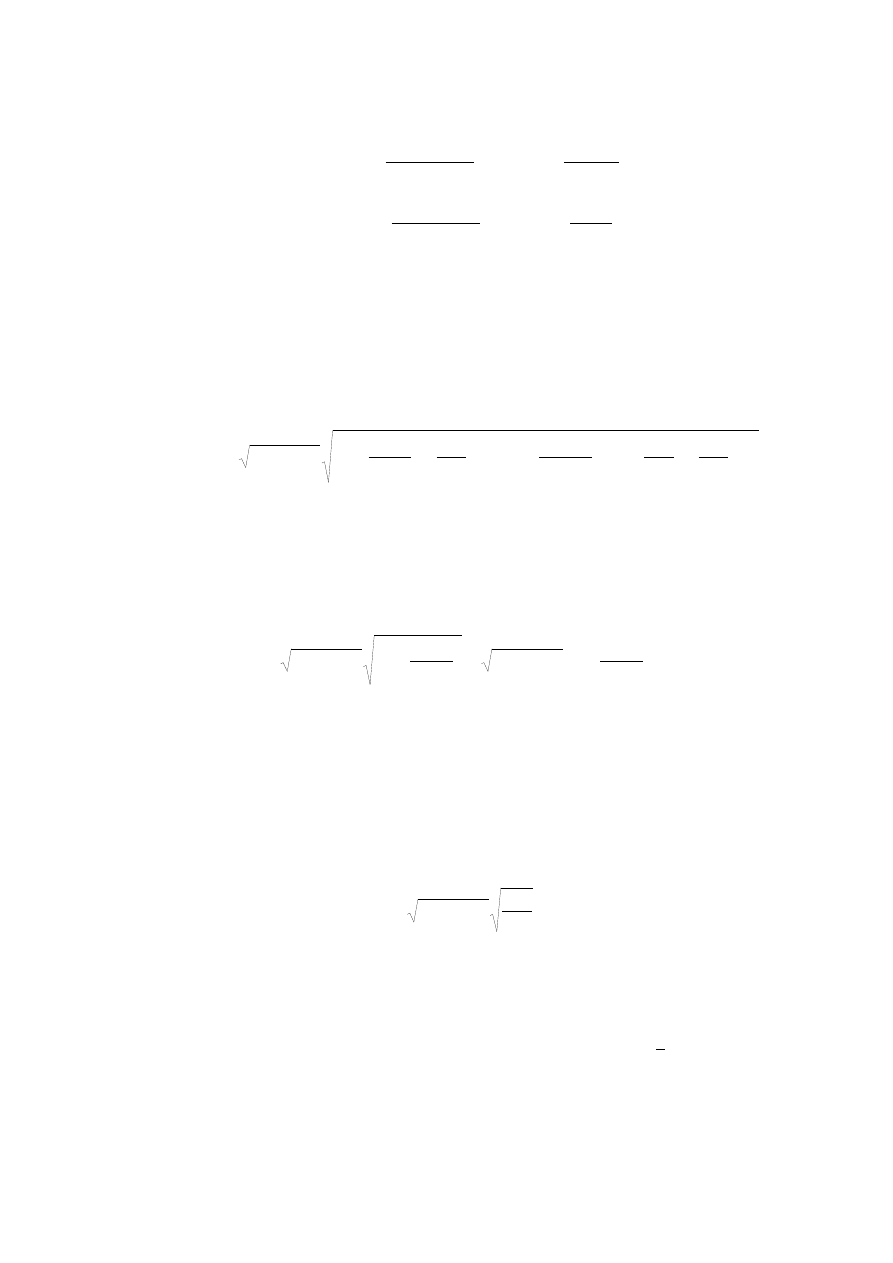
Rozwiązanie równania (5) przy założeniu, że w głębi półprzewodnika panuje neutralność
elektryczna (warunki brzegowe
ϕ
(x) = 0,
ρ
(x) = 0) prowadzi do wyrażenia opisującego zależność
całkowitego ładunku zgromadzonego w półprzewodniku (Q
S
) od potencjału powierzchniowego:
( )
−
−
−
+
−
+
−
−
=
1
kT
φ
q
kT
φ
q
exp
kT
φ
2
q
exp
1
kT
φ
q
kT
φ
q
exp
kT
N
ε
2
φ
sgn
Q
S
S
F
S
S
A
S
S
S
(7)
W przypadku struktury z podłożem typu p, w zależności od stanu, w jakim znajduje się obszar
podbramkowy, wzór (7) można znacznie uprościć.
W stanie akumulacji, gdy
ϕ
S
< 0:
−
=
−
≈
kT
2
φ
q
exp
kT
N
ε
2
kT
φ
q
exp
kT
N
ε
2
Q
S
A
S
S
A
S
S
(8)
W stanie płaskich pasm, gdy
ϕ
S
= 0:
0
Q
S
=
(9)
W stanach zubożenia i słabej inwersji, gdy 0 <
ϕ
S
< 2
ϕ
F
:
kT
φ
q
kT
N
ε
2
Q
S
A
S
S
−
≈
(10)
W stanie słabej inwersji, gdy
ϕ
F
≤
ϕ
S
< 2
ϕ
F
, koncentracja elektronów jest niewielka i można
ją pominąć, stosując dla ułatwienia tzw.
przybliżenie zubożenia. Polega ono na założeniu, że w
przypowierzchniowej warstwie półprzewodnika do głębokości x = x
d
(
ang. depletion) wszystkie
atomy domieszki są odsłonięte (ich ładunek nie jest kompensowany przez nośniki większościowe, a
koncentracje nośników mniejszościowych zaniedbuje się), zaś w głębi półprzewodnika dla x > x
d
wszystkie ładunki są skompensowane. Wielkość x
d
nazywa się
szerokością obszaru zubożonego i
wyznacza się ją ze wzoru:

„Oddziaływanie polowe w kondensatorze MOS” (M)
8
A
S
S
d
qN
φ
ε
2
x
=
(11)
Przy takim uproszczeniu ładunek zgromadzony w półprzewodniku jest tylko ładunkiem
zjonizowanych centrów domieszkowych i wzór (10) można przekształcić do postaci:
d
A
S
x
qN
Q
≈
(12)
Na początku stanu silnej inwersji, gdy U
G
= U
T
, korzystając nadal z przybliżenia
zubożenia i podstawiając do wzoru (11)
ϕ
S
= 2
ϕ
F
otrzymuje się:
F
A
S
S
φ
q
N
ε
4
Q
≈
(13)
Przy wzroście napięcia bramki powyżej napięcia progowego, w pierwszym przybliżeniu
zakłada się, iż potencjał powierzchniowy
ϕ
S
nie wzrasta powyżej wartości 2
ϕ
F
. W tym zakresie już
niewielki wzrost
ϕ
S
powoduje bardzo duży przyrost ładunku warstwy inwersyjnej (patrz rys. 6.).
Można przyjąć, że warstwa ta ekranuje głębsze warstwy półprzewodnika od pola elektrycznego. W
związku z tym grubość warstwy zubożonej nie wzrasta ponad:
A
F
S
max
d
qN
φ
ε
4
x
=
(14)
Rys. 6. Wykres zależności modułu ładunku zgromadzonego w półprzewodniku od potencjału
powierzchniowego dla kondensatora z podłożem typu p.
-0.400
-0.200
0.000
0.200
0.400
0.600
0.800
1.000
Q
S
ϕ
S
ϕ
F
2
ϕ
F

„Oddziaływanie polowe w kondensatorze MOS” (M)
9
W zakresie silnej inwersji przyjmuje się w przybliżeniu, że ładunek zgromadzony w
półprzewodniku zmienia się wykładniczo wraz ze zmianami potencjału powierzchniowego. Wzory
matematyczne opisujące Q
S
zostały pominięte, ponieważ różne przybliżenia charakteryzują się
różną dokładnością w zakresach wartości
ϕ
S
bliskich i większych od 2
ϕ
F
.
Jak już wspomniano, napięcie pomiędzy bramką a podłożem kondensatora jest sumą
spadków napięć na warstwie dielektryka i na przypowierzchniowej warstwie półprzewodnika.
Uwzględniając istnienie kontaktowej różnicy potencjałów oraz wpływ nieskompensowanych
ładunków w tlenku podbramkowym można uzupełnić zależność (1) zapisując:
i
S
FB
G
φ
φ
U
U
+
=
−
(15)
Korzystając z prawa Gaussa ostatecznie:
ox
S
S
FB
G
C
Q
φ
U
U
−
=
−
(16)
Numeryczne rozwiązanie równania (16) wraz z odpowiednim równaniem opisującym
zależność Q
S
od
ϕ
S
pozwala na znalezienie zależności pomiędzy napięciem bramki a ładunkiem
zgromadzonym w półprzewodniku.
5. Charakterystyka pojemnościowo-napięciowa kondensatora MOS
Pojemność różniczkowa kondensatora MOS (czyli jego pojemność dla małych amplitud
prądu zmiennego) jest zdefiniowana równaniem:
G
S
G
G
dU
dQ
A
dU
dQ
A
C
−
=
=
(17)
gdzie A jest polem powierzchni bramki kondensatora, a Q
G
ładunkiem zgromadzonym na bramce.
Oczywistym jest, że Q
G
= – Q
S
(przypomnienie: są to ładunki określane na jednostkę powierzchni).
W przypadku idealnej struktury MOS, korzystając z zależności (1) można zapisać:
(
)
ox
S
S
i
S
S
S
i
S
S
G
AC
1
AC
1
dQ
φ
d
dQ
φ
d
A
1
dQ
φ
φ
d
A
1
dQ
dU
A
1
C
1
+
=
−
−
=
+
−
=
−
=
(18a)
ox
S
ox
S
C
C
C
C
A
C
+
=
(18b)

„Oddziaływanie polowe w kondensatorze MOS” (M)
10
Postać wzoru (18a) wskazuje na to, iż najprostszy schemat zastępczy kondensatora MOS
składa się ze stałej pojemności dielektryka:
ox
ox
ox
t
ε
C
=
(19)
oraz połączonej szeregowo zmiennej (zależnej od napięcia) pojemności półprzewodnika (rys. 7.).
Rys. 7. Schemat zastępczy kondensatora MOS
Korzystając z zależności podanych w poprzednim punkcie instrukcji, całkowitą pojemność
kondensatora MOS można opisać w uproszczony sposób dla każdego stanu przypowierzchniowej
warstwy półprzewodnika.
W stanie akumulacji ładunek Q
S
jest ładunkiem nośników większościowych, który
wykładniczo zależy od potencjału powierzchniowego (wzór (8)). Ta silna zależność od
ϕ
S
oznacza,
ż
e pojemność półprzewodnika jest bardzo duża i pojemność całkowita jest bliska znacznie
mniejszej pojemności C
ox
:
MAX
ox
ox
ox
C
t
ε
A
AC
C
=
=
≈
(20)
W tym zakresie napięć bramki charakterystyka pojemnościowo-napięciowa kondensatora osiąga
swoje maksimum.
W stanie płaskich pasm pojemność półprzewodnika wynosi:
D
S
S
L
ε
C
=
(21)
gdzie L
D
jest tzw.
drogą Debye’a lub drogą ekranowania. Określa ona odległość, na której
potencjał elektryczny maleje e-krotnie, czyli praktycznie zanika pole elektryczne. Dla
półprzewodnika typu p:
A
2
S
D
N
q
ε
kT
L
=
(22)
AC
ox
AC
S
= f(U
G
)

„Oddziaływanie polowe w kondensatorze MOS” (M)
11
Całkowitą pojemność kondensatora w tym stanie oznacza się przez C
FB
, a jej wartość
wyznacza się korzystając z zależności (18b), (19) i (21) wraz z (22).
W stanie zubożenia ładunek Q
S
składa się głównie z ładunku jonów domieszek
nieskompensowanych przez nośniki większościowe. Zmiana tego ładunku odbywa się dzięki
przepływowi nośników większościowych, które podążając za zmianą potencjału powierzchniowego
zasłaniają lub odkrywają centra domieszkowe na końcu warstwy zubożonej x
d
:
d
S
S
x
ε
C
=
(23)
W tym zakresie całkowita pojemność kondensatora (18b) maleje wraz ze wzrostem U
G
, ponieważ
pojemność półprzewodnika (23) maleje, a C
S
< C
ox
.
W stanie silnej inwersji dominującym składnikiem Q
S
jest ładunek nośników
mniejszościowych. Koncentracja nośników mniejszościowych w półprzewodniku zmienia się
głównie wskutek procesów generacji-rekombinacji. Procesy te zachodzą ze skończoną szybkością,
która określana jest parametrem zwanym
czasem życia nośników mniejszościowych. Z tego
powodu, w tym stanie pracy kondensatora MOS obserwuje się jego różne odpowiedzi
pojemnościowe, w zależności od częstotliwości sygnału pobudzającego.
W przypadku powolnych zmian napięcia polaryzacji (
małej częstotliwości sygnału
pomiarowego) zmiany ładunku nośników mniejszościowych nadążają za zmianami potencjału
powierzchniowego. Jak już wspomniano, zmiany te są bardzo duże, a więc pojemność C
S
jest
bardzo duża i całkowita pojemność kondensatora MOS jest równa C
ox
(tak jak w stanie
akumulacji).
Przy
dużej częstotliwości sygnału pomiarowego ładunek nośników mniejszościowych nie
zmienia się, gdyż procesy generacji-rekombinacji nie nadążają za zmianami potencjału
powierzchniowego. Zmianie może ulegać tylko ładunek zjonizowanych centrów domieszkowych,
tak jak w stanie zubożenia. Jednakże w tym przypadku x
d
= x
dmax
, a zatem:
min
S
max
d
S
S
C
x
ε
C
=
=
(24)
W tym przypadku całkowitą pojemność kondensatora w stanie silnej inwersji wyznacza się
korzystając z zależności (18b), (19), (24) wraz z (14) i oznacza się ją przez C
MIN
.
Przebieg charakterystyki pojemnościowo-napięciowej kondensatora MOS z podłożem
typu p zilustrowano poglądowo na rys. 8. Przez LF oznaczono na nim część charakterystyki
odpowiadającą małym częstotliwościom sygnału pomiarowego (
ang. Low Frequency), zaś przez
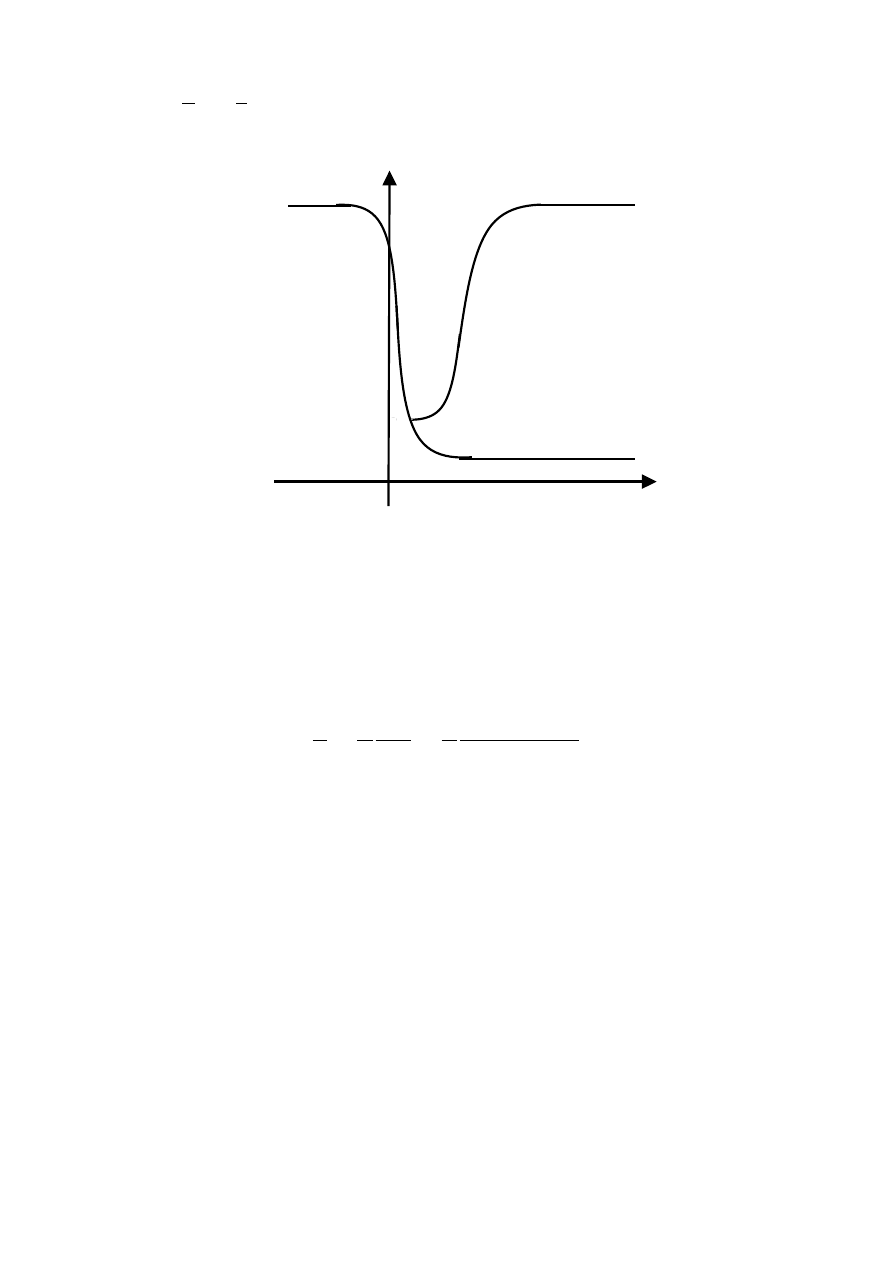
„Oddziaływanie polowe w kondensatorze MOS” (M)
12
HF (
ang. High Frequency) część charakterystyki, jaką uzyska się przy pomiarach
wysokoczęstotliwościowych.
Rys. 8. Charakterystyka pojemnościowo-napięciowa kondensatora MOS z podłożem typu p.
Należy podkreślić, że w dotychczasowych rozważaniach nie uwzględniono reakcji
ładunków zgromadzonych w tlenku podbramkowym na pobudzenie struktury MOS sygnałem
zmiennym. W przypadku rzeczywistego kondensatora MOS do zależności (17) należy podstawić
wzór (15). Wówczas:
(
)
S
i
S
FB
S
G
dQ
φ
φ
U
d
A
1
dQ
dU
A
1
C
1
+
+
−
=
−
=
(25)
Szczegółowa analiza zachowania różnych (np. ruchomych i nieruchomych) ładunków
zgromadzonych w tlenku oraz na powierzchni półprzewodnika przy pobudzeniu sygnałami o różnej
częstotliwości wykracza poza tematykę tego ćwiczenia. Zapamiętać należy, że istnienie tych
ładunków powoduje przesunięcie charakterystyk C-U kondensatora MOS równolegle do osi U
G
oraz zmianę kształtu i nachylenia charakterystyk w różnych jej zakresach. Analizując tak
zniekształcone charakterystyki można wyznaczyć wiele ważnych parametrów przyrządu, a co za
tym idzie np. wnioskować o jakości technologii, w jakiej go wykonano.
C
C
MAX
U
G
C
MIN
akumulacja
zubożenie
silna inwersja
LF
HF

„Oddziaływanie polowe w kondensatorze MOS” (M)
13
6. Wyznaczanie parametrów kondensatora MOS na podstawie zmierzonej
wysokoczęstotliwościowej charakterystyki pojemnościowo-napięciowej
1) Grubość tlenku podbramkowego
Korzystając z zależności (20):
MAX
ox
ox
ox
ox
C
ε
A
C
ε
t
=
=
(26)
gdzie C
MAX
jest zmierzoną w stanie akumulacji maksymalną wartością pojemności.
2) Koncentracja domieszek w podłożu półprzewodnikowym
Przekształcając wzory (14) i (24) otrzymuje się:
S
F
2
min
S
A
ε
q
φ
C
4
N
=
(27)
Pojemność C
Smin
wyznacza się ze wzoru:
MAX
MIN
ox
MIN
min
S
C
1
C
1
1
A
1
C
1
C
1
1
A
1
C
−
=
−
=
(28)
gdzie C
MIN
jest zmierzoną w zakresie silnej inwersji minimalną wartością pojemności.
Ponieważ potencjał Fermiego
ϕ
F
jest również funkcją koncentracji domieszek:
i
A
F
n
N
ln
q
kT
φ
=
(29)
wartość N
A
wyznacza się iteracyjnie ze wzorów (27) i (29) (szczegóły w
Instrukcji
wykonawczej).
3) Napięcie płaskich pasm
Podstawiając do wzoru (18a) zależności (20) – (22) można wyprowadzić wzór na całkowitą
pojemność kondensatora MOS w stanie płaskich pasm:
MAX
A
S
FB
C
1
N
ε
kT
qA
1
1
C
+
=
(30)
Znając wartość C
FB
należy znaleźć na charakterystyce punkt, dla którego C = C
FB
.
Odpowiadająca mu wartość napięcia bramki jest poszukiwaną wartością U
FB
.
4) Ładunek efektywny w tlenku podbramkowym
Jeżeli znany jest materiał, z którego wykonana jest bramka kondensatora MOS, to znana jest
wartość kontaktowej różnicy potencjałów
ϕ
ms
. Wartość Q
eff
oblicza się z przekształconego
wzoru (4):
(
)
FB
ms
ox
ox
eff
U
φ
t
ε
Q
−
=
(31)
„Oddziaływanie polowe w kondensatorze MOS” (M)
14
II. Zastosowanie oddziaływania polowego w strukturze MOS
1. Diagnostyka produkcji układów scalonych
Projektując maski technologiczne potrzebne do wykonania układu scalonego umieszcza się
na nich dodatkowe testowe struktury kondensatorów MOS. Po wykonaniu wszystkich (lub części)
procesów technologicznych, gdy kondensatory są już gotowe, dokonuje się pomiaru ich
charakterystyk pojemnościowo-napięciowych. Na ich podstawie wyznacza się wiele istotnych
parametrów kondensatorów MOS. Parametry te są również źródłem informacji o poprawności
przebiegu procesów technologicznych, a także o parametrach wytworzonych układów scalonych.
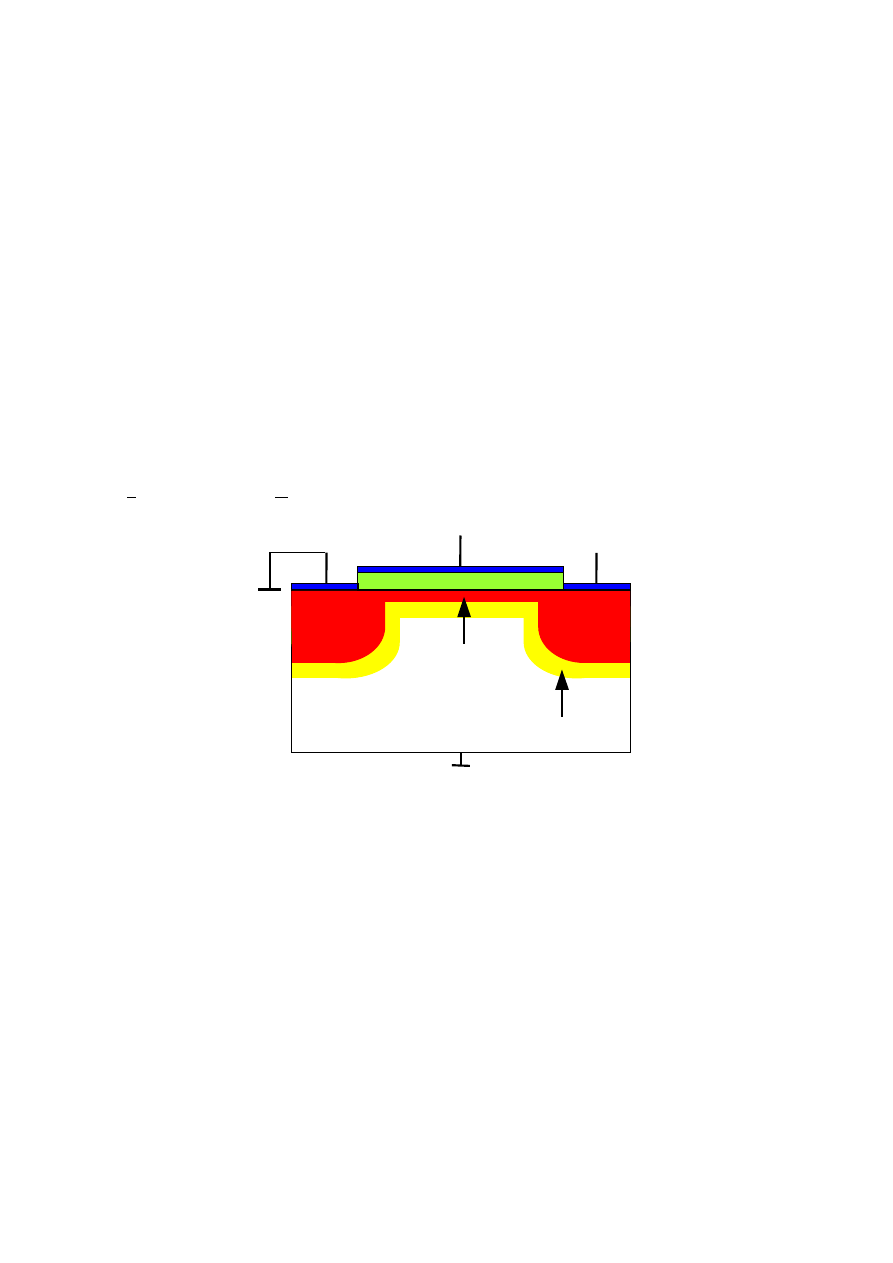
2. Tranzystor MOS
Tranzystor MOS działa w oparciu o to samo oddziaływanie polowe, co kondensator MOS.
W jego strukturze można wyróżnić dwa dodatkowe obszary przeciwnego typu niż podłoże: źródło
(
ang. Source) i dren (ang. Drain). Schematyczny przekrój tranzystora MOS pokazano na rys. 9.
Rys. 9. Schematyczny przekrój tranzystora MOS (U
DS
> 0 wywołuje przepływ prądu I
D
pomiędzy
ź
ródłem a drenem, gdy tranzystor jest włączony, czyli przy U
GS
≥
U
T
).
Przyłożenie do bramki napięcia większego niż napięcie progowe (U
GS
> U
T
) powoduje
wprowadzenie przypowierzchniowego obszaru półprzewodnika w stan silnej inwersji. Powstała
warstwa inwersyjna (zwana kanałem) łączy dren ze źródłem, umożliwiając przepływ
elektronowego prądu drenu I
D
przy polaryzacji drenu napięciem U
DS
> 0.
3. Zastosowania w układach scalonych
Zarówno kondensatory MOS, jak i tranzystory MOS są najczęściej stosowanymi w układach
scalonych
elementami
półprzewodnikowymi.
Są
podstawowymi
składnikami
pamięci
półprzewodnikowych, mikroprocesorów i wielu innych układów cyfrowych wykonanych np. w
technologiach CMOS, BiCMOS.
p
n++
n+
n+
+
n+
+
Warstwa
zubożona
Gate
U
GS
> U
T
Drain
U
DS
> 0
Source
Warstwa
inwersyjna
(kanał)

„Oddziaływanie polowe w kondensatorze MOS” (M)
15
III. Przykładowe pytania (zagadnienia) sprawdzające stan przygotowania do ćwiczenia
1) Co to jest kondensator MOS?
2) Omów stany, w jakich może znajdować się przypowierzchniowy obszar półprzewodnika przy
różnych napięciach polaryzacji bramki. Odpowiedź zilustruj odpowiednimi modelami
pasmowymi struktury MOS.
3) Wyjaśnij pojęcie napięcia progowego. Odpowiedź zilustruj odpowiednim modelem pasmowym
struktury MOS.
4) Wyjaśnij pojęcie kontaktowej różnicy potencjałów.
5) Wyjaśnij pojęcie napięcia płaskich pasm. Odpowiedź zilustruj odpowiednim energetycznym
modelem pasmowym struktury MOS.
6) Wyjaśnij pojęcie przybliżenia zubożenia. Dlaczego w warstwie zubożonej gęstość ładunku jest
stała niezależnie od położenia?
7) Dlaczego można przyjąć, że w stanie silnej inwersji potencjał powierzchniowy przestaje rosnąć
wraz ze wzrostem napięcia polaryzacji bramki?
8) Jak jest zdefiniowana pojemność kondensatora MOS?
9) Naszkicuj charakterystyki pojemnościowo-napięciowe kondensatora MOS. Wyjaśnij przyczynę
różnicy w przebiegu charakterystyk wysokoczęstotliwościowej i niskoczęstotliwościowej.
10) W jaki sposób można wyznaczyć podstawowe parametry kondensatora MOS na podstawie
pomiarów jego wysokoczęstotliwościowej charakterystyki C-U?
„Oddziaływanie polowe w kondensatorze MOS” (M)
16
IV. Instrukcja wykonawcza
do ćwiczenia pod tytułem:
„Oddziaływanie polowe w kondensatorze MOS”
(M)
1. Pomiar wysokoczęstotliwościowej charakterystyki C-U kondensatora MOS
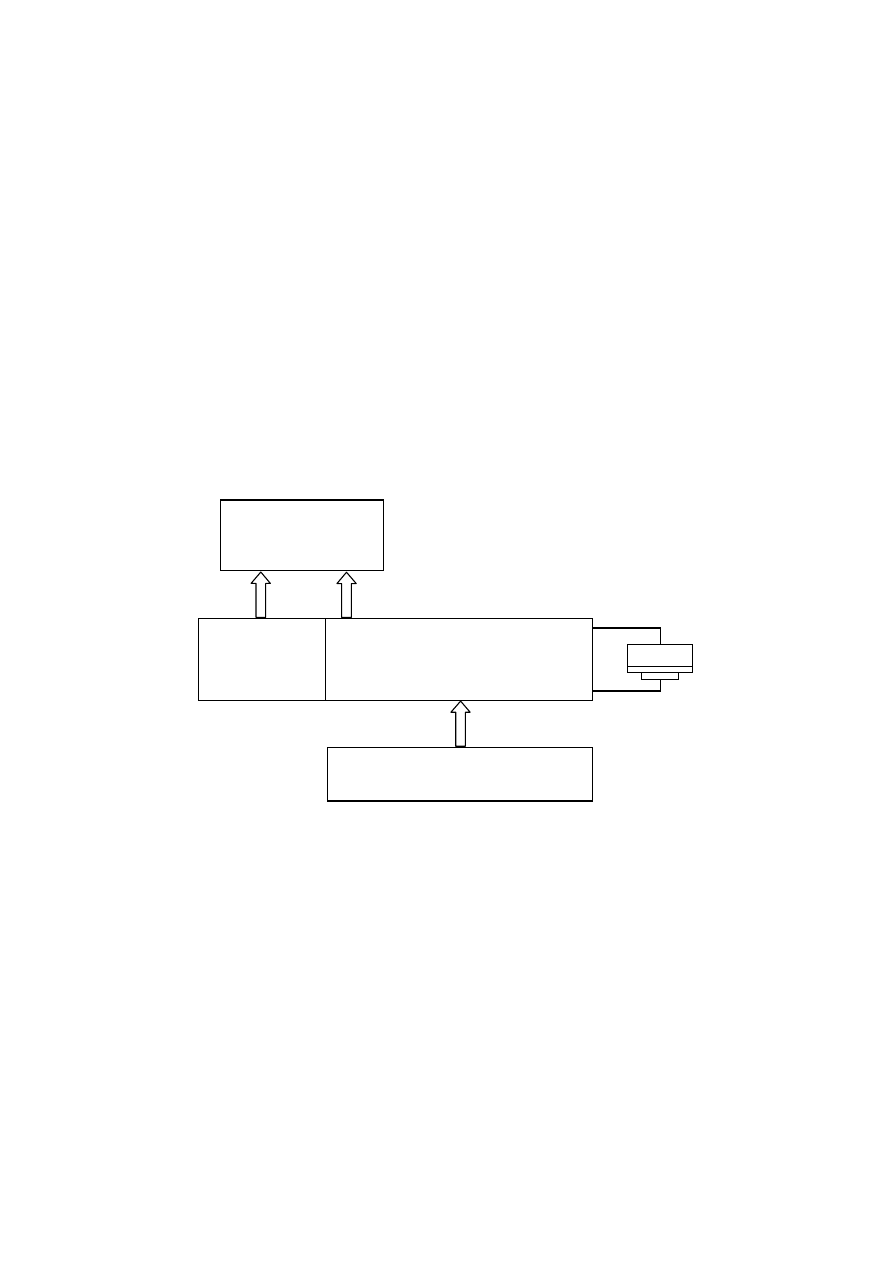
Schemat zestawu pomiarowego wykorzystywanego w niniejszym ćwiczeniu przedstawiono
na rys. 1. Na schemacie tym:
– miernik pojemności różniczkowej jest miernikiem typu FC-520 lub FC-522,
– C
X
oznacza gniazda dla minimanipulatora ostrzowego,
– zespół woltomierza C/U z wyświetlaczem cyfrowym pozwala odczytywać wartość
napięcia lub pojemności (opis sposobu odczytu zamieszczony na obudowie),
– zespół polaryzacji pozwala na regulację napięcia polaryzacji struktury MOS w zakresie
napięć ujemnych i dodatnich (za pomocą regulatora wieloobrotowego).
Rys. 1. Schemat zestawu pomiarowego (instrukcja obsługi zestawu u Prowadzącego).
Przed rozpoczęciem pomiarów należy wykonać następujące czynności:
1)
Na polecenie Prowadzącego załączyć do sieci miernik pojemności, woltomierz,
oraz generator sygnałowy.
2) Odczekać 10 min.
3)
Wraz z Prowadzącym dokonać zerowania miernika pojemności.
4)
Wraz z Prowadzącym dokonać kalibracji miernika pojemności.
Następnie należy zmierzyć charakterystykę C-U kondensatora MOS w zakresie napięć
polaryzacji bramki
od +4V do –4V. Punkty pomiarowe rozmieścić:
•
co 0.5V w zakresach inwersji i akumulacji (kiedy mierzona pojemność jest stała),
•
co 0.2V w pozostałych zakresach.
G
GENERATOR
SYGNAŁOWY ~1MHz / 0.5V
ZESPÓŁ
WOLTOMIERZA
C/U
MIERNIK POJEMNOŚCI
C
X
FC-52X
HI
LO
ZESPÓŁ
POLARYZACJI
„Oddziaływanie polowe w kondensatorze MOS” (M)
17
2. Wyznaczanie parametrów kondensatora MOS na podstawie zmierzonej charakterystyki
Badane kondensatory wykonane zostały na podłożu krzemowym (Si) typu p. Rolę
dielektryka podbramkowego spełnia dwutlenek krzemu (SiO
2
). Bramka kondensatora ma kształt
koła (jego średnicę
d poda Prowadzący) i została wykonana z aluminium (Al).
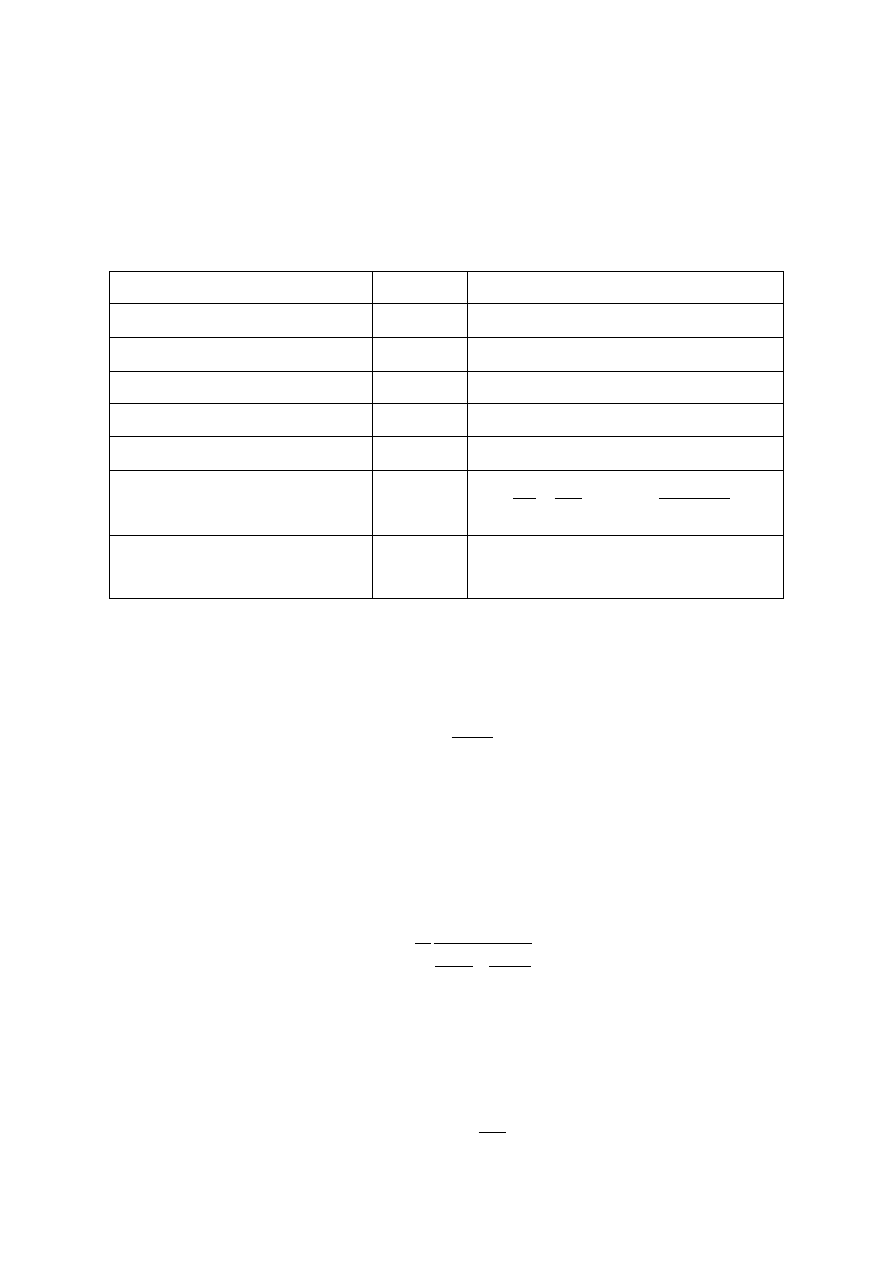
Podstawowe stałe oraz wzory wykorzystywane przy obliczeniach:
Nazwa
Symbol
Wartość lub wzór
ładunek elementarny
q
1.6
⋅
10
-19
C
stała Boltzmana
k
1.38
⋅
10
-23
J/K
temperatura
T
300 K
przenikalność dielektryczna Si
ε
S
1
⋅
10
-12
F/cm
przenikalność dielektryczna SiO
2
ε
ox
3.45
⋅
10
-13
F/cm
potencjał Fermiego
ϕ
F
[ ]
3
10
3
A
i
A
F
cm
10
cm
N
ln
026
.
0
n
N
ln
q
kT
φ
−
−
≈
=
[V]
kontaktowa różnica potencjałów
(wzór empiryczny dla bramki Al)
ϕ
ms
ϕ
ms
= – 0.6V –
ϕ
F
[V]
1) Na podstawie zmierzonej w zakresie akumulacji maksymalnej wartości pojemności C
MAX
wyznaczyć
grubość tlenku podbramkowego:
MAX
ox
ox
C
ε
A
t
=
(1)
2) Na podstawie zmierzonej w zakresie silnej inwersji minimalnej wartości pojemności C
MIN
oraz
wykorzystywanej
już
wartości
C
MAX
wyznaczyć
minimalną
wartość
pojemności
półprzewodnika:
MAX
MIN
min
S
C
1
C
1
1
A
1
C
−
=
(2)
3) W sposób iteracyjny wyznaczyć
koncentrację domieszek w półprzewodniku:
•
założyć
ϕ
F
np.: 0.3V i obliczyć N
A
ze wzoru:
S
F
2
min
S
A
ε
q
φ
C
4
N
=
(3)

„Oddziaływanie polowe w kondensatorze MOS” (M)
18
•
otrzymaną wartość N
A
podstawić do wzoru:
i
A
F
n
N
ln
q
kT
φ
=
(4)
i wyznaczyć wartość
ϕ
F
,
•
otrzymaną wartość
ϕ
F
podstawić do wzoru (3) i wyznaczyć wartość N
A
itd.
Obliczenia powtarzać aż, do momentu, gdy kolejna wartość N
A
różni się od poprzedniej o mniej
niż 5%.
4) Wyznaczyć całkowitą pojemność kondensatora MOS w stanie płaskich pasm:
MAX
A
S
FB
C
1
N
ε
kT
qA
1
1
C
+
=
(5)
5) Ustawić na zasilaczu takie napięcie polaryzacji bramki, aby mierzona pojemność kondensatora
była równa wartości C
FB
obliczonej ze wzoru (5). Ustawione napięcie jest
napięciem płaskich
pasm U
FB
.
6) Wyznaczyć
ładunek efektywny w tlenku podbramkowym:
(
)
FB
ms
ox
ox
eff
U
φ
t
ε
Q
−
=
(6)
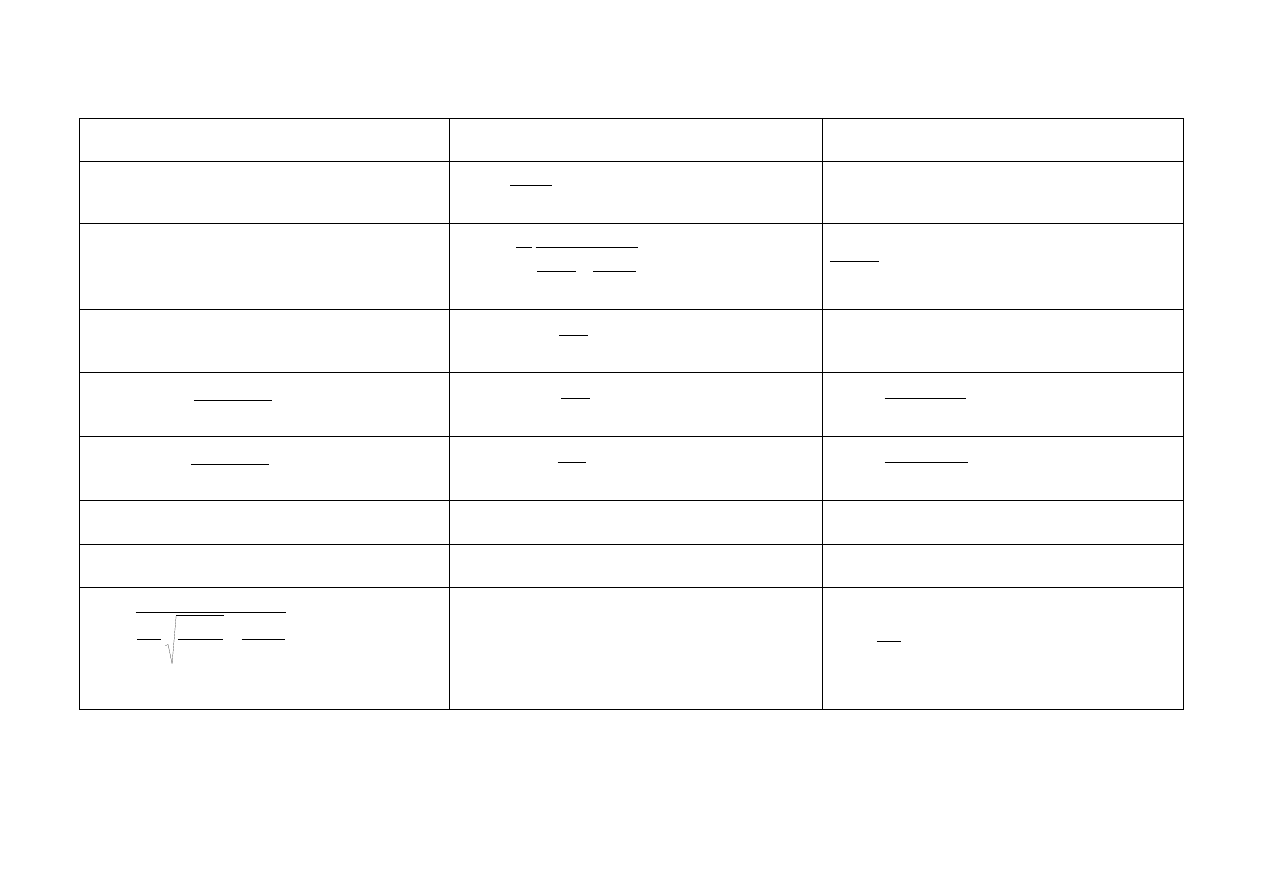
Na następnej stronie zamieszczono tabelę, którą można wydrukować i wykorzystać
pomocniczo do obliczeń.
Niezależnie należy sporządzić klasyczne sprawozdanie z przebiegu laboratorium
począwszy od protokołu pomiarowego, przez obliczenia, na wnioskach skończywszy.
Nie dopuszcza się używania komputerów osobistych („laptopów”) w trakcie laboratorium.
Studenci zobowiązani są przynieść na zajęcia kalkulatory.
„Oddziaływanie polowe w kondensatorze MOS” (M)
19
q = 1.6
⋅
10
-19
C
k = 1.38
⋅
10
-23
J/K
T = 300 K
ε
S
= 1
⋅
10
-12
F/cm
ε
ox
= 3.45
⋅
10
-13
F/cm
d [mm] =
d [cm] =
A [cm
2
] =
C
MAX
[F] =
MAX
ox
ox
C
ε
A
t
=
[cm] =
t
ox
[nm] =
C
MIN
[F] =
MAX
MIN
min
S
C
1
C
1
1
A
1
C
−
=
[F/cm
2
] =
S
2
min
S
ε
q
C
4
[V
-1
cm
-3
] =
ϕ
F1
[V] =
S
1
F
2
min
S
1
A
ε
q
φ
C
4
N
=
[cm
-3
] =
[ ]
3
10
3
1
A
2
F
cm
10
cm
N
ln
026
.
0
φ
−
−
=
[V] =
S
2
F
2
min
S
2
A
ε
q
φ
C
4
N
=
[cm
-3
] =
100
N
N
N
N
∆
1
A
2
A
1
A
A
⋅
−
=
[%] =
[ ]
3
10
3
2
A
3
F
cm
10
cm
N
ln
026
.
0
φ
−
−
=
[V] =
S
3
F
2
min
S
3
A
ε
q
φ
C
4
N
=
[cm
-3
] =
100
N
N
N
N
∆
2
3
A
2
A
A
⋅
−
=
[%] =
ϕ
F4
[V] =
N
A4
[cm
-3
] =
∆
N
A
[%] =
ϕ
F5
[V] =
N
A5
[cm
-3
] =
∆
N
A
[%] =
MAX
A
S
FB
C
1
N
ε
kT
qA
1
1
C
+
=
[F] =
U
FB
[V] =
ϕ
ms
= – 0.6V –
ϕ
F
[V] =
(
)
FB
ms
ox
ox
eff
U
φ
t
ε
Q
−
=
[C/cm
2
] =
Wyszukiwarka
Podobne podstrony:
cwiczenia 1 instrukcja 2010, BIOLOGIA UJ LATA I-III, ROK III, semestr I, Mikrobiologia, Cwiczenia
Instrukcja Z (2010)
cwiczenia 9 i 10 instrukcja 2010, BIOLOGIA UJ LATA I-III, ROK III, semestr I, Mikrobiologia, Cwiczen
egzamin optyka geometryczna i instrumentalna 2010
cwiczenia 8 instrukcja 2010, BIOLOGIA UJ LATA I-III, ROK III, semestr I, Mikrobiologia, Cwiczenia
Instrukcja 1 2010
cwiczenia 7B instrukcja 2010, BIOLOGIA UJ LATA I-III, ROK III, semestr I, Mikrobiologia, Cwiczenia
Instrukcja F (2010)
APP 05 Instrukcje 2010
cwiczenia 2 i 3 instrukcja 2010 Nieznany
cwiczenia 1 instrukcja 2010, BIOLOGIA UJ LATA I-III, ROK III, semestr I, Mikrobiologia, Cwiczenia
Instrukcja M (2010)
InstrukcjeĆw.2009 2010, Cw.1.E-01. Badanie właściwości elektrycznych kondensatora płaskiego, Laborat
PatchData key Ariva by MarcinO 03.06.2010-RAI 1234 na czerwiec, INSTRUKCJA WGRYWANIA KLUCZY do ARIVY
OSB Instrukcja montazu PL 03 2010
więcej podobnych podstron