Za rozwiàzanie

wszystkich zadaƒ

mo˝na otrzymaç

∏àcznie 50 punktów.

PRZYK¸ADOWY ARKUSZ

EGZAMINACYJNY Z MATEMATYKI

POZIOM PODSTAWOWY

Czas pracy: 170 minut

Instrukcja dla zdajàcego

1.

Sprawdê, czy arkusz zawiera 11 stron.

2.

W zadaniach od 1. do 21. sà podane 4 odpowiedzi:
A, B, C, D, z których tylko jedna jest prawdziwa. Wybierz
tylko jednà odpowiedê.

3.

Rozwiàzania zadaƒ od 22 do 31. zapisz starannie i czytel-
nie w wyznaczonych miejscach. Przedstaw swój tok rozu-
mowania prowadzàcy do ostatecznego wyniku.

4.

Pisz czytelnie. U˝ywaj d∏ugopisu/pióra tylko z czarnym
tuszem/atramentem.

5.

Nie u˝ywaj korektora. B∏´dne zapisy przekreÊl.

6.

Pami´taj, ˝e zapisy w brudnopisie nie podlegajà ocenie.

7.

Obok numeru ka˝dego zadania podana jest maksymal-
na liczba punktów mo˝liwych do uzyskania.

8.

Mo˝esz korzystaç z zestawu wzorów matematycznych,
cyrkla i linijki oraz kalkulatora.

˚yczymy powodzenia!

ARKUSZ 4

MATURA 2010

Arkusz opracowany przez Wydawnictwo Pedagogiczne OPERON

na wzór arkuszy opublikowanych przez Centralnà Komisj´ Egzaminacyjnà

ZADANIA ZAMKNI¢TE

W zadaniach od 1. do 21. wybierz i zaznacz na karcie odpowiedzi jednà poprawnà odpowiedê.

Zadanie 1. (1 pkt)

Wyra˝enie 4 16

2

1

3

$

$

zapisane w postaci pot´gi liczby 2, to:

A. 2

3

7

-

B. 2

3

4

-

C. 2

6

25

D. 2

6

26

Zadanie 2. (1 pkt)

Zmieszano 200 litrów mleka %

2

i 50 litrów mleka %

4

. Otrzymano mleko, które ma w sobie %

p

t∏uszczu. Wynika stàd, ˝e:
A. p

3

=

B.

,

p

2 4

=

C.

,

p

2 5

=

D.

,

p

3 2

=

Zadanie 3. (1 pkt)

Liczba

log

log

a

25

4

4

4

=

+

. Wynika stàd, ˝e:

A. a

4

=

B. a

8

=

C.

log

a

8

29

=

+

D.

log

a

8

29

=

+

Zadanie 4. (1 pkt)

JeÊli

,

,

,

A

B

4 5

5 6

= -

= #

-, to ró˝nica A B

[ jest równa:

A.

,

4 5

-

i

B.

,

4 6

-

i

C.

,

4 5

6

,

-

i

# -

D.

,

,

4 5

5 6

,

-

_

i

i

Zadanie 5. (1 pkt)

WartoÊç wyra˝enia

2

7

3

7

2

2

-

-

+

`

`

j

j

jest równa:

A. 1

-

B. 5

-

C. 1

2 7

- -

D. 5

2 7

- +

Zadanie 6. (1 pkt)

Zbiór liczb, których odleg∏oÊç na osi liczbowej od liczby

9

-

_

i

jest równa 4, mo˝na opisaç równaniem:

A. x

9

4

+

=

B. x

9

4

-

=

C. x

4

9

-

=

D. x

4

9

+

=

Zadanie 7. (1 pkt)

Dany jest wielomian ( )

W x

x

x

3

2

=

-

. WartoÊç tego wielomianu w punkcie 2

1

+

jest równa:

A. 3 2

8

-

-

B. 2

6

-

C. 3 2

4

+

D. 3 2

10

-

Zadanie 8. (1 pkt)

JeÊli do wykresu funkcji wyk∏adniczej f nale˝y punkt

,

P

1 3

= -

_

i

, to funkcja ta okreÊlona jest

wzorem:

A. ( )

f x

3

x

=

B. ( )

f x

9

x

=

C. f x

3

1

x

=

_

c

i

m

D. f x

9

1

x

=

_

c

i

m

Zadanie 9. (1 pkt)

Przedzia∏

,

6 11

-

_

i

jest zbiorem rozwiàzaƒ nierównoÊci:

A.

>

x

x

6 11

0

+

-

_

_

i

i

B.

<

x

x

6 11

0

-

-

_

_

i

i

C.

>

x

x

6

11

0

+

-

_

_

i

i

D.

<

x

x

6 11

0

-

+

_

_

i

i

Matematyka. Poziom podstawowy

3

Matematyka. Poziom podstawowy

Zadanie 10. (1 pkt)

Zbiór rozwiàzaƒ równania x

x

x

1

2

1

3

2

2

-

=

-

+

+

_

_

i

i

to:

A. 0

# -

B. 1

# -

C. R

D. Q

Zadanie 11. (1 pkt)

Proste o równaniach :

l

x

y

2

3

5

-

=

i :

k m

x

y

1

4

+

- =

_

i

sà równoleg∏e. Wynika stàd, ˝e:

A. m

3

= -

B. m

3

1

=

C. m

3

1

= -

D. m

1

=

Zadanie 12. (1 pkt)

Funkcja ( )

f x

m

m x

3

2

=

-

-

a

k

jest funkcjà sta∏à. Wynika stàd, ˝e:

A. m

1

=

B. m

0

=

C. m

m

1

0

0

= -

=

D. m

m

1

0

0

=

=

Zadanie 13. (1 pkt)

Funkcja okreÊlona wzorem ( )

f x

x

x

4

2

=

+

-

nie przyjmuje wartoÊci:

A. 5

-

B. 4

-

C. 0

D. 2

Zadanie 14. (1 pkt)

Odleg∏oÊç wierzcho∏ka paraboli ( )

f x

x

x

10

8

2

=

-

+

od osi OX jest równa:

A. 5

B. 17

C. 5

D. 17

Zadanie 15. (1 pkt)

Osià symetrii paraboli b´dàcej wykresem funkcji y

x

x

5

15

=

-

+

_

_

i

i

jest prosta o równaniu:

A. y

5

= -

B. y

5

=

C. x

5

= -

D. x

5

=

Zadanie 16. (1 pkt)

Dana jest funkcja okreÊlona wzorem ( )

f x

x

3

=

. WartoÊç tej funkcji w punkcie 5

2

-

jest równa:

A. 5

2

+

B. 3 5

3 2

+

C.

7

3 5

3 2

-

D.

7

3 5

3 2

+

Zadanie 17. (1 pkt)

JeÊli przyprostokàtne trójkàta prostokàtnego sà równe 6 i 3, a najmniejszy kàt ma miar´

a, to

wyra˝enie

sin

cos

W =

a

a ma wartoÊç:

A.

5

4 5

B.

5

2 5

C.

2

5

D.

5

2

Zadanie 18. (1 pkt)

Drugi wyraz ciàgu arytmetycznego jest równy 12, a trzeci wyraz jest równy 5. Wzór na ogólny wyraz
tego ciàgu to:
A. a

n

26

7

n

=

-

B. a

n

12

7

n

=

+

C. a

n

12

5

n

=

+

D. a

n

12

5

n

=

+

Zadanie 19. (1 pkt)

Dany jest ciàg geometryczny o wyrazie ogólnym a

5

3

n

n

= -

-

_

i

. Trzeci wyraz tego ciàgu jest równy:

A. 135

-

B. 45

-

C. 45

D. 135

4

Zadanie 20. (1 pkt)

Je˝eli promieƒ podstawy sto˝ka zwi´kszymy o

%

20

, a wysokoÊç zmniejszymy o

%

20

, to obj´toÊç

sto˝ka:
A. nie zmieni si´

B. zwi´kszy si´ o , %

15 2

C. zwi´kszy si´ o ,

%

1 52

D. zmniejszy si´ o %

4

Zadanie 21. (1 pkt)

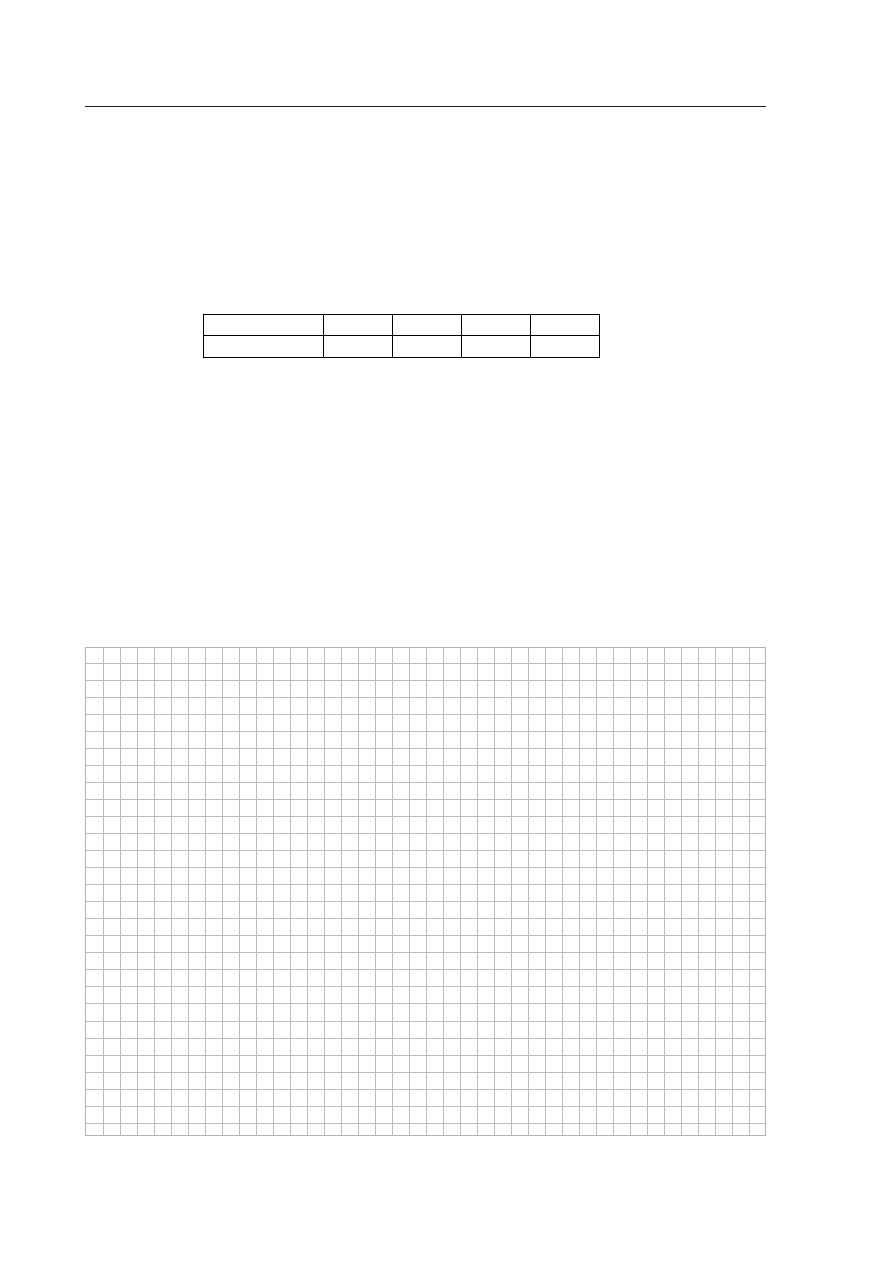
Ârednia wa˝ona danych z tabeli:

WartoÊç danej

4

5

6

8

Waga

2

1

1

3

jest równa:

A. .

2 3

B. ,

5 8

C. ,

5 75

D.

,

14 5

ZADANIA OTWARTE

Rozwiàzania zadaƒ o numerach od 22. do 31. nale˝y zapisaç w wyznaczonych miejscach pod

treÊcià zadania.

Zadanie 22. (2 pkt)

Wyznacz równanie prostej prostopad∏ej do prostej y

x

2

8

= -

+

przechodzàcej przez punkt

,

A

6

1

=

-

_

i

.

Matematyka. Poziom podstawowy

5

Brak poprawnej odpowiedzi !!!

Poprawna odpowiedz to 43/7 = 6,14

Matematyka. Poziom podstawowy

Zadanie 23. (2 pkt)

Kàt

a jest kàtem ostrym i tg

4

=

a

. Wyznacz sinus i cosinus tego kàta.

Zadanie 24. (2 pkt)

Wyznacz dziedzin´ funkcji ( )

f x

x

x

3

2

2

=

-

.

6

Zadanie 25. (2 pkt)

Ârednia arytmetyczna liczb:

, , , , , x

2 2 4 6 8

-

jest równa 5. Wyznacz liczb´ x.

Zadanie 26. (2 pkt)

Wyka˝, ˝e liczba x = 4

5 2

25

n

n

1

$

-

+

+

jest dla dowolnej liczby naturalnej n kwadratem liczby

ca∏kowitej.

Matematyka. Poziom podstawowy

7

Matematyka. Poziom podstawowy

Zadanie 27. (2 pkt)

Narysuj wykres funkcji ( )

,

,

f x

x

x

x

x

x

2

3

4

1

4

1 5

dla

dla

2

!

!

=

-

+

-

-

-

-

_

i

*

.

Zadanie 28. (2 pkt)

Liczby

,

,

x

x x

2

3 5

7

-

-

sà trzema poczàtkowymi wyrazami ciàgu arytmetycznego. Wyznacz liczb´ x.

8

Zadanie 29. (4 pkt)

Okràg o równaniu x

x

y

y

6

2

2

0

2

2

-

+

-

+

=

i prosta x

y

3

2

0

+

+

=

przecinajà si´ w punktach ,

A B

.

Wyznacz d∏ugoÊç ci´ciwy AB tego okr´gu.

Matematyka. Poziom podstawowy

9

Matematyka. Poziom podstawowy

Zadanie 30. (5 pkt)

Rzucono 8 razy monetà. Oblicz prawdopodobieƒstwo, ˝e wyrzucono or∏a:
a) co najmniej raz,
b) dok∏adnie 1 raz.

10

Zadanie 31. (6 pkt)

W ostros∏upie prawid∏owym trójkàtnym kraw´dzie boczne sà dwa razy d∏u˝sze od kraw´dzi
podstawy.
a) Wyznacz sinus kàta nachylenia Êciany bocznej ostros∏upa do p∏aszczyzny jego podstawy.

b) Wyznacz d∏ugoÊç kraw´dzi podstawy, tak aby obj´toÊç ostros∏upa wynosi∏a

3

2

11

.

Matematyka. Poziom podstawowy

11