02.05.2013  

1  

Pracownia Chemometrii Środowiska 

dr hab. Tomasz Puzyn, prof. UG 

Pracownia Chemometrii Środowiska 

e-mail: 

t.puzyn@qsar.eu.org

 

tel. (58) 523 54 51 

 

1  

Pracownia Chemometrii Środowiska 

 
1.  Analiza korelacji 

- wariancja i współczynnik korelacji 
- interpretacja współczynnika korelacji 
- wykresy korelacyjne 

 
2.  Regresja liniowa typu: y = ax + b 

- metoda najmniejszych kwadratów 
- szacowanie współczynników regresji 
- ocena istotności statystycznej modelu 
- ocena istotności statystycznej współczynników regresji 
- ocena jakości dopasowania modelu regresyjnego 
 

 
 
 

2  

Pracownia Chemometrii Środowiska 

 

1.

 

Analiza korelacji 
- wariancja i współczynnik korelacji 
- interpretacja współczynnika korelacji 
- wykresy korelacyjne 

 
2.  Regresja liniowa typu: y = ax + b 

- metoda najmniejszych kwadratów 
- szacowanie współczynników regresji 
- ocena istotności statystycznej modelu 
- ocena istotności statystycznej współczynników regresji 
- ocena jakości dopasowania modelu regresyjnego 
 

 
 
 

3  

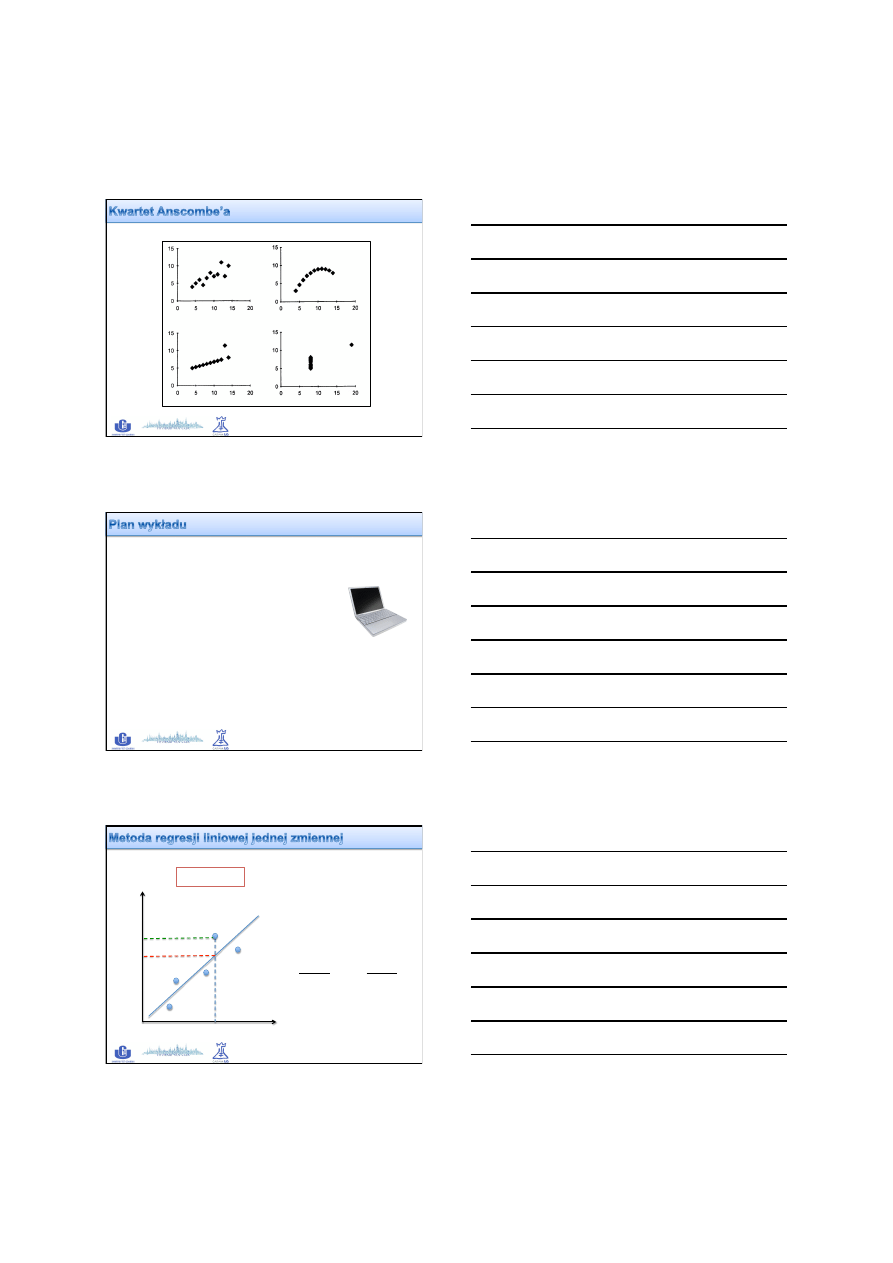
02.05.2013  

2  

Pracownia Chemometrii Środowiska 

r(x

k

, x

l

)

=

cov(x

k

, x

l

)

var(x

k

) var(x

l

)

cov(x

k

, x

l

)

=

(x

ik

− x

k

)(x

il

− x

l

)

i

=1

n

∑

n

− 1

var(x

k

)

=

(x

ik

− x

k

)

2

i

=1

n

∑

n

− 1

Wariancja 

Zmienność w wektorze x

k 

Kowariancja 

Współzmienność w wektorów x

k

 i x

l 

Współczynnik korelacji 

Współczynnik korelacji jest równy kowariancji dla danych standaryzowanych 

var(x

l

)

= 1

var(x

k

)

= 1

r(x

k

, x

l

)

= cov(x

k

, x

l

)

4  

Pracownia Chemometrii Środowiska 

•  Współczynnik korelacji r jest miarą 

współzmienności 

liniowej

 dwóch zmiennych 

x i y. 

 

•   

-1 ≤ r ≤ 1 

 

•  Jeżeli 

r > 0

 to ze wzrostem wartości 

zmiennej x 

rosną

 wartości zmiennej y. 

 

•  Jeżeli 

r < 0 

to ze wzrostem wartości 

zmiennej x 

maleją

 wartości zmiennej y. 

 

•  Współczynnik determinacji 

d = r

2

 

 wyraża 

ułamek ogólnej zmienności (wariancji) jednej 

zmiennej wyjaśnianej przez drugą.  

 

•  Współczynnik d wyraża się najczęściej w 

procentach. 

5  

r(x

k

, x

l

)

=

cov(x

k

, x

l

)

var(x

k

) var(x

l

)

Pracownia Chemometrii Środowiska 

6  

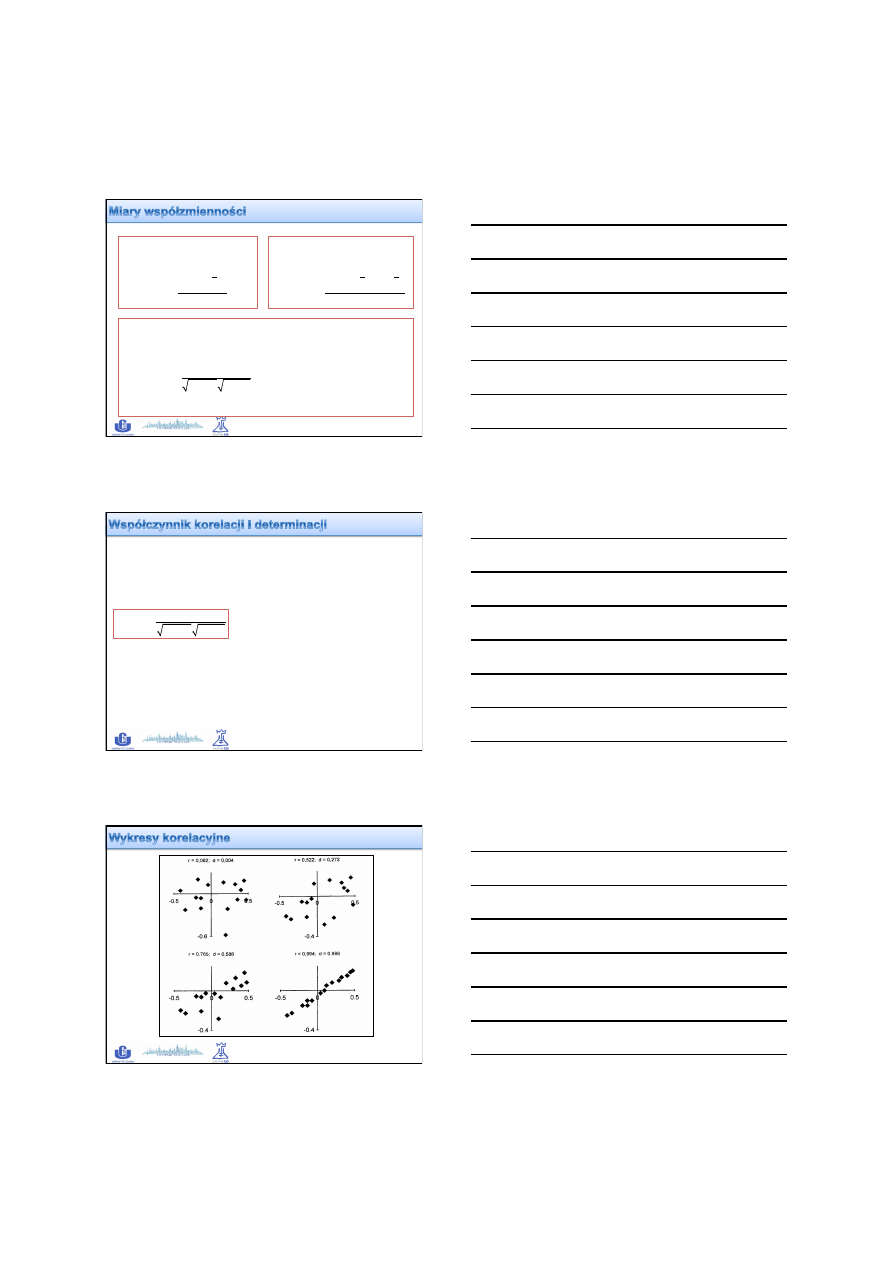
Żródło:  A  .  Mazerski,  Podstawy  chemometrii  

02.05.2013  

3  

Pracownia Chemometrii Środowiska 

7  

Żródło:  A  .  Mazerski,  Podstawy  chemometrii  

Pracownia Chemometrii Środowiska 

 
1.  Analiza korelacji 

- wariancja i współczynnik korelacji 
- interpretacja współczynnika korelacji 
- wykresy korelacyjne 

 

2.

 

Regresja liniowa typu: y = ax + b 
- metoda najmniejszych kwadratów 
- szacowanie współczynników regresji 
- ocena istotności statystycznej modelu 
- ocena istotności statystycznej współczynników regresji 
- ocena jakości dopasowania modelu regresyjnego 
 

 
 
 

8  

Pracownia Chemometrii Środowiska 

 

y

= ax + b

 

∂Φ a,b

( )

∂a

= 0

∂Φ a,b

( )

∂b

= 0

 

Φ a,b

( )

=

y

i

− ax

i

+ b

(

)

[

]

2

i

=1

n

∑

Φ =

(y

i

obs

− y

i

pred

)

2

i

=1

n

∑

9  

x 

y 

y

obs

 

y

pred

 

02.05.2013  

4  

Pracownia Chemometrii Środowiska 

 

y

= ax + b

 

a

=

n

x

i

y

i

i

=1

n

∑

−

x

i

i

=1

n

∑

y

i

i

=1

n

∑

n

x

i

2

i

=1

n

∑

−

x

i

i

=1

n

∑

⎛ 
⎝ ⎜ 

⎞ 
⎠ ⎟ 

2

=

xy

− x ⋅ y 

x

2

− x 

( )

2

=

cov x, y

( )

var x

( )

 

b

=

x

i

2

i

=1

n

∑

y

i

i

=1

n

∑

−

x

i

i

=1

n

∑

x

i

y

i

i

=1

n

∑

n

x

i

2

i

=1

n

∑

−

x

i

i

=1

n

∑

⎛ 
⎝ ⎜ 

⎞ 
⎠ ⎟ 

2

= y − ax 

 

var(x)

=

(x

i

− x )

2

i

=1

n

∑

n

−1

 

cov(x, y)

=

(x

i

− x )⋅(y

i

− y )

i

=1

n

∑

n

−1

 

r(x, y)

=

cov(x, y)

var(x)

⋅ var(y)

10  

Pracownia Chemometrii Środowiska 

Wariancja resztowa 

Wariancja modelu 

•  Im większa wartość statystyki F-Snedecora, tym model jest bardziej istotny statystycznie.  

 

•  Wartości krytyczne F znajdujemy w tablicach dla n-1 i n-p-1 stopni swobody odpowiednio dla 

licznika i mianownika (p - liczba parametrów modelu). 

Model istotny 

Model nieistotny 

11  

F = 0 

F > 0 

n – 1 

Pracownia Chemometrii Środowiska 

 

s

b

= s

E

2

⋅

x

i

2

i

=1

n

∑

n

⋅

x

i

2

−

x

i

i

=1

n

∑

⎛ 
⎝ ⎜ 

⎞ 
⎠ ⎟ 

i

=1

n

∑

2

 

s

a

=

s

E

2

x

i

2

− n ⋅

x

i

i

=1

n

∑

⎛ 
⎝ ⎜ 

⎞ 
⎠ ⎟ 

i

=1

n

∑

2

 

t

a

=

a

s

a

 

t

b

=

b

s

b

 

df

= n − 2

•  Jeżeli t ≤ t

kr

 => nie ma podstaw do odrzucenia H

0

 na założonym poziomie 

istotności. 

•  Jeżeli t > t

kr

 => H

0

 należy odrzucić na założonym poziomie istotności i przyjąć H

A. 

H

0

: a = 0 

H

A

: a 

≠

 0

  

H

0

: b = 0 

H

A

: b 

≠

 0

  

12  

02.05.2013  

5  

Pracownia Chemometrii Środowiska 

Miarą jakości dopasowania modelu jest 

współczynnik determinacji 

R

2

. Wyrażony w 

procentach określa, jaka część ogólnej zmienności 
odpowiedzi jest wyjaśniana przez model:  
 
 
 

Analiza rozkładu różnic: 

y

pred 

y

obs 

Inną stosowaną miarą dopasowania jest 

średniokwadratowy błąd kalibracji RMSEC 

(ang. 

root mean square error of calibration): 

R

2

= 1−

y

i

obs

− y

i

pred

(

)

2

i

=1

n

∑

y

i

obs

− y

obs

(

)

2

i

=1

n

∑

RMSE

C

=

y

i

obs

− y

i

pred

(

)

2

n

=1

n

∑

n

13