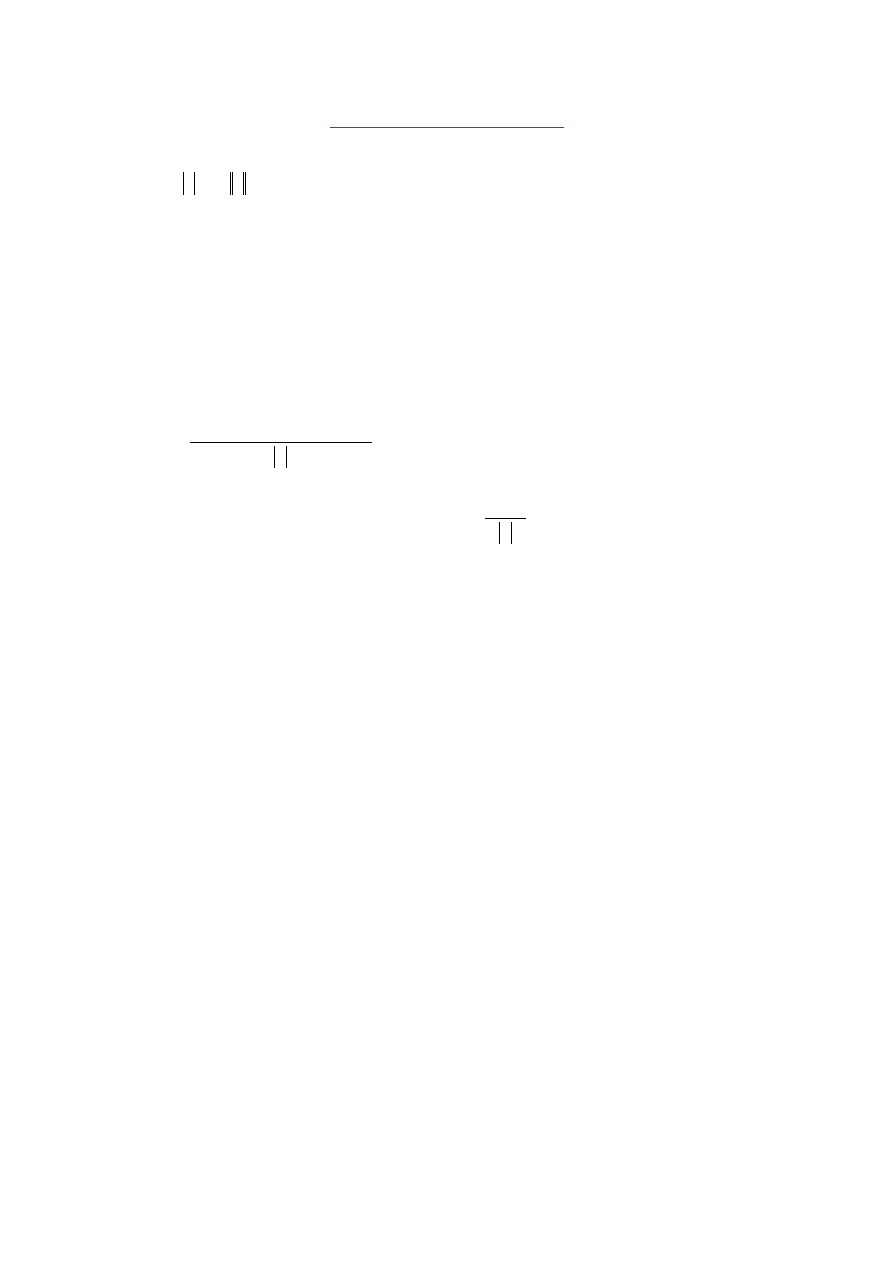
RÓŻNICZKA ZUPEŁNA
Niech
,
,
,
Y
X
przestrzenie unormowane nad K,
.
,
:
,
Top
0
U
x
Y
U
f
X
U
Różniczką zupełną
(
pochodną zupełną
)
odwzorowania f w punkcie x
0
nazywamy
odwzorowanie liniowe i ciągłe
0
x
L
L(
X, Y
)
spełniające warunek
U
h
x
h
o
h
L
x
f
h
x
f
x
0
0
0
dla
0
lub równoważnie
Y
h
h
L
x
f
h
x
f
x
h
0
lim
0
0
0
0
lub
.
0
lim
gdzie
,
0
0
0
0
0
0
h
h
r
h
r
h
L
x
f
h
x
f
x
h
x
x
Zatem funkcja f w punkcie x
0
ma rózniczkę zupełną, jeśli przyrost funkcji można rozłożyć na
część liniową i nieliniową resztę, która jest funkcją typu o(h).
Różniczkę odwzorowania f w punkcie x
0
oznaczamy też symbolem
.
'
lub
0
0
x
f
f
d
x
Definicja
Jeśli f jest różniczkowalna dla każdego
U
x
, to odwozorowanie
f
d
x
U
f
x
:'
L(
X,Y
)
nazywamy
odwzorowaniem pochodnym
funkcji f.
1
część reszta
liniowa
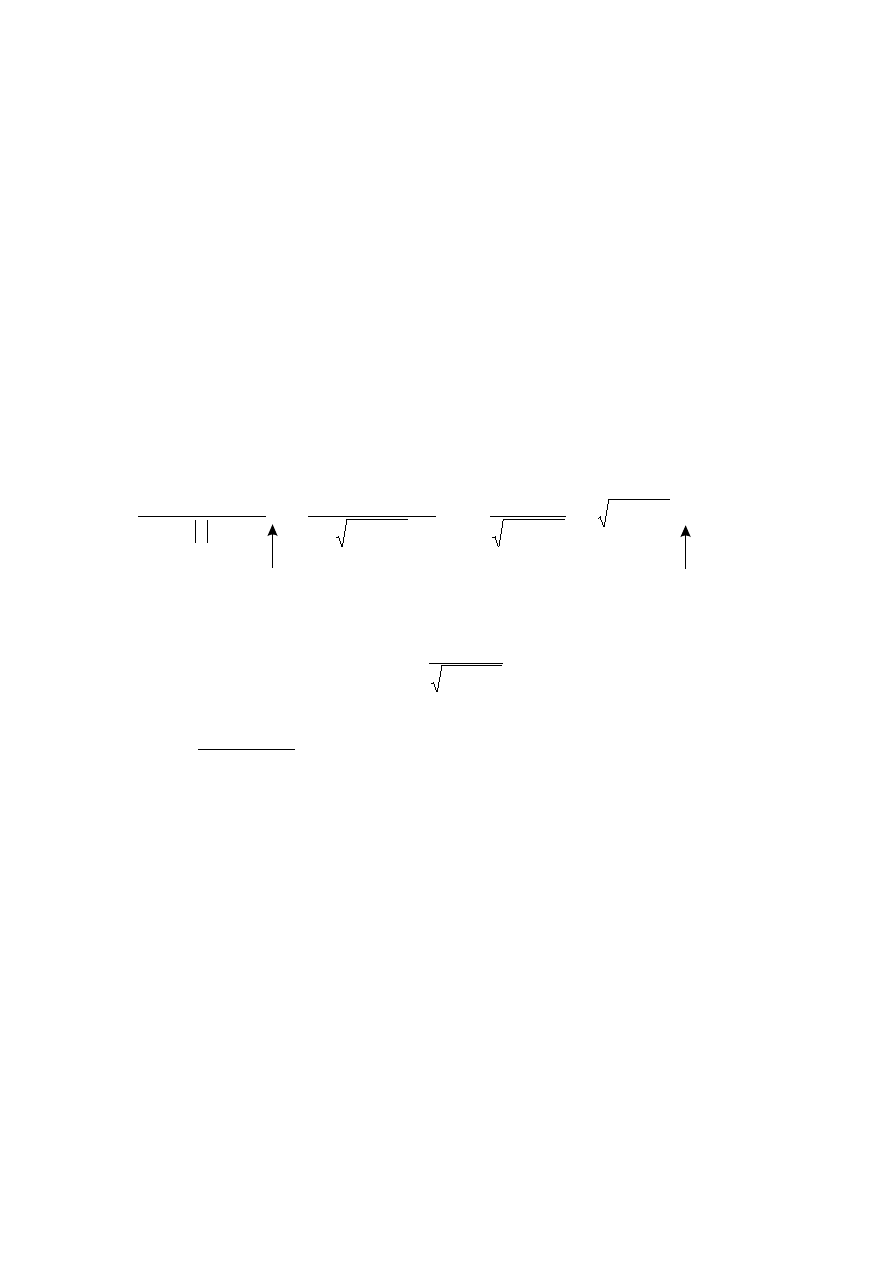
Przykład
Zbadać różniczkowalność funkcji
2
2
3
2
,
,
,
,
:
y
x
y
x
xy
y
x
f
f
R
R
w punkcie
(x
0
, y
0
)=(2, 1).
Wybieramy wektor h=[h
1
, h
2
] i obliczamy przyrost f
funkcji f w punkcie (x
0
, y
0
)
2
2
2
1
2
1
2
1
2
1
1
2
2
2
2
1
liniowe
2
1
liniowe
2
1
2
1
liniowe
1
2
2
2
2
1
2
1
2
1
2
1
0
0
2
0
1
0
,
0
,
2
4
,
,
2
2
4
,
,
2
5
,
3
,
2
1
2
,
3
,
1
2
1
,
2
1
,
2
,
,
h
h
h
h
h
h
h
h
h
h
h
h
h
h
h
h
h
h
h
h
h
h
h
h
h
h
f
h
h
f
y
x
f
h
y
h
x
f
f
Musimy pokazać, że część nieliniowa jest typu o(h).
skorzystalismy z
liczymy granicę dla
normy euklidesowej
każdej składowej osobno
gdzie granicę pierwszej składowej
2
2
2
1
2
1
0
,
0
,
2
1
lim
h
h
h
h
h
h
obliczyliśmy korzystając ze
współrzędnych biegunowych:
.
0
sin
cos
lim
sin
cos
lim
0
.
0
.
0
e
ograniczon
dow
r
dow
r
r
r
r
r
Zatem udowodniliśmy, że część liniowa należy do klasy
.
,
0
0
y
x
D
f
h
o
Część liniowa stanowi różniczkę, czyli
2
1
2
1
2
1
2
1
)
1
,
2
(
2
4
,
,
2
,
h
h
h
h
h
h
h
h
f
d
lub korzystajacąc z macierzowego zapisu odwzorowania liniowego
.
,
2
4
1
1
2
1
,
2
1
2
1
)
1
,
2
(
h
h
h
h
f
d
2
część część
liniowa nieliniowa
,
0
,
0
,
0
,
0
,
lim
,
0
,
lim
,
0
,
lim
2
2
2
1
2
2
2
1
2
1
0
0
2
2
2
1
2
2
2
1
2
1
0
2
2
2
1
2
1
0
2
1
h
h
h
h
h
h
h
h
h
h
h
h
h
h
h
h
h
h
h
h
h
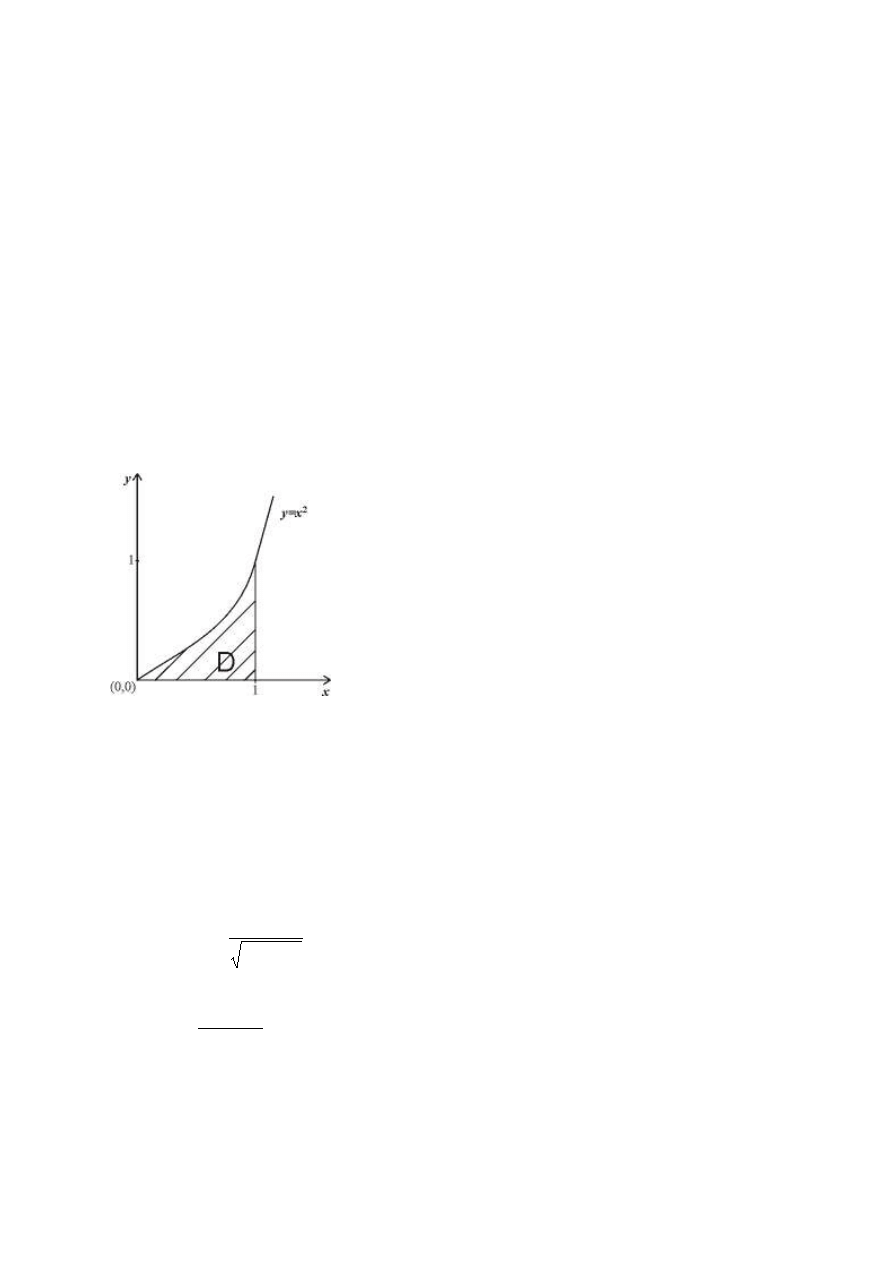
Twierdzenie
(
o jednoznaczności różniczki w punkcie
)
Jeśli istnieje różniczka
,
0
f
d
x
to jest jedyna.
Uwaga
Jedyność różniczki odwzorowania określonego w przestrzeni o wymiarze dimX >1
uzyskujemy dzięki temu, że dziedzina tego odwzorowania jest zbiorem otwartym.
Przykład
Niech
,
0
,
1
0
:
,
2
x
y
x
y
x
D
.
,
,
:
3
x
y
x
f
D
f
R
Dziedzina funkcji nie jest zbiorem otwartym,
.
Top
2
R
D
Wyznaczamy różniczkę w punkcie (x
0
, y
0
)=(0, 0), który jest punktem skupienia dziedziny D.
I. Rozłóżmy przyrost w punkcie (0,0) na część liniową i nieliniową
3
1
3
1
2
1
0
0
,
0
0
,
0
h
h
f
h
h
f
0
,
2
1
0
,
0
Zatem
h
h
L
jest różniczką funkcji w punkcie (0, 0), jeżeli
jest
)
,
(
3
1
2
1
h
h
h
r
).
(
typu
h
o
Sprawdzamy czy
h
o
h
r
:
,
0
lim
2
2
2
1
3
1
)
0
,
0
(
)
,
(
2
1
h
h
h
h
h
ponieważ
.
0
cos
lim
cos
lim
3
0
2
.
0
3
3
.
0
e
ograniczon
dow
r
dow
r
r
r
r
3
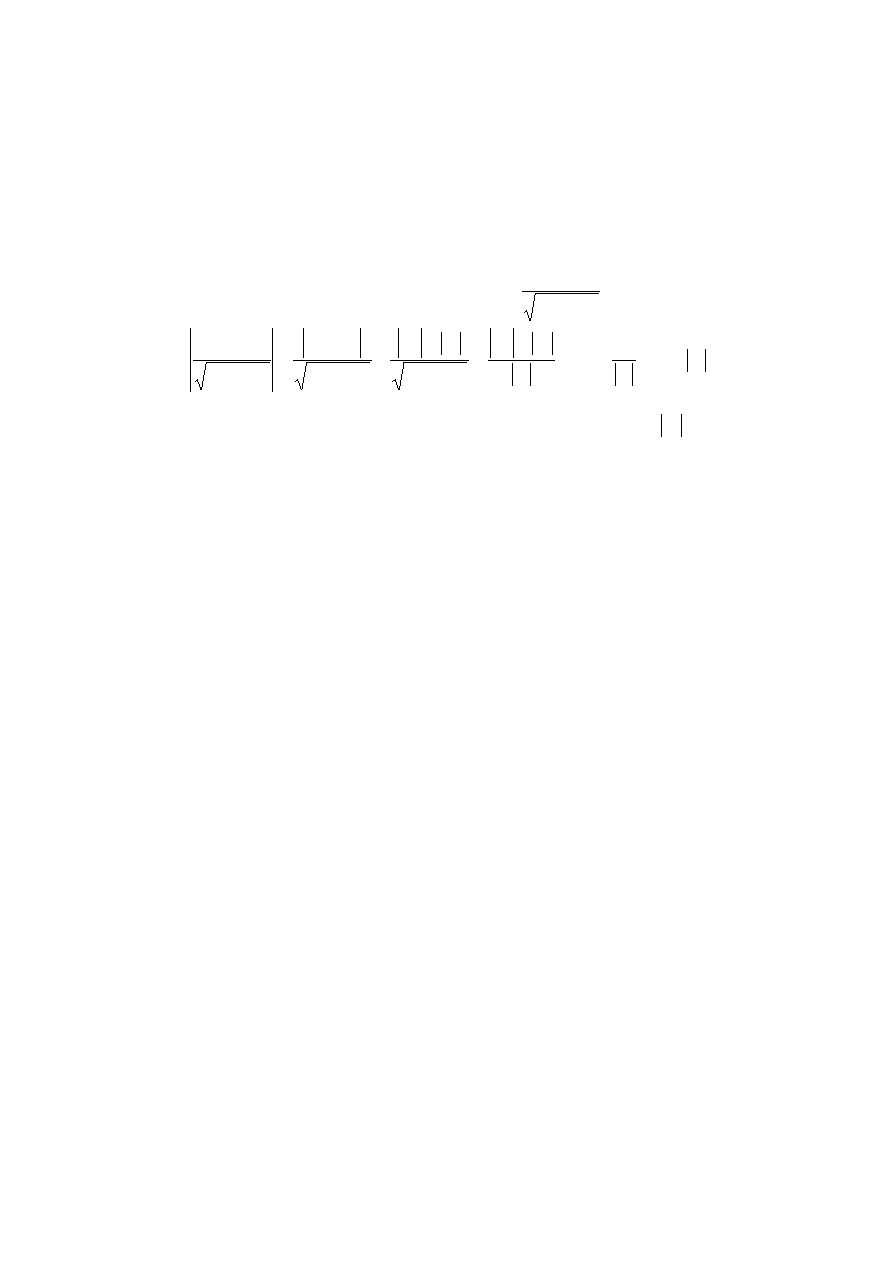
II. Wyznaczamy część liniową w inny sposób
.
0
,
0
,
2
3
1
2
2
1
nieliniowe
liniowe
h
h
h
f
h
h
f
,
,
2
2
1
0
,
0
Zatem
h
h
h
L
jeżeli
.
,
typu
jest
2
3
1
2
1
h
o
h
h
h
h
r
Sprawdzimy, czy reszta jest typu o(h).
,
0
lim
funkcjach
trzech
o
ia
twierdzen
podstawie
Na
2
2
2
1
2
3
1
)
0
,
0
(
)
,
(
2
1
h
h
h
h
h
h
bo
,
0
0
1
1
1
2
1
2
1
1
2
3
1
2
2
2
1
2
3
1
2
2
2
1
2
3
1
2
2
2
1
2
3
1
h
h
h
h
h
h
h
h
h
h
h
h
h
h
h
h
h
h
h
h
gdzie ostatnia nierówność jest spełniona ponieważ dla
D
h
h
2
1
,
zachodzi
2
1
2
h
h
.
Z I i II wynika, że funkcja nie ma jednoznacznie określonej różniczki.
Wniosek
Funkcja o dziedzinie nie będącej zbiorem otwartym nie ma jednoznacznie określonej
różniczki.
Twierdzenie
(
o liniowości różniczki względem odwzorowań
)
Niech
X,Y – przestrzenie unormowane nad ciałem K,
.
niech
oraz
,
,
,
:
,
,
Top
0
0
K
α,β
x
D
g
f
U
x
Y
U
g
f
X
U
Wtedy
)
(
0
g
f
d
x
(istnieje rózniczka kombincji liniowej funkcji f i g)
oraz
.
)
(
0
0
0
g
d
f
d
g
f
d
x
x
x
4
Twierdzenie
(
o różniczce iloczynu i ilorazu funkcji
)
Jeśli dodatkowo założymy, że Y=K, to
g
f
d
fg
d
x
x
0
0
)
(
(istnieją rózniczki iloczynu i ilorazu)
oraz
g
d
x
f
f
d
x
g
fg
d
x
x
x
0
0
0
0
0
)
(
i
.
0
,
0
2
0
0
0
gdy
0
0
0
x
g
x
g
g
d
x
f
f
d
x
g
g
f
d
x
x
x
Twierdzenie
(
o różniczce złożenia funkcji
)
Niech X,Y,Z – przestrzenie unormowane nad K,
.
)
(
,
,
:
,
:
,
Top
,
Top
0
0
0
V
x
f
y
U
x
Z
V
g
V
U
f
Y
V
X
U
Jeśli
,
0
0
g
d
f
d
y
x
to
f
g
d
x
0
i
f
d
g
d
f
g
d
x
y
x
0
0
0
Twierdzenie
(
o istnieniu pochodnej kierunkowej
)
.
,
:
,
Top
,
nad
unormowane
ie
przestrzen
,
Niech
0
U
x
Y
U
f
X
U
Y
X
K
Jeśli
,
0
f
d
x
to
).
(
)
(
:
1
,
0
0
0
h
f
d
x
f
D
x
f
D
h
X
h
x
h
h
pochodna kierunkowa
wartość różniczki
w kierunku
w punkcie x
0
wektora h
na wektorze h
5
Dowód
Niech
.
1
,
h
X
h
Wtedy
bo istnieje
różniczka jest
różniczka odwzorowaniem linowym
t
x
f
th
x
f
x
f
D
t
h
0
0
0
0
lim
t
th
o
th
f
d
x
t
)
(
lim
0
0
const
t
x
t
x
t
x
t
h
t
t
th
th
o
h
f
d
t
th
o
h
f
d
t
th
o
h
f
d
t
sgn
0
0
0
0
)
(
lim
)
(
lim
)
(
lim
0
0
0
0
h
f
d
x
0
c
Wniosek
(
o istnieniu pochodnych cząstkowych
)
Niech X=
.
n
K
Jeśli
,
0
f
d
x
to
)
(
0
0
0
j
x
j
j
e
f
d
x
x
f
x
x
f
.
...,
,
2
,
1
n
i
Twierdzenie
0
0
x
C
f
x
D
f
Dowód
Wynika bezpośrednio z definicji różniczki.
c
opracował Jacek Zańko
6