Astronomia geodezyjna z
geodynamiką - ćwiczenia

Dr Michał Kruczyk

[e-mail]

Astronomia geodezyjna z geodynamiką – ćwiczenia

1. Podstawy trygonometrii sferycznej. (zadanie domowe)
2. Astronomiczne układy współrzędnych. Transformacja między układami. (zadanie

domowe)

3. Ruch dobowy sfery niebieskiej – analiza zjawisk: wschód i zachód, kulminacje,

przejście przez pierwszy wertykał i elongacja, zmierzch. (zadanie domowe)

4. Ruch dobowy Słońca. Obliczanie parametrów wschodu i zachodu Słońca. (zadanie

domowe).

5. Rocznik Astronomiczny, katalogi gwiazd, oprogramowanie astronomiczne.
6. Czasy stosowane w astronomii i geodezji. Przeliczanie czasów. (zadanie domowe)
7. Wzory różniczkowe trygonometrii sferycznej. Efemerydy.
8. Miejsca pozorne ciał niebieskich. Analiza zjawisk wpływających na zmiany

współrzędnych pozornych. Analiza astronomicznych metod wyznaczania pozycji i
azymutu. Algorytmy redukcji obserwacji w różnych przypadkach.

Literatura

Podręczniki:



Barbara Kołaczek: „Astronomia sferyczna z ćwiczeniami” WPW 1976



Eugeniusz Rybka: „Astronomia ogólna” PWN 1983



Jan Mietelski: „Astronomia w geografii” PWN 1989



Tadeusz Jarzębowski: "Elementy astronomii." PPWK 1972



S. Wierzbiński: „Wstęp do astronomii matematycznej” 1950



J. Witkowski: „Astronomia sferyczna.” PWN 1953



F. Kępiński: „Astronomia sferyczna” WPW 1959



W. Szpunar: „Geodezja wyższa i astronomia geodezyjna” PWN 1963



L. Cichowicz: „Astronomia sferyczna” WPW 1965



W. Opalski, L. Cichowicz: „Astronomia geodezyjna” PPWK 1977



M. Karpowicz, K. Rudzki: „Zadania z astronomii ogólnej” PWN 1960

Lektury uzupełniające:



E. M. Rogers: „Fizyka dla dociekliwych Część II: Astronomia” PWN 1986



O. Wołczek: „Narodziny i rozwój Układu Słonecznego” ALFA 1985



J. M. Kreiner: „ Astronomia z astrofizyką” PWN 1988



E. Pittich, D. Klamancok: “Niebo na dłoni.” PW’ Wiedza powszechna’ 1988



M. Kubiak: „Gwiazdy i materia międzygwiazdowa” PWN 1994



P. Artymowicz: „Astrofizyka układów planetarnych” PWN 1995



K. Włodarczyk: „Przewodnik po gwiezdnym niebie” Wydawnictwo ‘Sport i turystyka’ 1989



„Fizyka z astronomią” – podręcznik dla klasy IV liceum ogólnokształcącego



T.Wilgat: „ Geografia astronomiczna ”



Michał Heller: „ Ewolucja kosmosu i kosmologii”



Frank Close: „ Kosmiczna cebula”



Steven Weinberg: „Pierwsze trzy minuty”

Ciekawe książki angielskojęzyczne:

Jean Kovalevsky, P. Kenneth Seidelmann “Fundamentals of Astrometry” Cambridge

University Press, 2004

Jean Meeus „Astronomical Algorithms”
Paul J. Heafnet “Fundamental Ephemeris Computations”
Guy Ottewell ” The Astronomical Companion”
V. Shebehely “Adventures in Celestial Mechanics”
O. Montenbruck, E. Gill „Satellite Orbits

Podstawy trygonometrii

sferycznej

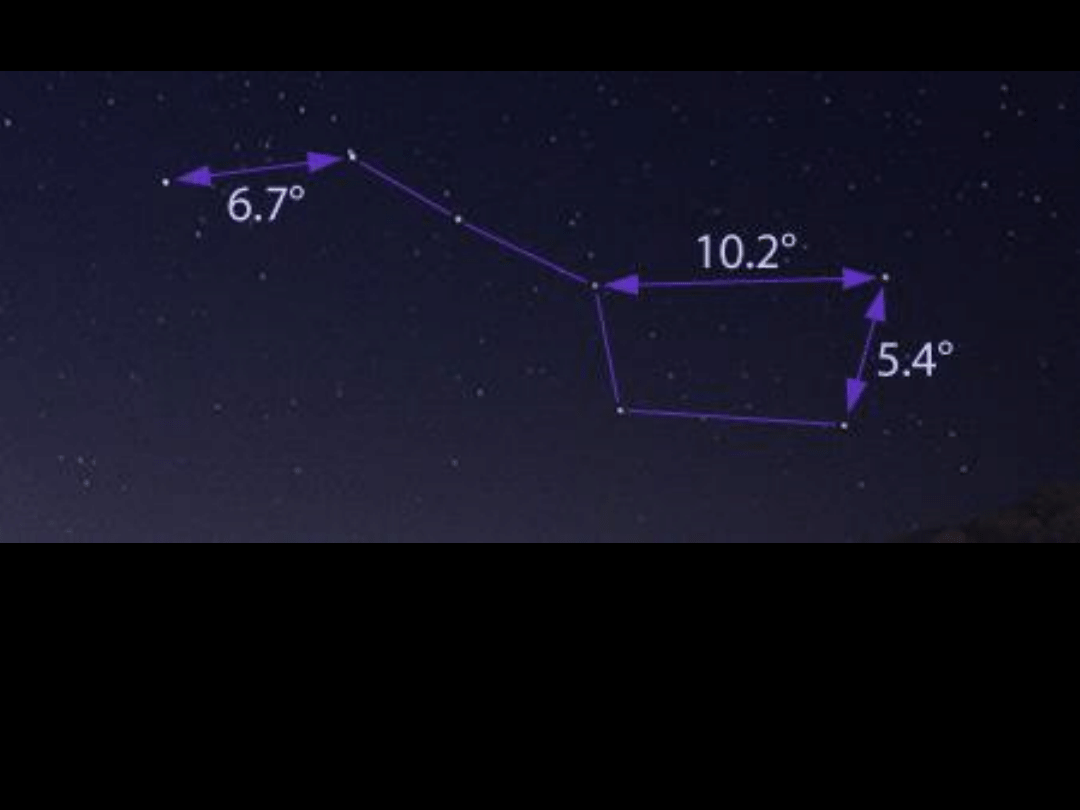
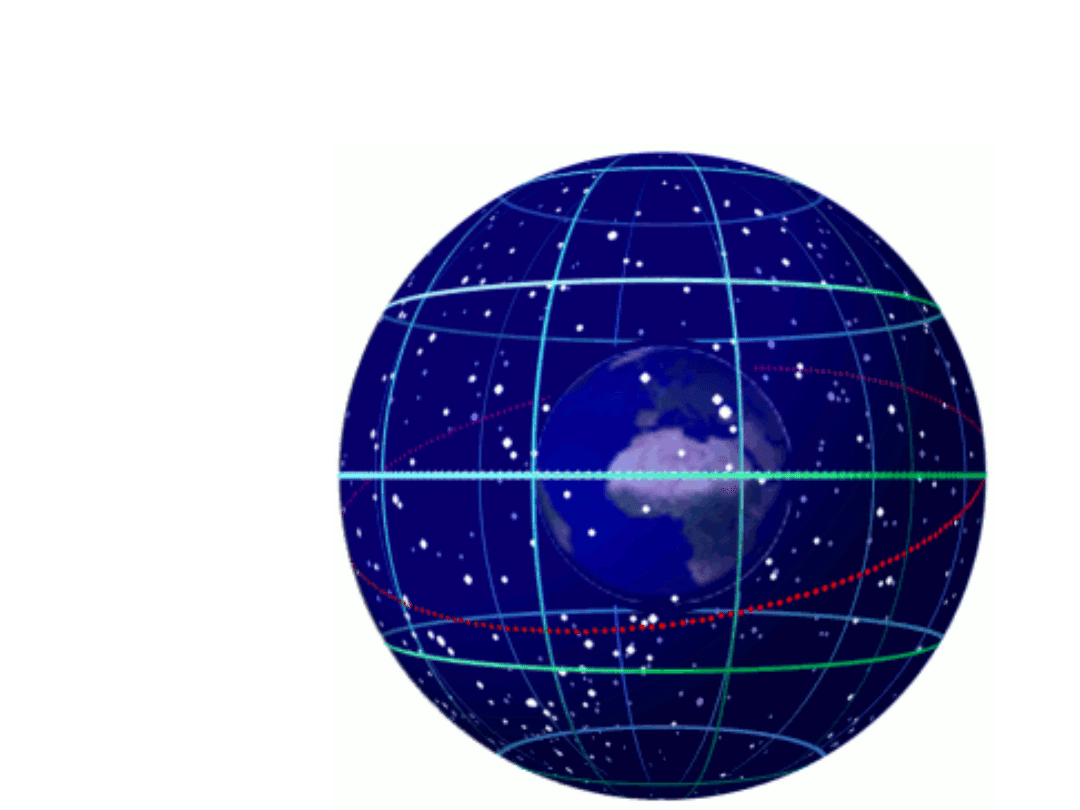
Trygonometria sferyczna dotyczy zarówno sfery niebieskiej jak
i pierwszego przybliżenia kształtu Ziemi. Jest obecna także w
fotogrametrii (orientacja kamery) czy chemii fizycznej (kształty
orbitali atomowych).

Podstawowe pojęcia trygonometrii sfery

Sfera niebieska jest sferą o nieokreślonym promieniu (np. jednostkowym) z obserwatorem w
jej środku. W astronomii sferycznej gwiazdy o bardzo różnych odległościach od Ziemi
rozpatrujemy tak jakby były one ‘zrzutowane’ na powierzchnię sfery. Interesują nas tylko ich
odległości sferyczne (kątowe) oraz położenia względem horyzontu obserwatora.

Ze względu na potrzeby dokładności wyróżniamy współrzędne sferyczne:

1. heliocentryczne (Słońce w środku sfery)
2. barycentryczne (barycentrum Układu Słonecznego lub układu Ziemia –Księżyc)
3. geocentryczne (Ziemia w środku sfery)
4. topocentryczne (obserwator – z uwzględnieniem jego pozycji względem środka

Ziemi)

Współrzędne heliocentryczne i barycentryczne różnią się bardzo nieznacznie. Jednak między
heliocentrycznymi a geocentrycznymi oraz topocentryznymi zachodzą zadaniczne różnice:
paralaksa i aberracja.

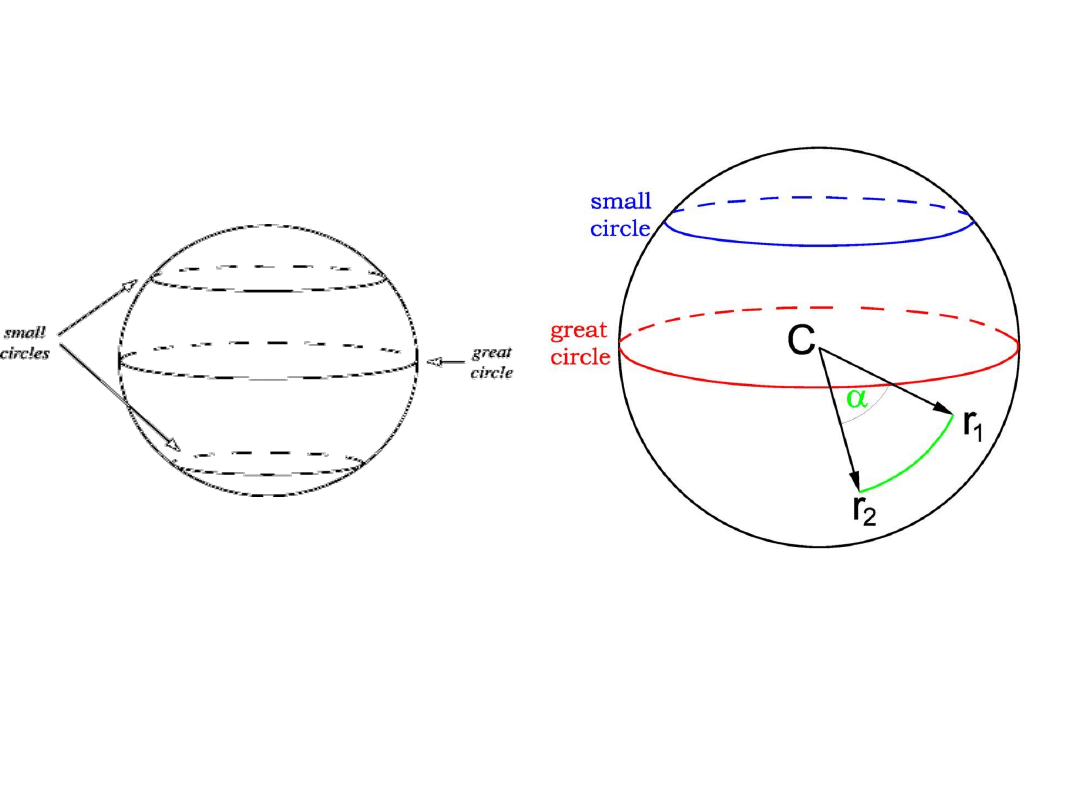
Koło wielkie i koło małe

Koło wielkie powstaje przez przecięcie sfery niebieskiej płaszczyzną przechodzącą
przez jej środek, a koło małe - nie przechodzącą przez jej środek.

Także odległość sferyczna to odcinek koła wielkiego.

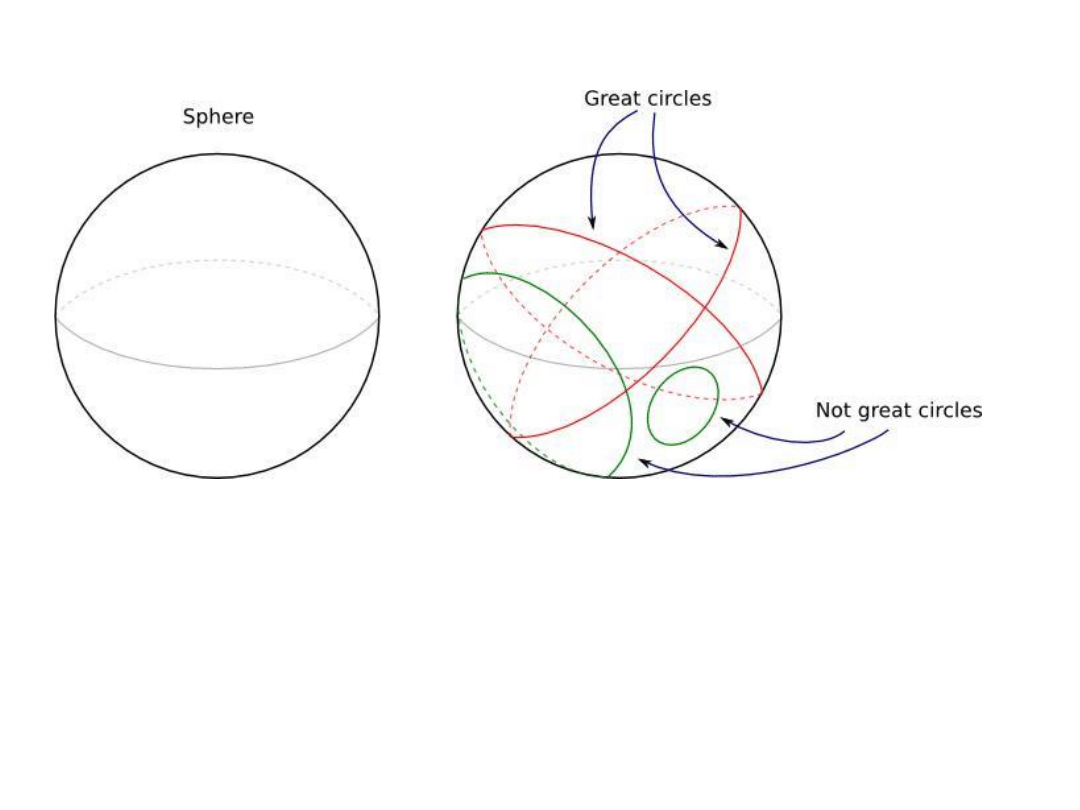
Koła wielkie mają taki sam rozmiar (i krzywiznę) - są podstawą
trygonometrii sferycznej.

Koła małe mogą mieć różną wielkość
– nie nadają się do konstruowania trójkątów sferycznych!

Kołami wielkimi na kulistej Ziemi są równik i południki
ale nie równoleżniki.

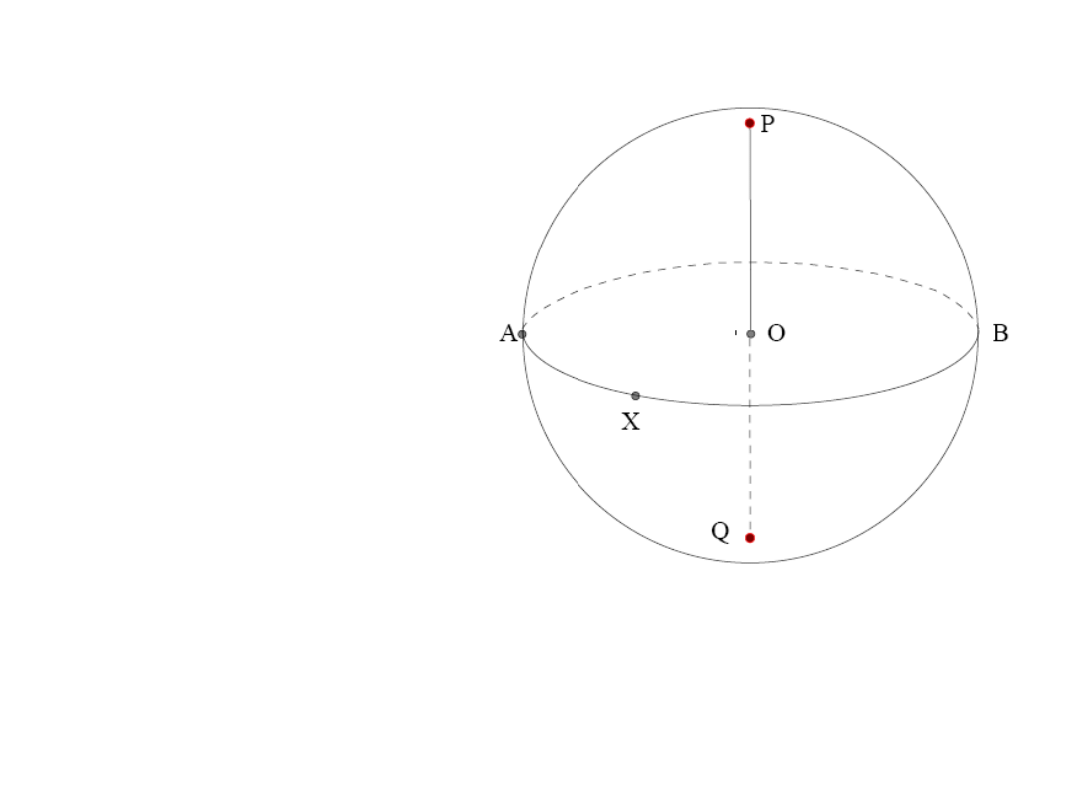
Każde koło wielkie ma dwa bieguny (tu P i Q)
- punkty odległe od niego o 90º)

Bieguny koła wielkiego

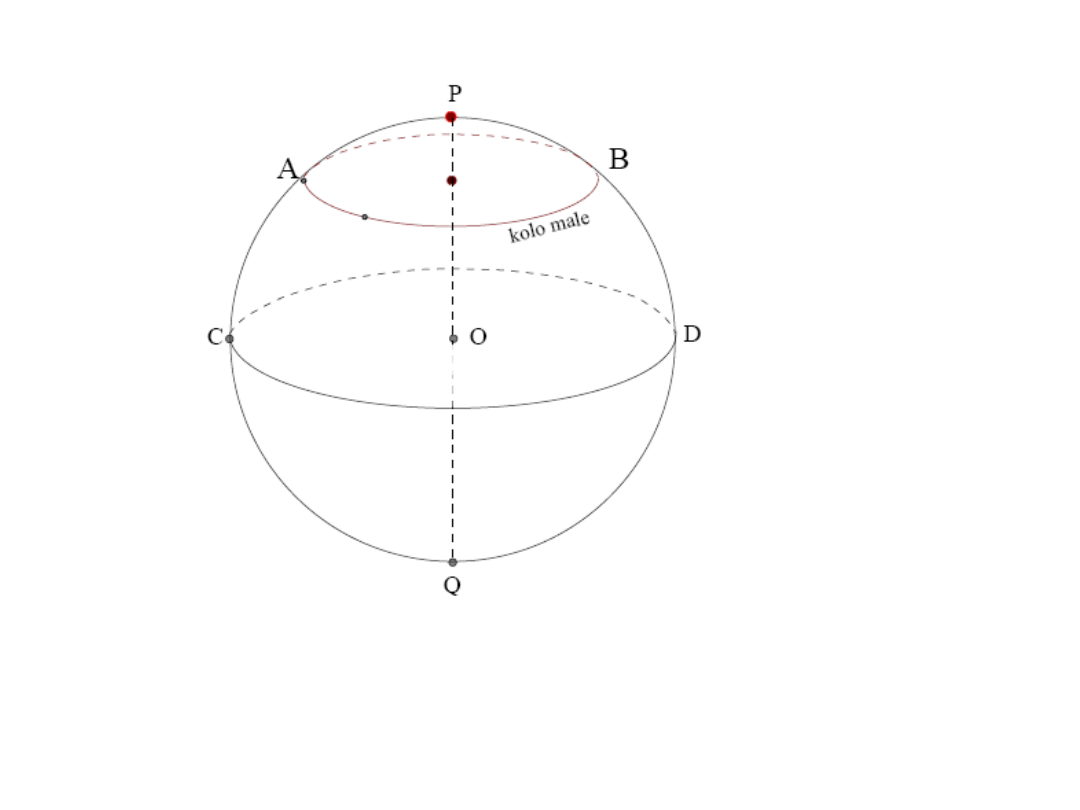
Koło małe ma także 2 bieguny.
Jego promień jest jednak zawsze mniejszy od promienia sfery.

Koła małe mogą być różnej wielkości i nie nadają się do
konstruowania trójkąta sferycznego.

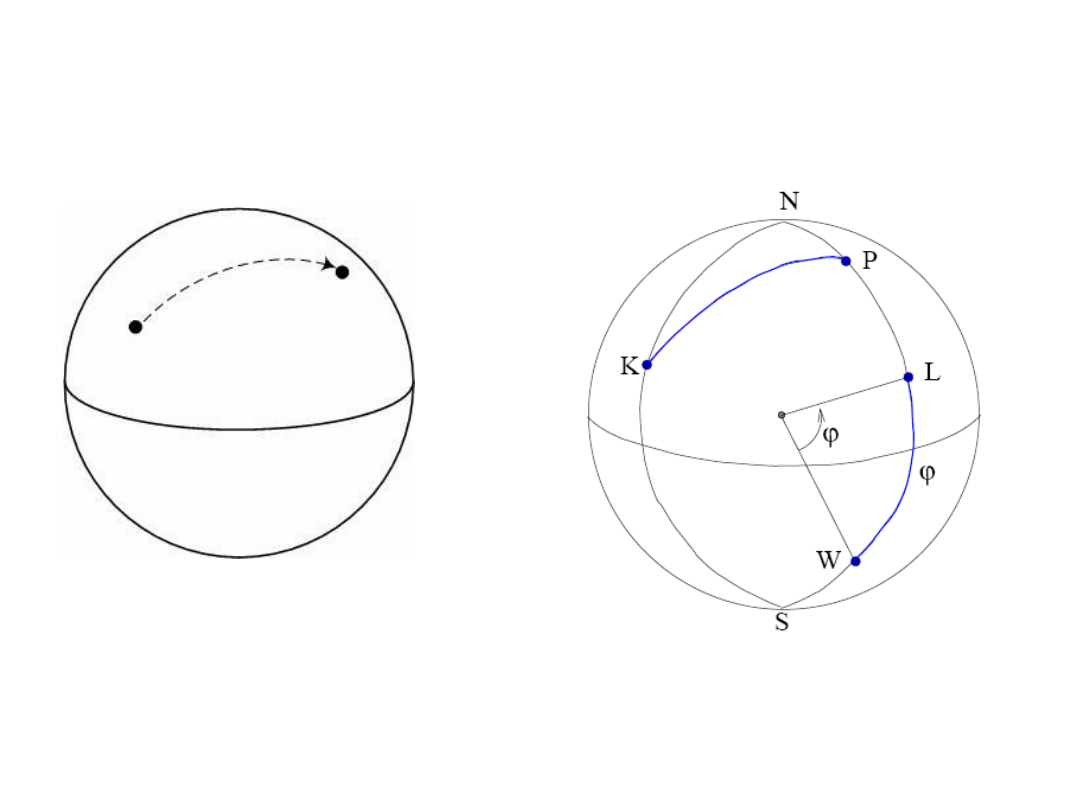
Odległość sferyczna to odcinek koła wielkiego (geodetyka)
- jej miarą jest kąt wierzchołkowy

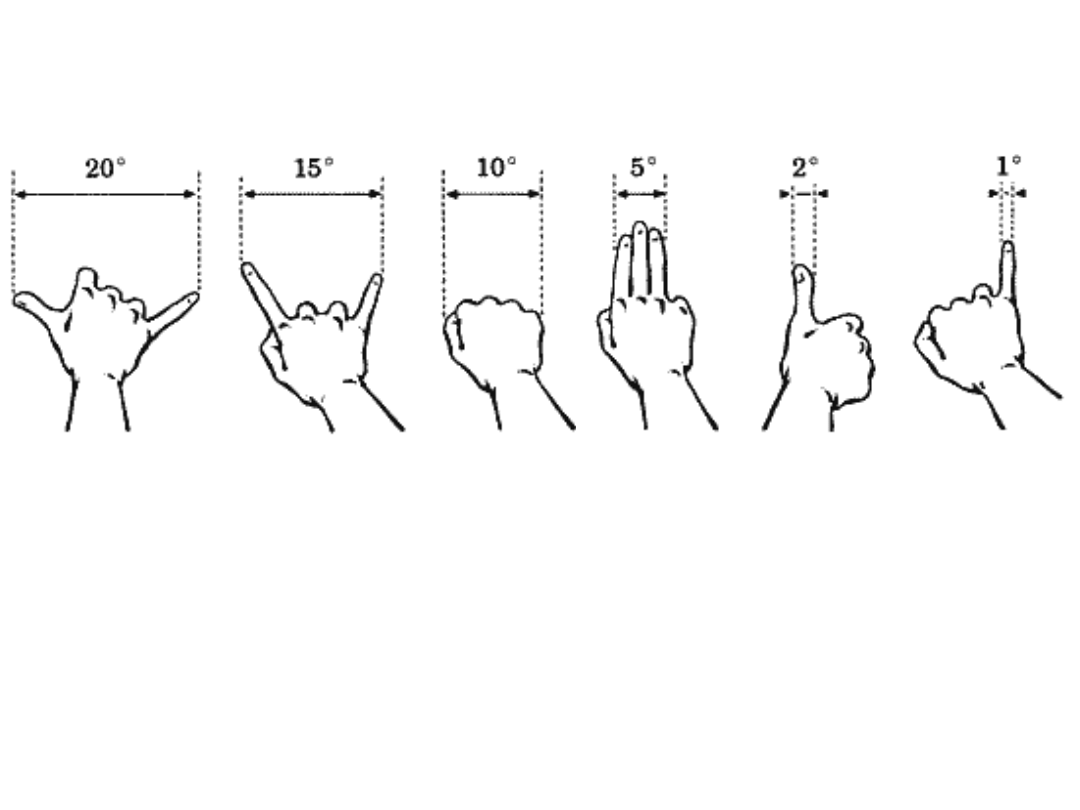
Metoda przybliżonego ‘mierzenia’ kątów na sferze niebieskiej

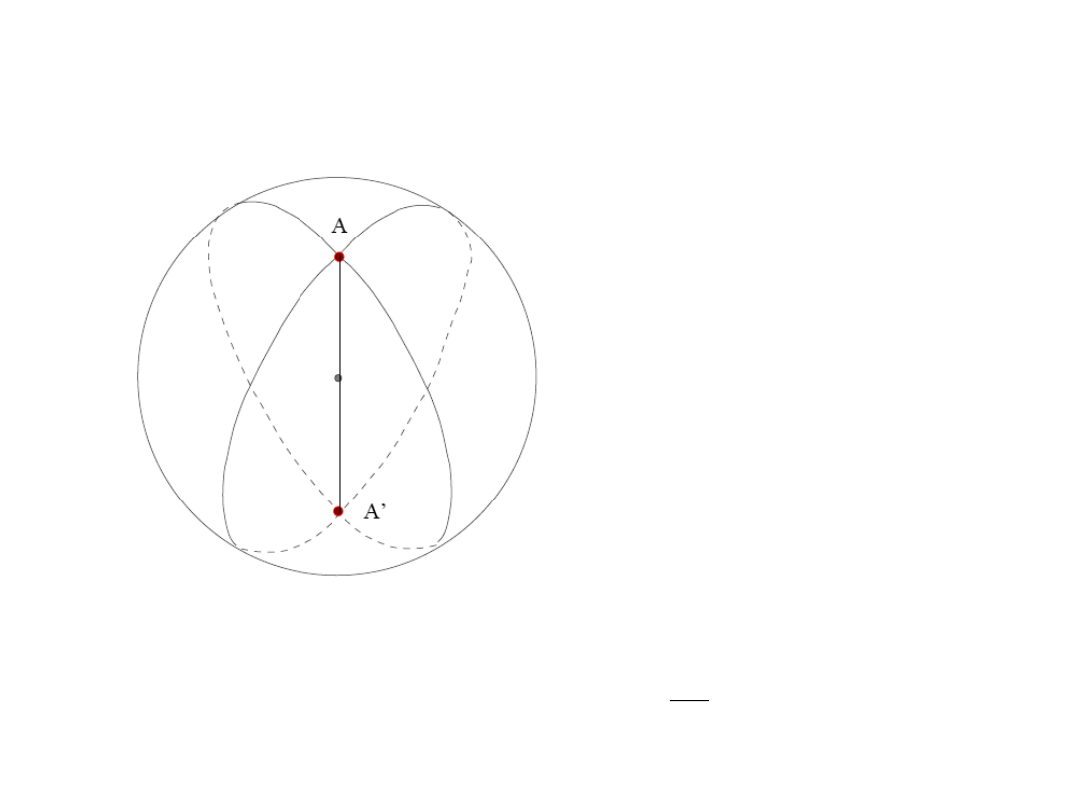
Podstawowe figury sferyczne: dwukąt sferyczny

Dwukąt sferyczny – najprostsza figura trygonometrii sferycznej – wycinek sfery utworzony

przez dwa niewspółpłaszczyznowe koła wielkie. Pole:

 

2

2

2

90

R

rad

R

P

















φ – miara dwukąta to kąt między płaszczyznami kół wielkich

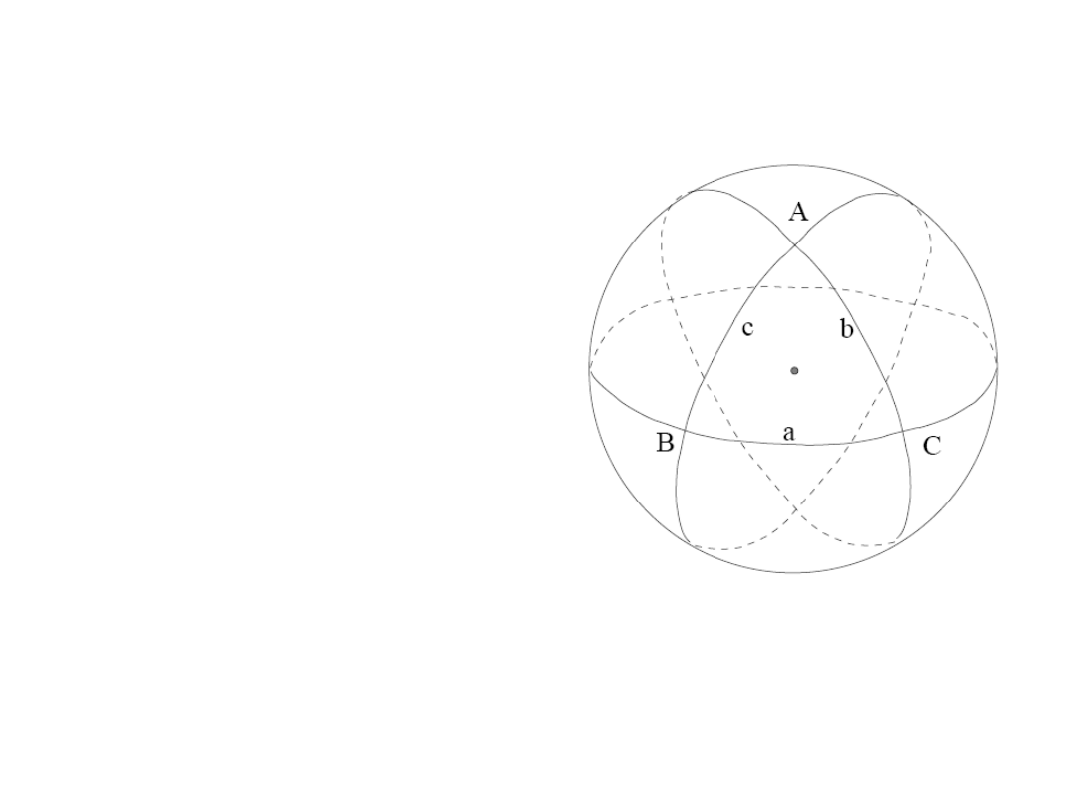
Podstawowe figury sferyczne: trójkąt sferyczny

Kąt trójkąta sferycznego to kąt dwuścienny
między płaszczyznami kół wielkich lub kąt między stycznymi.
Bok trójkąta sferycznego to odcinek koła wielkiego,
którego miarą jest kąt wierzchołkowy.

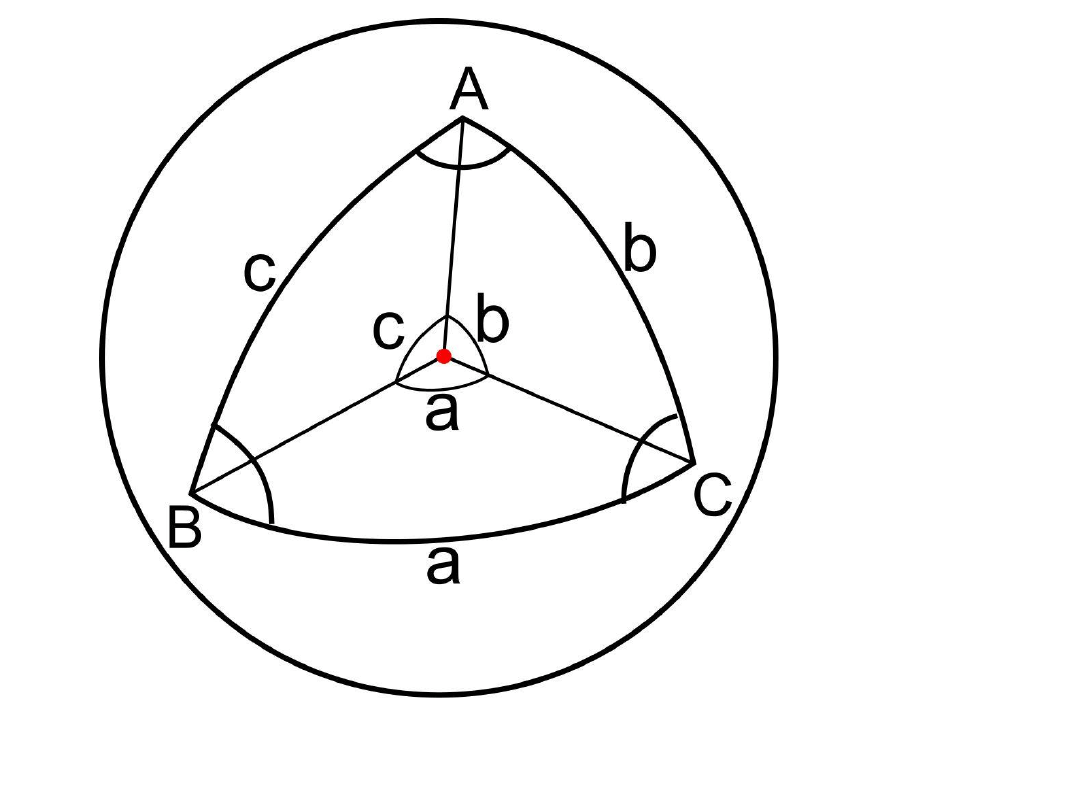
miara boku trójkąta = odległość sferyczna (kątowa) = kąt płaski =
= odcinek koła wielkiego

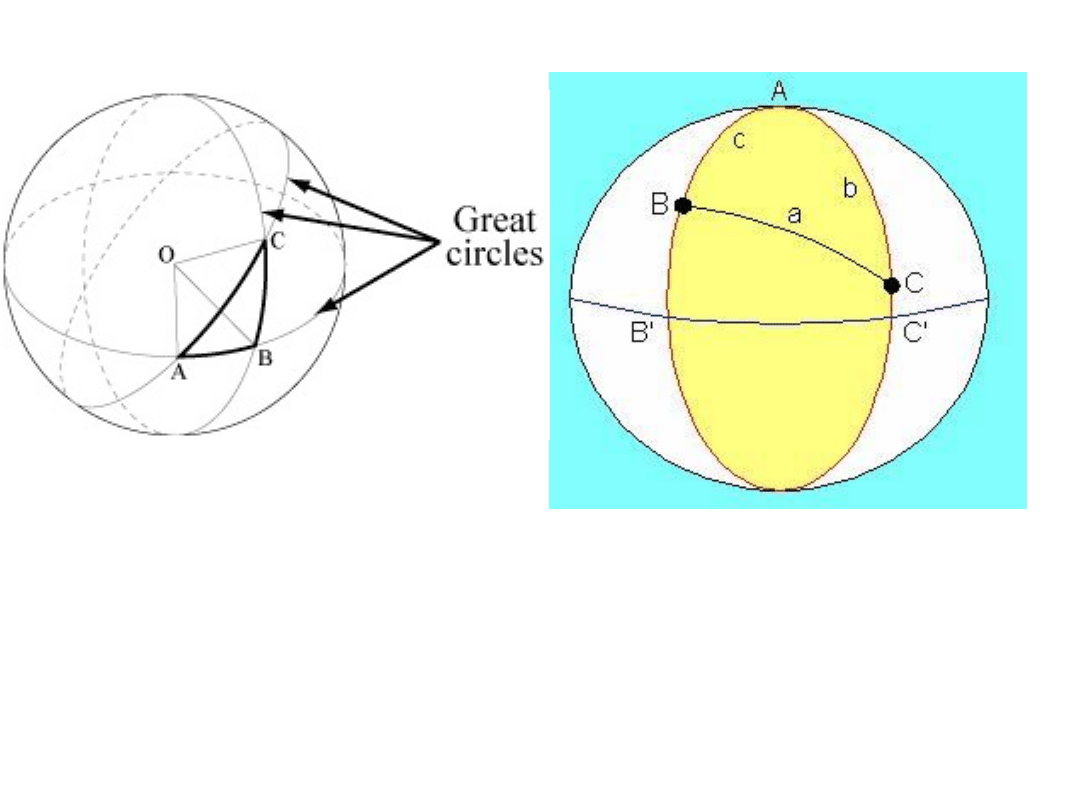
Bok trójkąta sferycznego jest odcinkiem koła wielkiego,
więc bok to zarazem geodetyka.
Miarą boku trójkąta sferycznego jest odległość kątowa między
danymi wierzchołkami.

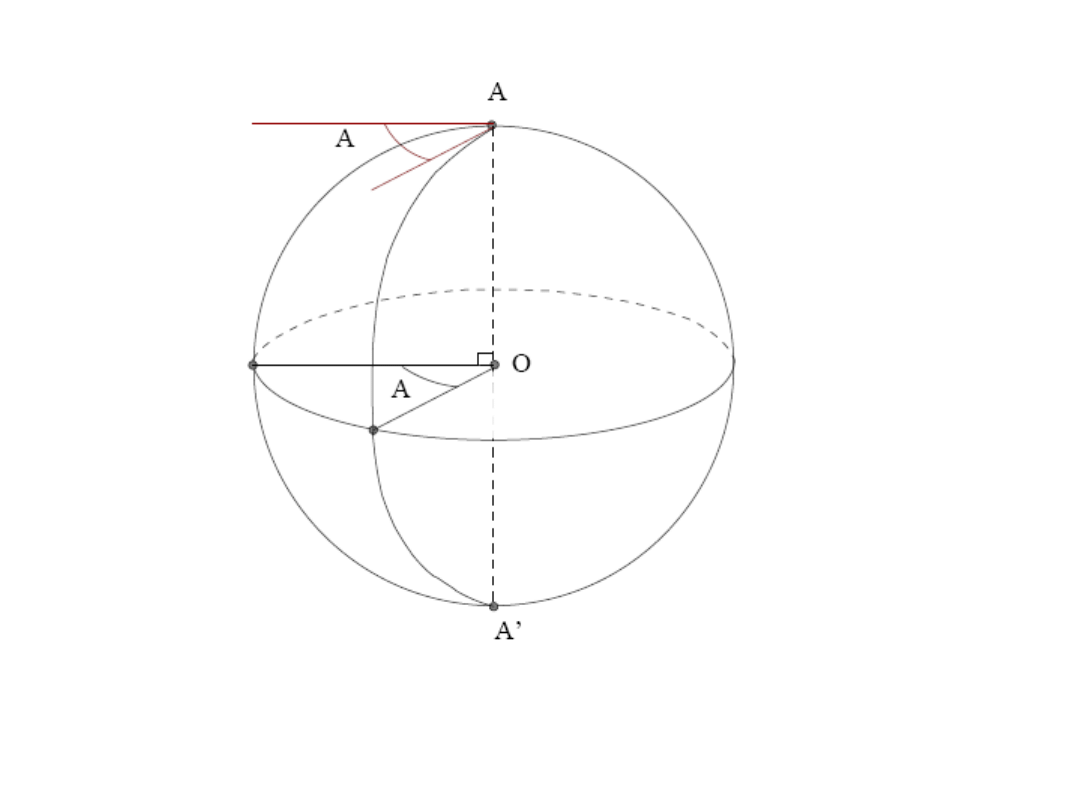
Kąt sferyczny A trójkąta sferycznego jest kątem dwuściennym
miedzy płaszczyznami boków (b i c) ale i między stycznymi
do danych boków w wierzchołku A.

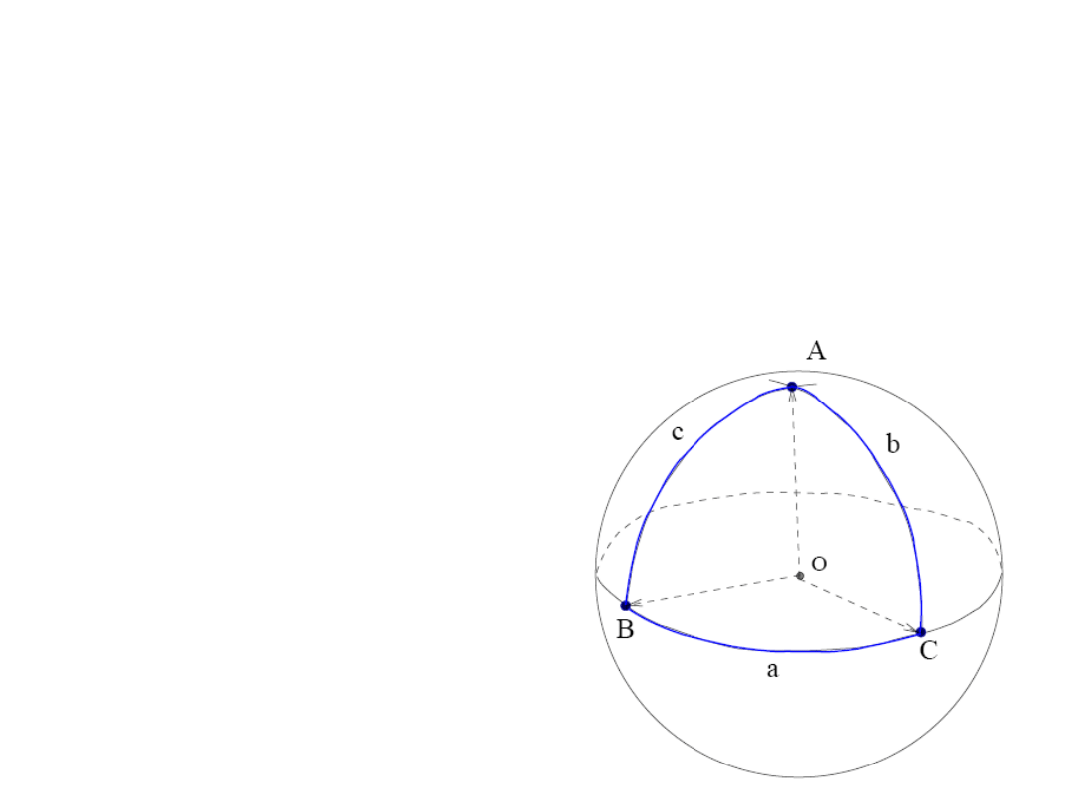
Własności trójkąta eulerowskiego:

1. a, b, c, A, B, C < 180



2. 180



< A+B+C < 540



3. naprzeciwko większego boku leży większy kąt
4. każdy bok jest większy od różnicy i mniejszy od sumy pozostałych

b-c < a < b+c itd.

5. suma boków mniejsza od 360



a+b+c < 360



6. A+B-C < 180



itd.

Trójkąt sferyczny ABC nazywamy
trójkątem eulerowskim, kiedy
wszystkie jego kąty i boki są
mniejsze od 180º

a,b,c, A,B,C < π

π < A+B+C < 3 π

Wzory podstawowe trygonometrii sferycznej

WZORY SINUSOWE


WZORY COSINUSOWE
cos a = cos b ∙ cos c + sin b ∙ sin c ∙ cos A
cos b = cos a ∙ cos c + sin a ∙ sin c ∙ cos B
cos c = cos a ∙ cos b + sin a ∙ sin b ∙ cos C

WZORY SINUSOWO-COSINUSOWE
sin a ∙ cos B = cos b ∙ sin c – sin b ∙ cos c ∙ cos A
sin a ∙ cos C = cos c ∙ sin b – sin c ∙ cos b ∙ cos A
sin b ∙ cos A = cos a ∙ sin c – sin a ∙ cos c ∙ cos B
sin b ∙ cos C = cos c ∙ sin a – sin c ∙ cos a ∙ cos B
sin c ∙ cos A = cos a ∙ sin b – sin a ∙ cos b ∙ cos C
sin c ∙ cos B = cos b ∙ sin a – sin b ∙ cos a ∙ cos C

WZORY DLA TRÓJKĄTA BIEGUNOWEGO
sin A ∙ sin b = sin a ∙ sin B
cos A =

־ cos B ∙ cos C + sin B ∙ sin C ∙ cos a

sin A ∙ cos b = cos B ∙ sin C + sin B ∙ cos C ∙ cos a
sin A ∙ cos c = cos C ∙ sin B + sin C ∙ cos B ∙ cos a

C

c

B

b

A

a

sin

sin

sin

sin

sin

sin





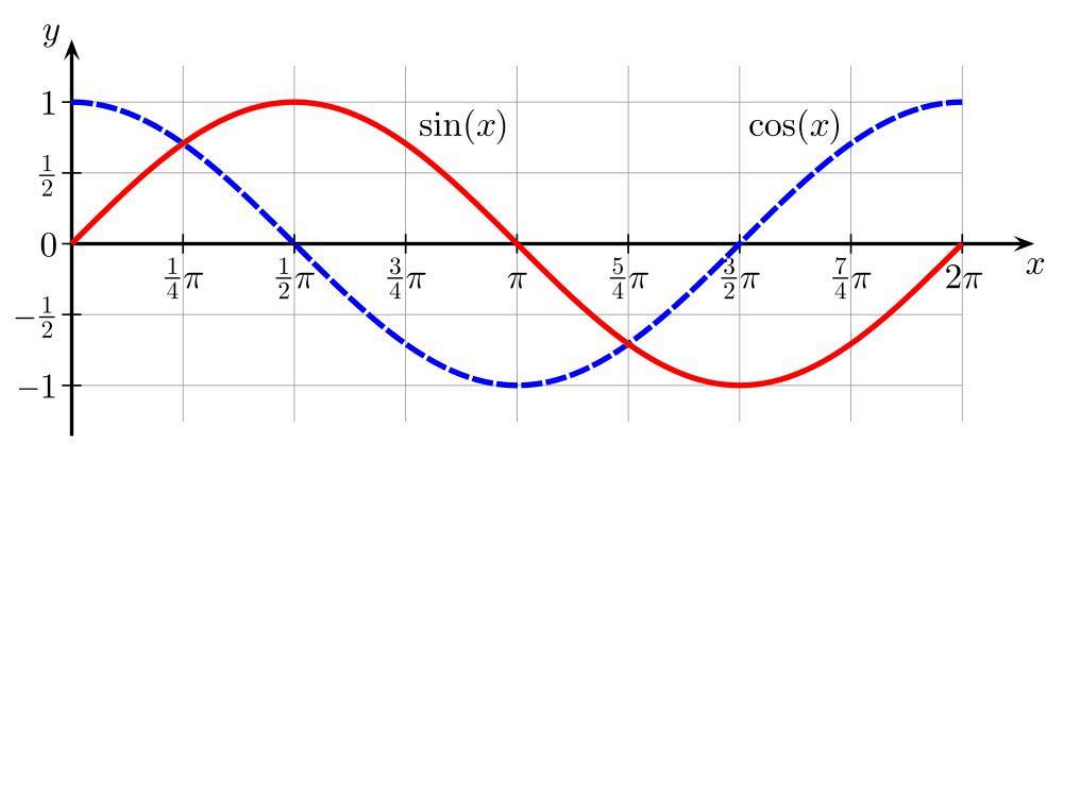
W przedziale szukania niewiadomych trójkąta eulerowskiego (0,π)
cosinus jest różnowartościowy (arc cos - jednoznaczny)
sinus ma dwa równoprawne rozwiązania.

Lepiej używać wzorów z cosinusem niewiadomej!

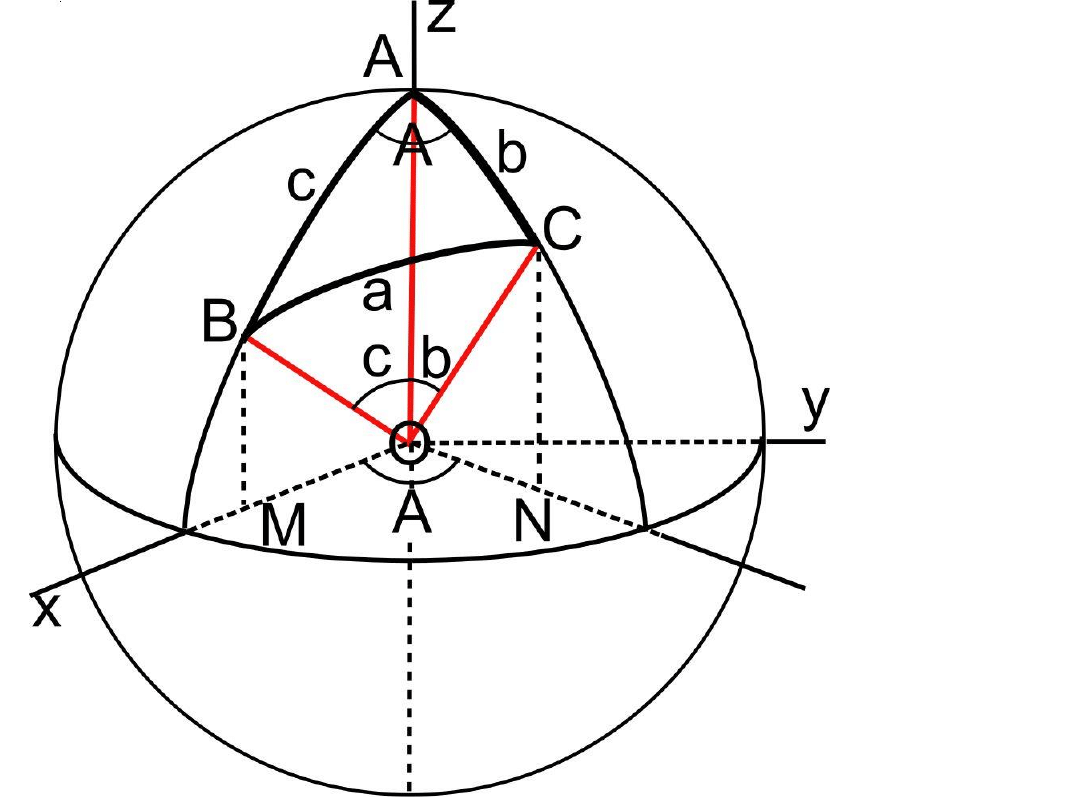
Trójkąt
sferyczny
w układzie
współrzędnych

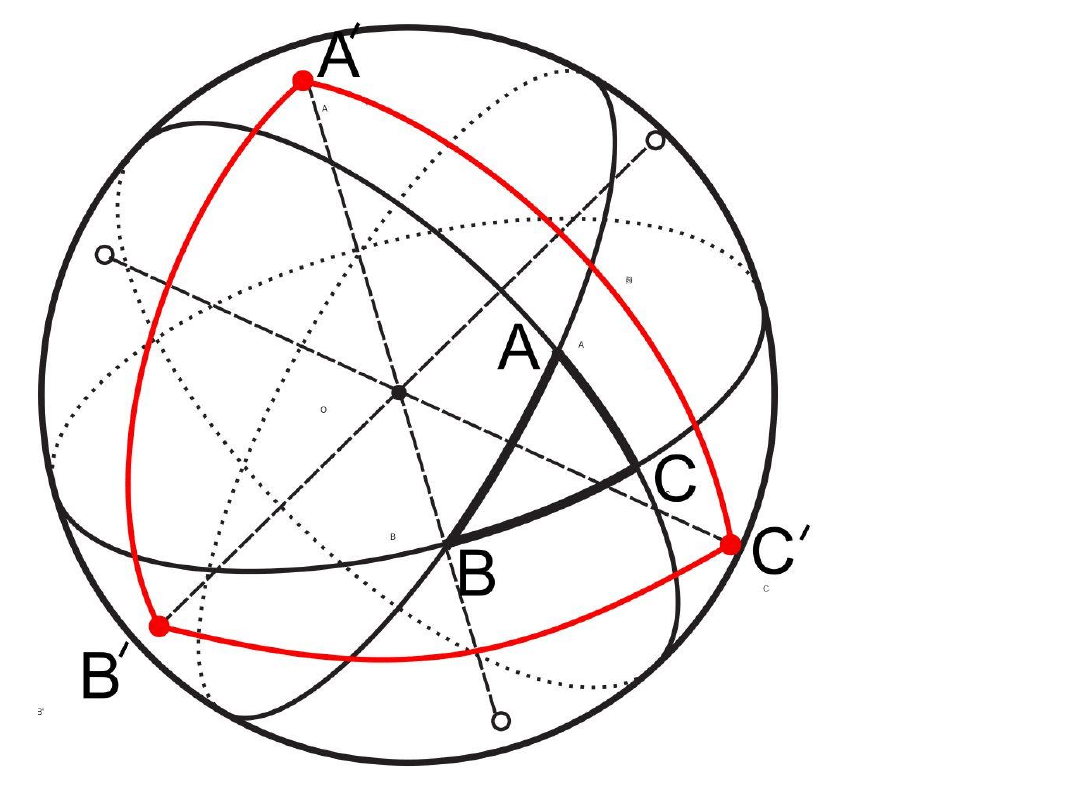
Trójkąt
biegunowy
(A’B’C’) w
stosunku do
trójkąta ABC

Trójkąt biegunowy

Definicja: Trójkąt biegunowy A’B’C’ względem trójkąta ABC nazywamy trójkąt utworzony
przez bieguny kół wielkich, których łuki tworzą boki tego trójkąta.
Pomiędzy elementami trójkąta ABC i biegunowego zachodzą zależności:













180

'

;

180

'

a

A

A

a

itd.

Wzory podstawowe trójkąta biegunowego (dotyczą każdego trójkąta sferycznego!)

B

a

b

A

a

B

C

B

C

c

A

a

C

B

C

B

b

A

a

C

B

C

B

A

sin

sin

sin

sin

cos

cos

sin

sin

cos

cos

sin

cos

cos

sin

sin

cos

cos

sin

cos

sin

sin

cos

cos

cos

















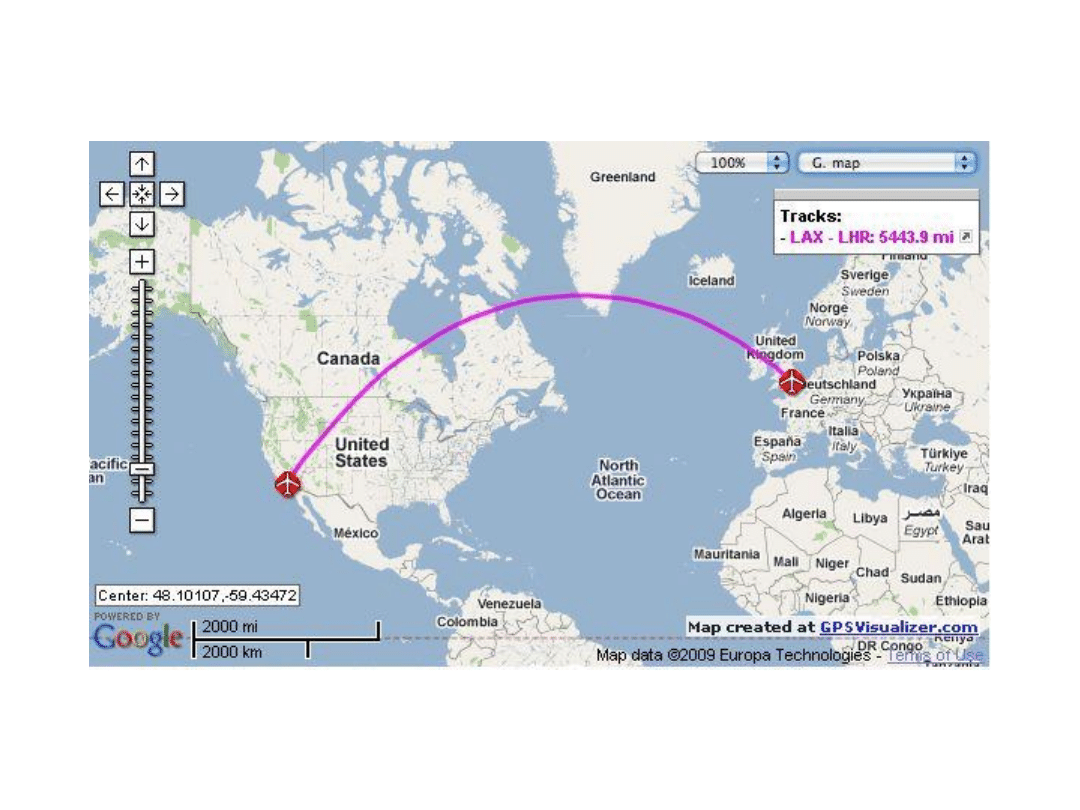
Dlaczego trasy samolotów na mapach są często tajemniczo wygięte?

Trasa lotu z Londynu do Los Angeles

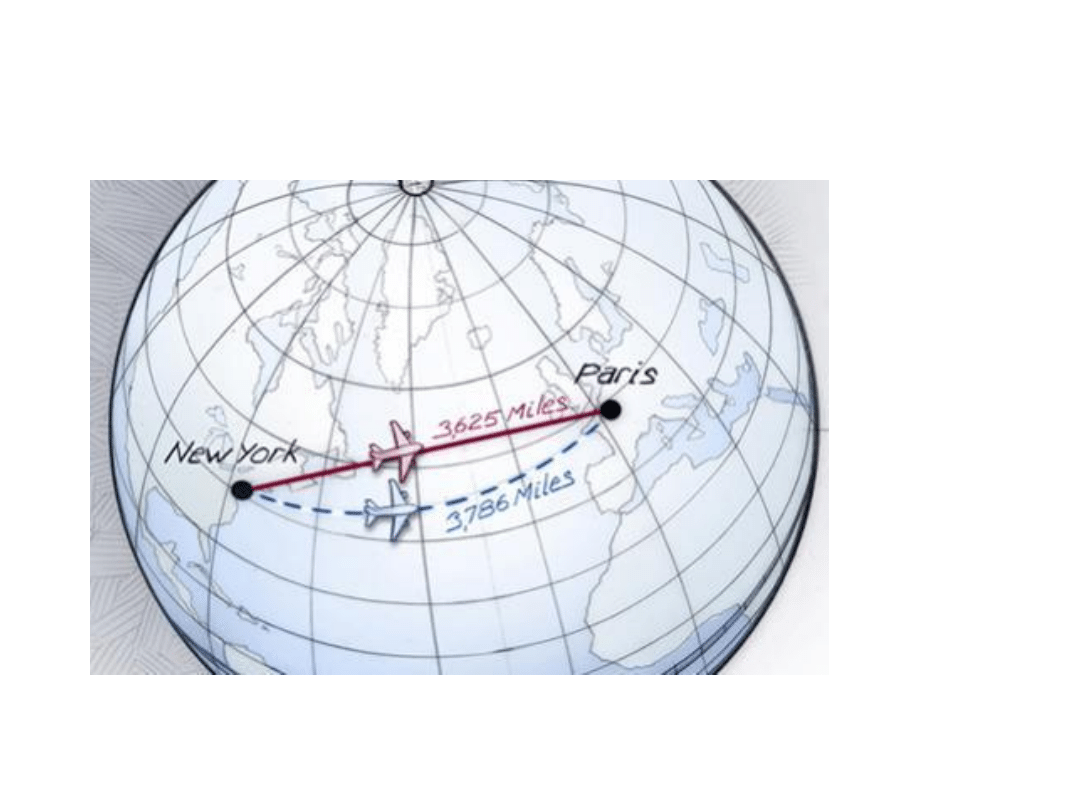
Samoloty oszczędzają paliwo i latają po geodetykach a więc
odcinkach kół wielkich. Widać to dobrze dopiero na globusie.

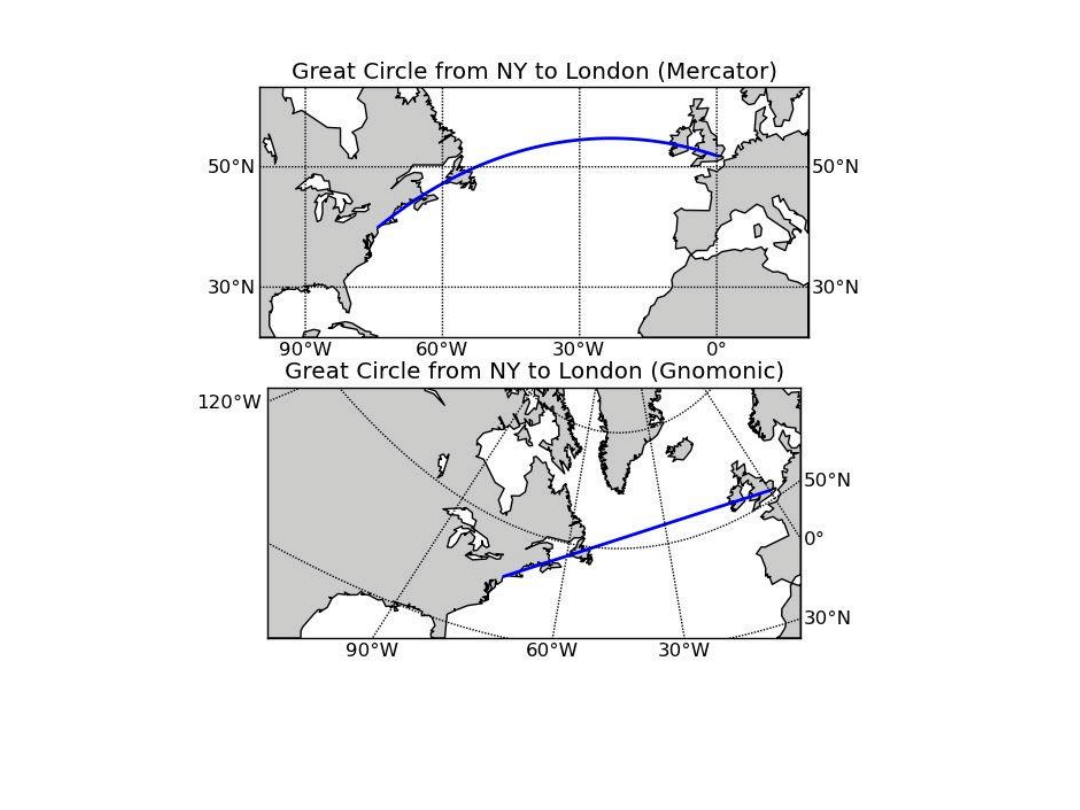
Problem można rozwiązać za pomocą odpowiedniego odwzorowania.

Wykorzystanie trójkąta paralaktycznego do obliczania odległości

Budujemy trójkąt, którego wierzchołkami są dwa punkty (miasta – odegłość między nimi
liczymy) i biegun. Jego boki to wówczas: r, (90º-φ

A

) i (90º-φ

B

), zaś kąt miedzy dwoma

ostatnimi bokami wyniesie (λ

B

-λ

A

). Z wzoru cosinusowego mamy:

Z

A

B

B

A

B

A

R

rad

d

km

D

d

























]

[

]

[

)

cos(

)

90

sin(

)

90

sin(

)

90

cos(

)

90

cos(

cos













Zadanie: policzyć odległość Teheran – Bydgoszcz;
Bydoszcz 53°07' N 18°00' E
Teheran 35.69°N 51.42° E

Pomiędzy dwoma gwiazdami na sferze niebieskiej (współrzędne: rektascenzja i deklinacja)
mamy tylko odległość kątową:

)

cos(

)

90

sin(

)

90

sin(

)

90

cos(

)

90

cos(

cos

1

2

2

1

2

1

































r

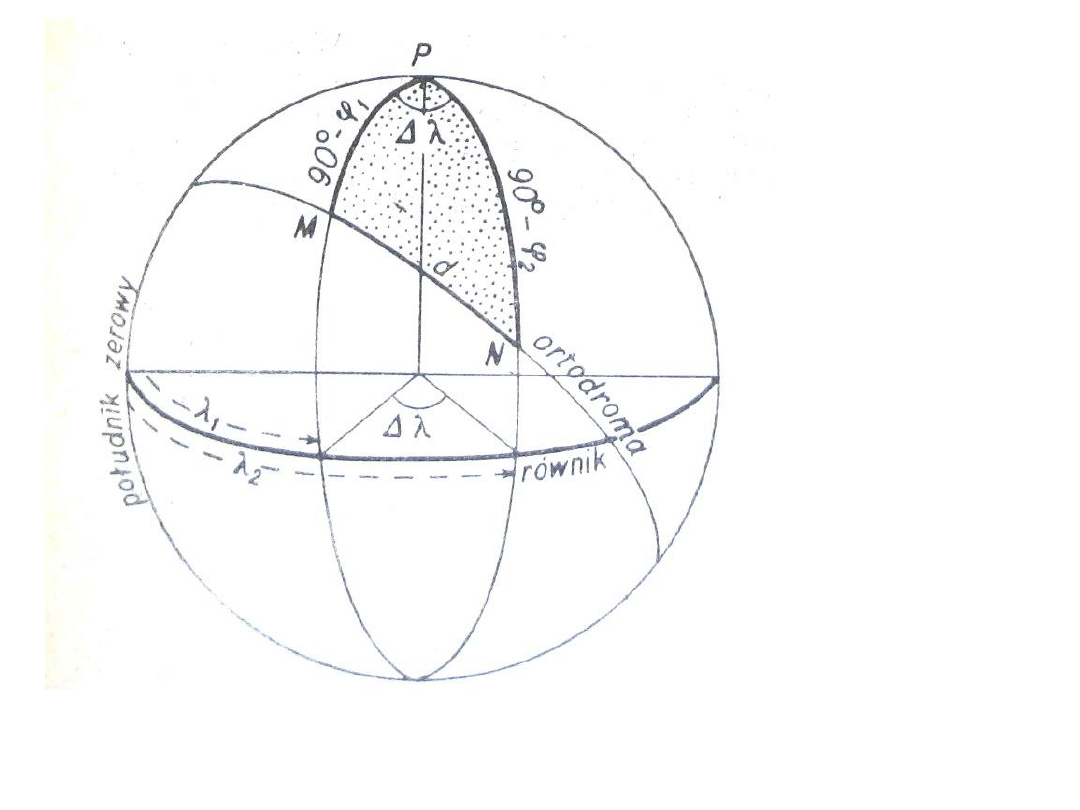
Trójkąt za pomocą którego obliczamy odległości (d) na sferze.
Miasta M i N mają szerokości geogr. φ

1

i φ

2

zaś różnicę długości geogr. Δλ

Przykładowe zadania:

1) dane: a, b, c - wzory cosinusowe
2) dane: a, b, C (dwa boki i kąt między nimi) - wzór cosinusowy
(nawet nie wymaga przekształcania)
6) dane: A, B, C - wzory cosinusowe trójkąta biegunowego

Na uwagę zasługuje też 3) dane: a, b, A (dwa boki i kąt przyległy „z boku”)

z wzoru sinusowego:

a

A

b

B

sin

sin

sin

sin





a c i C trzeba wyznaczyć z układu równań:

C

a

b

a

b

B

c

C

b

a

b

a

A

c

cos

cos

sin

sin

cos

cos

sin

cos

cos

sin

sin

cos

cos

sin









Nadmiar sferyczny jest miarą powierzchni trójkąta sferycznego:
Pole trójkąta sferycznego =





R

2

(R- promień sfery, ε w radianach !)

Pole pasa sferycznego
(np. dla pasa miedzy szerokościami



1

i



2

dla kulistej Ziemi):

)

sin

(sin

2

1

2

2











R

P

Nadmiar sferyczny

Nadmiar (eksces) sferyczny to nadwyżka sumy kątów trójkąta sferycznego ponad 180



.



≡ A+B+C – 180



Dla każdego trójkąta 0



<



<720



; dla trójkąta eulerowskiego: 0



<



<360



.

Dla trójkąta płaskiego



= 0



(i to świadczy, że nie jest to trójkąt sferyczny!)

Metody obliczania nadmiaru sferycznego

1. z definicji



= A+B+C – 180



2. wzór Cagnolii

itd. (przez podstawienie cykliczne)

3. Nadmiar sferyczny można też wyrazić przez dwa boki i kąt między nimi zawarty:

A

A

c

b

sin

cos

2

ctg

2

ctg

2

ctg







4. Wzór l’Huiliera

(Uwaga w skryptach często jest błąd)

5. Wzór przybliżony























24

3

1

sin

2

2

2

2

c

b

a

C

ab



C

c

b

a

sin

2

cos

2

sin

2

sin

2

sin





2

2

2

2

4

c

s

tg

b

s

tg

a

s

tg

s

tg

tg











)

(

2

1

c

b

a

s







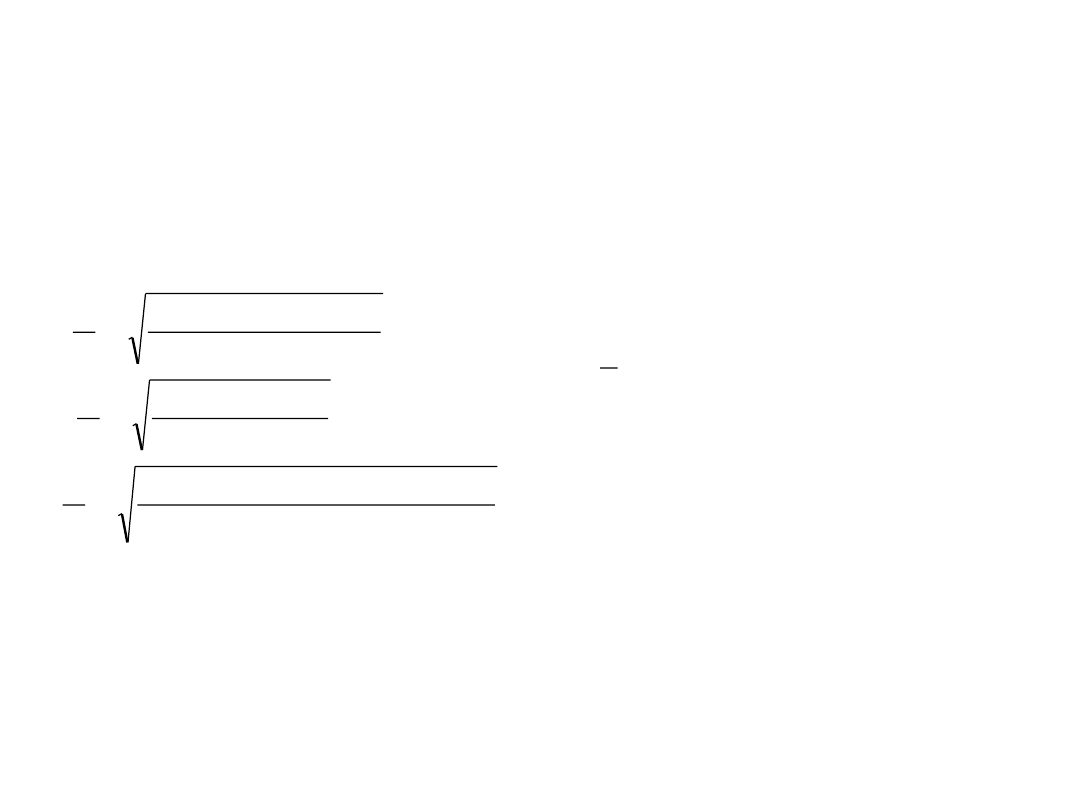
Inne wzory

Wzory cotangensowe:

Wzory Bordy (połówkowe)

Gdzie:

b

C

b

a

C

A

c

B

c

a

B

A

cos

cos

sin

ctg

sin

ctg

cos

cos

sin

ctg

sin

ctg









)

sin(

sin

)

sin(

)

sin(

)

sin(

2

tg

sin

sin

)

sin(

sin

2

cos

sin

sin

)

sin(

)

sin(

2

sin

a

s

s

c

s

b

s

a

s

A

c

b

c

s

s

A

c

b

c

s

b

s

A





























)

(

2

1

c

b

a

s







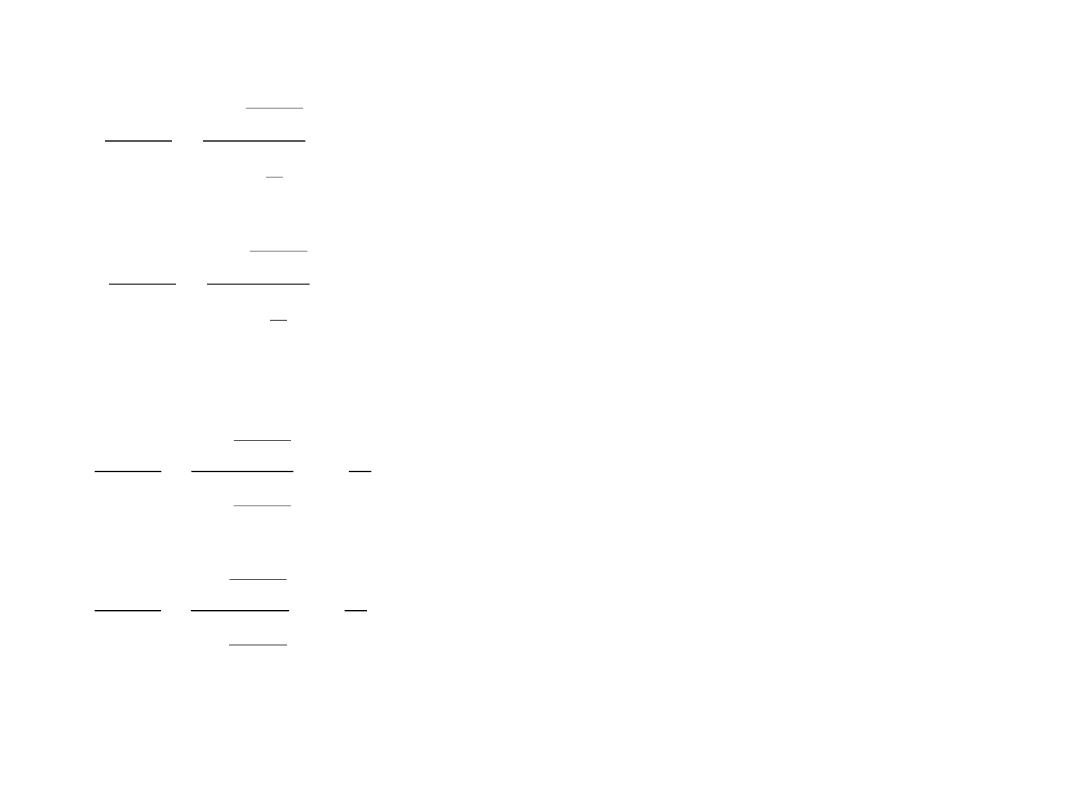
Wzory Gaussa-Delambre’a

Wzory Nepera (analogie Napiera):

C

c

b

a

B

A

C

c

b

a

B

A

sin

2

cos

2

cos

2

cos

cos

2

cos

2

cos

2

sin

















2

2

sin

2

sin

2

2

2

cos

2

cos

2

C

ctg

b

a

b

a

B

A

tg

C

ctg

b

a

b

a

B

A

tg





















Trójkąt prostokątny i prosto-boczny

Dla: A = 90° z wzorów podstawowych dostajemy:

b

a

B

c

C

c

a

C

b

B

B

b

C

a

c

C

c

B

a

b

C

B

c

b

a

tan

cot

sin

cos

cos

tan

cot

sin

cos

cos

cot

tan

sin

sin

sin

cot

tan

sin

sin

sin

cot

cot

cos

cos

cos





















dla: a =90° z wzorów podstawowych dostajemy:

B

A

b

C

c

C

A

c

B

b

b

B

c

A

C

c

C

b

A

B

c

b

C

B

A

tan

cot

sin

cos

cos

tan

cot

sin

cos

cos

cot

tan

sin

sin

sin

cot

tan

sin

sin

sin

cot

cot

cos

cos

cos





























Metody przybliżone rozwiązywania trójkątów sferycznych

Trójkąty wąskie:
Niech a, A małe, wobec tego także (b-c) małe:
sin a = a, sin A = A sin(b-c) = b-c
oraz cos a = cos A = cos(b-c) = 1
Wówczas wzory podstawowe tworzą zestaw:

C

a

c

A

B

a

b

A

c

b

C

a

b

c

B

a

sin

sin

sin

sin

cos

cos













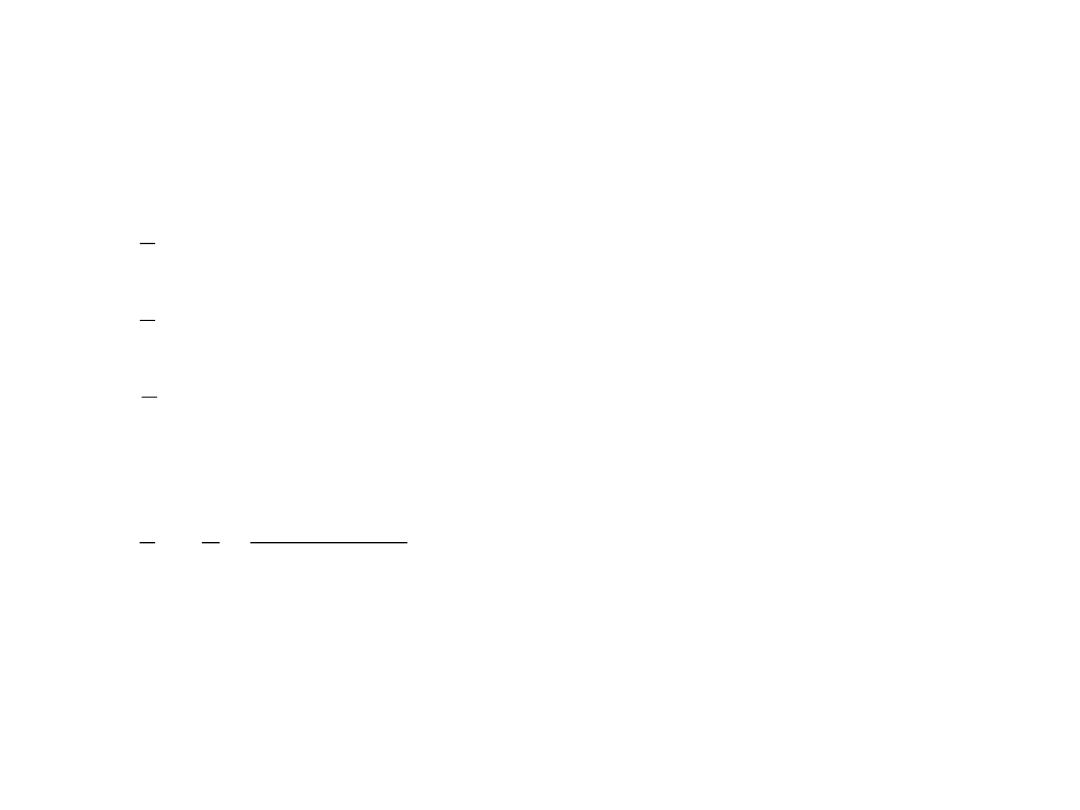
Trójkąt o małych bokach
(np. dla Ziemi mniejsze od 30 km, jeszcze dla 200 km błąd poniżej sekundy)
Twierdzenie Legendre’a:
Małe trójkąty sferyczne można traktować jak trójkąty płaskie o bokach równych sferycznym i
kątach:







3

1

'

3

1

'

3

1

'













C

C

B

B

A

A

dla nieco większych trójkątów trzeba zastosować wyrazy czwartego rzędu:

























2

2

2

2

60

2

3

3

1

'

R

a

c

b

A

A





Analogie trójkąta sferycznego i geometrii na płaszczyźnie:



wysokość trójkąta sferycznego

np. wysokość poprowadzona na bok a z wierzchołka A:

B

c

C

b

h

A

sin

sin

sin

sin

sin







promień okręgu (koła małego) opisanego (R) i wpisanego (r):

)

cos(

)

cos(

)

cos(

cos

tan

C

S

B

S

A

S

S

R











oraz

s

c

s

b

s

a

s

r

sin

)

sin(

)

sin(

)

sin(

tan









Interpretacja wektorowa trygonometrii sferycznej:
Jeśli wierzchołki trójkąta są rozpięte na wektorach (

C

B

A







,

,

), to odpowiednie boki

można wyznaczyć jako argumenty kosinusów kierunkowych tych wektorów.

C

B

a









cos

itd.

Normalne zorientowanej płaszczyzny koła wielkiego zawierającej boki a, b i c:

C

B

C

B

n

a

















,

A

C

A

C

n

b

















,

B

A

B

A

n

c

















pozwalają policzyć cosinusy kątów trójkąta sferycznego:

c

b

n

n

A











cos