Gliwice 2010

Kubatury Gaussa

(całka podwójna po trójkącie)

Gliwice 2010

Dana jest funkcja dwóch zmiennych

f (x, y)

ciągła

i ograniczona w obszarze trójkątnym

D.

Całka podwójna po trójkącie

Wierzchołki trójkąta wyznaczają punkty

(x

1

, y

1

)

,

(x

2

, y

2

)

,

(x

3

, y

3

)

nie leżące na jednej prostej.

Chcemy obliczyć całkę

( , ) d d

D

f x y

x y



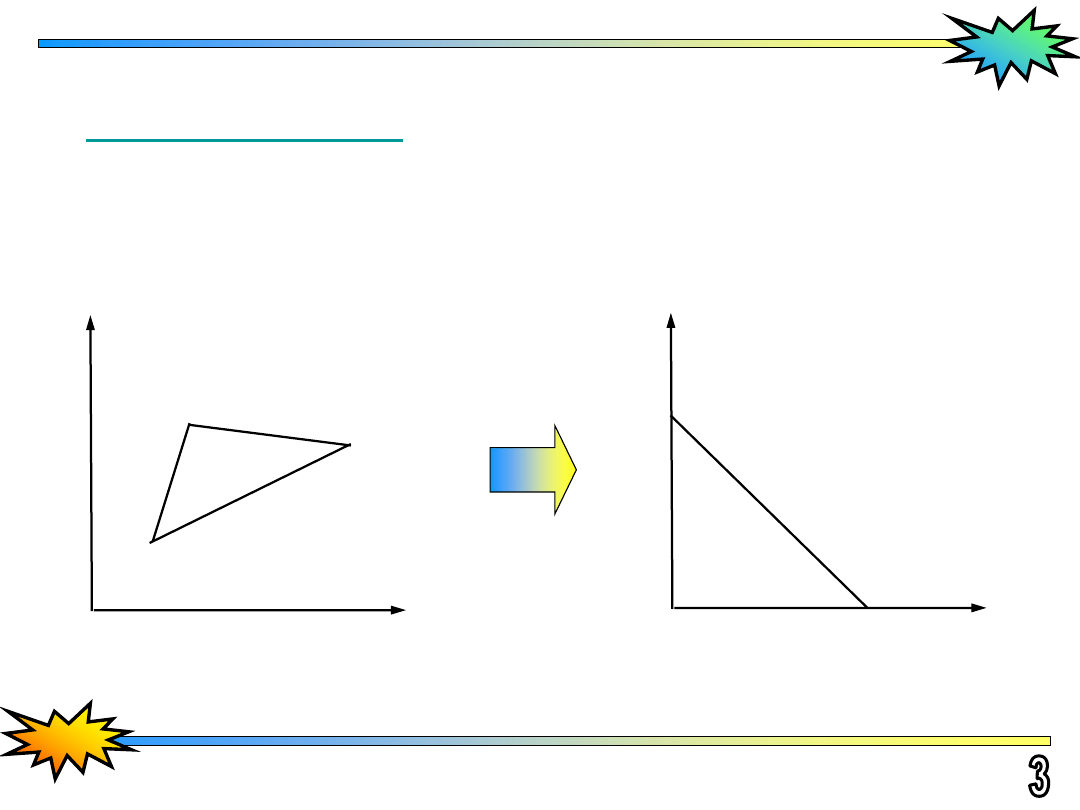
Gliwice 2010

Normalizujemy całkę

sprowadzając wyjściowy trójkąt

D

do trójkąta prostokątnego, równoramiennego o wierzchołkach:

(0,0)

,

(1,0)

,

(0,1)

Całka podwójna po trójkącie

x

y

D

(x

1

, y

1

)

(x

2

, y

2

)

(x

3

, y

3

)

(0,0)

η

ξ

(1,0)

(0,1)

Trójkąt wyjściowy i znormalizowany

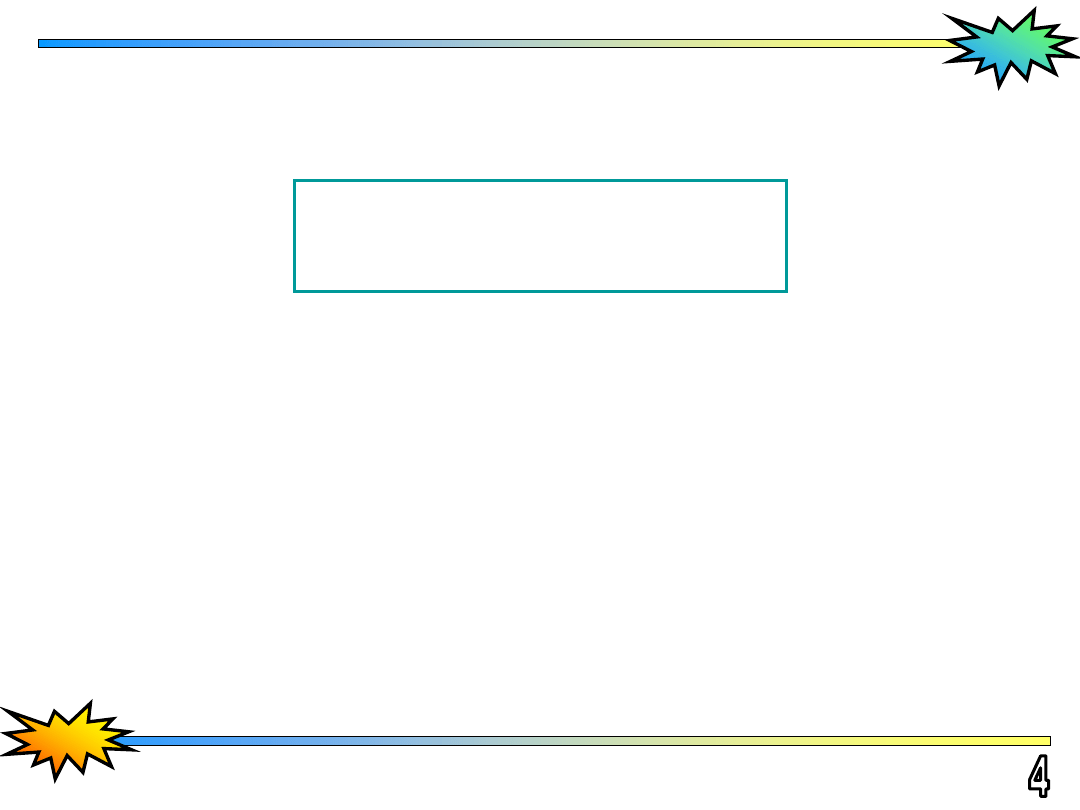
Gliwice 2010

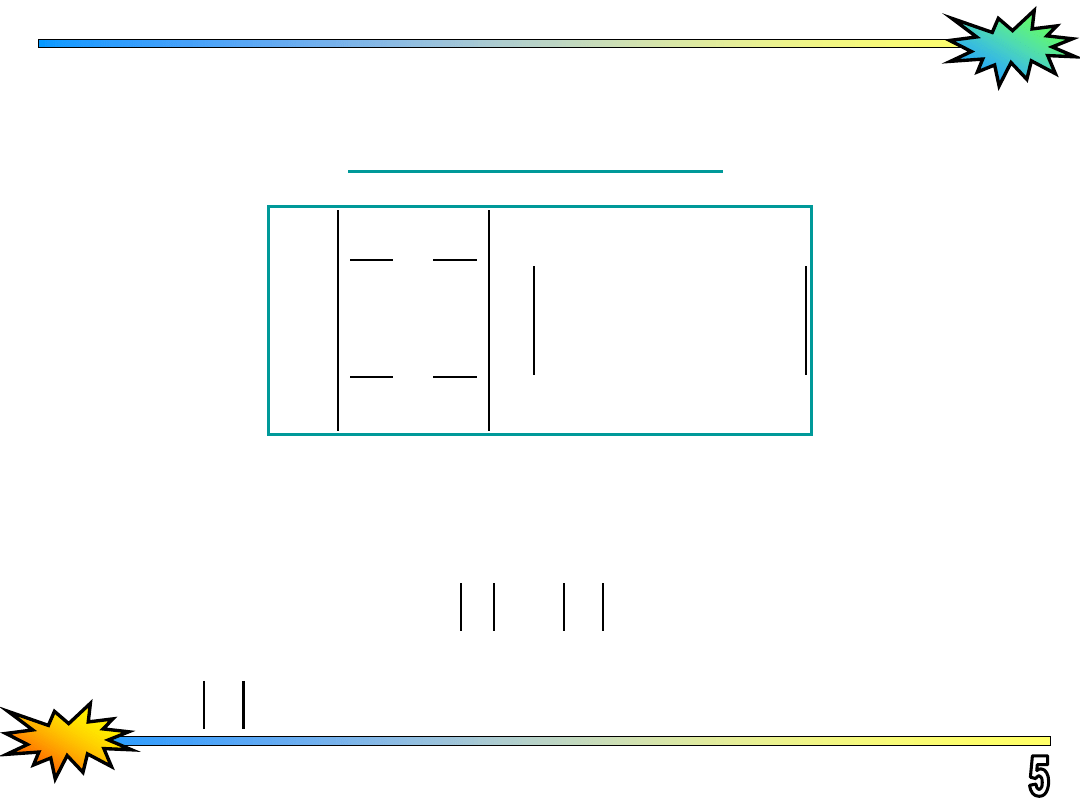
Normalizacji dokonujemy przez podstawienie:

Całka podwójna po trójkącie

Wierzchołki trójkątów odpowiadają sobie w następujący

sposób:

1

2

1

3

1

1

2

1

3

1

(

) ξ

(

) η

(

) ξ

(

) η

x

x

x

x

x

x

y

y

y

y

y

y

 







 







1

1

2

2

3

3

( ,

)

(0,0)

(

,

)

(1,0)

(

,

)

(0,1)

x y

x

y

x y







Gliwice 2010

Zmiana układu współrzędnych wymaga pomnożenia funkcji

podcałkowej przez

jakobian przekształcenia

Całka podwójna po trójkącie

- pole wyjściowego trójkąta

D

2

1

3

1

2

1

3

1

ξ

η

ξ

η

x

x

x

x

x

x

J

y

y

y

y

y

y





























2

1

3

1

3

1

2

1

(

)(

) (

)(

)

J

x

x

y

y

x

x

y

y













2

J

D



D

Gliwice 2010

Funkcja podcałkowa dla trójkąta znormalizowanego przyjmuje

postać:

Całka podwójna po trójkącie

1

2

1

3

1

1

2

1

3

1

[ (

(

) ξ

(

) η ,

(ξ , η

(

)

)

ξ (

) η]

J

f

x

x

x

x

x

y

F

y

y

y

y





















Gliwice 2010

Końcowy wzór do obliczania całki podwójnej metodą kubatur

Gaussa dla obszarów trójkątnych jest następujący

Całka podwójna po trójkącie

1 ξ

1

1

0

0

1

dξ

(ξ,η) dη

(ξ ,η )

2

n

i

i

i

i

F

F

w









 

gdzie:

- współrzędne punktów Gaussa,
- wagi dla punktów Gaussa,
- liczba punktów Gaussa w obszarze trójkąta

znormalizowanego.

ξ ,η

i

i

i

w

n

ξ ,η ,

i

i

i

w

Wartości odczytujemy z tablic (z literatury).

Gliwice 2010

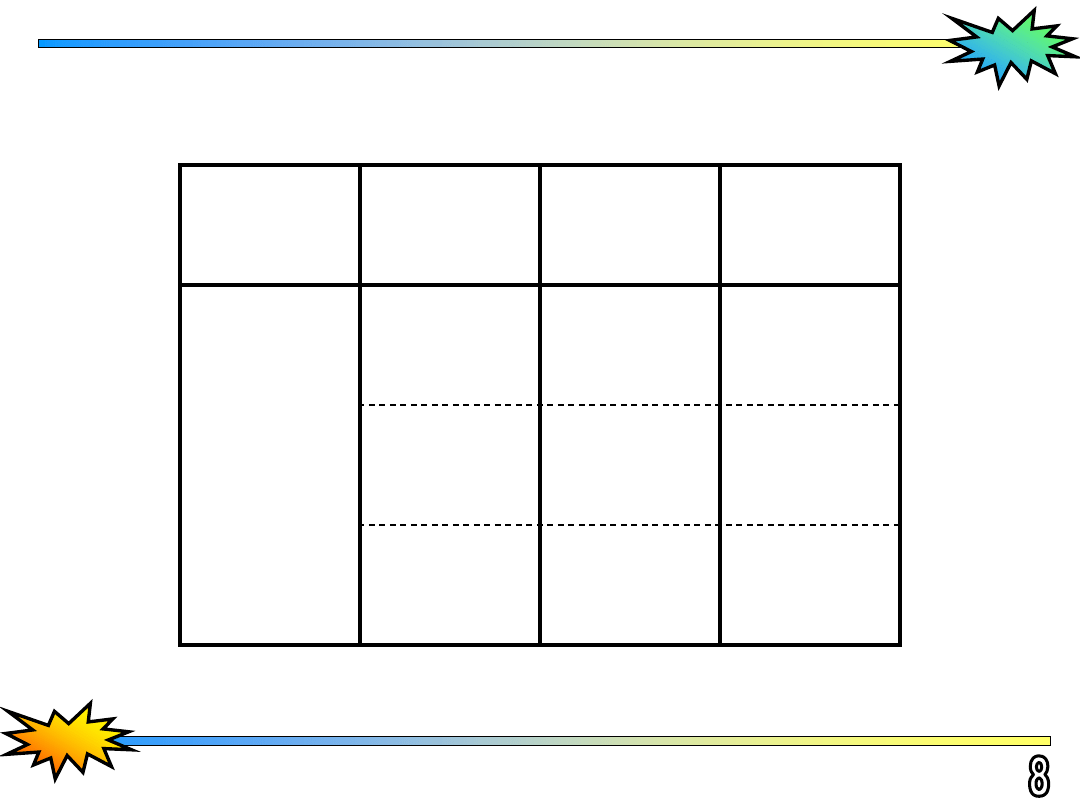
Całka podwójna po trójkącie

Współrzędne i wagi punktów Gaussa

n

ξ

i

η

i

i

w

3

1/3

1/3

1/3

1/2

1/2

0

1/2

1/2

0

Gliwice 2010

Przybliżone metody rozwiązywania

równań

Gliwice 2010

Rozwiązywanie równań

Przybliżone metody rozwiązywania równań

polegają

najczęściej na tworzeniu tzw. wzorów rekurencyjnych

określających sposób wyznaczania kolejnych wyrazów ciągu

liczbowego, którego granicą jest szukane rozwiązanie

równania typu

( )

0

F x



Większość metod obliczeniowych należy do typowych

metod iteracyjnych

.

Gliwice 2010

Podstawowe problemy tych metod to:

Lokalizacja pierwiastka (dobór punktu startowego).

Obliczanie przybliżeń pierwiastków.

Zbieżność procesu iteracyjnego.

Rozwiązywanie równań

Gliwice 2010

Metoda bisekcji

Popularnie stosowane metody iteracyjne

(metody kolejnych przybliżeń):

Rozwiązywanie równań

Metoda cięciw

Metoda stycznych

Gliwice 2010

Lokalizacja pierwiastków

Gliwice 2010

Twierdzenie 1 (Bolzano-Cauchy’ego):

Jeżeli funkcja

F(x)

jest ciągła w przedziale domkniętym

[a, b]

i na jego końcach przyjmuje wartości różnych

znaków, tzn.

F(a)



F(b) < 0

, to między punktami

a

i

b

znajduje się co najmniej jeden pierwiastek równania

F(x) = 0

.

Rozwiązywanie równań

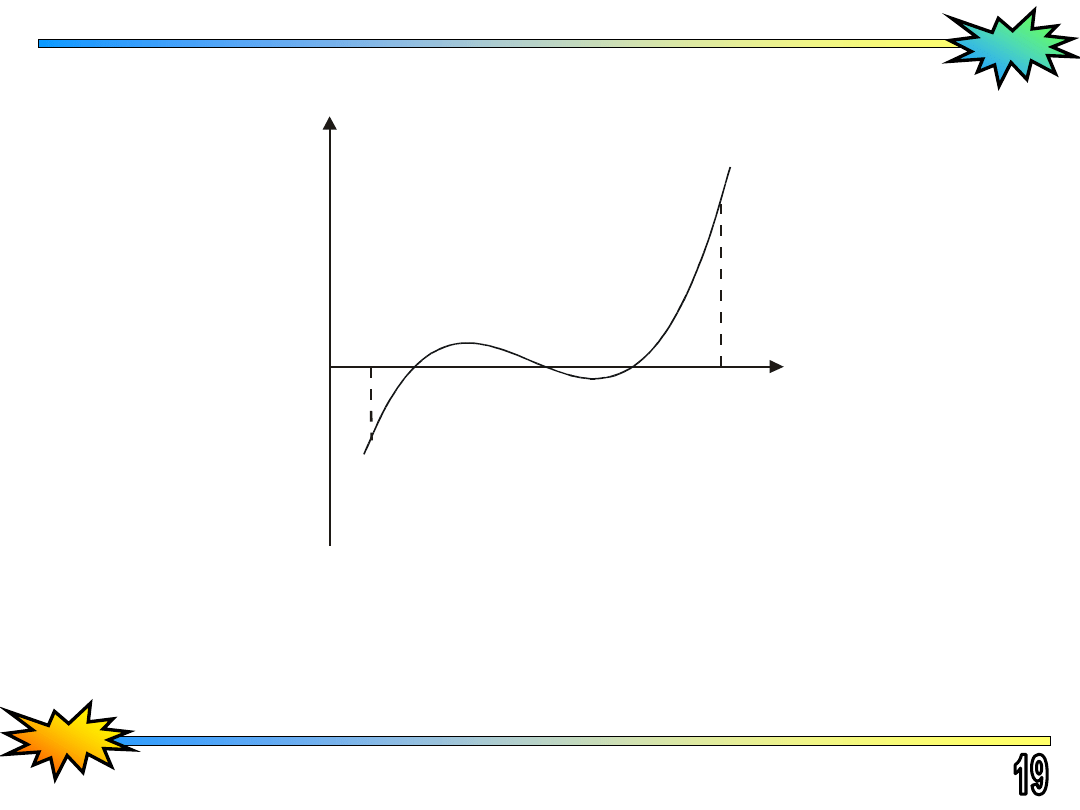
Gliwice 2010

y

x

F(x)

a

b

Przebieg funkcji między punktami

a

i

b

Rozwiązywanie równań

Gliwice 2010

Twierdzenie 2:

Jeżeli w przedziale

[a, b]

spełnione są założenia

twierdzenia Bolzano - Cauchy’ego i dodatkowo

F’(x)

jest

stałego znaku w tym przedziale

(co oznacza, że funkcja

jest stale rosnąca lub stale malejąca)

, to przedział ten

jest przedziałem izolacji pierwiastka równania

F (x) = 0

(w przedziale tym jest tylko jeden pierwiastek).

Rozwiązywanie równań

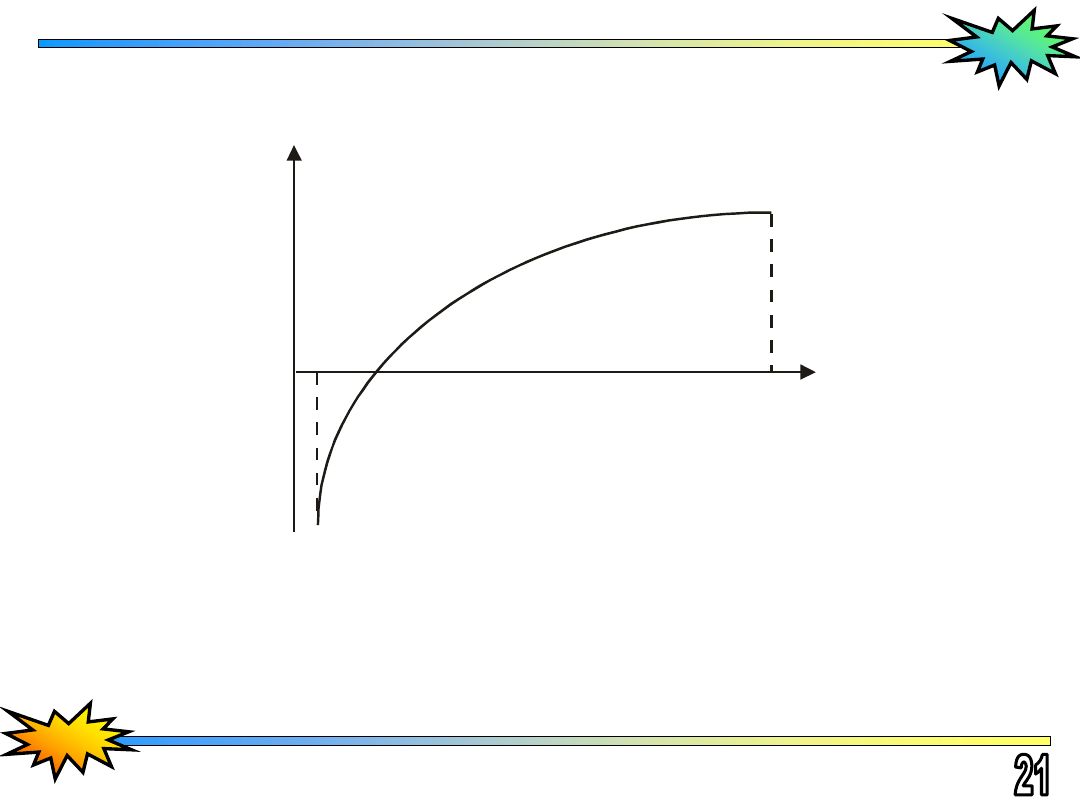
Gliwice 2010

y

x

F(x)

a

b

Przebieg funkcji między punktami

a

i

b

Rozwiązywanie równań

Gliwice 2010

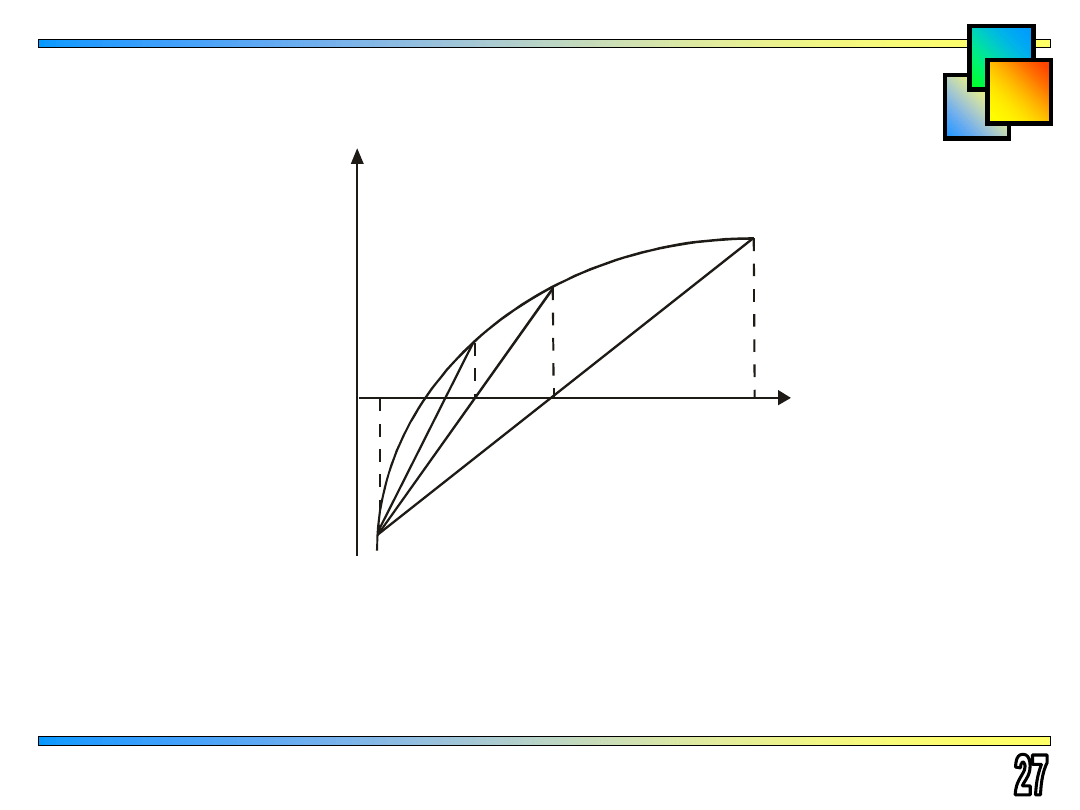
Metoda cięciw

Gliwice 2010

Rozwiązywanie równań

Jeżeli funkcja

F (x)

jest funkcją klasy

C

2

w przedziale izolacji

pierwiastka to rozwiązanie równania

( )

0

F x



przybliżamy ciągiem miejsc zerowych cięciw poprowadzonych

między punktami stanowiącymi końce kolejnych przedziałów

izolacji.

Gliwice 2010

x

4

x

1

x

2

y

x

F(x)

x

3

Kolejne przybliżenia poszukiwania pierwiastka w metodzie cięciw

Rozwiązywanie równań

Gliwice 2010

Równanie cięciwy można zapisać następująco

1

1

1

1

(

)

(

)

(

)

i

i

k

i

k

i

y

F x

x

x

F x

F x

x

x



















gdzie

x

k

jest drugim krańcem przedziału

[x

i



1

, x

k

]

, czyli pierwszą

cięciwę prowadzimy między punktami

( ,

( ) )

a F a

( ,

( ) )

b F b

i

Rozwiązywanie równań

Gliwice 2010

Rozwiązywanie równań

Podstawiając

y = 0

otrzymujemy wzór

1

1

1

1

(

)

(

)

(

)

k

i

i

i

i

k

i

x

x

x

x

F x

F x

F x

















Gliwice 2010

Założenie:

W przedziale

[a, b]

lub w kolejnym znalezionym przedziale

izolacji znak drugiej pochodnej funkcji

F (x)

nie zmienia się.

Wyrazy

ciągu

dają

przybliżenie

pierwiastka

z niedomiarem lub nadmiarem.

Rozwiązywanie równań

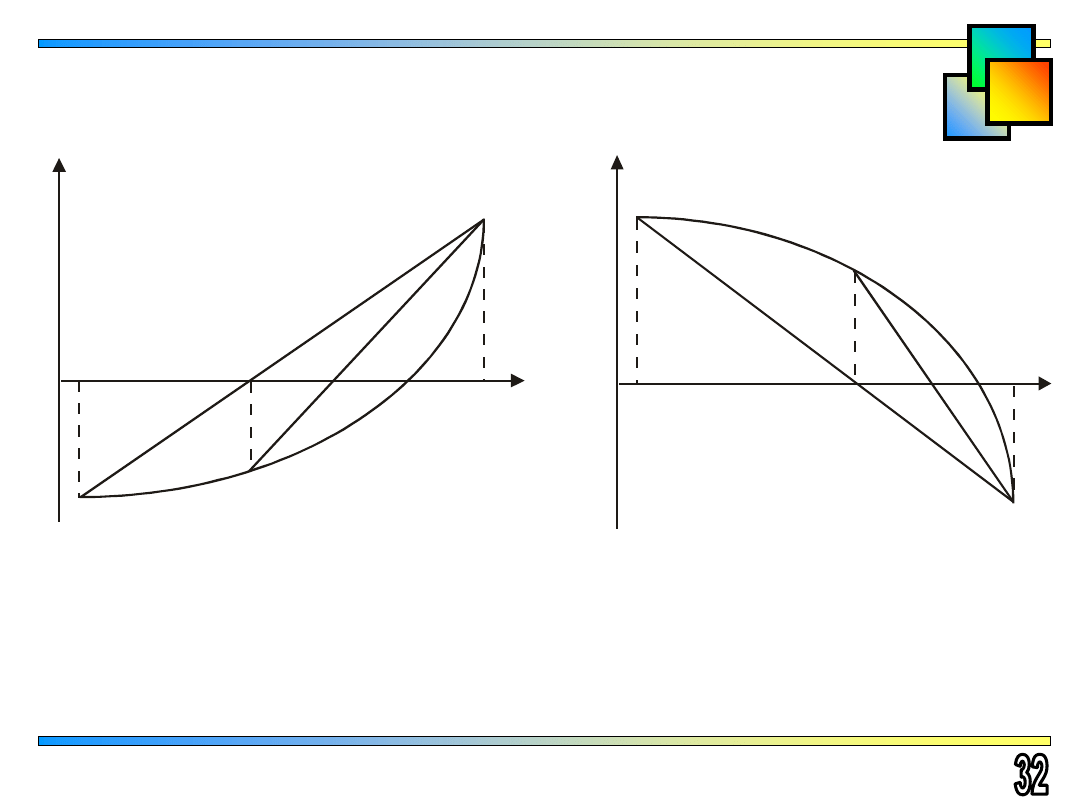
Gliwice 2010

Oszacowanie pierwiastka z niedomiarem

x

*

x

1

x

2

y

x

x

3

F’(x) > 0

F’’(x) > 0

x

4

x

*

x

1

x

2

y

x

x

3

F ’(x) < 0

F ’’(x) < 0

x

4

Rozwiązywanie równań

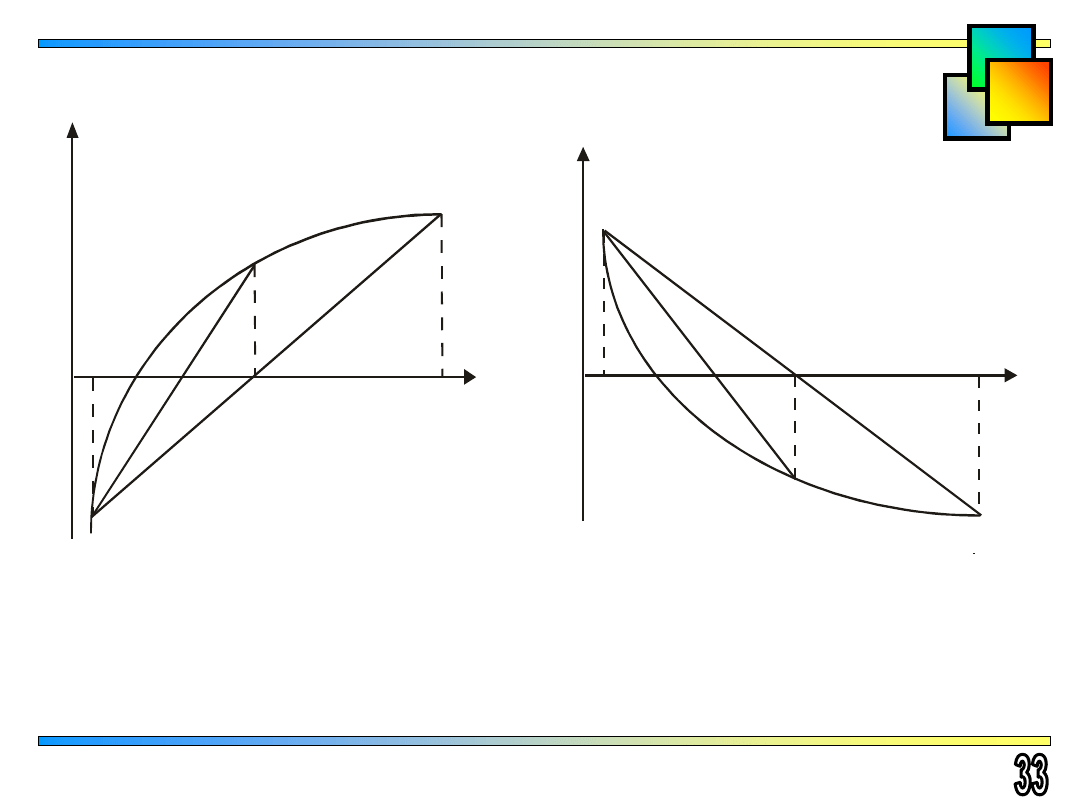
Gliwice 2010

Oszacowanie pierwiastka z nadmiarem

Rozwiązywanie równań

x*

x

1

x

2

y

x

x

3

F ’(x) > 0

F ’’(x) < 0

x

4

x*

x

1

x

2

y

x

x

3

F ’(x) < 0

F ’’(x) > 0

x

4

Gliwice 2010

Rozwiązywanie równań

Występujący w wzorze

punkt

x

k

jest lewym lub prawym końcem

przedziału

[a, b]

, czyli

x

k

= x

1

lub

x

k

= x

2

.

Określenie stałego punktu pęku cięciw:

2

[ , ] ,

'( )

''( )

0

k

x

a b

F x F

x

x

x

b













1

[ , ] ,

'( )

''( )

0

k

x

a b

F x F

x

x

x

a









 

Gliwice 2010

Metoda stycznych

(Newtona)

Gliwice 2010

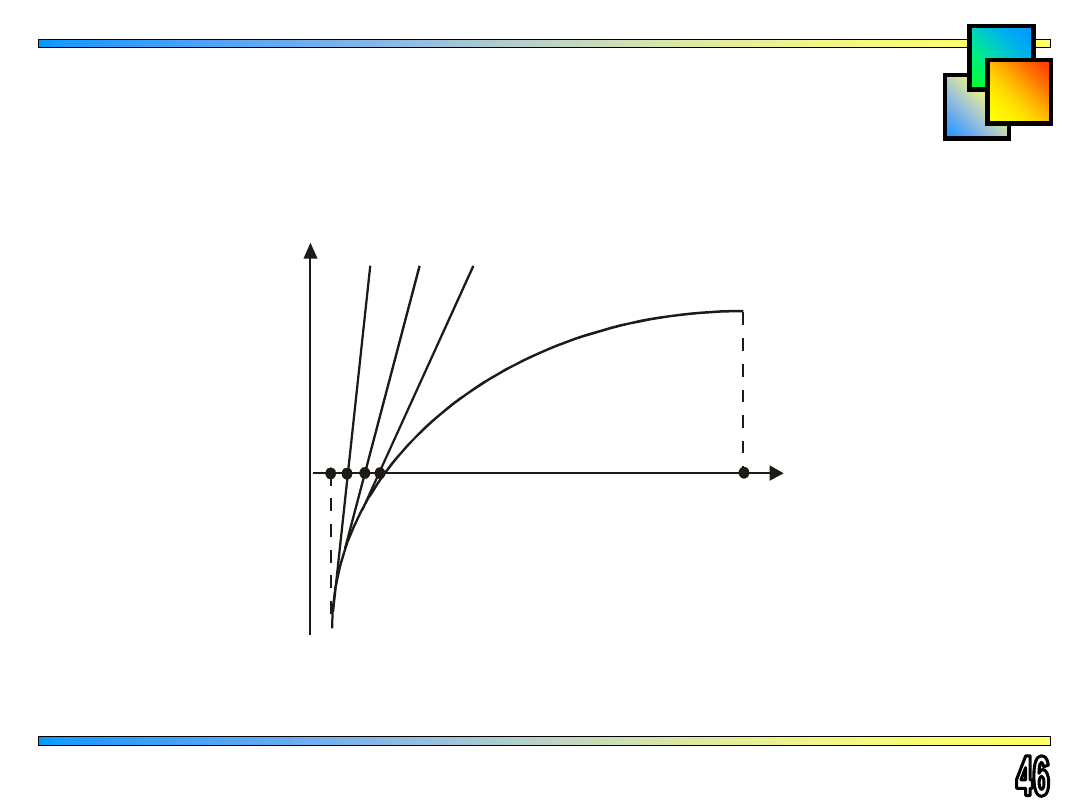
Rozwiązywanie równań

Kolejne przybliżenia poszukiwania pierwiastka

w metodzie stycznych

Rozwiązanie równania

F (x) = 0

w przedziale izolacji pierwiastka

[a, b]

przybliżamy wyrazami ciągu utworzonego przez miejsca

zerowe stycznych do funkcji

F (x)

.

y

x

F(x)

a

b

x

*

Gliwice 2010

Rozwiązywanie równań

Równanie stycznej w punkcie o odciętej

x

i



1

można zapisać

1

1

1

(

)

'(

) (

)

i

i

i

y

F x

F x

x

x











 

Podstawiając

y = 0

otrzymujemy wzór

1

1

1

(

)

,

1

'(

)

i

i

i

i

F x

x

x

i

F x













Gliwice 2010

Rozwiązywanie równań

Określenie punktu startowego do obliczeń:

Uwaga!

Jeżeli druga pochodna funkcji w przedziale izolacji nie ma

stałego znaku, to proces iteracyjny może być rozbieżny.

1

[ , ] ,

'( )

''( )

0

x

a b

F x F

x

x

b











1

[ , ] ,

'( )

''( )

0

x

a b

F x F

x

x

a











Gliwice 2010

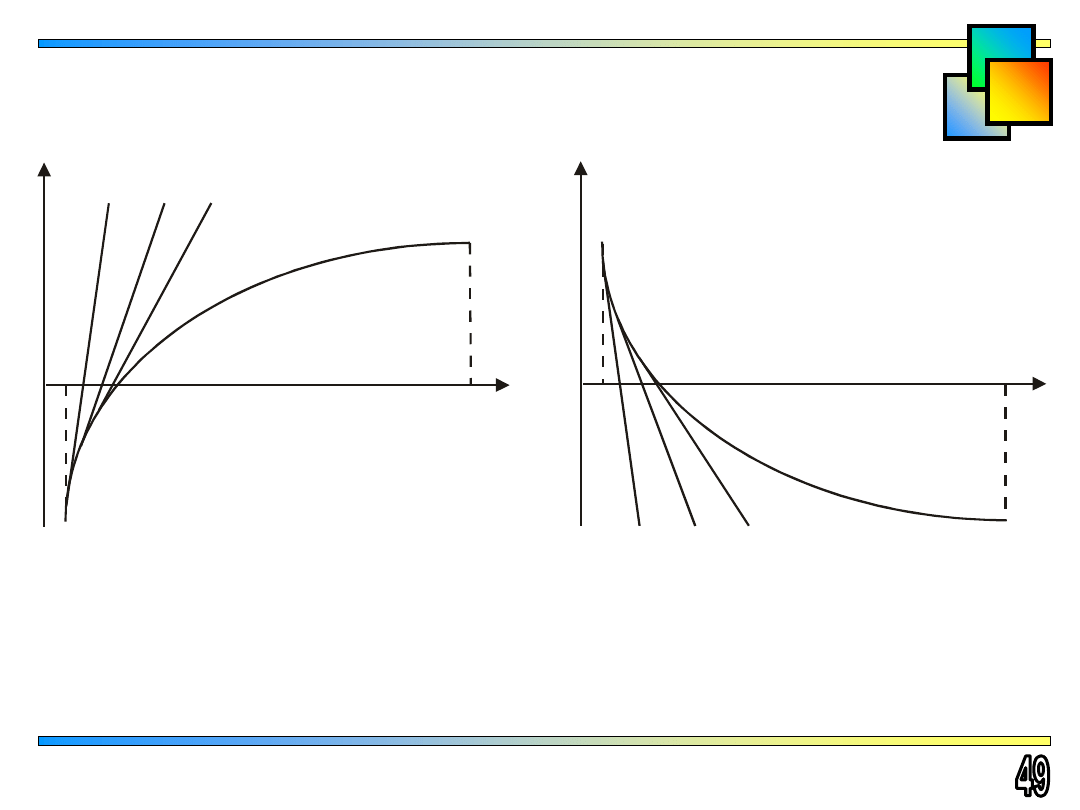
Wybór pierwszego przybliżenia w metodzie stycznych

Rozwiązywanie równań

x

*

x

1

b

y

x

F’(x) > 0

F’’(x) < 0

x

*

x

1

b

y

x

F’(x) < 0

F’’(x) > 0

Gliwice 2010

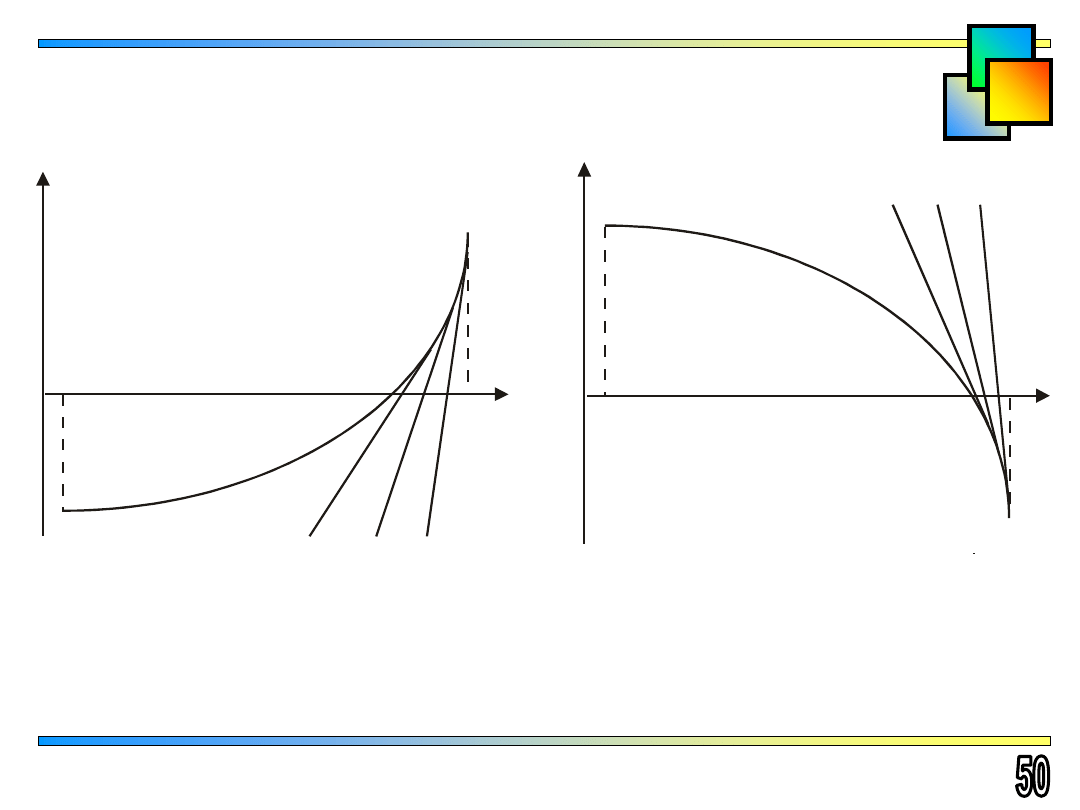
Wybór pierwszego przybliżenia w metodzie stycznych

Rozwiązywanie równań

x

*

a

x

1

y

x

F’(x) > 0

F’’(x) > 0

x

*

a

x

1

y

x

F’(x) < 0

F’’(x) < 0

Gliwice 2010