Gliwice 2010

Aproksymacja funkcji

Gliwice 2010

Definicja aproksymacji

Gliwice 2010

Definicja aproksymacji

 

( ) ,

,

y

f x

x

a b





Funkcja ta podana

jest w postaci wzoru

analitycznego

lub w postaci zbioru

punktów

1

1

2

2

( )

,

(

)

,

... ,

(

)

n

n

f x

y

f x

y

f x

y






Dana

jest

funkcja

jednej zmiennej

Należy dobrać taką funkcję

1

( ,

, ... ,

),

[ , ]

k

F x p

p

x

a b



aby w sensie przyjętego

kryterium, funkcja

1

( ,

, ... ,

)

k

F x p

p

możliwie dokładnie odtwa-

rzała przebieg funkcji

 

f x

p

1

,…,

p

k

- parametry

wzoru empirycznego

Gliwice 2010

Definicja aproksymacji

Funkcja

f (x)

może być zadana w postaci:

zbioru punktów (aproksymacja punktowa)

1

1

2

2

( )

,

( )

, ... ,

(

)

n

n

f x

y

f x

y

f x

y







wzoru analitycznego (aproksymacja integralna)

- rzadziej spotykany przypadek

Gliwice 2010

Definicja aproksymacji

Jeżeli rozpatrujemy funkcję wielu zmiennych

u = f (x, y, …)

,

to funkcja aproksymująca jest funkcją tych samych
argumentów i zawiera w sobie nieznane parametry

p

1

, …, p

k

1

( , ,...,

, ... ,

)

k

F x y

p

p

Gliwice 2010

Definicja aproksymacji

Kryterium aproksymacji punktowej dla funkcji jednej zmiennej
konstruuje się tak, aby różnice pomiędzy wartościami danej funkcji

f (x)

w punkcie

(x

i

, y

i

)

a wartościami funkcji

w

tych samych punktach były

minimalne

.

1

( ,

, ... ,

)

k

F x p

p

Wprowadza się pojęcie

odchyłki

ε

i

1

ε

( , , ... ,

)

i

i

k

i

F x p

p

y





gdzie:

1, 2, ... ,

i

n



Odchyłkę dla funkcji wielu zmiennych definiuje się analogicznie

1

ε

( , , ..., , ... ,

)

i

i

i

k

i

F x

y

p

p

u





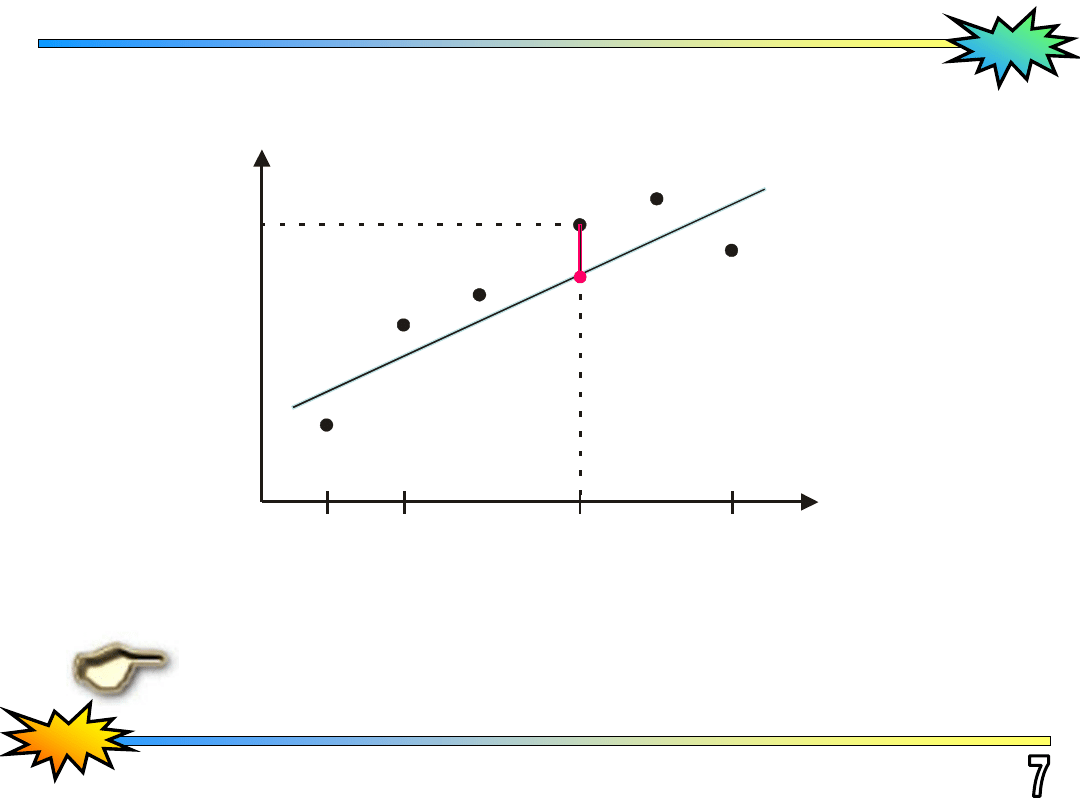
Gliwice 2010

Definicja aproksymacji

Ogólna postać funkcji

F

jest założona z góry,

natomiast

optymalizacja

dotyczy

nieznanych

parametrów

p

1

, …, p

k

Graficzna interpretacja odchyłki dla aproksymacji funkcji

y

i

x

1

x

i

x

n

x

x

2

y

e

i

F(x, p

1

, ... , p

k

)

Gliwice 2010

Definicja aproksymacji

Typowe metody aproksymacji funkcji jednej zmiennej

lub wielu zmiennych

Dobór parametrów

p

1

, …,

p

k

wzoru empirycznego, w taki

sposób aby spełnione było założone kryterium dotyczące

minimalizacji odchyłek

Gliwice 2010

Definicja aproksymacji

Kryteria minimalizacji odchyłek

metoda wybranych punktów

metoda średnich

metoda sumowania bezwzględnych wartości

metoda najmniejszych kwadratów

Gliwice 2010

Metoda najmniejszych kwadratów

Gliwice 2010

Metoda najmniejszych kwadratów

Kryterium

tej

metody

polega

na

takim

doborze

współczynników funkcji

, aby

1

( ,

, ... ,

)

k

F x p

p





2

2

1

1

1

1

(

, ... ,

)

ε

( , , ... ,

)

min

n

n

k

i

i

k

i

i

i

S p

p

F x p

p

y

















gdzie:

n

- ilość punktów

Gliwice 2010

Metoda najmniejszych kwadratów

Zalety:

kryterium jest „mocne” - zawiera kwadraty odchyłek, czyli

liczby nieujemne

prostota obliczeń minimum funkcji, pod warunkiem że

rozpatruje

się

aproksymację

w

klasie

wielomianów

uogólnionych, czyli

1

1

1

( ,

, ... ,

)

φ ( ) ...

φ ( )

k

k

k

F x p

p

p

x

p

x



 

Gliwice 2010

Aproksymacja liniowa funkcji

jednej zmiennej

Gliwice 2010

Aproksymacja liniowa funkcji jednej zmiennej

Rozpatrujemy zbiór punktów

(x

1

, y

1

)

,

(x

2

, y

2

)

, …,

(x

n

, y

n

)

Aproksymacją tego zbioru ma być funkcja liniowa

1

2

y

p

p x





Zgodnie z kryterium metody najmniejszych kwadratów





2

1

2

1

2

1

(

,

)

min

n

i

i

i

S p p

p

p x

y













Gliwice 2010

Aproksymacja liniowa funkcji jednej zmiennej

Wykorzystujemy warunek

konieczny istnienia

ekstremum funkcji dwóch

zmiennych

i otrzymujemy układ równań

1

2

1

1

2

2

(

,

)

0

(

,

)

0

S p p

p

S p p

p









































1

2

1

2

1

1

1

2

1

2

1

2

,

2

0

,

2

0

n

i

i

i

n

i

i

i

i

S p p

p

p x

y

p

S p p

p

p x

y

x

p







 



















 





 











Gliwice 2010

Aproksymacja liniowa funkcji jednej zmiennej

Po podzieleniu obu równań przez 2 otrzymujemy

1

2

1

1

2

1

2

1

1

1

n

n

i

i

i

i

n

n

n

i

i

i

i

i

i

i

p n

p

x

y

p

x

p

x

x y

















































1

2

1

1

2

1

0

0

n

i

i

i

n

i

i

i

i

p

p x

y

p

p x

y

x

























 







Układ ten zapisujemy w formie

Gliwice 2010

Aproksymacja liniowa funkcji jednej zmiennej

Układ równań można zapisać w postaci macierzowej

1

1

1

2

2

1

1

1

n

n

i

i

i

i

n

n

n

i

i

i

i

i

i

i

n

x

y

p

p

x

x

x y



























 













 









 





















 



Z powyższego układu wyznaczamy brakujące parametry

p

1

,

p

2

 

X P

Y

1







P

X

Y

Gliwice 2010

Aproksymacja funkcji

jednej zmiennej - inna funkcja

aproksymująca

Gliwice 2010

Aproksymacja liniowa funkcji

dwóch zmiennych

Gliwice 2010

Aproksymacja liniowa funkcji dwóch zmiennych

Dany jest zbiór punktów:

Aproksymacją tego zbioru ma być funkcja liniowa

Kryterium metody najmniejszych kwadratów

1

1

1

2

2

2

( ,

, ), (

,

,

), ... , (

,

,

)

n

n

n

x y z

x y z

x

y z

1

2

3

1

2

3

( , ,

,

,

)

z

F x y p p p

p

p x

p y













2

1

2

3

1

2

3

1

(

,

,

)

= min

n

i

i

i

i

S p p p

p

p x

p y

z













Gliwice 2010

Aproksymacja liniowa funkcji dwóch zmiennych

Wykorzystujemy warunek konieczny istnienia ekstremum

funkcji trzech zmiennych

























1

2

3

1

2

3

1

1

1

2

3

1

2

3

1

2

1

2

3

1

2

3

1

3

,

,

2

0

,

,

2

0

,

,

2

0

n

i

i

i

i

n

i

i

i

i

i

n

i

i

i

i

i

S p p p

p

p x

p y

z

p

S p p p

p

p x

p y

z

x

p

S p p p

p

p x

p y

z

y

p









 



















 







 











 







 











Gliwice 2010

Aproksymacja liniowa funkcji dwóch zmiennych

Układ równań w postaci macierzowej

1

1

2

1

1

1

2

1

1

1

n

n

i

i

i

i

n

n

n

i

i

i

i

i

i

i

n

n

n

i

i

i

i

i

i

i

n

x

y

x

x

x y

y

x y

y











































































1

2

3

p

p

p

 

  

 

 

 

1

1

1

n

i

i

n

i i

i

n

i i

i

z

x z

y z





















































Z powyższego układu równań wyznacza się

1

2

3

,

,

p

p

p

Gliwice 2010