WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA WIT

REPETYTORIUM (2)

J.Sikorski

Strona 1 / 14

REPETYTORIUM Z KOMBINATORYKI

Relacja binarna

R

⊆

X

×

Y

Relacja binarna w zbiorze X:

R

⊆

X

×

X

Może być określona za pomocą:

zdania logicznego

xRy

⇔

   

y

x

=

,

zbioru par uporządkowanych

{(x, y), (x, x), ...},

grafu relacji

tablicy relacji

x y z ...

x 1 0 1

y 0 1 0

z 1 1 0

...

Cechy relacji binarnej w zbiorze X:

•

zwrotna,

jeśli

∀

x

∈

X : xRx

•

przechodnia,

jeśli

∀

x, y, z

∈

X : ( xRy

∧

yRz ) ⇒ xRz

•

symetryczna,

jeśli

∀

x, y

∈

X : xRy ⇒ yRx

•

antysymetryczna, jeśli

∀

x, y

∈

X : ( xRy

∧

yRx ) ⇒ x

=

y

Relacja równoważności jest zwrotna, przechodnia i symetryczna.

Relacja porządku jest zwrotna, przechodnia i antysymetryczna.

WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA WIT

REPETYTORIUM (2)

J.Sikorski

Strona 2 / 14

Dla zbioru skończonego | X |

=

n :

liczba wszystkich relacji binarnych w X wynosi

2

2

n

,

liczba wszystkich zwrotnych relacji w X wynosi

)

(

1

2

−

n

n

,

liczba wszystkich symetrycznych relacji w X wynosi

2

1

2

)

(

+

n

n

,

liczba wszystkich antysymetrycznych relacji w X wynosi

2

1

3

2

)

(

−

⋅

n

n

n

,

liczba wszystkich relacji równoważności w X wynosi B

n

(liczby Bella),

∑

=













=

n

k

n

k

n

B

0

;

i

n

i

n

B

i

n

B

⋅













=

∑

=

+

0

1

Każdej relacji równoważności E w zbiorze X można wzajemnie

jednoznacznie przyporządkować podział zbioru X na bloki:

X|E

=

{ a|E : a

∈

X } ,

gdzie pojedynczy blok a|E

=

{ b

∈

X : aEb } nazywany jest

klasą abstrakcji elementu a.

Jeżeli G jest grupą permutacji zbioru X, to szczególna rolę odgrywa

relacja indukowana w zbiorze X przez grupę G (oznaczana R

G

).

Relacja indukowana R

G

jest relacją równoważności.

Każdą z klas abstrakcji relacji indukowanej R

G

nazywamy orbitą

działania grupy G. Symbol o(G) oznacza liczbę orbit.

Zbiór orbit działania jest podziałem zbioru X na o(G) bloków.

∑

∈

=

G

p

p

Inv

G

G

o

)

(

)

(

1

,

gdzie Inv(p) jest liczbą niezmienników permutacji p

∈

G.

WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA WIT

REPETYTORIUM (2)

J.Sikorski

Strona 3 / 14

Relacja porządku

p

wraz ze zbiorem , w którym została

zdefiniowana tworzy zbiór uporządkowany (X,

p

).

Dwa elementy x, y

∈

X nazywamy porównywalnymi, jeśli x

p

y

lub y

p

x , w przeciwnym przypadku są one nieporównywalne.

Jeśli każde dwa elementy x, y

∈

X są porównywalne, to parę (X,

p

)

nazywamy zbiorem liniowo uporządkowanym.

W zbiorze uporządkowanym (X,

p

) wprowadzamy „ostrą” relację

x

p

y

⇔

x

p

y

∧

x

≠

y

Jeżeli dla dwóch elementów s, t

∈

X zachodzi s

p

t i nie istnieje taki

element u

∈

X , że s

p

u i u

p

t , to s nazywamy bezpośrednim

poprzednikiem t, a t – bezpośrednim następnikiem s.

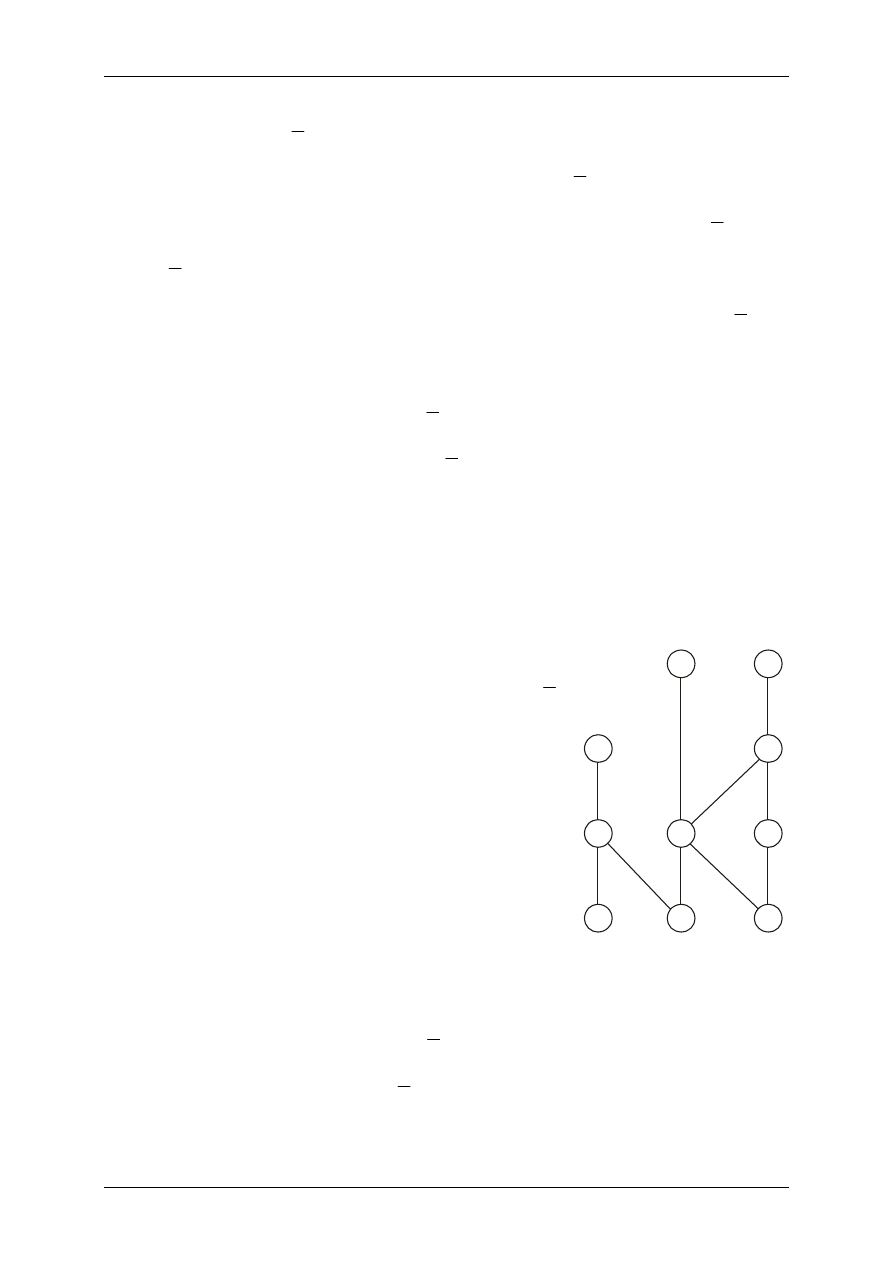
Wygodnym i czytelnym sposobem

przedstawienia zbioru uporządkowanego (X,

p

)

jest tzw. diagram Hassego, na którym łączymy

odcinkami tylko bezpośrednie poprzedniki z ich

następnikami i następniki umieszczamy

powyżej poprzedników.

Np.:

100

50

25

70

12

6

3

2

10

5

Element x

o

∈

X nazywamy elementem maksymalnym w zbiorze

częściowo uporządkowanym (X,

p

), jeśli w zbiorze X nie istnieje

element x

≠

x

o

, dla którego x

o

p

x .

WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA WIT

REPETYTORIUM (2)

J.Sikorski

Strona 4 / 14

Element x

o

∈

X nazywamy elementem minimalnym w zbiorze

częściowo uporządkowanym (X,

p

), jeśli w zbiorze X nie istnieje

element x

≠

x

o

, dla którego x

p

x

o

.

Element x

o

∈

X nazywamy elementem największym w zbiorze

częściowo uporządkowanym (X,

p

), jeśli dla każdego x

∈

X zachodzi

zależność x

p

x

o

.

Element x

o

∈

X nazywamy elementem najmniejszym w zbiorze

częściowo uporządkowanym (X,

p

), jeśli dla każdego x

∈

X zachodzi

zależność x

o

p

x .

W zbiorze częściowo uporządkowanym istnieje co najwyżej jeden

element największy i co najwyżej jeden element najmniejszy.

Przy tym element największy jest elementem maksymalnym, a element

najmniejszy jest elementem minimalnym.

Jeśli (X,

p

) jest zbiorem liniowo uporządkowanym oraz X jest

zbiorem skończonym i niepustym, to w (X,

p

) istnieją elementy

największy i najmniejszy.

Element x

o

∈

X nazywamy ograniczeniem dolnym zbioru A

⊆

X ,

jeśli dla każdego x

∈

A zachodzi zależność x

o

p

x .

Element x

o

∈

X nazywamy ograniczeniem górnym zbioru A

⊆

X ,

jeśli dla każdego x

∈

A zachodzi zależność x

p

x

o

.

Jeśli zbiór ograniczeń górnych zbioru A ma element najmniejszy, to

nazywamy go kresem górnym zbioru A i oznaczamy sup A .

WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA WIT

REPETYTORIUM (2)

J.Sikorski

Strona 5 / 14

Jeśli zbiór ograniczeń dolnych zbioru A ma element największy, to

nazywamy go kresem dolnym zbioru A i oznaczamy inf A .

Pokryciem zbioru X nazywamy taką rodzinę jego podzbiorów

{ Y

1

, Y

2

, ..., Y

k

} (Y

i

⊆

X), dla której zachodzi X

=

Y

1

∪

Y

2

∪

...

∪

Y

k

.

Mówimy, że rodzina { Y

1

, Y

2

, ..., Y

k

} pokrywa zbiór X.

Łańcuchem z zbiorze uporządkowanym (X,

p

) nazywamy taki

podzbiór L

⊆

X , w którym każde dwa elementy x, y

∈

L są

porównywalne, tzn. zawsze zachodzi x

p

y lub y

p

x .

Antyłańcuchem z zbiorze uporządkowanym (X,

p

) nazywamy taki

podzbiór A

⊆

X , w którym żadne dwa różne elementy x, y

∈

L nie są

porównywalne, tzn. zawsze zachodzi x

p

y

⇔

x

=

y .

W każdym skończonym zbiorze częściowo uporządkowanym (X,

p

)

maksymalna liczność antyłańcucha jest równa minimalnej liczbie

łańcuchów pokrywających zbiór X, a maksymalna liczność łańcucha

jest równa minimalnej liczbie antyłańcuchów pokrywających zbiór X.

Funkcja

f : X

→

→

→

→

Y

jest relacją binarną f

⊆

X

×

Y taką, że dla każdego x

∈

X istnieje

dokładnie jedna para postaci ( x, y

=

f (x) )

∈

f

Funkcja f jest injekcją (funkcją różnowartościową, „1

−

1”), jeśli

∀

x, y

∈

X x

≠

y ⇒ f (x)

≠

f (y)

Funkcja f jest surjekcją (funkcją „na”), jeśli

∀

y

∈

Y

∃

x

∈

X f (x)

=

y

WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA WIT

REPETYTORIUM (2)

J.Sikorski

Strona 6 / 14

Funkcja f jest bijekcją , jeśli jest jednocześnie injekcją i surjekcją.

Fun(X, Y) oznacza zbiór wszystkich funkcji z X w Y,

Inj(X, Y) oznacza zbiór wszystkich injekcji z X w Y,

Sur(X, Y) oznacza zbiór wszystkich surjakcji z X na Y,

Bij(X, Y) oznacza zbiór wszystkich bijekcji z X w Y,

Bij(X, Y)

=

Sur(X, Y)

∩

Inj(X, Y)

Dla zbiorów skończonych |

X

|

=

n i |

Y

|

=

m:

|

Fun(X, Y)

|

=

m

n

|

Inj(X, Y) |

=

m

n

(dla n

≤

m )

| Sur(X, Y) |

=













⋅

=

m

n

m

s

m

n

!

,

=

∑

−

=

−













−

1

0

1

m

i

n

i

i

m

i

m

)

(

)

(

|

Bij(X, Y)

|

=

n

n

=

n!

Zasada równoliczności pozwala rozstrzygać o liczbie elementów

jednego zbioru na podstawie liczby elementów drugiego po

skonstruowaniu bijekcji pomiędzy tymi zbiorami.

Jeżeli Bij(X, Y)

≠

∅

, to |

X

|

=

|

Y

|

=

n

Rozmieszczeniem uporządkowanym nazywamy wskazanie pewnej

funkcji f : X

→

Y wraz z określeniem uporządkowań we wszystkich

zbiorach f

−

1

({y}) dla y

∈

Y .

Liczba wszystkich rozmieszczeń uporządkowanych wynosi m

n

.

Przy zliczaniu funkcji f : X

→

Y stosujemy często zasadę mnożenia:

jeżeli X

=

X

1

∪

X

2

i Y

=

Y

1

∪

Y

2

oraz spełnione są warunki X

1

∩

X

2

=

∅

, f (

X

1

)

⊆

Y

1

i f (

X

2

)

⊆

Y

2

,

to

|

Fun(X, Y)

|

=

|

Fun(X

1

, Y

1

)

|

⋅

|

Fun(X

2

, Y

2

)

| ;

WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA WIT

REPETYTORIUM (2)

J.Sikorski

Strona 7 / 14

jeżeli ponadto Y

1

∩

Y

2

=

∅

,

to

|

Inj(X, Y)

|

=

|

Inj(X

1

, Y

1

)

|

⋅

|

Inj(X

2

, Y

2

)

| .

Jeżeli na zbiorze X zdefiniowano funkcję f w zbiór Y , to obowiązuje

także zasada szufladkowa:

jeżeli dla zbiorów X i Y zachodzi | X | > r

⋅

| Y | dla r > 0 , to

dla każdej funkcji f

∈

Fun(X, Y) warunek | f

−

1

({y}) | > r jest spełniony

dla co najmniej jednego y

∈

Y .

Permutacją zbioru X nazywamy bijekcję

p : X

→

X

|

Bij(X, X)

|

=

n!

S

n

oznacza zbiór wszystkich permutacji zbioru {1, 2, ..., n}.

Zbiór S

n

wraz z operacja składania permutacji tworzy grupę.

Operacja składania permutacji jest łączna, ale nie jest przemienna.

W zbiorze S

n

istnieje element neutralny operacji składania e

(permutacja identycznościowa) i dla każdego p

∈

S

n

istnieje element

odwrotny p

−

1

∈

S

n

(permutacja odwrotna).

Permutacja p może być określona za pomocą:

tablicy













=

4

1

2

3

5

5

4

3

2

1

p

,

grafu

1

4

5

2

3

.

WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA WIT

REPETYTORIUM (2)

J.Sikorski

Strona 8 / 14

Każdą permutację p

∈

S

n

można przedstawić w postaci złożenia

rozłącznych cykli:

p

=

[ 1, 5, 4 ] [ 2, 3 ]

Każdą permutację p

∈

S

n

można scharakteryzować przez podanie jej

typu:

n

n

λλλλ

λλλλ

λλλλ

...

2

1

2

1

, gdzie

λλλλ

i

oznacza liczbę cykli o długości i .

Parę (a

i

, a

j

), gdzie p(i

)

=

a

i

i p( j )

=

a

j

dla i

<

j

≤

n, nazywamy

inwersją permutacji p

∈

S

n

, jeśli a

i

>

a

j

.

I( p) oznacza liczbę wszystkich inwersji w permutacji p

∈

S

n

.

Znakiem permutacji p

∈

S

n

nazywamy liczbę

)

(

)

(

)

sgn(

p

I

p

1

−

=

.

Dla permutacji typu

n

n

λλλλ

λλλλ

λλλλ

...

2

1

2

1

jej znak





∑

−

=

=

2

1

2

1

n

j

j

f

λλλλ

)

(

)

sgn(

.

Znak cyklu o długości k jest równy (

−

1)

k

−

1

.

Dla permutacji p, s

∈

S

n

zachodzi równość sgn( p s)

=

sgn( p)

⋅

sgn(s).

Transpozycją nazywamy cykl o długości 2.

Transpozycją sąsiednią nazywamy cykl postaci [i, i

+

1].

Każdą permutację p

∈

S

n

można przedstawić w postaci złożenia

I( p) transpozycji sąsiednich, np. p

=

[2, 3] [3, 4] [4, 5] [1, 2].

Każda transpozycja ma znak równy –1.

Element i

∈

{1, 2, ..., n} nazywamy niezmiennikiem permutacji

p

∈

S

n

, jeśli p(i)

=

i.

Inv(p) oznacza liczbę niezmienników permutacji p.

Nieporządkiem nazywamy taką permutację p

∈

S

n

,

dla której Inv(p)

=

0.

D

n

oznacza zbiór wszystkich nieporządków w zbiorze S

n

.

WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA WIT

REPETYTORIUM (2)

J.Sikorski

Strona 9 / 14

| D

n

|

=

∑

=

−

n

i

i

i

n

0

1

!

)

(

!

Rodzina podzbiorów zbioru X:

(X)

=

{ Y : Y

⊆

X}

Każdy podzbiór Y

∈

(X) może być jednoznacznie określony przez

swój wektor charakterystyczny

ξ

( Y )

=

( b

1

, b

2

, ..., b

n

)

∈

{0, 1}

n

według wzoru:

b

x

Y

x

Y

i

i

i

=

∈
∉







1

0

jeśli

jeśli

,

dla X

=

{ x

1

, ..., x

n

}.

|

(X) |

=

2

n

Wektory charakterystyczne są wygodnym narzędziem do generowania

wszystkich elementów rodziny (X) .

Podzbiory k-elementowe zbioru X ( | X |

=

n ):

| { Y

∈

(X) : | Y |

=

k } |

=

k

k

n

n

n

k

n

k

n

k

n

k

n

k

⋅

⋅

⋅

+

−

−

=

−

=

=













...

)

(

...

)

(

)!

(

!

!

!

2

1

1

1

n

k

n

n

k











=

−











,

n

k

n

k

n

k











=

−











+

−
−











1

1

1

,

n

i

i

n

n











=

=

∑

0

2 ,

n

i

i

n

i

n

n











=

=

−

∑

0

1

2

,

Rozbiciem zbioru X na m podzbiorów o zadanych liczbach

elementów k

1

, k

2

, ..., k

m

nazywamy taką rodzinę rozłącznych zbiorów

{ X

1

, X

2

, ..., X

m

}, dla której spełnione są warunki:

m

X

X

X

X

∪

∪

∪

=

...

2

1

,

∅

=

∩

j

i

X

X

dla 1

≤

i

<

j

≤

m i

i

i

k

X

=

.

Liczba wszystkich rozbić zbioru X wynosi:

!

...

!

!

!

...

m

m

k

k

k

n

k

k

k

n

⋅

⋅

⋅

=













2

1

2

1

WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA WIT

REPETYTORIUM (2)

J.Sikorski

Strona 10 / 14

Zbiór z powtórzeniami

A

=

< k

1

∗

x

1

, ..., k

n

∗

x

n

>

określony jest przez podanie wektora krotności (k

1

, ..., k

n

) dla zbioru

bazowego X

=

{ x

1

, ..., x

n

}.

Liczba elementów w zbiorze z powtórzeniami A wynosi

| A |

=

k

1

+

...

+

k

n

Liczba wszystkich podzbiorów zbioru z powtórzeniami A wynosi

( k

1

+

1)

⋅

( k

2

+

1)

⋅

...

⋅

( k

n

+

1)

Liczba k-elementowych podzbiorów zbioru z powtórzeniami

< k

∗

x

1

, ..., k

∗

x

n

> (szczególny przypadek k

i

=

k) wynosi













−

+

=

k

k

n

k

n

k

1

!

Funkcja tworząca dla ciągu liczb podzbiorów k-elementowych

zbioru z powtórzeniami A ma postać

A(x)

=

∑

=

A

k

k

k

x

c

0

=

(1

+

x

+

...

+

1

k

x )

⋅

...

⋅

(1

+

x

+

...

+

n

k

x

) ;

c

k

jest liczbą podzbiorów k-elementowych zbioru z powtórzeniami A.

Liczba całkowitych nieujemnych rozwiązań liniowego równania

diofantycznego x

1

+

x

2

+

...

+

x

n

=

k dla całkowitego i nieujemnego

k wynosi













−

+

=

k

k

n

k

n

k

1

!

Podziałem zbioru X ( | X |

=

n ) na k bloków nazywamy taką

rodzinę niepustych zbiorów

π

=

{ A

1

, ..., A

k

} , dla której zachodzi

X

=

A

1

∪

...

∪

A

k

, A

i

∩

A

j

=

∅

dla 1

≤

i

<

j

≤

k oraz A

i

≠

∅

.

WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA WIT

REPETYTORIUM (2)

J.Sikorski

Strona 11 / 14

Π

k

(X) oznacza zbiór wszystkich podziałów zbioru X na k bloków.

Π

(X) oznacza zbiór wszystkich podziałów zbioru X.

|

Π

k

(X) |

=













k

n

(liczby Stirlinga 2 rodzaju)













k

n

=













−

−

1

1

k

n

+

k













−

k

n 1

, dla 0 < k < n













n

n

=

1,













0

n

=

0 dla n

≥

0;













1

n

=

1, dla n > 0

∑

∑

−

=

−

=

⋅

−

−

−

=

−













−

=













1

0

1

0

1

1

1

m

i

n

i

m

i

n

i

i

i

m

i

m

i

m

i

m

m

m

n

!

)!

(

)

(

)

(

)

(

)

(

!

∑

∑

=

−

=

⋅













⋅

−

=

⋅













=

n

k

k

k

n

n

k

k

n

m

k

n

m

k

n

m

0

0

1)

(

zachodzi dla m, n

∈

|

Π

(X)|

=

∑

=













=

n

k

n

k

n

B

0

(liczby Bella)

i

n

i

n

B

i

n

B

⋅













=

∑

=

+

0

1

Każdemu podziałowi

π

∈

Π

(X) można jednoznacznie przyporząd-

kować relację równoważności E(

π

) w zbiorze X , definiując ją jako

U

π

π

∈

×

=

A

A

A

E

)

(

tzn. dwa elementy x, y

∈

X są w relacji E(

π

), czyli x E(

π

) y

wtedy i tylko wtedy, kiedy x i y należą do tego samego bloku podziału.

Podziałem liczby n na k składników ( n, k

∈

{ 1, 2, ... } ) nazywamy

taki skończony ciąg całkowity a

1

, a

2

, ..., a

k

, dla którego zachodzi

WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA WIT

REPETYTORIUM (2)

J.Sikorski

Strona 12 / 14

n

=

a

1

+

...

+

a

k

i a

1

≥

a

2

≥

...

≥

a

k

> 0

P(n, k) oznacza liczbę podziałów liczby n na k składników.

P(n)

=

∑

=

n

k

k

n

P

1

)

,

(

oznacza liczbę wszystkich podziałów liczby n.

P

k

(n) oznacza liczbę podziałów liczby n o największym składniku

równym k.

P(n, k)

=

P

k

(n) ,

dla k

≤

n

P(n, k)

=

P(n

−

1, k

−

1)

+

P(n

−

k, k) dla n

≥

k > 0

P(0, 0)

=

P(0)

=

1

P(n, k)

=

∑

=

−

k

i

i

k

n

P

0

)

,

(

i P

k

(n)

=

∑

=

k

i

i

n

P

1

)

,

(

dla n

≥

k > 0

Zasada włączania-wyłączania to sposób wyznaczania liczby

elementów w sumie mnogościowej skończonej liczby zbiorów

(niekoniecznie rozłącznych):

| A

∪

B |

=

| A |

+

| B |

−

| A

∩

B |

| A

∪

B

∪

C |

=

=

| A |

+

| B |

+

| C |

−

| A

∩

B |

−

| A

∩

C |

−

| B

∩

C |

+

| A

∩

B

∩

C |

∑

∑

⊆

=

−

=

∩

∩

∩

−

=

}

,...,

{

}

,...,

,

{

|

...

|

)

(

n

p

p

p

p

p

p

n

i

i

n

i

i

i

i

A

A

A

A

1

1

1

1

2

1

2

1

1

U

Funkcją tworzącą dla ciągu liczbowego (a

i

)

=

(a

0

, a

1

, a

2

, ..., a

i

, ... )

nazywamy szereg potęgowy

∑

∞

=

=

0

i

i

i

z

a

z

A )

(

dla zmiennej zespolonej z.

WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA WIT

REPETYTORIUM (2)

J.Sikorski

Strona 13 / 14

Funkcje tworzące wybranych ciągów:

Ciąg

Funkcja tworząca

(1, 8, 28, 56, 70, 56, 28, 8, 1, 0, 0, ...),













=

i

a

i

8

(1

+

z)

8

(0, ..., 0, 1, 0, ...., 0, ... ), a

n

=

1 i a

i

=

0 dla i

≠

n

z

n

(1, 1, ..., 1, ... ), a

i

=

1 dla i

=

0, 1, ...

z

−

1

1

(c

0

, c

1

, c

2

, ..., c

i

, ... ), a

i

=

c

i

dla i

=

0, 1, ...

z

c

⋅

−

1

1

Operacjom na ciągach odpowiadają operacje na funkcjach tworzących:

Operacja na ciągu

Operacja na funkcjach

tworzących

mnożenie przez liczbę:

(a

i

)

→

(c

⋅

a

i

)

A(z)

→

c

⋅

A(z)

dodawanie ciągów:

(a

i

), (b

i

)

→

(a

i

+

b

i

)

A(z), B(z)

→

A(z)

+

B(z)

przesunięcie w prawo o m pozycji:

(a

i

)

→

(0, ..., 0, a

0

, a

1

, a

2

, ..., a

i

, ... )

(a

i

=

0 dla i

=

0, 1, ..., m

−

1)

A(z)

→

z

m

⋅

A(z)

Za pomocą funkcji tworzącej można otrzymać nierekurencyjny wzór

na kolejny wyraz ciągu Fibonacciego.

Wzór rekurencyjny:

F

i

=

F

i

−

1

+

F

i

−

2

+

i

=

1

dla i

=

0, 1, 2, 3, ... (F

i

=

0 dla i < 0)

Równanie dla funkcji tworzącej:

WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA WIT

REPETYTORIUM (2)

J.Sikorski

Strona 14 / 14

F(z)

=

z

2

⋅

F(z)

+

z

⋅

F(z)

+

z

Funkcja tworząca:

∑

∞

=

=

−

−

=

0

2

1

i

i

i

z

F

z

z

z

z

F

)

(

Wzór na kolejne wyrazy ciągu:



























−

−













+

=

i

i

i

F

2

5

1

2

5

1

5

1

dla i

=

0, 1, 2, ...

Za pomocą funkcji tworzącej można rozwiązać rekurencyjne równanie

dla złożoności rekurencyjnego algorytmu dla problemu wież Hanoi.

Wzór rekurencyjny:

T

i

=

2

⋅

T

i

−

1

+

1

−

i

=

0 dla i

=

0, 1, 2, ... (T

i

=

0 dla i < 0)

Równanie dla funkcji tworzącej:

T(z)

=

2

z

⋅

T(z)

+

z

−

1

1

−

1

Funkcja tworząca:

)

)(

(

)

(

z

z

z

z

T

2

1

1

−

−

=

Wzór na zależność liczby ruchów od liczby krążków:

T

i

=

2

i

– 1 dla i

=

0, 1, 2, ...