Matematyka dyskretna – dr Marcin Raniszewski, dr inż. Witold Staszewski 

Matematyka Dyskretna – ćw. 5 

Kombinatoryka 1 

Zasada włączeń i wyłączeń, prawo mnożenia, 

wariacje i kombinacje 

 

Zasada włączeń i wyłączeń dla dwóch skończonych zbiorów: 

                              

Zasada włączeń i wyłączeń dla trzech skończonych zbiorów: 

                                                                          

Prawo mnożenia (dla zbiorów skończonych): 

  

 

   

 

       

 

      

 

      

 

          

 

  

Zad. 1. Ile jest liczb trzycyfrowych podzielnych przez 8 lub 12? 

Zad. 2. Ile jest liczb czterocyfrowych podzielnych przez 3 lub 11 lub 12? 

Zad.  3.  Niech: 

                        ,                   

 

         

 

     ,     

                                          

 

   

 

 . Oblicz liczbę elementów zbioru          . 

Niech dany będzie zbiór 

 

 

 złożony z n elementów. 

k-elementową  (

     )  wariacją  bez  powtórzeń   

 

 

  ze  zbioru 

 

 

  nazywamy  każdy  k-elementowy  ciąg 

utworzony z elementów zbioru 

 

 

 taki, że elementy w tym ciągu nie mogą się powtarzać. 

Liczba wszystkich k-elementowych wariacji bez powtórzeń ze zbioru 

 

 

 wyraża się wzorem: 

  

 

 

   

  

        

                                

Jeśli 

      to wariację bez powtórzeń nazywamy permutacją  

 

 zbioru 

 

 

. Czyli: 

 

 

   

 

 

. 

Liczba wszystkich permutacji zbioru 

 

 

 wyraża się wzorem: 

  

 

      

 

 

   

  

        

 

  
  

     

k-elementową  wariacją  z  powtórzeniami 

 

 

 

  ze  zbioru 

 

 

  nazywamy  każdy  k-elementowy  ciąg  utworzony 

z elementów zbioru 

 

 

 taki, że elementy w tym ciągu mogą się powtarzać. 

Liczba wszystkich k-elementowych wariacji z powtórzeniami ze zbioru 

 

 

 wyraża się wzorem: 

  

 

 

     

 

 

 

Matematyka dyskretna – dr Marcin Raniszewski, dr inż. Witold Staszewski 

k-elementową (

     ) kombinacją bez powtórzeń  

 

 

 ze zbioru 

 

 

 nazywamy każdy k-elementowy podzbiór 

utworzony z elementów zbioru 

 

 

. Skoro podzbiór, to elementy nie mogą się powtarzać. 

Liczba wszystkich k-elementowych kombinacji bez powtórzeń ze zbioru 

 

 

 wyraża się wzorem: 

  

 

 

     

 

    

  

           

 

k-elementową  kombinacją  z  powtórzeniami 

 

 

 

  ze  zbioru 

 

 

  nazywamy  każdy  k-elementowy  wielozbiór 

utworzony z elementów zbioru 

 

 

. Skoro wielozbiór, to elementy mogą się powtarzać. 

Liczba wszystkich k-elementowych kombinacji z powtórzeniami ze zbioru 

 

 

 wyraża się wzorem: 

  

 

 

              

 

   

            

           

 

 

Zad. 4. Na ile sposobów można sześć z dziesięciu osób wpisać na numerowaną listę? Na ile 
sposobów można ich wszystkich wpisać na numerowaną listę? 

Zad. 5. Ile zostanie rozegranych meczów w turnieju szachowym dziesięciu zawodników gdzie 
każdy grał z każdym dokładnie jeden raz? 

Zad.  6.  Ile  symboli  można  zakodować  w  alfabecie 

            używając  co  najwyżej  6 

znaków tego alfabetu? 

Zad.  7.  Na  ile  sposobów  można  pomalować  czterema  kolorami  sześć  nierozróżnialnych 
przedmiotów? 

Zad. 8. Ile jest dziewięciocyfrowych numerów rozpoczynających się od „609” zawierających 
dokładnie raz sekwencję „609”? 

Zad. 9. Ile jest pięciocyfrowych liczb parzystych, które mają dokładnie dwie cyfry parzyste? 

Zad.  10.  Ile  jest  sześciocyfrowych  liczb  nieparzystych  o  różnych  cyfrach,  które  mają 
dokładnie trzy cyfry parzyste? 

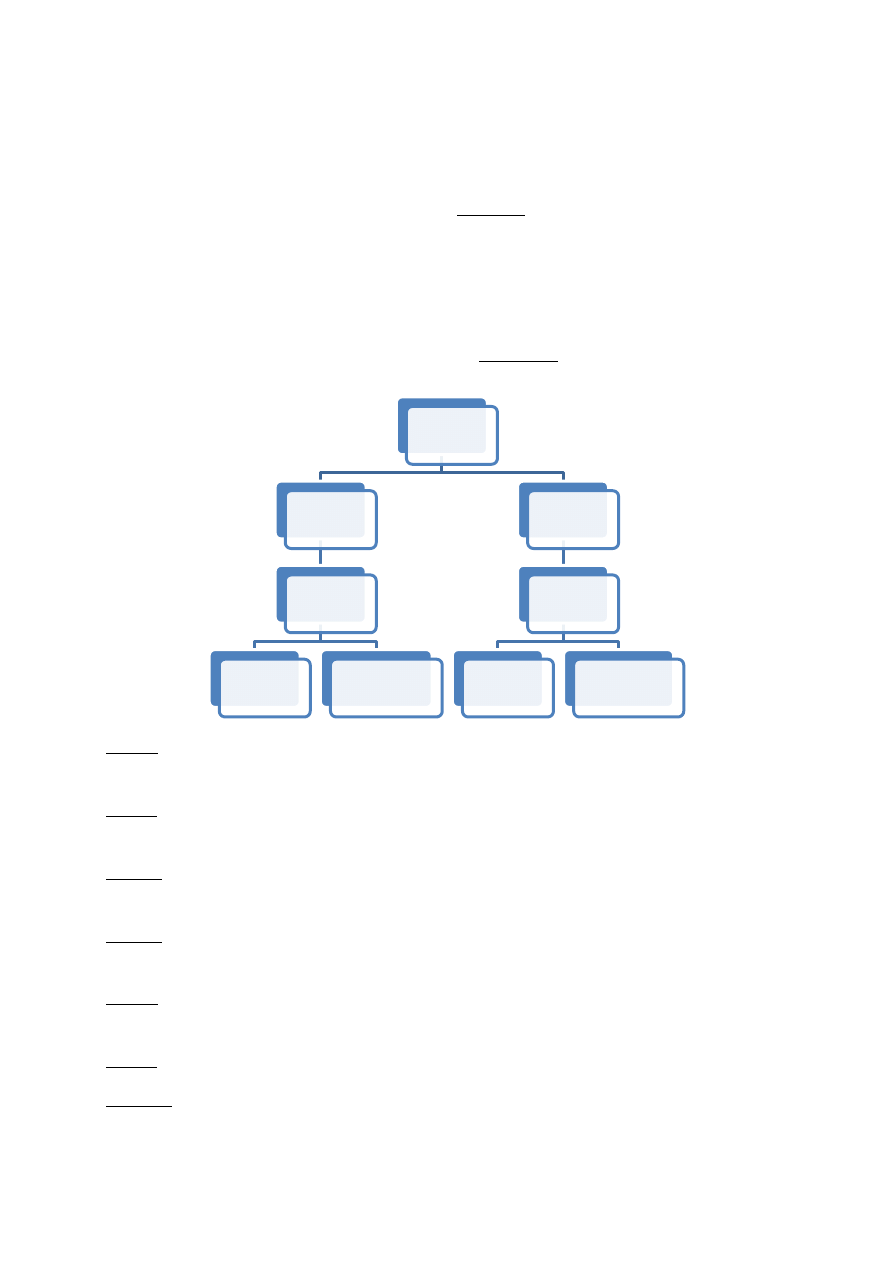
Czy liczy się 

kolejność? 

Nie 

Kombinacje 

Czy są 

powtórzenia? 

Nie 

Kombinacje 

bez powtórzeń 

Tak 

Kombinacje 

z powtórzeniami 

Tak 

Wariacje 

Czy są 

powtórzenia? 

Nie 

Wariacje 

bez powtórzeń 

Tak 

Wariacje 

z powtórzeniami