KATEDRA DRÓG I MOSTÓW

WYDZIAŁ BUDOWNICTWA

POLITECHNIKA OPOLSKA

Ćwiczenie z

Hydrauliki i Hydrologii

nr 5/a

Edyta Janota

rok III; grupa3

rok akademicki

2009/2010

I.

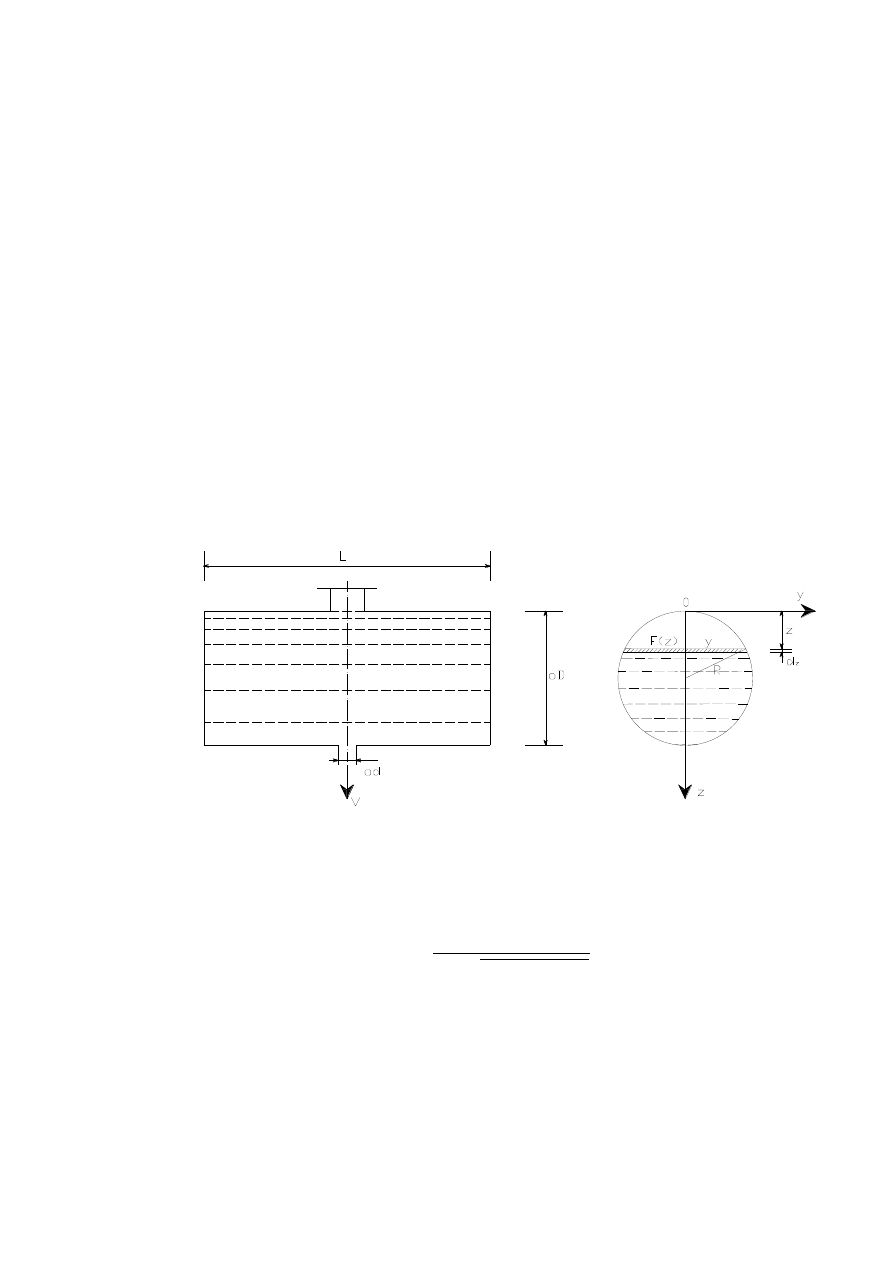
DANE:

𝑑 = 0,1 𝑚
𝐿 = 8 𝑚
𝐻 = 𝐷 = 3 𝑚
𝑔 = 9,81 𝑚/𝑠

2

II.

SZUKANE:

𝑡

𝑐

III.

ROZWIĄZANIE:

Elementarny czas wypływu:

𝑑𝑡 =

𝐹 𝑧 𝑑𝑧

𝑓 ∗ 2𝑔 ∗ (𝐻 − 𝑧)

Całkowity czas wypływu stanowi całkę czasu elementarnego,
zatem:

𝑡

𝑐

= 𝑑𝑡 =

𝐹 𝑧

𝑓 ∗ 2𝑔 ∗ (𝐻 − 𝑧)

𝑑𝑧

𝑡

𝑐

=

1

𝑓 2𝑔

𝐹 𝑧

𝐻 − 𝑧

𝑑𝑧

Z warunków zadania wzór na całkowity czas wypływu przyjmuje
postać:

𝑡

𝑐

=

1

𝑓 2𝑔

𝐹 𝑧

𝐻 − 𝑧

𝑑𝑧

𝐻

0

Wyznaczenie wartości f oraz F(z)

𝑓 =

𝜋𝑑

2

4

𝐹 𝑧 = 2𝑦 ∗ 𝐿

Korzystając z twierdzenia Pitagorasa można wyznaczyć wielkość y

𝐷

2

2

= 𝑦

2

+

𝐷

2

− 𝑧

2

Przekształcając powyższe równanie y wynosi:

𝑦 = 𝑧 ∗ (𝐷 − 𝑧)

Zatem F(z):

𝐹 𝑧 = 2 𝑧 ∗ (𝐷 − 𝑧) ∗ 𝐿

Podstawiając otrzymane wyniki, t

c

stanowi:

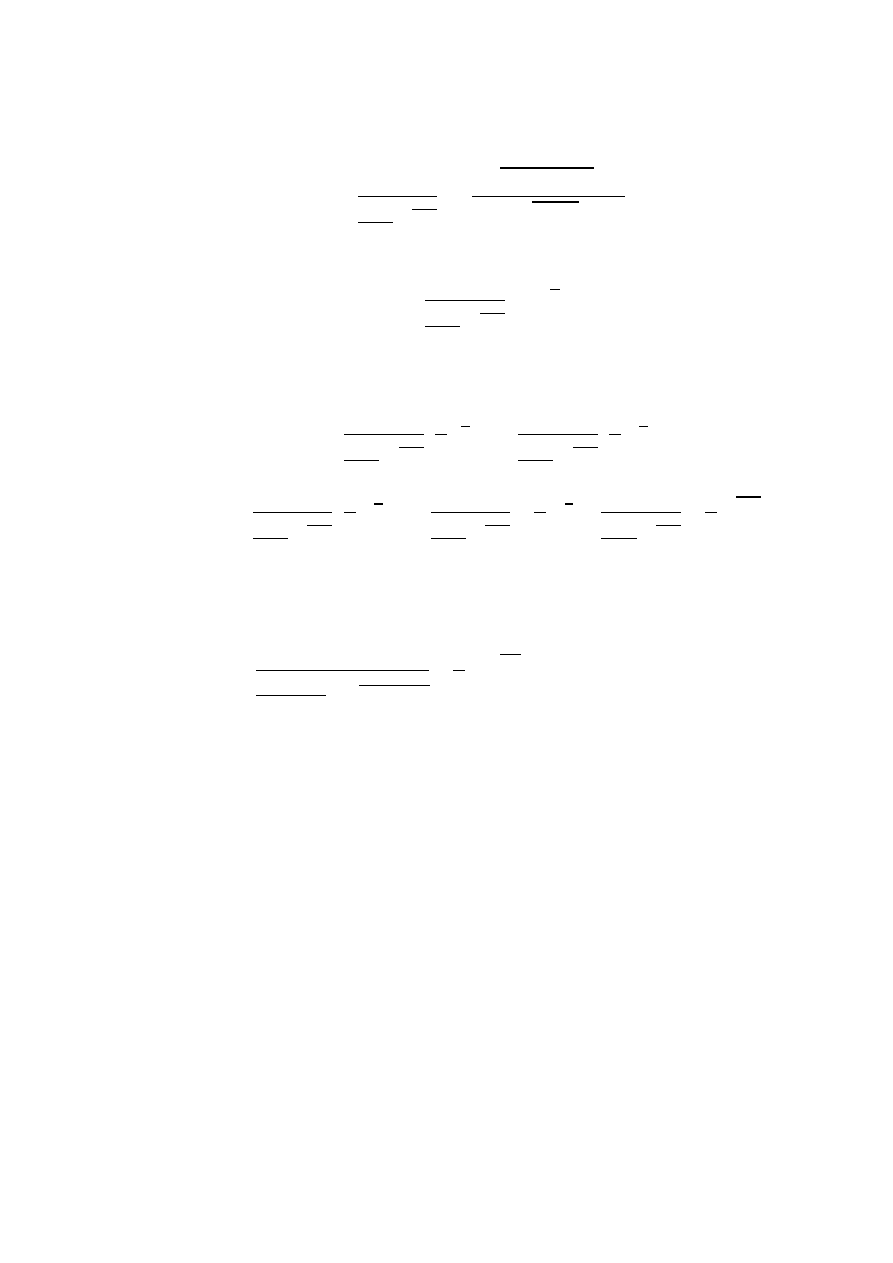
𝑡

𝑐

=

1

𝜋𝑑

2

4

2𝑔

2 𝑧 ∗ (𝐷 − 𝑧) ∗ 𝐿

𝐷 − 𝑧

𝑑𝑧

𝐷

0

𝑡

𝑐

=

2𝐿

𝜋𝑑

2

4

2𝑔

𝑧𝑑𝑧

𝐷

0

𝑡

𝑐

=

2𝐿

𝜋𝑑

2

4

2𝑔

2
3

𝑧

3
2

0

𝐷

=

2𝐿

𝜋𝑑

2

4

2𝑔

2
3

𝐷

3
2

0

𝐷

𝑡

𝑐

=

2𝐿

𝜋𝑑

2

4

2𝑔

2
3

𝐷

3
2

0

𝐷

=

2𝐿

𝜋𝑑

2

4

2𝑔

∗

2
3

𝐷

3
2

=

2𝐿

𝜋𝑑

2

4

2𝑔

∗

2
3

𝐷

3

Zatem czas wypływu będzie równy:

𝑡

𝑐

=

2 ∗ 8

𝜋 ∗ 0,1

2

4

∗ 2 ∗ 9,81

∗

2
3

∗ 3

3

= 1593 𝑠 ≈ 26,5 [𝑚𝑖𝑛]

IV.

ODPOWIEDŹ:
Czas wypływu benzyny z cysterny kolejowej wyniesie około 26,5
minuty.