Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Studium inżynierskie

Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, Prof. Antoni Kozioł

OGÓLNOTECHNICZNE

PODSTAWY BIOTECHNOLOGII

Z GRAFIKĄ INŻYNIERSKĄ

Wykład IX i X

Zasady termodynamiki

Proste przemiany termodynamiczne

Obiegi termodynamiczne

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

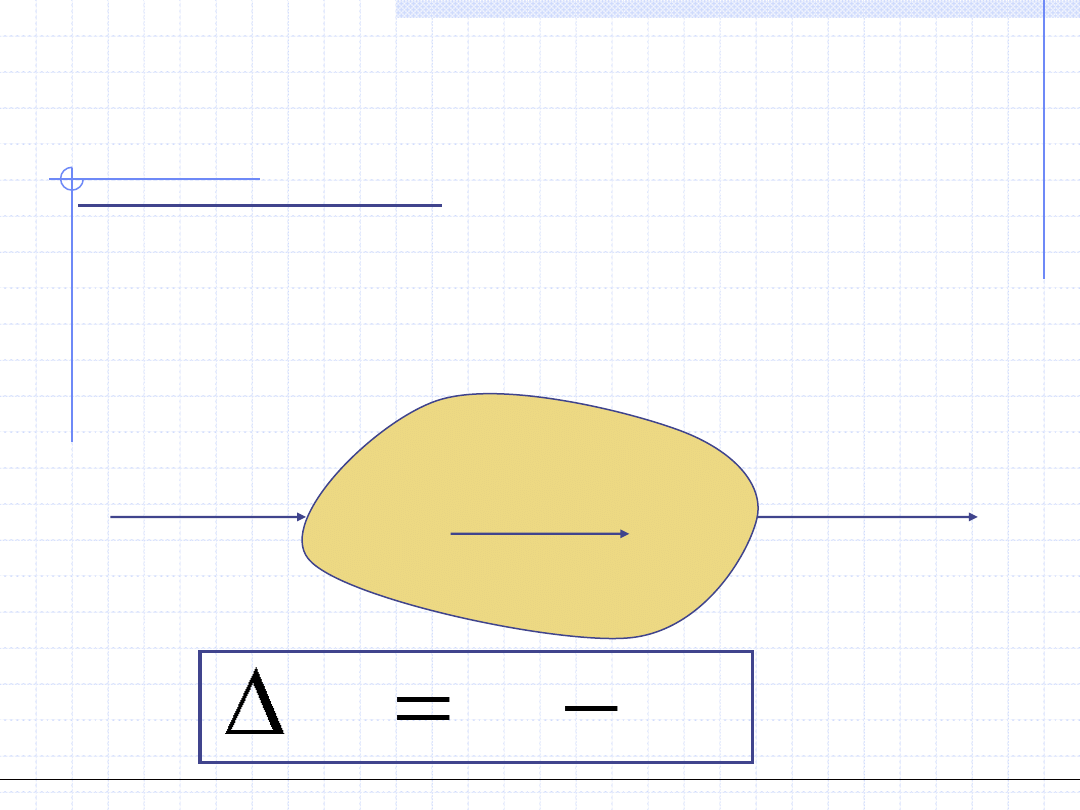
I ZASADA TERMODYNAMIKI

I zasada termodynamiki jest to w swojej istocie prawo zachowania

energii sformułowane dla dowolnej przemiany układu termodynamicznego.

I zasadę można formułować dla układów zamkniętych i otwartych.

Istnieje bardzo wiele matematycznych zapisów tej zasady. Przykładowo

napiszmy tą zasadę dla całkowej (nieróżniczkowej) przemiany układu

zamkniętego bazując na energii wewnętrznej.

Stan 1

U

1

Stan 2

U

2

ΔU=U

2

-U

1

Q

W

W

Q

U

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

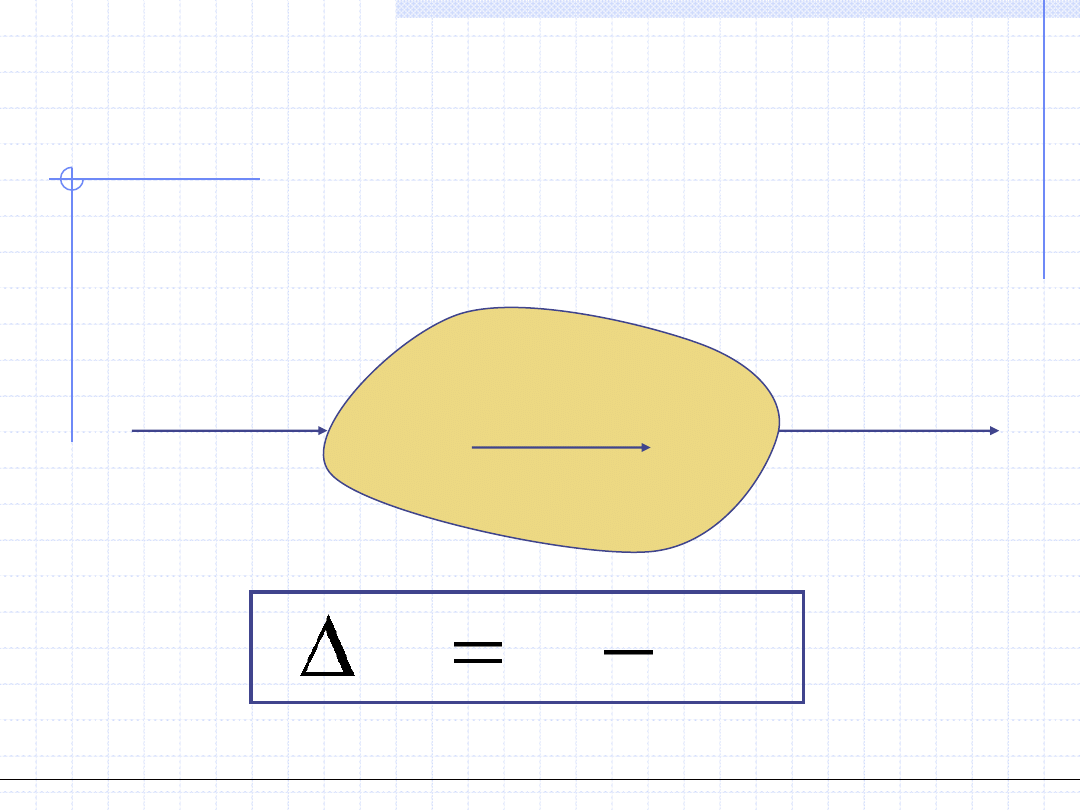
I ZASADA TERMODYNAMIKI

Stosunkowo często I zasada jest formułowana na bazie entalpii.

W takim przypadku w bilansie energetycznym zamiast pracy

objętościowej używa się pracy technicznej

Stan 1

H

1

Stan 2

H

2

ΔH=H

2

-H

1

Q

W

t

t

W

Q

H

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

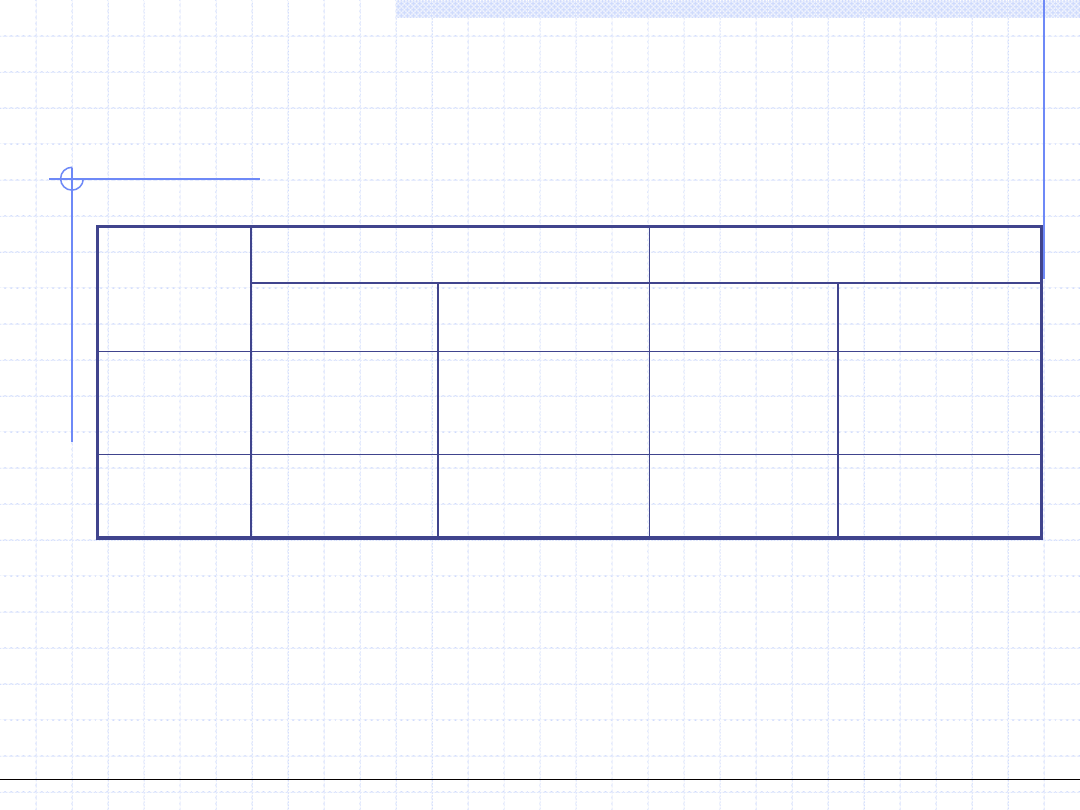
INNE SFORMUŁOWANIA PIERWSZEJ

ZASADY TERMODYNAMIKI

dh=δq-δw

t

Δh=q-w

t

dH=δQ-δW

t

ΔH=Q-W

t

Baza:

Entalpia

du=δq-δw

Δu=q-w

dU=δQ-δW

ΔU=Q-W

Baza:

Energia

wewnętrzna

Przem. różnicz.

Przem. całk.

Przem. różniczk.

Przem.

całkowa

Wielkości właściwe

Wielkości ekstensywne

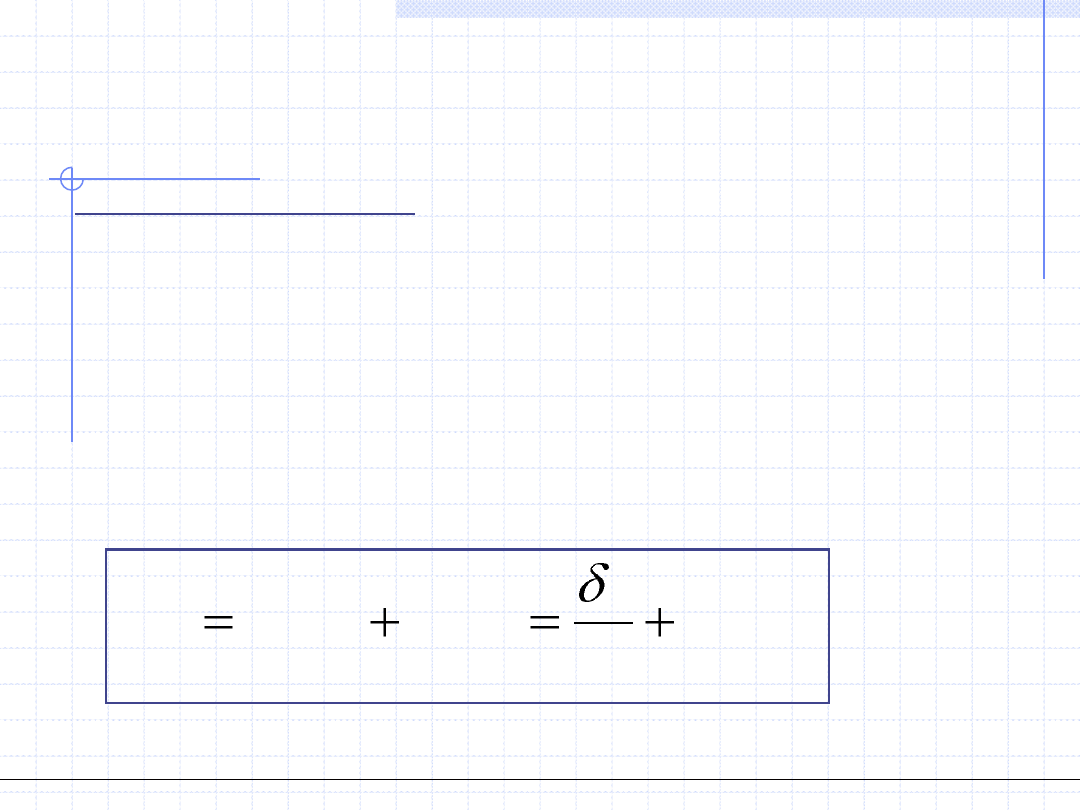
Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

II ZASADA TERMODYNAMIKI

II zasada termodynamiki posiada ogromną liczbę bardzo różnych sformułowań.

Dla celów termodynamiki procesowej podam sformułowanie oparte na tzw.

nierówności Clausiusa. Sformułowanie to opisuje zjawisko nieodwracalności

przemian termodynamicznych oraz uwzględnia klasyczną definicję entropii.

Załóżmy, że układ ulega dowolnej (odwracalnej lub nieodwracalnej) różniczkowej

przemianie termodynamicznej. W tej przemianie układ wymienia z otoczeniem

ciepło δq. W czasie przemiany zmieniać się mogą wszystkie parametry stanu.

Zmiana entropii wyniesie ds. Istnieją dwie przyczyny zmiany entropii:

1 - zmiana stanu energetycznego układu związana z wymianą ciepła,

2 - zmiana liczby dostępnych stanów energetycznych związana z

nieodwracalnymi efektami przemiany. Fakt ten można zapisać równaniem:

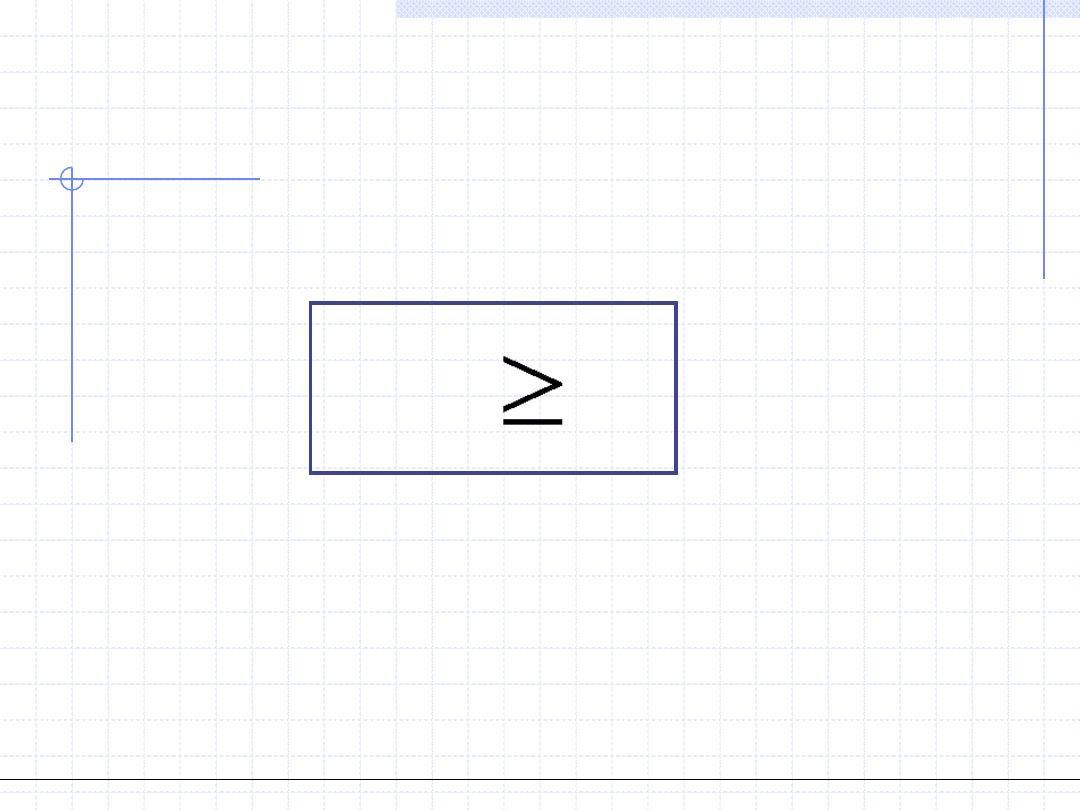
i

i

r

ds

T

q

ds

ds

ds

)

(

)

(

)

(

r – oznacza zmiany związane z odwracalnością przemiany (reversible)

i – oznacza zmiany związane z nieodwracalnością przemiany (irreversible)

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

II ZASADA TERMODYNAMIKI cd.

Nierówność Clausiusa dotyczy tej części zmiany entropii, która jest związana

z nieodwracalnością przemian i stanowi jedno z wielu sformułowań II zasady
termodynamiki.

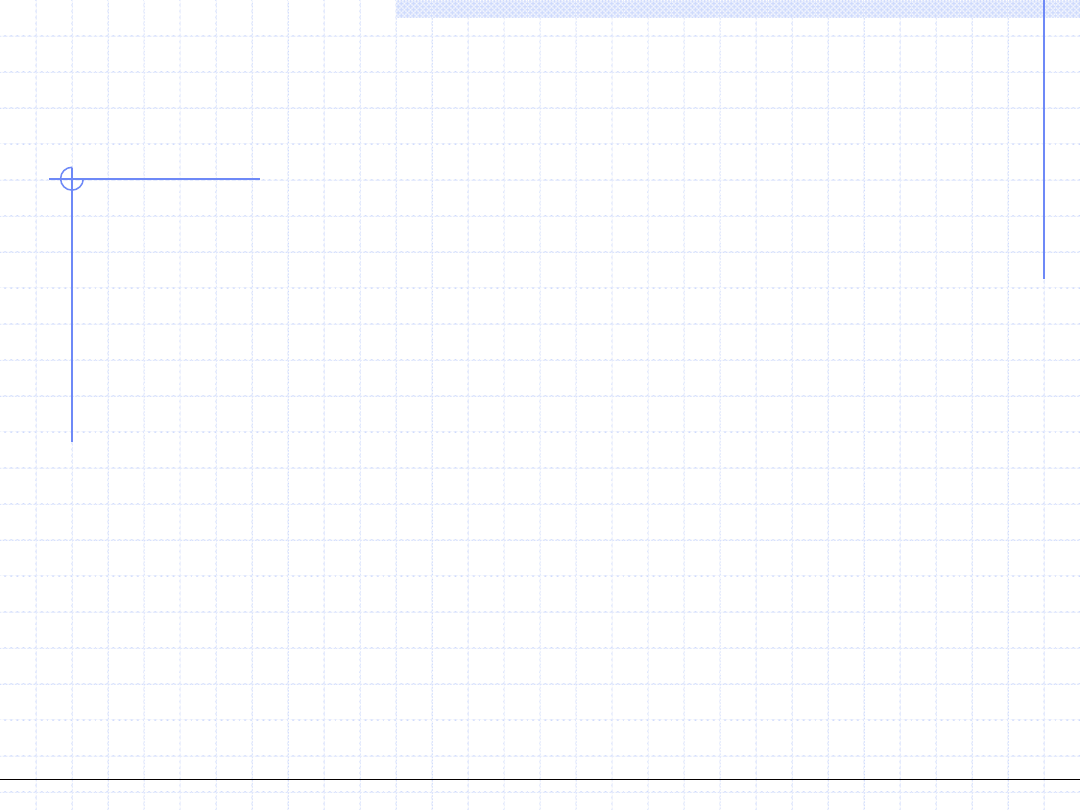
0

i

ds

Słownie oznacza to, że każda nieodwracalność powoduje wzrost entropii.

Ponieważ wszystkie przemiany samorzutne (odbywające się bez ingerencji

z zewnątrz) są nieodwracalne, z nierówności Clausiusa wynika, że w takich

przemianach entropia rośnie osiągając wartość maksymalną w stanie

równowagi, w którym mogą zachodzić tylko przemiany odwracalne.

Równość zachodzi tylko

w przypadku przemian

odwracalnych

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

Proste przemiany

termodynamiczne

Spośród bardzo wielu możliwych przemian termodynamicznych szczególną

rolę odgrywają przemiany spełniające pewien prosty warunek. Warunek

ten najczęściej określa stałość określonego parametru lub funkcji stanu.

W nazwie stałość ta jest opisana za pomocą przedrostka „izo”.

Mamy zatem następujące przemiany proste:

1. Przemiana izochoryczna – V=const.

2. Przemiana izobaryczna – p=const.

3. Przemiana izotermiczna – T=const.

4. Przemiana izentropowa – S=const. (przemiana adiabatyczna)

5. Przemiana politropowa – C=const.

Teraz omówimy po kolei omówimy poszczególne przemiany.

Przemiany te będziemy ilustrować wykresami w układzie p – v

tzn. ciśnienie – objętość właściwa (będziemy zakładać przemiany

w układach zamkniętych czyli n=const.)

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

Przemiana izochoryczna

.)

(

0

0

.

1

2

1

2

const

n

dla

v

v

dv

V

V

dV

const

V

0

0

0

0

.

w

w

pdv

w

dv

const

v

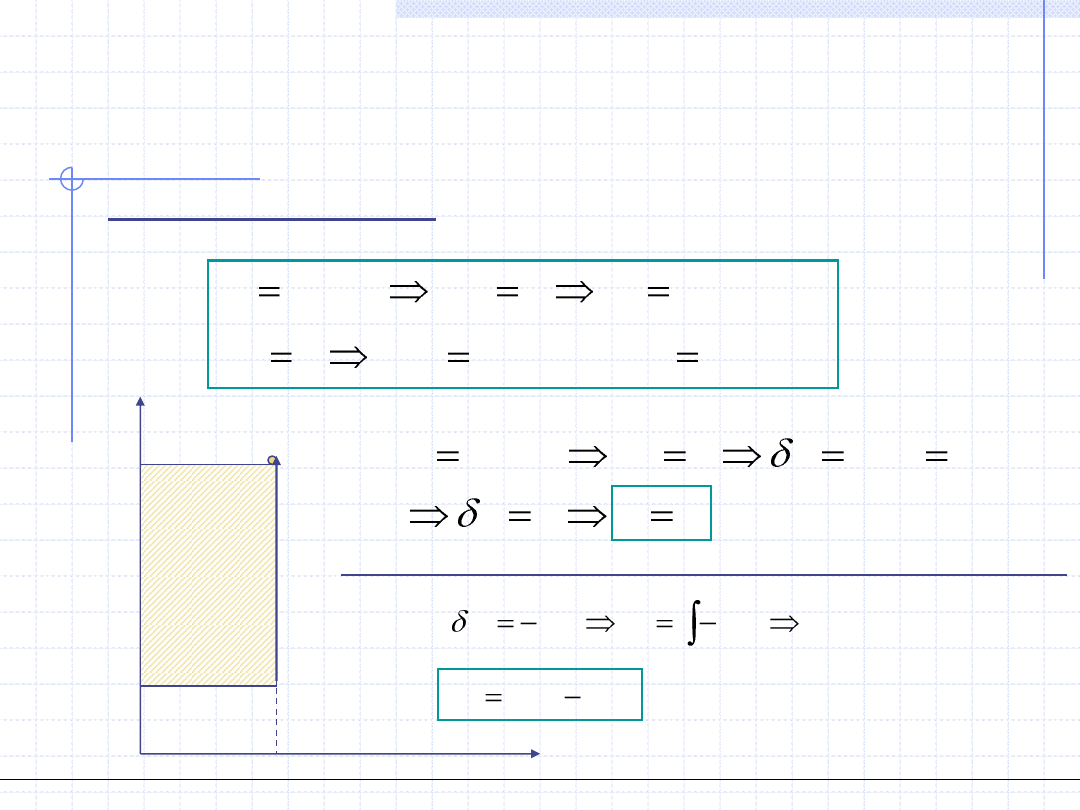
Przemiana izochoryczna odbywa się przy stałej objętości:

p

v

w

t

v=const.

p

1

,T

1

p

2

,T

2

Praca objętościowa w przemianie izochorycznej jest równa 0.

)

(

2

1

2

1

p

p

v

w

vdp

w

vdp

w

t

p

p

t

t

Wartość pracy technicznej przemiany

izochorycznej jest równa polu

zakreskowanego prostokąta.

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

Przemiana izochoryczna cd.

du

q

w

w

du

q

0

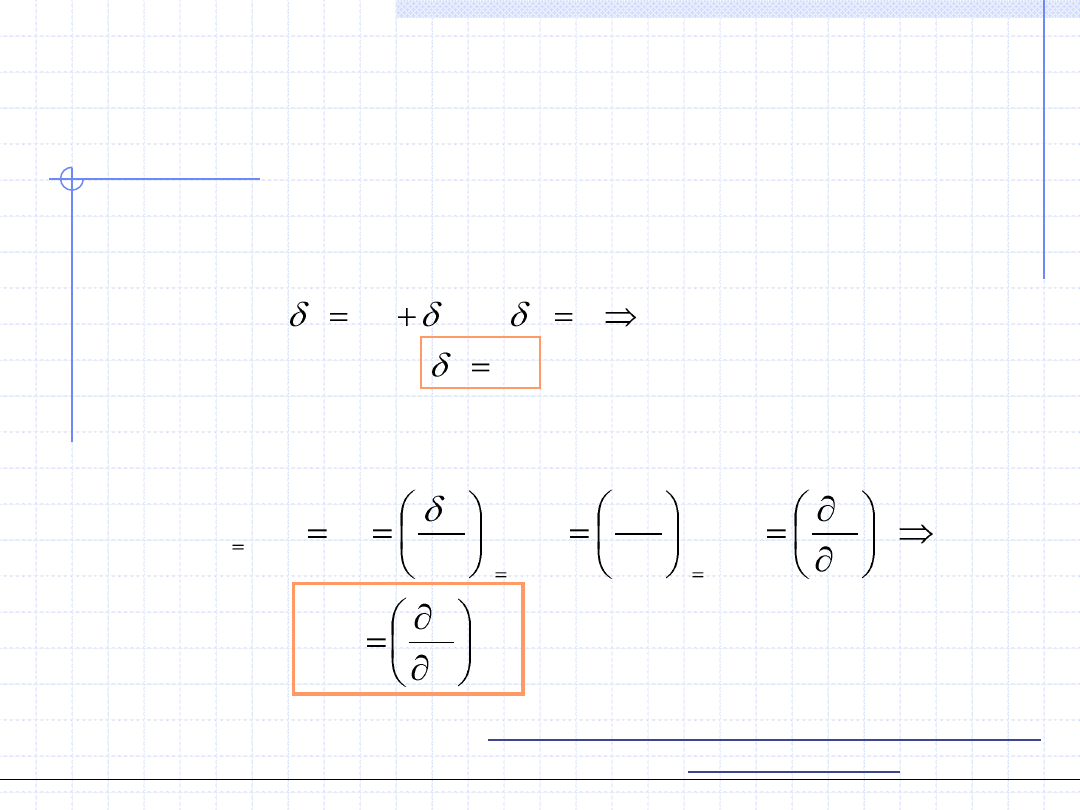
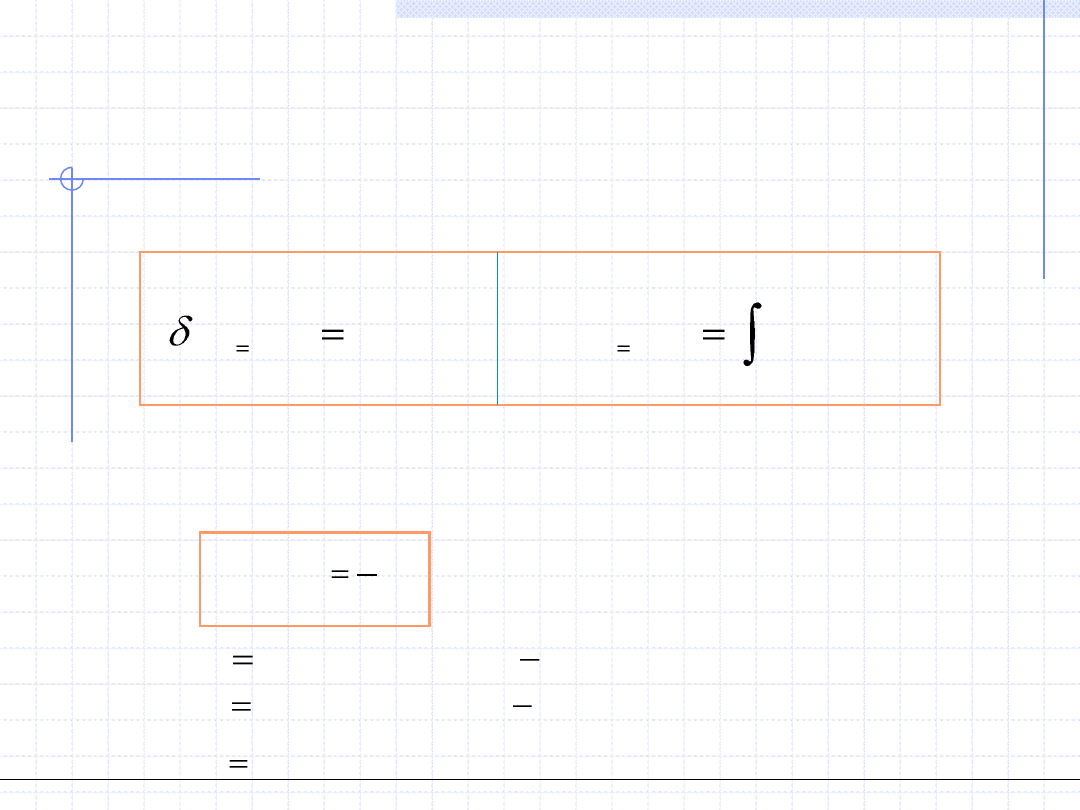
Rozpatrzmy teraz pojemność cieplną układu podczas przemiany

izochorycznej. Na mocy I zasady termodynamiki dla różniczkowej

przemiany można napisać:

Przypomnijmy teraz definicję właściwej pojemności cieplnej dla

rozważanej przemiany:

v

v

v

const

v

const

v

v

const

v

T

u

c

T

u

dT

du

dT

q

c

c

.

.

.

)

(

Wzór powyższy dowodzi, że pojemność cieplna w przemianie izochorycznej

jest pochodną funkcji stanu a zatem również jest funkcją stanu.

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

Przemiana izochoryczna cd.

2

1

)

(

)

(

)

(

.

.

T

T

v

const

v

v

const

v

dT

T

c

q

dT

c

q

:

2

)

(

)

(

gdzie

R

k

c

GD

v

atomowych

gazów

dla

k

1

3

Wielkość c

v

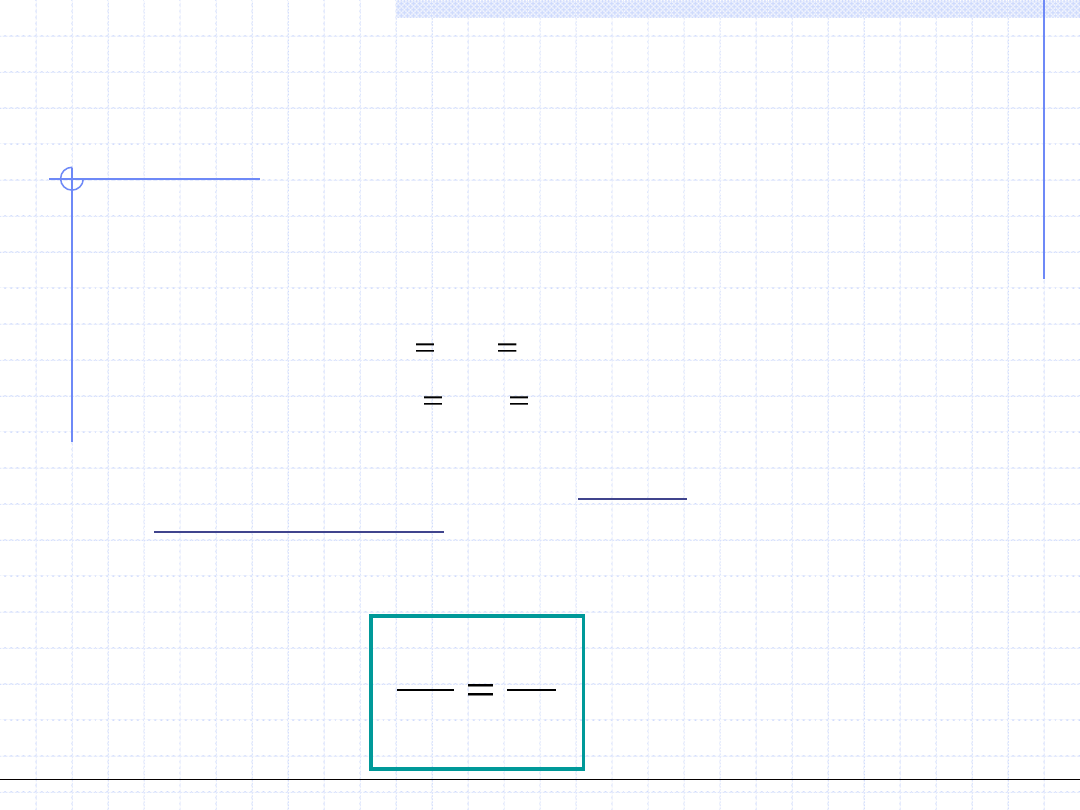
zależy od temperatury, ciśnienia i rodzaju ośrodka. Zależność

od temperatury pozwala na wyznaczenie ciepła przemiany izochorycznej:

Dla gazów doskonałych, z teorii kinetycznej wynika że wielkość c

v

powinna

być stała i równa:

atomowych

gazów

dla

k

2

5

wych

wieloatomo

gazów

dla

k

6

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

Przemiana izochoryczna cd.

2

2

2

2

1

1

1

1

RT

v

p

v

p

RT

v

p

v

p

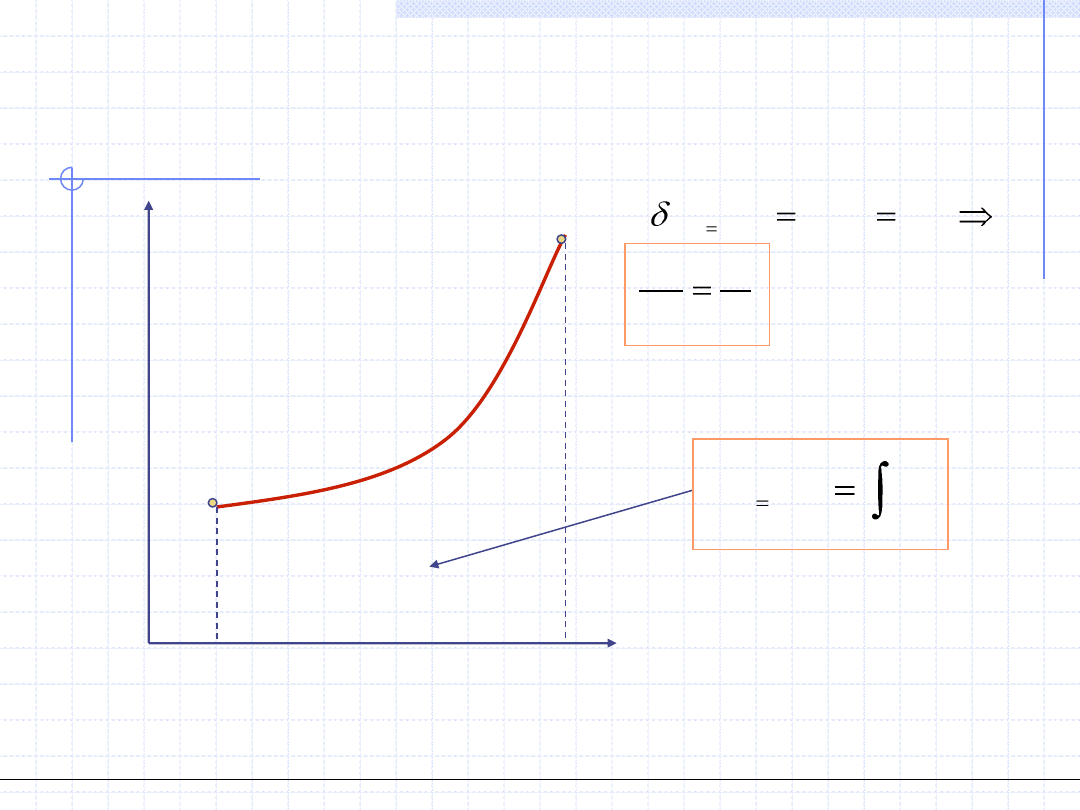
Rozpatrzmy jeszcze dokładniej przemianę izochoryczną gazów doskonałych.

W każdy punkcie takiej przemiany musi być spełnione równanie stanu gazu

doskonałego. Dla punku początkowego i końcowego mamy:

Dzieląc stronami otrzymujemy tzw. równanie

przemiany izochorycznej uzależniające ciśnienie

i temperaturę w skrajnych punktach przemiany:

1

2

1

2

T

T

p

p

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

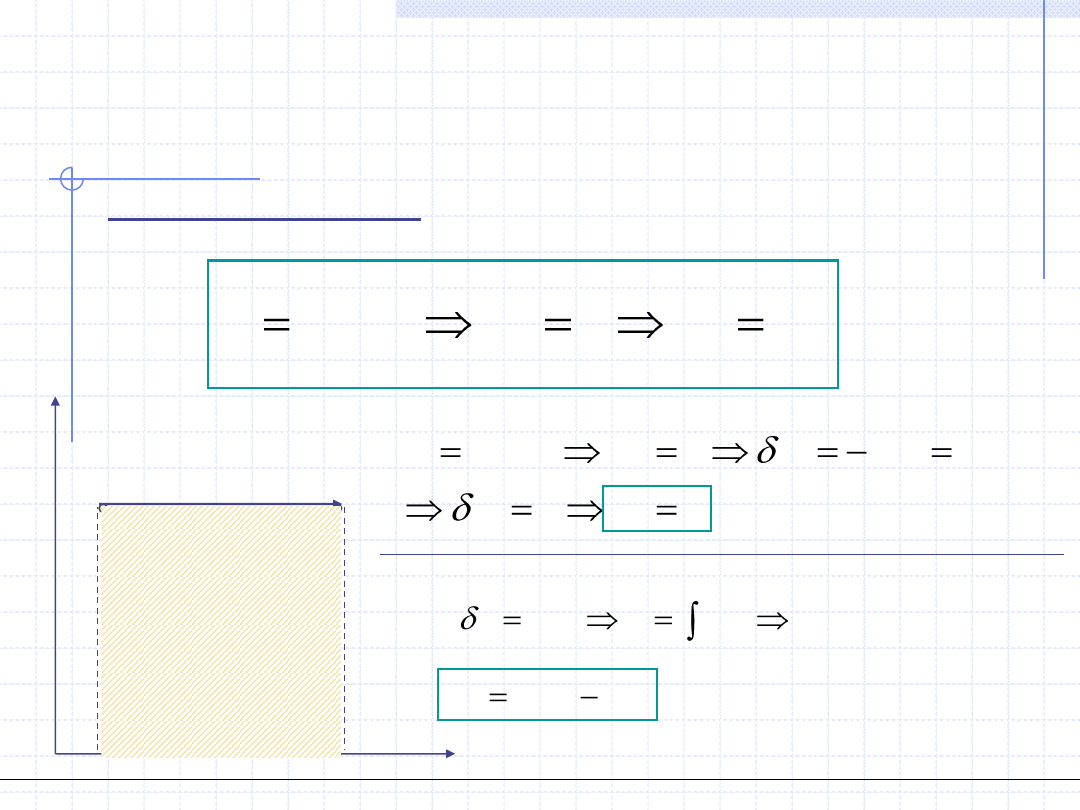
Przemiana izochoryczna cd.

2

1

.

)

(

s

s

const

v

Tds

q

T

s

1

2

s

1

s

2

v

v

const

v

c

T

ds

dT

Tds

dT

c

q

.

)

(

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

Przemiana izobaryczna

1

2

0

.

p

p

dp

const

p

0

0

0

0

.

t

t

t

w

w

vdp

w

dp

const

p

Przemiana izobaryczna odbywa się przy stałym ciśnieniu:

p

v

p=const.

v

1

,T

1

v

2

,T

2

Praca techniczna w przemianie izobarycznej jest równa 0.

)

(

1

2

2

1

v

v

p

w

pdv

w

pdv

w

v

v

Praca objętościowa przemiany

izobarycznej jest równa polu

zakreskowanego prostokąta.

w

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

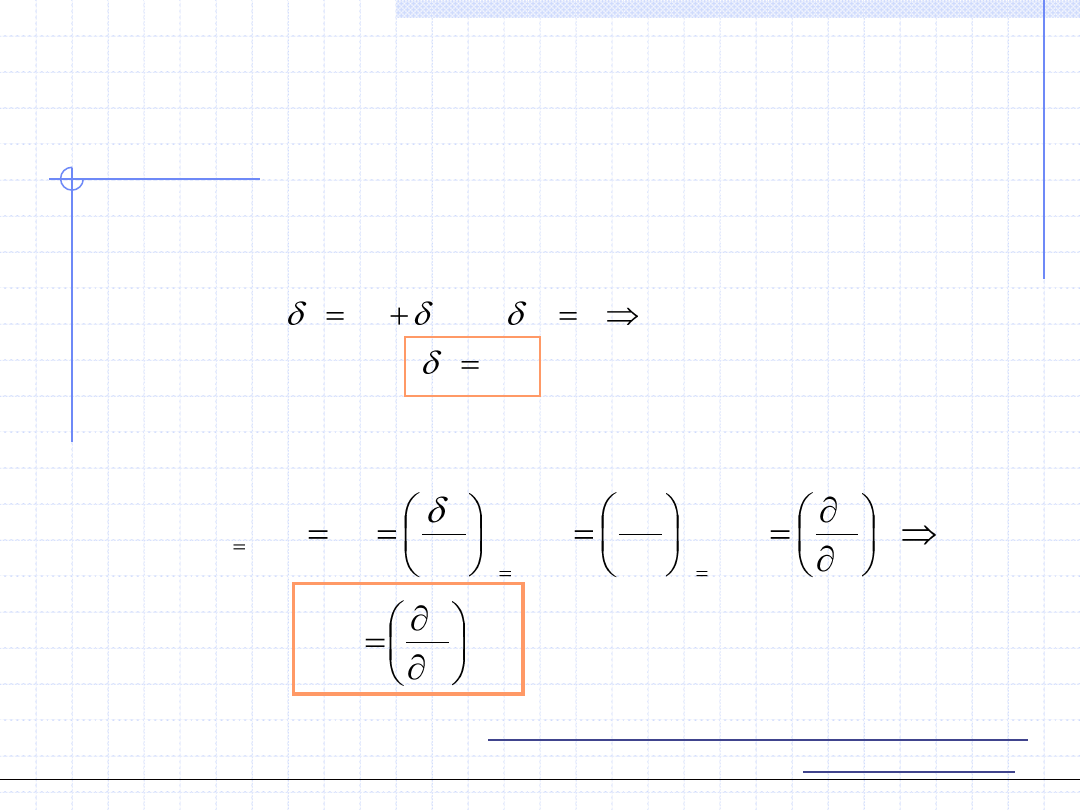
Przemiana izobaryczna cd.

dh

q

w

w

dh

q

t

t

0

Rozpatrzmy teraz pojemność cieplną układu podczas przemiany

izobarycznej. Na mocy I zasady termodynamiki dla różniczkowej

przemiany można napisać:

Przypomnijmy teraz definicję właściwej pojemności cieplnej dla

rozważanej przemiany:

v

p

p

const

p

const

p

p

const

p

T

h

c

T

h

dT

dh

dT

q

c

c

.

.

.

)

(

Wzór powyższy dowodzi, że pojemność cieplna w przemianie izobarycznej

jest pochodną funkcji stanu (entalpii) a zatem również jest funkcją stanu.

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

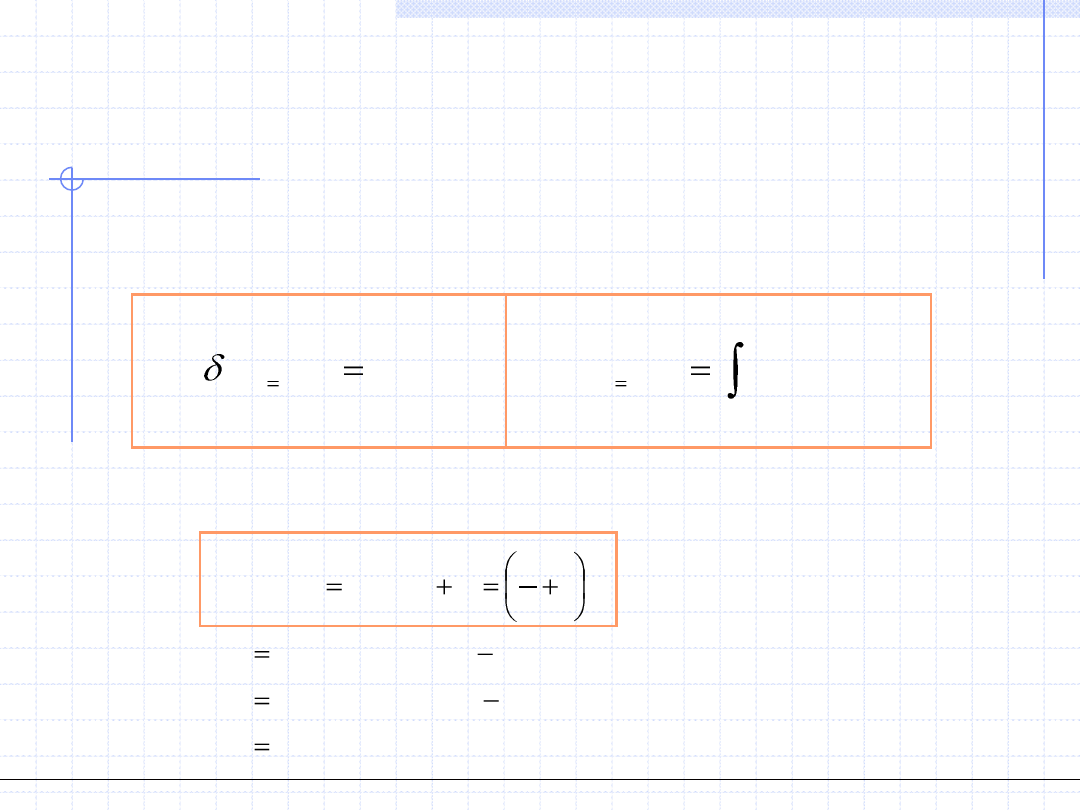
Przemiana izobaryczna cd.

2

1

)

(

)

(

)

(

.

.

T

T

p

const

p

p

const

p

dT

T

c

q

dT

c

q

Wielkość c

p

zależy od temperatury, ciśnienia i rodzaju ośrodka. Zależność

od temperatury pozwala na wyznaczenie ciepła przemiany izobarycznej:

Dla gazów doskonałych, z teorii kinetycznej wynika że wielkość c

p

powinna

być stała i równa:

wych

wieloatomo

gazów

dla

k

atomowych

gazów

dla

k

atomowych

gazów

dla

k

gdzie

R

k

R

c

c

GD

v

GD

p

6

2

5

1

3

:

1

2

)

(

)

(

)

(

)

(

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

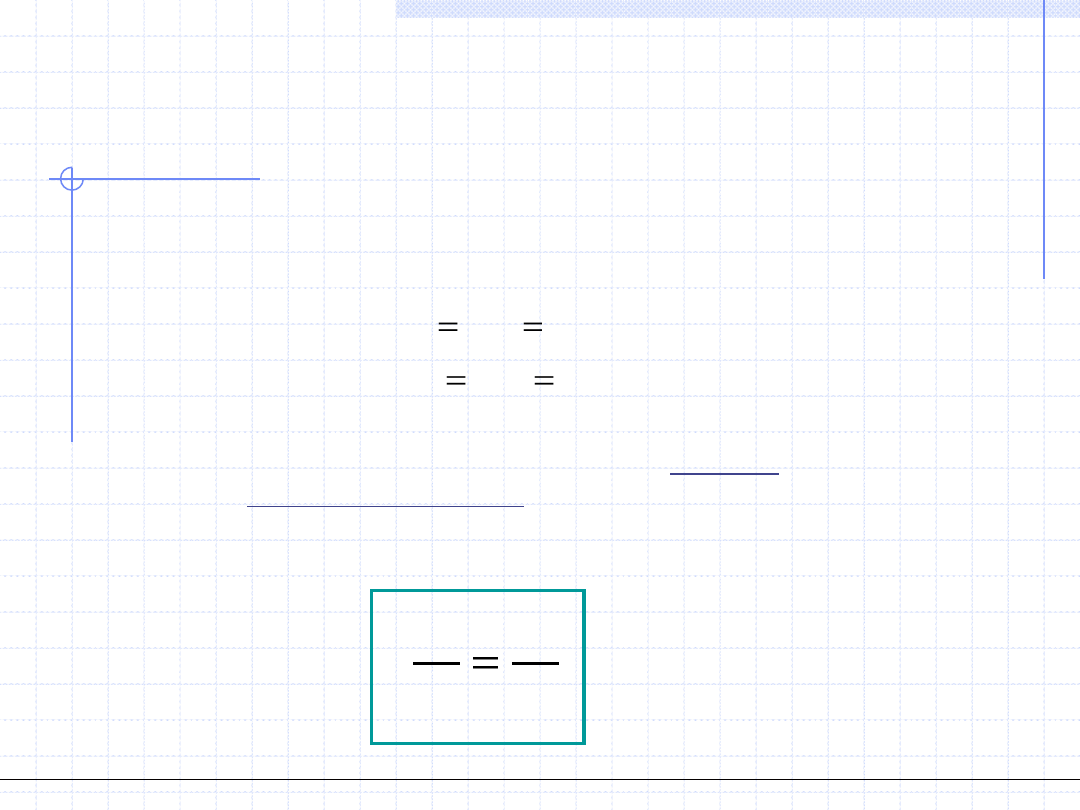
Przemiana izobaryczna cd.

2

2

2

2

1

1

1

1

RT

pv

v

p

RT

pv

v

p

Rozpatrzmy jeszcze dokładniej przemianę izobaryczną gazów doskonałych.

W każdy punkcie takiej przemiany musi być spełnione równanie stanu gazu

doskonałego. Dla punku początkowego i końcowego mamy:

Dzieląc stronami otrzymujemy tzw. równanie

przemiany izobarycznej uzależniające objętość

i temperaturę w skrajnych punktach przemiany:

1

2

1

2

T

T

v

v

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

2

1

.

)

(

s

s

const

p

Tds

q

T

s

1

2

s

1

s

2

p

p

const

p

c

T

ds

dT

Tds

dT

c

q

.

)

(

v=const.

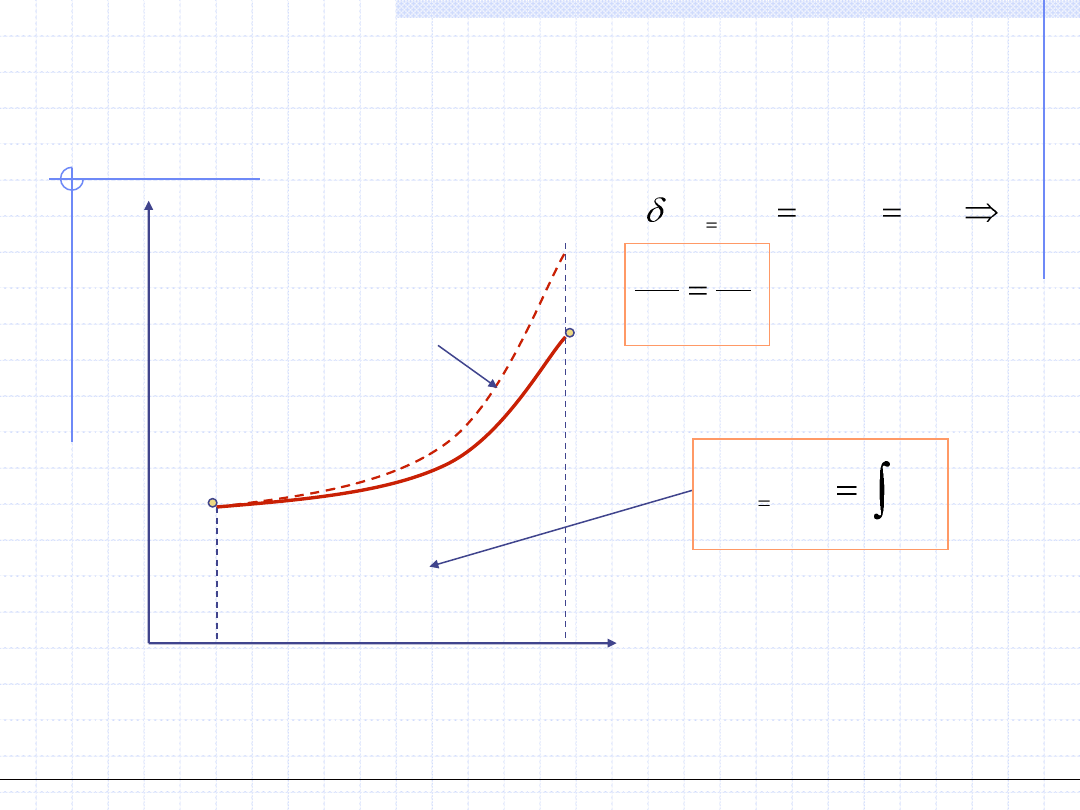
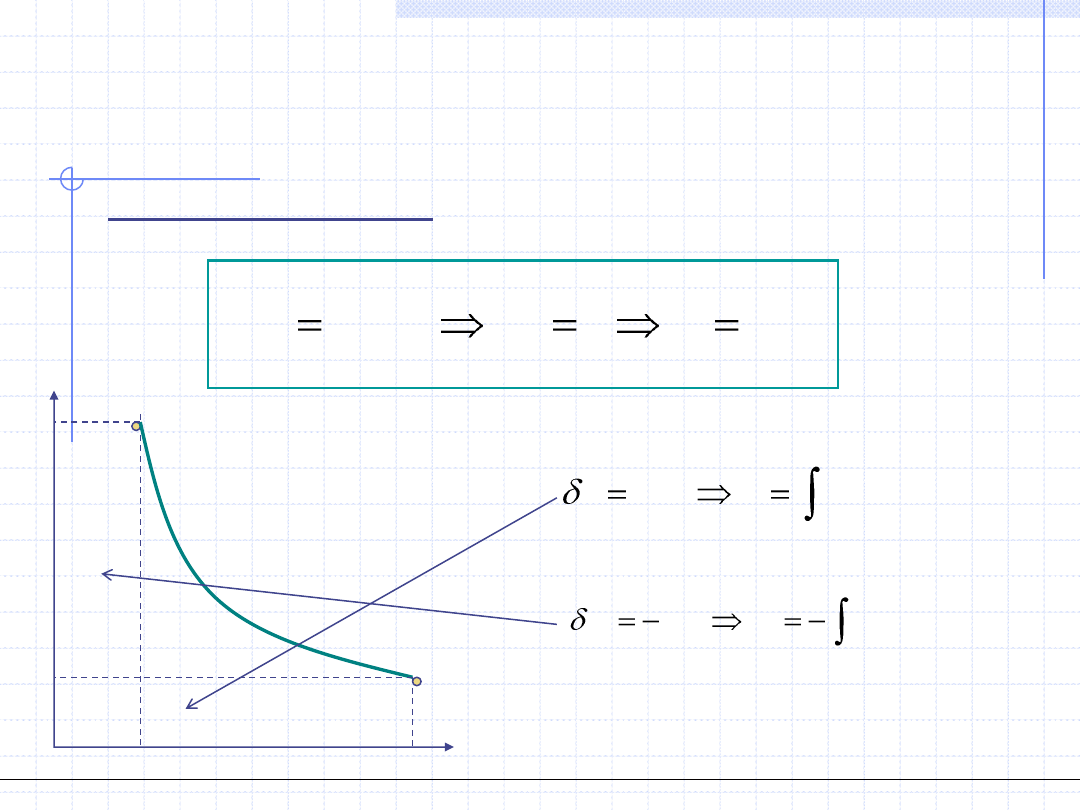
Przemiana izobaryczna cd.

Ale c

p

>c

v

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

18

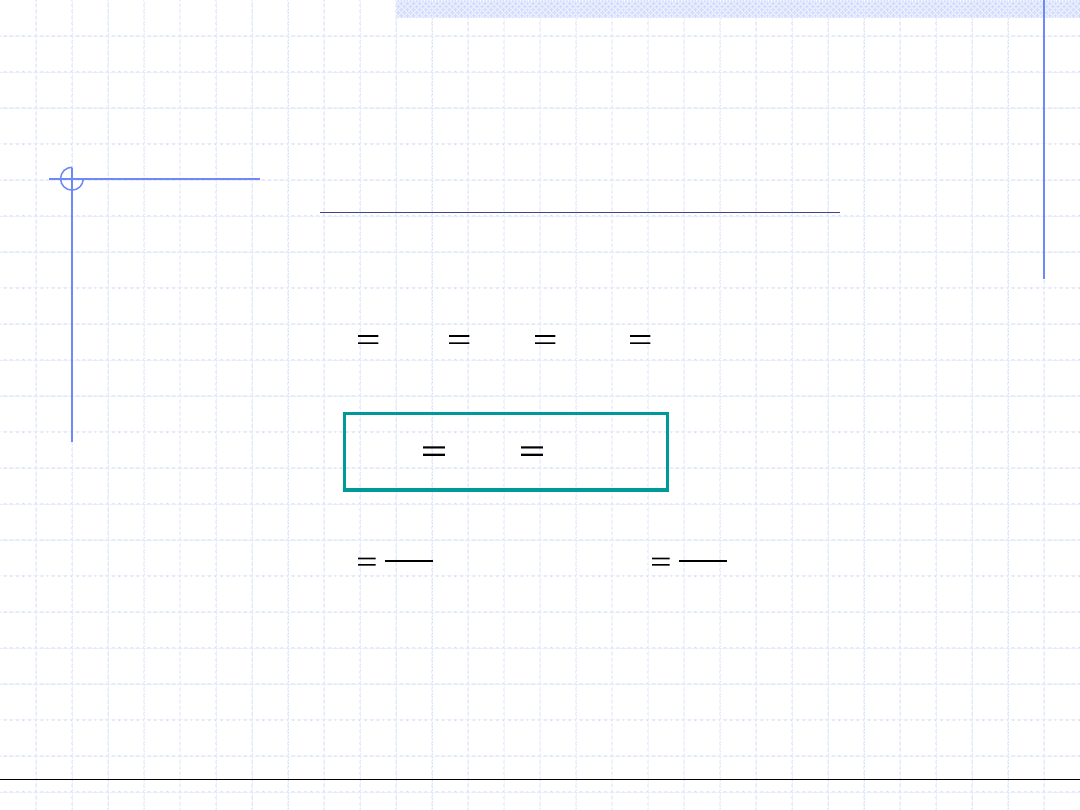
Przemiana izotermiczna

1

2

0

.

T

T

dT

const

T

2

1

)

(

v

v

dv

v

p

w

pdv

w

Przemiana izotermiczna odbywa się w stałej temperaturze:

p

v

v

1

,p

1

v

2

,p

2

2

1

)

(

p

p

t

t

dp

p

v

w

vdp

w

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

19

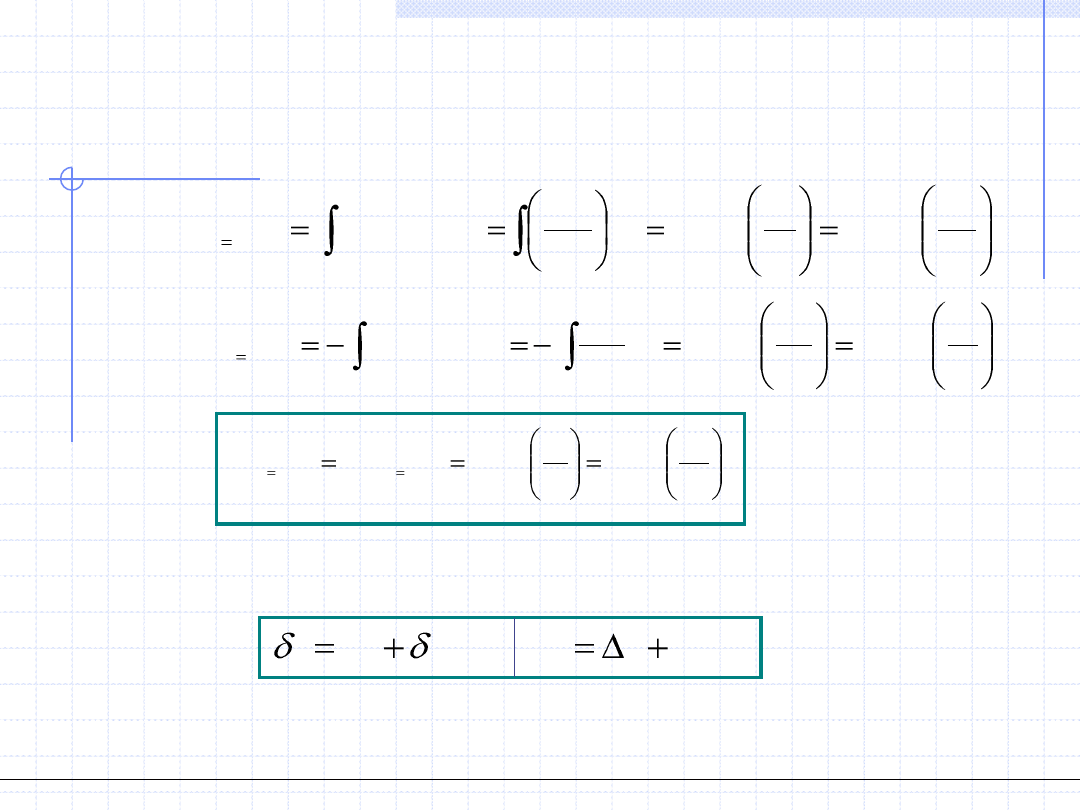
Przemiana izotermiczna cd.

2

2

2

1

1

1

v

p

RT

RT

RT

v

p

p

RT

p

v

v

RT

v

p

GD

GD

)

(

)

(

)

(

)

(

Rozpatrzmy teraz przemianę izotermiczną gazów doskonałych.

W każdy punkcie takiej przemiany musi być spełnione równanie stanu gazu

doskonałego. Dla punku początkowego i końcowego mamy:

Wyrażenia powyższe pozwalają na wyprowadzenie wzorów określających

pracę oraz pracę techniczną w przemianie izotermicznej gazów doskonałych:

.

const

RT

pv

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

20

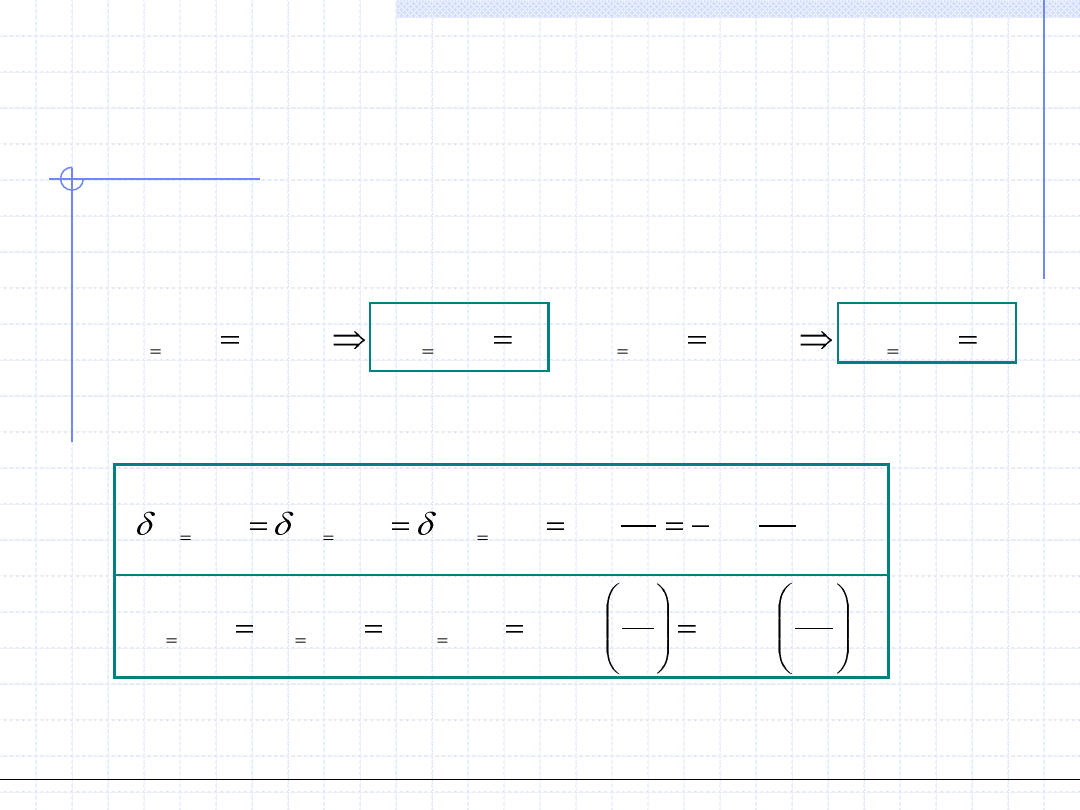
Przemiana izotermiczna cd.

w

u

q

w

du

q

2

1

1

2

)

(

)

(

.

ln

ln

)

(

)

(

2

1

2

1

p

p

RT

v

v

RT

dv

v

RT

dv

v

p

w

v

v

v

v

GD

GD

const

T

2

1

1

2

)

(

.

)

(

.

ln

ln

)

(

)

(

p

p

RT

v

v

RT

w

w

GD

const

T

t

GD

const

T

W celu wyznaczenia ciepła przemiany izotermicznej należy zastosować

I zasadę termodynamiki:

1

2

2

1

)

(

)

(

.

ln

ln

)

(

)

(

2

1

2

1

v

v

RT

p

p

RT

dp

p

RT

dp

p

v

w

p

p

p

p

GD

GD

const

T

t

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

21

Przemiana izotermiczna cd.

2

1

1

2

)

(

.

,

)

(

.

)

(

.

)

(

.

,

)

(

.

)

(

.

ln

ln

p

p

RT

v

v

RT

w

w

q

p

dp

RT

v

dv

RT

w

w

q

GD

const

T

t

GD

const

T

GD

const

T

GD

const

T

t

GD

const

T

GD

const

T

W przypadku przemiany gazu doskonałego można zauważyć, że jego

energia wewnętrzna i entalpia zależą tylko od temperatury. Zatem w stałej

temperaturze zarówno „u” jak i „h” są stałe czyli:

0

.

0

.

)

(

.

)

(

.

)

(

.

)

(

.

GD

const

T

GD

const

T

GD

const

T

GD

const

T

dh

const

h

du

const

u

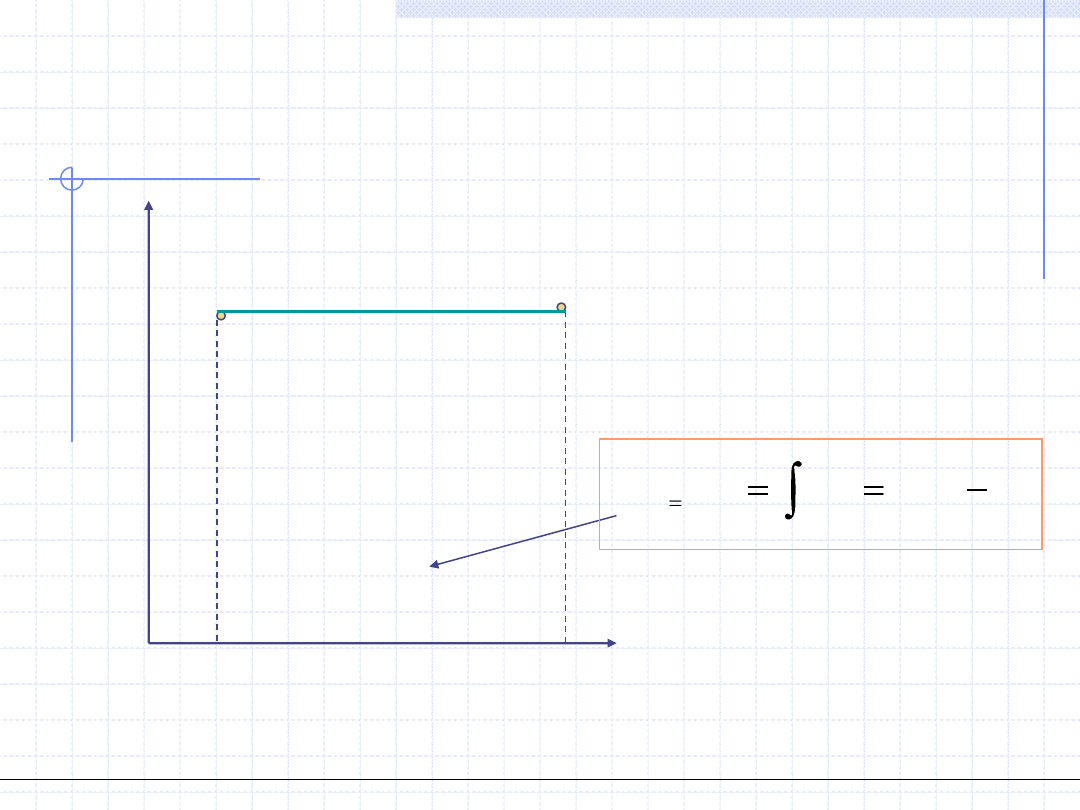
Uwzględniając I zasadę termodynamiki otrzymujemy wzory określające

ciepło przemiany izotermicznej gazów doskonałych:

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

22

)

(

)

(

1

2

.

2

1

s

s

T

Tds

q

s

s

const

T

T

s

1

2

s

1

s

2

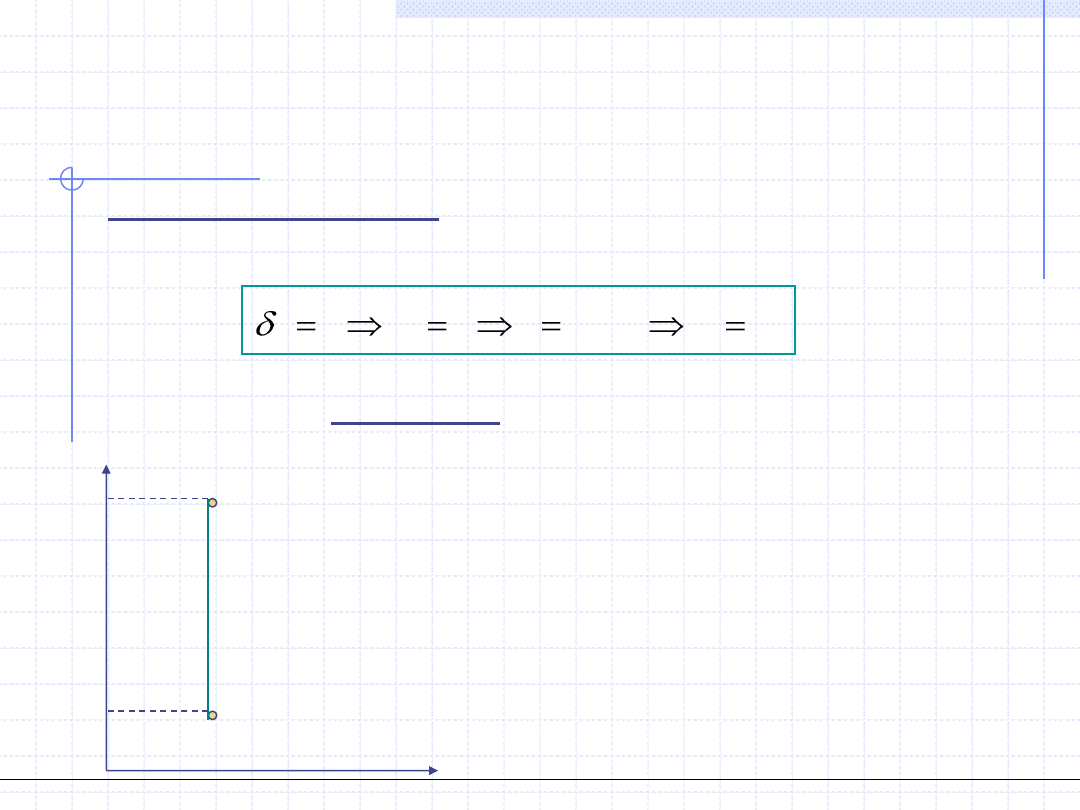
Przemiana izotermiczna cd.

T=const.

Wykres przemiany izotermicznej w układzie T – s jest

szczególnie prosty:

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

23

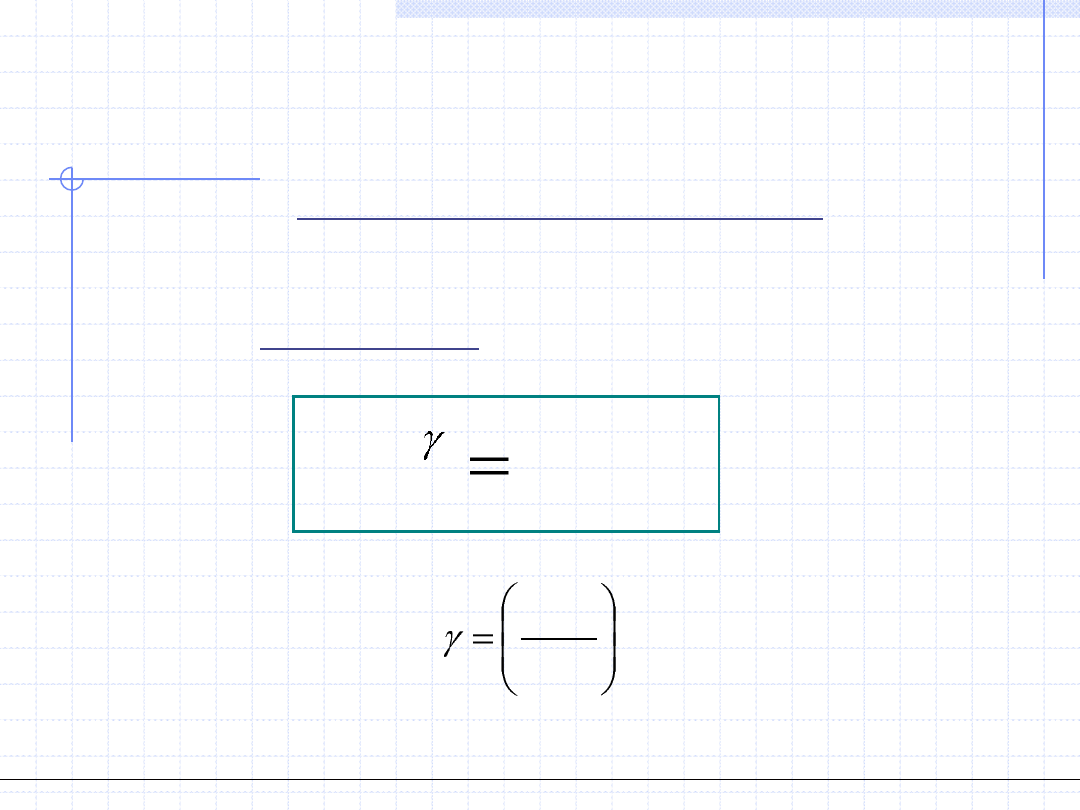
Przemiana adiabatyczna

(izentropowa)

1

2

0

0

s

s

const

s

ds

q

Przemiana adiabatyczna odbywa się w układzie adiabatycznym tzn. bez

wymiany ciepła z otoczeniem. Jeżeli jednocześnie jest to przemiana

odwracalna to wtedy:

Oznacza to, że odwracalna przemiana adiabatyczna odbywa się przy stałej

entropii czyli jest izentropowa. Wykres przemiany izentropowej jest

szczególnie prosty w układzie T – s.

T

s

1

2

W przemianie adiabatycznej układ może

wymieniać z otoczeniem energię mechaniczną

czyli wykonywać pracę (lub praca może być

wykonana na układzie). W celu wyznaczenia

tej pracy konieczna jest znajomość zależności

ciśnienia od objętości czyli konieczna jest

znajomość tzw. równania przemiany. Równanie

to można wyprowadzić dla gazu doskonałego.

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

24

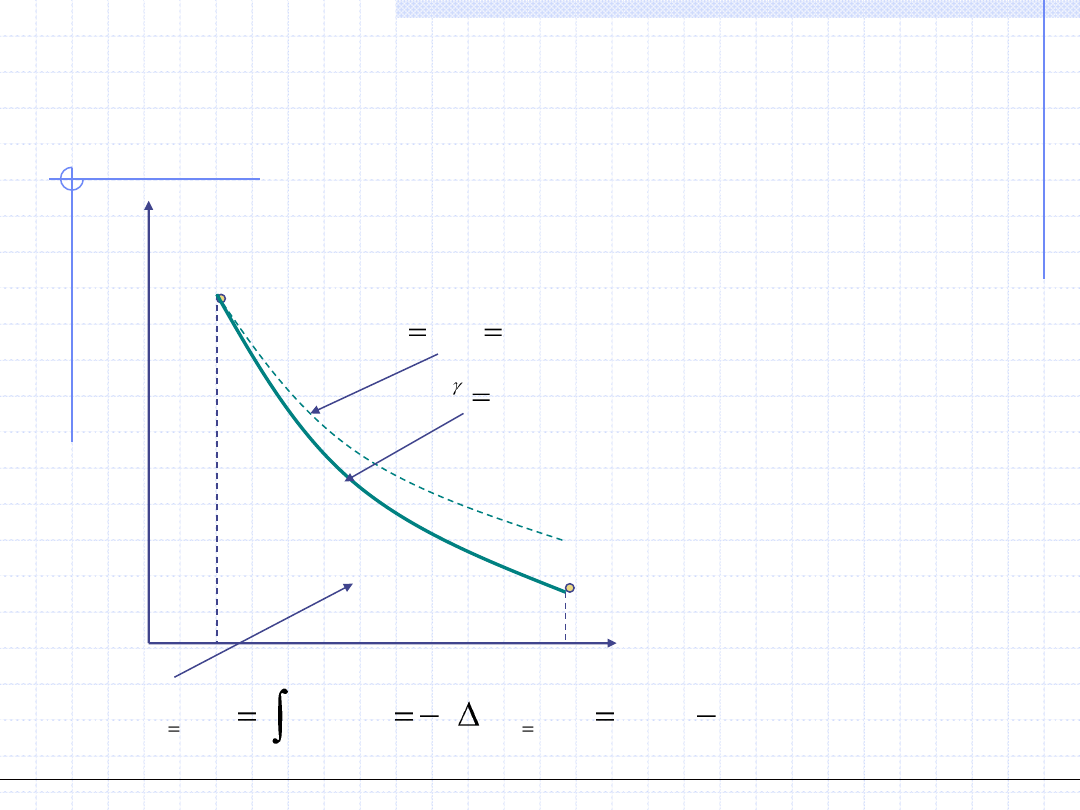
Przemiana adiabatyczna gazu

doskonałego

Rozpatrzmy teraz przemianę adiabatyczną gazów doskonałych.

Wychodząc z I zasady termodynamiki oraz uwzględniając własności gazów

doskonałych można wyprowadzić zależność między ciśnieniem a objętością

w postaci tzw. równania adiabaty:

const

pv

)

(

)

(

GD

v

GD

p

c

c

gdzie

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

25

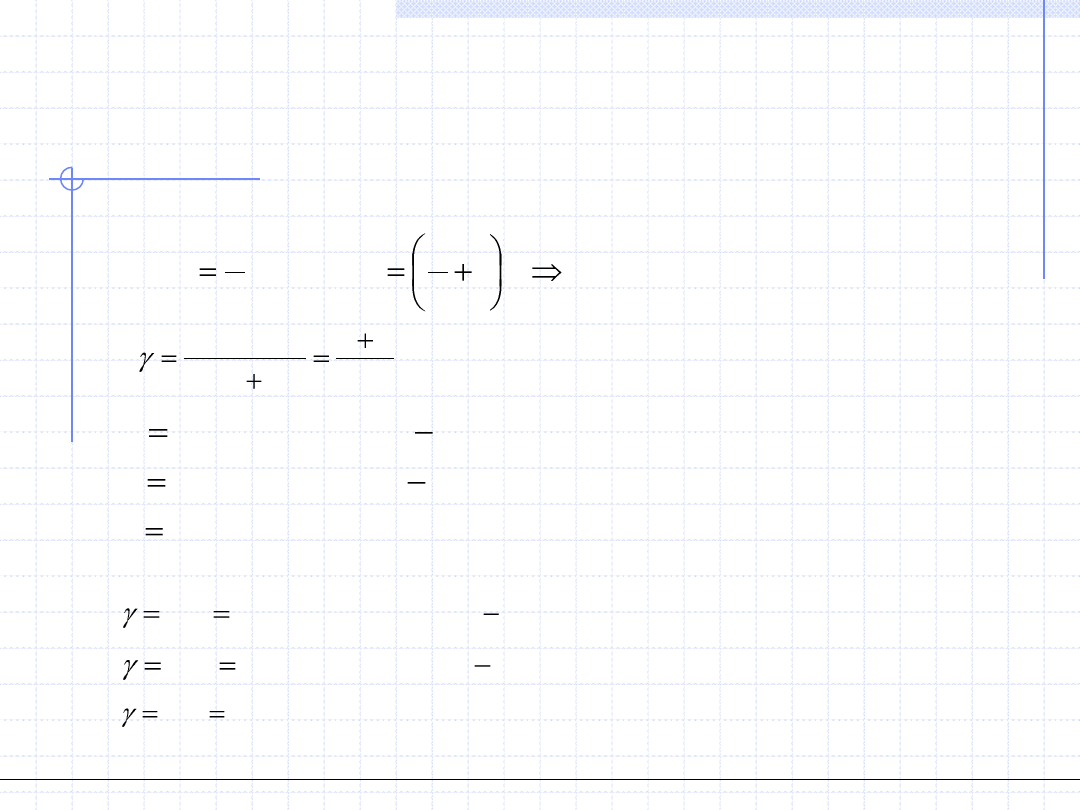
Przemiana adiabatyczna gazu

doskonałego

Wielkość γ dla gazów doskonałych jest stała i wynosi:

R

k

c

R

k

c

GD

p

GD

v

1

2

2

)

(

)

(

:

2

)

1

2

/

(

)

2

/

(

gdzie

k

k

R

k

R

k

atomowych

gazów

dla

k

1

3

atomowych

gazów

dla

k

2

5

wych

wieloatomo

gazów

dla

k

6

atomowych

gazów

dla

1

667

.

1

3

/

5

atomowych

gazów

dla

2

4

.

1

5

/

7

wych

wieloatomo

gazów

dla

333

.

1

6

/

8

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

26

)

(

)

(

)

(

)

(

2

1

)

(

.

)

(

2

1

T

T

c

u

dv

v

p

w

v

GD

const

s

v

v

GD

const

s

p

v

1(p

1

,v

1

,T

1

)

2(p

2

,v

2

,T

2

)

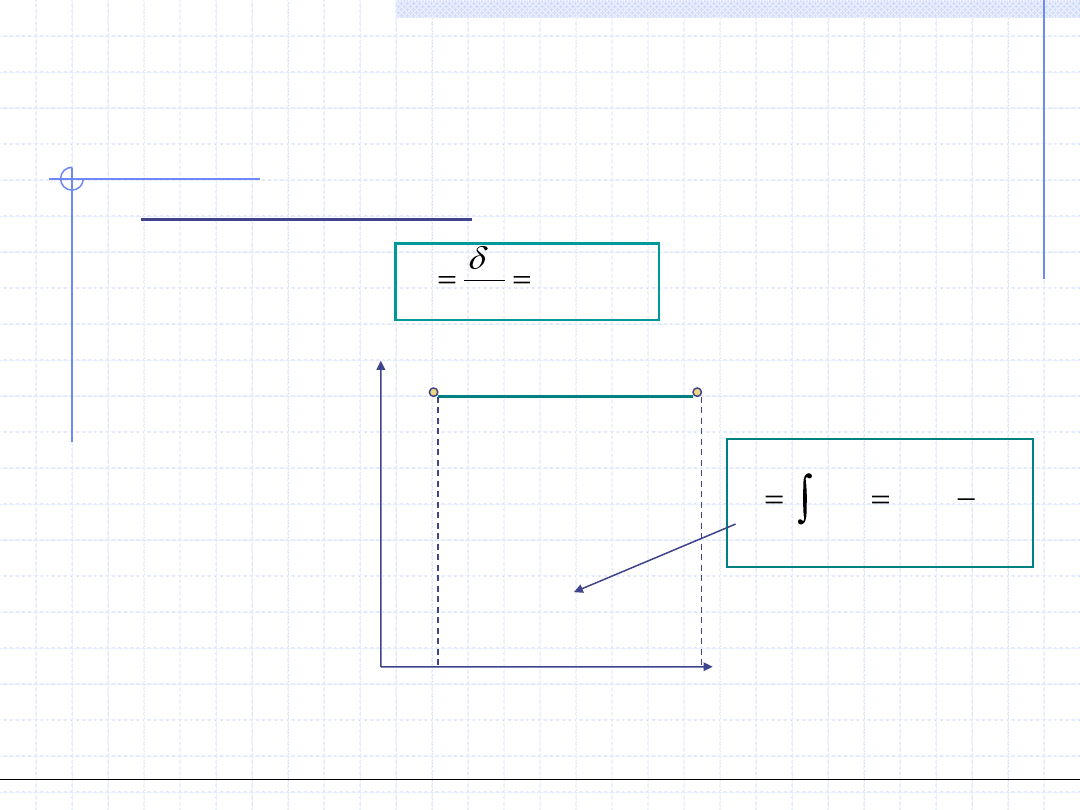
Przemiana adiabatyczna cd.

.

const

RT

pv

.

const

pv

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

27

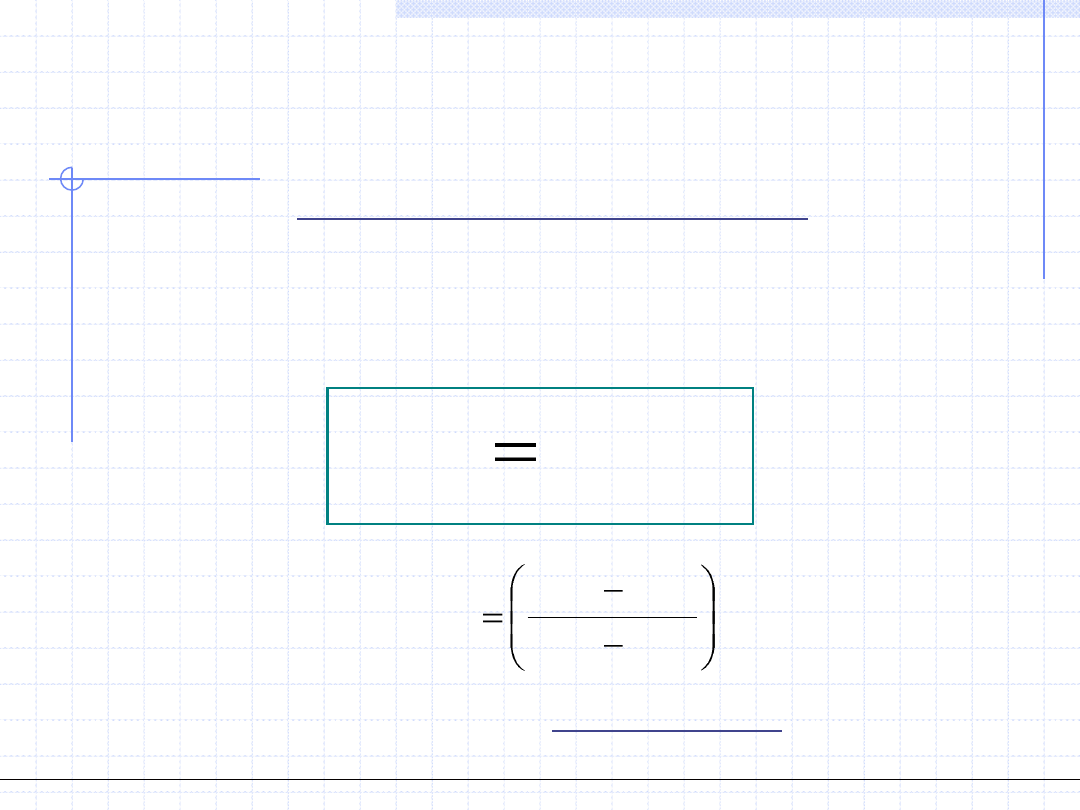
Przemiana politropowa

.

const

dT

q

c

W przemianie politropowej stała jest pojemność cieplna układu:

T

1(p

1

,v

1

,T

1

)

2(p

2

,v

2

,T

2

)

c

2

1

)

(

1

2

T

T

T

T

c

cdT

q

Szczególnie proste do obliczenia w przemianie politropowej jest ciepło przemiany,

które jest równe polu prostokąta na wykresie c – T.

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

28

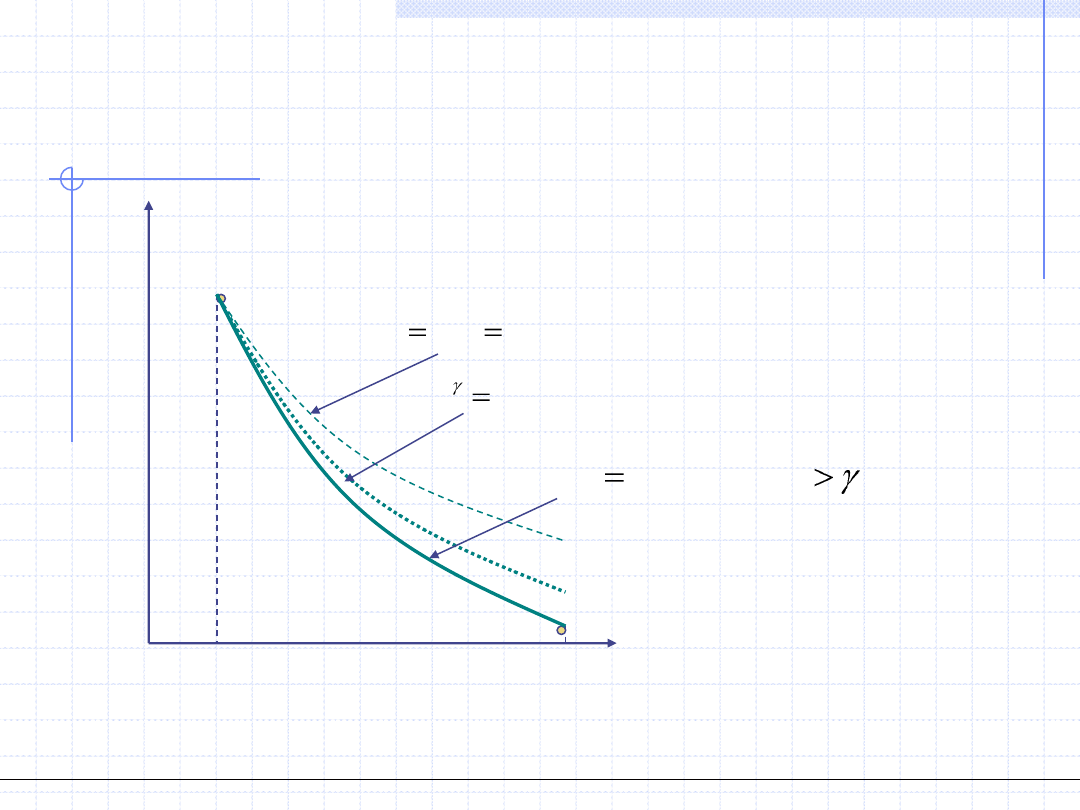
Przemiana politropowa gazu

doskonałego

Rozpatrzmy teraz przemianę politropową gazów doskonałych.

Podobnie jak dla przemiany adiabatycznej wychodząc z I zasady termodynamiki

i uwzględniając własności gazów doskonałych oraz definicję pojemności cieplnej

można wyprowadzić tzw. równanie politropy:

const

pv

m

)

(

)

(

)

(

)

(

GD

GD

v

GD

GD

p

c

c

c

c

m

gdzie

Bezwymiarowa wielkość „m” jest to wykładnik politropy i ma znaczenie

analogiczne jak wykładnik adiabaty.

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

29

)

(

.

m

const

pv

m

p

1(p

1

,v

1

,T

1

)

2(p

2

,v

2

,T

2

)

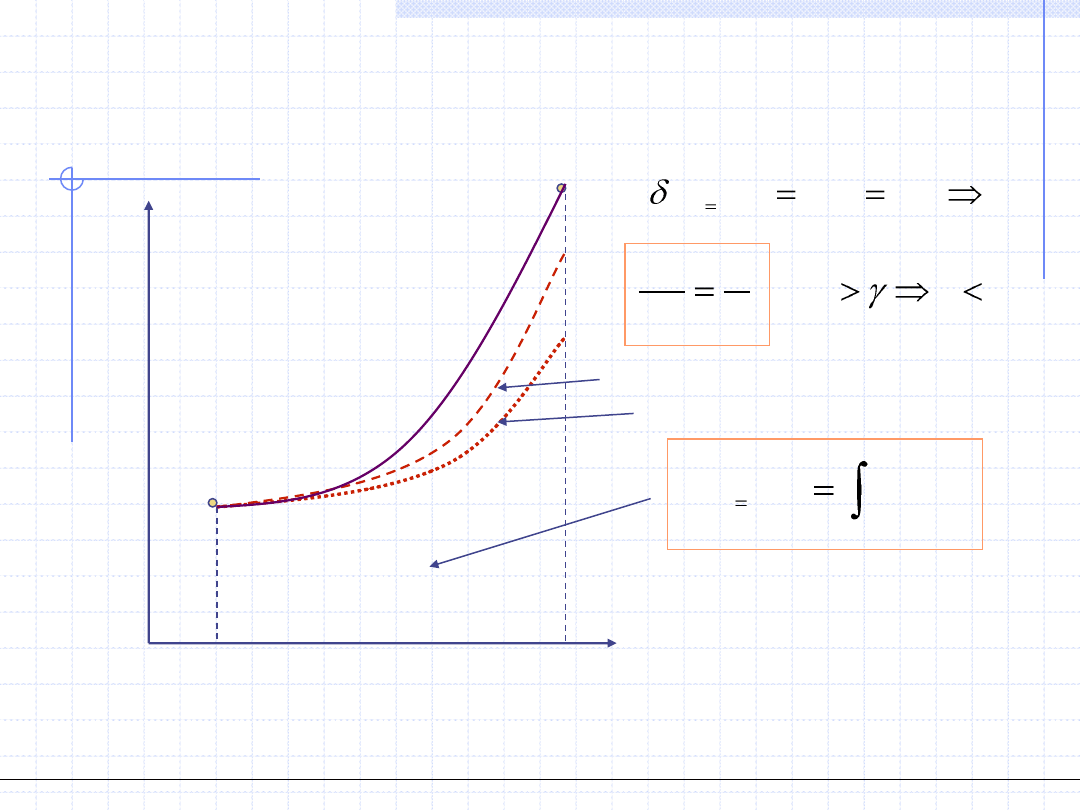
Przemiana politropowa

Wykres w układzie p - v

.

const

RT

pv

.

const

pv

v

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

30

2

1

)

(

)

(

.

s

s

const

c

ds

s

T

q

T

s

1

2

s

1

s

2

Tds

cdT

q

const

c

.

)

(

v=const.

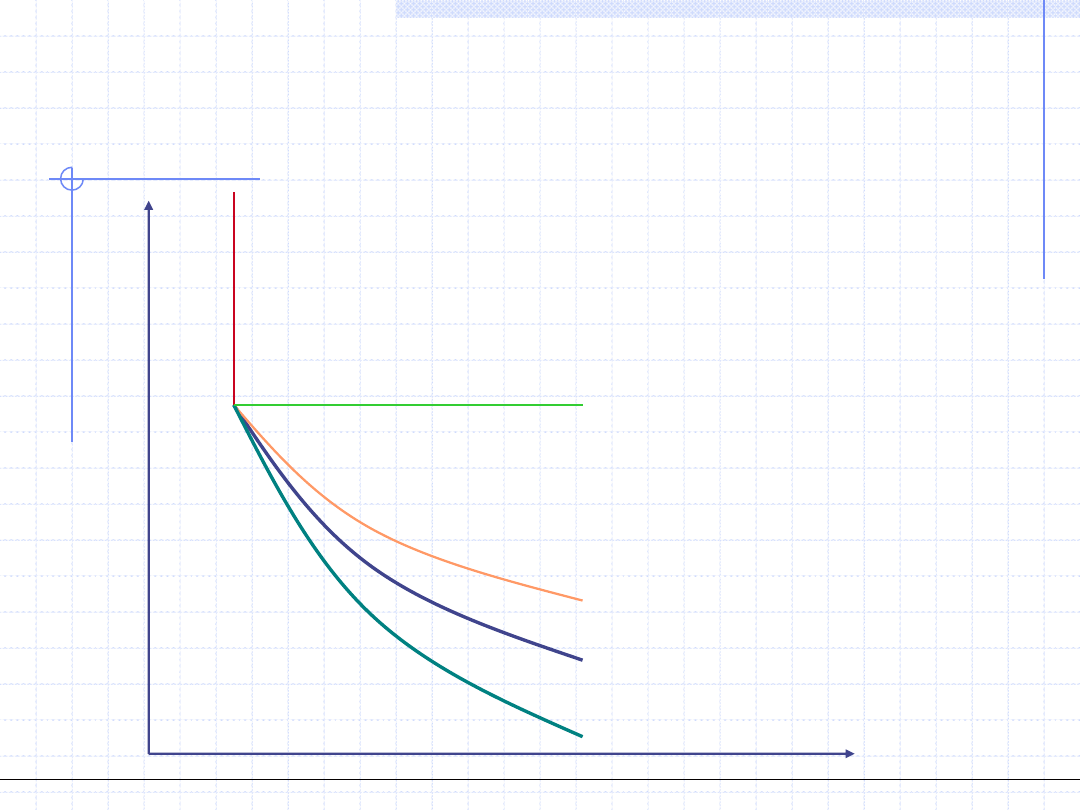
Przemiana politropowa

Wykres w układzie T - s

p=const.

v

c

c

m

c

T

ds

dT

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

31

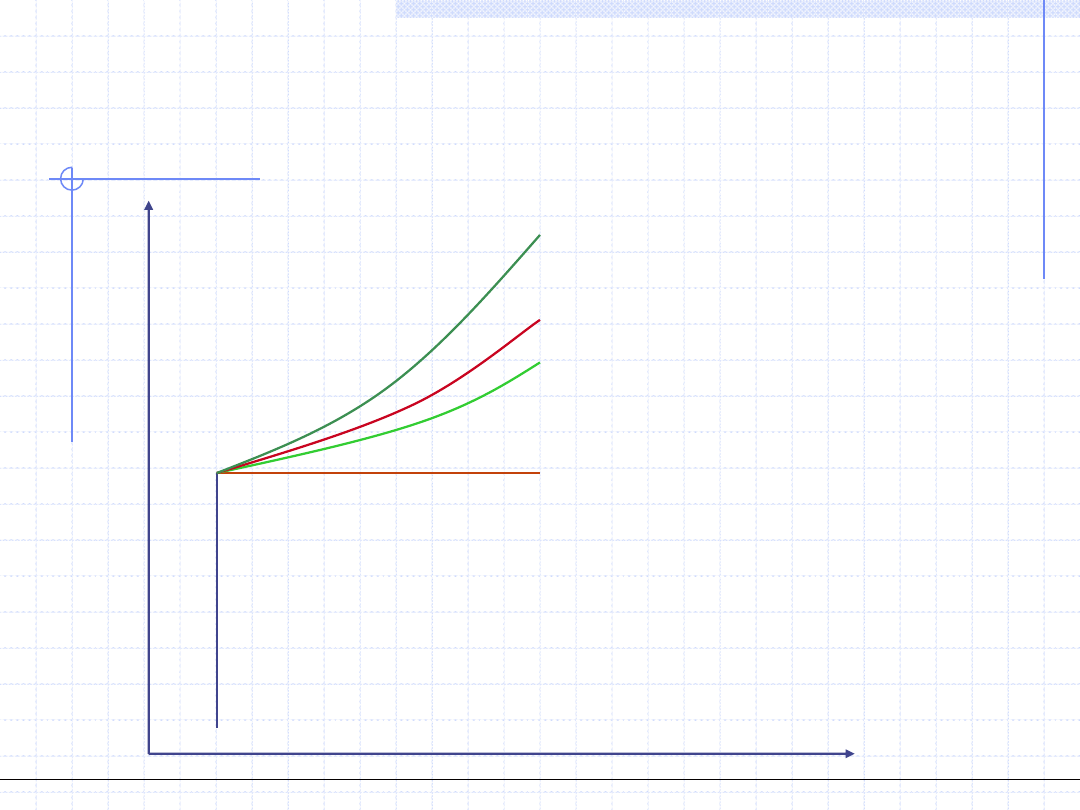
p

Porównanie przemian na

wykresie p -v

v

v=const., izochora

p=const., izobara

T=const., izoterma

s=const., izentropa(adiabata)

c=const., politropa (m>γ)

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

32

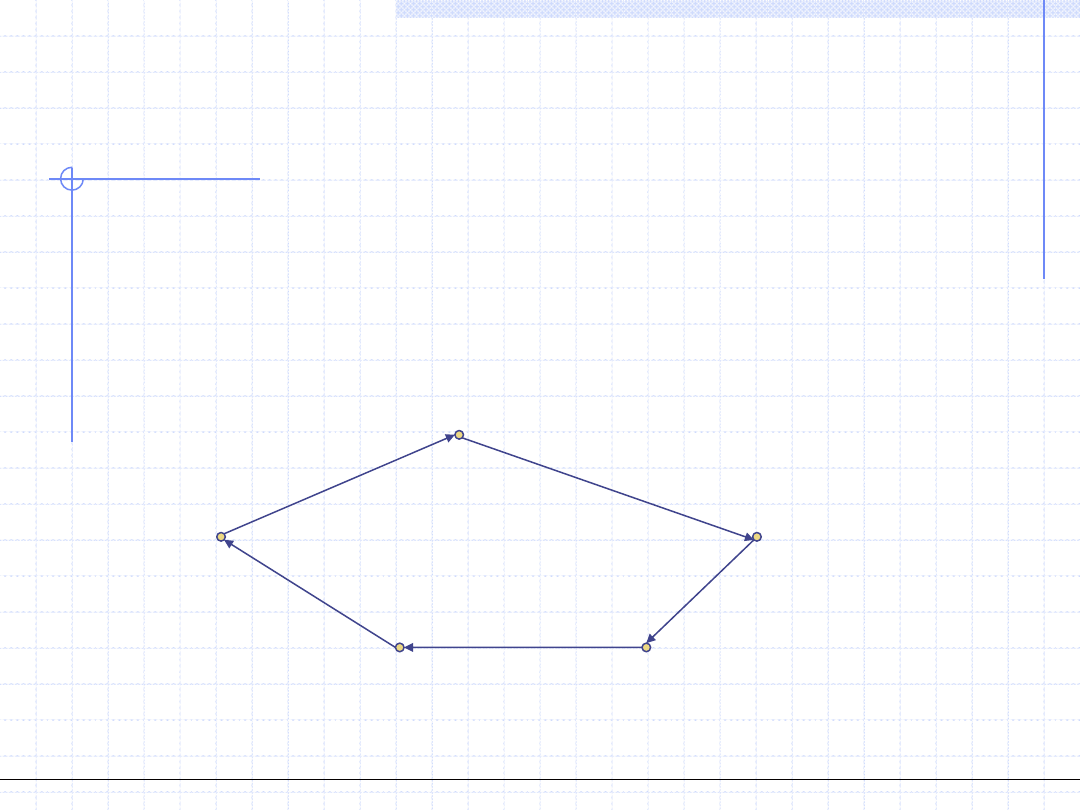
T

Porównanie przemian na

wykresie T - s

s

v=const., izochora

p=const., izobara

T=const., izoterma

s=const., izentropa(adiabata)

c=const., politropa (m>γ)

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

33

4

3

2

1

5

33

Obiegi termodynamiczne

Definicja i ilustracja

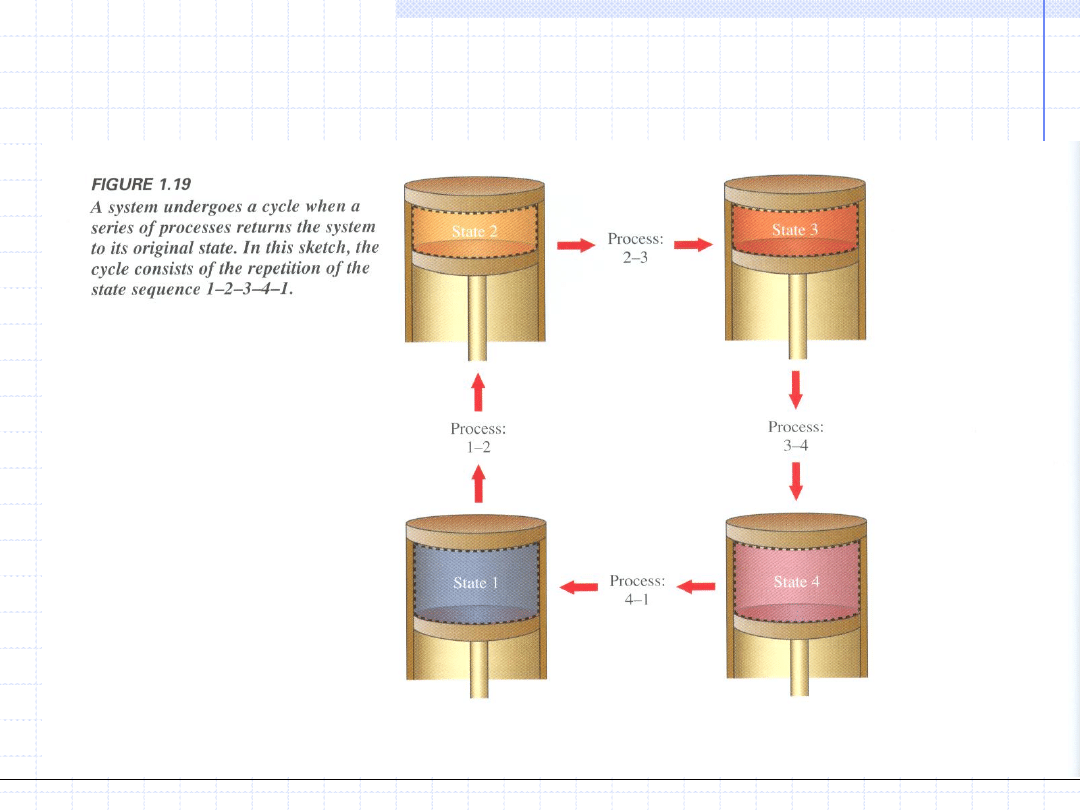
Obiegiem (cyklem) termodynamicznym nazywamy szereg następujących

po sobie przemian, w wyniku których układ wraca do stanu wyjściowego.

Pojęcie obiegu (cyklu) termodynamicznego jest bardzo ważne dla zrozumienia

istoty działania zarówno silników cieplnych jak i urządzeń chłodniczych.

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

34

Ilustracja cyklu

termodynamicznego

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

35

35

Obiegi termodynamiczne

Uwagi ogólne

Jeżeli wszystkie przemiany są odwracalne to również obieg nazywamy

odwracalnym. Jeżeli chociaż jedna z przemian cyklu jest nieodwracalna to

cały obieg również jest nieodwracalny.

Czynnikiem podlegającym przemianom może być gaz doskonały lub

substancje rzeczywiste. W praktyce bardzo ważne są obiegi, w których

czynnikiem jest woda i para wodna.

Graficznie obiegi przedstawia się najczęściej w układach p – v i T – s.

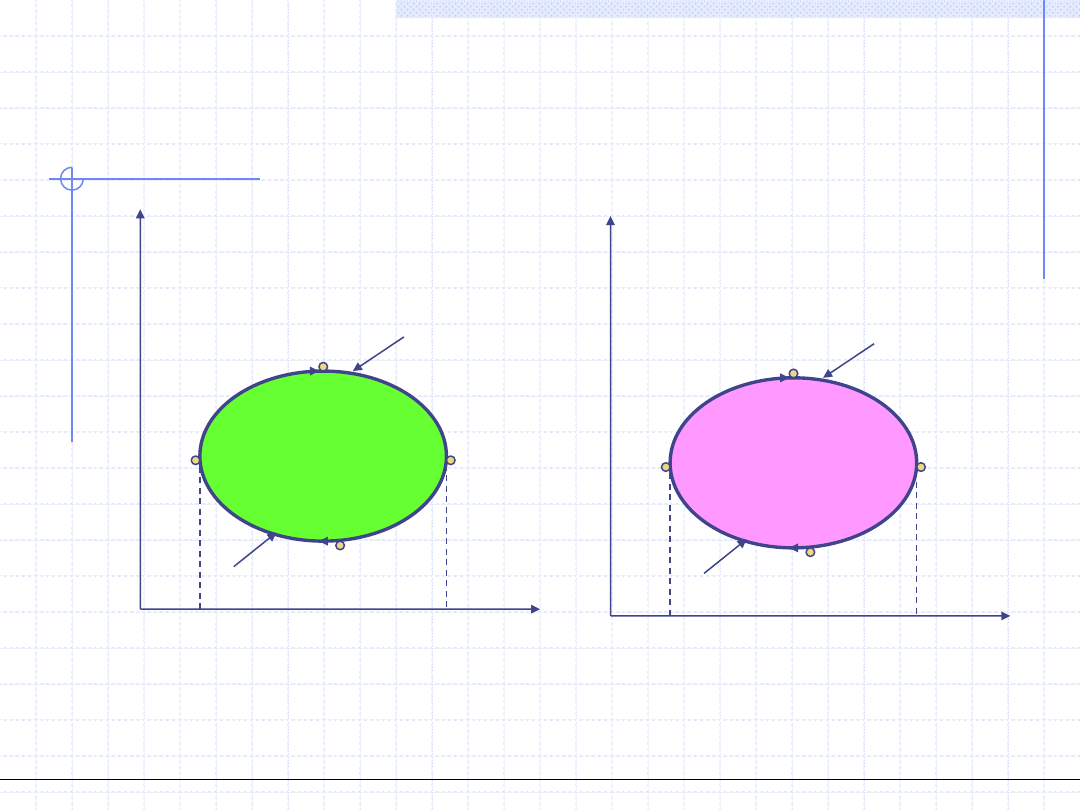
Bardzo ważną cechą obiegów jest kierunek przemian zachodzących

w układzie. W zależności od tego kierunku odróżnia się obiegi prawobieżne,

w których kierunek przemian na wykresach p – v i T – s jest zgodny z ruchem

wskazówek zegara i obiegi lewobieżne, w których kierunek przemian

jest przeciwny do ruchu wskazówek zegara.

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

36

36

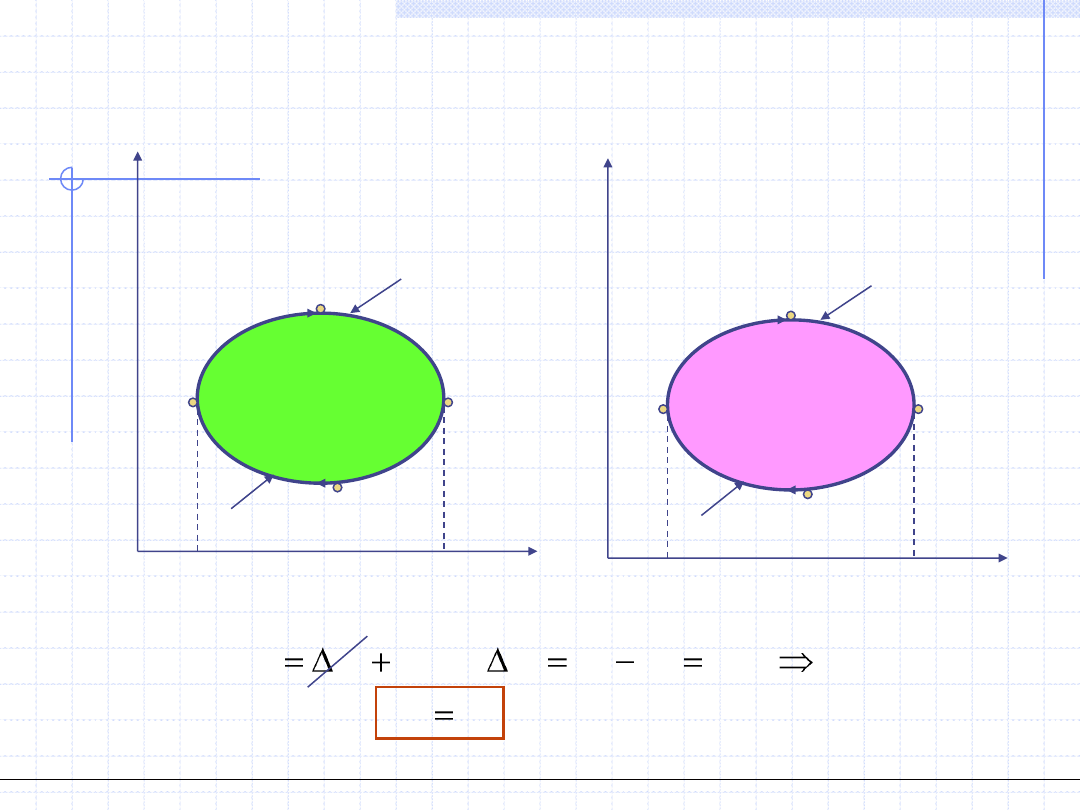
Obiegi prawobieżne - silnikowe

w

o

p

v

A

B

C

D

E

F

p

g

p

d

q

o

T

s

A’

B’

C’

D’

E’

F’

T

g

T

d

w

o

=w

g

+w

d

=Pole(ABCEFA)-Pole(CDAFEC)=Pole(ABCDA)

q

o

=q

g

+q

d

=Pole(A’B’C’E’F’A’)-Pole(C’D’A’F’E’C’)=Pole(A’B’C’D’A’)

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

37

37

Obiegi prawobieżne – silnikowe cd.

w

o

p

v

A

B

C

D

E

F

p

g

p

d

q

o

T

s

A’

B’

C’

D’

E’

F’

T

g

T

d

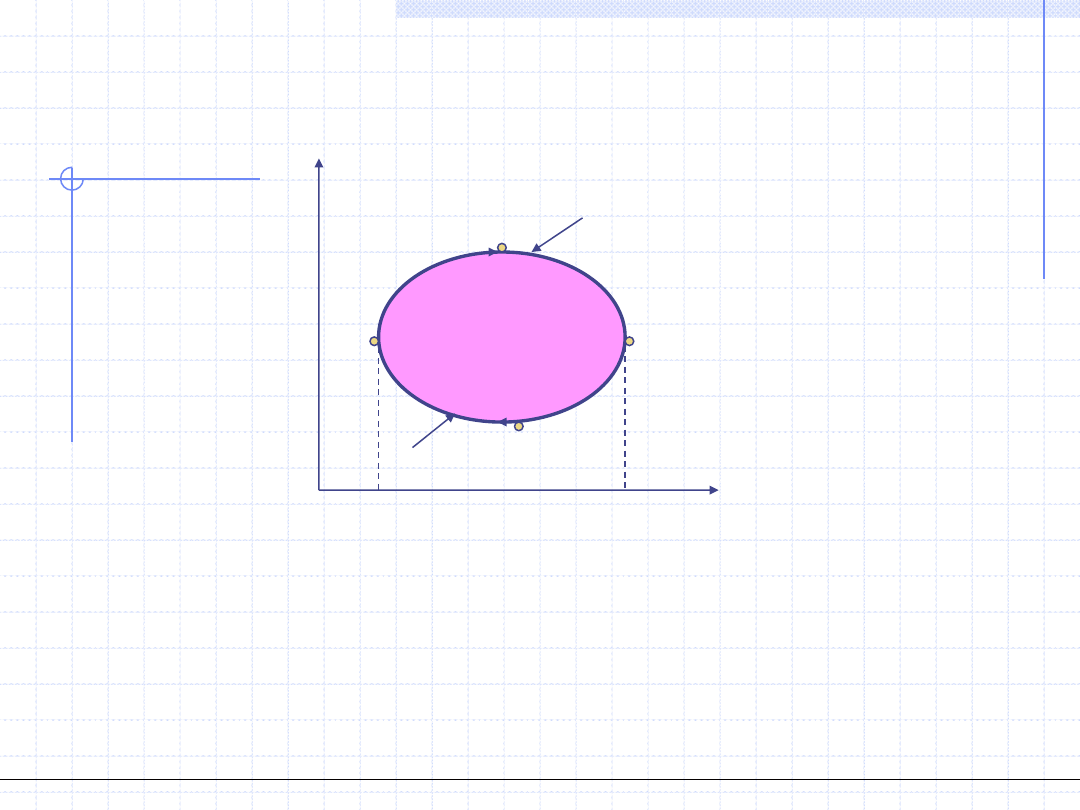
Na mocy I zasady termodynamiki możemy napisać dla dowolnego obiegu:

o

o

A

A

o

o

o

o

q

w

u

u

u

w

u

q

0

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

38

38

Obiegi prawobieżne – silnikowe

Sprawność obiegu silnikowego

w

o

=q

o

T

s

A’

B’

C’

D’

E’

F’

T

g

T

d

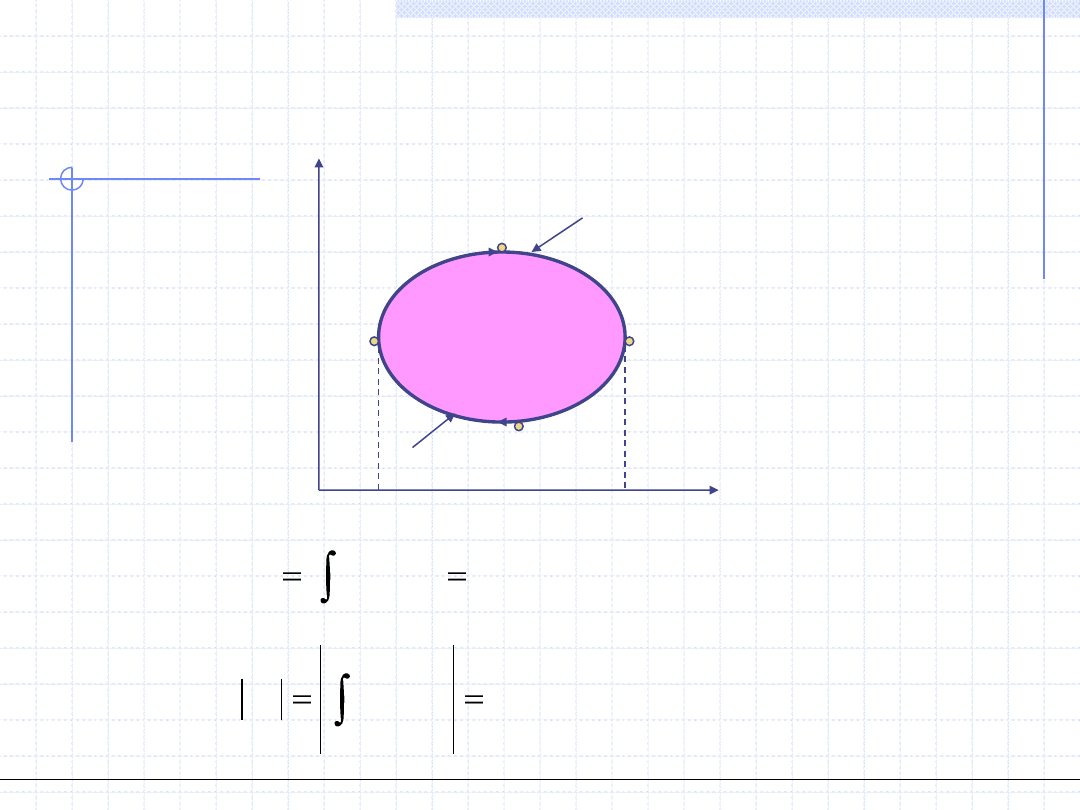
Celem obiegu silnikowego jest ciągłe przetwarzanie energii cieplnej (ciepła)

w energię mechaniczną (pracę). Aby ten cel zrealizować konieczne jest

dostarczenie do układu pewnej ilości ciepła – q

g

w temperaturze T

g

i odebranie

od układu części tego ciepła – q

d

w temperaturze T

d

.

Różnica tych wartości zostanie zamieniona na pracę w

o

. Ciepło q

g

jest równe

polu pod krzywą T

g

czyli polu figury A’B’C’E’F’A’. Ciepło q

d

ma znak ujemny

(jest odbierane z układu) a jego wartość jest polem pod krzywą T

d

czyli polem figury C’D’A’F’E’C’.

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

39

39

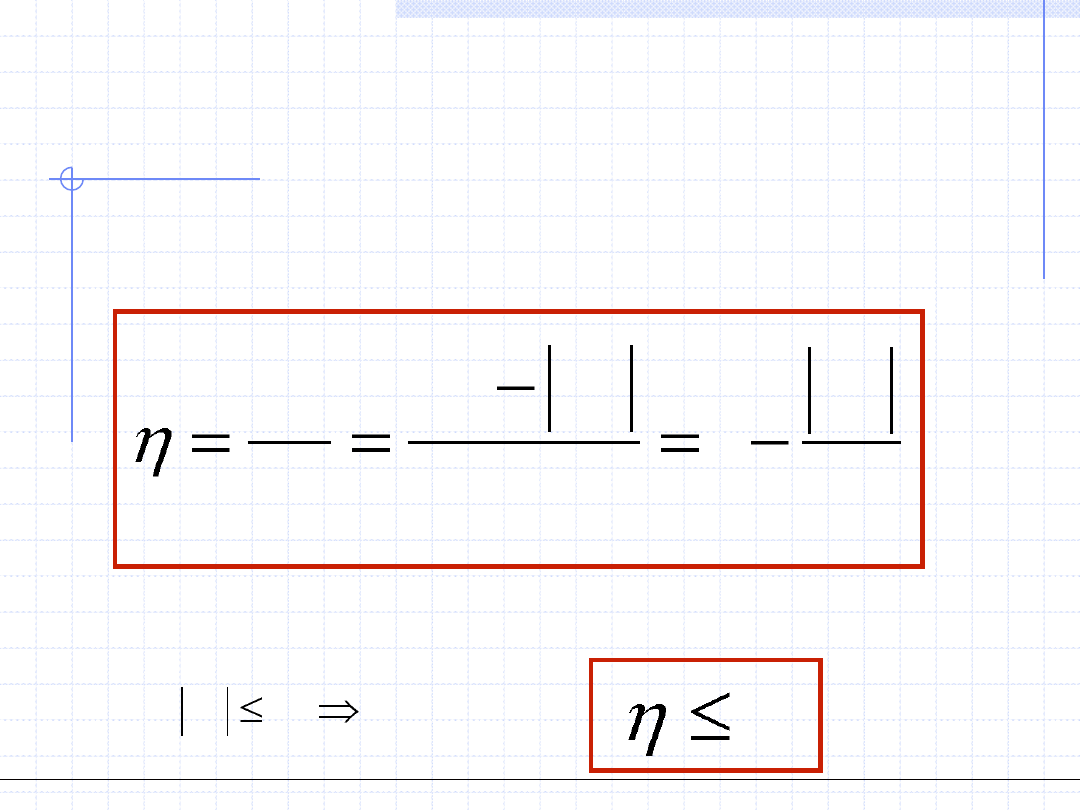
Obiegi prawobieżne – silnikowe

Sprawność obiegu silnikowego cd.

w

o

=q

o

T

s

A’

B’

C’

D’

E’

F’

T

g

T

d

)

'

'

'

'

'

'

(

)

(

)

'

'

'

'

'

'

(

)

(

'

'

'

'

A

F

E

C

D

A

Pole

ds

s

T

q

A

F

E

C

B

A

Pole

ds

s

T

q

C

A

C

A

s

s

d

d

s

s

g

g

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

40

40

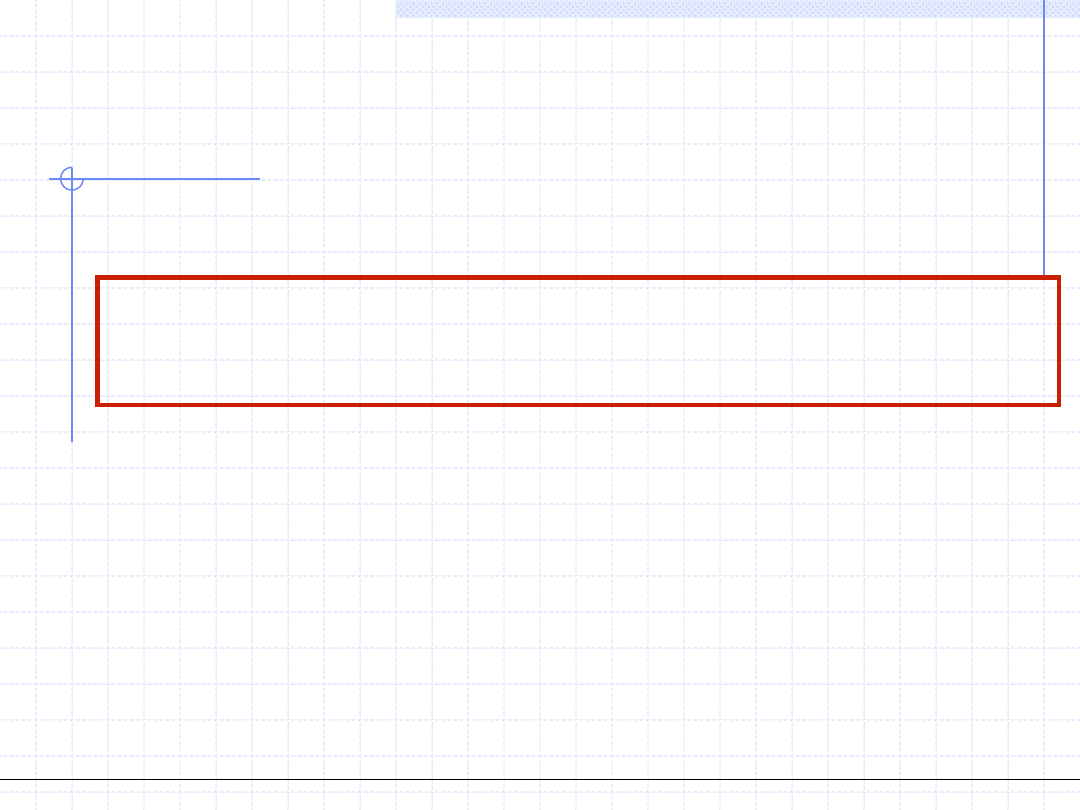
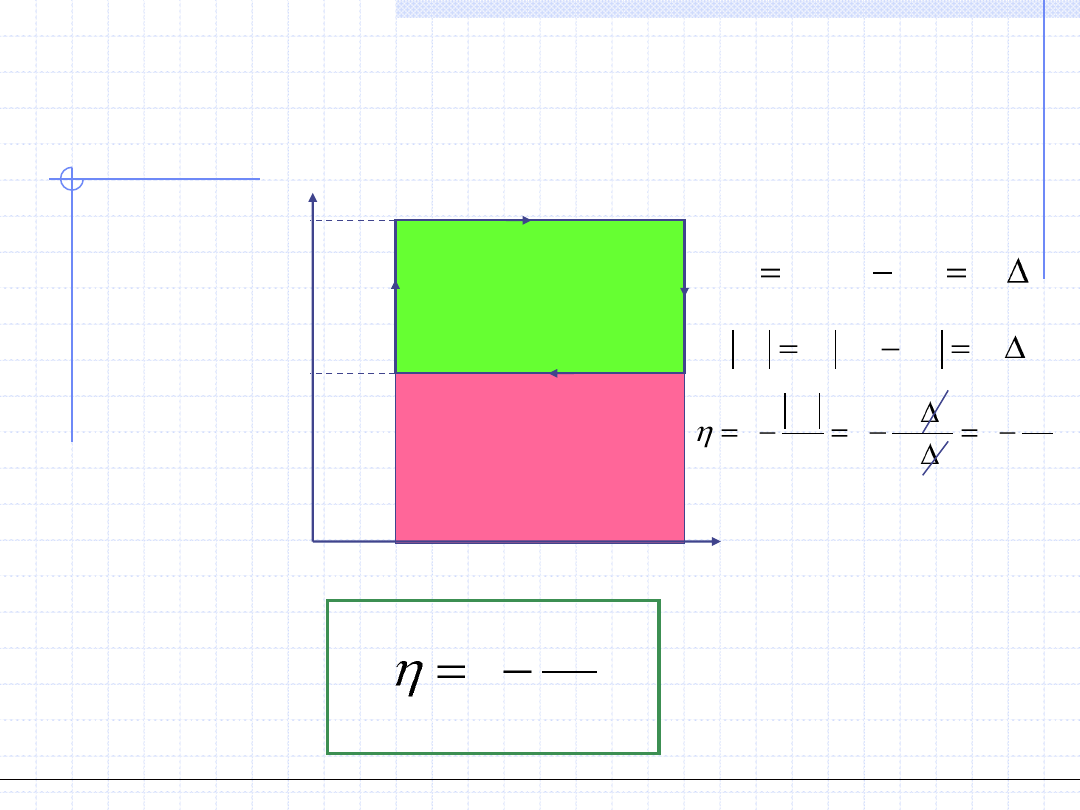
Obiegi prawobieżne – silnikowe

Sprawność obiegu silnikowego cd.

g

d

g

d

g

g

o

q

q

q

q

q

q

w

1

g

d

q

q

Stosunek otrzymanej w obiegu pracy do ciepła dostarczonego nazywamy

sprawnością obiegu silnikowego.

Z I zasady termodynamiki czyli z prawa zachowania energii wynika że:

1

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

41

41

Obieg silnikowy a II zasada

termodynamiki

Działanie obiegu silnikowego jest ściśle związane z II zasadą termodynamiki.

Jedno z wielu sformułowań tej zasady jest następujące:

Ciągłe przetwarzanie ciepła na pracę jest możliwe tylko za pomocą

obiegu silnikowego, w którym układ pobiera ciepło w temperaturze

wyższej i oddaje ciepło w temperaturze niższej.

W związku z tym w każdym obiegu silnikowym można wyróżnić część otoczenia

z którego będzie pobierane ciepło w temperaturze T

g

. Część tą będziemy

nazywać źródłem górnym lub grzejnikiem. W innej części otoczenia

o temperaturze T

d

będzie się odbywało oddawanie przez układ części ciepła

otoczęniu. Ta część otoczenia jest nazywana źródłem dolnym lub chłodnicą.

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

42

42

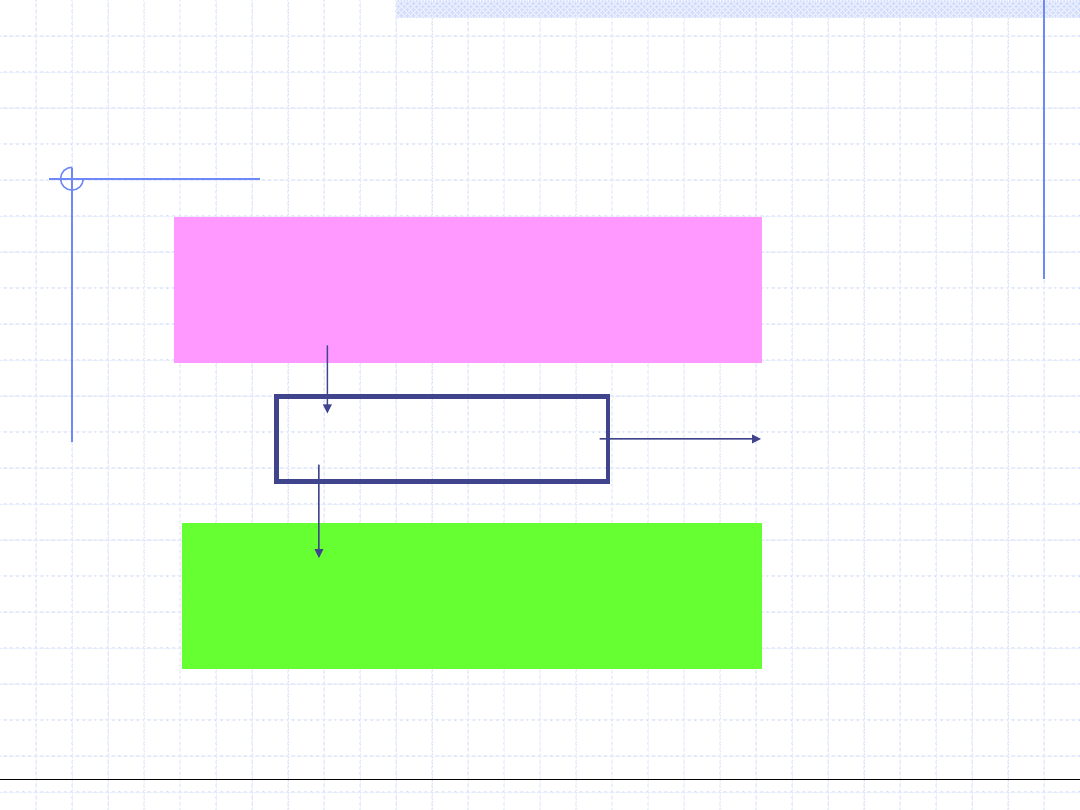
Schemat obiegu silnikowego

Źródło górne (grzejnik)

T

g

T

d

Źródło dolne (chłodnica)

q

g

|q

d

|

w

o

=q

g

-|q

d

|

Silnik

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

43

43

Obieg Carnota

Wzorcowym obiegiem silnikowym jest obieg rozważany przez francuskiego

uczonego Carnota na początku XIX wieku. Czynnikiem w obiegu Carnota jest

gaz doskonały. Na obieg składają się dwie przemiany izotermiczne i dwie

przemiany adiabatyczne. Na wykresie p – v obieg wykres obiegu Carnota

jest dosyć prosty:

p

v

1

2

3

T

g

=const., pv=const., q

g

>0

q=0, s=const., pv

γ

=

const.

T

d

=const., pv=const., q

d

<0

q=0, s=const., pv

γ

=const.

4

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

44

|q

d

|

44

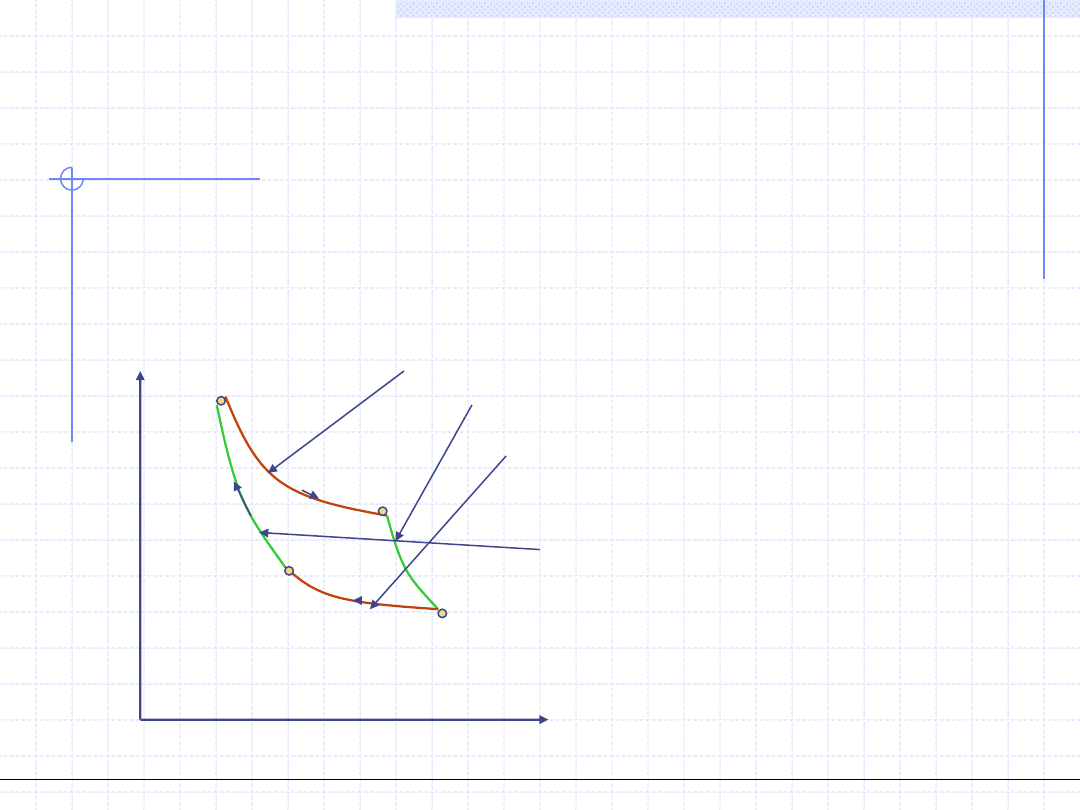
Obieg Carnota cd.

s

T

s

s

T

q

g

g

g

)

(

1

2

Wykres obiegu Carnota jest szczególnie prosty w układzie T - s:

T

s

w

o

=q

o

=q

g

-|q

d

|

1

2

3

4

T

g

=T

1

=T

2

T

d

=T

3

=T

4

s

1

=s

4

s

2

=s

3

g

d

T

T

1

s

T

s

s

T

q

d

d

d

)

(

3

4

g

d

g

d

g

d

T

T

s

T

s

T

q

q

1

1

1

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

45

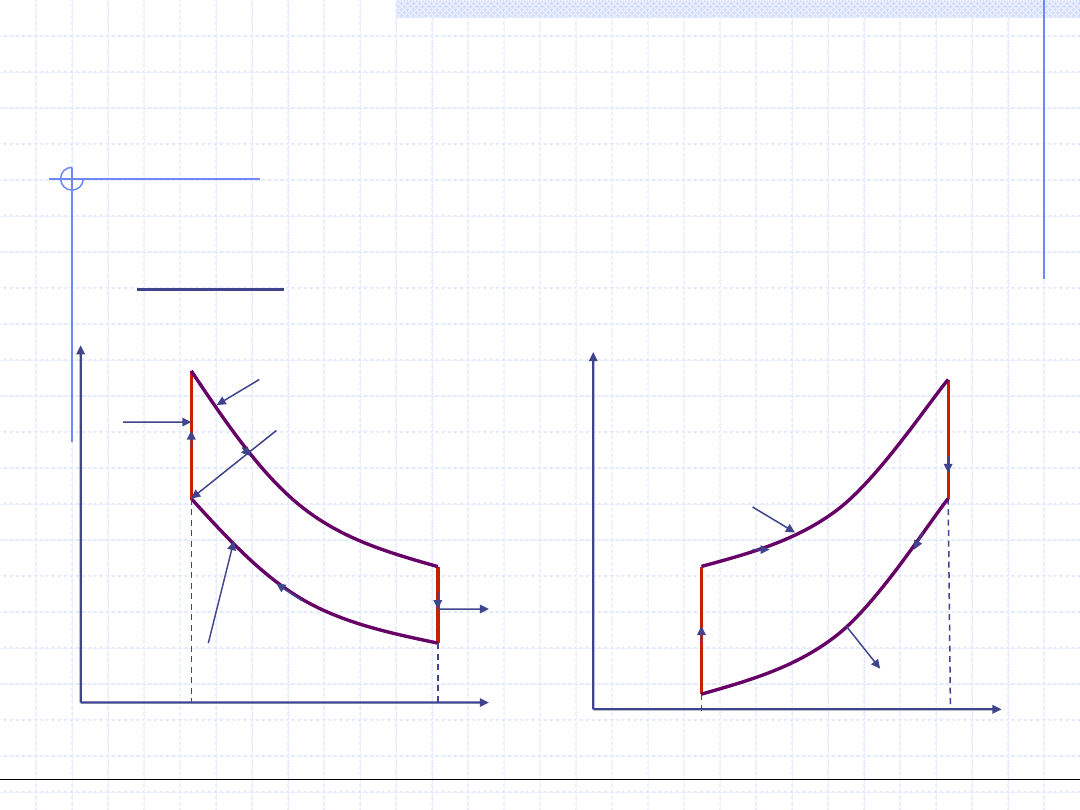
Rzeczywiste obiegi silnikowe

Obieg Carnota jest obiegiem idealnym w rzeczywistości trudno realizowalnym.

W szczególności trudne do przeprowadzenia są przemiany izotermiczne.

Rzeczywiste realizacje silników są modelowane za pomocą szeregu różnych

obiegów, z których najważniejsze są obieg Otto i obieg Diesla.

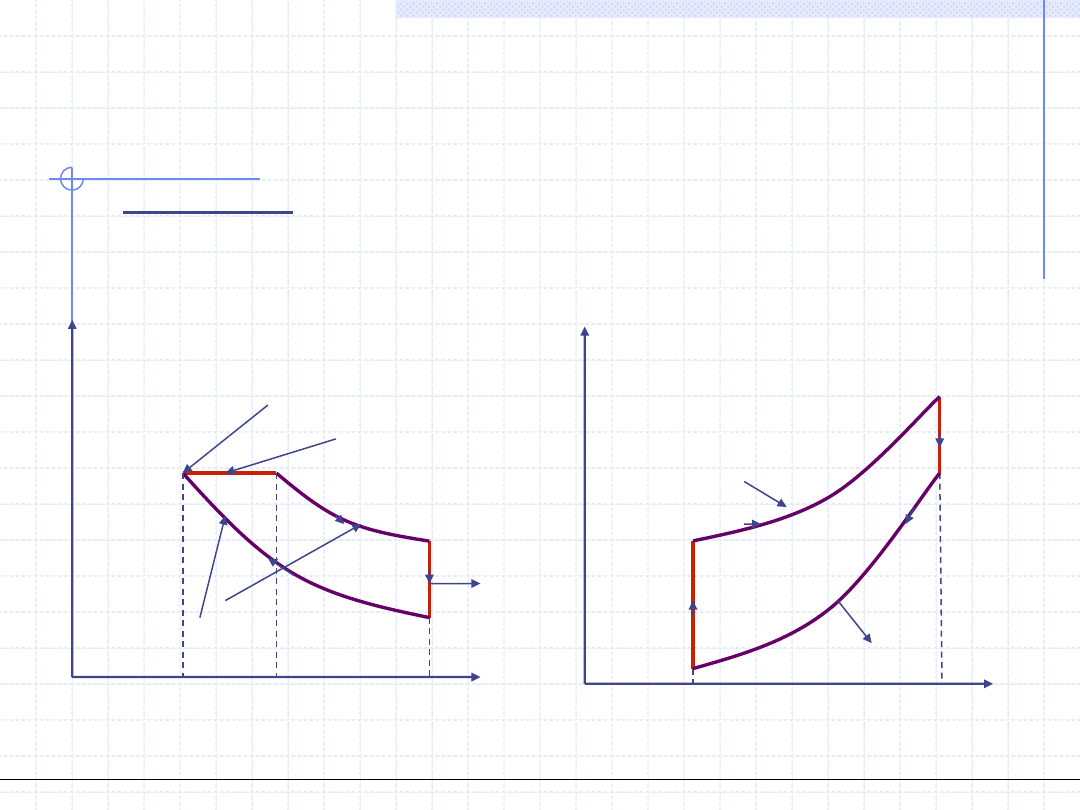
Obieg Otto jest to wzorcowy obieg silnika spalinowego z zapłonem iskrowym

(niskoprężnego) składający się z dwu izochor i dwu adiabat:

p

v

1

2

3

4

v

2

=v

3

v

1

=v

4

w

o

=q

o

q=0, pv

γ

=const.

q

g

q

d

q=0, pv

γ

=const.

zapłon paliwa

s

1

2

3

4

s

1

=s

2

s

3

=s

4

T

q

d

,v=const.

q

g

,v=const.

q

o

=w

o

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

46

46

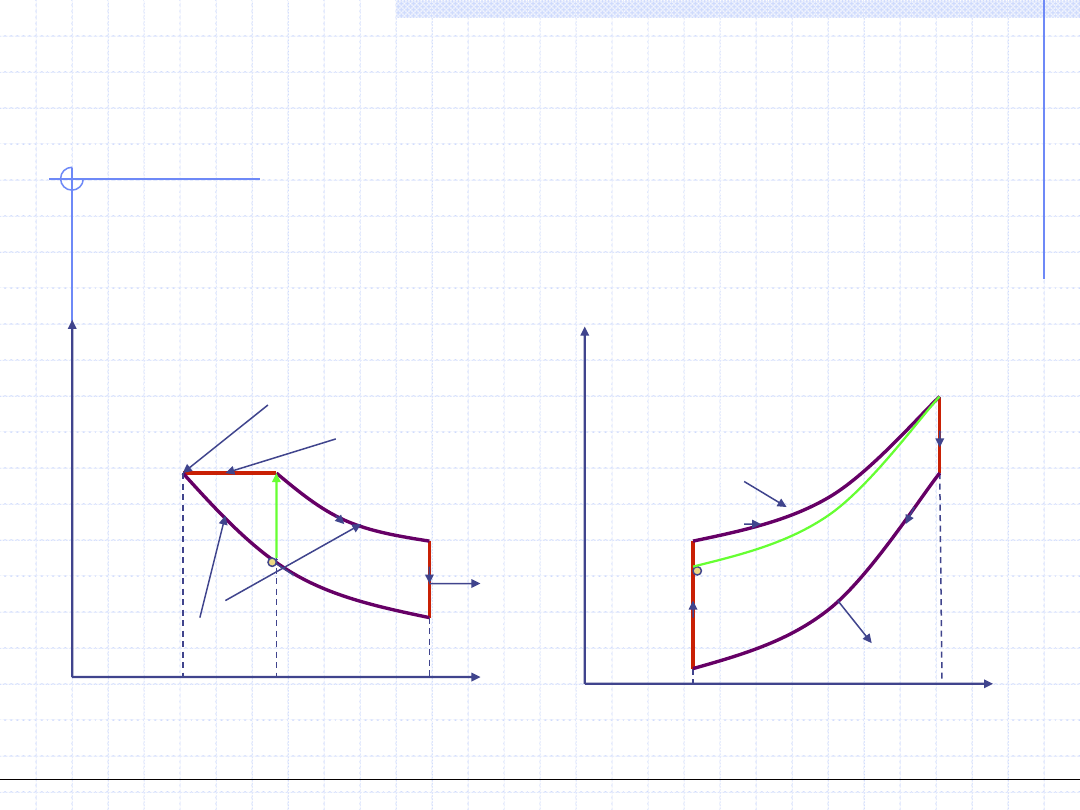
Obieg Diesla

Obieg Diesla jest to wzorcowy obieg silnika spalinowego z zapłonem

samoczynnym (wysokoprężnego) składający się z dwu adiabat, jednej izobary

oraz jednej izochory:

p

v

1

2

3

4

v

2

v

3

v

1

=v

4

w

o

=q

o

q

g

q

d

q=0, pv

γ

=const.

zapłon paliwa

s

1

2

3

4

s

1

=s

2

s

3

=s

4

T

q

d

,v=const.

q

g

,p=const.

q

o

=w

o

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

47

47

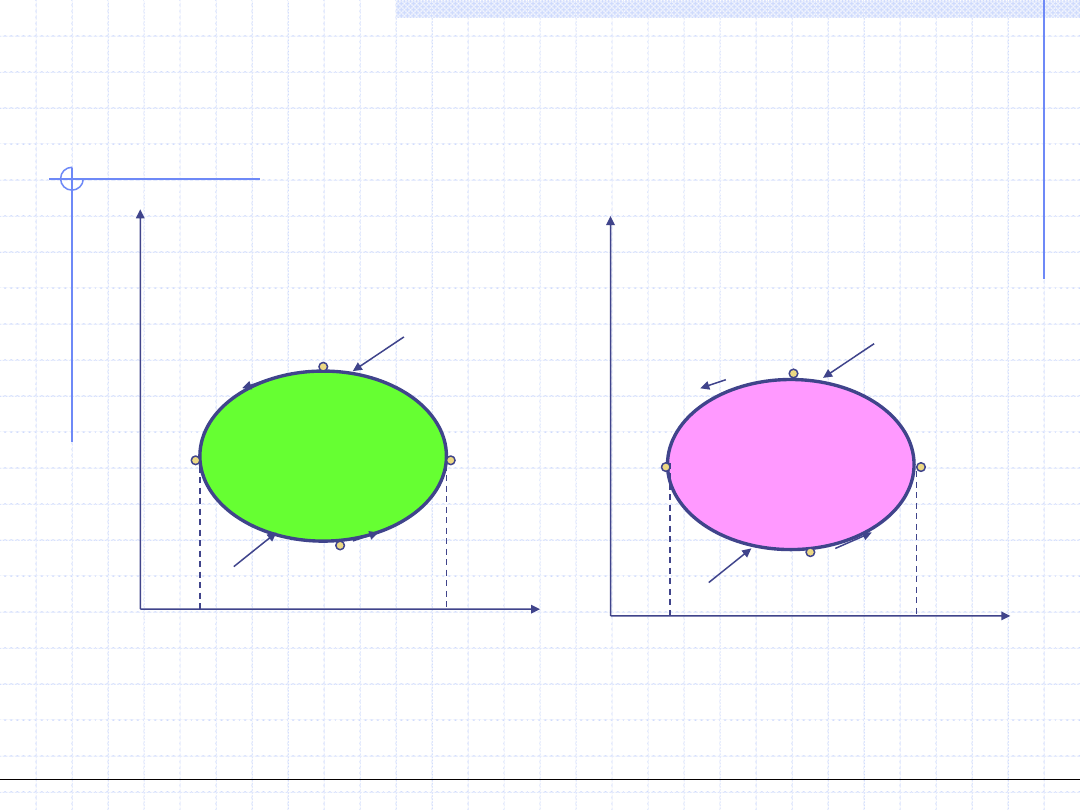
Obieg Diesla

Porównajmy obieg Diesla z obiegiem Otto:

p

v

1

2

3

4

v

2

v

3

v

1

=v

4

w

o

=q

o

q

g

q

d

q=0, pv

γ

=const.

zapłon paliwa

s

1

2

3

4

s

1

=s

2

s

3

=s

4

T

q

d

,v=const.

q

g

,p=const.

q

o

=w

o

2’

2’

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

48

48

Obiegi lewobieżne - chłodnicze

-w

o

p

v

A

B

C

D

E

F

p

g

p

d

-q

o

T

s

A’

B’

C’

D’

E’

F’

T

g

T

d

-w

o

=-w

g

-w

d

=Pole(ABCEFA)-Pole(CDAFEC)=Pole(ABCDA)

-q

o

=-q

g

-q

d

=Pole(A’B’C’E’F’A’)-Pole(C’D’A’F’E’C’)=Pole(A’B’C’D’A’)

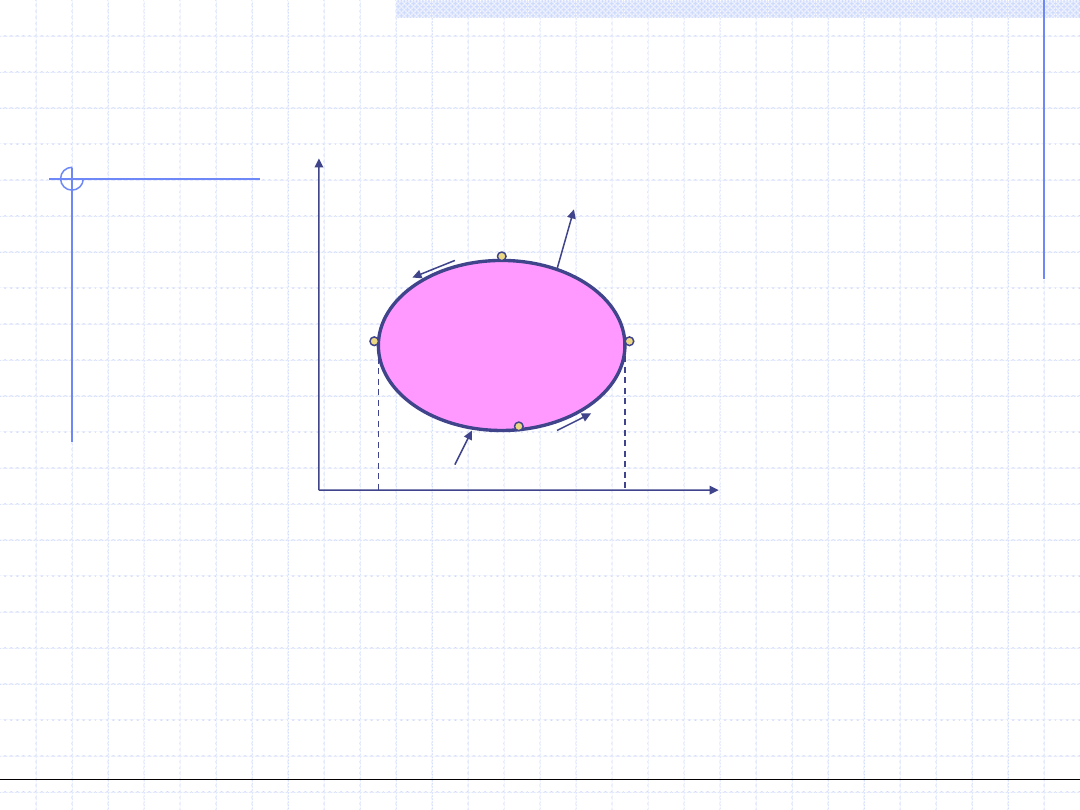
Obiegi, w których kierunek przemian jest przeciwny do ruchu wskazówek

zegara nazywamy lewobieżnymi lub chłodniczymi.

Wykresy takich obiegów są analogiczne jak silnikowych, z tym że kierunki

wszystkich przemian są odwrotne a znaki ciepła i pracy przeciwne.

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

49

49

Obiegi lewobieżne – chłodnicze cd.

-w

o

=-q

o

T

s

T

g

T

d

q

g

<0

q

d

>0

W wyniku działania obiegu chłodniczego następuje transport ciepła ze

źródła dolnego do źródła górnego. Aby ten transport był możliwy na układzie

należy wykonać pracę –w

o

, której wartość bezwzględna jest określona polem

figury opisującej obieg. Schematycznie obieg chłodniczy można zilustrować

podobnie jak obieg silnikowy:

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

50

50

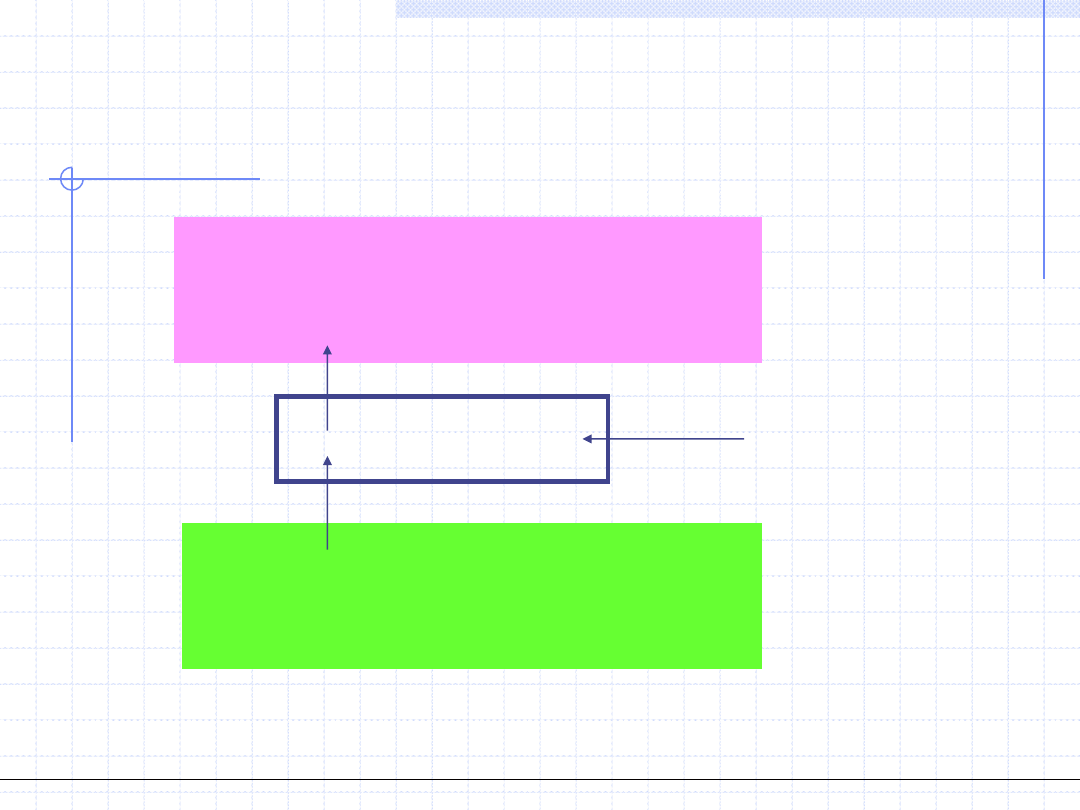
Schemat obiegu chłodniczego

Źródło górne (chłodnica)

T

g

T

d

Źródło dolne (zamrażalnik)

-q

g

q

d

-w

o

=-q

g

-q

d

Lodówka

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

51

51

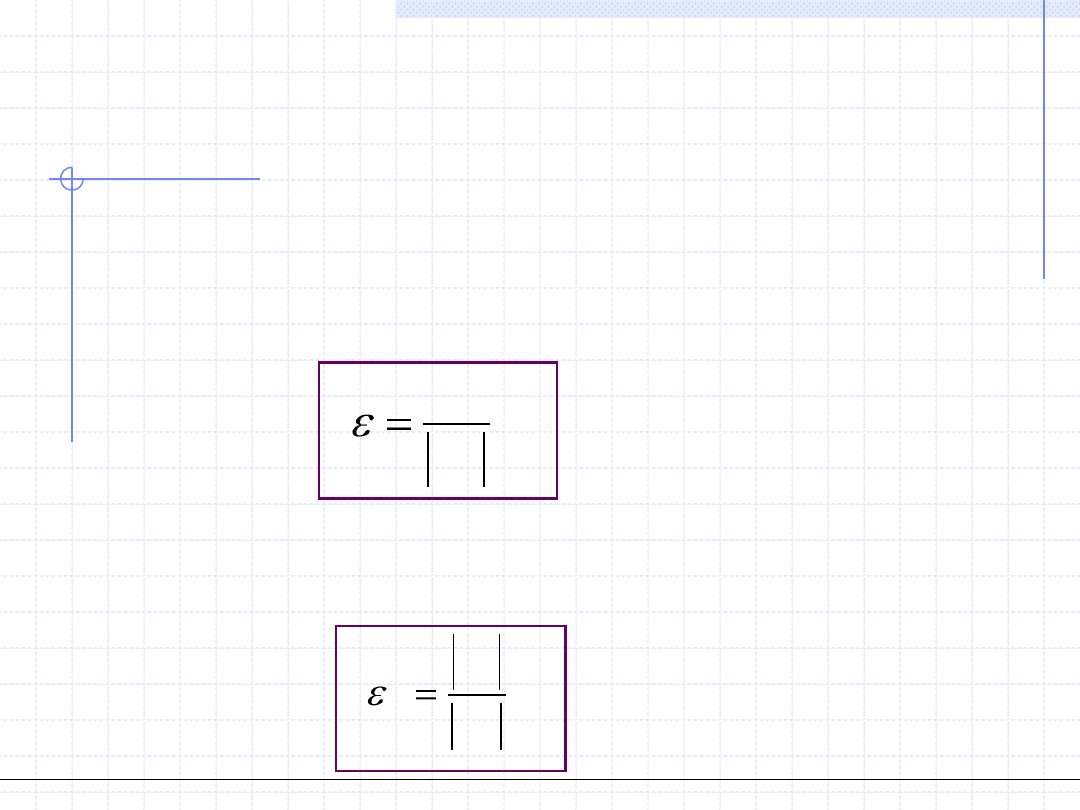
Obiegi chłodnicze - realizacje

o

d

w

q

Obiegi lewobieżne mogą mieć dwa cele praktyczne:

1. Cel pierwszy to odebranie pewnej ilości ciepła ze źródła dolnego.

Urządzenie realizujące taki cel nazywamy chłodziarką lub lodówką.

Sprawność takiego urządzenia jest określona wzorem:

Sprawność chłodziarki może mniejsza

lub większa od jedności.

2. Cel drugi obiegu lewobieżnego to dostarczenie ciepła do źródła górnego

czyli jego ogrzanie. Urządzenie o taki celu nazywamy pompą cieplną.

Sprawność pompy cieplnej określamy wzorem:

o

g

p

w

q

Można zauważyć, że sprawność pompy

cieplnej jest zawsze liczbą większą od 1.

Ogólnotechniczne podstawy biotechnologii z grafiką inżynierską, Wydział Chemiczny Politechniki Wrocławskiej, 2009/2010, prof. Antoni Kozioł

52

Na tym kończymy wykłady

z „Ogólnotechnicznych podstaw biotechnologii

z grafiką inżynierską”

Dziękuję bardzo Państwu za uwagę

i życzę powodzenia w zaliczeniu,

które odbędzie się:

15.01.2010 – termin podstawowy

- godz. 11.15 nieparzyste numery albumu

- godz. 12.15 parzyste numery albumu

22.01.2010 – termin poprawkowy