© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

1

OGÓLNOTECHNICZNE

PODSTAWY BIOTECHNOLOGII

Z GRAFIKĄ INŻYNIERSKĄ

Wykład V

Podstawowe zasady statyki

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ELEMENTY STATYKI

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

POJĘCIA STOPNIA SWOBODY I WIĘZÓW

W statyce bardzo ważną rolę odgrywają pojęcia stopni swobody

oraz więzów.

Stopniem swobody nazywamy możliwość wykonywania przez dane

ciało pewnego ruchu niezależnego od innych ruchów.

Punkt materialny ma na płaszczyźnie 2, a w przestrzeni 3 stopnie

swobody.

Ciało doskonale sztywne ma na płaszczyźnie 3, a w przestrzeni 6

stopni swobody.

Więzami nazywamy warunki ograniczające ruch punktu lub ciała.

Więzy zawsze zmniejszają liczbę stopni swobody.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

AKSJOMATY STATYKI

Statyka, podobnie jak większość nauk opiera się na zestawie pewnych

twierdzeń zaczerpniętych z innych dziedzin, które przyjmuje się jako

prawdziwe. Twierdzenia te nazywamy aksjomatami.

Aksjomaty statyki wynikają z podstawowych praw fizyki i zasad

rachunku wektorowego.

Ja przedstawię Państwu ujęcie, w którym funkcjonuje 6 aksjomatów.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

AKSJOMATY STATYKI

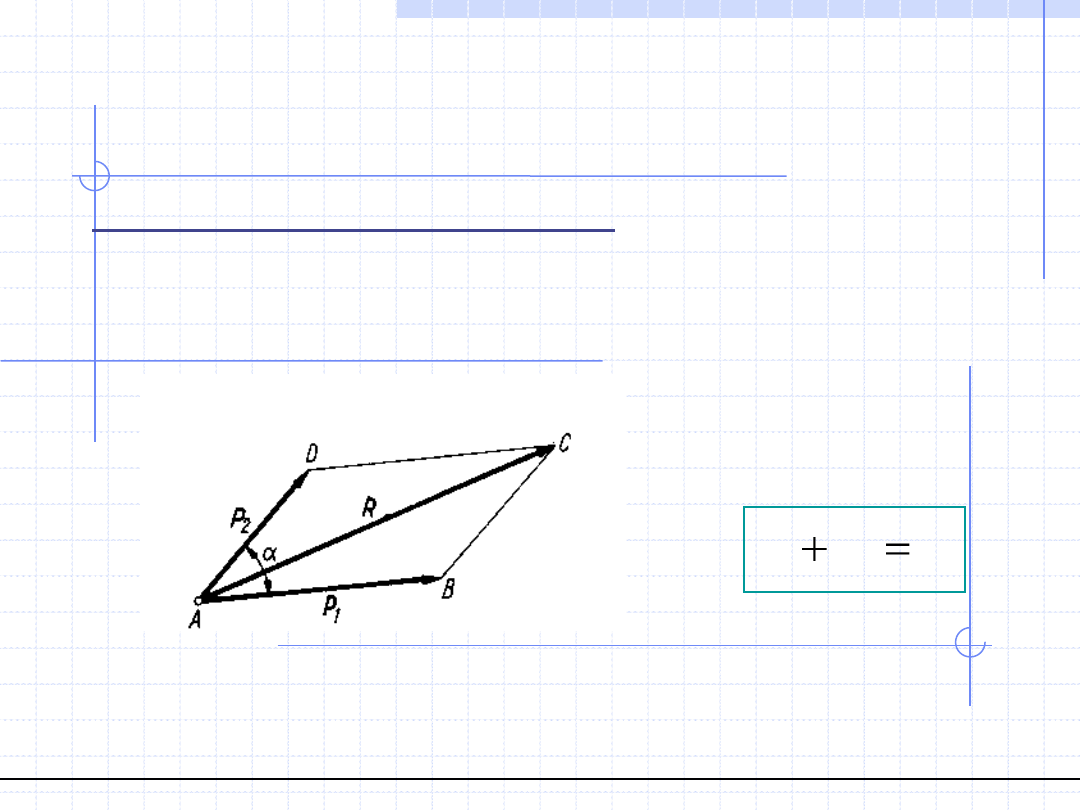
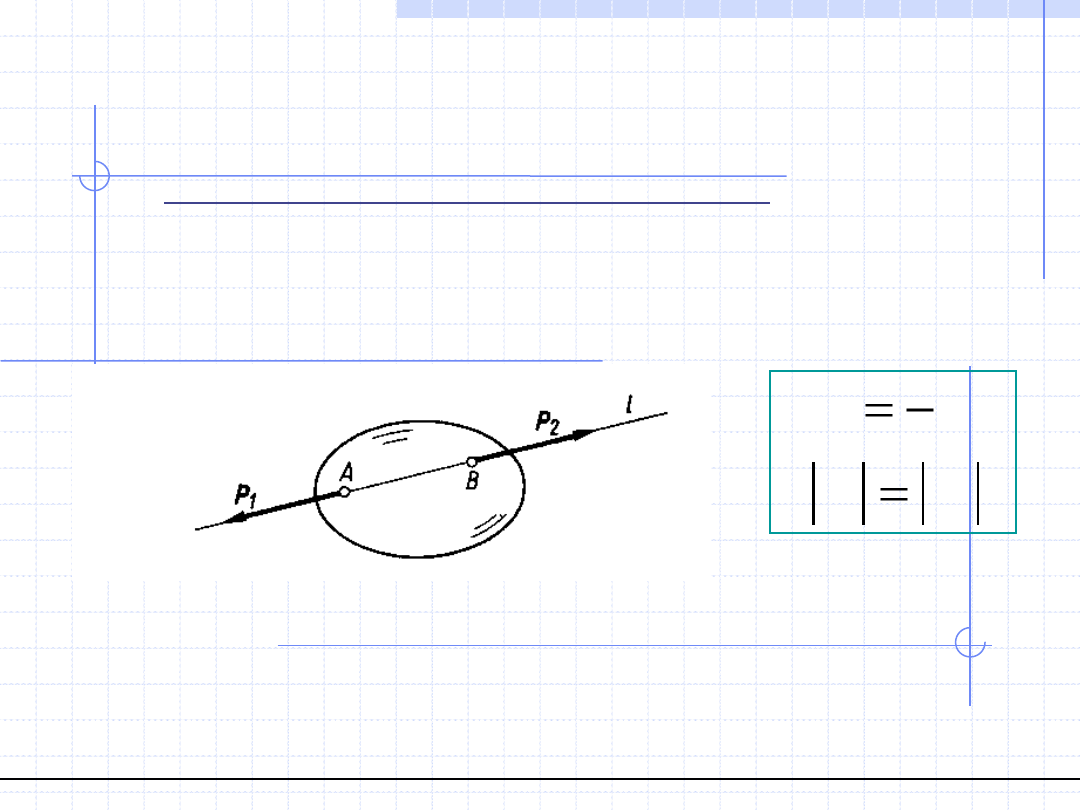
Aksjomat I (zasada dodawania sił):
Dwie siły P1 i P2 działające na ten sam punkt można zastąpić jedną

siłą R działającą w tym samym punkcie i będącą sumą wektorową

wektorów P1 i P2.
Siłę R nazywamy wypadkową układu sił P1 i P2.

R

P

P

2

1

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

AKSJOMATY STATYKI cd.

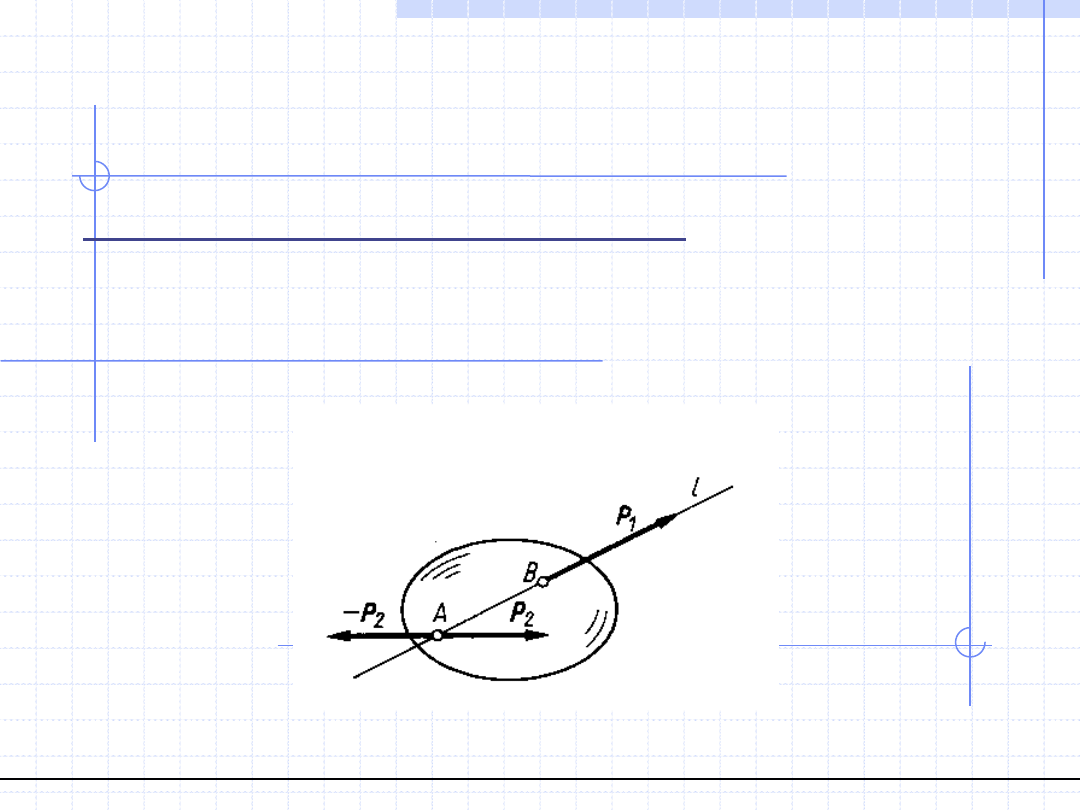
Aksjomat II (zasada równoważności sił):
Jeżeli do ciała przyłożone są dwie siły P

1

i P

2

to równoważą się

one tylko wtedy, kiedy mają tę samą linię działania, te same

wartości liczbowe i przeciwne zwroty.

2

1

2

1

P

P

P

P

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

AKSJOMATY STATYKI cd.

Aksjomat III (zasada układu zerowego):

Skutek działania dowolnego układu sił, przyłożonego do ciała nie zmieni

się, jeżeli do tego układu dodamy lub odejmiemy dowolny układ

równoważących się sił P

2

i -P

2

czyli tzw. układ zerowy.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

AKSJOMATY STATYKI cd.

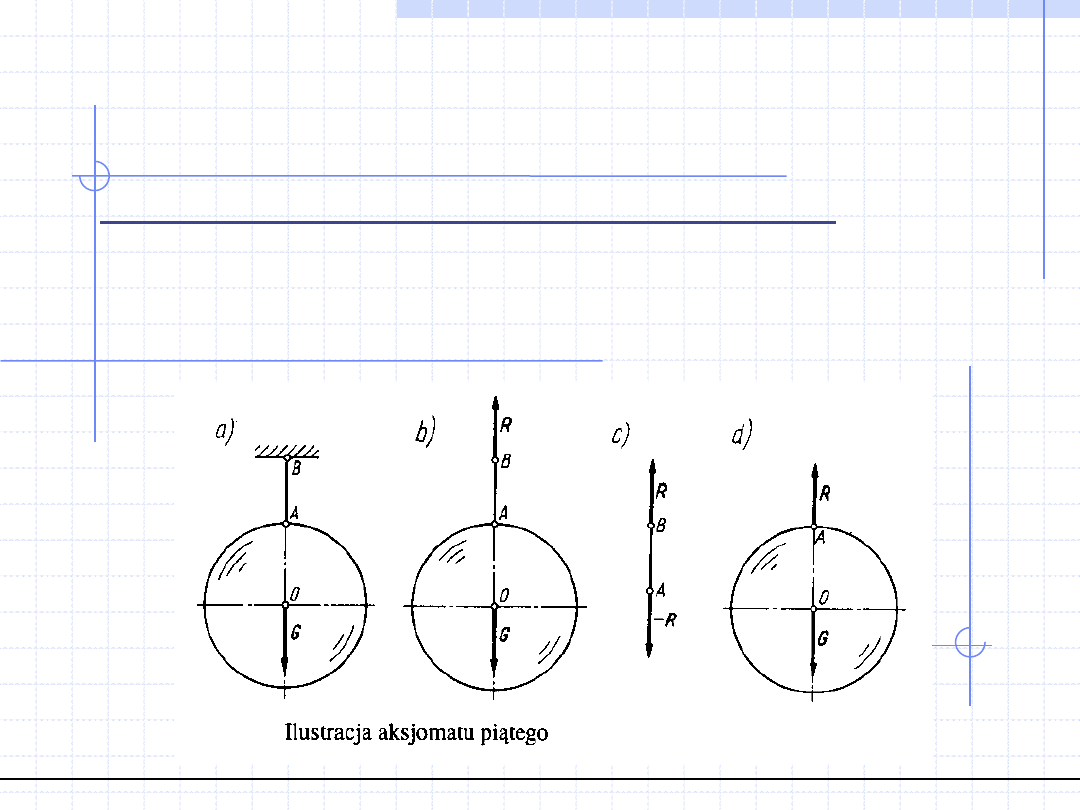
Aksjomat IV (zasada zesztywnienia):

Jeżeli ciało odkształcalne znajduje się w równowadze pod

działaniem pewnego układu sił, to również pozostanie w

równowadze ciało doskonale sztywne (nieodkształcalne)

identyczne geometrycznie, pod wpływem tego samego

układu sił.

Stwierdzenie odwrotne nie jest prawdziwe, tzn. że

równowaga ciała doskonale sztywnego jest konieczna ale nie

wystarczająca do równowagi ciała rzeczywistego.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

AKSJOMATY STATYKI cd.

Aksjomat V (zasada działania i przeciwdziałania):

Każdemu działaniu towarzyszy równe co do wartości o przeciwnym

zwrocie i leżace na tej samej prostej przeciwdziałanie. To

przeciwdziałanie nazywamy siłą reakcji.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

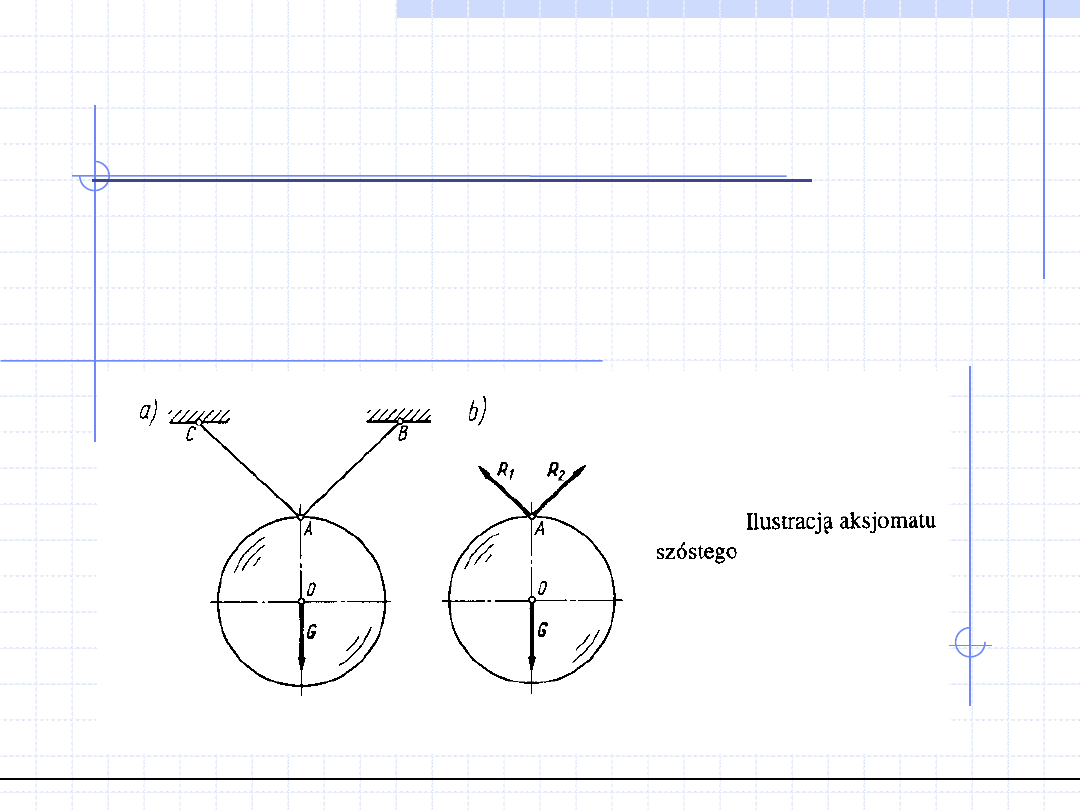
AKSJOMATY STATYKI cd.

Aksjomat VI (zasada oswobodzenia od więzów):

Każde ciało nieswobodne (ograniczone więzami) można myślowo

oswobodzić z więzów, zastępując ich działania reakcjami, a następnie

rozpatrywać ciało swobodne (bez więzów) znajdujące się

pod działaniem sił czynnych i biernych (reakcji więzów).

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

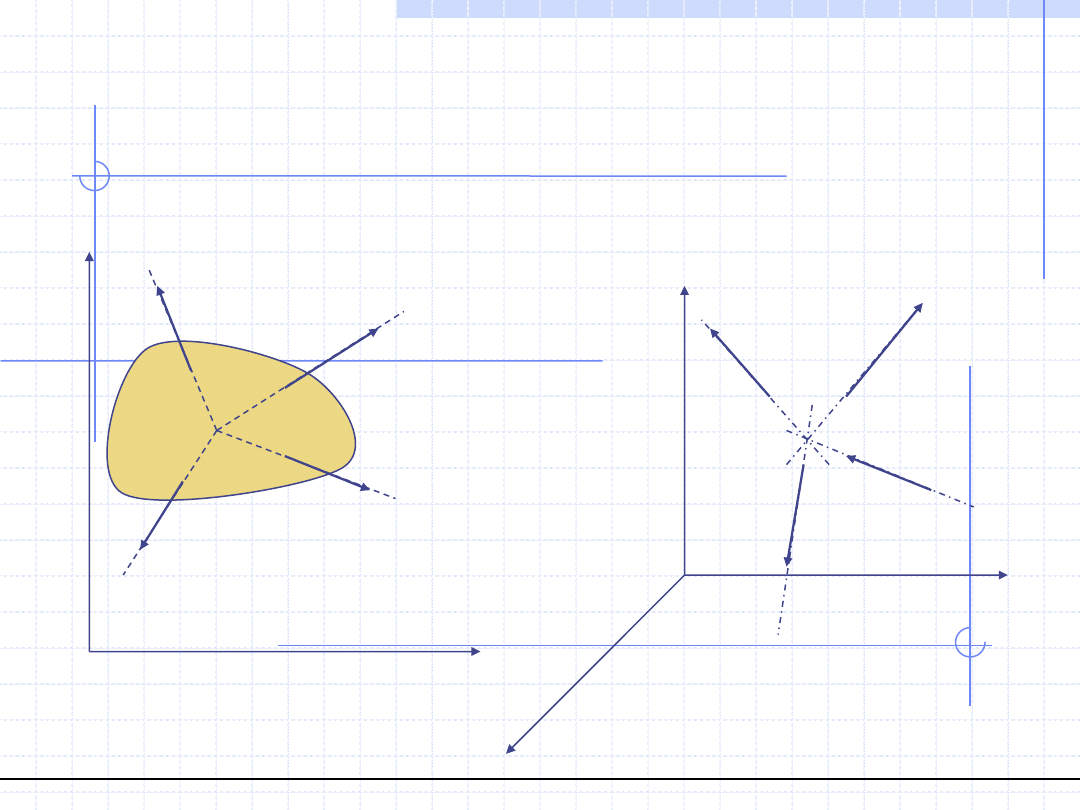
ZBIEŻNE UKŁADY SIŁ

Układy sił, których linie działania przecinają się w jednym punkcie nazywamy

zbieżnymi układami sił. Takie układy mogą być płaskie lub przestrzenne.

x

y

z

M

F

1

F

2

F

3

F

4

x

y

M

F

1

F

2

F

3

F

4

O

O

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

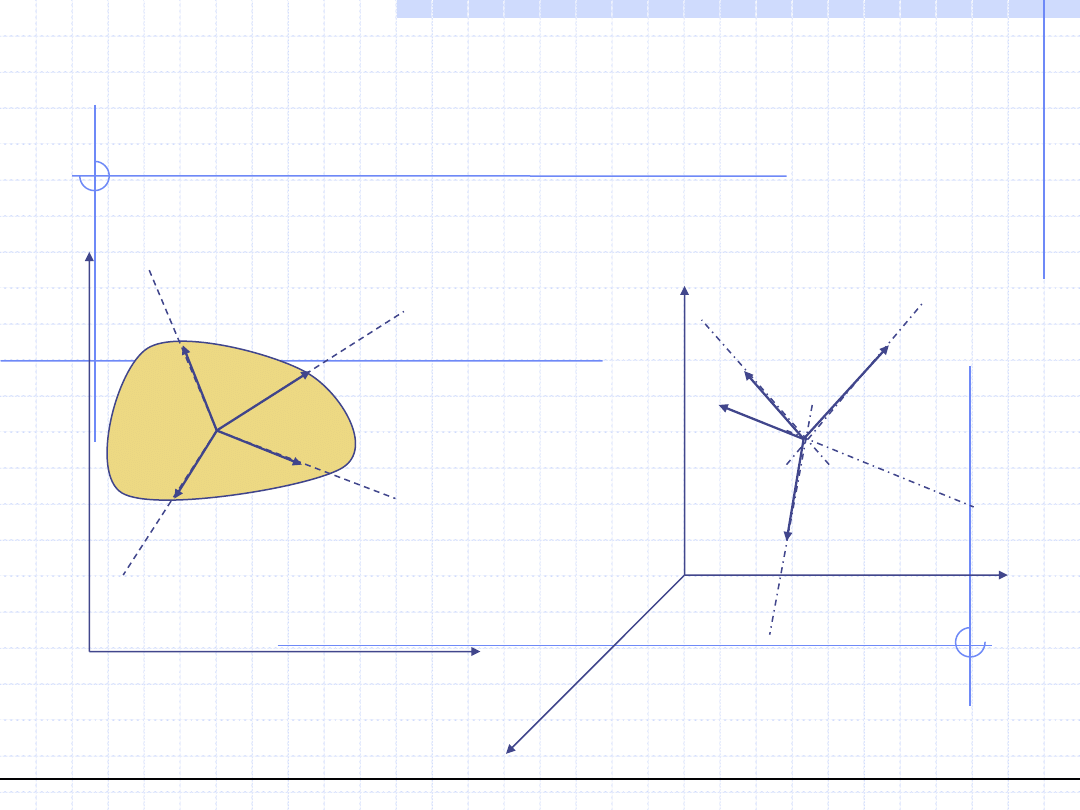
ZBIEŻNE UKŁADY SIŁ

WYZNACZANIE WYPADKOWEJ

Wypadkową zbieżnego układu sił wyznacza się przesuwając wszystkie siły do punktu

przecięcia i dodając wektory dowolną metodą.

x

y

z

M

F

1

F

2

F

3

F

4

x

y

M

F

1

F

2

F

3

F

4

O

O

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

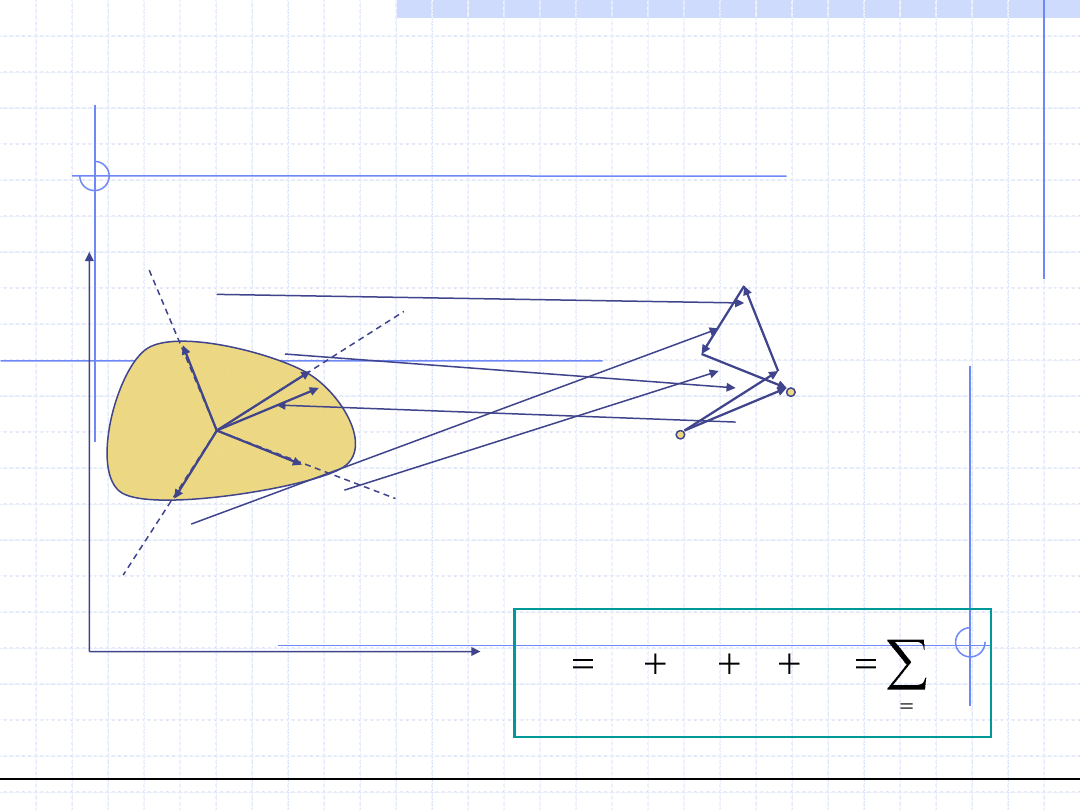
ZBIEŻNE UKŁADY SIŁ

WYZNACZANIE WYPADKOWEJ cd.

W przypadku płaskiego układu sił możemy zastosować metodę wieloboku. W przypadku

układu przestrzennego należy geometrycznie dodawać kolejne siły metodą równoległoboku

lub zbudować przestrzenny wielobok sił.

x

y

M

F

1

F

2

F

3

F

4

O

W

W

A

K

Stosując algebraiczny zapis sił jako wektorów

znajdowanie wypadkowej polega na dodawaniu

wektorowym wszystkich sił składowych, czyli:

n

i

i

n

F

F

F

F

W

1

2

1

...

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ZBIEŻNE UKŁADY SIŁ

PODSTAWOWE TWIERDZENIE O RÓWNOWADZE

n

i

i

F

1

0

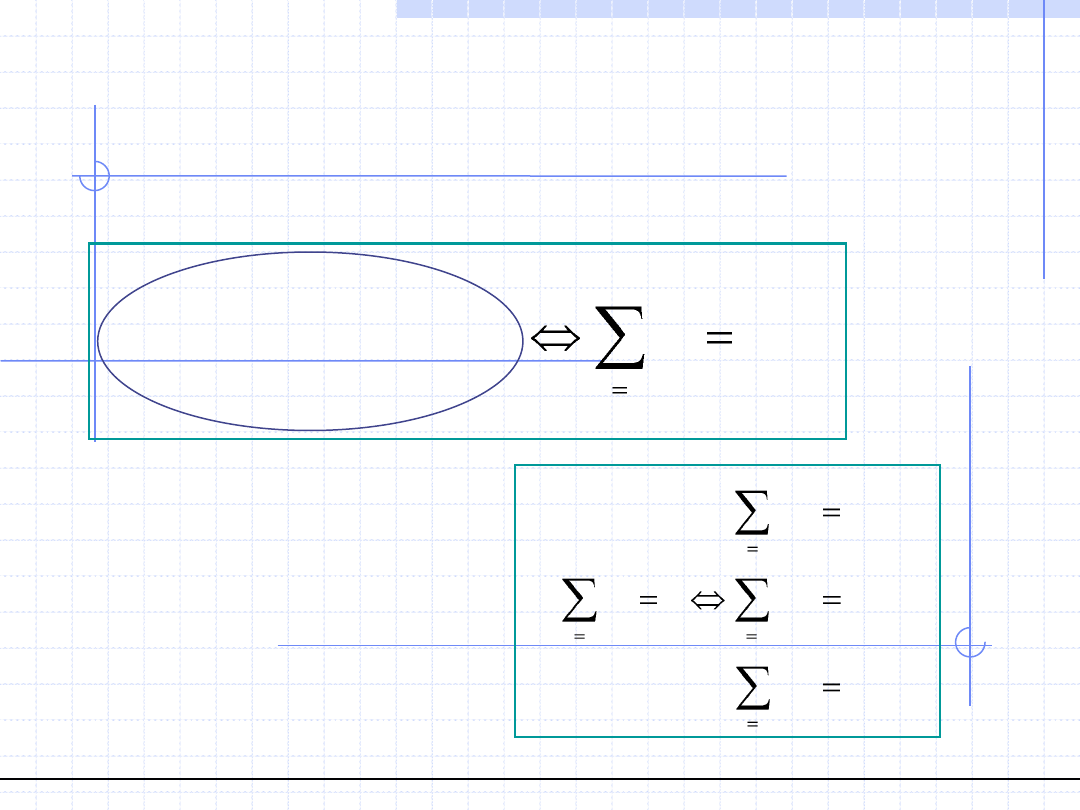
Z podstawowych praw fizyki wynika twierdzenie o równowadze ciała na które

działa zbieżny układ sił:

Ciało na które działa układ

sił zbieżnych F

1

,F

2

,…F

n

jest w równowadze statycznej

Warunek po prawej stronie równoważności

można zapisać algebraicznie za pomocą

trzech równań dotyczących składowych:

n

i

zi

n

i

yi

n

i

xi

n

i

i

F

F

F

F

1

1

1

1

0

0

0

0

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

MOMENT SIŁY WZGLĘDEM PUNKTU

F

r

M

O

x

Pojęcie momentu siły jest nieodzowne przy rozpatrywaniu sił niezbieżnych

działających na ciało płaskie lub przestrzenne. Istnieją różne momenty sił.

Najważniejszy jest moment siły względem punktu.

F

r

O

A

B

M

O

.

h

y

z

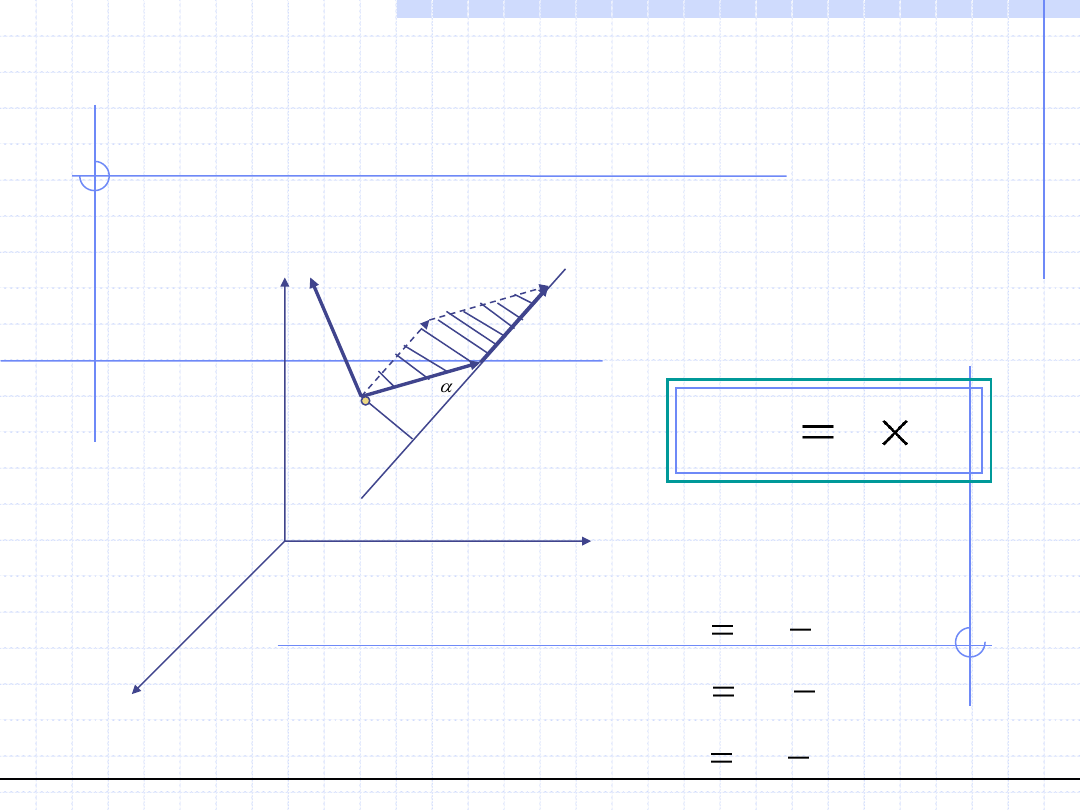
Momentem siły F względem punktu O

nazywamy wektor M

O

będący iloczynem

wektorowym wektorów r i F czyli

Wektor r określa wzajemne położenie

punktu O i punktu zaczepienia siły A.

Składowe wektora r można obliczyć

za pomocą wzorów:

O

A

z

O

A

y

O

A

x

z

z

r

y

y

r

x

x

r

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

MOMENT SIŁY WZGLĘDEM PUNKTU cd.

x

Definicja momentu siły łącznie z definicją iloczynu wektorowego wyznaczają

podstawowe własności momentu siły.

F

r

O

A

B

M

O

.

h

y

z

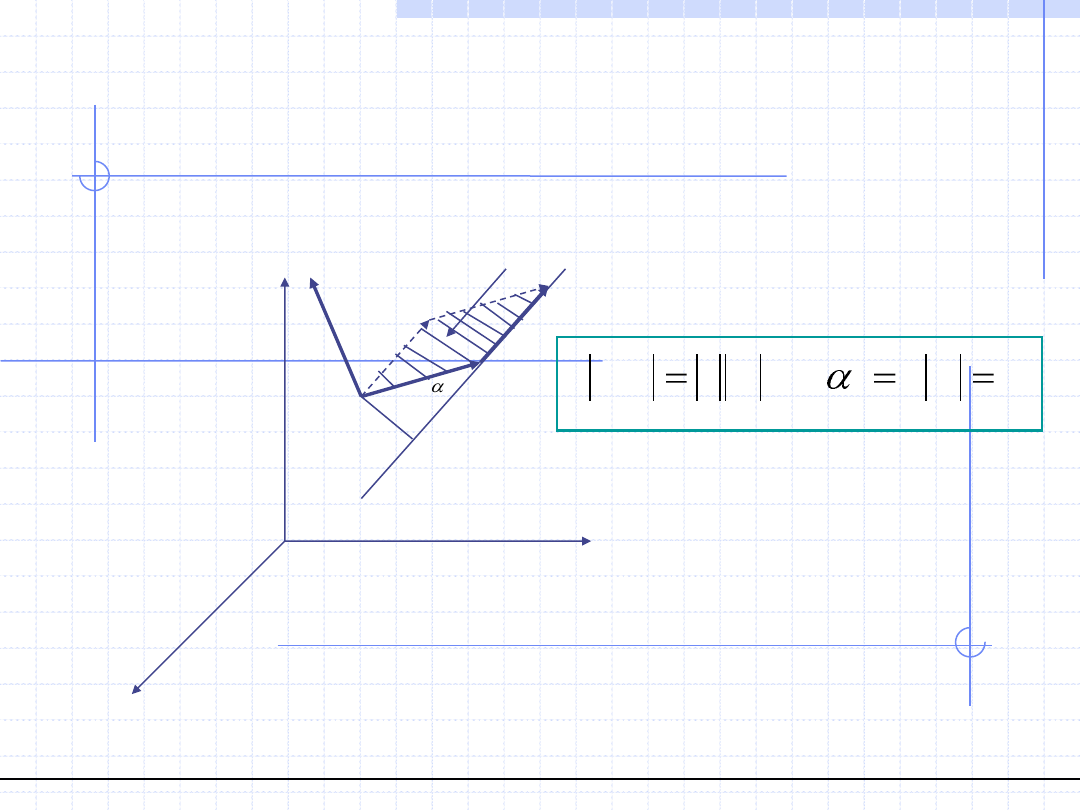
1.

Długość momentu jest określona

wzorem:

S

F

h

F

r

M

O

)

sin(

S

2.

Kierunek momentu siły jest prostopadły

do płaszczyzny wyznaczonej przez

wektory r i F.

3.

Zwrot wektora momentu siły wyznaczają

reguły korkociągu lub prawej dłoni.

4.

Wektor M

O

jest wektorem swobodnym.

W razie potrzeby najczęściej zaczepia

się go w punkcie O.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

MOMENT SIŁY WZGLĘDEM PUNKTU cd.

x

F

r

O

A

B

M

O

.

h

y

z

S

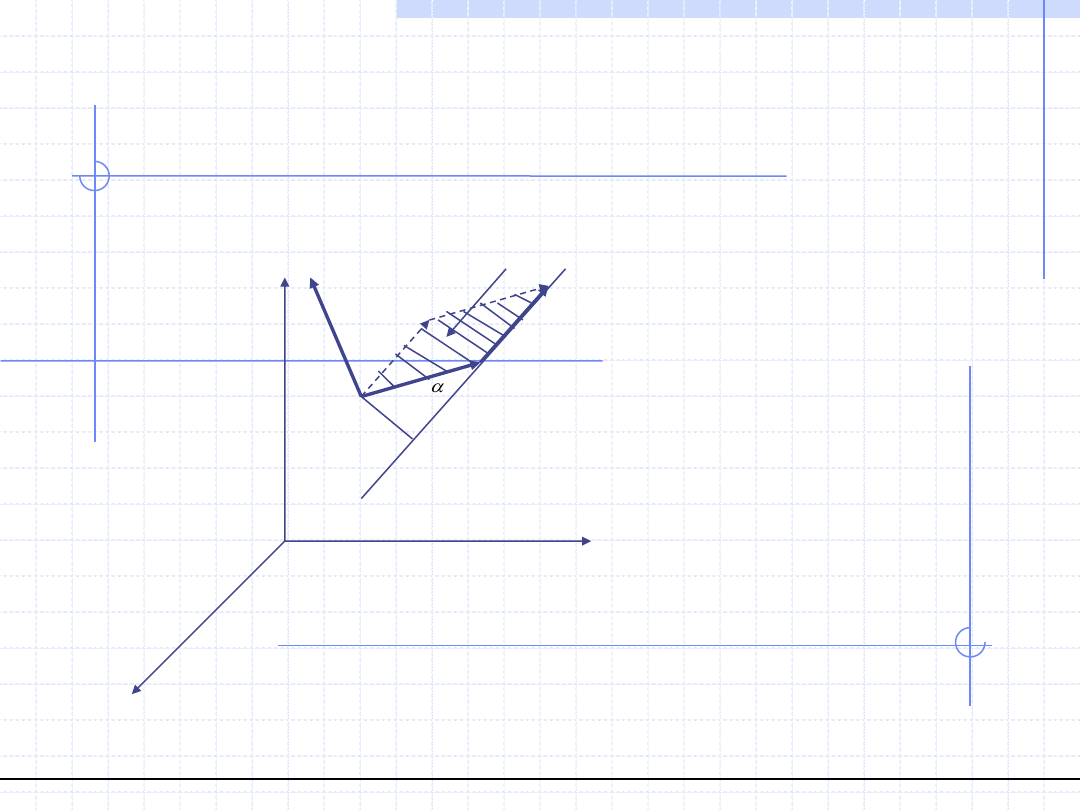
5.

Moment siły nie zależy od punktu

zaczepienia siły. Wynika to ze wzoru

określającego długość, w którym

wielkość h oznacza odległość punktu O

od linii działania siły. Odległość h

nazywana jest ramieniem siły

względem punktu O.

6.

Moment siły względem punktu leżącego

na jej linii działania jest wektorem

zerowym.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

MOMENT SIŁY WZGLĘDEM PUNKTU

Twierdzenie Varignona

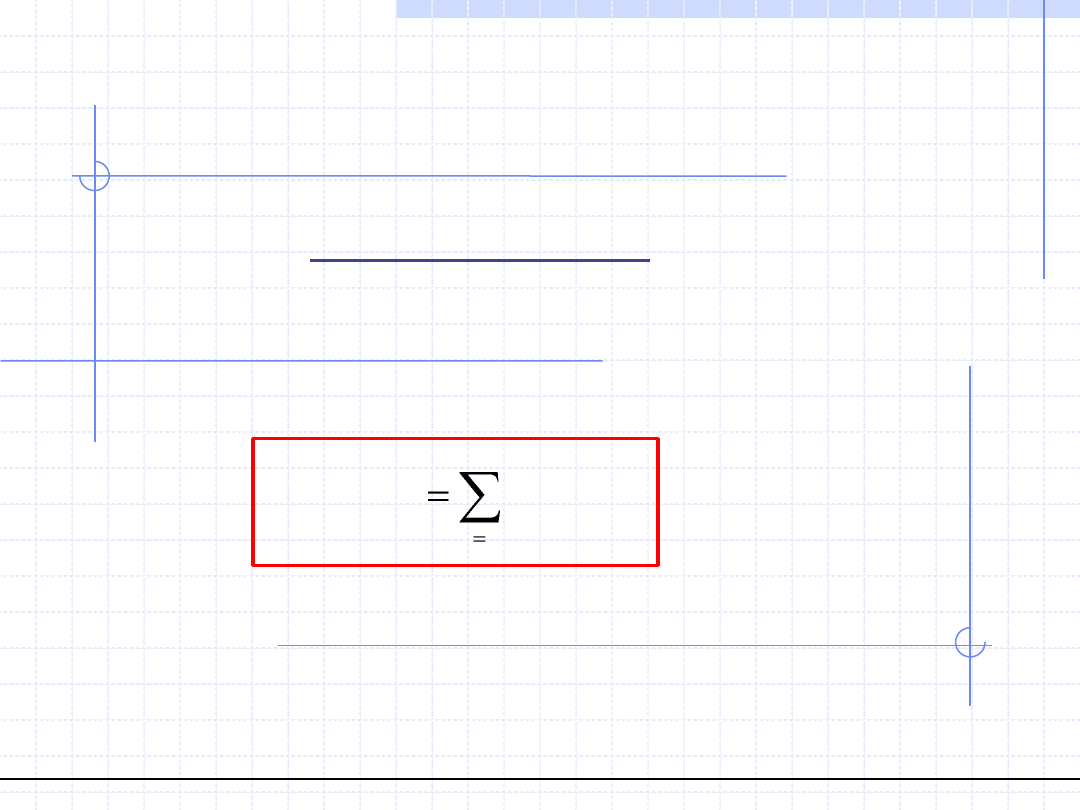
Z pojęciem momentu siły względem punktu wiąże się ważne

w statyce tzw. twierdzenie Varignona dotyczące układów sił.

Jeżeli na ciało działa dowolny układ sił P

1

,P

2

,…,P

n

a wypadkowa

tego układu wynosi W to moment siły tej wypadkowej jest równy

sumie momentów poszczególnych sił co można zapisać:

n

i

i

O

O

P

M

W

M

1

)

(

)

(

Oczywiście wszystkie momenty liczone są względem tego

samego punktu O.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

NIEZBIEŻNE UKŁADY SIŁ

Układ sił równoległych

2

1

F

F

W

Układ sił, których linie działania nie przecinają się w jednym punkcie nazywamy niezbieżnym.

Najprostszym niezbieżnym układem jest układ dwu sił równoległych na płaszczyźnie.

Zasadniczym problemem dla takiego układu jest wyznaczenie wypadkowej tzn. jednej siły,

której skutek działania jest taki sam jak danego układu. Wyznaczenie wektora wypadkowej jest
bardzo proste. Rozważmy dwa przypadki, gdy dane siły równoległe są zgodne i przeciwne.

F

1

F

2

F

1

F

2

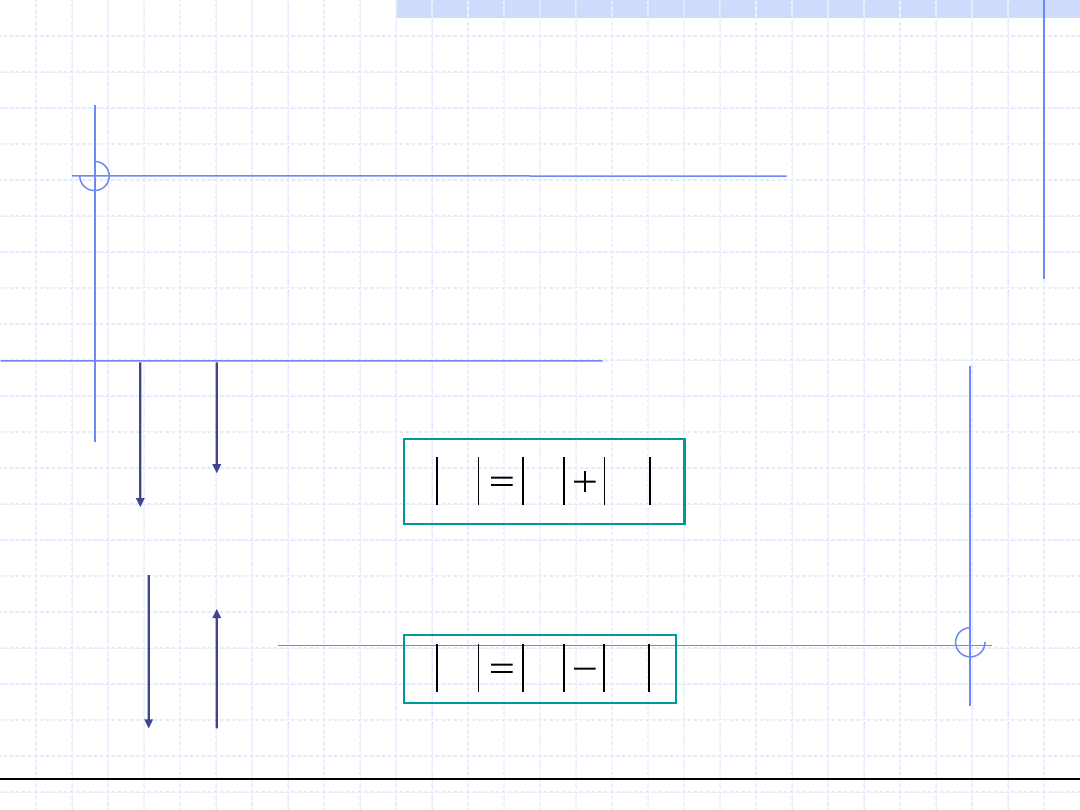
Wartość wypadkowej jest sumą wartości sił układu. Kierunek i zwrot jest

oczywiście zgodny z kierunkiem i zwrotem sił równoległych.

Wartość wypadkowej jest różnicą wartości siły większej i mniejszej. Kierunek

jest taki sam, natomiast zwrot jest zgodny ze zwrotem siły większej.

W obydwu przypadkach do wyznaczenia pozostaje linia działania wypadkowej.

2

1

F

F

W

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

NIEZBIEŻNE UKŁADY SIŁ

Układ sił równoległych cd.

Linię działania układu sił równoległych można wyznaczyć metodą geometryczną (wykreślną)

i analityczną która wykorzystuje pojęcie momentu siły względem punktu.

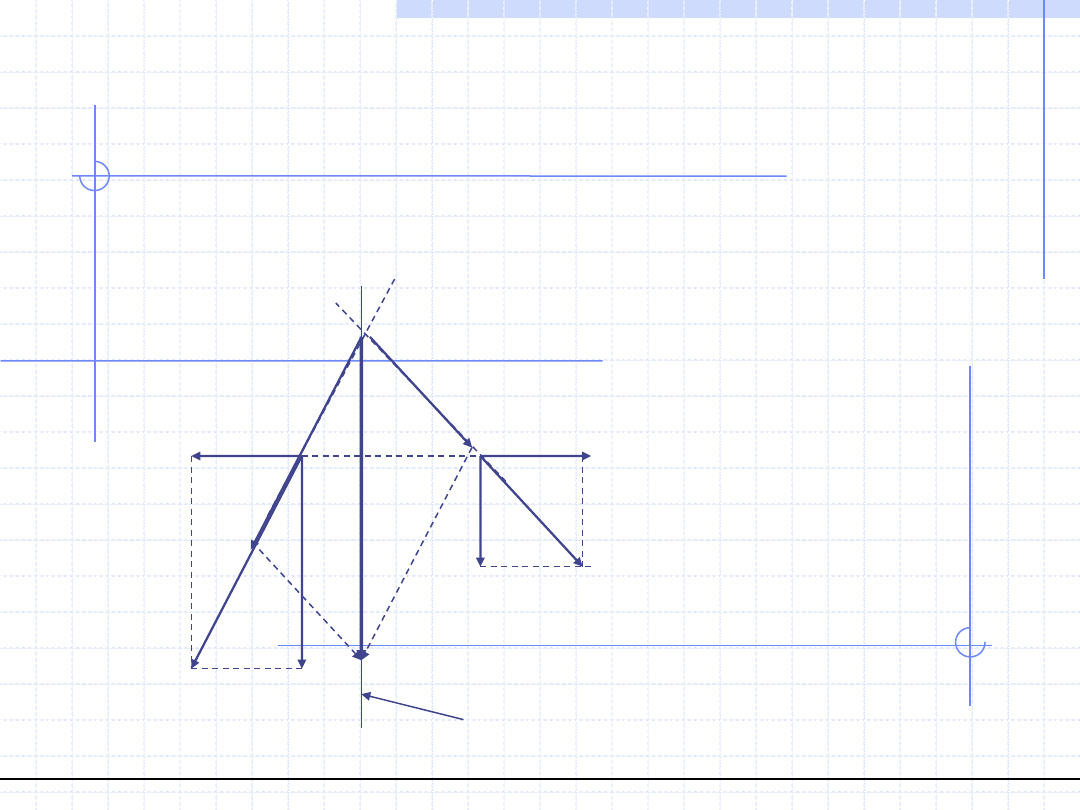
Metoda geometryczna oparta jest na III aksjomacie statyki czyli zasadzie układu zerowego.

Na podstawie tego aksjomatu do dowolnego układu można dodać układ zerowy np. dwie równe
siły o przeciwnych zwrotach.

F

1

F

2

S

1

S

2

=-S

1

R

2

R

1

W

W=R

1

+R

2

=F

1

+F

2

Linia działania wypadkowej W

O

K

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

NIEZBIEŻNE UKŁADY SIŁ

Układ sił równoległych cd.

n

i

n

i

i

O

O

i

F

M

W

M

F

W

1

1

)

(

)

(

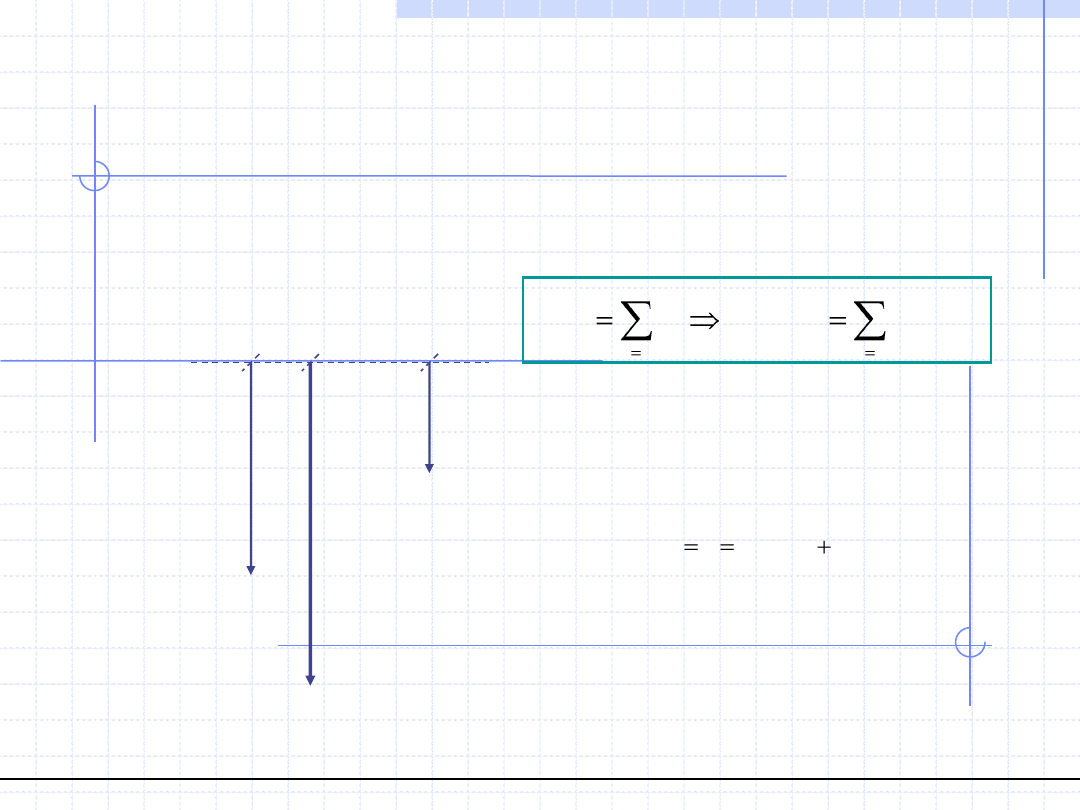
Metoda analityczna wyznaczania położenia linii działania siły wypadkowej wykorzystuje

tzw. twierdzenie Varignona, które mówi że moment siły wypadkowej dowolnego układ

względem dowolnego punktu O jest równy sumie momentów wszystkich sił układu

względem tego samego punktu O:

F

2

W

F

1

A O B

r

1

r

2

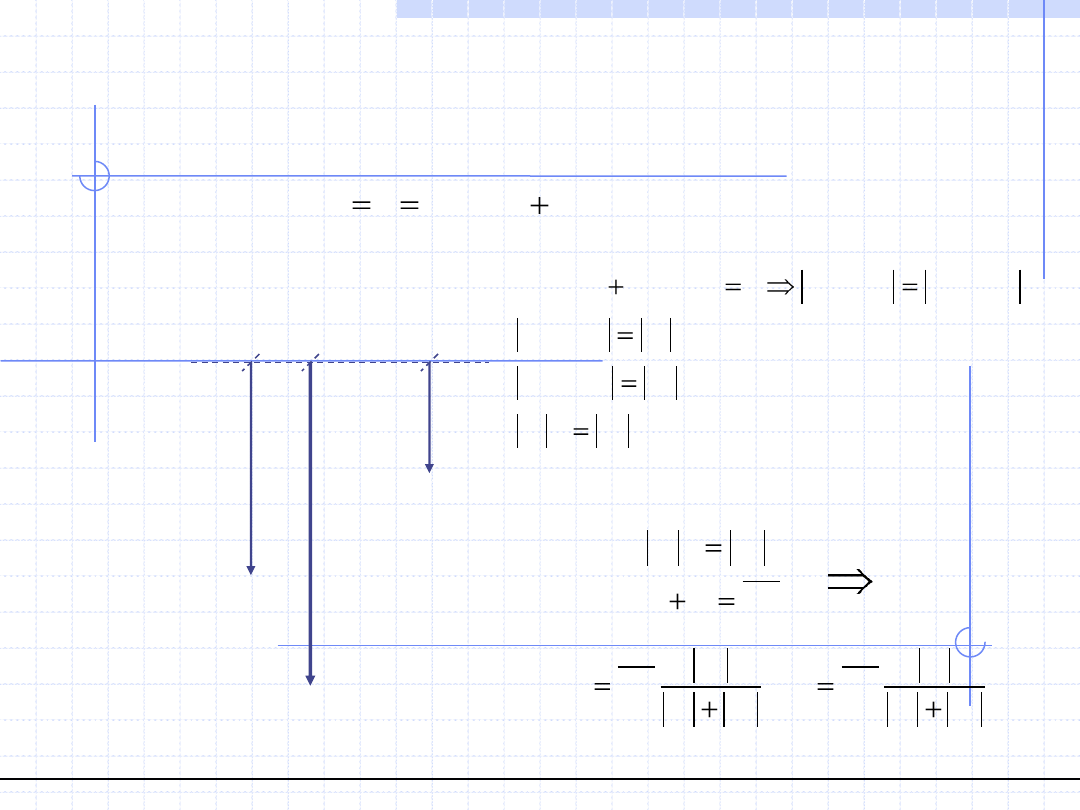
Załóżmy że dane są wartości sił |F

1

| i |F

2

| oraz odległość

ich linii działania czyli długość odcinka AB. Załóżmy że

linia działania wypadkowej układu przechodzi przez punkt O.

Punkt ten wyznacza odcinki r

1

=AO i r

2

=OB. Odcinki te

będziemy nazywać ramieniami sił. Na mocy twierdzenia

Varignona możemy napisać:

)

(

)

(

0

)

(

2

1

F

M

F

M

W

M

O

O

O



Zatem znaki (zwroty) momentów obydwu sił względem

punktu O muszą być przeciwne. Na podstawie dowolnej

reguły określającej zwrot momentów możemy stwierdzić,

że w przypadku gdy zwroty sił są zgodne punkt O musi

leżeć między siłami a w przypadku gdy zwroty są sił

przeciwne punkt O musi leżeć na zewnątrz odcinka AB.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

NIEZBIEŻNE UKŁADY SIŁ

Układ sił równoległych cd.

)

(

)

(

0

)

(

2

1

F

M

F

M

W

M

O

O

O



F

2

W

F

1

A O B

r

1

r

2

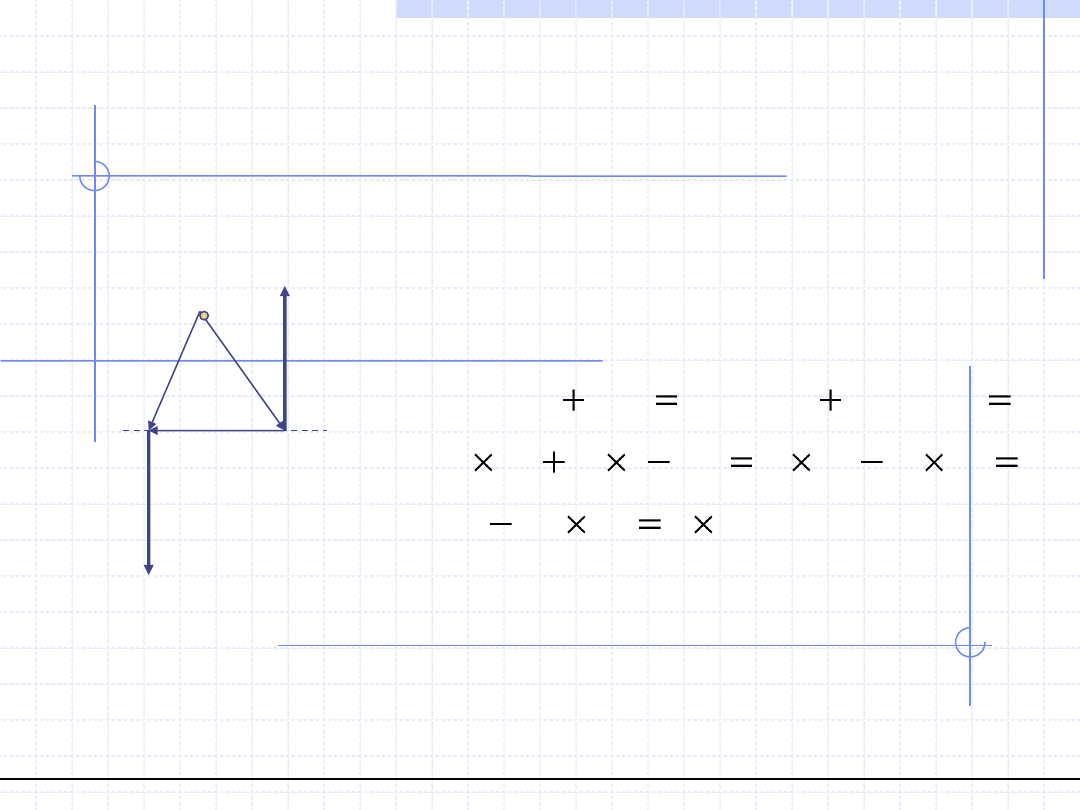
Rozpatrzmy teraz wartości powyższych momentów:

2

2

1

1

2

2

2

1

1

1

2

1

2

1

)

(

)

(

)

(

)

(

0

)

(

)

(

r

F

r

F

r

F

F

M

r

F

F

M

F

M

F

M

F

M

F

M

O

O

O

O

O

O



Ostatnia równość nazywana jest regułą dźwigni.

Wartości r

1

i r

2

możemy otrzymać rozwiązując układ

równań:

AB

r

r

r

F

r

F

2

1

2

2

1

1

2

1

1

2

2

1

2

1

F

F

F

AB

r

F

F

F

AB

r

Podobne wzory można otrzymać dla przypadku, gdy siły mają przeciwne zwroty. Wtedy, wypadkowa

leży na zewnątrz po stronie siły większej.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

NIEZBIEŻNE UKŁADY SIŁ

Para sił

F

2

=-F

1

F

1

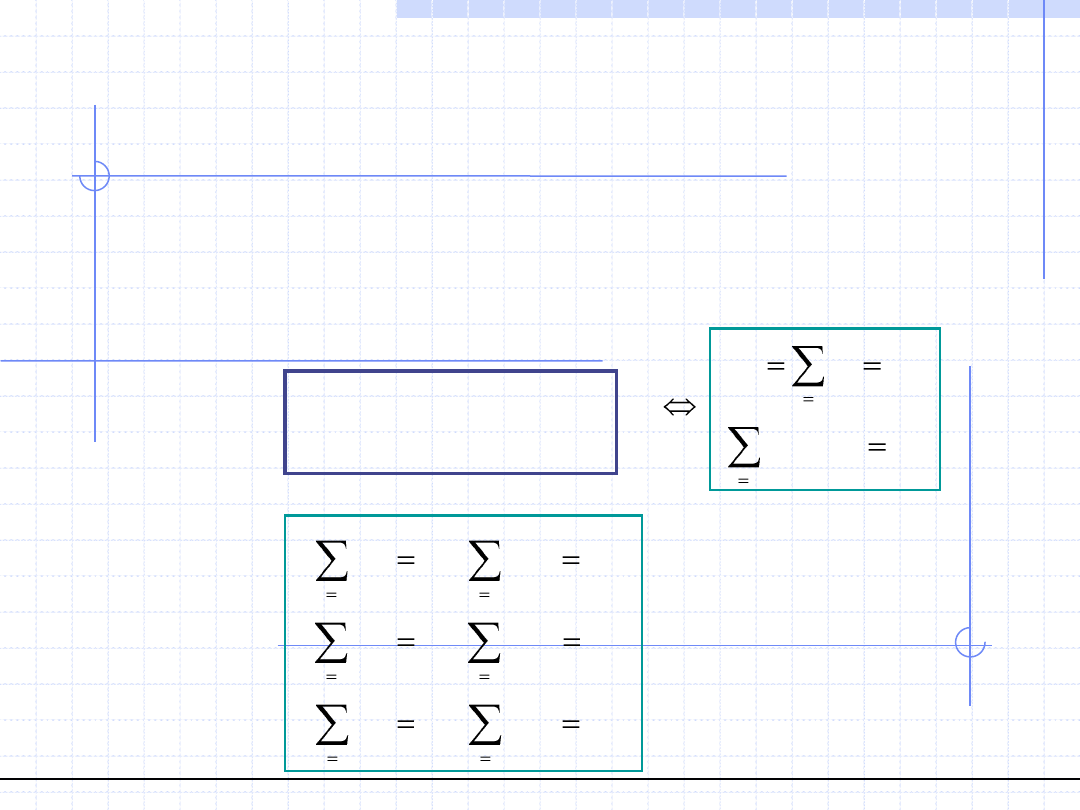
Ważnym pojęciem w statyce jest przypadek sił równoległych o takich samych

wartościach ale przeciwnych zwrotach. Przypadek taki nazywamy parą sił.

Jest oczywiste, że długość wypadkowej pary sił wynosi 0.

Jednakże nieprawdą jest że układ, na który działa para

sił jest zrównoważony. Obliczmy bowiem sumaryczny

moment pary sił względem dowolnego punktu O.

O

r

1

r

2

1

1

2

1

1

2

1

1

1

2

1

1

2

1

2

1

)

(

)

(

)

(

)

(

)

(

F

r

F

r

r

F

r

F

r

F

r

F

r

F

M

F

M

F

F

M

O

O

O

r=r

1

-r

2

Widzimy, że moment pary sił nie jest wektorem zerowym

oraz że nie zależy on od wyboru punktu O. Wektor r

nazywamy ramieniem pary sił.

Zasadniczym skutkiem działania pary sił jest obrót ciała.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

NIEZBIEŻNE UKŁADY SIŁ

Podstawowe twierdzenie statyki

n

i

i

O

n

i

i

F

M

F

W

1

1

0

)

(

0





Kluczowe znaczenie w statyce ma twierdzenie o niezbieżnym układzie sił.

Załóżmy, że siły F

1

, F

2

,…F

n

tworzą niezbieżny układ sił. Układ ten jest w równowadze

statycznej (tzn. nie porusza się lub porusza się ruchem jednostajnym prostoliniowym)

wtedy i tylko wtedy gdy jego wypadkowa jest wektorem zerowym a suma momentów

wszystkich sił względem dowolnego punktu również jest również wektorem zerowym.

Układ F

1

, F

2

,…F

n

jest

w równowadze statycznej

Algebraiczny zapis powyższych warunków jest układem 6-ciu równań dla odpowiednich składowych:

n

i

zi

n

i

yi

n

i

xi

n

i

zi

n

i

yi

n

i

xi

M

M

M

F

F

F

1

1

1

1

1

1

0

0

0

0

0

0

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

Dziękuję bardzo Państwu za uwagę