1

OGÓLNOTECHNICZNE

PODSTAWY BIOINŻYNIERII

Wykład VII

Podstawy techniki cieplnej i

termodynamiki procesowej

22

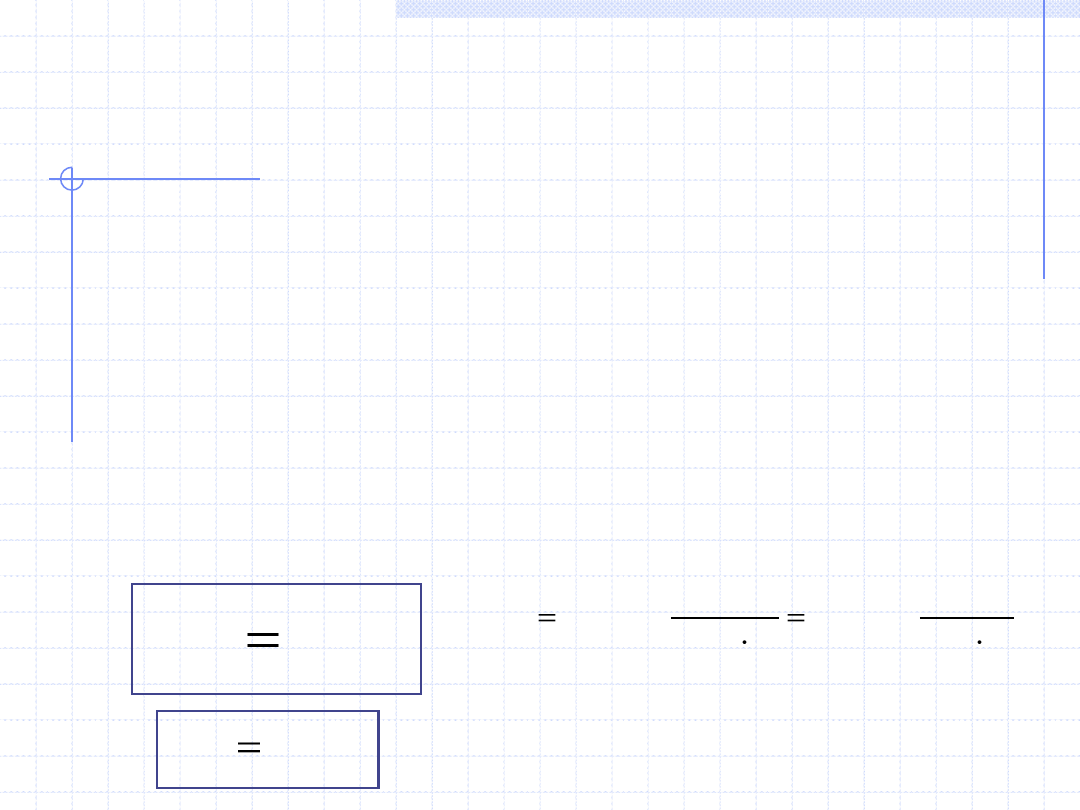
POJĘCIE GAZU DOSKONAŁEGO

nRT

pV

K

mol

J

K

kmol

J

R

31447

.

8

47

.

8314

Inną ważną idealizacją w termodynamice jest pojęcie tzw. gazu

doskonałego.

Gazem doskonałym nazywamy ciągły ośrodek termodynamiczny,

którego cząsteczki spełniają warunki:

1 - nie posiadają objętości własnej tzn. są traktowane jak punkty

materialne.

2 - nie oddziaływują ze sobą tzn. ani się nie przyciągają ani nie

odpychają.

Na podstawie kinetyki statystycznej można wykazać że gaz doskonały

musi spełniać tzw. równanie stanu gazu doskonałego:

- uniwersalna stała gazowa

RT

pv

n – liczność substancji zawartej

w układzie [kmol]

33

WŁASNOŚCI GAZU

DOSKONAŁEGO

0

p

T

Gazy rzeczywiste na ogół nie spełniają warunków gazu doskonałego,

niemniej jednak w wielu przypadkach odchylenia od tych warunków

nie są duże, tak że w przybliżeniu można je traktować jak gazy

doskonałe. Te warunki to przede wszystkim niskie ciśnienie i wysoka

temperatura.

Gaz rzeczywisty

Gaz doskonały

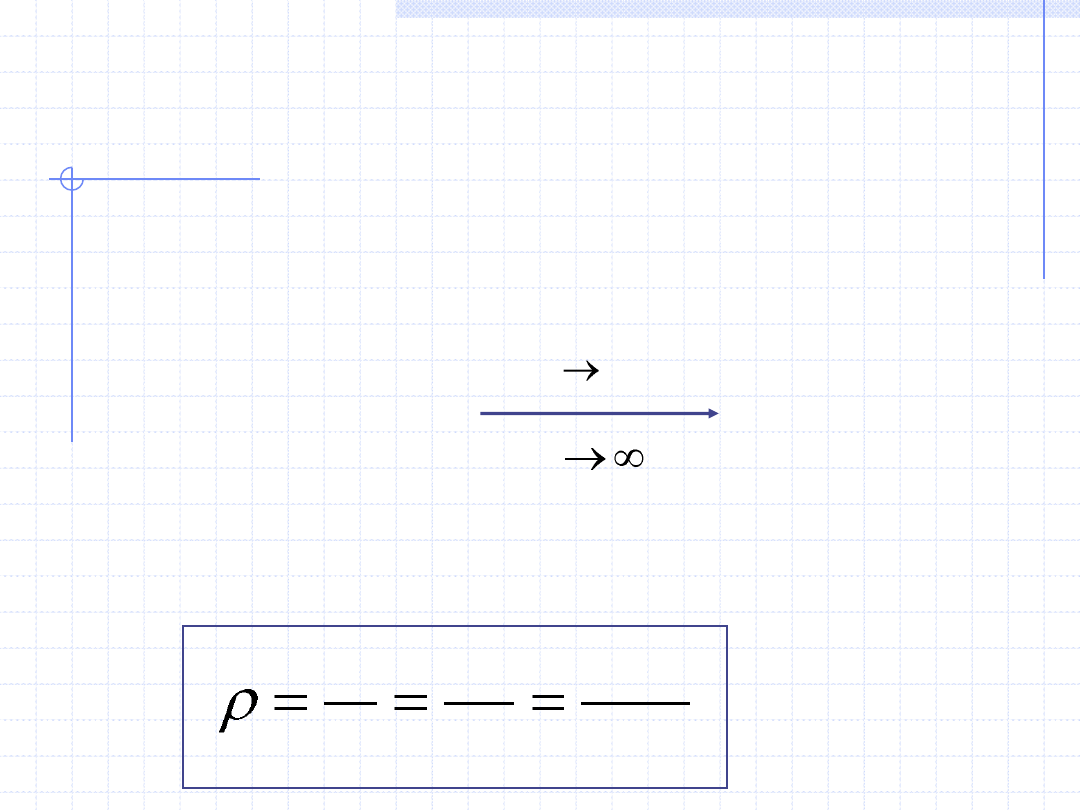
Założenie, że dany ośrodek zawarty w układzie jest gazem doskonałym
znakomicie upraszcza wiele zależności. Przykładowo gęstość gazu
doskonałego można obliczyć ze wzoru:

RT

pM

v

M

V

m

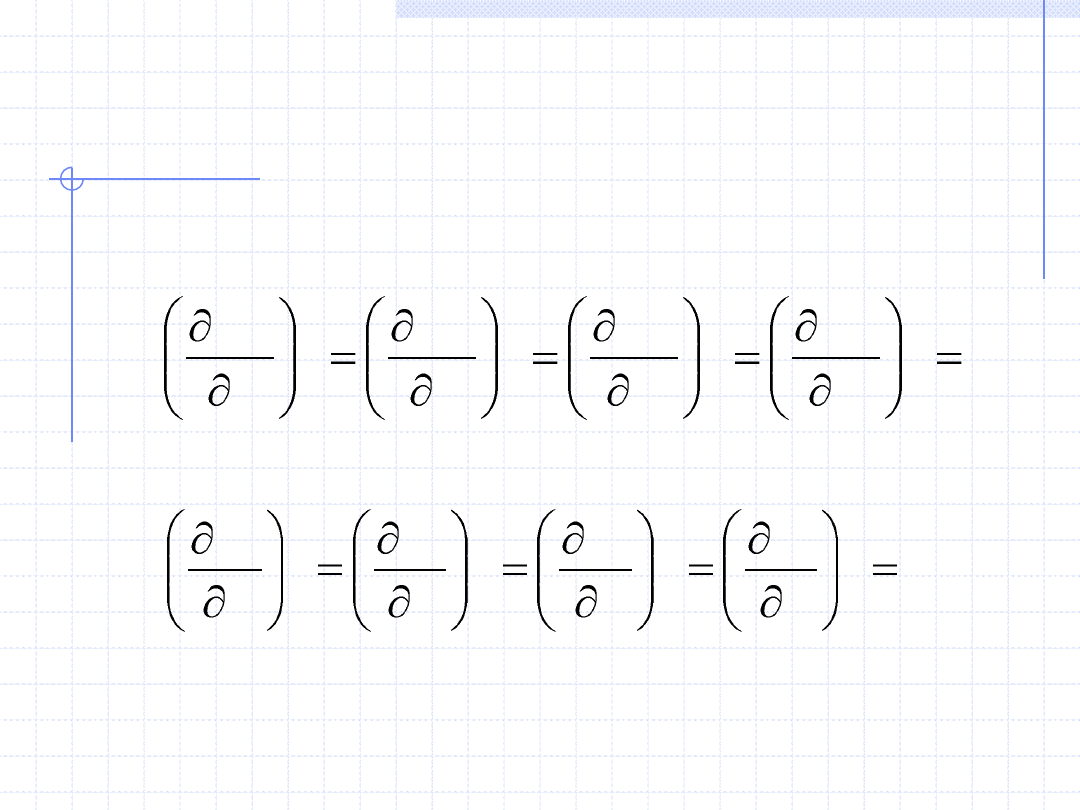
44

WŁASNOŚCI GAZU

DOSKONAŁEGO cd.

0

T

d

T

d

T

d

T

d

V

H

V

U

p

H

p

U

Gazy doskonałe posiadają szereg ważnych własności. Oto niektóre z nich:

• Ich energia wewnętrzna i entalpia zależą tylko od temperatury, a nie zależą

od ciśnienia i objętości co można zapisać różniczkowo:

0

T

d

T

d

T

d

T

d

v

h

v

u

p

h

p

u

lub dla wielkości właściwych:

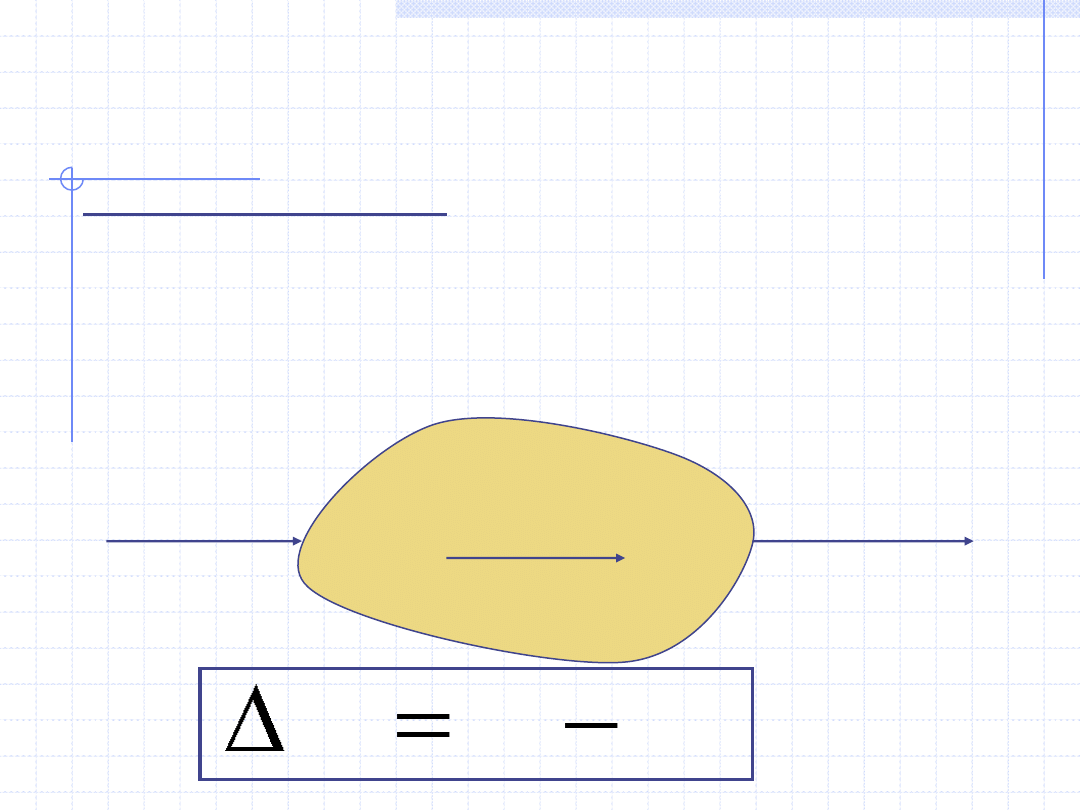
I ZASADA TERMODYNAMIKI

I zasada termodynamiki jest to w swojej istocie prawo zachowania

energii sformułowane dla dowolnej przemiany układu termodynamicznego.

I zasadę można formułować dla układów zamkniętych i otwartych.

Istnieje bardzo wiele matematycznych zapisów tej zasady. Przykładowo

napiszmy tą zasadę dla całkowej (nieróżniczkowej) przemiany układu

zamkniętego bazując na energii wewnętrznej.

Stan 1

Stan 2

ΔU=U

2

-U

1

Q

W

W

Q

U

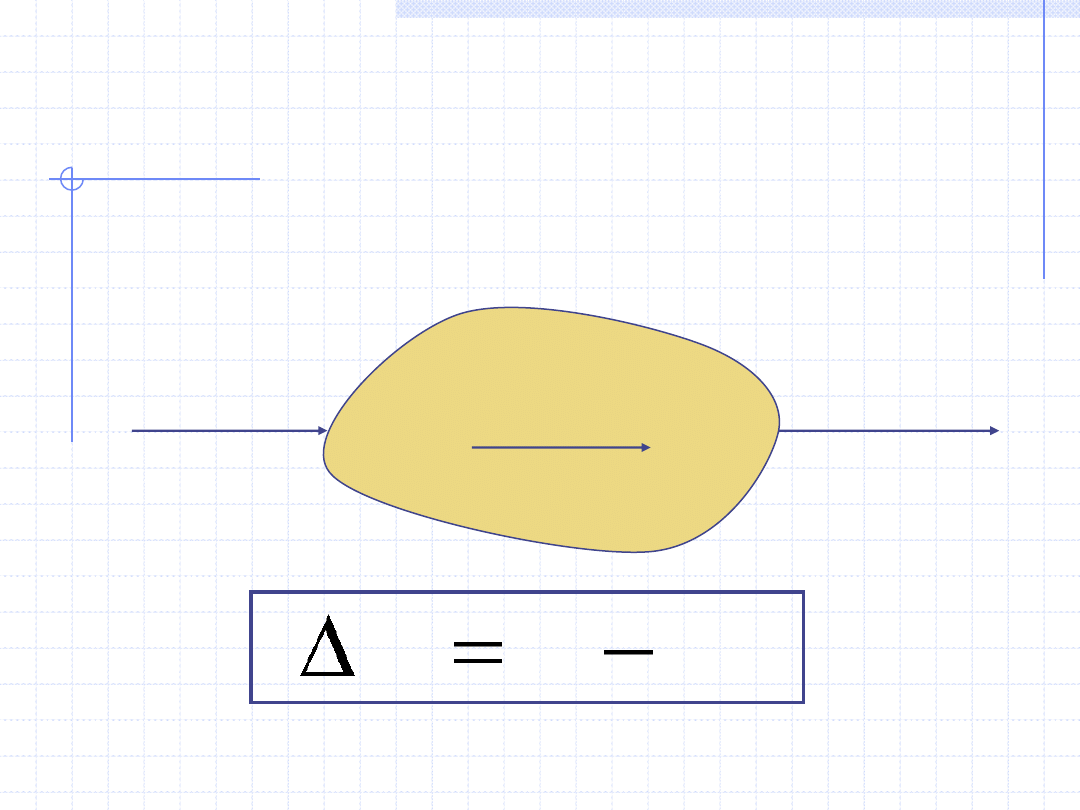
I ZASADA TERMODYNAMIKI

Stosunkowo często I zasada jest formułowana na bazie entalpii.

W takim przypadku w bilansie energetycznym zamiast pracy

objętościowej używa się pracy technicznej

Stan 1

Stan 2

ΔH=H

2

-H

1

Q

W

t

t

W

Q

H

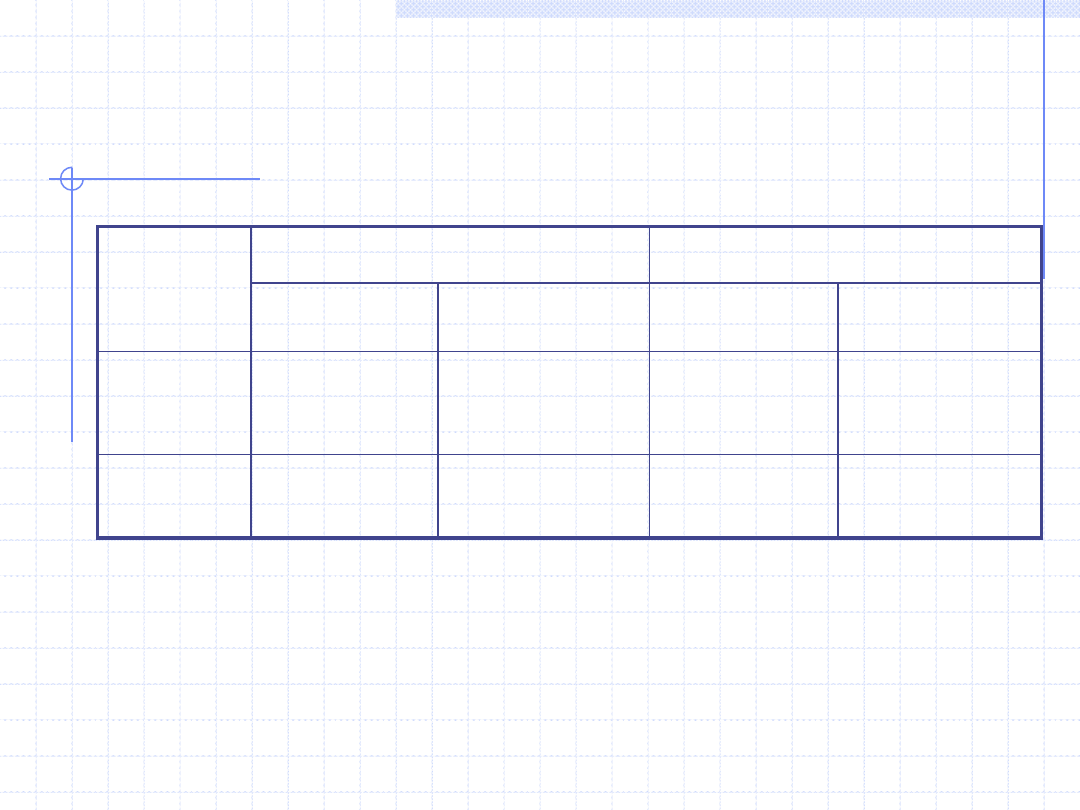
INNE SFORMUŁOWANIA PIERWSZEJ

ZASADY TERMODYNAMIKI

dh=δq-δw

t

Δh=q-w

t

dH=δQ-δW

t

ΔH=Q-W

t

Baza:

Entalpia

du=δq-δw

Δu=q-w

dU=δQ-δW

ΔU=Q-W

Baza:

Energia

wewnętrzna

Przem. różnicz.

Przem. całk.

Przem. różniczk.

Przem.

całkowa

Wielkości właściwe

Wielkości ekstensywne

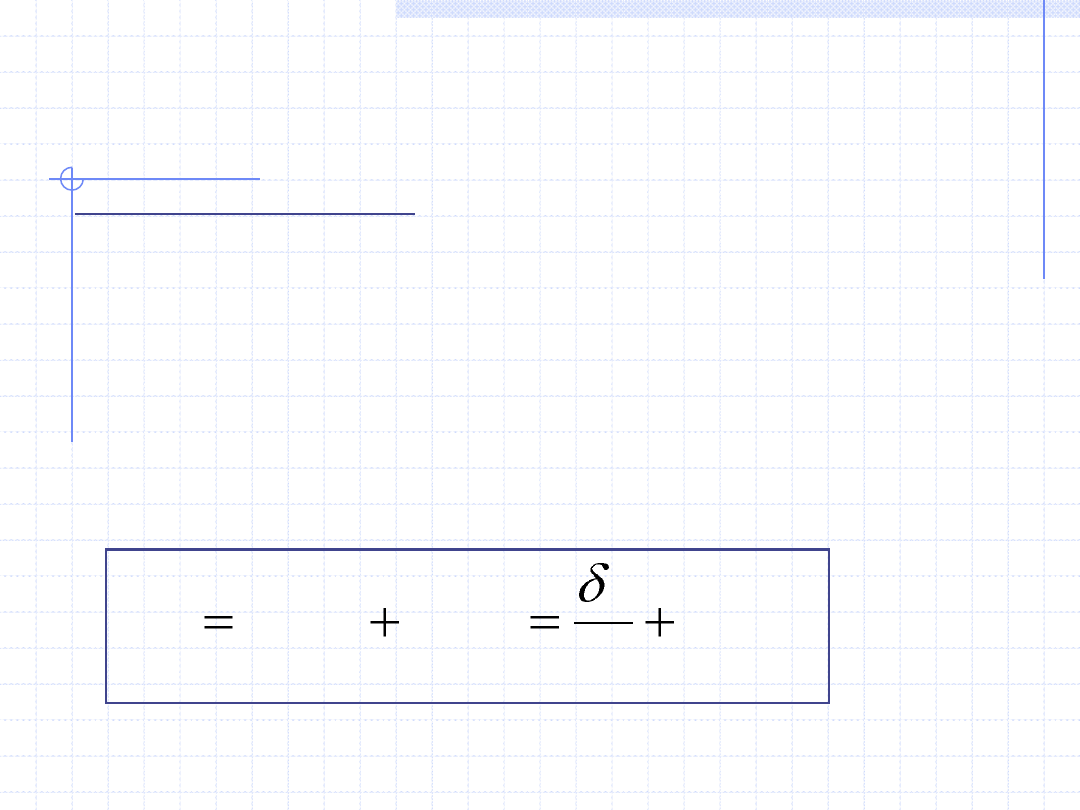
II ZASADA TERMODYNAMIKI

II zasada termodynamiki posiada ogromną liczbę bardzo różnych sformułowań.

Dla celów termodynamiki procesowej podam sformułowanie oparte na tzw.

nierówności Clausiusa. Sformułowanie to opisuje zjawisko nieodwracalności

przemian termodynamicznych oraz uwzględnia klasyczną definicję entropii.

Załóżmy, że układ ulega dowolnej (odwracalnej lub nieodwracalnej) różniczkowej

przemianie termodynamicznej. W tej przemianie układ wymienia z otoczeniem

ciepło δq. W czasie przemiany zmieniać się mogą wszystkie parametry stanu.

Zmiana entropii wyniesie ds. Istnieją dwie przyczyny zmiany entropii:

1 - zmiana stanu energetycznego układu związana z wymianą ciepła,

2 - zmiana liczby dostępnych stanów energetycznych związana z

nieodwracalnymi efektami przemiany. Fakt ten można zapisać równaniem:

i

i

r

ds

T

q

ds

ds

ds

)

(

)

(

)

(

r – oznacza zmiany związane z odwracalnością przemiany (reversible)

i – oznacza zmiany związane z nieodwracalnością przemiany (irreversible)

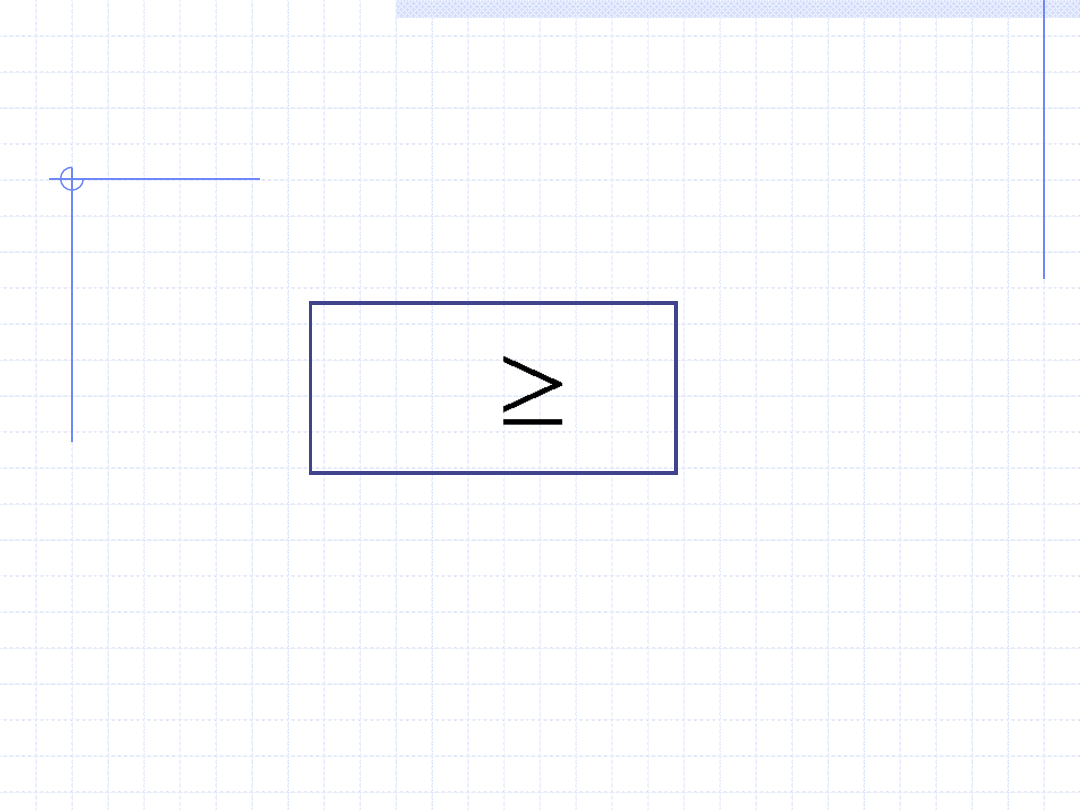
II ZASADA TERMODYNAMIKI cd.

Nierówność Clausiusa dotyczy tej części zmiany entropii, która jest związana

z nieodwracalnością przemian i stanowi jedno z wielu sformułowań II zasady
termodynamiki.

0

i

ds

Słownie oznacza to, że każda nieodwracalność powoduje wzrost entropii.

Ponieważ wszystkie przemiany samorzutne (odbywające się bez ingerencji

z zewnątrz) są nieodwracalne, z nierówności Clausiusa wynika, że w takich

przemianach entropia rośnie osiągając wartość maksymalną w stanie

równowagi, w którym mogą zachodzić tylko przemiany odwracalne.

Równość zachodzi tylko

w przypadku przemian

odwracalnych

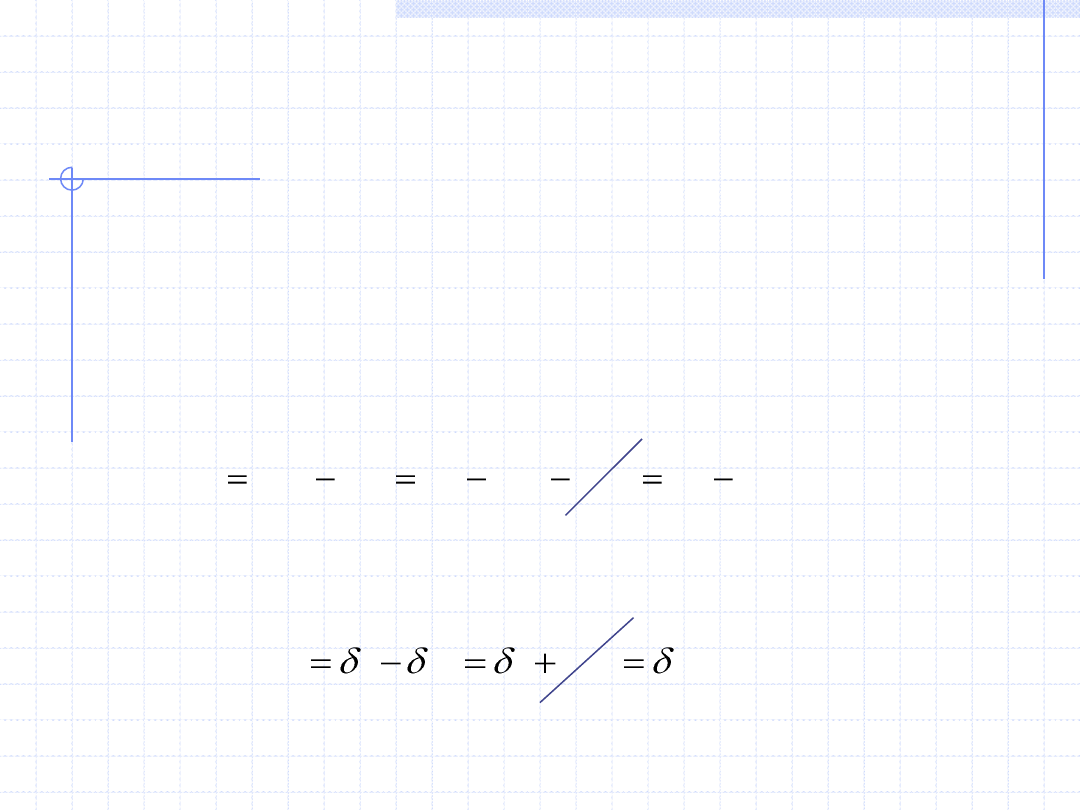
WNIOSKI Z II ZASADY TERMODYNAMIKI

Tds

dh

sdT

Tds

dh

Ts

h

d

dg

)

(

q

vdp

q

w

q

dh

t

W związku z rozważaniem stanów równowagi termodynamicznej, bardzo

ważny jest wniosek wynikający z II zasady zastosowanej do przemian,

w których układ dąży do stanu równowagi po ustaleniu się temperatury

i ciśnienia. Rozważamy zatem izotermiczno-izobaryczną przemianę

nieodwracalną (T=const., dT=0 p=const., dp=0). Rozpatrzmy jak będzie

się zachowywać w takiej przemianie entalpia swobodna (energia Gibbsa) g.

Na podstawie definicji entalpii swobodnej możemy napisać wzór

określający jej różniczkę dg:

Uwzględniając I zasadę termodynamiki oraz wzór określający różniczkową

pracę techniczną dostajemy:

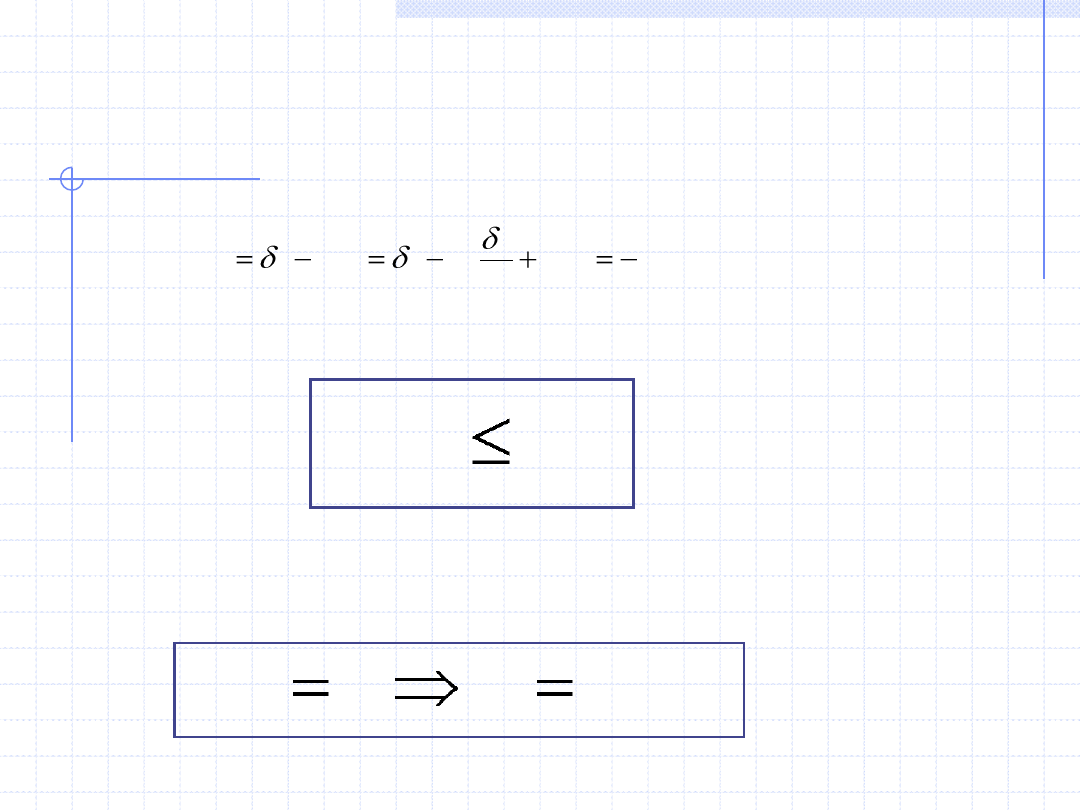
WNIOSKI Z II ZASADY TERMODYNAMIKI cd.

i

i

Tds

ds

T

q

T

q

Tds

q

dg

)

(

0

dg

Podstawiając uzyskany wynik do wyrażenia na dg otrzymujemy:

Uwzględniając nierówność Clausiusa dostajemy warunek, który spełnia

entalpia swobodna w przemianach samorzutnych:

Słownie oznacza to, że w przemianach samorzutnych dążących do stanu

równowagi, entalpia swobodna (G lub g) maleje i w stanie równowagi osiąga

wartość minimalną. Warunkiem równowagi termodynamicznej w stałej
temperaturze i pod stałym ciśnieniem jest zatem równość różniczkowa:

.

min

0

g

dg

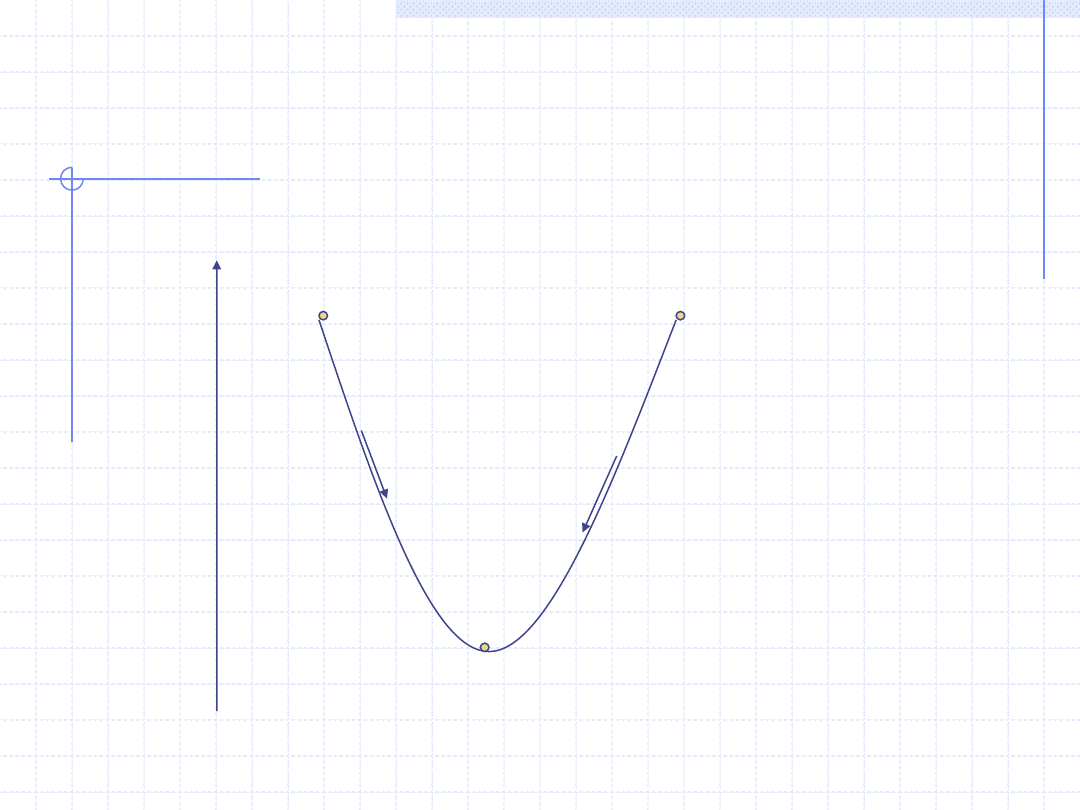
WNIOSKI Z II ZASADY TERMODYNAMIKI cd.

Graficznie wniosek ten można opisać następująco:

T=const, p=const

g

Brak równowagi

Brak równowagi

Stan równowagi termodynamicznej g=min.

Proste przemiany

termodynamiczne

Spośród bardzo wielu możliwych przemian termodynamicznych szczególną

rolę odgrywają przemiany spełniające pewien prosty warunek. Warunek

ten najczęściej określa stałość określonego parametru lub funkcji stanu.

W nazwie stałość ta jest opisana za pomocą przedrostka „izo”.

Mamy zatem następujące przemiany proste:

1. Przemiana izochoryczna – V=const.

2. Przemiana izobaryczna – p=const.

3. Przemiana izotermiczna – T=const.

4. Przemiana izentropowa – S=const. (przemiana adiabatyczna)

5. Przemiana politropowa – C=const.

Teraz omówimy po kolei omówimy poszczególne przemiany.

Przemiany te będziemy ilustrować wykresami w układzie p – v

tzn. ciśnienie – objętość właściwa (będziemy zakładać przemiany

w układach zamkniętych czyli n=const.)

Przemiana izochoryczna

.)

(

0

0

.

1

2

1

2

const

n

dla

v

v

dv

V

V

dV

const

V

0

0

0

0

.

w

w

pdv

w

dv

const

v

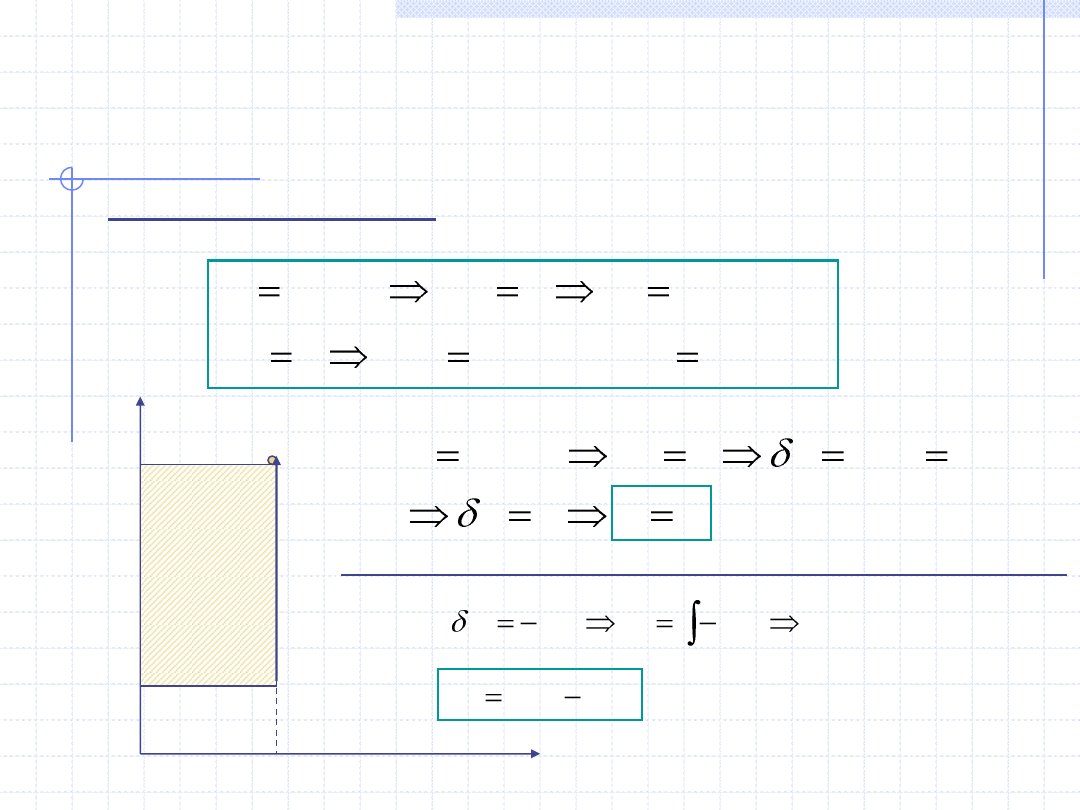
Przemiana izochoryczna odbywa się przy stałej objętości:

p

v

w

t

v=const.

p

1

,T

1

p

2

,T

2

Praca objętościowa w przemianie izochorycznej jest równa 0.

)

(

2

1

2

1

p

p

v

w

vdp

w

vdp

w

t

p

p

t

t

Wartość pracy technicznej przemiany

izochorycznej jest równa polu

zakreskowanego prostokąta.

Przemiana izochoryczna cd.

du

q

w

w

du

q

0

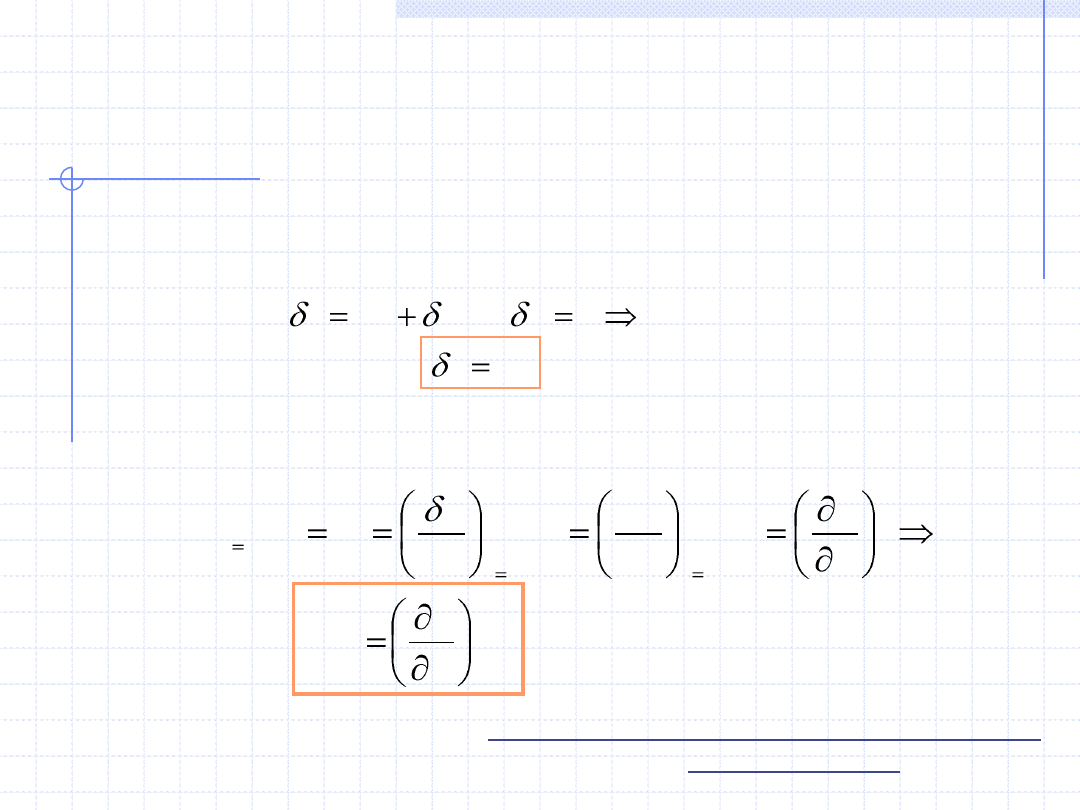
Rozpatrzmy teraz pojemność cieplną układu podczas przemiany

izochorycznej. Na mocy I zasady termodynamiki dla różniczkowej

przemiany można napisać:

Przypomnijmy teraz definicję właściwej pojemności cieplnej dla

rozważanej przemiany:

v

v

v

const

v

const

v

v

const

v

T

u

c

T

u

dT

du

dT

q

c

c

.

.

.

)

(

Wzór powyższy dowodzi, że pojemność cieplna w przemianie izochorycznej

jest pochodną funkcji stanu a zatem również jest funkcją stanu.

Przemiana izochoryczna cd.

2

1

)

(

)

(

)

(

.

.

T

T

v

const

v

v

const

v

dT

T

c

q

dT

c

q

:

2

)

(

)

(

gdzie

R

k

c

GD

v

atomowych

gazów

dla

k

1

3

Wielkość c

v

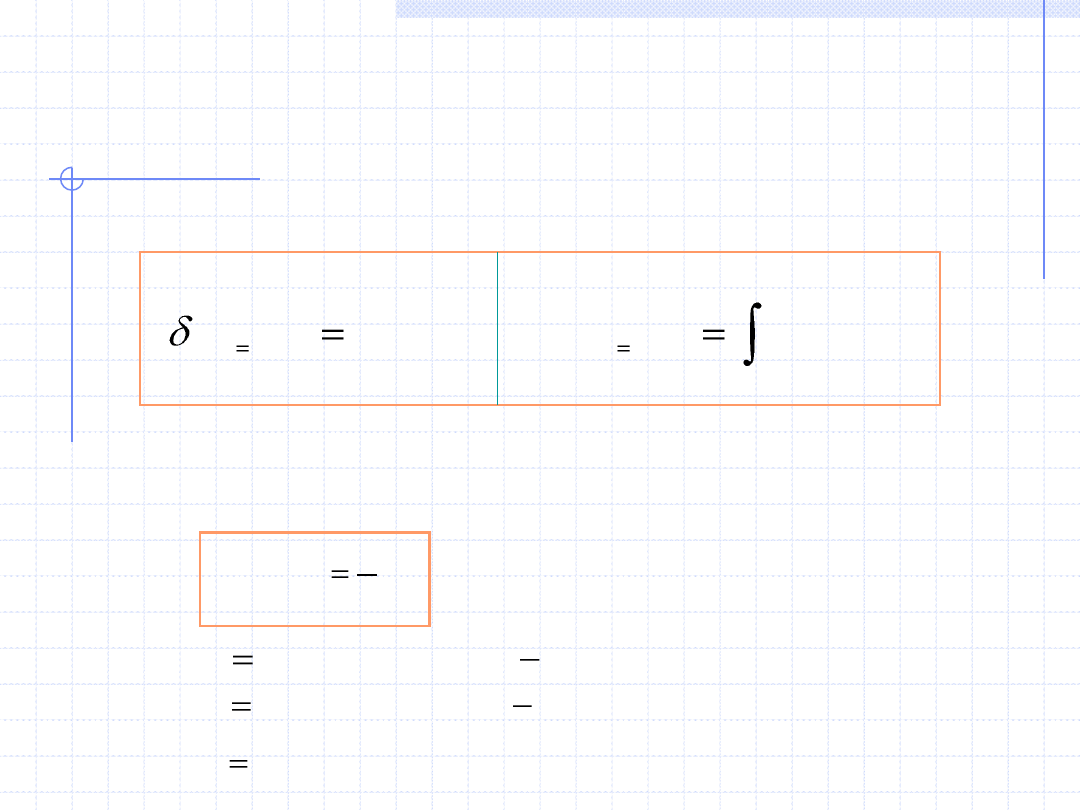
zależy od temperatury, ciśnienia i rodzaju ośrodka. Zależność

od temperatury pozwala na wyznaczenie ciepła przemiany izochorycznej:

Dla gazów doskonałych, z teorii kinetycznej wynika że wielkość c

v

powinna

być stała i równa:

atomowych

gazów

dla

k

2

5

wych

wieloatomo

gazów

dla

k

6

Przemiana izochoryczna cd.

2

2

2

2

1

1

1

1

RT

v

p

v

p

RT

v

p

v

p

1

)

(

1

)

(

)

(

1

2

1

)

(

)

(

.

1

2

1

)

(

1

1

1

2

)

(

1

2

)

(

)

(

)

(

.

2

1

p

p

T

c

q

p

p

T

c

T

T

p

p

c

T

T

c

dT

c

q

GD

v

GD

const

v

GD

v

GD

v

GD

v

T

T

GD

v

GD

const

v

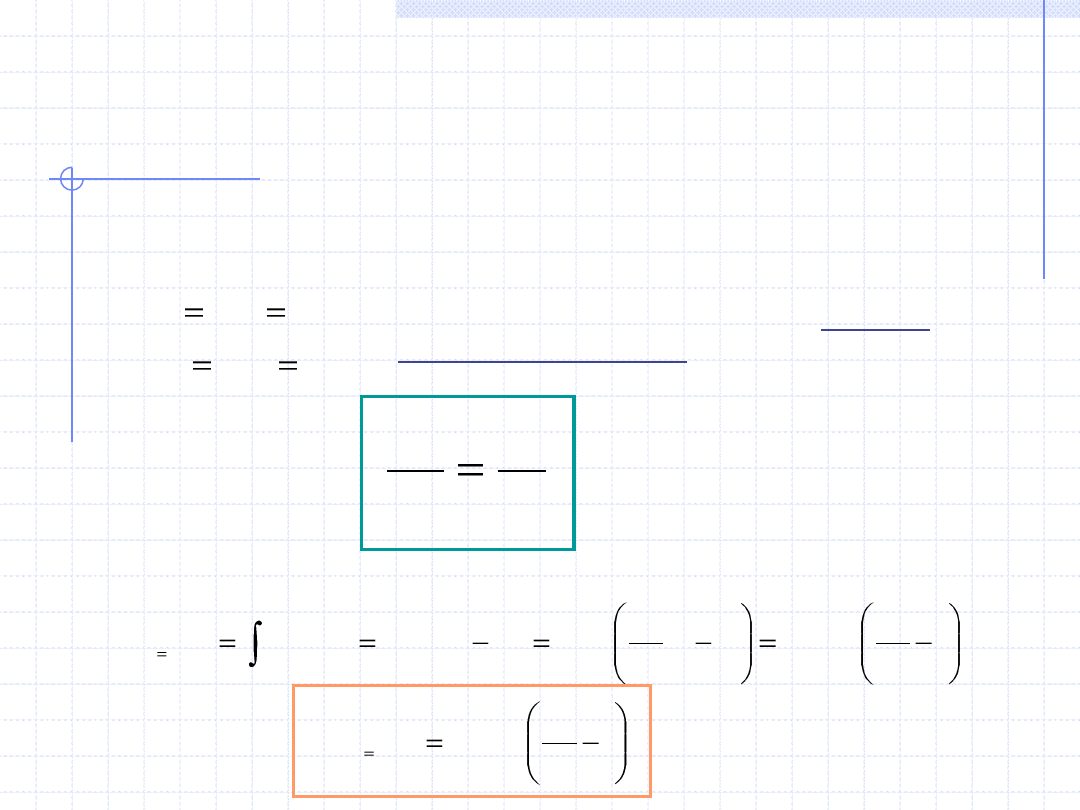
Rozpatrzmy jeszcze dokładniej przemianę izochoryczną gazów doskonałych.

W każdy punkcie takiej przemiany musi być spełnione równanie stanu gazu

doskonałego. Dla punku początkowego i końcowego mamy:

Dzieląc stronami otrzymujemy tzw. równanie

przemiany izochorycznej uzależniające ciśnienie

i temperaturę w skrajnych punktach przemiany:

Dla gazów doskonałych również wzór określający ciepło ma prostą postać:

1

2

1

2

T

T

p

p

Przemiana izochoryczna cd.

1

)

(

)

(

)

(

)

(

)

(

)

(

1

2

1

)

(

)

(

.

)

(

.

.

.

.

.

p

p

T

c

q

u

q

u

du

dq

GD

v

GD

const

v

GD

const

v

const

v

const

v

const

v

const

v

1

)

(

)

(

1

)

(

1

)

(

)

(

)

(

)

(

)

(

)

(

1

2

1

)

(

2

1

1

1

1

2

1

)

(

2

1

1

2

1

)

(

)

(

.

)

(

.

)

(

.

.

.

.

p

p

T

R

c

p

p

p

RT

p

p

T

c

p

p

v

p

p

T

c

w

q

h

vdp

dT

c

w

q

dh

w

q

h

w

q

dh

w

dh

q

GD

v

GD

v

GD

v

GD

const

v

t

GD

const

v

GD

const

v

v

const

v

t

const

v

const

v

t

t

t

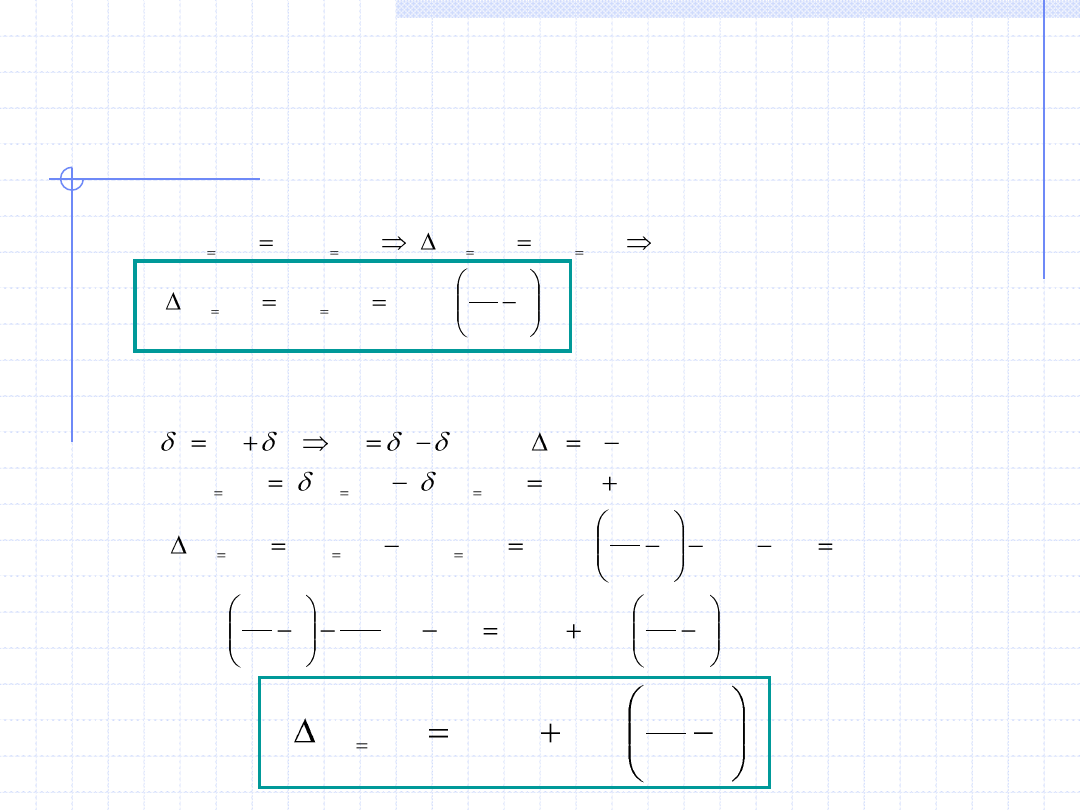
Na koniec określimy wzory określające przyrosty (zmiany) najważniejszych

funkcji stanu w przemianie izochorycznej gazów doskonałych.

a) Energia wewnętrzna – u.

Na podstawie I zasady termodynamiki mamy:

b) Entalpia – h.

Na podstawie I zasady termodynamiki mamy:

1

)

(

)

(

1

2

1

)

(

)

(

.

p

p

T

R

c

h

GD

v

GD

const

v

Przemiana izochoryczna cd.

1

2

)

(

)

(

)

(

.

.

.

.

ln

)

(

)

(

)

(

)

(

)

(

2

1

2

1

T

T

c

dT

T

c

s

dT

T

T

c

s

T

dT

c

T

q

ds

GD

v

T

T

GD

v

GD

const

v

T

T

v

const

v

v

const

v

const

v

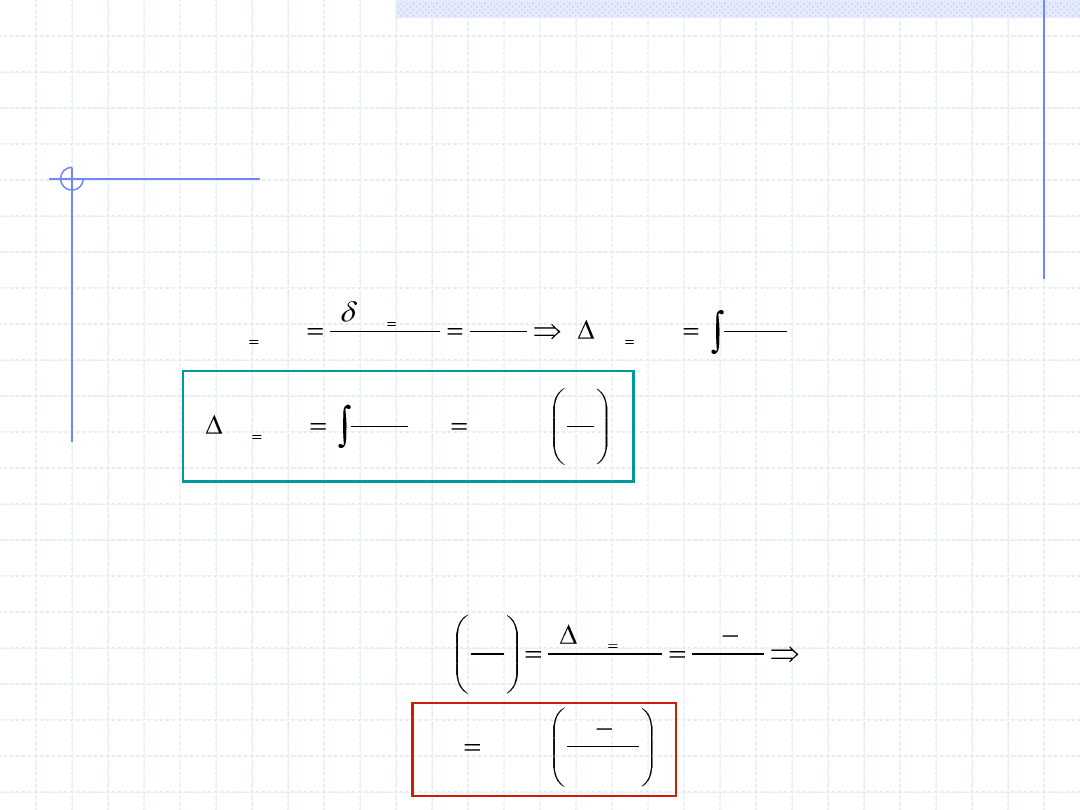
c) Entropia – s.

Przy założeniu, że nasza przemiana izochoryczna jest odwracalna

można napisać:

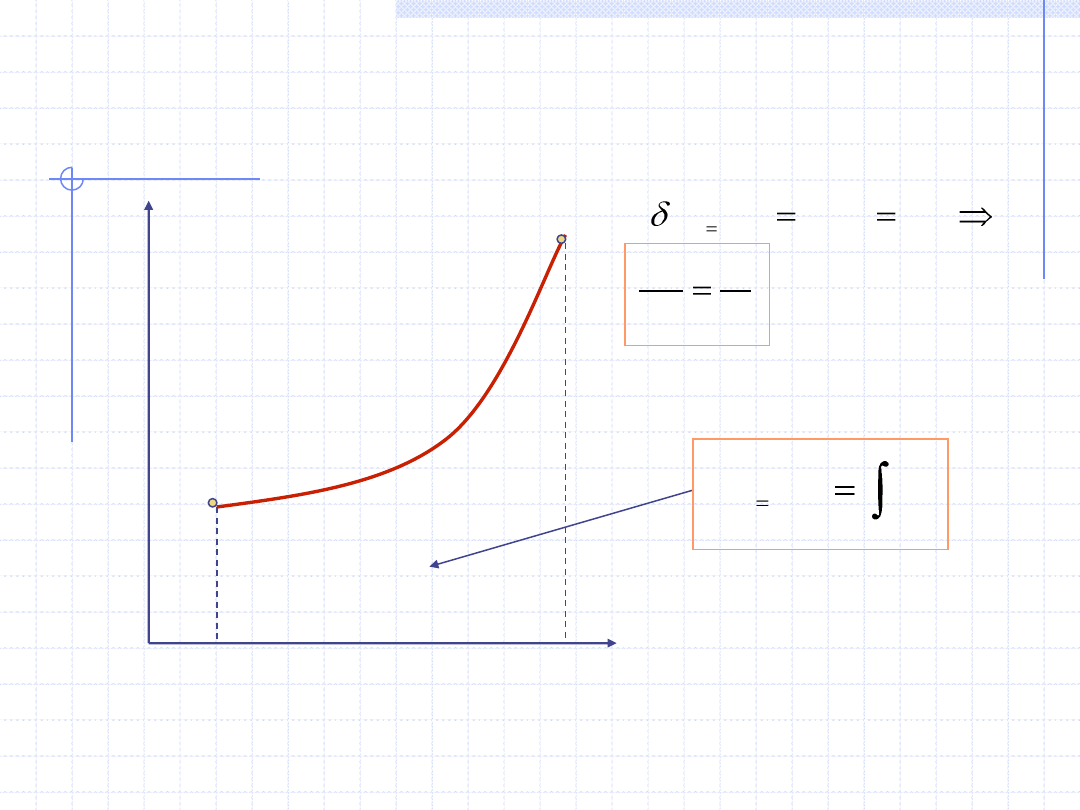
Wzór powyższy określający przyrost entropii w przemianie izochorycznej

gazu doskonałego można przekształcić otrzymując zależność temperatury

od entropii. Zależność taką można wykorzystać przy konstrukcji wykresu

przemiany w układzie T – s.

)

(

1

2

1

2

)

(

1

2

)

(

)

(

.

1

2

exp

)

(

ln

GD

v

GD

v

GD

v

GD

const

v

c

s

s

T

T

c

s

s

c

s

T

T

Przemiana izochoryczna cd.

2

1

.

)

(

s

s

const

v

Tds

q

T

s

1

2

s

1

s

2

v

v

const

v

c

T

ds

dT

Tds

dT

c

q

.

)

(

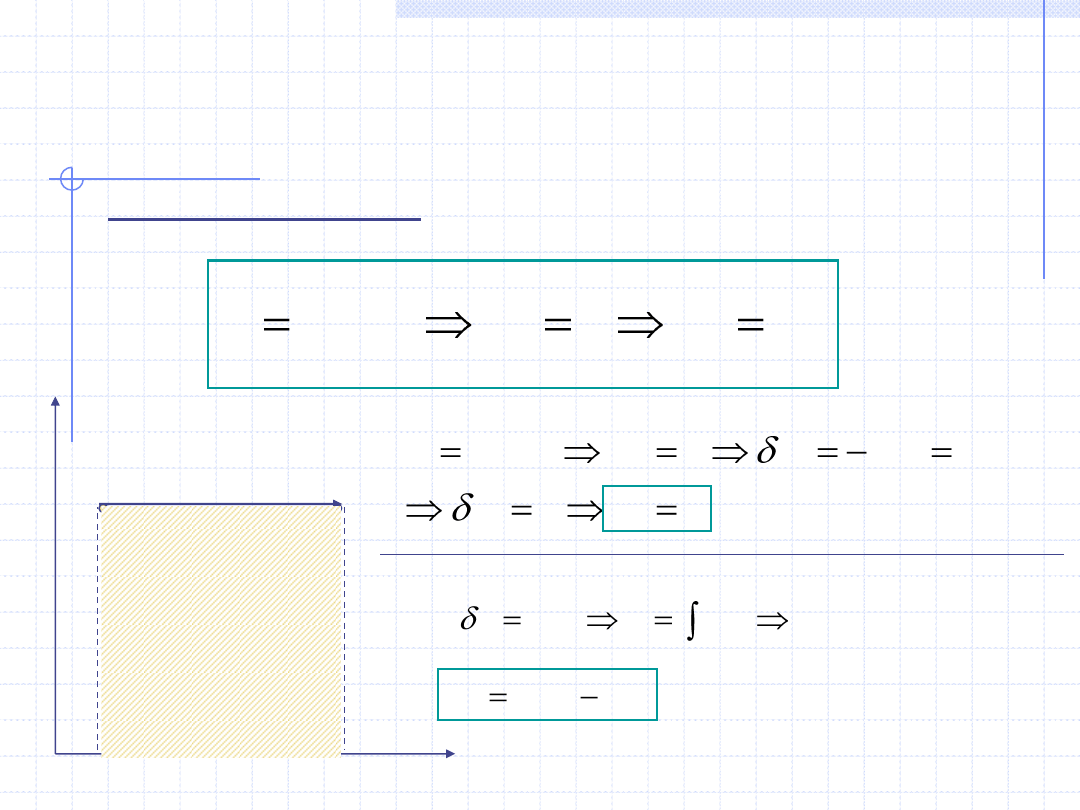
Przemiana izobaryczna

1

2

0

.

p

p

dp

const

p

0

0

0

0

.

t

t

t

w

w

vdp

w

dp

const

p

Przemiana izobaryczna odbywa się przy stałym ciśnieniu:

p

v

p=const.

v

1

,T

1

v

2

,T

2

Praca techniczna w przemianie izobarycznej jest równa 0.

)

(

1

2

2

1

v

v

p

w

pdv

w

pdv

w

v

v

Praca objętościowa przemiany

izobarycznej jest równa polu

zakreskowanego prostokąta.

w

Przemiana izobaryczna cd.

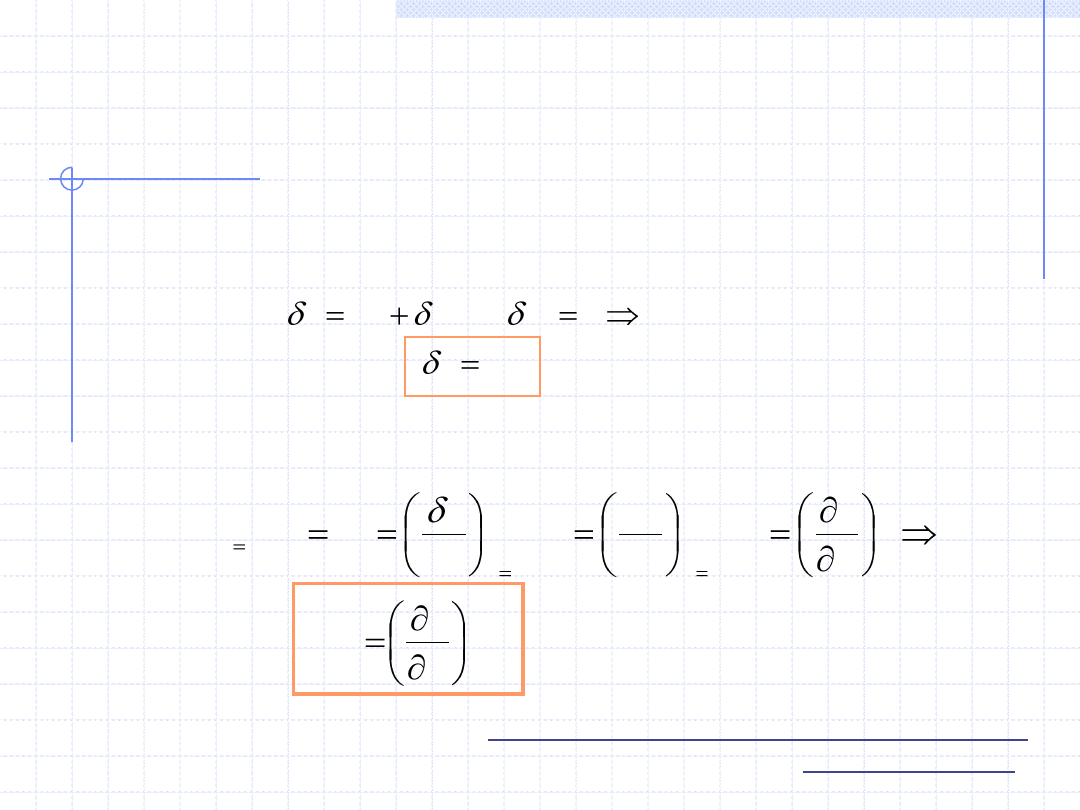
dh

q

w

w

dh

q

t

t

0

Rozpatrzmy teraz pojemność cieplną układu podczas przemiany

izobarycznej. Na mocy I zasady termodynamiki dla różniczkowej

przemiany można napisać:

Przypomnijmy teraz definicję właściwej pojemności cieplnej dla

rozważanej przemiany:

v

p

p

const

p

const

p

p

const

p

T

h

c

T

h

dT

dh

dT

q

c

c

.

.

.

)

(

Wzór powyższy dowodzi, że pojemność cieplna w przemianie izobarycznej

jest pochodną funkcji stanu (entalpii) a zatem również jest funkcją stanu.

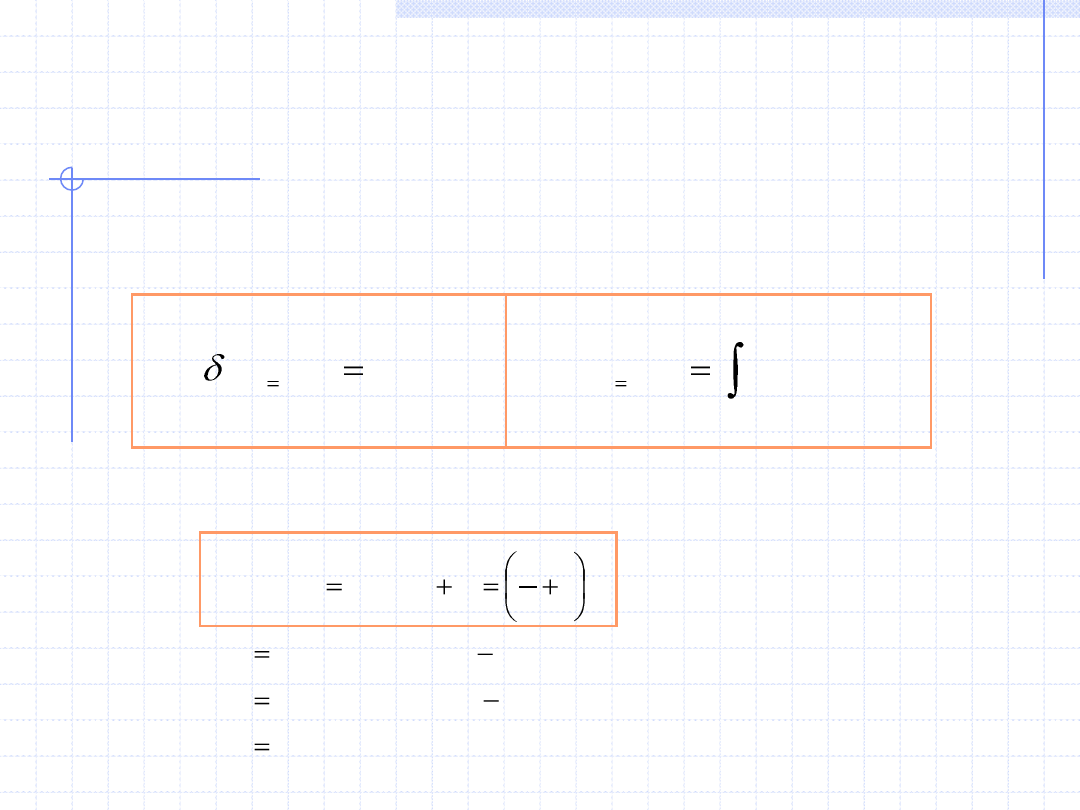
Przemiana izobaryczna cd.

2

1

)

(

)

(

)

(

.

.

T

T

p

const

p

p

const

p

dT

T

c

q

dT

c

q

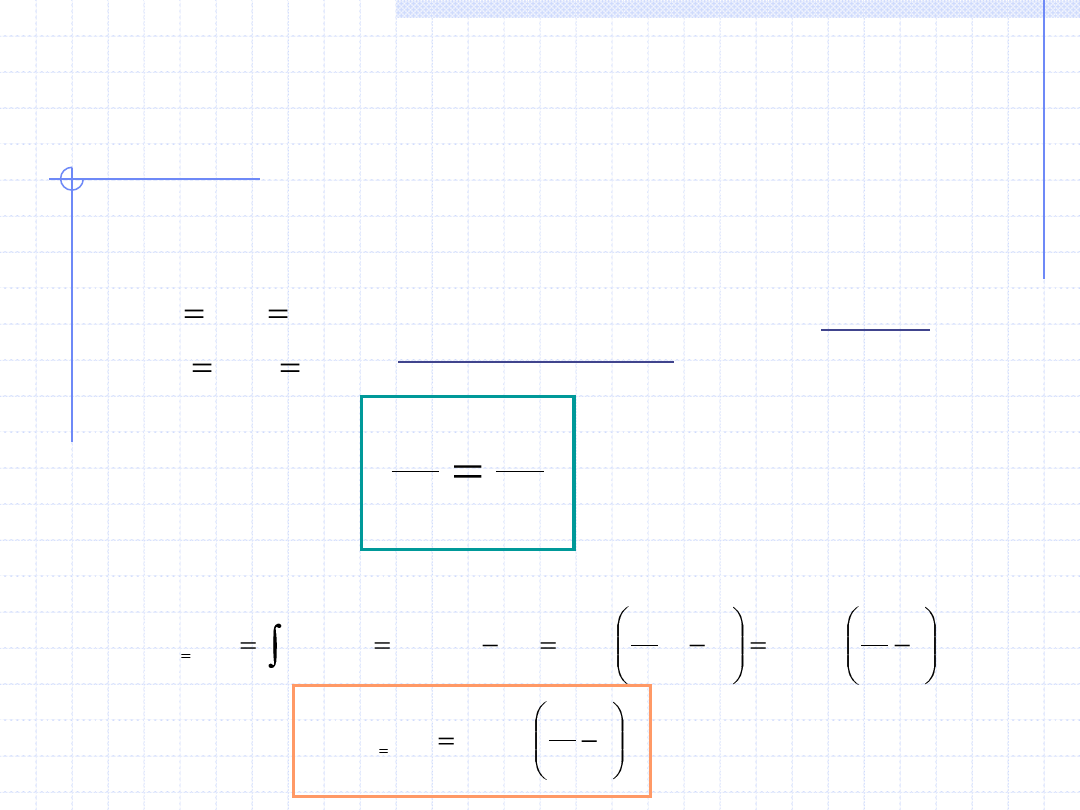
Wielkość c

p

zależy od temperatury, ciśnienia i rodzaju ośrodka. Zależność

od temperatury pozwala na wyznaczenie ciepła przemiany izobarycznej:

Dla gazów doskonałych, z teorii kinetycznej wynika że wielkość c

p

powinna

być stała i równa:

wych

wieloatomo

gazów

dla

k

atomowych

gazów

dla

k

atomowych

gazów

dla

k

gdzie

R

k

R

c

c

GD

v

GD

p

6

2

5

1

3

:

1

2

)

(

)

(

)

(

)

(

Przemiana izobaryczna cd.

2

2

2

2

1

1

1

1

RT

pv

v

p

RT

pv

v

p

1

)

(

1

)

(

)

(

1

2

1

)

(

)

(

.

1

2

1

)

(

1

1

1

2

)

(

1

2

)

(

)

(

)

(

.

2

1

v

v

T

c

q

v

v

T

c

T

T

v

v

c

T

T

c

dT

c

q

GD

p

GD

const

p

GD

p

GD

p

GD

p

T

T

GD

p

GD

const

p

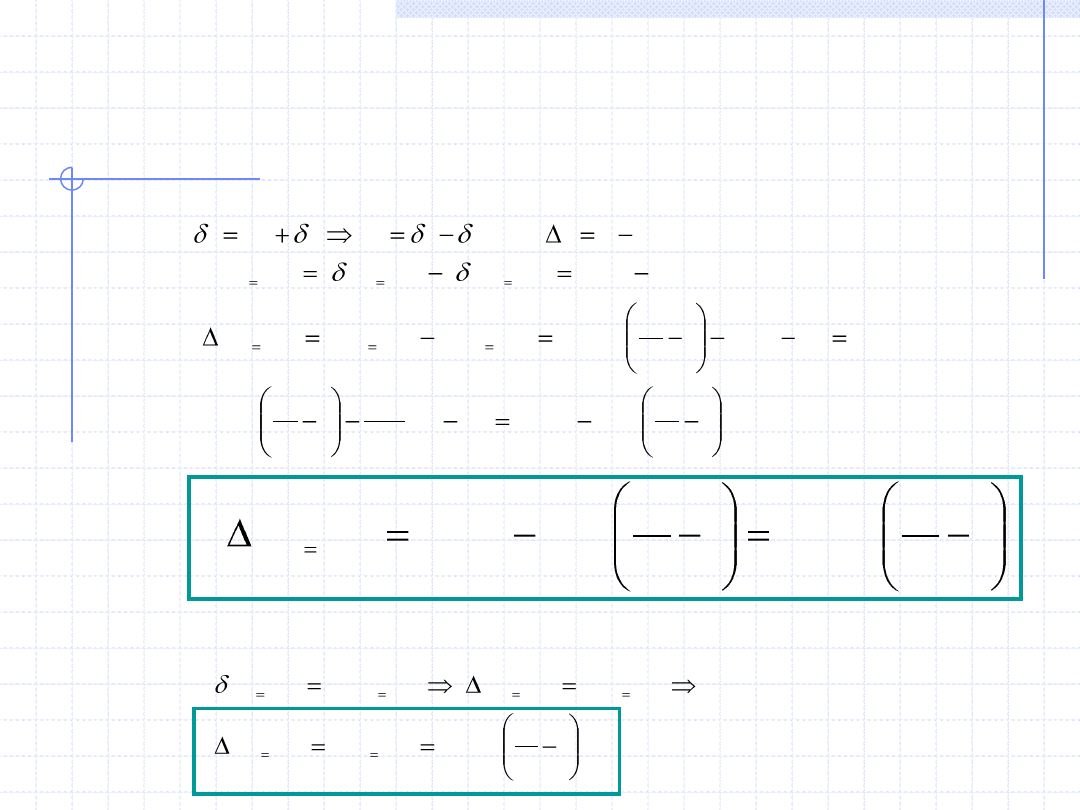
Rozpatrzmy jeszcze dokładniej przemianę izobaryczną gazów doskonałych.

W każdy punkcie takiej przemiany musi być spełnione równanie stanu gazu

doskonałego. Dla punku początkowego i końcowego mamy:

Dzieląc stronami otrzymujemy tzw. równanie

przemiany izobarycznej uzależniające objętość

i temperaturę w skrajnych punktach przemiany:

Dla gazów doskonałych również wzór określający ciepło ma prostą postać:

1

2

1

2

T

T

v

v

Przemiana izobaryczna cd.

1

)

(

)

(

)

(

)

(

)

(

)

(

1

2

1

)

(

)

(

.

)

(

.

.

.

.

.

v

v

T

c

q

h

q

h

dh

q

GD

p

GD

const

p

GD

const

p

const

p

const

p

const

p

const

p

1

)

(

)

(

1

)

(

1

)

(

)

(

)

(

)

(

)

(

)

(

1

2

1

)

(

1

2

1

1

1

2

1

)

(

1

2

1

2

1

)

(

)

(

.

)

(

.

)

(

.

.

.

.

v

v

T

R

c

v

v

v

RT

v

v

T

c

v

v

p

v

v

T

c

w

q

u

pdv

dT

c

w

q

du

w

q

u

w

q

du

w

du

q

GD

p

GD

p

GD

p

GD

const

p

GD

const

p

GD

const

p

p

const

p

const

p

const

p

Na koniec określimy wzory określające przyrosty (zmiany) najważniejszych

funkcji stanu w przemianie izobarycznej gazów doskonałych.

a) Energia wewnętrzna – u.

Na podstawie I zasady termodynamiki mamy:

b) Entalpia – h.

Na podstawie I zasady termodynamiki mamy:

1

1

)

(

)

(

1

2

1

)

(

1

2

1

)

(

)

(

.

v

v

T

c

v

v

T

R

c

u

GD

v

GD

p

GD

const

p

Przemiana izobaryczna cd.

1

2

)

(

)

(

)

(

.

.

.

.

ln

)

(

)

(

)

(

)

(

)

(

2

1

2

1

T

T

c

dT

T

c

s

dT

T

T

c

s

T

dT

c

T

q

ds

GD

p

T

T

GD

p

GD

const

p

T

T

p

const

p

p

const

p

const

p

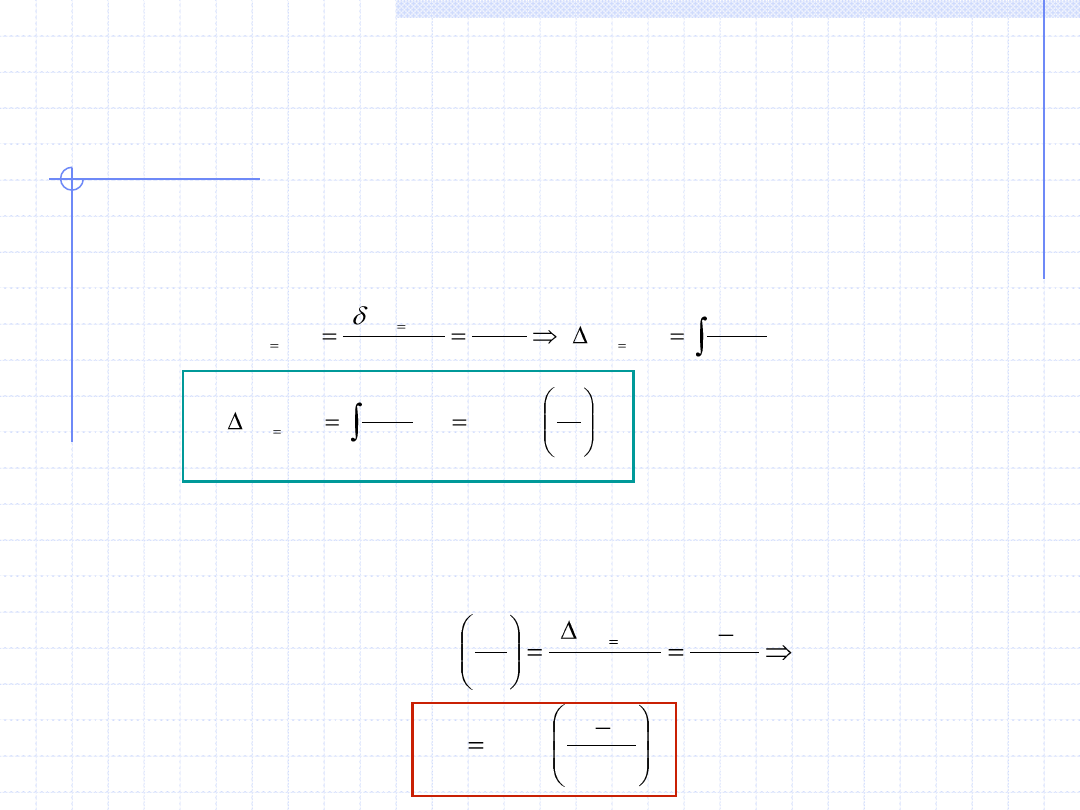
c) Entropia – s.

Przy założeniu, że nasza przemiana izobaryczna jest odwracalna

można napisać:

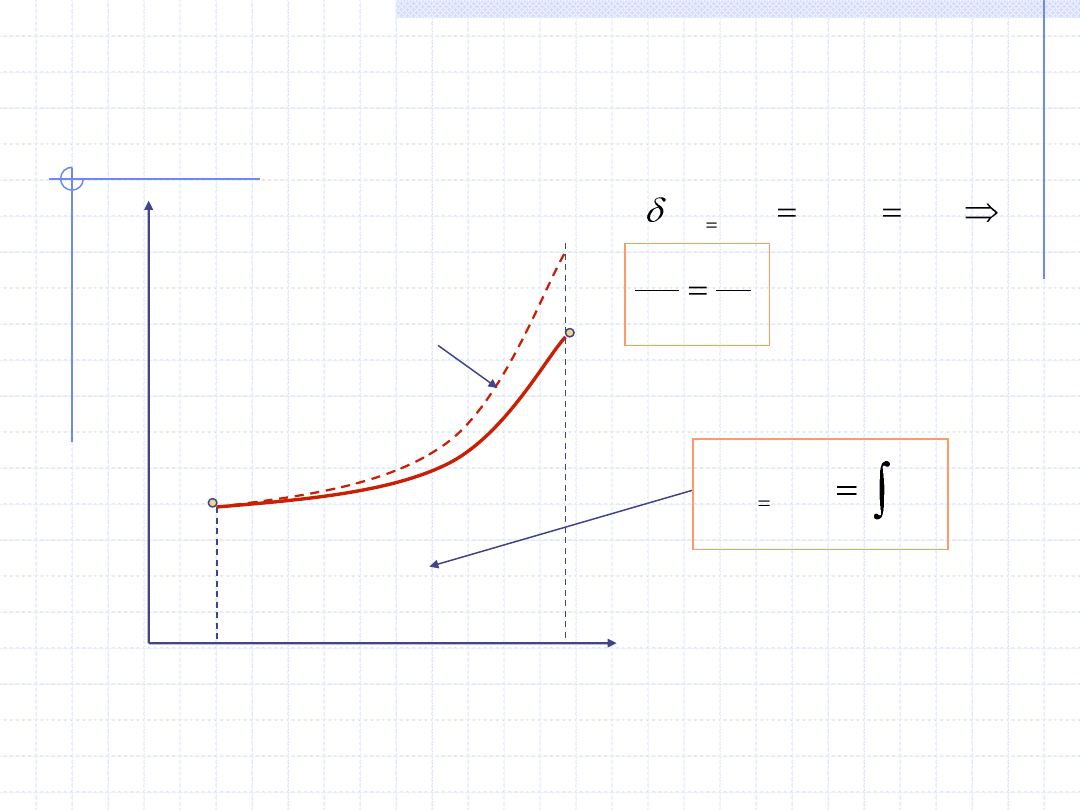
Wzór powyższy określający przyrost entropii w przemianie izobarycznej

gazu doskonałego można przekształcić otrzymując zależność temperatury

od entropii. Zależność taką można wykorzystać przy konstrukcji wykresu

przemiany w układzie T – s.

)

(

1

2

1

2

)

(

1

2

)

(

)

(

.

1

2

exp

)

(

ln

GD

p

GD

p

GD

p

GD

const

p

c

s

s

T

T

c

s

s

c

s

T

T

2

1

.

)

(

s

s

const

p

Tds

q

T

s

1

2

s

1

s

2

p

p

const

p

c

T

ds

dT

Tds

dT

c

q

.

)

(

v=const.

Przemiana izobaryczna cd.

Ale c

p

>c

v

28

To na dzisiaj tyle.

Dziękuję bardzo Państwu za uwagę.