©2004 Przemysław Baran – www.ar.krakow.pl\~pbaran
1
Ruch wody w gruncie – rozwiązanie ogólne
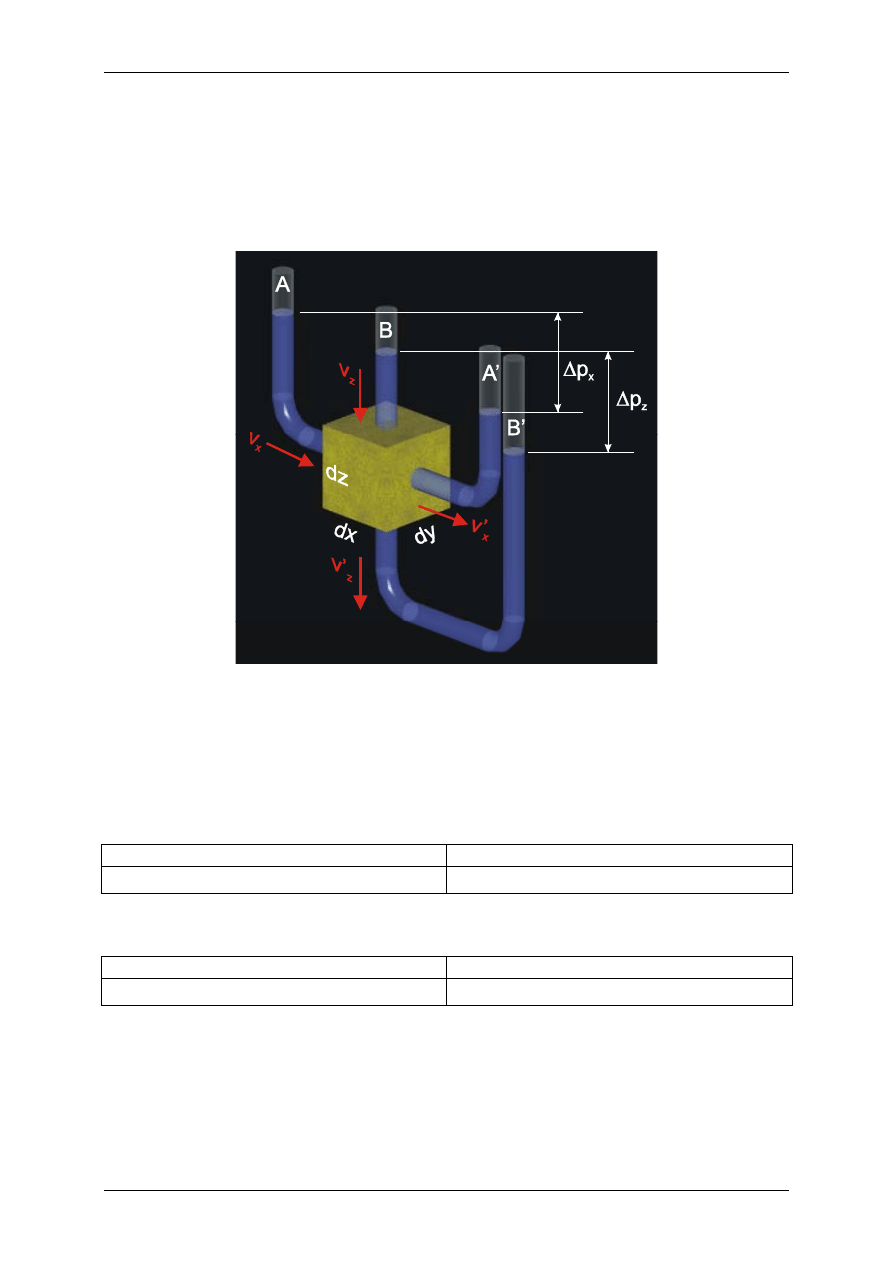
Do „myślowo” wyodrębnionego prostopadłościanu gruntu o wymiarach
nieskończenie małych, podłączono piezometry (Rys. 1). Zakładamy, że na kierunku y
grunt się nie zmienia, zatem skoncentrujemy się na przepływie w kierunku x
(poziomo) i z (pionowo).
Rys. 1 Filtracja przez elementarny prostopadłościan gruntu
Prędkość wody dopływającej do gruntu z kierunku x oznaczmy przez v
x
i
analogicznie, prędkość wody dopływającej z kierunku z przez v
z
. Przy przejściu przez
grunt woda nie ma już prędkości wejściowej (opory tarcia), zatem oznaczmy jej
prędkość na wyjściu z kierunku x przez v’
x
, a z kierunku z przez v’
z
. Przepływ na
wejściu do prostopadłościanu wyniesie odpowiednio:
kierunek x
kierunek z
dy
dz
v
q
x
x
⋅
⋅
=
dy
dx
v
q
z
z
⋅
⋅
=
I odpowiednio na wyjściu z prostopadłościanu:
kierunek x
kierunek z
dy
dz
v
q
x
x
⋅
⋅
= '
'
dy
dx
v
q
z
z
⋅
⋅
= '
'
Ponieważ opory tarcia zmniejszają prędkość, zmniejszają również wysokość
ciśnienia, czego skutkiem jest spadek zwierciadła wody pomiędzy piezometrami A i
A’, oraz B i B’ (Rys. 1). Zatem, można napisać, że nastąpiła zmiana prędkości
wejściowej na danym kierunku.
©2004 Przemysław Baran – www.ar.krakow.pl\~pbaran
2
Stąd:
kierunek x
kierunek z
dy
dz
dx
x
v
v
q
dx
x
v
v
v
x
x
x
x
x
x
⋅
⋅
⎟
⎠
⎞
⎜
⎝
⎛
⋅
∂
∂
+
=
⋅
∂
∂
+
=
'
'
dy
dx
dz
z
v
v
q
dz
z
v
v
v
z
z
z
z
z
z
⋅
⋅
⎟
⎠
⎞
⎜
⎝
⎛
⋅
∂
∂
+
=
⋅
∂
∂
+
=
'
'
Zakładamy, że :
- ruch wody jest ustalony;
- szkielet gruntu i woda są praktycznie nieściśliwe;
- w wodzie nie może powstawać próżnia
W związku z powyższym, ilość wody dopływającej do prostopadłościanu jak i z niego
wypływającej w danym czasie musi być sobie równa, a zatem:
0
;
;
'
'
=
⋅
⋅
⋅
∂
∂
+
⋅
⋅
⋅
∂
∂
⋅
⋅
⋅
∂
∂
+
⋅
⋅
+
⋅
⋅
⋅
∂
∂
+
⋅
⋅
=
⋅
⋅
+
⋅
⋅
+
=
+
dy
dx
dz
z
v
dy
dz
dx
x
v
dy
dx
dz
z
v
dy
dx
v
dy
dz
dx
x
v
dy
dz
v
dy
dx
v
dy
dz
v
q
q
q
q
z
x
z
z
x
x
z
x
z
x
z
x
Po uproszczeniu otrzymujemy równanie różniczkowe ciągłości filtracji:
0
=
∂
∂
+
∂
∂
z
v
x
v
z
x
Ruch wody w gruncie odbywa się zgodnie z prawem Darcy, zatem dla gruntu
izotropowego (k
x
= k
z
= k) prędkości filtracji wyniosą :
kierunek x
kierunek z
x
H
k
v
x
∂
∂
⋅
−
=
z
H
k
v
z
∂
∂
⋅
−
=
gdzie:
x
H
∂
∂
i
z
H
∂
∂
są spadkami hydraulicznymi odpowiednio w kierunku x i z. Znak
minus przy współczynniku filtracji oznacza, że kierunek dodatni prędkości jest w
stronę zmniejszającego się ciśnienia.
Po podstawieniu do równania ciągłości filtracji otrzymamy:
0
;
0
2
2
2
2
=
∂
∂
⋅
+
∂
∂
⋅
=
∂
⎭
⎬
⎫
⎩
⎨
⎧
∂
∂
⋅
−
∂
+
∂
⎭
⎬
⎫
⎩
⎨
⎧
∂
∂
⋅
−
∂
z
H
k
x
H
k
z
z
H
k
x
x
H
k
©2004 Przemysław Baran – www.ar.krakow.pl\~pbaran
3
Upraszczając przez k, dostajemy dwuwymiarowe równanie Laplace’a:
0
2
2
2
2
=
∂
∂
+
∂
∂
z
H
x
H
a wprowadzając operator „nabla”:
z
H
x
H
H
∂
∂
+
∂
∂
=
∇
, otrzymamy:
0
2
=
∇ H
Rozwiązanie powyższego równania oznacza znalezienie takiej wartości H
(wartości potencjału), która będzie średnią wszystkich wartości H na nieskończenie
małym okręgu otaczającym dany punkt w całym obszarze analizy, przy znanych
warunkach brzegowych. Aby móc znaleźć szukaną wartość H można posłużyć się
jedną z metod przybliżonych (numerycznych) – np. metodą różnic skończonych
(MRS). W naszym wypadku zastąpimy różnice nieskończenie małe we wzorze
Laplace’a, różnicami skończonymi. Przed dokonaniem tej „operacji” musimy
przeprowadzić tzw. dyskretyzację obszaru analizy. Ponieważ szukamy wartości H
jako średniej z otaczających ją wartości, wydzielamy, na rozpatrywanym przez nas
obszarze, siatkę punktów. Pamiętać tutaj należy, iż podział siatką punktów musi być
na tyle gęsty, aby różnice w odległościach były małe, co prowadzić będzie do
dokładniejszego rozwiązania.
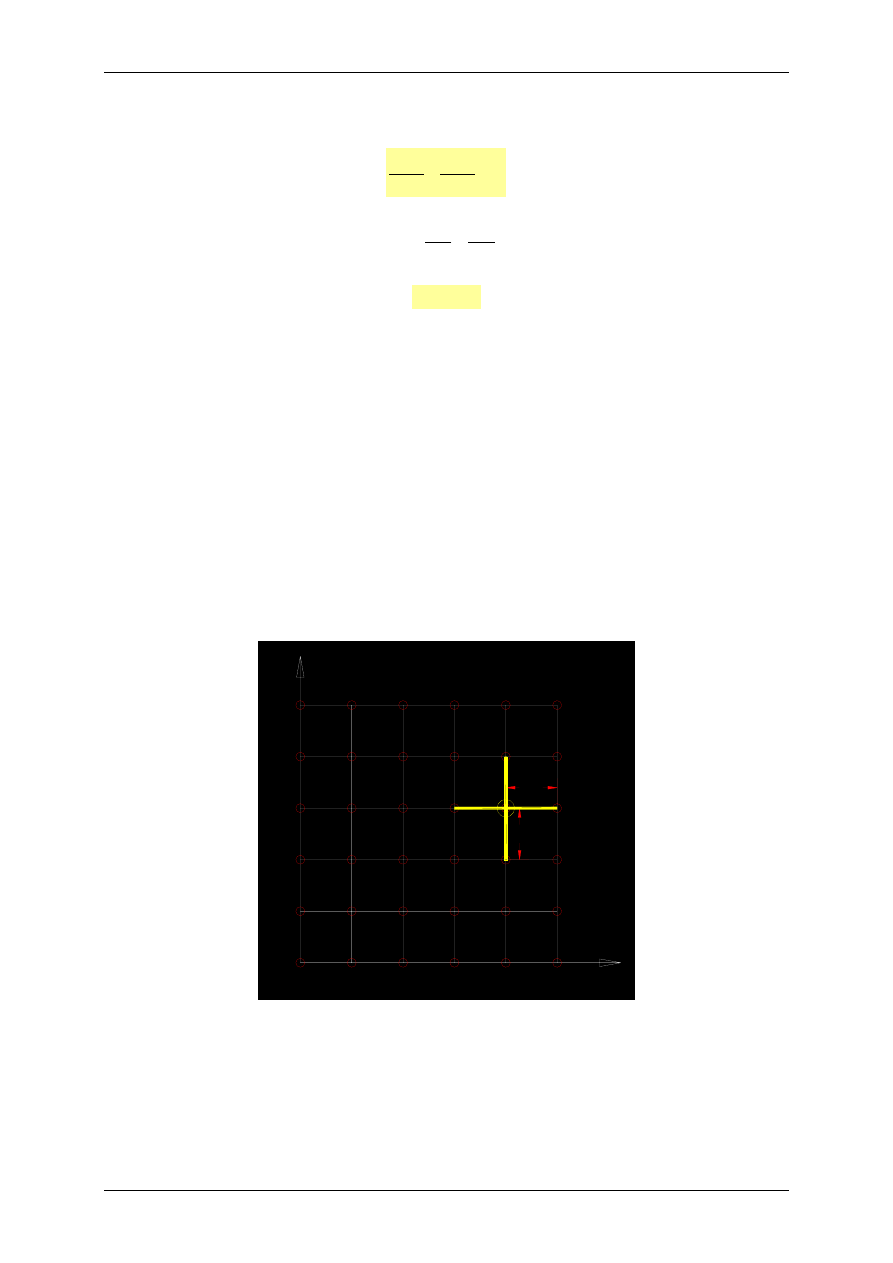
Zaprezentuję tutaj tok postępowania dla siatki kwadratowej (Rys. 2) (można
dyskretyzować również siatką trójkątną i sześciokątną).
∆
x
∆
x
X
Z
j=4
i=1
i=0
i=2
i=3
i=4
i=5
j=5
j=3
j=2
j=1
j=0
Rys. 2 Dyskretyzacja obszaru kwadratową siatką punktów
Skoncentrujmy się na żółtym węźle (i=4; j=3). Ma on czterech sąsiadów (3; 3),
(4; 4), (5; 3) i (4; 2), którzy stanowią jego otoczenie. Zakładamy, że są oni oddaleni
od węzła „żółtego” o skończenie małą wartość
∆
x. Nasze zadanie będzie polegało na
znalezieniu formuły przybliżonej, obliczającej drugą pochodną H względem x i z dla

©2004 Przemysław Baran – www.ar.krakow.pl\~pbaran
4
żółtego węzła. Ponieważ H jest funkcją x i z, do wyznaczenia pochodnych
skorzystamy z rozwinięcia funkcji w szereg Taylora:
( ) ( )
(
)
(
)
...
2
2
2
2
+
−
⋅
+
−
⋅
+
=
a
x
da
f
d
a
x
da
df
a
f
x
f
W naszym przypadku, na kierunku x, dla sąsiadów węzła „żółtego” otrzymamy:
x
X
x
∆
+
=
dla (5; 3)
x
X
x
∆
−
=
dla (3; 3)
oraz:
X
a
=
stąd po podstawieniu:
(
)
(
)
( )
(
)
(
)
( )
...
2
)
(
)
(
...;
2
)
(
)
(
:
)
(
...
2
)
(
)
(
...;
2
)
(
)
(
:
)
(
2
2
2
2
2
2
2
2
2
2
2
2
+
∆
⋅
+
∆
⋅
−
=
∆
−
+
−
∆
−
⋅
+
−
∆
−
⋅
+
=
∆
−
∆
−
+
∆
⋅
+
∆
⋅
+
=
∆
+
+
−
∆
+
⋅
+
−
∆
+
⋅
+
=
∆
+
∆
+
x
dX
f
d
x
dX
df
X
f
x
X
H
X
x
X
dX
f
d
X
x
X
dX
df
X
f
x
X
f
x
X
x
dX
f
d
x
dX
df
X
f
x
X
f
X
x
X
dX
f
d
X
x
X
dX
df
X
f
x
X
f
x
X
teraz dodajemy te formuły do siebie:
(
) (
)
( )
( )
(
) (
)
( )
(
) (
)
( )
(
) (
)
( )
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
)
(
2
;
)
(
2
;
2
2
)
(
2
;
2
)
(
2
)
(
x
dX
f
d
X
f
x
X
f
x
X
f
x
dX
f
d
X
f
x
X
f
x
X
f
x
dX
f
d
X
f
x
X
f
x
X
f
x
dX
f
d
x
dX
df
X
f
x
dX
f
d
x
dX
df
X
f
x
X
f
x
X
f
∆
⋅
=
⋅
−
∆
−
+
∆
+
∆
⋅
+
⋅
=
∆
−
+
∆
+
⎥
⎦
⎤
⎢
⎣
⎡
∆
⋅
⋅
+
⋅
=
∆
−
+
∆
+
∆
⋅
+
∆
⋅
−
+
∆
⋅
+
∆
⋅
+
=
∆
−
+
∆
+
stąd wzór na drugą pochodną f względem x przybierze postać:
(
) (
)
( )
2
2
2
)
(
2
x
X
f
x
X
f
x
X
f
dX
f
d
∆
⋅
−
∆
−
+
∆
+
≈
analogicznie dla f względem z:

©2004 Przemysław Baran – www.ar.krakow.pl\~pbaran
5
(
) (
)
( )
2
2
2
)
(
2
x
Z
f
x
Z
f
x
Z
f
dZ
f
d
∆
⋅
−
∆
−
+
∆
+
≈
Jak już było wspomniane, H jest funkcją zmiennych x i z, podstawiając powyższe
formuły do równania Laplace’a otrzymamy:
(
)
(
)
(
)
(
)
(
)
( )
(
)
(
)
( )
(
)
(
)
(
)
(
)
0
)
,
(
2
,
,
)
,
(
2
,
,
;
0
)
,
(
2
,
,
)
,
(
2
,
,
;
0
,
,
,
2
2
2
2
2
2
2
=
⋅
−
∆
−
+
∆
+
+
⋅
−
∆
−
+
∆
+
=
∆
⋅
−
∆
−
+
∆
+
+
∆
⋅
−
∆
−
+
∆
+
=
∂
∂
+
∂
∂
=
∇
Z
X
H
x
Z
X
H
x
Z
X
H
Z
X
H
Z
x
X
H
Z
x
X
H
x
Z
X
H
x
Z
X
H
x
Z
X
H
x
Z
X
H
Z
x
X
H
Z
x
X
H
Z
Z
X
H
X
Z
X
H
Z
X
H
Zatem, równanie Laplace’a w zapisie różnic skończonych przybierze postać:
(
)
(
)
(
)
(
)
(
)
0
)
,
(
4
,
,
,
,
,
2
=
⋅
−
∆
−
+
∆
+
+
∆
−
+
∆
+
≈
∇
Z
X
H
x
Z
X
H
x
Z
X
H
Z
x
X
H
Z
x
X
H
Z
X
H
Stąd, wartość H dla węzła centralnego (otoczonego czterema sąsiadami) będzie
równa:
(
)
(
)
(
)
(
)
4
,
,
,
,
)
,
(
x
Z
X
H
x
Z
X
H
Z
x
X
H
Z
x
X
H
Z
X
H
∆
−
+
∆
+
+
∆
−
+
∆
+
=
Zamiast współrzędnymi x i z (przy stałym wymiarze oczka siatki), lepiej operować
pozycją węzła (i; j). Wówczas, powyższy wzór otrzyma następującą formę:
( )
(
)
(
)
(
)
(
)
4
1
,
1
,
,
1
,
1
,
−
+
+
+
−
+
+
=
j
i
H
j
i
H
j
i
H
j
i
H
j
i
H
Zaprezentuję tutaj procedurę obliczeniową zwaną „metodą relaksacji”,
polegającą na wyliczaniu nowych wartości H w kolejnych iteracjach, na podstawie
dowolnych założonych wartości. Procedura jest o tyle interesująca, gdyż co byśmy
nie założyli, rozwiązanie zawsze nastąpi. Przytoczę w tym miejscu dwie techniki
iteracyjne:
Jakobiego (wolna ale prosta):
( )
(
)
(
)
(
)
(
)
4
1
,
1
,
,
1
,
1
,
1
m
m
m
m
m
j
i
H
j
i
H
j
i
H
j
i
H
j
i
H
−
+
+
+
−
+
+
=
+
Nad-relaksacyjna (szybka ale bardziej złożona):
( )
(
) ( )
(
)
(
)
(
)
(
)
[
]
4
1
,
,
1
1
,
,
1
,
1
,
1
1
1
+
+
+
−
+
−
+
+
+
+
⋅
⋅
⋅
−
=
m
m
m
m
m
m
j
i
H
j
i
H
j
i
H
j
i
H
j
i
H
j
i
H
ω
ω
gdzie: m jest numerem iteracji,
ω
współczynnikiem nad-relaksacji (1.5
÷1.85).
Obliczenia prowadzimy do chwili, gdy różnice pomiędzy wartościami z dwóch
ostatnich iteracji będą odpowiednio małe:

©2004 Przemysław Baran – www.ar.krakow.pl\~pbaran
6
( )
( )
0
,
,
max
1
≈
−
+
m
m
j
i
H
j
i
H
Kolejna rzecz: wartości brzegowe. Najczęściej posługujemy się dwoma rodzajami
wartości brzegowych. Pierwszy opisuje znaną wartość potencjału H (warunek
Dirichleta); drugi znaną wartość prędkości filtracji v (warunek Neumanna). Potencjał
może być (i najczęściej jest) rozumiany jako piezometryczny poziom wody (poziom
zwierciadła w piezometrze) mierzony od założonego poziomu odniesienia. Z kolei,
warunek brzegowy dla prędkości jest znacznie bardziej skomplikowany. Popatrzmy
niżej:
Vz
i,j
i,j+1
i+1,j
i-1,j
Rys. 3 Warunek brzegowy dla prędkości
Jeżeli prędkość w którymś z punktów analizowanego obszaru jest znana, wówczas
zastępujemy węzeł będący na kierunku jej działania, a zamiast niego wprowadzamy
wektor prędkości (Rys. 3). Rozpatrzmy znaną wartość prędkości na kierunku z.
Zgodnie z prawem Darcy będzie ona równa:
( )
z
z
x
H
k
z
H
k
v
z
∂
∂
⋅
−
=
∂
∂
⋅
−
=
,
Wartość pierwszej pochodnej H względem z otrzymamy z wykorzystanego wcześniej
rozwinięcia funkcji w szereg Taylora:
(
)
(
)
...
)
(
)
(
...;
)
(
)
(
:
)
(
...
)
(
)
(
...;
)
(
)
(
:
)
(
+
∆
⋅
−
=
∆
−
+
−
∆
−
⋅
+
=
∆
−
∆
−
+
∆
⋅
+
=
∆
+
+
−
∆
+
⋅
+
=
∆
+
∆
+
x
dZ
df
Z
f
x
Z
H
Z
x
Z
dZ
df
Z
f
x
Z
f
x
Z
x
dZ
df
Z
f
x
Z
f
Z
x
Z
dZ
df
Z
f
x
Z
f
x
Z

©2004 Przemysław Baran – www.ar.krakow.pl\~pbaran
7
Po odjęciu powyższych równań:
(
) (
)
( )
( )
(
) (
)
(
) (
)
x
x
Z
f
x
Z
f
dZ
df
x
dZ
df
x
Z
f
x
Z
f
x
dZ
df
Z
f
x
dZ
df
Z
f
x
Z
f
x
Z
f
∆
⋅
∆
−
−
∆
+
=
∆
⋅
⋅
=
∆
−
−
∆
+
⎥⎦
⎤
⎢⎣
⎡
∆
⋅
−
−
∆
⋅
+
=
∆
−
−
∆
+
2
2
Dla funkcji H(i, j) otrzymamy następujący wzór na pierwszą pochodną H względem z:
( )
(
)
(
)
x
j
i
H
j
i
H
dZ
j
i
dH
∆
⋅
−
−
+
≈
2
1
,
1
,
,
Stąd:
(
)
(
)
x
j
i
H
j
i
H
k
v
z
∆
⋅
−
−
+
⋅
−
=
2
1
,
1
,
Ponieważ na kierunku z nie ma węzła (i, j-1) (Rys. 3), musimy go wyeliminować przez
połączenie powyższego równania z równaniem Laplace’a:
(
)
(
)
(
)
(
)
(
)
(
)
( )
(
)
(
)
(
)
(
)
4
2
1
,
1
,
,
1
,
1
,
;
2
1
,
1
,
;
1
,
1
,
2
;
2
1
,
1
,
⎥⎦
⎤
⎢⎣
⎡
∆
⋅
⋅
+
+
+
+
+
−
+
+
=
∆
⋅
⋅
+
+
=
−
−
−
+
=
∆
⋅
⋅
−
∆
⋅
−
−
+
⋅
−
=
k
x
v
j
i
H
j
i
H
j
i
H
j
i
H
j
i
H
k
x
v
j
i
H
j
i
H
j
i
H
j
i
H
k
x
v
x
j
i
H
j
i
H
k
v
z
z
z
z
Zatem, dla warunku brzegowego przy znanej prędkości w kierunku pionowym
otrzymamy następujący wzór na potencjał w węźle (i, j):
( )
(
)
(
)
(
)
k
x
v
j
i
H
j
i
H
j
i
H
j
i
H
z
⋅
∆
⋅
+
−
+
+
+
+
⋅
=
2
4
,
1
,
1
1
,
2
,
I analogicznie w kierunku poziomym:
( )
(
)
(
)
(
)
k
x
v
j
i
H
j
i
H
j
i
H
j
i
H
x
⋅
∆
⋅
+
−
+
+
+
+
⋅
=
2
4
1
,
1
,
,
1
2
,

©2004 Przemysław Baran – www.ar.krakow.pl\~pbaran
8
Podsumowując:
&
Podstawy teoretyczne MRS są raczej proste, a tok postępowania w przypadku
korzystania z tej metody jest łatwy do wytłumaczenia.
&
Niewątpliwym atutem metody jest prostota działań arytmetycznych. W zasadzie
są to mnożenia i dodawania, czyli operacje, które są najszybciej wykonywane
przez komputer. Do przeprowadzenia takich obliczeń możemy skorzystać nawet
ze zwykłego arkusza kalkulacyjnego.
&
Obliczenia z zasady są stabilne i istnieje zawsze rozwiązanie (metoda relaksacji).
'
Niestety, aby móc skorzystać ze wzoru Laplace’a, należy znać wartości brzegowe
otaczające cały obszar analizy. Jest to czasami bardzo trudne do ustalenia, np.
położenie i kształt krzywej depresji. Sięga się wtedy do metod uproszczonych,
pozwalających określić wzmiankowane cechy krzywej depresji, a kiedy już jest to
znane, prowadzi się obliczenia rozkładu potencjałów. Oczywiście istnieją sposoby
na „obejście” tego typu postępowania, ale o tym powiemy sobie przy następnej
okazji.
'
Kolejna kwestia jest związana z samą dyskretyzacją za pomocą siatki punktów –
czasami ciężko ją zaadoptować do realnych warunków, zwłaszcza przy
skomplikowanej geometrii obszaru analizy.
Wyszukiwarka
Podobne podstrony:
ACTOR NETWORK THEORY id 51034 Nieznany (2)
Laplace example id 263400 Nieznany
aq cable theory id 67384 Nieznany
Laplace 5 id 263390 Nieznany
5 Laplace id 40231 Nieznany (2)
laplace 6 id 263391 Nieznany
Laplace 5 id 263390 Nieznany
Abolicja podatkowa id 50334 Nieznany (2)
4 LIDER MENEDZER id 37733 Nieznany (2)
katechezy MB id 233498 Nieznany
metro sciaga id 296943 Nieznany
perf id 354744 Nieznany
interbase id 92028 Nieznany
Mbaku id 289860 Nieznany
Probiotyki antybiotyki id 66316 Nieznany
miedziowanie cz 2 id 113259 Nieznany
LTC1729 id 273494 Nieznany
D11B7AOver0400 id 130434 Nieznany
więcej podobnych podstron