Prawdopodobieństwo i statystyka

17.03.2008 r.

___________________________________________________________________________

Zadanie 1.

Niech

będzie zmienną losową o rozkładzie jednostajnym na przedziale (0,1),

zmienną losową o rozkładzie jednostajnym na przedziale

1

X

2

X

(

)

1

,

0 X

,

zmienną losową

o rozkładzie jednostajnym na przedziale

3

X

(

)

2

,

0 X

i tak dalej. Niech N oznacza

zmienną losową o rozkładzie geometrycznym

K

,

3

,

2

,

1

gdy

)

1

(

)

(

1

=

−

=

=

−

n

q

q

n

N

P

n

,

gdzie

jest ustaloną liczbą. Zmienna N jest niezależna od zmiennych

.

)

1

,

0

(

∈

q

K

,

,

,

3

2

1

X

X

X

Obliczyć

.

)

(

2

1

N

X

X

X

E

⋅

⋅

⋅

K

(A)

(

)

q

e

q

q

q

−

−

−

1

1

2

(B)

(

)

1

1

−

−

q

e

q

q

(C)

)

2

(

)

1

(

2

q

q

q

−

−

(D)

q

q

−

−

2

1

(E)

q

e

q)

1

(

−

1

Prawdopodobieństwo i statystyka

17.03.2008 r.

___________________________________________________________________________

Zadanie 2.

Zmienna losowa

ma rozkład normalny z wartością oczekiwaną

,

i macierzą kowariancji

)

,

,

(

Z

Y

X

2

,

0

=

=

EY

EX

1

=

EZ

⎥

⎥

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎢

⎢

⎢

⎣

⎡

4

1

2

1

0

2

1

2

2

1

0

2

1

2

.

Obliczyć .

))

2

(

(

Z

Y

X

Var

−

(A)

4

13

(B)

4

17

(C)

4

5

(D)

4

9

(E)

2

2

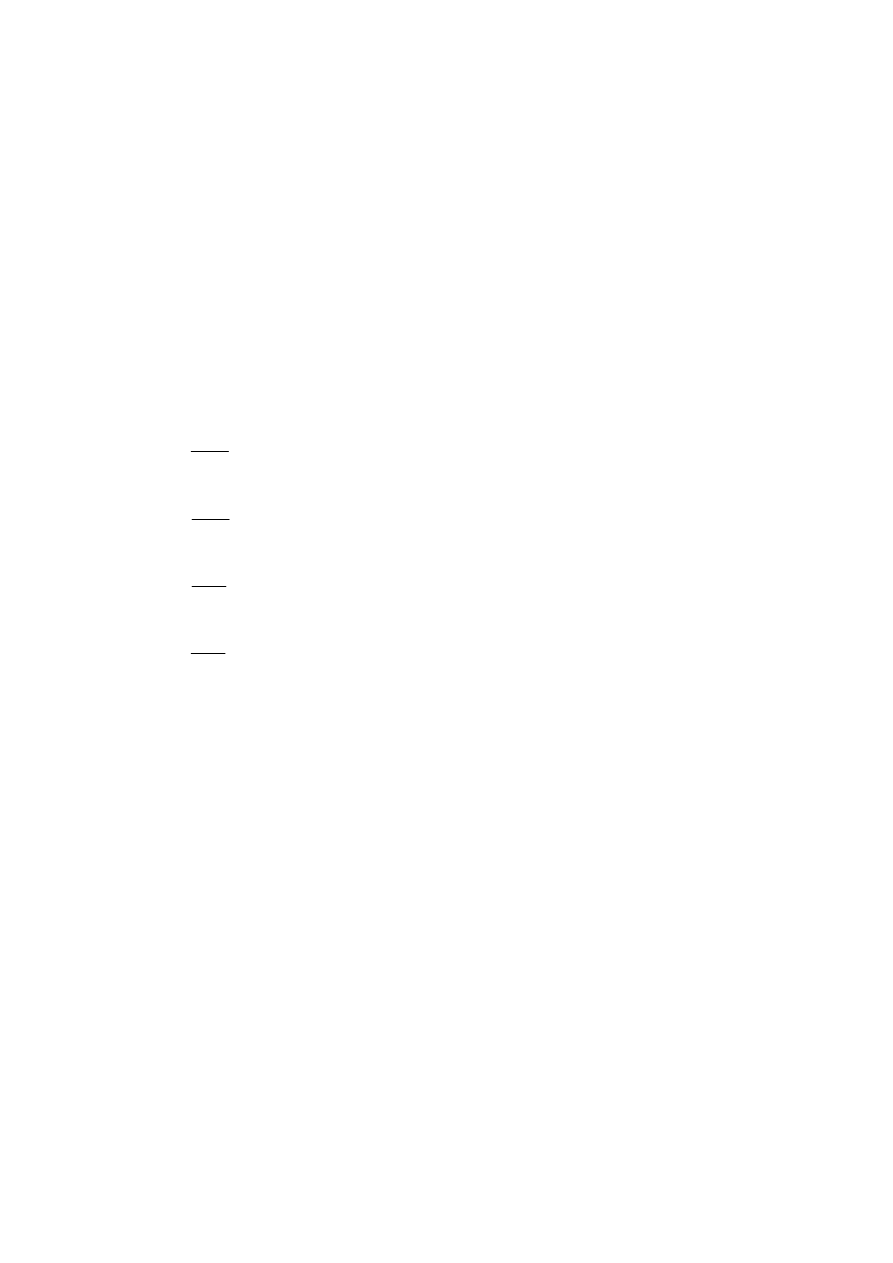
Prawdopodobieństwo i statystyka

17.03.2008 r.

___________________________________________________________________________

Zadanie 3.

Zmienna losowa X ma rozkład Weibulla o gęstości

⎩

⎨

⎧

≤

>

−

=

0

0

0

)

exp(

2

)

(

2

x

gdy

x

gdy

x

x

x

p

θ

θ

θ

,

gdzie

0

>

θ

jest nieznanym parametrem. Statystyk nie obserwuje zmiennej X,

uzyskuje tylko informację, gdy zmienna X przekroczy wartość d, a mianowicie
obserwuje zmienną Y równą X , gdy zmienna X jest większa niż d. W wyniku takiej
obserwacji uzyskuje prostą próbę losową

,

. Wartość oczekiwana

estymatora największej wiarogodności parametru

k

Y

Y

Y

,

,

,

2

1

K

2

>

k

θ uzyskanego na podstawie próby

losowej

jest równa

k

Y

Y

Y

,

,

,

2

1

K

(A)

θ

(B)

θ

2

−

k

k

(C)

θ

k

k

2

−

(D)

θ

k

k

1

−

(E)

θ

1

−

k

k

3

Prawdopodobieństwo i statystyka

17.03.2008 r.

___________________________________________________________________________

Zadanie 4.

Załóżmy, że niezależne zmienne losowe

mają rozkłady wykładnicze o

wartościach oczekiwanych

4

3

2

1

,

,

,

X

X

X

X

1

1

=

EX

, 2

4

3

2

=

=

=

EX

EX

EX

.

Obliczyć

.

{

}

(

)

4

3

2

1

1

,

,

,

max

X

X

X

X

X

P

=

(A)

35

5

(B)

5

1

(C)

10

1

(D)

35

16

(E)

30

1

4

Prawdopodobieństwo i statystyka

17.03.2008 r.

___________________________________________________________________________

Zadanie 5.

Niech będzie dwuwymiarową zmienną losową o funkcji gęstości

)

,

(

Y

X

⎩

⎨

⎧

<

+

>

>

=

przypadku.

przeciwnym

w

0

1

i

0

i

0

gdy

8

)

,

(

2

2

y

x

x

y

xy

y

x

f

Niech

2

2

2

Y

X

X

V

+

=

i

2

2

Y

X

Z

+

=

. Wtedy

(A) zmienne

X i Y są niezależne

(B) funkcja

gęstości rozkładu brzegowego zmiennej V wyraża się wzorem

dla

v

v

g

2

)

(

=

)

1

,

0

(

∈

v

(C) funkcja

gęstości rozkładu brzegowego zmiennej V wyraża się wzorem

dla

1

)

(

=

v

g

)

1

,

0

(

∈

v

(D)

6

1

)

,

(

=

V

Z

Cov

(E) funkcja

gęstości rozkładu brzegowego zmiennej Z wyraża się wzorem

dla

1

)

(

=

z

h

)

1

,

0

(

∈

z

5

Prawdopodobieństwo i statystyka

17.03.2008 r.

___________________________________________________________________________

Zadanie 6.

Niech

,

, będzie próbką losową z rozkładu normalnego

, gdzie oba parametry są nieznane. Bezpośrednio dostępne są tylko

obserwacje

, ale dodatkowo znamy średnią

m

n

n

X

X

X

X

+

,

,

,

,

,

2

1

K

K

1

,

>

n

m

)

,

(

2

σ

μ

N

n

X

X

X

,

,

,

2

1

K

∑

+

=

+

+

=

m

n

i

i

m

n

X

n

m

X

1

1

.

Budujemy estymator parametru

postaci

2

σ

(

2

1

1

1

∑

=

+

−

−

=

n

i

m

n

i

X

X

n

T

)

. Obciążenie tego

estymatora, czyli wielkość

jest równa

2

σ

−

ET

(A)

2

)

)(

1

(

σ

m

n

n

m

+

−

(B)

2

)

)(

1

(

σ

m

n

n

n

+

−

(C)

2

)

)(

1

(

1

σ

m

n

n

m

n

+

−

−

+

(D)

2

1

σ

m

n

+

−

(E)

2

1

σ

n

−

6

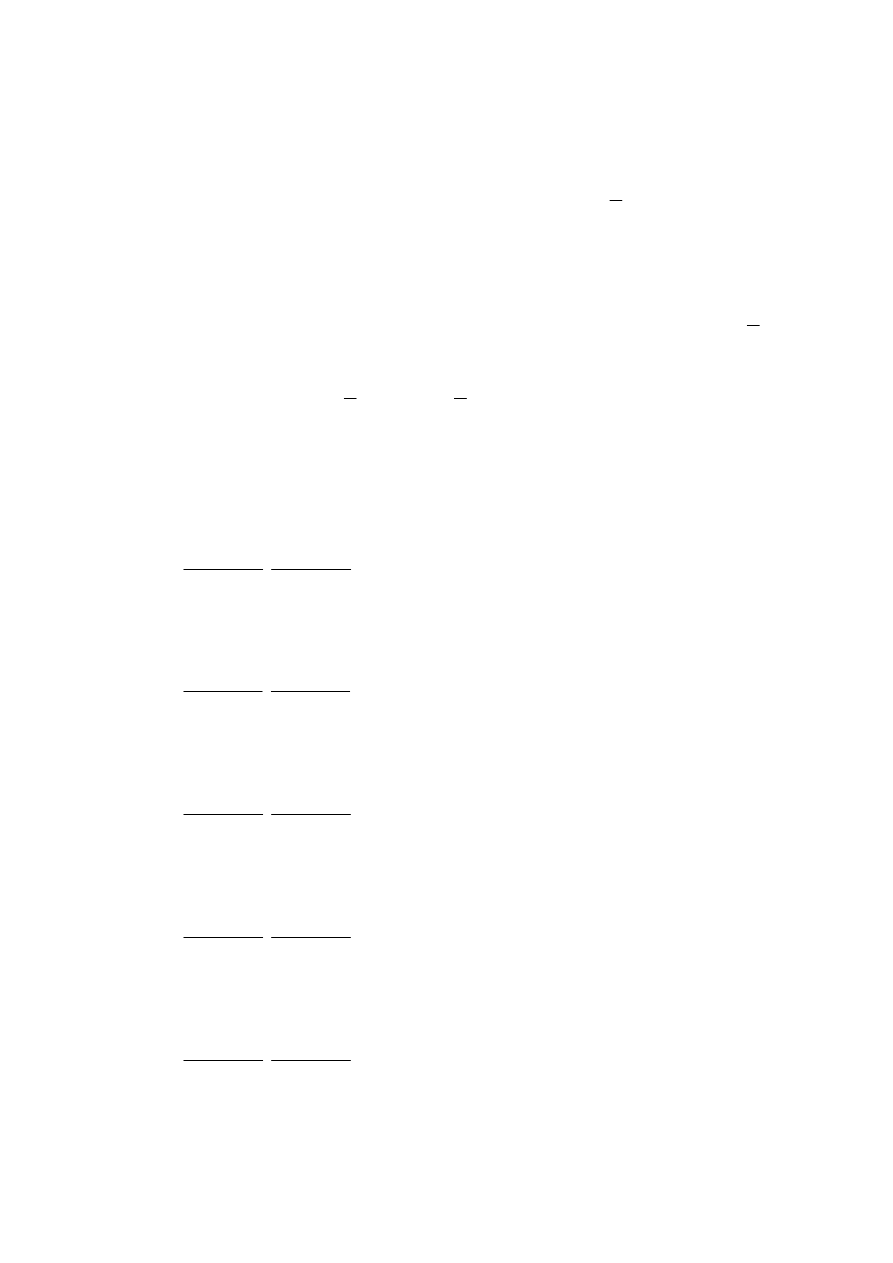
Prawdopodobieństwo i statystyka

17.03.2008 r.

___________________________________________________________________________

Zadanie

7.

Niech

będą niezależnymi zmiennymi losowymi o tym samym

rozkładzie normalnym z wartością oczekiwaną 0 i wariancją

6

2

1

,

,

,

X

X

X

K

θ

1

, gdzie

0

>

θ

jest

nieznanym parametrem. Zakładamy, że parametr

θ ma rozkład a priori o gęstości

(

)

⎩

⎨

⎧

≤

>

−

=

0

0

0

exp

)

(

2

θ

θ

βθ

θ

β

θ

gdy

gdy

p

,

gdzie 0

>

β

jest znane. Wyznaczamy bayesowski przedział ufności dla parametru

θ

1

postaci

[

, taki że

]

b

a,

05

,

0

|

1

|

1

=

⎟

⎠

⎞

⎜

⎝

⎛ >

Π

=

⎟

⎠

⎞

⎜

⎝

⎛ <

Π

x

b

x

a

θ

θ

,

gdzie

oznacza prawdopodobieństwo przy rozkładzie a posteriori, gdy

zaobserwowana wartość próbki losowej jest równa

(

x

|

⋅

Π

)

(

)

6

2

1

,

,

,

x

x

x

x

K

=

. Tak otrzymany

przedział jest równy

(A)

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎢

⎣

⎡

+

+

∑

∑

=

=

962

,

7

2

,

296

,

26

2

6

1

2

6

1

2

i

i

i

i

x

x

β

β

(B)

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎢

⎣

⎡

+

+

∑

∑

=

=

940

,

3

2

,

307

,

18

2

6

1

2

6

1

2

i

i

i

i

x

x

β

β

(C)

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎢

⎣

⎡

+

+

∑

∑

=

=

881

,

7

2

,

614

,

36

2

6

1

2

6

1

2

i

i

i

i

x

x

β

β

(D)

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎢

⎣

⎡

+

+

∑

∑

=

=

291

,

2

2

,

141

,

22

2

6

1

2

6

1

2

i

i

i

i

x

x

β

β

(E)

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎢

⎣

⎡

+

+

∑

∑

=

=

146

,

1

2

,

071

,

11

2

6

1

2

6

1

2

i

i

i

i

x

x

β

β

7

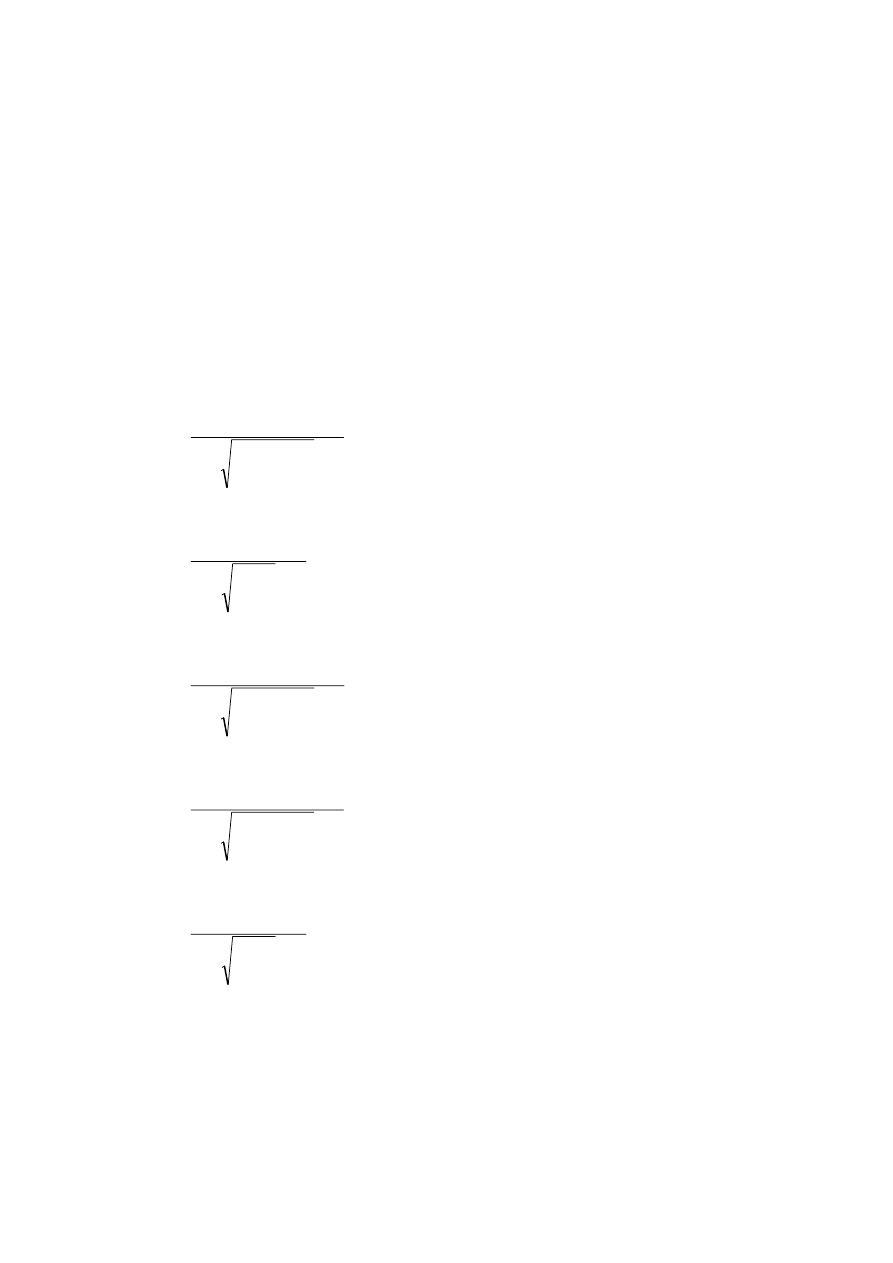
Prawdopodobieństwo i statystyka

17.03.2008 r.

___________________________________________________________________________

Zadanie

8.

Zakładamy, że zależność czynnika Y od czynnika x (nielosowego) opisuje model
regresji liniowej

i

i

i

x

Y

ε

β

β

+

+

=

1

0

, gdzie błędy

i

ε

są niezależne i mają rozkłady

normalne o wartości oczekiwanej 0 i wariancji 4. Obserwujemy zmienne losowe

przy danych wartościach

. Test najmocniejszy dla

weryfikacji hipotezy

n

Y

Y

Y

,

,

,

2

1

K

n

x

x

x

,

,

,

2

1

K

1

i

1

:

1

0

0

=

=

β

β

H

przy alternatywie

2

i

1

:

1

0

1

=

−

=

β

β

H

na poziomie istotności 0,05 odrzuca hipotezę

, gdy spełniona jest nierówność

0

H

(A)

290

,

3

)

2

(

)

2

)(

1

(

1

2

1

>

−

−

−

−

∑

∑

=

=

n

i

i

n

i

i

i

i

x

x

x

Y

(B)

645

,

1

)

1

(

1

2

1

>

−

−

∑

∑

=

=

n

i

i

n

i

i

i

i

x

x

x

Y

(C)

290

,

3

)

2

(

)

2

)(

1

(

1

2

1

>

−

−

−

−

∑

∑

=

=

n

i

i

n

i

i

i

i

x

x

x

Y

(D)

645

,

1

)

2

(

)

2

)(

1

(

1

2

1

>

−

−

−

−

∑

∑

=

=

n

i

i

n

i

i

i

i

x

x

x

Y

(E)

290

,

3

)

1

(

1

2

1

>

−

−

∑

∑

=

=

n

i

i

n

i

i

i

i

x

x

x

Y

8

Prawdopodobieństwo i statystyka

17.03.2008 r.

___________________________________________________________________________

Zadanie

9.

Zmienne losowe

i

są niezależne. Każda ze

zmiennych losowych

ma jednakowy rozkład prawdopodobieństwa

n

Z

Z

Z

,

,

,

2

1

K

)

,

(

,

),

,

(

),

,

(

2

2

1

1

n

n

Y

X

Y

X

Y

X

K

i

Z

(

)

(

0

1

1

=

)

−

=

=

=

i

i

Z

P

p

Z

P

. Każda ze zmiennych losowych

ma jednakowy

rozkład prawdopodobieństwa taki, że

)

,

(

i

i

Y

X

m

EY

EX

i

i

=

=

i

i

współczynnik korelacji

2

2

4

,

σ

σ

=

=

i

i

VarY

VarX

ρ

=

)

,

(

i

i

Y

X

Corr

. Niech

∑

=

=

n

i

i

i

n

X

Z

n

S

1

1

i

∑

=

=

n

i

i

i

n

Y

Z

n

T

1

1

.

Zbadać zbieżność rozkładów prawdopodobieństwa zmiennych

(

)

n

T

S

n

n

−

przy

+∞

→

n

(A)

(

)

))

2

5

(

)

1

(

2

,

0

(

2

ρ

σ

−

−

→

−

p

p

N

n

T

S

n

n

(B)

(

)

))

2

5

(

,

0

(

2

ρ

σ

−

→

−

p

N

n

T

S

n

n

(C)

(

)

))

4

5

(

,

0

(

2

2

ρ

σ

−

→

−

p

N

n

T

S

n

n

(D)

(

)

))

4

5

(

,

0

(

2

ρ

σ

−

→

−

p

N

n

T

S

n

n

(E)

(

)

n

T

S

n

n

−

nie jest ciągiem zbieżnym do rozkładu normalnego

9

Prawdopodobieństwo i statystyka

17.03.2008 r.

___________________________________________________________________________

Zadanie

10.

Wylosowano niezależnie 14 liczb z rozkładu symetrycznego ciągłego i ustawiono je w
ciąg według kolejności losowania. Otrzymano 8 liczb dodatnich (każdą z nich
oznaczmy symbolem a) i 6 ujemnych (każdą z nich oznaczmy symbolem b). Obliczyć
prawdopodobieństwo, że otrzymano 6 serii, gdzie serią nazywamy ciąg elementów
jednego typu, przed i za którym występuje element drugiego typu, na przykład w
ciągu : aaabbbbaabbbbba jest 5 serii (3 serie elementów typu a i 2 serie elementów
typu b).

(A)

143

30

(B)

143

40

(C)

143

20

(D)

143

10

(E)

143

50

10

Prawdopodobieństwo i statystyka

17.03.2008 r.

___________________________________________________________________________

Egzamin dla Aktuariuszy z 17 marca 2008 r.

Prawdopodobieństwo i statystyka

Arkusz odpowiedzi

*

Imię i nazwisko : .......................K L U C Z O D P O W I E D Z I.............................

Pesel ...........................................

Zadanie nr

Odpowiedź Punktacja

♦

1 A

2 D

3 E

4 C

5 C

6 A

7 B

8 A

9 D

10 C

*

Oceniane są wyłącznie odpowiedzi umieszczone w Arkuszu odpowiedzi.

♦

Wypełnia Komisja Egzaminacyjna.

11